Dynamics of Train–Track–Subway System Interaction—A Review

Abstract

This study provides a comprehensive review of advancements in the field of train–track–subway system interaction dynamics and suggests future directions for research and development. Mathematical modeling of train–track–subway interaction system is addressed, including wheel–track contact mechanics and wear, train multibody dynamics, train–track system coupling dynamics, track slab subsystem dynamics, subway tunnel–ground interaction models, building vibration excited by ground-borne seismic waves, and noise. Advanced computing and simulation techniques used for numerical studies of the dynamics of train–track–subway system interaction in the past two decades are also addressed, including high-performance computing with efficient algorithms, multi-physics and multi-scale simulation, real-time hardware-in-the-loop simulation, and laboratory and field validation. The study extends the applications of train–track–subway interaction dynamics to subway route planning, structural and material design, subway maintenance, operations safety and reliability, and passenger comfort. Emerging technologies and future perspectives are also reviewed and discussed, including artificial intelligence, smart sensing and real-time monitoring, digital twin technology, and sustainable design integration.

1. Introduction

Subways have been developed significantly in various cities around the world due to their relatively low energy consumption, low rates of environmental pollution, and high levels of safety [1]. Over the past three decades, mechanical and environmental research on vibrations and noise has expanded, driven by public concern over new rail projects [2,3]. Environmental impact studies and vibration assessments prevail. These are implemented through establishing methods to predict and mitigate train-induced subway vibration in complex settings, such as soft soils, tunnel propagation, and noise [4,5].

To achieve accurate and reliable prediction of train-induced vibrations, it is essential to develop robust predictive models using more systematic and adaptive approaches. A systematic framework is needed for guiding the development of such models, where the level of detail, dimensionality (2D vs. 3D), boundary conditions, input parameter resolution, and coupling mechanisms (e.g., vehicle–track–soil–structure interactions) are tailored to the characteristics of the targeted project. Such a framework should incorporate all relevant influencing factors, including site-specific geotechnical conditions, structural configurations, operational scenarios (e.g., type of rolling stock, speed, and axle loads), and the proximity of vibration-sensitive structures. Ultimately, the goal of such a systematic framework would be to support cost–risk-informed decision making by delivering accurate, context-adaptive, and computationally feasible vibration and noise predictions. It would not only improve the design of vibration mitigation strategies but also enhance the planning and route selection processes for metro systems, reducing the likelihood of future community complaints and regulatory non-compliance.

The study of train–track–subway interaction dynamics is grounded in the interplay between rolling stock and railways that dictates performance, safety, and durability. Understanding the dynamic interaction between trains, tracks, and subways provides essential fundamentals for environmental impact assessment, subway route planning, design, operations, maintenance, and passenger safety and ride quality. As the performance of subway infrastructure deteriorates, the life-cycle operations and maintenance cost increase. Smart subway infrastructure utilizing emerging information and communication technologies, Internet of Things (IoT) sensor technologies, digital twins, artificial intelligence, and green construction and maintenance represents the future for safe, affordable, efficient, resilient, and sustainable subway transportation for densely populated metropolitan areas.

This study sheds light on future perspectives of train–track–subway interaction and provides a comprehensive review of the state of the art in train–track–subway interaction dynamics. Section 2 addresses mathematical modeling of train–track–subway interaction systems. Section 3 addresses advanced computing and simulation techniques. Section 4 addresses applications of train–track–subway interaction dynamics. Section 5 addresses emerging technologies and future perspectives. Conclusions are drawn in Section 6.

2. Mathematical Modeling of Train–Track–Subway Interaction System

2.1. Wheel–Rail Contact Mechanics and Wear

Central to wheel–rail interaction is Hertzian contact theory, as shown in Figure 1, which describes the localized deformation and stress distribution that occurs when wheel and rail surfaces converge under load [6,7]. In Figure 1 the red and green lines represent the contact interface between the wheel and the track. The resulting contact area, much smaller than the dimensions of the interacting bodies, produces principal stresses along the x, y, and z axes. These stresses depend on factors such as contact force, relative displacement, material properties, and the geometric alignment of the wheel tread and rail surface [8,9]. This nonlinear Hertzian contact spring, constrained by unilateral conditions, serves as the foundation for computing normal loads and deformations. The Hertzian normal contact model is computationally efficient but less accurate than non-Hertzian normal contact models in representing contact patch geometry under large yaw angles or severe wear conditions.

Non-Hertzian normal contact models calculate penetration volumes to determine pressure distributions without relying on elliptical contact assumptions [10], essential for analyzing flange contact in tight curves or turnout zones, where contact stress concentrations can be 1.5–2.0 times higher than Hertzian predictions [11].

Figure 1. Wheel–rail Hertz normal contact model implementation in PFC 6.0 [12].

Figure 1. Wheel–rail Hertz normal contact model implementation in PFC 6.0 [12].

Relative motion between wheels and rails gives rise to creepage, a phenomenon critical to traction, braking, and steering dynamics. Tangential contact models integrate Shen–Hedrick–Elkins theory with Kalker’s linear theory and the FASTSIM algorithm, which incorporates micro-slippage and energy dissipation effects, and they have been used to compute creep forces, accounting for velocity-dependent friction coefficients that range from 0.3 under dry conditions to 0.1 in lubricated scenarios [13]. While Kalker’s linear theory and the FASTSIM algorithm are widely used to address tangential contact problems, their precision declines as the semi-axes ratio of the contact ellipse grows [14]. The FaStrip method overcomes this limitation by integrating Kalker’s strip theory with simplified formulations, enhancing the accuracy of shear stress distribution and stick–slip division across varied contact geometries [14,15].

Advancements in contact mechanics also include the MKP-Yaw and FaStrip-Yaw models, which incorporate wheelset yaw motion to refine the calculation of creep forces and moments under complex loading conditions [11,16]. These models are particularly relevant for metro subway systems, where frequent traction/braking cycles and tight radius curves intensify dynamic interactions [17].

Dynamic forces and inadequate maintenance exacerbate wear at the wheel–rail interface, leading to material degradation of wheel flanges and rail heads. Turnout zones present distinct challenges due to discontinuous contact geometries and abrupt transitions between rail segments. The quasi-Hertz method and finite element analysis demonstrate how interacting profiles redistribute contact stresses, with severe wear often concentrated in turnout areas due to multi-point contact and stress concentrations [6]. Polygonal wear, marked by primary and secondary wavelengths, emerges when wheel perimeter divisions coincide with excitation frequencies. This results in vibration amplitudes of 30 dB/mm (0.03 mm) at specific harmonics, such as the 23rd order (118 mm wavelength) [18]. Such wear patterns mirror rail corrugation effects, contributing to abnormal noise and component fatigue, highlighting the interdependence between wheel–rail geometry and system dynamics.

The mechanical compatibility between train and subway rolling stock and track infrastructure is also illustrated through the early operation of the Los Angeles Metro Red Line (a heavy-rail subway) [19]. The trains were designed with relatively large-diameter wheels for high-speed stability, but the track was built according to a typical metro geometry for smaller wheels. This mismatch led to severe wheel and rail wear, loud curve squeal, and even wheel flange climb derailments in sharp curves. A minor derailment at only 12 mph exposed the problem. Comprehensive wheel–rail interface remediation measures were taken, including using new wheel and rail profiles, improved curving suspension, track lubricators, and adjusted crossovers for reduced wear, friction, and noise, particularly on curved sections of track. These strategies improve the dynamic interaction between the wheels and rails, not only leading to better performance and reduced maintenance costs, but also extending wheel life from ~30,000 miles to over 200,000 miles.

2.2. Train Multibody Dynamics

Multibody dynamics serves as a robust framework for modeling the complex mechanical behavior of railway vehicles, capturing translational and rotational movements of rigid body components [14,20]. A train subsystem can be represented by rigid bodies—car bodies, bogies, wheelsets, and axle boxes—connected through spring–damper elements, while the track is modeled as a layered elastic structure consisting of rails, sleepers, and a foundation [21,22]. The equation of motion for a train subsystem takes the form

$${\mathbf{M}}_{\mathbf{T}\mathbf{r}\mathbf{a}\mathbf{i}\mathbf{n}}{\ddot{X}}_{\mathrm{R}\mathrm{a}\mathrm{i}\mathrm{l}}\left(t\right)+{\mathbf{C}}_{\mathbf{T}\mathbf{r}\mathbf{a}\mathbf{i}\mathbf{n}}{\dot{X}}_{\mathrm{R}\mathrm{a}\mathrm{i}\mathrm{l}}\left(t\right)+{\mathbf{K}}_{\mathbf{T}\mathbf{r}\mathbf{a}\mathbf{i}\mathbf{n}}{X}_{\mathrm{R}\mathrm{a}\mathrm{i}\mathrm{l}}\left(t\right)={\mathbf{F}}_{\mathbf{T}\mathbf{r}\mathbf{a}\mathbf{i}\mathbf{n}}(t)$$

(1)

where ${\mathbf{M}}_{\mathbf{T}\mathbf{r}\mathbf{a}\mathbf{i}\mathbf{n}},{\mathbf{C}}_{\mathbf{T}\mathbf{r}\mathbf{a}\mathbf{i}\mathbf{n}},{\mathbf{K}}_{\mathbf{T}\mathbf{r}\mathbf{a}\mathbf{i}\mathbf{n}}$, and ${\mathbf{F}}_{\mathbf{T}\mathbf{r}\mathbf{a}\mathbf{i}\mathbf{n}}$ are, respectively, the mass matrix, damping matrix, spring matrix, and force vector exerted by the rail-track with respect to the train, and ${\ddot{X}}_{\mathrm{T}\mathrm{r}\mathrm{a}\mathrm{i}\mathrm{n}}\left(t\right), {\dot{ X}}_{\mathrm{T}\mathrm{r}\mathrm{a}\mathrm{i}\mathrm{n}}\left(t\right),\mathrm{a}\mathrm{n}\mathrm{d}{ X}_{\mathrm{T}\mathrm{r}\mathrm{a}\mathrm{i}\mathrm{n}}\left(t\right)$ are, respectively, the acceleration, vertical velocity, and displacement of the train.

A 17-degree-of-freedom whole-vehicle vertical model has been developed for collision analysis, integrating spatial effects like car body bounce, pitch, and roll, alongside wheelset bounce and roll motions [23]. This model simplifies components as rigid masses concentrated at centroids, representing coupler and buffer devices and energy-absorbing anti-climbing devices through equivalent stiffness and damping parameters, and uses D’Alembert’s principle to derive 38 motion equations for car bodies, bogies, and wheelsets [23]. Advanced multibody dynamics methodologies address nonlinear phenomena in coupled oscillator chains, such as Duffing-type nonlinearities and kinematic harmonic excitations. Classical averaging techniques approximate vibrational amplitudes and phases, revealing conditions for synchronous steady states like in-phase and anti-phase motions [24].

Modern software packages like ADAMS/Rail leverage template-based assemblies to simulate rail vehicles, enabling analyses ranging from preload and linear stability assessments to dynamic curve negotiation and derailment studies [25]. Computational efficiency in multibody dynamics models depends on accurate descriptions of wheel–rail contact mechanics [16]. Commercial tools such as GENSYS and DIFF3D utilize pre-calculated look-up tables for contact geometry, interpolating data during time integration to simulate low-frequency (0–20 Hz) and extended-frequency (up to several hundred Hz) dynamics. For example, the Y25 bogie model in GENSYS incorporates Coulomb friction for couplings between side beams and transverse center beams, while DIFF3D’s finite element-based track model accounts for spatial flexibility variations in UIC60 turnouts, including rail bending and sleeper torsion. These tools validate simulations against field measurements, such as strain gauge-instrumented wheelset sampling at 9.6 kHz to capture vertical and lateral contact forces during turnout traversals at speeds of up to 100 km/h.

2.3. Train–Track System Coupling Dynamics

The dynamic interaction between moving train subsystems and rail-track subsystems constitutes an interconnected rigid body and flexible multibody problem. This coupling phenomenon involves bidirectional energy exchange between the train’s suspension system and the track’s elastic components, mediated through the wheel–rail interface. The equation of motion for the rail-track subsystem takes the form

$${\mathbf{M}}_{\mathbf{R}\mathbf{a}\mathbf{i}\mathbf{l}}{\ddot{X}}_{\mathrm{R}\mathrm{a}\mathrm{i}\mathrm{l}}\left(t\right)+{\mathbf{C}}_{\mathbf{R}\mathbf{a}\mathbf{i}\mathbf{l}}{\dot{X}}_{\mathrm{R}\mathrm{a}\mathrm{i}\mathrm{l}}\left(t\right)+{\mathbf{K}}_{\mathbf{R}\mathbf{a}\mathbf{i}\mathbf{l}}{X}_{\mathrm{R}\mathrm{a}\mathrm{i}\mathrm{l}}\left(t\right)={\mathbf{F}}_{\mathbf{R}\mathbf{a}\mathbf{i}\mathbf{l}}(t)$$

(2)

where ${\mathbf{M}}_{\mathbf{R}\mathbf{a}\mathbf{i}\mathbf{l}},{\mathbf{C}}_{\mathbf{R}\mathbf{a}\mathbf{i}\mathbf{l}},{\mathbf{K}}_{\mathbf{R}\mathbf{a}\mathbf{i}\mathbf{l}}$, and ${\mathbf{F}}_{\mathbf{R}\mathbf{a}\mathbf{i}\mathbf{l}}$ are, respectively, the mass matrix, damping matrix, spring matrix, and force vector exerted by the train to the rail-track, and ${\ddot{X}}_{\mathrm{R}\mathrm{a}\mathrm{i}\mathrm{l}}\left(t\right), {\dot{ X}}_{\mathrm{R}\mathrm{a}\mathrm{i}\mathrm{l}}\left(t\right),\mathrm{a}\mathrm{n}\mathrm{d}{ X}_{\mathrm{R}\mathrm{a}\mathrm{i}\mathrm{l}}\left(t\right)$ are, respectively, the acceleration, vertical velocity, and displacement of the rail-track. Recent advances incorporate stochastic analysis frameworks to account for parameter uncertainties, treating track irregularities and material properties as random fields rather than deterministic values [21].

Figure 2 shows a rail-track as a beam on a viscoelastic foundation subjected to a moving dynamic load [26]. Rail structure modeling in vehicle–track coupling analysis primarily relies on two models: the continuous Bernoulli–Euler beam and the continuous Timoshenko beam, resting on discrete elastic supports [26,27,28,29,30,31]. While effective for capturing vertical dynamics, Bernoulli–Euler beam theory neglects shear deformation and rotational inertia effects [22]. Timoshenko beam theory further refines rail modeling by accounting for shear deformation and rotational inertia, which become particularly significant in high-frequency domains [32]. Comparative studies demonstrate that Timoshenko-based models offer superior accuracy in predicting rail head deformation patterns, especially for frequencies exceeding 500 Hz or 1000 Hz [21,22,32]. Track models further distinguish between ballasted and slab track configurations, with the latter employing triple-layer discrete support systems to represent rail fastener–slab interactions in modern metro systems [13].

Co-simulation platforms have substantially improved the fidelity of vehicle–track interaction studies. Contemporary frameworks combine multibody dynamics software (e.g., SIMPACK) with finite element analysis tools, enabling simultaneous resolution of vehicle dynamics and structural wave propagation [33]. This integration is particularly critical for analyzing vibration transmission through tunnel structures, where track vibrations at 30–200 Hz frequencies induce ground-borne noise in adjacent buildings. The SAMS/2000 platform employs floating frame of reference formulations to predict displacements, accelerations, and stresses in adjacent structures, combining multibody dynamics with finite element representations of tracks and bridges [15].

2.4. Track Slab Subsystem Dynamics

The ballastless track slabs (BTSs) of high-speed railway systems in China are also used to some extent in metro subways in China. Since 2012, Sun and his associates have conducted a series of studies to develop a reliability-based life-cycle design theory and method for BTSs of high-speed railways. An overview of these studies is collected in Advancement in Basic Research on High-Speed Railway (2015–2019) [34].

Using SAP 2000, Sun, Chen, and Zelelew (2013) carried out a numerical analysis of stress and deflection responses of the BTSs of the China Rail Transit Summit type-II (CRTS-II) primarily used in China’s Beijing–Shanghai high-speed railway. The study showed that rail defection is only significantly impacted by rail fastening stiffness. To reduce high-speed rail deflection so as to mitigate riding discomfort, higher stiffness of the rail fastening is suggested. To reduce track slab bending stresses to prevent high-speed rails succumbing to structural failure, the following parameter design strategy can be used: a higher track slab thickness, a lower track slab stiffness, a lower rail fastening stiffness, a higher amount of CA mortar, and concrete supporting layer stiffness. The maximum shear stress of the BTS system is relatively low compared with the maximum bending stress of the BTS system [35].

Xia et al. [36] conducted dynamic analysis of a coupled train–ladder track–elevated bridge system as a new type of vibration reduction mechanism. Compared to the common slab track, adapting the ladder sleeper can effectively reduce the accelerations of the bridge girder and also reduce the car body accelerations and offload factors of the train vehicle [36]. Sun, Duan, and Yang [37] compared structural analysis models for CRTS II and CRTS III BTS subsystems of China’s high-speed railway. Sun, Duan, and Yang [37] studied the critical loading position and the most disadvantageous position of CRTS III BTSs in China’s high-speed railway. The results showed that the critical loading position of CRTS III ballastless track structures is the slab end position; the maximum transverse tensile stress is larger than the maximum longitudinal tensile stress at the bottom of the track slab, and the disadvantageous position is the slab corner; the maximum compressive stress of packed beds occurs under a load; the maximum longitudinal tensile stress is larger than the maximum transverse tensile stress on the support layer of a ballastless track structure on the subgrade, and the disadvantageous position is the load position; longitudinal tensile stress does not occur on the base plate of a ballastless track structure on a bridge; and transverse tensile stress occurs on the longitudinal edge of the support layer.

Sun et al. [38] conducted dynamic response analysis of CRTS II BTSs and obtained the first ten modals and dynamic characteristics of BTSs at different train speeds. They concluded that the natural frequency of CRTS II slab tracks on a bridge is larger than the specification limit, and therefore the bridge has sufficient rigidity to ensure safety and comfort; as the first of ten modals of a slab track on a bridge structure is lateral torsion, the lateral stiffness of the bridge structure is relatively low, so the lateral stability of the bridge should be noted; the vertical displacement, vertical acceleration, and bottom horizontal tensile stress in each component of the ballastless track structure (BTS) and the vertical stress of the concrete asphalt (CA) mortar layer gradually increase with the increasing speed of the trains; and the vertical stress of the top surface under line infrastructure has a turning point.

Sun, Duan, and Zhao [38] studied critical loading positions and the most unfavorable positions for CRTS II BTSs in the Beijing–Shanghai high-speed railway in China. Wang et al. studied the influence of uneven settlement of bridge piers on the running safety of a German ICE3 high-speed train running on the 32 m three-span simple-supported beam. The results show that most cumulative settlement occurs in the range of 10 m below the pile bottom. The relative camber of the bridge induced by adjacent pile settlement is more dangerous to the running safety of the train because the train bears a vertical centrifugal force in the direction opposite to the settlement direction when it runs on the bridge with a camber [39].

Zhang et al. [40] evaluated the vehicle–track–bridge interaction system for the continuous CRTS-II non-ballast track slab. In this study, the train subsystem was established by the rigid body dynamics method, the track subsystem and the bridge subsystem were established by the finite element method, and the wheel–rail contact relation was defined by the corresponding assumption in the vertical direction and the Kalker linear creep theory in the lateral direction. The in-span spring element was derived to model the track–bridge interaction; equal-bandwidth storage was adopted to fit the track structure with a multilayer uniform section beam; and the dynamic equilibrium equations were solved by the inter-history iteration method. As a case study, the response of a CRH2 high-speed train as it traversed a simply supported bridge with successive 31.5 m double-bound pre-stress beams was simulated. The results show that using the vehicle–track–bridge interaction model instead of the vehicle–bridge interaction model helps predict the rotation angle at beam ends and choose an economic beam vertical stiffness [40].

Ou et al. [41] analyzed the temperature field of BTSs based on meteorological data along the Beijing–Shanghai high-speed railway. It was found that the maximum positive temperature gradient appears between 12:00 noon and 2:00 p.m. and the minimum negative temperature gradient appears between 3:00 a.m. and 5:00 a.m. Solar radiation, wind speeds, and air temperatures are the main factors affecting the temperature distribution inside the BTSs [41].

Ou and Sun (2015) developed a simplified method for predicting nonlinear temperature effects of BTSs of high-speed railways. It was found that the axial uniform thermal stress of a track slab under different moments of the day consists of the mean and variation around the mean. Variation was related to the daily temperature variation at the slab surface. When a simplified temperature gradient is defined to replace the equivalent nonlinear temperature gradient, the resulting error is marginal and can be ignored. The maximum values of the nonlinear self-equilibrating thermal stress either appeared on the top or at the bottom of the track slab [42].

Ou, Sun, and Cheng [43] derived a simplified temperature field equation from the thermal transmission theory and the simplified meteorological boundary condition to account for temperature distribution in BTSs of China’s high-speed railway. The prediction and measurement results reveal that the temperature of a BTS is significantly affected by the atmospheric temperature, especially at a BTS depth of 0~0.2 m. The daily maximum value of the positive temperature gradient appears between 1:00 p.m. and 3:00 p.m., and it is affected by the thickness of the BTS. The maximum value of the positive temperature gradient varies with the seasons, the largest occurring in summer and the smallest in winter [43].

Ou et al. [44,45] developed an extreme-value probability model to describe the linear thermal gradient action (temperature gradient) in the BTSs of China’s high-speed railway. The results indicate that the daily maximum value of the positive temperature gradient for the yearly period satisfies an extreme-value I distribution in the city of Harbin; a Weibull distribution in Beijing, Shenyang, Urumqi, and Lanzhou; and a one-sided normal distribution in Wuhan, Shanghai, and Guangzhou. The daily maximum value of the absolute negative temperature gradient satisfies a normal distribution in Harbin, Shenyang, Urumqi, and Lanzhou and a Weibull distribution in Beijing, Wuhan, Shanghai, Guangzhou, and Kunming. The model provides a useful tool for fast determination of the track slab linear thermal gradient [44,45].

Zhao et al. [46] developed an effective method for determining a negative temperature gradient-induced gap at the corner of a slab. The method simulates a deformation curve in the process of warping based on the principle of minimum potential energy and a determinate curve using a quasi-Newtonian iterative algorithm. The measured warping displacements are close to the computed ones. The results show that the temperature gradients and warp of CRTS II BTSs have a positive correlation. Increasing the foundation coefficient can effectively reduce the warp caused by temperature [46]. Zhao et al. [47] developed a new model for predicting the thermal stress of CRTS II BTSs of high-speed railways under uniform cooling conditions using the Laplace transform.

Ou and Sun [48] studied the flexural fatigue–life reliability of frost-damaged concrete using three-point bending tests. Based on experimental and theoretical studies, the relationship between the fatigue life–fatigue strength and the P-S-N curve was obtained. It was shown that static flexural strength, flexural fatigue strength, and life significantly decrease as the number of freeze–thaw cycles (FTCs) increases. The results of the K-S test indicate that the two-parameter Weibull distribution function can appropriately describe the probability distribution of flexural fatigue life. The results indicate that as the number of FTCs increases, the scattering of the flexural fatigue life increases and the reliability probability (safety factor) of the flexural fatigue life of the frost-damaged concrete decreases [48].

Ou and Sun [44] developed an extreme-value probability model to describe the linear thermal gradient effect in high-speed railway ballastless track slabs. The distribution function and the statistical parameters of the daily maximum value of the positive temperature gradient and the minimum value of the negative temperature gradient for the yearly period were investigated by the estimation of the observed temperature gradient sample, which was calculated using the track slab temperature field equation with national historical meteorological data. Based on the estimated distribution function and the developed extreme-value probability model, the calculation formulas for the fractiles of the daily maximum value in the positive temperature gradient and minimum value in the negative temperature gradient for the design reference period were derived. Moreover, the curves of the fractile values and the safety probabilities for different design reference periods, and the recommended characteristic values were presented. It was indicated that the daily maximum values of the positive temperature gradient for the yearly period exhibited an extreme-value I distribution in the city of Harbin; a Weibull distribution in Beijing, Shenyang, Urumqi, and Lanzhou; and a one-sided normal distribution in Wuhan, Shanghai, and Guangzhou, while the daily maximum values of the absolute negative temperature gradient exhibited a normal distribution in Harbin, Shenyang, Urumqi, and Lanzhou and a Weibull distribution in Beijing, Wuhan, Shanghai, Guangzhou, and Kunming. This presented method provides a useful tool for a faster determination of the track slab linear thermal gradient action in a design procedure.

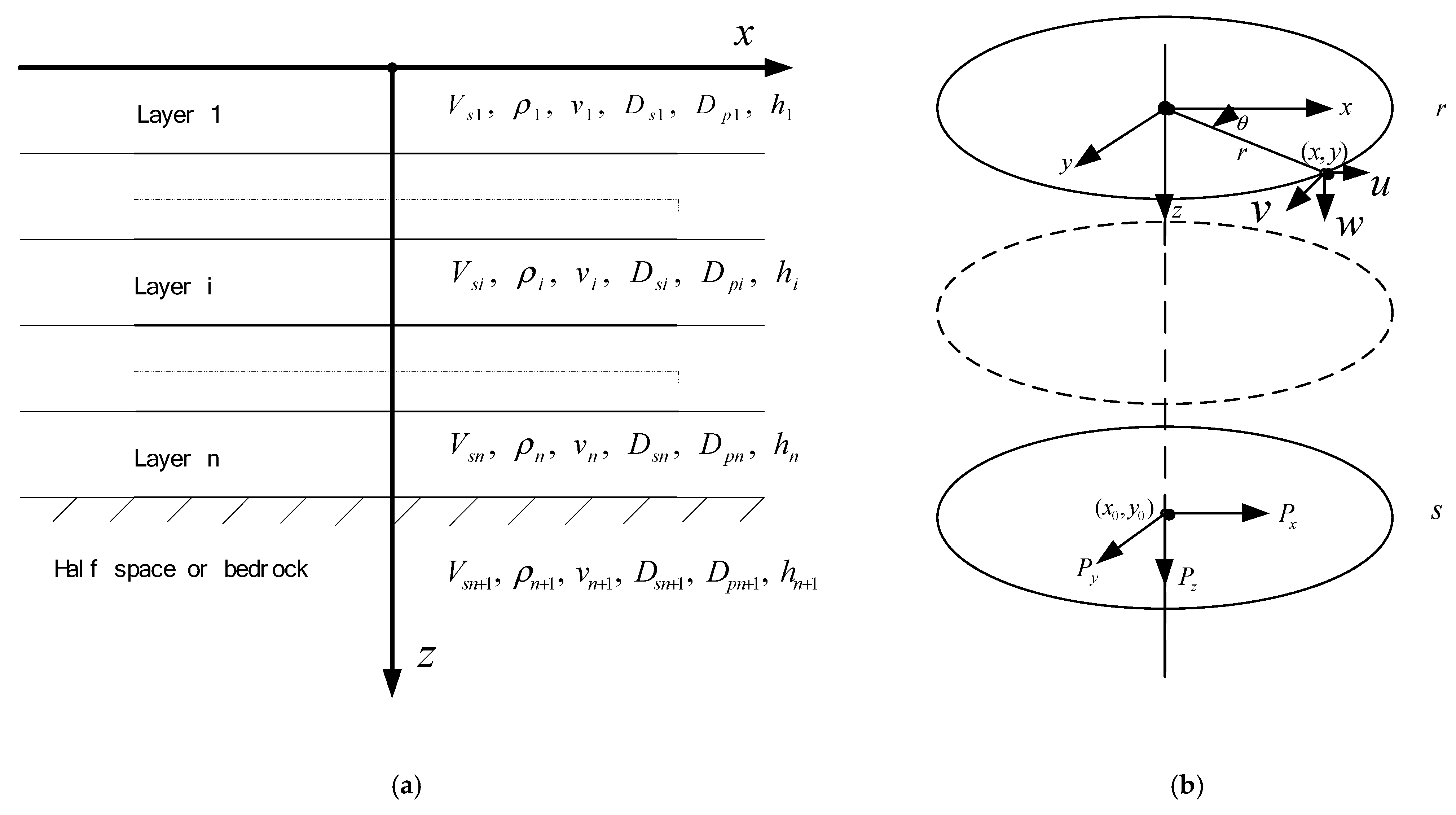
2.5. Subway Tunnel–Ground Interaction Models

Understanding how vibrations propagate through tunnel structures into surrounding soil media requires advanced theoretical models capable of capturing the intricate wave propagation phenomena in three-dimensional heterogeneous geological formations. A tunnel functions as a waveguide for structural vibrations. The complexity arises in solving boundary-value problems in elastodynamics involving moving sources within complex connected continua [49].

Vertical vibrations dominate within the tunnel and nearby soil layers, whereas horizontal vibrations can surpass vertical components at surface locations during curve negotiation [16]. Accelerometer data indicates a sharp reduction in vibration energy (8–71.4% decrease in acceleration effective values) between the rail and tunnel lining, followed by unexpected amplification near the surface—a phenomenon linked to wave-focusing effects in shallow soil layers [50]. The frequency spectra consistently exhibit peak energy concentrations in the 30–80 Hz range, corresponding to the P2 resonance frequency, which aligns with wheel–rail interaction dynamics and significantly influences building vibrations [50]. These empirical observations contradict conventional decay models, emphasizing the necessity of incorporating soil stratification in theoretical frameworks of train–track–subway system interaction.

The tunnel–soil interface plays a crucial role in vibration energy partitioning, with contact conditions significantly affecting wave transmission coefficients. Rough interface models incorporating micro-slip behavior predict 18–22% higher vibration transmission compared to perfect bond assumptions at frequencies above 50 Hz [49]. This effect is particularly pronounced in older tunnels where liner–soil contact quality has degraded due to wear. Measurements reveal that impedance discrepancies at segment joints can create localized vibration hotspots with 6–8 dB increases in specific octave bands [50]. Research indicates that a 30% increase in soil stiffness contrast between layers can alter surface vibration levels by 12–15 dB in critical frequency bands, underscoring the importance of precise geotechnical characterization [49]. The presence of groundwater further complicates the dynamics, as pore pressure buildup reduces effective stress and bearing capacity, potentially amplifying long-term soil deformations around tunnels. The incorporation of probabilistic methods further enhances predictive capability by accounting for uncertainties in soil conditions and material properties, which field tests identify as major contributors to model discrepancies [50].

Train-induced structural vibrations significantly impact underground station environments. Measurements from Rome’s Cassia–Montemario tunnel demonstrate frequency-dependent attenuation in vibration transmission through tunnel linings, with the dominant energy concentrated between 30 and 60 Hz during train arrivals and 20 and 50 Hz during departures [49]. Field data from Shanghai’s Line 9 curve segments reveals that vibration acceleration levels decrease by approximately 40% at 15 m from the tunnel wall yet remain perceptible to station occupants [50]. Mitigation strategies, including Vanguard dampers and 100 mm isolation trenches, reduce secondary vibrations in adjacent structures by 6–8 dB, while steel spring floating slab tracks achieve similar attenuation through mass–spring decoupling [51]. Zhou et al. [52] investigated how train-induced vibrations propagate through rails, track beds, and tunnel walls in a subway environment. The results indicate that vibration amplitude attenuates from rails to tunnel walls, but the presence of structural cracks can amplify peak vibration levels by 100–300% in tunnel components.

2.6. Building Vibration Excited by Ground-Borne Seismic Waves

The increasing adoption of metro subway systems in densely populated urban regions introduces a pressing challenge: train-induced ground-borne vibrations adversely affect nearby buildings, sensitive infrastructure, and the comfort of residents. Heavier mainline trains generally generate greater vibration energy than lighter metro trains, especially at low frequencies [52]. Subway trains in tunnels can induce significant vibrations transmitted through tunnel walls and surrounding soil, leading to ground-borne noise in nearby buildings. Train mass and speed critically shape the vibration frequency spectrum: heavier trains yield higher low-frequency vibration energy, whereas higher speeds shift energy to higher frequencies. Comparative measurements in buildings have shown that both surface rail and underground subways can produce perceptible vibrations, potentially disturbing occupants or sensitive equipment. Factors like train speed also affect frequency content—higher speeds shift vibration energy to higher frequencies [52,53,54,55].

Train-induced vibrations received by the buildings adjacent to subway networks pose one of the most controversial challenges in using subway transit systems in populated urban areas and communities [56,57]. Researchers have proposed various solutions and tried to predict and reduce train-induced vibrations with limited success [58]. Building vibrations are complex phenomena influenced by multiple interacting parameters such as railway track structure, vehicle dynamics, soil properties, and building characteristics, and they require a multi-scale, interdisciplinary approach for effective mitigation. To predict these effects, researchers employ methodologies such as field vibration measurements, impedance and finite element modeling, and one-third octave band spectral analysis [52].

Assessing building vibrations requires special attention to wave propagation paths in over-track structures, where vibrations transmit directly through columns and foundations rather than through the ground. Resonance can occur if train wheel loads excite the natural frequencies of tunnels, bridges, or station structures. Train-induced vibrations received by buildings adjacent to the railway network depends on various factors, such as railway track structure, tunnel characteristics, train properties, vibration receiver properties, the characteristics of the path between the vibration source and receiver, the distance between the vibration source and receiver, and building structure. Kouroussis et al. [59] reviewed how vehicle characteristics (unsprung mass and suspension) influence ground vibration, while Eitzenberger [60] surveyed tunnel vibration phenomena.

Field data from the Chengdu Metro shows that such structures exhibit 16 dB higher floor vibrations at natural frequencies compared to free-field measurements, highlighting the limited effectiveness of geometric attenuation in built environments [49]. The monolithic track bed commonly used in subway systems exacerbates this effect by channeling vibration energy directly into supporting structures, bypassing soil damping mechanisms that would otherwise mitigate far-field transmission. Validation against field measurements shows that coupled train–track–subway interaction models can predict building vibration levels with 3 dB accuracy when properly calibrated with site-specific soil parameters and structural properties [49].

Research in the field of train-induced vibration mitigation can be divided into three categories of approach: reduction of train-induced vibrations at the source of vibration (i.e., train and railway track; Figure 3a); reduction of vibrations along the path between the source and the receiver (Figure 3b); and reduction of train-induced vibrations at the receiver of vibrations (Figure 3c). Although all three categories of approach can be used for vibration mitigation in different stages of the subway life cycle, including planning, environmental assessment, design, construction, operations, safety, and maintenance, the cost and feasibility associated with these approaches differ dramatically.

In the first category of approach (a), various solutions have been proposed to increase damping and decrease the magnitude of vibrations by reducing the stiffness of various railway track components. For instance, the use of super-elastic fastening systems (fastening systems with low stiffness and high damping), the use of super-elastic layers under sleepers (i.e., floating sleepers), and the use of super-elastic layers and components under concrete slabs (i.e., floating track slabs) are common solutions for decreasing the vibration level at the source [64,65,66,67,68]. The first category of approach can generate a greater influencing range than the other two categories of approach [65]. European Standards include solutions that reduce vibration and increase durability, e.g., Under Sleeper Pads [69], Under Ballast Mats [70], and Under Slab Mats [71].

In the second category (b), digging a trench next to the railway track or next to the vibration receiver, or constructing buried walls with different materials on the path between the source and receiver are viable solutions which to some extent decrease train-induced vibration [72,73,74,75].

In the third category (c), designated vibration-absorbing components, such as dampers and energy absorbers, devices placed under building foundations, have been used to reduce the vibrations received by specific buildings, such as those with vibration-sensitive equipment or residences [76,77].

Choosing an appropriate approach to mitigate train-induced vibration is challenging not only because it depends on many factors such as the type of building, the type of vibration-sensitive equipment used in the building, the level of vibrations reaching the building, and the status of the subway (e.g., under planning and construction, or in operation), but also because all of the approaches are very expensive, while the consequence of the decision (i.e., effectiveness of vibration mitigation) is highly uncertain beforehand (i.e., high risk). For instance, if the second and third categories of approach are adopted, a large number of geotechnical, structural, and material parameters along the wave propagation path need to be collected in the field, which is very costly, almost prohibiting extensive applications for all communities and buildings along metro subway lines.

2.7. Noise

Noise is an issue accompanying vibration. When subway trains operate in proximity to buildings, noise becomes a critical concern. Wheel–rail noise (rolling noise and curve squeal) tends to increase with heavier vehicles and poor interface conditions. Studies in Australia, for instance, applied the TWIN noise model to rail systems and found that rail grinding could reduce rolling noise by ~4–9 dB, and installing rail dampers provided further attenuation of high-frequency noise [19]. These mitigation techniques are directly applicable to shared train–subway corridors where noise standards must be met. Resonance effects can also occur in special situations: for example, when a train’s axle repetition rate matches a bridge’s natural frequency or when tunnel wall modes are excited by passing trains. Li et al. [74] analyzed a high-speed train on a viaduct entering a tunnel and observed amplified vibrations at frequencies matching bridge and tunnel modes. Studies attempt to identify such resonant conditions via modal analysis and to design countermeasures (e.g., tuned mass dampers and softer fasteners) in advance.

3. Advanced Computing and Simulation Techniques

3.1. High-Performance Computing with Efficient Algorithms

Accurate prediction of train-induced ground-borne vibration is a complex and computationally demanding task, primarily due to the intricate interactions between the train and track structure at the local scale, and the subway, surrounding soil, and built environment at the large scale. To capture these interactions while a train is moving with sufficient fidelity, researchers typically rely on large-scale numerical simulation methods using advanced computational techniques. The generalized Duhamel integral method for moving loads [78], the finite element method (FEM), the boundary element method (BEM), and the discrete element method (DEM) each offer different advantages.

The generalized Duhamel integral method established by Sun [78] constructs the analytical form of a solution for continuum media for an arbitrary moving load using Green’s function. The method is based on Duhamel’s principle or, more fundamentally, the superposition principle of inhomogeneous linear partial differential systems. It is named after Jean-Marie Duhamel, who first applied the principle to the inhomogeneous heat equation [79]. The generalized Duhamel integral method represents the solution in analytical form or closed form, not only providing mathematical–physical insights to the problem, but also allowing efficient computation [30]. Although Duhamel’s principle or the superposition principle does not hold for nonlinear partial differential equations because nonlinear operators do not satisfy the property of adding solutions, it can still be used to study nonlinear partial differential equations such as the Navier–Stokes equations and nonlinear Schrödinger equation, where one treats nonlinearity as an inhomogeneity.

A variety of analytical solutions and closed-form solutions have been obtained by Sun and his associates for 1D, 2D, and 3D structures under moving loads. Sun [26,28,29,80,81,82] studied the dynamic responses of beams and plates under moving loads for different scenarios, including a concentrated load, a distributed load, a harmonic load, and an impulsive load at hypersonic speed, subsonic speed, and critical speed for elastic foundation and for viscoelastic foundation. Sun, Luo, and Chen [82]; Sun and Luo [27,83]; Sun et al. [84]; Sun et al. [85]; Luo et al. [86]; and Sun et al. [87] studied dynamic responses of half-space and layered medium subjects to a moving load in the form of steady-state harmonic loads, transient time-varying loads, and high-order models. Vehicle load, considering random irregularities and tire footprints on wheel–track roughness, have been studied by Sun and Deng [31]; including the damage caused by random loading and road-friendly vehicle suspension designs using a genetic algorithm [81].

FEM is well-suited for modeling complex geometries and heterogeneous materials [88]. It serves as a fundamental tool for modeling the structural and dynamic behavior of train–track–subway systems, providing high-fidelity simulations of complex interactions among rolling stock, track infrastructure, and surrounding environments. By discretizing continuous domains into finite elements, FEM approximates field variables across intricate geometries like wheel–rail interfaces and tunnel structures [89].

FEM proves especially useful for analyzing localized phenomena, including contact stresses at the wheel–rail interface, where nonlinear material behavior and transient loading conditions often render analytical solutions impractical [6]. Widely adopted commercial software packages like ANSYS and ABAQUS facilitate these simulations, utilizing extensive element libraries and solver capabilities to manage large-scale models with millions of degrees of freedom [15]. Three-dimensional FE models of wheelsets and rails, for example, have been developed to investigate vibration and sound radiation characteristics, accounting for gyroscopic and centrifugal effects caused by wheel rotation [7]. Such models typically employ solid elements (e.g., SOLID187 in ANSYS) to represent rails and sleepers, with contact algorithms simulating interactions between moving wheels and irregular rail profiles [90]. Simulation accuracy depends heavily on mesh refinement in critical zones; studies highlight the importance of uniform grids near contact areas in minimizing errors due to inconsistent element shapes [6]. For instance, a slab track model using CRTS II technology incorporated 5538 solid elements and 23,328 degrees of freedom to accurately predict dynamic responses under high-speed conditions [13].

FEM also enables system-wide evaluations of vehicle–track–tunnel interactions. Researchers have integrated FEM with multibody dynamics frameworks to incorporate infrastructure flexibility, allowing comprehensive assessments of vibration transmission through layered soil media and structural foundations [33]. Boundary conditions in FEM present a source of error for wave propagation, refraction, and reflection simulations. Artificial boundaries, whether absorbing or fixed, are commonly employed in FEM to truncate the space domain under investigation. However, if not properly defined, these boundaries can introduce artificial wave reflections or distortions that compromise the accuracy and reliability of the results, especially when simulating transient wave propagation in continuum media such as soil. BEM is advantageous for problems involving infinite or semi-infinite domains, such as wave propagation in soil and far-field radiation conditions [13].

DEM is effective in simulating granular media and contact interactions. Ren and Sun [91] used DEM and experimental testing to study the heterogeneous fracture process of a series of edge cracked semi-circular bend (SCB) tests under different porosities, void sizes, and void distributions in mode I fracturing, mode II fracturing, and mixed mode I and II fracturing at temperatures of 6 C and 10 C. The fracture toughness and the time at which peak load occurs reduced with the increasing porosity and void size. The impact of void size is more significant than that of porosity. At 6 C, the impact of void characteristics on crack propagation is not significant, except in mode II fracturing. The cracks in mode II fracturing no longer pass through aggregates and tend to bypass aggregates with increasing porosity. At 10 C, cracks tend to move away from the aggregate/mastic interface and pass through mastic with increasing porosities and void sizes. The distribution of voids in crack initiation zones is a key factor in the fracture performance and crack propagation of asphalt concrete. Ren and Sun [92] further developed a generalized Maxwell viscoelastic contact model for DEM based on a finite difference scheme. The relationship between microscale model input and macroscale properties of asphalt mastics and coarse aggregates was derived to calibrate contact parameters of the proposed DEM model. Dynamic modulus tests, static creep tests, bending tests at low temperature, and corresponding DEM simulations were implemented.

Despite their strengths, high-fidelity 3D numerical models based on FEM, BEM, or DEM are inherently computationally intensive. These models require high-resolution meshes, fine time steps, large-scale models, extensive processing times and computer memory, and high-energy consumption to achieve realistic results, even when using high-performance computing platforms. Such drawbacks make computationally intensive models impractical for large-scale routine applications where efficiency is crucial. Moreover, the iterative nature of vibration prediction tasks, such as parametric studies for design optimization, sensitivity analyses, and scenario testing, further amplifies the computational burden, making these methods impractical for real-time applications or routine use in early-stage design. The computational intensity of high-fidelity numerical computing and simulation models has spurred the development of reduced-order modeling techniques. Figure 4 outlines five efficient methods for numerical computation in the context of train–track–subway interaction dynamics.

Model simplification relies on assumptions in order to reduce the complexity of train–track–subway models. For instance, train loads can be idealized as moving concentrated loads, neglecting the coupling effect or even interaction between the vehicle, track, and ground system. Rail-track irregularities (i.e., rail roughness), which can significantly influence vibration generation and propagation, are often overlooked. Although these simplifications reduce the computational burden of train–track–subway interaction, the accuracy and realism of the model predictions are undermined.

Modal decomposition of finite element track models with truncated modal information incorporated into multibody dynamics can maintain computational efficiency while preserving essential dynamic characteristics [15]. This approach reduces computation time by 40–60% compared to full FE coupling without sacrificing accuracy in the 0–300 Hz bandwidth relevant for human vibration perception. Component mode synthesis methods condense track models by retaining only dominant vibration modes, typically reducing system degrees of freedom by 80–90% while preserving essential dynamic features below 500 Hz [13].

Parallel computing further accelerates solution times, enabling near real-time simulation for applications like digital twin systems. These computational optimizations facilitate parametric studies that would otherwise be impractical, such as analyzing 100+ vehicle-passing scenarios to assess long-term track degradation patterns or evaluating various wheel profile designs against standardized wear indices [14].

The coupled FEM-BEM method balances computational efficiency with accuracy in predicting ground-borne vibrations [49,93,94] and the FEM component discretizes the tunnel and adjacent soil domains, while BEM handles semi-infinite far-field radiation conditions. Advanced implementations utilize 2.5D methodologies, leveraging translational symmetry along the tunnel axis to simplify three-dimensional problems into two-dimensional cross-sections with wavenumber-domain solutions along the longitudinal direction. This approach is particularly effective for analyzing moving loads, as it inherently accounts for load movement in the normal direction without requiring full 3D discretization. Comparative studies demonstrate that 2.5D models achieve an accuracy comparable to that of full 3D simulations for frequencies below 250 Hz while reducing computation times by 60–75%, enabling efficient parametric studies of moving-load effects [49,94]. Models also reveal frequency-dependent attenuation patterns, demonstrating that low-frequency vibrations (<10 Hz) propagate farther than high-frequency components due to reduced material damping [95].

The generalized Duhamel integral-based thin-layer method for modeling arbitrarily layered half-spaces to account for soil inhomogeneity provides a greater advantage in capturing moving-load-generated wave propagation and vibration transmission over long distances, as shown in Figure 5. This approach discretizes the soil profile into horizontal layers with varying elastic properties, solving wave propagation efficiently through recursive stiffness matrix formulations. The higher-order thin-layer method developed by Sun and his associates [30,78,87] achieved an excellent accuracy while maintaining computational complexity at an acceptable level.

3.2. Multi-Physics and Multi-Scale Simulation

Modern train–subway system simulations demand an integrated approach to capture the uncoupled or coupled multi-physics interplay of mechanical, electrical, and thermal phenomena—a complexity beyond the scope of traditional single-physics (i.e., mechanical) models. A key focus lies in developing effective and efficient simulation capabilities rigorously validated against experimental data, ensuring both predictive accuracy and computational tractability.

By addressing interdependent processes like electromagnetic forces in traction systems, aerodynamic loads at high speeds, and thermal effects on braking performance, multi-physics coupling methods provide a comprehensive framework for analysis [96]. This paradigm is indispensable for contemporary rail systems, where high-speed operations and energy recovery during regenerative braking necessitate coupled evaluations across physical domains to ensure both safety and efficiency. Battery electric trains exemplify this need, requiring the integration of electrochemical energy storage models with mechanical vehicle dynamics and electrical power distribution characteristics [96]. Such simulations uncover energy consumption variations under diverse acceleration profiles or gradient conditions, facilitating optimizations in vehicle design and operational strategies.

Wheel–rail contact analysis represents a key application area of multi-physics simulation, where mechanical wear, frictional heat generation, and electrical conductivity for signaling systems interact dynamically. Contact forces at the interface produce not only mechanical stress but also localized heat, altering material properties and accelerating wear [25]. Coupled computational models combining FEM with iterative thermal solvers predict temperature distributions during emergency braking, where rail-head temperatures may surpass 400 °C, critically affecting microstructure and fatigue life [25]. Tribometer test validations demonstrate strong predictive accuracy for wear rates when thermal–mechanical coupling is incorporated, reducing discrepancies to less than 8% compared to uncoupled simulations [25].

High-speed trains operating above 300 km/h highlight the importance of aerodynamic–thermal–structural coupling. Integrated computational fluid dynamics and structural dynamics simulations reveal that aerodynamic loads significantly influence vehicle stability, particularly for tail cars experiencing lift forces nearing 10 kN at 350 km/h [97].

The interplay between traction power systems and mechanical dynamics introduces further complexity, particularly in AC electrified networks. Simulations merging vehicle multibody dynamics with electrical network models can predict harmonic distortions due to variable-frequency drives or regenerative braking currents, which may disrupt signaling equipment or other trains sharing the power supply [96]. For metro systems, these models identify resonance frequencies where mechanical vibrations of overhead lines coincide with electrical load fluctuations, leading to pantograph–catenary contact loss. Research on subway traction systems indicates that coupled electro-mechanical simulations reduced pantograph arcing incidents by 30% through optimized overhead wire tensioning and vehicle suspension damping [96].

3.3. Real-Time Hardware-in-the-Loop Simulation

Instantaneous feedback using real-time simulation provides extra value for train–subway operations. One notable approach is hardware-in-the-loop (HIL) simulation, which integrates physical components with virtual dynamics models to validate control algorithms under realistic conditions, demonstrating exceptional efficacy in evaluating braking performance, with HIL systems achieving millisecond-level synchronization between physical actuator responses and simulated track profiles [98]. Achieving real-time execution demands computational efficiency, often requiring strategic simplifications of models while preserving critical dynamics [99]. By relying on experimental data rather than first-principles equations for brake system modeling, the software meets real-time computational constraints, allowing operators to interactively adjust parameters like pneumatic pressure or regenerative braking ratios during simulations [100]. These platforms have reduced latency to under 10 ms per cycle, a threshold necessary for accurately replicating high-frequency dynamics in electro-mechanical systems [98]. A LabVIEW-based graphical interface paired with a Matlab-Simulink core facilitates seamless data exchange with programmable logic controllers used in actual subway operations, enabling scenario replay functionality and allowing operators to repeatedly simulate rare but critical events like low-adhesion starts on steep grades under varying weather conditions [101].

3.4. Laboratory and Field Validation

Validation with methodologies ranging from experimental modal analysis to field measurements remains crucial for verifying mathematical model accuracy, ensuring model reliability and predictive performance [102]. Laboratory-based techniques, including roll vibration tests for high-speed train bogies, offer controlled conditions to verify dynamic stability. Such tests generate baseline data essential for calibrating multibody dynamics models, particularly for extreme operational scenarios difficult to replicate in field environments. Multi-scale validation strategies are indispensable for applications requiring high spatial resolution, such as predicting vibration transmission through layered geological strata surrounding deep tunnels, fatigue life prediction, noise mitigation, and predictive maintenance [103].

Operational datasets enhance model credibility through data-driven validation frameworks. In Portland’s light rail system, longitudinal train dynamics models were calibrated using constrained nonlinear optimization, with effectiveness evaluated via acceleration/velocity and acceleration/distance phase-space comparisons [104]. This approach identified systematic biases in jerk predictions during braking maneuvers, leading to a 21% reduction in lateral ride index discrepancies after parameter adjustments.

The Manchester Benchmarks for Rail Vehicle Simulation established experimental protocols and performance metrics for simulation tools to evaluate critical aspects like hunting stability and wheel–rail contact force transients through predefined test cases [33,105]. Two simple vehicles and four matching track cases were defined to allow comparison of the capabilities of the various computer simulation packages currently used to model the dynamic behavior of railway vehicles. Simulations have been carried out with five of the major software packages [105]. For subway-induced vibrations, the Bakerloo line tunnel study developed a comprehensive validation framework by measuring vibrations at multiple locations—including axle boxes, rails, the tunnel invert, and the free field—while simultaneously characterizing soil dynamics and track properties [106].

Field measurements using instrumented wheelsets and track-mounted accelerometers show that properly calibrated models can predict vertical wheel–rail forces within 8–12% error margins and lateral forces within margins of 15–20% across speed ranges of 30–120 km/h [102]. Discrepancies often stem from unmodeled environmental factors, such as temperature-induced rail stress variations or moisture-dependent ballast stiffness changes. Coupled periodic FE-BE model predictions exhibited less than 3 dB deviation from measured surface vibrations across the 30–100 Hz frequency range. de Oliveira, et al. [107] conducted an experimental investigation using multiple very-low-cost inertial-based devices for ride comfort assessment and rail-track monitoring.

A recent study focused on wave attenuation in shallow soil layers. Field measurements from Shanghai Metro Line 9 reveal the anisotropic nature of vibration transmission. The study shows 8–71.4% reductions in vibration energy between rails and tunnel linings, followed by surface amplifications due to stratified soil effects [94]. Wear prediction models for CRH3 trains on the Wuhan–Guangzhou line achieved 88% correlation with measured tread wear patterns when trained on hybrid datasets combining simulation outputs and ultrasonic inspection results [14]. Emerging hybrid testing architectures combine physical components with virtual models to enhance validation. Hardware-in-the-loop (HIL) platforms for pantograph–catenary systems integrate actual current collectors with simulated overhead line dynamics, achieving millisecond-level synchronization for contact force validation [98]. ADAMS/Rail models of passenger coaches validated against Corus Rail Technologies’ track data demonstrated 92% accuracy in reproducing lateral force distributions during curve negotiation [25]. Real-time monitoring data extends validation to operational phases, where continuous comparisons between simulated and actual vibration spectra detect anomalies at 15% deviation thresholds.

4. Applications of Train–Track–Subway Interaction Dynamics

4.1. Planning of a Subway Line

When a metro subway line is under planning, a major challenge lies in the selection of routes for the subway line, a matter of high-cost and high-risk decision making. It involves environmental assessment, including evaluating vibration and noise along the metro subway line with only a limited amount of information and a limited degree of certainty. In practice, it has been found that metro subway lines are chosen mainly based on travel demand, without deliberate consideration of train-induced vibration and noise, which leads to complaints being made afterwards by the community residents in the operational stage of the subway. A high-fidelity computational model that can provide accurate prediction and assessment of the train-induced vibration and noise levels that will occur in surrounding buildings along the selected routes of a subway line that has not yet been constructed that accord with environmental regulations is highly desirable for cost-effective decision making for a subway line section [108,109,110,111].

4.2. Structural and Material Design of a Subway

For the structural and material design of a subway, a number of train-induced prediction models have been developed and reported in the literature based on empirical data collected from existing metro lines, including those of Lai et al. [49], Nicolosi et al. [110], Tao et al. [14], Sadeghi et al. [61], Ma et al. [109]. Auersch [63,112], Cao et al. [113], Kedia et al. [108], and Kolhatkar [15]. While these models may work well under similar conditions, they may not be applicable to conditions involving different types of soil, track structures, or operational requirements. The challenges posed by train-induced prediction models are many. One example is the failure to encompass the full spectrum of frequencies (e.g., 1 to 80 Hz and beyond) that are relevant for both human perception and the proper functioning of vibration-sensitive equipment for reducing the computational burden. Another example is the inadequate calibration and validation of theoretical models using field measurements, making models questionable and risky for real-world decision making. Insertion loss is another key parameter in dynamic analyses of vibration and noise [114,115,116,117]. Other challenges include the ignorance of the inherent variability in operational input parameters and assumptions of train type, speed, axle load, track defects, operational schedules, soil modulus, damping ratio, Poisson’s ratio, and pad stiffness as fixed constants. In reality, these parameters vary significantly both spatially and temporally. Ignoring this variability can result in significant discrepancies between predicted and actual vibration and noise levels.

4.3. Subway Maintenance

Figure 6 shows various superstructures of slab tracks [61], including a conventional slab track with a conventional fastening system, a floating slab track with a superior elastic fastening system, and a slab mat. The dynamic behaviors of train–subway systems significantly shape infrastructure maintenance demands, with wear mechanisms and vibration patterns serving as pivotal indicators for predictive maintenance strategies. In the context of vibration mitigation strategies for slab track systems, the first category of approach in Section 2.6 has been widely used, which involves manipulating the mechanical stiffness of key components, such as the rail fastening system (e.g., rail pads) and the layer beneath the concrete slab (e.g., slab mats or resilient base layers), as shown in Figure 6.

Numerous experimental, numerical, and field-based investigations have demonstrated that the stiffness characteristics of these components play a decisive role in determining the dynamic response of a slab track under train-induced loading and consequently affect both ride quality and structural longevity [65,118,119,120]. A significant reduction in the stiffness of rail pads, often introduced intentionally to isolate high-frequency vibrations and reduce noise emission, can lead to unintended consequences. While softer rail pads may offer improved vibration attenuation, they also result in increased relative movement between the rail and the fastening system. This increased flexibility elevates dynamic contact forces at the wheel–rail interface, intensifies wear processes, and accelerates the development of rail surface irregularities, commonly referred to as rail roughness. The propagation of rail irregularities over time not only deteriorates ride quality but also amplifies the excitation of the entire track structure, setting off a feedback loop of increased vibration and accelerated degradation.

On the other hand, reducing the stiffness of the layer beneath a concrete slab, typically through the use of elastomeric slab mats or other resilient materials designed to protect nearby structures from ground-borne vibrations, can adversely affect the fatigue performance of the concrete slab itself. While these soft sublayers are effective in vibration isolation, their high deformability increases the dynamic deflections experienced by the concrete slab under cyclic axle loads. These increased flexural and tensile stresses result in higher strain amplitudes, faster accumulation of fatigue damage, and, ultimately, a reduction in the fatigue life of the concrete slab. In slab track systems, where concrete is subjected to millions of load repetitions over its service life, maintaining fatigue durability is crucial for minimizing maintenance interventions and ensuring long-term performance.

The above findings highlight a fundamental trade-off in slab track design between vibration isolation and structural durability. While softer materials in a rail pad or slab mat can improve environmental performance by reducing vibration transmission, their indiscriminate use may compromise track geometry stability (via increased rail roughness) and structural integrity (via reduced slab fatigue life). These complex and interdependent behaviors underline the importance of adopting a system-level approach when designing for vibration control in modern railway slab tracks, particularly in sensitive urban environments such as metro systems, where both vibration mitigation and structural resilience are paramount.

Parameterized simulation platforms incorporate vehicle–track coupling dynamics to refine maintenance strategies and operational parameters. These platforms analyze wheel–rail contact forces and derailment risks through time-domain integrations of nonlinear differential equations using Runge–Kutta or Newmark methods [121]. Parameter sensitivity studies highlight the strong dependence of vehicle–track coupling dynamics on suspension characteristics and track support conditions. Primary suspension stiffness values between 1000 and 1450 kN/m and damping coefficients of 30 kN·s/m predominantly influence wheelset oscillation modes in the 50–80 Hz range. Secondary suspension parameters—230–240 kN/m stiffness and 29.5 kN·s/m damping—primarily affect car body vibrations below 10 Hz (Wang, Ding, and Lou, 2010). Track parameters such as fastener stiffness (50 kN/m) and ballast/subgrade support modulus (50–100 MPa) significantly impact vibration transmission, with 10% variations in these parameters causing 15–20% changes in rail displacement amplitudes under identical loading conditions [95].

Wheel–rail wear modeling enhances maintenance planning by pinpointing high-risk zones for material loss. Wear primarily occurs within ±25 mm of the nominal rolling circle. Modern wheel designs can reduce flange zone wear intensity by 20–50% through optimized profiles [6]. The relationship between wheel diameter differences and dynamic instability illustrates that deviations exceeding 2.5 mm lead to continuous flange–switch rail contact, accelerating wear despite improving vehicle stability. Maintenance protocols must enforce strict tolerances, limiting in-phase diameter differences to 2 mm to optimize wear reduction and operational reliability [122].

Track maintenance strategies also benefit from dynamic interaction analysis, particularly in addressing rail corrugation and vibration-induced degradation. Sensitivity studies on metro systems reveal that adjusting track stiffness (e.g., modifying fastener and steel spring vertical/horizontal stiffness) effectively disrupts resonant conditions driving corrugation formation. The inner rail corrugation of steel spring floating slab tracks is primarily caused by the bending vibration of the wheelset, while the outer rail corrugation is primarily caused by the bending vibration of the rail itself. The formation mechanisms of the inner and outer rail corrugation of long sleeper-embedded tracks are similar, both primarily caused by the lateral bending vibration of the rail [123].

Dynamic-based maintenance yields substantial economic benefits, particularly for turnouts, which account for 25–35% of total track maintenance costs due to complex load transitions and multi-point contact mechanics [102]. Field tests demonstrate how instrumented wheelset measurements validate simulation models, enabling predictive replacement of switch rails before fatigue cracks propagate. This data-driven approach reduces turnout life-cycle costs by 15–20% through optimized replacement schedules and fewer emergency repairs. Similarly, wear prediction models for high-order polygonal wear of wheels show that resonant frequencies near 589 Hz (bogie frame) and 601 Hz (wheelset) accelerate polygonal wear, prompting revised inspection intervals when detected during vibration monitoring [18].

Shifting predictive maintenance systems toward “foresight-based” models that anticipate faults before they occur can significantly boost reliability and safety. Optimizing axle bridge structures demonstrates how mass reduction and natural frequency adjustments can reduce lateral wheel–rail forces and derailment coefficients while lowering wear-related maintenance costs [124]. Advanced wheel designs further complement these measures, reducing flange-zone contact pressure by 50% compared to conventional profiles, thereby extending maintenance intervals and lowering life-cycle costs [6].

4.4. Operations Safety and Reliability

Evaluating safety margins and system reliability in train–subway interactions necessitates a thorough analysis of dynamic behaviors across varied operating conditions, with a focus on derailment risks measured by the lateral-to-vertical force ratio, structural integrity, and operational stability. When a metro is in operation, train-induced vibration reaching a building can be measured in the field. The dynamic response of vehicles to track irregularities also affects safety margins, as evidenced by the relationship between wheel diameter variations and instability. Deviations surpassing 2.5 mm may lead to persistent flange–switch rail contact, increasing wear while paradoxically enhancing stability [14]. Secondary suspension systems can ensure operational safety by balancing load distribution across railway vehicles. Refinements to secondary spring load forecasting models, which account for car body elastic deformation, have yielded more accurate predictions of load distribution patterns [125]. Rapidly progressing polygonal wear generates intense vibration and noise in the train–track system, potentially causing component fractures and operational hazards [18].

Longitudinal dynamics during traction and braking cycles introduce further safety considerations, particularly concerning wheel–rail adhesion limits. Excessive traction or braking forces under low adhesion conditions can induce wheel slip/slide phenomena, activating anti-slip controllers to maintain longitudinal creep rates within control thresholds. These dynamics are particularly pronounced in metro systems, where frequent acceleration–deceleration cycles occur. Simulation tools like RailSIM effectively model these interactions, with acceleration outputs typically being ±2.0 m/s² and jerk values below 2.0 m/s³—parameters that ensure both safety and passenger comfort [126].

Onboard monitoring systems, including traction equipment, anti-slip devices, and axle temperature sensors, can detect anomalies such as bogie instability or abnormal thermal conditions. For steel spring floating slab tracks, simulations confirm that vehicles operating below 100 km/h maintain adequate safety margins with substantial design buffers across all dynamic indicators [127]. Human factors significantly influence operational reliability, particularly in scenarios requiring rapid responses to dynamic disturbances [128].

4.5. Passenger Comfort

Passenger comfort in train–subway systems is related to vibration characteristics, noise levels, and physiological responses quantified by ride quality. Sperling’s ride index remains a foundational metric; its limitation to frequencies below 40 Hz poses challenges for modern systems incorporating high-frequency components [129]. Broader standards (UIC 513 and ISO 2631) address this gap by extending evaluation ranges to 80 Hz and incorporating frequency-weighted acceleration measurements for seated and standing passengers [129]. According to ISO 2631-1 [130], vertical vibrations become perceptible at 0.01 m/s² RMS acceleration, with lower floors in buildings near tracks experiencing heightened vibrations due to reduced structural damping [15]. Human sensitivity to lateral vibrations peaks between 1 and 2 Hz, necessitating design measures to avoid aligning vehicle body eigenfrequencies with this critical range [89].

Vibration transmission pathways play a pivotal role in comfort, where seat-to-head transmissibility (STHT) and apparent mass (AM) indicate how vibrations propagate through the human body. Direct model parameters significantly influence STHT, particularly in low-frequency ranges where resonant vibrations affect the head, thorax, and abdominal organs [131]. The SEAT (Seat Effective Amplitude Transmissibility) metric evaluates vibration attenuation efficacy, with values below 100% indicating effective isolation [132]. Experimental data shows that polygonal wheel wear at specific diameters exacerbates high-frequency vibrations, with resonant frequencies near 589 Hz (bogie frame) and 601 Hz (wheelset) accelerating wear patterns and amplifying noise levels [18]. Wheel diameter differences exceeding 2 mm induce unstable running conditions, degrading Sperling comfort indices in both vertical and lateral directions [122].

Noise pollution significantly impacts comfort, with interior noise levels closely tied to track design and wheel–rail interface conditions. Floating slab track systems demonstrate superior noise reduction, lowering axle-box vibration dominant frequencies from 66 Hz (conventional fasteners) to 43 Hz while reducing interior noise by 2.28 dB (A) [133]. Rail corrugation exacerbates high-frequency vibrations, generating discomfort-inducing noise and compromising running stability [123]. The CR400AF/BF Fuxing trains exemplify design improvements, achieving 1–3 dB reductions in cabin noise and 6–7 dB attenuation in pantograph areas compared to earlier Harmony series trains. Bridge–train interactions further modulate vibration propagation, with simulations confirming that vehicles operating below 100 km/h on steel spring floating slab tracks maintain acceptable vibration levels in the 40–100 Hz range [127].

Operational parameters also influence comfort metrics, where acceleration and jerk thresholds ensure safe yet comfortable travel. RailSIM simulations indicate that maintaining accelerations within ±2.0 m/s² and jerk below 3.0 m/s³ achieves an optimal balance between schedule adherence and passenger comfort [126]. The Train Energy and Dynamics Simulator (TEDS) incorporates comfort evaluation algorithms that adjust speed profiles based on interstation track conditions, identifying sections requiring speed moderation to meet UIC 513 comfort criteria [134,135]. Metro systems face unique challenges due to frequent start–stop cycles, where traction system vibrations transmitted through pneumatic brakes and inverter controls create distinct noise signatures in older rolling stock [136]. Modern trains mitigate these effects through improved suspension design and lightweight body structures, though trade-offs between weight reduction and structural stiffness require careful optimization to minimize flexible vibration modes between 4 and 12 Hz [136].

Integrating multibody dynamics models with human vibration sensitivity data enables predictive comfort assessments, as demonstrated in studies where 5 h exposure to 8–10 Hz vibrations induced muscle spasms and abdominal pain as per ISO 2631 thresholds [130,131]. Structural vibrations transmitted through tunnel walls into adjacent buildings exhibit frequency-dependent characteristics, with horizontal vibrations dominating below 5 Hz and vertical components prevailing at higher frequencies [137].

5. Emerging Technologies and Future Perspectives

5.1. Artificial Intelligence

The integration of artificial intelligence (AI) and machine learning (ML) into the analysis and prediction of train–subway dynamic interactions marks a transformative shift in urban subway design, operation, maintenance, and management. Machine learning algorithms have been applied to model wheel–rail contact forces, where neural networks trained on historical operational data achieve up to 96.2% accuracy in predicting vibration patterns and wear mechanisms—surpassing traditional methods like the GBDT algorithm by 7.8% [52]. Such capabilities are invaluable for maintenance planning, enabling early anomaly detection and reducing unplanned downtime. Machine learning algorithms trained on historical simulation data further enhance this predictive capability, classifying emerging fault patterns with 88% accuracy across diverse operational contexts [98].

Neural networks approximating coupled thermal–mechanical responses of brake discs achieve 95% prediction accuracy while reducing computation times from hours to seconds [97]. Deep learning architectures excel at capturing the nonlinear interactions between these subsystems. Attention mechanisms (AMs), for instance, have been used to identify key features in input data, particularly those influencing vibration propagation and energy dissipation [113]. These models not only enhance simulation efficiency but also support real-time decision making by offering actionable insights into system performance under diverse operational conditions. The iterative coupling approach, augmented by AI, strikes an effective balance between computational accuracy and efficiency, making it well-suited for large-scale network simulations [94]. Meanwhile, the integration of physics-informed neural networks with finite element analysis offers a hybrid approach that combines the interpretability of mechanistic models with the adaptability of data-driven methods. Standardized datasets and benchmarking frameworks will be critical to ensuring the reproducibility and scalability of these AI applications across diverse subway transit systems.

AI has shown promising capabilities in tasks involving design optimization, structural health monitoring, predictive maintenance, and decision making under uncertainty. Notably, machine learning (ML) algorithms, including neural networks, decision trees, support vector machines, and deep learning models, have been successfully used to analyze large volumes of railway operation data, identify patterns, and predict system behavior with remarkable accuracy and speed [63,138,139].

AI models, once trained, can produce near-instantaneous predictions with minimal computational overhead, making them especially suitable for applications where real-time monitoring, rapid assessment, or iterative design evaluations are required. Additionally, AI can effectively handle multi-dimensional data from heterogeneous sources (such as acceleration data, soil profiles, track geometry, and environmental conditions) thus offering a holistic framework for vibration-related problems. By integrating AI methodologies with domain knowledge in railway engineering and structural dynamics, robust, efficient, and scalable solutions can be developed. These solutions not only reduce reliance on resource-intensive numerical models but also enhance the responsiveness, adaptability, and effectiveness of vibration prediction and mitigation strategies in metro railway systems, enabling a new generation of intelligent, data-driven infrastructure design and management tools for modern rail transit systems.

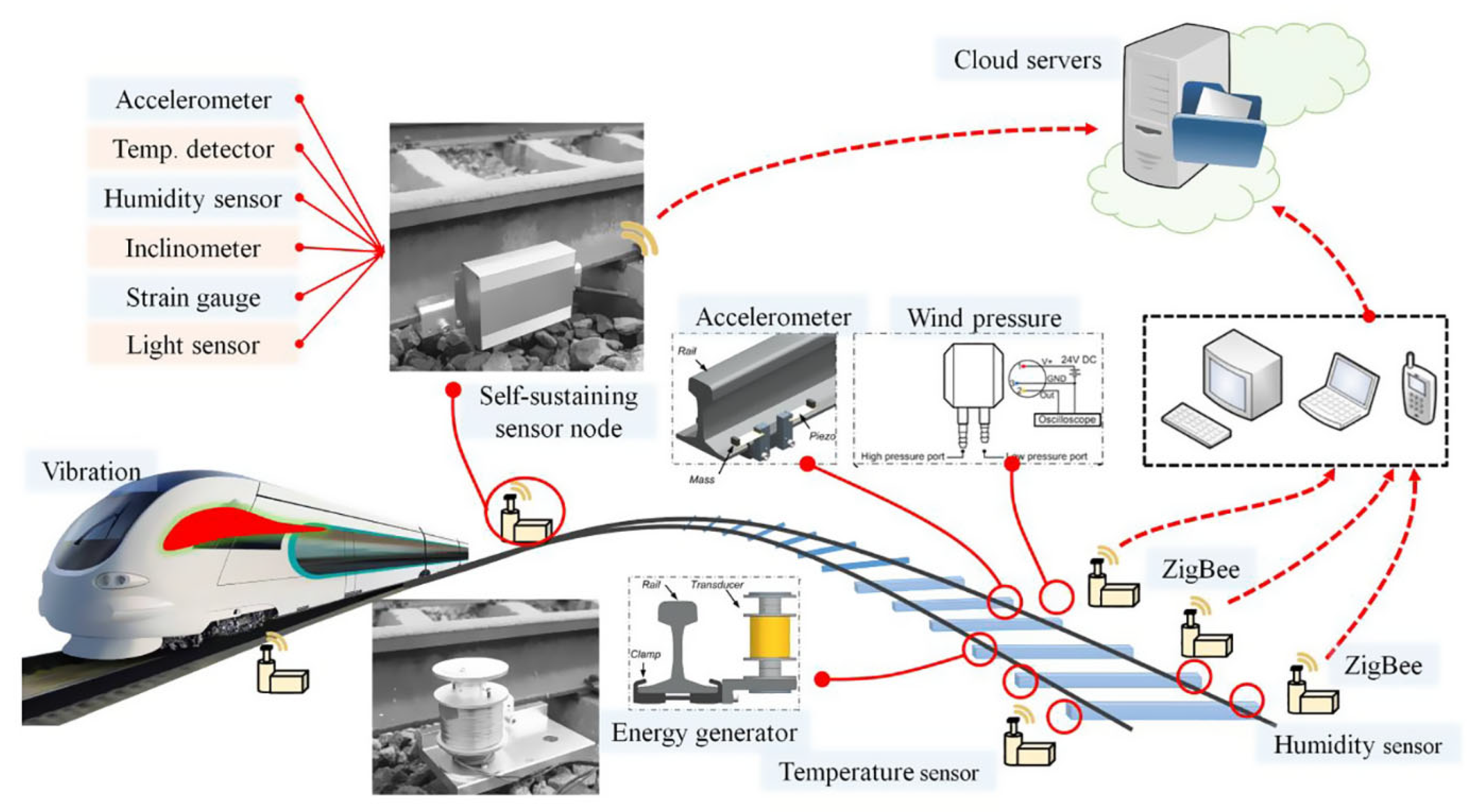
5.2. Smart Sensing and Real-Time Monitoring

Metro subway lines are typically constructed in densely populated urban areas, where space constraints, the proximity of buildings, and public sensitivity to environmental disturbances necessitate careful engineering consideration. Train-induced vibration can affect both the structural safety of nearby buildings and the comfort and well-being of the local population, as shown in Figure 7. As a result, the measurement, monitoring, and assessment of train-induced vibration have become essential components of ensuring the sustainable, safe, and socially acceptable operation of metro systems [140,141,142,143].

When metro lines are routed near vibration-sensitive structures (such as historic landmarks, museums, research laboratories, hospitals, or heritage buildings), the implementation of a permanent vibration monitoring system becomes critical. These systems provide continuous real-time data on vibration levels, enabling the detection of anomalous conditions, assessment of long-term trends, and verification of compliance with vibration limits established by regulatory guidelines or preservation standards [56]. Such data is invaluable for ensuring that the structural integrity and functional performance of sensitive buildings are not compromised over time by the dynamic loads transmitted from metro trains.

In contrast, temporary vibration monitoring systems are often deployed in response to specific events or concerns, particularly when complaints are received from residents or occupants of buildings adjacent to metro lines. In these cases, a short-term monitoring campaign may be initiated to quantify the magnitude and frequency characteristics of the vibrations, identify potential sources, and evaluate whether the measured vibration levels exceed accepted thresholds for human comfort or structural impact. The findings from such investigations can inform decisions regarding mitigation measures, such as retrofitting the track structure, enhancing the vibration isolation system, or modifying train operational parameters [145].

Advanced monitoring systems play an important role in addressing wear-related failures. For example, CR400AF/BF utilizes over 2500 monitoring points to track 1500 vehicle state parameters, facilitating real-time anomaly detection, such as abnormal wheel–rail temperatures or bogie lateral instability. When predefined thresholds are exceeded, the system automatically enforces speed restrictions or halts operations while generating targeted repair recommendations, minimizing unplanned downtime by prioritizing interventions based on actual component degradation rather than rigid schedules.

Smart sensing technologies allow for precise real-time data acquisition and analysis of critical operational parameters. Integrating vehicle-mounted accelerometers with track-side monitoring systems creates closed-loop feedback for maintenance decision making [50]. Smart sensors provide continuous monitoring of key parameters such as wheel–rail forces and vibration patterns. High-speed trains like France’s AGV and Italy’s ETR1000 demonstrate this capability through integrated onboard diagnostic networks, which include speed sensors, axle temperature monitors, and wheel imbalance detectors. These systems enable continuous condition monitoring, with radar-based speed measurement devices achieving sub-meter accuracy in line tests [98]. Distributed sensor architectures now address challenges in capturing transient wheel–rail contact phenomena, overcoming limitations regarding signal-to-noise ratios and sampling frequencies that plagued traditional methods [90]. Strain gauge instrumentation on wheel discs has proven particularly effective for measuring contact forces at frequencies up to 2 kHz, as evidenced by Swedish turnout field tests [102]. Accelerometer arrays deployed along tunnel walls and surrounding strata in Shanghai Metro Line 9’s vibration assessment program map energy propagation from rail-heads to the surface using dense sensor grids [50]. Multi-point measurement strategies facilitate spatial analysis of vibration transmission, offering valuable insights for evaluating floating slab track systems where wave propagation patterns influence rail corrugation development [127].

Laser-based sensing technologies represent a leap forward in environmental perception for collision avoidance. Millimeter-wave radar and LiDAR arrays generate high-resolution point clouds of track geometry, detecting potential obstructions with centimeter-level precision. These active sensing modalities perform reliably in low-light tunnel environments, while integrated processing algorithms eliminate false positives from rail fasteners and ballast particles. The resulting real-time hazard maps feed into predictive braking controllers, contributing to the train protection systems.

Fiber-optic sensing networks offer scalable solutions for large-scale subway tunnel monitoring. Distributed acoustic sensing (DAS) networks repurpose existing communication cables as continuous vibration sensors, achieving meter-scale spatial resolution across entire tunnel sections to detect rail defects and loose fasteners through characteristic frequency signatures, outperforming conventional accelerometer-based approaches.

Data fusion of these diverse sensor streams requires advanced data processing frameworks. Onboard computers use time-synchronization protocols to align measurements from inertial measurement units (IMUs), acoustic emission sensors, and strain gauges, creating unified representations of vehicle–track interaction dynamics. Edge computing performs initial feature extraction at measurement nodes, reducing bandwidth demands while preserving critical transient data for central analysis. For high-speed operations, decision latencies remain below 50 milliseconds, demanding a distributed processing approach that supports real-time condition assessment without sacrificing temporal resolution.

Future directions may exploit smart sensing for real-time model calibration, as demonstrated by the European Rail Research Institute (ERRI) DZ14 Committee’s harmonic decomposition methods for bridge vibration analyses, which avoid time-domain integrations by leveraging modal superposition and FFT techniques [94]. A prominent methodological advancement involves multi-time-step solution techniques, which integrate implicit and explicit integration methods to enhance computational efficiency for large-scale train–track–substructure systems. Advanced control algorithms and real-time monitoring systems play a pivotal role in adaptive optimization, balancing operational safety, reliability, and passenger comfort.

Future advancements will prioritize sensor durability and self-diagnostic capabilities to minimize maintenance requirements. Harsh operational conditions demand robust packaging solutions that can endure prolonged exposure to vibration, moisture, and electromagnetic interference without compromising accuracy. Emerging self-calibrating sensor designs incorporate reference standards and built-in test functions to mitigate drift in long-term deployments. These innovations collectively enhance the reliability and maintainability of monitoring systems, supporting predictive maintenance strategies in next-generation subway networks.

Most existing train-induced vibration monitoring systems are designed in a site-specific manner, lacking standardization or generalizable frameworks. Each system tends to be tailored to the unique characteristics of the local soil conditions, building sensitivities, metro train configurations, and urban constraints. While this customization is sometimes necessary, it highlights a broader challenge in the field: the absence of a unified methodology for the design, deployment, and operation of vibration monitoring systems in metro applications.

Therefore, there is an urgent need to develop a systematic framework for defining the technical characteristics, functional requirements, and deployment protocols of both permanent and temporary train-induced vibration monitoring systems. Such a framework should include clearly defined steps for system planning, sensor type selection (e.g., geophones and accelerometers), sensor placement strategies, data acquisition and processing methods, threshold setting based on standards (e.g., ISO 2631 and DIN 4150), long-term maintenance, and interpretation of results [130,146]. By establishing such a comprehensive methodology, practitioners can ensure that vibration monitoring not only fulfills regulatory and community expectations but also contributes to the resilience, reliability, and public acceptance of metro infrastructure in complex urban environments.

5.3. Digital Twin Technology

A digital twin refers to a virtual representation of a physical system (in this context, a subway system) that mirrors its behavior, structure and real-time data streams. It enables simulation, monitoring, optimization and predictive analytics across the life-cycle of the asset.

Digital twins are transforming system optimization by simulating operational conditions through high-fidelity virtual replicas that mirror physical train–subway interactions. Building on real-time data integration from advanced sensor networks, this approach enables synchronized digital models capable of predictive analysis and performance optimization. The Functional Mock-Up Unit (FMU) framework exemplifies this integration, allowing specialized domain models to be encapsulated within a cohesive system. Such co-simulation frameworks have proven effective in railway traction energy modeling, driver behavior analysis, and infrastructure digital twins, demonstrating their adaptability to complex multi-physics challenges [128].

Unlike traditional mathematical models, which are simplifications of real-world conditions and often deviate from real-world conditions, digital twin representations rely on empirical traction and braking data, ensuring alignment with actual operational scenarios. For example, curve-fitting techniques applied to experimental datasets reduce computational demands while preserving accuracy, enabling real-time simulations for controller development and system validation [98]. This approach resolves a critical limitation in prior research by unifying traction and braking processes within a single model—a capability absent in earlier studies that treated these phenomena independently. The resulting digital twins provide robust platforms for assessing energy efficiency, wear patterns, and safety margins across diverse operational conditions.

Collaborative potential is further unlocked through joint simulation techniques, such as those combining ADAMS and ANSYS for container crane systems. Although originally developed for freight handling, these principles are directly applicable to rail dynamics. By integrating Solidworks geometric models with multibody dynamics simulations, researchers can analyze coupled vibrations during acceleration and braking—a capability previously unattainable with simplified real-time motion models [25].

Digital twins also excel in operational optimization, particularly in traction energy management. Co-simulation frameworks facilitate scenario testing with variable driving strategies and headway configurations. For instance, defensive driving styles in tightly spaced timetables exhibit distinct energy consumption patterns compared to aggressive acceleration profiles, with following trains showing intermediate power draw when maintaining shorter inter-train distances [128].

Future advancements will likely focus on improving interoperability across simulation platforms and expanding real-time data assimilation. Current challenges include reconciling disparate model architectures and ensuring temporal synchronization across distributed computing nodes. Emerging solutions leverage edge processing for localized feature extraction, reducing latency while maintaining data resolution for centralized analysis. Research focusing on distributed computing architectures that partition simulation tasks across GPU clusters while maintaining deterministic timing is also promising [101]. Digital twin technologies can be further revolutionized through multi-physics coupling and real-time simulation. Achieving this requires reduced-order models that maintain coupling fidelity while minimizing computational costs, which is currently tackled via machine learning trained on offline simulations. By continuously comparing simulated and actual sensor data from in-service trains, discrepancies in vibration spectra or braking response times can signal component degradation before failures occur [97].

5.4. Sustainable Design Integration

Sustainable design principles are increasingly integrated to reduce environmental impact without compromising performance. The integration of environmental considerations into dynamic interaction analysis marks a pivotal advancement in rail transit design, balancing operational efficiency with ecological sustainability. This holistic approach mitigates unforeseen operational challenges, such as inadequate battery recharge intervals during turnarounds and seasonal factors like heating, ventilation, and air conditioning (HVAC) demands and extreme weather conditions [128]. The adoption of battery–electric trains eliminates localized emissions and reduces dependence on overhead contact networks [96]. These systems utilize non-contact power supply technologies, leveraging high-frequency electromagnetic induction between primary and secondary coils to enable efficient energy transfer without physical wear or visual disruption, thereby addressing urban aesthetic and safety concerns while ensuring reliability. Energy efficiency optimization intersects with sustainable design through co-simulation platforms that synchronize disparate subsystems. The timetable planning, traction power draw, and driver behavior models can be integrated to evaluate energy consumption across diverse operational scenarios [128]. Lightweight composite train bodies reduce traction energy demands by up to 15% compared to traditional steel structures, while regenerative braking systems recover kinetic energy during deceleration.

6. Conclusions

Based on this comprehensive review, the following concluding remarks can be made.

• Prediction of vibration and noise levels transmitted from the metro subway lines to nearby building structures and the automated development, deployment, and operation of vibration monitoring systems for temporary investigations and permanent installations are crucial for subway life cycles, including feasibility studies, environmental assessment and planning, design, operations, and maintenance.
• High-fidelity numerical simulation models of train–track–subway interaction dynamics offer greater precision but are often impractical for large-scale applications due to computational cost or early-stage evaluations due to uncertainties and challenges in measuring a variety of parameters. An optimal simulation model must balance the trade-off between model accuracy and computational efficiency and adapt its complexity based on the specific requirements and constraints of the project and its stage during the subway life cycle, including planning, design, and operations.
• Subway authorities in different countries enforce different environmental vibration regulations, including varied vibration threshold levels and frequency-weighting methods (e.g., ISO 2631 and DIN 4150) [130,146]. An effective simulation model must be tailored to align with the applicable regulatory requirements. This includes ensuring that the model’s frequency range covers the critical bandwidth requirements relevant to human perception and equipment sensitivity set forth by different countries.
• There is a lack of empirical data on long-term subway maintenance costs. For instance, there is no comprehensive study quantifying how much extra wear occurs when lighter and heavier vehicles share tracks over decades. As ultra-high-speed rail emerges, questions arise about whether future very fast trains could use metro corridors with mitigations for pressure waves, which is largely unstudied. Resonance in special conditions, such as high-speed trains in shallow urban subway tunnels, warrants further research to preempt issues as speeds increase.
• Vibration and noise could be mitigated through optimal design of railway concrete slab tracks and optimal design and placement of elastic vibration isolation elements under building foundations adjacent to metro lines to decrease train-induced vibrations. Future investigations should aim to define acceptable stiffness ranges or optimal design envelopes that enable vibration reduction without triggering undesirable mechanical consequences. Moreover, such studies should not treat the effects of rail pad and slab mat stiffness in isolation but should instead explore their interaction within the broader dynamic system of the track. This includes analyzing how changes in component stiffness affect load transfer paths, resonance frequencies, energy dissipation, and the evolution of track geometry over time. Thus, it will be possible to formulate design guidelines that balance the dual goals of vibration mitigation and track durability, ultimately supporting the development of high-performance slab track systems that meet the stringent operational and environmental demands of modern railway infrastructure. All of these require accurate and efficient prediction of vibration and noise levels.
• Mathematical modeling of wheel–rail contact mechanics and wear, train multibody dynamics, train–track system coupling dynamics, track slab subsystem dynamics, subway tunnel–ground interaction models, building vibrations excited by ground-borne seismic waves, and noise is becoming mature. New developments in these areas lie in high-fidelity numerical simulation with greater accuracy and resolution; high-efficiency, high-performance computing algorithms for rapid evaluation; multi-physics and multi-scale studies on coupled effects of different physical phenomena, such as thermal–hydro-mechanical–chemical (THMC) processes; real-time hardware-in-the-loop simulation; and laboratory and field validation of numerical simulations.
• AI, smart sensing and real-time monitoring, digital twin technology, and sustainable design integration are emerging in the study of train–track–subway interaction dynamics and its application to the life cycle of subway planning, design, construction, operations, maintenance, safety, and passenger comfort or ride quality. AI is most promising for delivering very fast prediction for train–track–subway system interaction dynamics by mimicking the mechanism of partial differential equation systems that govern system behavior, vibration, and noise, enabling a wide variety of applications in the life-cycle processes of subways.
• Smart sensing and real-time monitoring along with hardware-in-the-loop simulation augmented the capability for the safe and efficient operation of subways.
• Digital twins simulate operational conditions through high-fidelity virtual replicas that mirror physical train–track–subway interactions. Digital twins enable synchronized digital models capable of predictive analysis and performance optimization when jointly used with simulation software packages, such as ADAMS, ANSYS, and Solidworks for finite element analysis and Revit, Civil3D, and Micro-station for 3D information modeling of buildings and subway infrastructure. This two-way communication and control between physical and virtual worlds holds promise in effective railway traction energy modeling and driver behavior analysis.
• Sustainable design integrates environmental considerations into rail transit and subway design, balancing design longevity and operational efficiency with ecological sustainability. This may include but is not limited to the adoption of renewable energy for train HVAC systems, battery–electric trains, lightweight composite train bodies, and regenerative braking systems.