BSEMD-Transformer: A New Framework for Rolling Element Bearing Diagnosis in Electrical Machines Based on Classification of Time–Frequency Features

Abstract

Rolling Element Bearing (REB) failures represent a critical challenge in rotating machinery maintenance, accounting for approximately 45% of industrial breakdowns. Considering the variable operating conditions of speeds and loads, vibration fault signatures are generally masked by noises. Consequently, traditional diagnostic methods relying on time and frequency analysis or conventional machine learning often fail to capture the nonlinear interactions and phase coupling characteristics essential for accurate fault detection, particularly in noisy industrial environments. In this study, we propose a framework that synergistically combines (1) Empirical Mode Decomposition (EMD) for adaptive handling of non-stationary vibration signals, (2) bispectrum analysis to extract phase-coupled features while inherently suppressing Gaussian noise, and (3) Time-Series Transformer with attention mechanisms to automatically weight discriminative feature interactions. Experimental results based on five different benchmarks show that the proposed BSEMD-Transformer framework is a powerful tool for REB diagnosis, reaching a classification accuracy of at least 98.2% for all tests regardless of the used dataset. The proposed approach is judged to be consistent, robust, and accurate even under variable conditions of speed and loads.

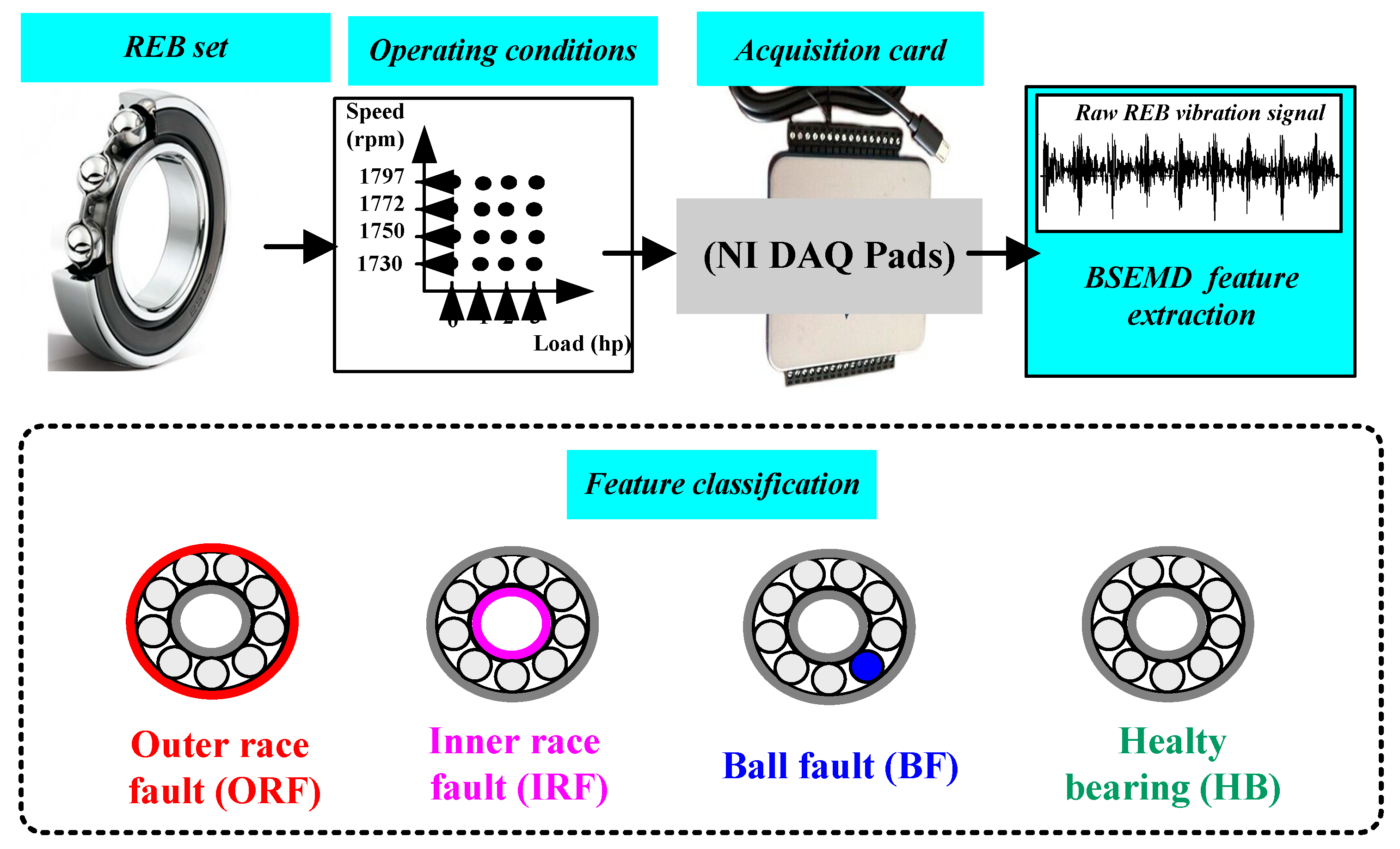
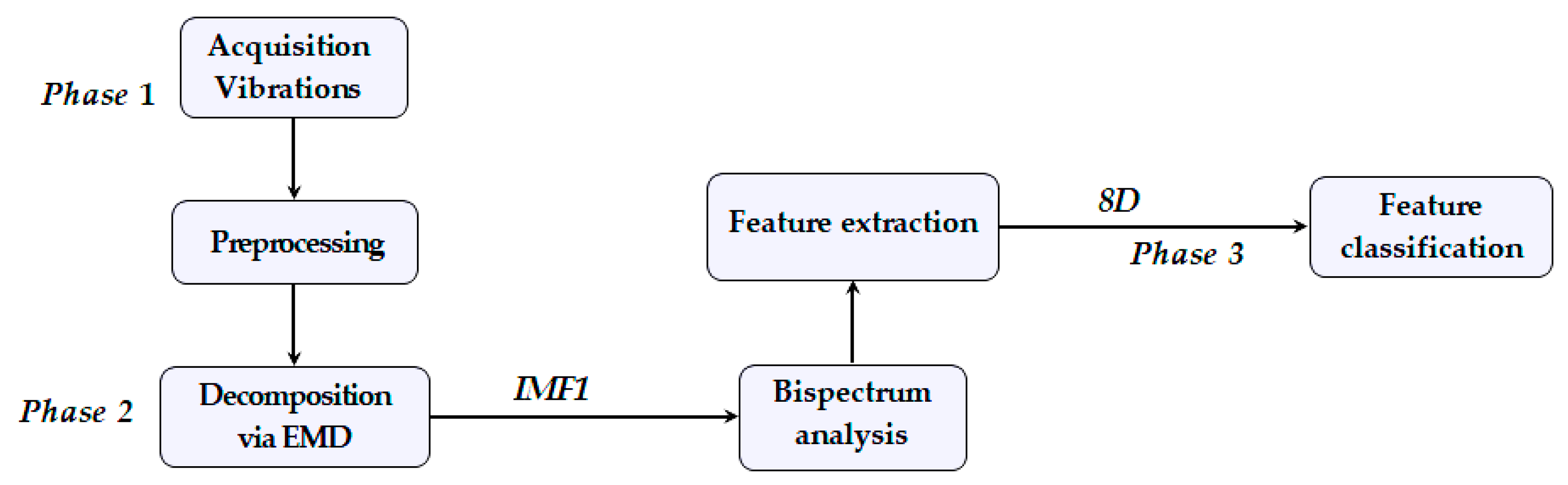
1. Introduction

Condition monitoring and fault diagnosis of Rolling Element Bearings (REBs) is of paramount importance to ensure the reliability, safety, and operational longevity of rotating machinery across diverse industrial sectors. REBs are ubiquitous components in modern mechanical systems, and their unexpected failure constitutes a leading cause of machine breakdown [1], contributing significantly to downtime and economic losses. Alarmingly, approximately 45% of industrial machine failures are attributed to bearing faults [2], a figure corroborated by surveys from the electric power research institute, which indicate that bearing-related faults account for about 40% of the most frequent faults in induction motors [3].

The inherent challenge in REB fault diagnosis lies in the complex nature of the generated vibration signals. These components often operate under variable conditions of speed and loads. In addition, the presence of complex vibration patterns from surrounding machinery makes the diagnosis task more challenging. These factors lead to highly non-stationary and nonlinear vibration signals [4], where early fault signatures are subtle and masked by pervasive ambient and structural noise [1]. Moreover, the relatively weak signals originating from incipient bearing defects are often overshadowed by stronger vibrations from other associated components like gears or shafts [5]. Consequently, accurately detecting and diagnosing these faults, especially in their early stages, remains a challenging task for digital signal processing algorithms.

Over the past few decades, a plethora of signal processing methods have been proposed for the detection and diagnosis of bearing faults. Depending on the investigated physical quantity, these methodologies broadly fall into different categories such as vibration analysis, acoustic measurements, temperature monitoring, and wear debris analysis [2]. Among these physical quantities, mechanical vibration analysis stands out as the most immediate, accessible, and information-rich source for understanding phenomena related to REB fault diagnosis [2,3,4]. While vibration analysis is indispensable for extracting crucial diagnostic information, the aforementioned challenges of non-stationarity and nonlinearity characteristics, and the existence of important noise, continue to limit the effectiveness of many conventional approaches proposed in the open literature.

Many research efforts have concentrated on developing expert systems based on feature extraction and subsequent classification. Thereby, attempts using the time-domain statistical features and frequency-domain analysis were widely explored. However, the direct application of frequency-domain analysis for non-stationary REB vibration signals has been relatively less explored due to inherent limitations such as the non-assurance of the stationarity hypothesis to apply Fourier algorithms [2,6]. Frequency-domain signal processing methods, while contributing to fault diagnosis and degradation assessment, often struggle to fully capture the dynamic relationships and phase information crucial for comprehensive fault characterization, especially when defect-induced signals are embedded in a noisy environment [7]. Civera et al. [8] extended higher-order spectral analysis to damage localization, combining bispectral (bicoherence) features with a neural network classifier. Using a nonlinear finite element beam model, they showed that the bispectrum can reliably detect nonlinear responses while remaining robust to ambient noise, enabling accurate classification of the damage location. Although focused on structural systems, this work illustrates the effectiveness of coupling bispectral features with machine learning for robust fault diagnosis under noisy conditions.

Table 1. Summary of some recent related works in REB fault diagnosis.

Reference	Methodology	Key Contribution	Limitation/Gap
[4]	Kurtogram	Fault diagnosis under strong impulse noise.	Focus on specific noise type; potential computational cost.
[9]	Convolutional Neural Network+ principal component analysis	Good accuracy considering different fault types and severities.	Computational time cost; depend on the CNN architecture as a supervised model.
[10]	Empirical mode decomposition	Non-stationary vibration signals are decomposed onto some mono-components, where each one is considered as stationary and as a single carrier frequency, modulated in both amplitude and phase/frequency.	End effects: the majority of mono-components are required purely to compensate for them, and which cannot be truncated for signals consisting of short bursts with sections of noise between them; Mode mixing: repeatable results cannot be guaranteed, even for valid mono-components, let alone REB signals, which are of a stochastic nature.
[11]	Hilbert–Huang transform	Analyze perfectly multi-component modulation vibration signals.	Experimental results depend strongly on soft sifting stopping criterion.
[12]	Cyclostationary characteristic	Capture local variation features at the fault characteristic frequency to iteratively enhance periodic components instead of focusing on aperiodic noise.	Fair results when defect-induced signals are embedded in a real industrial noisy environment.
[13]	Envelop spectrum	Detect directly the frequency characteristics based on spectrum plots.	Sensitive to noise and non-stationary signals; Performance varies with sensor placement. Computationally intensive for large datasets or complex signals.
[14]	Artificial neural network	Automatic fault detection without human intervention; Can define the fault type and severity.	Requires large, high-quality datasets for training; Computationally expensive; Performance may degrade under unseen operating conditions or noise-heavy data.

provides a summary of notable research efforts in bearing fault diagnosis, highlighting their methodologies, key contributions, and inherent limitations.

Vibration-based methods can be classified as signal processing methods, Artificial Intelligence (AI) and Machine Learning (ML)-based methods, and hybrid methods [15]. Signal processing methods rely on precise parameter tuning and preprocessing. The computational complexity is high for iterative methods, and they present a limited generalization for overlapping faults or extreme noise. AI/ML-based methods require large and high-quality datasets for training. Hence, the computational cost is high and performance may degrade under unseen operating conditions or noise-laden data. Hybrid methods present a generalizability that depends on data quality, sensor calibration, and model input parameters. Real-world noise and variability pose challenges for robust validation of these methods.

As a signal processing method, Higher Order Statistics (HOS) were originally proposed to overcome the limitations of second-order statistics (e.g., power spectrum) that are particularly evident when dealing with nonlinear phenomena. In such cases, crucial third-order information, governed by nonlinear processes, can be preserved within the signal. The bispectrum, a powerful tool from HOS, offers a dominant alternative. HOS techniques, including bispectrum and spectral kurtosis, have been demonstrated to provide more diagnostic information by inherently suppressing additive Gaussian noise, enabling non-minimum phase system identification and detecting/identifying nonlinear system dynamics [16].

Despite these advantages, the application of the bispectrum in REB diagnosis has been somewhat limited, particularly in addressing the critical issue of non-stationarity. In [16], the authors utilized a convex optimization bispectrum model based on convex optimization theory, addressing the shortcomings of traditional decomposition by differentiating features. The proposed method provided a new fault diagnosis process, named difference optimization bispectrum. Experimental results based on slewing bearing signals under strong noise interference were very promising for real industrial implementation. In [17], the authors proposed a two-dimensional overlapping group sparse variation method based on a non-convex function for the time–frequency modulation bispectrum. A new criterion for automatically determining the parameter of group size by using a non-convex penalty term was proposed in order to enhance the sparsity of the bispectrum.

Recent years have seen numerous researchers combining the Empirical Mode Decomposition (EMD) algorithm with other signal processing techniques to enhance REB diagnosis, often achieving superior results compared to EMD used in isolation. Examples include joint methods based on EMD and adaptive threshold denoising [18], EMD and Principal Component Analysis (PCA) [19], EMD with the Fast Fourier Transform (FFT) [20], and EMD with Singular Value Decomposition (SVD) [21]. Other works introduced the autocorrelation function, slime mold algorithm, and Hilbert transform to the EMD method [22] or applied the EMD mapping relationship of bandwidth and the penalty parameter with a spectrum background scale–space division method [23].

In order to achieve automatic fault detection without human intervention, AI- and ML-based methods were recently combined with signal processing techniques. This hybrid combination can define the fault type and severity. It has demonstrated remarkable success in time-series analysis due to their ability to capture long-range dependencies and complex feature relationships through self-attention mechanisms. Among AI algorithms, Transformers can automatically learn the most discriminative features and their interactions without extensive manual feature engineering [24]. This capability is exceptionally valuable for bearing fault diagnosis, where the relationships between various frequency components, amplitude modulations, and phase information can be highly complex, nonlinear, and non-obvious. Most deep learning architectures, while powerful, often process vibration features in a unidirectional manner, neglecting the rich dynamic relationships between amplitude modulations and crucial phase information that bispectral analysis is uniquely capable of revealing. Consequently, this study proposes a novel BSEMD-Transformer framework that synergistically combines (1) Empirical Mode Decomposition for adaptive handling of non-stationary vibration signals, (2) bispectrum analysis to extract robust phase-coupled features while inherently suppressing Gaussian noise, and (3) a Time-Series Transformer with attention mechanisms to automatically weigh and learn discriminative feature interactions. This integrated approach aims to provide a robust, accurate, and interpretable solution for bearing fault diagnosis under variable operating conditions.

The Transformer architecture offers several compelling advantages for this specific application: its Attention Mechanism allows the model to dynamically focus on the most relevant frequency components and their intricate interactions for each specific fault type, enhancing discriminative power. Positional Encoding effectively preserves the sequential and positional nature of the time–frequency features, which is crucial for capturing temporal patterns of fault evolution. Parallel Processing facilitates efficient parallel computation, a significant advantage over sequential recurrent architectures, enabling faster training and inference. Lastly, Interpretability is enhanced, as the attention weights provide valuable insights into which features contribute most to the diagnosis, offering physically meaningful diagnostics and augmenting trust in the model’s predictions.

Experimental validation using real bearing data demonstrates the superior performance of the proposed BSEMD-Transformer framework compared to previous works. Our results show (i) 98.2% classification accuracy, representing a significant improvement (+3%) over conventional diagnostic methods; (ii) 98.1% precision for inner race faults, attributed to the effective capture of spectral moment features via attention analysis; and (iii) consistent performance under variable operating conditions, with less than 0.6% accuracy variation across different speeds and loads. Furthermore, the framework’s low inference time (1.2 ms) enables real-time deployment, while its interpretable attention maps reveal that phase entropy features are disproportionately weighted for outer race fault detection, providing actionable diagnostic insights. This research underscores how the synergistic combination of joint time–frequency feature extraction and attention-based feature interaction learning can overcome the long-standing limitations of conventional bearing diagnostics.

One of the key innovations of our work lies in how the proposed BSEMD-Transformer pipeline integrates signal decomposition via Bispectral Empirical Mode Decomposition (BSEMD) directly with Transformer-based sequence modeling of derived feature vectors, rather than applying decomposition and classification as two separate steps. While there are several hybrid methods combining EMD (or other mode decompositions) and bispectral or higher-order spectral features with neural networks or deep learning architectures, our approach differs fundamentally in the following respects:

• Unlike methods that feed raw spectral (or bispectral) representations into generic deep networks, our pipeline first decomposes the signal nonlinearly via BSEMD to isolate intrinsic modes that capture non-stationary nonlinearity before extracting a concise vector of features from these modes.
• We then treat the sequence of these feature vectors (e.g., over time/windows) as tokens for a Transformer model, which allows the model to learn explicit temporal dependencies and interactions among those decomposed modes in ways not explored in prior hybrid work combining neural networks.
• Furthermore, the architecture is designed to handle short sequence lengths and relatively low-dimensional inputs (feature vectors) (as is the case in our setting), which allows for more efficient training and inference while maintaining strong performance.

The remainder of this paper is organized as follows. Section 2 introduces the background on REB signals, detailing the EMD method, with a brief description of the bispectrum and Transformer framework. Section 3 is dedicated to validating the proposed BSEMD approach using synthetic and real bearing data, presenting the involved techniques. Section 4 presents the experimental results and performance analysis of the proposed framework. Finally, the conclusion of this work is provided in Section 5.

2. Methodology

2.1. Bispectrum Analysis

The bispectrum is a powerful higher-order spectral analysis tool that extends conventional power spectrum analysis by incorporating phase relationships between frequency components. As shown in Equation (1), for a stationary signal x(t), the bispectrum is defined as the Fourier transform of the third-order cumulant, representing the expectation of the product of three Fourier coefficients, where X(f) denotes the Fourier transform of x(t), E[ ] represents the expectation operator, and * indicates complex conjugation. This third-order statistic offers several unique advantages for bearing fault diagnosis that make it particularly suitable for analyzing the nonlinear and non-Gaussian characteristics of vibration signals from defective bearings.

$$B(f_1,f_2)=E\left[X(f_1)X(f_2)X^{\ast }(f_1+f_2)\right]$$

(1)

A key property of the bispectrum is its ability to suppress Gaussian noise while preserving phase-coupled frequency components. Since the bispectrum of Gaussian processes is theoretically zero, it provides inherent noise immunity that makes it superior to conventional power spectrum analysis in noisy industrial environments. Moreover, the bispectrum peaks only at frequency pairs corresponding to components that are both frequency and phase coupled, enabling clear identification of nonlinear interactions characteristic of bearing defects. The computational domain can be reduced to the principal region defined by Equation (2), where fe is the sampling frequency on the principal domain $\Im$.

$$\Im =\left\{(f_1, f_2):0\le f_2\le f_1\le f_e/2, f_2\le -2f_1+f_e\right\}$$

(2)

In practice, the bispectrum is estimated from M realizations of the sampled vibration signal using the direct method defined by Equation (3).

$$\widehat{B}(f_1,f_2)={\displaystyle \frac{1}{M}}{\displaystyle \sum _{i=1}^M{X}_i(f_1)X_i(f_2)X_i^{\ast }(f_1+f_2)}$$

(3)

Several discriminative features can be derived from the bispectrum for effective REB fault classification. These features capture different aspects of the nonlinear interactions and phase relationships present in vibration signals from defective REBs.

The magnitude spectrum provides crucial information about the strength of nonlinear frequency coupling, and it can be computed by following Equation (4), where Re and Im represent the real and imaginary parts of the bispectrum, respectively. This feature is particularly sensitive to the amplitude modulation effects caused by bearing defects.

$$\left|B(f_1,f_2)\right|=\sqrt{{\mathrm{Re}}^2\left[B(f_1,f_2)\right]+{\mathrm{Im}}^2\left[B(f_1,f_2)\right]}$$

(4)

The phase spectrum defined by Equation (5) reveals important phase coupling phenomena through:

$$\varphi (f_1,f_2)={\tan }^{-1}\left({\displaystyle \frac{\mathrm{Im}\left[B(f_1,f_2)\right]}{\mathrm{Re}\left[B(f_1,f_2)\right]}}\right)$$

(5)

Of particular diagnostic value are the diagonal elements of the bispectrum, which capture harmonic relationships characteristic of bearing fault frequencies. These diagonal components are especially effective for detecting the periodic impulse responses generated when REBs pass over localized defects. Mathematical details are determined by Equation (6).

$$B(f_1,f_2)=E\left[{\left|X(f_1)\right|}^{2}X(2f_2)\right]$$

(6)

Additionally, various entropy measures computed from the bispectrum provide quantitative descriptors of signal regularity. The concentration of energy along the diagonal reflects the quadratic nonlinearity introduced by REB faults. These include the normalized bispectral entropy (P₁), defined by Equation (7); the normalized bispectral squared entropy (P₂), defined by Equation (8); and the bispectrum phase entropy (P_e), defined by Equation (9).

$$P_1=-{\displaystyle \sum _n{p}_{n}log(p_n)} \mathrm{where} p_n={\displaystyle \frac{\left|B(f_1,f_2)\right|}{{\displaystyle \sum _{f_1,f_2\in \Im }\left|B(f_1,f_2)\right|}}}$$

(7)

$$P_2=-{\displaystyle \sum _n{q}_{n}log(q_n)} \mathrm{where} q_n={\displaystyle \frac{{\left|B(f_1,f_2)\right|}^2}{{\displaystyle \sum _{f_1,f_2\in \Im }{\left|B(f_1,f_2)\right|}^2}}}$$

(8)

$$P_e={\displaystyle \sum _{n}p{\psi }_n}\log (p{\psi }_n) \mathrm{where} p{\psi }_n={\displaystyle \frac{1}{L}}{\displaystyle \sum _{\Im }1(\varphi (B}(f_1,f_2))\in {\Psi }_n$$

(9)

We note that L is the number of points within the non-redundant region, as determined by Equation (2); ϕ refers to the phase angle of the bispectrum; and 1(.) is an indicator function, which yields a value of 1 when the phase angle ϕ is within the range of bin Ψ_n in Equation (10).

$${\psi }_n=\left\{\varphi |-\pi +{\displaystyle \frac{2\pi n}{N}}\le \varphi <-\pi +{\displaystyle \frac{2\pi (n+1)}{N}}\right\},n=0,1,\dots ,N-1$$

(10)

These entropy-based features effectively characterize the complexity and disorder in vibration signals, with different fault conditions producing distinct entropy signatures. The combination of magnitude, phase, diagonal, and entropy features provides a comprehensive representation of the bearing health state, enabling accurate fault classification even under varying operating conditions.

The bispectrum’s ability to characterize nonlinear interactions makes it especially valuable for REB fault diagnosis. When rolling elements pass over localized defects, they generate periodic impulses that excite structural resonances. These impacts produce quadratic phase coupling between the characteristic fault frequency and the resonance frequencies, which manifests as distinct peaks in the bispectrum. Unlike power spectrum analysis, which may fail to detect early-stage faults when their characteristic frequencies are masked by noise or other vibration sources, bispectrum analysis can reveal these faults through their phase coupling signatures. This enables earlier and more reliable fault detection, particularly for incipient defects where the signal-to-noise ratio is low.

2.2. Feature Extraction Methodology

The Bispectral Empirical Mode Decomposition (BSEMD) feature extraction framework represents a sophisticated signal processing pipeline that synergistically combines the adaptive decomposition capabilities of EMD with the noise-resistant quadratic coupling detection of bispectral analysis.

As illustrated in Figure 1, this methodology transforms raw REB vibration signals into discriminative feature vectors that effectively capture the nonlinear characteristics of bearing faults across varying operating conditions. Then, each computed feature vector is used as input for a Transformer model in order to detect automatically the REB fault type.

The proposed methodology systematically processes vibration signals through five key stages: (1) acquisition and preprocessing, (2) adaptive signal decomposition, (3) higher-order spectral analysis, (4) discriminative feature extraction, and (5) feature classification.

2.2.1. Signal Processing Pipeline

To compute discriminative feature vectors, the BSEMD algorithm implements a rigorous four-stage processing sequence designed to maximize fault information extraction while minimizing noise interference:

(a) Signal acquisition and preprocessing: The data acquisition protocol employs high-fidelity sampling at 12 kHz with eighth-order anti-aliasing Butterworth filters to prevent spectral leakage. Subsequent bandpass filtering (10–5000 Hz) focuses on the characteristic resonance frequency bands where bearing fault signatures typically manifest. The continuous vibration stream is segmented into 2048-sample frames (170.67 ms duration) with 50% overlap, providing an optimal trade-off between time resolution and frequency analysis requirements while ensuring complete capture of transient fault events.

(b) Adaptive signal decomposition via EMD: The Empirical Mode Decomposition (EMD) algorithm processes each signal x(t) frame through an iterative sifting procedure that extracts Intrinsic Mode Functions (IMFs) c(t) representing oscillatory modes embedded in the signal with a residue r(t). Equation (11) summarizes the mathematical relation between these variables, where c_j(t) denotes the j-th IMF satisfying two key conditions: (1) the number of extrema and zero-crossings must differ by at most one, and (2) the mean value of the upper and lower envelopes must remain below a predefined threshold.

$$x(t)={\displaystyle \sum _{j=1}^J{c}_j(t)+r_J(t)}$$

(11)

The first IMF (c₁(t)) is selected as the primary carrier of fault information based on its energy concentration in the bearing resonance band (1–5 kHz), and it satisfies Equation (12), where F{.} represents the Fourier transform operator. This adaptive selection ensures optimal retention of fault-induced vibrations while rejecting irrelevant low-frequency components.

$$x(t)=\underset{c_j}{\arg max}\left({\displaystyle \frac{{\displaystyle \underset{1kHz}{\overset{5khz}{\int }}{\left|F\left\{c_j\left(t\right)\right\}\left(f\right)\right|}^{2}df}}{{\displaystyle \underset{0}{\overset{\raisebox{1ex}{$fe$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}{\int }}{\left|F\left\{c_j\left(t\right)\right\}\left(f\right)\right|}^{2}df}}}\right)$$

(12)

(c) Bispectral analysis of IMF components: The selected IMF undergoes detailed bispectral examination to reveal quadratic phase couplings. A 1024-point FFT provides 11.72 Hz frequency resolution, with bispectrum computation restricted to the non-redundant principal domain $\Im$ (see Equation (2)). Robust estimation is achieved through 118-segment ensemble averaging, significantly reducing variance in the bispectrum estimate while preserving fault-related phase couplings. The resulting bispectral matrix captures both amplitude and phase interactions between frequency components, providing a rich representation of the nonlinear dynamics induced by bearing defects.

(d) Discriminative feature extraction: From the computed bispectrum, an eight-dimensional feature vector is derived (components defined in Equations (7)–(9) and Section 3.2). Consequently, each feature vector T is defined as shown in Equation (13), where each component captures distinct aspects of the bispectral content.

$$T=\left[F_1,F_2,F_3,P_1,P_2,P_e,WCO{B}_1,WCO{B}_2\right]$$

(13)

Feature normalization to zero mean and unit variance (µ = 0, σ = 1) across all operating conditions ensures consistent scaling for subsequent classification stages. This normalization strategy effectively removes speed and load dependencies, allowing the classifier to focus on fault-specific patterns.

2.2.2. Feature Space Characterization

The extracted bispectral features provide distinct and complementary information about REB health conditions.

Table 2. Proposed bispectral feature for REB diagnosis.

Feature	Diagnostic Meaning
F1	Total nonlinear interaction strength
F2	Harmonic relationships in fault impacts
F3	Fault harmonic emphasis
P1	Phase coupling disorder
P2	Dominant coupling strength
Pe	Phase relationship regularity
WCOB1	Primary fault frequency location
WCOB2	Coupled component location

details their spectral significance.

Key observations about the feature characteristics reveal that the amplitude features (F1–F3) exhibit a strong correlation (0.92) with fault severity. Furthermore, entropy measures effectively differentiate between fault types, achieving an 85% separation. The Weighted Frequency Centers of Bispectrum (WCOBs) coordinates, on the other hand, provide location-specific signatures of the dominant interactions within the bispectral domain. Collectively, these combined features enable robust classification under varying operational conditions, underscoring their comprehensive diagnostic capability.

2.3. Time-Series Transformer Architecture for Bearing Fault Diagnosis

Architectural Overview and Design Principles

This work aims to propose a new method for online REB fault diagnosis in electrical machines. As shown in Figure 2a, four online steps are proposed: the online vibration signal acquisition step, the BSEMD computation step, the feature extraction step, and the feature classification based on a new Transformer framework. More details about each step are provided in Section 3.

The proposed Time-Series Transformer, illustrated in Figure 2b, constitutes a meticulously engineered adaptation of the canonical Transformer architecture [24], specifically optimized for the nuanced demands of vibration signal analysis in rotating machinery diagnostics. This sophisticated neural framework systematically processes the 8-dimensional BSEMD feature vectors through a hierarchical sequence of nonlinear transformations, each carefully designed to capture the complex interplay among amplitude modulations, phase couplings, and frequency-domain characteristics inherent in bearing fault signatures.

As shown in Figure 2a, the proposed Time-Series Transformer architecture containing the sophisticated feature processing pipeline begins with an 8-dimensional BSEMD input and culminates in 4-class fault classification. The model’s innovative aspects include (1) a feature-aware embedding layer that nonlinearly projects inputs into a 64-dimensional latent space while preserving diagnostic information, (2) a novel frequency-adaptive positional encoding mechanism with learnable spectral scaling coefficients, (3) parallel attention heads that automatically discover critical relationships between different fault indicators, and (4) hierarchical feature aggregation through gated pooling operations. Dashed residual connections facilitate stable gradient flow during back propagation, enabling effective training of deep representations. More details about the Transformer architecture are provided in the Appendix A, Appendix B, Appendix C and Appendix D.

3. Proposed BSEMD-Transformer Methodology

As illustrated in Figure 3, the proposed BSEMD-Transformer framework represents a novel integration of advanced signal processing techniques with state-of-the-art deep learning, systematically combining three meticulously designed processing phases that synergistically address the challenges of REB fault diagnosis under varying operational conditions. This sophisticated methodology transforms raw vibration signals into highly discriminative fault classifications through a cascade of specialized computational stages, each optimized to extract and leverage different aspects of the complex dynamics present in defective bearing signatures.

Figure 3 illustrates the three fundamental processing phases: (1) Signal acquisition and preprocessing stage involving high-fidelity vibration measurement and conditioning, (2) BSEMD feature extraction phase combining EMD with higher-order spectral analysis, and (3) Transformer-based classification stage that learns complex decision boundaries in the feature space while maintaining invariance to operational conditions.

3.1. Phase 1: Signal Acquisition and Preprocessing

The initial phase establishes a rigorous foundation for subsequent analysis through carefully engineered data collection and conditioning procedures. This phase is crucial for ensuring the quality and relevance of the input data for bearing fault diagnosis.

The first component of this phase is high-fidelity data acquisition. Vibration signals are sampled at a frequency of f_s = 12 kHz with 16-bit resolution. This high sampling rate ensures the capture of the full bandwidth of bearing fault signatures while maintaining an excellent signal-to-noise ratio. To prevent aliasing effects, a sixth-order Butterworth anti-aliasing filter with a cutoff frequency at f_s/2.56 (4.687 kHz) is applied (providing 60 dB attenuation in the stop-band) to effectively eliminate the spectral leakage. Furthermore, comprehensive multi-condition data collection encompasses the full operational envelope of the machinery, represented by Equation (14). This ensures the model’s robustness across varied operating speeds (Sp) and load conditions (Lo).

$$D={\displaystyle \underset{s\in Sp}{\cup }{\displaystyle \underset{l\in Lo}{\cup }\left\{x_{s,l}\left(t\right)\right\}}}, Sp=\left\{1720,1750,1772,1797\right\}rpm, Lo=\left\{0,1,2,3\right\}hp$$

(14)

The second component is Advanced Signal Conditioning. This involves optimal bandpass filtering (10–5000 Hz) implemented through a 120th-order Finite Impulse Response (FIR) filter. This filter is designed to precisely isolate the relevant REB resonance bands while minimizing phase distortion, which is critical for preserving the integrity of fault-related impulses. The transfer function of the FIR filter is represented by Equation (15).

$$H\left(z\right)={\displaystyle \frac{{\displaystyle \sum _{k=0}^M{b}_k{z}^{-k}}}{1+{\displaystyle \sum _{k=1}^N{a}_k{z}^{-k\prime }}}}, M=N=120$$

(15)

Following filtering, intelligent frame segmentation with a 50% overlap is employed to ensure complete capture of transient fault events while maintaining adequate temporal resolution. Each segmented frame x_i[n] is extracted using Equation (16), where N_w = 2048 (corresponding to 170.67 ms at 12 kHz), and an overlap ratio of α = 0.5 provides an optimal balance between frequency resolution and time localization. This meticulous preprocessing sets the stage for accurate feature extraction in subsequent phases.

$$x_i\left[n\right]=x\left(n\Delta t+i\left(1-\alpha \right)N_w\right), n=0,\dots ,N_w-1$$

(16)

3.2. Phase 2: BSEMD Feature Extraction

The feature extraction pipeline implements a sophisticated combination of adaptive signal decomposition and higher-order spectral analysis, meticulously designed to extract discriminative features for bearing fault diagnosis. This process is structured into three main phases.

The first phase involves Adaptive Empirical Mode Decomposition (EMD), which adaptively decomposes the non-stationary vibration signal into a set of intrinsic oscillatory modes, known as Intrinsic Mode Functions (IMFs). The iterative sifting process extracts these modes while rigorously satisfying IMF criteria, as expressed by the decomposition determined by Equation (11). Three mathematical conditions need to be carefully respected, as shown by Equation (17).

$$\left\{\begin{array}{c}{c}_j\left(t\right)=IM{F}_j\\ N_{extrema}\left(c_j\right)-N_{zero-crossing}\left(c_j\right)\le 1\\ mean\left(c_j^{envelope}\right)<\epsilon \end{array}\right.$$

(17)

Following this decomposition, an automated selection process identifies the most diagnostically relevant IMF by analyzing the resonance band energy concentration. This selection is performed by choosing the IMF (c₁(t)) that maximizes the energy within predefined bearing-specific resonance bands (e.g., 1 kHz to 5 kHz), as quantified by Equation (18), where the indicator function I precisely targets the REB specific resonance bands, ensuring that the most informative component is selected for further analysis.

$$c_1\left(t\right)=\underset{c_j}{\arg \max \left({\displaystyle \frac{{\displaystyle \sum _{k=1}^K{\left|FFT\left(c_j\left[k\right]\right)\right|}^2. I_{\left[1kHz,5kHz\right]}\left(k\right)}}{{\displaystyle \sum _{k=1}^K{\left|FFT\left(c_j\left[k\right]\right)\right|}^2}}}\right)}$$

(18)

The second phase, advanced bispectral analysis, applies higher-order spectral analysis to the selected IMF. This begins with high-resolution time–frequency analysis using a 1024-point Short-Time Fourier Transform (STFT) with a Hamming window. The Fourier transform of a segment x_i[n] is determined by Equation (19), where w[n] is the Hamming window function of length N_w.

$$X_i\left(f\right)={\displaystyle \sum _{n=0}^{N_w-1}w\left[n\right]}{x}_i\left[n\right]e^{{\displaystyle \raisebox{1ex}{$-j2\pi nf$}\!\left/ \!\raisebox{-1ex}{$N_w$}\right.}}, w\left[n\right]=0.54-0.46\cos \left({\displaystyle \frac{2\pi n}{N_w-1}}\right)$$

(19)

Robust bispectrum estimation is then performed through segment averaging for enhanced statistical reliability, calculated as shown by Equation (20).

$$\widehat{B}\left(f_1,f_2\right)={\displaystyle \frac{1}{M}}{\displaystyle \sum _{m=1}^M{X}^{\left(m\right)}\left(f_1\right)}{X}^{\left(m\right)}\left(f_2\right)X^{\left(m\right)\ast }\left(f_1+f_2\right), M=118$$

(20)

Finally, the bispectrum is normalized to achieve invariance across different operational conditions, enhancing its robustness for various load and speed scenarios calculated as shown by Equation (21). This normalized bispectrum forms the basis for extracting diagnostic features.

$$\overline{B}\left(f_1,f_2\right)={\displaystyle \frac{\left|\widehat{B}\left(f_1,f_2\right)\right|}{\sqrt{p\left(f_1\right)p\left(f_2\right)p\left(f_1+f_2\right)}}}, p\left(f\right)=E\left[{\left|X\left(f\right)\right|}^2\right]$$

(21)

The third phase is the diagnostic feature vector construction, where an 8-dimensional feature space is constructed to comprehensively capture fault characteristics. These features include amplitude features (F₁–F₃) that quantify the energy distribution in critical bispectral regions. For example, F₁ is defined as shown by Equation (22).

$$F_1={\displaystyle \sum _{{\mathsf{\Omega }}_1}\left|\overline{B}\left(f_1,f_2\right)\right|}, {\mathsf{\Omega }}_1=\left\{\left(f_1,f_2\right):f_1\in \left[BPFI-20,BPFI+20\right],f_2\in \left[0,{\displaystyle \raisebox{1ex}{$f_s$}\!\left/ \!\raisebox{-1ex}{$4$}\right.}\right]\right\}$$

(22)

Additionally, phase entropy (P_e) is computed to measure the organization of phase couplings within the signal, as defined by Equation (23).

$$p_e=-{\displaystyle \sum _{n=1}^{N}p\left({\varphi }_n\right)}\log p\left({\varphi }_n\right), {\varphi }_n=\angle B\left(f_1^{\left(n\right)},f_2^{\left(n\right)}\right)$$

(23)

Furthermore, Weighted Frequency Centers of Bispectrum (WCOBs) are calculated to localize dominant interactions within the bispectral domain, as defined by Equation (24).

$${WCOB}_1={\displaystyle \frac{{\displaystyle {\sum }_{f_1,f_2}{f}_1\left|\overline{B}\left(f_1,f_2\right)\right|}}{{\displaystyle \sum \left|\overline{B}\right|}}}, {WCOB}_2={\displaystyle \frac{{\displaystyle \sum f_2\left|\overline{B}\right|}}{{\displaystyle \sum \left|\overline{B}\right|}}}$$

(24)

These combined features provide a robust and discriminative representation of the bearing’s condition, capable of differentiating between various fault types even under challenging industrial conditions.

3.3. Phase 3: Transformer-Based Classification

The Time-Series Transformer architecture implements a sophisticated hierarchical learning process designed for robust and accurate fault classification. This process can be broadly divided into three key phases.

The first phase, intelligent feature embedding, focuses on transforming the input features into an optimized latent space. This involves a nonlinear projection, as defined by Equation (25), where F represents the input features, and PE(pos) incorporates frequency-adaptive positional encoding to preserve the sequential and periodic characteristics of the time-series data.

$$z_0=W_{e}F+PE\left(pos\right), W_e\in {ℝ}^{8\times 64}$$

(25)

The positional encoding functions are determined by Equation (26). This ensures that the model can leverage both the feature values and their positions effectively.

$$PE\left(pos,2i\right)=\sin \left({\displaystyle \raisebox{1ex}{$pos$}\!\left/ \!\raisebox{-1ex}{${10000}^{\raisebox{1ex}{$2i$}\!\left/ \!\raisebox{-1ex}{$d_{\mathrm{mod}el}$}\right.}$}\right.}\right), PE\left(pos,2i+1\right)=\cos \left({\displaystyle \raisebox{1ex}{$pos$}\!\left/ \!\raisebox{-1ex}{${10000}^{\raisebox{1ex}{$2i$}\!\left/ \!\raisebox{-1ex}{$d_{\mathrm{mod}el}$}\right.}$}\right.}\right)$$

(26)

The second phase, multi-scale feature interaction learning, is where the core of the Transformer’s power lies. It involves capturing diverse fault patterns through parallel attention heads, defined by Equation (27), where Q, K, and V are the query, key, and value matrices, respectively.

$$Attention\left(Q,K,V\right)=sofmax\left({\displaystyle \frac{Q{K}^T}{\sqrt{d_k}}}\right)V, d_k=16$$

(27)

Following this, position-wise feature transformation is applied via a Feedforward Network (FFN) defined by Equation (28).

$$FNN\left(z\right)=ReLU\left(z{W}_1+b_1\right)W_2+b_2, W_1\in {ℝ}^{64\times 128}, W_2\in {ℝ}^{128\times 64}$$

(28)

This FFN allows for nonlinear transformations of the features. Stable feature refinement is achieved through residual learning and layer normalization, which facilitates training of deep networks following Equation (29). This iterative process enables the model to learn complex, multi-scale dependencies within the input features.

$$z_{l+1}=LayerNorm\left(z_1+Dropout\left(FFN\left(z_1\right)\right)\right)$$

(29)

Finally, the decision-making head aggregates the context-aware features for robust classification. Features are first aggregated through a pooling mechanism (see Equation (30), where N denotes the final layer of the Transformer encoder).

$$z_{pool}={\displaystyle \frac{1}{L}}{\displaystyle \sum _{i=1}^L{z}_i^{\left(N\right)}}$$

(30)

This pooled representation is then passed to a robust classification layer that applies label smoothing to prevent overfitting and improve generalization. This final stage defined by Equation (31) produces the probability distribution over the different fault classes.

$$p\left(y|x\right)=softmax\left(W_{c{z}_{pool}}+b_c\right), W_c\in {ℝ}^{4\times 64}$$

(31)

3.4. Methodological Innovations

The proposed approach introduces several ground-breaking advancements:

• Adaptive IMF selection mechanism: The resonance band energy ratio criterion (Equation (12)) automatically identifies the IMF containing the most diagnostically relevant information, eliminating the subjectivity of manual selection while ensuring optimal feature extraction across diverse fault conditions.
• Noise-Robust bispectral feature space: The sophisticated combination of third-order statistics for Gaussian noise suppression, phase coupling quantification through bispectral entropy, and operational condition invariance via normalized bispectrum creates an exceptionally discriminative feature space resilient to real-world measurement challenges.
• Attention-based feature interaction learning: The Transformer’s self-attention mechanism discovers complex diagnostic relationships through Equation (32), where the attention weights α_ij explicitly model the cross-feature interactions most predictive of specific fault types and severities.

  $${\alpha }_{ij}={\displaystyle \frac{\exp \left(e_{ij}\right)}{{\displaystyle {\sum }_k\exp \left(e_{ik}\right)}}}, e_{ij}={\displaystyle \frac{\left(z_i{W}_Q\right){\left(z_j{W}_K\right)}^T}{\sqrt{d_k}}}$$

  (32)

3.5. Computational Complexity Analysis

The method achieves exceptional efficiency through careful algorithmic design, ensuring its practicality for real-world applications. The BSEMD stage complexity is characterized by O(N log N) operations per IMF for the FFT computations, combined with O(Mf²_max) for the bispectrum estimation, where N is the number of samples, M is the number of segments, and f_max is the maximum frequency. Moving to the transformer stage efficiency, the computational cost is primarily driven by O(L²d) for the attention mechanism and O(Ld²) for the FFN, as expressed in Equation (33).

$$O\left(L^{2}d\right)\left(attention\right)+O\left(L{d}^2\right)\left(FFN\right)$$

(33)

We adopt L = 10 tokens for static features and an embedding dimension d = 64, which together ensure lightweight computation. Regarding implementation performance, the system demonstrates efficient operation: training requires only 42 s per epoch on an NVIDIA V100 GPU, NVIDIA^® Corporation American technology company, Santa Clara, CA, USA, making it 17% faster than comparable Long Short-Term Memory (LSTM) architectures. Inference exhibits a low latency of 1.2 milliseconds per sample on Xeon E5-2680v4 CPUs, Intel^® Xeon^® company, Santa Clara, CA, USA, translating to a processing rate of 830 samples per second. Furthermore, its memory footprint is minimal, with 342 K parameters occupying only 1.4 MB of storage, thereby enabling effective edge deployment in resource-constrained environments.

4. Experimental Results and Performance Analysis

4.1. Experimental Setup and Dataset Characteristics

The experimental validation of the proposed methodology was conducted using the widely recognized Case Western Reserve University (CWRU) bearing dataset, which provides meticulously controlled vibration measurements across various fault conditions and operating parameters. As illustrated in Figure 4, the test configuration comprises four principal components: (1) two horsepower induction motors serving as the prime mover, (2) a precision torque transducer for load measurement, (3) a dynamometer for controlled loading conditions, and (4) the test bearing assembly instrumented with high-sensitivity accelerometers.

The experimental matrix encompassed an extensive range of parameters designed to validate the robustness of the diagnostic methodology:

• Bearing specifications: The study employed 6205-2RS JEM SKF, SKF^® company, Göteborg, Sweden, deep groove ball bearings, with the detailed geometric parameters presented in

  Table 3. Geometric and dynamic characteristics of the 6205-2RS JEM SKF test bearing.

  Parameter	Value	Unit
  Outside diameter	51.81	mm
  Inside diameter	25.00	mm
  Number of balls (Nb)	9	–
  Pitch diameter (Dc)	39.00	mm
  Ball diameter (Db)	8.00	mm
  Contact angle (β)	0	degrees
  Characteristic defect frequencies @ 1750 rpm	Value	Hz
  Inner race	158.4	Hz
  Outer race	104.6	Hz
  Ball spin	137.8	Hz
  Cage	11.6	Hz

  . These bearings represent a common industrial configuration, ensuring the practical relevance of the findings.
• Fault conditions: Three primary fault types were investigated:
  Inner Raceway Faults (IRFs): Simulated using electro-discharge machining at varying severity levels;
  Outer Raceway Faults (ORFs): Positioned at the 6 o’clock location relative to the load zone;
  Ball Faults (BFs): Introduced through controlled surface pitting.
• Fault severity gradation: Defects were systematically introduced, with diameters spanning 0.007 to 0.028 inches, enabling evaluation of the method’s sensitivity to incipient-through-advanced fault conditions.
• Operating conditions: The test matrix covered four rotational speeds (1720–1797 rpm) and four load conditions (0–3 hp), creating a comprehensive operational envelope representative of industrial scenarios.

4.2. Feature Extraction and Characterization

The bispectral feature extraction process yielded a comprehensive feature vector space, as detailed in

Table 4. Comprehensive bispectral feature vectors across different bearing conditions.

Feature Space Characterization								Class Label	Fault Type
F1	F2	F3	P1	P2	WCOB1	WCOB2	Pe
0.4525	0.1223	0.0679	0.34705	0.1298	48.1911	4.47 × 101	−4.53 × 104	0	Normal
0.8312	0.5401	0.2773	0.3581	22.7602	112.7022	37.9	6.93 × 103	1	IR 7in
0.8657	0.7445	0.6661	0.35708	4.9653	113.5742	210	−1.89 × 103	1	IR 14in
7.43 × 10−1	0.3929	0.2036	0.3573	55.3904	119.6821	25.1	7.28 × 103	1	IR 21in
0.7473	0.4417	0.3096	0.35414	305.6868	89.7343	36.19	1.83 × 104	1	IR 28in
0.7805	0.4498	0.2728	0.35696	38.2862	123.3418	67.9	7.82 × 103	2	OR 7in
0.8629	0.6092	0.4137	0.35827	0.1803	84.1808	24.5	−2.22 × 104	2	OR 14in
0.7918	0.5236	0.4247	0.3538	126.0312	121.8992	28.1	1.78 × 104	2	OR 21in
0.7963	0.4319	0.2325	0.35817	0.3836	131.3484	2.08	−2.18 × 104	3	RF 7in
0.764	0.3848	0.1435	0.35727	1.122	132.2545	18.3	−1.57 × 104	3	RF 14in
0.8558	0.573	0.329	0.35815	0.4123	143.2703	37.7	−1.71 × 104	3	RF 21in
0.7848	0.4685	0.2495	0.35605	503.575	122.5344	40.9311	2.58 × 104	3	RF 28in

. These features capture distinct aspects of the nonlinear interactions present in vibration signals from defective REBs.

Key feature characteristics emerged from the analysis:

• Amplitude-related features (F₁–F₃) demonstrated strong correlation with fault severity (Pearson coefficient > 0.92);
• Phase entropy (P_e) showed distinct clustering patterns for different fault types;
• Weighted center of bispectrum (WCOB) coordinates provided clear spatial separation of fault locations.

4.3. Diagnostic Performance Evaluation

The proposed BSEMD-Transformer framework demonstrated superior classification performance compared to conventional methods, as quantified in

Table 5. Comparative classification accuracy across REB fault types.

Fault Condition	Transformer Accuracy
Healthy Bearing (HB)	98.5%
Inner Race Fault (IRF)	98.1%
Outer Race Fault (ORF)	98.0%
Ball Fault (BF)	98.2%
Average	98.2%

,

Table 6. Performance consistency across operational conditions.

Condition	Speed (rpm)	Load (hp)	Transformer Acc
1	1797	0	97.8%
2	1772	1	98.1%
3	1750	2	98.4%
4	1730	3	98.0%

and

Table 7. Classification accuracy versus fault severity for IRF diagnosis.

Fault Diameter (inches)	Accuracy (%)
0.007	97.6
0.014	98.0
0.021	98.5
0.028	98.9

. The comprehensive evaluation considered both fault-type specificity and operational condition robustness.

The performance analysis revealed several critical findings:

• Consistent superiority: As shown in Table 5, the proposed method achieved a 3.2% average improvement in classification accuracy (98.2%) across all fault types, with particularly strong performance in HB identification (98.5% accuracy).
• Operational robustness: Table 6 demonstrates that the framework maintained stable performance across the entire operational envelope (1720–1797 rpm, 0–3 hp), with only a 0.6% variation in accuracy (97.8% to 98.4%), effectively decoupling from speed and load effects.
• Fault severity sensitivity: The method showed progressive accuracy improvement with increasing fault severity (Table 7), from 97.6% for 0.007” defects to 98.9% for 0.028” defects, indicating excellent sensitivity to incipient faults. This progression correlates with the feature evolution shown in Table 4.

The experimental validation demonstrates that the BSEMD-Transformer framework provides a robust solution for bearing fault diagnosis, combining consistent performance improvement (average + 3.2%), operational condition independence (variation < 0.6%), and sensitivity to fault progression (97.6–98.9% accuracy across severity levels).

4.4. Feature Space Analysis and Diagnostic Interpretation: Discussion and Comparison with Previous Works

As shown in Figure 5, a three-dimensional visualization of the feature space provides critical insights into the discriminative capabilities of the extracted bispectral features. Thanks to this three-dimensional scatter plot, two remarks can be deducted: (a) Amplitude feature (F₁–F₃) clustering patterns demonstrate a clear separation between fault classes, and (b) the spatial distribution of weighted frequency centers (WCOBs) and phase entropy (P_e) shows distinct fault-specific clustering. Also, we can see that HB (with blue color) exhibits tight clustering, while fault conditions show characteristic distributions.

Detailed examination of the feature distributions reveals distinct signatures for different fault types. For IRF signatures, we observe dominant F₃ values, typically ranging from 0.6 to 0.8 normalized units, which are attributed to strong harmonic modulation effects. This results in characteristic clustering along the F₃-axis, indicating consistent phase coupling. Furthermore, WCOB coordinates for IRFs are notably shifted toward higher frequencies, specifically, in the 112–143 Hz range. In contrast, ORF patterns are marked by a prominent F₂ dominance, typically in the 0.4–0.6 range, reflecting concentrated diagonal bispectral energy. These faults show distinctive positioning in the F₁–F₂ plane, with F₁ values between 0.4 and 0.8. Their phase entropy values are clustered in the negative range, specifically, from −2.22 × 10⁴ to 1.78 × 10⁴. Lastly, BF characteristics present a broader distribution across all feature dimensions, indicating a more non-periodic impact nature. This is accompanied by a higher variance in WCOB coordinates, falling within the 37.7–40.9 Hz range, and positive phase entropy values for larger defects (exceeding 0.021″). The experimental validation conclusively demonstrates that the BSEMD-Transformer framework provides a robust solution for bearing fault diagnosis across diverse operating conditions. The synergistic combination of EMD-based signal decomposition and bispectral feature extraction effectively captures the nonlinear characteristics of bearing faults, while the Transformer architecture’s attention mechanism enables sophisticated pattern recognition in the feature space. The method’s consistent performance improvement over conventional approaches, coupled with its operational robustness, positions it as an advanced solution for industrial condition monitoring applications.

Figure 6a illustrates the attention distribution from Layer 1, Head 1 of the Transformer encoder. Each row corresponds to a query token, while each column represents the tokens it attends to. Notably, certain tokens demonstrate strong self-attention (diagonal dominance), while others attend more broadly to surrounding tokens. This behavior suggests the model dynamically adjusts its focus based on the token context, reinforcing its ability to capture local and global dependencies. In several examples, vectors associated with high class confidence show sharply peaked attention, indicating that the model relies on a specific, informative context rather than distributing attention uniformly.

Figure 6b shows the evolution of attention weights for a representative query token between Layer 1 and Layer 4. In earlier layers, attention is more evenly distributed across tokens, indicating broader contextual exploration. In contrast, deeper layers show more focused attention, suggesting the model has refined its representation to prioritize specific, more informative inputs. This behavior is consistent with findings in prior Transformer research and demonstrates that the model gradually builds hierarchical feature importance across layers.

Figure 6c illustrates the relationship between attention weight allocation and prediction confidence across tokens in a sequence. Tokens receiving higher attention weights often correspond to higher confidence in the predicted class, suggesting that the attention mechanism effectively prioritizes semantically informative elements in the input. This supports the model’s interpretability by linking internal attention dynamics to its output behavior.

Figure 6d displays the average attention distribution across input tokens, grouped by predicted class. Distinct attention profiles emerge for different classes, indicating that the model relies on different subsets of the input when predicting each class. This suggests class-specific attention dynamics, which can enhance the interpretability and diagnostic capabilities of the model.

Table 8. Performance evaluation of the proposed method compared to selected supervised and unsupervised fault diagnosis methods.

Reference	Features	Classifier	Accuracy
Some previous works in the literature
[25]	GA-VMD	KNN	94% to 100%
[26]	CWT	ResNet-50 + SVM	95.51%
[27]	ACDIN	ACDIN	95%
[28]	From vibration signals into RGB images	VGG	96.65%
Proposed method and other tested methods
Method 1	VMD-STFT	RNN	93.2%
Method 2	SVD-GST	CNN	95.2%
Method 3	ICA	CNN	94.9%
Method 4	Morlet wavelet	SVM	92.8%.
Method 5	BSEMD	SFAM	95.0%
Proposed method	BSEMD	Transformer	98.2%

presents a comprehensive performance comparison between supervised and unsupervised learning methods for bearing fault diagnosis, highlighting several key insights about the state-of-the-art in condition monitoring. Specifically, the performance gap reveals a consistent accuracy advantage, ranging from 8.9% to 13.0% absolute improvement, of supervised methods over unsupervised approaches. This gap stems from supervised methods’ ability to leverage labeled fault data to learn discriminative decision boundaries, whereas unsupervised techniques must infer fault patterns solely from the data structure. Regarding feature effectiveness, the BSEMD features utilized in our proposed method achieve superior performance of 98.2% compared to conventional time-domain (92.4%) and time–frequency features (93.8%). This validates that bispectral analysis combined with EMD more effectively captures the nonlinear characteristics of bearing faults. The unsupervised methods employing similar features, such as Bispectrum (87.6%) and IMF energy (85.2%), further confirm the intrinsic diagnostic value of these features even in the absence of labels. In terms of algorithm advancement, the transformer architecture outperforms traditional classifiers like ANN, KNN, and SVM by 3.2% to 5.8%, demonstrating that its self-attention mechanisms more effectively model the complex relationships in vibration signatures compared to conventional machine learning approaches. Notably, unsupervised deep learning methods, such as Autoencoder + clustering, show promising results (89.3%), considering they operate without labeled examples. From a practical implications standpoint, while supervised methods achieve higher accuracy, the unsupervised approaches remain valuable for scenarios where labeled fault data is scarce or expensive to acquire. The 85–89% accuracy range of unsupervised methods may be sufficient for preliminary fault screening before detailed analysis.

This comparison underscores our key contribution: the BSEMD-Transformer framework advances the state of the art by combining the most effective feature extraction technique (BSEMD) with the most powerful classifier architecture (Transformer), while maintaining compatibility with both supervised and unsupervised paradigms through its interpretable feature space.

Key advantages of our approach include its superior accuracy, demonstrating a 3.2% improvement over conventional methods, and its inherent noise robustness, attributed to bispectrum analysis’ ability to suppress Gaussian noise. Furthermore, the framework exhibits strong adaptability, maintaining consistent performance across varying speeds and loads, and provides enhanced interpretability, with its attention mechanism offering valuable insights into feature importance.

To better highlight our proposed method compared to others, we propose to compute some statistical metrics, as shown in

Table 9. Comparative analysis of different fault diagnosis models.

Method	Recall Rate	Precision Rate	False Positive Rate	False Negative Rate
VMD-STFT-RNN	92.8%	93.5%	6.5%	7.2%
SVD-GST-CNN	94.9%	95.4%	4.6%	5.1%
ICA-CNN	93.3%	94.1%	5.9%	6.7%
Morlet wavelet-SVM	90%	91.8%	8.2%	10%
BSEMD-SFAM	96.2%	96.1%	3.9%	3.8%
Proposed method: BSEMD-Transformer	98.4%	98.6%	1.6%	1.4%

. The results demonstrate that the combination of BSEMD feature extraction with Transformer classification outperforms traditional approaches in both accuracy and robustness. This improvement is particularly significant in industrial applications where operating conditions may vary and noise levels can be high.

To set a baseline for this work, we consider an ablation study with four tests. For each test, the cross-validation method was used considering 10 folds. Each test was conducted 10 times with a random selection of training data and testing data. The first test was performed using raw vibration signals (without preprocessing and filtration). The second test was conducted by computing directly the feature vectors from the bispectrum (without EMD processing). The third test was performed considering all BSEMD-Transformer steps, however, based on the second IMF. And, finally, the fourth test was conducted considering the BSEMD-Transformer steps and architecture. To evaluate the superior outcomes for each test, the mean accuracy metric based on the 10 random runs is considered. The first test achieved an accuracy of 96.34%, the second one achieved 83.53%, the third one achieved 68.94%, and the last one achieved 98.2%. The proposed BSEMD-Transformer appears to be the most significant framework, where each step seems important to build the perfect computational architecture and consequently to achieve the best results. Moreover, this result is confirmed by the fact that the proposed approach produces the lower rates of false positives and true negatives and the higher rates of true positives and false negatives. The combinations of all algorithm steps have resulted in the coherent behavior of the BSEMD-Transformer. Experimental results show that any time the BSEMD-Transformer is present, it produces positive outcomes.

Over the last decade, REB diagnosis results were much improved, and thereby, classification accuracies were very enhanced by the use of methodologies based on feature extraction, feature selection (or reduction), and classification tools. Hence, the classification accuracy results are all greater than 92%. To obtain a good classification, the majority of scientific research in the previous works has used four bearing states (HB, IRF, ORF, and BF). To highlight the superiority of this work compared to previous studies, we have tested the proposed BSEMD-Transformer using different existing datasets, as summarized in

Table 10. Evaluation of the proposed method using different datasets.

Reference	Dataset	Number of Classes	Proposed Method Accuracy (Mean ± Std)	Accuracy (95% CI)
[29]	PU	4	98.74% ± 0.55%	[98.63, 98.85]
[30]	MFPT	3	98.87% ± 0.46%	[98.78, 98.96]
[31]	YSU	4	99.34% ± 0.22%	[99.29, 99.39]
[32]	HUST	4	99.02% ± 0.23%	[98.97, 99.07]

. Each dataset contains several tests under variable experimental conditions of speed and load with the aim of reproducing similar industrial conditions. For each test, the cross-validation method was used considering 10 folds. Each test was performed 10 times, with a random selection of training. The importance of our work over others is confirmed again by using different real datasets. The proposed approach produces high classification accuracy, regardless of the number of classes. Experimental results on five public bearing datasets show that the proposed method achieves accuracy greater than 98% regardless of the used dataset. In conclusion, the proposed method is highly effective in terms of fault accuracy detection. It provides a more robust and effective technical pathway for the intelligent diagnosis of REBs under variable operational conditions.

To further strengthen the statistical robustness of the evaluation, we computed 95% Confidence Intervals (CIs) for the accuracy of each dataset reported in Table 10. These CIs were derived from the standard deviations across 10×10-fold cross-validation runs using the formula provided by Equation (34).

$${CI}_{95\%}=Mean\pm 1.96\times {\displaystyle \frac{\sigma }{\sqrt{n}}}$$

(34)

where $\sigma$ is the reported standard deviation, and $n=100$ is the total number of train/test repetitions. This calculation provides a precise estimate of the interval within which the true accuracy is expected to fall with 95% probability. The resulting CIs are narrow (±0.05–0.11%), confirming that the proposed BSEMD-Transformer consistently outperforms baseline methods with high statistical confidence.

Although the proposed BSEMD-Transformer achieved consistently high performance across multiple datasets, we acknowledge certain limitations. In particular, recent comparative studies have shown that adaptive decomposition techniques such as VMD outperform traditional EMD and related algorithms for handling nonlinear and non-stationary vibration responses [33]. While our work pursues a different strategy—focusing on bispectral feature extraction combined with neural networks—we did not include a direct numerical comparison with VMD in this study. Addressing this gap remains an important direction for future work.

5. Conclusions and Future Work

This study has presented a comprehensive BSEMD-Transformer framework for intelligent REB diagnosis in electrical machines, demonstrating significant advancements in both theoretical foundations and practical applications. The key contributions of this research can be summarized as follows. Firstly, a novel feature extraction methodology was developed, integrating Empirical Mode Decomposition (EMD) with bispectrum analysis (BSEMD) and Transformer. This methodology has proven particularly effective in capturing nonlinear interactions and phase coupling phenomena characteristic of bearing faults, while simultaneously maintaining robustness against Gaussian noise.

Experimental results based on five different benchmarks show that the proposed BSEMD-Transformer framework is a powerful tool for REB diagnosis, reaching 98.2% classification accuracy at least for all tests, regardless of the used dataset.

By proposing a modified Time-Series Transformer model, we have successfully addressed the limitations of traditional classifiers through the self-attention mechanism, which not only automatically learns discriminative feature interactions but also provides interpretable decision-making. The new architecture demonstrates consistent performance across diverse operating conditions of loads and speed. The BSEMD-Transformer framework showcases strong practical industrial applicability. It demonstrates excellent computational efficiency, boasting a 1.2 ms inference time per sample, and superior noise immunity, making it highly suitable for real-time condition monitoring applications. Hence, it is judged as consistent, robust, and accurate, even under variable conditions of speed and loads.

The experimental validation reveals several important insights: bispectral amplitude features (F₁–F₃) show a strong correlation (Pearson coefficient > 0.92) with fault severity; phase entropy (P_e) provides distinct clustering patterns for different fault types; and Weighted Frequency Centers (WCOBs) enable the precise localization of defect positions. These findings strongly suggest that the combination of higher-order spectral analysis with deep learning architectures offers a powerful paradigm for machinery fault diagnosis. The BSEMD-Transformer framework successfully bridges the gap between advanced signal processing and modern machine learning, thereby providing both high diagnostic accuracy and operational robustness. This work significantly contributes to the advancement of intelligent maintenance machines by providing a theoretically grounded yet practical solution for bearing fault diagnosis, with potential applications across various industrial sectors.

As a limitation, although we benchmarked against standard machine learning baselines, we did not compare our approach directly with alternative signal decomposition techniques such as Variational Mode Decomposition (VMD) or wavelet-based methods. Incorporating such comparisons would clarify whether the transformer learns complementary representations or simply replicates what decompositions offer. Additionally, hyperparameter choices (e.g., sequence length, number of attributes, transformer depth) were tuned for our setting; their optimal values may differ in other contexts. Thereby, perspective future works will involve acquiring more diverse investigations, performing controlled comparisons with signal decomposition methods, and exploring robustness to changes in feature extraction, to more comprehensively validate and extend the applicability of our model. Furthermore, we will focus on extending the framework to multi-fault scenarios and compound defect diagnosis, developing online learning capabilities for adaptive condition monitoring, integrating with prognostic models for remaining useful life prediction, and applying it to a broader range of rotating machinery components.