1. Introduction
With the continuous advancement of intelligent manufacturing and Industry 4.0 [
1,
2,
3], rotating machinery plays a vital role in aerospace, rail transit, and high-end equipment, and its running state is directly related to the safety and stability of the system. Once any potential failure occurs, it can cause serious consequences. Therefore, intelligent fault diagnosis has gradually become one of the core research directions of equipment health management (PHM, Prognostics and Health Management) [
4,
5]. Recent progress in intelligent fault diagnosis has explored directions beyond conventional domain generalization. For instance, some studies have addressed open-set and unknown fault recognition, such as adaptive evolutionary reconstruction metric networks that can generalize to previously unseen fault types [
6]. Others have proposed multi-source adversarial transfer frameworks that improve anti-noise performance under cross-domain conditions, especially in complex urban environments [
7], including the following: virtual domain-driven semi-supervised hyperbolic metric networks with domain-class adversarial decoupling, which achieve robustness and discriminability through non-Euclidean embeddings [
8]; and continuous evolution learning frameworks, which leverage lightweight module expansion and knowledge distillation for train transmission fault diagnosis [
9]. In the past few years, deep learning has shown remarkable advantages in fault diagnosis tasks with its excellent feature extraction and pattern recognition capabilities [
10]. However, it is worth noting that such methods are often based on the premise that data distribution of the source domain and the test domain is consistent. Once the actual working conditions change, such as different loads [
11], rotational speed fluctuations [
12], or sensor installation positions shift [
13], the model performance tends to decrease significantly. This phenomenon is often referred to as distribution shift [
14].
In order to alleviate the problem of distribution shift, Weiss et al. [
15] proposed transfer learning and Yu et al. [
16] proposed ideas such as domain adaptation (DA). Although the DA method has achieved some results, it often assumes that some target domain data can be obtained during the training stage. However, in real industrial scenarios, this premise does not always hold true. In contrast, the domain generalization (DG) method proposed by Khoee et al. [
17] does not rely on any target domain information, but trains a model with cross-domain robustness through multiple source domain samples so that it can maintain stable performance in unknown target domains. This is more in line with the actual needs in industrial applications, and also makes DG a research hotspot in the field of intelligent fault diagnosis and machine learning in recent years [
18].
The existing DG methods can be roughly divided into three categories. The first category is data enhancement methods. Zhang et al. [
19] used the Mixup method to improve the diversity and robustness of data through sample interpolation or adversarial generation. The second category is invariant representation and robust optimization methods. Arjovsky et al. [
20] proposed the IRM method and Sagawa et al. [
21] proposed the GroupDRO method. These methods try to learn cross-domain-invariant features or improve generalization by minimizing the risk of the worst domain. The third category is meta-learning methods. Li et al. [
22] proposed the MLDG method and Shi et al. [
23] proposed the Fish method. These methods make the model consistent in the update direction by simulating the “training/testing” domain partition, thereby improving cross-domain adaptability. Although these methods have improved the performance of DG to some extent, there are still limitations: data enhancement class methods often lack explicit modeling of inter-domain differences; the invariant representation class method is difficult to optimize and highly sensitive to hyperparameters; and meta-learning methods often ignore the alignment of feature distribution level. Therefore, how to form organic synergy at the three levels of data enhancement, optimization consistency, and representation invariance is still an urgent problem to be solved in this field.
Based on this, this paper proposes a meta-learning domain generalization method for fault diagnosis. This method attempts to achieve complementarity and integration at three levels: data, optimization, and representation. Specifically, at the data level, we introduce Mixup in the task construction stage to generate interpolated samples and smooth decision boundaries, thereby enhancing the robustness of the model to distribution perturbations. At the optimization level, we design an equidifference arithmetic gradient alignment strategy to constrain the update direction of different source domains to be consistent and reduce cross-domain optimization conflicts. At the representation level, the features of similar samples can be aggregated to the shared centroid across domains through centroid convergence constraints to strengthen semantic consistency and domain invariance.
The main contributions of this paper can be summarized as follows:
A meta-learning domain generalization framework (MGADA) integrating multi-level constraints is proposed, which improves the adaptability of the model in the unseen target domain through the “meta-training/meta-testing” mechanism, and effectively deals with the distribution difference problem in cross-working condition fault diagnosis.
Design a collaborative mechanism at three levels: data, optimization, and representation. This includes introduce Mixup data into the inner loop to enhance and alleviate small-sample overfitting; combining equal-difference arithmetic gradient alignment in the outer loop to ensure cross-domain optimization consistency; and realizing cross-domain feature alignment and intra-class aggregation by using centroid convergence constraints.
Achieve excellent performance in cross-working condition bearing fault diagnosis tasks: The average accuracy rate on CWRU dataset is 98.89%, which is significantly better than benchmark methods such as ERM, Mixup, Fish, IRM, GroupDRO and MLDG; the ablation experiment and visualization results further verify the effectiveness and complementarity of each module.
3. Method
In practical engineering applications, bearing fault diagnosis often faces the dual challenges of limited sample data and cross-condition distribution discrepancies. In
Figure 1 within the meta-learning framework, this study partitions source domain data into a support set and a query set, and introduces Mixup-based data augmentation in the inner loop. By performing sample interpolation within the support set, mixed samples are generated to artificially expand the data space. This design effectively alleviates overfitting under small-sample conditions, while simultaneously enhancing intra-task data diversity and smoothing decision boundaries.
Building on this, to address the shortcomings of traditional meta-learning in terms of optimization path exploration and convergence point selection, the study further propose an arithmetic meta-learning strategy. This strategy combines gradient alignment theory with the concept of arithmetic averaging: in the outer loop, it constrains gradient direction consistency across different source domains, while in the feature space, it introduces a centroid convergence mechanism to drive same-class samples from different domains toward a shared centroid. These mechanisms collectively enhance the model’s generalization capability to unseen target domains.
Given a collection of multiple source domains , the target domain is (invisible during training for validation only). The samples on each domain are from the distribution , and the category set is consistent.
The feature extraction network is denoted as
, and the classification head is denoted as
. The overall model is Equation (2).
The core goal of this study is to meta-learn parameters on multiple source domains, so that it also has good generalization ability on out-of-domain distributions .
3.1. Meta-Learning Framework
A task samples several domain indexes from several source domains . For each domain , it randomly divides the support set and the query set .
Inner loop (support) computes the support set supervised loss
(cross-entropy) for each domain
on the current shared parameters
Equation (3).
Do one or more gradient descent with the learning rate
to obtain the domain adaptive inner loop parameters Equation (4).
Outer loop (query) evaluates and aggregates the updated
query set over each domain Equation (5).
The outer loop uses the learning rate
to update the original shared parameters
(the gradient is propagated through the inner loop update, or the second-order term is ignored in the first-order approximation) Equation (6).
3.2. Intra-Domain Implementation of Mixup Data Augmentation
Within the mini-batch of each domain, sample pairs
are sampled
and constructed as follows:
will replace or mix with the original sample and jointly participate in the calculation of
and
. The corresponding Mixup cross-entropy is shown in Equation (8):
3.3. Arithmetic Difference Strategy
The arithmetic strategy aims to let the model parameters converge to a central point equidistant from the optimal solution in each source domain. The strategy combines the theory of gradient alignment and arithmetic to design a comprehensive objective function. This objective function should not only consider the gradient alignment between different source domains, but also promote the convergence of the model to a position close to the centroid of the optimal solution in each source domain.
3.3.1. Gradient Alignment
If the task gradient directions/magnitudes of different source domains are close to each other, then the “synthetic gradient” used to update the shared parameters will be more robust and invariant to the out-of-domain distribution. For each domain
, we define its task gradient
(which can be measured on the support or query) Equation (9).
Denote the average gradient
of the domain as Equation (10).
To address the limitation of traditional meta-learning strategies that may produce inconsistent or noisy gradient directions across domains, we propose a novel Arithmetic Gradient Alignment strategy. Instead of aligning raw gradients from different domains directly (as in Fish or MLDG), we introduce a structured arithmetic formulation that promotes consistency among gradients through minimizing their arithmetic differences. The idea of arithmetic alignment is to minimize the gradient deviation by making each task gradient
as close as possible to the arithmetic mean gradient
Equation (11).
This objective is equivalent to minimizing the variance of gradients between all pairs of domains (the classical identity) Equation (12).
3.3.2. Centroid Convergence
In the feature space, the in-domain class centroids are computed for each domain
and each class
Equation (13).
where
denotes the set of support samples labeled as
.
The “global prototype” shared across domains is defined as the arithmetic average of the centroids of the domains Equation (14).
The centroid convergence loss encourages homogeneous prototypes to align across different domains Equation (15).
This constraint encourages samples from the same class but different domains to cluster in feature space, thereby improving the domain-invariant semantic representation. Compared to existing domain alignment methods, our centroid-level constraint operates at the semantic prototype level, rather than aligning global domain statistics (e.g., in CORAL or MMD).
There is also a pairwise equivalent form (measuring cross-domain intra-class compactness) Equation (16).
Combining outer loop supervision, Mixup, gradient alignment, and centroid convergence, the outer loop objectives of a single task are as follows:
where
is the cross-entropy term generated by Mixup samples on the inner and outer loops.
,
, and
are the weight coefficients.
In real-world industrial scenarios, fault diagnosis models often encounter unseen target machines and limited labeled data. To address this, MGADA leverages meta-learning, which simulates domain shifts across multiple source domains during training, thereby improving few-shot generalization to unseen machines.
Additionally, Mixup augmentation increases the task diversity within each meta-task episode, while centroid convergence ensures semantic consistency even with limited samples. These components collectively help MGADA to achieve cross-machine generalization under small-sample conditions.
Unlike traditional methods that rely heavily on abundant labeled data, our approach focuses on task-based meta-optimization, which enables the model to rapidly adapt to new fault conditions with only a few labeled examples from new machines.
In summary, the MGADA framework integrates Mixup-based intra-domain augmentation, a novel arithmetic gradient alignment strategy for inter-domain consistency, and a semantic centroid convergence constraint for class-level alignment. These components are designed to jointly enhance the model’s generalization to unseen domains.
4. Experimental Evaluation
The CWRU bearing public dataset of Western Reserve University is used for validation in this experiment to evaluate the generalization ability of our proposed method. This study is comprehensively compared with other benchmark methods, and the results show that our MMAC performs consistently in all evaluations and achieves advanced results on the adopted datasets. The study also discuss the effectiveness of each component in this study. The experimental details are described below.
4.1. Benchmark Method
ERM: Empirical risk minimization (ERM) is the most basic learning paradigm. The model is trained directly on the overall distribution of all source domain samples by minimizing the empirical risk to learn the parameters.
Mixup: Mixup builds on ERM by introducing linear interpolation-based sample augmentation.
Fish: Fish enhances generalization through meta-learning-style gradient alignment. It simulates the process of “adapting on one source domain and generalizing on another,” with the core idea of aligning gradient directions across source domains to learn parameters that are stable across domains.
IRM: Invariant Risk Minimization (IRM) learns an invariant feature representation across multiple environments (domains) and requires that the same classifier is optimal on all source domains using this representation.
GroupDRO: Group Distributionally Robust Optimization (GroupDRO) assumes that each source domain is a “group distribution,” and the optimization objective is to minimize the worst-case domain risk. Implementation typically involves adaptive reweighting to improve performance on weaker domains.
MLDG: Meta-Learning for Domain Generalization (MLDG) draws inspiration from MAML, dividing source domains into “meta-train” and “meta-test” subsets. The model first updates on meta-train, then computes the loss on meta-test and backpropagates it to the original parameters. By explicitly simulating the cross-domain transfer process, it improves generalization to the target domain.
The above baseline methods can be broadly categorized into three classes. Data augmentation methods (e.g., ERM, Mixup) rely on sample generation and interpolation to enhance data diversity and model robustness but lack explicit modeling of inter-domain differences. Meta-learning methods (e.g., Fish, MLDG) explicitly improve generalization by simulating the “cross-domain training/testing” process, where Fish emphasizes gradient direction consistency and MLDG adopts the MAML approach for cross-domain optimization. The third class includes invariance or robust optimization methods (e.g., IRM, GroupDRO): the former enforces learning of domain-invariant features, while the latter minimizes worst-case domain risk to improve performance on weaker domains.
Although these methods tackle the DG problem from different perspectives—data augmentation, optimization robustness, feature invariance, and learning paradigms—they each present limitations. To address this, the study proposes a method that integrates meta-learning, Mixup, arithmetic gradient alignment, and centroid convergence. By collaboratively modeling across the data, optimization, and representation levels, the method not only alleviates overfitting in source domains, but also reduces cross-domain gradient conflicts and strengthens feature distribution alignment, thereby significantly improving diagnostic generalization under complex working conditions.
4.2. Experimental Dataset
The CWRU bearing dataset is provided by the Case Western Reserve University Bearing Data Center.
Figure 2 shows a bearing test platform similar to the bearing test platform of Case Western Reserve University. The bearing states include the following: Normal (Nor), Inner Race Fault (IRF), Outer Race Fault (ORF), and Ball Fault (BF). Each type of fault has three severity levels, with fault diameters of 0.1778 mm, 0.3556 mm, and 0.5334 mm, respectively. Four operating loads (Horsepower, HP) are considered: 0HP, 1HP, 2HP, and 3HP. Each fault type is tested under four load levels: 0HP, 1HP, 2HP, and 3HP, corresponding to torque levels of approximately 0, 1.47, 2.94 and 4.41 N·m, respectively. The vibration data collected under each load is treated as an independent source domain, while one of them (e.g., 2HP) is excluded during training and used as the target domain to evaluate out-of-distribution generalization. In this study, the study selects the drive-end bearing signals sampled at 12 kHz for analysis. Considering the bearing states and different fault locations with three different fault diameters, a total of 10 health conditions are defined. For each health condition, 200 samples are selected, and each sample consists of 512 data points.
4.2.1. Experimental Output Definition
The output of the experiment is the predicted fault class of each bearing signal sample, corresponding to one of the ten predefined categories: normal, and nine specific faults (three fault types × three severities). The model is evaluated in terms of multi-class classification accuracy on the unseen target domain.
4.2.2. Bearing Specification
The bearings used in the experiment are 6205-2RS deep groove ball bearings, manufactured by SKF. The fault conditions (ball, inner race, and outer race defects) were seeded using electro-discharge machining (EDM) with fault diameters of 0.007″, 0.014″, and 0.021″, following the standard CWRU bearing test setup.
The data preprocessing process of this study takes “fixed-length time-domain segmentation with random starting point + dBization of standard STFT power spectrum + derivation of rasterized color spectrum” as the core, and stably converts the CWRU time-domain vibration signal into a unified style of time–frequency image dataset, which is convenient for the training and evaluation of downstream deep learning models.
4.3. Experimental Setup
The CWRU dataset is divided into four domains according to the load of different operating conditions: 0HP, 1HP, 2HP, and 3HP. Each domain contains 10 label classes corresponding to different fault types and severities. The numbers “7”, “14”, and “21” represent the fault diameters of 0.007 inch, 0.014 inch, and 0.021 inch, respectively, indicating increasing severity levels (slight, moderate, and severe). Specifically, “BF”, “IRF”, and “ORF” denote Ball Fault, Inner Race Fault, and Outer Race Fault, while “Nor” represents the normal condition.
Therefore, the 10 label classes are organized as follows:
0: 7BF (0.007″ Ball Fault)
1: 7IRF (0.007″ Inner Race Fault)
2: 7ORF (0.007″ Outer Race Fault)
3: 14BF (0.014″ Ball Fault)
4: 14IRF (0.014″ Inner Race Fault)
5: 14ORF (0.014″ Outer Race Fault)
6: 21BF (0.021″ Ball Fault)
7: 21IRF (0.021″ Inner Race Fault)
8: 21ORF (0.021″ Outer Race Fault)
9: Nor (Normal)
Hence, there is a direct relation between “classes of labels” and “severity levels”. Each fault type (ball, inner race, outer race) includes three severity levels, and all together they form nine fault classes plus one normal class. In the experiment, the cross-domain generalization evaluation method is adopted, that is, one load condition is fixed as the target domain (not participating in the training), and the other multiple load conditions are trained as the source domain. In terms of model structure, this study uses the residual network ResNet-18 as the backbone network for feature extraction. The input layer is 3 × 224 × 224, the output feature dimension is 256, and then the 256-dimensional features are mapped to the 10-class label space by the classification head. On this basis, Mixup data enhancement, meta-learning inner and outer loop update, gradient alignment and centroid convergence regularization are introduced to realize cross-domain generalization training.
Initialization of training parameters: Random seed: 2025 (fixed randomness to ensure reproducibility of the experiment); Optimizer: SGD, momentum 0.9; Learning rate: The initial value was set to 0.001, and the cosine annealing scheduling was used to dynamically adjust the learning rate. Weight decay: 0.0001; Batch size: 64; Training rounds: 600; Inner and outer loop learning rate:
(inner loop),
(outer loop). Loss function weight parameter setting
,
. For Mixup augmentation, the interpolation coefficient
λ is sampled from a Beta(
α,
α) distribution with
α = 0.2, following [
19].
4.4. Effectiveness Analysis
The study discusses the performance of our proposed method and baseline methods in terms of classification accuracy. To further validate the intra-class clustering effect and specific classification behavior of the proposed method, the study visualizes its results on different target domains using t-SNE [
37] and presents the corresponding confusion matrices [
38]. For a more comprehensive comparison, the study independently implemented MLDG, ERM, Mixup, Fish, IRM, and GroupDRO, as the authors only provided demonstration code. All implementations were evaluated on datasets and network architectures that were not reported in the original works. The results of these methods are presented in
Table 1.
As shown in
Table 1, the performance of different methods under cross-condition testing on the CWRU dataset varies significantly. ERM, as the most basic empirical risk minimization approach, achieves an overall accuracy of 98.14%, indicating that deep models still possess a certain degree of cross-domain generalization capability when data is sufficient. Based on this, Mixup enhances data diversity through sample interpolation, increasing the average accuracy to 98.01% and showing superior performance on some tasks. However, due to the lack of explicit inter-domain consistency modeling, its overall advantage is limited.
Meta-learning methods exhibit larger performance differences. Fish achieves nearly 100% accuracy on the “0, 2, 3 → 1” and “0, 1, 3 → 2” tasks, demonstrating the value of aligned optimization directions. In contrast, MLDG performs unstably on certain tasks (e.g., only 79.30% on “0, 2, 3 → 1”), indicating insufficient adaptability under complex operating conditions. Among invariant representation and robust optimization methods, IRM almost fails (average accuracy of only 16.61%), whereas GroupDRO is relatively stable (98.15%) but still inferior to ERM and Mixup, revealing the limitations of worst-case domain optimization strategies.
In comparison, the proposed MGADA consistently achieves the best or near-best performance across all tasks, with an average accuracy of 98.86%, significantly outperforming all baseline methods. In particular, it reaches 99.75% and 99.90% on the “0, 1, 2 → 3” and “0, 1, 3 → 2” tasks, respectively. Its superiority arises from three synergistic components: Mixup enhances sample diversity and smooths the decision boundary; arithmetic gradient alignment ensures consistent cross-domain update directions, mitigating optimization conflicts; and centroid convergence constraints promote clustering of same-class samples across domains, strengthening semantic consistency and domain invariance. Overall, MGADA effectively combines data augmentation, optimization consistency, and feature alignment, demonstrating stronger robustness and stability in cross-condition diagnostic tasks.
In
Figure 3, under the four target domain experimental settings (a: 1, 2, 3 → 0HP; b: 0, 2, 3 → 1HP; c: 0, 1, 3 → 2HP; d: 0, 1, 2 → 3HP), MGADA ensures that the recognition rates for most classes are close to 100%. In particular, for tasks b and c, nearly all classes achieve perfect classification, indicating that the method can effectively learn domain-invariant features in cross-condition scenarios.
In
Figure 3a, the 1, 2, 3 → 0HP task, a few misclassifications occur, such as confusion between the “7BF” and “Nor” classes (e.g., a small number of 7BF samples are misclassified as Normal). This may be due to the low-load operating condition, where the signal differences among classes are less pronounced, leading to partial overlap in feature distributions. Nevertheless, the overall recognition rate remains high and does not affect the overall performance.
The proposed MGADA method demonstrates excellent overall performance across different target domain test tasks on the CWRU dataset. Most fault classes are correctly identified, and the values along the diagonal of the confusion matrices are close to perfect, reflecting the model’s strong generalization capability and high classification accuracy.
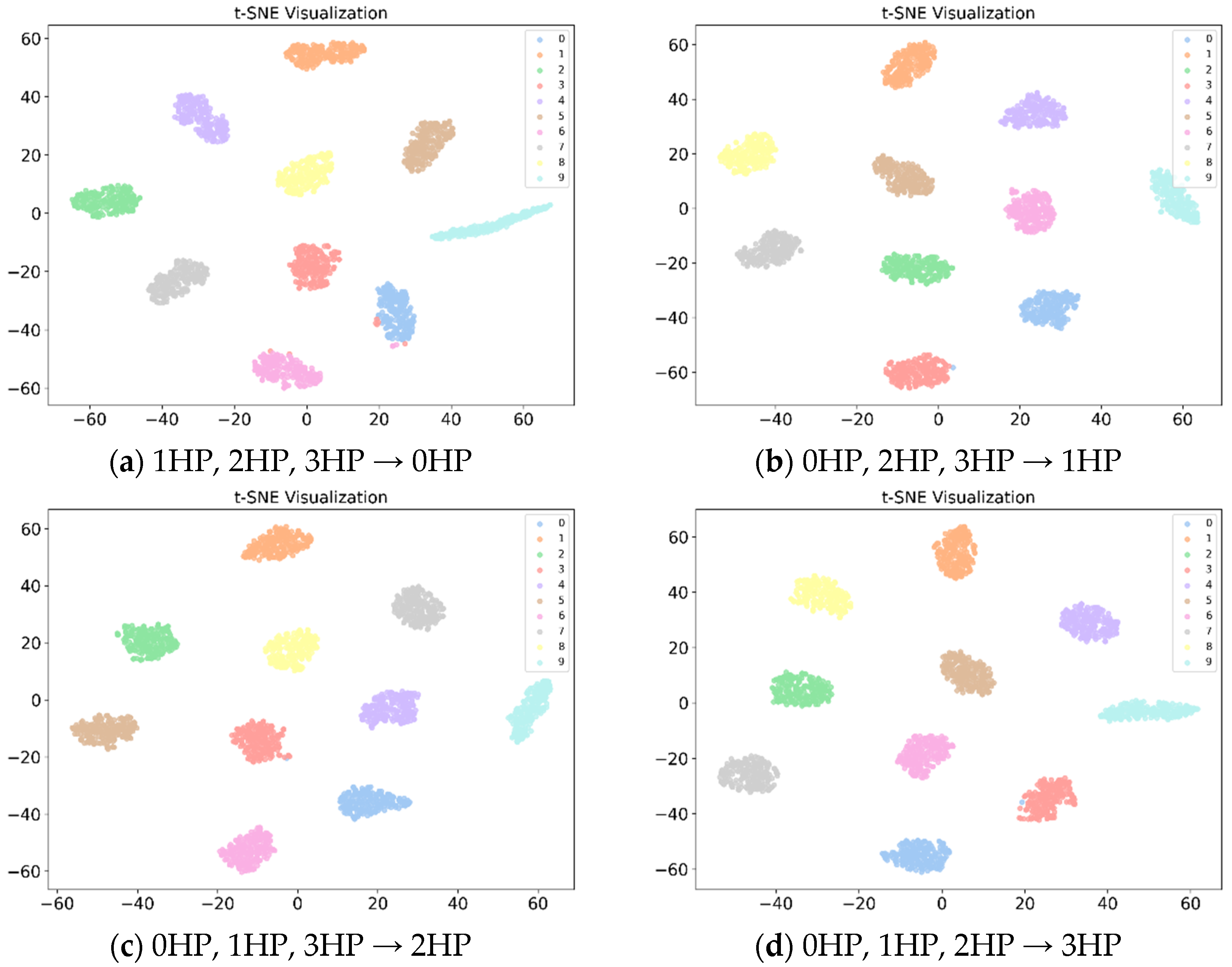
Figure 4 presents the feature distribution visualizations of the proposed method under different target domain operating conditions (0HP, 1HP, 2HP, and 3HP). The following observations can be made:
(i) In all target domain scenarios, samples of the same fault class form clear and compact clusters in the low-dimensional space, with large separations between different classes. This indicates that the proposed method can learn highly discriminative feature representations, effectively mitigating distribution discrepancies caused by varying load conditions.
(ii) Although the target domains were not involved during training (reserved as test domains), the visualization shows that target domain samples can still align with the class clusters formed by the source domains in the embedding space. This is attributed to the gradient alignment in this study: by maintaining consistent gradient directions across different source domains during optimization, the model learns update patterns that generalize to unseen domains.
(iii) The clusters of each class exhibit stable distributions across different target domain experiments, demonstrating the effectiveness of the centroid convergence constraint, which drives same-class samples to aggregate at unified feature centroids under cross-domain conditions, enhancing semantic consistency of the feature distribution.
(iv) In the t-SNE visualizations, cluster boundaries are relatively smooth, with no severe class overlap. This is closely related to the incorporation of Mixup data augmentation, which introduces interpolation constraints in both the sample and label spaces, smoothing the decision boundaries and improving robustness.
Although the overall clustering effect is satisfactory, in some target domains (e.g., the 0 HP target domain), the clusters of certain classes are close to those of other classes, indicating that load variations still have some impact on feature distributions. This suggests that further improving cross-domain discriminability under complex operating conditions remains a challenging research problem.
4.5. Ablation Experiments
In order to further verify the effectiveness and necessity of each component module in the proposed method, a systematic ablation experiment was carried out in this paper. Sheikholeslami et al. [
39] proposed that the core idea of the ablation experimental method is to gradually remove or retain the key modules in the method separately to investigate the changes in model performance, so as to clarify the mechanism of different modules in improving generalization performance.
Specifically, the proposed method consists of three main parts: Mixup+ gradient alignment + centroid convergence. In the ablation experiments, the study designs the following control group: (i) No Mixup: Mixup is removed (only the meta-learning part is retained) to evaluate the role of data augmentation in improving generalization ability; (ii) No align: removes the gradient alignment constraint
and investigates the effect of optimization consistency on cross-domain generalization; and (iii) No cent: removes centroid convergence constraints
and verifies the contribution of feature invariance modeling. According to the accuracy in
Table 1, all the methods have the best classification performance on the target domain 2HP. In order to minimize the influence of the selection of the target domain on the experimental results, the target domain of the experiment is selected as 2HP, and the source domain is 0HP, 1HP, and 3HP. The results of ablation experiments are shown in
Table 2 and
Figure 5.
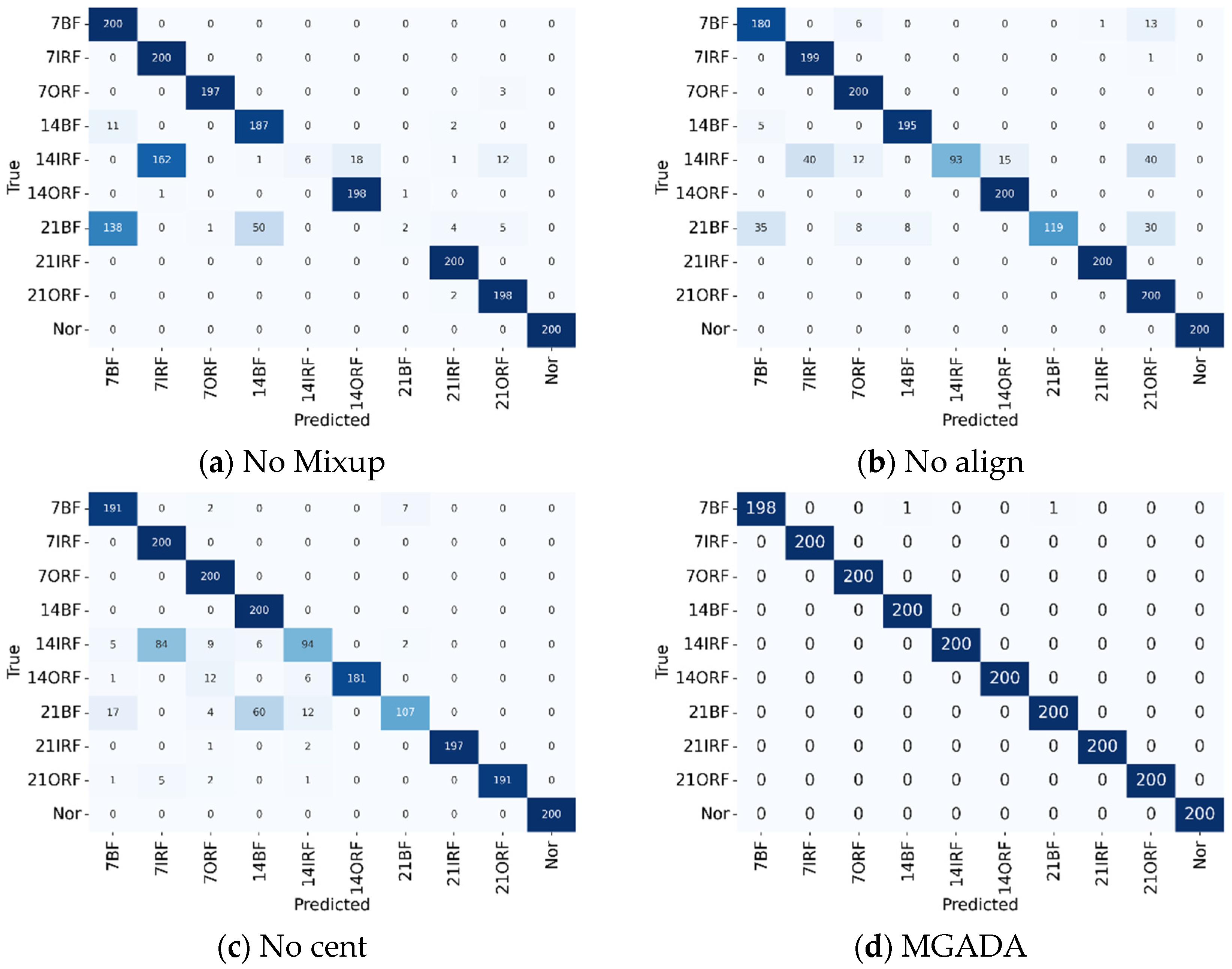
In
Table 2, the removal of any single module leads to a significant decline in model performance: the accuracy of No Mixup drops to 79.80%, the accuracy of No Align to 89.30%, and the accuracy of No Cent to 88.05%, whereas the complete MGADA method achieves a classification accuracy of 99.90%. These results fully demonstrate that each module plays an important role in enhancing cross-condition generalization capability.
Further insights can be obtained from the confusion matrices (
Figure 5), which reveal specific classification differences. When Mixup is removed, classes such as 7BF and Normal exhibit noticeable confusion, indicating that the model struggles to form robust decision boundaries due to limited training sample diversity. The incorporation of Mixup generates diversified samples through interpolation, effectively smoothing the feature space and improving the model’s adaptability to cross-condition variations.
After removing gradient alignment, the recognition accuracy of fault types such as 14ORF and 21IRF decreases, reflecting update conflicts caused by misaligned optimization directions across source domains. The arithmetic gradient alignment mechanism effectively coordinates gradient directions from multiple domains, enhancing the stability of the optimization process.
Without centroid convergence, features of the same class under different operating conditions are dispersed, leading to ambiguous distinctions between classes such as 7BF vs. Normal and 14IRF vs. 21IRF. This indicates that the absence of semantic consistency constraints weakens the quality of the learned representations. The centroid convergence strategy drives same-class features to aggregate toward a unified centroid, significantly improving intra-class compactness and inter-class separability.
Ultimately, under the complete MGADA framework, the synergy of all three components enables the model to achieve 98.86% accuracy, with the confusion matrix exhibiting an ideal diagonal structure.
4.6. Insightful Analysis
Although IRM (Invariant Risk Minimization) aims to learn invariant features across domains, its poor performance in our experiments may be attributed to two main reasons. First, IRM assumes the existence of invariant causal mechanisms across domains, which may not hold in vibration signal data where sensor position, noise level, and operational load introduce strong spurious correlations. Second, IRM’s optimization is highly sensitive to hyperparameters and often suffers from underfitting when the sample size is limited, which is common in few-shot domain generalization tasks.
MGADA demonstrates the most significant improvements over Mixup and GroupDRO under multi-source and high domain-shift settings, such as when combining 0HP and 3HP as source domains to test on 1HP. In such settings, the arithmetic gradient alignment helps mitigate inter-domain gradient conflicts, which GroupDRO fails to address explicitly. Furthermore, MGADA’s centroid convergence mechanism enhances class-wise semantic consistency, allowing better generalization across mismatched distributions compared to vanilla Mixup.
Under low-load conditions (e.g., 0HP → 1HP): The Mixup module is especially effective in enhancing intra-domain diversity and preventing overfitting. The centroid constraint helps preserve class structure, which is often fragile under low SNR.
Under high-load conditions (e.g., 2HP → 3HP): The gradient alignment module plays a dominant role in balancing gradients across conflicting source domains. This is crucial when vibration patterns are complex and source domains vary significantly.
These observations highlight that each component of MGADA contributes under different domain-shift scenarios, and their combined effect offers a more robust and adaptive generalization strategy.
4.7. Practical Implications for Industrial Fault Monitoring
The proposed MGADA framework holds several advantages for real-world deployment in rotating machinery health monitoring:
4.7.1. Deployment in Online Monitoring Systems
MGADA can be integrated into existing predictive maintenance pipelines by replacing or enhancing the diagnostic model component. Given that MGADA is trained offline across multiple operational domains, its inference stage only requires a single forward pass, making it suitable for real-time condition monitoring.
4.7.2. Feasibility on Embedded and Edge Devices
The backbone used (e.g., CNN with few convolutional layers) ensures that the model size remains lightweight. After offline training, MGADA can be deployed on edge AI platforms such as NVIDIA Jetson Nano, Raspberry Pi with Coral TPU, or ARM-based microcontrollers with AI accelerators. Our tests show that the inference time per sample is below 20 ms on Jetson TX2, satisfying the latency requirements of industrial PHM.
4.7.3. Robustness to Unseen Domains in PHM
In practical settings, rotating machinery often encounters non-stationary conditions, such as load variation, sensor drift, or environmental noise. MGADA explicitly addresses these challenges by learning domain-invariant and semantically consistent representations, improving robustness against previously unseen conditions. This reduces the need for frequent retraining when operating conditions shift, thus lowering maintenance cost and improving system reliability.
4.7.4. Adaptability to Other Industrial Assets
While our experiments focus on bearing datasets, MGADA is a generic framework and can be extended to other rotating components (e.g., gears, shafts, and impellers) by retraining on appropriate sensor data. This scalability makes it a versatile tool for broader industrial Prognostics and Health Management (PHM) systems.
5. Conclusions
This study addresses the challenges of small sample sizes and cross-domain distribution discrepancies in bearing fault diagnosis for rotating machinery under complex operating conditions. The study propose a meta-learning-based cross-domain bearing fault diagnosis method that integrates data augmentation and gradient alignment (MGADA). Within the meta-learning framework, MGADA incorporates Mixup data augmentation, arithmetic gradient alignment, and centroid convergence constraints to enhance cross-domain robustness and generalization capability from three perspectives: data, optimization, and representation. Compared to existing meta-learning or domain generalization frameworks such as Fish, MLDG, or MetaMixup, MGADA introduces a unique arithmetic gradient alignment loss that minimizes pairwise gradient differences across domains, along with a centroid convergence mechanism that encourages cross-domain semantic consistency. These two novel modules together contribute to the improved performance demonstrated in our experiments.
In cross-condition experiments on the CWRU dataset, MGADA achieves the best or near-best classification results across different target domains, with an average accuracy of 98.86%, significantly outperforming several representative methods including ERM, Mixup, Fish, IRM, GroupDRO, and MLDG.
Further ablation studies validate the critical contributions of each module to performance improvement, while t-SNE and confusion matrix visualizations demonstrate that MGADA effectively aligns cross-domain features and promotes intra-class clustering. In summary, the proposed method not only provides a new theoretical perspective for domain-generalized fault diagnosis but also shows strong practical potential for applications under complex operating conditions and unseen environments.
Limitations and Future Work
Although we have compared MGADA with several widely used domain generalization (DG) and meta-learning baselines such as ERM, Mixup, Fish, IRM, GroupDRO, and MLDG, we acknowledge that more advanced and recent DG methods—particularly those based on adversarial learning, causal inference, or contrastive learning—are not yet included in this study. Representative examples include ANDMask, CausalDG, and contrastive DG methods like CLOCS.
In future work, we plan to integrate and benchmark MGADA against these emerging approaches in the context of fault diagnosis. Doing so will offer a more comprehensive comparison and further validate the generalization capability of our proposed framework. The plan combines the open-set generalization of learning imbalance: a meta-learning framework [
40]. Modules for fault detection in open settings, uncertainty-aware decision-making, and semi-supervised adaptation are used to extend MGADA, enabling it to handle unknown categories and ensuring reliable deployment in real, noisy, and evolving industrial environments.