Abstract
This paper presents a lower-limb hip exoskeleton system integrated with an adjustable-stiffness flexible energy-storage module for three-dimensional gait correction. This system features a modular flexible mechanical design and a stiffness-gain scheduled PID control strategy for dynamic, personalized assistance. Based on biomechanical analysis of the hip joint, a 3D gait correction model was constructed targeting impairments in flexion, abduction, and adduction. The control strategy adjusts system stiffness in real-time according to gait phase and user-specific parameters. Experimental results demonstrated that the exoskeleton effectively reduced joint trajectory variability (22% decrease in standard deviation of hip flexion angle) and improved muscle activation patterns (21.4% increase in rectus femoris activity), thereby enhancing gait symmetry and stability. This study offers a feasible mechatronic solution for pathological gait correction with promising clinical applicability.
1. Introduction
Exoskeletons have gained significant interest in the realm of rehabilitation and assistive technology for their potential to restore mobility in people with lower-limb impairments. These wearable systems deliver mechanical assistance that augments muscle strength and improves gait function, showing considerable promise for rehabilitating individuals with neuromuscular and musculoskeletal disorders [1,2].
Despite notable advances, current lower-limb exoskeletons face limitations in addressing diverse abnormal gait patterns. Many users, such as stroke survivors or individuals with spinal cord injuries, suffer from motor dysfunctions like hemiplegia or muscle weakness. Their gait deficits vary significantly, complicating effective assistance. Most existing devices are built with rigid structures and metal linkages that transmit torque to joints. However, their bulky designs often constrain natural joint movement, and precise alignment with human joint centers is difficult, especially in asymmetric gait cases—resulting in discomfort and reduced effectiveness. Li et al. [3] found that exoskeletons with misaligned joints caused discomfort and reduced movement efficiency, especially in asymmetric gaits. Lobo-Prat et al. [4] highlighted that rigid exoskeletons restrict joint movement and lack adaptability to different body types. Abdikadirova et al. [5] showed that asymmetric stiffness in hip exoskeletons worsens gait asymmetry, impeding rehabilitation. Furthermore, most systems are designed for sagittal plane motion only, neglecting multi-planar dynamics crucial for natural walking and individualized rehabilitation [6,7]. For example, Rangan et al. [8] designed a 16 kg exoskeleton with fixed trajectories, which limited user engagement. Zhong et al. [9] introduced a knee-assist exoskeleton (NE-105) with two linear actuators but focused solely on sagittal plane motion. Yan et al. [10] simplified the model into a sagittal three-link leg, excluding the coordination necessary for dynamic balance across three dimensions.
Additionally, many exoskeletons rely on phase-based or motion-following control strategies that passively support movement but lack mechanisms for correcting pathological patterns. Gait correction control actively intervenes when abnormal patterns arise, helping retrain motor behavior [11,12]. Zhang et al. [13] proposed a self-learning controller to guide impaired limbs using healthy limb motion, but it failed to address bilateral impairments. Lee et al. [14] applied torque pulses at the hip using gait phase locking, though individual variability still affects consistency. Thalman et al. [15] used soft robotic systems to improve gait synchronization, but their open-loop approach lacked real-time adaptability. Kang et al. [16] used sinusoidal torque profiles for hip assistance, which may be too simplified for practical deployment. Firouzi et al. [17], explored feedback control for gait correction, adjusting in real-time to correct asymmetry but still facing challenges with user-specific gait variability. Li et al. [18] developed a multi-stage control system for hemiparetic gait but with limited adaptability to different walking speeds. Despite these advancements, most existing systems are limited by their inability to dynamically adapt to varying gait patterns and individual needs, which our research aims to address by introducing a flexible and adaptive gait correction model.
Therefore, this paper proposes a novel lower-limb hip exoskeleton with gait correction capabilities. A flexible energy-storing module with adjustable stiffness was developed to support personalized mechanical intervention. Based on a biomechanical model of the hip joint, a three-dimensional gait correction Equilibrium models were established, targeting the flexion, abduction, and adduction of the hip joint. A stiffness-gain scheduled PID control strategy was implemented to dynamically adjust the system’s stiffness. The complete exoskeleton prototype was built and verification experiments were conducted. Results verified the exoskeleton’s ability to reduce joint angle deviations and muscle compensation, demonstrating feasibility and clinical potential.
2. Materials and Methods
2.1. Apparatus Description
2.1.1. Structural Design
The adjustable-stiffness flexible energy-storing module, as shown in Figure 1, comprises three primary components: a drive box, an elastic element, and a control box. The elastic element is connected at both ends via Bowden cables, with the upper cable linked to the drive box and the lower cable extending to the region around the knee joint.
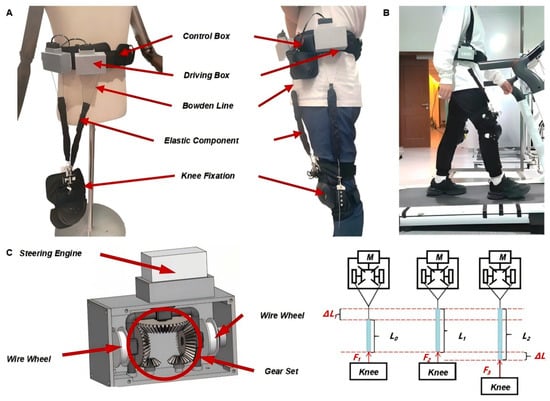
Figure 1.
Overall Mechanical Design and Human–Device Coupling of Lower-Limb Hip Exoskeleton: (A) Prototype of the Lower-Limb Hip Exoskeleton Mechanis. (B) Human–Exoskeleton Interface During Walking. (C) Drive Box Structure and Force Transmission Mechanism.
The internal mechanism of the drive box employs a coaxial counter-rotation system, wherein a top-mounted servo motor drives a gear assembly that synchronously actuates two symmetrically arranged cable reels. This design enables controlled winding and unwinding of the cable, allowing precise adjustment of the elastic element’s stiffness. The symmetrical configuration of the reels ensures mechanical balance during operation, mitigating the risk of misalignment due to unilateral tension. Additionally, a pair of small anti-slip gears is positioned beneath the main gear assembly to enhance transmission stability and prevent gear slippage. The drive box is ergonomically designed to minimize user burden, with compact dimensions (97 mm × 45 mm × 60 mm) and a total weight of approximately 1.6 kg. Except for the servo motors, all structural components are fabricated using 3D printing. A rear-mounted clip allows for rapid donning and doffing, and provides positional adjustability to accommodate different body types. The control box integrates the power supply and control circuitry, supplying energy to the servo motors and supporting system communication.
The mechanical structure of the hip exoskeleton adopts a flexible cable-driven design without rigid joint alignment. It applies assistive torques through externally mounted elastic elements connected via Bowden cables. The assistive force is transmitted to the hip joint through the relative movement of the anchoring points on the pelvis and thigh. Human–device coupling is realized using a lightweight wearable interface consisting of a waist belt and thigh cuffs made from breathable, adjustable straps. These interfaces are positioned based on anatomical landmarks (e.g., anterior superior iliac spine, greater trochanter) to ensure effective force transmission and comfort. The elastic elements are routed along the lateral and anterior surfaces of the lower body and do not interfere with joint rotation.
2.1.2. Hardware Design
An integrated control system (Figure 2), comprising four subsystems—a controller, a sensing unit, a servo drive system, and an execution unit—is introduced in this work to regulate the stiffness of the flexible energy-storing module. The controller is built on an Arduino UNO R3 (Arduino, Elegoo, Shenzhen, China) integrating an ATmega328P microcontroller (Atmel, Microchip Technology Inc., Shanghai, China). With a 16 MHz clock and up to 16 MIPS throughput, it provides sufficient compute for real-time embedded control and system coordination. The sensing unit acquires biomechanical data in real time—joint angles, linear acceleration, and angular velocity—using an MPU6050 inertial measurement unit (IMU) connected via daisy-chained cabling. Communication with the controller uses the IIC protocol, closing the loop for accurate exoskeleton control. The servo drive system executes commands issued directly by the controller or generated from sensor feedback. A dedicated multi-channel servo controller communicates with the Arduino over a UART-based asynchronous serial bus, enabling centralized command distribution to multiple actuators. Angular-position feedback from each servo is continuously monitored to ensure precise actuation.
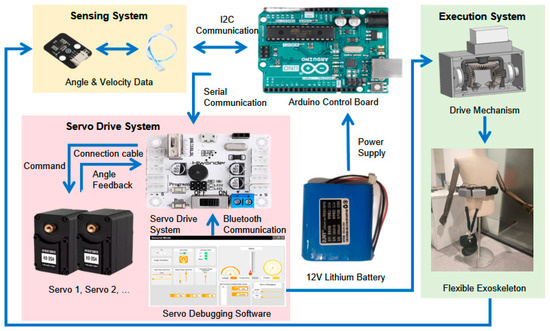
Figure 2.
System Architecture of the Hip Exoskeleton: Sensing, Control, and Actuation Modules.
The MPU6050 IMU (InvenSense, TDK InvenSense Inc., Shenzhen, China) provides 6-degree-of-freedom sensing through a combination of a 3-axis gyroscope and a 3-axis accelerometer. Joint angles are estimated using a complementary filter that fuses data from both sensors: the accelerometer estimates static orientation based on gravitational acceleration, while the gyroscope captures dynamic rotational changes. The filtered angle is calculated as:
where is a filter coefficient typically ranging from 0.96 to 0.98. Relative orientation between adjacent IMUs (e.g., pelvis and thigh) is then used to determine joint angles, consistent with methods reported in the GaitMotion dataset.
The execution unit integrates the mechanical drive and the flexible exoskeleton interface. Actuation modulates cable tension to adjust the elastic element’s stiffness; forces are transmitted through Bowden cables to the wearable interface, delivering targeted assistive and corrective torques at the lower-limb joints. Collectively, the system enables dynamic support and gait correction during walking.
2.2. Analysis of 3D Gait Correction Based on Human-Assistance Coupled Model
2.2.1. Analysis of Abnormal Lower-Limb Gait Characteristics
Circumduction gait caused by hemiparesis is one of the most common abnormal gait patterns among patients with central nervous system injuries and represents a key target population for exoskeleton-assisted rehabilitation. In this study, circumduction gait was selected as the representative pathological gait for modeling and analysis, with the goal of enhancing the study’s specificity and clinical relevance by enabling the development of targeted assistance strategies [19]. This type of gait is frequently observed in post-stroke patients and is characterized by the inability of the affected limb to clear the ground during the swing phase, primarily due to muscle weakness, restricted joint mobility, or impaired intermuscular coordination. A lateral arc swing of the affected leg—known as circumduction—typically results from pelvic elevation and hip abduction, which patients employ as a compensatory strategy to achieve forward progression.
In this work, the GaitMotion multi-task gait dataset developed by the University of British Columbia was used as a reference [20]. Based on this dataset, joint angle trajectories of both normal gait and circumduction gait across the complete gait cycle were extracted and visualized (shown in Figure 3).
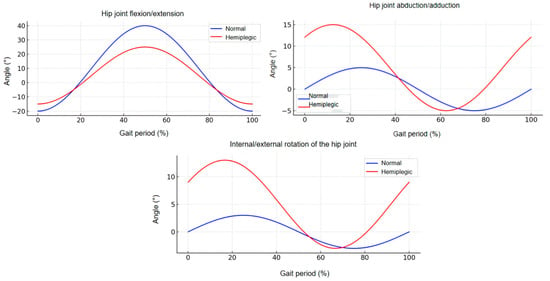
Figure 3.
Lower-Limb Joint Angle Differences Between Normal and Hemiparetic Circumduction Gait.
Hemiparetic gait is characterized by insufficient hip flexion and excessive abduction based on the kinematic perspective [21]. Patients with weakened hip flexor muscles often struggle to actively lift the leg during the swing phase, resulting in reduced hip flexion angles. Abnormal hip abduction is consequently employed to facilitate foot clearance as a compensatory strategy [17]. Although this mechanism allows basic locomotion, it compromises both gait efficiency and stability.
External torques must be applied at the hip joint by the exoskeleton system, enabling the user to achieve the desired joint trajectories as a means of correcting such abnormal gait patterns [22]. Hip joint torque is generated through the coordinated action of muscles, ligaments, and bones, and is closely associated with joint angles and movement velocity. Its magnitude is influenced by factors such as angular acceleration, muscle contraction force, and segmental moment of inertia.
2.2.2. Hip Flexion Correction Equilibrium Model
The model for generating hip flexion assistive torque was established by utilizing the energy storage and release characteristics of elastic elements in this paper [23]. As illustrated in Figure 4, the hip exoskeleton assists flexion through a mechanical structure in which Ph denotes the rotational center of the hip joint. The upper anchor point Uh is fixed at the anterior superior iliac spine, while the lower anchor point Dh is located on the upper section of the knee fixation mechanism. The elastic element is connected between Uh and Dh. Point P is the projection of Uh on the torso, and point H is the projection of h on the midline of the thigh. In Figure 4A,B, the yellow dashed line represents the extension of PPh, defined as the initial reference position. The angle between the yellow dashed line and PhH is defined as the hip joint angle θh, with Figure 4A representing positive hip flexion and Figure 4B representing negative hip extension.
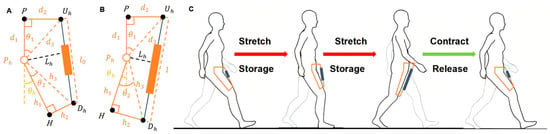
Figure 4.
Hip Flexion Assistance Model Based on Exoskeleton Mechanism: (A) Model representation at maximum hip flexion; (B) Model representation at maximum hip extension; (C) Operating principle of the elastic element during flexion assistance. (Ph: hip joint center; Uh: upper anchor point on pelvis; Dh: lower anchor point near knee; P, H: projections used to define hip angle θh; θh: angle between PhH and PPh).
The operational principle of the elastic element during walking is illustrated in Figure 4C. Mechanical energy is stored through elastic stretching during the stance phase and subsequently released in the swing phase to facilitate hip flexion [24].
As shown in Equation (2), a formulation is used for modeling the exoskeleton-assisted hip flexion mechanism.
where Mh is the torque generated by the elastic element at the hip joint; Kh is the stiffness coefficient of the elastic element; l is the current length of the elastic element; l0 is the initial (unstretched) length of the elastic element; Lh is the moment arm of the elastic force with respect to the hip joint rotation center.
The length of the elastic element is calculated using Equation (2), and the moment arm is given by Equation (4):
where θh is the hip joint angle; θ1, θ2, d3 and h3 are auxiliary geometric parameters, which can be determined using the following sub-equations.
where d1 denotes the vertical distance from point Uh to Ph, d2 is the horizontal distance from Uh to Ph, h1 is the distance from H to Ph, and h3 represents the distance from point Dh to H.
2.2.3. Hip Abduction Correction Equilibrium Model
As shown in Figure 5, the diagram illustrates the biomechanical model for exoskeleton-assisted hip abduction. Here, denotes the rotational center of the hip joint. The upper anchor point is located on the inner side of the thigh’s longitudinal axis, while the lower anchor point is attached to the knee-binding mechanism. The elastic element is positioned between and . is the projection of on the thigh’s midline, and is the projection of on the same axis.
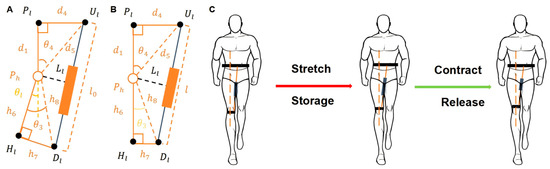
Figure 5.
Hip Abduction Assistance Model Based on Exoskeleton Mechanism: (A) Model representation at maximum hip extension during abduction; (B) Model representation at maximum hip flexion during abduction; (C) Operating principle of the elastic element during abduction assistance. (Ul: upper anchor on inner thigh; Dl: lower anchor near knee; Pl: projection of Ul; Hl: projection of Dl on thigh; θl: angle between PhHl and PlPh).
In Figure 5A, the yellow dashed line represents the extension of , defined as the initial reference position. The angle between the dashed line and represents the abnormal hip abduction angle, denoted as . Figure 5B shows the hip joint in a state of positive-angle abduction, while Figure 5B shows the corrected posture after exoskeleton-assisted abduction. The operational process of the elastic element during walking is shown in Figure 5C: the element is stretched during the stance phase to store energy, which is subsequently released during the swing phase to assist hip abduction.
As shown in Equation (9), a formulation is used for modeling the exoskeleton-assisted hip flexion mechanism.
where Mh is the torque generated by the elastic element at the hip joint; Kh is the stiffness coefficient of the elastic element; l is the current length of the elastic element; l0 is the initial (unstretched) length of the elastic element; is the moment arm of the elastic force with respect to the hip joint rotation center.
The length of the elastic element is calculated using Equation (9), and the moment arm is given by Equation (11):
where θh is the hip joint angle; θ3, θ4, d5 and h8 are auxiliary geometric parameters, which can be determined using the following sub-equations.
where d1 denotes the vertical distance from point Pl to Ph, d4 is the horizontal distance from Ul to Ph, h6 is the distance from Hl to Ph, and h8 represents the distance from point Dl to Hl.
2.2.4. Hip Adduction Correction Equilibrium Model
As shown in Figure 6, the diagram illustrates the hip adduction assistance model using an exoskeleton. denotes the rotational center of the hip joint. The upper anchor point is located on the inner side of the thigh’s midline, and the lower anchor point is placed on the knee-binding mechanism. The elastic element is connected between and . is the projection of onto the thigh’s longitudinal axis, and point is the projection of onto the same axis. In Figure 6A, the yellow dashed line represents the extended line of , which is defined as the initial reference position. The angle between the yellow line and represents the abnormal hip abduction angle θk. Figure 6A shows the joint in a state of abnormal abduction, while Figure 6B depicts the corrected, normal alignment after exoskeleton-assisted adduction. The operational process of the elastic element during human walking is illustrated in Figure 6C. During the stance phase, the elastic element is stretched to store energy, which is then released during the swing phase to assist the hip joint in completing the adduction motion.
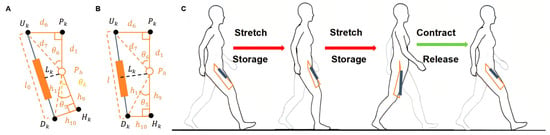
Figure 6.
Hip Adduction Assistance Model Based on Exoskeleton Mechanism: (A) Model representation at maximum hip extension during abduction; (B) Model representation at maximum hip flexion during abduction; (C) Operating principle of the elastic element during abduction assistance. (Uk: upper anchor on inner thigh; Dk: lower anchor near knee; Pk, Hk: projection points; θk: adduction angle defined between PhHk and PkPh).
As shown in Equation (16), a formulation is used for modeling the exoskeleton-assisted hip flexion mechanism.
where Mh is the torque generated by the elastic element at the hip joint; Kh is the stiffness coefficient of the elastic element; l is the current length of the elastic element; l0 is the initial (unstretched) length of the elastic element; is the moment arm of the elastic force with respect to the hip joint rotation center.
The length of the elastic element is calculated using Equation (17), and the moment arm is given by Equation (18):
where θ5, θ6, d7 and h11 are auxiliary geometric parameters, which can be determined using the following sub-equations.
where d1 denotes the vertical distance from point Pk to Ph, d2 is the horizontal distance from Uk to Ph, h1 is the distance from Hk to Ph, and h3 represents the distance from point Dk to Hk.
3. Gait Correction Control Strategy Based on Stiffness Gain
This paper introduces a Stiffness-Gain Scheduled PID Control Strategy, which incorporates a “stiffness regulation” mechanism to improve the stability of the control system under varying load conditions [25]. The strategy integrates the mechanical property of “stiffness” into the gain-scheduling PID control framework, enabling dynamic adjustments to the control gain related to stiffness, thus allowing precise regulation of system stiffness [18].
In this context, “stiffness” is defined as the ratio of the restoring force from the elastic element to its displacement. By adjusting the element’s initial stretch and dynamic range, the system delivers personalized assistive force based on walking speed. To enable this, the concept of “stiffness gain” is introduced—a dynamic parameter linked to gait speed. As the user walks faster, the gain increases to enhance support; at slower speeds, the gain decreases, making the system more compliant.
In this context, “stiffness” refers to the elastic response of the assistive system. The parameter Kg represents the dynamically adjusted stiffness gain, influenced by the user’s walking speed. To achieve speed-adaptive modulation, a speed sensitivity coefficient αs is introduced:
Ks denotes the baseline stiffness gain, αs adjusts the responsiveness to gait speed v. Although this formulation is similar in form to damping (i.e., force proportional to velocity), in this context it does not represent viscous resistance. Instead, it modulates the magnitude of stiffness gain in a gain-scheduling control scheme. The term “restoring force” has been removed to avoid confusion with classical elastic or damping forces.
The core of this control strategy lies in introducing the stiffness gain, which enables the controller to adjust the system’s parameters based on its current state and the external dynamic disturbances. The introduction of the stiffness gain not only strengthens the system’s responsiveness but also improves the robustness of the control system under complex environments. The stiffness gain PID controller can be expressed as:
where Ks is the stiffness gain, and f(t) represents the dynamic input from external disturbances or load changes [26].
In this control strategy, the goal of adjusting the stiffness gain is to fine-tune the PID controller parameters in response to the speed variations during walking, as illustrated in Figure 7.
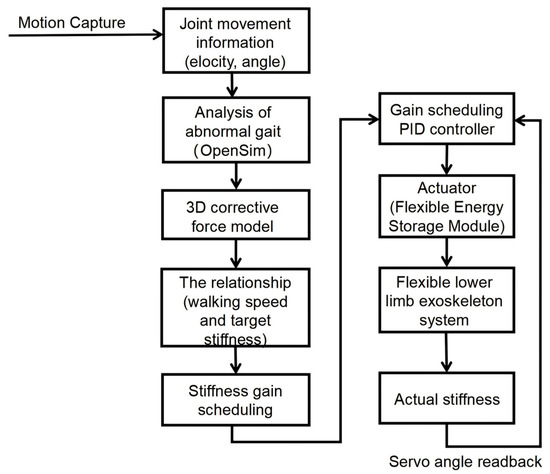
Figure 7.
Stiffness Adjustment Procedure.
- Motion capture and data collection: Joint kinematics were recorded under both normal and abnormal gait to parameterize subsequent simulations and analyses.
- Abnormal gait analysis and corrective-force modeling: Using OpenSim (version 4.5, Stanford University, Stanford, CA, USA), the primary muscle groups underlying the pathological pattern were identified; time-varying corrective forces were then applied to the target muscles. The gait model’s speed was concurrently adjusted to satisfy optimal correction requirements.
- Stiffness-gain computation and scheduling: Based on the required corrective forces, speed-dependent stiffness-gain values were derived from the 3D gait-correction model, providing real-time guidance for the controller.
- Personalized stiffness-adjustment system design: Simulation outcomes determined the number and placement of adjustable flexible energy-storage modules. The empirically derived speed–stiffness map was embedded in the controller to enable closed-loop, real-time assistance and dynamic gait correction for the wearable device [27].
This paper adopts the optimal stiffness from gait simulations as the control target and applies a stiffness-gain PID control strategy to track it. As shown in Figure 8, the system estimates real-time stiffness from servo feedback and cable tension. The error between the target and estimated stiffness is fed into the PID controller, which adjusts cable tension to modulate the elastic element accordingly. This approach enables real-time stiffness adaptation, maintains consistent joint torque output, and ensures robust performance across varying walking speeds and external disturbances.
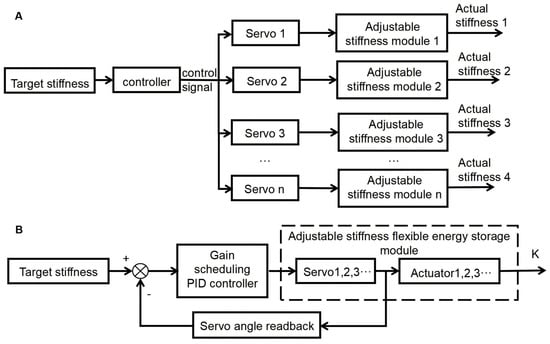
Figure 8.
Stiffness Adjustment and Control Strategy for Exoskeleton: (A) Methods for Adjusting the Stiffness of the Exoskeleton; (B) Overall Block Diagram of Stiffness Gain PID Control.
4. Experiment Protocol and Data Processing
A preliminary study was conducted using a single-subject, within-subject design in order to evaluate the assistive and corrective effects of the exoskeleton. From three screened volunteers, one male (height 168 cm, weight 68 kg) exhibiting a marked deviation from normal lower-limb joint angles—specifically an abnormal adduction range in the right limb—was selected. The participant provided written informed consent, and all procedures were performed in a quiet, comfortable laboratory environment [28]. In the main experiment, the subject walked with and without the exoskeleton, and changes in lower-limb joint angles and muscle activation were quantified. Prior to data collection, the participant completed standardized training to familiarize himself with the protocol and potential risks.
The device incorporates a multi-layered safety and fail-safe architecture to ensure safe operation during rehabilitation. Real-time monitoring of joint angles, estimated stiffness, and actuator states triggers a graded soft shutdown when abnormalities are detected. Mechanical end-stops limit elastic-element excursion to prevent excessive restoring forces, while a firmware watchdog manages control-loop or communication faults. All skin-contact interfaces use soft, breathable materials to minimize the risk of irritation during prolonged use. An easily accessible emergency-stop button allows immediate deactivation by the user or therapist. Together, these measures enhance system stability and user safety, align with ethical standards for clinical rehabilitation, and support reliable deployment in both supervised clinical and home settings.
4.1. Indicator Selection and Data Collection
4.1.1. Indicator Selection
Joint angles and EMG signals are key parameters for assessing the corrective effects of exoskeletons [29]. Firstly, joint angles provide a direct reflection of the lower limb joint movements during gait, particularly the flexion, abduction, and adduction angles of the hip, knee, and ankle. By comparing the differences in joint angles before and after wearing the exoskeleton, the effectiveness of the exoskeleton in gait correction can be objectively evaluated, particularly in improving hip flexion angles and gait symmetry [30]. Joint angle data not only quantifies gait improvement but also reveals changes in abnormal gait patterns, such as gait asymmetry in hemiparetic patients.
Secondly, EMG signals offer a detailed analysis of muscle activation, reflecting the impact of exoskeleton assistance on muscle load. By analyzing the EMG signals, changes in the activation levels of relevant muscle groups under exoskeleton assistance can be assessed, especially regarding muscle fatigue and coordination patterns. Combining joint angles and EMG signals enables a comprehensive evaluation of the exoskeleton’s performance in gait correction, particularly in terms of gait smoothness, stability, and muscle load distribution [31]. In summary, joint angles and EMG signals provide multidimensional quantitative indicators that effectively support the evaluation of exoskeleton corrective effects.
4.1.2. Experiment Device
IMUs and EMG sensors (MyoMOTION, Noraxon, Scottsdale, AZ, USA) were used to capture and display three-dimensional joint angles and accelerations of the human body in real-time using data acquisition software (MR3, Noraxon, Scottsdale, AZ, USA). Five IMUs were affixed to specific anatomical locations: the pelvis, left thigh, left shank, right thigh, and right shank. EMG sensors were placed on the rectus femoris, adductor longus, and gluteus medius muscles to measure muscle activation levels during the gait cycle. The placement of these sensors followed standard anatomical guidelines to ensure accurate data collection. The sampling frequency was set to 100 Hz. Each IMU provided angle measurements with a static accuracy of ±0.2° and a dynamic accuracy of ±0.4°.
Joint angle measurements were obtained using a motion-capture system (Nokov, Nokov Science&Technology, Beijing, China). Nineteen reflective markers were positioned on specific anatomical landmarks according to the Davis protocol [32,33]. The trajectories of these markers were tracked and analyzed using the motion capture software. The average and standard deviation of lower-limb joint angles were calculated. From the data, joint angles at critical points during the gait cycle, such as heel strike and toe-off, were extracted across multiple consecutive cycles. These parameters include the hip, knee, and ankle angles during both the stance and swing phases, as well as the total duration of each gait cycle.
4.2. Experiment Protocol
4.2.1. EMG Acquisition Experiment
- To ensure the objectivity of the EMG data (shown in Figure 9), participants refrained from intense physical activity within 24 h prior to the experiment. EMG sensors were placed on the rectus femoris, adductor longus, and gluteus medius according to anatomical landmarks. Prior to placement, the skin was cleaned with alcohol to remove any debris that could interfere with signal quality.
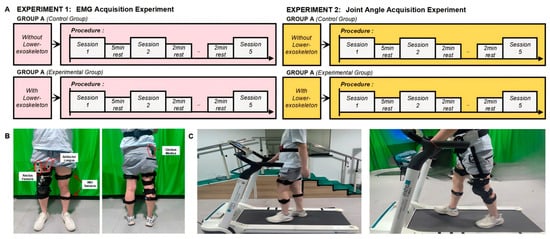 Figure 9. Experimental Setup for Gait Analysis: Walking with and without Exoskeleton Assistance: (A) Experimental Procedure; (B) IMU and EMG Sensor Placement; (C) Experimental Process (Without and with exoskeleton).
Figure 9. Experimental Setup for Gait Analysis: Walking with and without Exoskeleton Assistance: (A) Experimental Procedure; (B) IMU and EMG Sensor Placement; (C) Experimental Process (Without and with exoskeleton). - After the sensors were applied, participants rested for 5 min to relax the muscles.
- Group A: Participants walked on a treadmill at a speed of 2.5 km/h for 1 min, repeating the walk five times with a 5 min rest between each trial. After completing the experiment, they proceeded to Group B.
- Group B: After donning the exoskeleton, participants walked on the treadmill at the same speed of 2.5 km/h for 1 min, repeating the walk five times with a 5 min rest in between each trial.
4.2.2. Joint Angle Acquisition Experiment
- Fifteen reflective markers were applied to the participants’ lower limbs (shown in Figure 9), with the following placement locations: anterior superior iliac spine, posterior superior iliac spine, greater trochanter, lateral and medial femoral condyles, mid-lateral thigh, lateral and medial tibial condyles, tibial tuberosity, head of the fibula, lateral and medial malleolus (distal fibula and tibia), heel (calcaneus), and the base of the fifth metatarsal and the head of the first metatarsal.
- After all the markers were applied, participants rested for 5 min to relax their muscles.
- Group A: Participants walked on a treadmill at a speed of 2.5 km/h for 1 min, repeating the walk five times with a 5 min rest between each trial. After completing the experiment, they proceeded to Group B.
- Group B: After donning the exoskeleton, participants walked on the treadmill at the same speed of 2.5 km/h for 1 min, repeating the walk five times with a 5 min rest between each trial.
4.3. Data Processing
4.3.1. EMG Signal
To quantify the muscle activation, this study uses the Root Mean Square (RMS) method for analyzing the EMG signal [34]. RMS is a common indicator that represents the maximum muscle signal intensity, effectively reflecting the level of muscle activation during the movement process. The higher the RMS value, the greater the muscle activation during the analyzed time segment. The calculation of RMS is given by:
where EMGi is the EMG signal at each time point, and N is the total number of selected sampling points. To ensure the stability and representativeness of the analysis results, the study selected the last 20 complete gait cycles from the subject as the statistical sample for EMG analysis.
4.3.2. Coefficient of Variation
To evaluate the fluctuation and stability of the EMG signal, the coefficient of variation (CV) was used for statistical analysis [35], expressed as:
where σ is the standard deviation and μ is the mean value. A higher CV indicates greater fluctuation in muscle activation during the gait cycle.
4.3.3. Joint Angle
Joint angle data from multiple gait cycles are normalized to eliminate individual differences, in order to obtain a representative gait pattern [36], thereby enabling comparison across cycles. The normalization formula is:
where θ(t) is the original joint angle at a given time, θmin and θmax are the minimum and maximum joint angles within the gait cycle, respectively, and θnorm(t) is the normalized joint angle, expressed as a percentage for easy comparison across different gait cycles.
The representative gait is derived by averaging the normalized angles across all cycles, using:
where θavg is the average normalized joint angle for the gait cycle, and N represents the number of sampling points in the cycle. This approach provides a standardized dataset for gait analysis and correction.
5. Results
This study aimed to investigate the effects of exoskeleton assistance on gait by analyzing EMG signals, joint angles, and the CV of the gait cycle. The results provide valuable insights into how exoskeletons assist in correcting abnormal gait patterns, as evidenced by the comparison of data collected with and without the exoskeleton.
5.1. EMG Signals
The analysis of EMG signals revealed significant differences between the wearing and non-wearing conditions. The rectus femoris showed the most notable increase in muscle activation with a 21.4% (p < 0.01, shown in Figure 10) difference between the wearing and non-wearing conditions. This suggests that the exoskeleton provides additional assistance to the muscle, likely due to its role in supporting hip flexion and aiding the movement of the lower limbs during walking. The gluteus medius showed a minimal increase in activation, only 0.3% (p < 0.05), indicating that the exoskeleton has little impact on this muscle’s activity. Conversely, the long adductor muscle exhibited a 6.8% (p < 0.05) increase in activation with the exoskeleton, suggesting a moderate effect in aiding the adduction movement during the gait cycle. These results suggest that the exoskeleton assists in redistributing the muscle load, particularly in the major muscle groups involved in walking, which may reduce the effort required by the user.
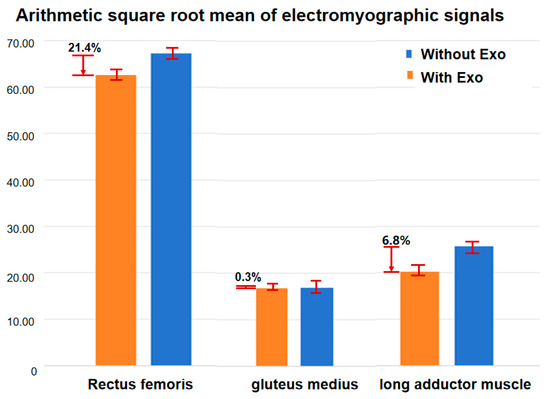
Figure 10.
Activation of the rectus femoris, vastus coeruleus, and gluteus medius muscles before and after exoskeleton wear.
5.2. CV in Muscle Activation
CV analysis offers insight into the consistency and stability of muscle activation during the gait cycle. Lower CV values indicate more stable muscle activation, while higher values suggest greater fluctuations in muscle use. As seen in the EMG data, the rectus femoris exhibited a relatively lower CV in the wearing condition, indicating more consistent activation of the muscle when the exoskeleton was used (shown in Figure 11). In contrast, muscles like the gluteus medius and long adductor muscle showed higher CV values in the non-wearing condition, indicating less stable muscle activation. The exoskeleton’s influence on reducing variability in muscle activation reflects its potential for providing more reliable and steady assistance, thus enhancing overall gait stability.
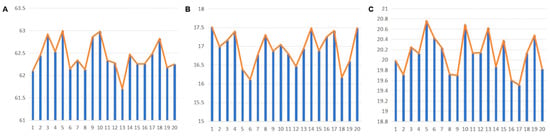
Figure 11.
Muscle Activation Levels over 20 Gait Cycles After Wearing the Exoskeleton: (A) Rectus Femoris; (B) Gluteus Medius; (C) Long Adductor. Blue bars indicate muscle activation levels, and orange lines represent the average activation trend.
5.3. Joint Angles
The joint angle data provided further insights into the exoskeleton’s effects on gait. As shown in the figures, the hip joint abduction/adduction and hip flexion/extension profiles differed between the conditions of wearing and not wearing the exoskeleton. In the hip joint abduction/adduction graph, wearing the exoskeleton resulted in a more symmetrical movement pattern with reduced deviations, suggesting that the device helps to stabilize the gait and improve balance. The joint angle data provide further evidence of the exoskeleton’s impact on gait performance. As illustrated in the figures, notable differences were observed in the hip joint abduction/adduction and flexion/extension trajectories between the assisted and unassisted conditions. When wearing the exoskeleton, the hip abduction/adduction pattern appeared more symmetrical and exhibited reduced fluctuations, suggesting improved mediolateral stability and gait balance. Similarly, the flexion/extension profile demonstrated smoother and more continuous transitions, indicative of enhanced sagittal-plane motion and better coordination during walking. These trends support the hypothesis that exoskeleton assistance promotes more natural joint kinematics, particularly in individuals with pathological gait patterns. Quantitatively, the standard deviation in hip flexion angle—measured as the standard deviation across gait cycles—was reduced by 22% with exoskeleton support, while standard deviation in the knee and ankle joints decreased by 15% and 12% (p < 0.05, shown in Figure 12). These findings underscore the exoskeleton’s ability to stabilize joint motion in both the frontal and sagittal planes, thereby enhancing overall gait consistency and biomechanical efficiency.
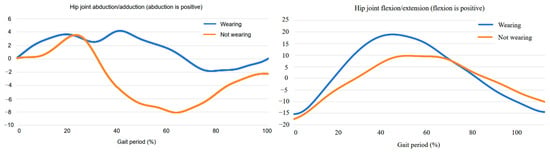
Figure 12.
Angle Variation Curves Before and After Wearing the Exoskeleton: (left) Hip Abduction/Adduction Angle; (right) Hip Flexion/Extension Angle.
6. Discussion
6.1. Equilibrium Gait Correction Models
In this paper, a three-dimensional dynamic gait correction model is proposed to enable real-time gait support through the exoskeleton. The model is based on the biomechanics of the hip joint and incorporates dynamic adjustments to apply corrective forces during the gait cycle. By accounting for the varying kinematic parameters of the lower limbs—such as the hip, knee, and ankle joints—this model simulates realistic and natural movement patterns. The dynamic nature of the model allows the exoskeleton to not only assist in improving joint angles but also to adjust dynamically based on the user’s movement and walking speed.
The model’s effectiveness was validated experimentally, showing a reduction in deviations from healthy gait dynamics. Specifically, joint angle variations decreased by 22% in hip flexion, 15% in the knee, and 12% in the ankle. These results confirm the robustness of the model in guiding the exoskeleton to improve gait performance, particularly in individuals with abnormal gait patterns, such as hemiparetic circumduction gait.
The stiffness calculation was simplified to a constant value using a dynamic stiffness adjustment approach, in order to optimize the model’s real-time adaptability and ensure its practical application. This approach balances the system’s theoretical biomechanical effectiveness with its real-time usability. Through these adjustments, the exoskeleton can effectively provide dynamic support and improve gait efficiency, even with hardware limitations. The model’s accuracy in simulating joint movements further demonstrates its potential for personalized gait assistance and correction, particularly for rehabilitation and assistive mobility applications.
6.2. Gait Correction Control Method
The three-dimensional dynamic gait correction model introduced in this study plays a pivotal role in enabling the exoskeleton to provide adaptive, real-time gait support. By incorporating the biomechanics of the hip joint and allowing for dynamic adjustments, this model enables the exoskeleton to apply corrective forces throughout the gait cycle. Specifically, it considers the varying kinematic parameters of the lower limbs—such as the hip, knee, and ankle joints—simulating natural and realistic movement patterns. The dynamic nature of the model allows the exoskeleton not only to assist in improving joint angles but also to adjust based on the user’s movement and walking speed, enhancing both precision and efficiency.
Experimental validation of the model demonstrated its effectiveness in reducing deviations from healthy gait dynamics. Specifically, joint angle variations were reduced by 22% in hip flexion, 15% in the knee, and 12% in the ankle. These results indicate that the model effectively guides the exoskeleton in improving gait performance, especially in individuals with abnormal gait patterns, such as hemiparetic circumduction gait. The findings confirm the robustness of the three-dimensional dynamic model in providing accurate real-time corrections and highlights its potential for improving the overall stability and efficiency of walking in users with gait abnormalities.
6.3. Usability and Limitations
The exoskeleton system developed in this study shows strong potential for improving gait correction, particularly for individuals with abnormal gait patterns. Its core innovation, the adjustable stiffness module, allows for real-time adaptation to varying walking speeds and individual gait needs, enhancing comfort and efficiency during use. The system integrates a dynamic gait correction control strategy, providing personalized support that optimizes movement patterns. The experimental results confirm the exoskeleton’s ability to adjust hip, knee, and ankle joint angles, aligning them with preset healthy gait dynamics. Furthermore, EMG analysis showed that muscle activation patterns were redistributed, alleviating strain and enhancing muscle coordination during walking. This suggests that the exoskeleton could benefit patients with neurological or musculoskeletal disorders, improving gait stability and reducing fatigue.
However, several limitations must be addressed to fully realize the system’s potential. The small sample size used for experimental validation limits the generalizability of the findings, as it may not represent the full spectrum of gait abnormalities. A larger and more diverse group of participants is necessary to assess the system’s adaptability across various conditions. Additionally, while the exoskeleton is relatively lightweight, its reliance on external power sources and potential for discomfort during long-term use may limit its practical application. Future versions should focus on improving portability, battery life, and overall user comfort. Moreover, while the system performed well in controlled environments, its performance in real-world settings—such as on varied terrain or during dynamic movements—remains untested. Long-term effects on muscle adaptation and dependency also require further investigation. In summary, while the exoskeleton shows promising results, ongoing research is needed to optimize its design, enhance its applicability, and ensure its effectiveness for a broader range of users.
7. Conclusions
This paper proposes a novel lower-limb hip exoskeleton system that integrates an adjustable-stiffness flexible energy-storage module for targeted gait correction and dynamic support. Unlike traditional rigid exoskeletons, which often limit natural joint movement and adaptability, the modular mechanical design of this system accommodates varying gait patterns, enabling personalized assistance tailored to individual needs. A three-dimensional gait correction model was constructed based on hip biomechanics, focusing on flexion, abduction, and adduction impairments. To support real-time intervention, a stiffness-gain scheduled PID control strategy was developed, allowing dynamic modulation of system stiffness according to gait phase and user-specific parameters. A functional prototype was built and validated through motion capture and surface EMG experiments. Experimental results revealed that the exoskeleton reduced joint trajectory variability, with a 22% decrease in the standard deviation of hip flexion angle, and 15% and 12% reductions at the knee and ankle, respectively. EMG analysis showed improved muscle activation, including a 21.4% increase in rectus femoris, 6.8% in gluteus medius, and 0.3% in adductor longus, indicating better muscle coordination compared to previous studies. These results confirm the effectiveness of the proposed structural and control strategies in enhancing gait coordination and muscle engagement, setting this exoskeleton apart from existing technologies that lack such adaptability. The system demonstrates strong clinical potential for gait rehabilitation in populations with motor impairments, offering improved symmetry, reduced compensatory effort, and more stable, natural walking patterns.
Author Contributions
Z.S. and T.X. contributed equally to this work. Conceptualization, T.X. and R.K.T.; Methodology, Z.S. and Q.M.; Data curation, Y.Z.; Writing—review & editing, S.L., H.T. and H.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Key R&D Program of China (Grant No. 2023YFC3604302).
Institutional Review Board Statement
The ethics committee of Shanghai University of Medicine & Health Sciences approved the procedures of the study (Approval Code: 2024-SZR-04-420300197109053525), and all experiments were conducted in accordance with the Declaration of Helsinki (1964).
Informed Consent Statement
Informed consent was obtained from all participants prior to the experiment.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Acknowledgments
The authors would like to express special thanks to Qingyun Meng from Shanghai University of Medicine & Health Sciences for her valuable support and assistance with this paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Edwards, D.J.; Forrest, G.; Cortes, M.; Weightman, M.M.; Sadowsky, C.; Chang, S.H.; Furman, K.; Bialek, A.; Prokup, S.; Carlow, J.; et al. Walking improvement in chronic incomplete spinal cord injury with exoskeleton robotic training (WISE): A randomized controlled trial. Spinal Cord. 2022, 60, 522–532. [Google Scholar]
- Louie, D.R.; Eng, J.J.; Lam, T. Gait speed using powered robotic exoskeletons after spinal cord injury: A systematic review and correlational study. J. NeuroEng. Rehabil. 2015, 12, 82. [Google Scholar] [CrossRef]
- Li, Y.; Wang, H.; Zhao, X.; Chen, Q.; Zhang, J. Design, Simulation and Functional Testing of a Novel Ankle Exoskeleton with 3DOFs. Sensors 2024, 24, 6160. [Google Scholar] [CrossRef]
- Lobo-Prat, J.; Font-Llagunes, J.M.; Rodríguez-Fernández, A.; Pons, J.L. Systematic review on wearable lower-limb exoskeletons for gait training in neuromuscular impairments. J. NeuroEng. Rehabil. 2021, 18, 22. [Google Scholar]
- Abdikadirova, B.; Price, M.; Moreno Jaramillo, J.; Hoogkamer, W.; Huber, M.E. Gait Adaptation to Asymmetric Hip Stiffness Applied by a Robotic Exoskeleton. IEEE Trans. Neural Syst. Rehabil. Eng. 2024, 32, 1101–1111. [Google Scholar] [CrossRef]
- Calafiore, D.; Negrini, F.; Tottoli, N.; Ferraro, F.; Ozyemisci-Taskiran, O.; De Sire, A. Efficacy of robotic exoskeleton for gait rehabilitation in patients with subacute stroke: A systematic review. Eur. J. Phys. Rehabil. Med. 2022, 58, 1–8. [Google Scholar] [PubMed]
- Abdullah, M.; Hulleck, A.A.; Katmah, R.; Khalaf, K.; El-Rich, M. Multibody dynamics-based musculoskeletal modeling for gait analysis: A systematic review. J. NeuroEng. Rehabil. 2024, 21, 178. [Google Scholar]
- Rangan, R.P.; Maheswari, C.; Vaisali, S.; Sriram, K.; Stonier, A.A.; Peter, G.; Ganji, V. Design, Development, and Model Analysis of Lower Extremity Exoskeleton. Med. Eng. Phys. 2022, 106, 103830. [Google Scholar] [CrossRef] [PubMed]
- Zhong, L.; Guan, X.; Li, H.; Liu, Y.; Mao, X.; Li, X.; Xu, C. Numerical Study on Dynamics of Exoskeleton with Rigid-Flexible Coupling Knees Based on Sagittal Gait Plan. J. Adv. Mech. Des. Syst. Manuf. 2019, 13, 625–634. [Google Scholar]
- Yan, L.J.; Shen, Q.M.; Yang, D.; Qiao, J.M.; Datseris, P. Kinematic and Dynamic Modeling and Analysis of a Lower Extremity Exoskeleton. J. Adv. Mech. Des. Syst. Manuf. 2019, 13, 501–513. [Google Scholar]
- Zhang, S.; Guan, X.; Ye, J.; Chen, G.; Zhang, Z.; Leng, Y. Gait Deviation Correction Method for Gait Rehabilitation with a Lower Limb Exoskeleton Robot. IEEE Trans. Med. Robot. Bionics 2022, 4, 754–764. [Google Scholar]
- Hidayah, R.; Bishop, L.; Jin, X.; Chamarthy, S.; Stein, J.; Agrawal, S.K. Gait adaptation using a cable-driven active leg exoskeleton (C-ALEX) with post-stroke participants. IEEE Trans. Neural Syst. Rehabil. Eng. 2020, 28, 1984–1994. [Google Scholar]
- Zhang, Q.; Wu, Q.; Chen, B.; Zhu, Y. Gait self-learning control based on reference trajectory generation online for an asymmetric limb rehabilitation exoskeleton. Mechatronics 2024, 104, 103262. [Google Scholar] [CrossRef]
- Lee, J.; Huber, M.E.; Hogan, N. Gait Entrainment to Torque Pulses From a Hip Exoskeleton Robot. IEEE Trans. Neural Syst. Rehabil. Eng. 2022, 30, 656–664. [Google Scholar]
- Thalman, C.M.; Debeurre, M.; Lee, H. Entrainment During Human Locomotion Using a Soft Wearable Ankle Robot. IEEE Robot. Autom. Lett. 2021, 6, 4265–4272. [Google Scholar] [CrossRef]
- Kang, I.; Kunapuli, P.; Young, A.J. Real-Time Neural Network-Based Gait Phase Estimation Using a Robotic Hip Exoskeleton. IEEE Trans. Med. Robot. Bionics 2020, 2, 28–37. [Google Scholar] [CrossRef]
- Firouzi, V.; Seyfarth, A.; Song, S.; von Stryk, O.; Sharbafi, M.A. Biomechanical Models in the Lower-Limb Exoskeletons Development: A Review. J. NeuroEng. Rehabil. 2025, 22, 56. [Google Scholar]
- Li, C.; Luo, L.; Liu, Z.; Wang, H.; Zhang, Y.; Du, F. Adaptive Control of Lower-Limb Exoskeletons for Walking Assistance Based on Inter-Joint Coordination. J. Bionic Eng. 2024, 21, 1775–1787. [Google Scholar]
- Zhang, W.; Zhang, H.; Jiang, Z.; Wang, J.; Servati, A.; Servati, P. GaitMotion: A multitask dataset for pathological gait forecasting. arXiv 2024, arXiv:2405.09569. [Google Scholar] [CrossRef]
- Pan, Y.T.; Kang, I.; Joh, J.; Kim, P.; Herrin, K.R.; Kesar, T.M.; Sawicki, G.S.; Young, A.J. Effects of Bilateral Assistance for Hemiparetic Gait Post-Stroke Using a Powered Hip Exoskeleton. Ann. Biomed. Eng. 2023, 51, 410–421. [Google Scholar] [PubMed]
- Sekiguchi, Y.; Owaki, D.; Honda, K.; Izumi, S.-I. Kinetic Interjoint Coordination in Lower Limbs during Gait in Patients with Hemiparesis. Biomechanics 2022, 2, 466–477. [Google Scholar] [CrossRef]
- Naghavi, N.; Akbarzadeh, A.; Khaniki, O.; Kardan, I.; Moradi, A. Assist-As-Needed Control of a Hip Exoskeleton Using Central Pattern Generators in a Stride Management Strategy. J. Intell. Robot. Syst. 2023, 107, 53. [Google Scholar] [CrossRef]
- Lee, K.-J.; Nam, Y.-G.; Yu, J.-H.; Kim, J.-S. Effect of Wearable Exoskeleton Robots on Muscle Activation and Gait Parameters on a Treadmill: A Randomized Controlled Trial. Healthcare 2025, 13, 700. [Google Scholar] [CrossRef] [PubMed]
- Lin, X.; Du, F.; Song, J.; Yin, C.; Zhang, Y.; Li, Y.; Liu, W. Robust Continuous Sliding Mode Torque Tracking Control for Compliant Actuators with Prescribed Performance. Int. J. Control Autom. Syst. 2025, 23, 882–895. [Google Scholar] [CrossRef]
- Yang, T.; Yang, C.; Jiang, F.; Tian, B. Design and Evaluation of a Novel Variable Stiffness Hip Joint Exoskeleton. Sensors 2024, 24, 6693. [Google Scholar] [CrossRef]
- Wang, R.; Lin, X.; Yin, C.; Liu, Z.; Zhang, Y.; Liu, W.; Du, F. Robust Continuous Sliding-Mode-Based Assistive Torque Control for Series Elastic Actuator-Driven Hip Exoskeleton. Actuators 2025, 14, 239. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, R.; Miao, Y.; An, M.; Wang, S.; Zhang, Y. PI2-Based Adaptive Impedance Control for Gait Adaption of Lower Limb Exoskeleton. IEEE/ASME Trans. Mechatron. 2024, 29, 4251–4261. [Google Scholar] [CrossRef]
- Puyuelo-Quintana, G.; Cano-de-la-Cuerda, R.; Plaza-Flores, A.; Garcés-Castellote, E.; Sanz-Merodio, D.; Goñi-Arana, A.; Marín-Ojea, J.; García-Armada, E. A New Lower Limb Portable Exoskeleton for Gait Assistance in Neurological Patients: A Proof of Concept Study. J. NeuroEng. Rehabil. 2020, 17, 60. [Google Scholar] [CrossRef]
- Celik, Y.; Stuart, S.; Woo, W.L.; Godfrey, A. Gait Analysis in Neurological Populations: Progression in the Use of Wearables. Med. Eng. Phys. 2021, 87, 9–29. [Google Scholar] [CrossRef]
- Yeung, L.F.; Ockenfeld, C.; Pang, M.K.; Wai, H.W.; Soo, Y.O.Y.; Li, S.W.; Tong, K.Y. Design of an Exoskeleton Ankle Robot for Robot-Assisted Gait Training of Stroke Patients. Front. Neurosci. 2017, 11, 14. [Google Scholar]
- De Luca, A.; Bellitto, A.; Mandraccia, S.; Marchesi, G.; Pellegrino, L.; Coscia, M.; Leoncini, C.; Rossi, L.; Gamba, S.; Massone, A.; et al. Exoskeleton for Gait Rehabilitation: Effects of Assistance, Mechanical Structure, and Walking Aids on Muscle Activations. Appl. Sci. 2019, 9, 2868. [Google Scholar] [CrossRef]
- Rodríguez-Fernández, A.; Lobo-Prat, J.; Font-Llagunes, J. Systematic Review on Wearable Lower-Limb Exoskeletons for Gait Training in Neuromuscular Impairments. J. NeuroEng. Rehabil. 2021, 18, 22. [Google Scholar] [CrossRef]
- Cottam, D.S.; Campbell, A.C.; Davey, P.M.; Clarke, J.; James, D. Measurement of uni-planar and sport-specific trunk motion using magneto-inertial measurement units: The concurrent validity of Noraxon and Xsens systems relative to a retro-reflective system. Gait Posture 2022, 92, 129–134. [Google Scholar] [CrossRef] [PubMed]
- Sul, J.-H.; Piyathilaka, L.; Moratuwage, D.; Dunu Arachchige, S.; Jayawardena, A.; Kahandawa, G.; Preethichandra, D.M.G. Electromyography Signal Acquisition, Filtering, and Data Analysis for Exoskeleton Development. Sensors 2025, 25, 4004. [Google Scholar] [CrossRef] [PubMed]
- Park, Y.; Bae, Y. Increased Variability in Lower Limb Muscle Activation Is Observed with Increasing Walking Speed in Fall-Risk Older Adults. Life 2024, 14, 1551. [Google Scholar] [CrossRef] [PubMed]
- Seel, T.; Raisch, J.; Schauer, T. IMU-Based Joint Angle Measurement for Gait Analysis. Sensors 2014, 14, 6891–6909. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).