Wear Analysis of Conical Picks with Different Self-Rotatory Speeds
Abstract
1. Introduction
2. Methods
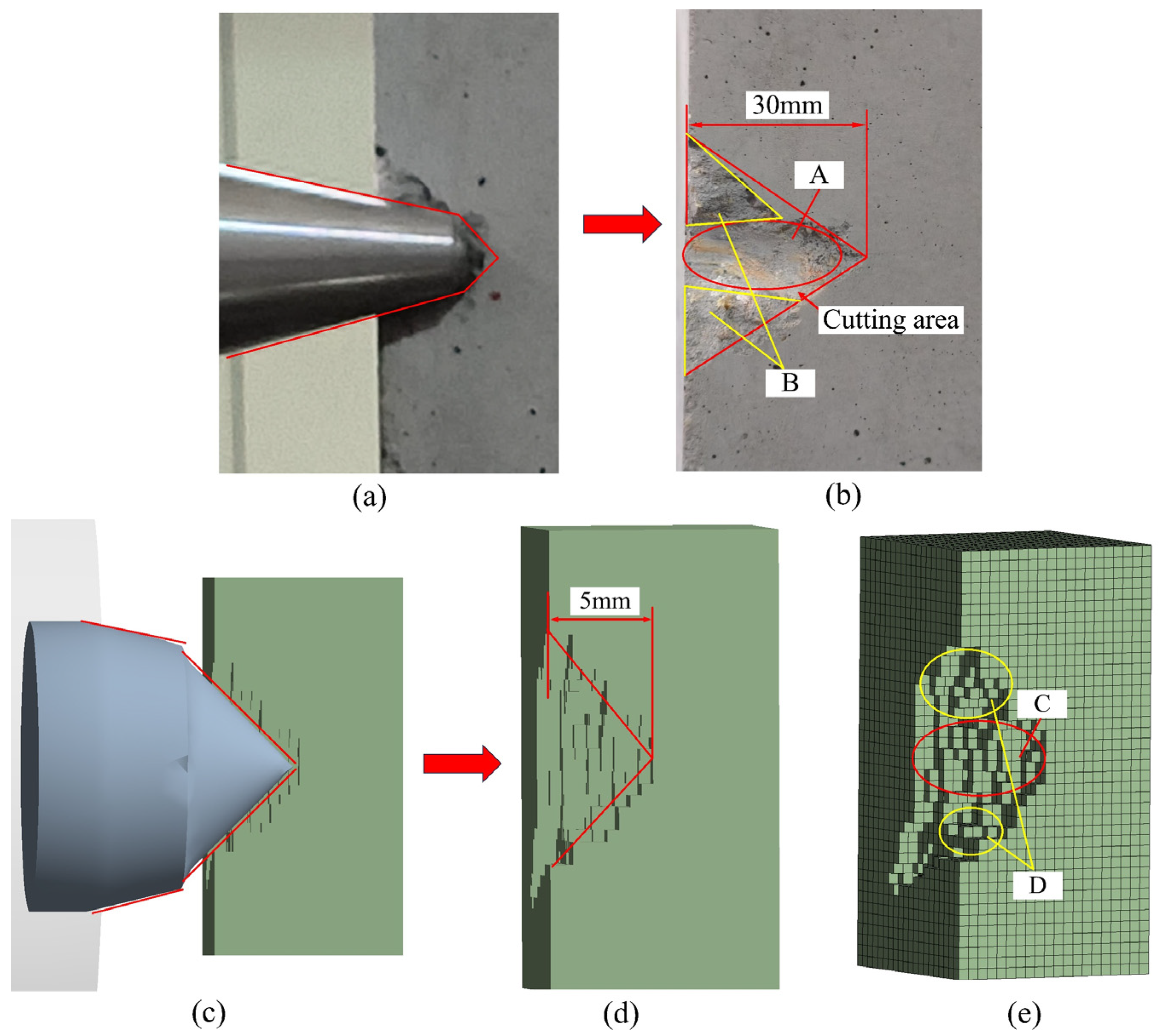
2.1. Experimental Methods
2.2. Simulation Methods
3. Results and Discussion
3.1. Qualitative Experimental Analysis of Self-Rotatory Speed and Wear
3.1.1. Weight Loss
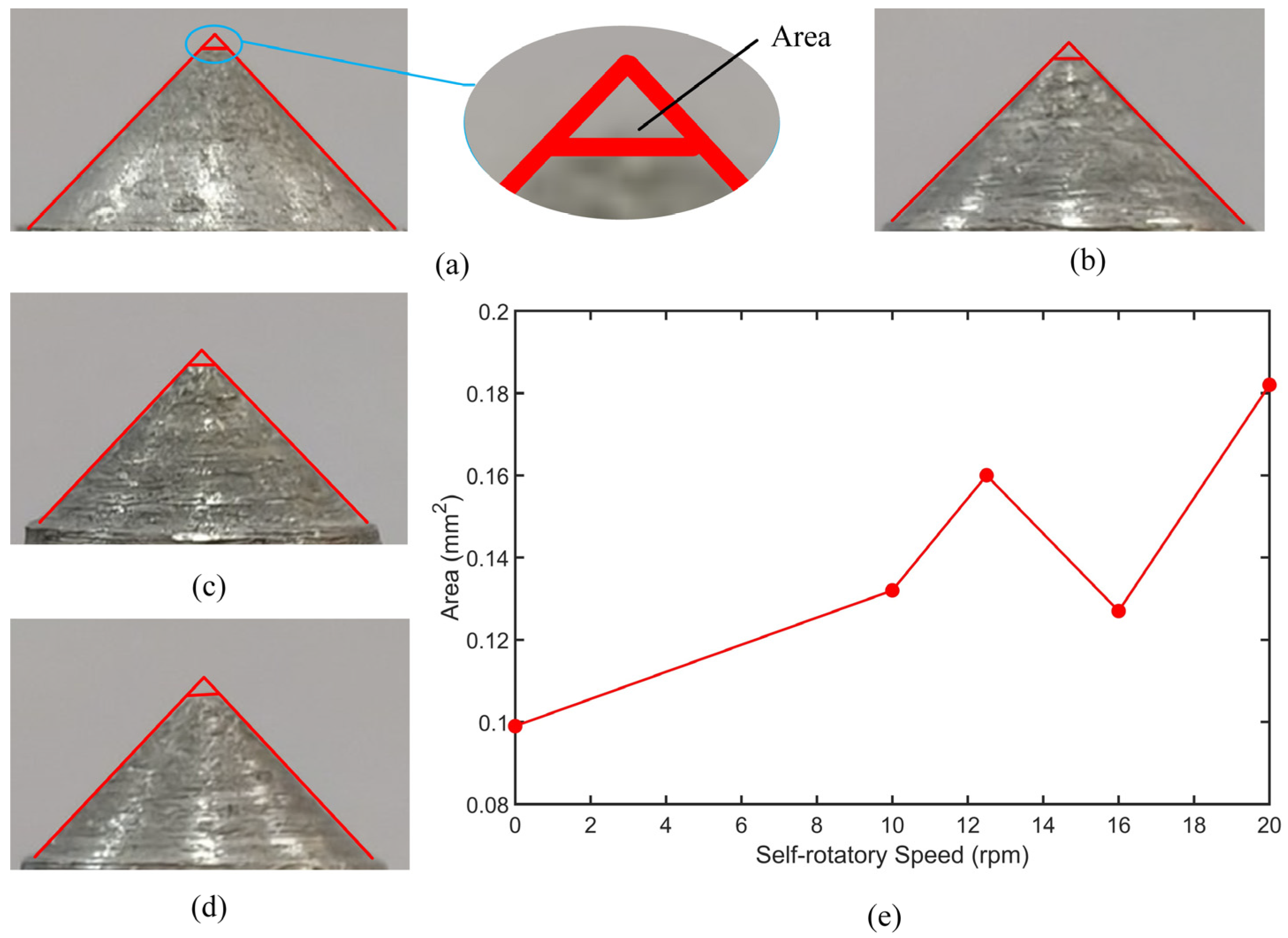
3.1.2. Wear Areas
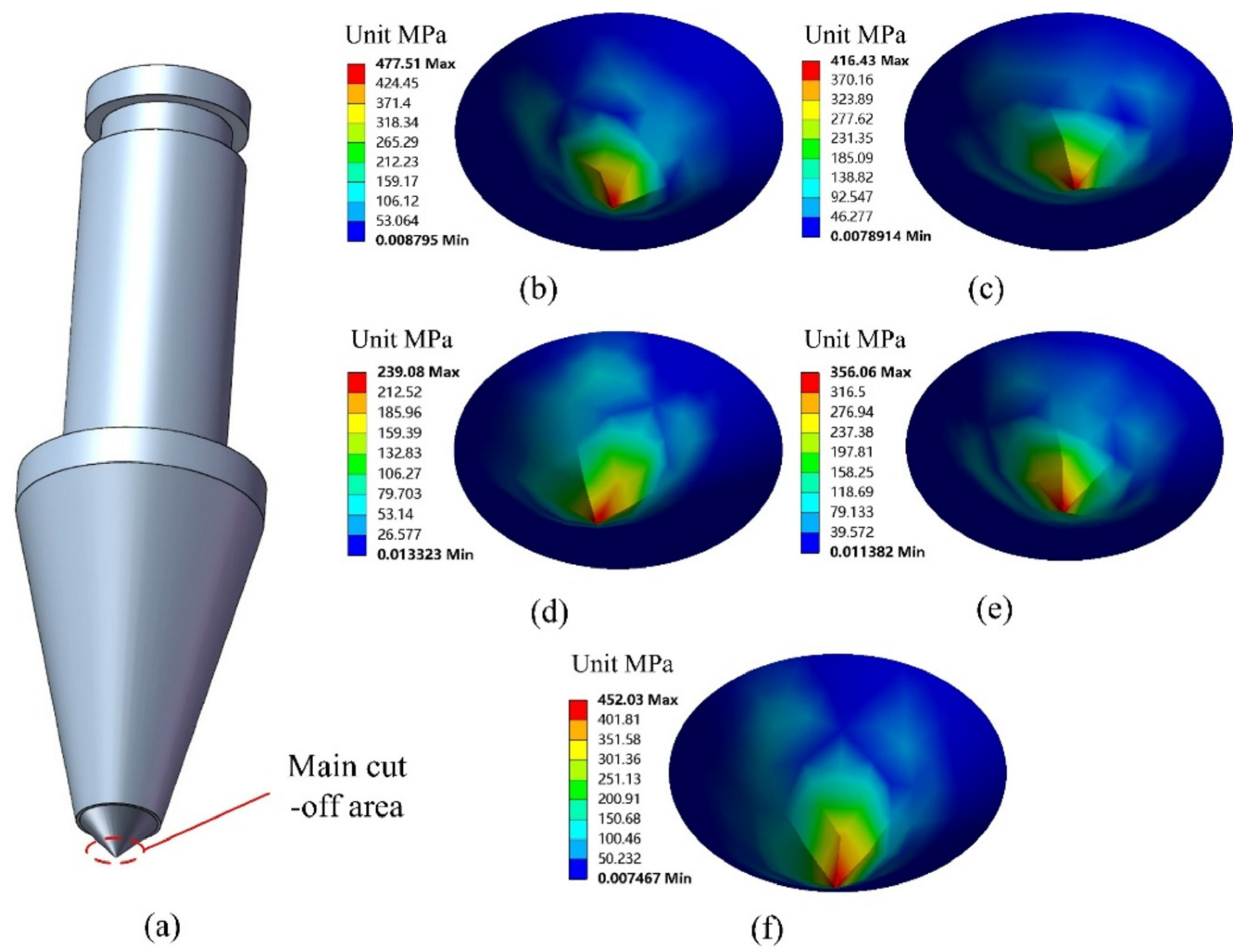
3.2. Simulation Analysis of Self-Rotatory Speed and Wear
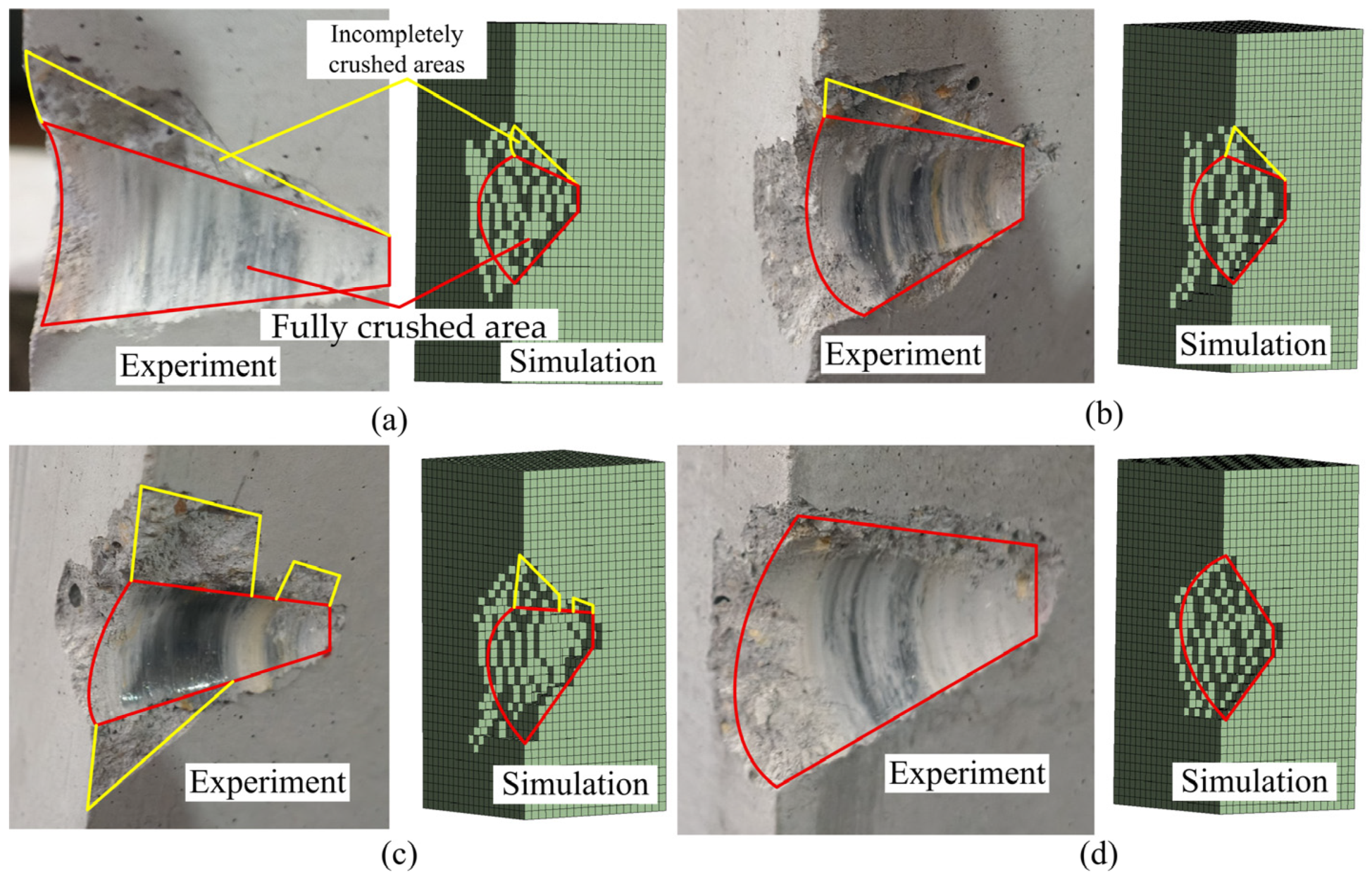
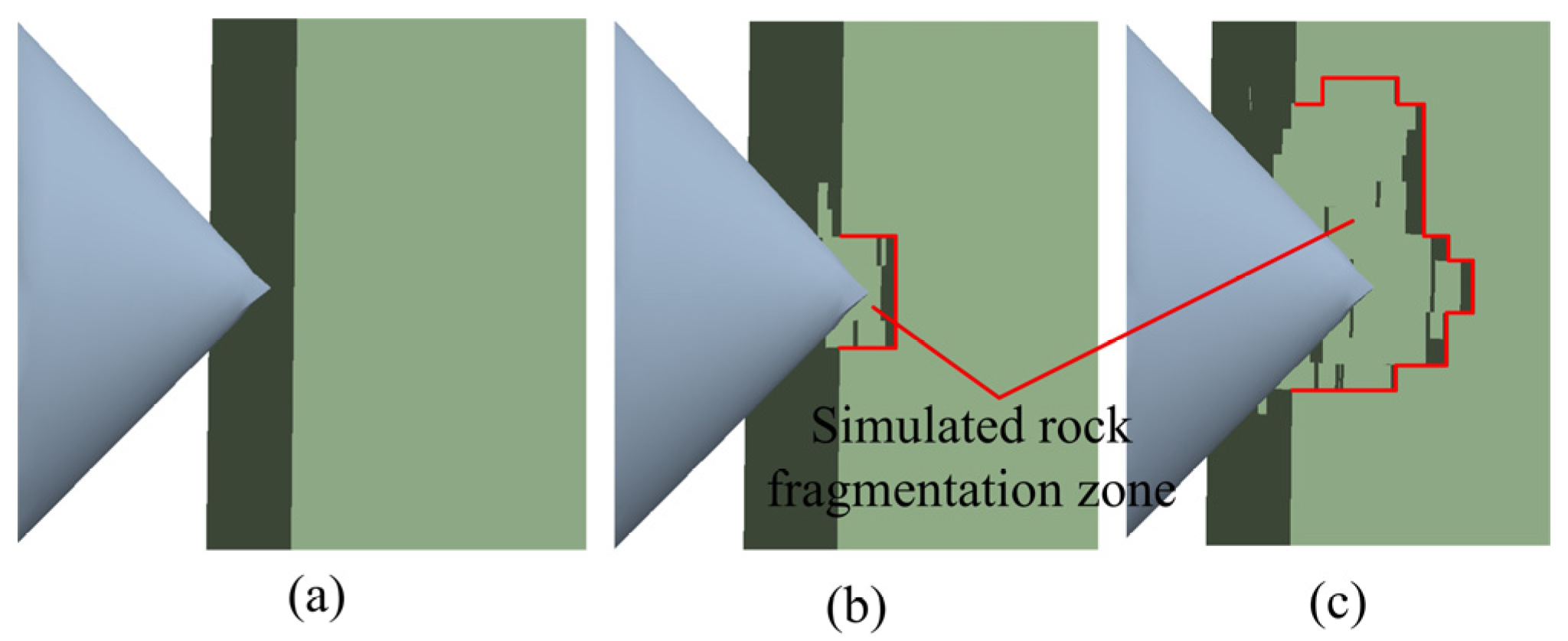
3.2.1. Consistency Analysis Between Simulation and Experiment in the Degree of Rock Fragmentation
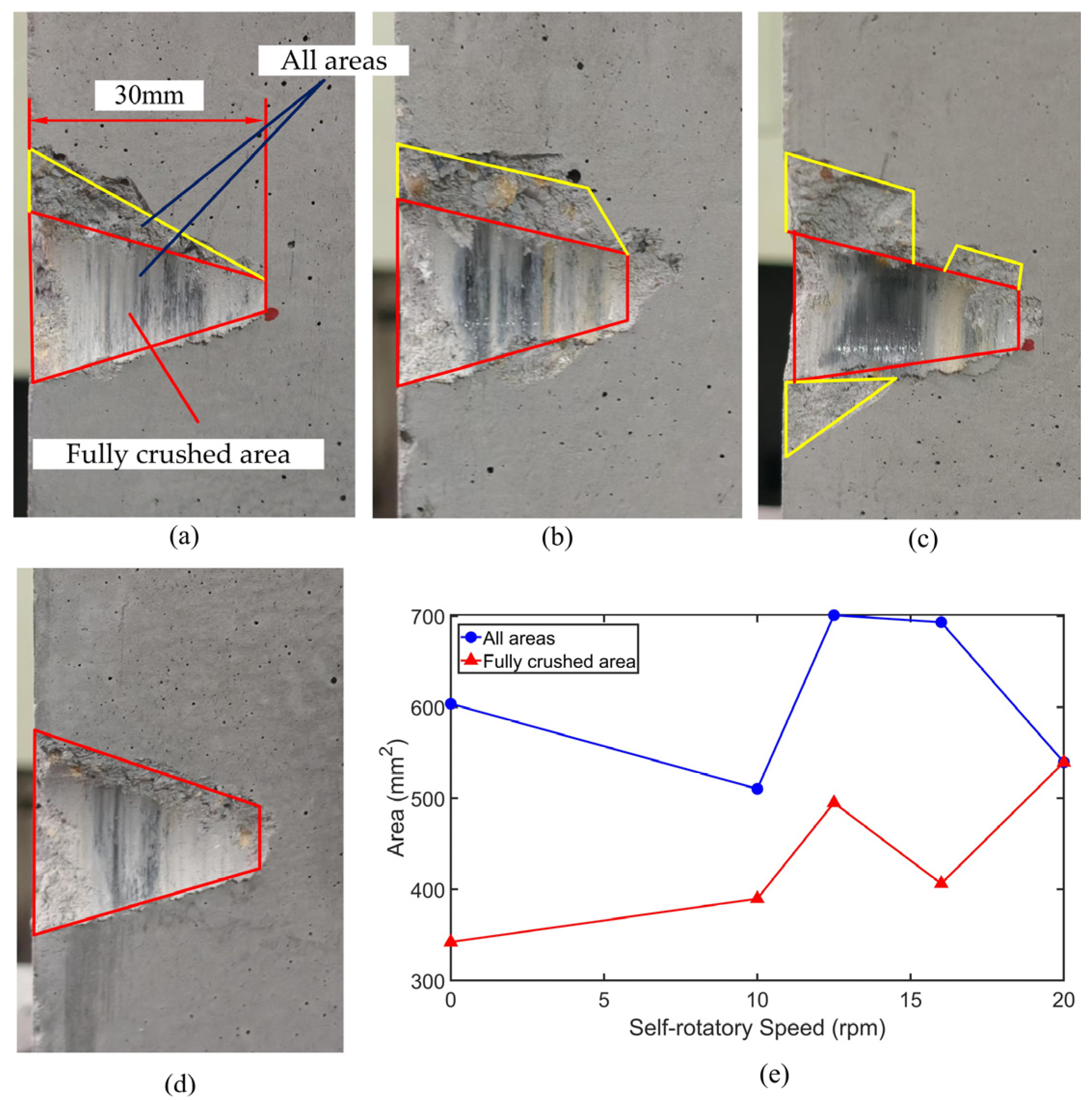
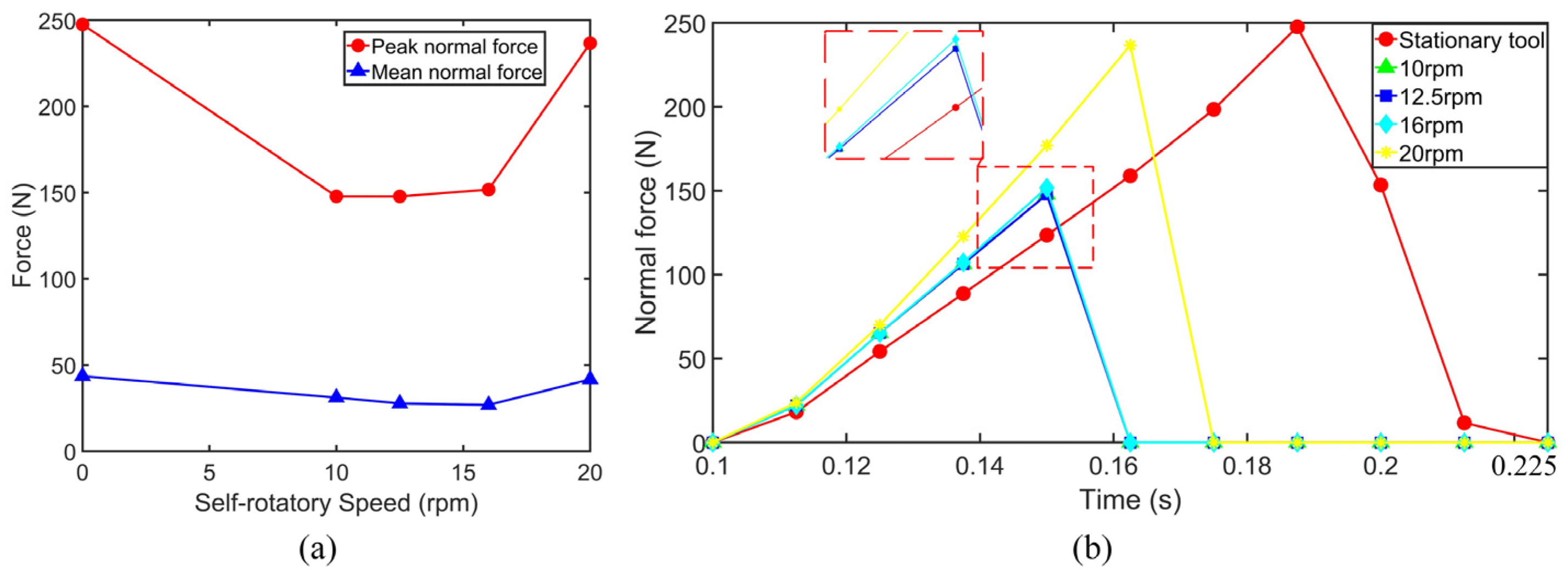
3.2.2. Analysis of the Correlation Between Self-Rotatory Speed and Wear of Conical Pick
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ergin, H.; Acaroglu, O. The effect of machine design parameters on the stability of a roadheader. Tunn. Undergr. Space Technol. 2007, 22, 80–89. [Google Scholar] [CrossRef]
- Prokopenko, S.; Li, A.; Kurzina, I.; Sushko, A. Improved Operating Performance of Mining Machine Picks. IOP Conf. Ser. Mater. Sci. Eng. 2016, 142, 012115. [Google Scholar] [CrossRef]
- Hoseinie, S.H.; Ataei, M.; Khalokakaie, R.; Ghodrati, B.; Kumar, U. Reliability analysis of drum shearer machine at mechanized longwall mines. J. Qual. Maint. Eng. 2012, 18, 98–119. [Google Scholar] [CrossRef]
- Hoseinie, S.H.; Ataei, M.; Khalokakaie, R.; Kumar, U. Reliability and maintainability analysis of electrical system of drum shearers. J. Coal Sci. Eng. China 2011, 17, 192–197. [Google Scholar] [CrossRef]
- Dewangan, S.; Chattopadhyaya, S.; Hloch, S. Wear Assessment of Conical Pick used in Coal Cutting Operation. Rock Mech. Rock Eng. 2015, 48, 2129–2139. [Google Scholar] [CrossRef]
- Dewangan, S.; Chattopadhyaya, S. Characterization of Wear Mechanisms in Distorted Conical Picks After Coal Cutting. Rock Mech. Rock Eng. 2016, 49, 225–242. [Google Scholar] [CrossRef]
- Krauze, K.; Mucha, K.; Wydro, T.; Pieczora, E. Functional and operational requirements to be fulfilled by conical picks regarding their wear rate and investment costs. Energies 2021, 14, 3696. [Google Scholar] [CrossRef]
- Luo, Y.; Zhang, D.; Wang, Q.; Liu, H.; Cheng, G.; Ge, S. Preparation and properties of a new cutting pick of coal shearers. Int. J. Min. Sci. Technol. 2010, 20, 794–796. [Google Scholar] [CrossRef]
- Eshaghian, O.; Hoseinie, S.H.; Salimi Jazi, H. Effects of Ni-based composite coatings on failure mechanism and wear resistance of cutting picks on coal shearer machine. Eng. Fail. Anal. 2023, 151, 107342. [Google Scholar] [CrossRef]
- Jiang, H.; Meng, D. Experimental Research on the Specific Energy Consumption of Rock Breakage Using Different Waterjet-Assisted Cutting Heads. Adv. Mater. Sci. Eng. 2018, 2018, 3853980. [Google Scholar] [CrossRef]
- Zhou, X.; Guo, C.; Zhang, H.; Liu, Y.; Bai, J.; Wang, F. Experimental and numerical investigation on rock breaking of conical pick assisted by abrasive water jet gridding pre-cutting method. J. Braz. Soc. Mech. Sci. Eng. 2023, 45, 599. [Google Scholar] [CrossRef]
- Sun, Y.; Li, X.S.; Harbers, C.; Williams, D.; Boland, J.N. Wear and cutting temperature of thermally stable diamond composite tipped pick in hard rock cutting. Wear 2023, 523, 204848. [Google Scholar] [CrossRef]
- Zhang, X.; Li, X.; Xu, W.; Gao, K.; Jiang, K.; Wang, X.; Wei, H. Experimental investigation of the failure of conical picks under thermal and abrasive effects. Eng. Fail. Anal. 2024, 156, 107737. [Google Scholar] [CrossRef]
- Li, X.; Wang, S.; Ge, S.; Malekian, R.; Li, Z. A Theoretical Model for Estimating the Peak Cutting Force of Conical Picks. Exp. Mech. 2018, 58, 709–720. [Google Scholar] [CrossRef]
- Wang, Z.; Zeng, Q.; Wan, L.; Lu, Z.; Wang, H. Investigation of the Influence of Cutting Parameters on Conical Pick Cutting Performance and Rock Damage. Machines 2022, 10, 1034. [Google Scholar] [CrossRef]
- Fan, Q.; Chen, C.; Zhang, Q.; Liu, G. A dynamic analysis of a conical pick during rock-cutting process based on the smooth finite element method. Wear 2023, 512–513, 204523. [Google Scholar] [CrossRef]
- Liu, S.F.; Lu, S.F.; Wan, Z.J.; Cheng, J.Y. Investigation of the influence mechanism of rock damage on rock fragmentation and cutting performance by the discrete element method. R. Soc. Open Sci. 2019, 6, 190116. [Google Scholar] [CrossRef]
- Wang, S.; Shi, X.; Wu, Y. DEM-based 2D numerical simulation of the rock cutting process using a conical pick under confining stress. Comput. Geotech. 2024, 165, 105885. [Google Scholar] [CrossRef]
- Menezes, P.L.; Lovell, M.R.; Avdeev, I.V.; Lin, J.S.; Higgs, C.F. Studies on the formation of discontinuous chips during rock cutting using an explicit finite element model. Int. J. Adv. Manuf. Tech. 2014, 7, 635–648. [Google Scholar] [CrossRef]
- Liu, X.; Tang, P.; Li, X.; Tian, M. Self-rotatory performance of conical cutter interacted with rock material. Eng. Fail. Anal. 2017, 80, 197–209. [Google Scholar] [CrossRef]
- Liu, X.; Geng, Q. Effect of contact characteristics on the self-rotation performance of conical picks based on impact dynamics modelling. R. Soc. Open Sci. 2020, 7, 200362. [Google Scholar] [CrossRef]
- Yasar, S.; Odoom, K.; Shepel, T.; Bretschneider, J.; Drebenstedt, C. Rotation Enhancement of Conical Picks Coupled with Springs. Rock Mech. Rock Eng. 2023, 56, 5447–5453. [Google Scholar] [CrossRef]
- Hekimoglu, O.Z. Suggested methods for optimum rotative motion of point attack type drag tools in terms of skew angles. Int. J. Min. Reclam. Environ. 2020, 34, 573–591. [Google Scholar] [CrossRef]
- Akintunde, I.B.; Lindsay, E.E.; Olakanmi, E.O.; Prasad, R.V.S.; Matshediso, B.I.; Motimedi, T.; Botes, A.; Pityana, S.L. Performance evaluation and failure analysis of conical picks used in a Botswana (Ngwato) mine. Eng. Fail. Anal. 2023, 143, 106872. [Google Scholar] [CrossRef]
- Luo, P.; Li, D.; Ru, W.; Gong, H.; Wang, M. Hard rock fragmentation by dynamic conical pick indentation under confining pressure. Int. J. Rock Mech. Min. Sci. 2024, 183, 105932. [Google Scholar] [CrossRef]
- Jiang, H.; Meng, D. 3D numerical modelling of rock fracture with a hybrid finite and cohesive element method. Eng. Fract. Mech. 2018, 199, 280–293. [Google Scholar] [CrossRef]
- Wang, S.; Li, X.; Du, K.; Wang, S. Experimental investigation of hard rock fragmentation using a conical pick on true triaxial test apparatus. Tunn. Undergr. Space Technol. 2018, 79, 210–223. [Google Scholar] [CrossRef]
- Yang, D.; Jianping, L.I.; Zheng, K.; Jiang, H.; Handong, X.U.; Liu, S. High-hardness alloy substituted by low hardness during drilling and cutting experiments of conical pick. Int. J. Rock Mech. Min. Sci. 2017, 95, 73–78. [Google Scholar] [CrossRef]
- Liu, S.; Ji, H.; Liu, X.; Jiang, H. Experimental research on wear of conical pick interacting with coal-rock. Eng. Fail. Anal. 2017, 74, 172–187. [Google Scholar] [CrossRef]
- Zhao, H.; Zhang, L.; Wu, Z.; Liu, A. A new discrete element model for rock-like materials. Comput. Struct. 2022, 261–262, 106730. [Google Scholar] [CrossRef]
- Lu, Z.; Wan, L.; Zeng, Q.; Zhang, X.; Gao, K. Numerical Simulation of Fragment Separation during Rock Cutting Using a 3D Dynamic Finite Element Analysis Code. Adv. Mater. Sci. Eng. 2017, 2017, 3024918. [Google Scholar] [CrossRef]
- Wicaksana, Y.; Jeong, H.; Jeon, S. Numerical simulation of rock cutting process induced by a pick cutter considering dynamic properties of rock at intermediate strain rate. Bull. Eng. Geol. Environ. 2021, 80, 9049–9069. [Google Scholar] [CrossRef]
- Evans, I. A Theory of the Basic Mechanics of Coal Ploughing. In Proceedings of the International Symposium on Mining Research, Columbia, MO, USA, February 1961; Pergamon Press: Oxford, UK, 1962; pp. 761–798. [Google Scholar] [CrossRef]
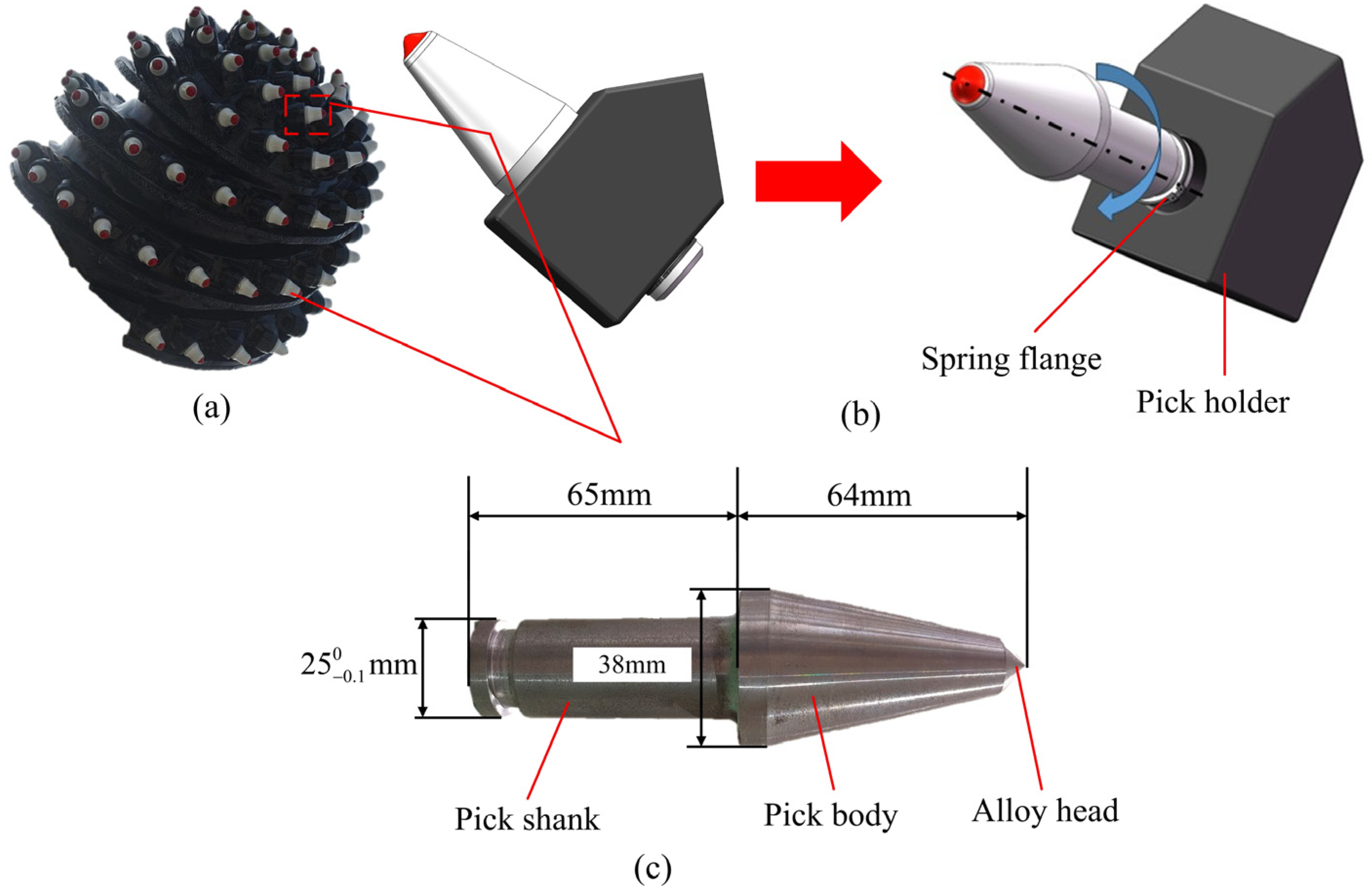
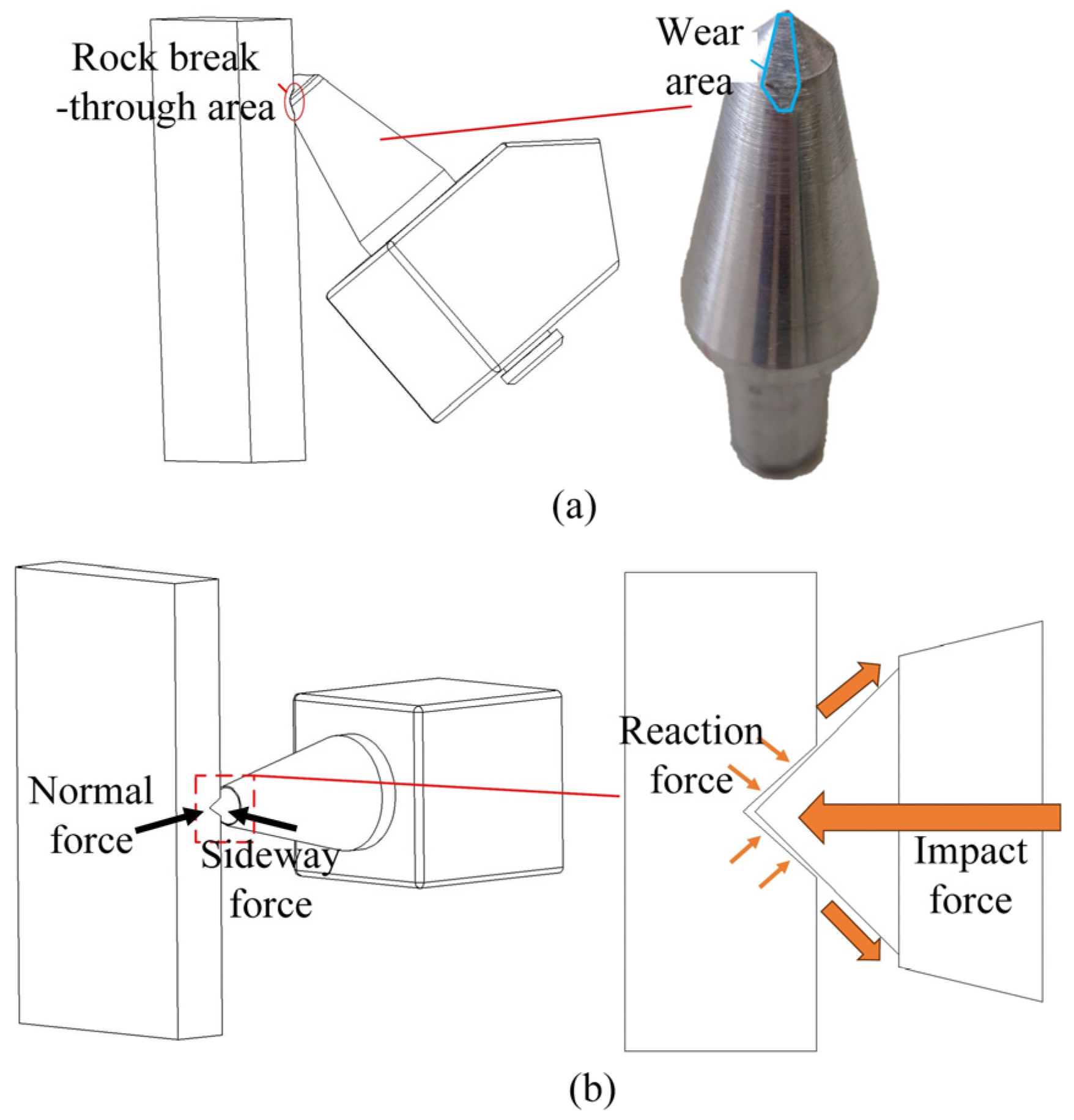



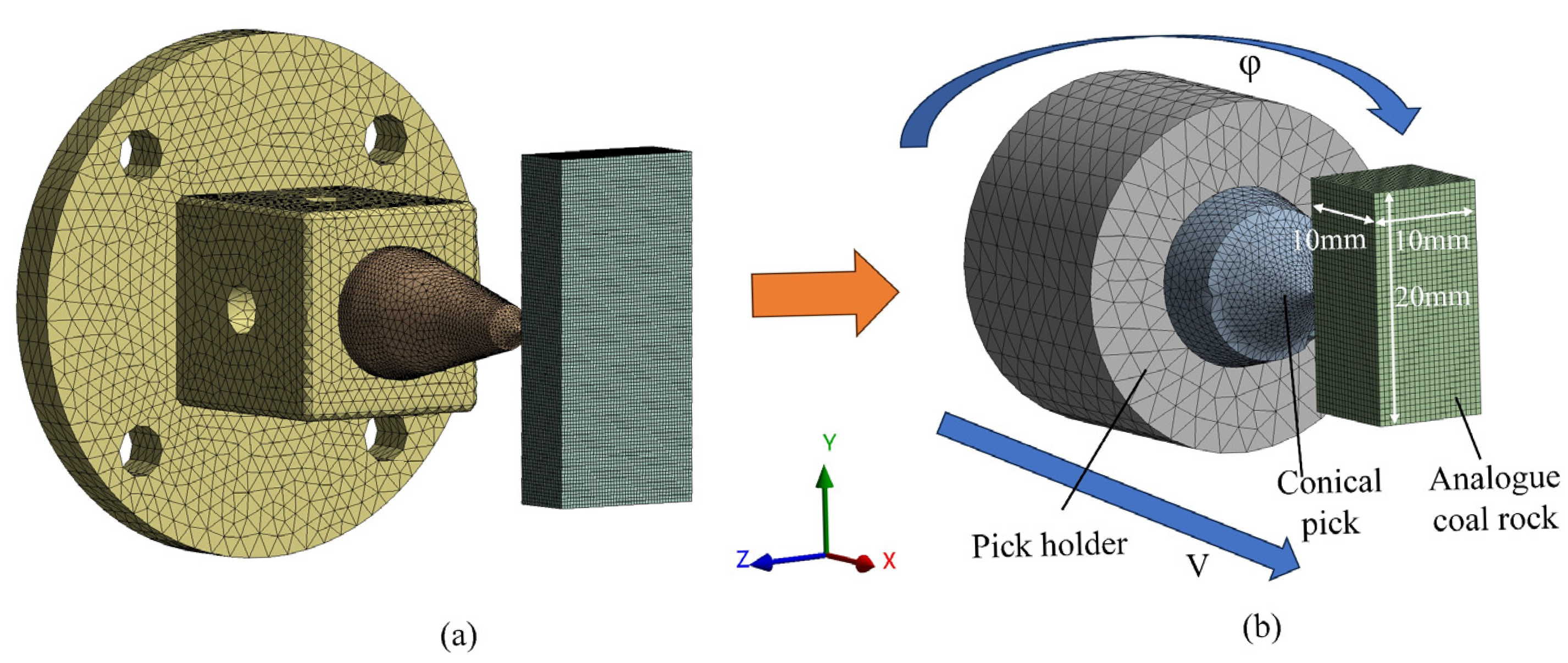
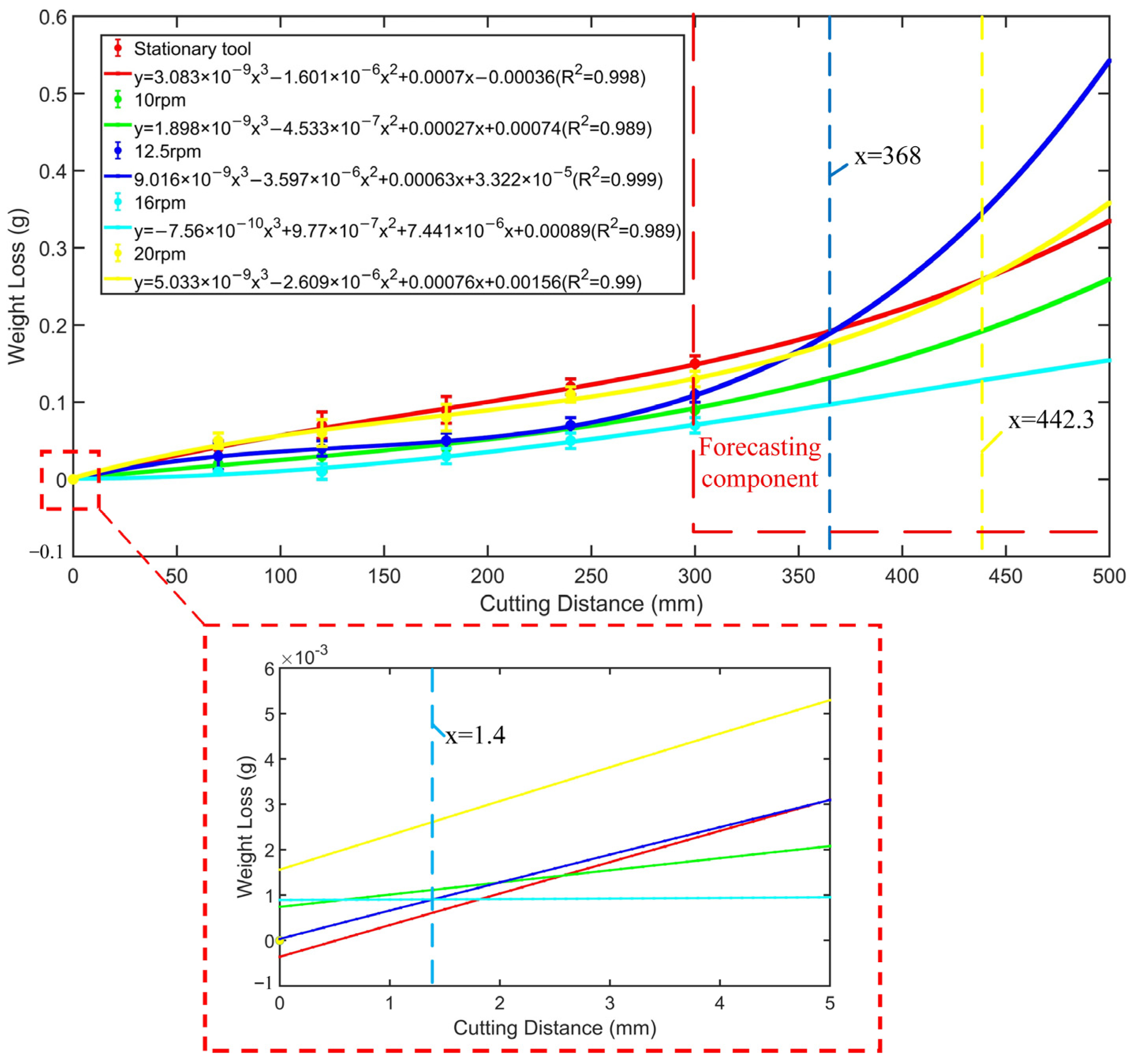


| Material | Density (g/cm3) | Young’s Modulus (GPa) | Poisson’s Ratio | Tensile Stress (MPa) | Compressive Strength (MPa) | |
|---|---|---|---|---|---|---|
| A3 | 7.85 | 205.8 | 0.3 | 500 | ||
| Test specimen | 2.236 | 2.0308 | 0.22 | 1.01 | 15 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, Y.; Peng, X.; Ma, Z.; Li, F. Wear Analysis of Conical Picks with Different Self-Rotatory Speeds. Machines 2025, 13, 957. https://doi.org/10.3390/machines13100957
Zhou Y, Peng X, Ma Z, Li F. Wear Analysis of Conical Picks with Different Self-Rotatory Speeds. Machines. 2025; 13(10):957. https://doi.org/10.3390/machines13100957
Chicago/Turabian StyleZhou, Youhang, Xin Peng, Zhuxi Ma, and Fang Li. 2025. "Wear Analysis of Conical Picks with Different Self-Rotatory Speeds" Machines 13, no. 10: 957. https://doi.org/10.3390/machines13100957
APA StyleZhou, Y., Peng, X., Ma, Z., & Li, F. (2025). Wear Analysis of Conical Picks with Different Self-Rotatory Speeds. Machines, 13(10), 957. https://doi.org/10.3390/machines13100957






