Design of a PM-Assisted Synchronous Reluctance Motor with Enhanced Performance and Lower Cost for Household Appliances

Abstract

Conventional permanent magnet-assisted synchronous reluctance machine (PMaSynRM) suffers from limited power factor and efficiency. To boost these, the use of sintered rare earth permanent magnets (PMs) is an option, with respect to sintered ferrite, resulting in a high-performance PMaSynRM (HP-PMaSynRM). However, the increasing price of rare earth PM can lead to an overall increase in machine cost. To overcome this issue, a novel HP-PMaSynRM is presented in this paper. Structurally, the proposed four-pole HP-PMaSynRM rotor is characterized by two fluid-shaped flux barriers filled with sintered ferrite, as well as a cut-off region. Based on the finite element analysis (FEA) results, the proposed HP-PMaSynRM exhibits higher performance compared with the conventional HP-PMaSynRM with rare earth PMs. It is shown that the proposed HP-PMaSynRM has higher power factor, efficiency, and better torque quality over a wide range of operating conditions. Moreover, the HP-PMaSynRM presented incurs lower cost. Finally, the proposed HP-PMaSynRM is manufactured, tested, and compared with the conventional benchmark HP-PMaSynRM, proving its advantages, including higher power factor, higher efficiency, lower torque oscillation, and lower cost.

1. Introduction

Electrical motors are widely used in various applications such as aerospace, automotive, industry, and household appliances [1,2,3,4]. These motors have different topologies, depending on the corresponding application cases [5,6,7,8,9]. In household applications, the motor cost is one of the key performance indicators, in addition to the efficiency and torque requirements. Thus, synchronous reluctance motors (SynRMs) have gained increasing interest in this application, thanks to their lower cost and higher efficiency compared with traditional induction motors (IMs) [10].

Generally, rotors of SynRMs are characterized by multilayer flux barriers. SynRMs exhibit only reluctance torque owing to the absence of PMs, which limits the power factor, torque density, and efficiency level of the motor [11]. Various methods have been researched in the literature in order to enhance the anisotropy for better performance of such motor topology [12,13,14]. A common solution is to use regular-shaped rectangular sintered PM in the center part of each flux barrier layer. Normally, sintered ferrite PMs are utilized for economic considerations [15]. In this paper, a PMaSynRM with only regular-shaped rectangular sintered ferrite is referred to as a conventional PMaSynRM.

Conventional PMaSynRMs exhibit higher efficiency and power factor compared with SynRMs since the existence of ferrite PMs not only assists the saturation of the rotor ribs, but also contributes a small amount of torque production [16]. In [17], a number of studies investigating to enhance the performance of conventional PMaSynRM are reviewed in the literature. It is demonstrated that torque ripple can be significantly reduced by adopting an optimal rotor design or skewing techniques [18,19,20]. Research in [21] indicates that torque ripple resulting from the reluctance can be reduced while maintaining the average torque by designing a rotor with sinusoidal lamination. However, the rotor lamination disparity requires additional manufacturing cost, and the rotor complexity can be an impediment in assembly. Another strategy implemented to minimize the torque ripple is by optimizing the flux barrier angles and insulation ratio [22]. It is also illustrated that, by combining rotor asymmetry with rotor parameter optimization, torque ripple in conventional PMaSynRM can be limited within a small value [23]. Apart from the torque ripple, limited power factor and efficiency are also considered as downsides of conventional PMaSynRMs when directly compared with permanent magnet synchronous motors (PMSMs) with rare earth PMs [24]. In recent literature, some alternative solutions using asymmetrical topologies with the magnet-axis-shift (MAS) effect are proposed in order to maximize the average torque capacity, power factor, and efficiency [25]. However, the improvement from the MAS effect is limited. The electromagnetic performance of conventional PMaSynRMs is still not competitive against PMSMs owing to the disparity between ferrite and rare earth PMs [26]. Therefore, in conventional HP-PMaSynRMs, regular-shaped rectangular sintered rare earth PMs (e.g., NdFeB) are partially or completely used instead of only sintered ferrite PMs in conventional PMaSynRMs to satisfy the higher efficiency, power, and torque density demands [27]. In [28], a PMaSynRM with NdFeB bonded magnets in U shape is designed and tested, showing its enhanced power factor and torque capability over traditional SynRM. However, the remanence of the bonded NdFeB is even lower than some sintered ferrites. As a result, it is not a cost-effective method from the electromagnetic point of view.

Conventional HP-PMaSynRMs possess excellent performance since the high remanence and coercivity of the sintered rare earth PMs provide strong rotor field excitation [29], whereas their limited availability and harmful environmental impact increase the final motor cost [30]. This issue is critical in applications that need mass production and strict cost constraints such as household appliances [31].

In this paper, a complete rare earth free novel HP-PMaSynRM is proposed aiming to demonstrate that PMaSynRM with only ferrite PMs is possible to have better performance than conventional HP-PMaSynRMs with rare earth PMs in terms of power factor, efficiency, and torque quality. Moreover, the cost advantage of the proposed motor is highlighted. Such HP-PMaSynRM is designed and manufactured with two fluid-shaped flux barriers filled with sintered ferrite PMs and a cut-off region. The proposed HP-PMaSynRM introduces a novelty with respect to the state of the art for this machine class.

This paper is organized as follows: In Section 2, the conventional benchmark HP-PMaSynRM (M1) is introduced. In Section 3, the proposed novel HP-PMaSynRM (M2) is characterized, and a detailed comparison with M1 is performed via FEA, indicating the advantages of M2 in terms of higher electromagnetic performance including higher average torque capability, lower torque ripple, higher power factor, and higher efficiency over a wide range of operating conditions. Moreover, the cost advantage of M2 is highlighted. A structural FEA of M2 is also carried out in this section in order to ensure the structural robustness of M2. In Section 4, the experimental results are shown to prove the reliability of the FEA analysis. Finally, the conclusion of the paper is presented in Section 5.

2. Reference Conventional HP-PMaSynRM

Figure 1 shows one pole of the conventional three-phase four-pole HP-PMaSynRM motor (M1). A single-layer integral slot distributed winding (ISDW) is used in the stator winding configuration in order to guarantee the highest saliency ratio to exhibit the highest reluctance torque [32].

As shown in Figure 1, the rotor of the conventional HP-PMaSynRM is characterized by three flux barrier layers. PMs are inserted in the middle part of each barrier layer mainly to saturate the flux leakage in the q-axis for higher rotor anisotropy and to contribute a portion of magnetic torque. Consequently, the overall torque of the HP-PMaSynRM motor is the sum of both magnetic torque and reluctance torque, as shown in the following Equation (1):

$${\mathit{T}}_{\mathit{e}}={\displaystyle \frac{3}{2}}p({\lambda }_{pm}{i}_d+(L_d-L_q)i_d{i}_q)$$

(1)

where $T_e$ is the total electromagnetic torque; p is the number of pole pairs; ${\lambda }_{pm}$ is the flux linkage of the magnet; $L_d$ and $L_q$ are the d-axis and q-axis inductance, respectively; and $i_d$ and $i_q$ are the d-axis and q-axis current, respectively.

A sketch of one pole of the M1 rotor is shown in Figure 2 with geometrical identifications. Both the center ribs and the tangential ribs in Figure 2 exist to guarantee the mechanical property of the iron lamination within the maximum operating speed 7200 rpm for the required safety margin.

Table 1. M1 parameters.

Rotor Geometry	Label	Value	Unit
Rotor outer diameter	$D_{re}$	53.3	mm
Rotor inner diameter	$D_{ri}$	12.96	mm
Pole pairs	p	2	-
Radial rib thickness	$W_{rad}$	0.45	mm
Tangential rib thickness	$W_{tan}$	0.45	mm
First layer PM width	$W_{pm1}$	5.4	mm
First layer PM height	$h_{pm1}$	1.8	mm
Second layer PM width	$W_{pm2}$	10.8	mm
Second layer PM height	$h_{pm2}$	2.4	mm
Third layer PM width	$W_{pm3}$	10.8	mm
Third layer PM height	$h_{pm3}$	2.4	mm
Rated Condition Performance	Label	Value	Unit
Rated torque	$T_{av}$	1.9	Nm
Rated speed	$\omega$	5400	r/min
Rated power	$P_{out}$	1074.4	W
DC-link voltage	$V_{dc}$	310	V
Rated phase current	$I_{ph}$	3.4	Arms
Rated phase voltage	$V_{ph}$	118.6	Vrms
Power factor	$\lambda$	0.925	-
Copper loss	$P_{copper}$	37.89	W
Iron loss	$P_{iron}$	30.2	W
Efficiency	$\eta$	94.04	%
Torque ripple percentage	$T_{ripple}$	14.57	%

reports M1 parameters, including rotor geometry and performance.

3. HP-PMaSynRM with Enhanced Performance

To further improve the motor performance such as power factor and efficiency, the option is either to increase the magnetic torque component or to enhance the reluctance torque component in Equation (1) so that the motor can exhibit higher overall torque. However, the simple additional insertion of N30H would increase the motor cost. Thus, ferrite is introduced to replace the role of the rare earth PM N30H.

In this section, a ferrite-assisted HP-PMaSynRM M2 is presented, and the exact optimal shape of ferrite to produce the best torque capability is investigated. The motor output results are compared with the conventional M1 in the previous section in order to show the unique advantage of the proposed new HP-PMaSynRM.

3.1. Motor Characterization

In general, M2 shares the same stator, winding configuration, stack length, rotor outer and inner diameters, and iron material with M1. The only difference is ferrite Y-40 is inserted in the rotor barrier in M2 instead of using rare earth PM material N30H in M1.

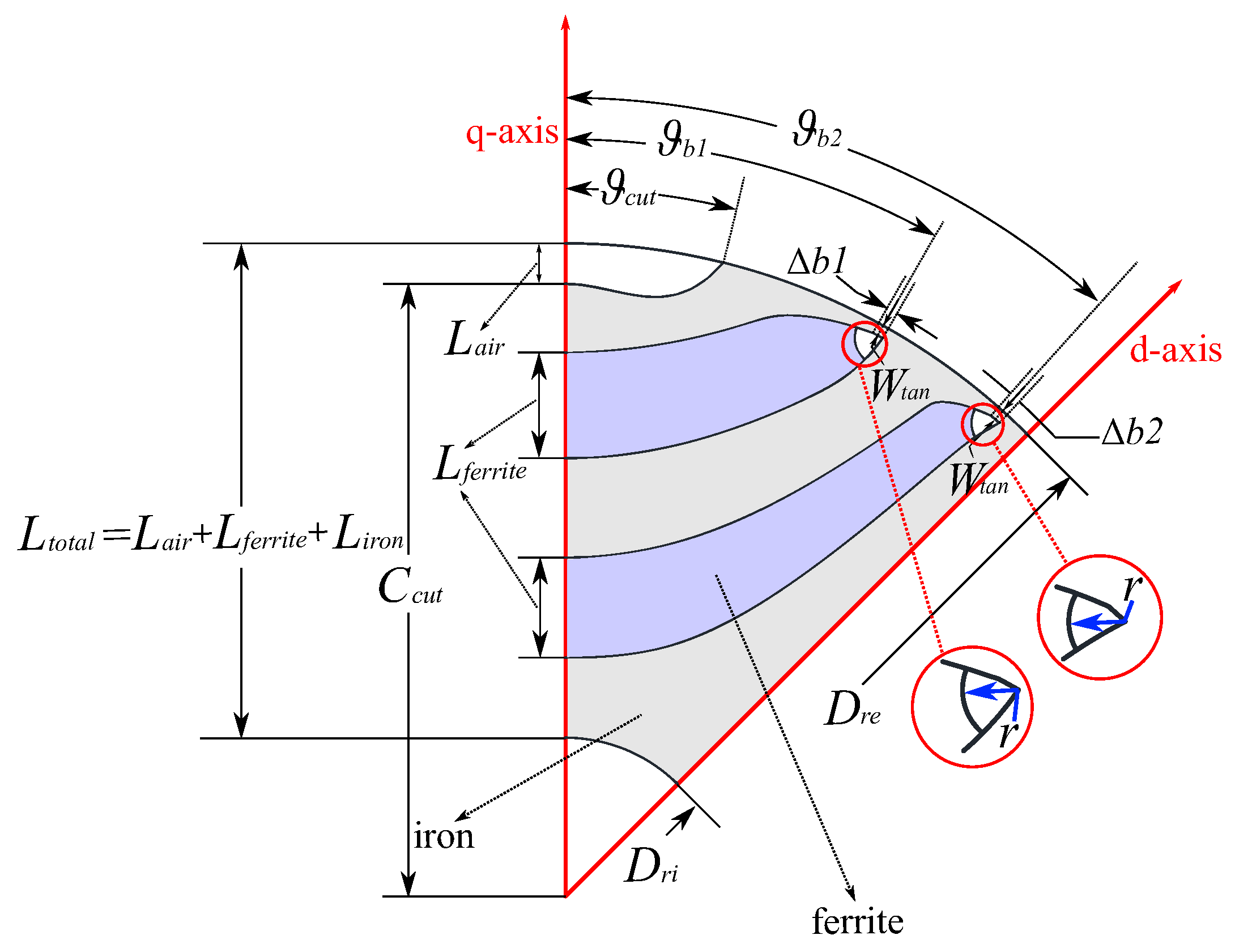
Figure 3 shows half a pole of the M2 rotor. It is characterized by two fluid-shaped flux barriers filled with ferrite magnets. In addition, the M2 rotor also has a cut-off region at the q-axis.

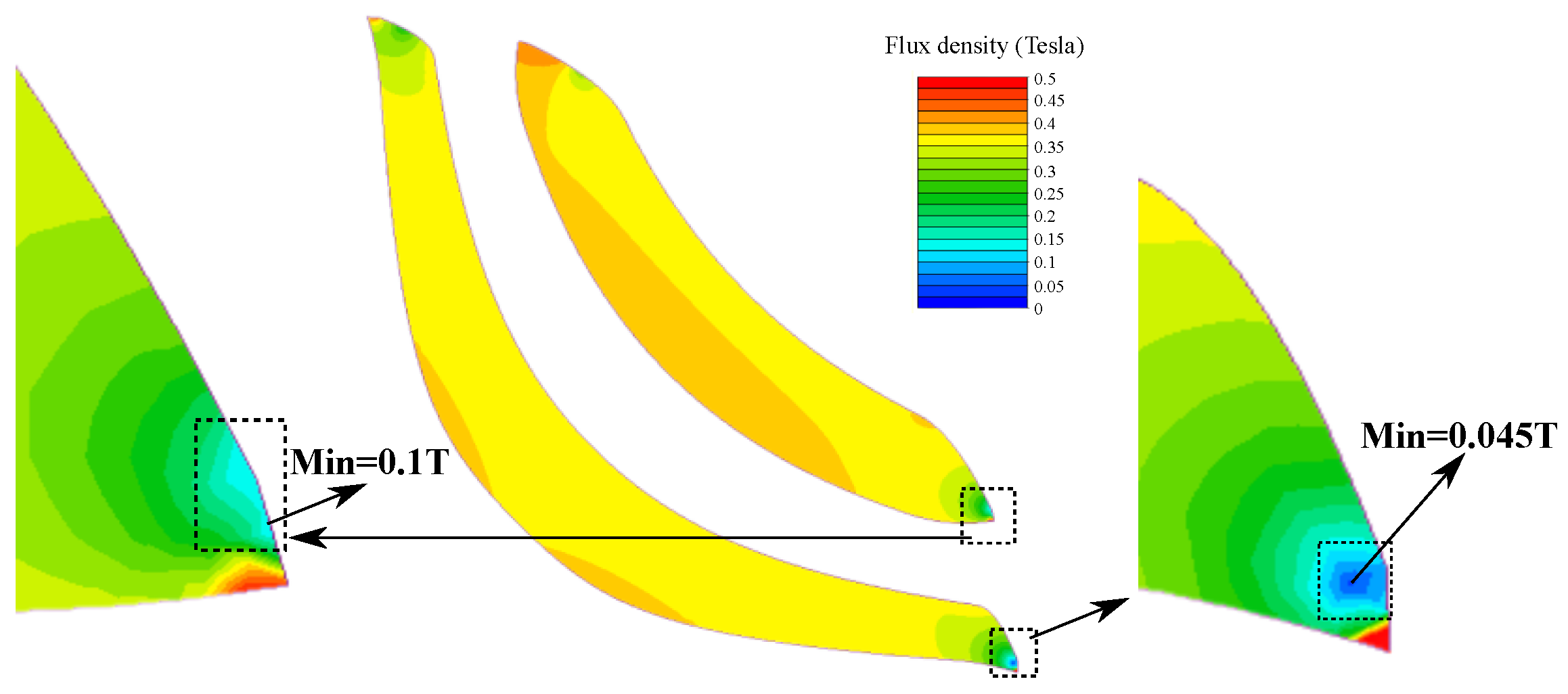
Ferrite in M2 shares the same magnetic flux direction in q-axis. At each flux barrier end of the rotor, there is a small region with air instead of ferrite, which is highlighted in Figure 3. This is mainly for the purpose of avoiding ferrite demagnetization owing to the high saturation level over the tangential rib region. As shown in Figure 4, the flux density of the ferrite on the barrier end would be below the demagnetization knee value if the air region highlighted in Figure 3 is not added. However, as illustrated in Figure 5, the flux density of the ferrite on the barrier end would be safely above the demagnetization knee value according to

Table 2. Ferrite Y-40 property.

Property Item	Label	Value	Unit
Coercivity	$H_{cb}$	342.4	kA/m
Intrinsic coercivity	$H_{cj}$	357.26	kA/m
Remanence	$B_r$	0.45	T
Demagnetization knee	$B_{md}$	0.12	T

, thanks to the air region. A detailed flux density behavior analysis on the ferrite end during a full electrical cycle is recorded in Figure 6, showing the minimum value of 0.1789 T, which is above the demagnetization knee value 0.12 T.

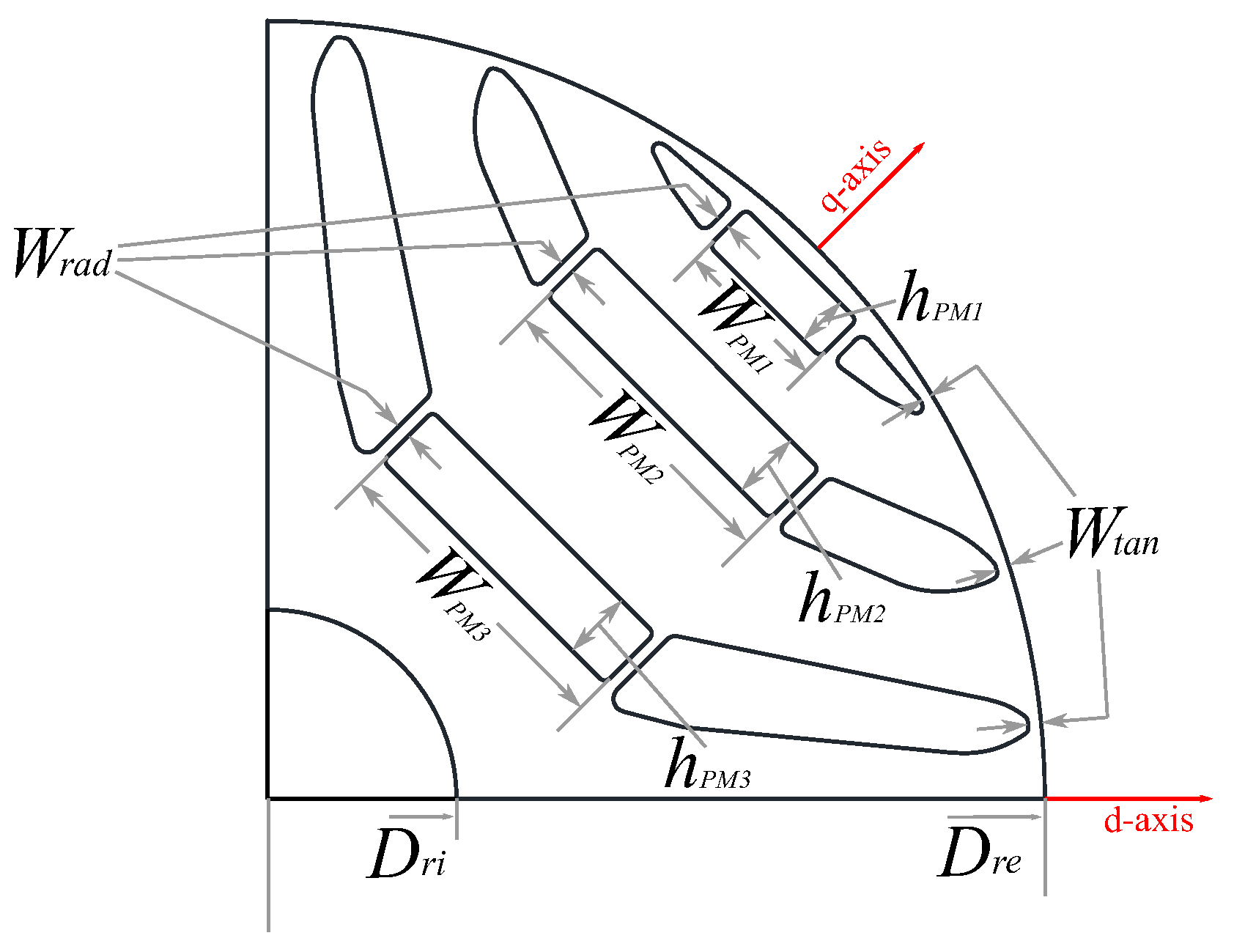
The main geometrical parameters considered in Figure 3 can be summarized below:

• $D_{re}$ and $D_{ri}$ are rotor outer and inner diameters;
• ${\vartheta }_{b1}$ and ${\vartheta }_{b2}$ are barrier angles;
• $W_{tan}$ is tangential rib thickness;
• $\mathrm{\Delta }b1$ and $\mathrm{\Delta }b2$ are flux barrier end opening angles;
• $L_{ferrite}$ and $L_{iron}$ are ferrite and iron length in q-axis correspondingly, $L_{total}$ is the total length in q-axis, $L_{air}$ is the air length in q-axis;
• $C_{cut}$ is the length from the center of the cut-off region to the rotor center in q-axis and ${\vartheta }_{cut}$ is the cut-off region angle.

The geometrical dimensions of the M2 rotor in Figure 3 are summarized in

Table 3. M2 rotor geometrical dimension parameters.

Rotor Parameters	M2	Unit
$D_{re}$	53.3	mm
$D_{ri}$	12.96	mm
$W_{tan}$	0.45	mm
r	1.15	mm
${\vartheta }_{b1}$	29.1 *	degree
${\vartheta }_{b2}$	42 *	degree
$\mathrm{\Delta }b1$	1	degree
$\mathrm{\Delta }b2$	1	degree
$k_{ferrite}$	0.42 *	-
$C_{cut}$	26.65 *	mm
${\vartheta }_{cut}$	11.15 *	degree

* Optimized parameters.

, where the parameters with * are optimized values through a MOGA-II genetic algorithm optimization via ModeFrontier [33]. The method has been well established in [15]. The two objectives are to minimize the torque ripple and to maximize the average torque in order to have the best torque quality. Since PMaSynRM is originally derived from SynRM, it is logical to define a $k_{ferrite}$ representing the insulation level in the q-axis since ferrite has nearly the same permeability as air [34]. $k_{ferrite}$ in Table 3 is defined in Equation (2) as

$${\mathit{k}}_{\mathit{ferrite}}={\displaystyle \frac{L_{ferrite}}{L_{total}}}$$

(2)

As shown in the M2 rotor in Figure 3, the edges of the two ferrite filled flux barriers are drawn on the basis of the N. E. Joukowski air potential function [35], which is an applied mathematical model to describe ‘natural flux’. The method was first proposed in [36], indicating that by applying ‘natural flux’-shaped barriers, reluctance torque could be produced to the maximum extent. The center of each arc lies on the q-axis due to rotor symmetry. Moreover, a cut-off region is introduced in M2. The cut-off curve is modified by a cubic function dominated by two the independent parameters ${\vartheta }_{cut}$ and $C_{cut}$. 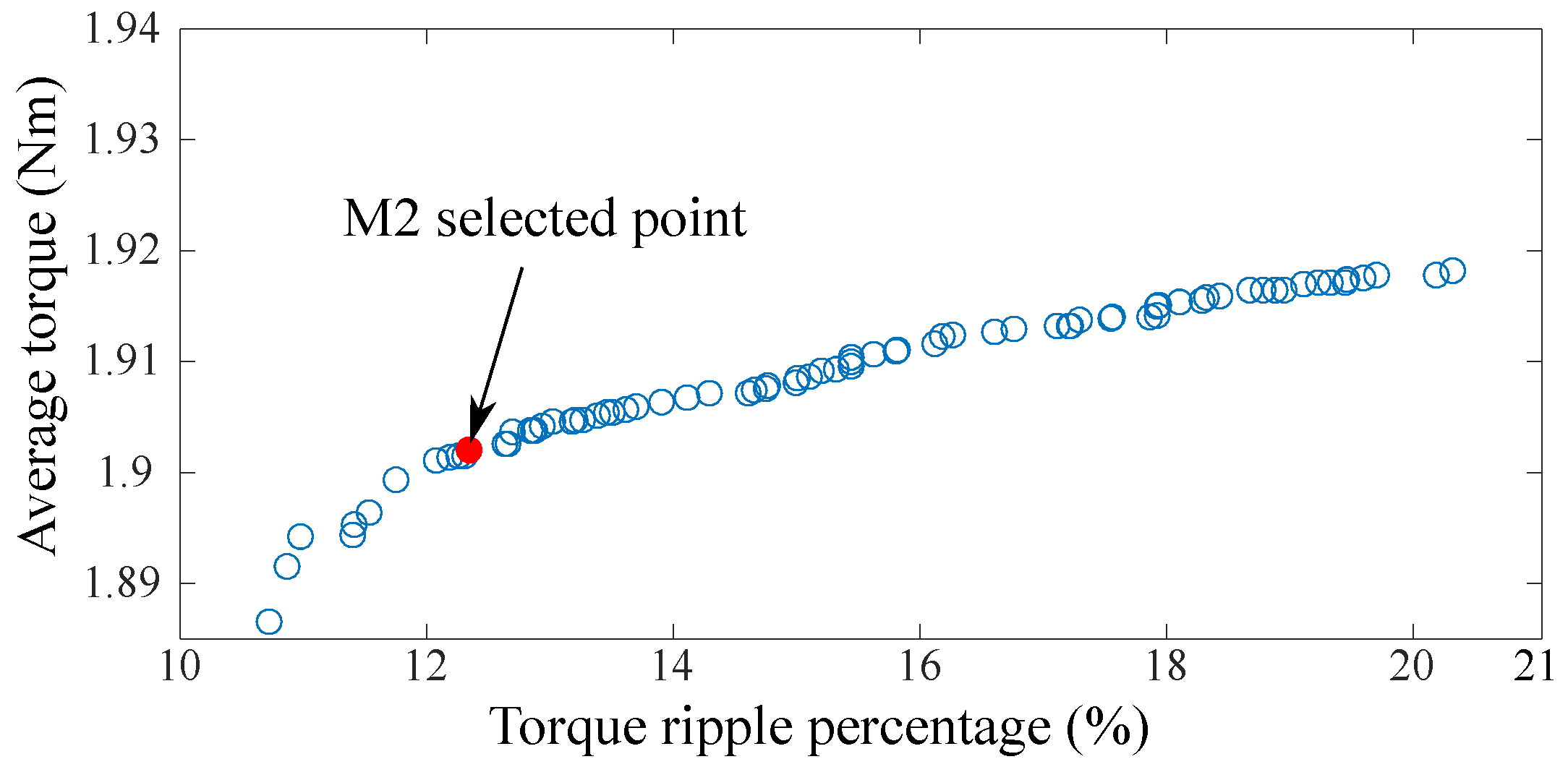The purpose of setting this cut-off region is to acquire a desired saturation level in the iron region around the cut-off, in which way the motor would produce a minimized torque ripple. 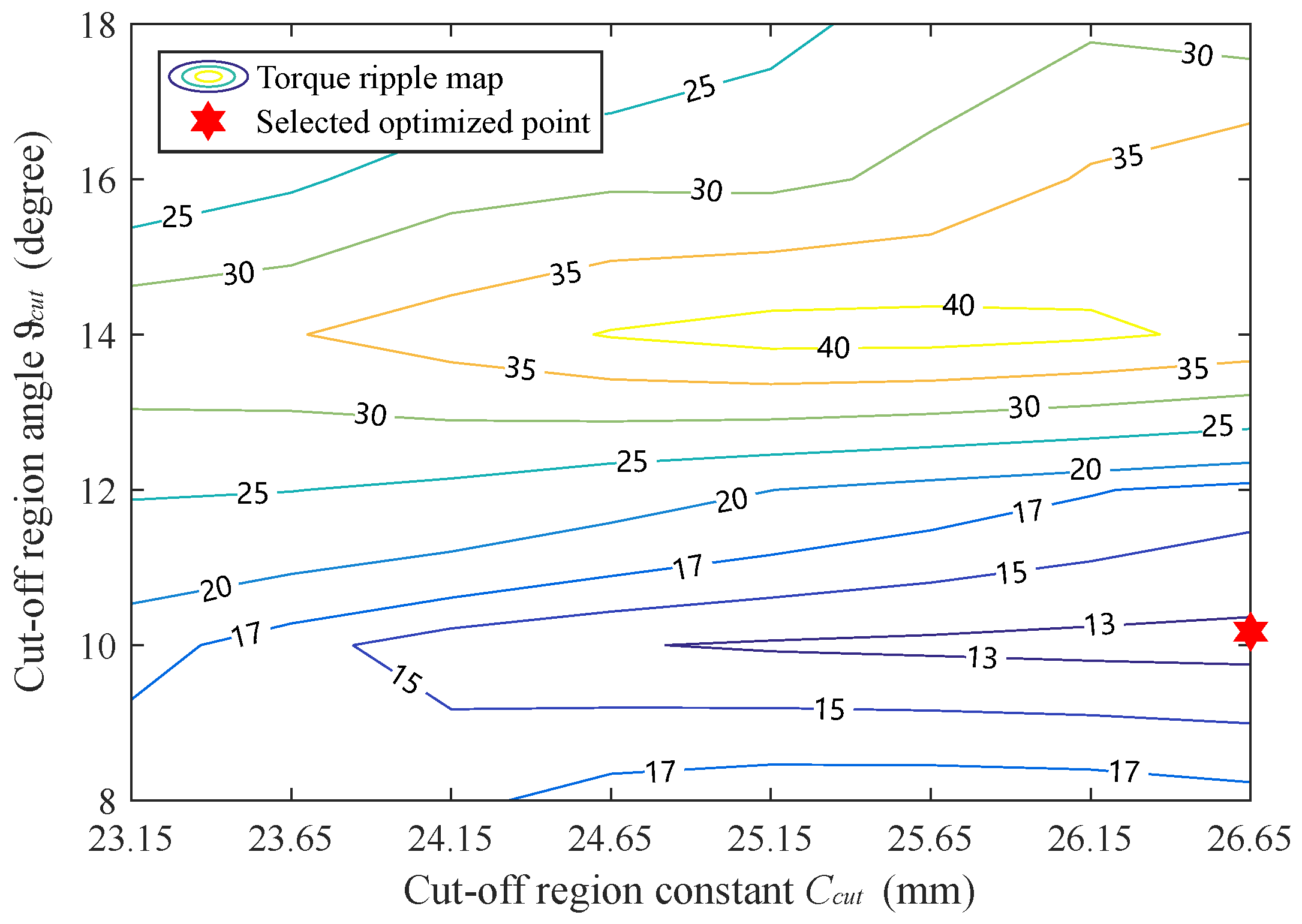The Pareto front solutions of M2 are shown in Figure 7. The solutions are all recorded under MTPA (Maximum Torque Per Ampere) mode with the same rated phase current of 3.26 Arms. Among the Pareto front solutions, the final solution is selected, as marked in Figure 7.

Figure 8 and Figure 9 elaborate the sensitivity analysis of torque ripple from the cut-off region constant $C_{cut}$ and the cut-off region angle ${\vartheta }_{cut}$. As shown in Figure 8, the variations of $C_{cut}$ and ${\vartheta }_{cut}$ give different effects on the torque ripple. Starting from the selected optimized point with $C_{cut}$ 26.6 mm and ${\vartheta }_{cut}$ 11.15 degrees, further decrease in $C_{cut}$ would increase the torque ripple from the optimized 12.34% to around 18% and further decrease or increase in ${\vartheta }_{cut}$ would increase the torque ripple. It is worth noticing that the maximum torque ripple over 40% occurs with $C_{cut}$ at around 25.5 mm and ${\vartheta }_{cut}$ at around 14 degrees, which is over three times larger than the optimized torque ripple value at 12.34%. 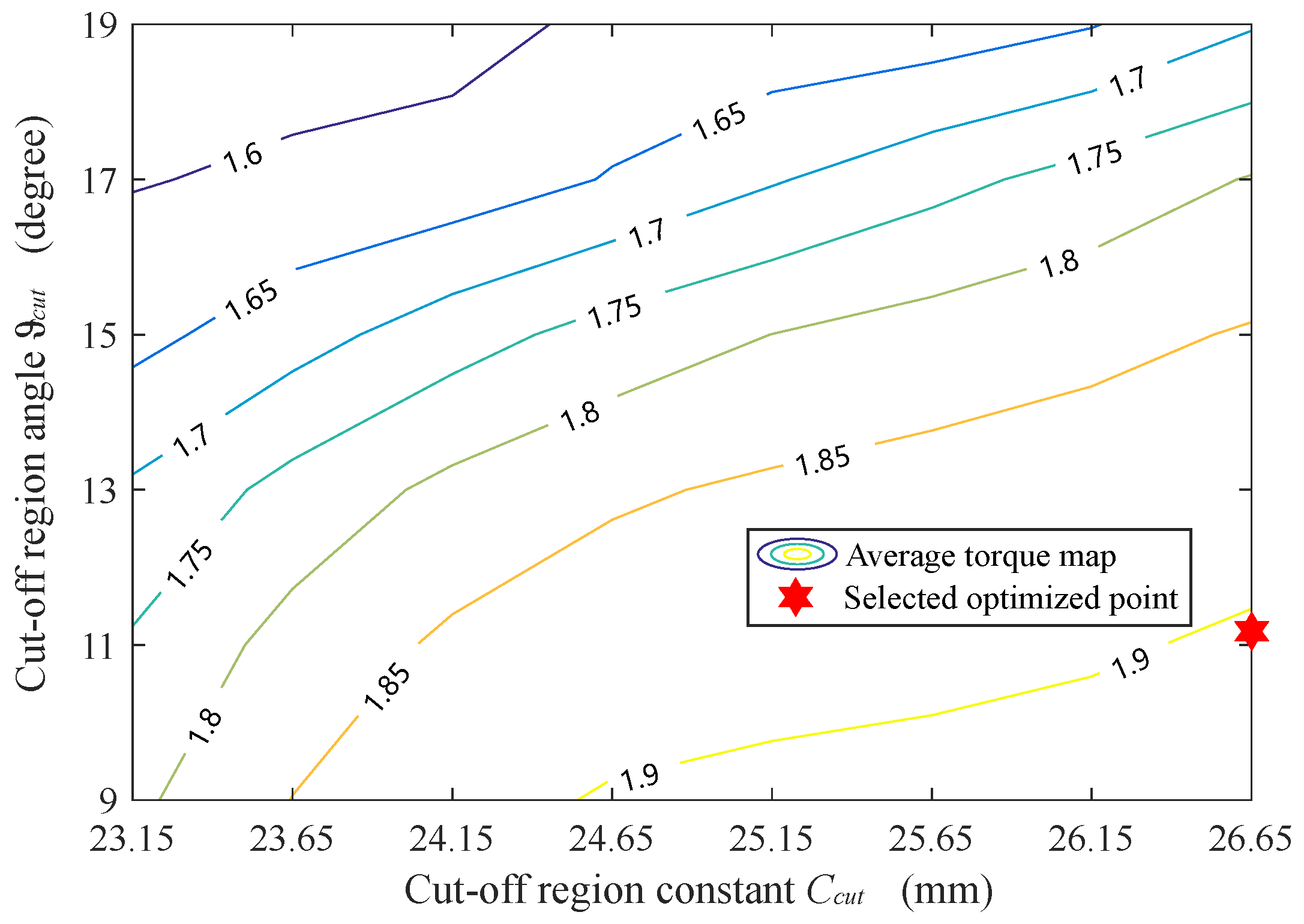The influence of $C_{cut}$ and ${\vartheta }_{cut}$ on average torque is presented in Figure 9. It can be seen that the average torque is not as sensitive to $C_{cut}$ and ${\vartheta }_{cut}$ as torque ripple. Although further decrease in ${\vartheta }_{cut}$ from the optimized 11.15 degrees to 9 degrees would increase the average torque value from 1.907 Nm to 1.915 Nm, it results in an over 17% torque ripple, which is not preferred. To conclude, the above analysis confirms the importance of selecting suitable cut-off region parameters in order to reduce the torque ripple.

In the next section, the M2 solution is compared and analyzed in detail with respect to the reference M1 regarding average torque, torque ripple, efficiency, etc.

3.2. M1 and M2 Performance and Cost Comparison

In this section, M1 and M2 mentioned in the previous sections are selected for comparison.

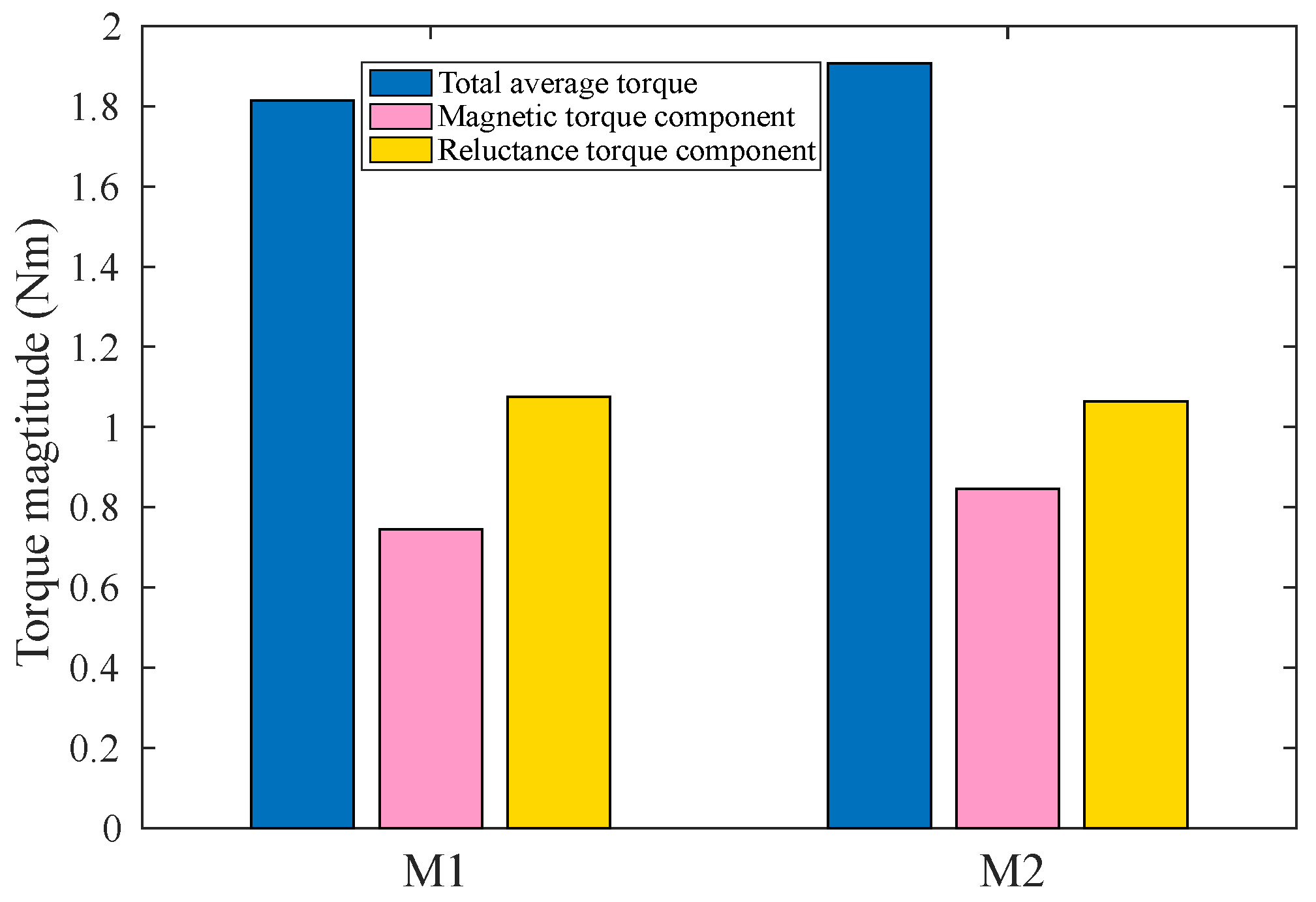
Both motors are simulated under the same phase current at 3.26 Arms by means of FE software MagNet (version 2019.1.0.33). The torque results under MTPA mode are shown in Figure 10. It can be noted that M2 with the insertion of ferrite in a particular flux barrier shape can contribute more average torque compared with M1 with rare earth PM.

The exact torque component values are reported in Table 4. As shown in Table 4, the magnetic torque component is increased by 13.15% in M2 compared with M1. Even though the reluctance torque component is decreased very little by 0.56% in M2, the total average torque is improved from 1.815 Nm in M1 by 5.07% to 1.907 Nm in M2, thanks to the increase in the magnetic torque component. It is interesting to notice that both reluctance torque and magnetic torque contribute in relatively the same order of magnitude in M1 and M2.

It has been clearly shown in Figure 10 and Table 4 that M2 with ferrite in fluid barrier shape can produce more average torque due to the additional magnetic torque component. Therefore, it is necessary to conclude the exact motor performance of the two motors at a rated condition considering other evaluations such as efficiency and power factor. The performance results of M1 and M2 at a rated condition are summarized in Table 5, and rotor material cost results are listed in Table 6. It can be noticed from Table 5 that iron loss in M1 and M2 has insignificant difference, and the total loss is mainly determined by the copper loss. To summarize, it is clearly indicated that M2 presents the following benefits:

• The phase current is reduced by about 4.12% in M2 compared with 3.4 Arms in M1.
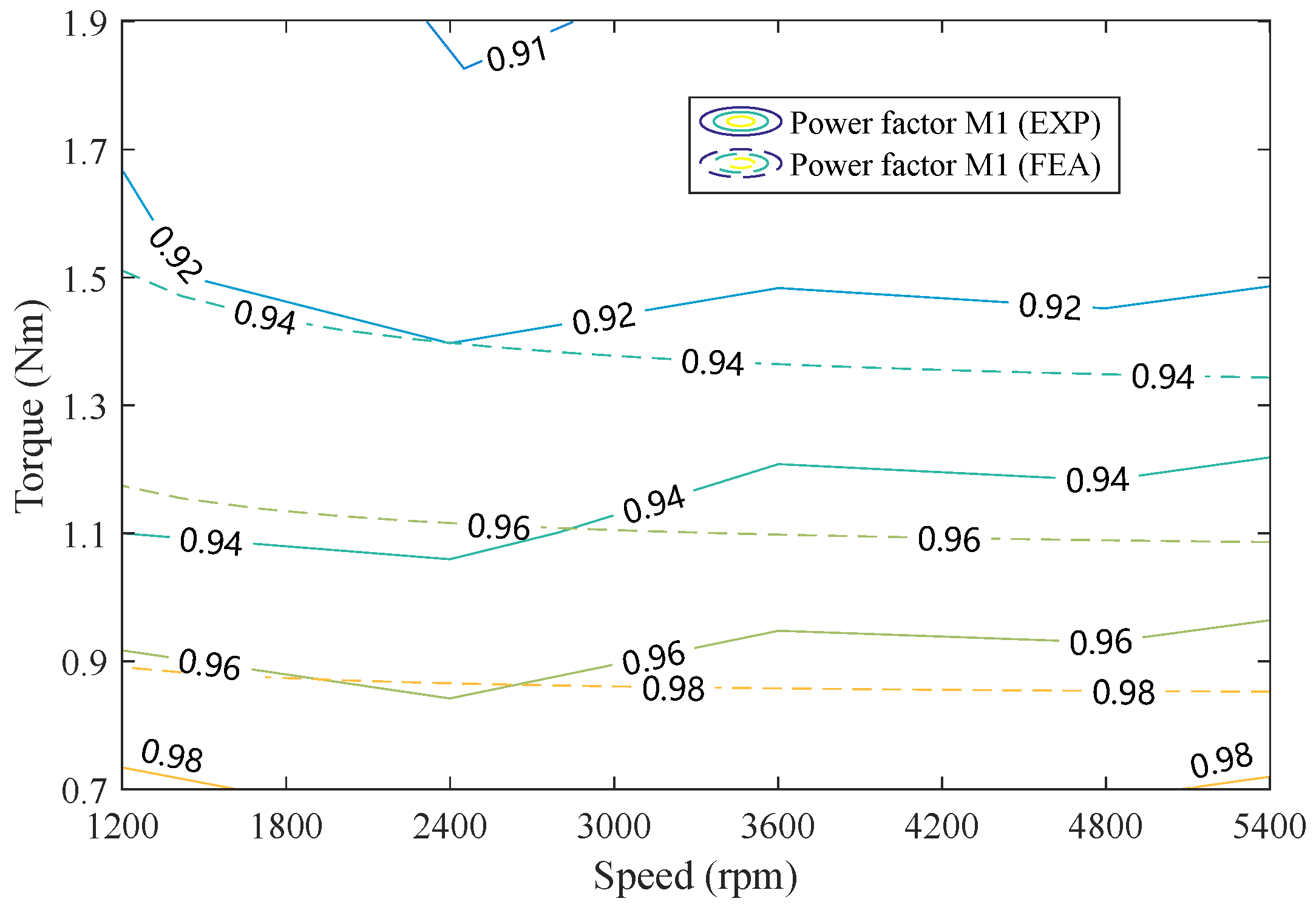
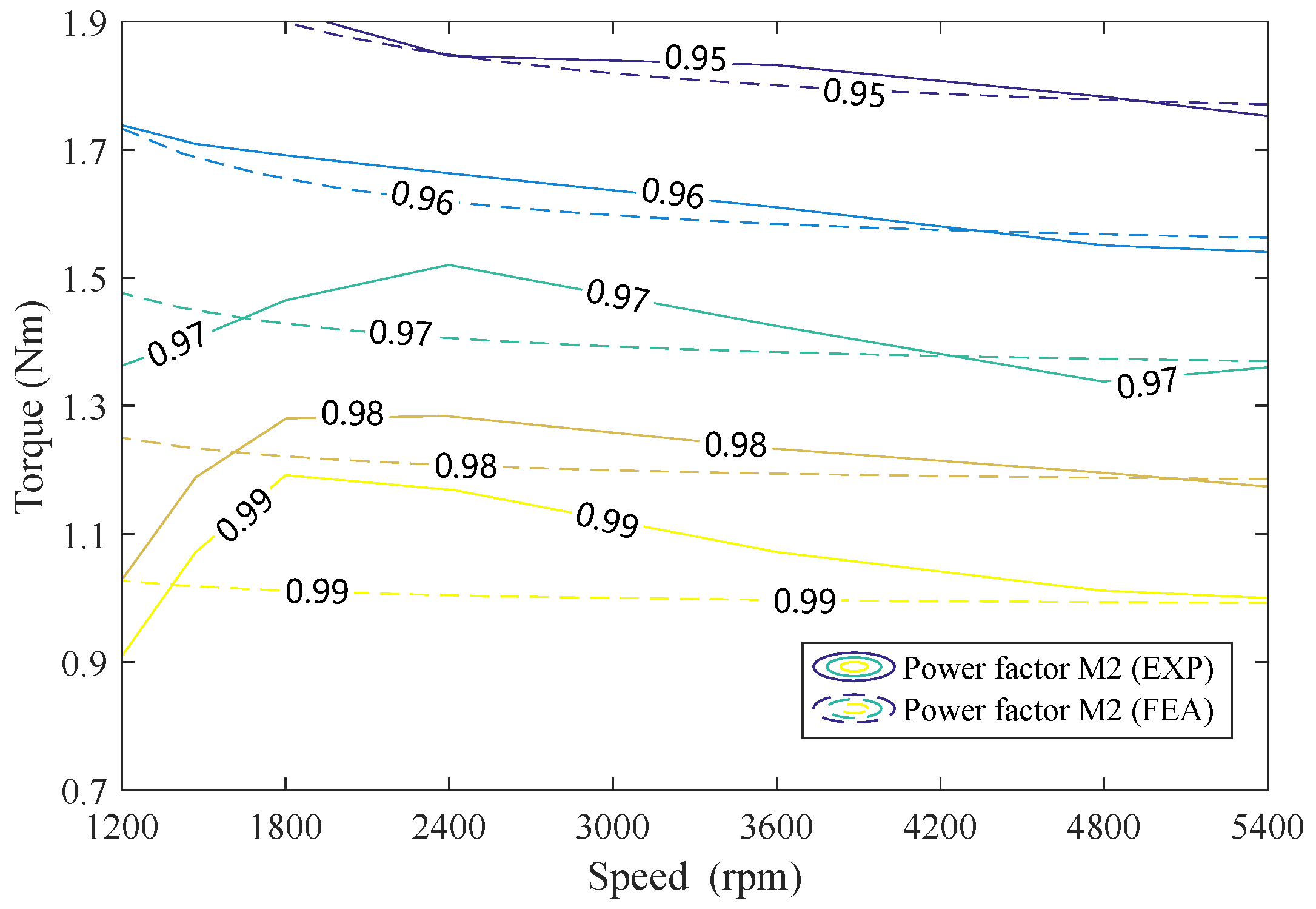
• The power factor is improved from the original 0.925 in M1 to 0.944 in M2. The increase is about 2.05%.
• Copper loss in M2 is reduced compared with M1, thanks to the lower current, which contributes to the eventual efficiency improvement from 94.04% in M1, by 0.23% to 94.27% in M2.
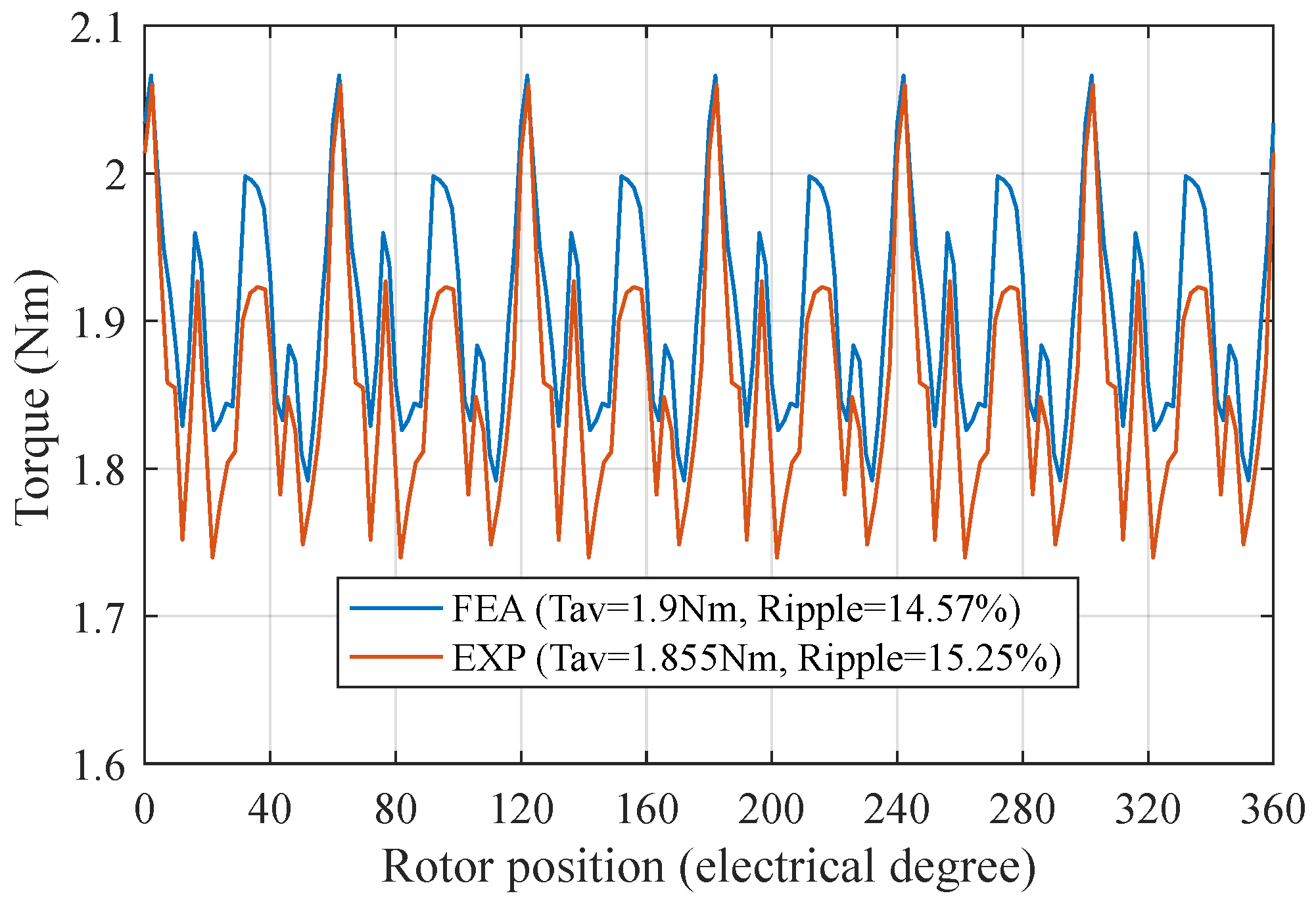
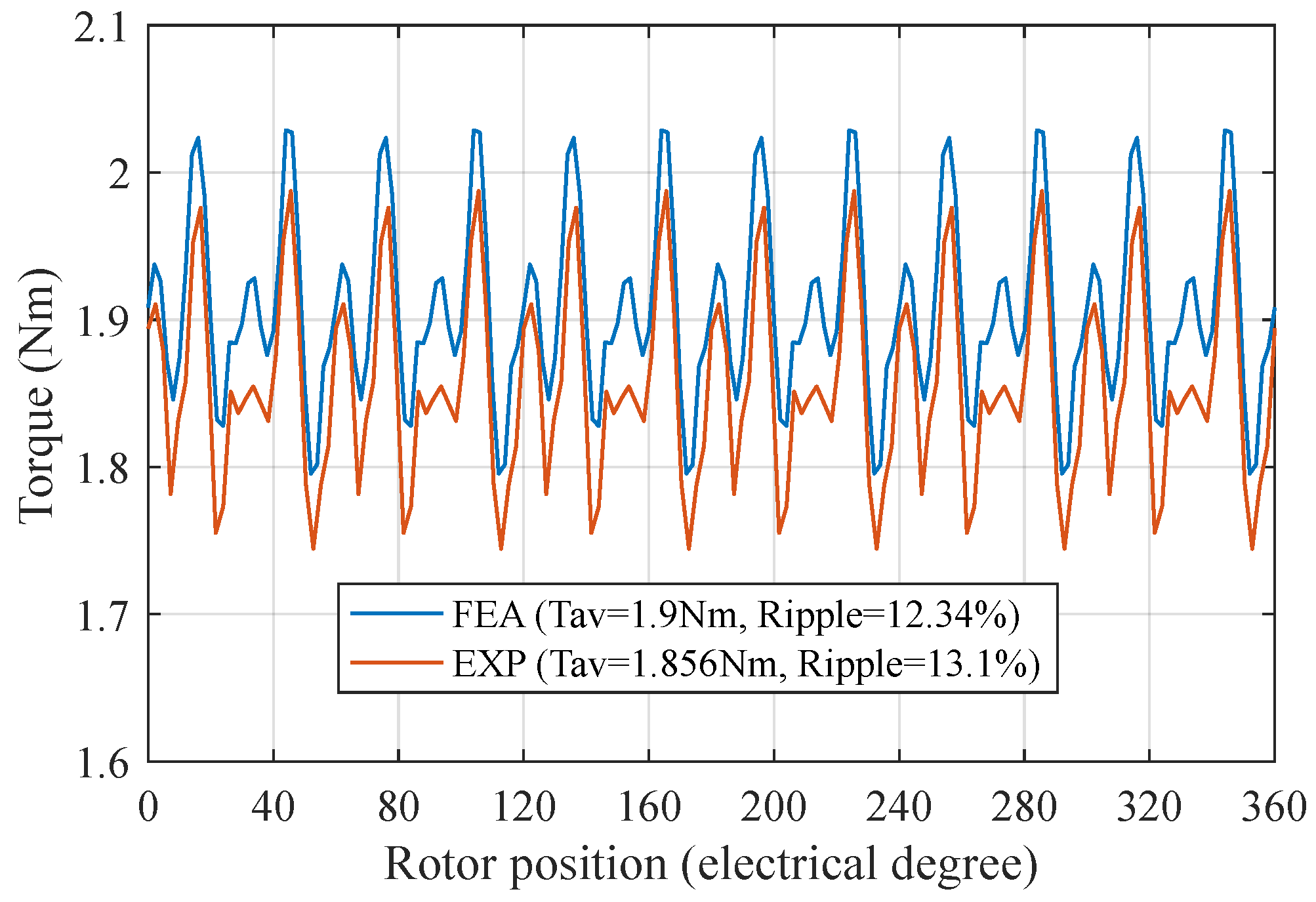
• M2 has the lower torque pulsation of 12.34% compared with 14.57% in M1.
• The PM cost of M2 is reduced to only 35.6% of M1, thanks to the remarkably cheaper price of ferrite Y-40 compared with rare earth PM N30H. Meanwhile, rotor iron cost is decreased by about 14.7% in M2. Generally, the rotor material cost of M2 is reduced by 59.6% compared with M1, which is an obvious price advantage.

Table 4. Torque component data under phase current at 3.26 Arms in MTPA.

Torque	M1	M2	Unit
Total average torque	1.815	1.907	Nm
Improvement	-	+5.07	%
Reluctance torque	1.07	1.064	Nm
Improvement	-	−0.56	%
Magnetic torque	0.745	0.843	Nm
Improvement	-	+13.15	%
Reluctance torque proportion	58.95	55.79	%
Magnetic torque proportion	41.05	44.21	%

Table 4. Torque component data under phase current at 3.26 Arms in MTPA.

Torque	M1	M2	Unit
Total average torque	1.815	1.907	Nm
Improvement	-	+5.07	%
Reluctance torque	1.07	1.064	Nm
Improvement	-	−0.56	%
Magnetic torque	0.745	0.843	Nm
Improvement	-	+13.15	%
Reluctance torque proportion	58.95	55.79	%
Magnetic torque proportion	41.05	44.21	%

Table 5. Motor performance comparison at rated condition.

Rated Condition	Label	M1	M2	Unit
Average torque	$T_{av}$	1.9	1.9	Nm
Speed	$\omega$	5400	5400	rpm
Power	$P_{out}$	1074.4	1074.4	W
Torque ripple percentage	$T_{ripple}$	14.57	12.34	%
MTPA phase current	$I_{ph}$	3.4	3.26	Arms
Current reduction	-	-	4.12	%
Power factor	$\lambda$	0.925	0.944	-
Power factor increase	-	-	2.05	%
Copper loss	$P_{copper}$	37.89	35.01	W
Iron loss	$P_{iron}$	30.2	30.6	W
Efficiency	$\eta$	94.04	94.27	%
Efficiency increase	-	-	0.23	%

Table 5. Motor performance comparison at rated condition.

Rated Condition	Label	M1	M2	Unit
Average torque	$T_{av}$	1.9	1.9	Nm
Speed	$\omega$	5400	5400	rpm
Power	$P_{out}$	1074.4	1074.4	W
Torque ripple percentage	$T_{ripple}$	14.57	12.34	%
MTPA phase current	$I_{ph}$	3.4	3.26	Arms
Current reduction	-	-	4.12	%
Power factor	$\lambda$	0.925	0.944	-
Power factor increase	-	-	2.05	%
Copper loss	$P_{copper}$	37.89	35.01	W
Iron loss	$P_{iron}$	30.2	30.6	W
Efficiency	$\eta$	94.04	94.27	%
Efficiency increase	-	-	0.23	%

Table 6. Rotor cost comparison.

Rotor Material Cost	M1	M2	Unit
PM volume	16,044	54,607	mm3
PM material	N30H	Y-40	-
PM unit price 1	68.5	10.96	US$/kg
PM cost	8.24	2.93	US$
Rotor iron volume	93,925	80,275	mm3
Rotor iron material	M235-35A	M235-35A	-
Rotor iron cost	0.88	0.75	US$
Rotor material cost	9.12	3.68	US$
Rotor material cost reduction	-	59.6	%

¹ Based on the quotes from manufacturers in 2022.

Table 6. Rotor cost comparison.

Rotor Material Cost	M1	M2	Unit
PM volume	16,044	54,607	mm3
PM material	N30H	Y-40	-
PM unit price 1	68.5	10.96	US$/kg
PM cost	8.24	2.93	US$
Rotor iron volume	93,925	80,275	mm3
Rotor iron material	M235-35A	M235-35A	-
Rotor iron cost	0.88	0.75	US$
Rotor material cost	9.12	3.68	US$
Rotor material cost reduction	-	59.6	%

¹ Based on the quotes from manufacturers in 2022.

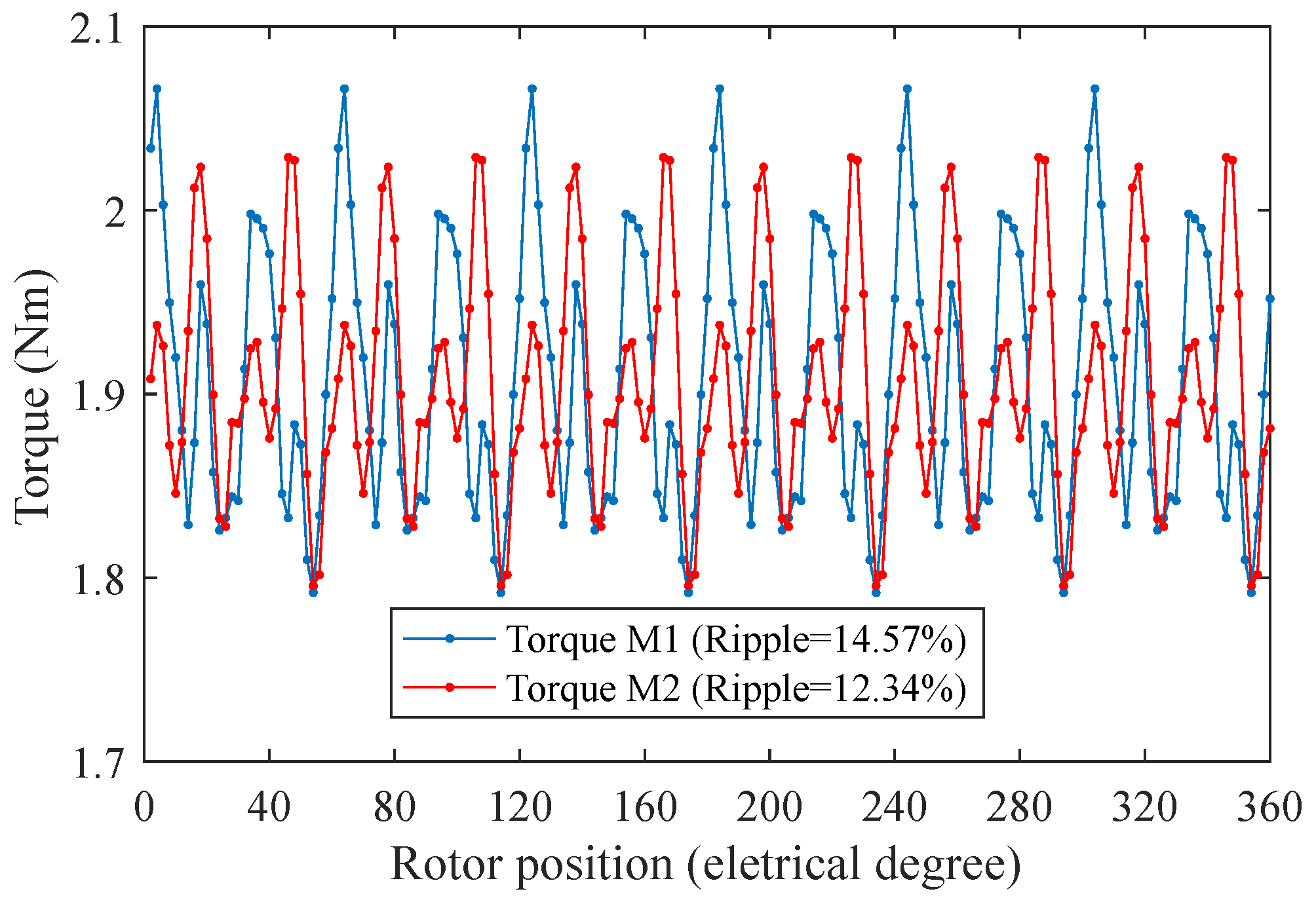
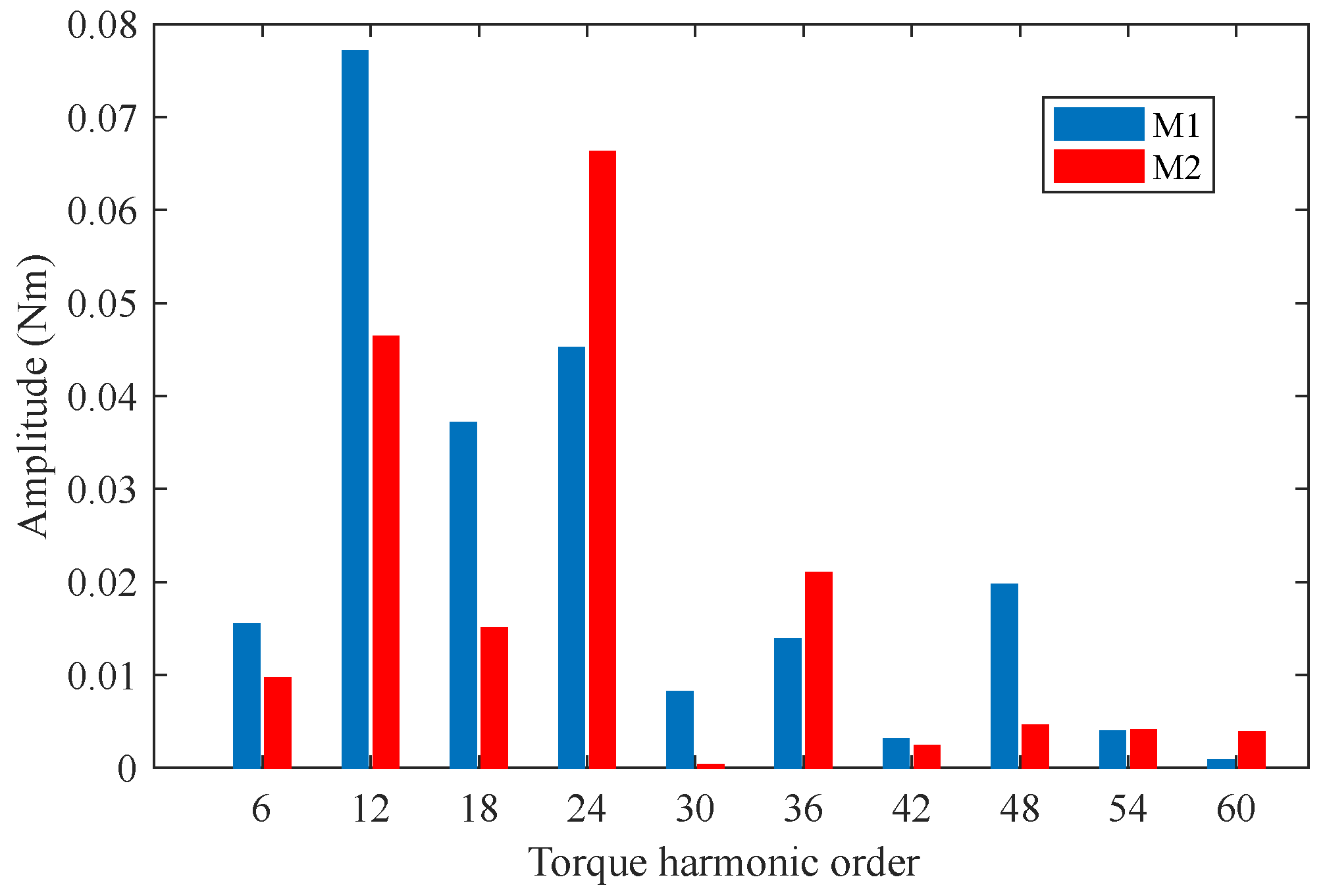
Under a rated condition, M2 exhibits lower torque ripple at 12.34% compared with 14.57% in M1, as reported in Table 5. The instantaneous torque of the two motors over one electrical period is included in Figure 11, which clearly indicates the instantaneous torque differences. This is because M2 has generally lower torque ripple harmonic amplitudes compared with M1. As shown in Figure 12, the amplitude of the 6th harmonic order in M2 is only around 63% of that in M1. Compared with M1, M2 also has obviously smaller 12th and 18th harmonic order values. In general, M2 exhibits lower torque ripple harmonic order values compared with M1 apart from the 24th and 36th.

To conclude, M2 exhibits higher efficiency, higher power factor, and lower torque ripple and costs less compared with M1. It is proved that the HP-PMaSynRM with fluid-shaped ferrite PMs could be provided with higher performance and lower price compared with traditional HP-PMaSynRM with rectangular-shaped rare earth PMs. As a result, the following part is to include a deeper comparison study between M2 and M1 to verify the efficiency and power factor advantages of M2 regarding a wide operating speed range.

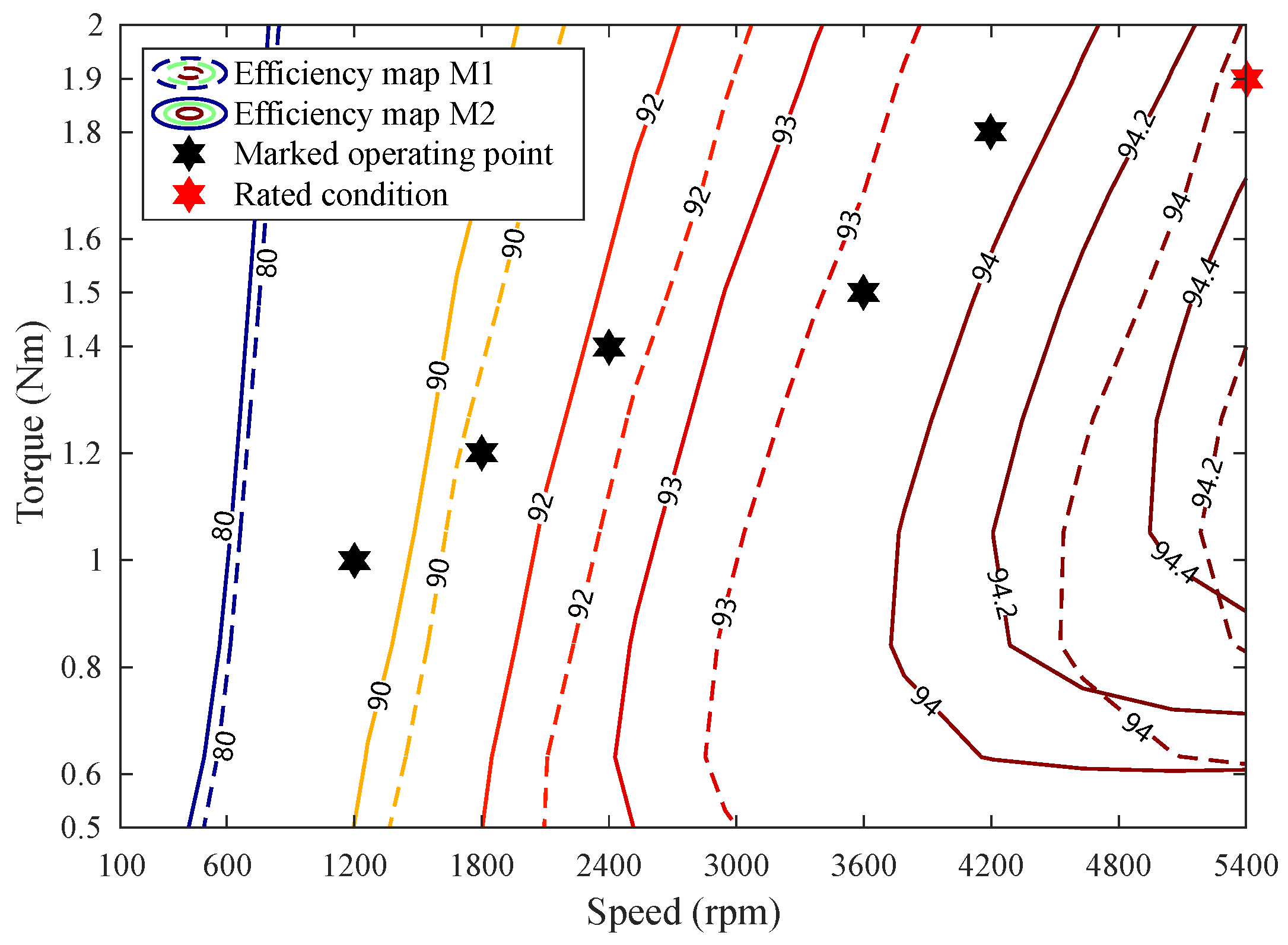
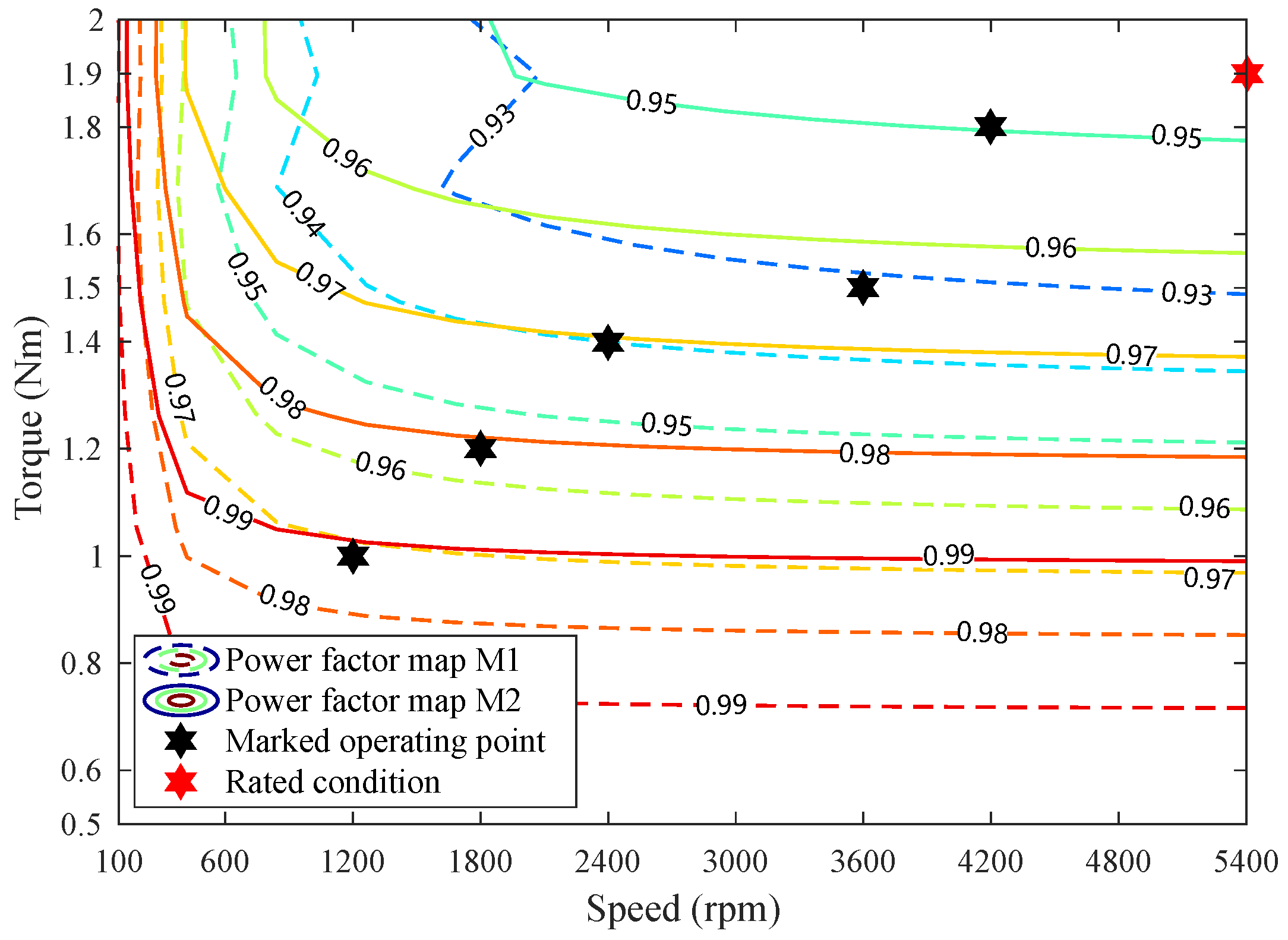
Figure 13 and Figure 14 report the efficiency and power factor of M1 and M2 over the speed range from 100 rpm to rated 5400 rpm and torque range from 0.5 Nm to 2 Nm (rated 1.9 Nm included). As shown in Figure 13, M2 is provided with higher efficiency at every operating point within the scope. In M1, the highest efficiency is limited to below 94.2%, whereas in M2, the highest efficiency can reach over 94.4%. Moreover, M2 is provided with an obvious wider range of efficiency over 94% compared with M1. In Figure 14, it can be evidently indicated that M2 exhibits a higher power factor. Within the speed and torque range, the power factor in M2 is over 0.94 and can reach over 0.99 at torque load conditions below 1 Nm. However, in M1, the power factor is only 0.925 at a rated condition. Moreover, a power factor over 0.96 occupies almost a 75% region in M2, whereas it is only around 50% in M1.

Table 7. Efficiency and power factor comparison between M1 and M2.

Operating Point	Speed (rpm)	Average Torque (Nm)	Efficiency (%)			Power Factor (-)
			M1	M2	Increase	M1	M2	Increase
1	1200	1.0	88.38	88.71	+0.33	0.971	0.991	+0.02
2	1800	1.2	90.65	91.07	+0.42	0.955	0.981	+0.03
3	2400	1.4	91.80	92.27	+0.47	0.940	0.970	+0.03
4	3600	1.5	93.25	93.66	+0.41	0.931	0.964	+0.03
5	4200	1.8	93.49	93.86	+0.37	0.928	0.950	+0.02
6 (rated)	5400	1.9	94.04	94.27	+0.23	0.925	0.944	+0.02

reports the detailed values of efficiency and power factor on the marked operating point to show the obvious advantage of M2. As reported in Table 7, the efficiency and power factor of M2 are apparently higher at the six chosen operating points. The data of the rated operating point is also included in Table 7, which is also reported specifically in Table 5.

3.3. Structural Analysis

A structural FEA is performed for M2 via ANSYS software 2024R2 in order to ensure the rotor mechanical integrity against centrifugal force at the designed 7200 rpm maximum rotating speed. The analysis is carried out by simulating one rotor pole to save computing time cost, thanks to the symmetry.

Table 8. Rotor material properties.

Property	M235-35A	Y-40	Unit
Mass density	7600	4900	kg/m3
Young’s modulus	185	180	GPa
Poisson’s ratio	0.3	0.28	-
Tensile Strength	460	35	MPa

reports the mechanical properties that are fully considered in the mechanical simulation. All contact regions between the iron and ferrite are set as frictional, meaning that sliding and separation are taken into account in order to simulate the worst circumstances when the bondings lose effectiveness. The results at the 7200 rpm maximum rotor speed are presented in Figure 15. As shown in Figure 15, the maximum von Mises stress lies in the tangential rib region of the second-layer barrier end. The maximum von Mises stress value is around 92 Mpa, and it is purely safe compared with the 460 Mpa tensile strength capability included in Table 8; moreover, the maximum deformation at 7200 rpm is only 1.6 μm.

4. Experimental Validation

In order to verify the FEA results of the proposed M2 and traditional M1, M1 and M2 have been manufactured and tested. The experimental measurements are collected from the platform shown in Figure 16. The test machine is coupled with a SUGAWARA rig. SUGAWARA is a precise dynamometer with a speed capability of 100–25,000 rpm and a torque capability of 0.06–2 Nm. The torque resolution of SUGAWARA can reach 0.001 Nm. The test motor is driven by a cheap STM32-based controller for economic consideration. Prototypes of M1 and M2 are shown in Figure 17.

Results of the six operating points in Table 7 have been tested regarding both M1 and M2, including the actual speed, average torque, phase current, output power, power factor, and efficiency, as highlighted in

Table 9. Experimental results comparison between M1 and M2.

Operating Point	Motor	Speed	Average Torque	Phase Current	Output Power	Power Factor	Efficiency
		(rpm)	(Nm)	(Arms)	(W)	(-)	(%)
1	M1	1199	1.001	2.096	125.659	0.952	87.0
	M2	1199	0.998	2.071	125.256	0.981	87.64
2	M1	1799	1.200	2.396	226.050	0.931	90.15
	M2	1798	1.200	2.333	225.842	0.991	90.62
3	M1	2401	1.400	2.748	351.955	0.921	91.32
	M2	2401	1.402	2.658	352.384	0.975	91.72
4	M1	3601	1.500	2.839	565.568	0.919	92.98
	M2	3601	1.500	2.717	565.521	0.967	93.48
5	M1	4200	1.800	3.301	791.857	0.911	93.19
	M2	4200	1.802	3.174	792.519	0.952	93.48
6 (rated)	M1	5401	1.902	3.498	1075.925	0.915	93.48
	M2	5401	1.905	3.357	1077.751	0.939	93.85

. The experimental results regarding the power factor and efficiency show a good agreement with the ones from FEA in Table 7 for both M1 and M2. It can be easily noticed that M2 exhibits reduced current with the same torque requirement. Considering the rated operating point 6 (5400 rpm, 1.9 Nm), the phase current in M2 is 3.357 Arms, which is 4.1% smaller than 3.498 Arms in M1. Additionally, the power factor and efficiency test results of M2 show an obvious advantage compared with M1.

Figure 18 and Figure 19 present the efficiency and power factor maps comparisons of M1 between experimental and FEA results. It can be seen that the experimental results align closely with the FEA results in both efficiency and power factor cases. Even though the efficiency of M1 could not reach 94% experimentally within the tested speed and torque range as shown in Figure 18, the difference is minor. At a rated condition, M1’s efficiency is 93.48%, which is only 0.56% lower than the FEA value of 94.04%. The experimental power factor values of M1 are slightly lower than the FEA ones, as shown in Figure 19, with a difference of less than 0.02, which is acceptable. Similarly, Figure 20 and Figure 21 show that the efficiency and power factor maps of M2 also agree well between experimental and FEA results. Moreover, it is evident that M2 performs better than M1 in terms of both efficiency and power factor at a wide range of operating conditions experimentally by comparing Figure 20 with Figure 18 and Figure 21 with Figure 19 correspondingly.

The torque ripple validation is characterized on a test rig presented in Figure 22. The tested M1 and M2 are performed at a very low speed of 10 rpm/min so that the nature of torque oscillations can be captured. As shown in Figure 22, the tested motor is connected through a torque transducer to a master commercial servo motor. An irreversible gear box with a 1:50 ratio is coupled between the master motor and the torque transducer in order to reduce the actual speed on the tested motor side. The control of the tested motor is driven by a STM32-based controller, which has already been shown in Figure 16. Current values of M1 and M2 are controlled under the rated condition referring to Table 5. The torque ripple results of both M1 and M2 have been collected and are shown in Figure 23 and Figure 24 correspondingly.

It can be observed that the torque ripple waveform from FEA matches quite well with the experimental results. As shown in Figure 23, the M1 measured torque ripple is 15.25% with an average torque of 1.855 Nm, whereas the FEA simulation gives a 14.57% torque ripple with an average torque of 1.9 Nm. The difference in average torque is around 2.4%, and the difference value in torque ripple is only 0.68%. As shown in Figure 24, the measured torque ripple of M2 is 13.1% with an average torque of 1.856 Nm, and it is 12.34% and 1.9 Nm in FEA simulation. The difference in average torque is around 2.3%, and the difference value in torque ripple is only 0.76%. Moreover, it is obvious that the oscillation trends of the FEA and experimental results are quite similar in both M1 and M2 cases.

Based on the results presented in this section, it is proved that the FEA simulation results predict the performance of M1 and M2 quite accurately.

5. Conclusions

This paper has proposed a complete rare earth free novel HP-PMaSynRM (M2). The proposed M2 is characterized by two fluid-shaped flux barriers filled with sintered ferrite PMs and one cut-off region. A comprehensive comparison between M2 and the benchmark conventional HP-PMaSynRM with rare earth PMs (M1) on torque, power factor, and efficiency via FEA is made, indicating that M2, even with only ferrite PMs and without rare earth PMs, can exhibit 5.07% higher average torque capability at the same current of 3.26 Arms and reduce torque ripple value by 15.3% at a rated condition. M2 can provide a 2% higher power factor and a 0.23% increase in efficiency at a rated condition. Moreover, the power factor and efficiency advantages of M2 exist within a wide speed operating range. Apart from the electromagnetic advantages, the cost of the M2 rotor is 59.6% lower than that of the M1 rotor, thanks to the significantly cheaper price of ferrite Y40 (10.96 USD/kg) compared with rare earth PM N30H (68.5 USD/kg).

The experimental results of M1 and M2 match the ones from FEA, including average torque, power factor, efficiency, and torque ripple, which validates the reliability of the FEA results. It is proved that the proposed rare earth free HP-PMaSynRM, with only ferrite PMs, can be designed to be better than rare earth HP-PMaSynRM, enabling better performance at lower cost.