Adaptive Trigger Compensation Neural Network for PID Tuning in Virtual Autopilot Heading Control
Abstract
1. Introduction
2. Preliminaries
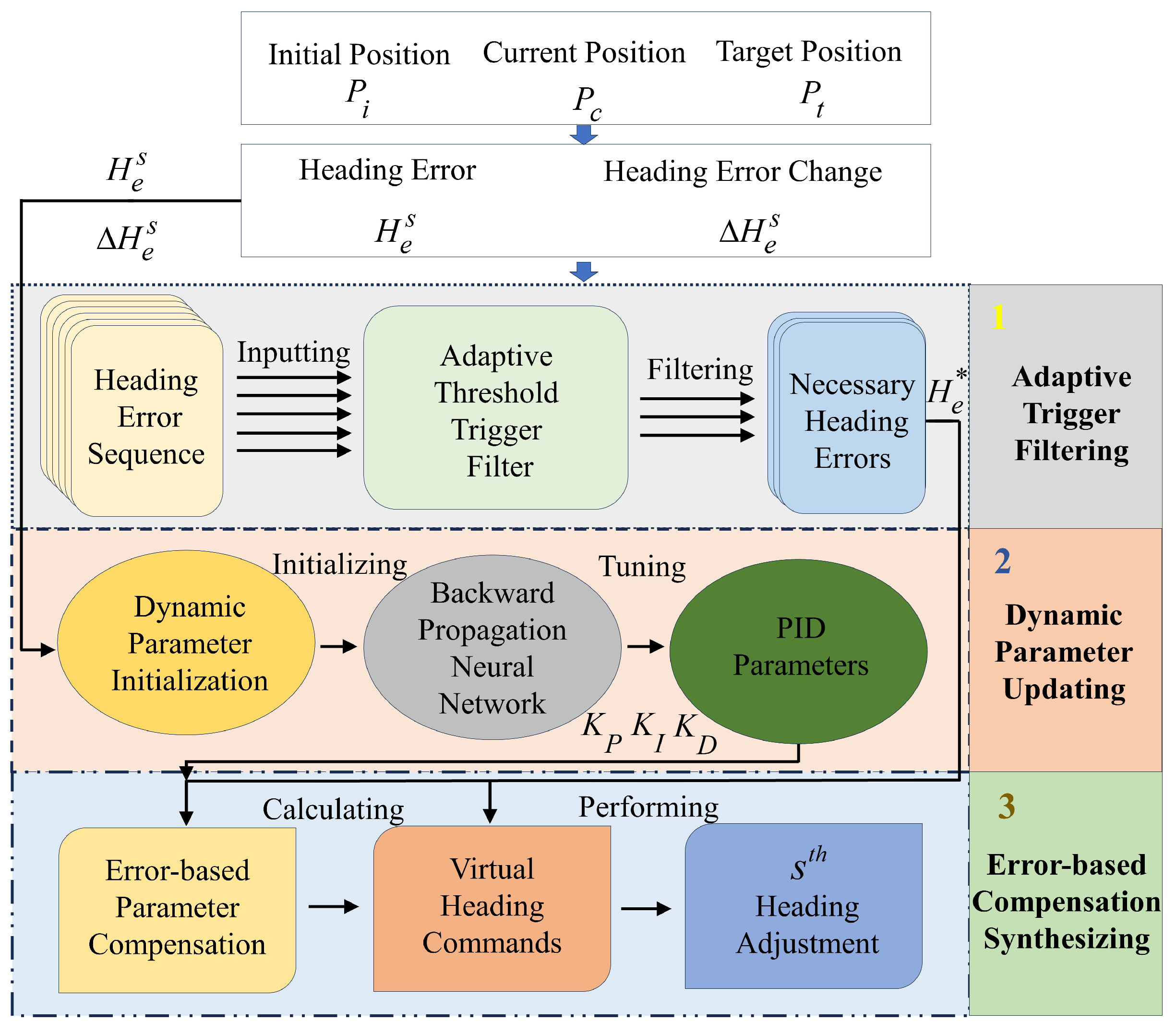
3. Methodology
3.1. Adaptive Trigger Filtering
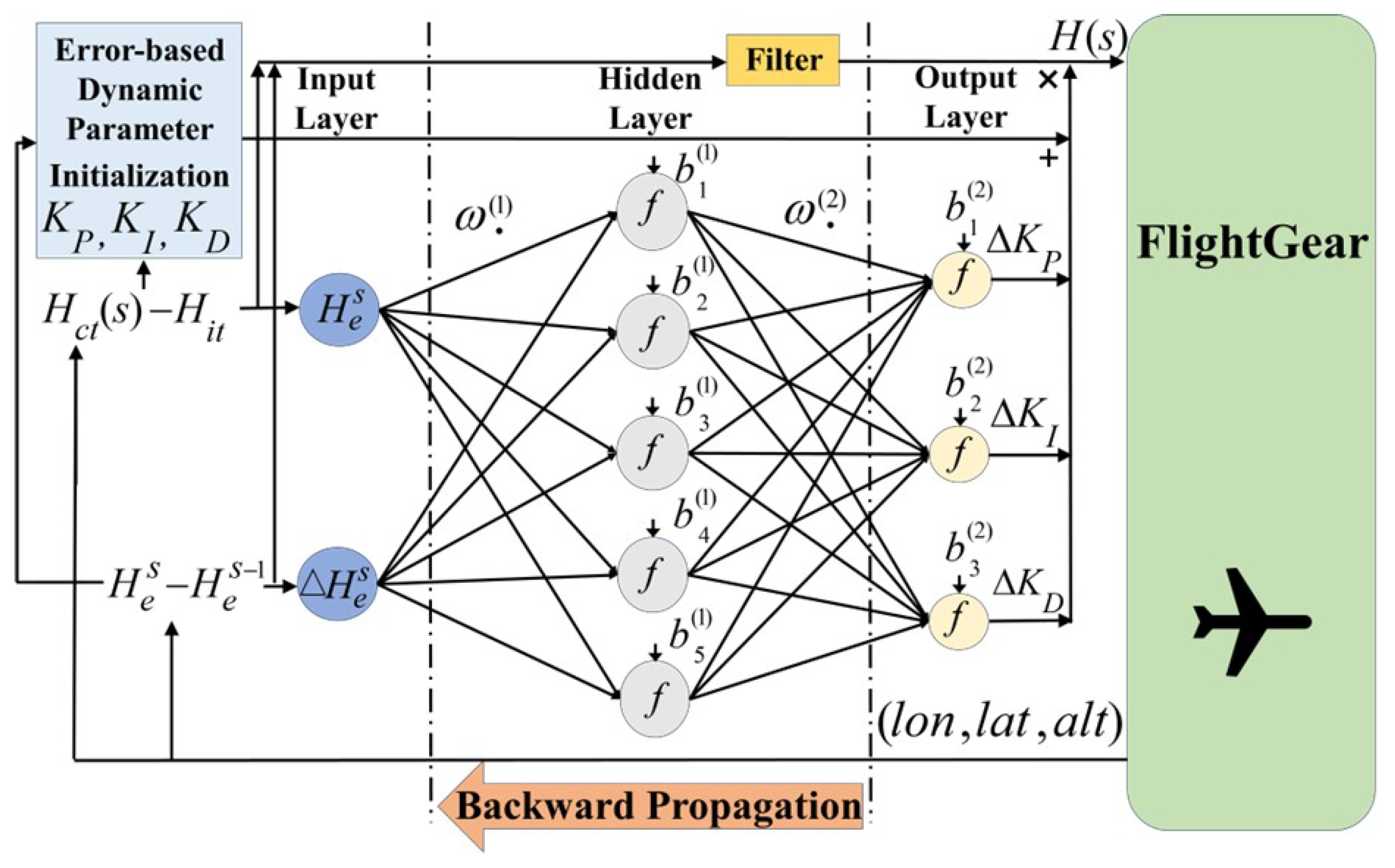
3.2. Dynamic Parameter Updating
3.3. Error-Based Compensation Synthesizing
| Algorithm 1 Q-waypoint flight mission using ATC-NN-PID method |
 |
4. Experiments and Discussion
4.1. Even-Waypoint Simulation
4.2. Odd-Waypoint Simulation
4.3. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Rahman, M.H.; Xie, C.; Sha, Z.H. Predicting sequential design decisions using the function-behavior-structure design process model and recurrent neural networks. J. Mech. Des. 2021, 143, 081706. [Google Scholar] [CrossRef]
- Gnjatovic, M.; Delic, V. Cognitively-inspired representational approach to meaning in machine dialogue. Knowl.-Based Syst. 2024, 71, 25–33. [Google Scholar] [CrossRef]
- Yi, S.H.; Shamsudin, S.S.; Pairan, M.F. Flight control system design for a rotorcraft-based unmanned aerial system using pole placement and LQR-based PID tuning techniques. J. Aeronaut. Astronaut. Aviat. 2024, 56, 615–636. [Google Scholar] [CrossRef]
- Miao, C.X.; Fang, J.C. The design and implement of micro autopilot system for low-altitude mapping of MAV. In Proceedings of the 2011 Second International Conference on Mechanic Automation and Control Engineering, Bao Tou, China, 15–17 July 2011; pp. 1744–17488. [Google Scholar] [CrossRef]
- Li, L.; Zhang, X.B.; Qian, C.X.; Wang, R.H.; Zhao, M.H. Autopilot controller of fixed-wing planes based on curriculum reinforcement learning scheduled by adaptive learning curve. IEEE Trans. Emerg. Top. Comput. Intell. 2024, 8, 2182–2196. [Google Scholar] [CrossRef]
- Madhuranthakam, C.R.; Singh, J.; Elkame, A.; Budman, H. Optimal PID controller parameters for first order and second order systems with time delay using a connectionist approach. Eng. Optim. 2010, 42, 295–303. [Google Scholar] [CrossRef]
- Cao, Y.; Zhang, L.; Yao, Y.; Wang, Y.; Liu, H.; Jie, Y. Research on frequency stabilization method of PID controller based on BP neural network optimization for POINT system on EAST. In Proceedings of the 7th International Conference Frontiers in Diagnostic Technologies, Frascati, Italy, 21–23 October 2024; Volume 20, pp. 1–7. [Google Scholar] [CrossRef]
- Liu, J.; Zhang, Z.; Zhang, J.; Chen, J.A. Application of a neural network on steam drum pressure control in a fixed-bed reactor for exothermic reactions. Appl. Sci. 2024, 14, 3052. [Google Scholar] [CrossRef]
- Kumar, N.; Thakur, N.; Gupt, Y. Optimisation of synchronisation control parameters for enhanced bilateral teleoperation system. Robotica 2024, 42, 3639–3656. [Google Scholar] [CrossRef]
- Talebi, S.P.; Darvishi, H.; Werner, S.; Rossi, P.S. Gradient-descent adaptive filtering using gradient adaptive step-size semantic search result. In Proceedings of the 2022 IEEE 12th Sensor Array and Multichannel Signal Processing Workshop (SAM), Trondheim, Norway, 20–23 June 2022; pp. 321–325. [Google Scholar] [CrossRef]
- Arthanari, S.; Jeong, J.H.; Joo, Y.H. Learning multi-regularized mutation-aware correlation filter for object tracking via an adaptive hybrid model. Neural Netw. 2025, 191, 107746. [Google Scholar] [CrossRef]
- Li, J.; He, X.; Zhou, Q.; Anthony, C.; Wang, B.; Lu, G.X.; Xu, H.M. Heuristic information-rich evolutionary modelling for engine soft sensors of hybrid electric vehicles. Appl. Soft Comput. 2025, 180, 113468. [Google Scholar] [CrossRef]
- Chen, L.G.; Zhu, P.C.; Qiang, W.; Zhang, X.B.; Wang, S.F. Fuzzy backpropagation neural network PID control of a 6-DOF parallel robot. In Proceedings of the International Conference on Mechanical Design and Simulation, Xi’an, China, 29 February–2 March 2024; pp. 1375–1384. [Google Scholar] [CrossRef]
- Qian, R.H.; Wu, R.P.; Wu, H. Research on adaptive control of six-degree-of-freedom manipulator based on fuzzy PID. Syst. Sci. Control Eng. 2025, 13, 2498912. [Google Scholar] [CrossRef]
- Liu, Z.L.; Lv, X.F.; Gan, S.K.; Yang, K.K. Application of particle swarm optimization-based BP neural network PID controller in spray humidification. Eng. Res. Express 2025, 7, 025412. [Google Scholar] [CrossRef]
- Mao, Q.H.; Chong, S.M.; Chai, J.Q.; Qin, S.; Zhang, F. Research on deviation correction control method of full-width horizontal-axis roadheader based on PSO-BP neural network PID. Actuators 2025, 14, 362. [Google Scholar] [CrossRef]
- Wu, L.F.; Wang, Z.H.; Rastgaar, M.; Mahmoudian, N. Adaptive velocity control for UAV boat landing: A neural network and particle swarm optimization approach. J. Intell. Robot. Syst. 2025, 111, 6. [Google Scholar] [CrossRef]
- Nangrani, S.P.; Singh, A.R.; Chandan, A. Chaos driven instability control using interval type-2 fuzzy logic controller for better performance. J. Intell. Fuzzy Syst. 2018, 34, 1491–1501. [Google Scholar] [CrossRef]
- Deng, X.K.; Chen, J.B.; Chen, C.Z.; Zhang, Y.Y.; Zhang, Z.Y. UAV path planning with improved PSO al-gorithm based on levy flight. In Proceedings of the 6th International Conference on Control and Computer Vision-ICCCV-Annual, Tianjin, China, 13–15 June 2024; pp. 86–91. [Google Scholar] [CrossRef]
- Srinivasan, A.V.; Jayarajan, N.; Ganesan, T. Optimizing UAV trajectory tracking using neural network-based PID control in dynamic environments. In Proceedings of the 2025 International Conference on Computational Innovations and Engineering Sustainability (ICCIES), Coimbatore, India, 24–26 April 2025; pp. 1–8. [Google Scholar] [CrossRef]
- Marino, A.; Neri, F. PID tuning with neural networks. In Intelligent Information and Database Systems. ACIIDS 2019; Nguyen, N., Gaol, F., Hong, T.P., Trawiński, B., Eds.; Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2019; Volume 11431, pp. 476–487. [Google Scholar] [CrossRef]
- Zhou, Y.T. Ternary correlation adaptive tuning for virtual autopilot commands. J. Guid. Control Dyn. 2024, 47, 1946–1951. [Google Scholar] [CrossRef]
- Rachmanto, A.D.; Iswanto, I.; Hernawati, H. Simulation and modeling of aircraft movements passing through VOR. Iop Conf. Ser. Mater. Sci. Eng. 2020, 830, 032021. [Google Scholar] [CrossRef]
- Hussein, H.H.; Ahmed, H.M.; Kandil, S.A.; Alexan, W. Unveiling diverse solitons in the quintic perturbed Gerdjikov-Ivanov model via a modified extended mapping method. Sci. Rep. 2025, 15, 15881. [Google Scholar] [CrossRef]
- Zhang, W.; Wang, Z.L.; Wang, H.Y.; Li, Z.W.; Wang, Y.F.; Zhao, Z.Y. AEK-MFIS: An adaptive ensemble of Kriging models based on multi-fidelity simulations and importance sampling for small failure probabilities. Comput. Methods Appl. Mech. Eng. 2025, 441, 117952. [Google Scholar] [CrossRef]
- Benrabah, M.; Kara, K.; AitSahed, O.; Hadjili, M.L. Adaptive Fourier series neural network PID controller. Int. J. Control Autom. Syst. 2021, 19, 3388–3399. [Google Scholar] [CrossRef]
- Ahmadi, A.; Esfanjani, R.M. Improved machine learning based approach for autotuning PID controller using genetic algorithms and parallel processing. J. Sci. Ind. Res. 2025, 84, 269–277. [Google Scholar] [CrossRef]
- Singh, A.; Yadav, S.; Tiwari, N.; Nishad, D.K.; Khalid, S. Optimized PID controller and model order re-duc-tion of reheated turbine for load frequency control using teaching learning-based optimization. Sci. Rep. 2025, 15, 3759. [Google Scholar] [CrossRef]
- Perry, A.R.; Olson, C. The FlightGear Flight Simulator History, Status and Future; Citeseer: Princeton, NJ, USA, 2021; Available online: https://kruimel.snt.utwente.nl/pub/software/flightgear/www/old/Papers/LinuxTag-2001/fgfs.pdf (accessed on 14 August 2025).
- Wang, L.; Li, Y.K.A. A multi-objective optimization method based on dimensionality reduction mapping for path planning of a HALE UAV. In Proceedings of the Chinese Automation Congress (CAC), Hangzhou, China, 22–24 November 2019; pp. 3189–3194. [Google Scholar] [CrossRef]
- Zhan, T.; Chen, W.T.; Xu, C.C.; Li, L.X.; Ding, X.X. Attention mechanism-based feature fusion and degra-dation state classification for rolling bearing performance assessment. Sensors 2025, 25, 4951. [Google Scholar] [CrossRef] [PubMed]
- Ma, B.; Dong, S.M. A novel hybrid efficiency prediction model for pumping well system based on MDS-SSA-GNN. Energy Sci. Eng. 2024, 12, 3272–3288. [Google Scholar] [CrossRef]
- Xue, H.; Xu, X.P.; Meng, X. Variety classification and identification of maize seeds based on hyperspectral imaging method. Optoelectron. Lett. 2025, 21, 234–241. [Google Scholar] [CrossRef]

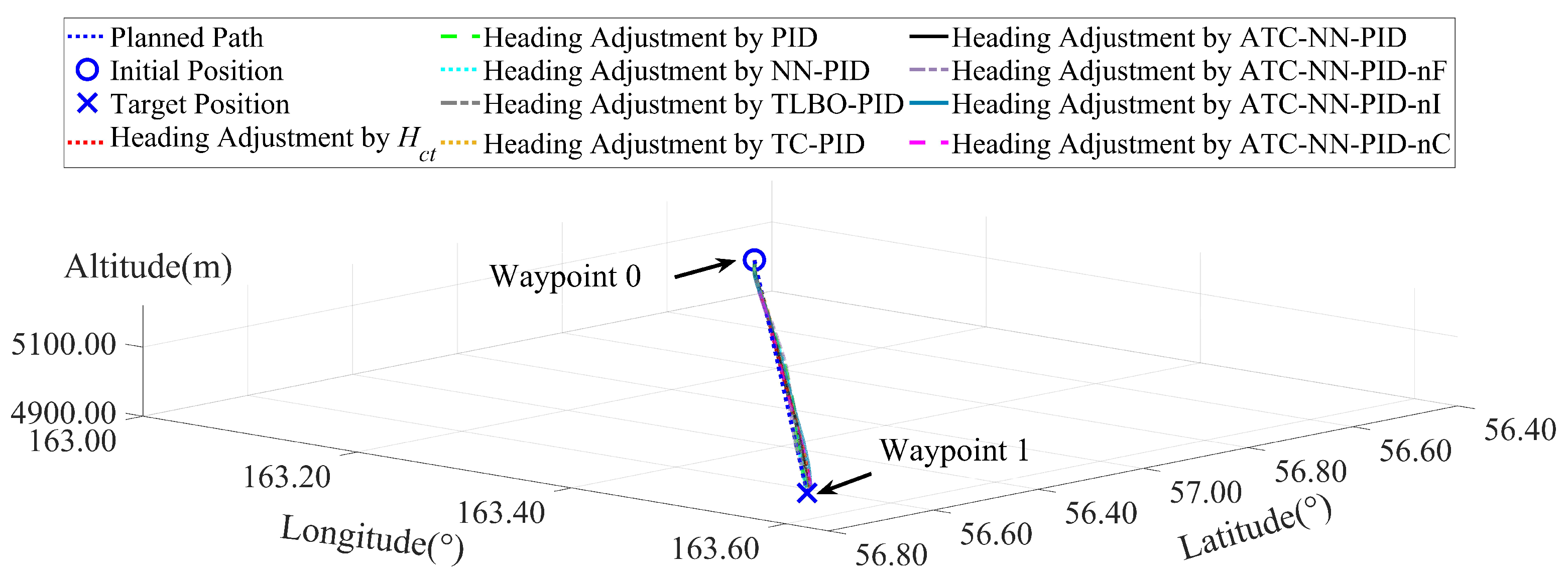
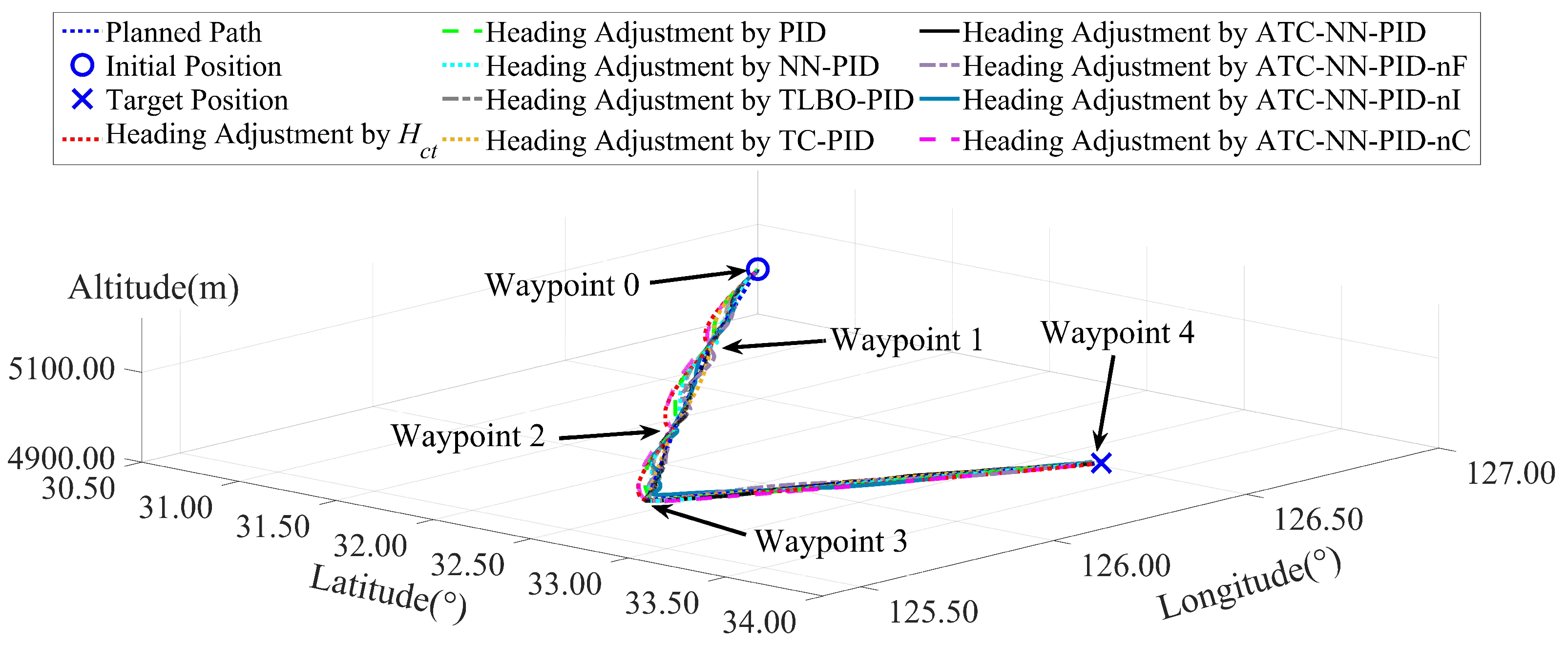
| Waypoint | Latitude (°) | Longitude (°) | Altitude (m) |
|---|---|---|---|
| 0 | 56.42 | 163.00 | 5000.00 |
| 1 | 57.00 | 164.55 | 5000.00 |
| Method | AFT (s) | AFD (m) | AHAT (Times) | AEM (m) | AEStd (m) | R |
|---|---|---|---|---|---|---|
| 753.62 | 112,642.64 | 17 | 686.90 | 333.03 | 0.84 | |
| 753.83 | 112,665.83 | 10 | 614.65 | 347.32 | 0.86 | |
| 752.90 | 112,629.55 | 10 | 535.54 | 302.36 | 0.99 | |
| 744.29 | 112,613.97 | 6 | 562.97 | 324.05 | 0.98 | |
| 754.37 | 112,624.83 | 9 | 556.06 | 247.38 | 0.99 | |
| 753.02 | 112,627.48 | 5 | 518.67 | 238.82 | 0.99 | |
| 754.08 | 112,633.67 | 21 | 533.46 | 336.87 | 0.98 | |
| 753.97 | 112,638.00 | 18 | 614.27 | 286.01 | 0.98 | |
| 753.77 | 112,632.98 | 12 | 533.78 | 244.10 | 0.96 |
| Method | NFT | NFD | NHAT | NEM | NEStd |
|---|---|---|---|---|---|
| 11.64 | 11.27 | 1.84 | 5.92 | 5.24 | |
| 11.15 | 13.02 | 1.65 | 5.65 | 5.23 | |
| 11.06 | 12.78 | 1.37 | 5.64 | 5.13 | |
| 11.32 | 12.99 | 1.50 | 5.63 | 4.95 | |
| 11.42 | 12.85 | 0.72 | 5.69 | 4.83 | |
| 11.02 | 12.96 | 1.49 | 5.61 | 4.65 | |
| 12.38 | 11.36 | 2.28 | 5.63 | 5.29 | |
| 12.96 | 11.34 | 2.15 | 5.64 | 5.02 | |
| 13.03 | 11.31 | 1.26 | 5.62 | 4.67 |
| Waypoint | Latitude (°) | Longitude (°) | Altitude (m) |
|---|---|---|---|
| 0 | 30.50 | 127.00 | 5000.00 |
| 1 | 31.25 | 126.50 | 5000.00 |
| 2 | 32.15 | 125.95 | 5000.00 |
| 3 | 32.90 | 125.50 | 5000.00 |
| 4 | 33.75 | 126.25 | 5000.00 |
| Method | AFT (s) | AFD (m) | AHAT (Times) | AEM (m) | AEStd (m) | R |
|---|---|---|---|---|---|---|
| 3010.40 | 419,704.13 | 77 | 2518.51 | 1151.65 | 0.77 | |
| 3005.91 | 419,197.00 | 76 | 1577.62 | 951.20 | 0.78 | |
| 2999.03 | 418,132.58 | 48 | 1097.12 | 846.06 | 0.86 | |
| 3001.63 | 418,482.46 | 72 | 1042.42 | 770.71 | 0.89 | |
| 3004.79 | 419,120.52 | 116 | 1085.30 | 608.11 | 0.83 | |
| 3043.90 | 424,571.25 | 98 | 880.43 | 606.60 | 0.94 | |
| 3057.99 | 427,338.67 | 93 | 927.25 | 715.48 | 0.80 | |
| 3019.01 | 421,028.54 | 79 | 1418.08 | 897.77 | 0.68 | |
| 3063.99 | 427,907.67 | 98 | 940.59 | 650.94 | 0.93 |
| Method | NFT | NFD | NHAT | NEM | NEStd |
|---|---|---|---|---|---|
| 13.65 | 11.81 | 3.97 | 7.41 | 6.34 | |
| 13.59 | 11.77 | 3.12 | 7.06 | 6.58 | |
| 14.09 | 12.25 | 3.00 | 7.02 | 6.56 | |
| 12.00 | 13.97 | 3.68 | 6.43 | 6.37 | |
| 14.39 | 12.39 | 4.37 | 6.72 | 5.96 | |
| 14.43 | 12.46 | 3.73 | 5.84 | 5.84 | |
| 14.18 | 12.22 | 3.84 | 5.90 | 5.99 | |
| 14.18 | 12.19 | 3.52 | 6.74 | 6.35 | |
| 13.84 | 11.91 | 3.83 | 6.04 | 5.68 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, Y.; Fu, S. Adaptive Trigger Compensation Neural Network for PID Tuning in Virtual Autopilot Heading Control. Machines 2025, 13, 933. https://doi.org/10.3390/machines13100933
Zhou Y, Fu S. Adaptive Trigger Compensation Neural Network for PID Tuning in Virtual Autopilot Heading Control. Machines. 2025; 13(10):933. https://doi.org/10.3390/machines13100933
Chicago/Turabian StyleZhou, Yutong, and Shan Fu. 2025. "Adaptive Trigger Compensation Neural Network for PID Tuning in Virtual Autopilot Heading Control" Machines 13, no. 10: 933. https://doi.org/10.3390/machines13100933
APA StyleZhou, Y., & Fu, S. (2025). Adaptive Trigger Compensation Neural Network for PID Tuning in Virtual Autopilot Heading Control. Machines, 13(10), 933. https://doi.org/10.3390/machines13100933







