Fabric Flattening with Dual-Arm Manipulator via Hybrid Imitation and Reinforcement Learning
Abstract
1. Introduction
2. Related Work
3. Materials and Methods
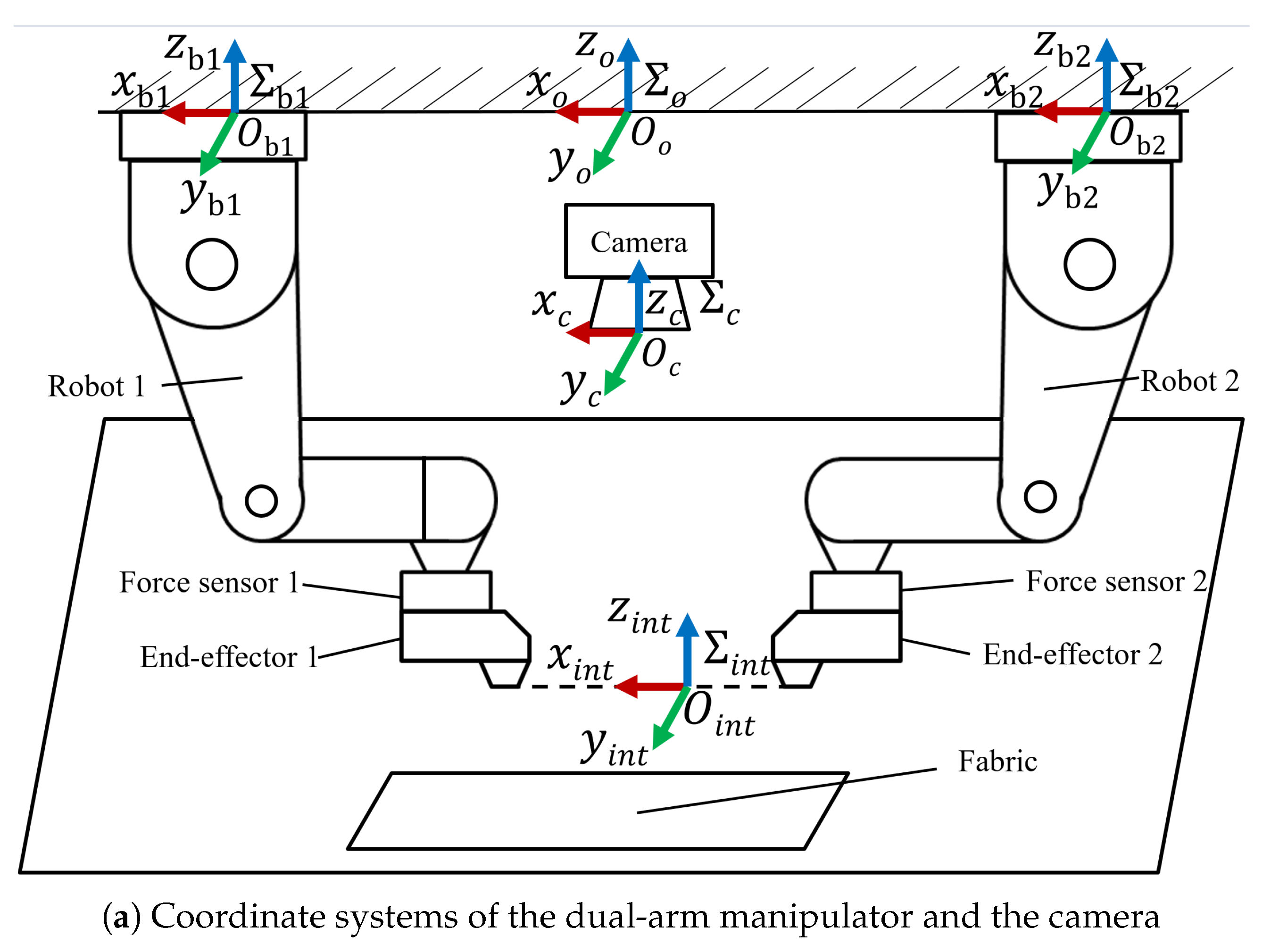
3.1. Robot System Setup
3.1.1. Manipulator
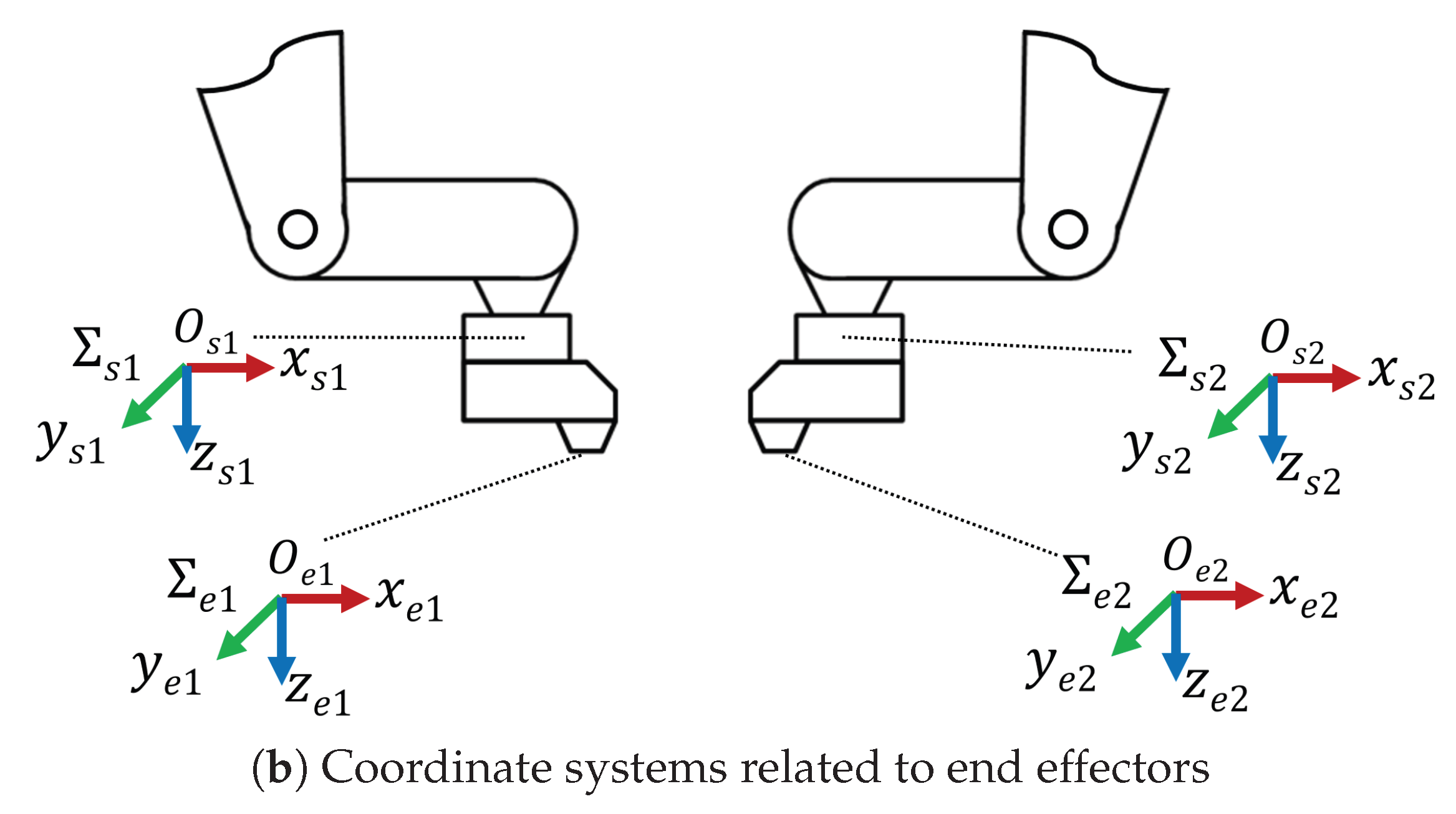
3.1.2. F/T Sensor
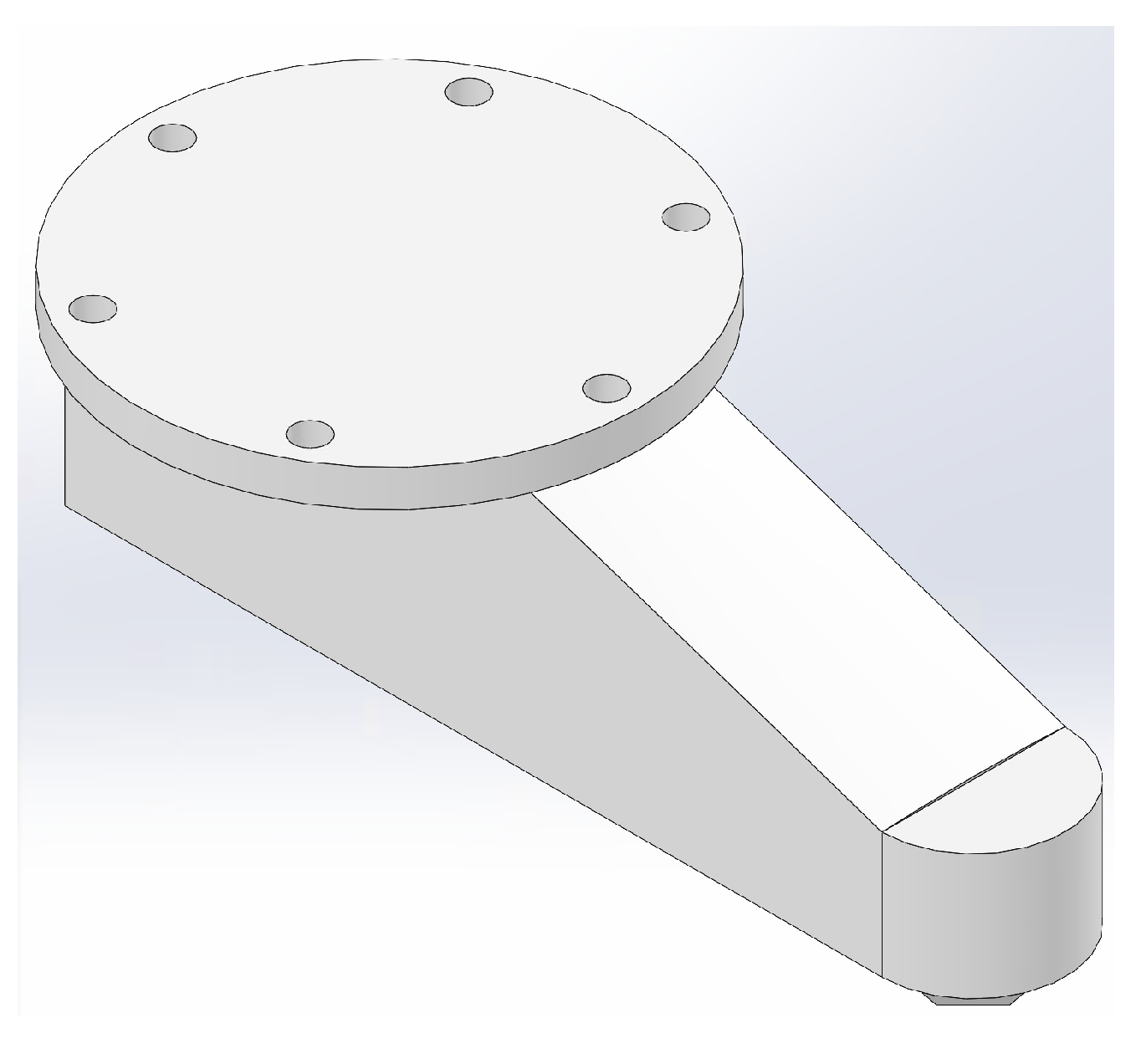
3.1.3. End-Effector
3.1.4. Vision System
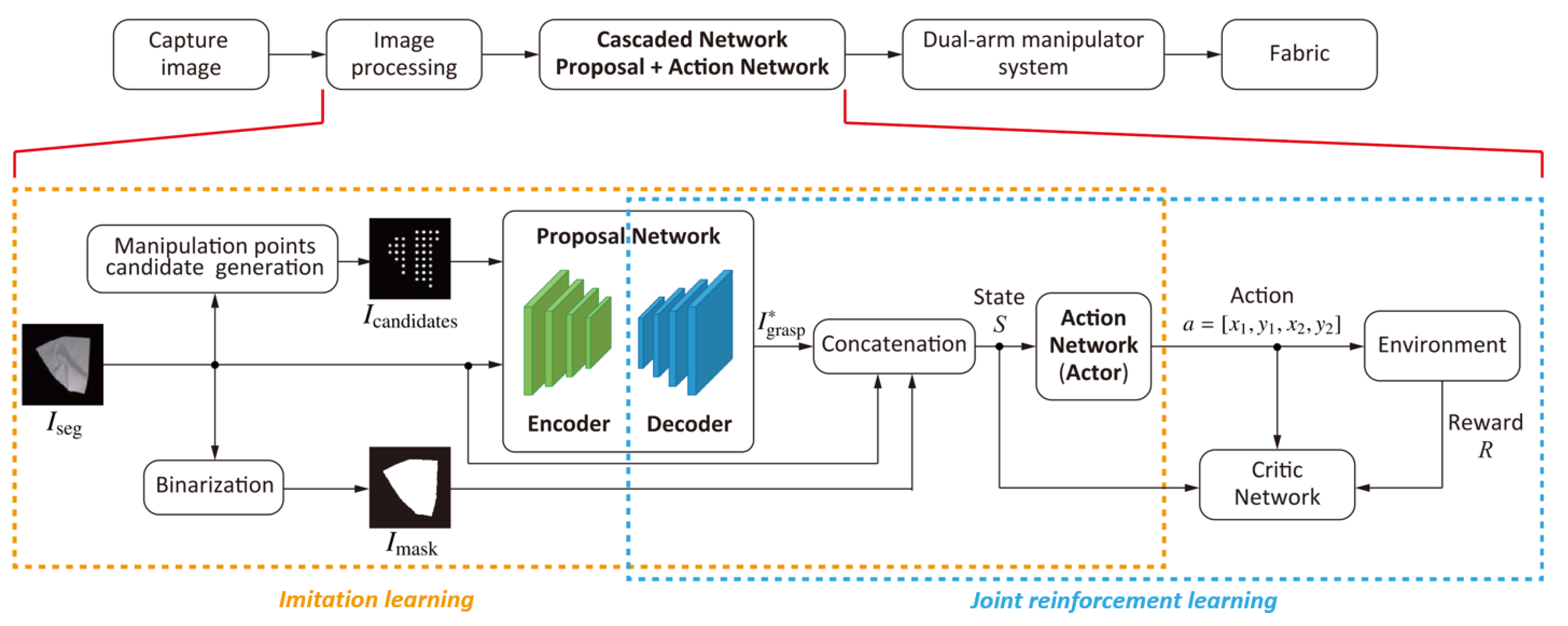
3.2. Imitation Learning Based on Human Demonstration
3.2.1. Human Demonstration
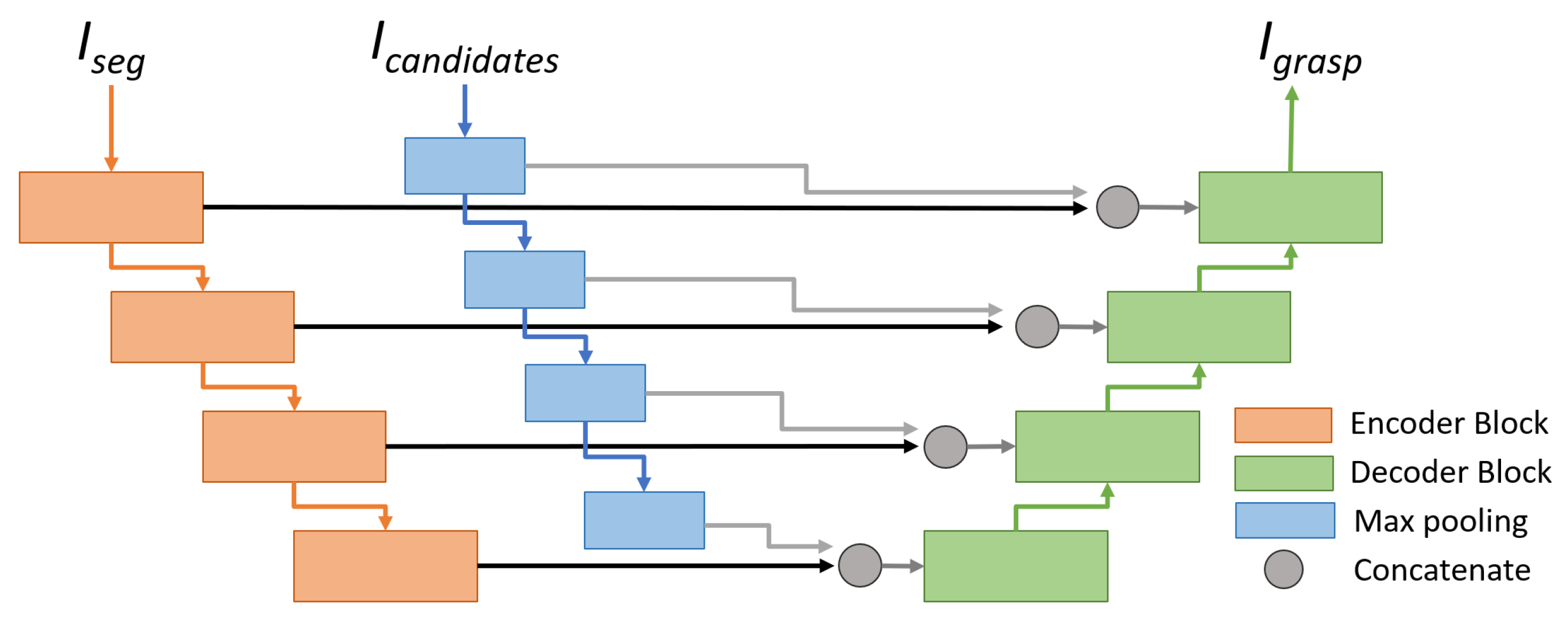
3.2.2. PN Architecture and Training
3.2.3. AN Architecture and Training
3.3. Joint Reinforcement Learning
3.3.1. Dataset for Offline Reinforcement Learning
3.3.2. Learning Strategies
4. Results
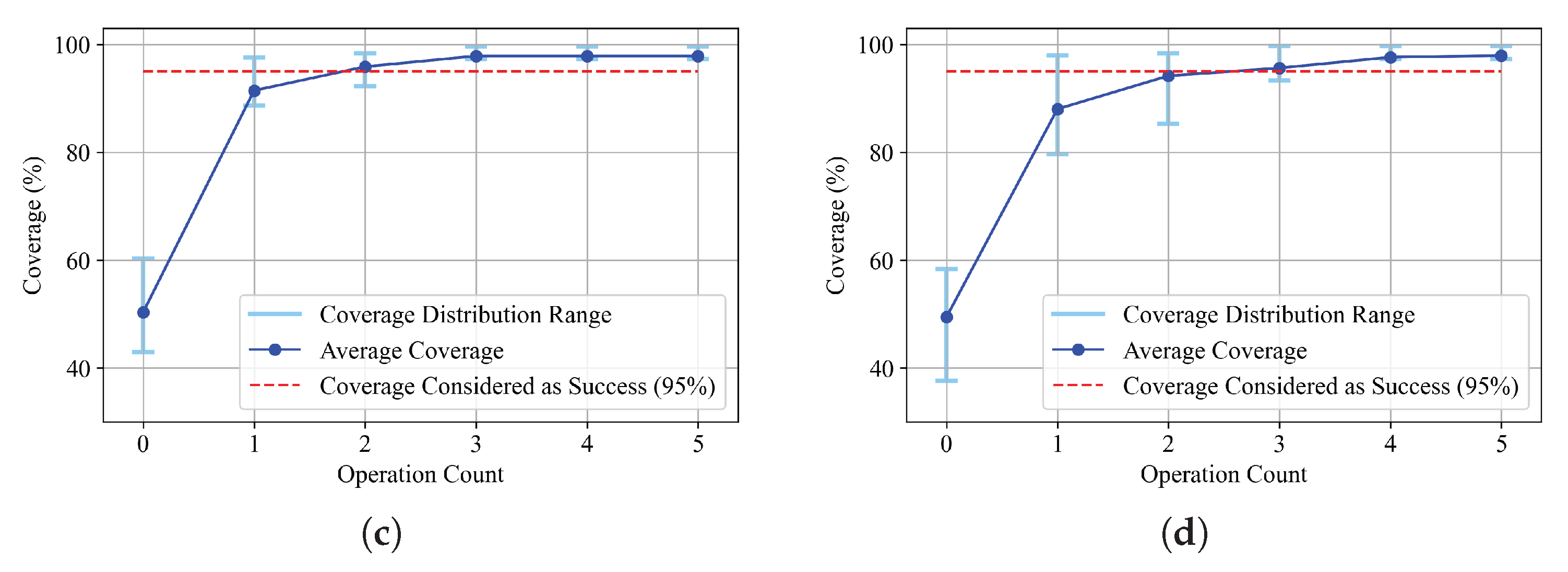
4.1. Proposal Network
4.2. Pre-Training for Action Network
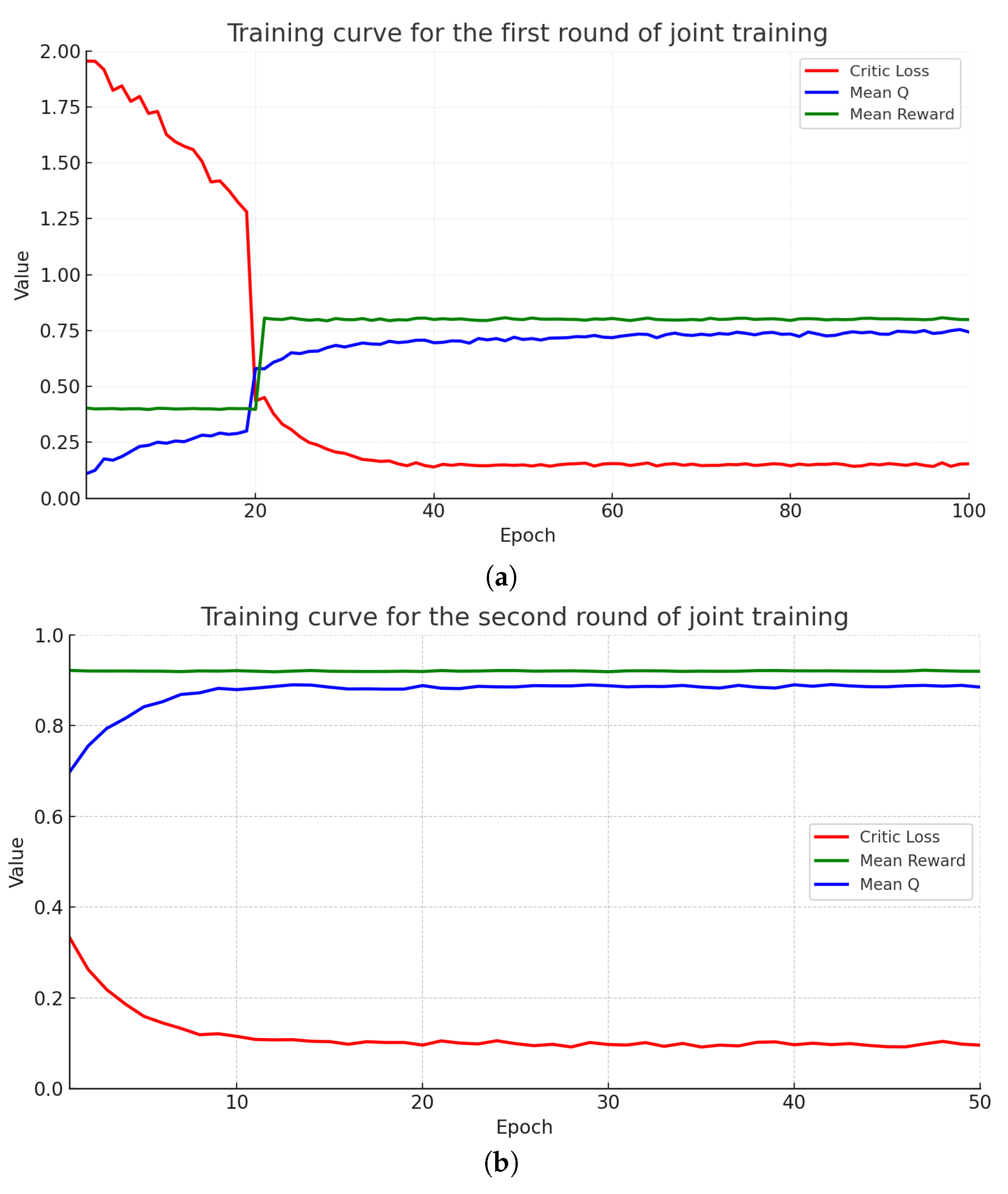
4.3. Joint Reinforcement Learning
4.4. Flattening Evaluation on Different Types of Fabric
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| lL | Imitation learning |
| RL | Reinforcement learning |
| PN | Proposal network |
| AN | Action network |
| BCE | Binary cross-entropy |
| HWD | Haar wavelet down-sampling |
| MSE | Mean squared error |
| SD | standard deviation |
References
- Tang, K.; Tokuda, F.; Seino, A.; Kobayashi, A.; Tien, N.C.; Kosuge, K. Time-Scaling Modeling and Control of Robotic Sewing System. IEEE/ASME Trans. Mechatronics 2024, 29, 3166–3174. [Google Scholar] [CrossRef]
- Tang, K.; Huang, X.; Seino, A.; Tokuda, F.; Kobayashi, A.; Tien, N.C.; Kosuge, K. Fixture-Free Automated Sewing System Using Dual-Arm Manipulator and High-Speed Fabric Edge Detection. IEEE Robot. Autom. Lett. 2025, 10, 8962–8969. [Google Scholar] [CrossRef]
- Zhu, J.; Cherubini, A.; Dune, C.; Navarro-Alarcon, D.; Alambeigi, F.; Berenson, D.; Ficuciello, F.; Harada, K.; Kober, J.; Li, X.; et al. Challenges and Outlook in Robotic Manipulation of Deformable Objects. IEEE Robot. Autom. Mag. 2022, 29, 67–77. [Google Scholar] [CrossRef]
- Seita, D.; Florence, P.; Tompson, J.; Coumans, E.; Sindhwani, V.; Goldberg, K.; Zeng, A. Learning to Rearrange Deformable Cables, Fabrics, and Bags with Goal-Conditioned Transporter Networks. In Proceedings of the 2021 IEEE International Conference on Robotics and Automation (ICRA), Xi’an, China, 30 May–5 June 2021; pp. 4568–4575. [Google Scholar] [CrossRef]
- Shehawy, H.; Pareyson, D.; Caruso, V.; Zanchettin, A.M.; Rocco, P. Flattening Clothes with a Single-Arm Robot Based on Reinforcement Learning. In Proceedings of the Intelligent Autonomous Systems 17 (IAS 2022), Zagreb, Croatia, 13–16 June 2022; Petrovic, I., Menegatti, E., Marković, I., Eds.; Lecture Notes in Networks and Systems. Springer: Cham, Switzerland, 2023; Volume 577, pp. 580–595. [Google Scholar] [CrossRef]
- Seita, D.; Ganapathi, A.; Hoque, R.; Hwang, M.; Cen, E.; Tanwani, A.K.; Balakrishna, A.; Thananjeyan, B.; Ichnowski, J.; Jamali, N.; et al. Deep Imitation Learning of Sequential Fabric Smoothing From an Algorithmic Supervisor. In Proceedings of the 2020 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Las Vegas, NV, USA, 25–30 October 2020; pp. 9651–9658. [Google Scholar] [CrossRef]
- Qiu, Y.; Zhu, J.; Della Santina, C.; Gienger, M.; Kober, J. Robotic fabric flattening with wrinkle direction detection. In Proceedings of the International Symposium on Experimental Robotics, Chiang Mai, Thailand, 26–30 November 2023; Springer: Berlin/Heidelberg, Germany, 2023; pp. 339–350. [Google Scholar]
- Sun, L.; Aragon-Camarasa, G.; Rogers, S.; Siebert, J.P. Accurate garment surface analysis using an active stereo robot head with application to dual-arm flattening. In Proceedings of the 2015 IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26–30 May 2015; pp. 185–192. [Google Scholar]
- Ma, Y.; Tokuda, F.; Seino, A.; Kobayashi, A.; Hayashibe, M.; Jin, B.; Kosuge, K. Partial Fabric Flattening for Seam Line Region Using Dual-Arm Manipulation. In Proceedings of the 2025 IEEE International Conference on Mechatronics and Automation (ICMA), Beijing, China, 3–6 August 2025; pp. 1173–1178. [Google Scholar]
- Islam, S.; Owen, C.; Mukherjee, R.; Woodring, I. Wrinkle Detection and Cloth Flattening through Deep Learning and Image Analysis as Assistive Technologies for Sewing. In Proceedings of the 17th International Conference on Pervasive Technologies Related to Assistive Environments, Crete, Greece, 26–28 June 2024; pp. 233–242. [Google Scholar]
- Li, C.; Fu, T.; Li, F.; Song, R. Design and Implementation of Fabric Wrinkle Detection System Based on YOLOv5 Algorithm. Cobot 2024, 3, 5. [Google Scholar] [CrossRef]
- Yamazaki, K.; Inaba, M. Clothing classification using image features derived from clothing fabrics, wrinkles and cloth overlaps. In Proceedings of the 2013 IEEE/RSJ International Conference on Intelligent Robots and Systems, Tokyo, Japan, 3–8 November 2013; pp. 2710–2717. [Google Scholar]
- Yang, H. 3D Clothing Wrinkle Modeling Method Based on Gaussian Curvature and Deep Learning. In Proceedings of the 2024 IEEE Asia-Pacific Conference on Image Processing, Electronics and Computers (IPEC), Dalian, China, 12–14 April 2024; pp. 136–140. [Google Scholar]
- Lee, R.; Abou-Chakra, J.; Zhang, F.; Corke, P. Learning Fabric Manipulation in the Real World with Human Videos. In Proceedings of the 2024 IEEE International Conference on Robotics and Automation (ICRA), Yokohama, Japan, 13–17 May 2024; pp. 3124–3130. [Google Scholar] [CrossRef]
- Doumanoglou, A.; Kargakos, A.; Kim, T.K.; Malassiotis, S. Autonomous active recognition and unfolding of clothes using random decision forests and probabilistic planning. In Proceedings of the 2014 IEEE International Conference on Robotics and Automation (ICRA), Hong Kong, China, 31 May–7 June 2014; pp. 987–993. [Google Scholar]
- Xue, H.; Li, Y.; Xu, W.; Li, H.; Zheng, D.; Lu, C. Unifolding: Towards sample-efficient, scalable, and generalizable robotic garment folding. arXiv 2023, arXiv:2311.01267. [Google Scholar]
- Ganapathi, A.; Sundaresan, P.; Thananjeyan, B.; Balakrishna, A.; Seita, D.; Grannen, J.; Hwang, M.; Hoque, R.; Gonzalez, J.E.; Jamali, N.; et al. Learning Dense Visual Correspondences in Simulation to Smooth and Fold Real Fabrics. In Proceedings of the 2021 IEEE International Conference on Robotics and Automation (ICRA), Xi’an, China, 30 May–5 June 2021; pp. 11515–11522. [Google Scholar] [CrossRef]
- Kant, N.; Aryal, A.; Ranganathan, R.; Mukherjee, R.; Owen, C. Modeling Human Strategy for Flattening Wrinkled Cloth Using Neural Networks. In Proceedings of the 2024 IEEE International Conference on Systems, Man, and Cybernetics (SMC), Kuching, Malaysia, 6–10 October 2024; pp. 673–678. [Google Scholar] [CrossRef]
- Weng, T.; Bajracharya, S.M.; Wang, Y.; Agrawal, K.; Held, D. Fabricflownet: Bimanual cloth manipulation with a flow-based policy. In Proceedings of the Conference on Robot Learning, PMLR, Auckland, New Zealand, 14–18 December 2022; pp. 192–202. [Google Scholar]
- Seita, D.; Jamali, N.; Laskey, M.; Tanwani, A.K.; Berenstein, R.; Baskaran, P.; Iba, S.; Canny, J.; Goldberg, K. Deep Transfer Learning of Pick Points on Fabric for Robot Bed-Making. In Proceedings of the Robotics Research, Geneva, Switzerland, 25–30 September 2022; Asfour, T., Yoshida, E., Park, J., Christensen, H., Khatib, O., Eds.; Springer: Cham, Switzerland, 2022; pp. 275–290. [Google Scholar]
- Avigal, Y.; Berscheid, L.; Asfour, T.; Kröger, T.; Goldberg, K. SpeedFolding: Learning Efficient Bimanual Folding of Garments. In Proceedings of the 2022 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Kyoto, Japan, 23–27 October 2022; pp. 1–8. [Google Scholar] [CrossRef]
- Hietala, J.; Blanco–Mulero, D.; Alcan, G.; Kyrki, V. Learning Visual Feedback Control for Dynamic Cloth Folding. In Proceedings of the 2022 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Kyoto, Japan, 23–27 October 2022; pp. 1455–1462. [Google Scholar] [CrossRef]
- Puthuveetil, K.; Kemp, C.C.; Erickson, Z. Bodies Uncovered: Learning to Manipulate Real Blankets Around People via Physics Simulations. IEEE Robot. Autom. Lett. 2022, 7, 1984–1991. [Google Scholar] [CrossRef]
- Antonova, R.; Shi, P.; Yin, H.; Weng, Z.; Jensfelt, D.K. Dynamic environments with deformable objects. In Proceedings of the 35th Conference on Neural Information Processing Systems Datasets and Benchmarks Track (Round 2), Virtual (Online), 6–14 December 2021. [Google Scholar]
- Kober, J.; Bagnell, J.A.; Peters, J. Reinforcement Learning in Robotics: A Survey. Int. J. Robot. Res. 2013, 32, 1238–1274. [Google Scholar] [CrossRef]
- Levine, S.; Finn, C.; Darrell, T.; Abbeel, P. End-to-End Training of Deep Visuomotor Policies. J. Mach. Learn. Res. 2016, 17, 1–40. [Google Scholar]
- Lillicrap, T.P.; Hunt, J.J.; Pritzel, A.; Heess, N.; Erez, T.; Tassa, Y.; Silver, D.; Wierstra, D. Continuous Control with Deep Reinforcement Learning. In Proceedings of the 4th International Conference on Learning Representations (ICLR), San Juan, PR, USA, 2–4 May 2016. [Google Scholar]
- Schulman, J.; Wolski, F.; Dhariwal, P.; Radford, A.; Klimov, O. Proximal Policy Optimization Algorithms. arXiv 2017, arXiv:1707.06347. [Google Scholar] [CrossRef]
- Zeng, A.; Song, S.; Yu, K.; Donlon, E.; Hogan, F.; Bauza, M.; Rodriguez, A. Learning Synergies between Pushing and Grasping with Self-supervised Deep Reinforcement Learning. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA), Brisbane, QLD, Australia, 21–25 May 2018; pp. 747–754. [Google Scholar]
- Shehawy, H.; Pareyson, D.; Caruso, V.; De Bernardi, S.; Zanchettin, A.M.; Rocco, P. Flattening and folding towels with a single-arm robot based on reinforcement learning. Robot. Auton. Syst. 2023, 169, 104506. [Google Scholar] [CrossRef]
- Lee, R.; Ward, D.; Dasagi, V.; Cosgun, A.; Leitner, J.; Corke, P. Learning arbitrary-goal fabric folding with one hour of real robot experience. In Proceedings of the Conference on Robot Learning, PMLR, London, UK, 8–11 November 2021; pp. 2317–2327. [Google Scholar]
- Ha, H.; Song, S. Flingbot: The unreasonable effectiveness of dynamic manipulation for cloth unfolding. In Proceedings of the Conference on Robot Learning, PMLR, Auckland, New Zealand, 14–18 December 2022; pp. 24–33. [Google Scholar]
- Sun, Z.; Wang, Y.; Held, D.; Erickson, Z. Force-Constrained Visual Policy: Safe Robot-Assisted Dressing via Multi-Modal Sensing. IEEE Robot. Autom. Lett. 2024, 9, 4178–4185. [Google Scholar] [CrossRef]
- Vecerik, M.; Hester, T.; Scholz, J.; Wang, F.; Pietquin, O.; Piot, B.; Heess, N.; Rothörl, T.; Lampe, T.; Riedmiller, M. Leveraging demonstrations for deep reinforcement learning on robotics problems with sparse rewards. arXiv 2017, arXiv:1707.08817. [Google Scholar]
- Ho, J.; Ermon, S. Generative adversarial imitation learning. In Proceedings of the Advances in Neural Information Processing Systems, Barcelona, Spain, 5–10 December 2016; Volume 29. [Google Scholar]
- Tsurumine, Y.; Matsubara, T. Goal-aware generative adversarial imitation learning from imperfect demonstration for robotic cloth manipulation. Robot. Auton. Syst. 2022, 158, 104264. [Google Scholar] [CrossRef]
- Fujimoto, S.; Meger, D.; Precup, D. Off-policy deep reinforcement learning without exploration. In Proceedings of the International Conference on Machine Learning, PMLR, Long Beach, CA, USA, 9–15 June 2019; pp. 2052–2062. [Google Scholar]
- Salhotra, G.; Liu, I.C.A.; Dominguez-Kuhne, M.; Sukhatme, G.S. Learning Deformable Object Manipulation from Expert Demonstrations. IEEE Robot. Autom. Lett. 2022, 7, 8775–8782. [Google Scholar] [CrossRef]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In Proceedings of the Medical Image Computing and Computer-Assisted Intervention–MICCAI 2015: 18th International Conference, Munich, Germany, 5–9 October 2015; Proceedings, Part III 18. Springer: Berlin/Heidelberg, Germany, 2015; pp. 234–241. [Google Scholar]
- Bridle, P. Probabilistic Interpretation of Feedforward Classification Network Outputs, with Relationships to Statistical Pattern Recognition. Neurocomputing 1990, 2, 227–236. [Google Scholar]
- Li, X.; Sun, X.; Meng, Y.; Liang, J.; Wu, F.; Li, J. Dice Loss for Data-imbalanced NLP Tasks. In Proceedings of the 58th Annual Meeting of the Association for Computational Linguistics, Online, 5–10 July 2020; pp. 465–476. [Google Scholar] [CrossRef]
- Wu, T.; Tang, S.; Cai, Q.; Zhang, C.; Torr, P.H. Haar wavelet downsampling: A simple but effective downsampling module for semantic segmentation. In Proceedings of the European Conference on Computer Vision (ECCV), Tel Aviv, Israel, 23–27 October 2022; Springer: Berlin/Heidelberg, Germany, 2022. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, L.; Polosukhin, I. Attention is all you need. In Proceedings of the Advances in Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; Volume 30. [Google Scholar]
- Mnih, V.; Badia, A.P.; Mirza, M.; Graves, A.; Lillicrap, T.; Harley, T.; Silver, D.; Kavukcuoglu, K. Asynchronous methods for deep reinforcement learning. In Proceedings of the International Conference on Machine Learning, New York, NY, USA, 19–24 June 2016; pp. 1928–1937. [Google Scholar]









| Method | Valid Cases | Fabric Images with Invalid Points |
|---|---|---|
| MSE | 86% (43/50) | 14% (7/50) |
| MSE + | 98% (49/50) | 2% (1/50) |
| Policy | Final Success Rate | One-Time Success Rate | Average Operation Count |
|---|---|---|---|
| Trained by human demonstration | 82% (41/50) | 74% (37/50) | – |
| One-round joint reinforcement learning | 94% (47/50) | 90% (45/50) | – |
| Two-round joint reinforcement learning | 100% (50/50) | 94% (47/50) | 1–3 |
| Wrinkle detection with dual-arm [9] | 84% (42/50) | 30% (15/50) | 3–9 |
| Wrinkle detection with single-arm [7] | – | – | 7–9 |
| Deep imitation learning [6] | – | – | 4–8 |
| Properties | Type I | Type II | Type III | Type IV |
|---|---|---|---|---|
| Specimen |  |  |  |  |
| Material | Cotton | Cotton | Cotton | Linen |
| () | 0.26 | 0.24 | 0.08 | 0.13 |
| T (mm) | 0.28 | 0.27 | 0.14 | 0.18 |
| G (N/mm) | 0.39 | 0.64 | 0.47 | 0.68 |
| E (MPa) | 17.31 | 6.60 | 22.80 | 14.96 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, Y.; Tokuda, F.; Seino, A.; Kobayashi, A.; Hayashibe, M.; Kosuge, K. Fabric Flattening with Dual-Arm Manipulator via Hybrid Imitation and Reinforcement Learning. Machines 2025, 13, 923. https://doi.org/10.3390/machines13100923
Ma Y, Tokuda F, Seino A, Kobayashi A, Hayashibe M, Kosuge K. Fabric Flattening with Dual-Arm Manipulator via Hybrid Imitation and Reinforcement Learning. Machines. 2025; 13(10):923. https://doi.org/10.3390/machines13100923
Chicago/Turabian StyleMa, Youchun, Fuyuki Tokuda, Akira Seino, Akinari Kobayashi, Mitsuhiro Hayashibe, and Kazuhiro Kosuge. 2025. "Fabric Flattening with Dual-Arm Manipulator via Hybrid Imitation and Reinforcement Learning" Machines 13, no. 10: 923. https://doi.org/10.3390/machines13100923
APA StyleMa, Y., Tokuda, F., Seino, A., Kobayashi, A., Hayashibe, M., & Kosuge, K. (2025). Fabric Flattening with Dual-Arm Manipulator via Hybrid Imitation and Reinforcement Learning. Machines, 13(10), 923. https://doi.org/10.3390/machines13100923







