Lightweight Design and Research of Electric Towing Winch Based on Kriging-NSGA-III-TOPSIS Multi-Objective Optimization Technology
Abstract
1. Introduction
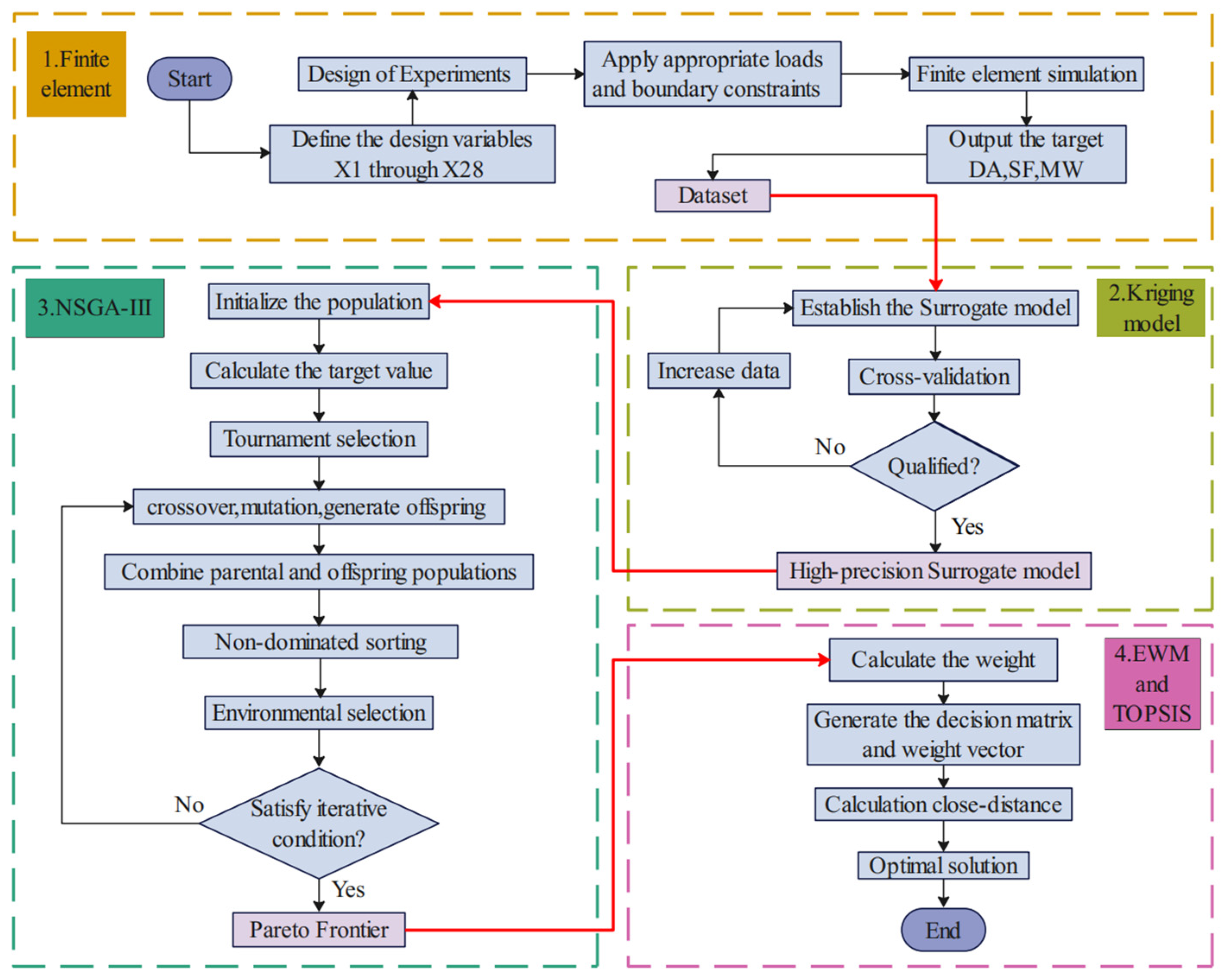
2. Multi-Objective Optimization Framework
2.1. Principles of Kriging Interpolation Models
2.2. NSGA-III Optimization Algorithm
2.3. EWM and TOPSIS
3. Simulation Experiments and Optimization Models
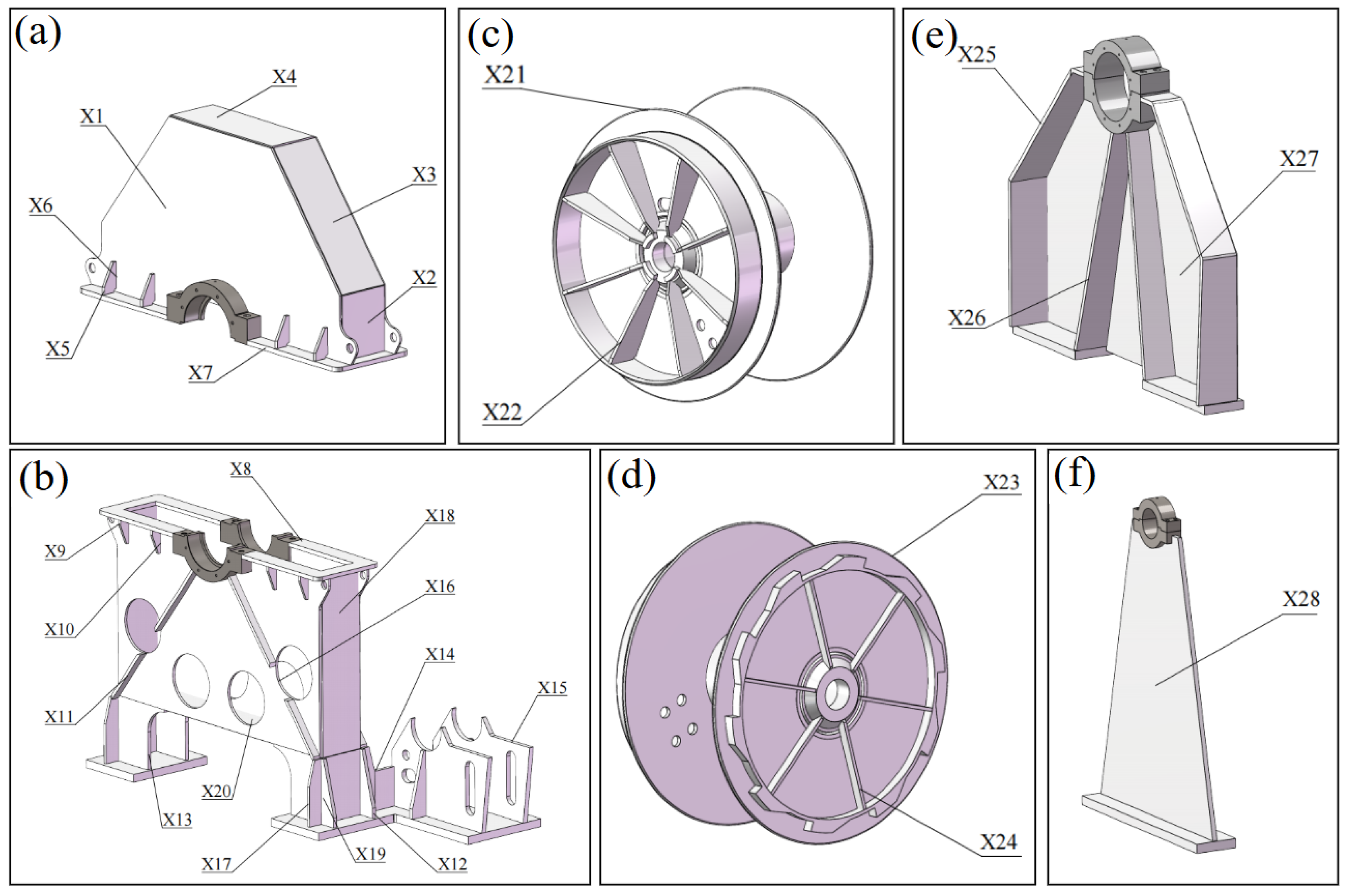
3.1. Engineering Case Model
- (1)
- Gravity on the rope on the drum:
- (2)
- Workload torque on the reel:
- (3)
- Braking torque of the brake on the drum:
- (4)
- The pressure exerted by the cable on the drum.
- (5)
- The pressure exerted by the cable on the flange plate. During layer transition winding (crossover from drum end to new layer), cable wedging generates axial thrust at the transition loop. This force induces flange bending and significant stress concentration at the flange-drum interface. During multilayer winding, every crossover segment applies compressive loading on the flange. Furthermore, crossover segments distribute circumferentially with minimal inter-layer spacing. Consequently, total compressive load is modeled as uniformly distributed flange pressure:
3.2. Establishment of an Optimized Model
3.3. DoE Experiment
4. Results Analysis
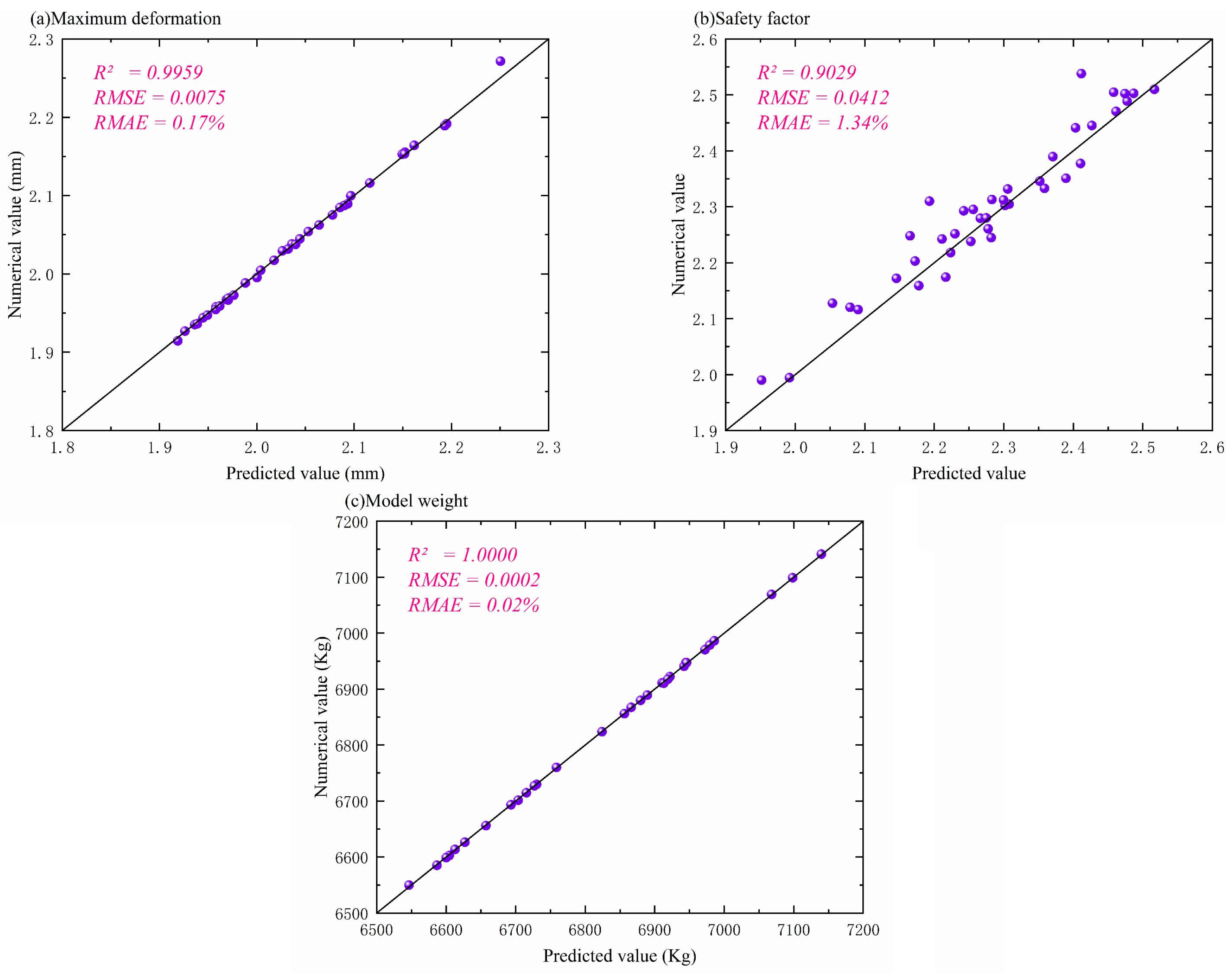
4.1. Kriging Model Prediction Results
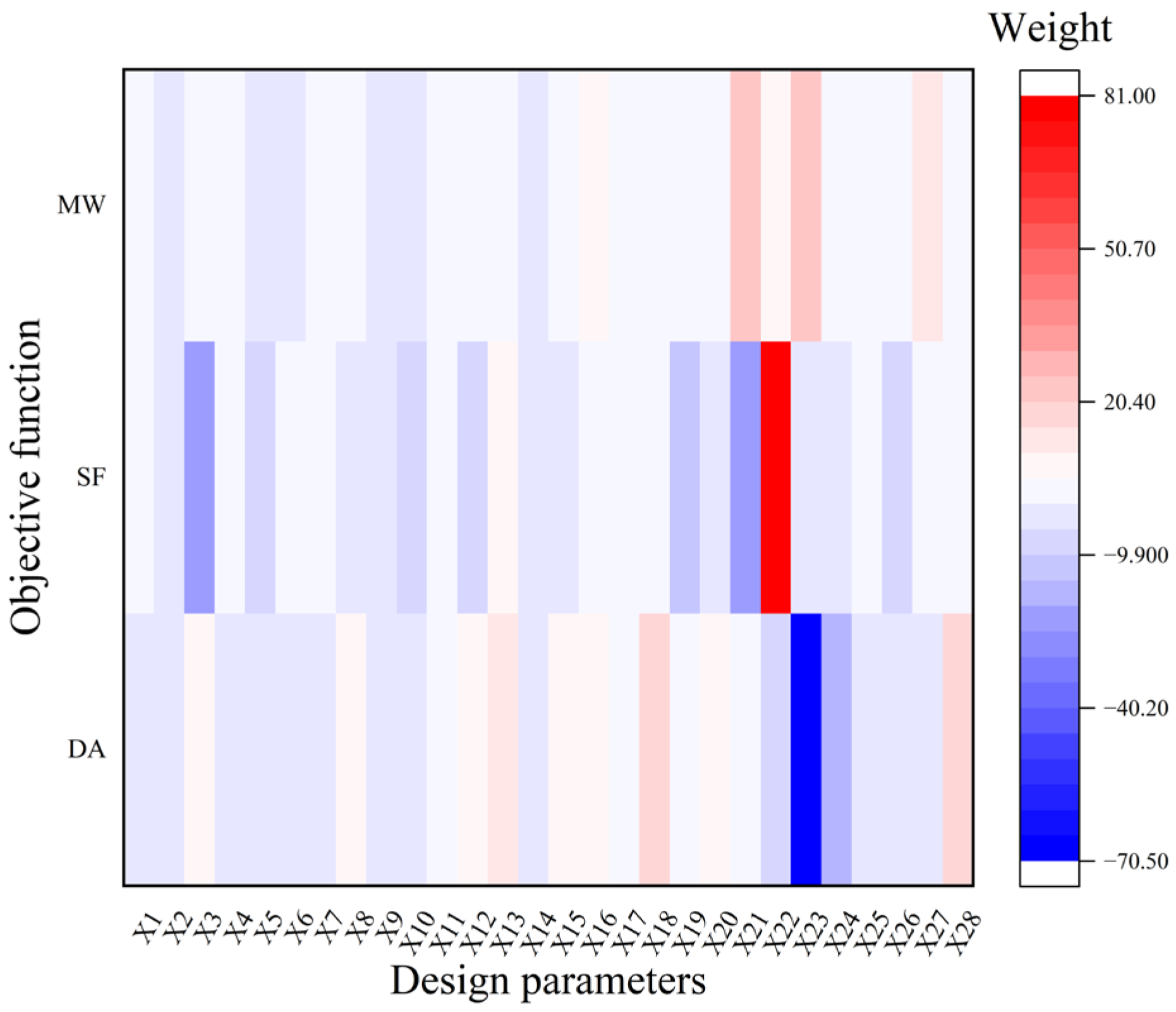
4.2. Sensitivity Analysis
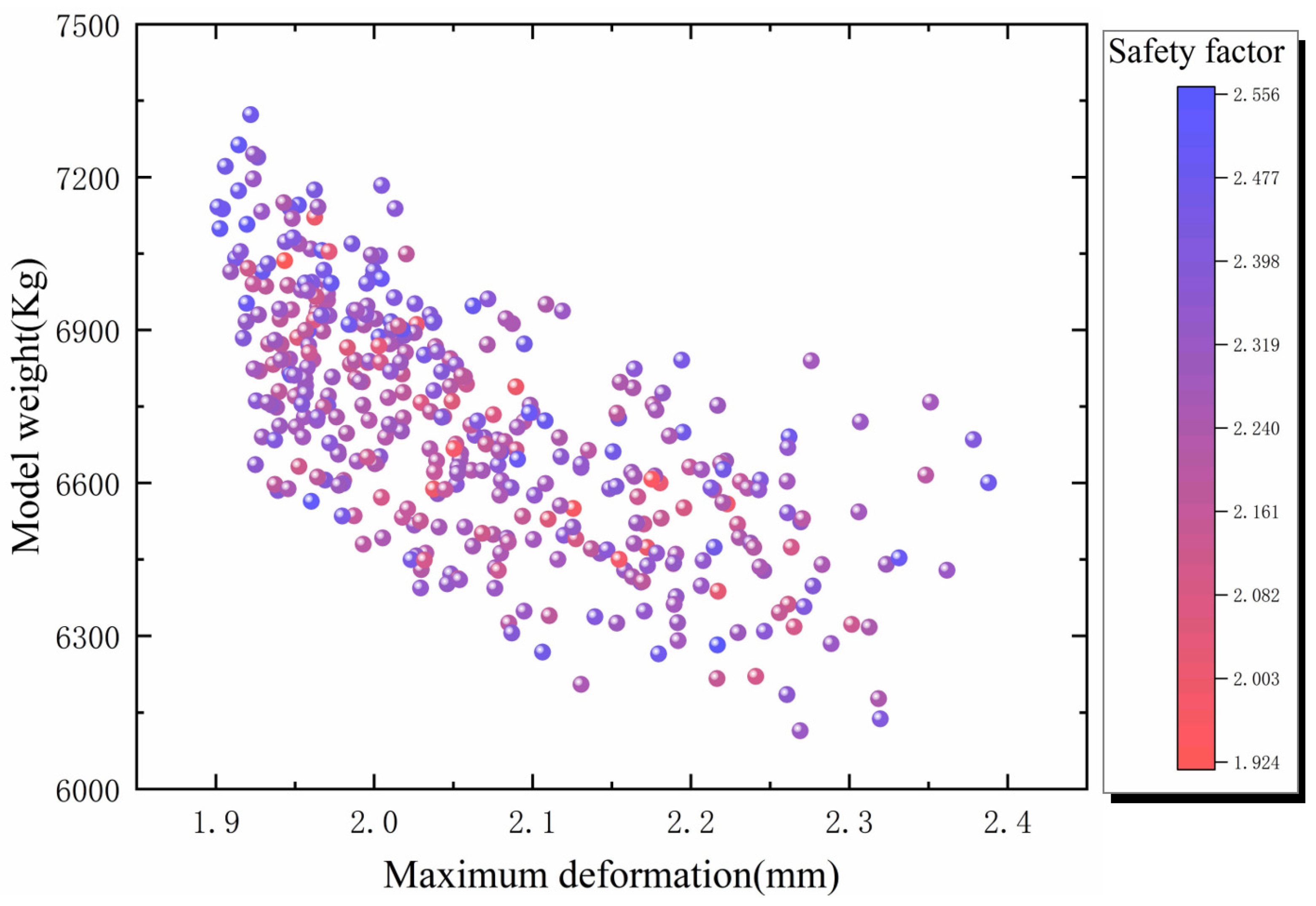
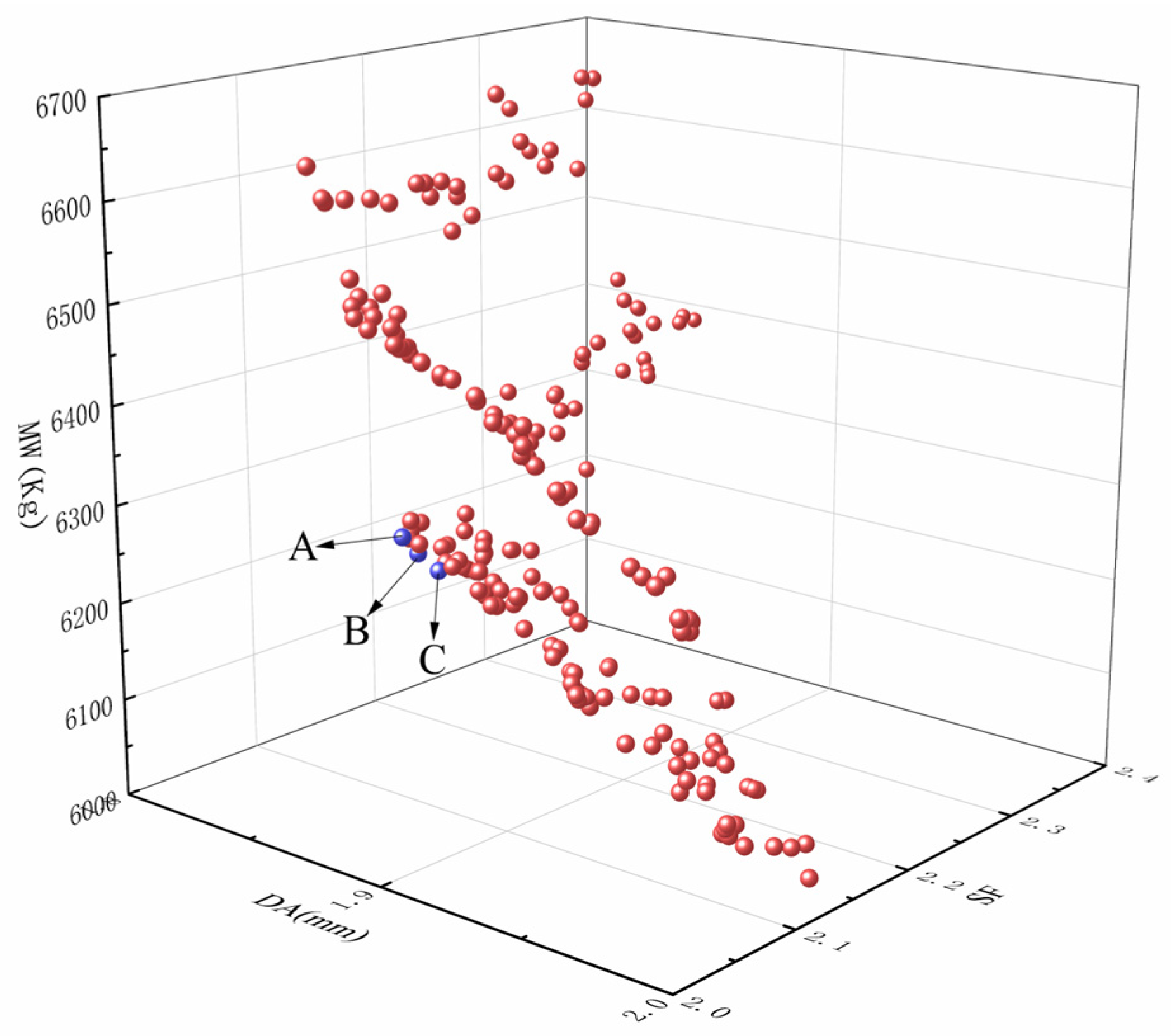
4.3. Optimized Solution
5. Conclusions
- High Efficiency and Reliability of the Integrated Framework: By integrating high-precision Kriging modeling, NSGA-III algorithms, and EWM-TOPSIS decision-making, the proposed framework significantly reduces reliance on computationally intensive simulations. This provides a systematic, efficient, and reliable methodology for the co-optimization of lightweighting and reliability in complex three-dimensional structures.
- Significant Optimization Outcomes for Electric Cable Winches: The framework achieved intelligent optimization of critical structural parameters, targeting reinforcement in high-stress zones and rational reduction in low-stress zones. The optimized design, which strictly adheres to corporate technical specifications and operational requirements, achieved a 7.32% weight reduction, a 7.34% increase in the safety factor, and a 4.57% decrease in maximum deformation. These results fully validate the framework’s engineering effectiveness.
- High Industry Value of the Framework: This framework effectively balances conflicting design objectives. The established optimization process provides an efficient, scalable paradigm for intelligent and lean design of marine deck winch machinery. It holds significant practical implications for advancing marine engineering equipment toward high performance, low material consumption, and high reliability.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Xu, M.; Shen, Y.; Zhu, Y.; Hong, L.; Ma, M.; Lü, L.; Li, K.X. Identification of critical sets of ports in cascading failures of global liner shipping network. Transp. Res. Part E 2025, 200, 104184. [Google Scholar] [CrossRef]
- Wang, L.; Yang, Y.; Mei, Q.; Song, R. Generational evolution and spatial distribution characteristics of ports along the belt and road initiative. J. Transp. Geogr. 2025, 128, 104343. [Google Scholar] [CrossRef]
- Carral Couce, L.; Carral Couce, J.C.; Fraguela Formoso, J.A. Operation and Handling in Escort Tugboat Manoeuvres with the aid of Automatic Towing Winch Systems. J. Navig. 2015, 68, 71–88. [Google Scholar] [CrossRef]
- Saito, D.G.H.; Santos, M.V.d.; Souza, C.B. Dynamic modelling, simulation, and control of hybrid power systems for escort tugs and shuttle tankers. J. Energy Storage 2023, 72, 108091. [Google Scholar] [CrossRef]
- Solovyov, V.; Cherniavsky, A. Computational and experimental analysis of trawl winches barrels deformations. Eng. Fail. Anal. 2013, 28, 160–165. [Google Scholar] [CrossRef]
- Ye, H.; Li, W.; Lin, S.; Ge, Y.; Han, F.; Sun, Y. Experimental investigation of spooling test on the multilayer oceanographic winch with high-performance synthetic fibre rope. Ocean Eng. 2021, 241, 110037. [Google Scholar] [CrossRef]
- Jin, C.; Zhu, L.; Liu, Q.; Lin, J. Multi-Objective Optimization of Marine Winch Based on Surrogate Model and MOGA. Comput. Model. Eng. Sci. 2025, 143, 1689–1711. [Google Scholar] [CrossRef]
- Huang, X.; Wang, P.; Wang, Q.; Zhang, L.; Yang, W.; Li, L. An improved adaptive Kriging method for the possibility-based design optimization and its application to aeroengine turbine disk. Aerosp. Sci. Technol. 2024, 153, 109495. [Google Scholar] [CrossRef]
- Kumar, R.; Prasad, K.J.; Keprate, A.; Sen, S. Addressing material uncertainty in reliability analysis of floating offshore mooring through probabilistic meta-model developed with Stochastic Kriging technique. Ocean Eng. 2025, 335, 121697. [Google Scholar] [CrossRef]
- Jiang, Z.; Chen, J.; Xie, S.; Li, X.; Liu, H.; Wang, L.; Hong, C.; Li, G.; Li, H.; Chen, K. Establishment of CFD-ANN-NSGA-II model for stirred reactor design. Chem. Eng. Sci. 2025, 311, 121614. [Google Scholar] [CrossRef]
- Liu, F.; Deng, X. Multi-objective optimization of an autonomous underwater vehicle shape based on an improved Kriging model. Ocean Eng. 2024, 313, 119388. [Google Scholar] [CrossRef]
- Lin, J.; Liu, Q. TRAA: A two-risk archive algorithm for expensive many-objective optimization. Complex Intell. Syst. 2024, 10, 7349–7371. [Google Scholar] [CrossRef]
- Axay, T.; Atin, R.; Subrata, C. Reliability analysis of underground tunnel by a novel adaptive Kriging based metamodeling approach. Probabilistic Eng. Mech. 2022, 70, 103351. [Google Scholar] [CrossRef]
- Zhao, Q.; Duan, J.; Wu, T.; Hong, J. Time-dependent reliability analysis under random and interval uncertainties based on Kriging modeling and saddlepoint approximation. Comput. Ind. Eng. 2023, 182, 109391. [Google Scholar] [CrossRef]
- Park, J. Central Limit Theorem for Multi-Point Functions of the 2D Discrete Gaussian Model at High Temperature. Commun. Math. Phys. 2025, 406, 234. [Google Scholar] [CrossRef]
- Deb, K.; Jain, H. An Evolutionary Many-Objective Optimization Algorithm Using Reference-Point-Based Nondominated Sorting Approach, Part I: Solving Problems With Box Constraints. IEEE Trans. Evol. Comput. A Publ. IEEE Neural Netw. Counc. 2014, 18, 577–601. [Google Scholar] [CrossRef]
- Li, Y.; Xie, H.; Deng, X.; Zhang, J.; Liu, S.; Wang, L. Inventory optimisation based on NSGA-III algorithm. Int. J. Space-Based Situated Comput. 2023, 9, 158–164. [Google Scholar] [CrossRef]
- Chowdhury, S.; Bohre, A.K.; Saha, A.K. Meta-Heuristic Optimization for Hybrid Renewable Energy System in Durgapur: Performance Comparison of GWO, TLBO, and MOPSO. Sustainability 2025, 17, 6954. [Google Scholar] [CrossRef]
- Gu, Q.; Li, K.; Wang, D.; Liu, D. A MOEA/D with adaptive weight subspace for regular and irregular multi-objective optimization problems. Inf. Sci. 2024, 661, 120143. [Google Scholar] [CrossRef]
- Reddy, S.; Dulikravich, G.S. A self-adapting algorithm for many-objective optimization. Appl. Soft Comput. J. 2022, 129, 109484. [Google Scholar] [CrossRef]
- Zhao, T.; Wu, L.; Cui, Z.; Qin, A.K. An adaptive strategy based multi-population multi-objective optimization algorithm. Inf. Sci. 2025, 686, 120913. [Google Scholar] [CrossRef]
- Abdel-Basset, M.; Mohamed, R.; Abouhawwash, M. Balanced multi-objective optimization algorithm using improvement based reference points approach. Swarm Evol. Comput. 2021, 60, 100791. [Google Scholar] [CrossRef]
- Hu, Y.; Peng, J.; Ou, J.; Li, Y.; Zheng, J.; Zou, J.; Jiang, S.; Yang, S.; Li, J. The IGD-based prediction strategy for dynamic multi-objective optimization. Swarm Evol. Comput. 2024, 91, 101713. [Google Scholar] [CrossRef]
- Liu, H.; Wang, C.H. SEAMS: A surrogate-assisted evolutionary algorithm with metric-based dynamic strategy for expensive multi-objective optimization. Expert Syst. Appl. 2025, 265, 126050. [Google Scholar] [CrossRef]
- Ravichandran, S.; Manoharan, P.; Sinha, D.K.; Jangir, P.; Abualigah, L.; Alghamdi, T.A.H. Multi-objective resistance-capacitance optimization algorithm: An effective multi-objective algorithm for engineering design problems. Heliyon 2024, 10, e35921. [Google Scholar] [CrossRef] [PubMed]
- Yin, Y.; Song, C.; Jing, Y.; Zhang, S.; Ye, S.; Wang, Y.; Gao, P. EWMS: A software tool for interactively using entropy weight coefficient method for aggregating sustainability indicators. Environ. Model. Softw. 2025, 191, 106500. [Google Scholar] [CrossRef]
- Liu, H.; Wang, Y. TOPSIS method for ability evaluation of industrial internet platform energizing digital transformation of manufacturing with DHHFLTSs. Int. J. Knowl.-Based Intell. Eng. Syst. 2025, 29, 336–347. [Google Scholar] [CrossRef]
- Du, Y.; Mao, K.; Lei, X.; Ma, W.; Liang, Q.; Tu, J. Multi-objective optimization of process parameters for laser cladding of Cr3C2/15-5PH composite coatings on 20CrMnTi using RSM-CMOPSO-EWM-CV. J. Mater. Res. Technol. 2025, 36, 5632–5645. [Google Scholar] [CrossRef]
- Li, G.; Yang, J.; Wang, W.; Zhang, Z.; Zhang, W.; Wu, Z. Augmented RBF metamodel for global sensitivity analysis enhanced by recursive evolution LHD and efficient K-fold cross-validation. J. Mech. Sci. Technol. 2022, 36, 4127–4142. [Google Scholar] [CrossRef]
- Sengupta, P.; Chakraborty, S. Bayesian model updating in an active Kriging-based metamodeling framework. Appl. Math. Model. 2025, 142, 115981. [Google Scholar] [CrossRef]
- Yuan, Y.; Au, F.T.K.; Yang, D.; Zhang, J. Active learning structural model updating of a multisensory system based on Kriging method and Bayesian inference. Comput.-Aided Civ. Infrastruct. Eng. 2022, 38, 353–371. [Google Scholar] [CrossRef]
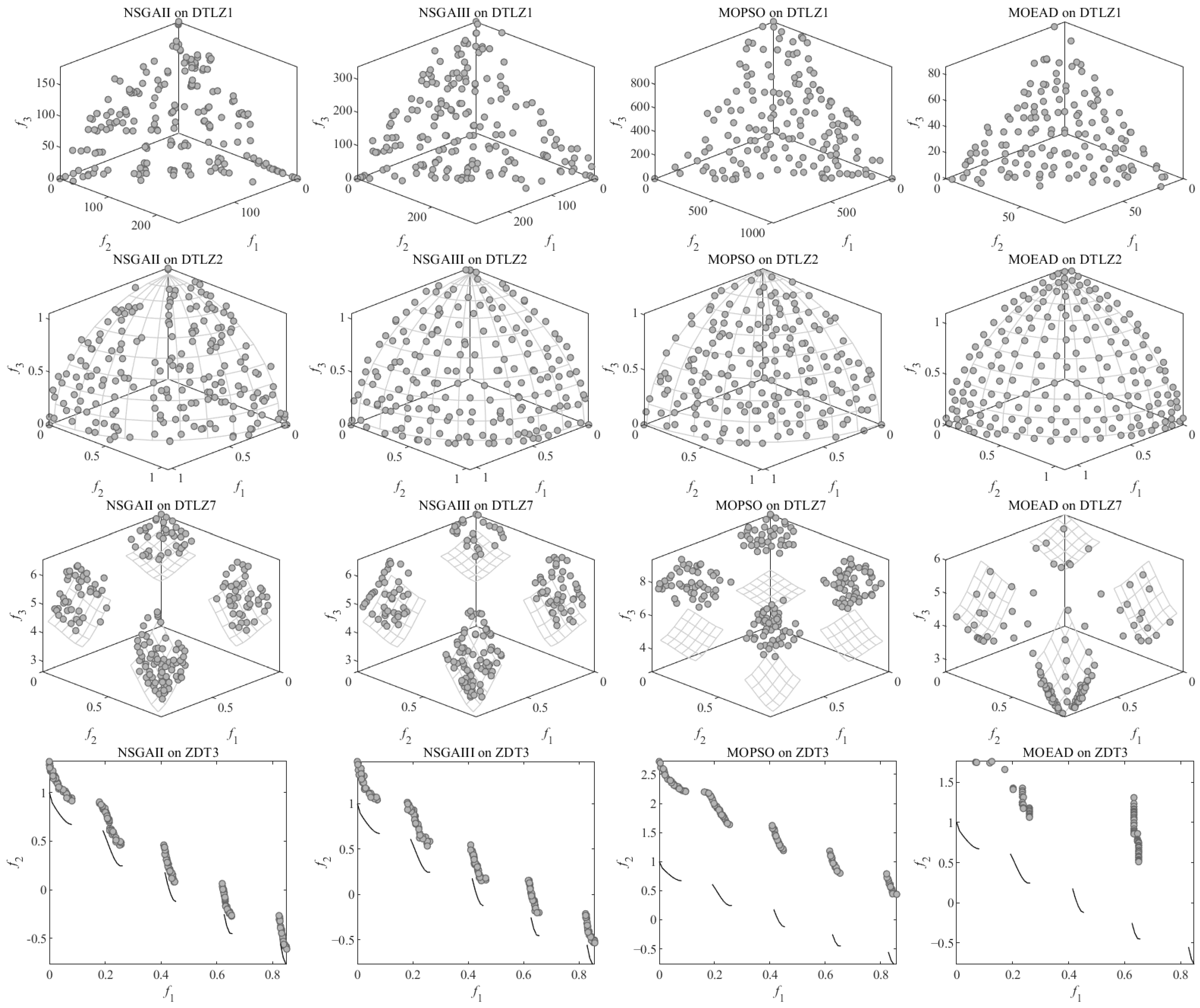



| Test Function | Objective Function and Constraint Conditions | Design Variable |
|---|---|---|
| DTLZ1 | ||
| DTLZ2 | ||
| DTLZ7 | ||
| ZDT3 |
| Test Function | Indicator | NSGA-II | NSGA-III | MOPSO | MOEA/D |
|---|---|---|---|---|---|
| DTLZ1 | 9.09 × 101 (1.72 × 101) | 1.19 × 102 (1.36 × 101) | 4.16 × 102 (2.98 × 101) | 4.57 × 101 (1.48 × 101) | |
| 1.36 × 101 (2.24 × 100) | 1.70 × 101 (2.25 × 100) | 3.49 × 101 (3.05 × 100) | 4.39 × 100 (1.26 × 100) | ||
| DTLZ2 | 7.08 × 10−2 (4.02 × 10−3) | 6.52 × 10−2 (3.31 × 10−3) | 4.88 × 10−2 (1.57 × 10−3) | 7.04 × 10−2 (1.01 × 10−2) | |
| 4.13 × 10−2 (2.07 × 10−3) | 4.56 × 10−2 (1.81 × 10−3) | 3.65 × 10−2 (3.87 × 10−3) | 3.58 × 10−2 (1.75 × 10−3) | ||
| DTLZ7 | 1.88 × 10−1 (3.32 × 10−2) | 2.24 × 10−1 (5.35 × 10−2) | 1.59 × 100 (4.35 × 10−1) | 1.70 × 10−1 (1.74 × 10−1) | |
| 4.43 × 10−2 (4.24 × 10−3) | 4.12 × 10−2 (3.31 × 10−3) | 3.66 × 10−2 (1.00 × 10−2) | 1.01 × 10−1 (2.35 × 10−2) | ||
| ZDT3 | 1.05 × 10−1 (1.47 × 10−2) | 1.52 × 10−1 (1.18 × 10−2) | 6.21 × 10−1 (5.63 × 10−2) | 4.69 × 10−1 (8.88 × 10−2) | |
| 9.59 × 10−3 (1.00 × 10−3) | 1.52 × 10−2 (2.56 × 10−3) | 1.28 × 10−2 (4.79 × 10−3) | 1.77 × 10−2 (7.97 × 10−3) |
| Technical Parameters | Workload (N) | Brake Load (N) | Rated Speed (m/min) | Cable Diameter (mm) | Cable Length (m) |
|---|---|---|---|---|---|
| Main drum | 3.00 × 104 | 1.73 × 106 | 60 | 104 | 200 |
| Anchor chain wheel | 3.33 × 104 | 4.49 × 104 | 15 | 28 | 100 |
| Variable Parameters | Lower Limit (mm) | Original Value (mm) | Upper Limit (mm) |
|---|---|---|---|
| X1 | 7 | 10 | 13 |
| X2 | 7 | 10 | 13 |
| X3 | 7 | 10 | 13 |
| X4 | 7 | 10 | 13 |
| X5 | 10 | 14 | 18 |
| X6 | 91 | 130 | 169 |
| X7 | 14 | 20 | 26 |
| X8 | 14 | 20 | 26 |
| X9 | 10 | 14 | 18 |
| X10 | 91 | 130 | 169 |
| X11 | 11 | 16 | 21 |
| X12 | 14 | 20 | 26 |
| X13 | 14 | 20 | 26 |
| X14 | 14 | 20 | 26 |
| X15 | 18 | 25 | 33 |
| X16 | 10 | 14 | 18 |
| X17 | 10 | 14 | 18 |
| X18 | 10 | 14 | 18 |
| X19 | 231 | 330 | 429 |
| X20 | 10 | 14 | 18 |
| X21 | 21 | 30 | 39 |
| X22 | 18 | 25 | 33 |
| X23 | 21 | 30 | 39 |
| X24 | 18 | 25 | 33 |
| X25 | 14 | 20 | 26 |
| X26 | 14 | 20 | 26 |
| X27 | 21 | 30 | 39 |
| X28 | 14 | 20 | 26 |
| Fold | DA | SF | MW | ||||||
|---|---|---|---|---|---|---|---|---|---|
| (%) | (%) | (%) | |||||||
| 1 | 0.9952 | 0.0078 | 0.19 | 0.8965 | 0.0431 | 1.42 | 1.0000 | 0.0002 | 0.02 |
| 2 | 0.9963 | 0.0072 | 0.16 | 0.9082 | 0.0398 | 1.28 | 0.9999 | 0.0002 | 0.02 |
| 3 | 0.9957 | 0.0076 | 0.18 | 0.9012 | 0.0415 | 1.36 | 1.0000 | 0.0002 | 0.02 |
| 4 | 0.9949 | 0.008 | 0.20 | 0.8958 | 0.0433 | 1.45 | 1.0000 | 0.0002 | 0.02 |
| 5 | 0.9961 | 0.0074 | 0.17 | 0.9047 | 0.0406 | 1.31 | 1.0000 | 0.0002 | 0.01 |
| 6 | 0.9955 | 0.0077 | 0.18 | 0.8993 | 0.0422 | 1.38 | 1.0000 | 0.0002 | 0.02 |
| 7 | 0.9960 | 0.0073 | 0.16 | 0.9071 | 0.0401 | 1.29 | 0.9999 | 0.0003 | 0.02 |
| 8 | 0.9958 | 0.0075 | 0.17 | 0.9036 | 0.041 | 1.33 | 0.9999 | 0.0002 | 0.02 |
| 9 | 0.9953 | 0.0079 | 0.19 | 0.9054 | 0.0404 | 1.3 | 1.0000 | 0.0002 | 0.02 |
| 10 | 0.9962 | 0.0071 | 0.15 | 0.9008 | 0.0418 | 1.37 | 0.9999 | 0.0002 | 0.02 |
| Option | DA (mm) | SF (-) | MW (t) |
|---|---|---|---|
| A | 1.931 | 2.412 | 6.200 |
| B | 1.933 | 2.409 | 6.198 |
| C | 1.859 | 2.478 | 6.371 |
| Variable Parameters | Original Value (mm) | Optimization Value (mm) |
|---|---|---|
| X1 | 10 | 7 |
| X2 | 10 | 12 |
| X3 | 10 | 7 |
| X4 | 10 | 12 |
| X5 | 14 | 12 |
| X6 | 130 | 169 |
| X7 | 20 | 14 |
| X8 | 20 | 14 |
| X9 | 14 | 10 |
| X10 | 130 | 120 |
| X11 | 16 | 12 |
| X12 | 20 | 14 |
| X13 | 20 | 14 |
| X14 | 20 | 15 |
| X15 | 25 | 18 |
| X16 | 14 | 10 |
| X17 | 14 | 10 |
| X18 | 14 | 10 |
| X19 | 330 | 232 |
| X20 | 14 | 10 |
| X21 | 30 | 21 |
| X22 | 25 | 30 |
| X23 | 30 | 34 |
| X24 | 25 | 32 |
| X25 | 20 | 14 |
| X26 | 20 | 14 |
| X27 | 30 | 21 |
| X28 | 20 | 14 |
| DA (mm) | SF (-) | MW (t) | |
|---|---|---|---|
| Original plan | 2.035 | 2.276 | 6.711 |
| Predicted results | 1.932 | 2.436 | 6.221 |
| Real solution | 1.942 | 2.443 | 6.220 |
| Prediction error | 0.51% | 0.29% | 0.02% |
| Optimize boost rate | −4.57% | +7.34% | −7.32% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Q.; Feng, L.; Wang, Y.; Lin, J.; Zhu, L. Lightweight Design and Research of Electric Towing Winch Based on Kriging-NSGA-III-TOPSIS Multi-Objective Optimization Technology. Machines 2025, 13, 922. https://doi.org/10.3390/machines13100922
Liu Q, Feng L, Wang Y, Lin J, Zhu L. Lightweight Design and Research of Electric Towing Winch Based on Kriging-NSGA-III-TOPSIS Multi-Objective Optimization Technology. Machines. 2025; 13(10):922. https://doi.org/10.3390/machines13100922
Chicago/Turabian StyleLiu, Quanliang, Lu Feng, Ya Wang, Ji Lin, and Linsen Zhu. 2025. "Lightweight Design and Research of Electric Towing Winch Based on Kriging-NSGA-III-TOPSIS Multi-Objective Optimization Technology" Machines 13, no. 10: 922. https://doi.org/10.3390/machines13100922
APA StyleLiu, Q., Feng, L., Wang, Y., Lin, J., & Zhu, L. (2025). Lightweight Design and Research of Electric Towing Winch Based on Kriging-NSGA-III-TOPSIS Multi-Objective Optimization Technology. Machines, 13(10), 922. https://doi.org/10.3390/machines13100922





