Effects of Roller End/Rib Curvature Ratio on Friction and Accuracy in Tapered Roller Bearings

Abstract

To address the uncertainty in selecting the optimal spherical base curvature radius (SR) for tapered roller bearings, this study develops dynamic and friction torque models under combined loading conditions to evaluate three SR configurations—0.85ρ_p, 0.90ρ_p, and 0.95ρ_p, where ρ_p represents the curvature radius of the inner rib—in terms of load capacity, friction losses, and operational precision. The results indicate that (1) the 0.85ρ_p configuration minimizes friction by optimizing the contact zone’s f_V parameter under combined loads, making it ideal for low-friction applications; (2) the 0.95ρ_p design achieves superior operational accuracy; (3) the intermediate value of 0.90ρ_p offers an optimal compromise, balancing friction torque reduction with operational precision. These findings establish quantitative guidelines for SR selection based on specific bearing performance requirements.

1. Introduction

Tapered roller bearings (TRBs) are extensively employed in transmission systems owing to their exceptional load-carrying capacity, demountability, and adjustable clearance. Significant research efforts have focused on optimizing their mechanical performance, including load capacity, fatigue resistance, stiffness, and load distribution [1,2,3,4]. With growing emphasis on energy efficiency, secondary contact interfaces—particularly the roller end/rib interaction—have emerged as critical determinants of tribological performance. Under high axial loads, this contact dominates frictional losses and power dissipation [5,6], necessitating detailed analysis of its unique geometric and kinematic behavior.

The roller end/rib interface exhibits fundamentally distinct behavior compared to classical elasto-hydrodynamic lubrication (EHL) point contacts. Its operation under combined moderate loads and high sliding velocities requires specialized consideration of geometric pairing effects and spinning friction [7]. Research has established that curvature radii and geometric configurations profoundly influence tribological performance, affecting both load capacity and friction losses. Quasi-static and dynamic modeling approaches have been widely adopted to quantify contact loads and sliding velocities. Gupta’s foundational work [8] derived roller motion equations demonstrating the direct relationship between frictional behavior and roller skew, later refined by Majdoub et al. [9], who identified tangential flange forces as the primary skew mechanism. Subsequent studies [10,11,12] developed nonlinear dynamic models revealing three key trends: (i) friction power scales positively with rim angle, (ii) larger roller end radii reduce friction, and (iii) flange contact friction governs skew generation. Wingertszahn et al. [13] advanced these insights through multibody simulations, confirming the pivotal role of curvature matching in contact mechanics.

At low speeds, mixed lubrication conditions prevail, with sliding friction dominating roller/rib interactions [14]. EHL analyses by Wang et al. [15] and Fujiwara et al. [16] converged on optimal radius ratios (0.6~0.8 and 0.6~0.85, respectively), balancing fluid film retention and skew mitigation. Recent methodological innovations include Li et al.’s [17] unified friction coefficient model spanning dry-to-EHL regimes, and Liu et al.’s [18] thermal EHL framework incorporating Carreau rheology, which identified an optimal curvature ratio minimizing friction. Experimental techniques have similarly progressed, with Cai et al. [19] quantifying rib/roller friction dominance in heavy-load conditions, while Majdoub et al. [20] enabled precise skew measurement via inductive sensors. Collectively, these works demonstrate that spherical/toroidal roller ends with medium radii (on toroidal ribs) optimize film thickness and load capacity; a fundamental trade-off exists between these objectives.

Despite these advances, no systematic methodology exists to reconcile operational precision with friction optimization through SR selection. This study addresses this gap by developing a principled framework for matching macro-geometric parameters in roller end/rib contacts, accounting for complex kinematics and mating geometry constraints. The proposed framework integrates advanced numerical simulation tools with foundation tests, offering a comprehensive approach to enhancing the energy efficiency and operational stability of TRBs in diverse applications.

2. Materials and Methods

This study adopts a high-fidelity modeling approach where all bearing components are represented with their true geometries. The present work describes the most detailed model configuration, explicitly defining (i) component bodies and reference frames, (ii) force interactions, and (iii) system boundary conditions. All geometric parameters, material properties, and lubricant characteristics are obtained directly from the computational core.

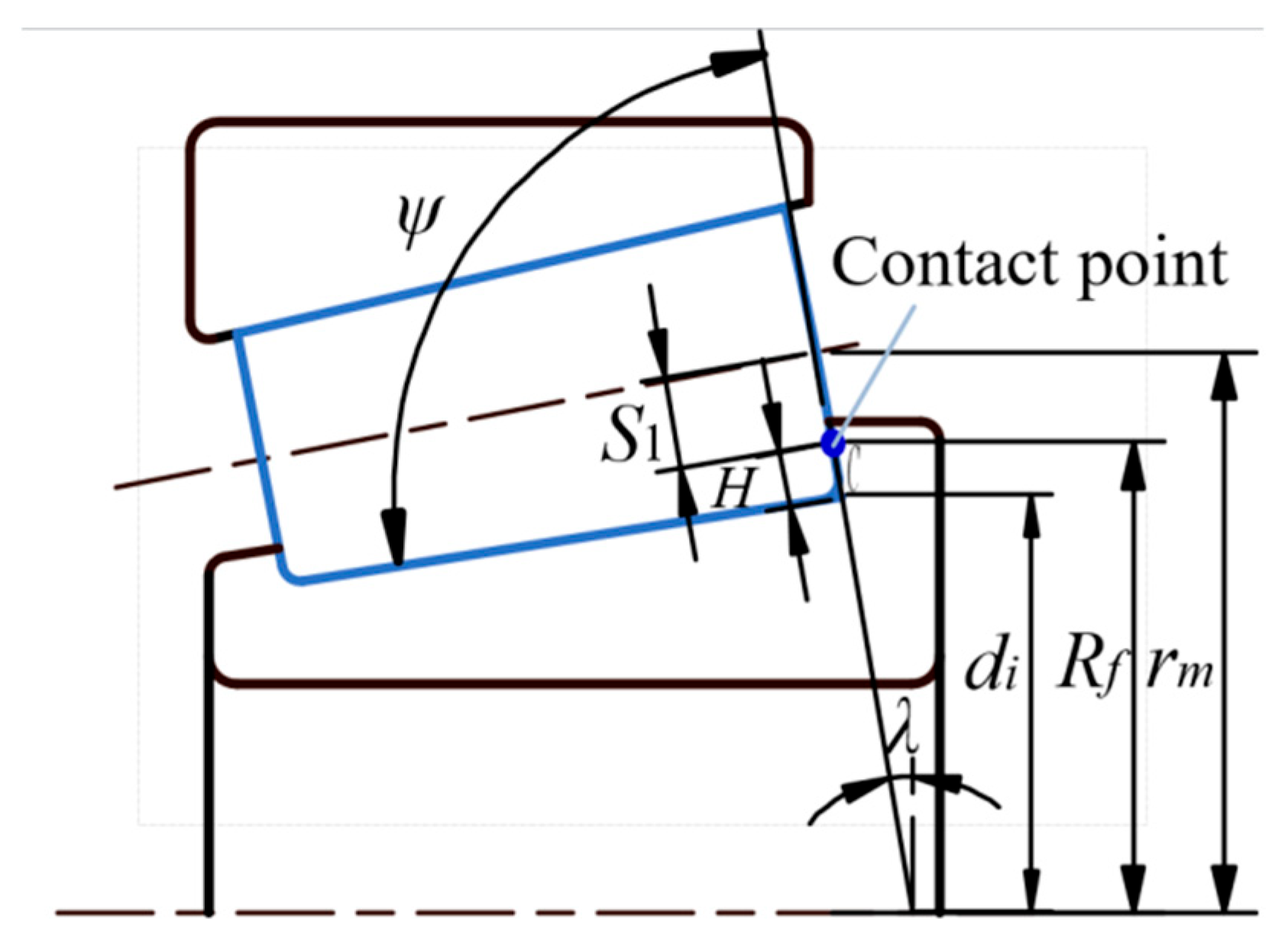
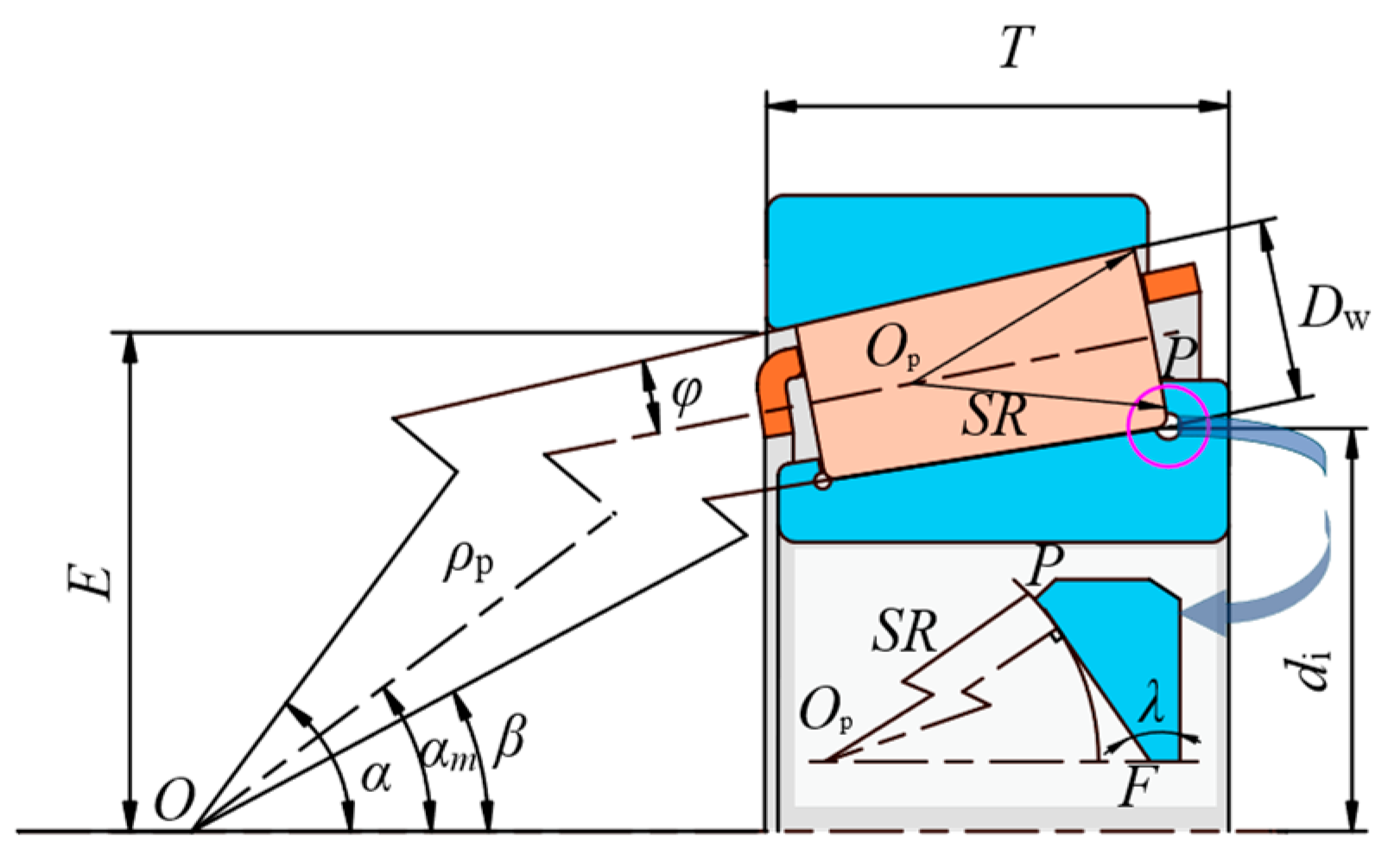
2.1. Geometric Relationship

Figure 1 shows the geometric relationship of tapered roller bearings: P is the cone top, FO_p is the axis, and PF is a round table surface of the bus bar.

The formula for calculating the angle λ between the cone and the end face of the large rib of the inner circle is as follows [21]:

$$\lambda ={\sin }^{-1}\left[{\displaystyle \frac{d_i^{\prime }+d_2}{4SR}}-{\displaystyle \frac{h\sin (\alpha -\phi )}{SR}}\right]$$

(1)

$$h={\rho }_{\mathrm{p}}\cos \phi -\sqrt{S{R}^2-D_w^2/4}$$

(2)

$$d_i^{\prime }=2{\rho }_{\mathrm{p}}\sin \beta$$

(3)

$${\rho }_{\mathrm{p}}=\left({\displaystyle \frac{E}{2\tan \alpha }}+T-a_0\right)/\cos (\alpha -2\phi )$$

(4)

In this formula, E is the nominal small inner diameter of the outer circle; a₀ is the thickness of the inner circle large flange; φ is the roller half cone angle; β is the angle between the inner raceway bus bar and its center line; T is the bearing assembly height; $d_i^{\prime }$ is the maximum diameter of the raceway in the initial inner circle; d₂ is the diameter of the large flange of the inner circle; α is the nominal contact angle of the bearing; D_w is the diameter of the big end of the roller.

Angle ψ between the cone of the inner circle and the raceway is

$$\psi =90-\lambda +\beta$$

(5)

The position of the contact point between the inner rim and the base surface of the roller ball is

$$H={\displaystyle \frac{SR}{\tan \psi -\arctan \zeta }}$$

(6)

$$\zeta ={\displaystyle \frac{\left[\frac{D_w}{2\tan \phi }-\sqrt{S{R}^2-D_w^2/4}\right]\sin \phi }{\frac{d_i}{2\sin \beta }\left[\frac{D_w}{2\tan \phi }-\sqrt{S{R}^2-D_w^2/4}\right]\cos \phi }}$$

(7)

In this formula, d_i is the maximum diameter of the inner ring raceway.

2.2. Contact Modeling

The contact area requires proper discretization, for roller/raceway line contact; therefore, this study employs the roller slicing technique (RST) [11], which accounts for edge loading and angular misalignment effects. In contrast, face-to-rib contact deviates significantly from ideal point/line conditions, necessitating a cell-based approach.

Figure 2a presents the fundamental model for bearing load transmission and rotational functionality, which determines the load-carrying capacity, fatigue life, stiffness, and frictional losses of the bearing. Figure 2b illustrates the secondary interactions among rollers, guiding ribs, and the cage within the bearing assembly. These interactions become particularly critical under high-speed operation, light loading conditions, or inadequate lubrication, and may serve as primary contributors to bearing failure. These two models represent core concepts in the dynamic analysis of rolling bearings, characterizing the complex force and kinematic relationships among internal components during bearing operation.

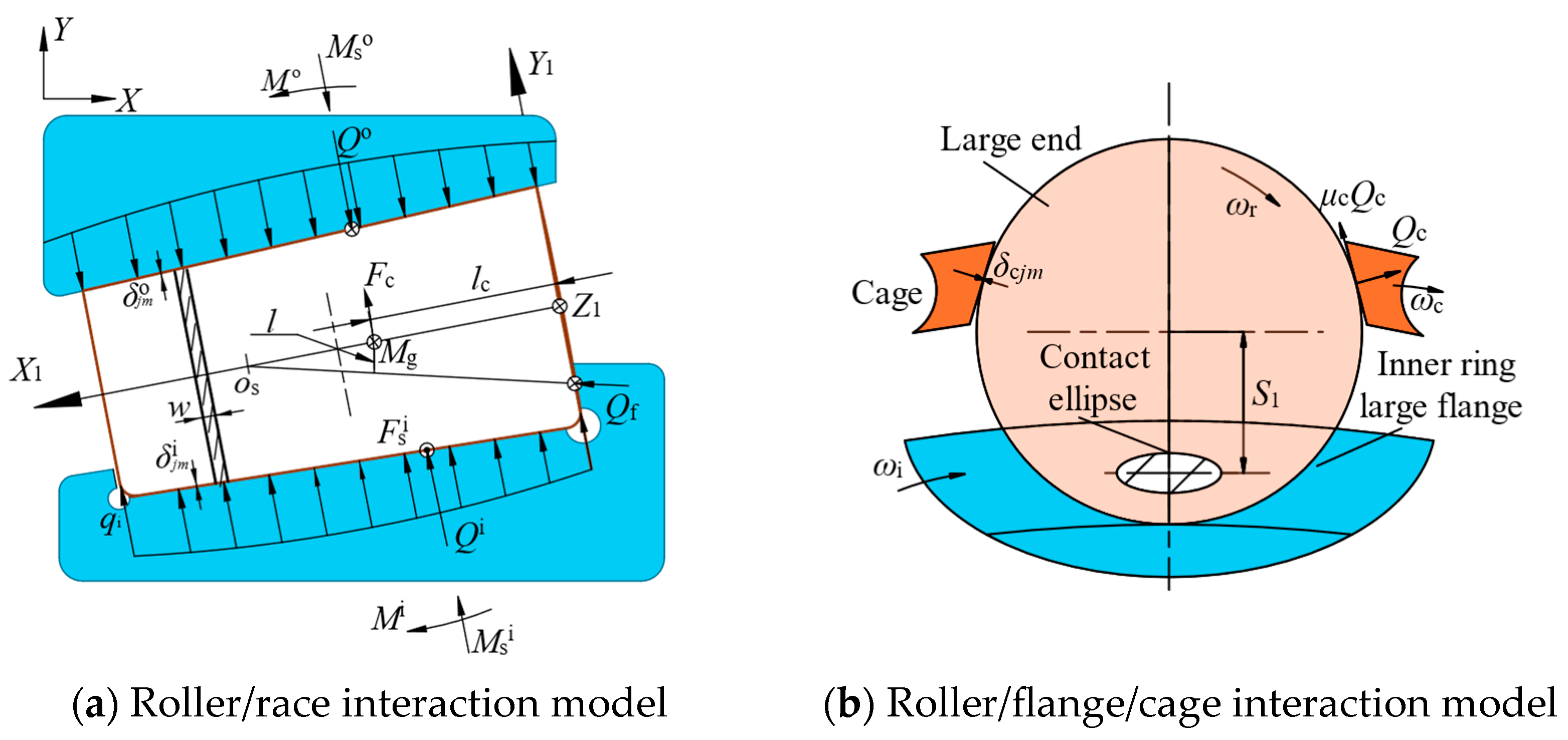
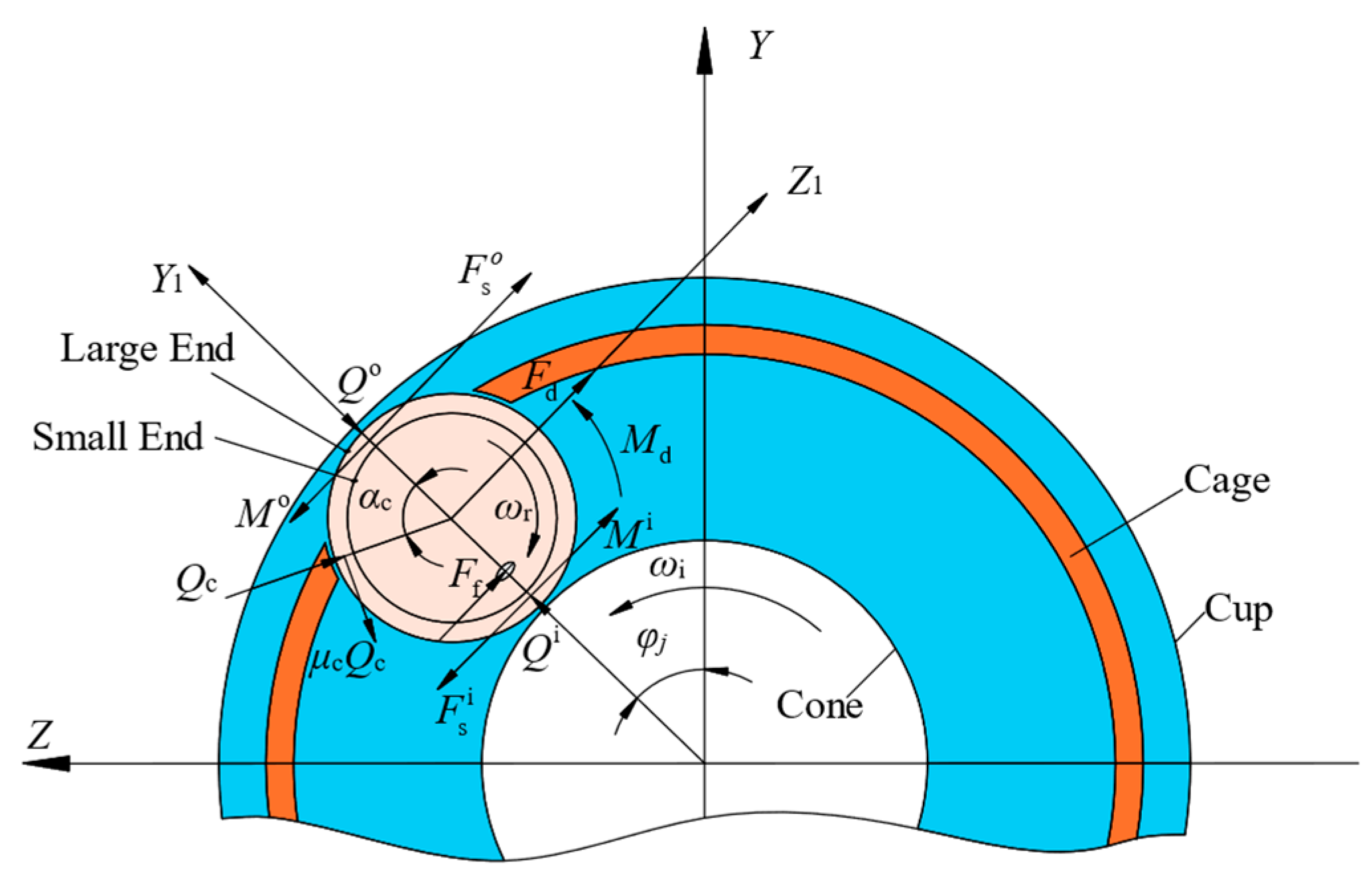
2.2.1. Roller/Race Contact Model

According to Hertz’s theory and Palmgren’s work, normal force between the mth lamina of the jth roller and raceway can be calculated. The specific lamina’s contact load per unit length is given by

$${\overline{q}}_{jm}^{\mathrm{k}}=\left\{\begin{array}{l}{\displaystyle \frac{{({\delta }_{jm}^{\mathrm{k}})}^{1.11}}{A^{1.11}{L}^{0.11}}},\hspace{1em}\hspace{1em}{\delta }_{jm}^{\mathrm{k}}>0\\ 0,\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}{\delta }_{jm}^{\mathrm{k}}\le 0\end{array}\right.$$

(8)

where k = o(i) represents the outer (inner) raceway; A denotes the deformation constant; L signifies the effective length of the roller; and ${\delta }_{jm}^{\mathrm{k}}$ symbolizes the elastic deformation between the mth lamina of the jth roller and raceway.

The normal force of the jth roller and raceway is

$$Q_j^{\mathrm{k}}={{\displaystyle \sum _{m=1}^{N_{\mathrm{P}}}({\delta }_{jm}^{\mathrm{k}})}}^{1.11}{\displaystyle \frac{w}{L^{0.11}{A}^{1.11}}}\hspace{1em}j=1,\cdots ,N_{\mathrm{Z}}$$

(9)

The integrated friction force per lamina yields the magnitude of the friction force as follows:

$$F_{sj}^{\mathrm{k}}={\displaystyle \sum _{m=1}^{N_{\mathrm{P}}}{\mu }_{\mathrm{k}}{\overline{q}}_{jm}^{\mathrm{k}}}$$

(10)

where N_P represents the total number of laminas, N_Z the total number of rollers, and w the width of each lamina, calculated as q = L/N_P. Additionally, ${\mu }_{\mathrm{k}}$ denotes the traction coefficient, as detailed in Section 2.3.

2.2.2. Roller Large End/Inner Ring Back Face Rib Contact Model

Hertz’s elliptical contact theory is employed to ascertain the contact force arising from the interaction, with the normal force [22] as specified in Equation (11):

$$Q_{\mathrm{f}j}={\displaystyle \frac{\pi E^{\prime }k}{3}}{\left[2\epsilon {\mathrm{R}}_{\mathrm{eff}}{\left({\displaystyle \frac{{\delta }_{\mathrm{f}j}}{F}}\right)}^3\right]}^{{\displaystyle \frac{1}{2}}}$$

(11)

The meaning of the variables in the formula is shown in Appendix A.

The friction force of the roller end and flange is

$$F_{\mathrm{f}j}={\mu }_{\mathrm{f}}{Q}_{\mathrm{f}j}$$

(12)

where ${\mu }_{\mathrm{f}}$ is the friction coefficient (see Section 2.3).

2.2.3. Roller/Cage Contact Model

The normal force is

$$Q_{\mathrm{c}j}=\left\{\begin{array}{ll}0& ({\delta }_{\mathrm{c}jm}\le 0)\\ {\displaystyle \sum _{m=1}^{N_{\mathrm{P}}}{({\delta }_{\mathrm{c}jm})}^{1.11}\frac{w}{L^{0.11}{A}^{1.11}}}& ({\delta }_{\mathrm{c}jm}>0)\end{array}\right.$$

(13)

where ${\delta }_{\mathrm{c}jm}$ is the contact deformation between the mth lamina of the jth roller and cage pocket.

The friction force is given by Equation (14):

$$F_{\mathrm{c}j}={\mu }_{\mathrm{c}}{Q}_{\mathrm{c}j}$$

(14)

${\mu }_{\mathrm{c}}$ is the friction coefficient (see Section 2.3).

2.3. Traction Coefficient

In the elasto-hydrodynamic lubrication framework, the traction coefficient is a time-dependent variable that depends on the slide/roll ratio and other parameters. It is determined using an experimental regression formula provided in Ref. [23]. The traction coefficient is given by Equation (15):

$$\mu =(A_u+B_{u}s)e^{-s{C}_u}+D_u$$

(15)

where A_u, B_u, C_u and D_u are the functions dependent on the normal load, the lubricant’s inlet temperature, and the velocity of the two contacting objects, respectively; s represents the slide/roll ratio.

The traction coefficient under the boundary lubrication model is given by Equation (16):

$$\mu =(-0.1+22.28s)e^{-181.46s}+0.1$$

(16)

As shown in Ref. [24], the traction coefficient within the mixed lubrication model is determined through a smooth interpolation, utilizing coefficients from both the boundary and hydrodynamic lubrication models.

2.4. Damping Considerations

Due to complex influencing factors, parametric damping models are adopted. Material damping arises from elastic deformations, while lubricant film damping occurs in the elasto-hydrodynamic lubrication (EHL) contact zone [25].

This study employs a parametric damping model for interactions between raceways, ribs, and cage pockets. The damping force is governed by two key parameters: the maximum damping coefficient (d_max) and the critical penetration depth (δ_max), beyond which damping saturates. The model is applied locally to each disc or cell, depending on the contact geometry. Equations (17) and (18) employ a widely-used model that incorporates maximum damping saturation, based on the hyperbolic tangent (tanh) function. This model represents the ratio of the maximum damping force achievable at the contact interface to the relative velocity. At high relative velocities, the damping force asymptotically approaches a saturation limit, preventing unbounded increase. F_D: Damping force, d_max: Maximum damping coefficient.

$$\overrightarrow{F_D}\left(\overrightarrow{v_N},{\delta }_{max},d_{max}\right)=-\overrightarrow{v_N}\cdot d$$

(17)

$$d=\left\{\begin{array}{c}0 for \delta <0\\ {\displaystyle \frac{-2\cdot d_{max}}{{\delta }_{max}^3}}\cdot {\delta }^3+{\displaystyle \frac{3\cdot d_{max}}{{\delta }_{max}^2}}\cdot {\delta }^2 for 0\le \delta <{\delta }_{max}\\ d_{max} for \delta \ge {\delta }_{max}\end{array}\right.$$

(18)

2.5. Bearing Friction Torque

Friction torque mainly includes the contact friction torque between the roller and the raceway, the elastic hysteresis friction torque, the contact friction torque between the base surface of the big end ball of the roller and the big guard edge, the collision friction torque of the cage, and the viscous resistance moment of the lubricating oil [10,26].

There are both friction resistance and viscous resistance moments of the lubricant on rollers between rollers and raceways. The friction power consumption generated by contact between rollers and raceways is as follows:

$$H_{\mathrm{r}}^k={\displaystyle {\int }_0^{2\pi }[({\displaystyle {\int }_{-L_s/2}^{L_s/2}{F}_{sj}^k\Delta V_{jm}^{k}d{x}_r})+M_j^k{\omega }_{\mathrm{b}j}]d\varphi }$$

(19)

$$M_j^k=14.2E_0{L}_s{R}_0^2{U}^{0.75}{G}^{-0.04}{W}^{0.08}$$

(20)

where L_s is the effective contact length of the roller; $\Delta V_{jm}^k$ represents the relative sliding speed between the roller and the raceway; ω_bj is the angular rotation speed of the roller; E₀ and R₀ are the equivalent elastic modulus and radius of curvature between the contacting bodies, respectively; U, G, and W are the velocity, material, and load parameters, respectively.

Due to the elastic hysteresis property of the material, the energy loss generated by tapered roller bearings is

$$H_{\mathrm{e}}^{\mathrm{k}}={\displaystyle {\int }_0^{2\pi }\left[{\displaystyle {\int }_{-L_s/2}^{L_s/2}\xi \sqrt{\frac{\pi {\overline{q}}_{jm}^{\mathrm{k}}}{\eta D_{wjm}}}{\delta }_{jm}^{\mathrm{k}}\left|{\omega }_{\mathrm{i}}-{\omega }_{\mathrm{c}}\right|d{x}_r}\right]d\varphi }$$

(21)

where ξ is the elastic hysteresis coefficient of the material, which is desirable for steel ξ = 0.007; η represents the combined elastic coefficient of the two elastomers; D_wjm is the diameter of the k-th segment of the roller; ω_i is the inner circle’s angular velocity; ω_c is the angular velocity of the cage.

Relative sliding speed occurs when the base surface of the roller ball contacts with the inner circle’s large retaining edge, generating the following energy loss:

$$H_{\mathrm{f}}={\displaystyle {\int }_0^{2\pi }({\mu }_{\mathrm{f}j}{Q}_{\mathrm{f}j}\Delta V_{\mathrm{f}j})d\varphi }$$

(22)

where ΔV_fj is the relative sliding speed at the contact point between the big end face of the roller and the big rib of the inner circle (see Appendix B).

There are a collision and relative sliding between the roller and the cage pocket hole, and the resulting friction power consumption is

$$H_{\mathrm{c}}={\displaystyle {\int }_0^{2\pi }[{\displaystyle {\int }_{-L_s/2}^{L_s/2}{F}_{\mathrm{c}jm}\Delta V_{\mathrm{c}jm}d{x}_r}]d\varphi }$$

(23)

where F_cjm is the tangential friction force between the roller and the hole; ΔV_cjm is the relative sliding speed between the roller and cage hole.

The friction power consumption caused by the oil/gas resistance of the roller is

$$H_{\mathrm{oil}}={\displaystyle {\int }_0^{2\mathsf{\pi }}\frac{1}{8}{C}_d{\rho }_m{D}_{\mathrm{w}}l{(d_m{\omega }_{\mathrm{c}})}^{2}d\varphi }$$

(24)

where ρ_m is the density of oil and gas mixture; C_d is the resistance coefficient around the flow.

According to the law of conservation of energy, the total friction torque of tapered roller bearing is

$$M_{\mathrm{all}}={\displaystyle \frac{H_{\mathrm{r}}^k+H_{\mathrm{e}}^k+H_{\mathrm{f}}+H_{\mathrm{c}}+H_{\mathrm{oil}}}{\omega }}$$

(25)

In this formula, ω is the bearing speed.

2.6. Dynamic Differential Equations

Figure 3 shows the forces and moments acting on the jth tapered roller.

Based on Newton’s law of motion, the dynamic differential equations of the translational motion of the tapered roller can be expressed in the Cartesian coordinates as follows:

$$\begin{array}{l}{m}_{\mathrm{b}}{\ddot{x}}_{\mathrm{b}j}=-(Q_j^{\mathrm{i}}+Q_j^{\mathrm{o}})\sin \phi +Q_{\mathrm{f}j}\cos ({\alpha }_{\mathrm{m}}-\lambda )-F_{\mathrm{c}j}\sin {\alpha }_{\mathrm{m}}-Q_{\mathrm{c}j}\sin \phi \\ m_{\mathrm{b}}{\ddot{y}}_{\mathrm{b}j}=(Q_j^{\mathrm{i}}-Q_j^{\mathrm{o}})\cos \phi +Q_{\mathrm{f}j}\sin ({\alpha }_{\mathrm{m}}-\lambda )+F_{\mathrm{c}j}\cos {\alpha }_m-Q_{\mathrm{c}j}\cos \phi \cos {\alpha }_{\mathrm{c}}-{\mu }_{\mathrm{c}}{Q}_{\mathrm{c}j}\cos \phi \sin {\alpha }_{\mathrm{c}}\\ m_{\mathrm{b}}{\ddot{z}}_{\mathrm{b}j}=F_{\mathrm{s}j}^{\mathrm{o}}-F_{\mathrm{s}j}^{\mathrm{i}}+F_{\mathrm{f}j}+F_{\mathrm{d}j}+Q_{\mathrm{c}j}\cos \phi \sin {\alpha }_{\mathrm{c}}-{\mu }_{\mathrm{c}}{Q}_{\mathrm{c}j}\cos \phi \cos {\alpha }_{\mathrm{c}}\end{array}$$

(26)

where m_b is the mass of tapered roller; ${\ddot{x}}_{\mathrm{b}j}$, ${\ddot{y}}_{\mathrm{b}j}$, ${\ddot{z}}_{\mathrm{b}j}$ refer to the acceleration of the jth roller mass center; ωi is the inner circle’s angular velocity.

The dynamic differential equations of the rotational motion of the jth tapered roller around its mass center and cage equilibrium can be seen in Appendix C.

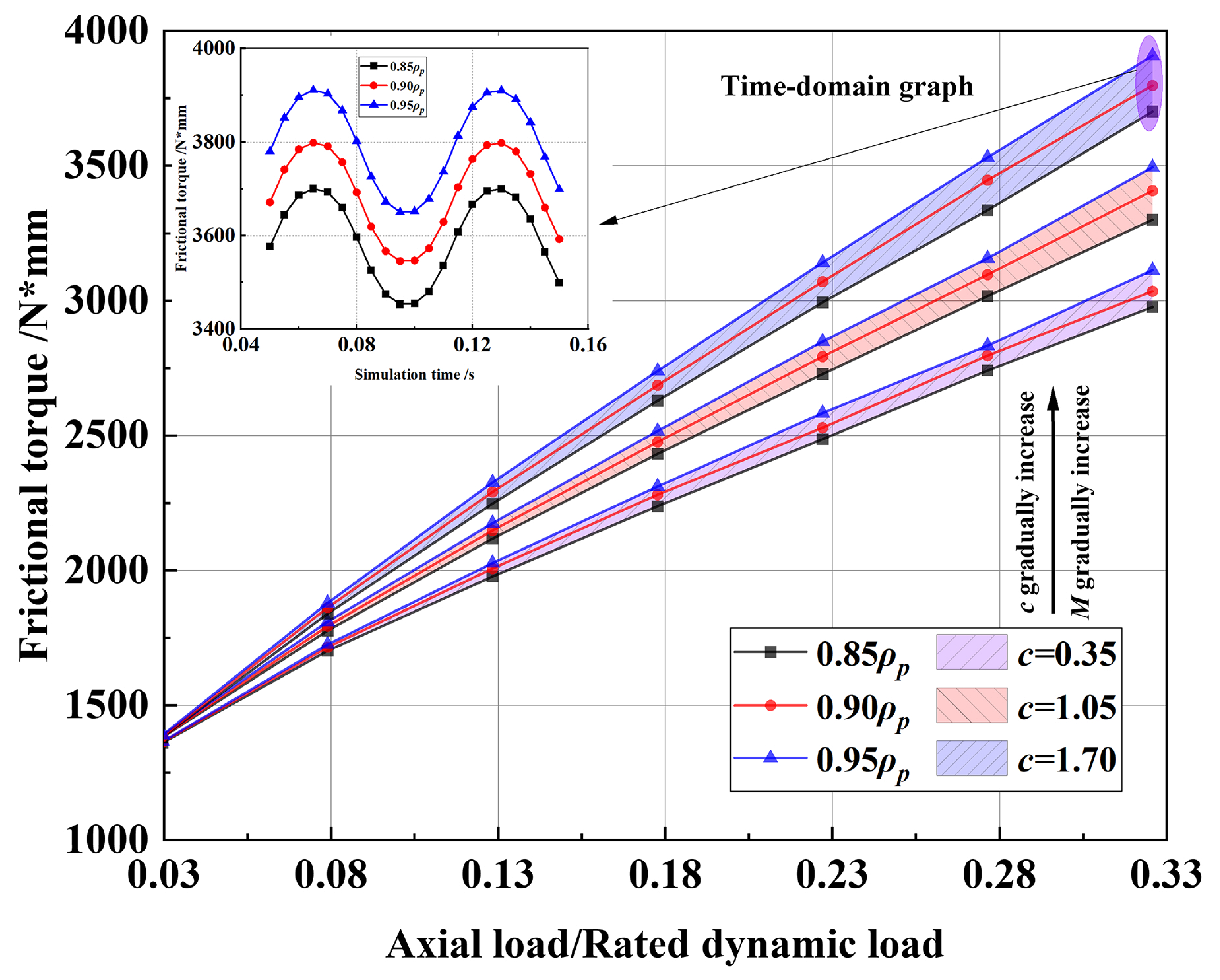
3. Result Analysis

This paper takes 32,208 tapered roller bearing as the research object. The main parameters are shown in

Table 1. Major parameters of bearing.

Argument	Numerical Value
Inside diameter/Outside diameter (mm)	40.0/80.0
Bearing width (mm)	24.75
Inner circle width (mm)	23.0
Outer circle width (mm)	19.0
Radius of the sphere base (mm)	144.0
Large flange Angle	89°28′55″
Large rib height (mm)	2.706
Roller small/big end diameter (mm)	9.46/10.63
Contact angle between roller and inner circle/outer circle/large rib	10/14/87
Number of rollers	17
Rated dynamic load	81.1 kN

. The axial load is 12 kN, the radial load is 24 kN, and the inner circle speed is 6000 r/min. SARB rolling bearing dynamic simulation analysis software v.2.1 was used to conduct the bearing performance simulation analysis [27]. The simulation calculation model was referred to in Ref. [28].

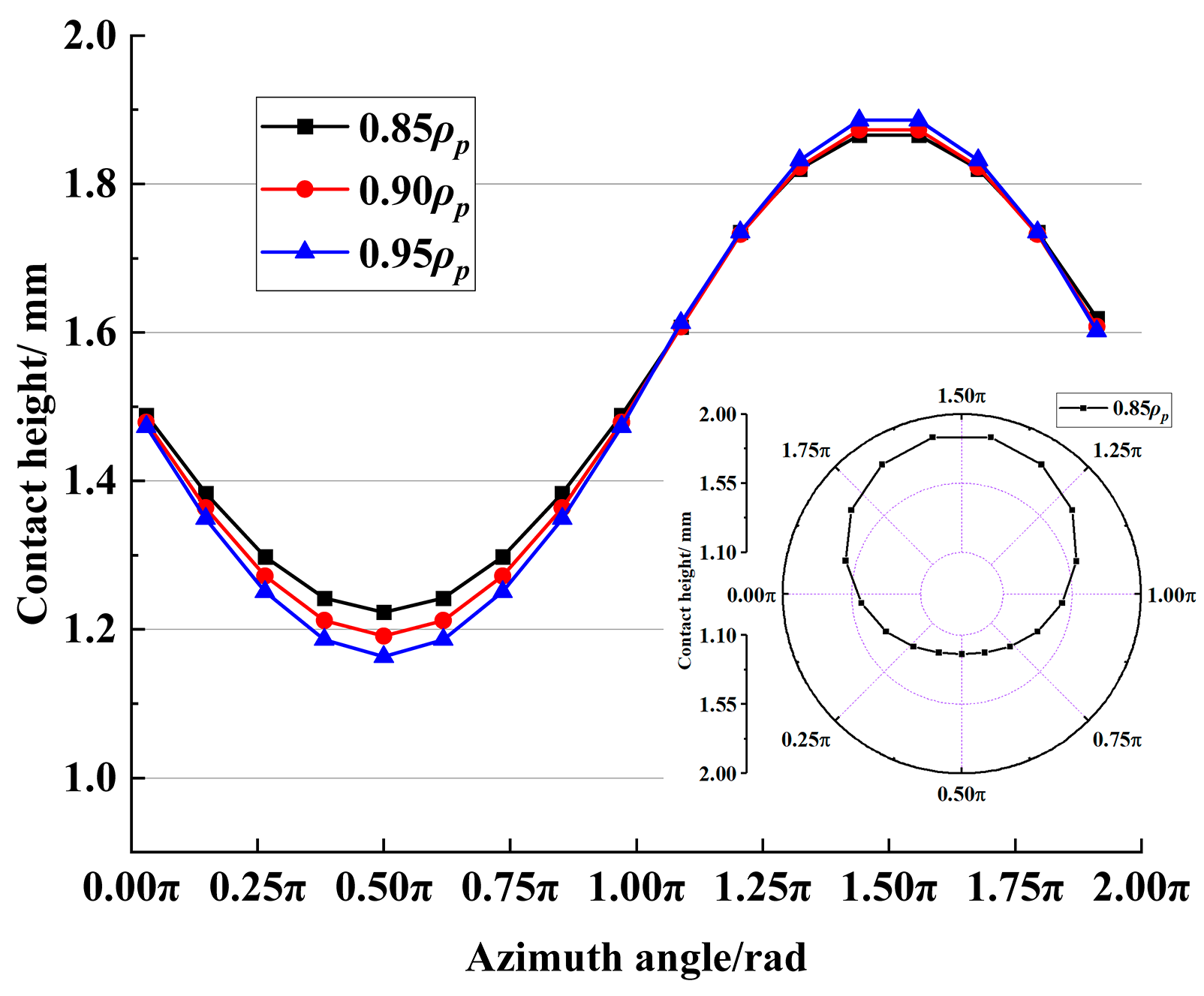
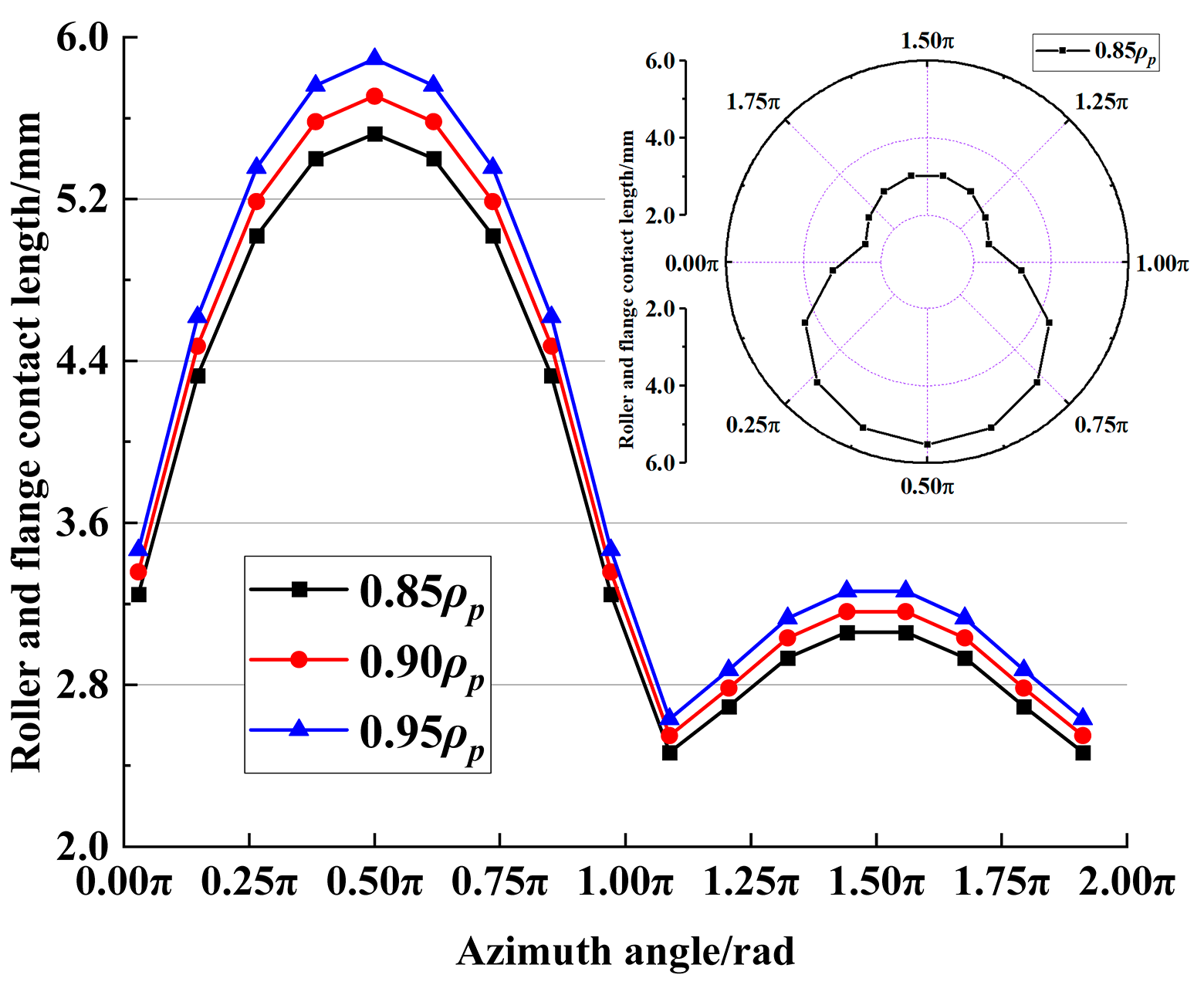
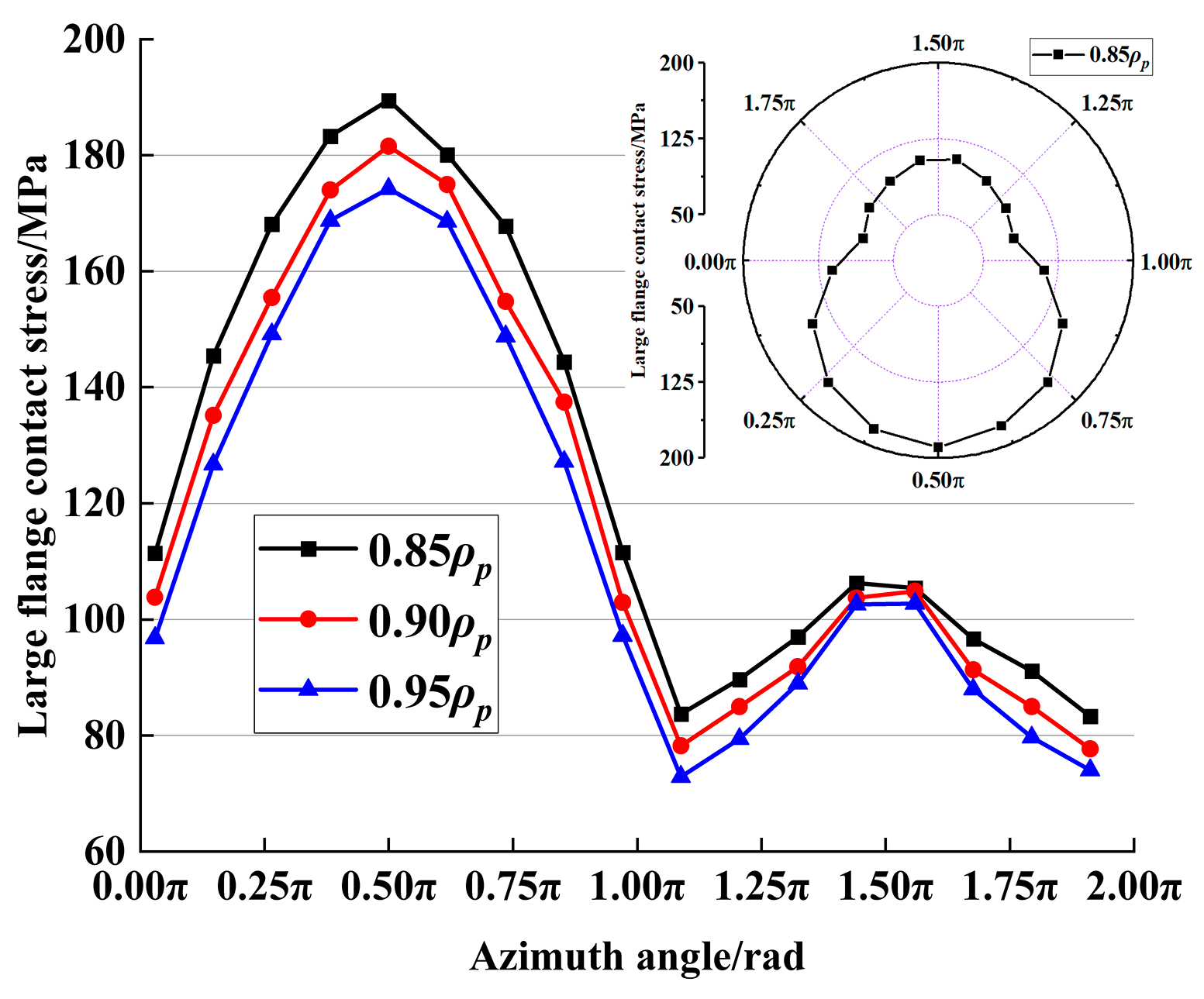
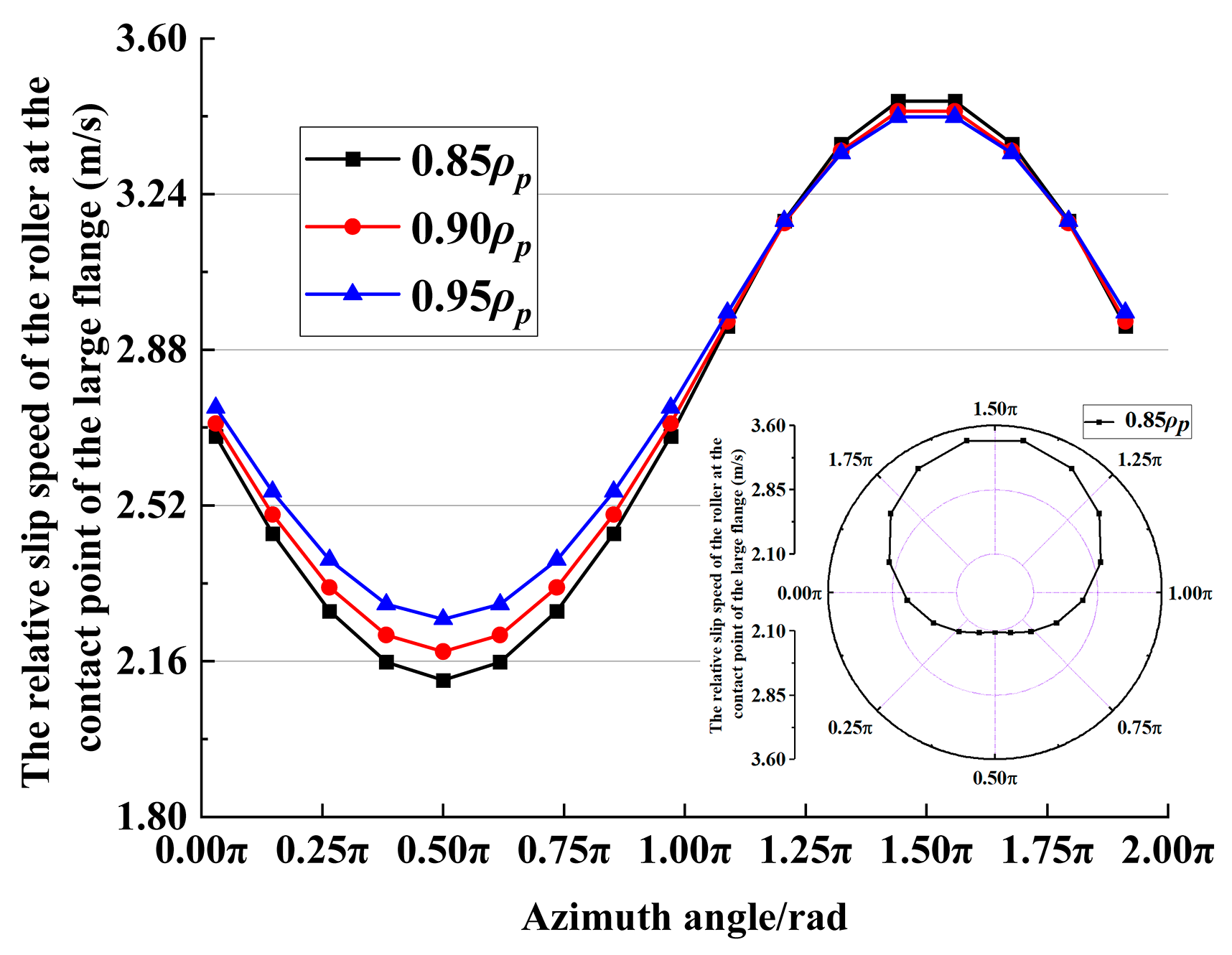
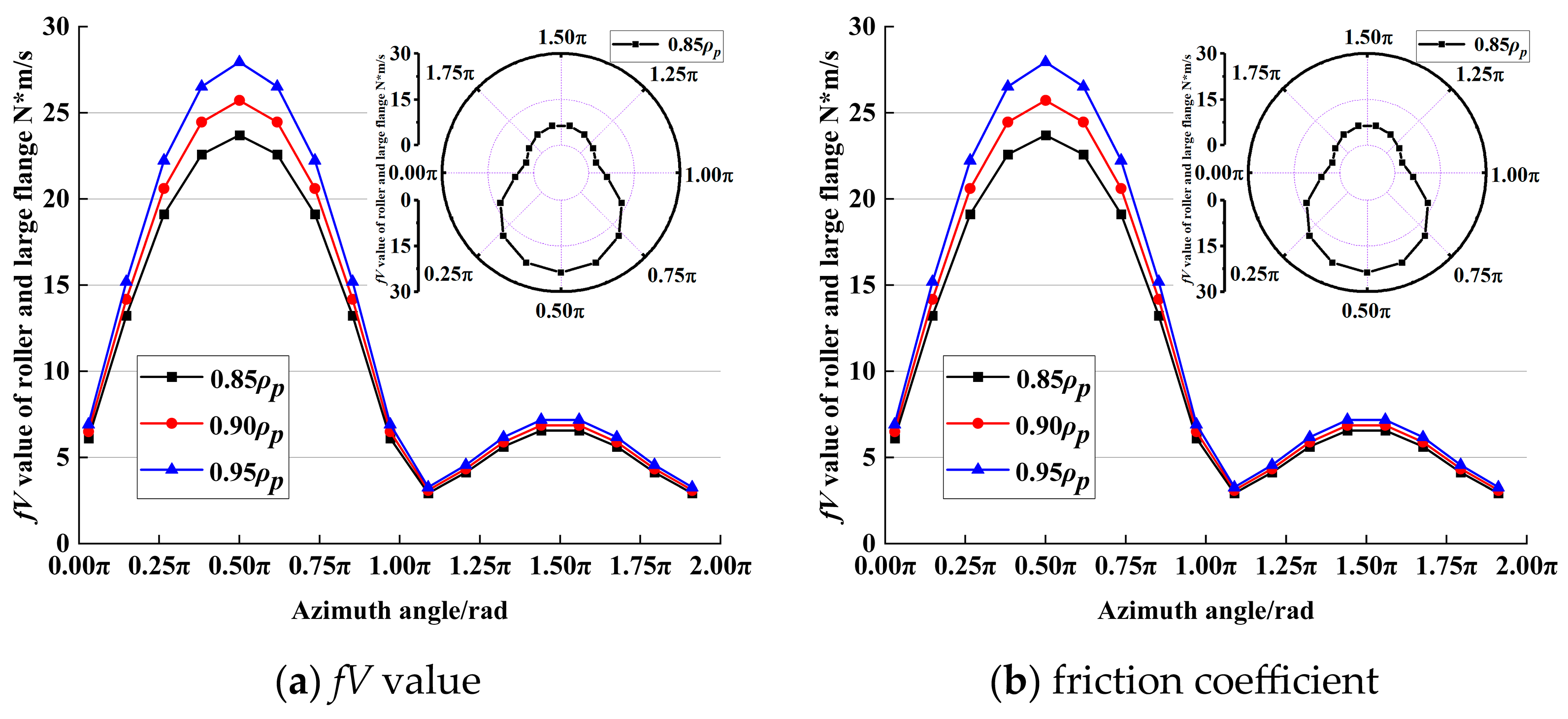
3.1. Contact State Analysis

The bearing is in the stable running stage, and the results are repeatable in each running cycle. In order to show the results of the stress and sliding speed of the bearing in the circular direction, the calculation results in a single cycle are described in this paper. In this paper, the load of a single roller is at maximum at the circular direction of 0.50π.

Figure 4 shows the contact height between the base surface of the roller ball and the large flange of the inner circle, and its value is jointly affected by geometric parameters, load, and azimuth angle. The existing research shows that the contact height is between 1/3 and 1/2 of the effective height of the big gear side. The contact height of the roller with the largest load is the smallest and has a large difference with the change of SR, and the value of the non-contact area is large and has a small change with SR. The azimuth angle is defined as the clockwise angular measurement in a horizontal plane from a reference direction to the line of sight of a target.

Figure 5 shows the length of the contact area between the base surface of the roller ball and the large flange of the inner circle. The contact length of the maximum loaded part of the flange is 5.52 mm and the contact length of 0.95ρ_p is 5.89 mm, with an increase of about 7%. The shorter contact length makes the sliding speed in the circular direction smaller and low friction torque easier to achieve.

Figure 6 shows the contact stress between the roller and the large flange, and its value is non-uniform distribution along the circumference direction, and the contact stress between the roller with the largest load and the large flange is also the largest. With the increase of SR, the contact stress between the roller and the large flange gradually decreases in the circular direction. In the range of 1.0π~2.0π, there is a small contact stress, which is because the bearing bears axial and radial loads at the same time, some rollers are not in the main bearing area, and the load is small.

Figure 7 shows the relative sliding speed at the contact point between the roller and the large flange. In the range of 0.0π~1.0π, the relative sliding speed increases with the increase of SR, and the maximum loading increase is about 6%. The relative sliding speed in the circumference direction is not fixed, and the sliding speed is the lowest in the area with a large load, and the sliding speed will change greatly when entering and leaving the bearing area, which will lead to the instability of the roller force for a short time.

Figure 8 shows the PV value of the contact area between the large flange of the inner circle and the base surface of the roller ball, which is defined as the product of contact stress P between the roller and the large flange and sliding speed V at the contact point. The PV value is usually used to describe the wear degree and heat degree of the two contact points. In the range of 0~π and π~2π, the dominant values are the P value and V value, and the increase of SR can reduce the PV value of the roller and the large flange.

Figure 9 shows the fV value of the contact area between the large flange of the inner circle and the base surface of the roller ball, which is defined as the product of the friction force f between the base surface of the roller ball and the large flange of the inner circle and the sliding speed V at the contact point. With the increase of SR, the fV value increases significantly in the bearing area, increasing by about 17% at 0.5π, which is the main reason for the difference in bearing friction torque. The smaller SR increases the wedge clearance between the roller and the large flange, and the relative sliding speed of the contact between the roller ball base and the large flange decreases (as shown in Figure 7), and the friction coefficient decreases (as shown in Figure 9), further reducing the friction torque of the bearing.

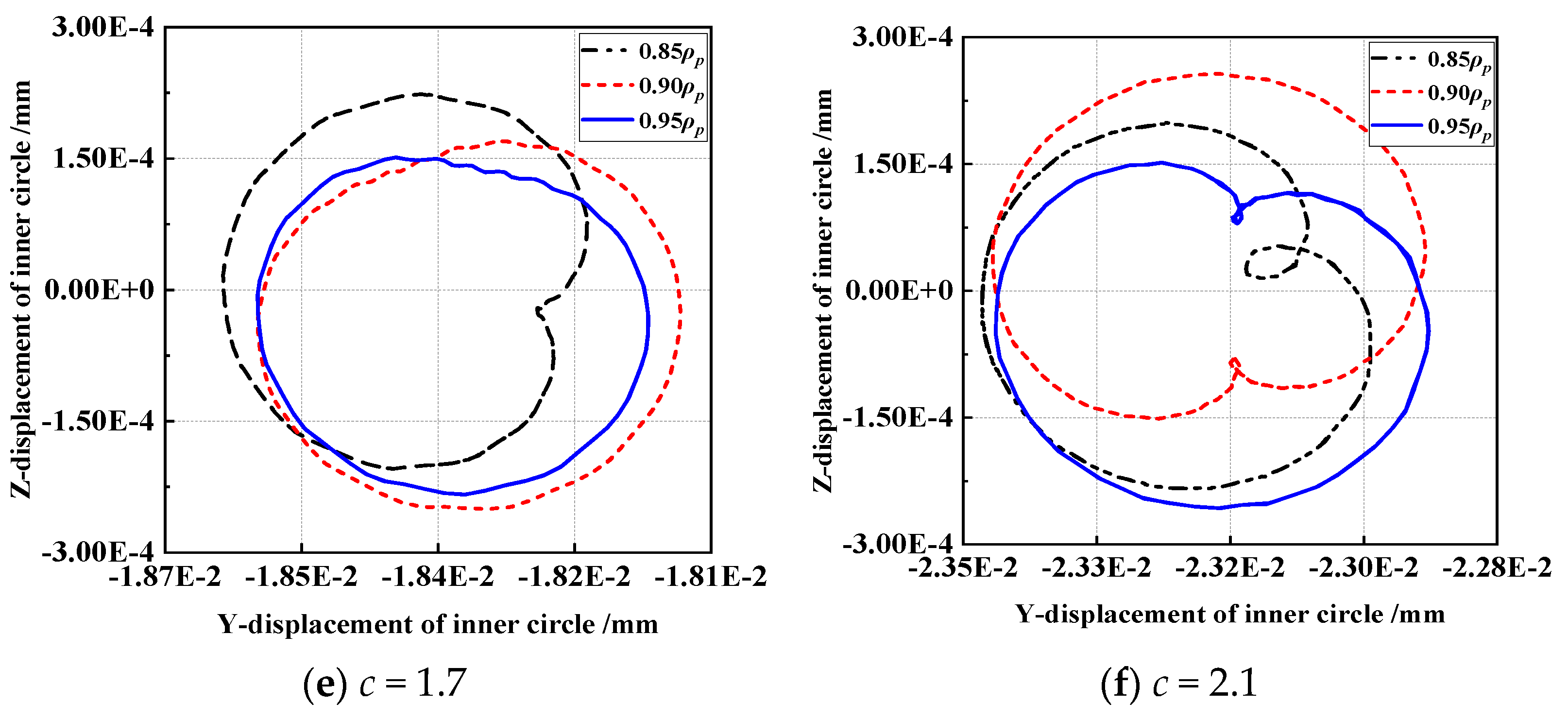
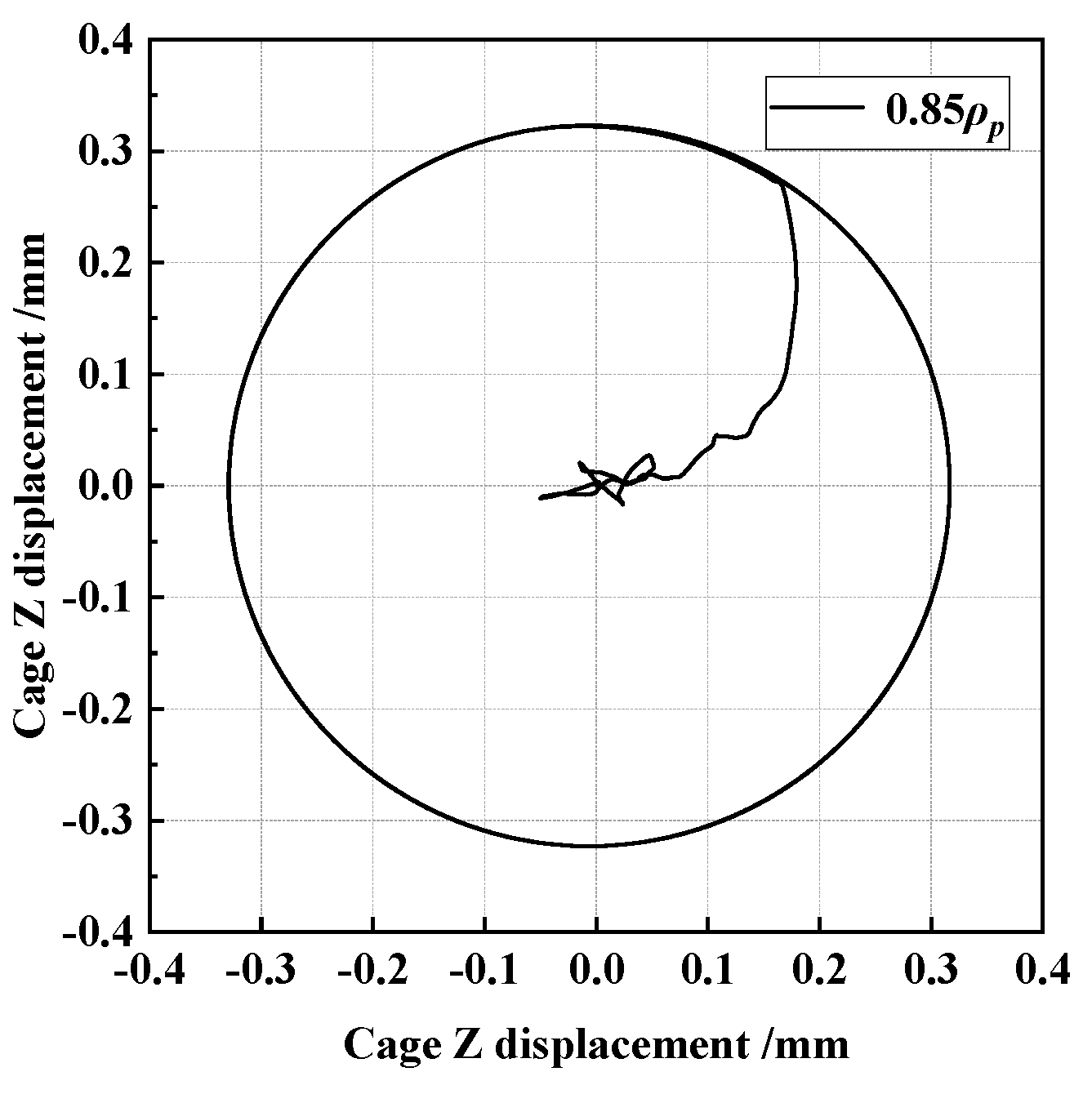
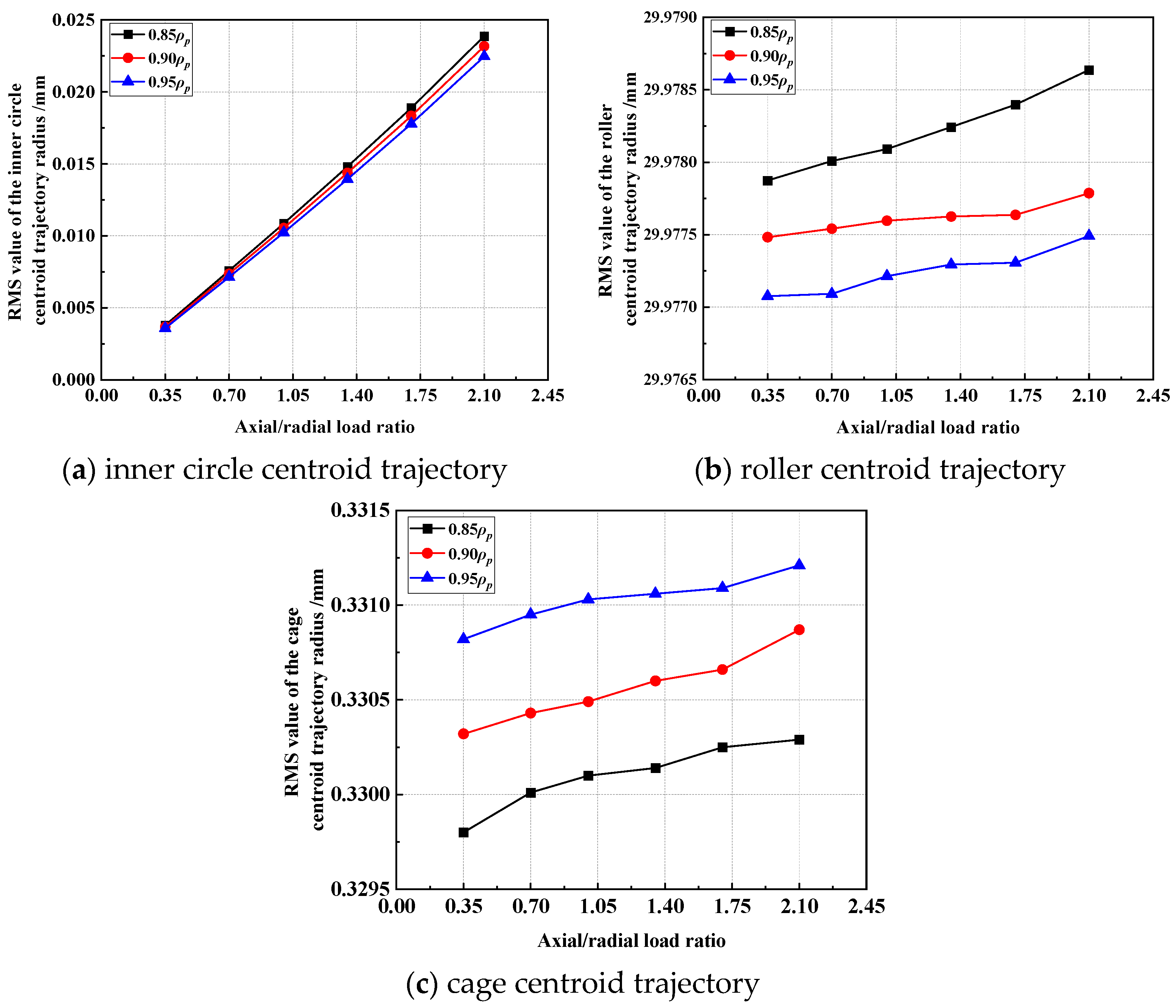
3.2. Analysis of Running Accuracy

Under the conditions of given load and speed, the running accuracy of tapered roller bearings can be judged by the inner circle centroid trajectory and cage centroid trajectory. The inner circle speed is selected as 6000 r/min, the axial load is 12 kN, and the radial load is changed. Figure 10 and Figure 11 show the centroid trajectory of the bearing inner circle and cage.

Figure 10 shows the inner circle centroid trajectory, and it defines the axial and radial load ratio c = Fa/Fr to describe the load state of the bearing. Figure 10a–f show the orbit of the centroid of the inner circle when c = 0.35, 0.7, 1.0, 1.35, 1.7, 2.1, respectively. In these figures, the x-axis represents the Y displacement of inner circle, while the y-axis represents the Z displacement of inner circle. As shown in Figure 10, the absolute value of Y displacement gradually increases due to the increase of radial load, while the orbit radius of the inner circle centroid increases and becomes irregular, indicating that the running accuracy of the bearing decreases.

Figure 11 shows the centroid trajectory of the cage when c = 1.0. At this time, the centroid trajectory of the cage is close to a circle, and the centroid trajectory of the cage is much larger than the change of the centroid trajectory of the inner circle. Due to the complexity of the description of the bearing component centroid trajectory, the RMS value of the inner circle/cage centroid trajectory radius R_st in the time domain is used to describe the running accuracy of the bearing. Among them, $R_{S\mathrm{t}}=\sqrt{{SY}_{\mathrm{t}}^2+{SZ}_{\mathrm{t}}^2}$; S represents the inner circle, cage, and roller components; SY_t, SZ_t represent the Y-direction and Z-direction displacement of the component at time t.

Figure 12 shows the root mean square (RMS) values of the centroid locus radius, respectively. The variation rule of the RMS value of the inner circle centroid trajectory and the roller centroid trajectory is consistent, and the RMS value of the centroid trajectory radius increases with the increase of SR and c. The RMS value of the cage centroid trajectory radius shows the opposite trend to that of the inner circle and roller centroid trajectory. The increase of the cage centroid trajectory radius is mainly due to the influence of the collision force between the roller and the cage, as the cage is in a suspended state during operation.

Figure 13 shows the friction torque of the bearing under different loads when the inner circle speed is 6000 r/min. Under the same main structural parameters and loading conditions of the bearing, the force between the rollers and the raceway is basically the same. The contact state between the large flange and the spherical base surface of the roller is the main reason for the difference in friction torque. When the axial load/rated dynamic load is 0.32 and c = 1.70, the total friction torque of the bearing decreases by approximately 9.7%. Moreover, the reduction is more significant under larger loads. As SR increases, the friction torque of the bearing gradually increases, mainly due to the changes in the contact force, contact position, sliding speed, and friction coefficient between the spherical base surface of the roller and the large flange, which causes the friction torque of the bearing to gradually increase with the increase of SR.

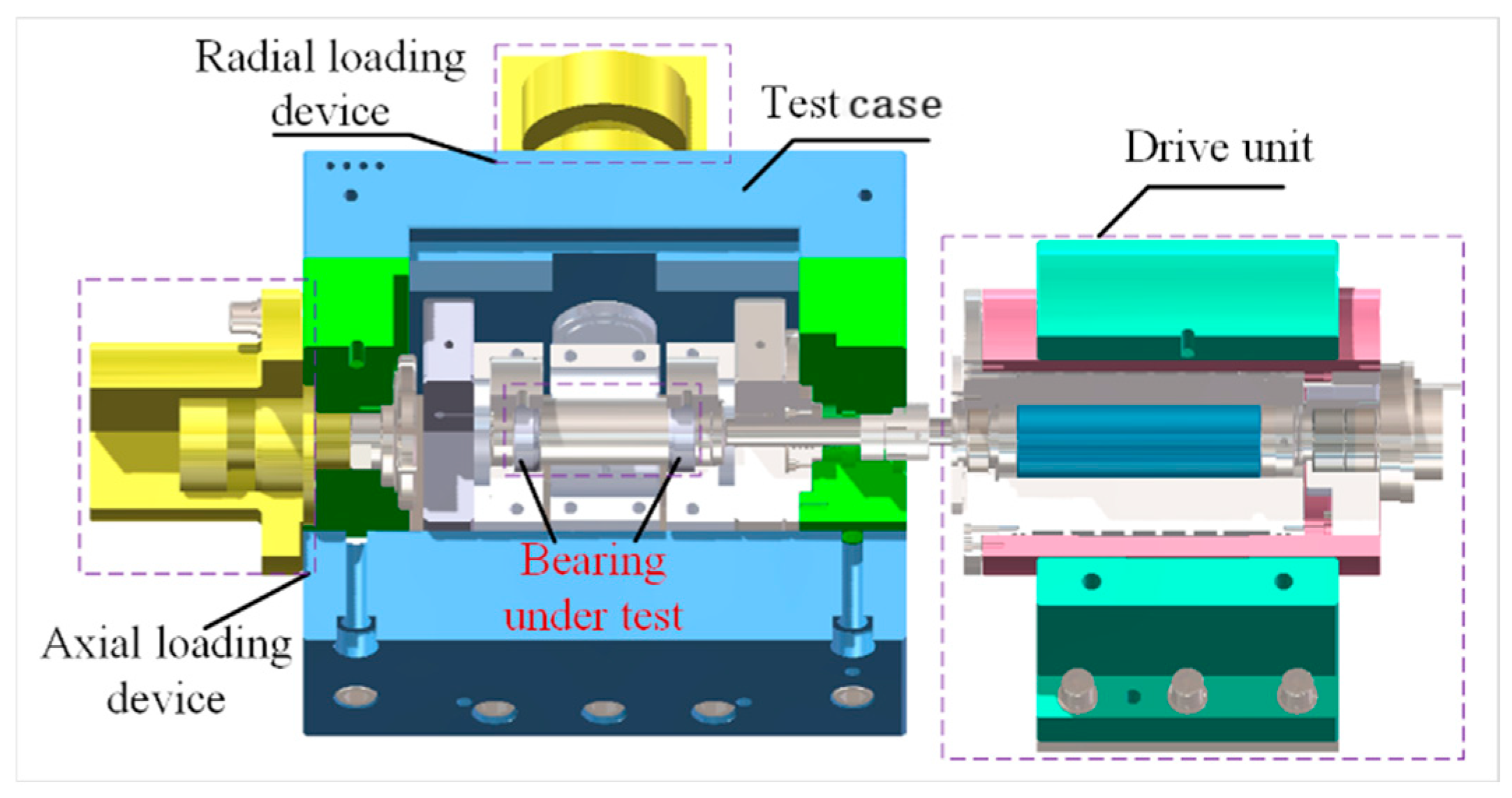
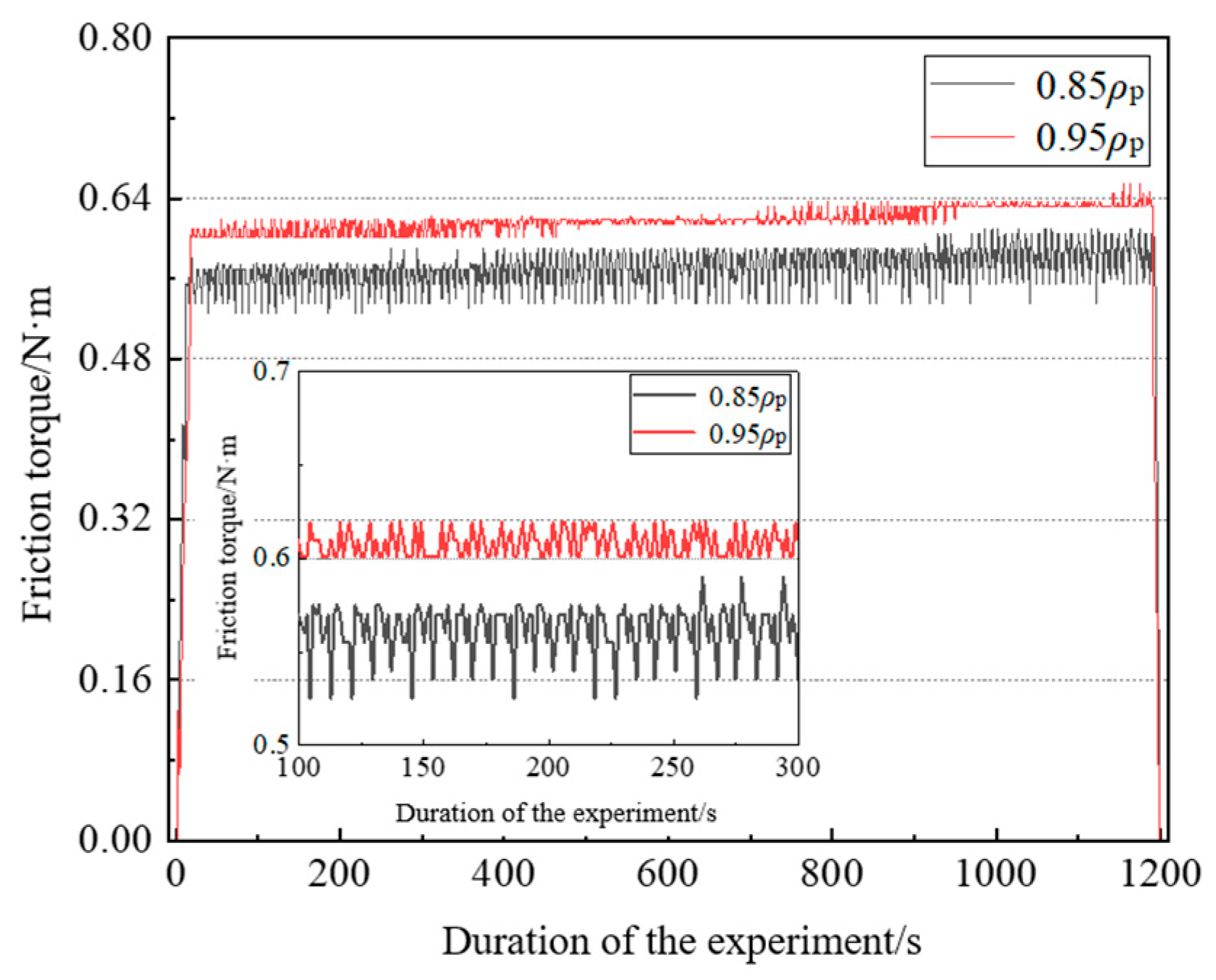
4. Test Verification

The 32,208 bearings were tested using a rolling bearing performance testing machine. The spindle structure of the testing machine is shown in Figure 14. The bearings are installed in type X mode and lubricated by oil injection. The inner circle speed is 1800 r/min and the axial load Fa is 2.16 kN. The torque sensor is used to measure the total friction torque of the two sets of bearings. Bearings SR= 0.85ρ_p and SR= 0.95ρ_p were selected for grouping measurement, and the friction torque results during stable operation for 10 min were captured, as shown in Figure 15.

Figure 15 shows the measurement results of the friction torque of a single set of tapered roller bearings when SR = 0.85ρ_p and SR = 0.95ρ_p. The average friction torques are 0.56 N·m and 0.61 N·m, respectively. When SR = 0.85ρ_p, the friction torque decreases by 8.2%. However, the friction torque fluctuates more significantly with a smaller SR value, with the maximum fluctuation being approximately 0.075 N·m (fluctuation value/maximum value = 14.1%), which is higher than 0.06 N·m (8.9%) when SR = 0.95ρ_p. This indicates that the bearing stability is lower with a smaller SR value, verifying the accuracy of the proposed model and the correctness of the analysis.

5. Conclusions

In this paper, the contact state, bearing friction torque, and running accuracy between the ball base and the large rib of the roller ball were analyzed when the curvature radius SR of the roller ball base was 0.85ρ_p, 0.90ρ_p, and 0.95ρ_p, and the basis for the value of SR under different performance design requirements was studied. The results are as follows:

(1)

The larger SR makes the contact stress, contact height, and PV value of the contact area between the base surface of the roller ball and the large flange smaller, but the relative sliding speed and fV value between the roller ball base and the contact area of the large flange is higher, and the final bearing friction torque increases with the increase of SR.

(2)

The increase of the SR value can increase the running accuracy of the bearing to a certain extent; it is recommended to select a larger value under high radial load conditions.

(3)

When SR is 0.85ρ_p, the friction torque is small; when SR is 0.95ρ_p, the bearing running accuracy is high. When SR is 0.90ρ_p, the bearing friction torque and running accuracy can be balanced.