A Novel Empirical-Informed Neural Network Method for Vehicle Tire Noise Prediction
Abstract
1. Introduction
- (1)
- This study proposes an Empirical-informed Neural Network (EINN) method. By redesigning the neural network’s loss function, the local vibro-acoustic mechanism is embedded in it in the form of constraints. Even in the absence of an accurate physical model, this method can use empirical data to guide network learning and construct a hybrid neural network model that combines knowledge and data-driven methods. This innovation successfully addresses the traditional physical information neural network’s reliance on precise physical models when handling complex systems, thereby greatly broadening its scope of application.
- (2)
- To enhance the model’s prediction performance further, this study introduces an adaptive weight mechanism. The mechanism can dynamically adjust the weight of each item in the loss function to ensure the numerical comparability of different weights, so as to effectively prevent gradient disappearance or gradient explosion and significantly improve the robustness of the training process.
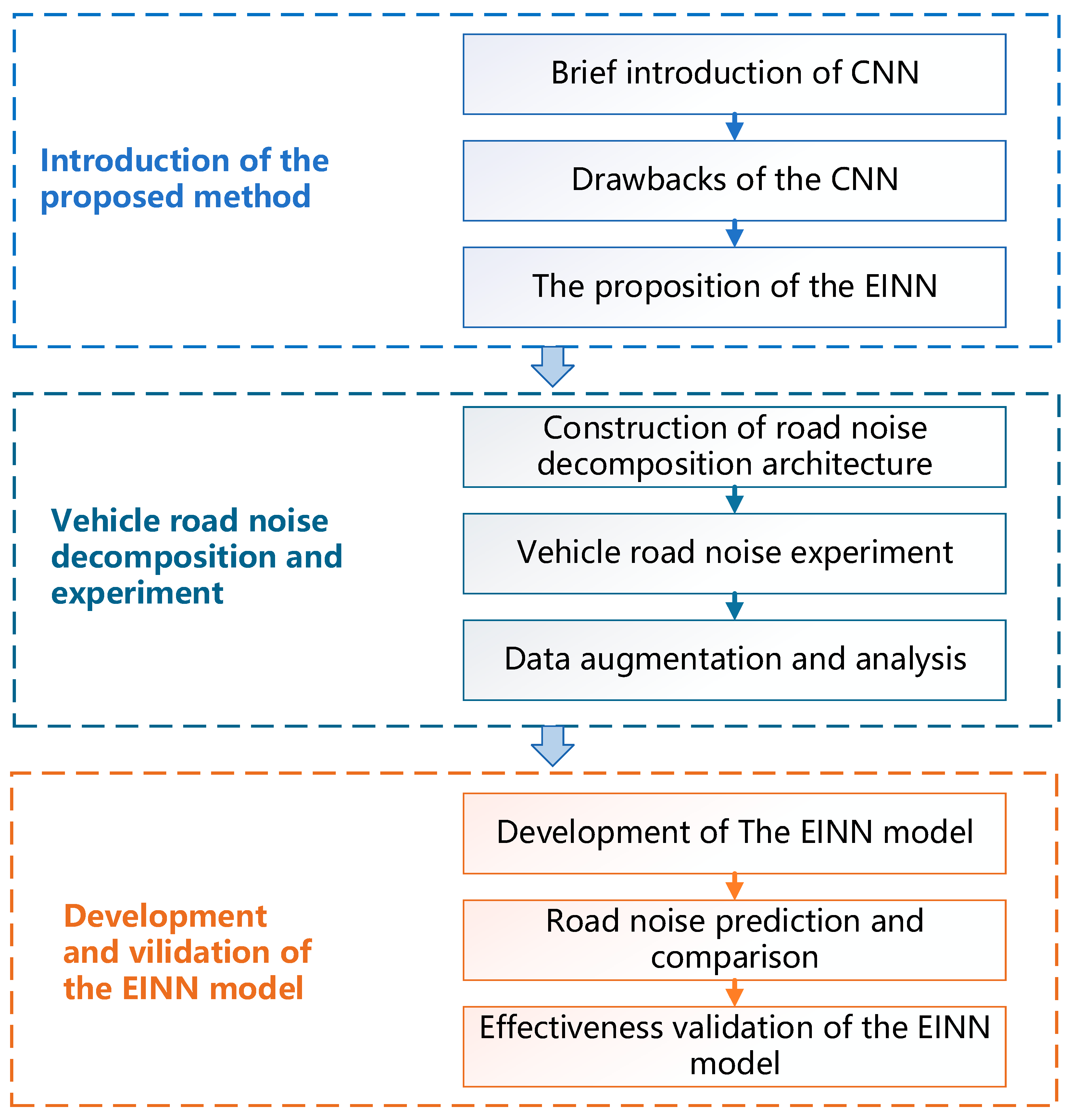
2. Method Proposed
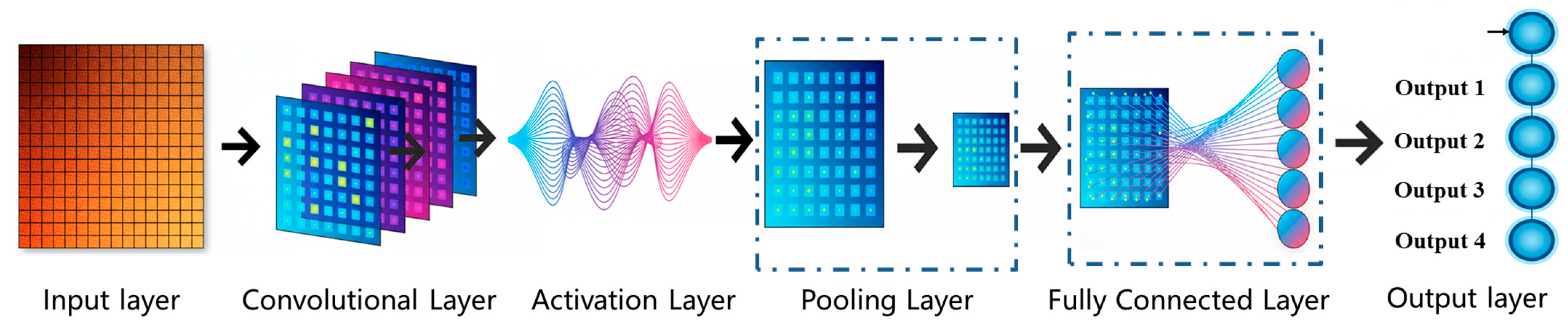
2.1. Introduction of CNN Structure
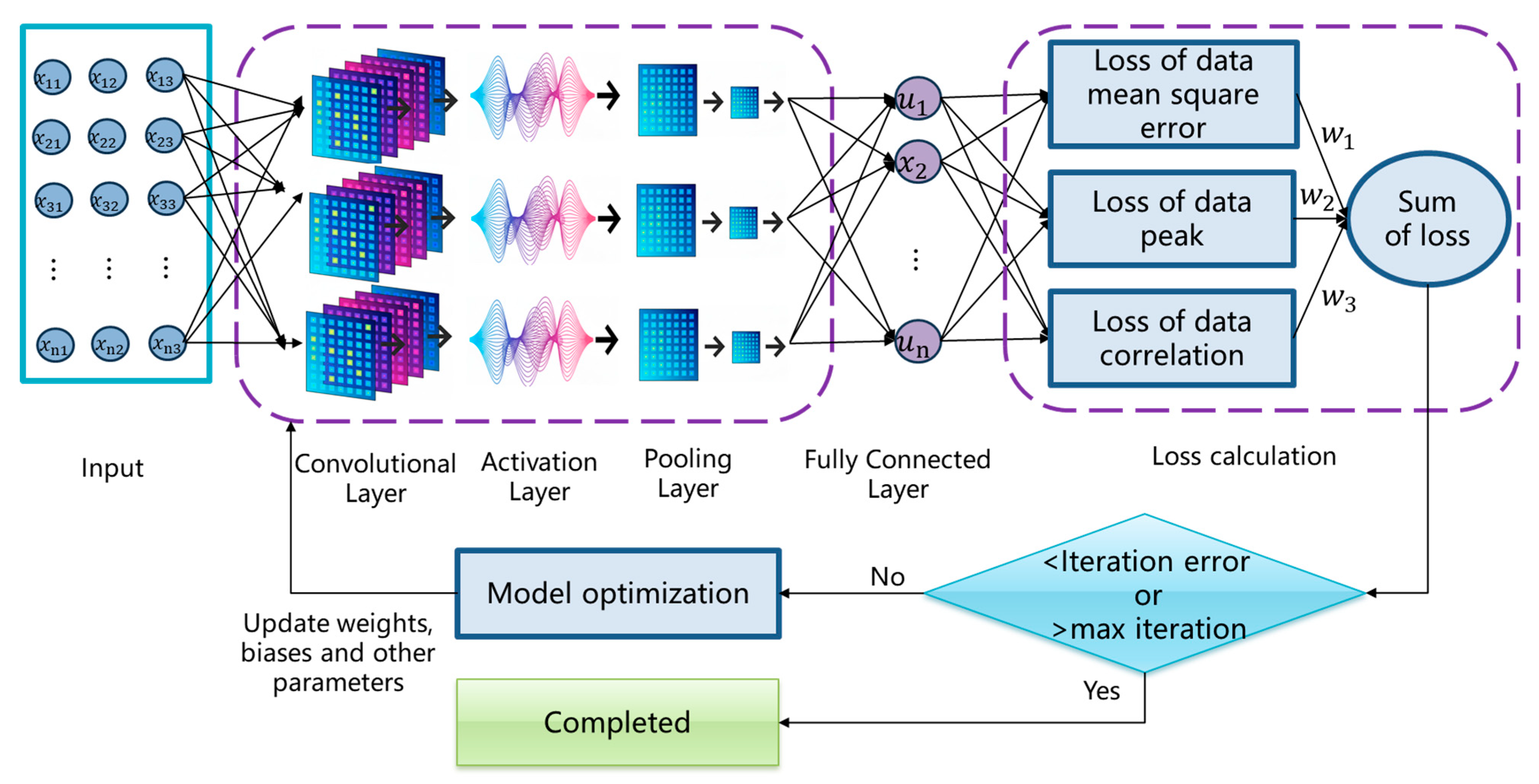
2.2. EINN Proposed
3. Vehicle Tire Noise Test and Analysis
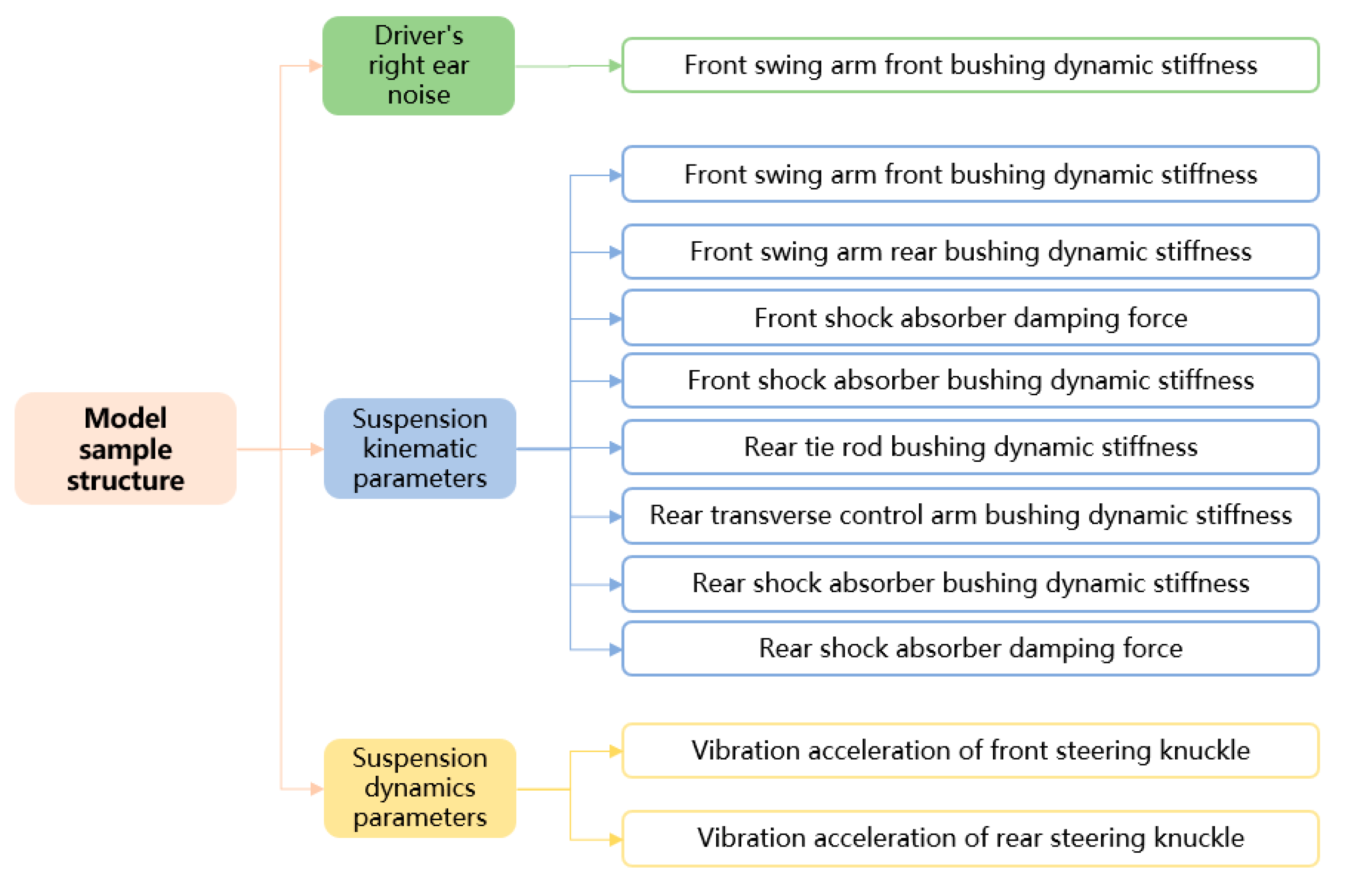
3.1. Analysis of Factors Affecting Tire Noise
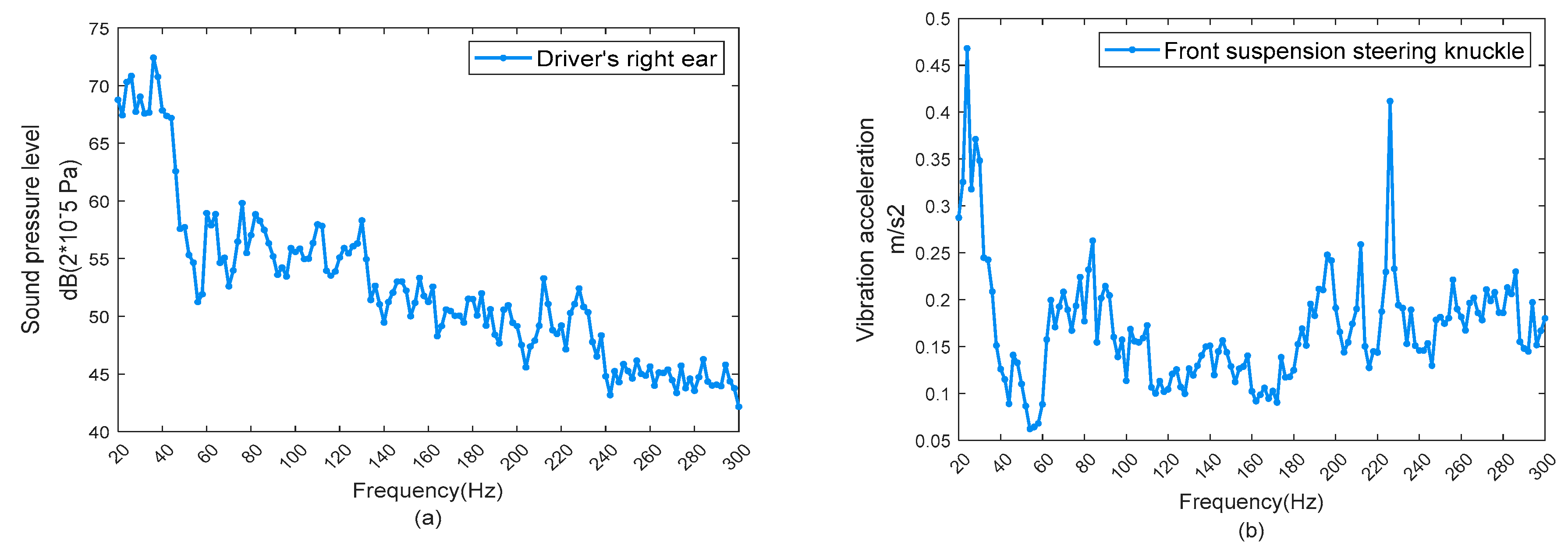
3.2. Tire Noise Road Test
3.3. Data Augmentation
4. Application and Verification of the Method
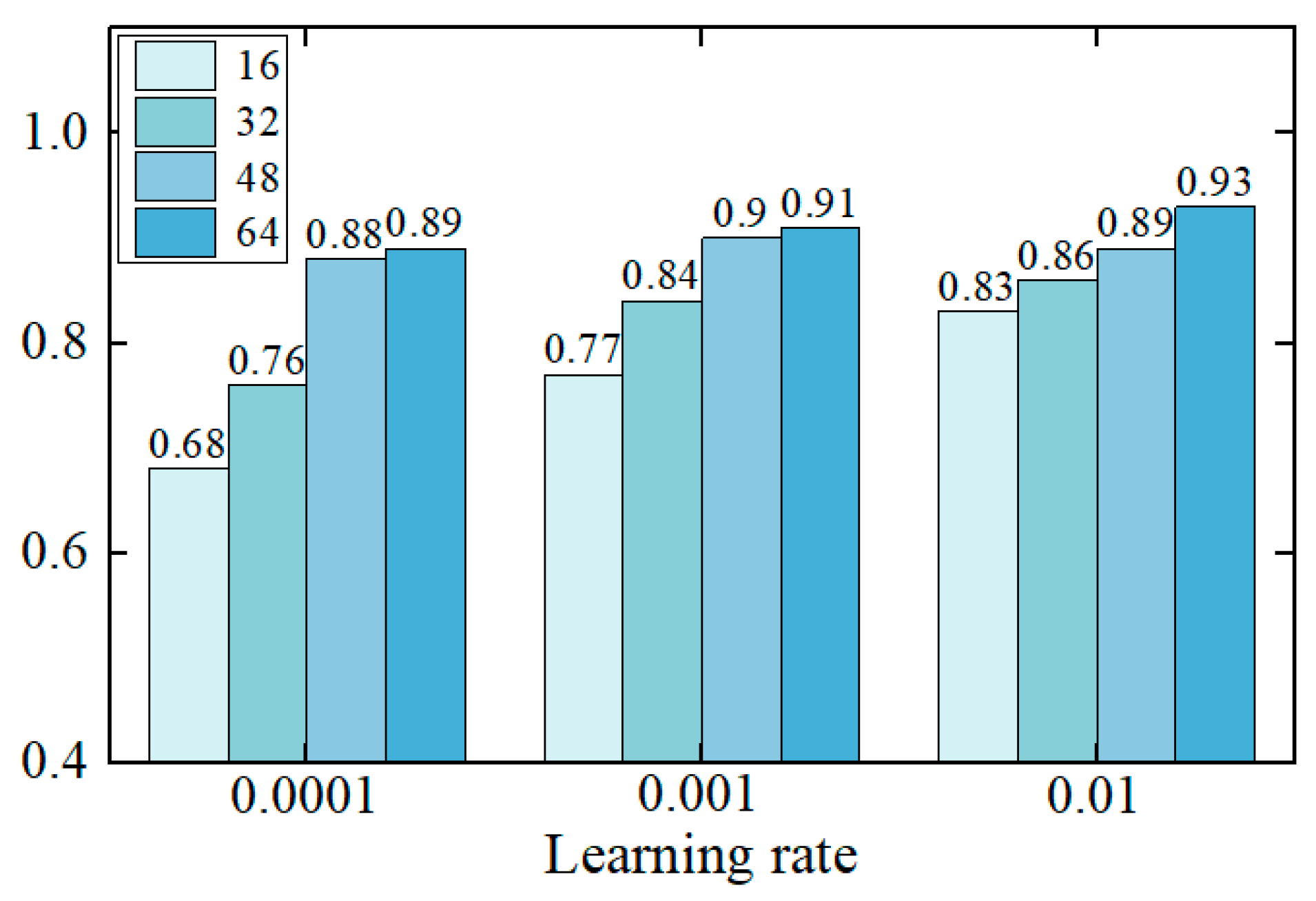
4.1. Development of a Tire Noise Prediction Model Using EINN
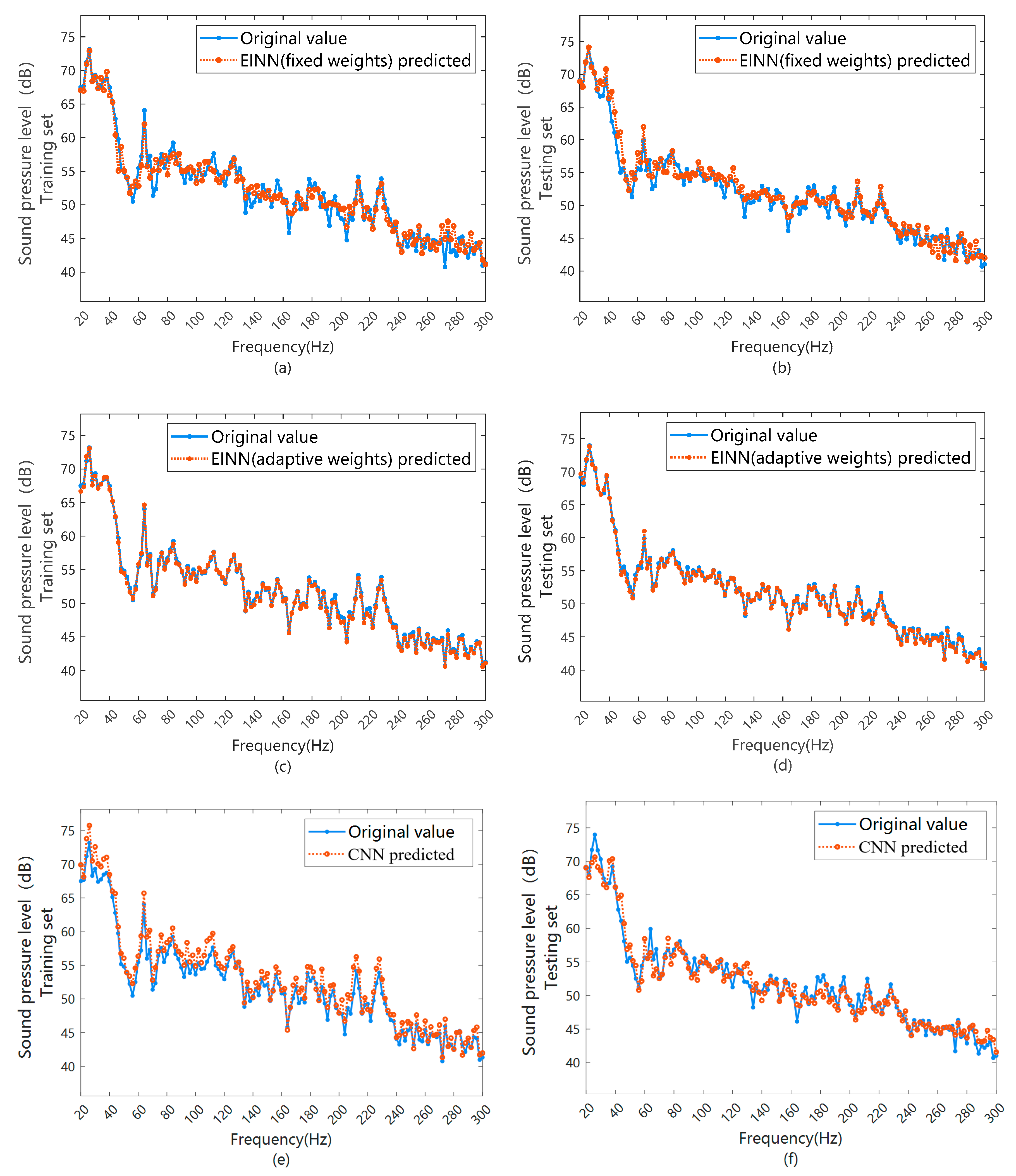
4.2. EINN Model Comparison and Verification
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Abidou, D.; Abdellah, A.H.; Haggag, S. Optimizing Rear Spoiler Angle for Enhanced Vehicle Braking Performance. SAE Int. J. Veh. Dyn. Stab. NVH 2025, 9, 10-09-04-0033. [Google Scholar] [CrossRef]
- Liu, K.; Liao, Y.; Wang, H.; Zhou, J. Road Noise Improvement Method for Battery Electric Vehicles Based on Bushing Stiffness Optimization. SAE Int. J. Veh. Dyn. Stab. NVH 2025, 9, 10-09-04-0032. [Google Scholar] [CrossRef]
- Zhu, H.; Zhao, J.; Wang, Y.; Ding, W.; Pang, J.; Huang, H. Improving of pure electric vehicle sound and vibration comfort using a multi-task learning with task-dependent weighting method. Measurement 2024, 233, 114752. [Google Scholar] [CrossRef]
- Li, X.; Lu, C.; Chen, W.; Zhu, Y.; Liu, Z.; Cheng, C.; Sun, M. A computationally efficient multichannel feedforward time–frequency-domain adjoint least mean square algorithm for active road noise control. Appl. Acoust. 2025, 231, 110441. [Google Scholar] [CrossRef]
- Raabe, J.; Fontana, F.; Neubeck, J.; Wagner, A. Contribution to the objective evaluation of combined longitudinal and lateral vehicle dynamics in nonlinear driving range. SAE Int. J. Veh. Dyn. Stab. NVH 2023, 7, 533–554. [Google Scholar] [CrossRef]
- Contartese, N.; Nijman, E.; Desmet, W. A procedure to restore measurement induced violations of reciprocity and passivity for FRF-based substructuring. Mech. Syst. Signal Process. 2022, 167, 108556. [Google Scholar] [CrossRef]
- Yuan, W.; Yang, Q. A Novel Method for Pavement Transverse Crack Detection Based on 2D Reconstruction of Vehicle Vibration Signal. KSCE J. Civ. Eng. 2023, 27, 2868–2881. [Google Scholar] [CrossRef]
- Huang, H.; Huang, X.; Ding, W.; Yang, M.; Fan, D.; Pang, J. Uncertainty optimization of pure electric vehicle interior tire/road noise comfort based on data-driven. Mech. Syst. Signal Process. 2022, 165, 108300. [Google Scholar] [CrossRef]
- Mikhailenko, P.; Piao, Z.; Kakar, M.R.; Bueno, M.; Athari, S.; Pieren, R.; Heutschi, K.; Poulikakos, L. Low-Noise pavement technologies and evaluation techniques: A literature review. Int. J. Pavement Eng. 2022, 23, 1911–1934. [Google Scholar] [CrossRef]
- Deubel, C.; Ernst, S.; Prokop, G. Objective evaluation methods of vehicle ride comfort—A literature review. J. Sound Vib. 2023, 548, 117515. [Google Scholar] [CrossRef]
- Dai, R.; Zhao, J.; Zhao, W.; Ding, W.; Huang, H. Exploratory study on sound quality evaluation and prediction for engineering machinery cabins. Measurement 2025, 253, 117684. [Google Scholar] [CrossRef]
- Huang, H.; Wang, Y.; Wu, J.; Ding, W.; Pang, J. Prediction and optimization of pure electric vehicle tire/road structure-borne noise based on knowledge graph and multi-task ResNet. Expert Syst. Appl. 2024, 255, 124536. [Google Scholar] [CrossRef]
- Chen, F.; Cao, Z.; Grais, M.E.; Zhao, F. Contributions and limitations of using machine learning to predict noise-induced hearing loss. Int. Arch. Occup. Environ. Health 2021, 94, 1097–1111. [Google Scholar] [CrossRef]
- He, X.; Chen, H.; Lv, C. Robust multiagent reinforcement learning toward coordinated decision-making of automated vehicles. SAE Int. J. Veh. Dyn. Stab. NVH 2023, 7, 475–488. [Google Scholar] [CrossRef]
- Raissi, M.; Perdikaris, P.; Karniadakis, G. Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J. Comput. Phys. 2019, 378, 686–707. [Google Scholar] [CrossRef]
- Feng, Y.; Wang, W. Energy Equalities of the Inhomogeneous Navier-Stokes Equations, MHD Equations and Hall-MHD Equations. Bull. Malays. Math. Sci. Soc. 2025, 48, 166. [Google Scholar] [CrossRef]
- Feng, M.; Sun, T. Error analysis of a hybrid numerical method for optimal control problem governed by parabolic PDEs in random cylindrical domains. Adv. Comput. Math. 2025, 51, 22. [Google Scholar] [CrossRef]
- Yang, C.; Wang, J.; Jian, M.; Dai, J. Synchronization Control of Complex Spatio-Temporal Networks Based on Fractional-Order Hyperbolic PDEs with Delayed Coupling and Space-Varying Coefficients. Fractal Fract. 2024, 8, 525. [Google Scholar] [CrossRef]
- Jin, X.; Cai, S.; Li, H.; George, E. Nsfnets (navier-stokes flow nets): Physics-informed neural networks for the incompressible navier-stokes equations. J. Comput. Phys. 2021, 426, 109951. [Google Scholar] [CrossRef]
- Xu, Y.; Zhang, Y.; Lu, X. MADAN: A multi-angle domain adversarial network for robust cross-condition rolling bearing fault diagnosis. Meas. Sci. Technol. 2025, 36, 096101. [Google Scholar] [CrossRef]
- Schiassi, E.; Furfaro, R.; Leake, C.; Mario, D.; Johnston, H.; Mortari, D. Extreme theory of functional connections: A fast physics-informed neural network method for solving ordinary and partial differential equations. Neurocomputing 2021, 457, 334–356. [Google Scholar] [CrossRef]
- Cai, S.; Wang, Z.; Wang, S.; Perdikaris, P.; Karniadakis, G. Physics-Informed Neural Networks for Heat Transfer Problems. J. Heat Transf. 2021, 143, 060801. [Google Scholar] [CrossRef]
- Li, X.; Zhang, W. Physics-informed deep learning model in wind turbine response prediction. Renew. Energy 2022, 185, 932–944. [Google Scholar] [CrossRef]
- Chen, K.; Wu, G.; Peng, S.; Zeng, X.; Ju, L. The vehicle speed strategy with double traffic lights based on reinforcement learning. Int. J. Veh. Perform. 2023, 9, 250–271. [Google Scholar] [CrossRef]
- Zhang, X.; Yi, Y.; Wang, L.; Xu, Z.; Zhang, T.; Zhou, Y. Deep Neural Networks for Modeling Astrophysical Nuclear Reacting Flows. Astrophys. J. 2025, 990, 105. [Google Scholar] [CrossRef]
- Dai, R.; Zhao, J.; Sui, Q.; Zhao, W.; Ding, W.; Huang, H. Multi-dimensional evaluation and prediction of vibration comfort in electric loaders using ACO-Transformer. Sound Vib. 2025, 59, 3523. [Google Scholar] [CrossRef]
- Luo, D.; Yang, W.; Wang, Y.; Han, Y.; Liu, Q.; Yang, Y. Investigation of regenerative braking for the electric mining truck based on fuzzy control. Int. J. Veh. Perform. 2024, 10, 73–95. [Google Scholar] [CrossRef]
- Tonelli, R.; Buckert, S.; Patrucco, A.; Perez, B.B.; Gutierrez, J.; Sanchez, A. Electric Vehicle Ride & Vibrations Analysis: Full Electric Vehicle MBD Model Development for NVH Studies. SAE Int. J. Adv. Curr. Pract. Mobil. 2024, 7, 1024–1034. [Google Scholar] [CrossRef]
- Lawal, Z.; Yassin, H.; Lai, D.; Idris, A. Physics-informed neural network (PINN) evolution and beyond: A systematic literature review and bibliometric analysis. Big Data Cogn. Comput. 2022, 6, 140. [Google Scholar] [CrossRef]
- Leung, W.; Lin, G.; Zhang, Z. NH-PINN: Neural homogenization-based physics-informed neural network for multiscale problems. J. Comput. Phys. 2022, 470, 111539. [Google Scholar] [CrossRef]
- Marral, U.I.; Du, H.; Naghdy, F. Multidimensional Coupling Effects and Vibration Suppression for In-Wheel Motor–Driven Electric Vehicle Suspension Systems: A Review. SAE Int. J. Veh. Dyn. Stab. NVH 2025, 9, 229–251. [Google Scholar] [CrossRef]
- Soresini, F.; Barri, D.; Ballo, F.; Manzoni, S.; Gobbi, M.; Mastinu, G. Noise, Vibration, and Harshness Countermeasures of Permanent Magnet Synchronous Motor with Viscoelastic Layer Material. SAE Int. J. Veh. Dyn. Stab. NVH 2025, 9, 1–18. [Google Scholar] [CrossRef]
- Nicho, M.; Cusack, B.; McDermott, D.; Girija, S. Assessing IoT intrusion detection computational costs when using a convolutional neural network. Inf. Secur. J. A Glob. Perspect. 2025, 34, 471–491. [Google Scholar] [CrossRef]
- Hatami, M.; Gharaee, H.; Mohammadzadeh, N. SADCNN: Supervised anomaly detection based on convolutional neural network models. Inf. Secur. J. A Glob. Perspect. 2025, 34, 455–470. [Google Scholar] [CrossRef]
- Hamrouni, C.; Alutaybi, A. Modeling and predicting the transmission efficiency of communication devices under joint noise and vibration disturbances. Sound Vib. 2025, 59, 2112. [Google Scholar] [CrossRef]
- Alutaybi, A.; Hamrouni, C. Impact of vibration on wind turbine efficiency and LSTM-based power conversion prediction. Sound Vib. 2025, 59, 2059. [Google Scholar] [CrossRef]
- Tian, J.; Wang, H.; He, J.; Pan, Y.; Cao, S.; Jiang, Q. Learning and interpreting gravitational-wave features from CNNs with a random forest approach. Mach. Learn. Sci. Technol. 2025, 6, 035045. [Google Scholar] [CrossRef]
- Elabd, E.; Hamouda, M.H.; Ali, M.; Fouad, Y. Correction: Climate change prediction in Saudi Arabia using a CNN GRU LSTM hybrid deep learning model in al Qassim region. Sci. Rep. 2025, 15, 31371. [Google Scholar] [CrossRef]
- Jin, M.; Zuo, S.; Wu, X.; Li, S.; Li, H.; Shi, L.; Chen, Y. Multistage operation transfer path analysis of an electric vehicle based on the regularization of total least squares. Mech. Syst. Signal Process. 2025, 225, 112250. [Google Scholar] [CrossRef]
- Elliott, A.S.; Moorhouse, A.T.; Huntley, T.; Tate, S. In-situ source path contribution analysis of structure borne road noise. J. Sound Vib. 2013, 332, 6276–6295. [Google Scholar] [CrossRef]
- Pu, Z.; Yi, J.; Liu, Z.; Qiu, T.; Sun, J.; Li, F. A review of research on group intelligent decision-making methods driven by knowledge and data synergy. J. Autom. 2022, 48, 1–17. [Google Scholar] [CrossRef]
- Liu, W.; Zhang, X.; Wang, Z.; Wang, Y.; Hu, B.; Zhuang, Y. Exploration of Vibration Signal Measurement Method of Automobile Parts Utilizing FPGA/Photoelectric Sensor. J. Nanoelectron. Optoelectron. 2021, 16, 1629–1637. [Google Scholar] [CrossRef]
- GB/T 18697-2002; Acoustics—Method for Measuring Vehicle Interior Noise. General Administration of Quality Supervision, Inspection and Quarantine of the People’s Republic of China, Standardization Administration of the People’s Republic of China: Beijing, China, 2002.
- Shields, M.; Zhang, J. The generalization of Latin hypercube sampling. Reliab. Eng. Syst. Saf. 2015, 148, 96–108. [Google Scholar] [CrossRef]
- Huang, H.; Huang, X.; Ding, W.; Yang, M.; Yu, X.; Pang, J. Vehicle vibro-acoustical comfort optimization using a multi-objective interval analysis method. Expert Syst. Appl. 2023, 213, 119001. [Google Scholar] [CrossRef]
- Pan, Z.; Yu, W.; Yi, X.; Khan, A.; Yuan, F.; Zheng, Y. Recent progress on generative adversarial networks (GANs): A survey. IEEE Access 2019, 7, 36322–36333. [Google Scholar] [CrossRef]
- Huang, J.; Yang, P.; Xiong, B.; Lv, Y.; Wang, Q.; Wan, B.; Zhang, Z.Q. Mixup-based data augmentation for enhancing few-shot SSVEP detection performance. J. Neural Eng. 2025, 22, 046038. [Google Scholar] [CrossRef] [PubMed]
- Tang, L.; Zhang, Z.; Yang, J.; Yong, F.; Wang, Q.; Sun, S.; Shao, H. Intervention-based Mixup Augmentation for Multiple Instance Learning in Whole-Slide Image Survival Analysis. IEEE Trans. Med. Imaging 2025. [Google Scholar] [CrossRef]
- Cao, K.; Peng, J.; Chen, J.; Hou, X.; Ma, J. Adversarial Style Mixup and Improved Temporal Alignment for Cross-Domain Few-Shot Action Recognition. Comput. Vis. Image Underst. 2025, 255, 104341. [Google Scholar] [CrossRef]
- Kwon, S.; Lee, Y. Explainability-based mix-up approach for text data augmentation. ACM Trans. Knowl. Discov. Data 2023, 17, 1–14. [Google Scholar] [CrossRef]
- Guo, H. Nonlinear mixup: Out-of-manifold data augmentation for text classification. Proc. AAAI Conf. Artif. Intell. 2020, 34, 4044–4051. [Google Scholar] [CrossRef]
- Kalange, N. Prediction of Stock Prices Using LSTM-ARIMA Hybrid Deep Learning Model. Asian J. Probab. Stat. 2025, 27, 28–39. [Google Scholar] [CrossRef]
- Tempone, G.; de Carvalho Pinheiro, H.; Imberti, G.; Carello, M. Control System for Regenerative Braking Efficiency in Electric Vehicles with Electro-Actuated Brakes. SAE Int. J. Veh. Dyn. Stab. NVH 2024, 8, 265–284. [Google Scholar] [CrossRef]
- Yang, M.; Dai, P.; Yin, Y.; Wang, D.; Wang, Y.; Huang, H. Predicting and optimizing pure electric vehicle road noise via a locality-sensitive hashing transformer and interval analysis. ISA Trans. 2025, 157, 556–572. [Google Scholar] [CrossRef] [PubMed]


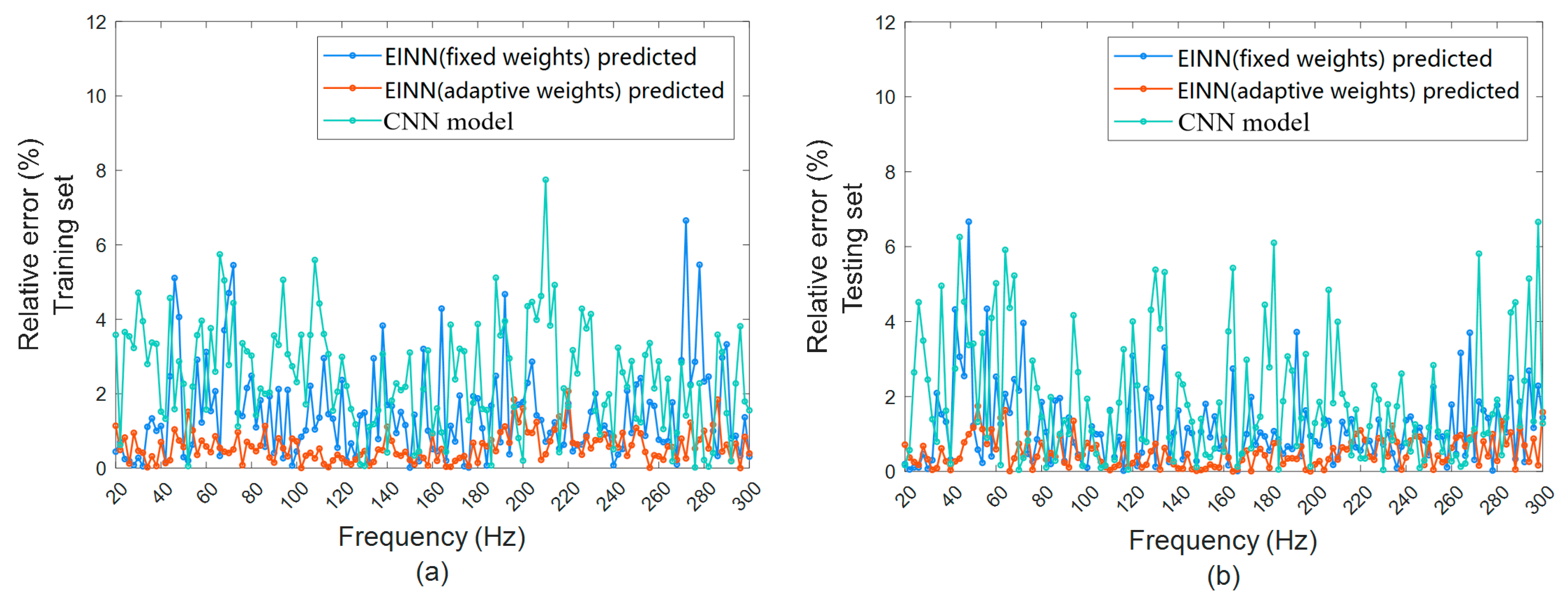
| MRE | MaxRE | MPE | MaxPE | ||
|---|---|---|---|---|---|
| EINN (Fixed weight) | Training | 2.2% | 6.3% | 2.3% | 3.3% |
| Testing | 2.5% | 5.8% | 2.1% | 3.4% | |
| EINN (Adaptive weight) | Training | 1.1% | 2.0% | 0.8% | 1.0% |
| Testing | 1.3% | 2.2% | 0.7% | 1.0% | |
| CNN | Training | 3.0% | 7.5% | 5.8% | 5.9% |
| Testing | 3.4% | 6.8% | 5.9% | 6.4% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dai, P.; Dai, R.; Yin, Y.; Wang, J.; Huang, H.; Ding, W. A Novel Empirical-Informed Neural Network Method for Vehicle Tire Noise Prediction. Machines 2025, 13, 911. https://doi.org/10.3390/machines13100911
Dai P, Dai R, Yin Y, Wang J, Huang H, Ding W. A Novel Empirical-Informed Neural Network Method for Vehicle Tire Noise Prediction. Machines. 2025; 13(10):911. https://doi.org/10.3390/machines13100911
Chicago/Turabian StyleDai, Peisong, Ruxue Dai, Yingqi Yin, Jingjing Wang, Haibo Huang, and Weiping Ding. 2025. "A Novel Empirical-Informed Neural Network Method for Vehicle Tire Noise Prediction" Machines 13, no. 10: 911. https://doi.org/10.3390/machines13100911
APA StyleDai, P., Dai, R., Yin, Y., Wang, J., Huang, H., & Ding, W. (2025). A Novel Empirical-Informed Neural Network Method for Vehicle Tire Noise Prediction. Machines, 13(10), 911. https://doi.org/10.3390/machines13100911







