Gear Target Detection and Fault Diagnosis System Based on Hierarchical Annotation Training
Abstract
1. Introduction
- 1.
- Hierarchical training is employed to enhance the gear fault localization capabilities of diagnostic models in complex environments.
- 2.
- Imbalanced datasets are generated for hierarchical annotation, where images are captured under complex backgrounds from varying distances and angles.
- 3.
- The model trained by using the proposed method is applied to actual sites and its excellent performance proves the effectiveness of the method.
2. Methodology
2.1. Data Acquisition
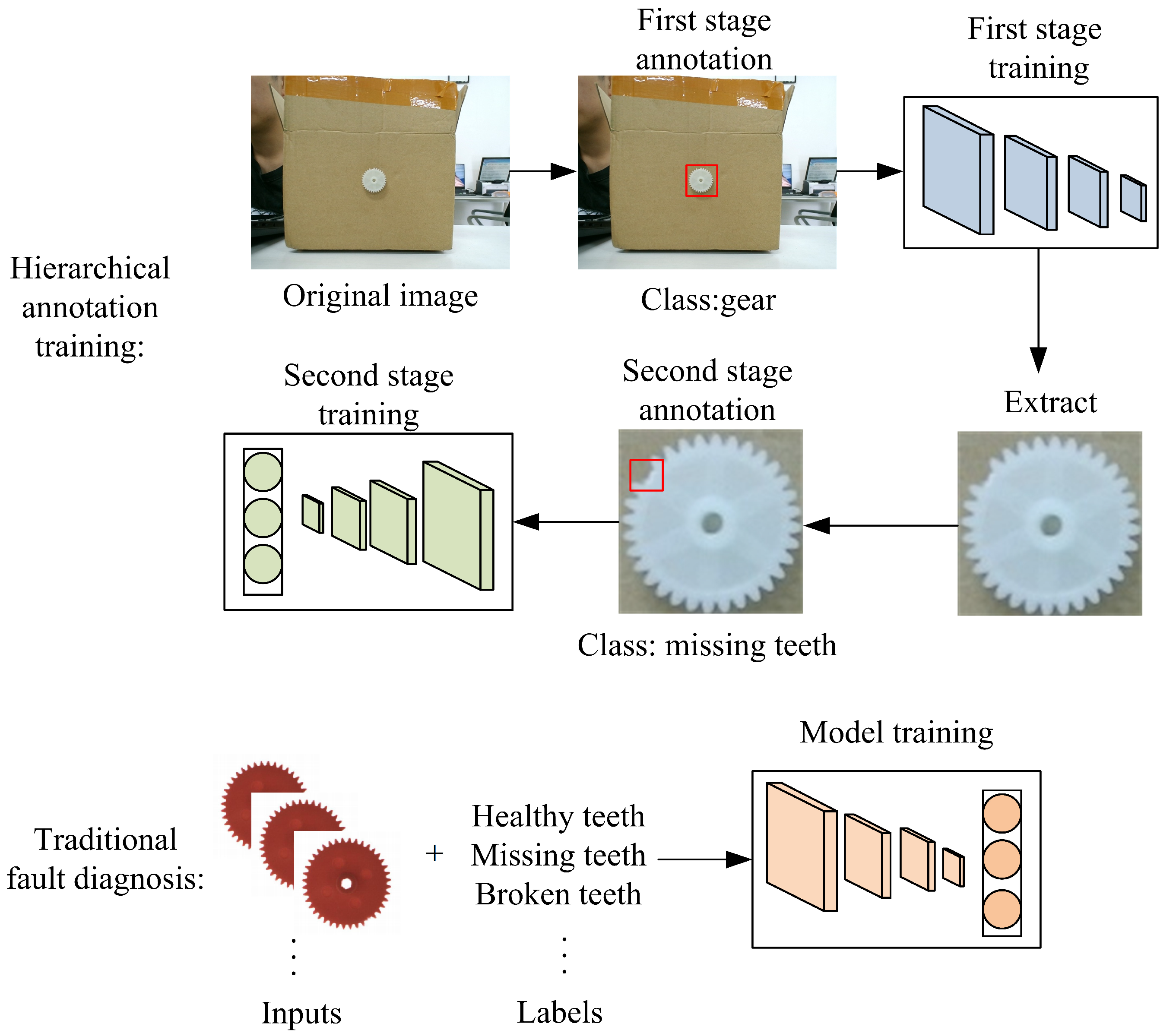
2.2. Hierarchical Annotation
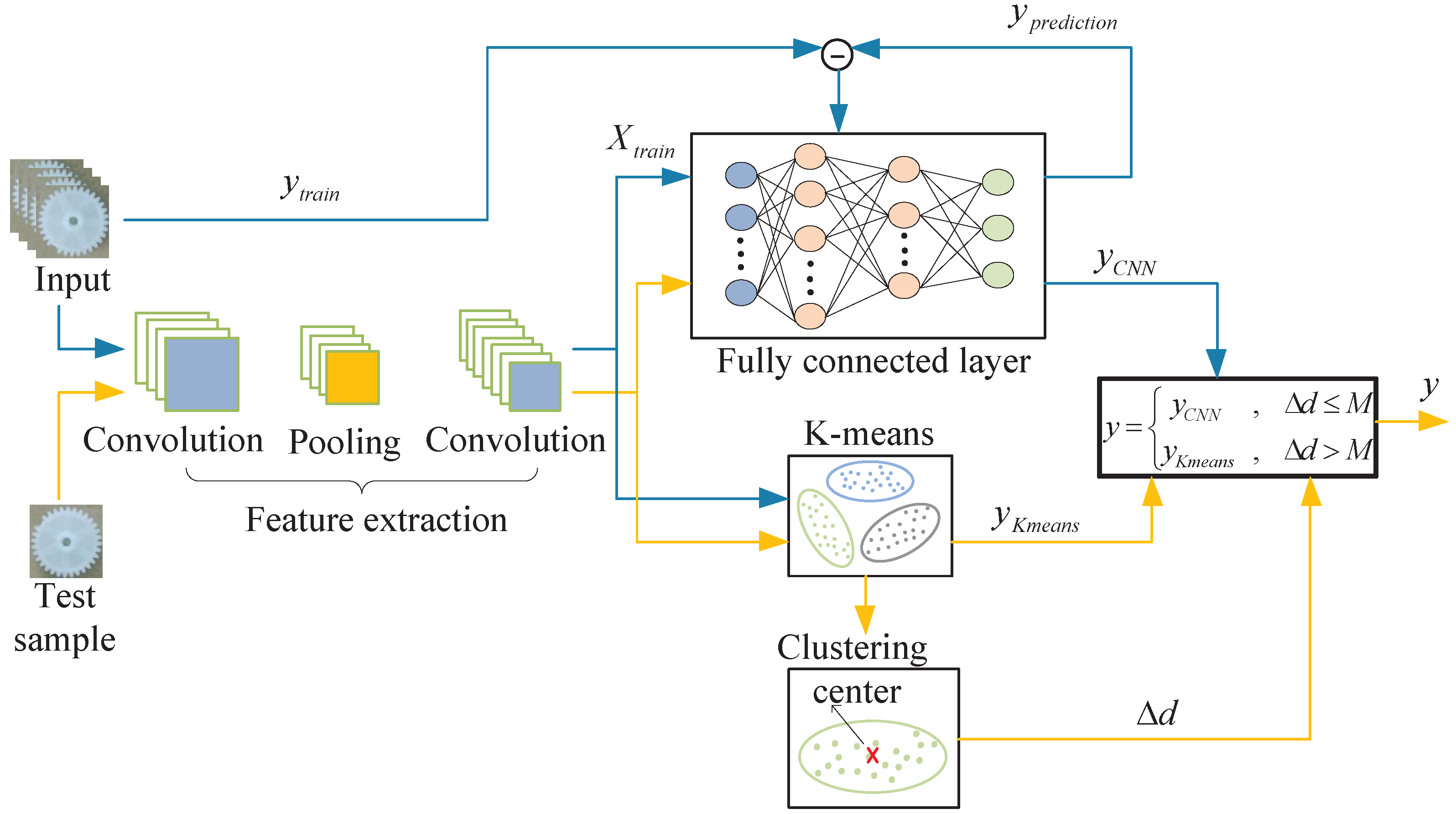
2.3. Semi-Supervised Learning Framework
3. Experimentation
3.1. Preparation
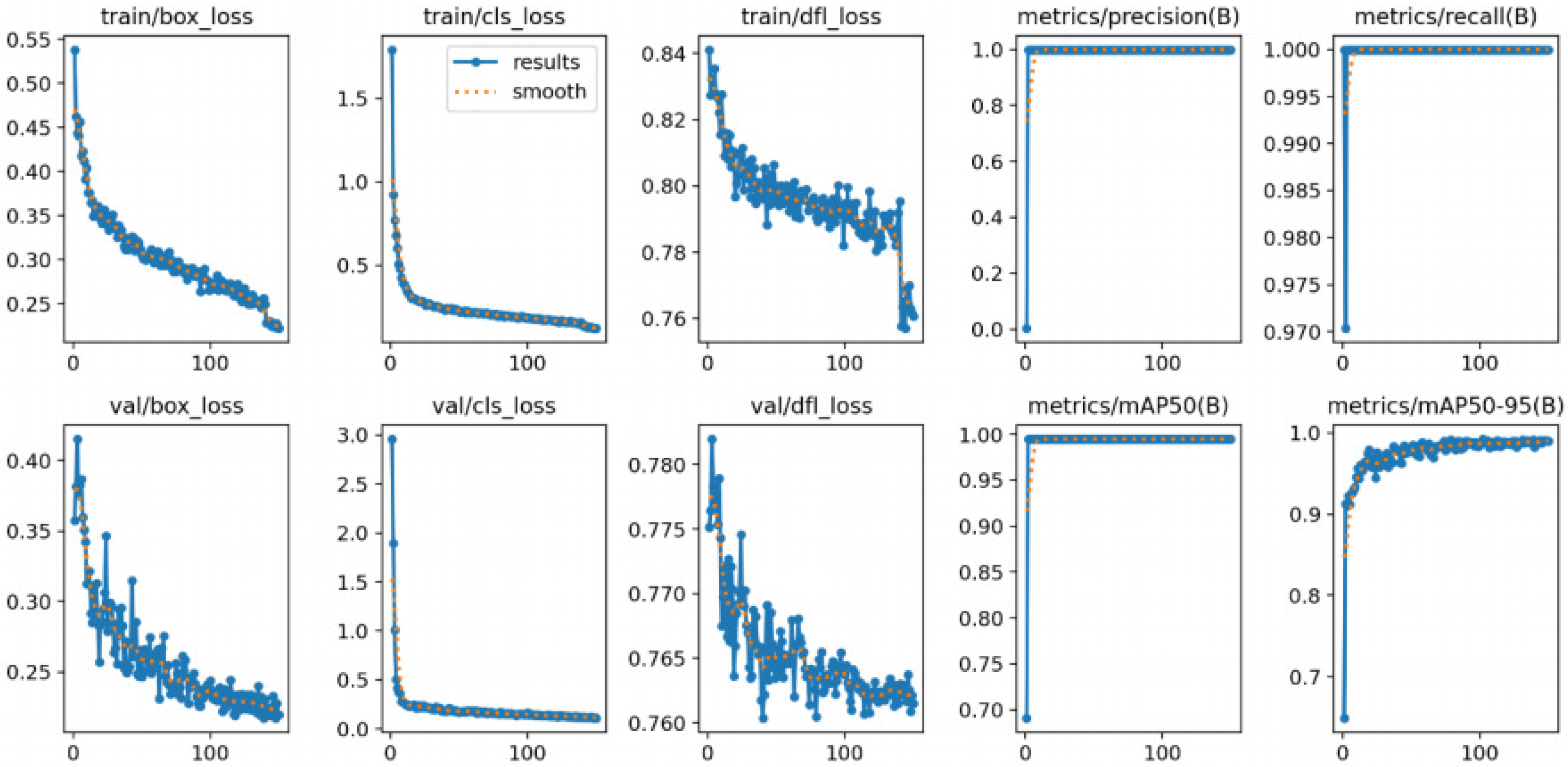
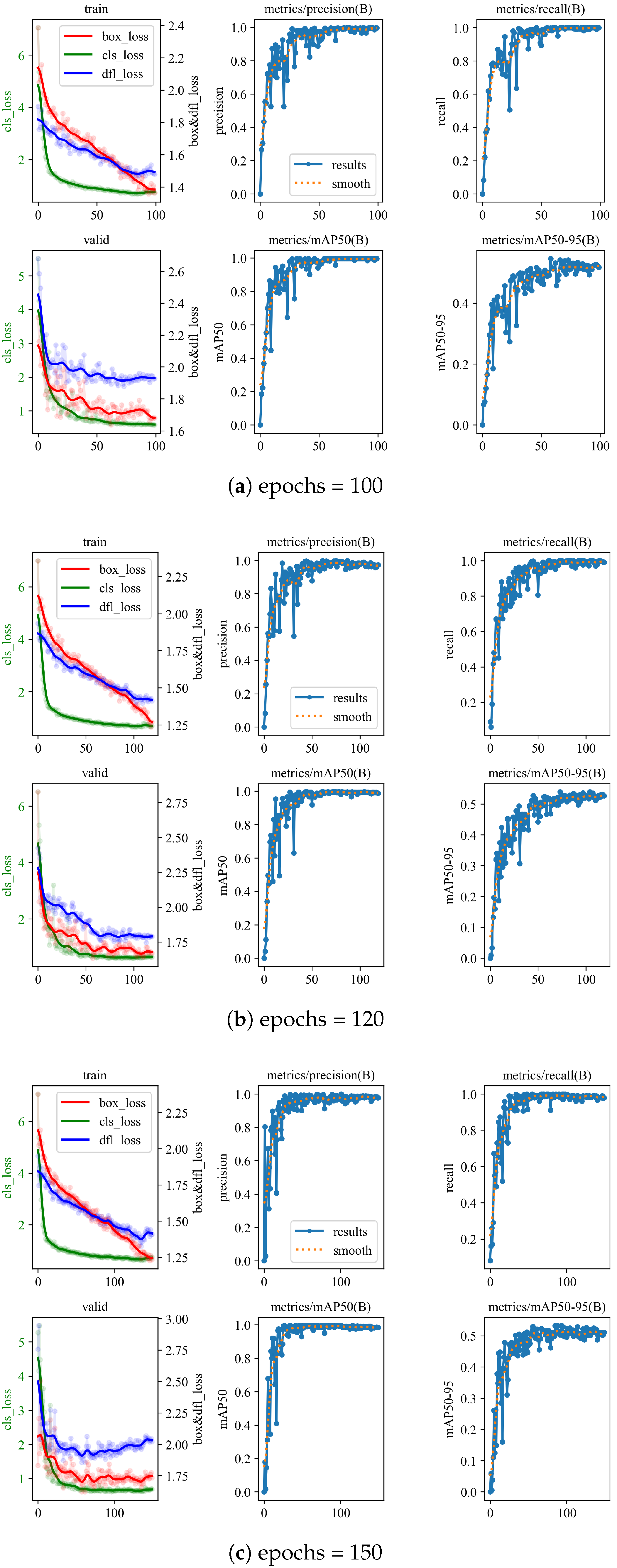
3.2. Hierarchical Training
3.3. Semi-Supervised Learning Framework
3.4. Comparison
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| CNN | Convolutional Neural Networks |
| mAP | mean Average Precision |
| IoU | Intersection of Union |
| G-mean | Geometric mean accuracy |
References
- Lv, H.; Chen, J.; Pan, T.; Zhang, T.; Feng, Y.; Liu, S. Attention mechanism in intelligent fault diagnosis of machinery: A review of technique and application. Measurement 2022, 199, 111594. [Google Scholar] [CrossRef]
- Feng, K.; Ji, J.; Ni, Q.; Beer, M. A review of vibration-based gear wear monitoring and prediction techniques. Mech. Syst. Signal Process. 2023, 182, 109605. [Google Scholar] [CrossRef]
- Liu, D.; Cui, L.; Wang, H. Rotating Machinery Fault Diagnosis Under Time-Varying Speeds: A Review. IEEE Sens. J. 2023, 23, 29969–29990. [Google Scholar] [CrossRef]
- Sharma, V.; Parey, A. A Review of Gear Fault Diagnosis Using Various Condition Indicators. Procedia Eng. 2016, 144, 253–263. [Google Scholar] [CrossRef]
- Xiao, J.; Ding, X.; Wang, Y.; Huang, W.; He, Q.; Shao, Y. Gear fault detection via directional enhancement of phononic crystal resonators. Int. J. Mech. Sci. 2024, 278, 109453. [Google Scholar] [CrossRef]
- Hashim, S.; Shakya, P. A spectral kurtosis based blind deconvolution approach for spur gear fault diagnosis. ISA Trans. 2023, 142, 492–500. [Google Scholar] [CrossRef] [PubMed]
- Junjun, Z.; Quansheng, J.; Yehu, S.; Chenhui, Q.; Fengyu, X.; Qixin, Z. Application of recurrent neural network to mechanical fault diagnosis: A review. J. Mech. Sci. Technol. 2022, 36, 527–542. [Google Scholar] [CrossRef]
- Mohammed, O.D.; Rantatalo, M. Gear fault models and dynamics-based modelling for gear fault detection—A review. Eng. Fail. Anal. 2020, 117, 104798. [Google Scholar] [CrossRef]
- Dadon, I.; Koren, N.; Klein, R.; Bortman, J. A realistic dynamic model for gear fault diagnosis. Eng. Fail. Anal. 2018, 84, 77–100. [Google Scholar] [CrossRef]
- Huang, H.; Peng, X.; Du, W.; Zhong, W. Robust Sparse Gaussian Process Regression for Soft Sensing in Industrial Big Data Under the Outlier Condition. IEEE Trans. Instrum. Meas. 2024, 73, 1–11. [Google Scholar] [CrossRef]
- Ahmad, H.; Cheng, W.; Xing, J.; Wang, W.; Du, S.; Li, L.; Zhang, R.; Chen, X.; Lu, J. Deep learning-based fault diagnosis of planetary gearbox: A systematic review. J. Manuf. Syst. 2024, 77, 730–745. [Google Scholar] [CrossRef]
- Shao, Z.; Zhang, T.; Kosasih, B. Compound Faults Diagnosis in Wind Turbine Gearbox Based on Deep Learning Methods: A Review. In Proceedings of the 2024 Global Reliability and Prognostics and Health Management Conference (PHM-Beijing), Beijing, China, 11–13 October 2024; pp. 1–8. [Google Scholar]
- Sowmya, S.; Saimurugan, M.; Edinbarough, I. Rotational Machine Fault Diagnosis Using Artificial Intelligence (AI) Strategies for the Operational Challenges Under Variable Speed Condition: A Review. IEEE Access 2024, 12, 144870–144889. [Google Scholar] [CrossRef]
- Gecgel, O.; Ekwaro-Osire, S.; Dias, J.P.; Serwadda, A.; Alemayehu, F.M.; Nispel, A. Gearbox Fault Diagnostics Using Deep Learning with Simulated Data. In Proceedings of the 2019 IEEE International Conference on Prognostics and Health Management (ICPHM), San Francisco, CA, USA, 17–20 June 2019; pp. 1–8. [Google Scholar]
- Heydarzadeh, M.; Kia, S.H.; Nourani, M.; Henao, H.; Capolino, G.A. Gear fault diagnosis using discrete wavelet transform and deep neural networks. In Proceedings of the IECON 2016—42nd Annual Conference of the IEEE Industrial Electronics Society, Florence, Italy, 23–26 October 2016; pp. 1494–1500. [Google Scholar]
- Saufi, S.R.; Ahmad, Z.A.B.; Leong, M.S.; Lim, M.H. Gearbox Fault Diagnosis Using a Deep Learning Model with Limited Data Sample. IEEE Trans. Ind. Inform. 2020, 16, 6263–6271. [Google Scholar] [CrossRef]
- Krawczyk, B. Learning from imbalanced data: Open challenges and future directions. Prog. Artif. Intell. 2016, 5, 221–232. [Google Scholar] [CrossRef]
- Nikpour, B.; Rahmati, F.; Mirzaei, B.; Nezamabadi-pour, H. A comprehensive review on data-level methods for imbalanced data classification. Expert Syst. Appl. 2026, 295, 128920. [Google Scholar] [CrossRef]
- Dablain, D.; Krawczyk, B.; Chawla, N.V. DeepSMOTE: Fusing Deep Learning and SMOTE for Imbalanced Data. IEEE Trans. Neural Netw. Learn. Syst. 2023, 34, 6390–6404. [Google Scholar] [CrossRef]
- Haixiang, G.; Yijing, L.; Shang, J.; Mingyun, G.; Yuanyue, H.; Bing, G. Learning from class-imbalanced data: Review of methods and applications. Expert Syst. Appl. 2017, 73, 220–239. [Google Scholar] [CrossRef]
- Wang, W.; Sun, D. The improved AdaBoost algorithms for imbalanced data classification. Inf. Sci. 2021, 563, 358–374. [Google Scholar] [CrossRef]
- Singh, A.; Ranjan, R.K.; Tiwari, A. Credit Card Fraud Detection under Extreme Imbalanced Data: A Comparative Study of Data-level Algorithms. J. Exp. Theor. Artif. Intell. 2022, 34, 571–598. [Google Scholar] [CrossRef]
- Ngo, G.; Beard, R.; Chandra, R. Evolutionary bagging for ensemble learning. Neurocomputing 2022, 510, 1–14. [Google Scholar] [CrossRef]
- Yang, X.; Song, Z.; King, I.; Xu, Z. A survey on deep semi-supervised learning. IEEE Trans. Knowl. Data Eng. 2022, 35, 8934–8954. [Google Scholar] [CrossRef]
- Odena, A. Semi-supervised learning with generative adversarial networks. arXiv 2016, arXiv:1606.01583. [Google Scholar] [CrossRef]
- Thekumparampil, K.K.; Wang, C.; Oh, S.; Li, L.J. Attention-based graph neural network for semi-supervised learning. arXiv 2018, arXiv:1803.03735. [Google Scholar]
- Rasmus, A.; Berglund, M.; Honkala, M.; Valpola, H.; Raiko, T. Semi-supervised learning with ladder networks. Adv. Neural Inf. Process. Syst. 2015, 28. [Google Scholar]
- Lee, D.H. Pseudo-label: The simple and efficient semi-supervised learning method for deep neural networks. In Proceedings of the Workshop on Challenges in Representation Learning, ICML, Atlanta, GA, USA, 20–21 June 2013. [Google Scholar]
- Yao, J.; Wang, M.; Mao, X. CDC-YOLO for Gear Defect Detection: Make YOLOv8 Faster and Lighter on RK3588. In Proceedings of the 2024 International Conference on Sensing, Measurement & Data Analytics in the era of Artificial Intelligence (ICSMD), Huangshan, China, 31 October–3 November 2024; pp. 1–6. [Google Scholar]
- Ioannou, I.; Christophorou, C.; Nagaradjane, P.; Vassiliou, V. Performance Evaluation of Machine Learning Cluster Metrics for Mobile Network Augmentation. In Proceedings of the 2024 International Conference on Wireless Communications Signal Processing and Networking (WiSPNET), Chennai, India, 21–23 March 2024; pp. 1–7. [Google Scholar]






| Parameters | Descriptions |
|---|---|
| pixel | 2 million |
| maximum resolution | |
| clarity | 1080p |
| communication interface | USB |
| sensor type | CMOS |
| support system | Windows, Mac OS, Android, Linux |
| Degree of Imbalance | Number of Healthy Gears | Number of Missing Gears | Number of Broken Gears |
|---|---|---|---|
| 2:1:1 | 500 | 250 | 250 |
| 5:1:1 | 500 | 100 | 100 |
| 10:1:1 | 500 | 50 | 50 |
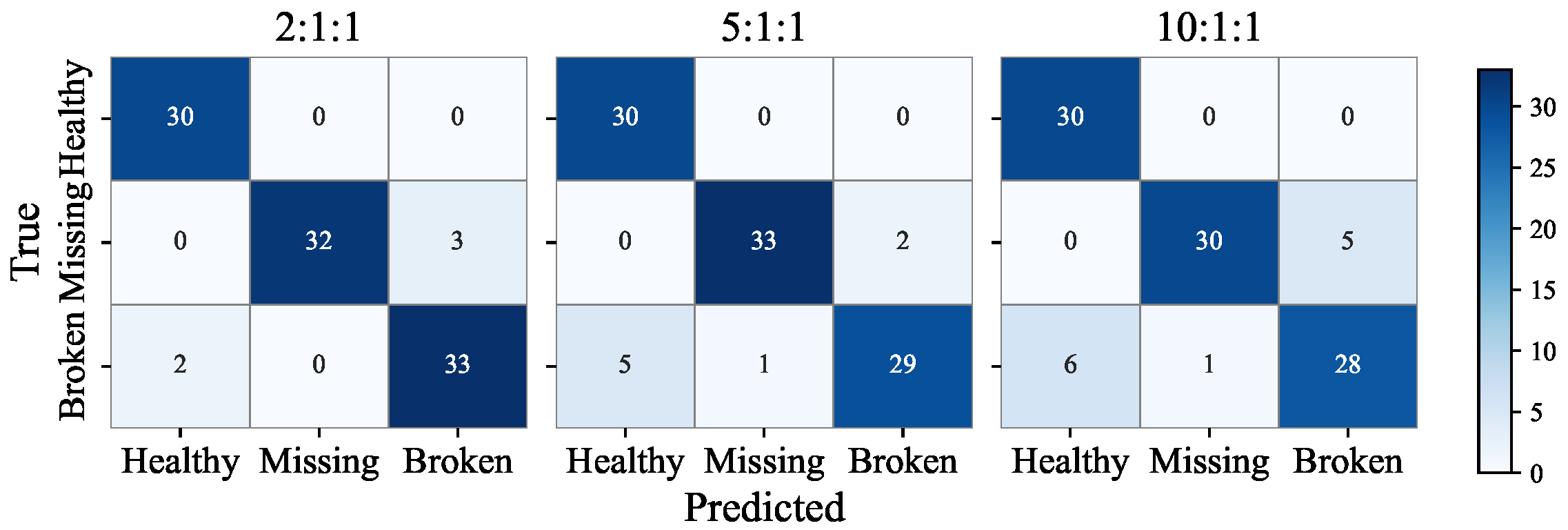
| Degree of Imbalance | Accuracy | Time | Category | Precision | Recall |
|---|---|---|---|---|---|
| 2:1:1 | 0.95 | First stage: 1.17 s | Healthy | 0.9375 | 1.0 |
| Second stage: 1.35 s | Missing | 1.0 | 0.9143 | ||
| Total: 2.52 s | Broken | 0.9167 | 0.9429 | ||
| 5:1:1 | 0.92 | First stage: 1.16 s | Healthy | 0.8571 | 1.0 |
| Second stage: 1.23 s | Missing | 0.9706 | 0.9429 | ||
| Total: 2.39 s | Broken | 0.9355 | 0.8286 | ||
| 10:1:1 | 0.88 | First stage: 1.17 s | Healthy | 0.8333 | 1.0 |
| Second stage: 1.35 s | Missing | 0.9677 | 0.8571 | ||
| Total: 2.52 s | Broken | 0.8485 | 0.80 |
| Degree of Imbalance | Accuracy | Time | Category | Precision | Recall |
|---|---|---|---|---|---|
| 2:1:1 | 0.94 | First stage: 1.21 s | Healthy | 0.8824 | 1.0 |
| Second stage: 1.33 s | Missing | 1.0 | 0.9429 | ||
| Total: 2.54 s | Broken | 0.9394 | 0.8857 | ||
| 5:1:1 | 0.94 | First stage: 1.16 s | Healthy | 0.8824 | 1.0 |
| Second stage: 1.24 s | Missing | 0.9714 | 0.9714 | ||
| Total: 2.40 s | Broken | 0.9677 | 0.8571 | ||
| 10:1:1 | 0.90 | First stage: 1.11 s | Healthy | 0.8571 | 1.0 |
| Second stage: 1.19 s | Missing | 0.9688 | 0.8857 | ||
| Total: 2.30 s | Broken | 0.8788 | 0.8286 |
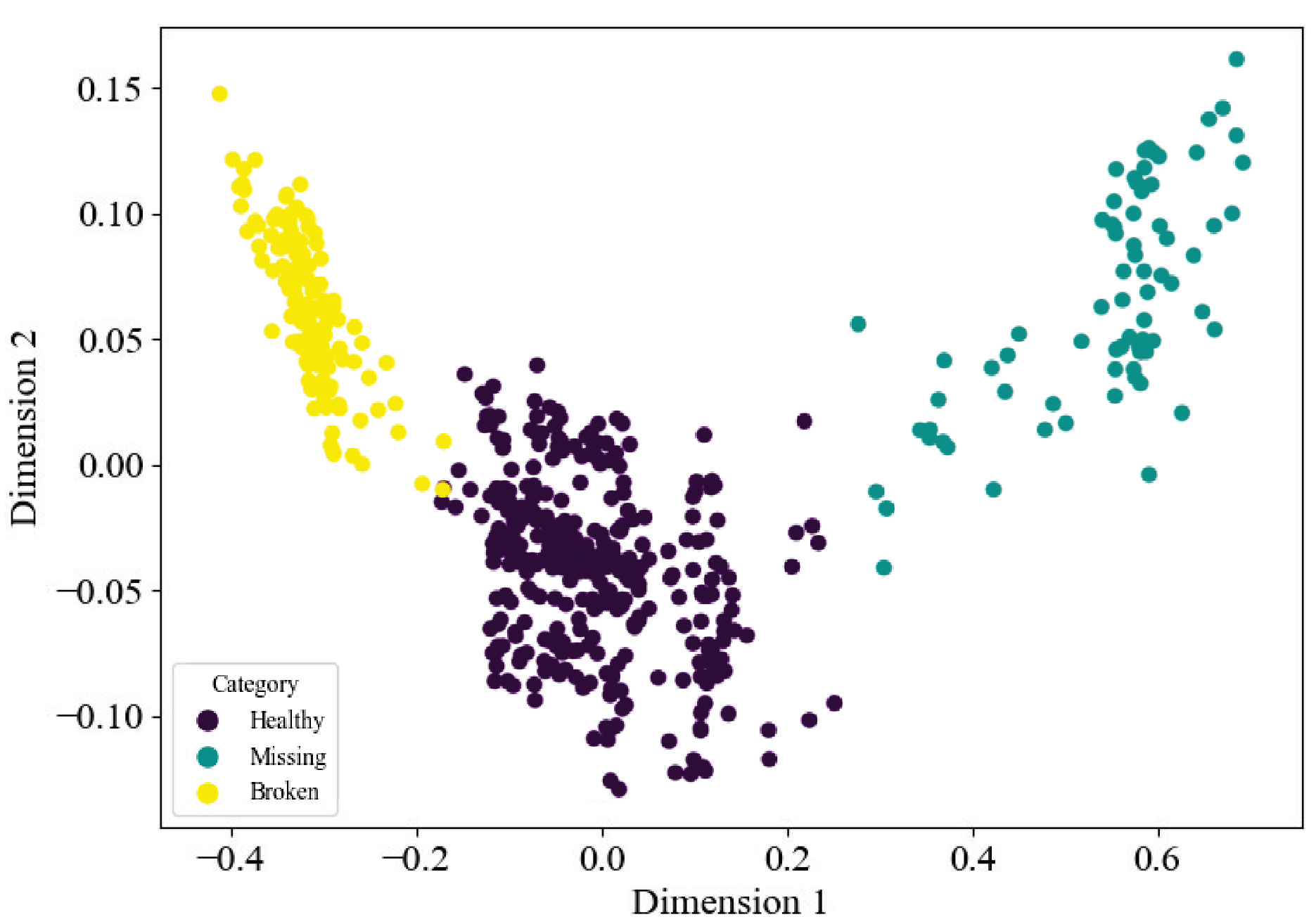
| Datasets | Imbalance Ratio | Frameworks | |
|---|---|---|---|
| Supervised | Semi-Supervised | ||
| Public | 1:1:1 | 0.155 | 0.035 |
| Self-constructed | 2:1:1 | 0.928 | 0.914 |
| 5:1:1 | 0.884 | 0.912 | |
| 10:1:1 | 0.828 | 0.857 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, H.; Liang, Q.; Wu, R.; Yang, D.; Wang, J.; Zheng, R.; Xu, Z. Gear Target Detection and Fault Diagnosis System Based on Hierarchical Annotation Training. Machines 2025, 13, 893. https://doi.org/10.3390/machines13100893
Huang H, Liang Q, Wu R, Yang D, Wang J, Zheng R, Xu Z. Gear Target Detection and Fault Diagnosis System Based on Hierarchical Annotation Training. Machines. 2025; 13(10):893. https://doi.org/10.3390/machines13100893
Chicago/Turabian StyleHuang, Haojie, Qixin Liang, Rui Wu, Dan Yang, Jiaorao Wang, Rong Zheng, and Zhezhuang Xu. 2025. "Gear Target Detection and Fault Diagnosis System Based on Hierarchical Annotation Training" Machines 13, no. 10: 893. https://doi.org/10.3390/machines13100893
APA StyleHuang, H., Liang, Q., Wu, R., Yang, D., Wang, J., Zheng, R., & Xu, Z. (2025). Gear Target Detection and Fault Diagnosis System Based on Hierarchical Annotation Training. Machines, 13(10), 893. https://doi.org/10.3390/machines13100893






