Multi-Objective Structural Parameter Optimization for Stewart Platform via NSGA-III and Kolmogorov–Arnold Network
Abstract
1. Introduction
- This work optimizes five key structural parameters within the maximum stroke. Compared with previous methods, the proposed approach demonstrates superior applicability to practical engineering scenarios and achieves significant improvements in critical performance metrics.
- This work employs NSGA-III to balance a large number of performance indicators. Compared with previous methods, the proposed approach can take more performance metrics into account and achieve better results.
- This work employs a Kolmogorov–Arnold Network to model each orientation and position within the maximum singularity-free workspace. Compared with previous methods, this network exhibits higher fitting accuracy than the traditional MLP and is well-suited for real-time computation.
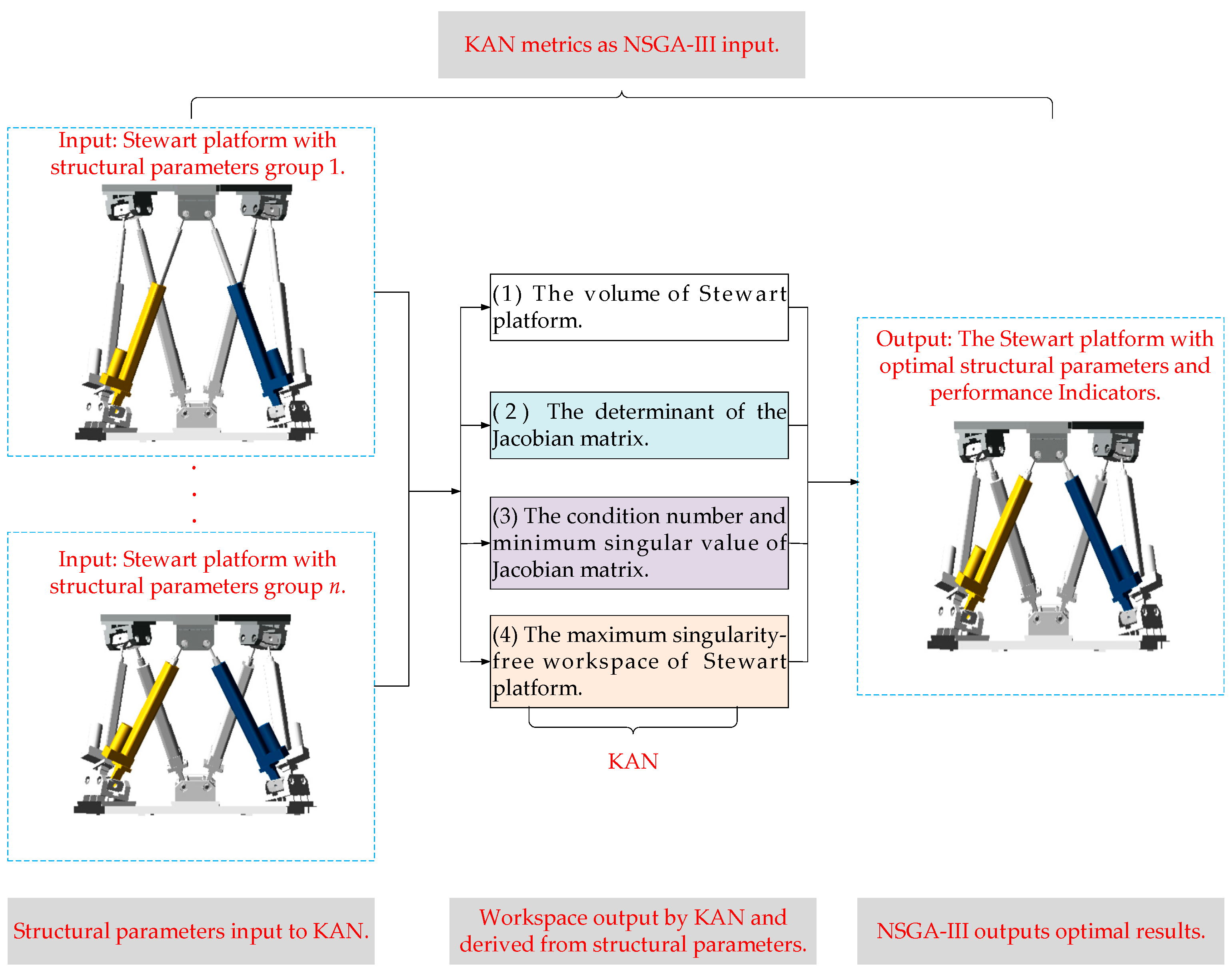
2. Overview
- Optimizes five key structural parameters of the Stewart platform, a critical kinematic system, under the platform’s stroke constraints. Unlike traditional methods that require comprehensive optimization of numerous parameters, our approach targets five primary parameters to enhance key performance metrics in Stewart platforms. This targeted strategy balances efficiency and precision, avoiding the complexity of adjusting excessive parameters while ensuring systematic performance improvement.
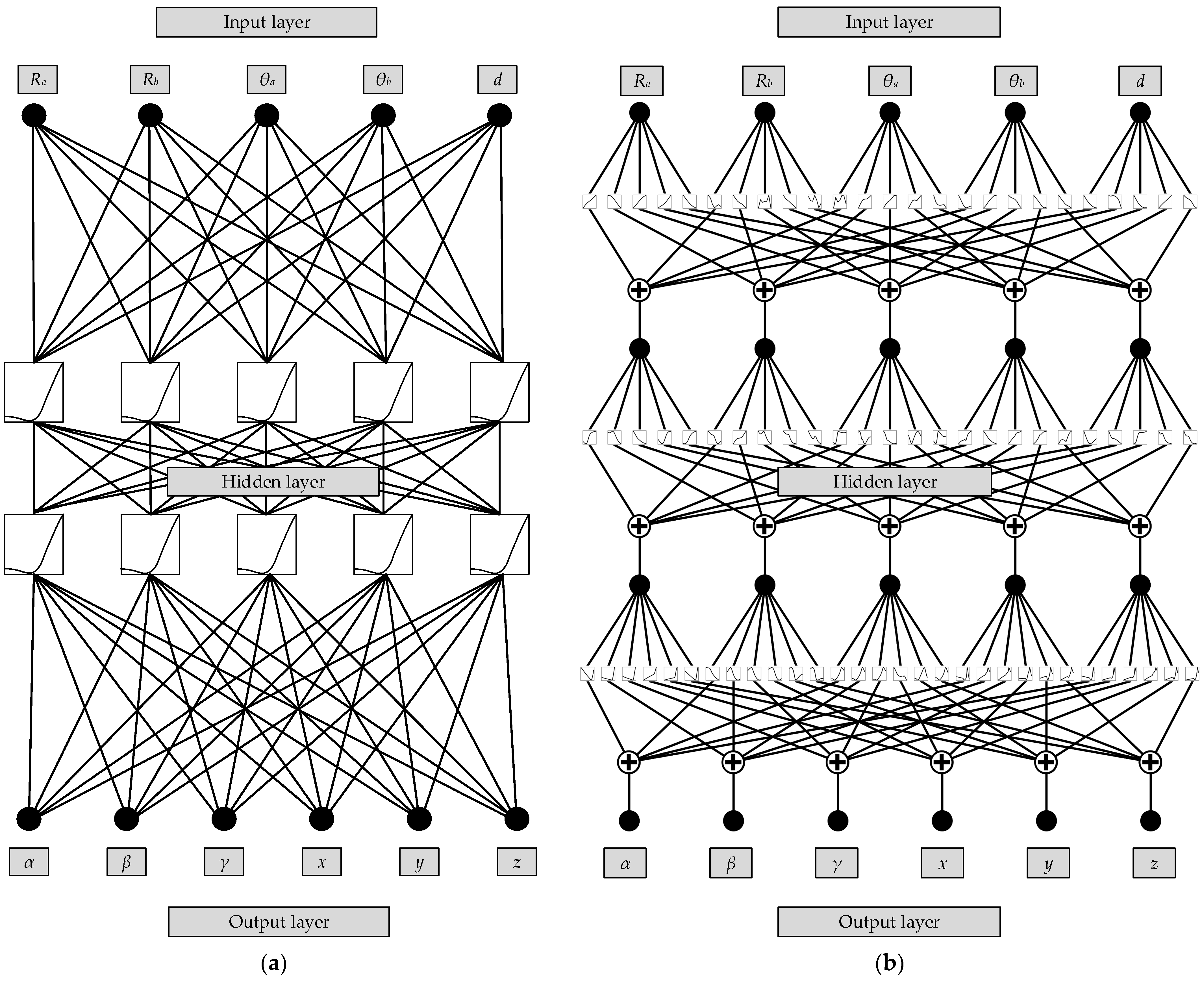
- Utilizes the KAN, a mathematically proven neural network, for efficient function approximation in the optimization framework. Notably, this approach has the advantage of reducing the computational complexity in genetic algorithms by leveraging a mathematically proven capability to represent any continuous function with minimal layers. Compared to MLPs, KAN outperforms conventional neural networks in both interpretability and approximation accuracy, which makes the KAN particularly suitable for real-time kinematic modeling.
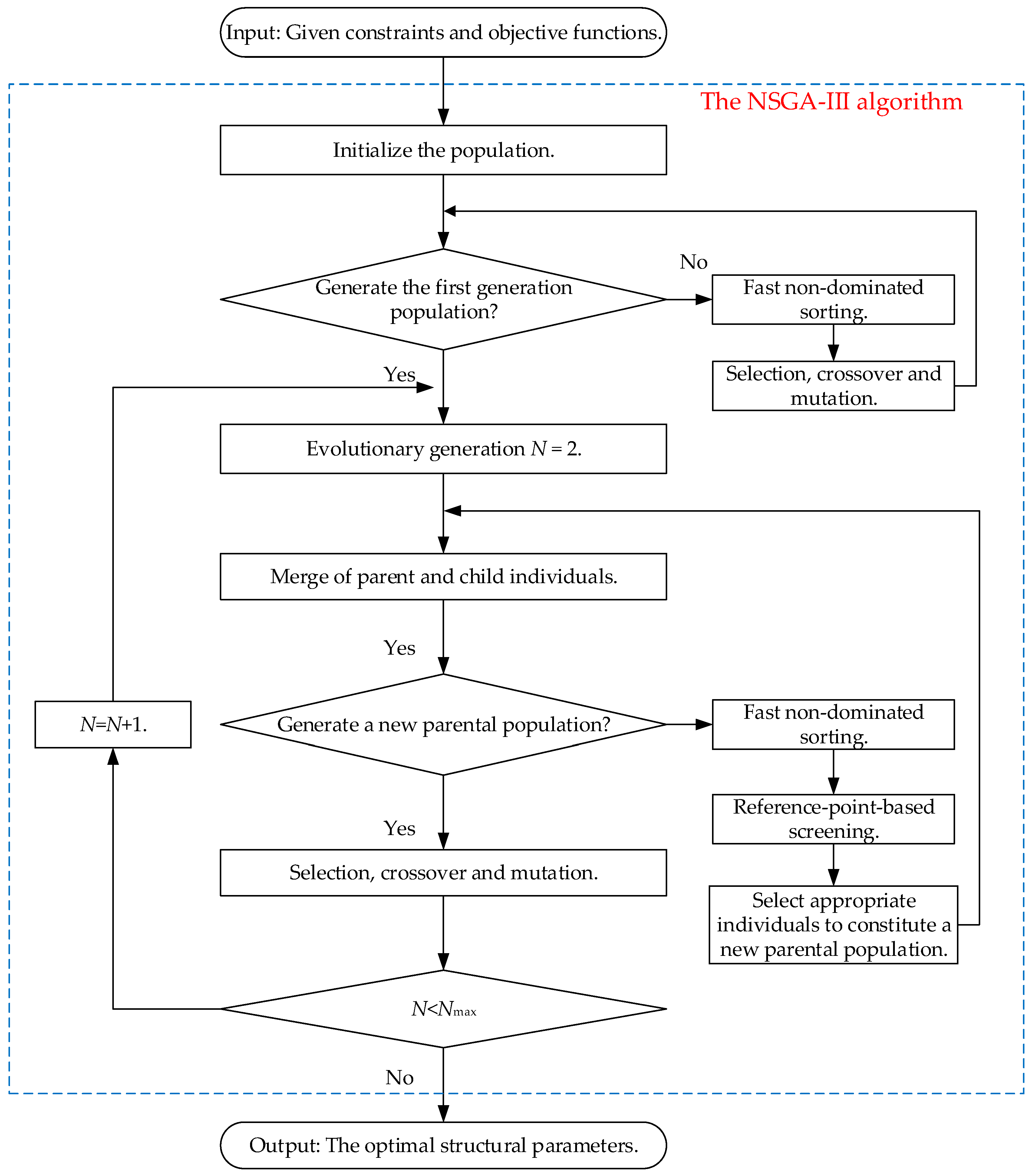
- Optimize the structural parameters of the Stewart platform using NSGA-III. In contrast to NSGA-II, NSGA-III demonstrates superior performance in addressing multiple conflicting objectives, characterized by uniform solution distribution across the Pareto front, accelerated convergence to optimal regions, and enhanced scalability in high-dimensional objective spaces.
3. Mathematical Modeling for Stewart Platform Optimization
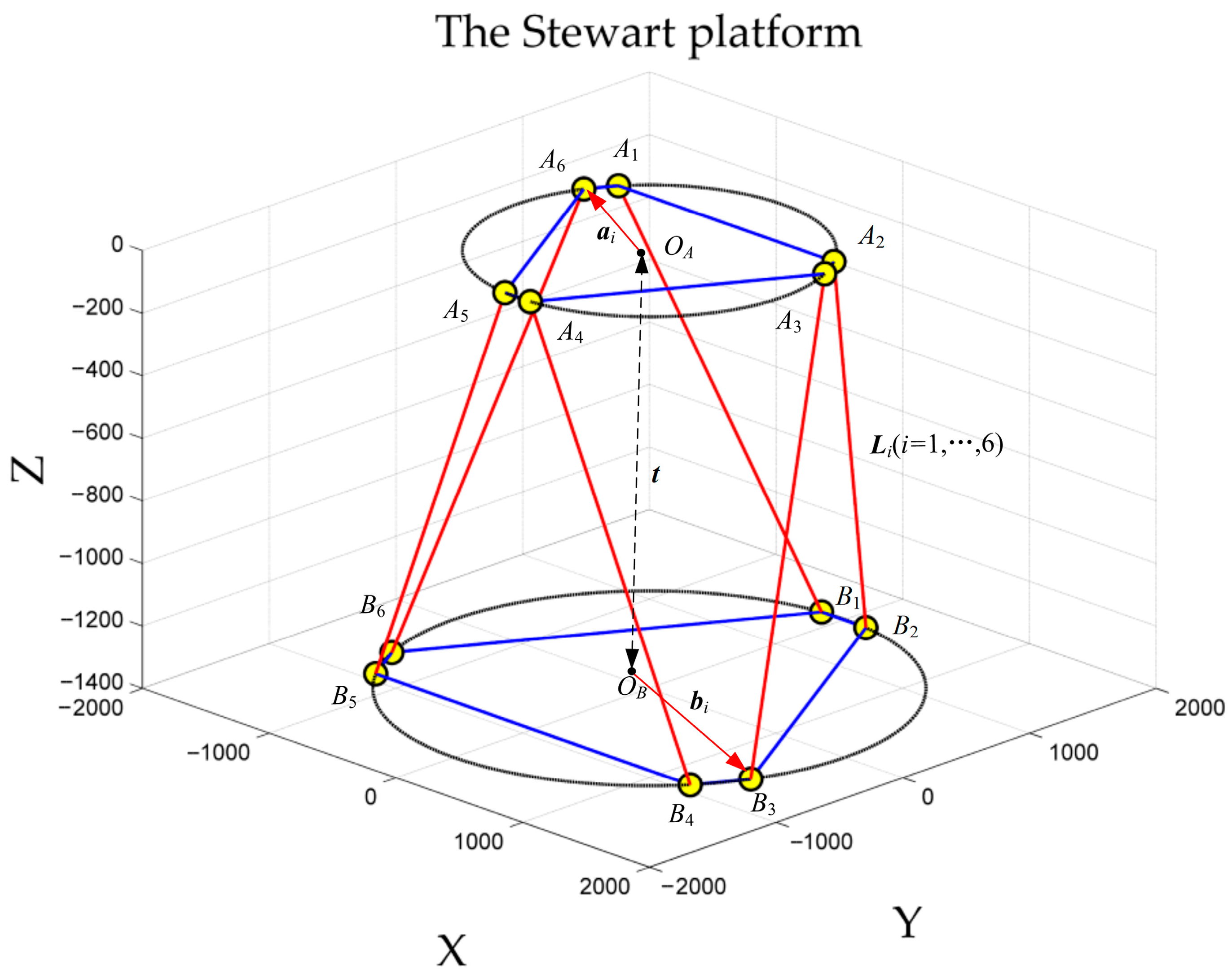
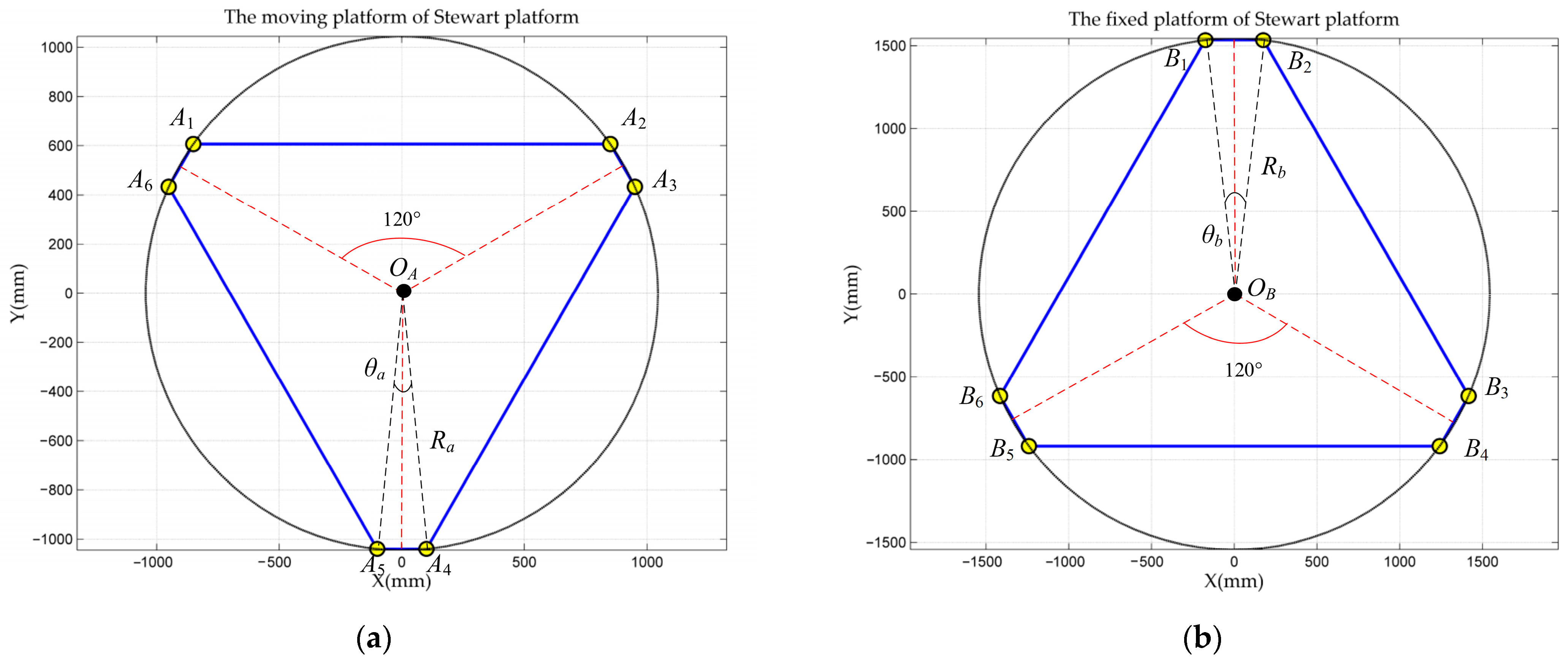
3.1. Structural and Kinematic Characteristics of the Stewart Platform
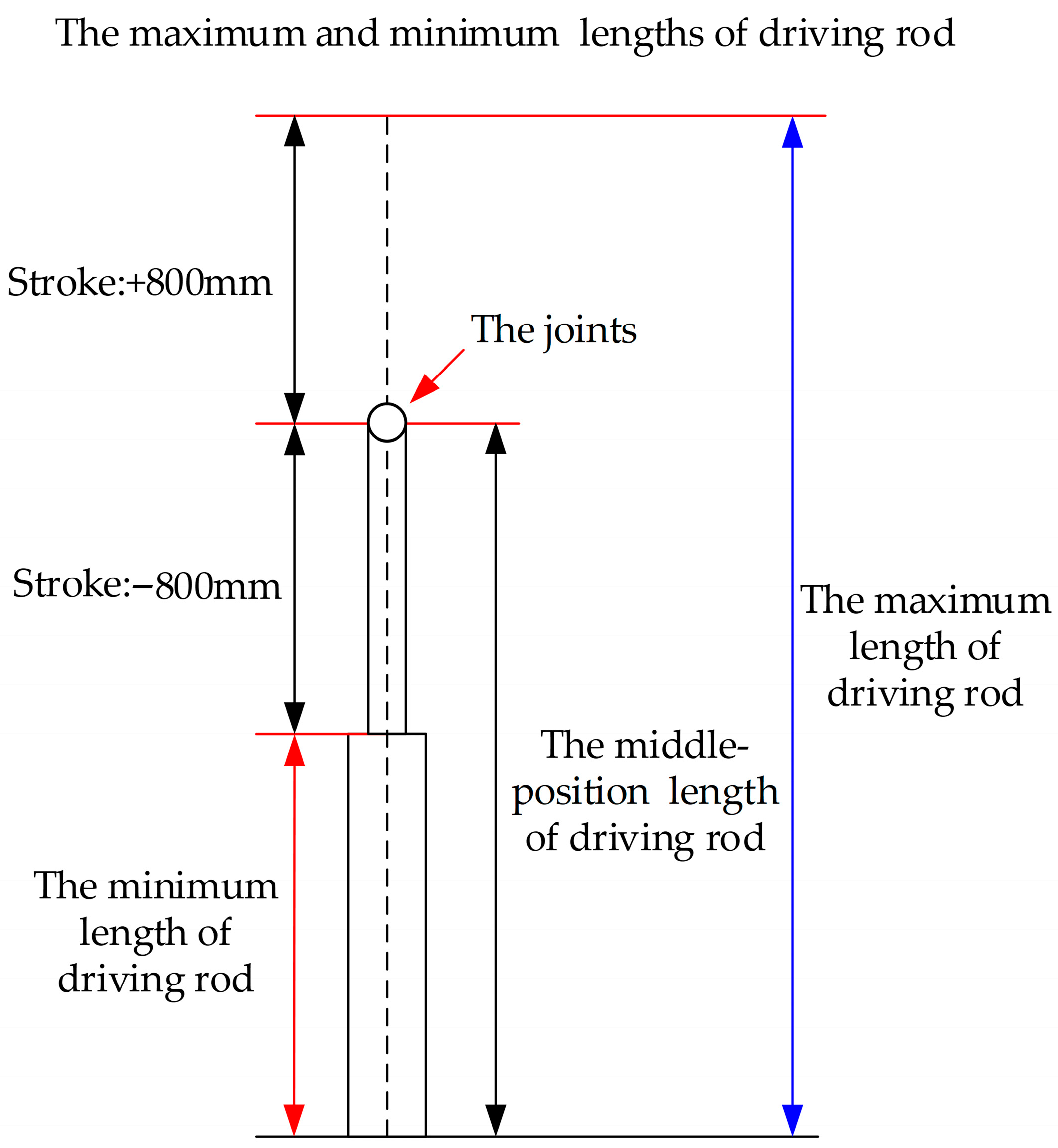
3.2. Optimization Constraint on Driving Rod Lengths Within Stroke Limits
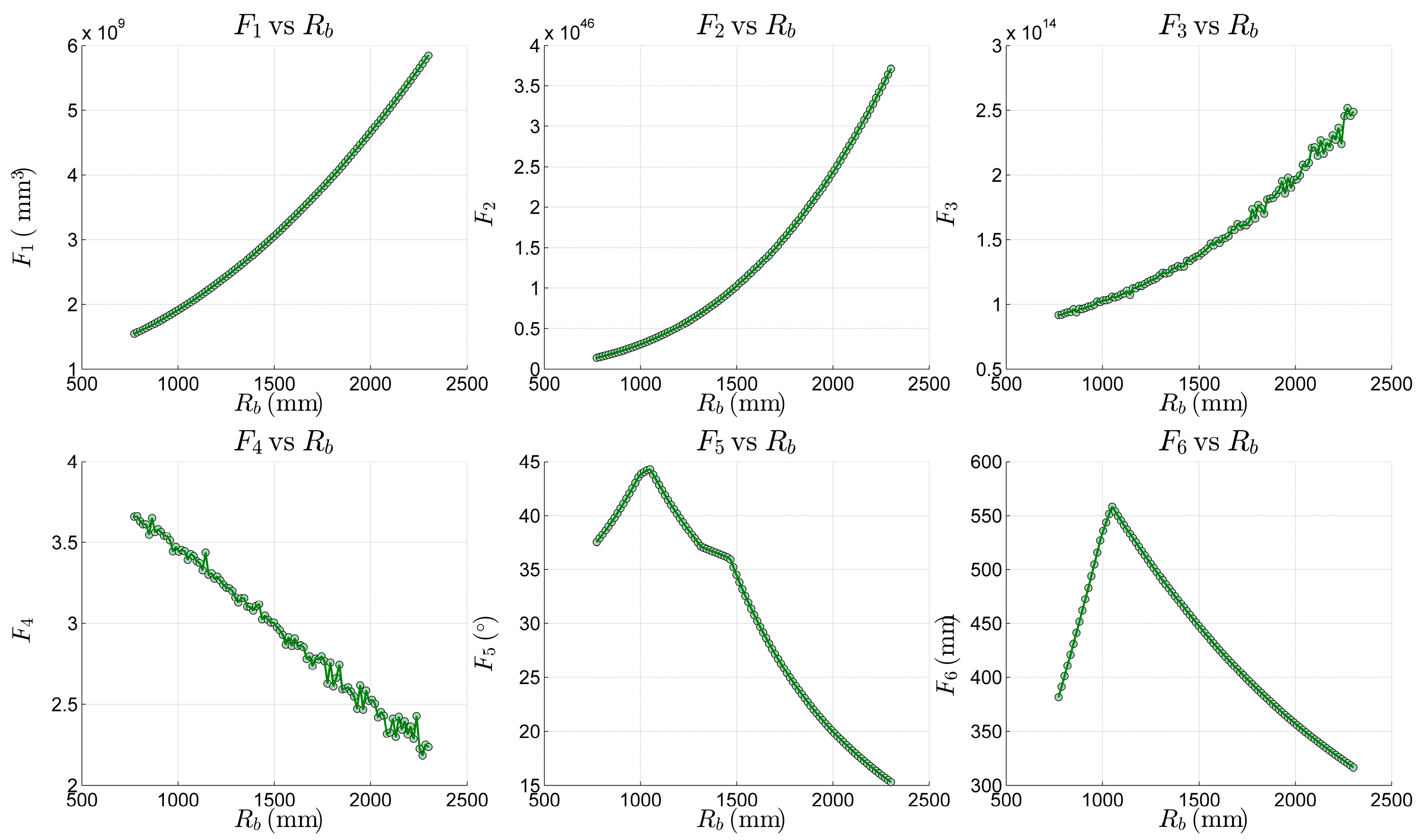
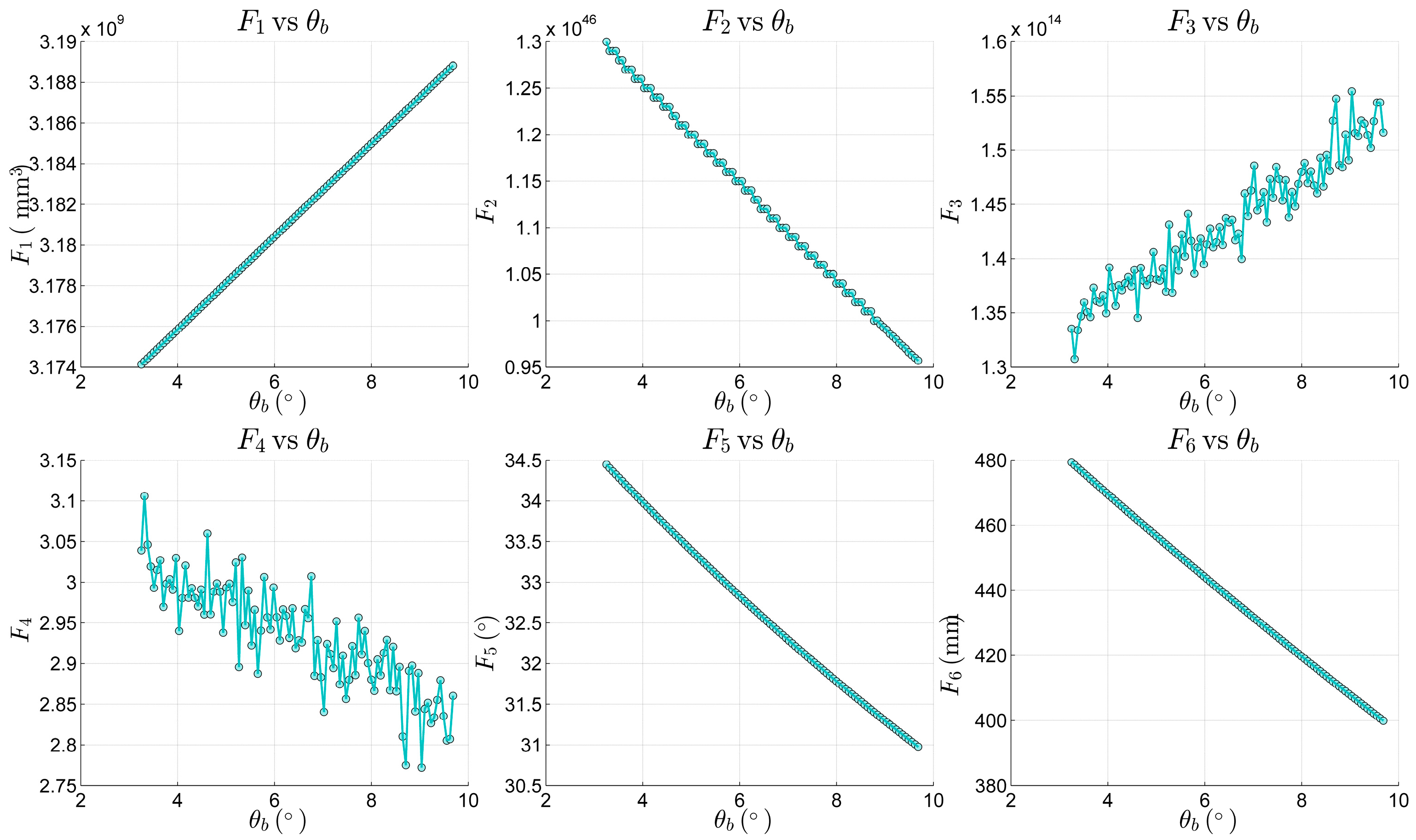
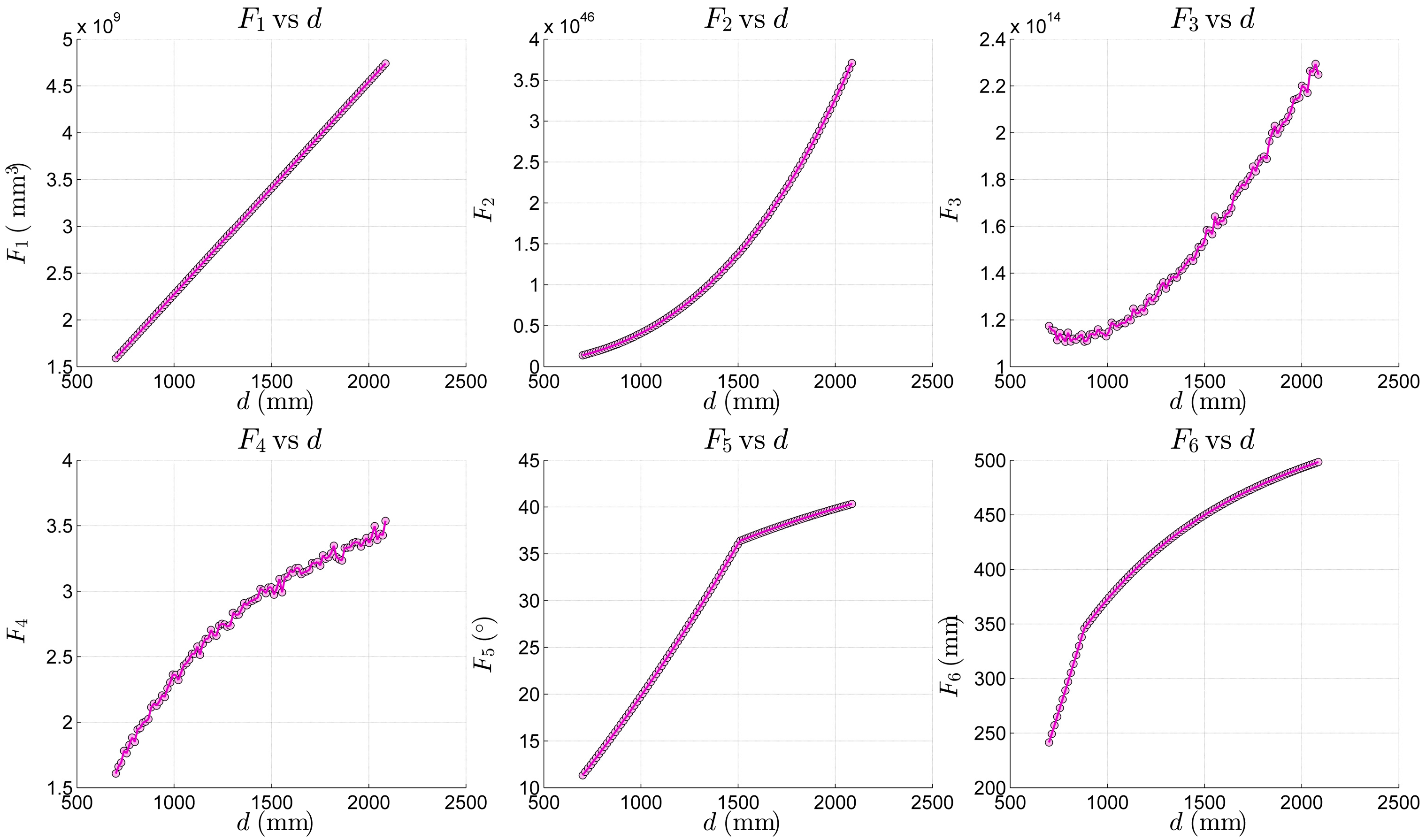
3.3. Performance Indicators for the Stewart Platform
- ●
- Minimize Structural Compactness ()
- ●
- Maximize Force Transmission Efficiency ()
- ●
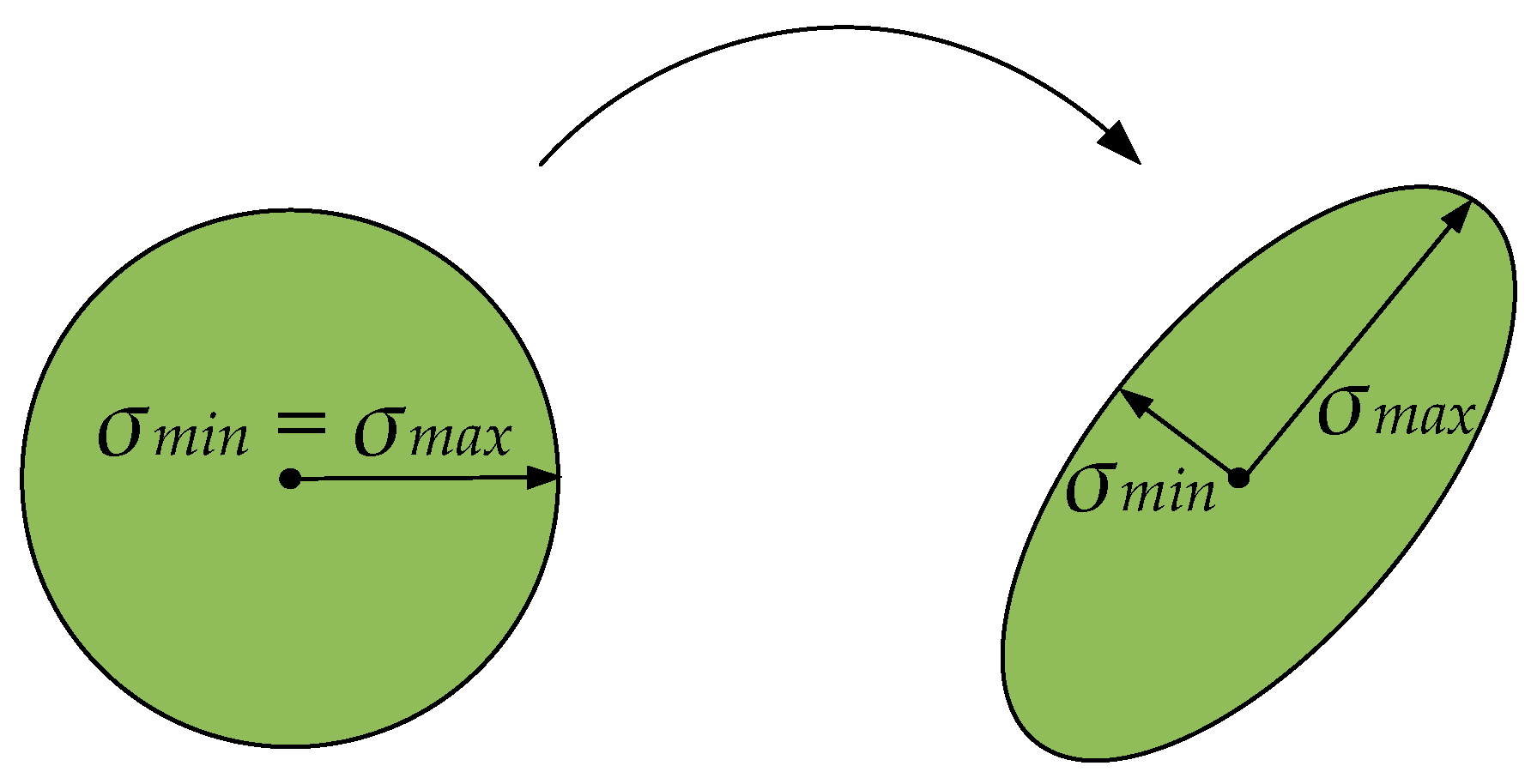
- Minimize Isotropy ()
- ●
- Maximize Singularity Resistance ()
- ●
- Maximize Orientational Workspace Capability ()
- ●
- Maximize Positional Workspace Capability ()
4. Optimizing the Structural Parameters of the Stewart Platform
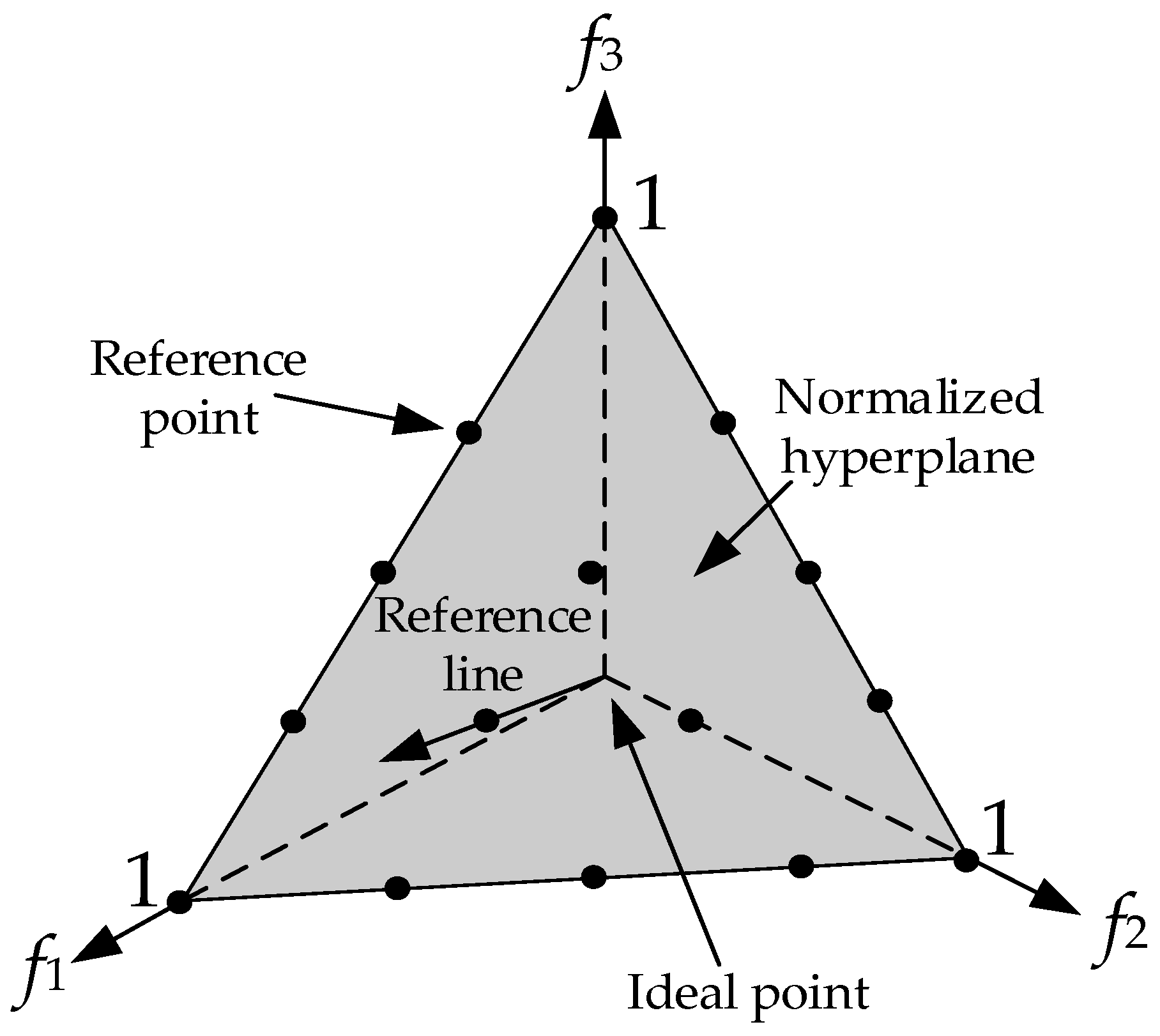
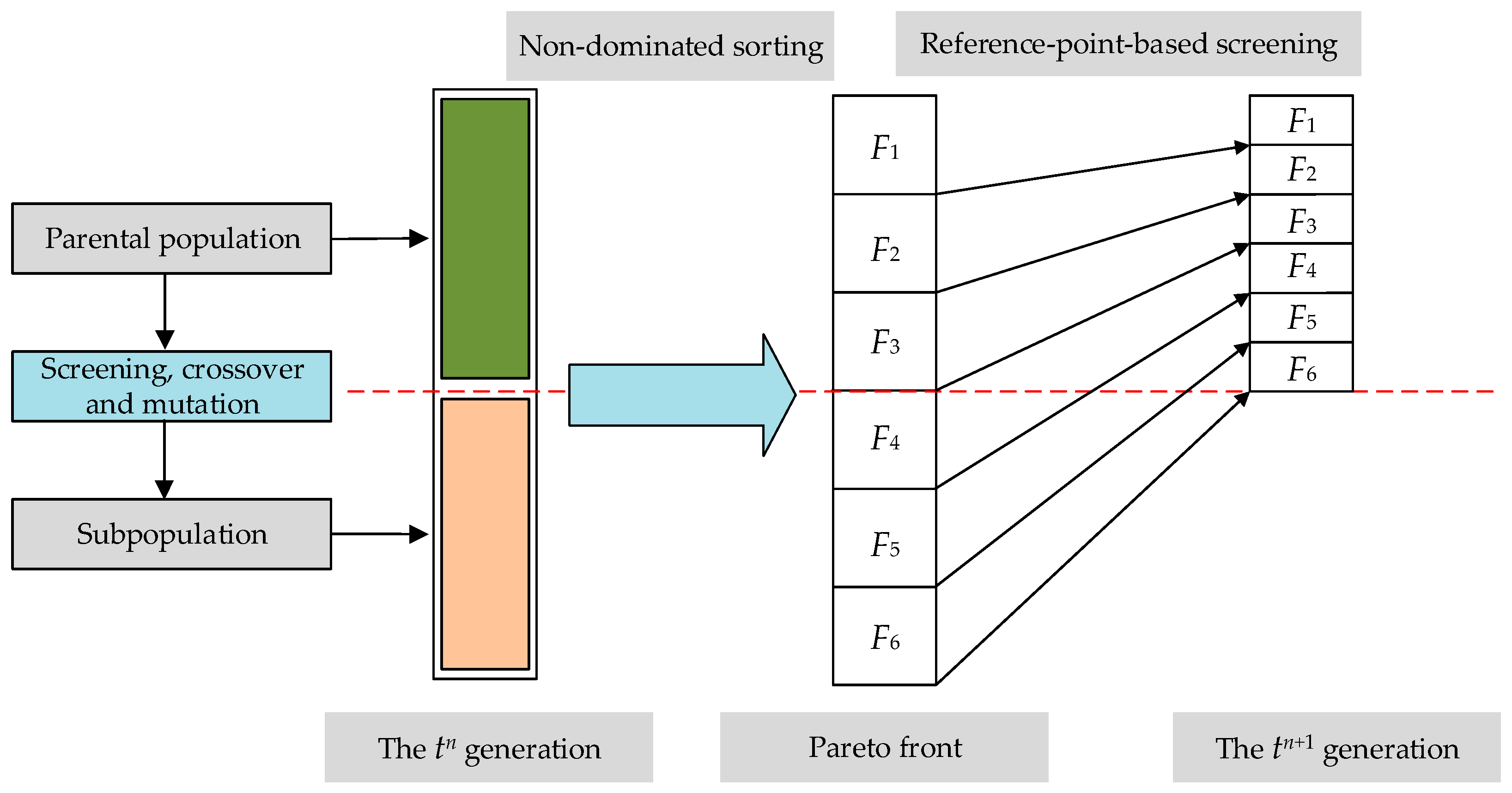
4.1. The Multi-Objective Optimization Algorithm NSGA-III
4.2. The Neural-Network-Fitting Algorithm KAN
5. Simulations and Experiments
5.1. Experimental Design and Condition
5.2. Experimental Results and Analysis
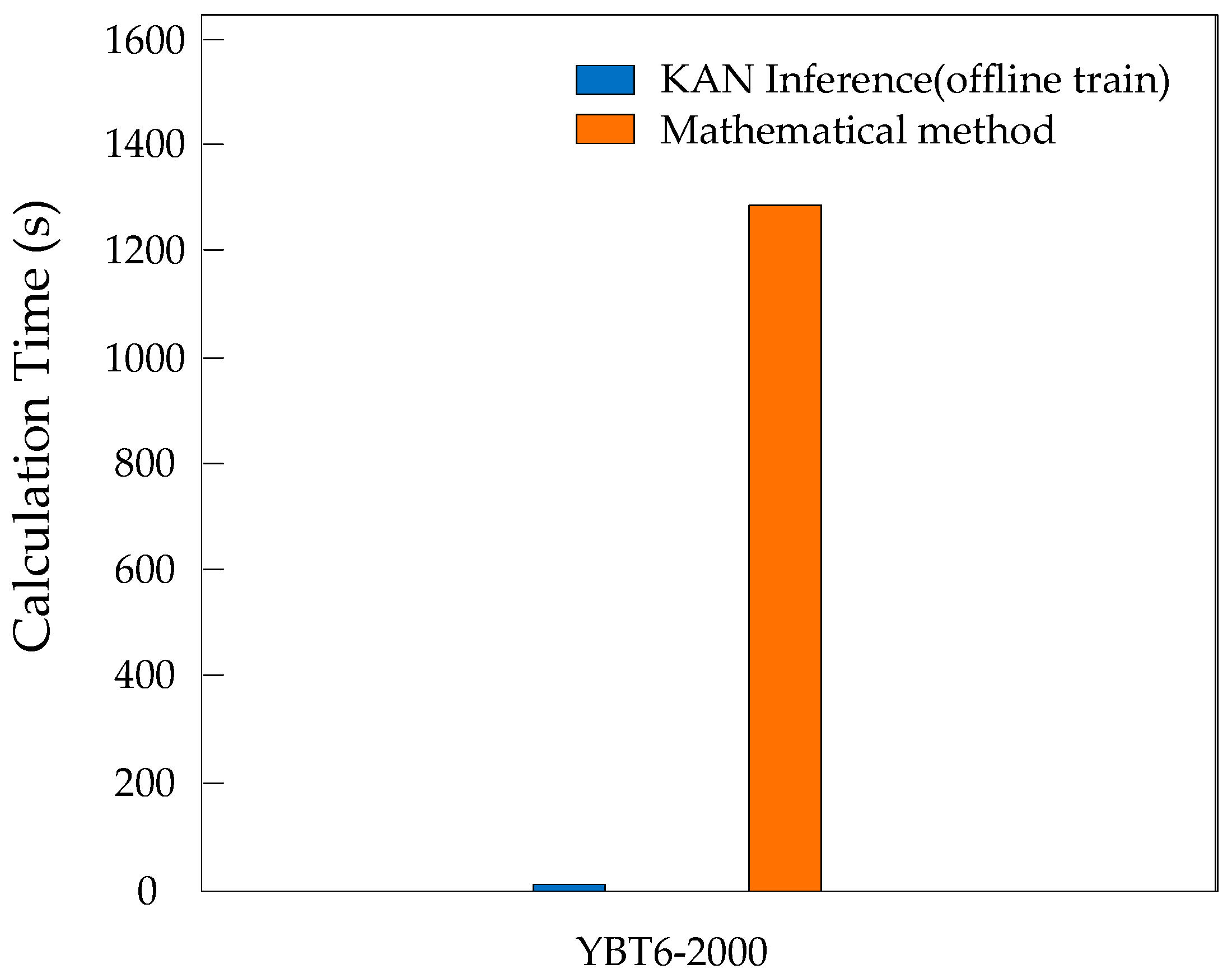
5.3. Comparison of Efficiency, Accuracy, and Multi-Objective Performance
6. Discussion
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Velasco, J.; Calvo, I.; Barambones, O.; Venegas, P.; Napole, C. Experimental Validation of a Sliding Mode Control for a Stewart Platform Used in Aerospace Inspection Applications. Mathematics 2020, 8, 2051. [Google Scholar] [CrossRef]
- Liu, Z.; Cai, C.; Yang, M.; Zhang, Y. Testing of a MEMS Dynamic Inclinometer Using the Stewart Platform. Sensors 2019, 19, 4233. [Google Scholar] [CrossRef]
- Li, D.; Wang, S.; Song, X.; Zheng, Z.; Tao, W.; Che, J. A BP-Neural-Network-Based PID Control Algorithm of Shipborne Stewart Platform for Wave Compensation. J. Mar. Sci. Eng. 2024, 12, 2160. [Google Scholar] [CrossRef]
- Cetin, K.; Tugal, H.; Petillot, Y.; Dunnigan, M.; Newbrook, L.; Erden, M.S. A Robotic Experimental Setup with a Stewart Platform to Emulate Underwater Vehicle Manipulator Systems. Sensors 2022, 22, 5827. [Google Scholar] [CrossRef]
- Gosselin, C.; Angeles, J. A global performance index for the kinematic optimization of robotic manipulators. J. Mech. Des. 1991, 113, 220–226. [Google Scholar] [CrossRef]
- Chiu, S. Kinematic characterization of manipulators: An approach to defining optimality. In Proceedings of the 1988 IEEE International Conference on Robotics and Automation, Philadelphia, PA, USA, 24–29 April 1988; pp. 828–833. [Google Scholar]
- Li, Y.; Yang, X.L.; Wu, H.T.; Chen, B. Optimal Design of a Six-Axis Vibration Isolator via Stewart Platform by Using Homogeneous Jacobian Matrix Formulation Based on Dual Quaternions. J. Mech. Sci. Technol. 2018, 32, 11–19. [Google Scholar] [CrossRef]
- Chablat, D.; Wenger, P.; Majou, F.; Merlet, J.-P. A novel method for the design of 2-dof parallel mechanisms for machining applications. Int. J. Robot. Res. 2007, 23, 615–624. [Google Scholar] [CrossRef]
- Salunkhe, D.H.; Michel, G.; Kumar, S.; Sanguineti, M.; Chablat, D. An Efficient Combined Local and Global Search Strategy for Optimization of Parallel Kinematic Mechanisms with Joint Limits and Collision Constraints. Mech. Mach. Theory 2022, 173, 104796. [Google Scholar] [CrossRef]
- Zhang, T.; Gong, X.; Zhang, L.; Yu, Y. A New Modeling Approach for Parameter Design of Stewart Vibration Isolation System Integrated into Complex Systems. Machines 2022, 10, 1005. [Google Scholar] [CrossRef]
- Tu, Y.Q.; Yang, G.L.; Cai, Q.Z.; Wang, L.F.; Zhou, X. Optimal design of SINS’s Stewart platform bumper for restoration accuracy based on genetic algorithm. Mech. Mach. Theory 2018, 124, 42–54. [Google Scholar] [CrossRef]
- Lee, C.J.; Chen, C.T. Reconfiguration for the Maximum Dynamic Wrench Capability of a Parallel Robot. Appl. Sci. 2016, 6, 80. [Google Scholar] [CrossRef]
- Liu, G. Optimal Kinematic Design of a 6-UCU Kind Gough-Stewart Platform with a Guaranteed Given Accuracy. Robotics 2008, 7, 30. [Google Scholar] [CrossRef]
- Zhu, M.; Huang, C.; Song, S.; Gong, D. Design of a Gough–Stewart Platform Based on Visual Servoing Controller. Sensors 2022, 22, 2523. [Google Scholar] [CrossRef] [PubMed]
- Germain, C.; Caro, S.; Briot, S.; Wenger, P. Optimal design of the IRSBot-2 based on an optimized test trajectory. In Proceedings of the 37th Mechanisms and Robotics Conference, Portland, OR, USA, 4–7 August 2013; American Society of Mechanical Engineers: Portland, OR, USA, 2013; pp. 1–11. [Google Scholar]
- Saadatzi, M.H.; Masouleh, M.T.; Taghirad, H.D.; Gosselin, C.; Teshnehlab, M. Multi-objective scale independent optimization of 3-RPR parallel mechanisms. In Proceedings of the 13th World Congress in Mechanism and Machine Science, Guanajuato, Mexico, 19–25 June 2011; pp. 1–11. [Google Scholar]
- Pu, H.; Cheng, H.; Wang, G.; Ma, J.; Zhao, J.; Bai, R.; Luo, J.; Yi, J. Dexterous Workspace Optimization for a Six Degree-of-Freedom Parallel Manipulator Based on Surrogate-Assisted Constrained Differential Evolution. Appl. Soft Comput. 2023, 139, 110228. [Google Scholar] [CrossRef]
- Gallant, M.; Boudreau, R. The Synthesis of Planar Parallel Manipulators with Prismatic Joints for an Optimal, Singularity-Free Workspace. J. Robot. Syst. 2002, 19, 13–24. [Google Scholar] [CrossRef]
- Li, J.; Li, W.; Zhang, X.; Huang, H. Design Optimization of a Hexapod Vibration Isolation System for Electro-Optical Payload. Chin. J. Aeronaut. 2024, 37, 330–342. [Google Scholar] [CrossRef]
- Sonmez, M. Artificial Bee Colony algorithm for optimization of truss structures. Appl. Soft Comput. 2011, 11, 2406–2418. [Google Scholar] [CrossRef]
- Saputra, V.B.; Ong, S.K.; Nee, A.Y.C. A PSO Algorithm for Mapping the Workspace Boundary of Parallel Manipulators. In Proceedings of the 2010 IEEE International Conference on Robotics and Automation, Anchorage, AK, USA, 3–8 May 2010; pp. 4691–4696. [Google Scholar]
- Wang, H.; Zhang, L.; Chen, G.; Huang, S. Parameter Optimization of Heavy-Load Parallel Manipulator by Introducing Stiffness Distribution Evaluation Index. Mech. Mach. Theory 2017, 108, 244–259. [Google Scholar] [CrossRef]
- Duyun, T.; Duyun, I.; Kabalyants, P.; Rybak, L. Optimization of a 6-DOF Platform for Simulators Based on an Analysis of Structural and Force Parameters. Machines 2023, 11, 814. [Google Scholar] [CrossRef]
- Pisarenko, A.; Malyshev, D.; Rybak, L.; Cherkasov, V.; Skitova, V. Application of Evolutionary PSO Algorithms to the Problem of Optimization of 6-6 UPU Mobility Platform Geometric Parameters. Procedia Comput. Sci. 2022, 213, 643–650. [Google Scholar] [CrossRef]
- Gill, P.E.; Murray, W.; Wright, M.H. Numerical Linear Algebra and Optimization; Addison-Wesley: Redwood City, CA, USA, 1991; Volume 1. [Google Scholar]
- Spellucci, P. A new technique for inconsistent QP problems in the SQP method. Math. Methods Oper. Res. 1998, 47, 355–400. [Google Scholar] [CrossRef]
- Byrd, R.H.; Hribar, M.E.; Nocedal, J. An interior point algorithm for large-scale nonlinear programming. SIAM J. Optim. 1999, 9, 877–900. [Google Scholar] [CrossRef]
- Hassan, A.; Abomoharam, M. Modeling and Design Optimization of a Robot Gripper Mechanism. Robot. Comput. Integr. Manuf. 2017, 46, 94–103. [Google Scholar] [CrossRef]
- Kucuk, S. A Dexterity Comparison for 3-DOF Planar Parallel Manipulators with Two Kinematic Chains Using Genetic Algorithms. Mechatronics 2009, 19, 868–877. [Google Scholar] [CrossRef]
- Gonzalez, S.; Guacheta, J.C.; Nunez, D.A.; Mauledoux, M.; Aviles, O.F. Multi-objective optimization of dynamic controllers on parallel platforms. J. Eng. Res. 2023, 11, 100025. [Google Scholar] [CrossRef]
- Muralidharan, V.; Bose, A.; Chatra, K.; Bandyopadhyay, S. Methods for Dimensional Design of Parallel Manipulators for Optimal Dynamic Performance over a Given Safe Working Zone. Mech. Mach. Theory 2020, 147, 103721. [Google Scholar] [CrossRef]
- Ganesh, S.; Koteswara Rao, A.; Sarath kumar, B. Design Optimization of a 3-DOF Star Triangle Manipulator for Machining Applications. Mater. Today Proc. 2020, 22, 1845–1852. [Google Scholar] [CrossRef]
- Leal-Naranjo, J.-A.; Soria-Alcaraz, J.-A.; Torres-San Miguel, C.-R.; Paredes-Rojas, J.-C.; Espinal, A.; Rostro-González, H. Comparison of Metaheuristic Optimization Algorithms for Dimensional Synthesis of a Spherical Parallel Manipulator. Mech. Mach. Theory 2019, 140, 586–600. [Google Scholar] [CrossRef]
- Ríos, A.; Hernández, E.E.; Valdez, S.I. A Two-Stage Mono- and Multi-Objective Method for the Optimization of General UPS Parallel Manipulators. Mathematics 2021, 9, 543. [Google Scholar] [CrossRef]
- Liu, Z.; Wang, Y.; Vaidya, S.; Ruehle, F.; Halverson, J.; Soljacic, M.; Hou, T.Y.; Tegmark, M. KAN: Kolmogorov–Arnold Networks. In Proceedings of the International Conference on Learning Representations (ICLR), Singapore, 24–28 April 2025. [Google Scholar]
- Lao, R. A Brief Analysis of the Hooke’s Joint. Zenodo 2018. [Google Scholar] [CrossRef]
- Tao, J.; Zhou, H.; Fan, W. Efficient and High-Precision Method of Calculating Maximum Singularity-Free Space in Stewart Platform Based on K-Means Clustering and CNN-LSTM-Attention Model. Actuators 2025, 14, 74. [Google Scholar] [CrossRef]
- Yang, Z.G.; Shao, M.L.; Shin, D.I. Kinematic Optimization of Parallel Manipulators with a Desired Workspace. Appl. Mech. Mater. 2015, 752–753, 973–979. [Google Scholar] [CrossRef]
- Yang, X.L.; Wu, H.T.; Li, Y.; Kang, S.Z.; Chen, B. Computationally Efficient Inverse Dynamics of a Class of Six-DOF Parallel Robots: Dual Quaternion Approach. J. Intell. Robot. Syst. 2019, 94, 101–113. [Google Scholar] [CrossRef]
- Tsai, L.W. Robot Analysis: The Mechanics of Serial and Parallel Manipulators; John Wiley & Sons: New York, NY, USA, 1999. [Google Scholar]
- Yoshikawa, T. Manipulability of Robotic Mechanisms. Int. J. Robot. Res. 1985, 4, 3–9. [Google Scholar] [CrossRef]
- Liang, C.; Li, W.; Huang, H.; Zheng, Y. Design and Experiment of a Multi-DOF Shaker Based on Rotationally Symmetric Stewart Platforms with an Insensitive Condition Number. Actuators 2023, 12, 368. [Google Scholar] [CrossRef]
- Tao, J.; Zhou, H.; Fan, W. A Hybrid Strategy for Forward Kinematics of the Stewart Platform Based on Dual Quaternion Neural Network and ARMA Time Series Prediction. Actuators 2025, 14, 159. [Google Scholar] [CrossRef]
- Deb, K.; Jain, H. An Evolutionary Many-Objective Optimization Algorithm Using Reference-Point-Based Nondominated Sorting Approach, Part I: Solving Problems With Box Constraints. IEEE Trans. Evol. Comput. 2014, 18, 577–601. [Google Scholar] [CrossRef]
- Zhang, Y.; Tang, H.; Wei, L.; Zheng, G.; Yang, G. Kolmogorov–Arnold Networks for Reduced-Order Modeling in Unsteady Aerodynamics and Aeroelasticity. Appl. Sci. 2025, 15, 5820. [Google Scholar] [CrossRef]




| Chain 1 | Chain 2 | Chain 3 | Chain 4 | Chain 5 | Chain 6 | |
|---|---|---|---|---|---|---|
| −850.585 | 850.585 | 950.725 | 100.139 | −100.139 | −950.725 | |
| 606.717 | 606.717 | 433.270 | −1039.987 | −1039.987 | 433.270 | |
| 0 | 0 | 0 | 0 | 0 | 0 | |
| −174.829 | 174.829 | 1416.295 | 1241.465 | −1241.465 | −1416.295 | |
| 1534.458 | 1534.458 | −615.822 | −918.636 | −918.636 | −615.822 | |
| −1399.760 | −1399.760 | −1399.760 | −1399.760 | −1399.760 | −1399.760 |
| KAN | MLP | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| MAE | MAPE | MSE | RMSE | MAE | MAPE | MSE | RMSE | |||
| /° | 0.9965 | 0.0131 | 0.6580 | 0.0004 | 0.0192 | 0.8554 | 0.0923 | 5.2134 | 0.0154 | 0.1241 |
| /° | 0.9957 | 0.0148 | 0.2543 | 0.0005 | 0.0228 | 0.7681 | 0.1298 | 2.2848 | 0.0283 | 0.1683 |
| /° | 0.9993 | 0.0097 | 0.0662 | 0.0003 | 0.0159 | 0.9311 | 0.0999 | 1.1111 | 0.0257 | 0.1603 |
| /mm | 0.9996 | 0.0072 | 0.0704 | 0.0001 | 0.0094 | 0.9688 | 0.0664 | 0.7322 | 0.0069 | 0.0830 |
| /mm | 0.9993 | 0.0081 | 0.0682 | 0.0001 | 0.0115 | 0.9634 | 0.0665 | 0.5770 | 0.0072 | 0.0851 |
| /mm | 0.9991 | 0.0087 | 0.1361 | 0.0001 | 0.0114 | 0.9035 | 0.0906 | 1.2665 | 0.0137 | 0.1169 |
| KAN | MLP | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| MAE | MAPE | MSE | RMSE | MAE | MAPE | MSE | RMSE | |||
| /° | 0.9961 | 0.0133 | 0.5686 | 0.0004 | 0.0197 | 0.8551 | 0.0892 | 3.0675 | 0.0143 | 0.1197 |
| /° | 0.9952 | 0.0156 | 1.1873 | 0.0006 | 0.0237 | 0.7543 | 0.1307 | 31.4181 | 0.0289 | 0.1699 |
| /° | 0.9993 | 0.0097 | 0.1417 | 0.0002 | 0.0156 | 0.9339 | 0.0950 | 1.5708 | 0.0235 | 0.1533 |
| /mm | 0.9995 | 0.0074 | 0.0916 | 0.0001 | 0.0098 | 0.9685 | 0.0644 | 0.5164 | 0.0064 | 0.0802 |
| /mm | 0.9993 | 0.0081 | 0.0800 | 0.0001 | 0.0114 | 0.9620 | 0.0653 | 0.6213 | 0.0069 | 0.0829 |
| /mm | 0.9990 | 0.0087 | 0.1227 | 0.0001 | 0.0115 | 0.8986 | 0.0915 | 1.1824 | 0.0136 | 0.1168 |
| Default Parameters | NSGA-II | NSGA-III | |
|---|---|---|---|
| (mm) | 1044.797 | 1195.286 | 966.856 |
| (mm) | 1544.386 | 1325.850 | 956.069 |
| (°) | 11 | 7.348 | 6.926 |
| (°) | 13 | 7.168 | 10.088 |
| (mm) | 1399.760 | 1724.218 | 1160.285 |
| Default Parameters | NSGA-II | NSGA-III | |
|---|---|---|---|
| () | 3.182 × 109 | 3.582 × 109 | 1.400 × 109 |
| 1.121 × 1046 | 2.439 × 1046 | 1.402 × 1045 | |
| 1.432 × 1014 | 1.631 × 1014 | 6.990 × 1013 | |
| 2.931 | 3.407 | 3.482 | |
| (°) | 32.557 | 44.756 | 47.537 |
| 437.901 | 650.974 | 501.412 |
| NSGA-II | NSGA-III | |
|---|---|---|
| SP | 0.040 | 0.018 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tao, J.; Xu, Y.; Chen, Y.; Cheng, P.; Zhang, H.; Wang, J.; Zhou, H. Multi-Objective Structural Parameter Optimization for Stewart Platform via NSGA-III and Kolmogorov–Arnold Network. Machines 2025, 13, 887. https://doi.org/10.3390/machines13100887
Tao J, Xu Y, Chen Y, Cheng P, Zhang H, Wang J, Zhou H. Multi-Objective Structural Parameter Optimization for Stewart Platform via NSGA-III and Kolmogorov–Arnold Network. Machines. 2025; 13(10):887. https://doi.org/10.3390/machines13100887
Chicago/Turabian StyleTao, Jie, Yafei Xu, Yongjun Chen, Pin Cheng, Haikun Zhang, Jianping Wang, and Huicheng Zhou. 2025. "Multi-Objective Structural Parameter Optimization for Stewart Platform via NSGA-III and Kolmogorov–Arnold Network" Machines 13, no. 10: 887. https://doi.org/10.3390/machines13100887
APA StyleTao, J., Xu, Y., Chen, Y., Cheng, P., Zhang, H., Wang, J., & Zhou, H. (2025). Multi-Objective Structural Parameter Optimization for Stewart Platform via NSGA-III and Kolmogorov–Arnold Network. Machines, 13(10), 887. https://doi.org/10.3390/machines13100887





