Deep Feature Decoupling Network for Ball Mill Load Signals

Abstract

Accurately identifying the load status of a ball mill is critical for optimizing grinding efficiency and ensuring operational stability. However, the one-dimensional vibration signals collected from ball mills exhibit strong non-stationarity and a high degree of entanglement between multi-scale local transient features and long-range temporal evolution patterns. To address this, rather than relying on a purely black-box approach, this paper introduces a novel Deep Multi-scale Spatial–Temporal Feature Decoupling Network (DMSTFD-Net) guided by a clear feature decoupling philosophy to enhance model interpretability. The core of DMSTFD-Net lies in its hierarchical collaborative feature refinement mechanism. It first utilizes a one-dimensional residual network (ResNet) to adaptively capture and preliminarily decouple multi-scale spatial characteristics from the raw signal. Subsequently, the extracted high-level feature sequences are fed into a bidirectional gated recurrent unit (Bi-GRU) to decouple high-order temporal dynamic patterns. Experiments on a multi-condition dataset demonstrate that the proposed network achieves a state-of-the-art accuracy of 97.65%. Furthermore, dedicated cross-condition experiments and t-SNE visualizations validate the framework’s effectiveness. The results confirm that DMSTFD-Net provides a powerful, robust, and more interpretable solution for ball mill load identification.

1. Introduction

The ball mill is a key piece of equipment in the ore dressing process. It enhances the recovery rate and yield of useful minerals by grinding materials. However, the grinding operation typically consumes a large amount of energy, and an improper load can lead to a surge in power consumption, accelerated liner wear, and severely compromised product quality due to over-grinding or under-grinding [1,2,3]. Therefore, developing a robust and accurate method for load identification is of great significance for improving the energy efficiency of grinding.

Traditionally, research on ball mill load identification has followed a paradigm based on signal processing and shallow machine learning. For instance, Feng et al. [4] used principal component analysis to extract power spectrum features as external characteristic information for mill load prediction and constructed a PCA-PSO-SVM model by optimizing SVM parameters with PSO. Pu et al. [5] denoised the collected grinding sound signals during mill operation, estimated the power spectrum using the Welch method, and extracted fundamental features from segments of the power spectrum via principal component analysis to be used as input for a load prediction model. While these machine learning-based methods have achieved decent extraction results, they possess inherent limitations: they are highly dependent on expert experience and a priori domain knowledge for feature design, lacking adaptability; the extracted features are often shallow and strongly coupled, failing to effectively disentangle the complex, overlapping information streams that reflect different physical mechanisms (e.g., material load variations versus grinding media dynamics). This fundamentally limits their generalization ability under different operating conditions [6]. Moreover, this traditional paradigm, which relies on manual feature engineering, can be subjective and time-consuming. The performance of such hybrid models is highly dependent on the expert’s choice of signal processing tools, such as selecting an appropriate wavelet basis or frequency bands for analysis. This process may lead to suboptimal feature representations that are not robust to changes in operational conditions. To overcome these limitations, our work adopts an end-to-end deep learning approach that learns feature representations directly from the raw signal data. This allows the model to adaptively capture the most discriminative information without manual intervention, thereby avoiding potential human-induced biases and enhancing its generalization capability.

With the rapid development of deep learning, neural networks capable of automatically learning hierarchical feature representations from raw data have become a powerful alternative, eliminating the need for laborious manual feature engineering [7]. Several studies have successfully applied deep learning in this domain. For example, Xu et al. [8] converted time-series vibration signals into two-dimensional images and fed them into a VGG19 network, and Kong et al. [9] used a ResNet-based network to identify mill load from audio signals. These methods have demonstrated the potential of deep learning.

However, many existing deep learning models still treat the feature extraction process as a “black box,” limiting interpretability. To address prevalent challenges such as handling non-stationary signals or improving generalization, the field has seen the emergence of highly sophisticated paradigms. In reference [10], the Time–Frequency Self-Similarity Enhancement Network (TFSSEN) was developed to enhance faint fault characteristics in wind turbine signals by modeling feature correlations within multi-scale time–frequency representations. In reference [11], to improve robustness to domain shift, the MixStyle network employs complex strategies like Batch Spectral Penalization to augment domain diversity during training. While these advanced methods have achieved breakthrough performance, their ever-increasing architectural complexity and reliance on specialized modules can obscure the underlying physical meaning of the learned features.

A key challenge that remains largely unresolved, and which this paper focuses on, is the intrinsic complexity of the one-dimensional vibration signal itself. The raw vibration signal from a ball mill is a complex tapestry woven from two distinct types of information: (1) multi-scale, short-term local transient features (the “spatial” dimension of the time-series, such as impacts and frequency shifts); and (2) long-range, slowly evolving temporal dynamic patterns (the “temporal” dimension, such as the gradual transition of load states). In most existing deep learning models, these two information streams are processed in a coupled manner, leading to a high degree of feature entanglement. This entanglement hinders the model from learning truly discriminative and robust representations, especially when faced with domain shift caused by different operating conditions [12].

To address this specific challenge, and guided by a clear “hierarchical decoupling” philosophy, this paper proposes a novel Deep Multi-scale Spatial–Temporal Feature Decoupling Network (DMSTFD-Net). In contrast to black-box approaches or those requiring complex signal pre-processing, our framework is designed with physical interpretability at its core. The network employs a hierarchical architecture to progressively decouple these entangled features. It first utilizes a one-dimensional ResNet to robustly represent and decouple local “spatial” features, and then employs a Bi-GRU to model and separate long-range “temporal” patterns. The main contributions of this paper are summarized as follows:

(1)

The primary contribution of this study is to systematically identify and define the problem of “spatial–temporal feature entanglement” in one-dimensional industrial vibration signals. We argue that this high degree of coupling at the signal level, arising from different physical mechanisms (such as short-term impacts and long-range load evolution), is a fundamental obstacle to building robust and highly generalizable recognition models.

(2)

Based on this problem modeling, we propose the DMSTFD-Net framework, an architecture designed with a clear physical decoupling interpretation. Unlike conventional end-to-end models, our framework assigns clear decoupling roles to its core components: the one-dimensional residual network (ResNet) is responsible for decoupling “spatial” transient features, while the bidirectional gated recurrent unit (Bi-GRU) handles the decoupling of “temporal” dynamic patterns. This design significantly enhances the interpretability of the model’s behavior.

(3)

Through comprehensive comparative experiments and t-SNE visualization, we provide strong validation for the effectiveness of our proposed decoupling approach. The experimental results not only demonstrate the model’s excellent performance but also intuitively showcase the process of features transitioning from a highly entangled state to clearly separated clusters layer by layer, thereby confirming the correctness of our framework’s design.

2. Related Work

2.1. Residual Network (ResNet) for Local Feature Representation

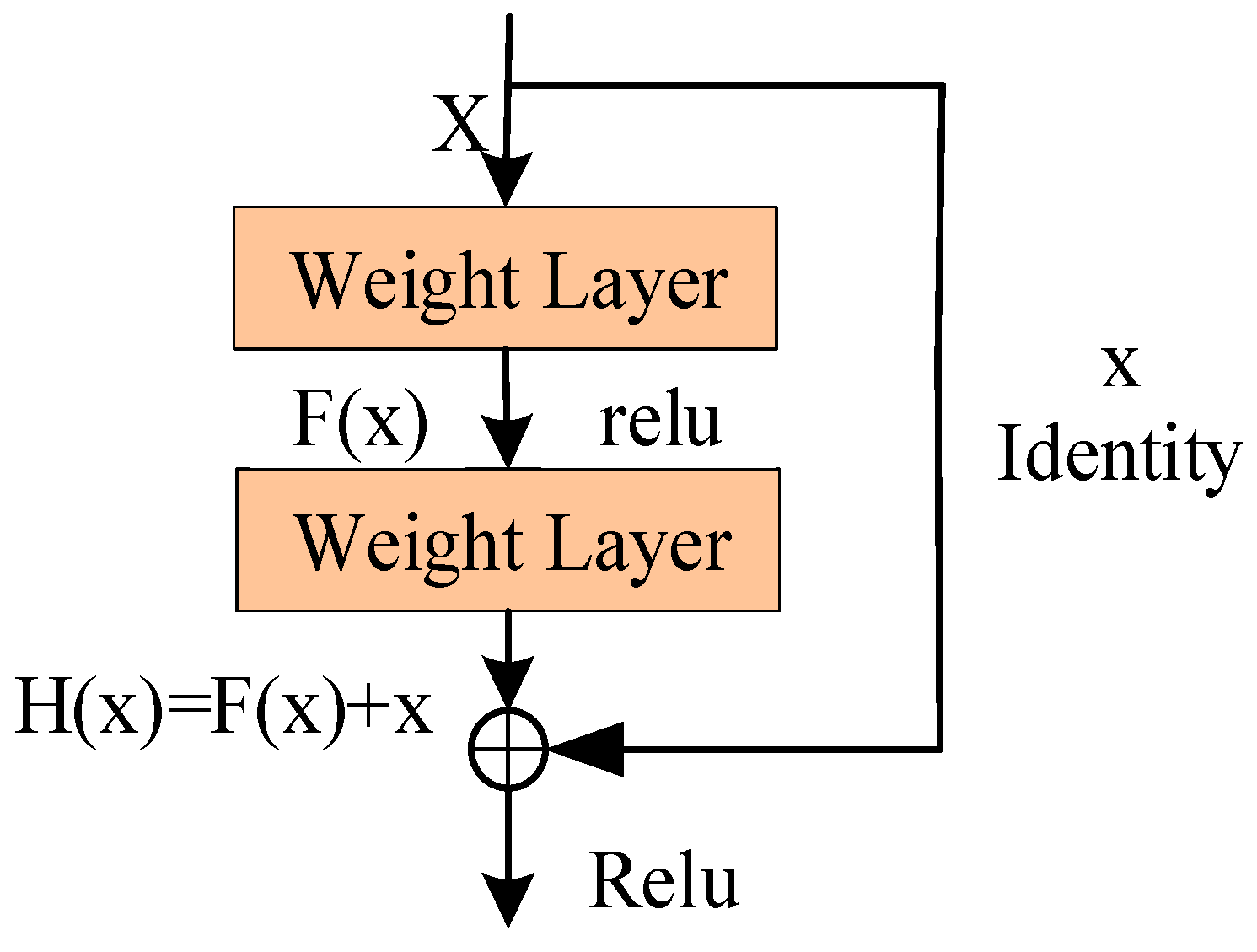
As deep neural networks become deeper, they often encounter a significant challenge known as performance degradation, where adding more layers leads to higher training error, a problem distinct from overfitting. To address this issue, He et al. introduced the Residual Network (ResNet), an innovative architecture that facilitates the training of extremely deep networks [13].

The core idea of ResNet is to learn residual functions with reference to the layer inputs, instead of learning unreferenced functions [14]. As shown in Figure 1, a residual block can be formally defined as:

$$H\left(x\right)=F\left(x\right) + x$$

(1)

where $x$ is the input to the block, and $F\left(x\right)$ is the residual mapping to be learned by a few stacked layers. The original mapping is recast into $F\left(x\right) + x$. The “shortcut connection” $x$ performs identity mapping, and its output is added to the output of the stacked layers. This structure allows gradients to flow more easily through the network during backpropagation, effectively mitigating the vanishing gradient problem. This mechanism enables the network to easily learn an identity mapping by driving the weights of $F\left(x\right)$ towards zero, ensuring that adding more layers does not degrade performance. Due to its powerful ability to learn deep and robust feature representations, ResNet has become a foundational architecture for various feature extraction tasks.

2.2. Bidirectional Gated Recurrent Unit (Bi-GRU) for Temporal Dependency Modeling

Modeling sequential data, such as industrial time-series signals, requires capturing temporal dependencies. While traditional Recurrent Neural Networks (RNNs) are designed for this purpose, they struggle to learn long-range dependencies due to the vanishing and exploding gradient problems. The Gated Recurrent Unit (GRU) is an advanced RNN architecture designed to overcome this limitation [15].

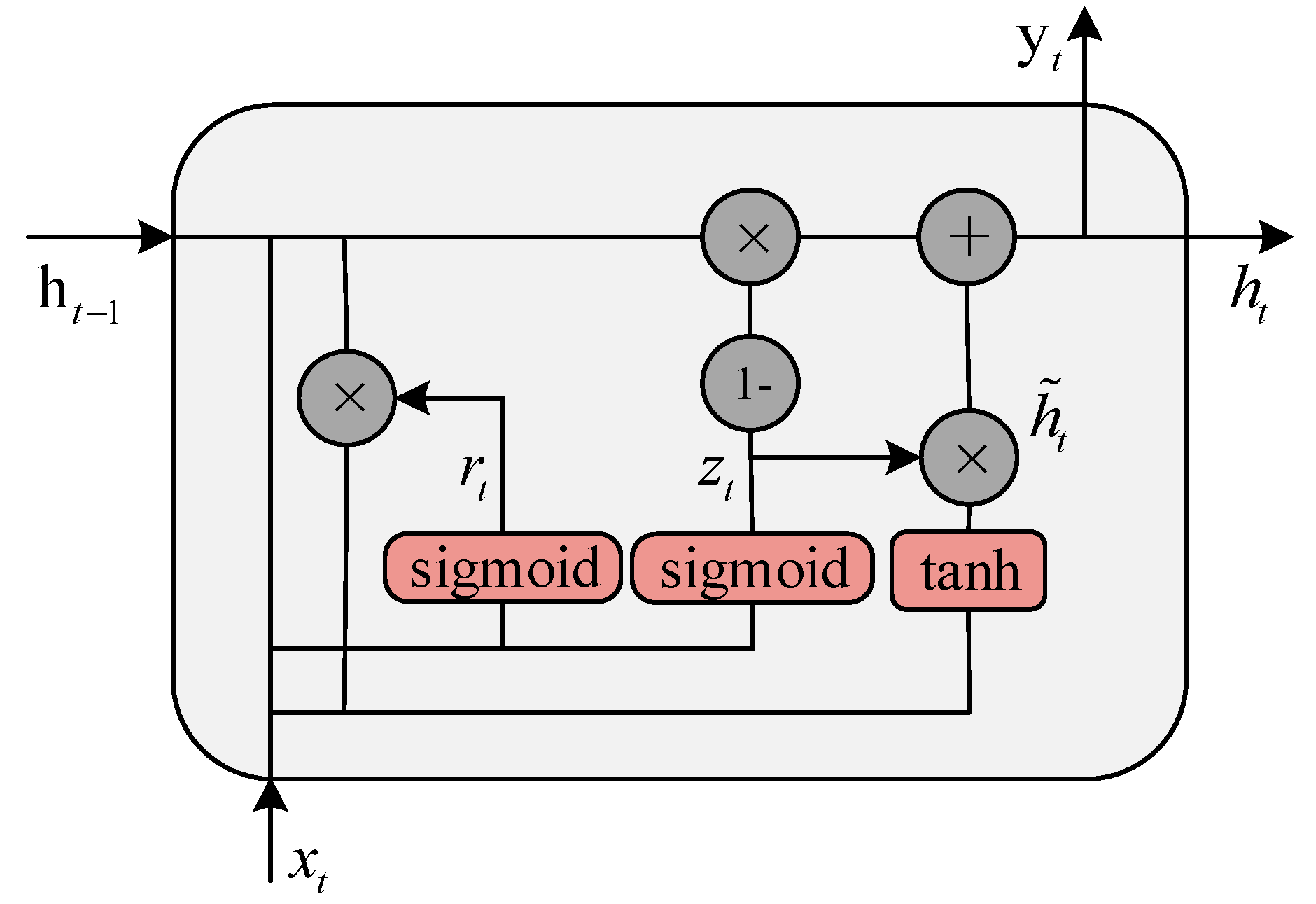
GRU contains two gating mechanisms: an update gate zₜ and a reset gate rₜ. Its gating mechanism effectively resolves the vanishing gradient problem of traditional RNNs, enabling it to effectively manage and transmit long-term dependency information. As shown in Figure 2, the GRU unit adaptively controls the flow of information between time steps through its gating mechanism, allowing the model to selectively remember or forget information when processing sequential data, thereby more effectively capturing complex temporal features. The update formulas for a GRU unit are as follows:

$$r_t=sigmoid(W_r·[h_{t-1},x_t]+b_r)$$

(2)

$$z_t=sigmoid(W_z.[h_{t-1},x_t]+b_z)$$

(3)

$${\tilde{h}}_t=\tan \mathrm{h}(W_{\tilde{h}}\left. [r_t\odot h_{t-1},x_t\right]+b_{\tilde{y}})$$

(4)

$$h_t=\left(1-z_t\right)\odot h_{t-1}+z_t\odot {\tilde{h}}_t$$

(5)

$$y_t=sigmoid(W_y·h_t+b_y)$$

(6)

where ⨀ denotes the element-wise product; sigmoid and tanh are activation functions; $W_r$, $W_{\tilde{h}}$, $W_z$, $W_y$ are weight matrices; and $b_r,b_z,b_{\tilde{y}}, b_y$ are the corresponding bias terms. The state vector $hₜ$ in the GRU is determined jointly by the current input $x_t$ and the state vector from the previous time step $h_{t-1}$, and it represents the final state of the entire sequence processing through a dynamic adjustment of information integration.

However, a standard GRU processes a sequence in a single direction (chronologically), which means the prediction at a given time step can only access past and current information. In many tasks, including load state analysis, future context can be equally important for understanding the current state. The bidirectional gated recurrent unit (Bi-GRU) solves this problem by using two independent GRU layers: one processes the input sequence in the forward direction (from start to end), and the other processes it in the backward direction (from end to start). Then, at each time step, the outputs of these two layers are typically concatenated. This structure allows the Bi-GRU to utilize both past (backward) and future (forward) context when making a prediction for any given point in the sequence, making it a highly effective tool for complex time-series analysis [16].

3. The Proposed DMSTFD-Net Method

To address the core challenge of deep entanglement between spatial and temporal features in raw vibration signals, this paper proposes a deep multi-scale Spatial-Temporal Feature Decoupling Network (DMSTFD-Net), an end-to-end framework designed to systematically disentangle these coupled information streams.

3.1. Overall Architecture

The overall architecture of the proposed DMSTFD-Net is shown in Figure 3. The network is designed with a modular, hierarchical structure to facilitate a progressive feature decoupling and refinement process. It is primarily composed of four key stages:

(1)

Input Layer: Receives the raw one-dimensional vibration signal as input.

(2)

Deep Robust Local Feature Decoupling Module: A deep one-dimensional residual network (ResNet) block that acts as a “spatial” feature decoupler, extracting robust, multi-scale local transient features from the noisy input signal.

(3)

High-Order Temporal Pattern Decoupling Module: A bidirectional gated recurrent unit (Bi-GRU) that acts as a “temporal” feature decoupler. It receives the sequence of high-level features from the ResNet module and models its long-range contextual dependencies.

(4)

Load State Discrimination Layer: A final classifier, consisting of a Global Average Pooling layer and a Fully Connected layer, which maps the refined feature representation to the final load state probabilities.

The entire network is trained in an end-to-end fashion, allowing each module to collaboratively optimize the feature learning and decoupling process under the guidance of a single loss function.

To ensure the full reproducibility of our research, the detailed layer-by-layer architecture and hyperparameters of the proposed DMSTFD-Net are provided in

Table 1. Detailed Architecture of the Proposed DMSTFD-Net.

Stage	Component	Details	Output Shape (Example)
Input	Raw Signal	4096 $\times$ 1 vector	(Batch, 4096, 1)
Stage 1: Initial Conv	1D Conv	64 filters, kernel = 7, stride = 2, padding = 3	(Batch, 2048, 64)
	Batch Norm 1D	-	(Batch, 2048, 64)
	ReLU	-	(Batch, 2048, 64)
	Max Pooling	kernel = 3, stride = 2, padding = 1	(Batch, 1024, 64)
Stage 2: ResNet Body	Residual Block Group 1	2 $\times$ Blocks, 64 filters, stride = 1	(Batch, 1024, 64)
	Residual Block Group 2	2 $\times$ Blocks, 128 filters, stride = 2	(Batch, 512, 128)
	Residual Block Group 3	2 $\times$ Blocks, 256 filters, stride = 2	(Batch, 256, 256)
	Residual Block Group 4	2 $\times$ Blocks, 512 filters, stride = 2	(Batch, 128, 512)
Stage 3: Pooling	Global Average Pooling 1D	-	(Batch, 512)
Stage 4: Temporal	Bi-GRU	256 hidden units	(Batch, 512)
Stage 5: Classifier	Fully Connected	9 output units	(Batch, 9)
	Softmax	-	(Batch, 9)

Note: The structure is based on a standard ResNet-18 architecture adapted for 1D time-series data. The specific convolution kernel sizes within residual blocks are 3 $\times$ 1.

. The model is conceptually based on a ResNet-18 backbone, specifically adapted for processing one-dimensional time-series signals, which is then connected to a Bi-GRU layer for temporal dependency modeling. The data flow and tensor shape transformations are also outlined to provide a clear understanding of the model’s inner workings.

The selection of these specific hyperparameters was meticulously performed. Key parameters, such as the ResNet-18 structure, were chosen based on established best practices for deep feature extraction. Other parameters, including the number of Bi-GRU units, were fine-tuned through a series of preliminary experiments to achieve an optimal balance between the model’s expressive capacity and its computational efficiency, while also mitigating the risk of overfitting.

3.2. Rationale for Architectural Choices

The architecture of DMSTFD-Net was purposefully designed to align with our “hierarchical decoupling” philosophy. The selection of a one-dimensional ResNet followed by a Bi-GRU was a deliberate, problem-driven choice over other advanced architectures.

ResNet as the Spatial Decoupler: We chose ResNet to first decouple local, transient features (the “spatial” dimension of the time-series). Its deep architecture with residual connections is exceptionally suited for learning hierarchical patterns from simple edges to complex impact events in the signal, while mitigating gradient vanishing issues common in deep networks.

Bi-GRU as the Temporal Decoupler: After extracting high-level spatial representations, a Bi-GRU was employed to model their long-range temporal dependencies. The load evolution is a continuous process where the significance of a vibration event often depends on both past and future context. The bidirectional nature of Bi-GRU is ideal for capturing these contextual dependencies. While architectures like Temporal Convolutional Networks (TCNs) are powerful for long sequences, their fixed convolutional structure is less flexible than the gating mechanism of GRU for handling the non-stationary dynamics of ball mill signals. Similarly, Transformers, despite their strength in capturing global dependencies, typically require vast datasets and their self-attention mechanism might re-entangle the spatial and temporal features we aim to separate, thus reducing the model’s physical interpretability.

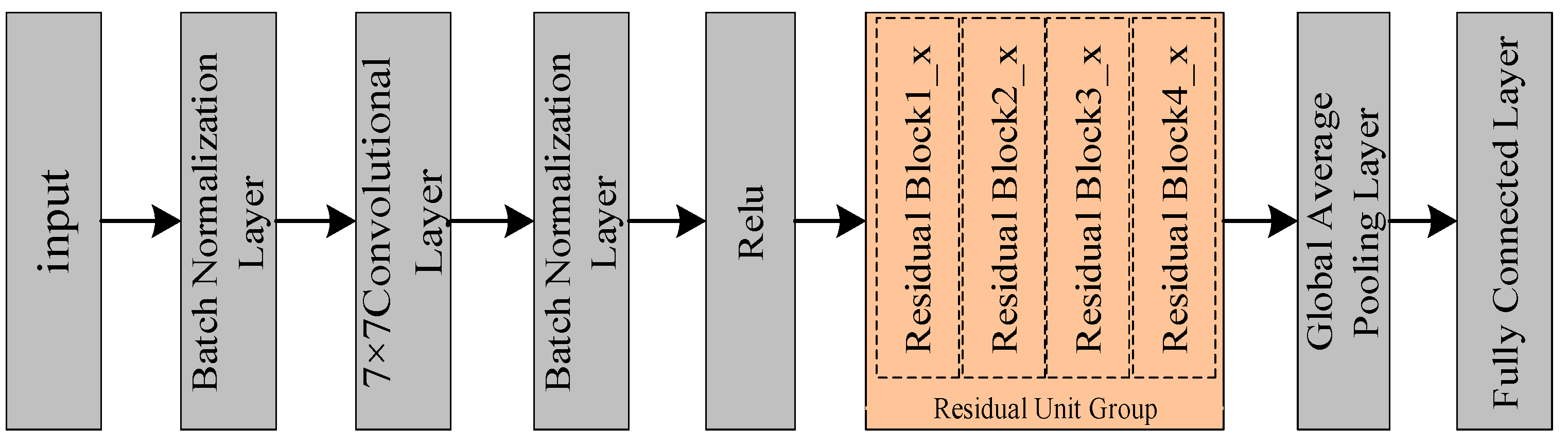
3.3. Deep Robust Local Feature Decoupling Module

The first key stage of our network is to extract and decouple robust local features from the raw, non-stationary vibration signal. This module, based on the one-dimensional ResNet architecture shown in Figure 4, is responsible for the initial “spatial” decoupling.

The module first processes the input signal with an initial convolutional layer to capture low-level local patterns. The resulting feature map is then fed into a series of stacked residual blocks for deep feature refinement. Each residual block contains convolutional layers, Batch Normalization (BN) layers, and ReLU activation functions. The inclusion of BN is crucial; it normalizes the distribution of activations, which accelerates convergence and enhances the model’s robustness against shifts in the input data distribution—a common phenomenon under varying operating conditions. The ReLU function introduces the necessary non-linearity, enabling the module to capture complex relationships within the signal.

By utilizing a deep ResNet architecture with varying filter sizes (from 64 to 512) and strides, this module can adaptively learn multi-scale, hierarchical local features. The residual connections ensure that discriminative information can propagate smoothly through the deep network. Ultimately, this module transforms the complex raw signal into a high-level, preliminarily decoupled sequence of local feature representations, providing a clean and information-dense input for the subsequent temporal analysis module.

In the context of this study, the term “spatial” refers to the localized, short-term structural patterns within the one-dimensional time-series signal, such as impacts, oscillations, and decays. The one-dimensional ResNet acts as a “spatial feature decoupler” by hierarchically breaking down the complex raw signal. The initial convolutional layers capture primitive features like sharp peaks or edges. As the signal propagates through deeper residual blocks, these primitives are progressively combined into more abstract and robust representations of complex events, such as a complete grinding impact event. The core function of decoupling here is to transform the highly entangled raw signal, where various physical phenomena are mixed, into a structured sequence of high-level, disentangled local features. This process effectively isolates and purifies the key spatial patterns, providing a clean and informative input for the subsequent temporal analysis module.

3.4. High-Order Temporal Pattern Decoupling Module

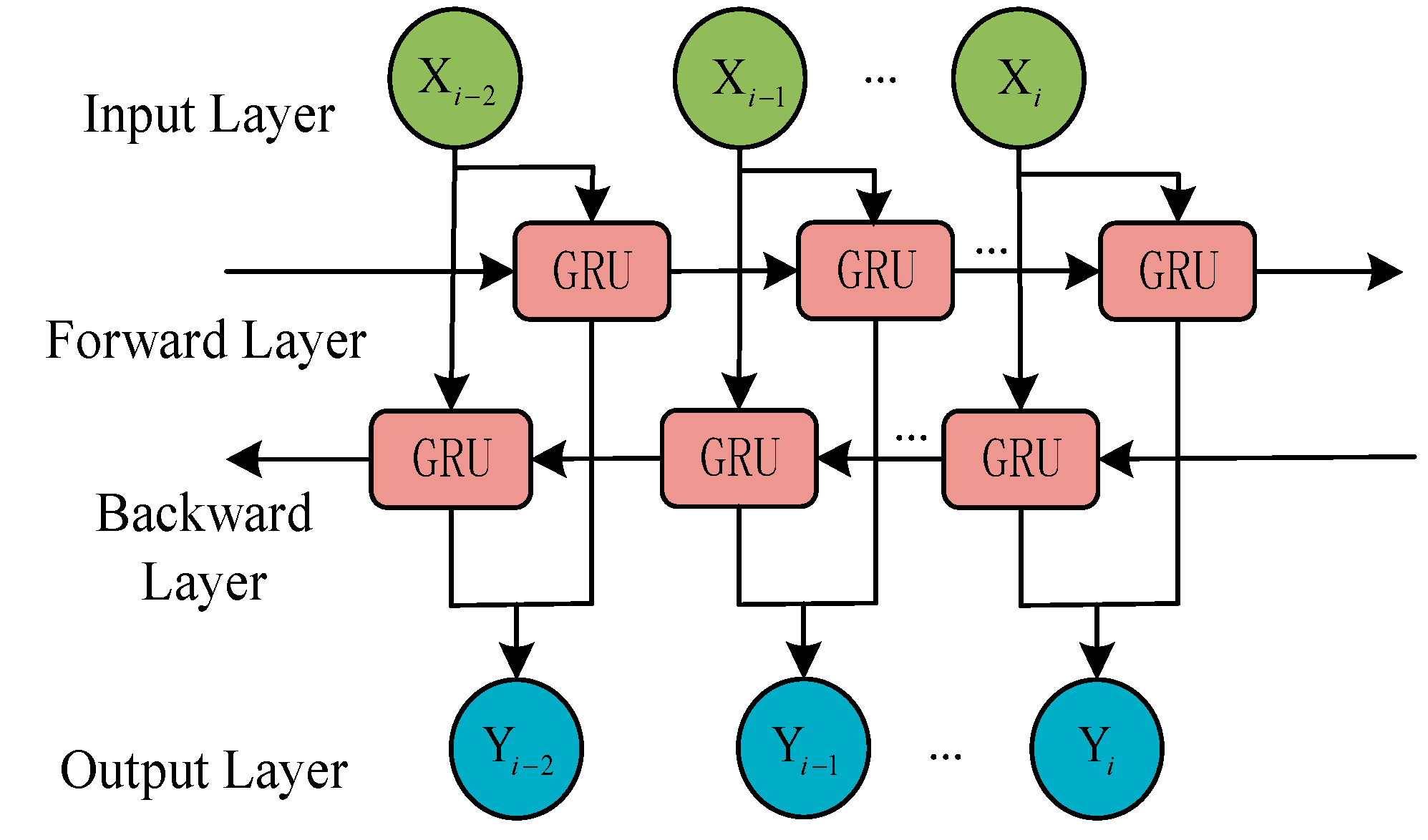
After the initial spatial decoupling, the sequence of extracted local features is fed into the high-order temporal pattern decoupling module. The purpose of this module is to model the long-range temporal dependencies and further disentangle the dynamic evolution patterns hidden within the feature sequence.

We employ a bidirectional gated recurrent unit (Bi-GRU) to accomplish this task, with its structure shown in Figure 5. The Bi-GRU processes the feature sequence in two directions simultaneously:

A forward GRU reads the sequence from the first time step to the last, capturing the “past-to-present” contextual information. A backward GRU reads the sequence from the last time step to the first, capturing the “future-to-present” contextual information.

At each time step, the hidden states from the forward and backward GRUs are concatenated. This creates a comprehensive representation that is aware of the complete temporal context of each local feature. This bidirectional processing is essential for accurately interpreting the state of the ball mill, as the significance of a particular vibration event can often only be understood by considering both what happened before and what happens next. This module effectively separates the pure temporal dynamics from the feature stream, completing the spatial-temporal decoupling process.

3.5. Load State Discrimination and Model Optimization

Once the features have been fully decoupled and refined, the final stage is to classify the load state. The output from the Bi-GRU module is first passed through a Global Average Pooling (GAP) layer. This layer aggregates the feature maps across the time dimension into a single, fixed-length vector, which significantly reduces the number of parameters and helps to prevent overfitting.

This aggregated feature vector is then fed into one or more Fully Connected (FC) layers, which perform the final high-level mapping from features to classes. The output layer uses a Softmax activation function to convert the network’s output logits into a probability distribution over the C possible load states. The probability ŷ_c for class c is calculated as:

$$\begin{array}{c}{\hat{y}}_c={\displaystyle \frac{e^{z_c}}{\sum _{k=1}^c{e}^{z_k}}}\end{array}$$

(7)

where z_c is the logit output for class c.

To train the entire network, we use the Cross-Entropy (CE) Loss function, which measures the dissimilarity between the predicted probability distribution ŷ and the true one-hot encoded label y. The loss is defined as:

$$L_{CE}=-{\displaystyle \frac{1}{N}}{\sum }_{i=1}^N{\sum }_{c=1}^C{y}_{ic}\mathrm{l}\mathrm{o}\mathrm{g}\left({\hat{y}}_{ic}\right)$$

(8)

where N is the total number of training samples, and y_ic is 1 if sample i truly belongs to class c, and 0 otherwise. By minimizing this loss function using an optimizer like SGD, the DMSTFD-Net learns to perform the feature decoupling and classification tasks in an optimized, end-to-end manner.

4. Experiments and Result Analysis

To comprehensively evaluate the performance of the proposed DMSTFD-Net, a series of systematic experiments were conducted on a real-world dataset collected from a laboratory-scale ball mill.

4.1. Experimental Setup and Dataset

Experimental Platform: Data was collected using the experimental platform shown in Figure 6. The platform consists of a laboratory-scale ball mill, a DH131 vibration sensor, and a DH5922N dynamic signal acquisition instrument. The vibration sensor was installed on the mill’s bearing housing to capture vibration signals, which were digitized by the acquisition instrument at a sampling frequency of 20 kHz and transmitted to a PC for storage and processing. Although the platform is also equipped with an acoustic sensor, this study focuses exclusively on the analysis of the one-dimensional vibration signal.

Dataset Construction: In order to conduct a proof-of-concept validation of the feature decoupling method proposed in this paper within a controllable yet challenging environment, a multi-condition dataset was constructed by varying two key parameters: the filling ratio and the material-to-ball ratio. In this context, the Material-to-Ball Ratio is defined as the volume ratio of the grinding material to the void volume between the grinding media (steel balls). These conditions cover a wide range of operations from low to high load. The specific parameters for each experimental condition are detailed in

Table 2. Experimental parameters for the multi-condition ball mill load dataset.

Filling Ratio	Material-to-Ball Ratio	Number of Steel Balls			Material Ratio 1:2:3:4 (kg)
		φ30 mm	φ40 mm	φ50 mm	+3–6 mm	+6–9 mm	+9–13 mm	+13–18 mm
0.2	0.1	27	23	17	0.178	0.356	0.534	0.712
	0.3	19	16	12	0.369	0.737	1.106	1.475
	0.5	15	12	9	0.482	0.964	1.445	1.927
	0.7	12	10	8	0.571	1.143	1.714	2.285
	0.9	11	9	7	0.645	1.291	1.936	2.582
	1.1	10	8	6	0.711	1.421	2.132	2.842
0.3	0.1	38	32	25	0.252	0.504	0.756	1.008
	0.3	26	22	17	0.512	1.024	1.536	2.048
	0.5	20	17	13	0.645	1.291	1.936	2.581
	0.7	16	13	10	0.726	1.453	2.179	2.905
	0.9	13	11	9	0.781	1.561	2.342	3.123
0.4	0.1	51	43	33	0.336	0.672	1.008	1.344
	0.3	34	29	22	0.683	1.365	2.048	2.731
	0.5	26	22	17	0.860	1.721	2.581	3.442
	0.7	21	18	14	0.968	1.937	2.905	3.874
	0.9	18	15	11	1.041	2.082	3.123	4.164
0.5	0.1	64	54	41	0.420	0.840	1.260	1.680
	0.3	43	36	28	0.853	1.707	2.560	3.414
	0.5	33	28	21	1.076	2.151	3.227	4.302
	0.7	26	22	17	1.211	2.421	3.632	4.842
	0.9	22	19	14	1.301	2.602	3.904	5.205
	1.1	19	16	12	1.366	2.733	4.099	5.466

.

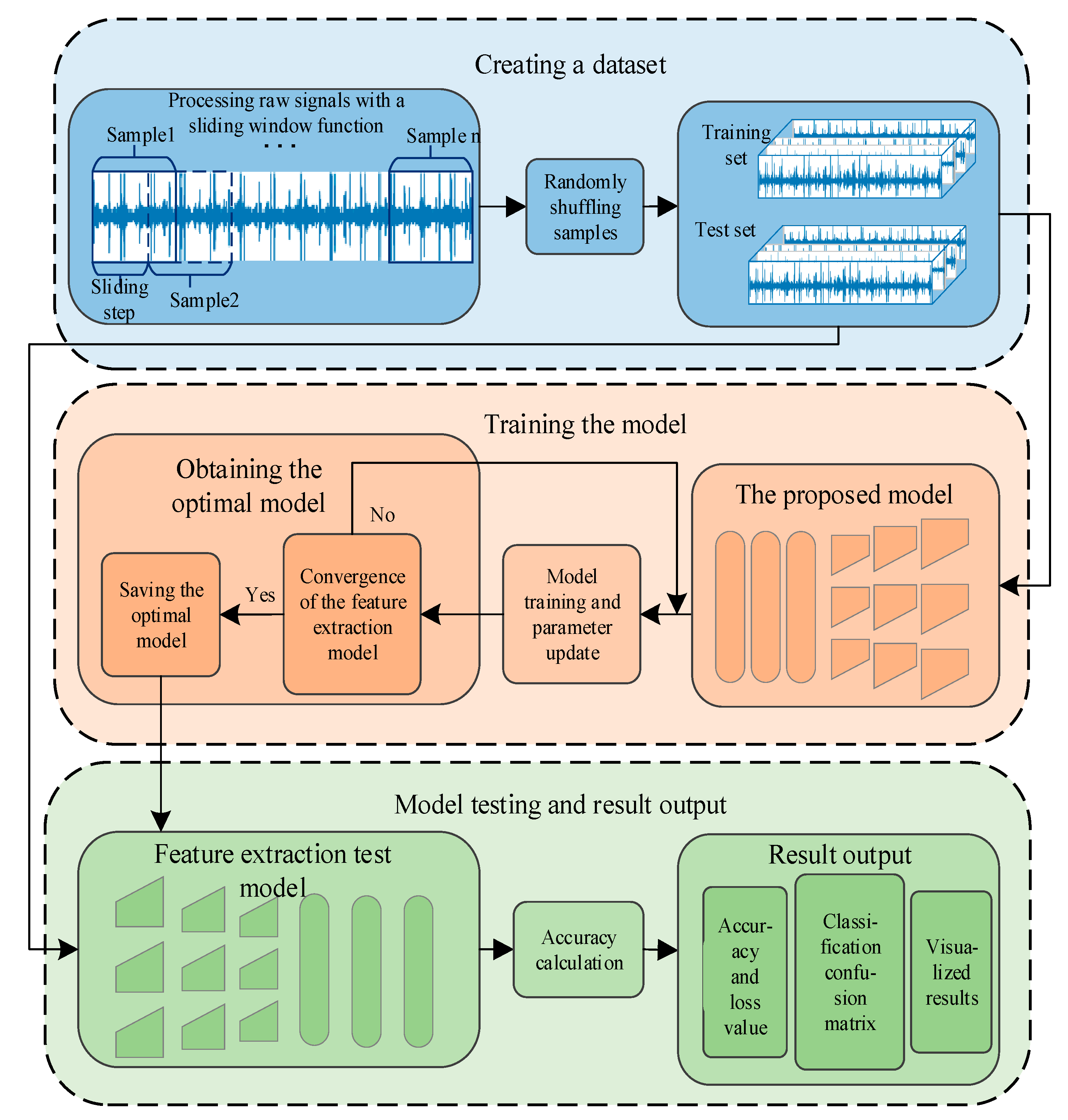
Data Preprocessing and Labeling: The overall data processing and sample construction pipeline is shown in Figure 7. The raw one-dimensional vibration signal for each condition was processed using a sliding window function to generate samples. Each sample has a fixed length of 4096 data points to ensure the capture of complete vibration cycles. To preserve the integrity of the original time-domain information, DMSTFD-Net directly takes these raw sequence samples as input, avoiding any information loss associated with feature engineering or time–frequency transformations.

All generated samples were then randomly shuffled and split into a training set and a testing set at a 4:1 ratio. This resulted in 3600 training samples and 900 testing samples. The nine different load states were assigned labels from 0 to 8, as detailed in

Table 3. Dataset division and labels for the multi-condition load states.

Filling Ratio	Material-to-Ball Ratio	Training/Test Set	Label	Data State (Filling Ratio/Material-to-Ball Ratio)
0.2	0.1	400/100	0	Low/Low
	0.3	400/100	0	Low/Low
	0.5	400/100	1	Low/Normal
	0.7	400/100	1	Low/Normal
	0.9	400/100	2	Low/High
	1.1	400/100	2	Low/High
0.3	0.1	400/100	3	Normal/Low
	0.3	400/100	3	Normal/Low
	0.5	400/100	4	Normal/Normal
	0.7	400/100	4	Normal/Normal
	0.9	400/100	5	Normal/High
0.4	0.1	400/100	3	Normal/Low
	0.3	400/100	3	Normal/Low
	0.5	400/100	4	Normal/Normal
	0.7	400/100	4	Normal/Normal
	0.9	400/100	5	Normal/High
0.5	0.1	400/100	6	High/Low
	0.3	400/100	6	High/Low
	0.5	400/100	7	High/Normal
	0.7	400/100	7	High/Normal
	0.9	400/100	8	High/High
	1.1	400/100	8	High/High

. This standardized dataset forms the basis for all subsequent model training and evaluation. To ensure a fair and unbiased evaluation of the model’s performance, the constructed dataset was balanced, with an equal number of samples for each of the nine defined load states.

4.2. Performance of the Proposed Model

This section evaluates the intrinsic performance of the proposed DMSTFD-Net on the constructed ball mill load dataset, with a focus on its convergence stability and classification accuracy.

(1)

Training Convergence Analysis: The convergence behavior of DMSTFD-Net was tracked by monitoring the accuracy and loss values on both the training and testing sets during the training process, with the results shown in Figure 8 and Figure 9, respectively.

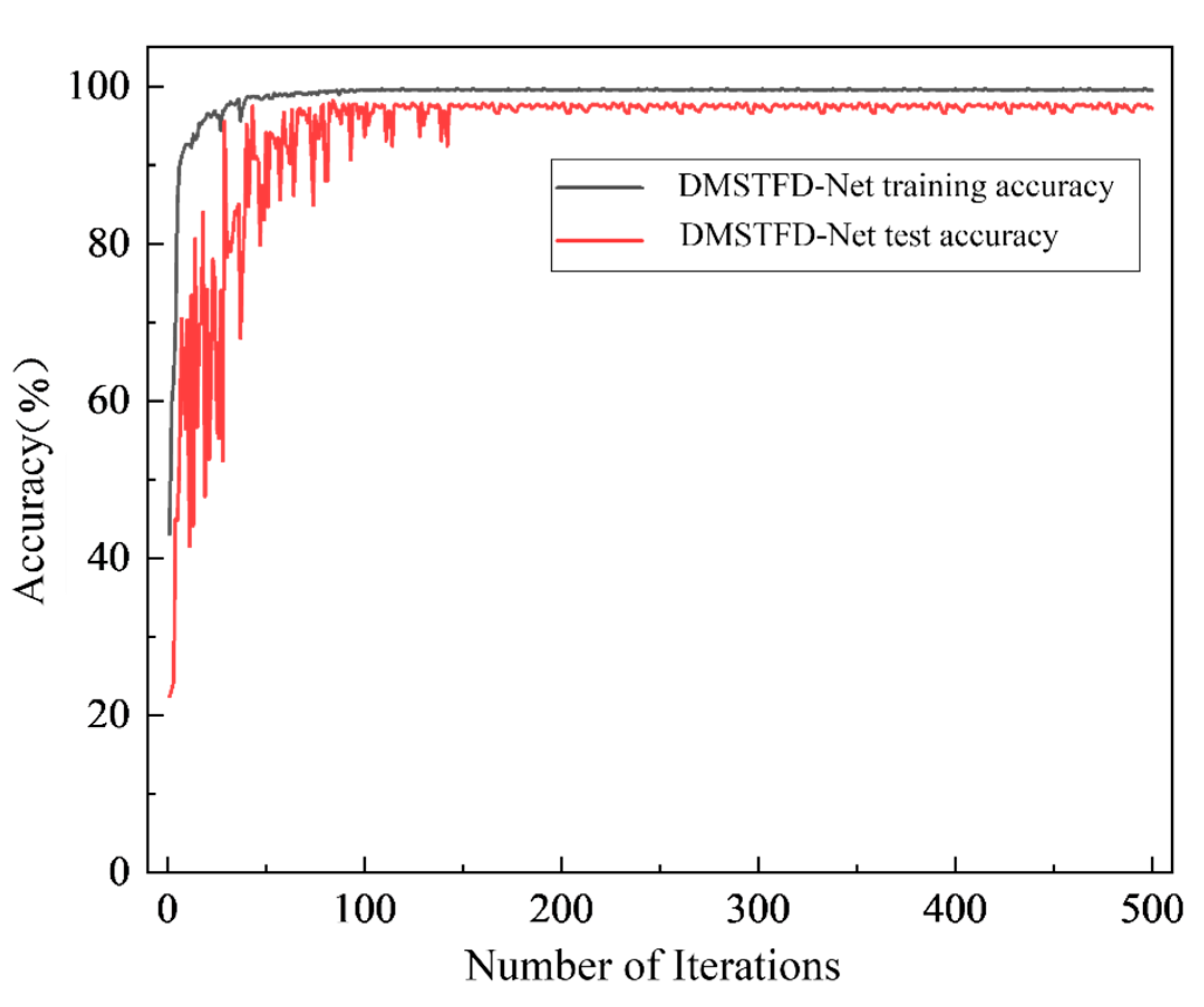
Figure 8 shows that the accuracy curves for both the training and testing sets exhibit a rapid upward trend in the initial training epochs, indicating that the model can quickly capture discriminative features from the raw vibration signals. As the number of epochs increases, the accuracy curves gradually plateau. The training accuracy ultimately stabilizes above 98%, while the testing accuracy stabilizes at approximately 97%, with a final average accuracy of 97.65%. The high degree of consistency between the two curves in their upward trend and final converged state demonstrates that DMSTFD-Net possesses excellent learning capabilities and effectively avoids overfitting.

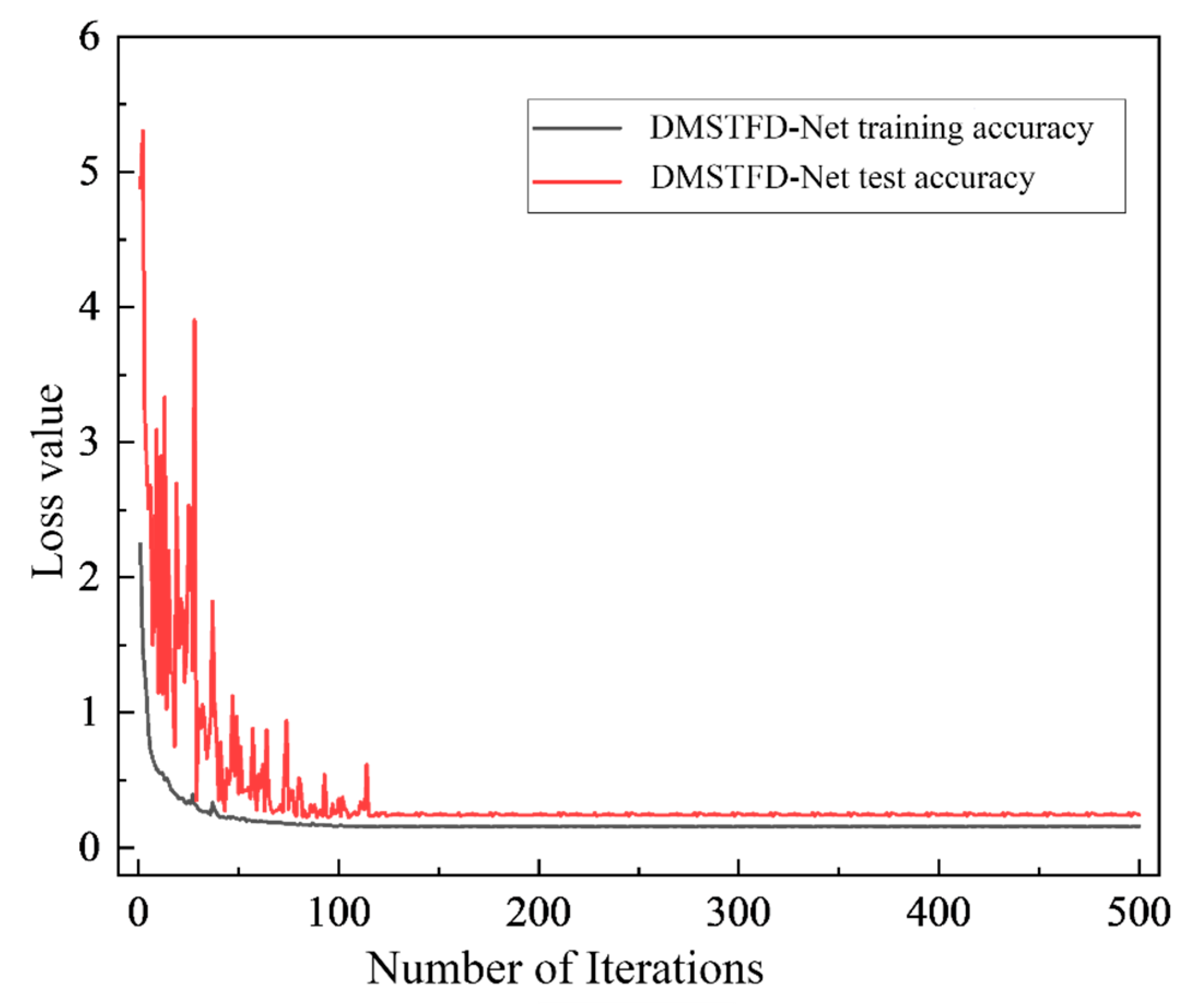
The change in loss value during the training process is depicted in Figure 9. The loss value drops sharply from a high initial point (close to 2.5), indicating that the model is efficiently learning the load features. Subsequently, the loss curves for both sets decrease steadily and converge to a very low value. Although the testing loss shows minor fluctuations initially, it generally follows the downward trend of the training loss and maintains a small gap. This comprehensive performance in both accuracy and loss demonstrates that DMSTFD-Net is a stable and highly effective model for the load feature extraction and discrimination task.

(2)

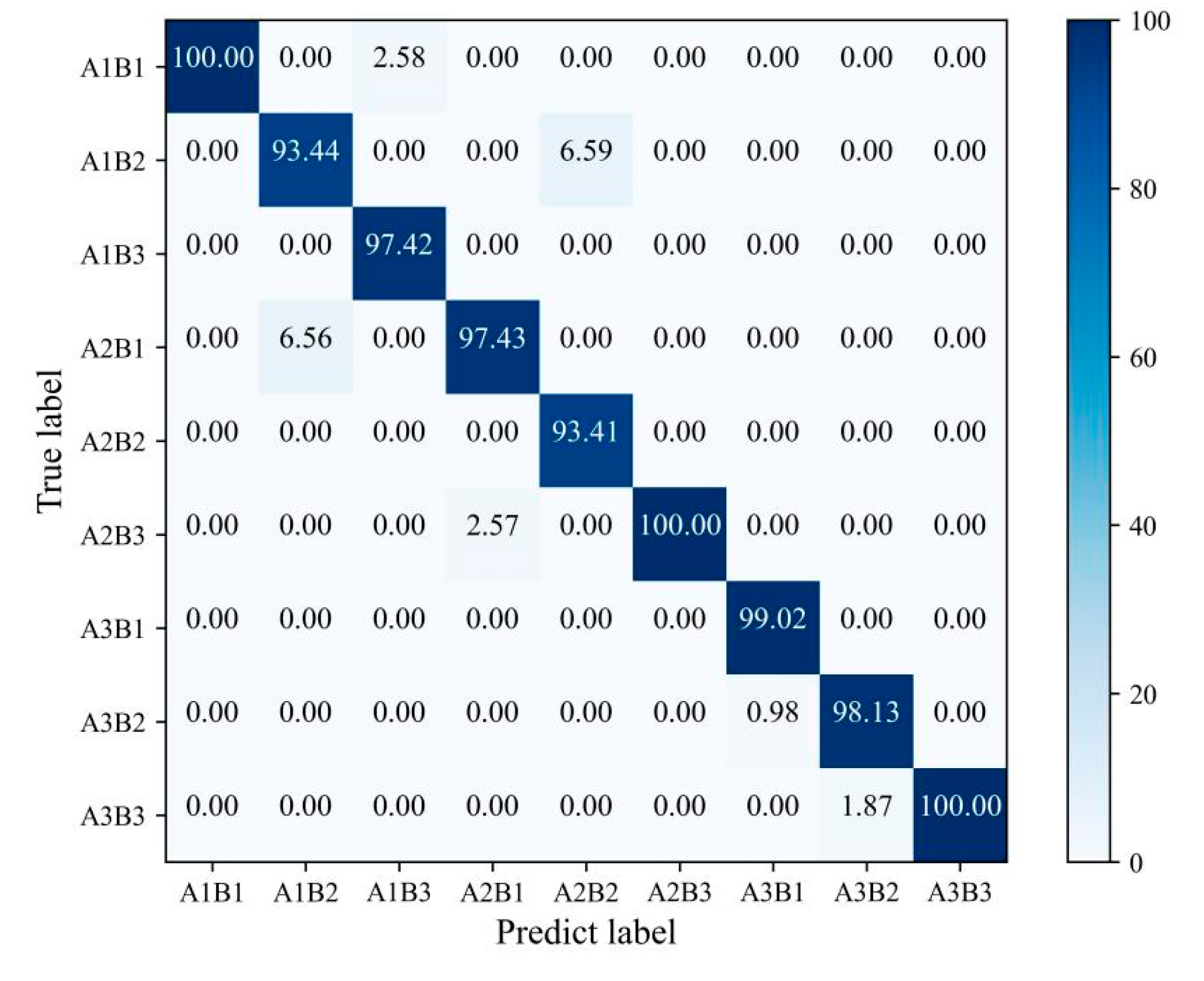
Classification Accuracy: To further quantify the classification performance of DMSTFD-Net on different load states, the confusion matrix on the test set was generated, as shown in Figure 10. The confusion matrix provides a detailed, class-by-class visualization of the model’s prediction performance, including correct classifications and misclassification patterns.

The diagonal elements of the matrix represent the percentage of correctly classified samples for each class. It is evident that the model achieves outstanding recognition performance. For instance, for load states A1B1 (Low/Low), A2B3 (Normal/High), and A3B3 (High/High), the model’s accuracy is nearly 100%. Even for the classes with some misclassifications, the error rates are extremely low. For example, in class A1B2 (Low/Normal), 93.44% of samples are correctly identified, with only a small portion (6.59%) being misclassified as A2B2 (Normal/Normal), which is a physically adjacent and easily confusable state.

Overall, the confusion matrix reveals that DMSTFD-Net is highly reliable and effective for ball mill load state discrimination. The average accuracy across all classes exceeds 97%, which preliminarily validates the model’s exceptional ability to extract discriminative features from raw vibration signals and classify complex load states.

4.3. Comparative Experiments

To rigorously validate the performance and advanced nature of the proposed DMSTFD-Net, an extensive benchmark was conducted against a diverse set of deep learning architectures. The selected baseline models represent a spectrum of design philosophies, enabling a multi-faceted analysis of the problem. The benchmark suite includes: (1) a Standard Convolutional Neural Network (CNN) to establish a foundational performance level [17]; (2) a Bidirectional Gated Recurrent Unit (Bi-GRU) to specifically evaluate a pure temporal modeling approach; (3) a CNN-LSTM architecture, representing a classic and strong baseline for combined spatial-temporal feature extraction; and (4) a standalone ResNet, to isolate the performance of the advanced spatial decoupling module.

For a holistic and comprehensive evaluation, all models were analyzed across a suite of metrics. Classification efficacy was measured by Accuracy, Precision, Recall, and F1-score. Model efficiency was assessed by the number of trainable parameters and the inference time per sample. All experiments were performed under identical protocols to ensure a fair and direct comparison.

The comprehensive benchmark results are summarized in

Table 4. Performance comparison results of DMSTFD-Net with mainstream methods.

Model	Accuracy (%)	Precision (%)	Recall (%)	F1-Score (%)	Parameters (M)	Inference Time (ms/Sample)
Standard CNN	90.35	90.41	90.35	90.33	0.03	0.2
Bi-GRU	91.57	91.63	91.57	91.56	0.40	1.1
CNN-LSTM *	94.20	94.25	94.20	94.19	0.23	1.0
ResNet	97.02	97.05	97.02	97.01	11.18	0.5
Proposed (DMSTFD-Net)	97.65	97.68	97.65	97.65	12.36	1.5

* The CNN-LSTM model was included as a strong and representative baseline for combined spatial-temporal modeling to provide a more comprehensive comparison.

, with a visual analysis of the performance-complexity trade-off presented in Figure 11.

The results presented in Table 4 and Figure 11 unequivocally demonstrate that the proposed DMSTFD-Net achieves state-of-the-art performance. It outperforms all baseline models across every classification metric, reaching a top accuracy of 97.65% and an F1-score of 97.65%. A detailed analysis of these results provides the following insights:

(1) Efficacy of Hierarchical Architectures:

As illustrated in Figure 11, there is a clear trend of performance improvement with architectural sophistication. A Standard CNN establishes a solid baseline with a 90.35% accuracy. The CNN-LSTM model, a canonical spatial–temporal architecture, significantly improves upon this to 94.20%. This result validates the core hypothesis that a hierarchical approach—first extracting local features and then modeling their temporal sequence—is fundamentally more effective for this task. However, the performance gap between CNN-LSTM and the ResNet-based models highlights the limitations of a simple convolutional frontend.

(2) The Critical Role of Advanced Feature Decoupling:

The most dramatic performance leap occurs with the introduction of the ResNet architecture. The standalone ResNet model achieves an exceptionally high accuracy of 97.02%. This is visually represented in Figure 11 by the sharp rise in both the F1-score bar and the parameter line plot. This underscores that a powerful, deep feature extractor capable of effective “spatial decoupling” is the single most critical factor for achieving high performance. However, the standalone Bi-GRU (91.57%), despite its temporal modeling capabilities, is outperformed by even the simple CNN, confirming that its effectiveness is severely constrained by the quality of input features.

(3) Synergistic Breakthrough and Efficiency of DMSTFD-Net:

The proposed DMSTFD-Net attains the highest performance by synergistically integrating the advanced spatial decoupling of ResNet with the temporal modeling of Bi-GRU. It surpasses the standalone ResNet, demonstrating that even after powerful spatial feature extraction, there remains valuable, extractable information within the temporal dependencies of the feature sequence.

From an efficiency standpoint, Figure 11 clearly illustrates the performance-complexity trade-off. The transition to the high-performance regime (>97% accuracy) necessitates a significant increase in model complexity, as shown by the jump in parameters for ResNet and our proposed model. Our DMSTFD-Net, with a parameter count of ~12.36 M, builds upon the ResNet backbone (~11.18 M) and uses the additional complexity to achieve the final, state-of-the-art result. This comprehensive analysis confirms that our proposed hierarchical decoupling architecture represents an effective and advanced solution for ball mill load identification.

4.4. Evaluation of Cross-Condition Generalization

To provide direct evidence for the model’s generalization capability on unseen operational conditions—a critical aspect for practical deployment—we conducted a dedicated cross-condition experiment. This evaluation protocol is significantly more challenging than the previous mixed-data tests, as it assesses the model’s ability to extrapolate knowledge to new domains.

For this purpose, we formulated a representative transfer task (L2 → L3) where models were trained exclusively on data from one filling rate condition (0.3) and subsequently evaluated on data from a completely different, unseen filling rate condition (0.4). The performance of the proposed DMSTFD-Net was benchmarked against the other representative models, with the results summarized in

Table 5. Model accuracy (%) on the unseen filling rate condition (L2 → L3 Task).

Model	Accuracy (%)	Performance Drop (%)
Standard CNN	81.33	−9.02
Bi-GRU	84.64	−6.93
CNN-LSTM	87.15	−7.05
ResNet	95.03	−1.99
Proposed (DMSTFD-Net)	97.59	−0.06

.

The results in Table 5 clearly demonstrate the superior cross-condition generalization of the proposed DMSTFD-Net. While all baseline models suffered a significant performance degradation when confronted with the unseen data, our model maintained an exceptionally high accuracy of 97.59%, with a negligible performance drop. This provides strong evidence that our hierarchical decoupling approach learns a more fundamental and robust representation of the grinding process, which is less sensitive to shifts in operational parameters.

While this preliminary experiment validates the effectiveness of our approach, a more extensive investigation across a wider range of transfer tasks is a key direction for our future work.

4.5. Visualization of Feature Decoupling

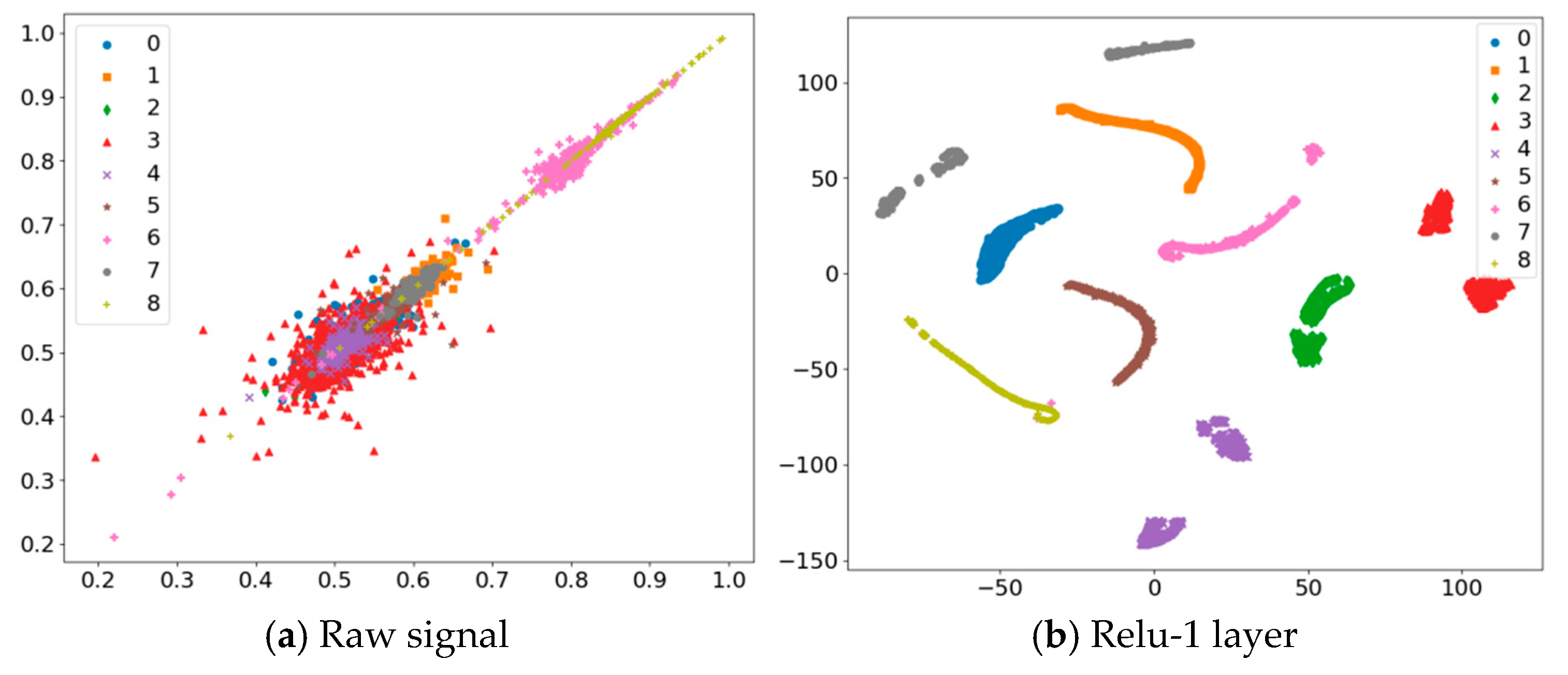
To intuitively verify the effectiveness of DMSTFD-Net in feature decoupling and cross-condition generalization, we employed the t-Distributed Stochastic Neighbor Embedding (t-SNE) algorithm. t-SNE is a powerful technique that can visualize high-dimensional data in a low-dimensional space (typically 2D or 3D) while preserving the local neighborhood structure. In our analysis, if the feature clusters for different classes become clearly separated and internally compact after passing through the network, it indicates that the model has successfully learned highly discriminative and well-decoupled feature representations.

We applied t-SNE to visualize the feature outputs at different stages of the DMSTFD-Net: the raw input signal, an intermediate layer of the ResNet module (Relu-1), the output of the Bi-GRU module (visualized after the Global Average Pooling layer), and the final fully connected layer. The results are shown in Figure 12.

(a)

Raw Input Signal: The visualization of the raw vibration signals in Figure 12a shows a state of high feature entanglement. Data points from different load states (represented by different colors and markers) are severely mixed and overlapped, making it nearly impossible to distinguish their class membership. This directly reflects the complexity, non-linearity, and high-order feature entanglement in the original signal space, validating the “feature entanglement” challenge proposed in the introduction.

(b)

ResNet Intermediate Layer (Relu-1 layer): After initial processing by the deep robust local feature decoupling module (ResNet), the feature distribution in Figure 12b begins to show a preliminary clustering trend. The data points of different load states start to separate from the entangled mass and gather towards their respective class centers. This demonstrates that the ResNet module has successfully extracted robust, multi-scale local invariant features and achieved an initial level of feature decoupling and noise suppression. Notably, some load states (such as labels 0, 1, 7) already exhibit a considerable degree of separation, laying a solid foundation for the subsequent temporal pattern decoupling.

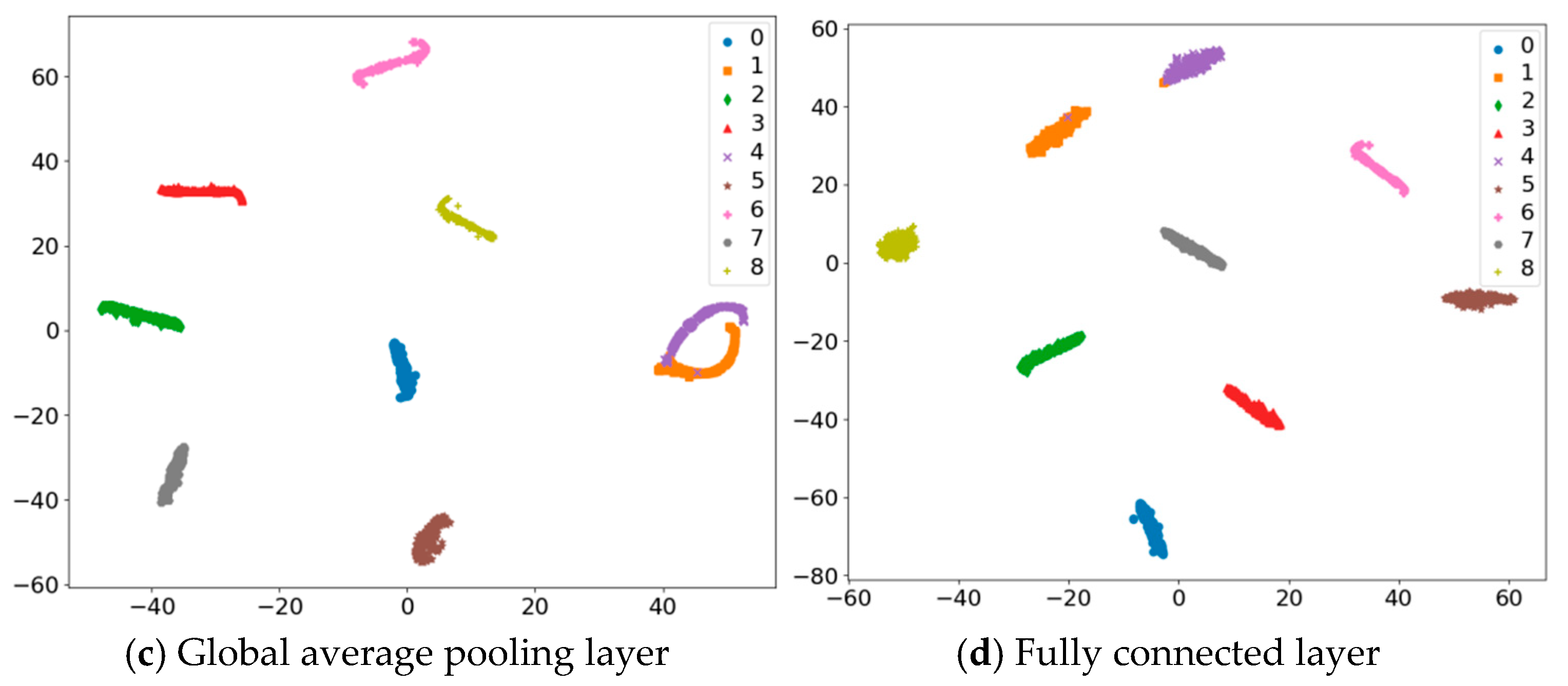
(c)

Bi-GRU Output (Global average pooling layer): After processing by the high-order temporal dynamic pattern decoupling module (Bi-GRU), the separation of features becomes significantly more pronounced, as shown in Figure 12c. Compared to the ResNet intermediate layer, the feature clusters for different load states are further apart, and the intra-class aggregation is much tighter. This intuitively demonstrates the effectiveness of the Bi-GRU module in capturing long-range temporal dependencies, as well as refining and decoupling high-order dynamic patterns. Although a slight overlap still exists between a few classes (such as labels 1 and 4), the overall degree of feature decoupling has been substantially enhanced.

(d)

Final Fully Connected Layer: In the final feature space before classification, shown in Figure 12d, all load state clusters exhibit an ultimate degree of separation and compactness. The overlapping phenomenon between different load states has almost completely disappeared, while the features within the same class have formed the tightest clusters. This provides powerful evidence that DMSTFD-Net’s hierarchical collaborative feature refinement and deep decoupling mechanism can extract highly discriminative and thoroughly decoupled load feature representations from multi-dimensional, highly entangled raw signals, ultimately achieving the highest possible separability for the ball mill load states.

5. Conclusions

The core contribution of this research is to first systematically identify and define a key bottleneck in the task of ball mill load identification: spatial-temporal feature entanglement. We posit that the high degree of coupling at the signal level—caused by short-term transient impacts and long-range evolution of operating conditions—is the fundamental reason limiting the generalization ability and interpretability of existing models. Based on this understanding, rather than merely pursuing an increase in black-box accuracy, we propose and validate an analysis framework guided by the core philosophy of “hierarchical decoupling” and designed with a clear physical interpretation: the Deep Feature Dec- ling Network (DMSTFD-Net). Within this framework, the one-dimensional residual network (ResNet) is assigned the role of a “spatial” transient feature decoupler, while the bidirectional gated recurrent unit (Bi-GRU) acts as a “temporal” dynamic pattern decoupler.

To comprehensively validate the effectiveness of this philosophy-guided framework, we conducted rigorous experimental evaluations. On our self-constructed multi-condition dataset, DMSTFD-Net achieved a recognition accuracy of up to 97.65%, significantly outperforming a series of benchmark models. While this top-tier performance necessitates a model of considerable complexity, we argue this trade-off is justified for critical industrial applications where gains in accuracy and robustness can lead to substantial economic and operational benefits. More importantly, the t-SNE visualization analysis provides compelling evidence for our decoupling philosophy: it intuitively demonstrates how the internal features progress from a highly entangled initial state to clearly defined, compact class clusters through layer-by-layer decoupling. This not only proves the model’s performance but also mechanistically confirms both the correctness and the enhanced interpretability of our framework’s design.

At the same time, we must acknowledge the limitations of this study, which also point to future research directions. First, the data for this research was collected from a laboratory-scale environment. Although we provided a strong Proof-of-Concept for the “spatial–temporal decoupling” approach by setting up multi-condition experiments, a significant Domain Gap undoubtedly exists between the laboratory and real-world industrial sites, which involve more complex noise, equipment aging, and variations in raw materials. Therefore, the top priority of our future work will be to deploy the proposed model on actual industrial production lines to test its robustness under more demanding conditions. Second, the high parameter count of the current model, while justified by its performance, motivates future research into lightweight model designs to meet the deployment requirements of resource-constrained edge computing devices in industrial settings.

In summary, this research not only provides a high-accuracy and robust solution for ball mill load identification but, more importantly, offers a more interpretable analysis paradigm for understanding and processing complex industrial time-series signals. We believe that this modeling approach, which starts from the essential nature of the problem and aims for clear physical decoupling, will serve as a valuable reference for advancing the intelligence and efficiency of industrial processes.