Optimizing Lightweight Material Selection in Automotive Engineering: A Hybrid Methodology Incorporating Ashby’s Method and VIKOR Analysis

Abstract

The automotive industry is responsible for about 20% of greenhouse gas emissions in Europe, and it is under notable pressure to meet the reduction targets set by the European Union for the next decades. In this context, lightweighting is a very effective design strategy for which materials selection plays a key role. One of the main challenges of lightweighting is selecting materials with enhanced structural properties but a reduced weight in comparison with traditional solutions. The spectrum of available materials is very large, and the choice needs to be carefully evaluated based on multiple factors, such as mechanical behavior, raw materials cost, the availability of manufacturing processes, and environmental impact. This article presents an innovative methodology for materials selection in the lightweight automotive field based on the Ashby approach for mechanical performance coefficients as an initial filtering criterion. Following this preliminary screening, this study adopts the VIKOR (Vise Kriterijumska Optimizacija I Kompromisno Resenje) MCDA (Multi-Criteria Decision Analysis) technique to rank feasible design solutions based on case study boundary conditions. The evaluation criterion of different design options encompasses crucial factors, such as mechanical properties, cost considerations, and environmental impact measures. The method is finally validated by the application of a redesign case study, a motor bracket of an electric commercial car.

1. Introduction

1.1. Lightweight Redesign

In 2022, global CO₂ emissions from energy and transport have increased, respectively, by 261 Mt and 254 Mt with respect to 2021 levels [1]. Considering the European area, the automotive industry accounts for 20% of the overall greenhouse gas (GHG) emissions [2]. In the light of achieving a 60% GHG emissions reduction in 2050 compared to 1990 levels (as mandated by European Union policies [3]), lightweighting design has recently been established as one of the most favorable strategies. Lightweight design strongly contributes to pollution reduction by lowering vehicle consumption, as provided by [4], which states that a 10% mass decrease allows for achieving a 5–8% abatement in energy absorption. By lowering fuel consumption, lightweighting also enables reducing exhaust gas emissions and, consequently, the environmental impact caused by passenger car transportation [5,6,7]. Several case studies from both research and industry fields deal with the replacement of conventional materials for specific car components through lighter solutions [8,9,10], providing several advantages in addition to consumption reduction, such as improved vehicle performances (in terms of both acceleration and top speed [11,12]), increased safety by enhancing stability, greater maneuverability, and reduced braking distances [13,14]. Current production and manufacturing technologies make available a wide range of materials that can be applied in the lightweight redesign context [15], with lightening potential, which strongly varies depending on the specific component and reference solution considered [16]. To date, the development of innovative design options in the area of lightweighting can be declined into the following three major approaches:

-

Lightweight materials. This strategy is focused on materials that offer advantageous structural characteristics while presenting very low density, especially if compared to steel, which historically has been the reference in the automotive industry [17,18]. Aluminum [15,18], titanium [18], magnesium [19], high-strength steels (HSS) [20], metal and plastic matrix composites [21] (even with natural fibers [20] or recycled fibers [20,22]), graphene [23], bio-based materials [24], and sandwich materials [25] represent the most common options. In this context, much research is devoted to the characterization of properties and behavior of these new and complex materials, with the scope to standardize their application [26];

-

Innovative manufacturing processes. The automotive industry is moving from traditional steel-based materials to innovative lightweight structures. This shift determines the investigation of innovative, high-performing, and economically viable manufacturing methods. New production technologies allow the realization of complex geometries and, at the same time, make possible materials combination, which permits a remarkable weight reduction while preserving structural integrity. Some examples of new industrial processes and methods to produce advanced materials are additive manufacturing [27], advanced sheet compression molding [28], reaction injection molding [29], and resin transfer molding [30];

-

Optimization and redesign of car components/assemblies. Design optimization and redesign of vehicle components represent another pillar of lightweighting. Such a strategy is based on implementing design modifications for single parts and systems (theoretically for all vehicle parts, from the body structure up to interior components), with the target of weight reduction without negatively affecting functionality and efficiency. A widespread simulation method in this area is topology optimization [31,32], which allows spatially optimizing material distribution within a specific domain while fulfilling at the same time predefined constraints and minimizing objective cost functions. The literature provides a series of case studies dealing with the most disparate car parts, the most common being closures [33], engine compartment components [34], exterior body panels [35], floor sections [36], and body-in-white [37].

1.2. Design Methods for Materials Selection

Concerning materials selection in the automotive field, a widely used method is the Ashby theory [38,39,40]. As also remarked by [40], the Ashby diagrams are a valuable tool for selecting optimal materials with respect to mechanical and structural integrity requirements. That said, the theory is complex due to the mathematics behind the selection procedure; it works well when there is the need to solve only a few specific problems (the increase in selection criteria strongly complicates the application), and it does not offer a ranking of materials. This last point represents an important limitation of the Ashby theory, which is not able to appropriately address potential trade-offs between different technical, economic, and environmental aspects while maintaining performance and safety standards [41]. This is because the main different requirements often conflict with each other, thus making more complex the overall material selection process [42].

On this aspect, a valuable strategy for considering various and concurrent design criteria is represented by Multi-Criteria Decision Analysis (MCDA) methods. In addition to engineering, this kind of approach finds extensive and effective application also in many other disciplines, such as geology, economics, computer science, and urban planning [43]. MCDA methods prove to be a valid option when the issue is represented not only by the presence of multiple decisional criteria but also by the vastity of alternatives to be compared. Regarding the field of materials selection for lightweighting, a wide range of MCDA methods have been applied in the past, the main discriminating point being the specific engineering problems to be addressed, such as the structural integrity, thermal integrity, durability, and manufacturability. In this area, MCDA methods widely used are the Technique of Order Preference by Similarity to Ideal Solution (TOPSIS), Vise Kriterijumska Optimizacija I Kompromisno Resenje (VIKOR), Complex Proportional Assessment (COPRAS), Preference Ranking Organization Method for Enrichment Evaluation (PROMETHEE), ELimination Et Choix Traduisant la REalité (ELECTRE), and Multi-Objective Optimization on the basis of Ratio Analysis (MOORA). TOPSIS is based on the research of the best option that provides the shortest Euclidean distance from the ideal solution [44], and it ranks the alternatives from the nearest to the farthest with respect to the optimal one. Introduced by [45], VIKOR is a method that handles a set of alternatives characterized by conflicting criteria, and it determines compromise solutions by establishing a ranking, which is calculated by averaging the maximum group utility and the individual regret [46]. COPRAS was developed by [47]. This method is based on the ranking of alternatives considering the ratio ideal–worst solution and the ratio alternative–ideal solution [48]. PROMETHEE in another MCDA method developed by [49]. The algorithm considered the amplitude of the deviation between the alternatives evaluation and considered the pairwise comparison of the alternatives [50]. The ELECTRE method [51] consists of two main procedures: an aggregation procedure to construct several outranking relations and an exploitation procedure to produce results [52]. MOORA is another algorithm developed by [53] with the main goal of comparing the normalized performance of alternative solutions with respect to a particular attribute and ranking these solutions with the summary of such a performance [54].

The literature provides a series of case studies in the automotive context where the above-mentioned MCDA methods are applied, for which some examples are [55,56,57,58,59,60,61]. Ref. [55] uses TOPSIS with an integrated approach to select the optimal materials for the exhaust manifold of a B-segment gasoline passenger car. The criteria used are surface hardness, core hardness, the surface fatigue limit, the bending fatigue limit, ultimate tensile strength, and cost. The results show that nitrided steel is identified as the best solution through the considered case study. Ref. [56] implements VIKOR alongside the house of quality tool to assign criteria and appropriate weights in a specific case study (valve seats of a high-performance engine), with fuzzy logic applied to manage data uncertainty. The researchers selected the CuBe2 for its technical characteristics, which make it the optimal solution for the considered case study. Ref. [57] adopts the VIKOR method to select materials for metallic bipolar plates for polymer electrolyte fuel cells used in electric vehicles. To define the list of acceptable materials, the authors use the following criteria: tissue tolerance, corrosion resistance, tensile strength, fatigue strength, relative toughness, relative wear resistance, elastic modulus, specific gravity, and cost. The method provides 316L austenitic stainless steel as the best choice. Ref. [58] adopts the Complex Proportional Assessment (COPRAS), integrated with the Digital Logic Method (DLM), to analyze various materials for the intermediate layer of laminated glass in the application to windshields and windows. Based on the five key criteria selected for the assessment (failure load, deflection, weight, load ratio, and cost), the poly-ethylene terephthalate with ethylene–vinyl acetate (XLAB) results as the preferable solution, followed in the ranking by ethylene–vinyl acetate (EVA) for glass interlayer materials. Ref. [59] describes a fuzzy version of the Preference Ranking Organization Method for Enrichment Evaluation (PROMETHEE) to select materials for a car instrument internal panel. The criteria used for this case study are the maximum temperature limit, recyclability, elongation, weight thermal conductivity, tensile strength, cost, and toxicity level. Styrene Maleic Anhydride and Polypropylene are determined as suitable materials for the case study. Ref. [60] applies the ELimination Et Choix Traduisant la REalité (ELECTRE) multi-criteria method to choose the materials most susceptible to corrosion in the body of a car. The criteria used are in compliance with international standard EN 10111:2008 [62], the percentage of use in the bodywork, and the steel thickness. The authors conclude that High-Elastic Limit (HLE) steels are the most susceptible to corrosion and are worthy of further investigation in this aspect. Ref. [61] compares five MCDM methods (COPRAS, MOORA, TOPSIS, VIKOR, and Additive Ratio Assessment—ARAS) for the selection of the optimal material for the connecting rod of a commercial car. The following criteria are used for the evaluation: cost, tensile strength, fatigue limit, fracture toughness, machinability, and first fracture brittleness. The article emphasizes that the choice may depend on the specific MCDM method used, as different methods can produce slightly diverse rankings. The authors suggest that TOPSIS and VIKOR are the most advisable methods for the specific case study.

In the light of the above literature review, the following can be summarized:

-

The Ashby method describes the inherent specificities of the considered case studies, using coefficients (the so-called performance indices) obtained by combining appropriate material properties. That said, it turns out to be effective only when a few parameters (2 or 3) need to be handled while resulting in complexity for managing more parameters. Indeed, although performance indices are effective and independent of the user experience, they are sufficient to properly carry out the choice of one option over the others. Additionally, in regards to the cost aspect, the reference is often based on raw material acquisition while not considering all the manufacturing processes that raise the component cost. At the same time, the environmental effect of End-of-Life (EoL) is often neglected, thus not taking into account the impacts of the entire dismantling/disposal stage (i.e., landfilling or incineration), as well as any credit from recovery processes (i.e., recycling or energy recovery);

-

The cited papers on MCDA methods perform materials selection based on single material properties functional to define the optimal solution based on criteria related to the specific application (i.e., failure load, deflection, tensile strength, fatigue limit, fracture toughness, cost, etc.). However, such an arbitrary choice of parameters dictated by designers’ experience certainly represents a valid way to treat the problem, but it does not allow for the systematic and automatic evaluation of the actual physical phenomena that characterize the specific application.

1.3. Targets and Objectives of This Paper

This article presents an innovative method to select materials for an automotive component from a lightweight and sustainable perspective. The conceived approach incorporates the objective functions provided by the Ashby theory as selection criteria to rank the alternatives in a Vise Kriterijumska Optimizacija I Kompromisno Resenje (VIKOR) modeling environment, considering not only the lightweight issue but also the requirements of production cost and environmental impact. The main innovation of the approach is represented by the integration of the Ashby and the Multi-Criteria Decision Analysis (MCDA) VIKOR methods, which emphasize the interaction between the selection criteria and the environmental aspect, thus offering a holistic approach addressing, at the same time, mechanical properties, cost-efficiency, and the environmental footprint. This represents a significant innovation in material selection methodology, when there is the need to replace a material with another more advantageous one, calculating the mass of the component in advance. This methodology bridges the gap between traditional selection processes and the urgent need for sustainable development in automotive engineering. The materials and methods section explains the model under consideration, detailing the design, cost, and environmental criteria used. The section dedicated to the case study illustrates the method application to a specific case study from the literature, along with objectives, boundary conditions, and constraints. Finally, the results and their implications are critically discussed.

2. Materials and Methods

The materials and method section is split into two paragraphs: The first one describes in detail the conceived approach for materials selection, and the second one provides the implementation of the method to a practical case study taken from the literature.

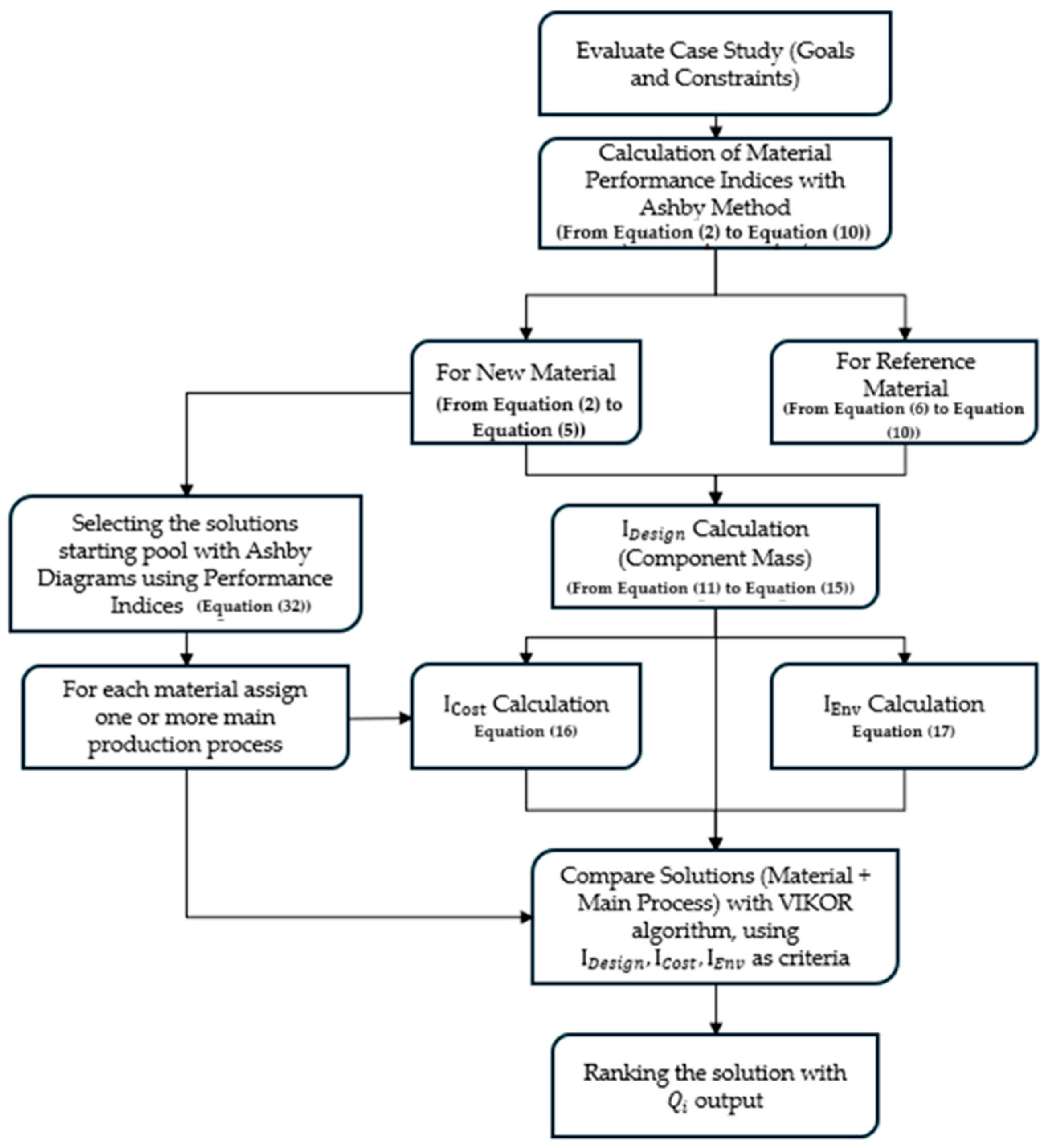
2.1. Method for Materials Selection

The conceived method explores the selection of new materials in an eco-design lightweight perspective based on the comparison with the reference material for a specific car component. For selecting new materials, the approach considers design, cost, and environmental aspects, which are accounted for by the following corresponding indices used by VIKOR to rank the alternatives: design index (I_Design), cost index (I_Cost), and environmental index (I_Env). The method provides that the different design solutions are compared and ranked by VIKOR through the calculation of a single score Q_i based on which alternatives are ranked from lowest to highest score. As the method considers the selection of both material and manufacturing process, the expression “design solution” means the combination of the base constituting material and primary manufacturing process to produce the component. A flowchart explaining the analytical approach followed is provided in Figure 1: Equations are explained in detail in the text.

From here onward, the conceived method is described referring to the specific case study investigated in this paper, a motor mounting bracket for a C-segment electric car subject to a torque load, whose description is provided in Section 2.2.

Design index (I_Design). The I_Design index coincides with the mass of the component. Mass calculation is carried out using performance indices provided by the Ashby theory [38] and based on load and stress type the component is subject to. In general, the component performance depends on component functional requirements, component geometry, and material properties. In regards to the definition of constraints and objectives, the goal for the case study considered is finding a solution that is strong and rigid but, at the same time, provides the lowest possible mass. More specifically, the target is obtaining a component that does not yield under tensile loads and resists torque bending loads. Additionally, it is essential that beyond withstanding loads, the bracket undergoes deformation as little as possible. The calculation of material property function provides inequalities that express the acceptability area for performance index and component mass, as reported in Equations (1) and (2). To reach the optimum design, the selection of component material and geometry that maximize/minimize the performance indices is performed according to Equation (1).

$${PI}_i\ge f{\left(F, G, M\right)}_i\to {PI}_i\ge f{\left(F\right)}_i\cdot f{\left(G\right)}_i\cdot f{\left(M\right)}_i$$

(1)

where PI_i is the performance index of the i-th material, f(F)_i are the functional requirements, f(G)_i are the component geometric parameters, and f(M)_i are material properties. When the groups of functional, geometric, and materials requirements are separable, the optimization of materials properties is independent of the other groups. As a consequence, the performance for ${\left(F\right)}_i\cdot f{\left(G\right)}_i$ is maximized by maximizing $f{\left(M\right)}_i$ [38].

For the design section, PI_i turns out to be m_i, the mass of the component made of the new material. Considering the specific case study of motor bracket, it provides tensile and compression loads: As a consequence, f(M)_i turns out to be $\left({\displaystyle \frac{{\rho }_i}{{\sigma }_{y_i}}}\right)$, which depends only on material type, as reported in Equation (2).

$$m_i\ge f{\left(F\right)}_i\cdot f{\left(G\right)}_i\cdot \left({\displaystyle \frac{{\rho }_i}{{\sigma }_{y_i}}}\right)$$

(2)

where ${\rho }_i$ is the material density [kg/m³], and ${\sigma }_{y_i}$ is the material yield strength [MPa].

The same reasoning applies to component stiffness with the same nature of loads, leading to inequality in Equation (3):

$$m_i\ge f{\left(F\right)}_i\cdot f{\left(G\right)}_i\cdot \left({\displaystyle \frac{{\rho }_i}{E_i}}\right)$$

(3)

where E_i is the Young’s modulus [GPa] of the new material.

In case torque bending load is considered, the inequalities reported in Equations (2) and (3) become the following:

$$m_i\ge f{\left(F\right)}_i\cdot f{\left(G\right)}_i\cdot \left({\displaystyle \frac{{\rho }_i}{\sqrt[3]{{\sigma }_{y_i}^2}}}\right)$$

(4)

$$m_i\ge f{\left(F\right)}_i\cdot f{\left(G\right)}_i\cdot \left({\displaystyle \frac{{\rho }_i}{\sqrt{E_i}}}\right)$$

(5)

Objective functions must also hold for the component with the reference material. Rewriting the inequalities (1)–(5), the following relations are obtained.

$$m_{ref}\ge f{\left(F\right)}_{ref}\cdot f{\left(G\right)}_{ref}\cdot \left({\displaystyle \frac{{\rho }_{ref}}{{\sigma }_{y_{ref}}}}\right)$$

(6)

$$m_{ref}\ge f{\left(F\right)}_{ref}\cdot f{\left(G\right)}_{ref}\cdot \left({\displaystyle \frac{{\rho }_{ref}}{E_{ref}}}\right)$$

(7)

$$m_{ref}\ge f{\left(F\right)}_{ref}\cdot f{\left(G\right)}_{ref}\cdot \left({\displaystyle \frac{{\rho }_{ref}}{\sqrt[3]{{\sigma }_{y_{ref}}^2}}}\right)$$

(8)

$$m_{ref}\ge f{\left(F\right)}_{ref}\cdot f{\left(G\right)}_{ref}\cdot \left({\displaystyle \frac{{\rho }_{ref}}{\sqrt{E_{ref}}}}\right)$$

(9)

$${PI}_{ref}\ge f{\left(F\right)}_{ref}\cdot f{\left(G\right)}_{ref}\cdot f{\left(M\right)}_{ref}$$

(10)

where the subscript “ref” (reference) is referred to the reference material.

Once PI_i and PI_ref are obtained, the method improved in this case study can calculate the ratio (PI_i/PI_ref) and use it to determine a unique value for PI, referred to the new solution. To complete this, the following assumptions are considered: f(F)_i = f(F)_ref and f(G)_i = f(G)_ref. This step involves evaluating and comparing Equation (6) with Equation (2), Equation (7) with Equation (3), Equation (8) with Equation (4), Equation (9) with Equation (5), and Equation (1) with Equation (10), from which the following equations are derived.

$${\left({\displaystyle \frac{P_i}{P_{ref}}}\right)}_j={\displaystyle \frac{f{\left(M\right)}_{ij}}{f{\left(M\right)}_{{ref}_j}}}$$

(11)

$${\left({\displaystyle \frac{m_i}{m_{ref}}}\right)}_1={\displaystyle \frac{{\rho }_i{\sigma }_{ref}}{{\rho }_{ref}{\sigma }_{y_i}}};{\left({\displaystyle \frac{m_i}{m_{ref}}}\right)}_2={\displaystyle \frac{{\rho }_i{E}_{ref}}{{\rho }_{ref}{E}_i}};{\left({\displaystyle \frac{m_i}{m_{ref}}}\right)}_3={\displaystyle \frac{{\rho }_i}{{\rho }_{ref}}}\sqrt[3]{{\left({\displaystyle \frac{{\sigma }_{ref}}{{\sigma }_{y_i}}}\right)}^2};{\left({\displaystyle \frac{m_i}{m_{ref}}}\right)}_4={\displaystyle \frac{{\rho }_i}{{\rho }_{ref}}} \sqrt{{\displaystyle \frac{E_{ref}}{E_i}}}$$

(12)

The first two equations consider tensional loads, while the other two equations consider torque bending load. Each of the four equations gives a different mass ratio depending on load type the material is subjected to and, therefore, four different mass values for the new component. To quantify a unique mass value, a weighted average is assumed, as reported in Equations (13)–(15).

$$\left({\displaystyle \frac{P_i}{P_{ref}}}\right)={\displaystyle \frac{{\sum }_{j=1}^n\left(w_j\frac{f{\left(M\right)}_{ij}}{f{\left(M\right)}_{{ref}_j}}\right)}{{\sum }_{j=1}^n{w}_j}} \to P_i=P_{ref}{\displaystyle \frac{{\sum }_{j=1}^n\left(w_j\frac{f{\left(M\right)}_{ij}}{f{\left(M\right)}_{{ref}_j}}\right)}{{\sum }_{j=1}^n{w}_j}}$$

(13)

$${\displaystyle \frac{m_i}{m_{ref}}}={\displaystyle \frac{w_1\frac{{\rho }_i{\sigma }_{ref}}{{\rho }_{ref}{\sigma }_{y_i}}+w_2\frac{{\rho }_i{E}_{ref}}{{\rho }_{ref}{E}_i}+w_3\frac{{\rho }_i}{{\rho }_{ref}}\sqrt[3]{{\left(\frac{{\sigma }_{ref}}{{\sigma }_{y_i}}\right)}^2}+w_4\frac{{\rho }_i}{{\rho }_{ref}} \sqrt{\frac{E_{ref}}{E_i}}}{{\sum }_{j=1}^4{w}_j}}$$

(14)

$$I_{{Design}_i}=m_i=m_{ref}{\displaystyle \frac{w_1\frac{{\rho }_i{\sigma }_{ref}}{{\rho }_{ref}{\sigma }_{y_i}}+w_2\frac{{\rho }_i{E}_{ref}}{{\rho }_{ref}{E}_i}+w_3\frac{{\rho }_i}{{\rho }_{ref}}\sqrt[3]{{\left(\frac{{\sigma }_{ref}}{{\sigma }_{y_i}}\right)}^2}+w_4\frac{{\rho }_i}{{\rho }_{ref}} \sqrt{\frac{E_{ref}}{E_i}}}{{\sum }_{j=1}^4{w}_j}}$$

(15)

where $m_{av{g}_i}$ is the mass of the lightweight component averaged based on different mass values derived from different PI ratios, while w_j are the corresponding weights.

For example, if in a different case study with respect to the bracket component, the tensile loads are considered more important than bending loads, weights w₃ and w₄ are lower than weights w₁ and w₂. On the contrary, in case material stiffness is assumed of lesser importance because the designer uses modification to component geometry to achieve greater stiffness, weights w₂ and w₄ are lower than weights w₁ and w₃. These corrective weights allow for expanding the perimeter research of the new lightweight solutions

-

Without the need of considering the assumptions f(F)_i = f(F)_ref and f(G)_i = f(G)_ref;

-

Setting parameters (PI_i/PI_ref)_j according to the needs of the specific case study.

Cost index (I_Cost). The cost index is defined to calculate the production cost of the component. I_Cost is defined as provided in Equation (16):

$$I_{{Cost}_{ik}}=m_i{\displaystyle \frac{C_{m_i}}{1-f_k}}+\left({\displaystyle \frac{C_{t_k}}{n}}\right)int\left({\displaystyle \frac{n}{n_{t_k}}}+0.51\right)+{\displaystyle \frac{1}{{\dot{n}}_k}}\left({\displaystyle \frac{{C_c}_k}{L_k\ast t_{{wo}_k}}}\right){\left(1+d\right)}^{t_{{wo}_k}}+{\displaystyle \frac{{\dot{C}}_{oh}}{{\dot{n}}_k}}$$

(16)

where k is the k-th industrial process, $C_{m_i}$ is the cost of raw material [EUR/kg], $f_k$ is the scrap fraction (fraction of primary material that ends up as sprues, risers, turnings, rejects, or waste) [−], $C_{t_k}$ is the cost of tooling when it needs to be replaced [EUR], n is the batch size considered for the production of the component [−], and $n_{t_k}$ is the tool life. It is the number of units that a set of tooling can produce before it has to be replaced [−], ${\dot{n}}_k$ is the production rate of the k-th process [1/hr], ${C_c}_k$ is the Capital Cost of Equipment [EUR], $L_k$ is the load factor, the fraction of time for which the equipment is productive [−], $t_{{wo}_k}$ is the capital write-off time [years], d is the discount rate [−], and ${\dot{C}}_{oh}$ is the overhead rate [EUR/hr].

Data characterizing both materials and industrial processes of the selected design solutions (mechanical, physical, economical, and environmental properties) are from the Granta Selector Database [63]. I_Cost is defined as considering only the primary production process of the component, while it does not account for any secondary processes or End-of-Life (EoL) treatments for the lack of data

Environmental index (I_Env). The environmental index is defined to quantify the Climate Change (CC) effect (in kilograms of CO₂_eq) due to the entire component Life Cycle (LC). The calculation of I_ENV is provided in Equation (17):

$$I_{{Env}_{ik}}=I_{{En{v}_{raw}}_{ik}}+I_{{En{v}_{use}}_i}+I_{{En{v}_{Eol}}_i}$$

(17)

where $I_{{En{v}_{raw}}_{ik}}$ quantifies the emissions due to raw materials acquisition considering also the increase in material quantity for primary process. $I_{{En{v}_{raw}}_{ik}}$ is calculated through the following relation:

$$I_{En{v}_{ra{w}_{ik}}}={\displaystyle \frac{m_i}{1-f_k}}\ast C{O_2}_i$$

(18)

where $C{O_2}_i$ is the CC due to extraction of 1 kg of the i-th material, and it is taken from Granta Selector (R2 2023) [63].

$I_{{Env\_Use}_i}$, in Equation (17), assesses the CC caused by component use stage, and it is quantified according to the following equation [64].

$$I_{{Env}_{{use}_i}}=m_i\ast IRV\ast mileage$$

(19)

where mileage is the distance traveled during component operation [km] (assumed equal to vehicle use stage mileage), and IRV is the Impact Reduction Value, defined as the CC caused by the production of 1 kWh electricity consumed by the vehicle on which the component is mounted [kWh/100 km100 kg].

As provided in

Table 1. IRV coefficient calculated by geographical relevance (NO: Norway, EU28: 28-country European average, PL: Poland) and standard driving cycle (NEDC: New European Driving Cycle, WLTC: Worldwide harmonized Light vehicles Test Cycles, ALDC: All-Long Driving Cycle) [64,65].

IRV (kgCO2_eq/(100 km × 100 kg))
	NEDC	WLTP	ALDC
NO	IRVNO_NEDC = 3.0 × 10−6 M + 0.0116	IRVNO_WLT P = 4.0 × 10−6 M + 0.0121	IRVNO_WLTP = 4.0 × 10−6 M + 0.0121
EU28	IRVEU28_NEDC = 4.7 × 10−5 M + 0.1591	IRVEU28_WLTP = 5.6 × 10−5 M + 0.1655	IRVEU28_ALDC = 1.2 × 10−4 M + 0.2231
PL	IRVPL_NEDC = 1.1 × 10−4 M + 0.3798	IRVPL_WLTP = 1.3 × 10−4 M + 0.3951	IRVPL_ALDC = 2.8 × 10−4 M + 0.5326

, the IRV coefficient depends on car mass (M), driving cycle, and grid mix assumed for electricity production.

For the motor bracket case study, the following boundary conditions are considered: 2 t car mass, 200,000 km LC mileage, 28 European countries (EU28) grid mix for electricity production, and WLTP driving cycle for the operation stage. Regarding EoL, the corresponding index ($I_{Env\_EoL}$) is calculated as follows [65]:

$$I_{En{v}_{Eo{l}_i}}={CC}_{Di{s}_i}+C{C}_{Sh{r}_i}+C{C}_{Se{p}_i}+C{C}_{Re{c}_i}+C{C}_{{Enr}_i}+C{C}_{Dis{p}_i}$$

(20)

$$C{C}_{{Dis}_i}=m_i\ast c{c}_{{Dis}_i}$$

$$C{C}_{Sh{r}_i}=m_i\ast c{c}_{Sh{r}_i}$$

$$C{C}_{{Sep}_i}=m_i\ast c{c}_{{Sep}_i}$$

$$C{C}_{{Rec}_i}={\eta }_{eff}\ast m_i\ast S{F}_i\ast c{c}_{{Mat}_i}$$

$$C{C}_{{Enr}_i}=m_i\ast \left(1-{\vartheta }_i\right)\left(c{c}_{{EnRec}_i}-H_i\ast {C{O}_{2}P}_i\ast {\eta }_{El}\right)$$

$$C{C}_{Dis{p}_i}=\left\{\begin{array}{c}{m}_i\ast c{c}_{{Disp}_i}\ast {\vartheta }_i\\ \left(1-{\eta }_{eff}\right)\ast m_i\ast c{c}_{{Disp}_i}\end{array}\right.$$

where ${CC}_{{Dis}_i}$ is the CC of component disassembly [kgCO₂_eq], $C{C}_{Sh{r}_i}$ is the CC of component shredding [kgCO₂_eq], $C{C}_{Se{p}_i}$ is the CC of materials separation after shredding [kgCO₂_eq], $C{C}_{Re{c}_i}$ is the CC credit achieved through recycling of separated materials [kgCO₂_eq], $C{C}_{En{Rec}_i}$ is the CC credit achieved through incineration with energy recovery of separated materials [kgCO₂_eq], $C{C}_{Dis{p}_i}$ is the CC of disposal phase of non-separated shredded materials [kgCO₂_eq], $c{c}_{{Dis}_i}$ is the mass-specific CC of disassembly step [kgCO₂_eq/kg], $c{c}_{Sh{r}_i}$ is the mass-specific CC of shredding phase [kgCO₂_eq/kg], $c{c}_{{Mat}_i}$ is the mass-specific CC in material stage [kgCO₂_eq/kg], $c{c}_{{EnRec}_i}$ is the mass-specific CC of incineration with energy recovery [kgCO₂_eq/kg], $c{c}_{{Disp}_i}$ is the mass-specific CC of disposal phase [kgCO₂_eq/kg], $S{F}_i$ is the recycling substitution factor (quota of avoided primary production impact due to recycling) $\left[-\right]$, ${\eta }_{eff}$ is a factor that quantifies efficiency of separation in post-shredding phase $\left[-\right]$, ${\vartheta }_i$ is the share of fibers in composite materials (applicable only for composite materials) $\left[-\right]$, $H_i$ is the combustion heat in incineration with energy recovery (net value) [MJ/kg], ${C{O}_{2}P}_i$ is the specific CC of incineration with energy recovery [kgCO₂_eq/MJ], and ${\eta }_{El}$ is the efficiency of waste-to-energy plant $\left[-\right]$.

Based on calculated values for I_Design, I_Cost, and I_Env, the method provides that VIKOR is applied to evaluate the above-mentioned indices and rank the feasible design options based on predefined weighting criteria. VIKOR is selected for integration with the Ashby method, as it is mathematically simpler to manage. Furthermore, unlike other algorithms such as TOPSIS, it does not compare solutions based on Euclidean distance between ideal solutions, but it gives full consideration to the preferences and the properties of conflict problem determination compromise. This is completed to help users make appropriate decisions by considering compromise criteria to identify optimal solutions when there is the need to meet different and contrasting requirements. A description of the algorithm is given below: After determining the pairwise matrix of dimensions mxn, where x_il is the value of lth criteria for the ith solution,

$$X=\left[\begin{array}{ccc}{x}_{11}& \cdots & x_{1n}\\ ⋮& x_{il}& ⋮\\ x_{m1}& \cdots & x_{mn}\end{array}\right]$$

(21)

The subsequent step is normalizing the matrix above, which is carried out as follows [66]:

$$f_{il}={\displaystyle \frac{x_{il}}{\sqrt{\sum _{i=1}^m\left(x_{il}^2\right)}}}$$

(22)

where f_il is the normalized value of lth criteria for the ith solution. After this, the worst-normalized value $\left(f_j^{-}\right)$ and the best-normalized value $\left(f_j^{+}\right)$ need to be determined for all criteria. If the criterion is a beneficial attribute, the following relations are considered:

$$\left\{\begin{array}{c}{f}_l^{-}=\underset{i}{\min }{f}_{il}\\ f_l^{+}=\underset{i}{\max }{f}_{il}\end{array}\right.$$

(23)

Otherwise, if the criterion is a cost attribute, the following relations are considered:

$$\left\{\begin{array}{c}{f}_l^{-}=\underset{i}{\max }{f}_{il}\\ f_l^{+}=\underset{i}{\min }{f}_{il}\end{array}\right.$$

(24)

These values are used to calculate S_i (group utility) and R_i (individual regret) with the following equations:

$$S_i={\sum }_{l=1}^n\left(w_l{\displaystyle \frac{f_l^{+}-f_{il}}{f_l^{+}-f_l^{-}}}\right)$$

(25)

$$R_i=\underset{l}{\mathit{max}}\left(w_l{\displaystyle \frac{f_l^{+}-f_{il}}{f_l^{+}-f_l^{-}}}\right)$$

(26)

where $w_l$ are the weights, respectively, for design, cost, and sustainability aspects defined as ${w_I}_{Design}$, ${w_I}_{Cost}$, and ${w_I}_{CC}$.

Finally, the single score Q_i is calculated as follows:

$$Q_i=v{\displaystyle \frac{S_i-S^{-}}{S^{+}-S^{-}}}+\left(1-v\right){\displaystyle \frac{R_i-R^{-}}{R^{+}-R^{-}}}$$

(27)

where v is a weight to support the maximum group utility strategy and varies between 0 and 1. Generally, it is assumed to be equal to 0.5 in the literature.

The values S⁺, S⁻, R⁺, and R⁻ are the defined as follows:

$$S^{+}=\underset{i}{\mathit{max}}{S}_i=\underset{i}{\mathit{max}}{\sum }_{l=1}^n\left(w_l{\displaystyle \frac{f_l^{+}-f_{il}}{f_l^{+}-f_l^{-}}}\right)$$

(28)

$$S^{-}=\underset{i}{\mathit{min}}{S}_i=\mathit{mi}{n}_i{\sum }_{l=1}^n\left(w_l{\displaystyle \frac{f_l^{+}-f_{il}}{f_l^{+}-f_l^{-}}}\right)$$

(29)

$$R^{+}=\underset{i}{\mathit{max}}{R}_i=\underset{i}{\mathit{max}}\left(\underset{l}{\mathit{max}}\left(w_l{\displaystyle \frac{f_l^{+}-f_{il}}{f_l^{+}-f_l^{-}}}\right) \right)$$

(30)

$$R^{-}=\underset{i}{\mathit{min}}{R}_i=\underset{i}{\mathit{min}}\left(\underset{l}{\mathit{max}}\left(w_l{\displaystyle \frac{f_l^{+}-f_{il}}{f_l^{+}-f_l^{-}}}\right) \right)$$

(31)

Then, the algorithm orders the alternatives in ascending order of the value of Q_i: The smaller the value, the higher the ranking.

2.2. Case Study

This section deals with the validation of the conceived method by applying it to a practical case study taken from literature. As already mentioned before, the chosen application is the redesign of a motor bracket of a passenger C-segment electric car treated by Celik et al. [67].

Table 2. Main technical features of bracket component in the reference design version (data from [67]).

Motor mounting Bracket Component
Material	AISI304 Stainless Steel
Mass	8.913 [kg]
Max torque without yielding	3 × 105 [N/mm]
Max displacement	0.284 [mm]
Max equivalent stress	170 [MPa]

reports the main technical features of the bracket component, which is chosen as reference design version for the implementation of materials selection method.

A first selection of materials applicable for lightweighting was carried out by considering the Ashby diagrams reported in Figure 2a,b, which are built by means of the Granta Selector software (R2 2023 version) [63]. The diagrams show how materials are arranged within the database:

-

The first one (Figure 2a) provides the ratio ${\displaystyle \frac{{\rho }_i}{{\sigma }_{y_i}}}$ on the x-axis and the ratio ${\displaystyle \frac{{\rho }_i}{E_i}}$ on the y-axis, thus highlighting the ability of the material under tensile/compression loads to be light but, at the same, time rigid and strong (the lower the values, the better the material);

-

The second one (Figure 2b) provides the ratio ${\displaystyle \frac{{\rho }_i}{\sqrt[3]{{\sigma }_{y_i}^2}}}$ on the x-axis and the ratio ${\displaystyle \frac{{\rho }_i}{\sqrt{E_i}}}$ on the y-axis, thus highlighting the ability of the material under torque bending loads to be light but, at the same time, rigid and strong (the lower the values, the better the material).

As provided in Figure 2, composite materials are located at the bottom left of both diagrams, stressing that they are the best-performing materials (low density associated with high structural integrity features). Regarding metals, ferrous materials are found in the upper part of diagrams, while for non-ferrous materials (such as aluminum and magnesium), the position varies when passing from one diagram to the other. Figure 2a shows that non-ferrous metals are overlapped with ferrous alloys, while in Figure 2b, non-ferrous materials are positioned in the central area of the diagram, demonstrating better performances in case of torque bending loads.

Taking into account the values of ${\displaystyle \frac{{\rho }_{ref}}{{\sigma }_{y_{ref}}}}$, ${\displaystyle \frac{{\rho }_{ref}}{E_{ref}}}$, ${\displaystyle \frac{{\rho }_{ref}}{\sqrt[3]{{\sigma }_{y_{ref}}^2}}}$, and ${\displaystyle \frac{{\rho }_{ref}}{\sqrt{E_{ref}}}}$ in the baseline design version (bracket made of AISI 304 stainless steel), it is assumed that all materials that provide a maximum deterioration of indices of up to 15% are considered as acceptable. The following equations provide the maximum acceptable value for indices above.

$${\left({\displaystyle \frac{{\rho }_i}{{\sigma }_{y_i}}}\right)}_{Max}=1.15\ast {\displaystyle \frac{{\rho }_{ref}}{{\sigma }_{y_{ref}}}}; {\left({\displaystyle \frac{{\rho }_i}{E_i}}\right)}_{Max}=1.15\ast {\displaystyle \frac{{\rho }_{ref}}{E_{ref}}};$$

$${\left({\displaystyle \frac{{\rho }_i}{\sqrt[3]{{\sigma }_{y_i}^2}}}\right)}_{Max}=1.15\ast {\displaystyle \frac{{\rho }_{ref}}{\sqrt[3]{{\sigma }_{y_{ref}}^2}}}; {\left({\displaystyle \frac{{\rho }_i}{\sqrt{E_i}}}\right)}_{Max}=1.15\ast {\displaystyle \frac{{\rho }_{ref}}{\sqrt{E_{ref}}}}$$

(32)

Due to functional features and operational conditions of the component, the following constraints are also assumed in the analysis: As the bracket is located close to an electric motor, a maximum operating temperature of 70 °C was considered, and the minimum yielding stress of the material was set at 170 MPa. Such a value is chosen based on [59], a redesign case study conducted on a similar application in terms of both component features and nature of the loads. Also, given the geometry and specifications of the bracket, only a part of the available processes in the Granta Database [63] was selected, that is, only those compatible with component and materials considered. Since not all materials can be produced by means of all industrial processes (due to technological constraints, materials features, and geometric reasons), only specific manufacturing technologies were selected for the bracket case study (see

Table 3. Manufacturing processes selected for the case study (data provided by Granta Selector Database [63]).

Industrial Processes	$1-{\mathit{f}}_{\mathit{k}}$	${\mathit{C}}_{{\mathit{t}}_{\mathit{k}}}$	${\mathit{n}}_{{\mathit{t}}_{\mathit{k}}}$	${\dot{\mathit{n}}}_{\mathit{k}}$	${\mathit{C}}_{{\mathit{C}}_{\mathit{k}}}$
Binder jetting	0.98	0.05	316,000	22.40	361,000
Squeeze casting	0.93	22,200	22,400	30.00	393,000
Gravity die casting	0.69	10,500	31,600	15.80	35,200
Investment casting, automated (lost wax process)	0.82	6810	1580	44.70	39,300
Evaporative pattern casting, automated	0.49	2980	7071	31.62	23,086
Shell casting	0.49	3930	3160	15.81	5560
Ferro die casting	0.80	44,500	7070	54.80	393,000
Green sand casting, automated	0.63	2150	31,600	77.50	39,300
Replicast casting	0.69	5560	3160	22.40	21,500
Press forming	0.75	78,600	100,000	77.50	278,000
Cold isostatic pressing (CIP)	0.99	1470	316	31.60	141,000

). For the identification of processes suitable for application in the automotive field, ref. [18] is assumed as reference. The choice of specific manufacturing processes that meet case study boundary conditions (batch production scale, applicability to component, technological maturity level, and compatibility with materials used) was performed by a targeted selection on the Granta Database based on technological, geographical, and temporal requirements.

The preliminary screening above provides 1151 materials. Considering the combination of industrial processes compatible with such materials, a set of 1850 possible design solutions (where a solution is intended as the association of base material with manufacturing technology) was obtained. Since the bracket equipped a mass-production car, a limitation was set on the increase in production cost of the lightweight alternative with respect to the baseline design. Such a limitation was defined through the coefficient expressed by Equation (33), that is, the ratio between cost and mass variation due to lightweight design:

$${\left({\displaystyle \frac{{\Delta }_{Cost}}{{\Delta }_{Mass}}}\right)}_{ik}={\displaystyle \frac{I_{Cos{t}_{ik}}-I_{Cos{t}_{ref}}}{m_{ref}-I_{Desig{n}_i}}}$$

(33)

where $m_{ref}$ and $I_{Desig{n}_i}$ are the same as Equation (15), $I_{Cos{t}_{ik}}$ is defined in Equation (16), and $I_{Cos{t}_{ref}}$ is the value of $I_{Cos{t}_{ik}}$ considering the reference (AISI304 stainless steel and assumed the component is produced by press forming).

Thus, the total cost of the bracket was put in relation to the lightweight potential offered by the specific design alternative: Negative values of ${\left({\displaystyle \frac{{\mathsf{\Delta }}_{Cost}}{{\mathsf{\Delta }}_{Mass}}}\right)}_{ik}$ were considered acceptable only if $I_{Cos{t}_{ik}}\le I_{Cos{t}_{ref}}$, while solutions which result in an increase in component mass ($m_{ref}<I_{Desig{n}_i}$) were discarded. As a consequence, only design options with a coefficient ${\left({\displaystyle \frac{{\mathsf{\Delta }}_{Cost}}{{\mathsf{\Delta }}_{Mass}}}\right)}_{ik}$ lower than the acceptable maximum value were compared and ranked through the VIKOR model: For the bracket component, such acceptability maximum value was set to 10 Eur/kg.

Regarding comparison and ranking of the selected 1850 solutions, the following considerations were made:

-

Parameters $L_k$, $t_{{wo}_k}$, d, and ${\dot{C}}_{oh}$ are those predefined by the Granta Selector software, and they were assumed constant for each industrial process: $L_k=0.5$, $t_{{wo}_k}=5 \mathrm{y}\mathrm{e}\mathrm{a}\mathrm{r}\mathrm{s}$, d = 0.05, and ${\dot{C}}_{oh}=150 \mathrm{E}\mathrm{U}\mathrm{R}/\mathrm{h}$;

-

As the case study deals with a large-scale production electric vehicle, parameter n was set to 100,000 units;

-

It was assumed that the bracket component was manually disassembled, so the specific environmental impact of disassembly step (cc_Dis) was set to 0 [kgCO₂_eq/kg];

-

The specific impact of the shredding phase ($c{c}_{Sh{r}_i}$) was assumed constant for all materials selected, and it was considered an average value taking into account the shredding of the entire vehicle (0.0175 [kgCO₂_eq/kg]), as provided by [64]. The same assumption was made for the disposal phase, for which $c{c}_{{Disp}_i}$ was assumed to be 0.03 [kgCO₂_eq/kg] (data from [68]);

-

Recycling was provided only for metals and metallic fibers. SF was considered constant for the same material, and it was assumed to be −0.25 for ferrous alloys and −0.15 for non-ferrous alloys. For other materials, SF was assumed to be 0;

-

${\eta }_{eff}$ was set to 0.98 for metal alloys, while for metallic fibers, it was calculated as $0.98\ast {\vartheta }_i$;

-

$H_i$ was provided by Granta Selector Database [63] for each material option explored;

-

${\eta }_{El}$ was set to 0.3;

-

${C{O}_{2}P}_i$ was derived from EcoInvent-APOS391 database considering the specific energy generation process “heat, district or industrial, natural gas | market for heat, district or industrial, natural gas/heat and power co-generation, natural gas, conventional power plant” [69];

-

Since the case study deals with a large volume production component for which optimization of manufacturing cost represent a crucial point, it was chosen to give priority to the cost aspect, for which the corresponding index (I_Cost) was assumed to be four times more relevant than the other two indices (I_Design and I_Env). Consequently, the resulting weights for design, cost, and sustainability aspects are, respectively, ${w_I}_{Design}=0.167$, ${w_I}_{Cost}=0.667$, and ${w_I}_{CC}=0.167$;

-

All three indices are considered “cost attributes”, so in the ranking performed through VIKOR, the lower the index value, the better the solution.

Weights related to performance indices were considered unitary: Sensitivity analysis of results based on variability of weights of different design criteria represents an interesting point for future development of this study.

3. Results and Discussion

Based on the acceptability criteria and parameters setting described in the previous section, the number of design solutions (the combination of materials and manufacturing processes automatically selected by the tool) that result as a viable option for the bracket component is 1316, which are ranked in order of preference through the VIKOR method.

Table 4. Results of materials selection: ranking of the first 20 lightweight options (only materials with a ${\displaystyle \frac{{\mathsf{\Delta }}_{Cost}}{{\mathsf{\Delta }}_{Mass}}}$ less than 10 Eur/kg and criteria weights $w_{Design}=0.167$, $w_{Cost}=0.667$, and $w_{CC}=0.167$).

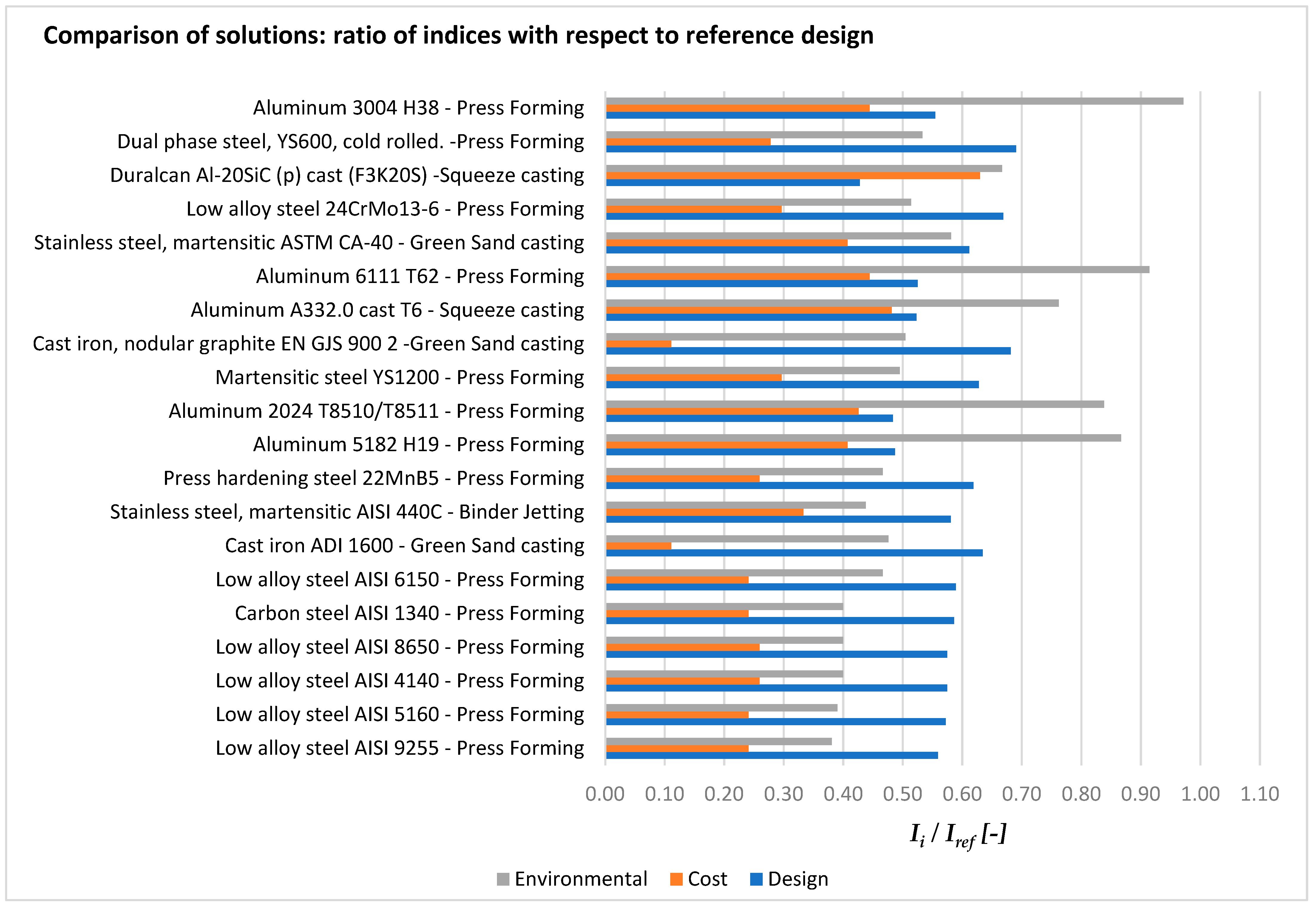
Ranking	Design Solution	Mass [kg]	Cost			CC [kgCO2_eq]		Qi
			Raw Material [EUR]	Total [EUR]	$\frac{{\mathsf{\Delta }}_{\mathit{C}\mathit{o}\mathit{s}\mathit{t}}}{{\mathsf{\Delta }}_{\mathit{M}\mathit{a}\mathit{s}\mathit{s}}}$ [EUR/kg]	Use	Total LC
	Ref: Stainless Steel Austenitic AISI 304 Annealed–Press Forming	REF: 8.91	REF: 50	REF: 54		REF: 49	REF: 105
1	Low-alloy steel, AISI 9255, oil quenched and tempered at 205 °C—press forming	4.98	9	13	−14	27.6	40	0.0149
2	Low-alloy steel, AISI 5160, oil quenched and tempered at 205 °C—press forming	5.10	9	13	−14	28.3	41	0.0195
3	Low-alloy steel, AISI 4140, oil quenched and tempered at 205 °C—press forming	5.12	10	14	−14	28.4	42	0.0211
4	Low-alloy steel, AISI 8650, oil quenched and tempered at 205 °C—press forming	5.12	11	14	−14	28.4	42	0.0225
5	Carbon steel, AISI 1340, oil quenched and tempered at 205 °C—press forming	5.22	9	13	−15	29	42	0.0242
6	Low-alloy steel, AISI 6150, oil quenched and tempered at 205 °C—press forming	5.25	10	13	−11	28.8	49	0.0268
7	Cast-iron, austempered ductile, ADI 1600—green sand casting, automated	5.65	4	6	−15	31.3	50	0.0340
8	Stainless steel, martensitic, AISI 440C, tempered at 316 °C—binder jetting	5.17	10	18	−10	28.7	46	0.0352
9	Press hardening steel, 22MnB5, austenized and H20 quenched, coated—press forming	5.51	10	14	−12	30.6	49	0.0396
10	Aluminum, 5182, H19—press forming	4.34	19	22	−7	24.1	91	0.0436
11	Aluminum, 2024, T8510/T8511—press forming	4.31	20	23	−7	23.3	88	0.0436
12	Martensitic steel, YS1200, hot rolled—press forming	5.59	12	16	−11	31	52	0.0483
13	Cast-iron, nodular graphite, EN GJS 900 2, hardened and tempered—green sand casting, automated	6.07	4	6	−17	33.7	53	0.0592
14	Aluminum, A332.0, cast, T6—squeeze casting	4.66	19	26	−7	25.8	80	0.0592
15	Aluminum, 6111, T62—press forming	4.68	20	24	−7	26	96	0.0615
16	Stainless steel, martensitic, ASTM CA-40, cast, tempered at 315 °C—green sand casting, automated	5.45	20	22	−9	30.3	61	0.0633
17	Low-alloy steel, 24CrMo13-6, quenched and tempered—press forming	5.96	13	16	−13	33	54	0.0650
18	Duralcan Al-20SiC (p) cast (F3K20S)—squeeze casting	3.81	28	34	−4	21.1	70	0.0691
19	Dual-phase steel, YS600, cold rolled—press forming	6.15	12	15	−14	34.1	56	0.0716
20	Aluminum, 3004, H38—press forming	4.94	21	24	−7	27.4	102	0.0771

shows the ranking of the first 20 lightweight options, for each of which the following parameters are reported:

-

Component mass (corresponding to $I_{Desig{n}_i}$, as provided by Equation (15));

-

Cost of raw materials (corresponding to $m_i$∗${\displaystyle \frac{C_{m_i}}{1-f_k}}$, as provided by Equation (16));

-

Total component cost ($I_{Cos{t}_{ik}}$, as provided by Equation (16));

-

Cost variation in relation to weight reduction (corresponding to coefficient ${\left({\displaystyle \frac{{\mathsf{\Delta }}_{Cost}}{{\mathsf{\Delta }}_{Mass}}}\right)}_{ik}$, as provided by Equation (33));

-

Environmental impact of component use stage ($I_{En{v}_{us{e}_i}}$, as provided by Equation (19));

-

Environmental impact of entire component LC ($I_{{Env}_{ik}}$, as provided by Equation (17));

-

Single score $Q_i$, based on which VIKOR provides the ranking of the solutions: The lower the value, the higher the solution’s ranking.

The first discussion point is represented by the fact that negative values of $\left({\displaystyle \frac{{\mathsf{\Delta }}_{Cost}}{{\mathsf{\Delta }}_{Mass}}}\right)$ correspond to an alternative with potential for cost saving, that is, a solution which provides lightweighting and at the same time cost reduction. Regarding the ranking of the selected lightweight options, wrought steels are placed in the top positions (from the first to the sixth), and all of these are produced through press forming as the primary manufacturing process. The reason steels rank so high is that, despite the lower mechanical strength with respect to other materials in the ranking (such as plastic matrix composites or metal matrix composites) and the consequent smaller weight reduction offered, they are definitely more economical (1.40 EUR/kg raw material cost for steel against 3.30 EUR/kg raw material cost for aluminum) and eco-friendly due to their low total emissions. Table 4 stresses that forging processes for press forming generally affect the final cost of the component by 3–4 EUR.

Regarding casting, traditional methods are the cheapest (green sand casting 2 EUR/piece), while the more innovative processes (such as squeeze casting) can achieve a cost of 6–7 EUR/piece. Finally, as known from the literature, additive manufacturing processes result to be the most expensive, accounting for 8 EUR/piece for binder jetting. Regarding the ranking of materials obtained, in the first position, a low-alloyed steel (low-alloy steel, AISI 9255, oil quenched and tempered at 205 °C), was manufactured through press forming. The comparison of such a lightweight option with the baseline (press-formed AISI304 stainless steel) stresses a mass decrease of around 44%, a 75% cost saving, and a CC reduction of around 60%. The following three positions (from the second to the fourth) also provide low-alloy steels, which provide very similar savings for all the assessment criteria considered: a mass reduction in the range of 5.10–5.12 kg, cost decrease in the range of 13–14 EUR, CC impact abatement in the range of 41–42 kgCO₂_eq. Among the low-alloy steel solutions, the fifth position is occupied by an alternative based on carbon steel, which involves a good lightweight potential (mass of the lightweight component of 5.22 kg) due to the mechanical properties comparable with the first position design (see

Table 5. Material properties of the top 20 design solutions.

Material	Price Raw Material [Eur/kg]	Density [kg/m3]	Young Modulus [GPa]	Yield Strength [MPa]	Primary Production CC (Virgin Grade) [kg/kg]
Ref: Stainless steel austenitic AISI 304 annealed	5.29	7850	196	252	5.73
Low-alloy steel, AISI 9255, oil quenched and tempered at 205 °C	1.38	7850	211	2040	2.33
Low-alloy steel, AISI 5160, oil quenched and tempered at 205 °C	1.36	7850	209	1780	2.33
Low-alloy steel, AISI 4140, oil quenched and tempered at 205 °C	1.44	7850	212	1630	2.33
Low-alloy steel, AISI 8650, oil quenched and tempered at 205 °C	1.56	7850	211	1660	2.33
Carbon steel, AISI 1340, oil quenched and tempered at 205 °C	1.36	7850	207	1580	2.33
Low-alloy steel, AISI 6150, oil quenched and tempered at 205 °C.	1.40	7850	206	1680	3.44
Cast-iron, austempered ductile, ADI 1600	0.50	7060	159	1360	2.43
Stainless steel, martensitic, AISI 440C, tempered at 316 °C	1.89	7800	200	1890	4.31
Press-hardening steel, 22MnB5, austenized and H20 quenched, coated	1.36	7850	210	1090	2.96
Aluminum, 5182, H19	3.23	2650	70	392	13
Aluminum, 2024, T8510/T8511	3.41	2770	76	398	12
Martensitic steel, YS1200, hot rolled	1.62	7850	210	1020	3.35
Cast-iron, nodular graphite, EN GJS 900 2, hardened and tempered	0.44	7150	172	749	2.33
Aluminum, A332.0, cast, T6	3.74	2700	73	280	12.5
Aluminum, 6111, T62	3.18	2710	69	320	12.6
Stainless steel, martensitic, ASTM CA-40, cast, tempered at 315 °C	2.29	7610	200	1140	4.15
Low-alloy steel, 24CrMo13-6, quenched and tempered	1.60	7800	200	831	3.16
Duralcan Al-20SiC (p) cast (F3K20S)	6.70	2810	101	355	11.9
Dual-phase steel, YS600, cold rolled	1.42	7850	210	671	3.28
Aluminum, 3004, H38	3.15	2720	70	250	12.6

) and also remarkable cost and CC savings (respectively, 75% and 53%). The seventh position provides a cast-iron (ADI 1600 austempered ductile) alternative produced by the green sand casting automated process. Cast materials have, in general, lower mechanical properties than wrought materials: This involves a lower mass decrease for the cast-iron bracket to withstand the loads the component is subjected to (5.65 kg). That said, the cost and CC reduction results are very high, respectively, 89% and 52%. The reason for the strong cost reduction is the very low cost of the raw material (0.44 EUR/kg). Another design alternative made of cast iron is found in the 13th position (nodular graphite, EN GJS 900 2, hardened and tempered), which is down in the ranking mainly because of the bigger mass despite the low cost of material acquisition.

In the eighth position, the ranking provides a martensitic stainless steel component (AISI 440C tempered at 316 °C) produced through additive manufacturing binder jetting that guarantees a 42% mass saving. Despite the cost reduction being very high (66%), such a solution is the worst among the steel design options in the top 20 positions: This is due to the high cost of the additive manufacturing technology, which amounts to 8 EUR to produce a bracket of 5.17 kg. In the 9th and 12th positions, the ranking provides, respectively, press hardening steel 22MnB5 and martensitic steel YS1200, both manufactured through the press forming process. These materials, typically used for crash management components, show worse mechanical properties than the low-alloy steels (as reported in Table 5), so the corresponding component mass results higher (around 5.5 kg for both alternatives), and this is reflected in the bigger cost and CC (14 EUR and 16 EUR; 49 kgCO₂_eq and 52 kgCO₂_eq).

Going down in the ranking, the classification provides five aluminum solutions: pressed-formed 5182 aluminum—H19 (in 10th position), pressed-formed 2024 aluminum—T8510/T8511 (in 11th position), squeeze-cast A332.0 aluminum (in 14th position), pressed-formed 6111 aluminum—T62 (in 15th position), and pressed-formed 3004 aluminum—H38 (in 20th position). In general, it can be said that the use of aluminum allows for achieving a bigger mass saving than the steel design options (in the range of 44–52%). That said, when evaluating the economic aspect, the very high costs of raw materials acquisition (definitely bigger than steels, see Table 5) partially counterbalance the low component mass, leading, however, to cost savings that remain very important (in the range 52–59%). On the other hand, the high environmental impact due to the strong energy intensity of aluminum extraction and production makes the CC saving relatively limited, from a maximum of 80 kgCO₂_eq for A332.0 T6 aluminum produced through squeeze casting (position n°14 in the ranking), up to an almost null reduction (3 kgCO₂_eq) for press-formed 3004 H38 aluminum (position n°20 in the ranking). As a confirmation, Table 3 shows a big difference in the CC between use and the entire LC, meaning that the vast majority of the environmental impact is concentrated in the materials acquisition stage.

Passing to the last positions, the Duralcan Al-20SiC design processed by squeeze casting is found on the 18th. The strength of this kind of material is the lightweight potential, which is comparable with low-alloy steels (57% mass saving), while considering cost and CC, the overall reduction is around 35%. Such an outcome is in line with the literature review presented in the introduction section, stressing that high-performance materials are often discarded for high-production volumes because of their notable manufacturing costs, which make those not sustainable for mass-market production.

Another design option for which similar considerations can be made is PolyAmide 66 (PA66) with 40% long carbon fibers produced by compression molding, which ranks 35th (out of the list of top 20 design alternatives but, however, worthy to be mentioned). Although such a solution allows for achieving a great mass saving (3.71 kg, resulting in more than a 58% reduction with respect to the reference), the main motivation for the low ranking is represented by the increase in both costs and environmental impact. Indeed, the PA66 bracket requires 69 EUR for its production (27% growth), while the CC amounts to even 161 kgCO₂_eq, thus proving a 53% increase with respect to the reference. Another relevant discussion point is the strong variability in indices among design options in the ranking. In this regard, Figure 3 provides the I_Design, I_Cost, and I_CC for the best 20 solutions in terms of ratio with respect to the baseline design, allowing us to evaluate how design solutions perform towards different aspects considered.

Another interesting observation deriving from the analysis of results is that the quota associated with manufacturing is definitely different when considering economic and environmental assessments. In the case of costs, the percentage contribution of production over total LC CC is comprised in the range of 56–91% depending on the design option considered, while the environmental impact of production is definitely lower, as it varies from a minimum of 26% to a maximum of around 68%. The notably smaller numbers in the case of environmental assessment are mainly due to the predominant effect of the use stage in the overall LC economy, which reaches the highest levels for those design solutions characterized by the highest mass values.

Figure 3 provides the design, cost, and environmental indices normalized with respect to the baseline design. As shown in the diagram, for the first five design alternatives, all three indices are more or less aligned on the same values. This is mainly due to the fact that the base material and manufacturing process remain substantially the same (low-alloy steel and press forming), with variations in mechanical properties (reported in Table 5) due to different chemical compositions not involving relevant discrepancies in terms of final component mass (variability range: 4.98–5.22 kg).

Regarding the aluminum materials (both alloys and aluminum-based matrices), Figure 3 shows that they are generally characterized by lower values of the design index ratio than low-alloy steels (in the range of 0.42–0.55), while the cost and environmental indices ratios are definitely bigger (in the range 0.41–0.62). Such an outcome can be explained by the strong energy consumption of extraction and refinement processes of the alumina mineral, which, on the one hand causes, a strong economic expenditure and, on the other hand, involves high greenhouse gas emissions for producing the amount of consumed energy. Differently, solutions based on martensitic, dual-phase steels and press-hardening lightweight design options provide similar (or slightly higher) design index ratios than low-alloy steels, but the cost and environmental indices ratios are bigger, these latter being the main cause for backward ranking. Finally, it has to be noted that cast-iron solutions (positioned in the 7th and 13th positions) present contrasting results with respect to the above-mentioned design alternatives. Indeed, against decisively worse performances in terms of lightweight potential and environmental effects than low-alloy steels, they provide a very low cost of primary material (cost index ratio below 0.13), which involves a mid-table positioning in the ranking of the best 20 solutions.

The strength of the conceived approach for materials selection is the integration of the Ashby and VIKOR methods, which represents an innovation in the automotive field. The result is a functional method to generate and rank alternative design solutions based on predictive estimation of component mass, thus allowing assessment at the same time as different and often conflicting design aspects. Such an ability constitutes a notable advancement with respect to the existing literature in this research area, the latter providing several approaches that are applied separately to the materials selection process [55,56,57,58,59,60,61]. In the light of the holistic perspective above-mentioned, the refined method makes available to car designers and product developers a valuable tool for redesigning specific car components when the main target is mass reduction while containing costs and environmental impact. This represents the main point of innovation provided by this paper, bridging the gap between traditional selection processes and the urgent need for sustainable development in automotive engineering.

Regarding future development of this work, the first point is represented by FEM analysis of both the baseline and innovative solutions identified, which would validate numerically the advantages provided by lightweight components. Another option for future development is represented by the application of topological optimization, targeted at optimizing component design, to achieve an extra weight reduction in addition to the one obtained by change in the material and manufacturing process. Topological optimization would also be useful to demonstrate the validity of the results of the preliminary mass calculation step, as well as to provide indications to adjust the weights of different design criteria. Finally, other possible improvements are as follows:

-

The extension to additional case studies to verify the generality of the method;

-

The implementation of a sensitivity analysis to assess how the final results are affected by a variation in weights associated with different design criteria.

4. Conclusions

This paper conceives a method for materials selection when redesigning an automotive component from a lightweight eco-design perspective. The strength of the refined method is considering, at the same time, the three major pillars of the design process: structural integrity, cost sustainability, and environmental sustainability; the latter is assessed by means of the CC impact category. The development of the method is based on Ashby theory indices, which are used to define design indicators customized according to the load and stress features of the specific case study. Cost and environmental aspects are evaluated by means of innovative indices, which enable assessing the most relevant phases within the LC of the considered car part. The design solutions (intended as a combination of component base material and primary manufacturing process) are ranked by a single score indicator calculated through the VIKOR MCDA model, which provides also weighting of the considered aspects according to the peculiarities of the specific case study. Based on such a ranking resulting from the assessment of multiple and concurring aspects, a wise and conscious selection of the optimal design solutions can be carried out.

The conceived method is validated through the application of a practical case study from the literature, a motor bracket mounted on an electric passenger car, which, in the reference design version, is made of AISI 304 produced through press forming. Considering industrial processes compatible with the chosen material options, the method provides 1850 possible alternatives. The constitutive equations of the model are applied to the case study, obtaining the selection of 1151 materials, which are characterized on the basis of data from the Granta Selector database. Regarding criteria weighting, I_Cost is assumed to be four times more relevant than the design and environmental indices, and a first screening of acceptable design options is made by assuming a limit to the cost increase of the lightweight solutions by means of the parameter ${\displaystyle \frac{{\mathsf{\Delta }}_{Cost}}{{\mathsf{\Delta }}_{Mass}}}$ (cost increase against mass reduction). The results stress that a bracket made of low-alloy steel (AISI 9255) processed through press forming is identified as the optimal solution in replacement of the stainless steel baseline component. Such a design alternative allows for achieving very high savings at the component level, both in terms of weight (44% decrease), cost (75% decrease), and CC effect (61% decrease). Other lightweight options providing notable improvement under the selection criteria considered are based on aluminum, martensitic steels, dual-phase steels, and cast-iron materials.

The main innovation provided by the refined approach for materials selection is represented by the integration of the Ashby and VIKOR methods, which allows the evaluation of a lightweight case study from the structural integrity, cost, and environmental impact points of view. This makes the method a valuable tool for designers and car developers to generate and, at the same time, assess several alternative design solutions.