RSSR Mechanism Design and Motion Control Strategy of a Carbon-Free Vehicle for Obstacle Avoidance Competition
Abstract
1. Introduction
2. Design Proposal
3. Mathematical Model
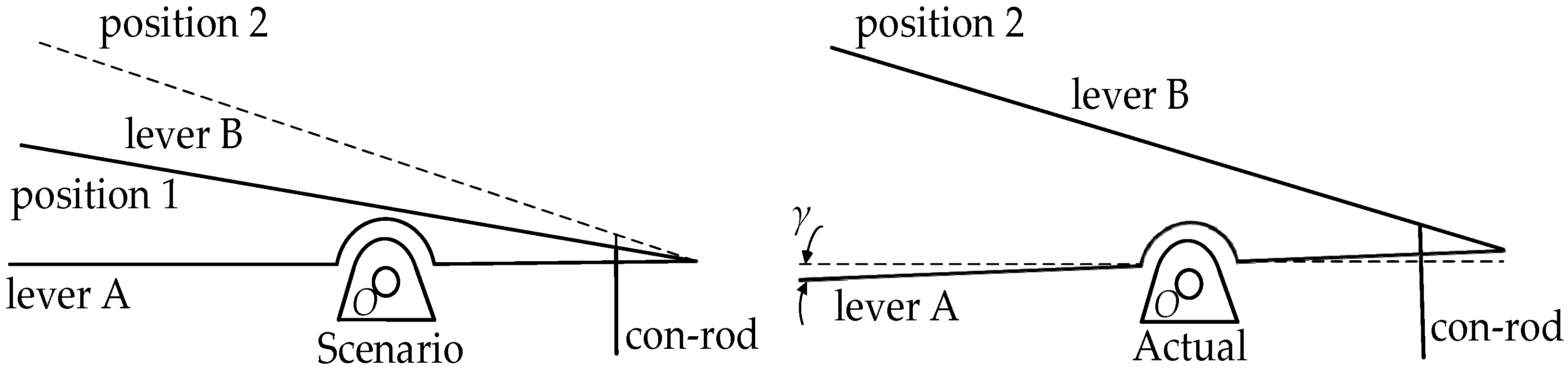
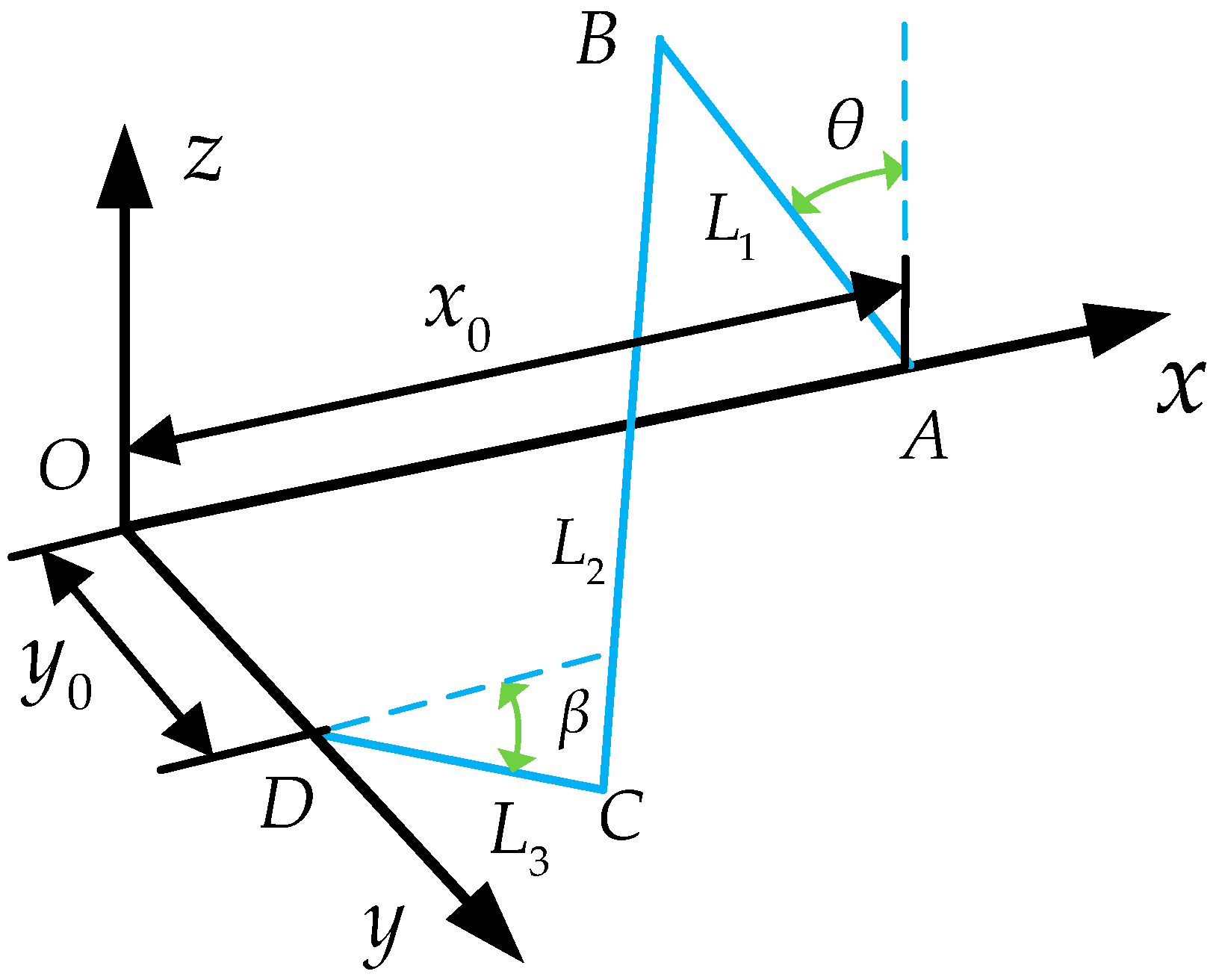
3.1. Motion Analysis of the RSSR Mechanism
- Then, it can be solved:
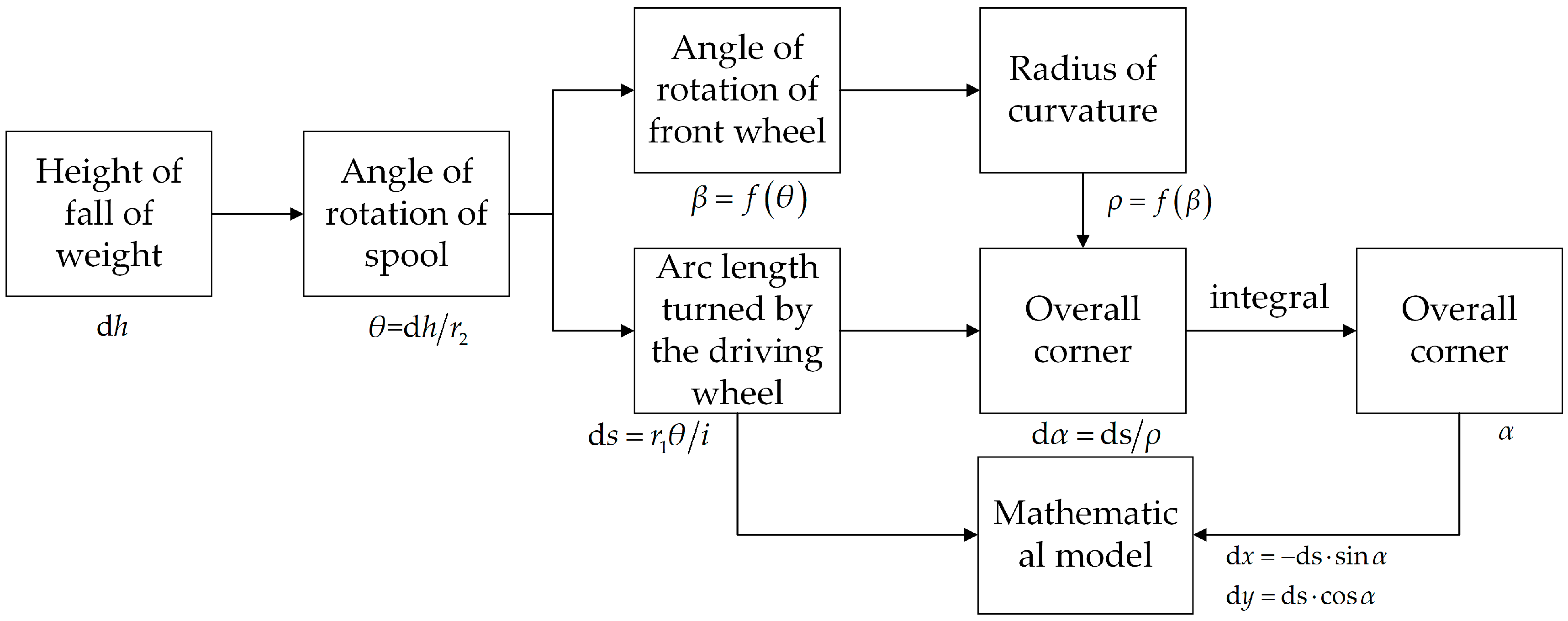
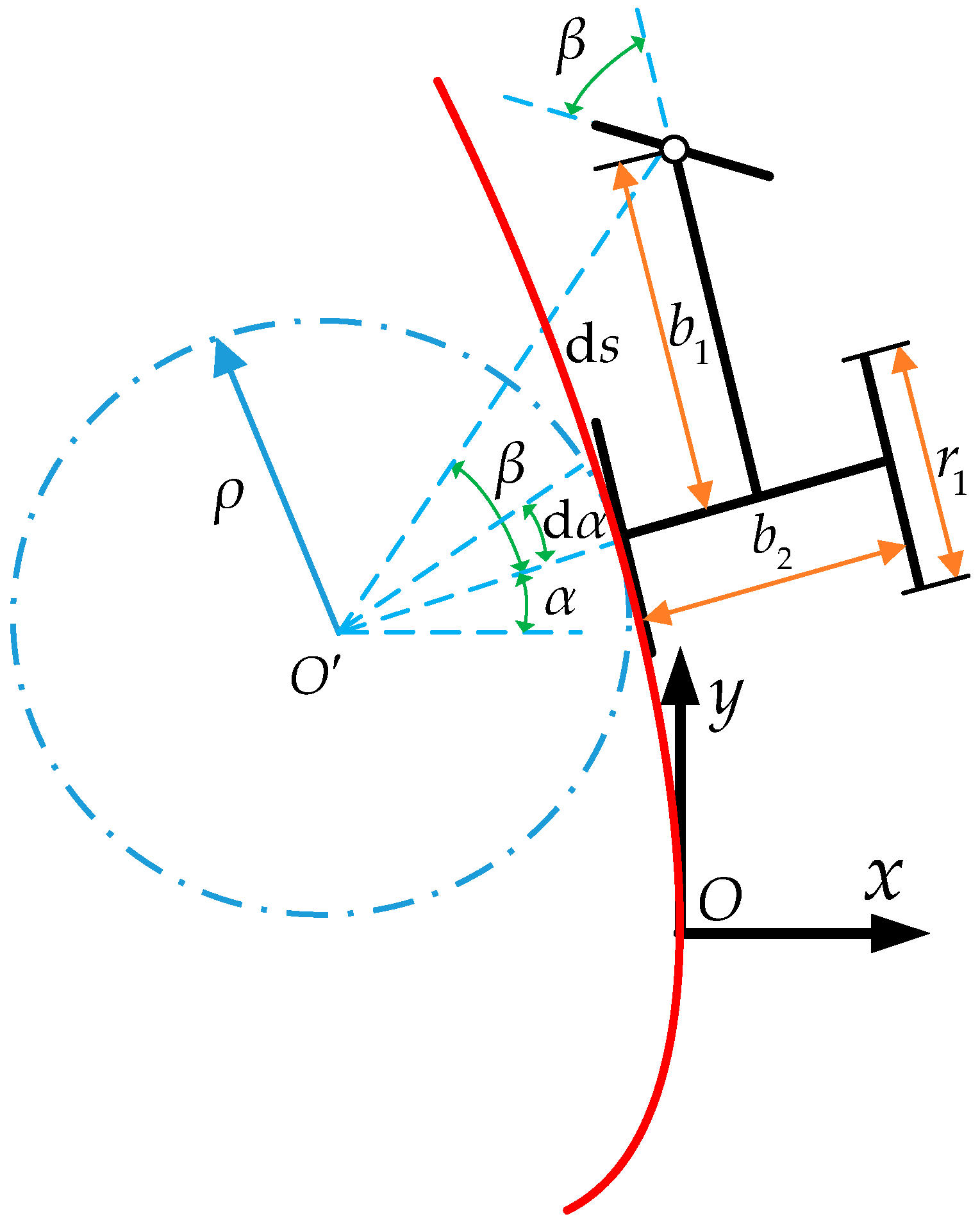
3.2. Motion Analysis of the Vehicle
4. Numerical Simulation and Analysis of Results
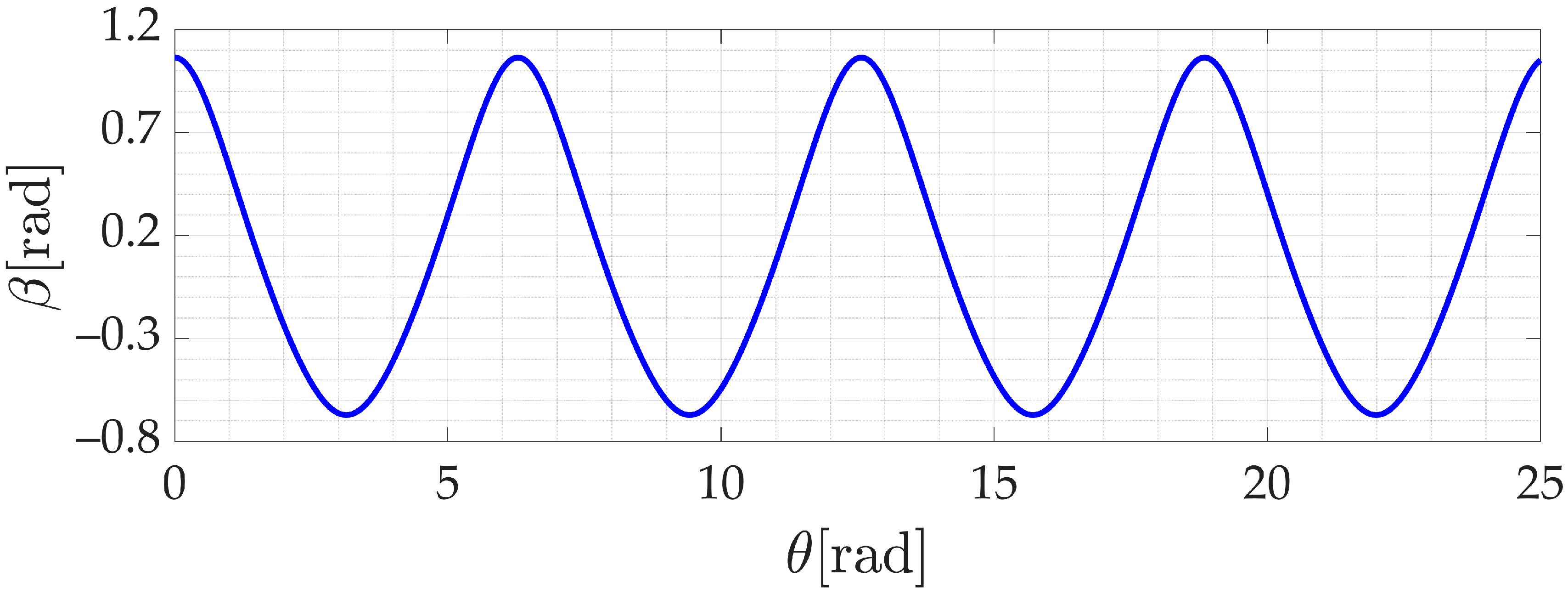
4.1. Kinematic Analysis
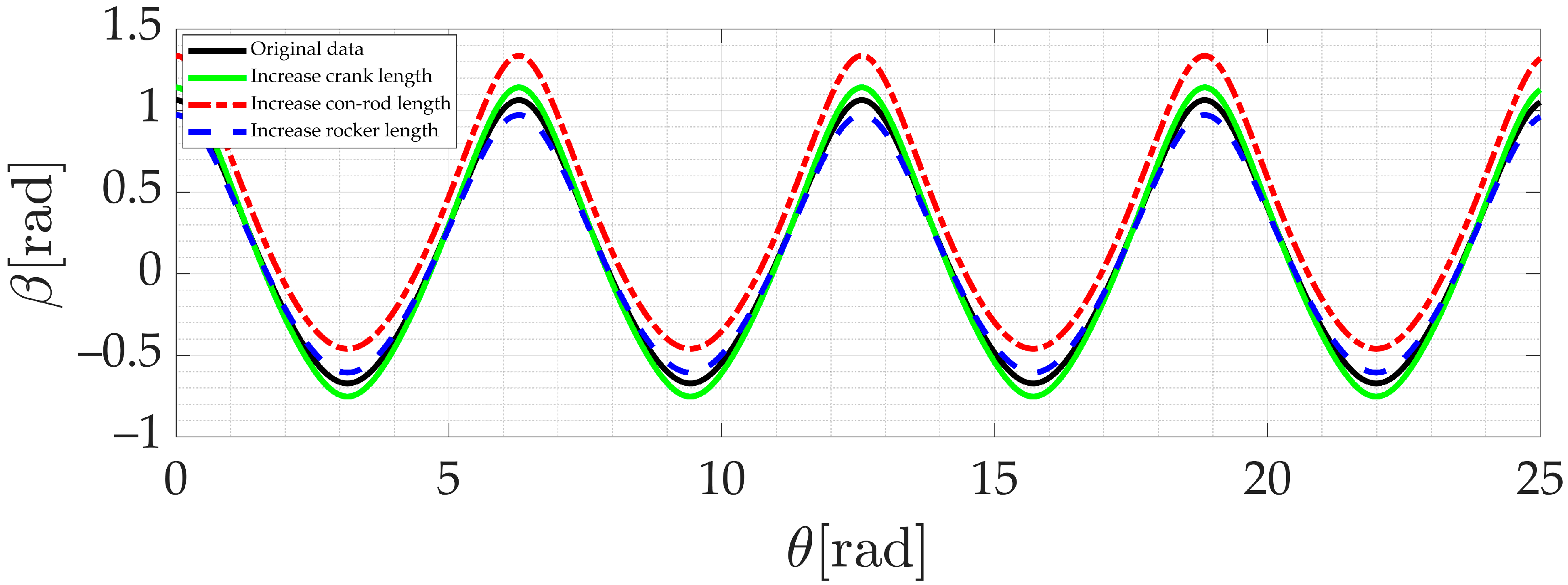
- When the lengths of the con-rod and rocker are kept constant, an increase or decrease in the crank length will directly affect the amplitude of the curve but has no effect on the periodicity of the curve change. This indicates that the crank length is the key factor that affects the amplitude of the motion without affecting the periodicity of the motion.
- With the crank and rocker lengths fixed, changing the length of the con-rod will cause the curve to translate in the direction of the longitudinal axis. This change does not affect the amplitude of the curve or its periodicity, indicating that the length of the con-rod mainly affects the starting position of the motion without changing the basic characteristics of the motion.
- Changing only the length of the rocker, we find that the effect is the same as when the length of the crank is changed. This further confirms that the crank and the rocker have similar roles in affecting the motion profile and that together they determine the magnitude of the profile.
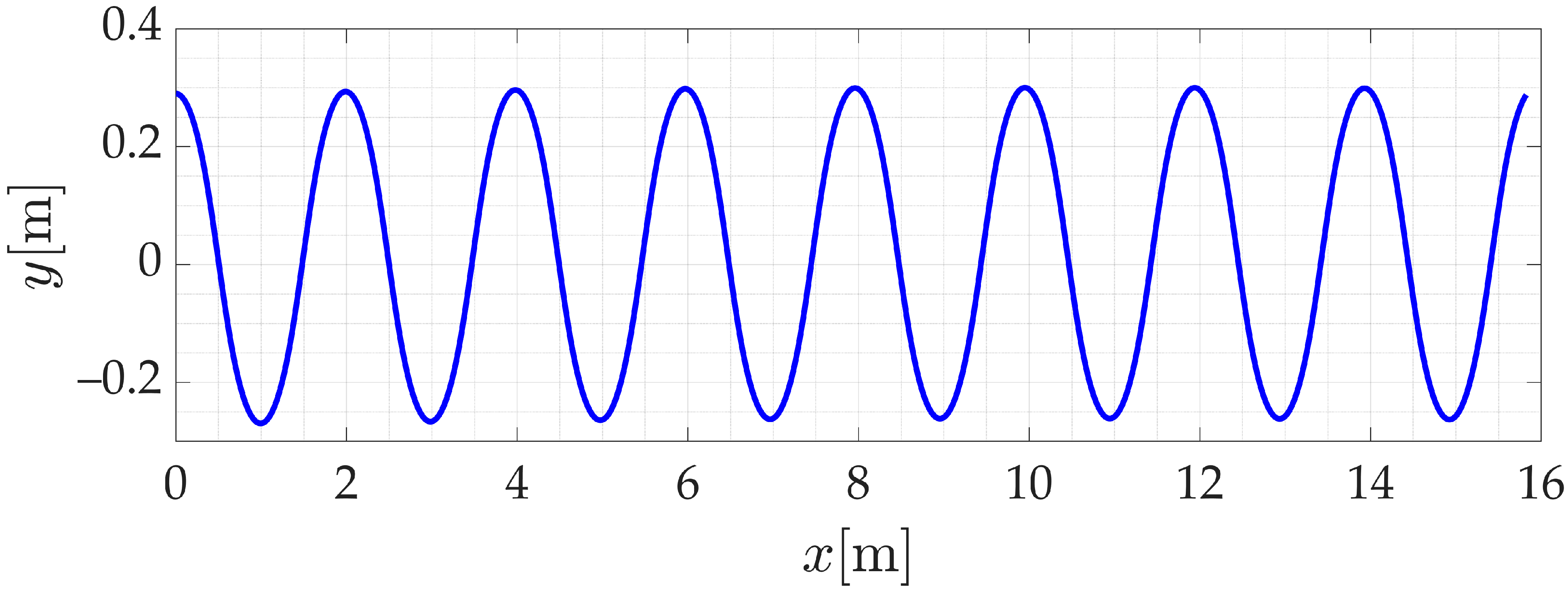
- Effect of crank length: when keeping the length of the con-rod and rocker constant, increasing or decreasing the crank length will result in a corresponding increase or decrease in the period of the trajectory curve. At the same time, this change will also cause the vehicle motion to deviate to one side, thus affecting the overall motion path of the vehicle.
- Effect of con-rod length: while keeping the crank and rocker lengths constant, changing the length of the con-rod will cause the car body to be deflected. However, this deflection has less effect on the cyclic variation of the trajectory curve. This implies that the adjustment of the con-rod length mainly affects the symmetry of the vehicle’s motion rather than its underlying motion period.
4.2. Physical Test Analysis
- Influence of the crank: the length of the crank directly affects the maximum curvature of the traveling trajectory of the vehicle. When the crank length increases, the left and right deflection angle of the front wheels of the vehicle will increase accordingly, which is manifested in the motion trajectory as the compression of the cycle and the deflection of the vehicle body.
- The role of the con-rod: the con-rod is the key component for adjusting the front wheel deflection angle distribution. It can adjust the size of the left and right deflection angles individually without changing the sum of the left and right deflection angles of the front wheels. This is reflected in the trajectory, as the motion cycle remains unchanged but the vehicle body is deflected. To ensure that the direction of operation of the vehicle is not deflected, the length of the con-rod needs to be precisely fine-tuned.
- Commissioning of the RSSR mechanism vehicle: for the vehicle with the RSSR mechanism, the crank length should be adjusted first to adapt the period of the running trajectory to the spacing of the obstacles when the key dimensions such as the diameter of the rear wheels, the transmission ratio, the length of the vehicle and the width of the vehicle have already been determined during the commissioning. Then, the con-rod length should be adjusted to correct the vehicle deflection. Alternatively, the V fine-tune structure can be used to directly adjust the left and right deflection angles of the front wheels by changing the size of the V tension angle until the vehicle movement is no longer deflected.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ma, X.; Wang, X.; Zhang, H.; Li, H. The Teaching Application of the Backward Design Method in Chinese National Undergraduate Engineering Training Integration Ability Competition: Take the Double 8 Carbon-Free Car as an Example. Appl. Sci. 2023, 13, 8829. [Google Scholar] [CrossRef]
- Yu, J.H.; Qiu, X.Y.; Tang, Y.H. Teaching reform of mechanical design course design based on discipline competition. J. Mech. Des. 2018, 35, 258–260. [Google Scholar]
- Liu, J.W.; Li, Y.H.; Yang, N.J. Innovative Design and Manufacture of “S” Type Carbon-Free Cars. MATEC Web Conf. 2017, 95, 09008. [Google Scholar] [CrossRef]
- Zhang, C.; Zheng, Y.B.; Ma, Y.C. Wide-angle turning performance optimization of gravitational potential energy driven three-wheeled car. J. Mech. Des. 2014, 31, 50–55. [Google Scholar]
- Zou, G.M.; Yang, X.G.; Huang, C.; Feng, J. Research on the potential energy-driven car with energy stored by vortex coil spring. J. Mech. Des. 2012, 29, 32–35. [Google Scholar]
- Wang, Z.; He, G.Q.; Hu, Z. Design of Carbon-Free Car Steering Mechanism Based on ADAMS Software. J. Hunan Univ. Sci. Technol. 2013, 27, 28–32. [Google Scholar]
- Ai, X.J.; Wang, Z.H.; Su, L.; Zhao, L.M. Design for Gravity-Driven and Direction-Control Carbon-Free Vehicle. Mach. Des. Manuf. 2016, 34, 157–160. [Google Scholar]
- Han, S.K.; Jie, M.Y.; Lin, C.X.; Lai, B.; Zhang, S.J. Tracing Principle Study and Structure Design of Double ‘8-shaped’ Trajectory Carbon-free Car. J. Mech. Transm. 2019, 43, 60–64. [Google Scholar]
- Han, S.K.; Jie, M.Y.; Lin, C.X.; Lai, B.; Zhang, S.J. The Key Structure Design and System of “Double 8-Shaped” Trajectory Carbon-Free Car. Mach. Des. Manuf. 2020, 3, 241–245. [Google Scholar]
- Fang, L.; Wu, Y.F.; Mou, Z.H.; Guo, Y.L. Reverse simulation analysis and design of “8”⁃shaped trajectory carbon⁃free car’ s cam. J. Mech. Des. 2023, 40, 106–111. [Google Scholar]
- Li, J. Trajectory and structural design of car-based on B-spline curve. J. Mech. Des. 2023, 40, 114–118. [Google Scholar]
- Zhou, Y.B.; Luo, Q.; Zhang, Y.W.; Wang, J.Y.; Feng, Q.; Wang, Y.S. Carbon-free Car Structure and Trajectory Simulation Design for Clocking the “Long March” Route. J. Mech. Transm. 2024, 48, 75–82. [Google Scholar]
- Hu, Z.; He, G.Q.; Wang, Z.; Chen, W.H. Design of Wheel Arrangement of Single-Drive Carbon-Free Car Based on Adams Software. J. Hunan Univ. Technol. 2013, 27, 53–56. [Google Scholar]
- Tiau, G.F.; Xu, Y.; Sun, S.H. Design and simulation of a new carbon-free vehicle. Machinery 2018, 56, 49–52. [Google Scholar]
- Chen, Y.L.; Gao, F.Q.; Xie, Z.L. Research and Test for the Cam Steering Mechanism of the S-shaped Carbon-free Car. J. Mech. Transm. 2017, 41, 106–110. [Google Scholar]
- Chen, L.F.; Wang, L.Q.; Zhu, P.C.; Feng, H.Z.; Tian, X.F. Optimal Design of RSSR Mechanism for Double “8” Carbonless Car. J. Hunan Univ. Sci. Technol. 2020, 35, 50–55. [Google Scholar]
- Gong, C.; Jiao, R.Q.; Ruan, W.L. Optimization Design of Variable Pitch Walk Carbon-free Vehicle with RSSR Steering Control. J. Hubei Polytech. Univ. 2020, 36, 10–14. [Google Scholar]
- Castro, J.; Nóbrega, J.M.; Costa, R. Computational Framework to Model the Selective Laser Sintering Process. Materials 2024, 17, 1845. [Google Scholar] [CrossRef]
- Siddiqui, S.; Surananai, S.; Sainath, K.; Zubair Khan, M.; Raja Pandiyan Kuppusamy, R.; Kempaiah Suneetha, Y. Emerging Trends in Development and Application of 3D Printed Nanocomposite Polymers for Sustainable Environmental Solutions. Eur. Polym. J. 2023, 196, 112298. [Google Scholar] [CrossRef]
- Rotzoll, M.; Regan, M.H.; Husty, M.L.; Hayes, M.J.D. Kinematic Geometry of Spatial RSSR Mechanisms. Mech. Mach. Theory 2023, 185, 105335. [Google Scholar] [CrossRef]
- Mazzotti, C.; Troncossi, M.; Parenti-Castelli, V. Dimensional Synthesis of the Optimal RSSR Mechanism for a Set of Variable Design Parameters. Meccanica 2017, 52, 2439–2447. [Google Scholar] [CrossRef]
- Liu, Y.F.; Xia, Y.L.; Liang, Z.H.; Chen, L.; Li, X.B. Track simulation and structural design of the double 8-typed carbon-free car based on MATLAB. J. Mech. Des. 2020, 37, 8–13. [Google Scholar]
- Li, L.S.; Wu, W.G. Optimization Design of Steering Mechanism for Carbon-free Car based on Matlab. J. Mech. Transm. 2019, 43, 59–63. [Google Scholar]




| Name | Gear Center Distance | Captain of Vehicle | Width of Vehicle | Gear Ratio | Rear Wheel Radius | Length of Crank | Length of Con-Rod | Length of Rocker |
|---|---|---|---|---|---|---|---|---|
| symbolic | d1 [mm] | b1 [mm] | b2 [mm] | i | r1 [mm] | L1 [mm] | L2 [mm] | L3 [mm] |
| value | 30 | 120 | 110 | 6 | 65 | 21 | 70 | 39 |
| Index | Length of Crank [mm] | Length of Con-Rod [mm] | Length of Rocker [mm] |
|---|---|---|---|
| 1 | 20.3 | 68.6 | 38.3 |
| 2 | 20.4 | 68.8 | 38.4 |
| 3 | 20.5 | 69.0 | 38.5 |
| … | … | … | … |
| 12 | 21.5 | 72.8 | 39.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, L.; Liu, Y.; Zhang, Y. RSSR Mechanism Design and Motion Control Strategy of a Carbon-Free Vehicle for Obstacle Avoidance Competition. Machines 2024, 12, 634. https://doi.org/10.3390/machines12090634
He L, Liu Y, Zhang Y. RSSR Mechanism Design and Motion Control Strategy of a Carbon-Free Vehicle for Obstacle Avoidance Competition. Machines. 2024; 12(9):634. https://doi.org/10.3390/machines12090634
Chicago/Turabian StyleHe, Long, Yang Liu, and Ya Zhang. 2024. "RSSR Mechanism Design and Motion Control Strategy of a Carbon-Free Vehicle for Obstacle Avoidance Competition" Machines 12, no. 9: 634. https://doi.org/10.3390/machines12090634
APA StyleHe, L., Liu, Y., & Zhang, Y. (2024). RSSR Mechanism Design and Motion Control Strategy of a Carbon-Free Vehicle for Obstacle Avoidance Competition. Machines, 12(9), 634. https://doi.org/10.3390/machines12090634







