A Generic Multi-Objective Optimization of Machining Processes Using an End-to-End Evolutionary Algorithm
Abstract
1. Introduction
- (1)
- During the objective modeling phase of optimization, conventional studies are often conducted under the assumption that modeling methods aimed at different objectives are the same. However, the characteristics of the different objectives vary greatly, resulting in variations in their representation. The lack of guidance in the construction of an objective model system for optimization leads to the poor adaptability of optimization systems to different types of machining processes. Accordingly, to help improve the generalization and flexibility of multi-objective optimization methods, a novel modeling framework that can be readily adapted to different machining optimization objectives is required.
- (2)
- During the multi-objective optimization stage of the machining process, conventional studies often use fixed optimized dimensions, and it is common practice to establish objective functions and constraints in a stationary state, which cannot be modified during the optimization process. In general, the machining steps and requirements are often changed during daily manufacturing operations, resulting in the state of the objective functions and constraints being dynamic. As a consequence, conventional single-step optimization methods are ineffective for different machining optimization tasks. While it is possible to develop a specialized optimization framework for each machining task, such an approach can be both costly and time-consuming.
- (3)
- Conventional studies have mostly conducted the multi-objective decision-making process in a subjective and specialized way to determine Pareto front solutions. This is effective when handling low-dimensional Pareto front searches. Unfortunately, in a multi-step machining process, the number of optimized dimensions is high. The conventional way of manually assigning weights and finding a final solution is prone to error, and it is hard for the operators to find the best approximate process parameters. On the basis of this, a novel method that can determine the final parameters for the operators in an objective and automated way is required.
- (1)
- A new approach is suggested for optimizing different CNC processes. This method is better equipped to handle the dynamic characteristics of the process and is therefore more appropriate for optimizing parameters in industrial settings compared with traditional methods.
- (2)
- A flexible optimization framework is proposed. Compared with conventional optimization studies, the proposed method can not only handle the variations in single-step machining optimization processes, but also those in the multi-step optimization process that was considered in this study.
- (3)
- A more objective method of determining parameters is proposed. Compared with the conventional method, the proposed method can be used to find the best approximate parameters not only from low-dimensional, but also high-dimensional Pareto front solutions in an automated way.
2. Optimization Problem Analysis
2.1. Analysis of the Optimization of the Parameters of a Machining Process
2.2. Optimization Problem in Machining Process
3. Proposed Optimization Method
3.1. Overall Framework
3.2. Objective Function Modeling Using the Proposed Method
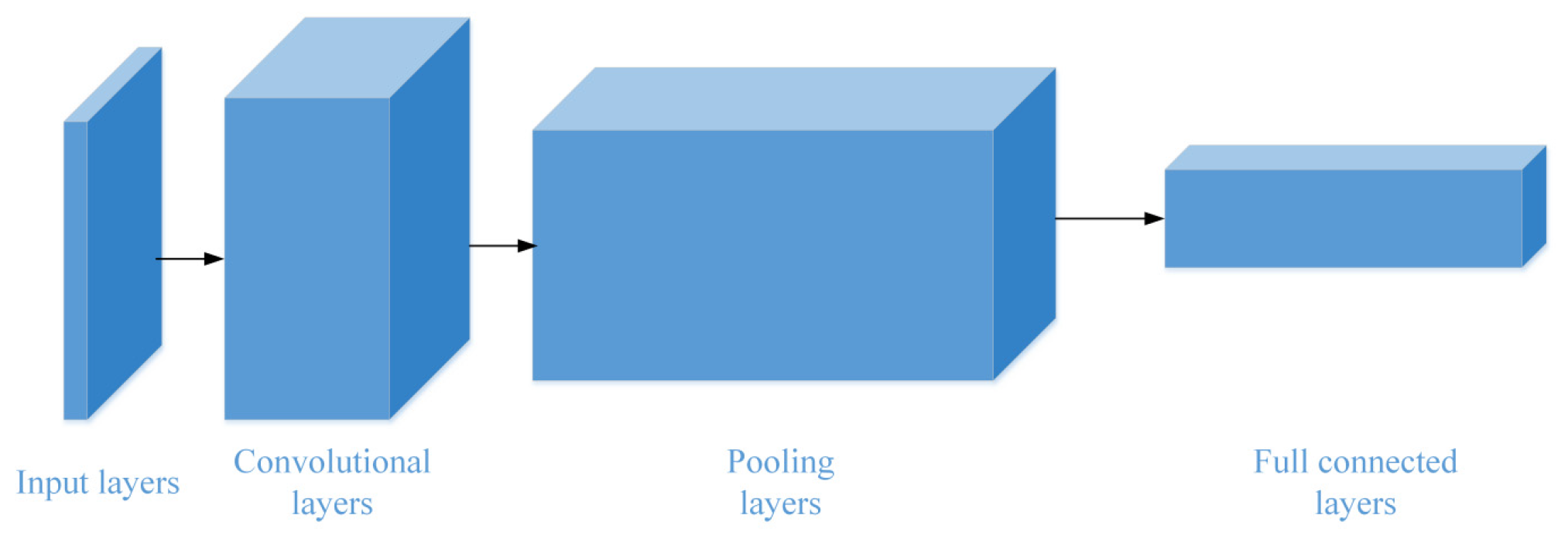
3.2.1. Data-Driven Model of Energy Consumption
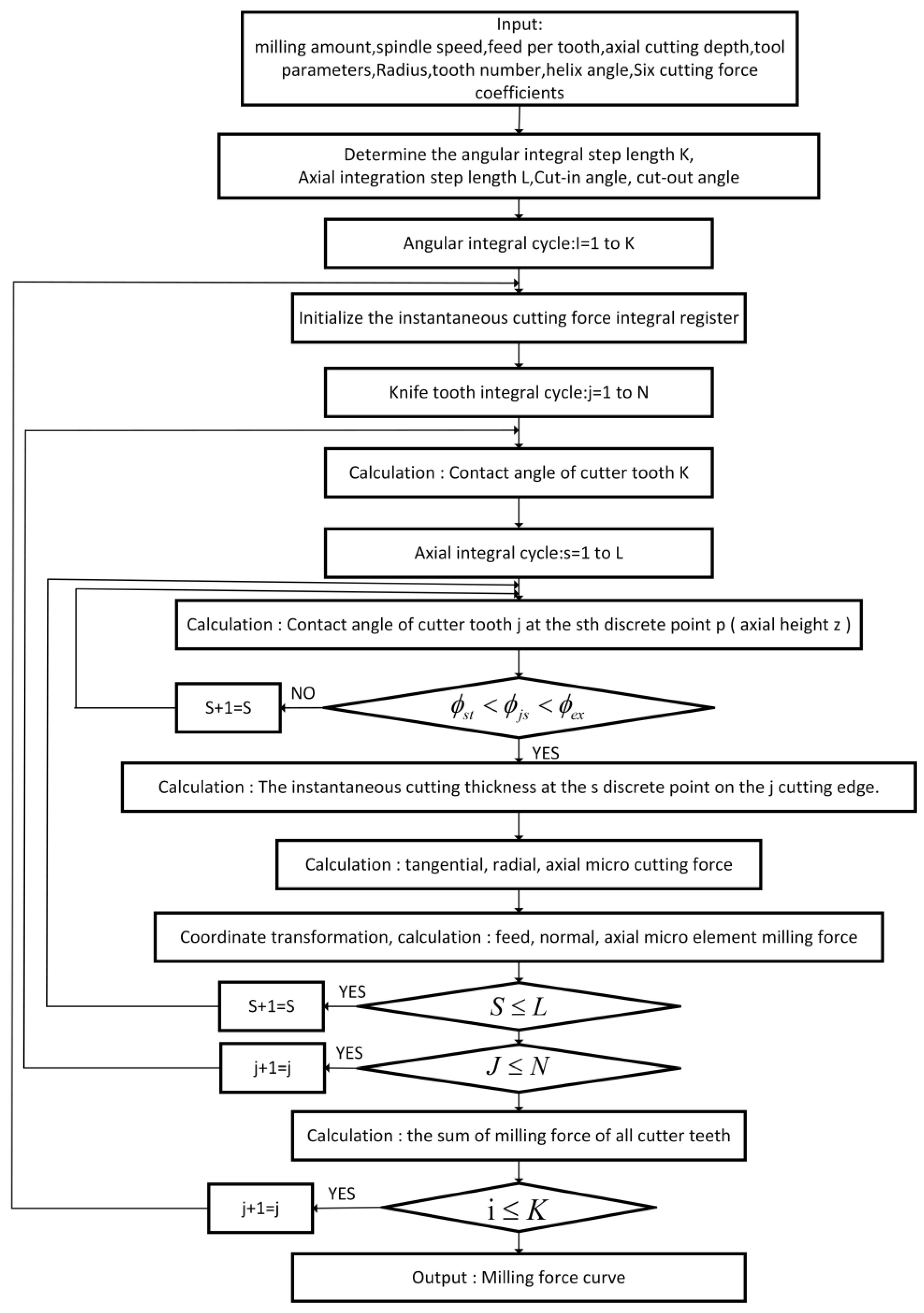
3.2.2. Physical Modeling of the Cutting Force
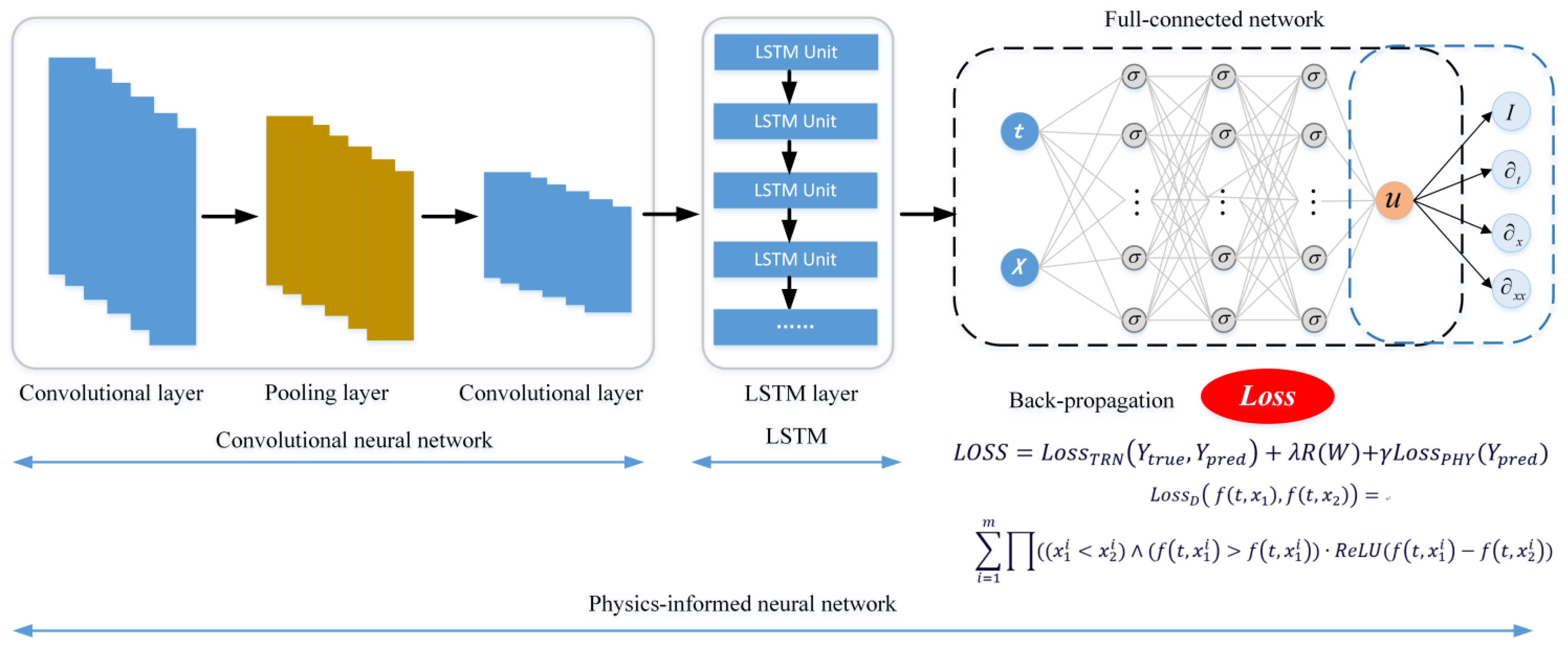
3.2.3. Physics-Informed Machine Learning for Surface Roughness
3.2.4. Empirical Functions for the Material Removal Rate
3.2.5. Surrogate Model for the Objectives
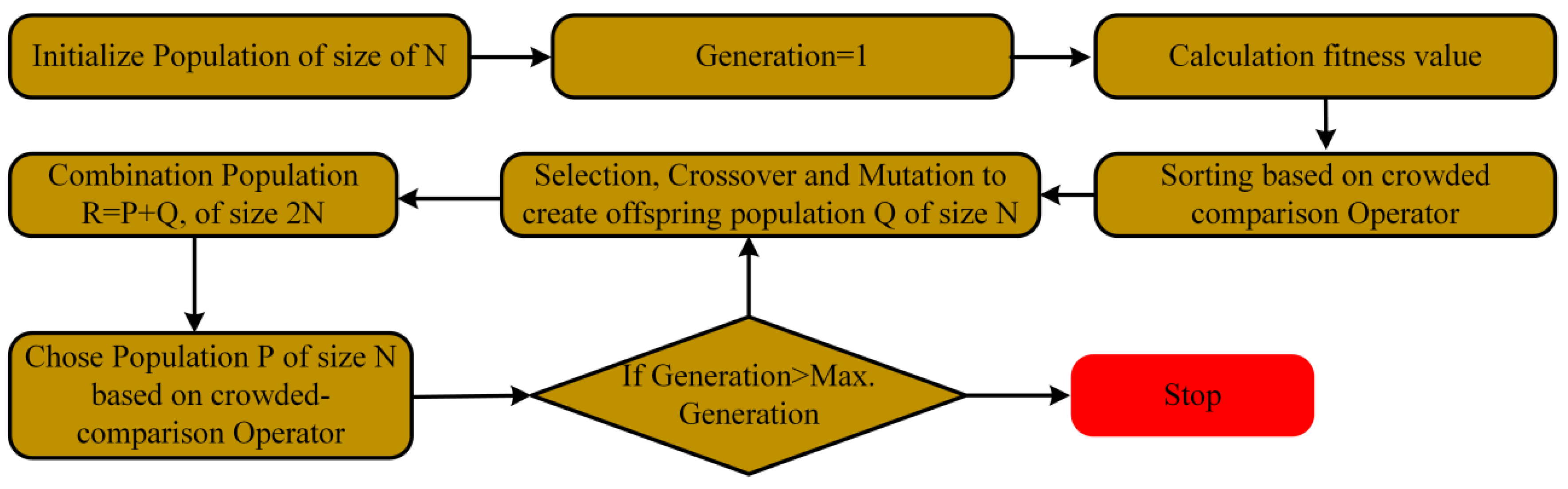
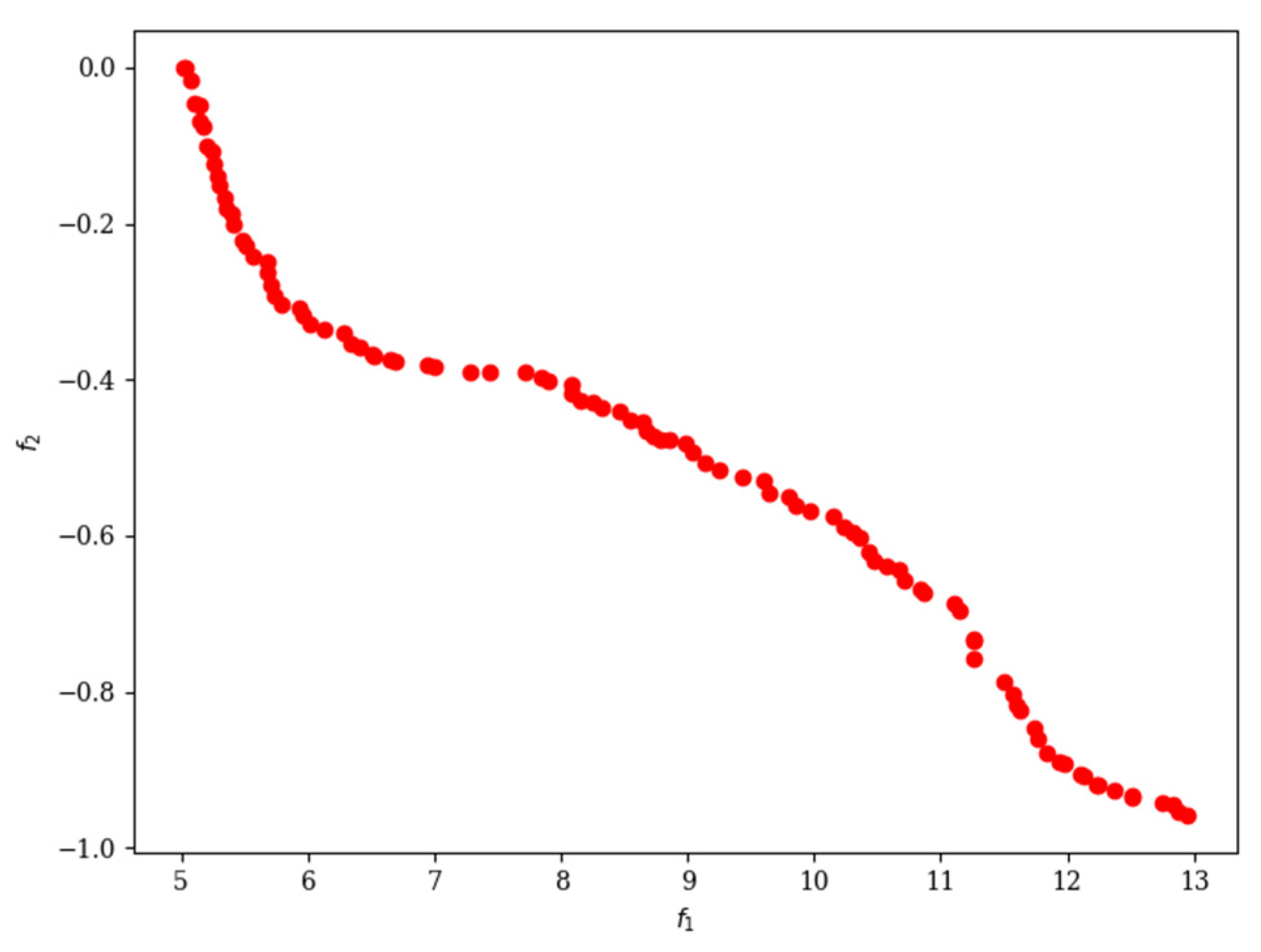
3.3. MODM Using NSGA-II
| Algorithm 1 Document clustering using NSGA-II |
Begin t  0 0CN  RANDOM (K) RANDOM (K)C  {CN1,CN2,…CNj} {CN1,CN2,…CNj}Initialize population P(t) While (not termination condition) do  compute objective functions P(t) compute objective functions P(t)   R(t)  P(t)+ Q(t) P(t)+ Q(t) fast nondominated sort R(t) fast nondominated sort R(t) fitness assignment fitness assignmentt  t+1 t+1end end |
3.4. Weight Determination Using CRITIC
3.5. MADM Using TOPSIS
| Algorithm 2 Steps of the TOPSIS method in pseudo-code format. | |
| 1. | Construction of the normalized decision matrix |
where denotes the elements of normalized decision matrix | |
| 2. | Construction of the weighted normalized decision matrix |
| 3. | ) solutions |
| where and are associated with the benefit and cost attributes, respectively. | |
| 4. | Calculation of the separation measure |
| 5. | Calculation of the relative closeness to the ideal solution |
| Ranking of alternatives according to the value of | |
4. Case Study
4.1. Experimental Setup
4.2. Statistical Analysis of the Prediction Model
4.3. Determination of the Boundary Conditions of the Machining Process
5. Results and Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, B.; Tao, F.; Fang, X.; Liu, C.; Liu, Y.; Freiheit, T. Smart manufacturing and intelligent manufacturing: A comparative review. Engineering 2021, 7, 738–757. [Google Scholar] [CrossRef]
- Rahmatullah, R.; Amiruddin, A.; Lubis, S. Effectiveness of CNC Turning and CNC Milling in Machining Process. Int. J. Econ. Technol. Soc. Sci. 2021, 2, 575–583. [Google Scholar] [CrossRef]
- Sreejith, P.S.; Ngoi, B.K.A. Material removal mechanisms in precision machining of new materials. Int. J. Mach. TOOLS Manuf. 2001, 41, 1831–1843. [Google Scholar] [CrossRef]
- Han, F.; Li, L.; Cai, W.; Li, C.; Deng, X.; Sutherland, J.W. Parameters optimization considering the trade-off between cutting power and MRR based on linear decreasing particle swarm algorithm in milling. J. Clean. Prod. 2020, 262, 121388. [Google Scholar] [CrossRef]
- He, K.; Tang, R.; Jin, M. Pareto fronts of machining parameters for trade-off among energy consumption, cutting force and processing time. Int. J. Prod. Econ. 2017, 185, 113–127. [Google Scholar] [CrossRef]
- Xiao, Y.M.; Jiang, Z.G.; Gu, Q.; Yan, W.; Wang, R.P. A novel approach to CNC machining center processing parameters optimization considering energy-saving and low-cost. J. Manuf. Syst. 2021, 59, 535–548. [Google Scholar] [CrossRef]
- Yusoff, Y.; Ngadiman, M.S.; Zain, A.M. Overview of NSGA-II for optimizing machining process parameters. Procedia Eng. 2011, 15, 3978–3983. [Google Scholar] [CrossRef]
- Yusup, N.; Zain, A.M.; Hashim, S.Z.M. Overview of PSO for Optimizing Process Parameters of Machining. Work. Inf. Electron. Eng. 2012, 29, 914–923. [Google Scholar] [CrossRef]
- Cui, Y.; Geng, Z.; Zhu, Q.; Han, Y. Multi-objective optimization methods and application in energy saving. Energy 2017, 125, 681–704. [Google Scholar] [CrossRef]
- Lipin, K.; Govindan, P. A review on multi objective optimization of drilling parameters using Taguchi methods. AKGEC Int. J. Technol. 2013, 4, 11–21. [Google Scholar]
- Sur, G.; Motorcu, A.R.; Nohutçu, S. Single and multi-objective optimization for cutting force and surface roughness in peripheral milling of Ti6Al4V using fixed and variable helix angle tools. J. Manuf. Process. 2022, 80, 529–545. [Google Scholar] [CrossRef]
- Sureban, R.; Kulkarni, V.N.; Gaitonde, V.N. Modern optimization techniques for advanced machining processes—A review. Mater. Today Proc. 2019, 18, 3034–3042. [Google Scholar] [CrossRef]
- Tzeng, C.-J.; Lin, Y.-H.; Yang, Y.-K.; Jeng, M.-C. Optimization of turning operations with multiple performance characteristics using the Taguchi method and Grey relational analysis. J. Mater. Process. Technol. 2009, 209, 2753–2759. [Google Scholar] [CrossRef]
- Sharma, S.; Kumar, V. A comprehensive review on multi-objective optimization techniques: Past, present and future. Arch. Comput. Methods Eng. 2022, 29, 5605–5633. [Google Scholar] [CrossRef]
- Patel, N.S.; Parihar, P.L.; Makwana, J.S. Parametric optimization to improve the machining process by using Taguchi method: A review. Mater. Today Proc. 2021, 47, 2709–2714. [Google Scholar] [CrossRef]
- Kalita, K.; Pal, S.; Haldar, S.; Chakraborty, S. A hybrid TOPSIS-PR-GWO approach for multi-objective process parameter optimization. Process Integr. Optim. Sustain. 2022, 6, 1011–1026. [Google Scholar] [CrossRef]
- Singh, O.P.; Kumar, G.; Kumar, M. Role of Taguchi and grey relational method in optimization of machining parameters of different materials: A review. Acta Electron. Malaysia 2019, 3, 19–22. [Google Scholar] [CrossRef]
- Kumar, S.; Jagadish; Ray, A. Multi-objective optimization of CNC drilling parameters on machining of HcHcr steel using Taguchi’s technique and grey relational analysis. In Advances in Thermal Engineering, Manufacturing, and Production Management: Select Proceedings of ICTEMA 2021; Springer: Cham, Switzerland, 2020; pp. 353–367. [Google Scholar]
- Li, C.B.; Xiao, Q.G.; Tang, Y.; Li, L. A method integrating Taguchi, RSM and MOPSO to CNC machining parameters optimization for energy saving. J. Clean. Prod. 2016, 135, 263–275. [Google Scholar] [CrossRef]
- Akhtar, M.N.; Sathish, T.; Mohanavel, V.; Afzal, A.; Arul, K.; Ravichandran, M.; Rahim, I.A.; Alhady, S.S.N.; Bakar, E.A.; Saleh, B. Optimization of process parameters in CNC turning of aluminum 7075 alloy using L27 array-based Taguchi method. Materials 2021, 14, 4470. [Google Scholar] [CrossRef]
- Shahane, S.; Aluru, N.; Ferreira, P.; Kapoor, S.G.; Vanka, S.P. Optimization of solidification in die casting using numerical simulations and machine learning. J. Manuf. Process. 2020, 51, 130–141. [Google Scholar] [CrossRef]
- Ghosh, T.; Martinsen, K. Generalized approach for multi-response machining process optimization using machine learning and evolutionary algorithms. Eng. Sci. Technol. Int. J. 2020, 23, 650–663. [Google Scholar] [CrossRef]
- Weichert, D.; Link, P.; Stoll, A.; Rüping, S.; Ihlenfeldt, S.; Wrobel, S. A review of machine learning for the optimization of production processes. Int. J. Adv. Manuf. Technol. 2019, 104, 1889–1902. [Google Scholar] [CrossRef]
- Shin, S.J.; Woo, J.; Rachuri, S. Energy efficiency of milling machining: Component modeling and online optimization of cutting parameters. J. Clean. Prod. 2017, 161, 12–29. [Google Scholar] [CrossRef]
- Wang, W.; Tian, G.; Chen, M.; Tao, F.; Zhang, C.; Abdulraham, A.-A.; Li, Z.; Jiang, Z. Dual-objective program and improved artificial bee colony for the optimization of energy-conscious milling parameters subject to multiple constraints. J. Clean. Prod. 2020, 245, 118714. [Google Scholar] [CrossRef]
- Wu, P.; He, Y.; Li, Y.; He, J.; Liu, X.; Wang, Y. Multi-objective optimisation of machining process parameters using deep learning-based data-driven genetic algorithm and TOPSIS. J. Manuf. Syst. 2022, 64, 40–52. [Google Scholar] [CrossRef]
- Cao, W.; Yu, Y.; Li, J.; Wu, D.; Ni, J.; Chen, X. High stability multi-objective decision-making approach of dry hobbing parameters. J. Manuf. Process. 2022, 84, 1184–1195. [Google Scholar] [CrossRef]
- Rajesh, N.; Yohan, M.; Venkataramaiah, P.; Pallavi, M.V. Optimization of Cutting Parameters for Minimization of Cutting Temperature and Surface Roughness in Turning of Al6061 Alloy. Mater. Today Proc. 2017, 4, 8624–8632. [Google Scholar] [CrossRef]
- Karandikar, J.; Schmitz, T.; Smith, S. Physics-guided logistic classification for tool life modeling and process parameter optimization in machining. J. Manuf. Syst. 2021, 59, 522–534. [Google Scholar] [CrossRef]
- Deng, Y.F.; Du, S.C.; Jia, S.Y.; Zhao, C.; Xie, Z.Y. Prognostic study of ball screws by ensemble data-driven particle filters. J. Manuf. Syst. 2020, 56, 359–372. [Google Scholar] [CrossRef]
- Giampieri, A.; Ling-Chin, J.; Ma, Z.; Smallbone, A.; Roskilly, A.P. A review of the current automotive manufacturing practice from an energy perspective. Appl. Energy 2020, 261, 114074. [Google Scholar] [CrossRef]
- Bhatt, D.; Patel, C.; Talsania, H.; Patel, J.; Vaghela, R.; Pandya, S.; Modi, K.; Ghayvat, H. CNN variants for computer vision: History, architecture, application, challenges and future scope. Electronics 2021, 10, 2470. [Google Scholar] [CrossRef]
- Alzubaidi, L.; Zhang, J.; Humaidi, A.J.; Al-Dujaili, A.; Duan, Y.; Al-Shamma, O.; Santamaría, J.; Fadhel, M.A.; Al-Amidie, M.; Farhan, L. Review of deep learning: Concepts, CNN architectures, challenges, applications, future directions. J. Big Data 2021, 8, 1–74. [Google Scholar]
- Wan, M.; Lu, M.S.; Zhang, W.H.; Yang, Y. A new ternary-mechanism model for the prediction of cutting forces in flat end milling. Int. J. Mach. Tools Manuf. 2012, 57, 34–45. [Google Scholar] [CrossRef]
- Wang, J.-J.J.; Zheng, C.M. An analytical force model with shearing and ploughing mechanisms for end milling. Int. J. Mach. Tools Manuf. 2002, 42, 761–771. [Google Scholar] [CrossRef]
- Gonzalo, O.; Beristain, J.; Jauregi, H.; Sanz, C. A method for the identification of the specific force coefficients for mechanistic milling simulation. Int. J. Mach. Tools Manuf. 2010, 50, 765–774. [Google Scholar] [CrossRef]
- Wu, P.; Dai, H.; Li, Y.; He, Y.; Zhong, R.; He, J. A physics-informed machine learning model for surface roughness prediction in milling operations. Int. J. Adv. Manuf. Technol. 2022, 123, 4065–4076. [Google Scholar] [CrossRef]
- Abdeljaber, O.; Avci, O.; Kiranyaz, M.S.; Boashash, B.; Sodano, H.; Inman, D.J. 1-D CNNs for structural damage detection: Verification on a structural health monitoring benchmark data. Neurocomputing 2018, 275, 1308–1317. [Google Scholar] [CrossRef]
- Chung, W.H.; Gu, Y.H.; Yoo, S.J. District heater load forecasting based on machine learning and parallel CNN-LSTM attention. Energy 2022, 246, 123350. [Google Scholar] [CrossRef]
- Ren, L.; Dong, J.; Wang, X.; Meng, Z.; Zhao, L.; Deen, M.J. A data-driven auto-CNN-LSTM prediction model for lithium-ion battery remaining useful life. IEEE Trans. Ind. Informatics 2020, 17, 3478–3487. [Google Scholar] [CrossRef]
- Deb, K.; Jain, H. An evolutionary many-objective optimization algorithm using reference-point-based nondominated sorting approach, part I: Solving problems with box constraints. IEEE Trans. Evol. Comput. 2013, 18, 577–601. [Google Scholar] [CrossRef]
- Krishnan, A.R.; Kasim, M.M.; Hamid, R.; Ghazali, M.F. A modified CRITIC method to estimate the objective weights of decision criteria. Symmetry 2021, 13, 973. [Google Scholar] [CrossRef]
- Diakoulaki, D.; Mavrotas, G.; Papayannakis, L. Determining objective weights in multiple criteria problems: The critic method. Comput. Oper. Res. 1995, 22, 763–770. [Google Scholar] [CrossRef]
- Yoon, K.P.; Hwang, C.-L. Multiple Attribute Decision Making: An Introduction; Sage Publications: New York, NY, USA, 1995. [Google Scholar]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]





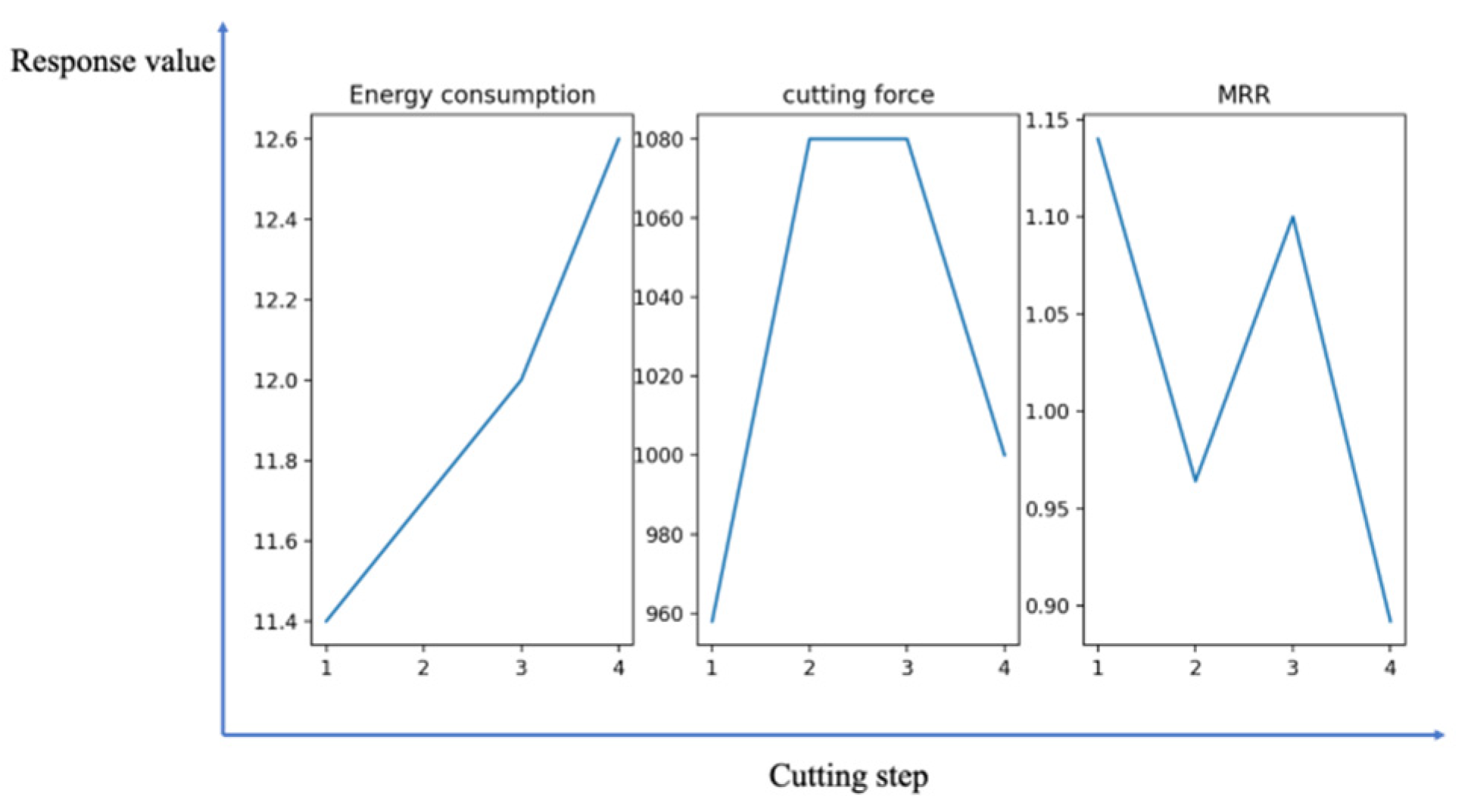
| Type | MAE | RMSE | MPA |
|---|---|---|---|
| PIM for surface roughness | 122.33 | 231.47 | 92.33% |
| CNN for energy consumption | 260.60 | 273.52 | 94.60% |
| Step | (10−2 ) | |||
|---|---|---|---|---|
| 1 | 97.997 | 0.497 | 9.310 | 3.899 |
| 2 | 99.809 | 0.490 | 9.741 | 3.903 |
| 3 | 99.698 | 0.496 | 9.997 | 3.861 |
| 4 | 97.758 | 0.192 | 9.979 | 3.104 |
| Step | (10−2) | MRR | ||||
|---|---|---|---|---|---|---|
| 1 | 97.348 | 0.429 | 9.958 | 3.223 | 11.92 | 8.900 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xun, C.; Wu, P. A Generic Multi-Objective Optimization of Machining Processes Using an End-to-End Evolutionary Algorithm. Machines 2024, 12, 635. https://doi.org/10.3390/machines12090635
Xun C, Wu P. A Generic Multi-Objective Optimization of Machining Processes Using an End-to-End Evolutionary Algorithm. Machines. 2024; 12(9):635. https://doi.org/10.3390/machines12090635
Chicago/Turabian StyleXun, Cheng, and Pengcheng Wu. 2024. "A Generic Multi-Objective Optimization of Machining Processes Using an End-to-End Evolutionary Algorithm" Machines 12, no. 9: 635. https://doi.org/10.3390/machines12090635
APA StyleXun, C., & Wu, P. (2024). A Generic Multi-Objective Optimization of Machining Processes Using an End-to-End Evolutionary Algorithm. Machines, 12(9), 635. https://doi.org/10.3390/machines12090635






