Thermo-Mechanical Coupling Analysis of Inserts Supporting Run-Flat Tires under Zero-Pressure Conditions
Abstract
1. Introduction
2. Theory of the SSTF of the ISRFT
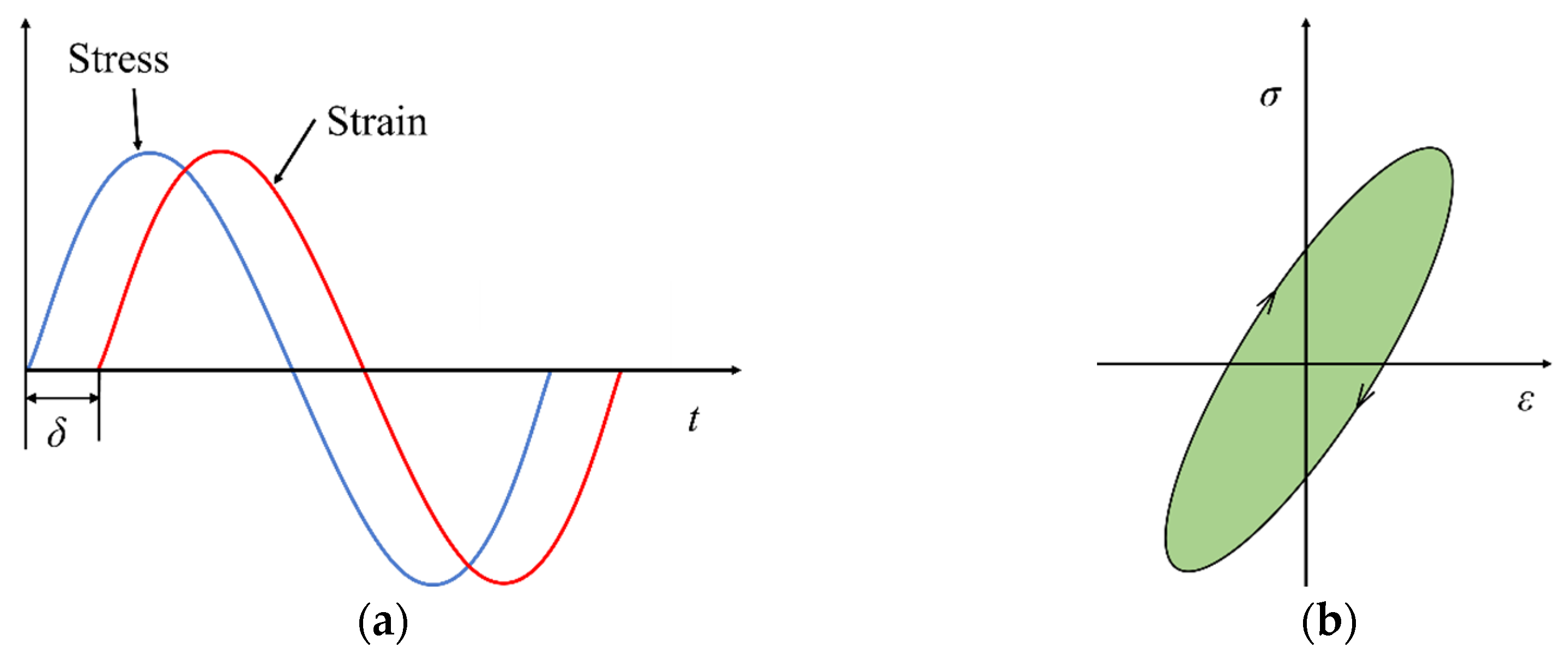
2.1. Theory of Hysteresis Loss in Viscoelastic Materials
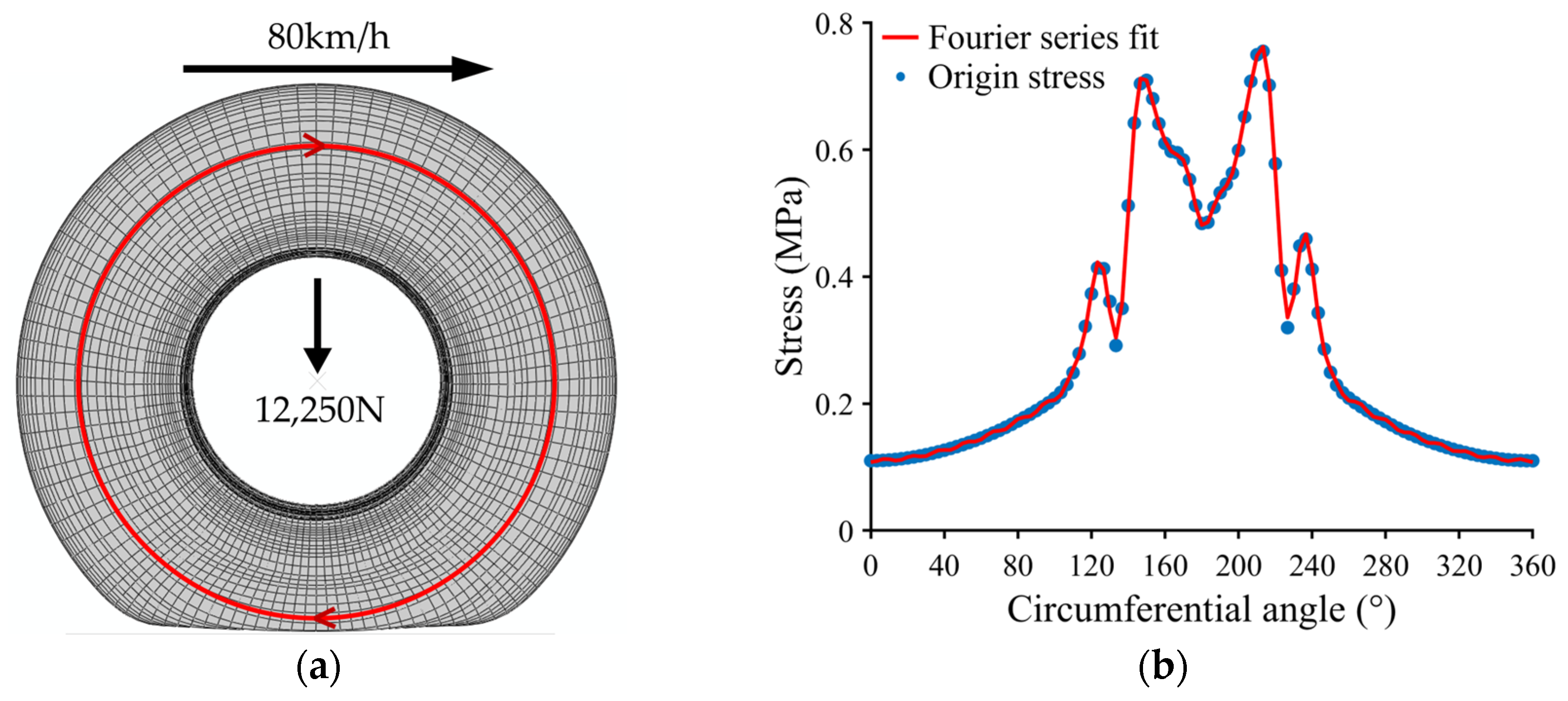
2.2. Fourier Series Fit Process
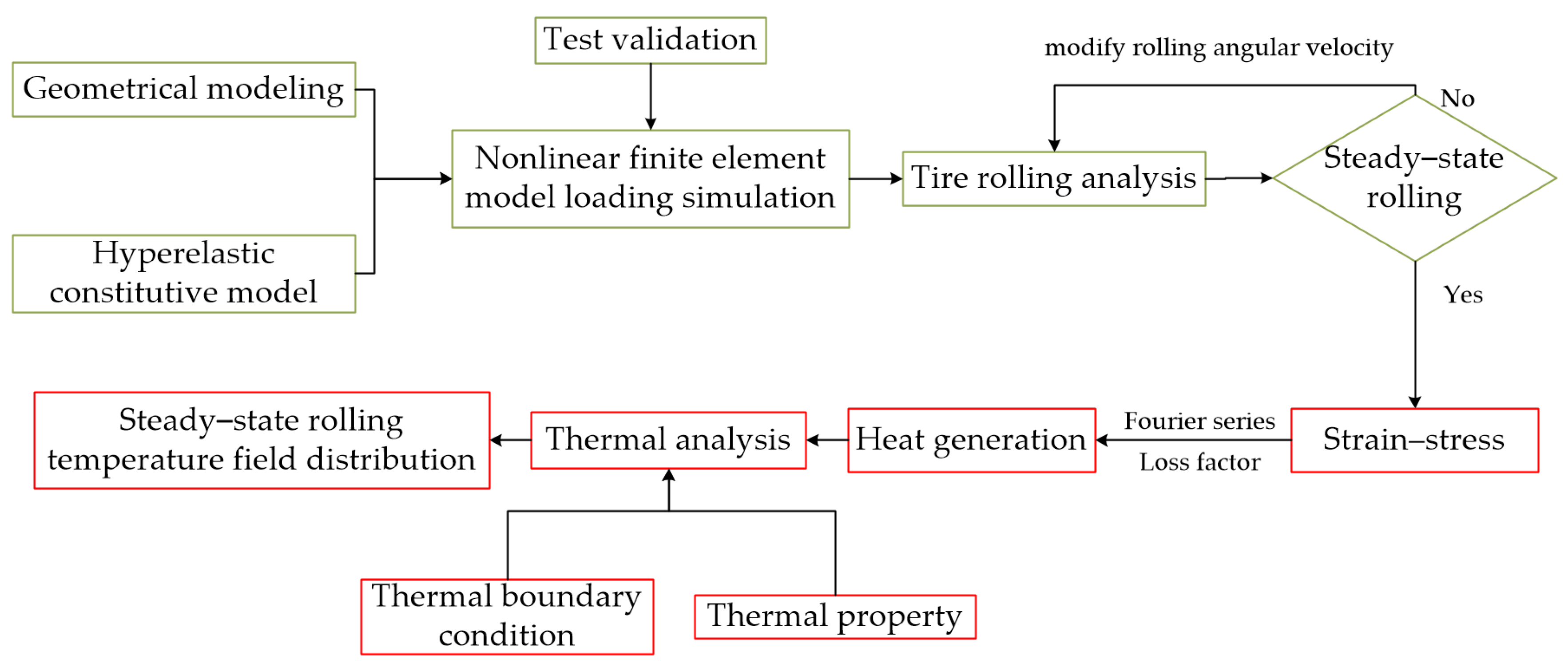
3. Simulations and Verifications
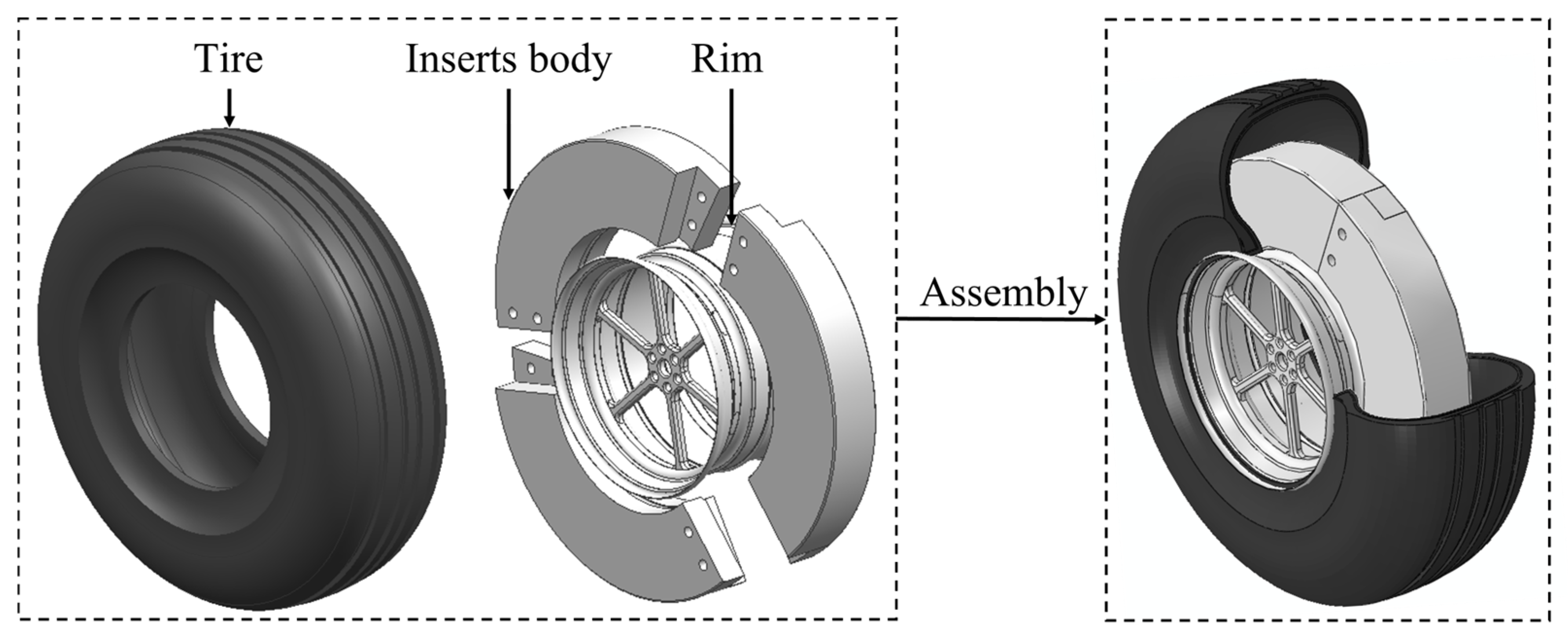
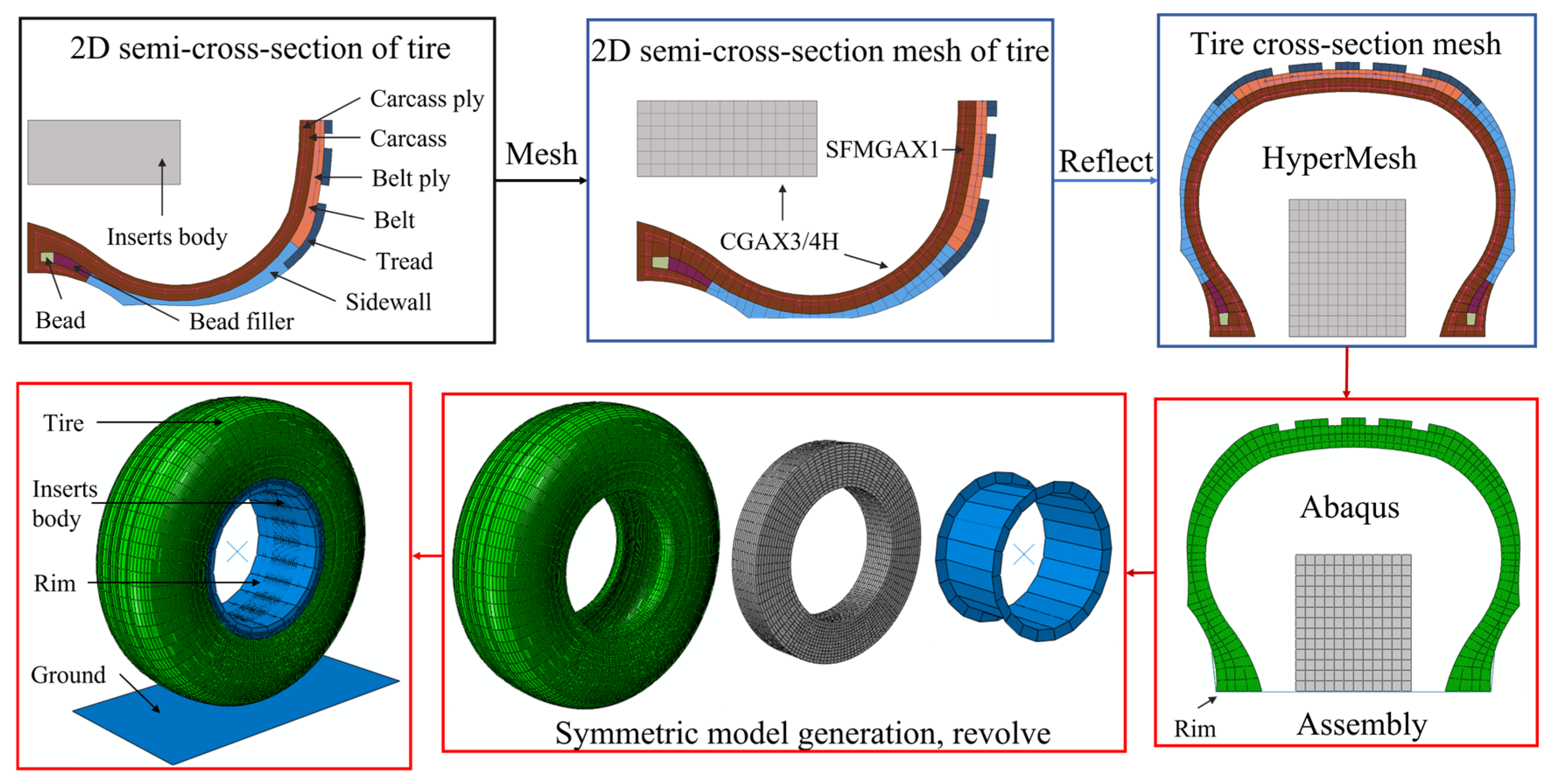
3.1. Finite Element Modelling of the ISRFT
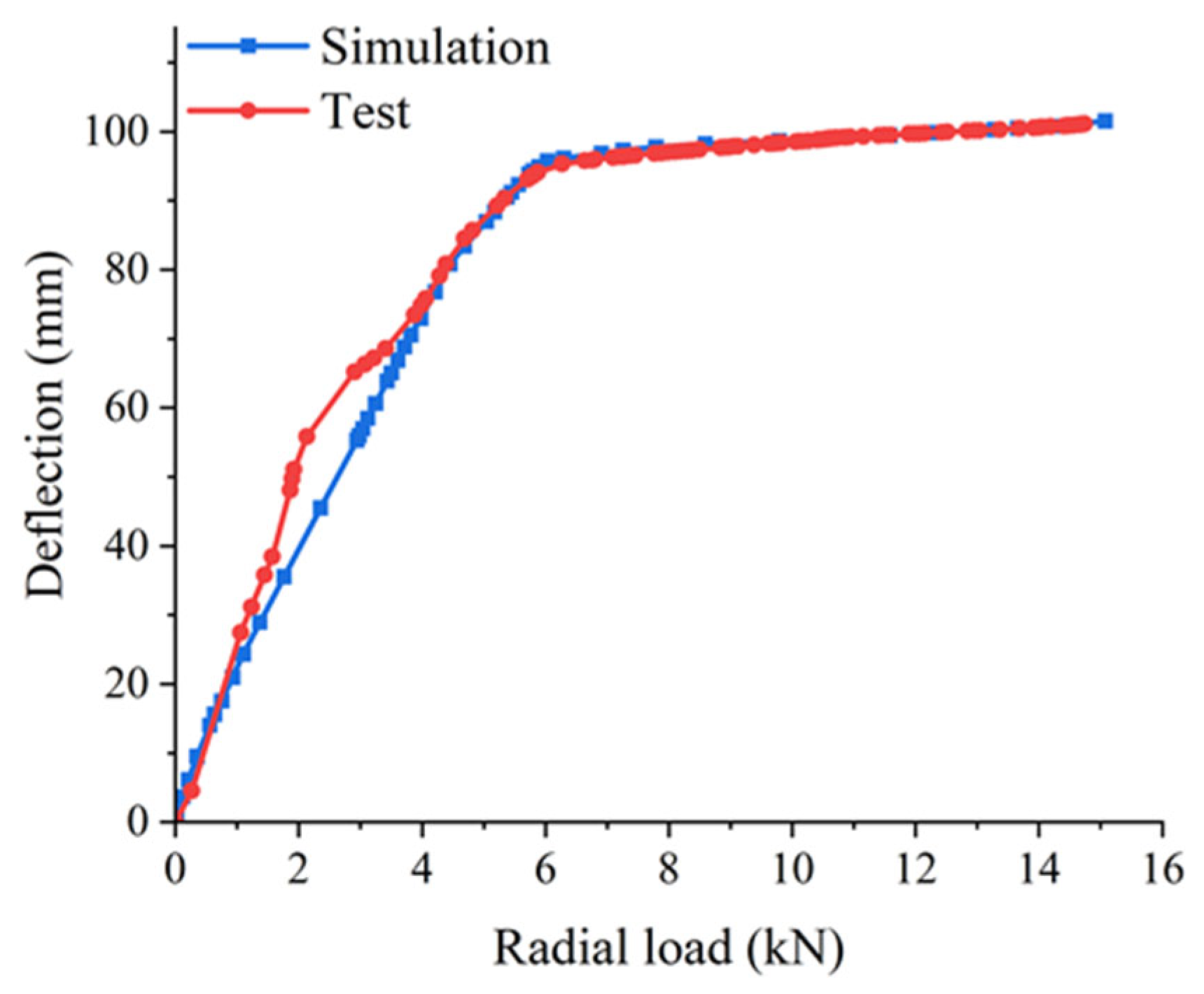
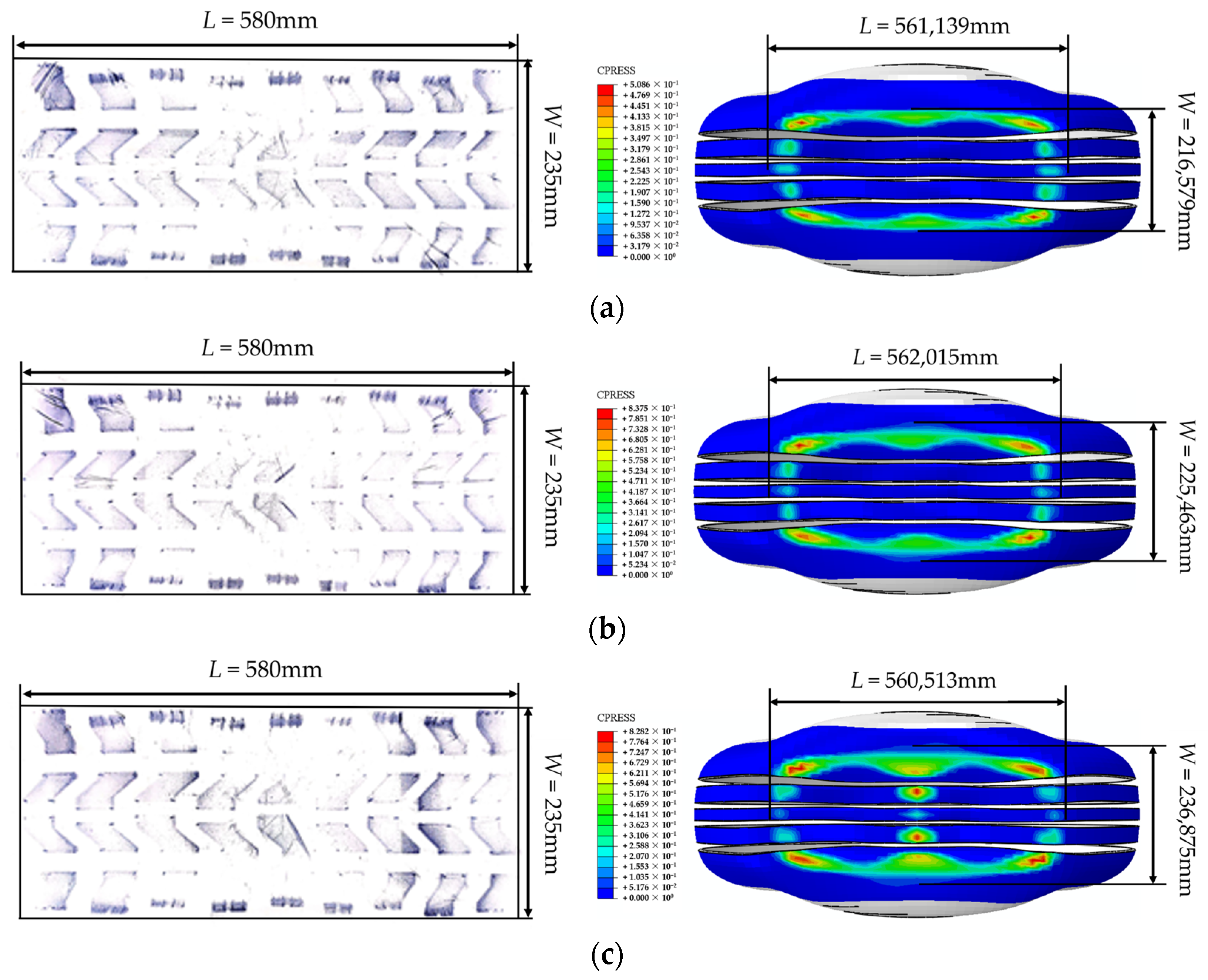
3.2. Bench Test of the ISRFT
4. Numerical Simulation Analysis
4.1. Steady-State Rolling Simulation
4.2. Thermal Boundary Condition Setting
- The properties of tire viscoelastic materials are not affected by temperature, and all the heat generated in the rolling process of the tire originates from hysteresis loss.
- The steady-state rolling of the tire does not take into account the circumferential temperature gradient, and the temperature is the same in each cross-section.
- When the tire is in thermal equilibrium, the thermo-physical parameters such as thermal conductivity, specific heat capacity and the loss factor of rubber material are regarded as constant.
- The rubber material used in tires is isotropic.
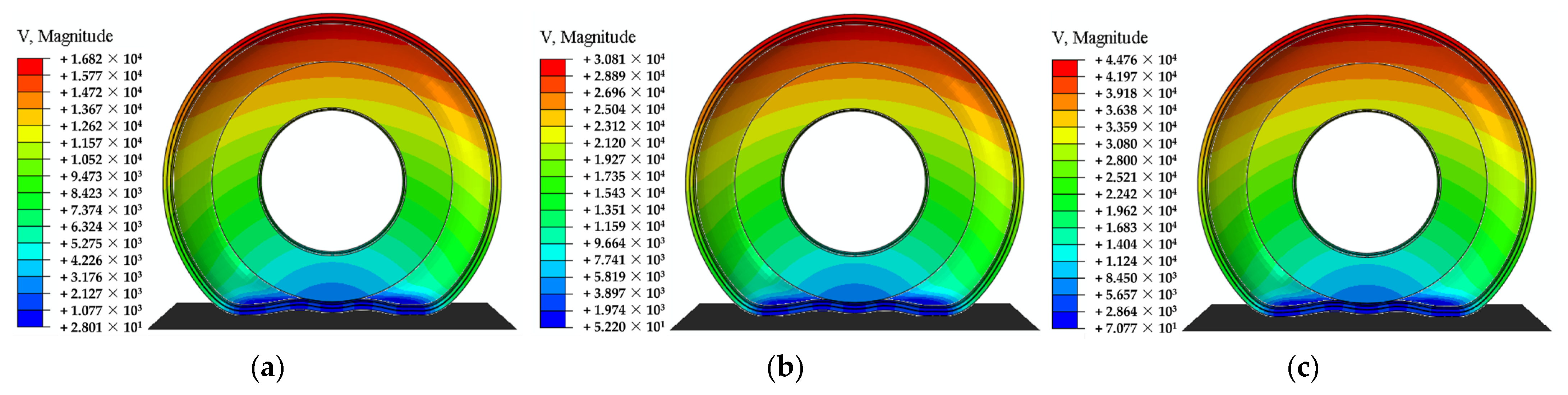
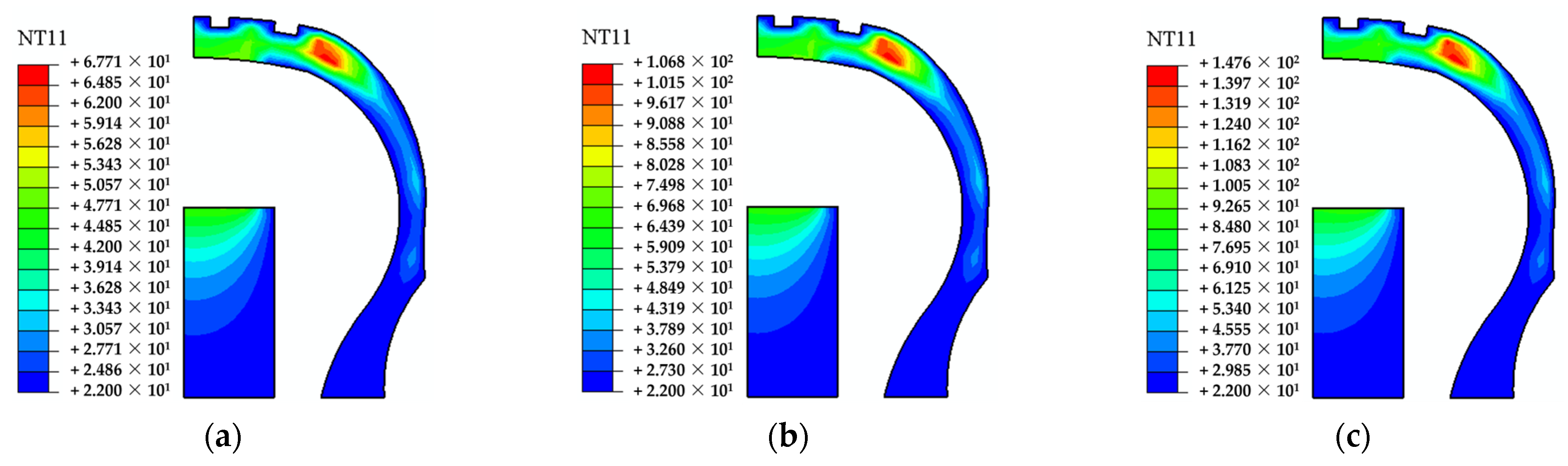
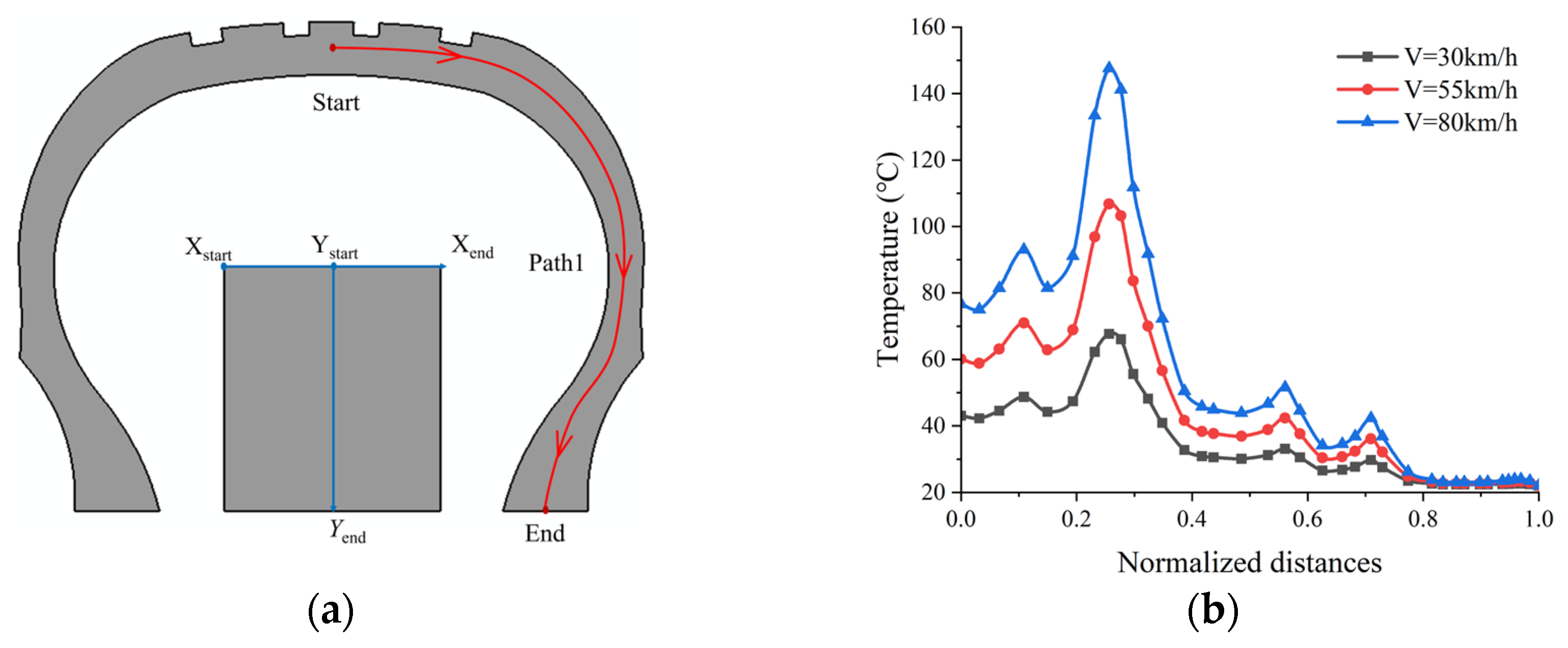
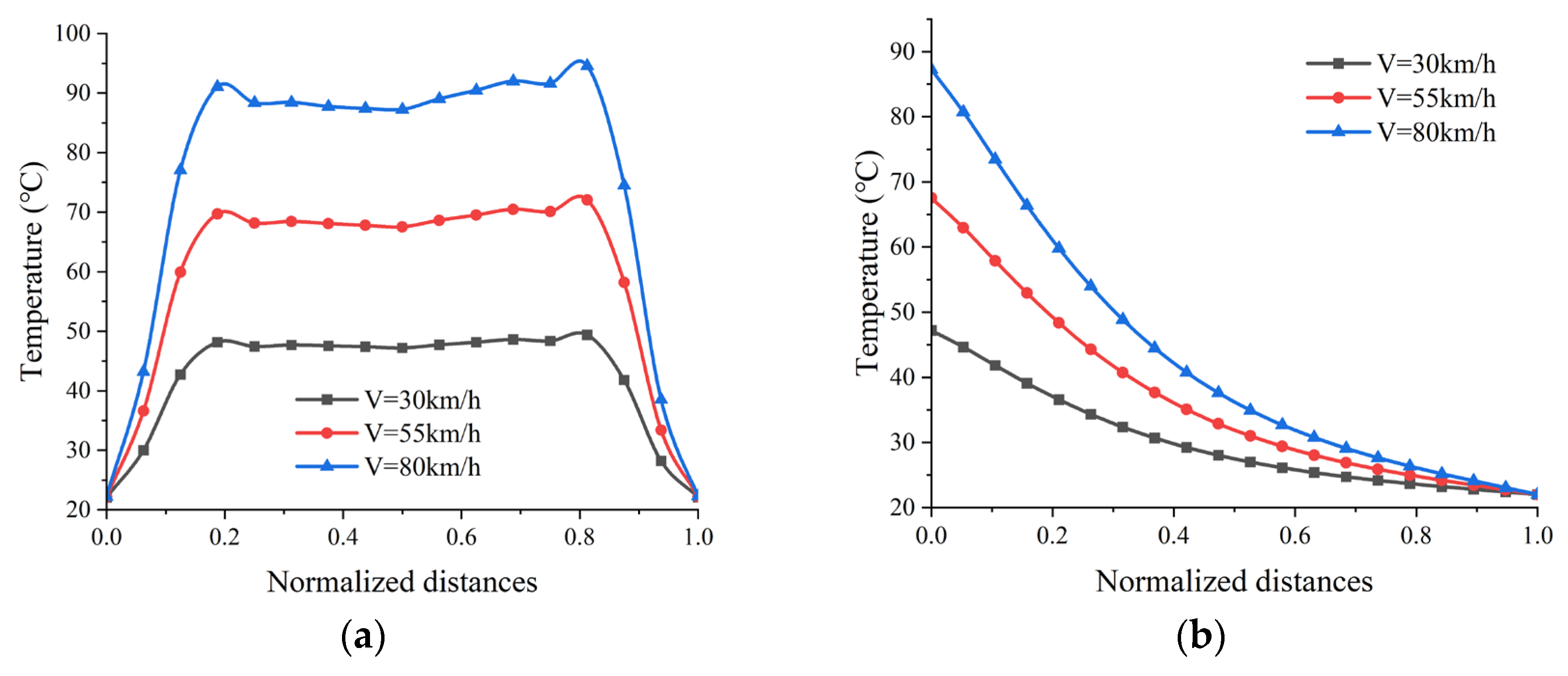
4.3. Results of SSTF Distribution
4.3.1. SSTF Distribution of ISRFT
4.3.2. SSTF Distribution of the Inserts Body
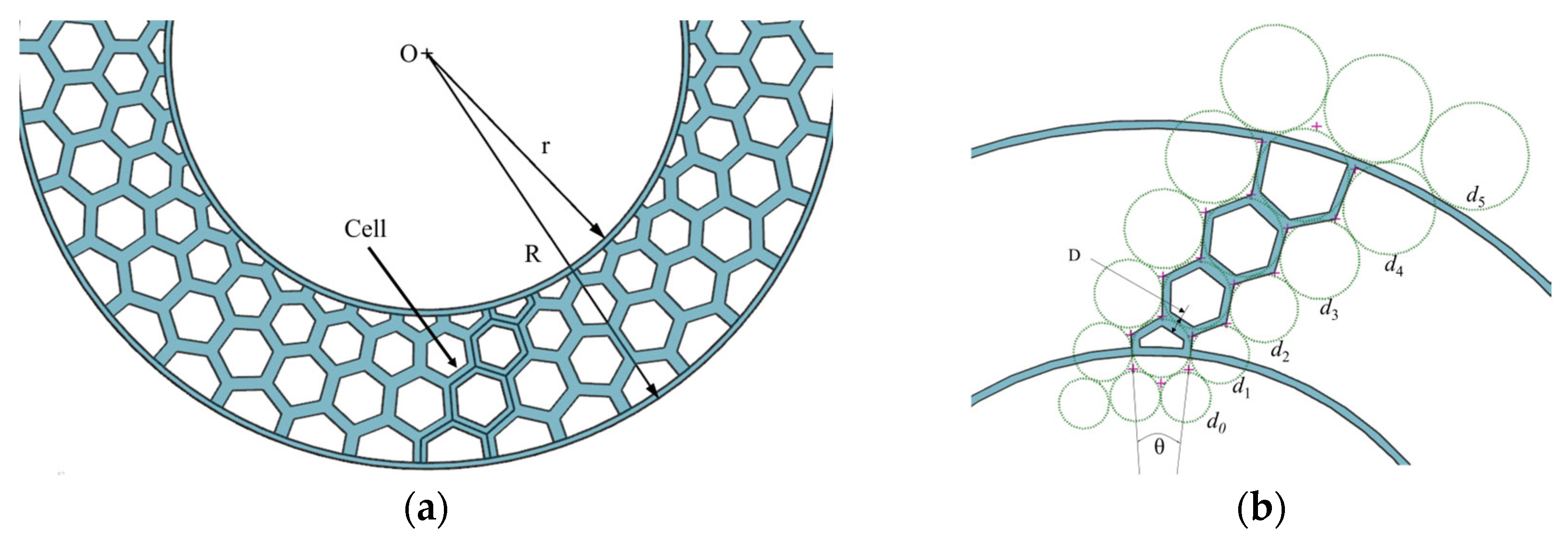
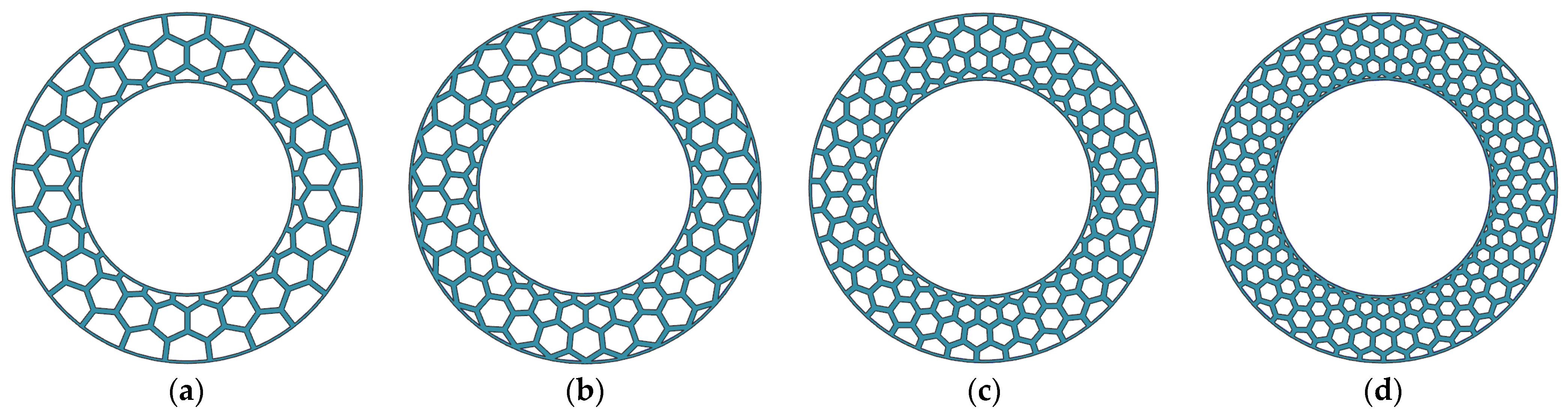
4.4. Honeycomb Structure Optimization
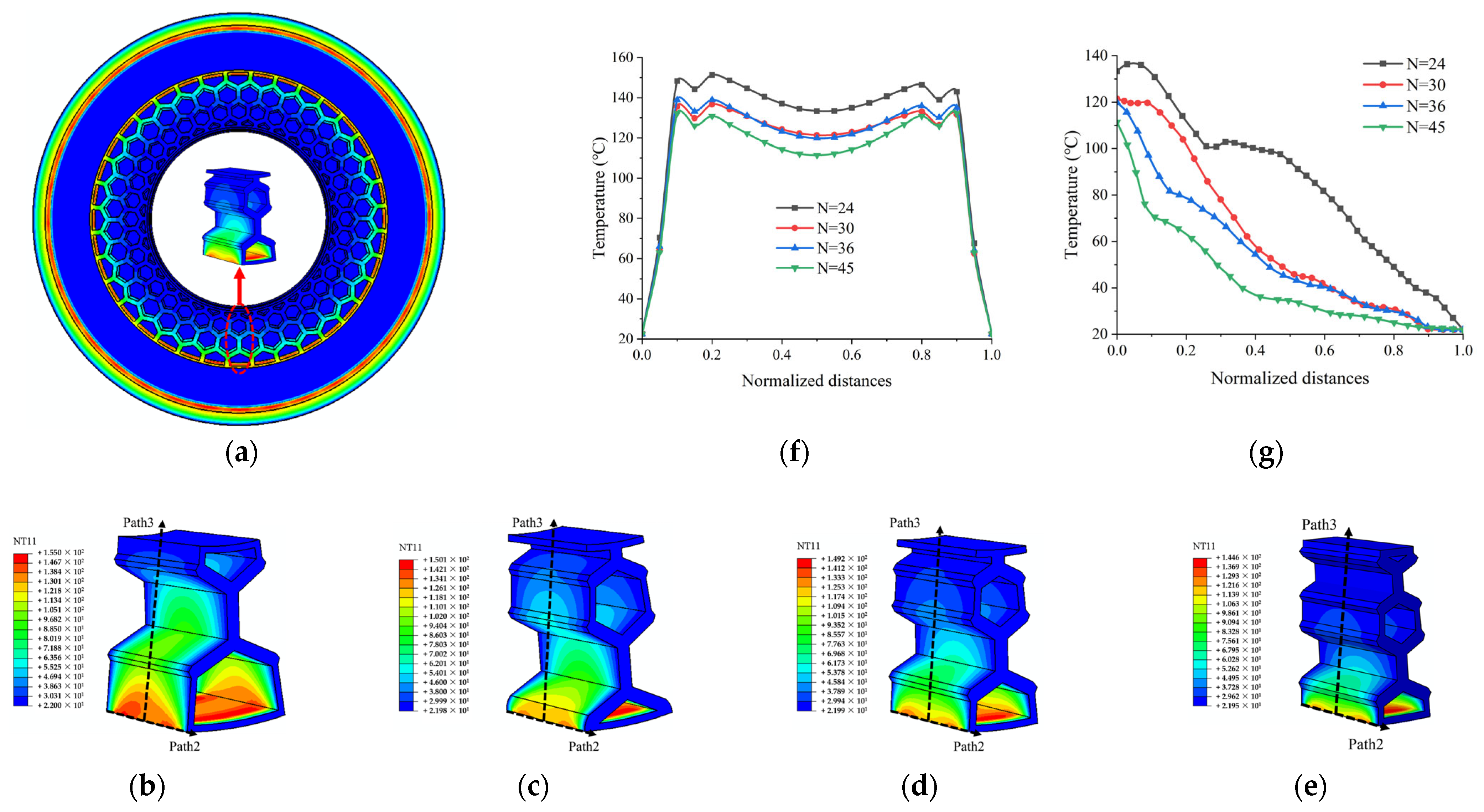
4.4.1. SSTF Distribution of Honeycomb ISRFTs
4.4.2. SSTF Distribution of the Honeycomb Inserts Body
5. Conclusions
- Under zero-pressure rated load conditions, for each 1 km/h increase in the operating speed of the ISRFT, the shoulder temperature rises by approximately 1.6 °C, the tread temperature by approximately 0.67 °C and the sidewall temperature by approximately 0.37 °C. The temperature rise of the bead and other components is relatively minor and less sensitive to speed.
- Compared to the original the ISRFT, the maximum temperature of the shoulder of the honeycomb ISRFT decreases by about 30 °C, and the SSTF distribution is more uniform. However, the maximum temperature of the tread increases by about 40 °C.
- Compared to the original inserts body, the four groups of the honeycomb inserts body exhibited a reduction in mass of 70.83%, 59.36%, 56.04% and 43.88%, respectively. This resulted in a notable enhancement in lightweight performance. The temperature of the honeycomb inserts body increased by 60.4 °C, 55.5 °C, 54.6 °C and 50 °C, respectively.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Jin, X.; Hou, C.; Fan, X.; Sun, Y.; Lv, J.; Lu, C. Investigation on the Static and Dynamic Behaviors of Non-Pneumatic Tires with Honeycomb Spokes. Compos. Struct. 2018, 187, 27–35. [Google Scholar]
- Sun, M.; Liu, W.; Zhang, Q.; Chen, Y.; Jiang, J.; Liu, X. Study on the Load-Bearing Characteristics Analysis Model of Non-Pneumatic Tire with Composite Spokes. Machines 2024, 12, 358. [Google Scholar] [CrossRef]
- Huang, S. The Development of Dongfeng “Mengshi” the First of 3rd Generation Off-road Vehicle in China. Automot. Eng. 2008, 30, 731–735. [Google Scholar]
- T/COS 015-2023; Specification for Aluminum-Based Support Body of Deflating Protection Wheels. China Ordnance Society: Beijing, China, 2023.
- Ejsmont, J.; Jackowski, J.; Luty, W.; Motrycz, G.; Stryjek, P.; Żurek, B. Analysis of Rolling Resistance of Tires with Run Flat Insert. Key Eng. Mater. 2014, 597, 165–170. [Google Scholar]
- Čukanović, D.; Bogdanović, G.; Radaković, A.; Milosavljević, D.; Veljović, L.; Balać, I. Comparative Thermal Buckling Analysis of Functionally Graded Plate. Therm. Sci. 2017, 21, 2957–2969. [Google Scholar]
- Radaković, A.; Čukanović, D.; Bogdanović, G.; Blagojević, M.; Stojanović, B.; Dragović, D.; Manić, N. Thermal Buckling and Free Vibration Analysis of Functionally Graded Plate Resting on an Elastic Foundation According to High Order Shear Deformation Theory Based on New Shape Function. Appl. Sci. 2020, 10, 4190. [Google Scholar] [CrossRef]
- Chen, D.; Wu, J.; Su, B.; Cui, B.; Teng, F.; An, S.; Bai, Y.; Liu, X.; Liu, Y.; Wang, Y. Thermo-mechanical-abrasive Coupling Analysis of Solid Rubber Tire Under High-Speed Rolling. Wear 2023, 512–513, 204546. [Google Scholar]
- Konstantinovich, L.P.; Aleksandrovich, Z.A. Current Issues of Implementation of Run Flat Technology in Production of Tires for Wheeled Vehicles. Mod. Technol. Sci. Technol. Prog. 2020, 1, 169–170. [Google Scholar]
- Wu, F. Finite Element Analysis of Temperature Distribution in Steady Rolling Tires. Ph.D. Thesis, University of Science and Technology of China, Hefei, China, 2009. [Google Scholar]
- Cho, J.; Lee, J.; Jeong, W.; Jeong, K.; Kim, K. Numerical Estimation of Rolling Resistance and Temperature Distribution of 3-D Periodic Patterned Tire. Int. J. Solids Struct. 2013, 50, 86–96. [Google Scholar]
- Liu, S.; Liu, W.; Zhou, S.; Li, X.; Zhang, Q. SSTF and Rolling Resistance Characteristics of Low-Velocity and Low-Load Capacity Non-Pneumatic Tires. Lubricants 2023, 11, 402. [Google Scholar]
- Zang, L.; Wang, X.; Zhao, Y.; Yin, R.; Lin, F.; Zhao, Z. Mechanical Characteristics of Inserts Supporting Run-Flat Tire under Zero-Pressure Conditions. Trans. CSAE 2020, 36, 80–86. [Google Scholar]
- Zang, L.; Wang, X.; Wu, C.; Teng, F.; Yang, S. Analysis of Load Characteristic and Contact Patch Characteristic of Support Insert Run-Flat Tire under Zero-Pressure Condition. Int. J. Automot. Technol. 2021, 22, 1141–1151. [Google Scholar]
- Behnke, R.; Kaliske, M. Numerical Modeling of Thermal Aging in Steady State Rolling Tires. Int. J. Nonlinear Mech. 2018, 103, 145–153. [Google Scholar]
- Shida, Z.; Koishi, M.; Kogure, T.; Kabe, K. A Rolling Resistance Simulation of Tires Using Static Finite Element Analysis. Tire Sci. Technol. 1999, 27, 84–105. [Google Scholar]
- Li, F.; Liu, F.; Liu, J.; Gao, Y.; Lu, Y.; Chen, J.; Yang, H.; Zhang, L. Thermo-mechanical Coupling Analysis of Transient Temperature and Rolling Resistance for Solid Rubber Tire: Numerical Simulation and Experimental Verification. Compos. Sci. Technol. 2018, 167, 404–410. [Google Scholar]
- Wei, Y.; Tian, Z.; Du, X. A Finite Element Model for the Rolling Loss Prediction and Fracture Analysis of Radial Tires. Tire Sci. Technol. 1999, 27, 250–276. [Google Scholar]
- Wu, W. Simulation Analysis of Tire Temperature Field. Master’s Thesis, Jilin University, Changchun, China, 2017. [Google Scholar]
- Yao, Q.; Dong, P.; Zhao, Z.; Li, Z.; Wei, T.; Wu, J.; Qiu, J.; Li, W. Temperature Dependent Tensile Fracture Strength Model of Rubber Materials Based on Mooney-Rivlin Model. Eng. Fract. Mech. 2023, 292, 109646. [Google Scholar]
- Wang, X.; Zang, L.; Wang, Z.; Zhao, Z.; Lin, F.; Teng, F. Analysis of Mechanical Characteristics of Inserts Supporting Run-Flat Tire During Pressure Relief. J. Braz. Soc. Mech. Sci. 2021, 43, 235. [Google Scholar]
- Genovese, A.; Garofano, D.; Sakhnevych, A.; Timpone, F.; Farroni, F. Static and Dynamic Analysis of Non-Pneumatic Tires Based on Experimental and Numerical Methods. Appl. Sci. 2021, 11, 11232. [Google Scholar] [CrossRef]
- Feng, X.; Wei, Y.; Zheng, X.; Li, H.; He, J. Study on Mechanics of Steady State Free Rolling Tires. China Rubber Ind. 2013, 60, 517–526. [Google Scholar]
- Zhuang, J.; Wei, D. Static and Dynamic Performances of Bionic Camel Foot Tire. Trans. CSAE 2006, 9, 30–33. [Google Scholar]
- Liu, H.; Pan, Y.; Bian, H.; Wang, C. Optimize Design of Run-Flat Tires by Simulation and Experimental Research. Materials 2021, 14, 474. [Google Scholar] [CrossRef] [PubMed]
- Deng, Y.; Wang, Z.; Shen, H.; Gong, J.; Xiao, Z. A Comprehensive Review on Non-Pneumatic Tyre Research. Mater. Des. 2023, 227, 111742. [Google Scholar]
- Deng, Y.; Wang, Z.; Liu, T.; Liang, W.; Shen, H.; Xiao, Z. Static and Dynamic Mechanical Characteristics of Honeycomb Non-Pneumatic Tire Under Structural Damage Condition. Eur. J. Mech. A/Solids 2023, 102, 105120. [Google Scholar]
- Zang, L.; Wang, X.; Yan, P.; Zhao, Z. Structural Design and Characteristics of a Non-Pneumatic Tire with Honeycomb Structure. Mech. Adv. Mater. Struct. 2022, 29, 4066–4073. [Google Scholar]



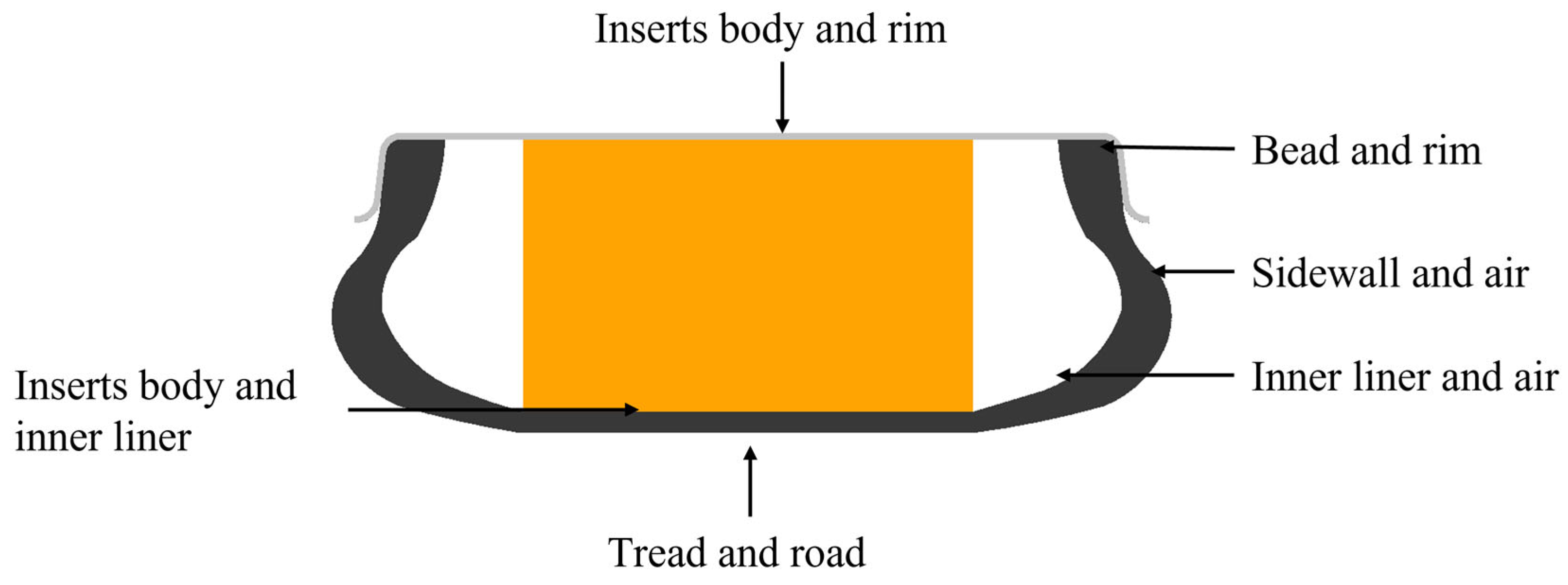

| Component | C01 (MPa) | C10 (MPa) | D01 (MPa) | Density (kg/m3) | Conductivity (W/(m·K)) | Specific Heat (J/(kg·K)) | tanδ |
|---|---|---|---|---|---|---|---|
| Tread | 0.5792 | 0.1448 | 0.01381 | 1112 | 0.341 | 1.406 | 0.182 |
| Belt | 1.0848 | 0.2712 | 0.00737 | 1144 | 0.285 | 1.060 | 0.11 |
| Sidewall | 0.524 | 0.131 | 0.01527 | 1110 | 0.311 | 1.372 | 0.087 |
| Bead filler | −1.6905 | 8.0598 | 0.00157 | 1025 | 0.323 | 1.450 | 0.049 |
| Carcass | 0.6159 | 0.154 | 0.01299 | 1058 | 0.291 | 1.283 | 0.082 |
| Component | Young’s Modulus (MPa) | Poisson’s Ratio | Density (kg/m3) | Conductivity (W/(m·K)) | Specific Heat (J/(kg·K)) | tanδ |
|---|---|---|---|---|---|---|
| Inserts body | 600 | 0.48 | 1200 | 0.24 | 1.334 | 0.445 |
| Bead | 166,000 | 0.3 | 7800 | 0.385 | 1.580 | 0.143 |
| Carcass ply | 10,549 | 0.4 | - | |||
| Belt ply | 205,351 | 0.3 | ||||
| Radial Load (N) | Test Width (mm) | Simulation Width (mm) | Test Length (mm) | Simulation Length (mm) | Test Area (mm2) | Simulation Area (mm2) | Area Error (%) |
|---|---|---|---|---|---|---|---|
| 9800 | 235 | 216.579 | 580 | 561.139 | 136,300 | 121,530 | 10.84 |
| 12,250 | 235 | 225.463 | 580 | 562.015 | 136,300 | 126,713 | 7.03 |
| 14,700 | 235 | 235.875 | 580 | 560.513 | 136,300 | 132,211 | 3 |
| Part | Coefficient of Convective Heat Transfer (w/m2k) |
|---|---|
| Tread | 118 |
| Sidewall | 90 |
| Rim | 168 |
| Inner liner | 52 |
| n | d0 (mm) | d1 (mm) | d2 (mm) | d3 (mm) | d4 (mm) | d5 (mm) | d6 (mm) |
|---|---|---|---|---|---|---|---|
| 24 | 43.21 | 54.24 | 68.08 | 85.46 | 107.28 | / | / |
| 30 | 36.33 | 43.57 | 52.25 | 62.66 | 75.15 | 90.12 | / |
| 36 | 31.28 | 36.39 | 42.33 | 49.25 | 57.30 | 66.66 | / |
| 45 | 25.72 | 29.03 | 32.76 | 36.98 | 41.73 | 47.11 | 53.17 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xue, C.; Zang, L.; Wei, F.; Feng, Y.; Zhou, C.; Lv, T. Thermo-Mechanical Coupling Analysis of Inserts Supporting Run-Flat Tires under Zero-Pressure Conditions. Machines 2024, 12, 578. https://doi.org/10.3390/machines12080578
Xue C, Zang L, Wei F, Feng Y, Zhou C, Lv T. Thermo-Mechanical Coupling Analysis of Inserts Supporting Run-Flat Tires under Zero-Pressure Conditions. Machines. 2024; 12(8):578. https://doi.org/10.3390/machines12080578
Chicago/Turabian StyleXue, Cheng, Liguo Zang, Fengqi Wei, Yuxin Feng, Chong Zhou, and Tian Lv. 2024. "Thermo-Mechanical Coupling Analysis of Inserts Supporting Run-Flat Tires under Zero-Pressure Conditions" Machines 12, no. 8: 578. https://doi.org/10.3390/machines12080578
APA StyleXue, C., Zang, L., Wei, F., Feng, Y., Zhou, C., & Lv, T. (2024). Thermo-Mechanical Coupling Analysis of Inserts Supporting Run-Flat Tires under Zero-Pressure Conditions. Machines, 12(8), 578. https://doi.org/10.3390/machines12080578






