Research on Scheduling Algorithm of Knitting Production Workshop Based on Deep Reinforcement Learning
Abstract
1. Introduction
2. Literature Review
3. Mathematical Modeling of Production Scheduling Problem in Knitting Workshop
3.1. System Model
- The same machine can only process a maximum of one workpiece at a given time;
- The same job can only be processed by one machine at the same time in the same process;
- Each process of each job cannot be interrupted once it starts (that is, each process is considered to be non-preemptive);
- Different artifacts have the same priority;
- There are no priority constraints between the processes for different jobs, but there are sequential constraints between processes for the same job;
- All jobs and machines are available within the dispatch scope until the dispatch is completed, regardless of equipment failures.
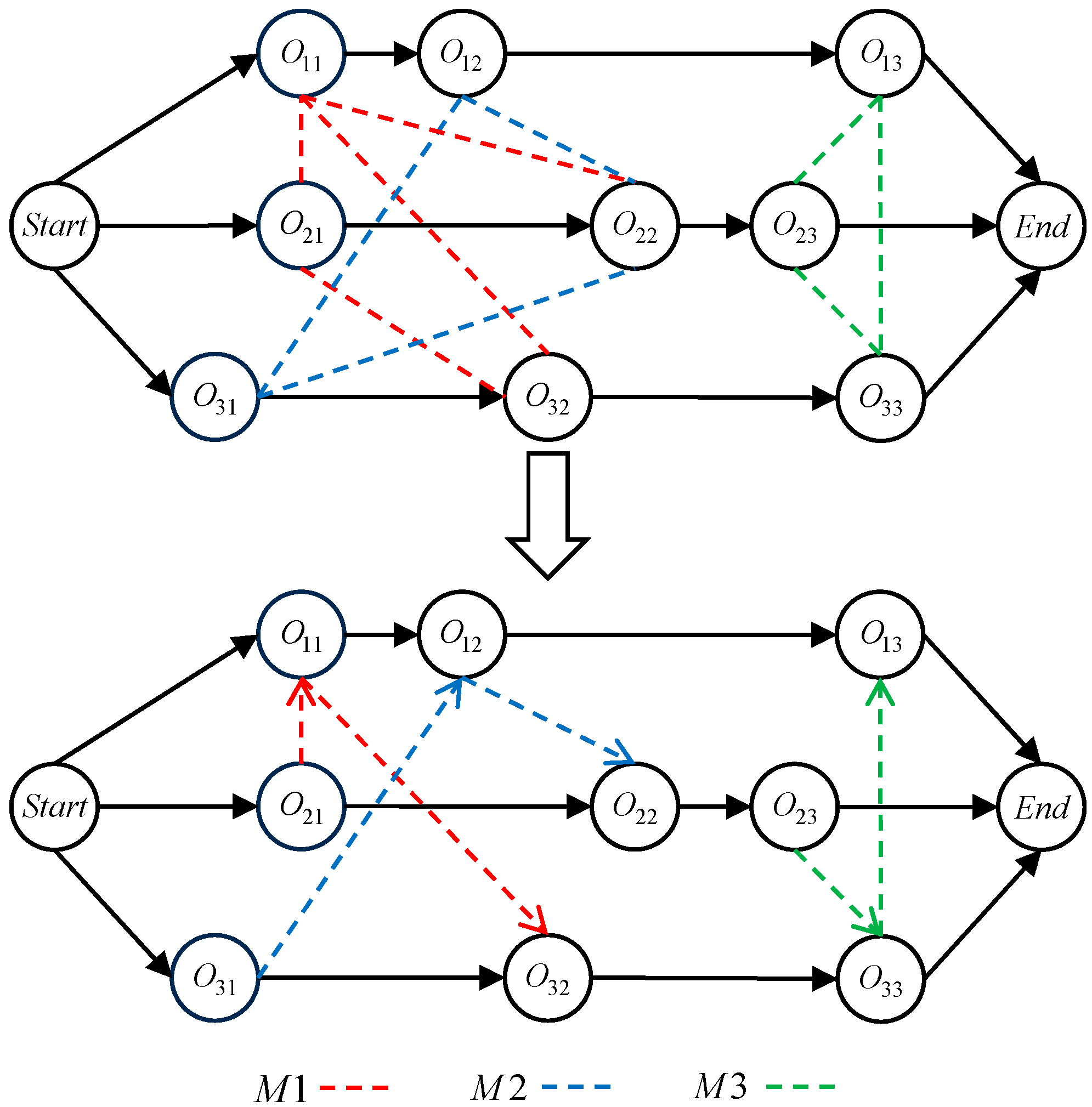
3.2. Problem Formulation
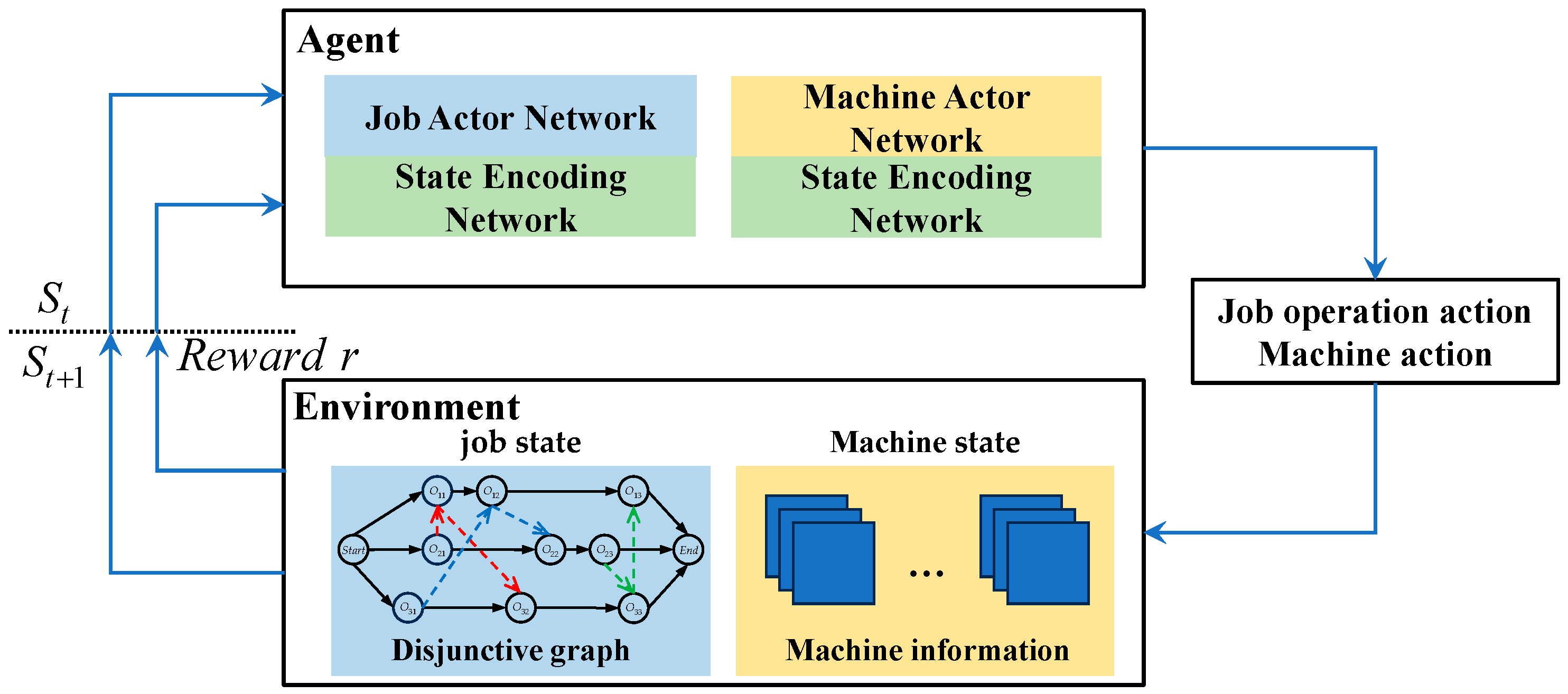
4. DRL Architecture for the Knitting Workshop Production Scheduling Problem
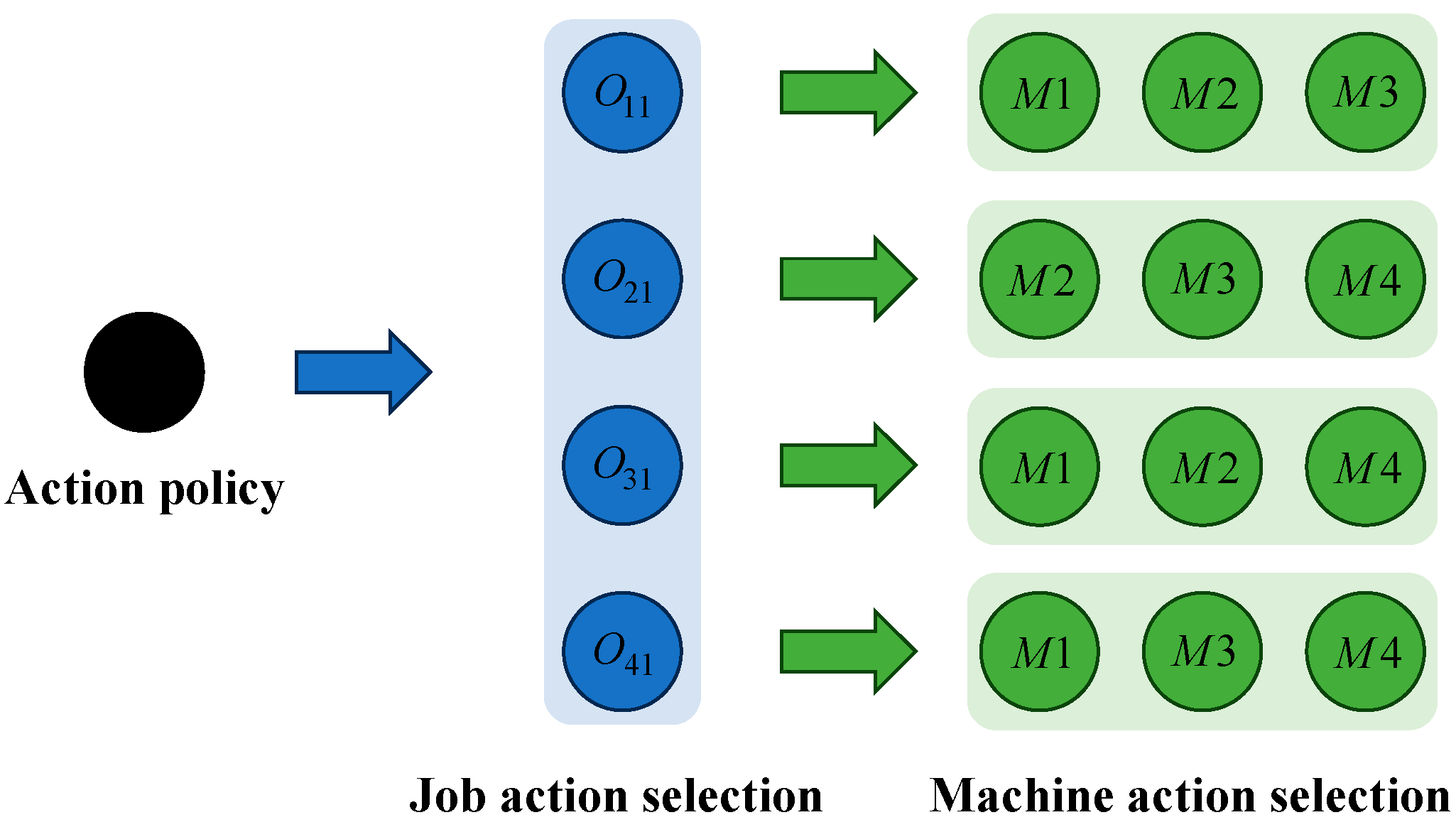
4.1. Problem Setting
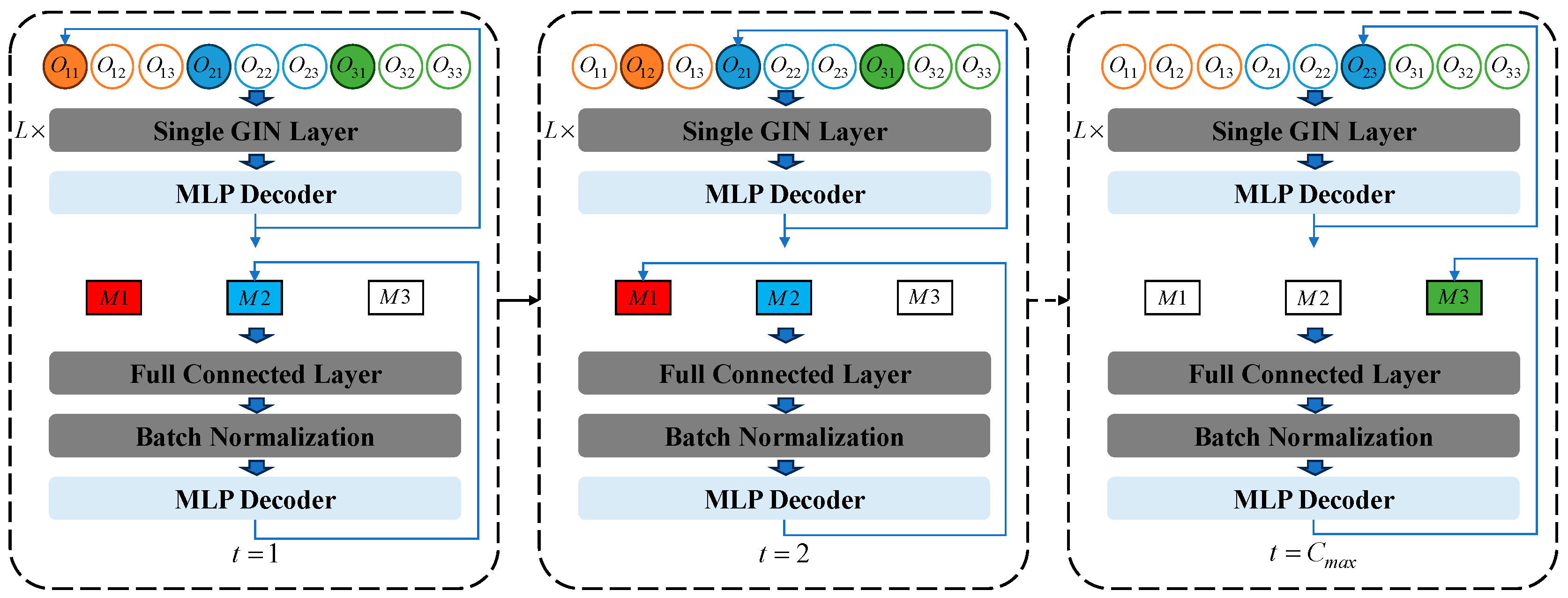
4.2. Multi-Proximal Policy Optimization
| Algorithm 1 Multi-PPO Algorithm |
| Parameters: Truncated factorization , number of sub-iterations , Input: Initial policy function parameters , initial value function parameters . Output: Optimal solution s Begin for k = 0, 1, 2, ⋯, do . . for do The Adam stochastic gradient ascent algorithm is used to maximize the objective function of PPO-Clip to update the policy: end for for do The value function is learned by minimizing the mean square error using the gradient descent algorithm: end for end for End |
5. Simulation Result and Analysis
5.1. Parameters and Training
5.2. System Validation Parameters
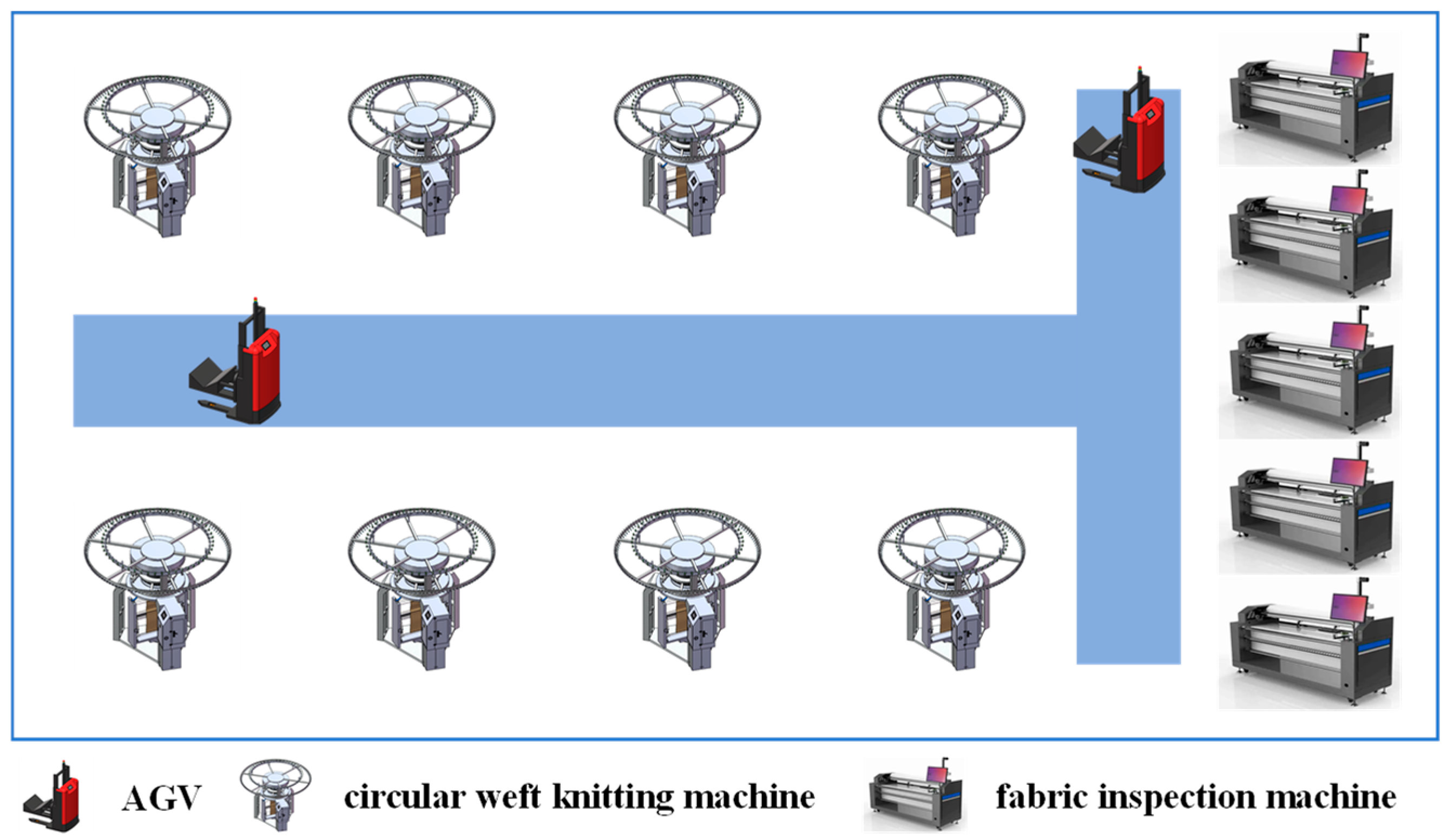
5.3. Knitting Intelligent Production Experiment Platform
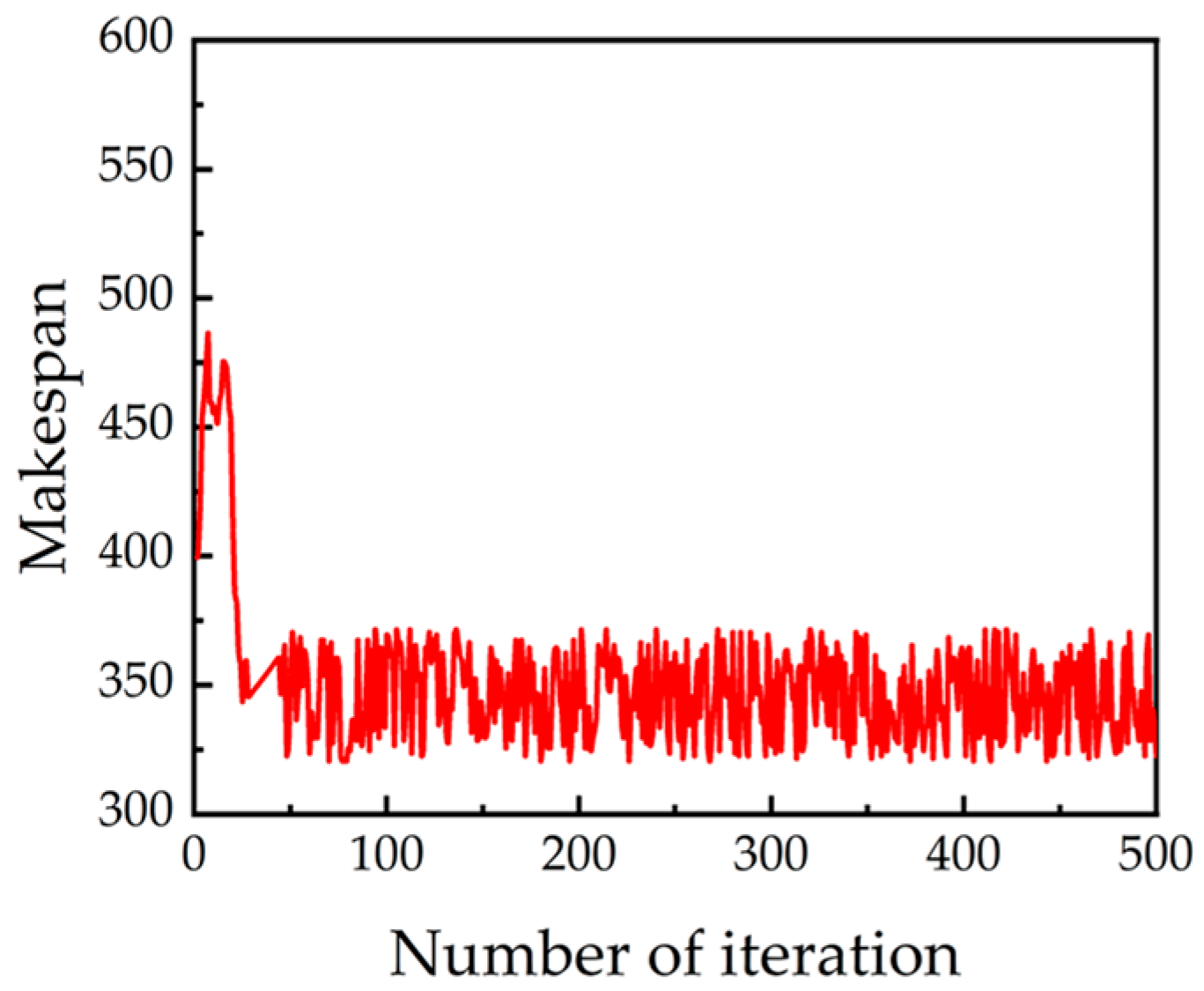
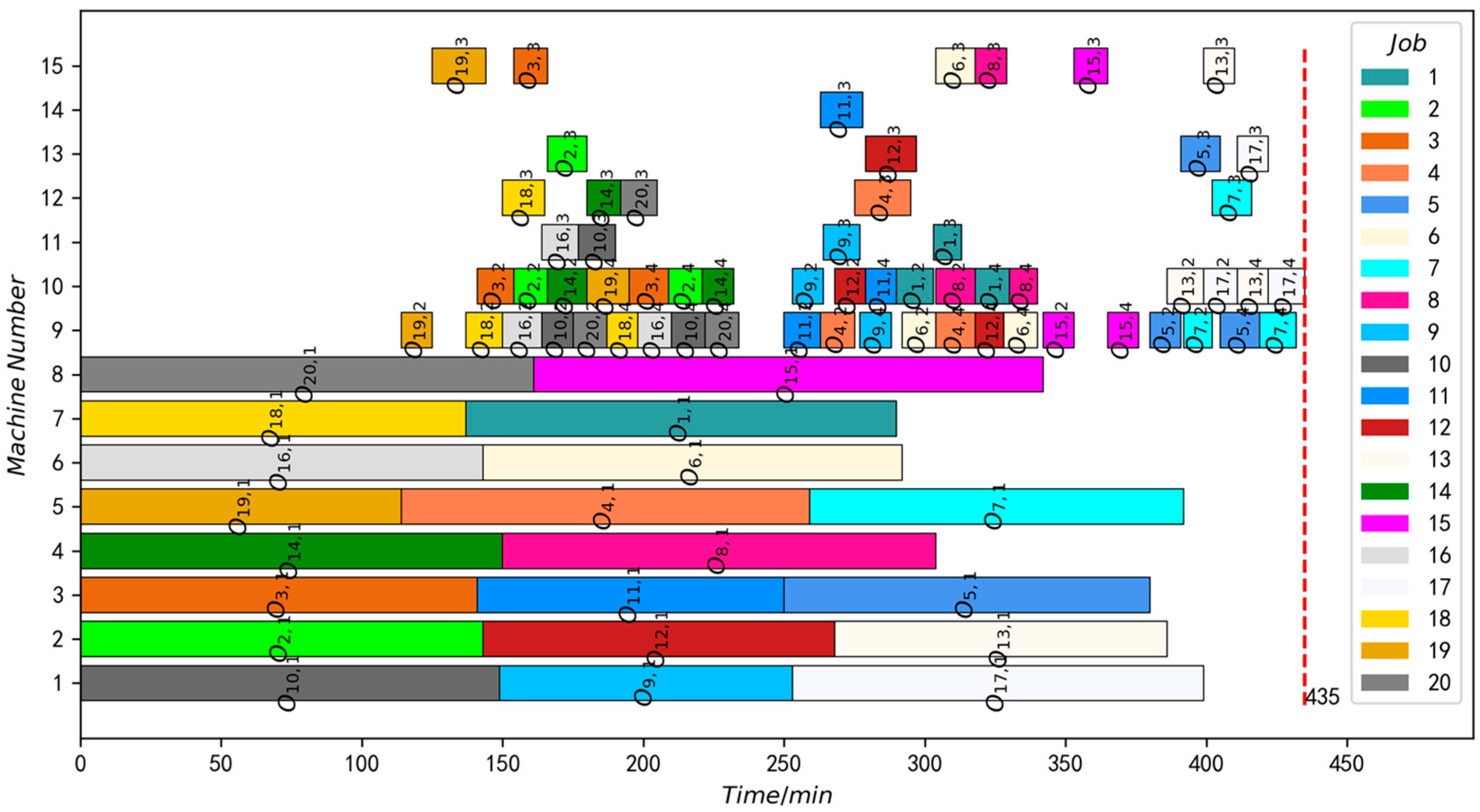
5.4. Multi-Proximal Policy Optimization
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sun, L.; Shi, W.M.; Wang, J.R.; Mao, H.M.; Tu, J.J.; Wang, L.J. Research on Production Scheduling Technology in Knitting Workshop Based on Improved Genetic Algorithm. Appl. Sci. 2023, 13, 5701. [Google Scholar] [CrossRef]
- Chen, X.J.; Cui, W.Z.; Wei, Y.L. Application of information technology in textile industry. Qing Fang Gong Ye YuJishu 2021, 50, 72–73. [Google Scholar]
- Wang, C.Y.; Li, Y.; Li, X.Y. Solving flexible job shop scheduling problem by a multi-swarm collaborative genetic algorithm. J. Syst. Eng. Electron. 2021, 32, 261–271. [Google Scholar] [CrossRef]
- Gen, M.; Lin, L.; Ohwada, H. Advances in Hybrid Evolutionary Algorithms for Fuzzy Flexible Job-shop Scheduling: State-of-the-Art Survey. In Proceedings of the 13th International Conference on Agents and Artificial Intelligence (ICAART), Electr Network, Online, 4–6 February 2021; pp. 562–573. [Google Scholar]
- Gao, K.Z.; Cao, Z.G.; Zhang, L.; Chen, Z.H.; Han, Y.Y.; Pan, Q.K. A Review on Swarm Intelligence and Evolutionary Algorithms for Solving Flexible Job Shop Scheduling Problems. IEEE-CAA J. Autom. Sin. 2019, 6, 904–916. [Google Scholar] [CrossRef]
- Wang, J.F.; Du, B.Q.; Ding, H.M. A Genetic Algorithm for the Flexible Job-Shop Scheduling Problem. In Proceedings of the International Conference on Advanced Research on Computer Science and Information Engineering, Zhengzhou, China, 21–22 May 2011; pp. 332–339. [Google Scholar]
- Sun, W.; Pan, Y.; Lu, X.H.; Ma, Q.Y. Research on flexible job-shop scheduling problem based on a modified genetic algorithm. J. Mech. Sci. Technol. 2010, 24, 2119–2125. [Google Scholar] [CrossRef]
- Zhang, G.H.; Shao, X.Y.; Li, P.G.; Gao, L. An effective hybrid particle swarm optimization algorithm for multi-objective flexible job-shop scheduling problem. Comput. Ind. Eng. 2009, 56, 1309–1318. [Google Scholar] [CrossRef]
- Nouiri, M.; Jemai, A.; Ammari, A.C.; Bekrar, A.; Niar, S. An effective particle swarm optimization algorithm for flexible job-shop scheduling problem. In Proceedings of the 5th International Conference on Industrial Engineering and Systems Management (IEEE IESM), Mohammadia Sch Engn, Rabat, Morocco, 28–30 October 2013; pp. 29–34. [Google Scholar]
- Devi, K.G.; Mishra, R.S.; Madan, A.K. A Dynamic Adaptive Firefly Algorithm for Flexible Job Shop Scheduling. Intell. Autom. Soft Comput. 2022, 31, 429–448. [Google Scholar] [CrossRef]
- Shapiro, J.F. Mathematical programming models and methods for production planning and scheduling. In Handbooks in Operations Research and Management Science; Elsevier: Amsterdam, The Netherlands, 1993; Volume 4, pp. 371–443. [Google Scholar]
- Özgüven, C.; Özbakir, L.; Yavuz, Y. Mathematical models for job-shop scheduling problems with routing and process plan flexibility. Appl. Math. Model. 2010, 34, 1539–1548. [Google Scholar] [CrossRef]
- Meng, L.L.; Zhang, B.; Gao, K.Z.; Duan, P. An MILP Model for Energy-Conscious Flexible Job Shop Problem with Transportation and Sequence-Dependent Setup Times. Sustainability 2023, 15, 776. [Google Scholar] [CrossRef]
- Yang, D.S.; Wu, M.L.; Li, D.; Xu, Y.L.; Zhou, X.Y.; Yang, Z.L. Dynamic opposite learning enhanced dragonfly algorithm for solving large-scale flexible job shop scheduling problem. Knowl.-Based Syst. 2022, 238, 16. [Google Scholar] [CrossRef]
- Sun, K.X.; Zheng, D.B.; Song, H.H.; Cheng, Z.W.; Lang, X.D.; Yuan, W.D.; Wang, J.Q. Hybrid genetic algorithm with variable neighborhood search for flexible job shop scheduling problem in a machining system. Expert Syst. Appl. 2023, 215, 18. [Google Scholar] [CrossRef]
- Pan, Z.X.; Lei, D.M.; Wang, L. A Bi-Population Evolutionary Algorithm with Feedback for Energy-Efficient Fuzzy Flexible Job Shop Scheduling. IEEE Trans. Syst. Man Cybern.-Syst. 2022, 52, 5295–5307. [Google Scholar] [CrossRef]
- Badia, A.P.; Piot, B.; Kapturowski, S.; Sprechmann, P.; Vitvitskyi, A.; Guo, D.; Blundell, C. Agent57: Outperforming the Atari Human Benchmark. In Proceedings of the International Conference on Machine Learning (ICML), Electr Network, Online, 13–18 July 2020. [Google Scholar]
- Bellemare, M.G.; Naddaf, Y.; Veness, J.; Bowling, M. The Arcade Learning Environment: An Evaluation Platform for General Agents. J. Artif. Intell. Res. 2013, 47, 253–279. [Google Scholar] [CrossRef]
- Shang, X.F. A Study of Deep Learning Neural Network Algorithms and Genetic Algorithms for FJSP. J. Appl. Math. 2023, 2023, 13. [Google Scholar] [CrossRef]
- Wang, L.; Hu, X.; Wang, Y.; Xu, S.; Ma, S.; Yang, K.; Liu, Z.; Wang, W. Dynamic job-shop scheduling in smart manufacturing using deep reinforcement learning. Comput. Netw. 2021, 190, 107969. [Google Scholar] [CrossRef]
- Lei, K.; Guo, P.; Zhao, W.C.; Wang, Y.; Qian, L.M.; Meng, X.Y.; Tang, L.S. A multi-action deep reinforcement learning framework for flexible Job-shop scheduling problem. Expert Syst. Appl. 2022, 205, 18. [Google Scholar] [CrossRef]
- Liang, X.J.; Song, W.; Wei, P.F. Dynamic Job Shop Scheduling via Deep Reinforcement Learning. In Proceedings of the 35th IEEE International Conference on Tools with Artificial Intelligence (ICTAI), Atlanta, GA, USA, 6–8 November 2023; pp. 369–376. [Google Scholar]
| Symbol | Definition |
|---|---|
| Total number of jobs | |
| Total number of machines | |
| Machine number, | |
| Job number, | |
| Number of processes for job | |
| Process number, | |
| The set of optional processing machines for process of job | |
| The number of optional processing machines for process of job | |
| The process for job | |
| The process of job is processed on machine | |
| The processing time on machine for process of job | |
| The processing start time of process of job | |
| The processing completion time of process of job | |
| The processing completion time of job | |
| The maximum completion time | |
| The total number of processes for all jobs, | |
| Workpiece | Process 1 | Process 2 | Process 3 | Process 4 |
|---|---|---|---|---|
| Job 1 | (M1,M2,M3,M4,M5,M6,M7,M8) | (M9,M10) | (M11,M12,M13,M14,M15) | (M9,M10) |
| Job 2 | (M1,M2,M3,M4,M5,M6,M7,M8) | (M9,M10) | (M11,M12,M13,M14,M15) | (M9,M10) |
| Job 3 | (M1,M2,M3,M4,M5,M6,M7,M8) | (M9,M10) | (M11,M12,M13,M14,M15) | (M9,M10) |
| Job 4 | (M1,M2,M3,M4,M5,M6,M7,M8) | (M9,M10) | (M11,M12,M13,M14,M15) | (M9,M10) |
| Job 5 | (M1,M2,M3,M4,M5,M6,M7,M8) | (M9,M10) | (M11,M12,M13,M14,M15) | (M9,M10) |
| Job 6 | (M1,M2,M3,M4,M5,M6,M7,M8) | (M9,M10) | (M11,M12,M13,M14,M15) | (M9,M10) |
| Job 7 | (M1,M2,M3,M4,M5,M6,M7,M8) | (M9,M10) | (M11,M12,M13,M14,M15) | (M9,M10) |
| Job 8 | (M1,M2,M3,M4,M5,M6,M7,M8) | (M9,M10) | (M11,M12,M13,M14,M15) | (M9,M10) |
| Job 9 | (M1,M2,M3,M4,M5,M6,M7,M8) | (M9,M10) | (M11,M12,M13,M14,M15) | (M9,M10) |
| Job 10 | (M1,M2,M3,M4,M5,M6,M7,M8) | (M9,M10) | (M11,M12,M13,M14,M15) | (M9,M10) |
| Job 11 | (M1,M2,M3,M4,M5,M6,M7,M8) | (M9,M10) | (M11,M12,M13,M14,M15) | (M9,M10) |
| Job 12 | (M1,M2,M3,M4,M5,M6,M7,M8) | (M9,M10) | (M11,M12,M13,M14,M15) | (M9,M10) |
| Job 13 | (M1,M2,M3,M4,M5,M6,M7,M8) | (M9,M10) | (M11,M12,M13,M14,M15) | (M9,M10) |
| Job 14 | (M1,M2,M3,M4,M5,M6,M7,M8) | (M9,M10) | (M11,M12,M13,M14,M15) | (M9,M10) |
| Job 15 | (M1,M2,M3,M4,M5,M6,M7,M8) | (M9,M10) | (M11,M12,M13,M14,M15) | (M9,M10) |
| Job 16 | (M1,M2,M3,M4,M5,M6,M7,M8) | (M9,M10) | (M11,M12,M13,M14,M15) | (M9,M10) |
| Job 17 | (M1,M2,M3,M4,M5,M6,M7,M8) | (M9,M10) | (M11,M12,M13,M14,M15) | (M9,M10) |
| Job 18 | (M1,M2,M3,M4,M5,M6,M7,M8) | (M9,M10) | (M11,M12,M13,M14,M15) | (M9,M10) |
| Job 19 | (M1,M2,M3,M4,M5,M6,M7,M8) | (M9,M10) | (M11,M12,M13,M14,M15) | (M9,M10) |
| Job 20 | (M1,M2,M3,M4,M5,M6,M7,M8) | (M9,M10) | (M11,M12,M13,M14,M15) | (M9,M10) |
| Workpiece | Process 1 (min) | Process 2 (min) | Process 3 (min) | Process 4 (min) |
|---|---|---|---|---|
| Job 1 | (194,153,174,173,179,163,153,189) | (13,13) | (10,11,16,16,13) | (12,12) |
| Job 2 | (171,143,196,183,153,195,195,170) | (12,12) | (22,21,14,19,21) | (13,12) |
| Job 3 | (183,197,141,166,158,138,157,165) | (12,13) | (19,15,13,20,12) | (15,14) |
| Job 4 | (182,201,173,188,145,173,184,188) | (12,12) | (20,20,20,22,25) | (14,14) |
| Job 5 | (211,208,130,174,214,135,210,151) | (11,14) | (19,19,14,16,14) | (14,15) |
| Job 6 | (201,190,166,182,166,149,205,197) | (12,12) | (18,23,18,25,14) | (12,12) |
| Job 7 | (174,197,150,180,133,154,183,200) | (10,12) | (16,14,14,20,17) | (13,14) |
| Job 8 | (183,163,193,154,156,207,216,179) | (14,14) | (21,14,20,16,11) | (12,10) |
| Job 9 | (104,159,114,191,192,179,117,192) | (12,11) | (13,15,18,14,20) | (11,13) |
| Job 10 | (149,168,152,203,141,193,207,206) | (11,12) | (13,20,17,18,19) | (12,12) |
| Job 11 | (199,209,109,150,179,187,144,146) | (13,15) | (20,23,20,15,16) | (11,11) |
| Job 12 | (123,125,141,199,179,132,192,120) | (14,11) | (19,19,18,19,20) | (10,13) |
| Job 13 | (122,118,122,197,187,127,169,180) | (12,13) | (14,14,17,16,11) | (12,11) |
| Job 14 | (201,200,151,150,169,176,153,201) | (13,14) | (18,12,19,18,13) | (11,11) |
| Job 15 | (164,157,173,194,196,199,150,181) | (11,12) | (23,20,18,14,12) | (11,11) |
| Job 16 | (195,198,148,193,164,143,160,145) | (14,15) | (13,20,14,15,19) | (12,12) |
| Job 17 | (146,193,168,137,189,200,139,139) | (12,12) | (13,11,11,16,13) | (12,13) |
| Job 18 | (208,203,208,152,203,197,137,181) | (13,13) | (17,15,15,20,16) | (11,11) |
| Job 19 | (122,152,143,159,114,189,152,159) | (11,12) | (22,21,21,20,19) | (12,15) |
| Job 20 | (191,188,181,185,181,212,212,161) | (12,11) | (20,13,19,19,18) | (12,12) |
| Experimental Algorithms | Algorithm Solution Results | Relative Error (%) | Running Time (s) |
|---|---|---|---|
| LPT | 462 | 5.84 | 0.57 |
| SPT | 527 | 17.46 | 0.59 |
| FIFO | 654 | 33.49 | 0.41 |
| Genetic algorithms | 437 | 0.46 | 6.83 |
| The algorithms in this paper | 435 | 0.00 | 1.08 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, L.; Shi, W.; Xuan, C.; Zhang, Y. Research on Scheduling Algorithm of Knitting Production Workshop Based on Deep Reinforcement Learning. Machines 2024, 12, 579. https://doi.org/10.3390/machines12080579
Sun L, Shi W, Xuan C, Zhang Y. Research on Scheduling Algorithm of Knitting Production Workshop Based on Deep Reinforcement Learning. Machines. 2024; 12(8):579. https://doi.org/10.3390/machines12080579
Chicago/Turabian StyleSun, Lei, Weimin Shi, Chang Xuan, and Yongchao Zhang. 2024. "Research on Scheduling Algorithm of Knitting Production Workshop Based on Deep Reinforcement Learning" Machines 12, no. 8: 579. https://doi.org/10.3390/machines12080579
APA StyleSun, L., Shi, W., Xuan, C., & Zhang, Y. (2024). Research on Scheduling Algorithm of Knitting Production Workshop Based on Deep Reinforcement Learning. Machines, 12(8), 579. https://doi.org/10.3390/machines12080579





