Flow Field Noise Analysis and Noise Reduction Research of Twin-Screw Air Compressor Based on Multi-Field Coupling Technology
Abstract
1. Introduction
2. Twin-Screw Compressor Flow Field Noise Calculation Method
2.1. Flow Field Analysis Methods
- (1)
- Mass conservation equations
- (2)
- Momentum conservation equation
- (3)
- The energy conservation equation
2.2. Sound Field Analysis Methods
- (1)
- Equation for acoustic waves in fluid media:
- (2)
- Helmholtz equation
3. Model Building and Solution Setup
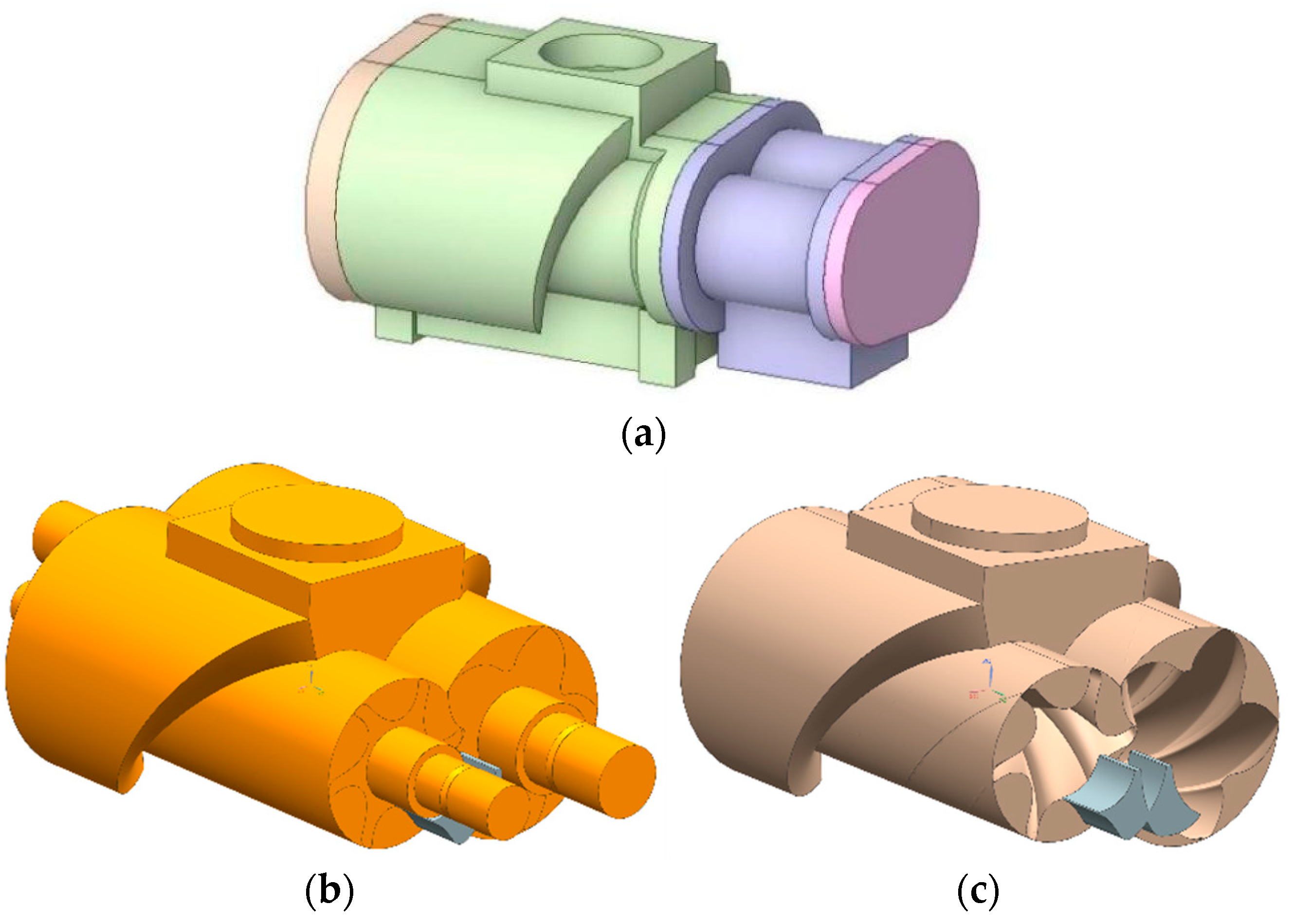
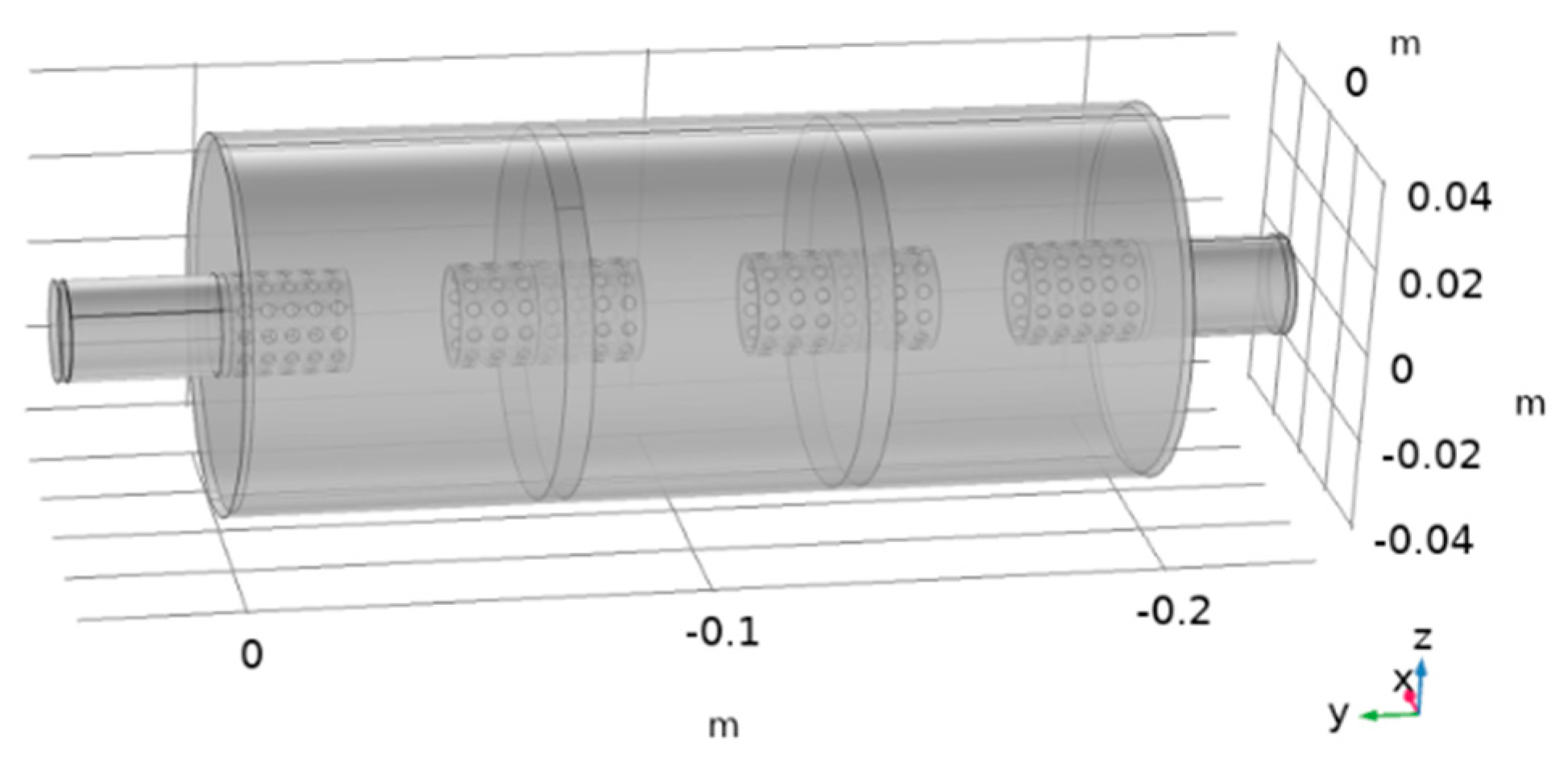
3.1. Modelling of the Flow Field
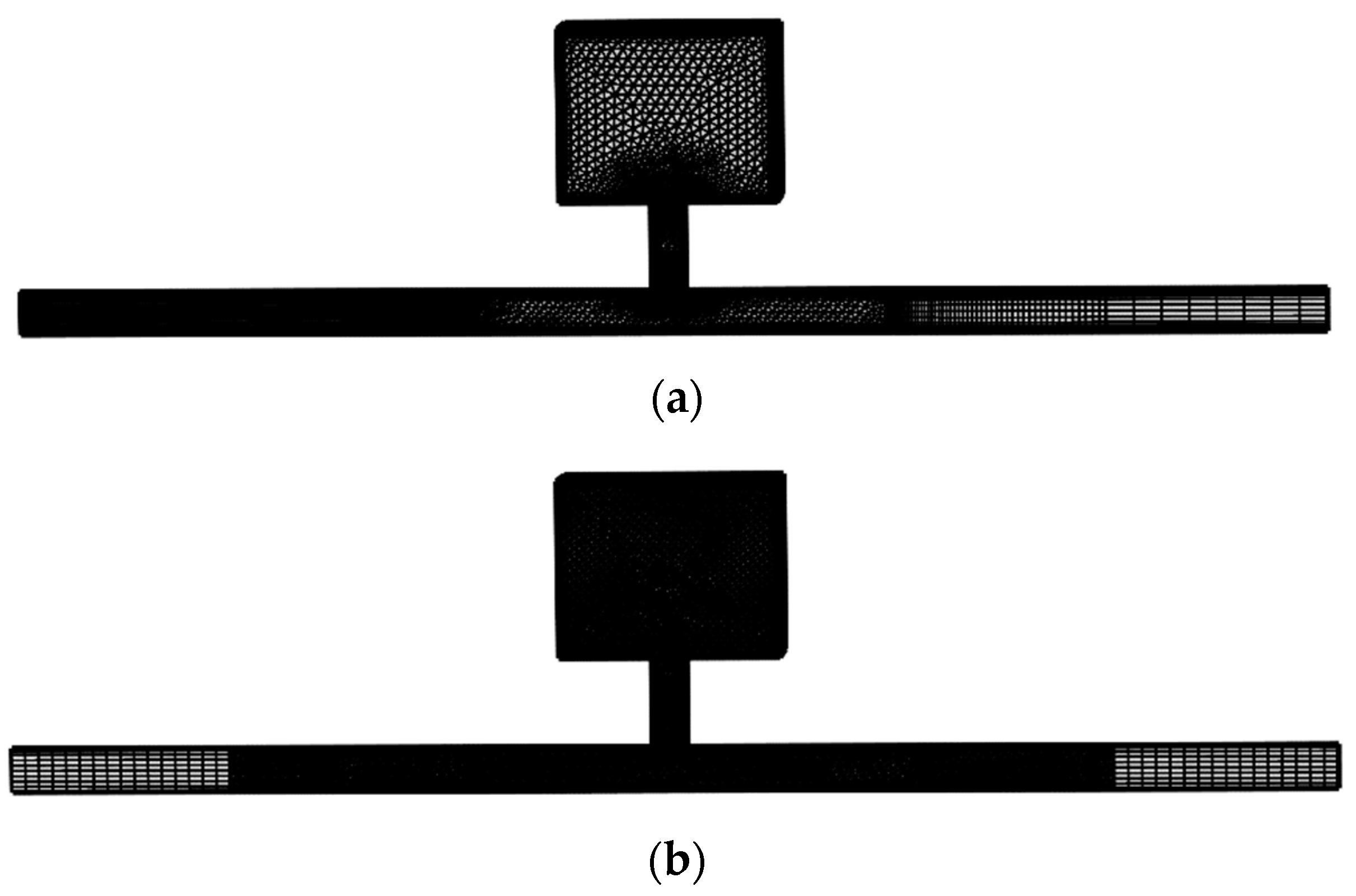
3.2. Mesh Division of Air Compressor Flow Field
3.3. Setting of Boundary Conditions
4. Twin-Screw Compressor Flow Field and Noise Calculation
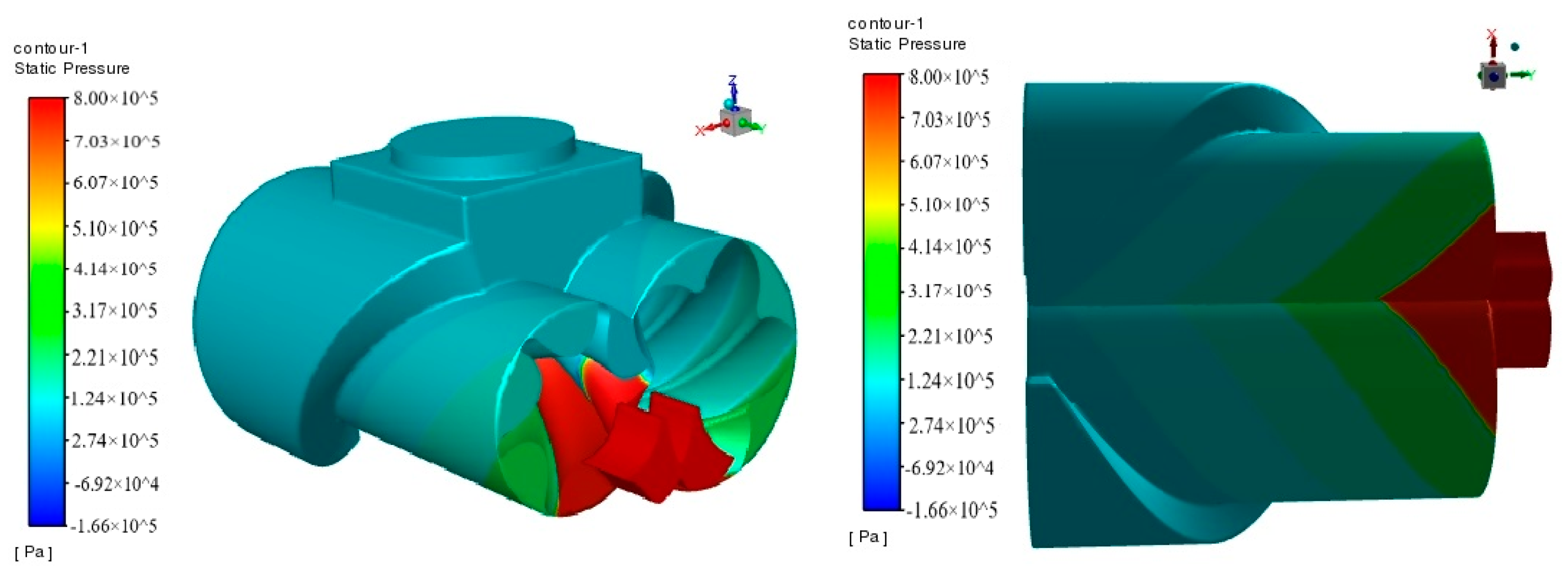
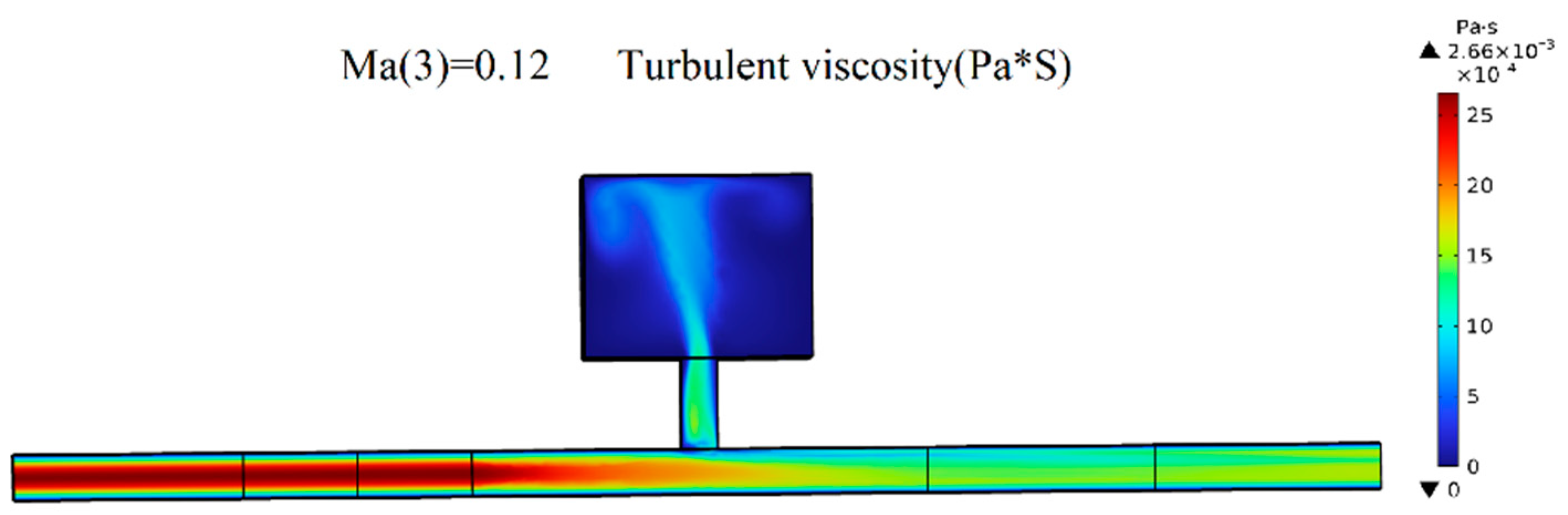
4.1. Flow Field Pressure Calculation
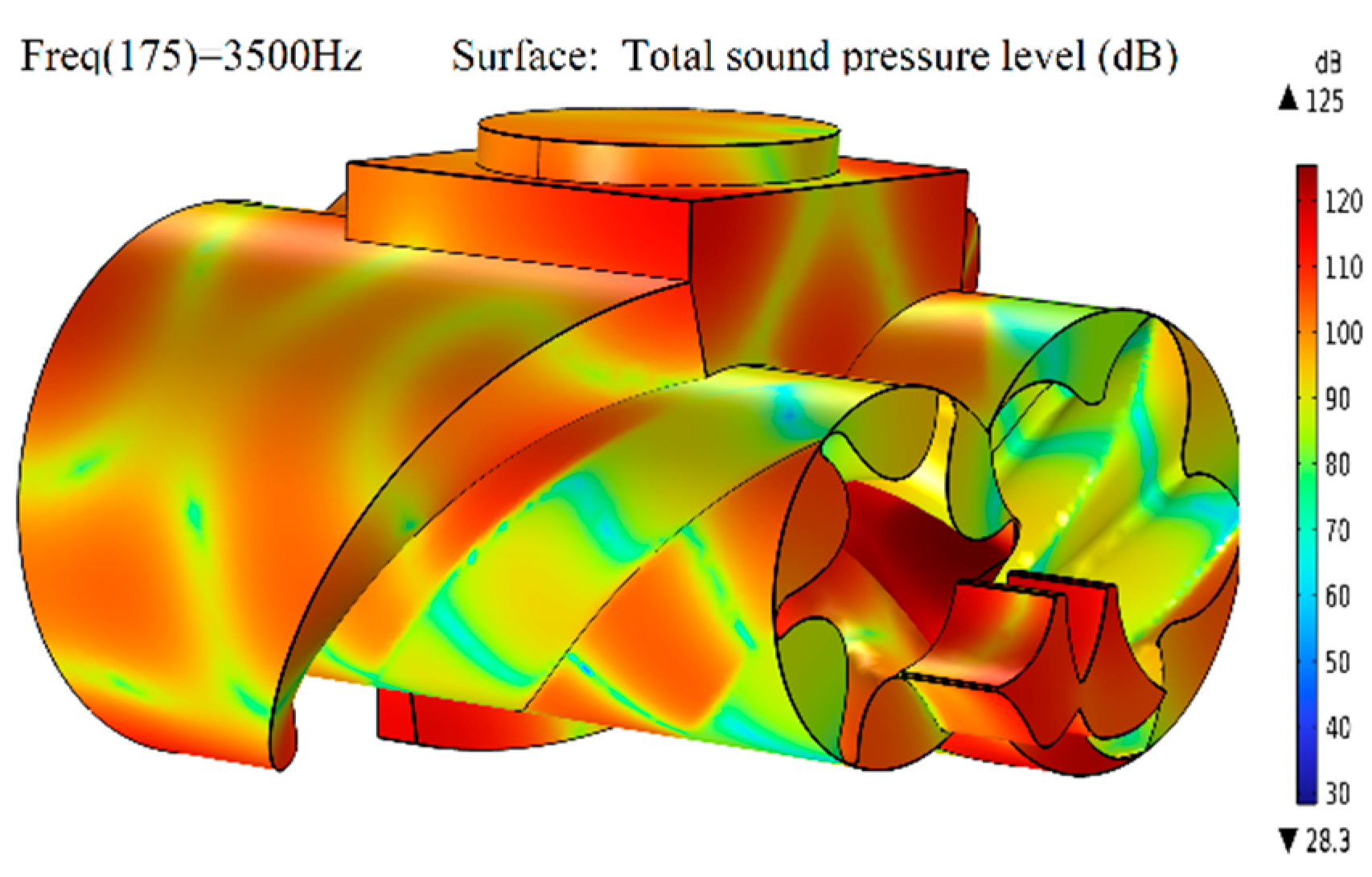
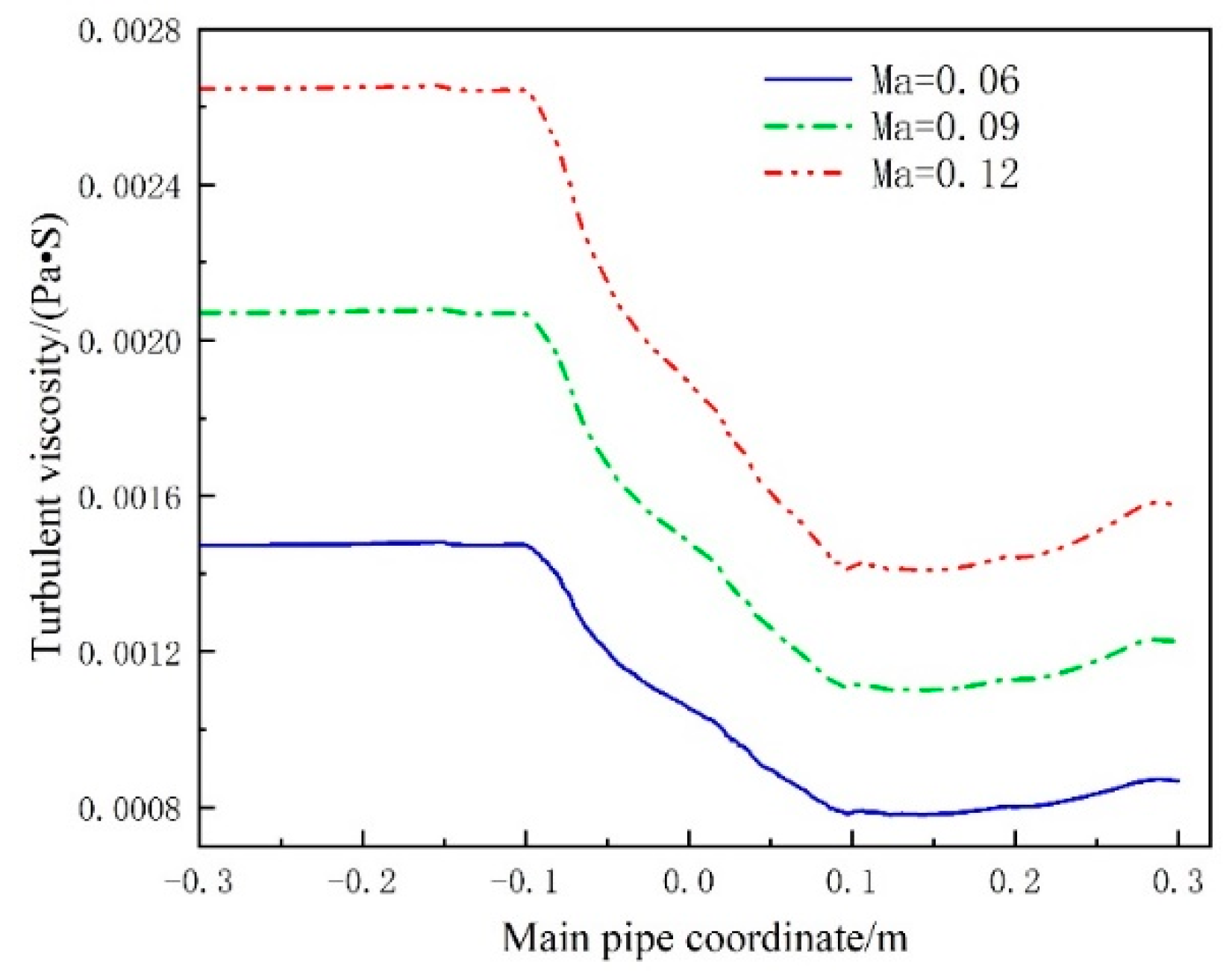
4.2. Flow Field Noise Analysis
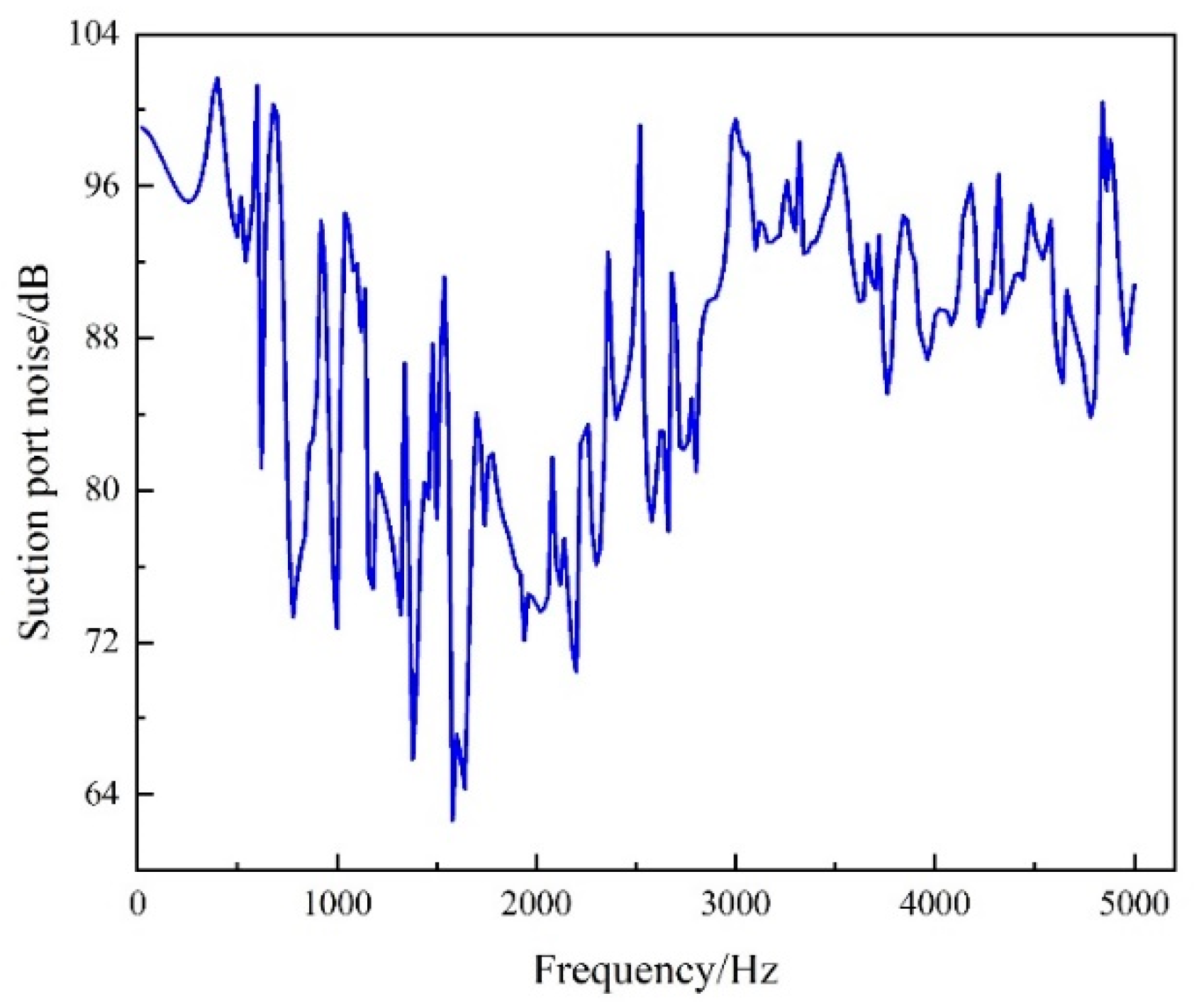
4.3. Numerical Calculation of Noise at the Suction and Exhaust Ports
4.4. Experimental Research and Analysis
- (1)
- Principle of operation of the test system
- (2)
- Comparative analysis of test data and simulation results
5. Exhaust Muffler Design and Air Compressor Noise Reduction Research
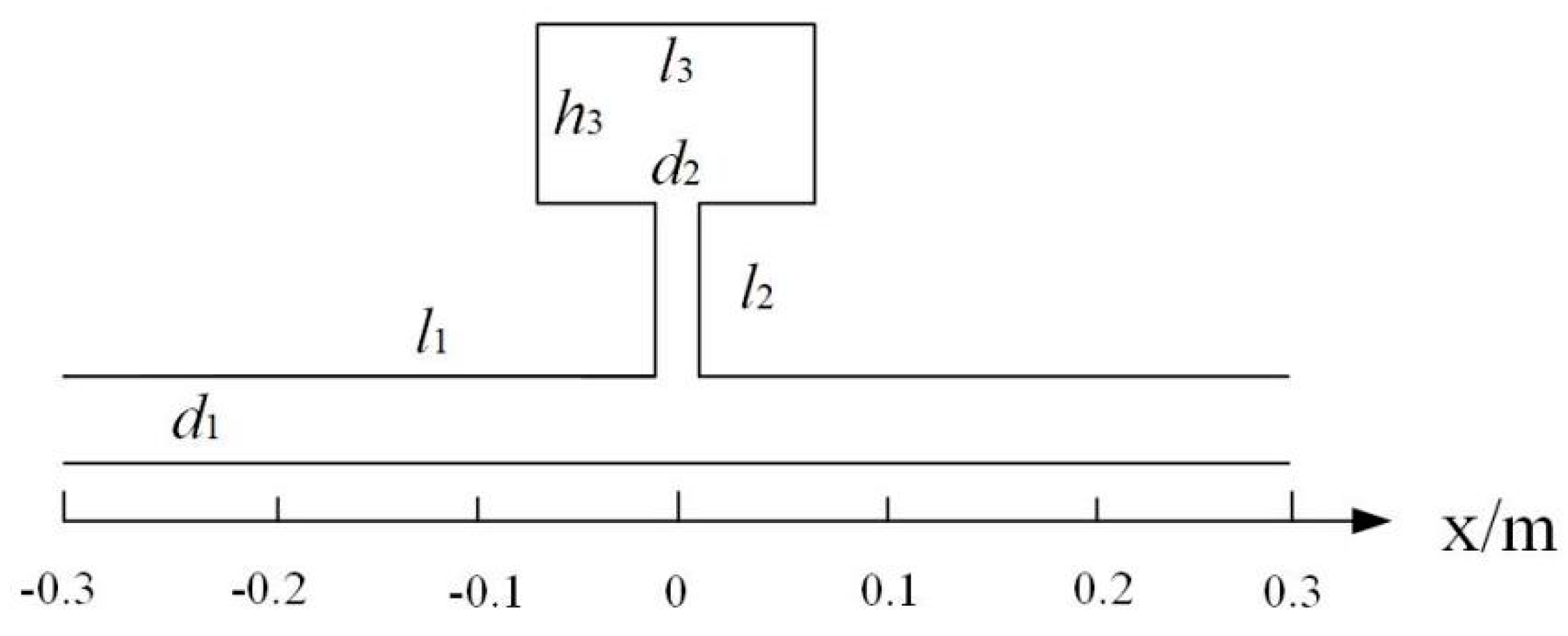
5.1. Design of Helmholtz Resonator
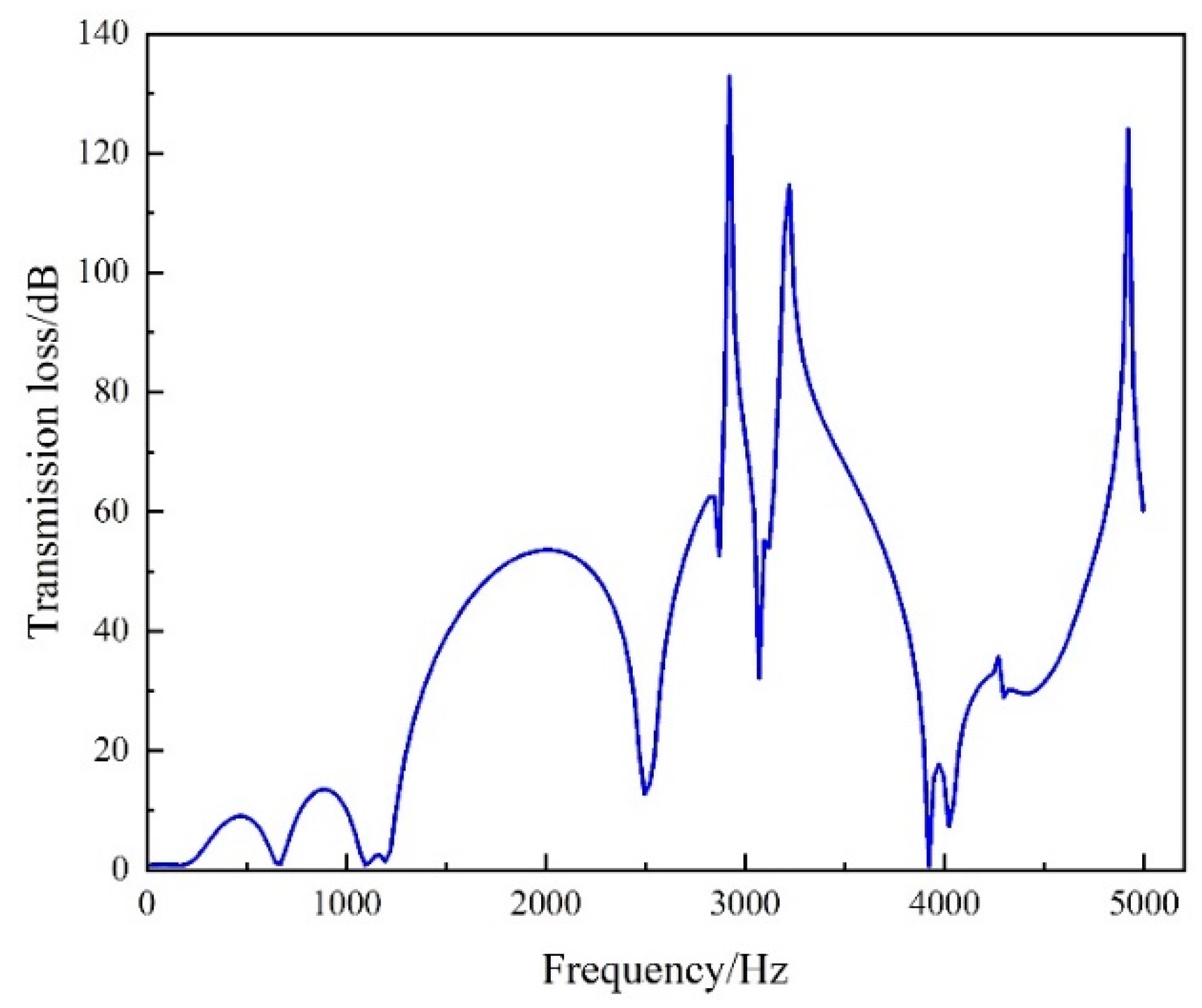
5.2. Calculation of Muffler Transmission Loss
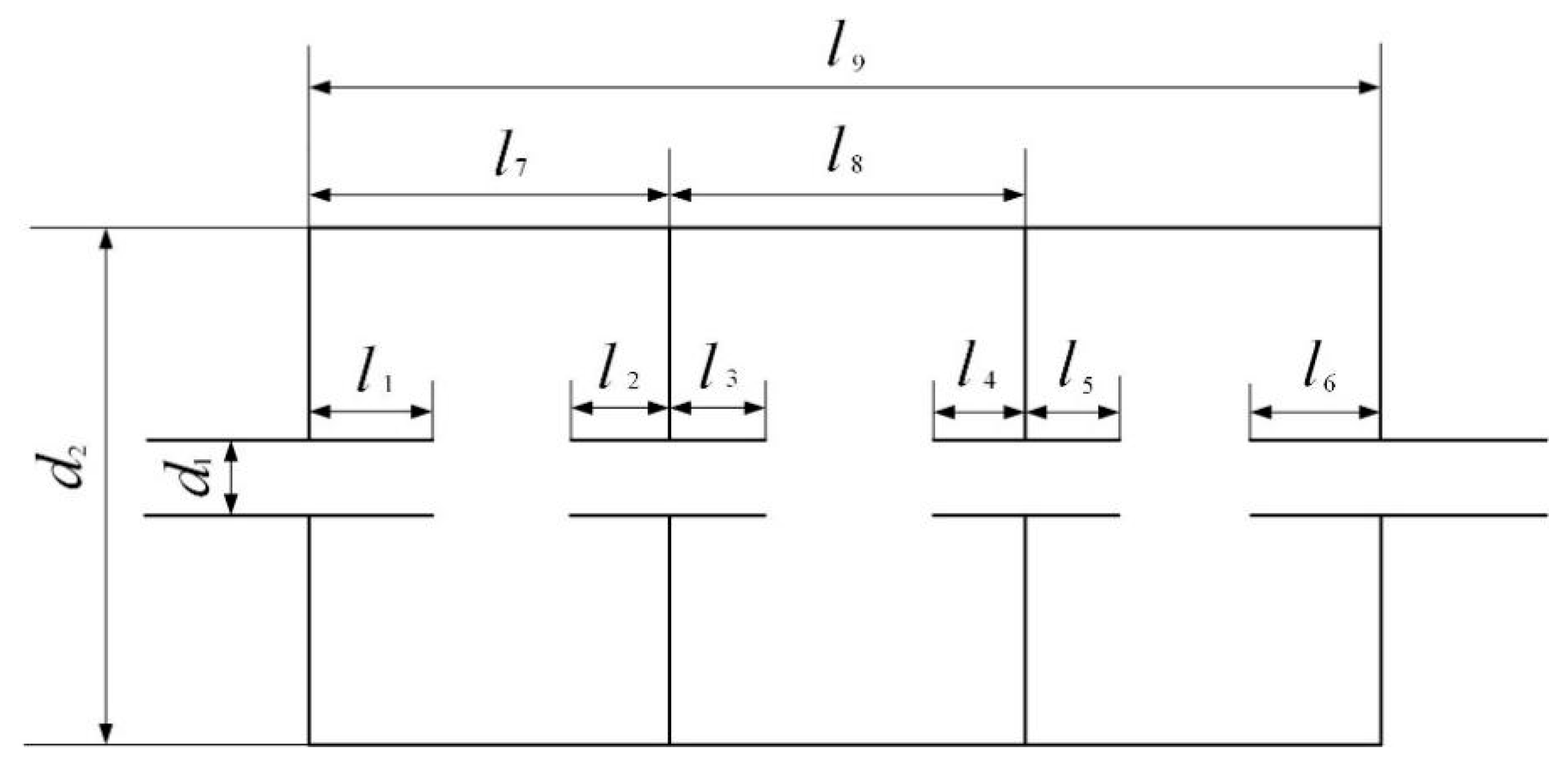
5.3. Design of Three-Cavity Interpolated Perforated Muffler
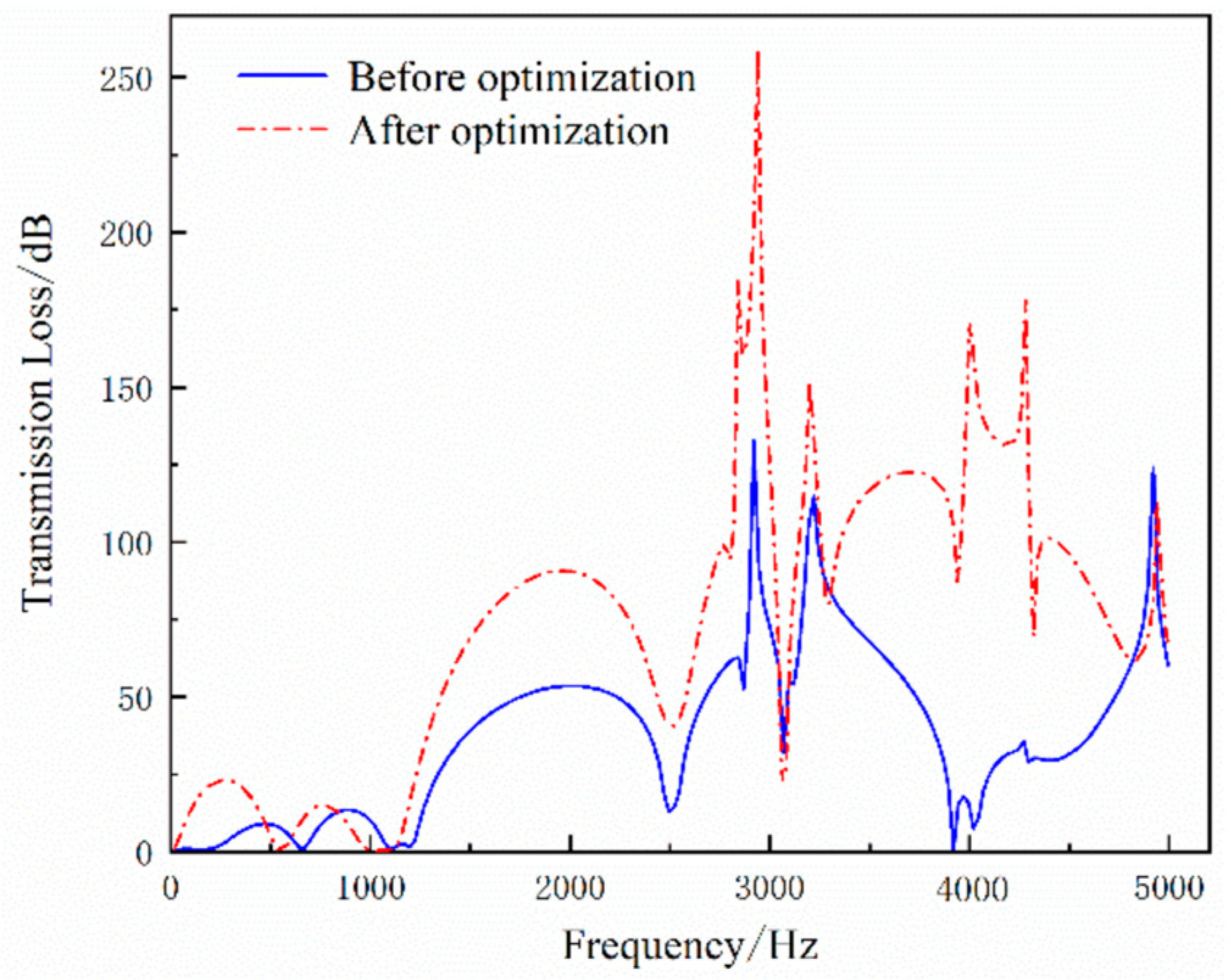
5.4. Optimized Design of Three-Cavity Interpolated Perforated Muffler Structure
- (1)
- Optimization Objectives
- (1)
- The insertion tube sudden expansion unit of the first cavity:
- (2)
- The straight tube unit of the first cavity
- (3)
- The insertion tube sudden contraction unit of the first cavity:
- x is the optimization variables;
- f1 is the lower limit of the objective function frequency (20 Hz);
- f2 is the objective function frequency upper limit (5000 Hz);
- TL(f) is the transfer loss theoretical equation.
- (1)
- Optimization variables and constraints
- (2)
- Constraint conditions
- (3)
- Optimization results and analysis
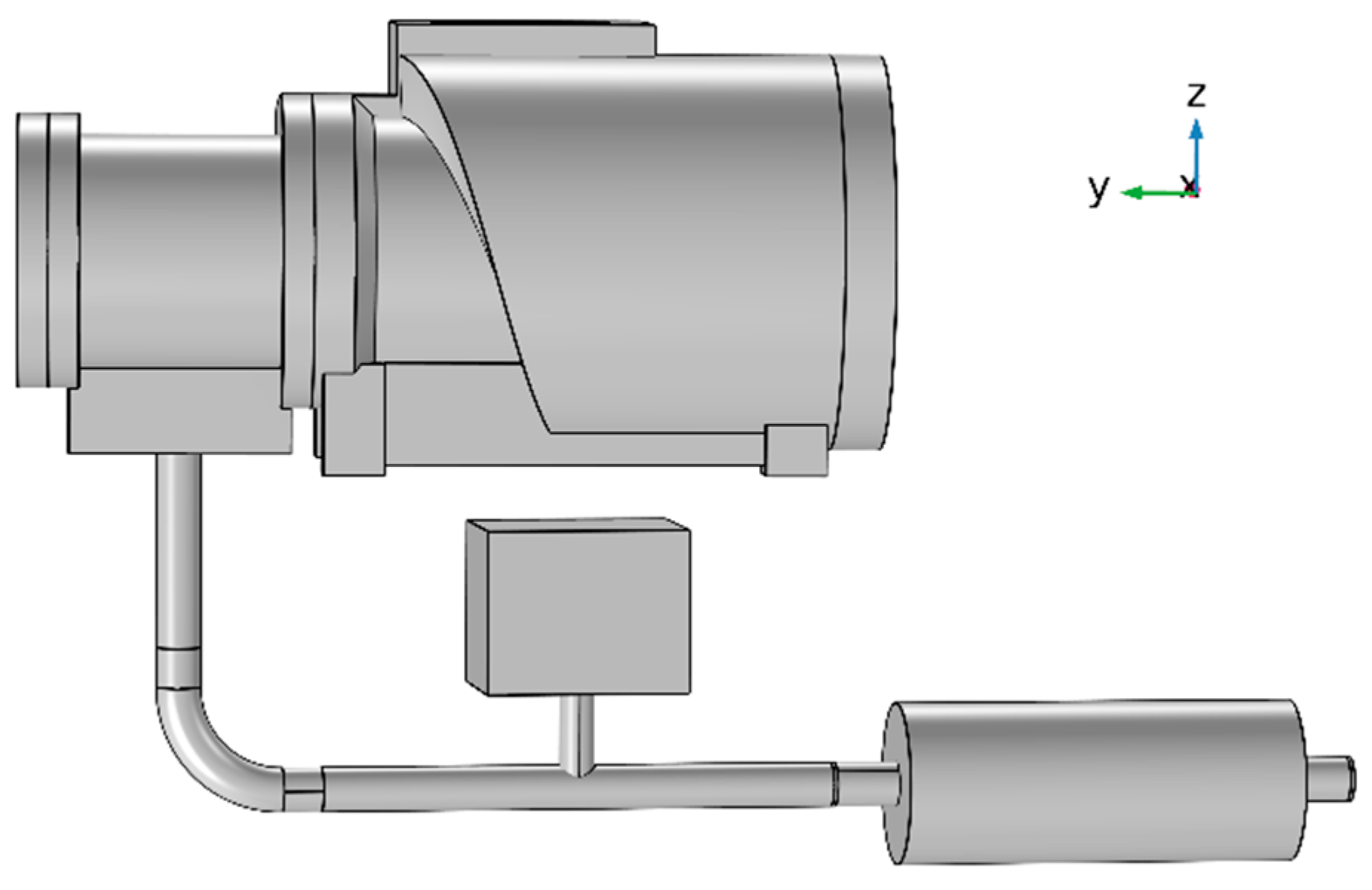
5.5. Study of Noise Reduction at Air Compressor Exhaust Ports
5.6. The Effect of Mufflers on the Performance of Air Compressors
6. Conclusions
- (1)
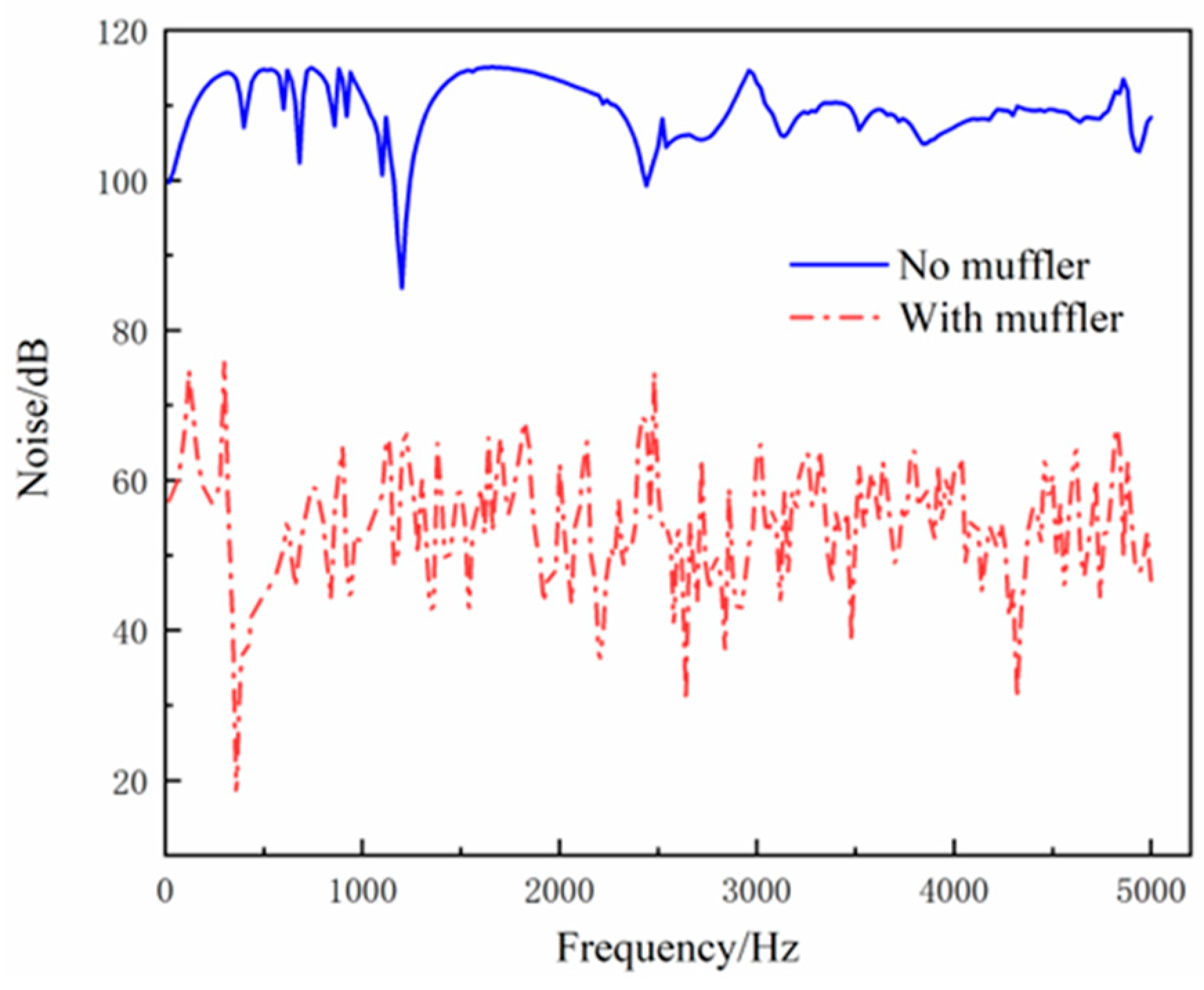
- By calculating the internal flow field of the twin-screw compressor, it was found that the noise at the air compressor inlet primarily ranges between 84 and 100 dB, while the noise at the exhaust port is predominantly between 100 and 114 dB. Notably, the noise at the exhaust port is significantly higher than that at the air inlet.
- (2)
- To address the issue of excessive noise at the exhaust port of the air compressor, a Helmholtz resonator was designed to function as a flow stabilizer. An acoustic fluid interaction analysis revealed that the resonator effectively stabilized gas flow and reduced noise in the low-frequency band. Additionally, a three-cavity interpolated perforated muffler was designed for full-frequency performance analysis, and its structure was optimized, resulting in enhanced noise reduction.
- (3)
- The designed Helmholtz resonator and three-cavity interpolated perforated muffler were installed sequentially at the exhaust port, followed by a noise reduction analysis. The results show that the exhaust port noise decreased significantly from 100–114 dB to 37–68 dB, demonstrating the effectiveness of the designed exhaust muffler in reducing noise. The findings of this study provide valuable insights for noise reduction in equipment with aerodynamic noise issues.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Milojevit, S.; Savic, S.; Mitrovit, B.P.V. Solving the Problem of Friction and Wear in Auxiliary Devices of Internal Combustion Engines on the Example of Reciprocating Air Compressor for Vehicles. Tech. Gaz. 2023, 30, 122–130. [Google Scholar]
- Sun, S.; Zhou, M.; Chen, W.; Wang, C.; Xing, Z.; Su, B. Experimental investigation of characteristics of discharge pressure pulsation in a twin-screw refrigeration compressor. J. Refrig. 2023, 1–8. [Google Scholar] [CrossRef]
- Wang, X.; Tian, G.; Tian, Q.; Xiong, G. Numerical study on discharge characteristics of balanced twin-screw compressor. Mach. Des. Manuf. 2019, 201–205. [Google Scholar] [CrossRef]
- Huang, P.X. A model for the transient pulsation generation at the discharge of a screw compressor by a shock tube analogy. IOP Conf. Ser. Mater. Sci. Eng. 2018, 425, 012022. [Google Scholar]
- Abdulrahem, A.A.G. Analysis of the jet engine noise emissions at the inlet air to the compressor and nozzle exhaust outlet. J. Eng. Res. 2023, 18, 11. [Google Scholar]
- Sun, S.; Xing, Z.; Li, Y.; Su, P.; Chen, W. Experimental investigation on twin screw refrigeration compressor with different capacity control methods. Int. J. Refrig. 2021, 130, 370–381. [Google Scholar]
- He, Y.; Xiao, C.; Zhang, W.; Wang, K. Study of noise and structural characteristics of twin-screw air compressor based on multi-physical field coupling. Sci. Rep. 2023, 13, 20879. [Google Scholar]
- Guerrato, D.; Nouri, J.M.; Stosic, N.; Arcoumanis, C. Flow and pressure characteristics within a screw compressor. J. Phys. Conf. Ser. 2007, 85, 012012. [Google Scholar]
- Fujiwara, A.; Matsuo, K.; Yamashita, H. Vibration analysis of oil-injected twin-screw compressors using simple simulated waveforms. Proc. Inst. Mech. Eng. Part E J. Process Mech. Eng. 2011, 225, 105–116. [Google Scholar]
- Willie, J.; Yonkers, S.W.; Huang, P.X.; Ganatra, R.B. Use of CFD to optimize the design of a shunt pulsation trap used for noise and vibration mitigation in oil free screw compressors. IOP Conf. Ser. Mater. Sci. Eng. 2022, 1267, 012017. [Google Scholar]
- Zhang, W.; Lu, Y. Experimental investigation on noise and vibration reduction in twin-screw refrigeration compressor unit. J. Refrig. 2012, 33, 50–54. [Google Scholar]
- Li, J.; Gen, M.; Jiang, H.; Wang, L.; Cui, D.; Li, X. Aerodynamic noise optimization design of dry twin screw air compressor. Hydraul. Pneum. Seals 2023, 43, 7–10. [Google Scholar]
- Shen, J.; Wang, R.; Zhou, M.; Chen, W. Numerical and experimental research on the discharge noise of twin-screw Refrigeration compressors. J. Mech. Eng. 2017, 53, 169–175. [Google Scholar]
- Liu, H.; Chen, C.; Zhou, H.; Su, X. Noise analysis and treatment of screw compressors. Mach. Des. Manuf. 2013, 229–231. [Google Scholar] [CrossRef]
- Cheng, S.; Li, G.; Zhang, Q. Research on Noise Control of Screw Compressor. Fluid Mach. 2007, 35, 43–45. [Google Scholar]
- Ji, J.; Tang, P.; Wu, X. Research on Low Frequency Noise Performance Control of Screw Compressor. Compress. Technol. 2017, 24–26+55. [Google Scholar]
- Niu, Q.; Qian, L.; Huang, J. Noise analysis and control of screw compressor. Noise Vib. Control 2007, 119–122. [Google Scholar]
- He, Z.; Han, Y.; Chen, W.; Zhou, M.; Xing, Z. Noise control of a two-stage screw refrigeration compressor. Appl. Acoust. 2020, 167, 107383. [Google Scholar]
- Mujic, E.; Kovacevic, A.; Stosic, N.; Smith, I.K. The influence of the discharge port shape on screw compressor performance and gas pulsations. In Proceedings of the International Compressor Engineering Conference 2008, West Lafayette, IN, USA, 14–17 July 2008. [Google Scholar]
- Shen, J.; Chen, W.; Yan, S.; Zhou, M.; Liu, H. Study on the noise reduction methods for a semi-hermetic variable frequency twin-screw refrigeration compressor. Int. J. Refrig. 2021, 125, 1–12. [Google Scholar]
- Li, Q. Simulation Analysis and Research on Internal Flow Field of Twin-Screw Compressor. Master’s Thesis, Chang’an University, Chang’an, China, 2020; pp. 33–34. [Google Scholar]
- Ji, Z.L. Muffler Acoustic Theory and Design; Science Press: Beijing, China, 2015; pp. 26–27. [Google Scholar]
- Fang, Z.Q. Aerodynamic Noise and Mufflers; Science Press: Beijing, China, 2015; pp. 157–158. [Google Scholar]
- Zhao, S. Noise Reduction and Isolation (Part II); Tongji University Press: Shanghai, China, 1989; pp. 63–77. [Google Scholar]





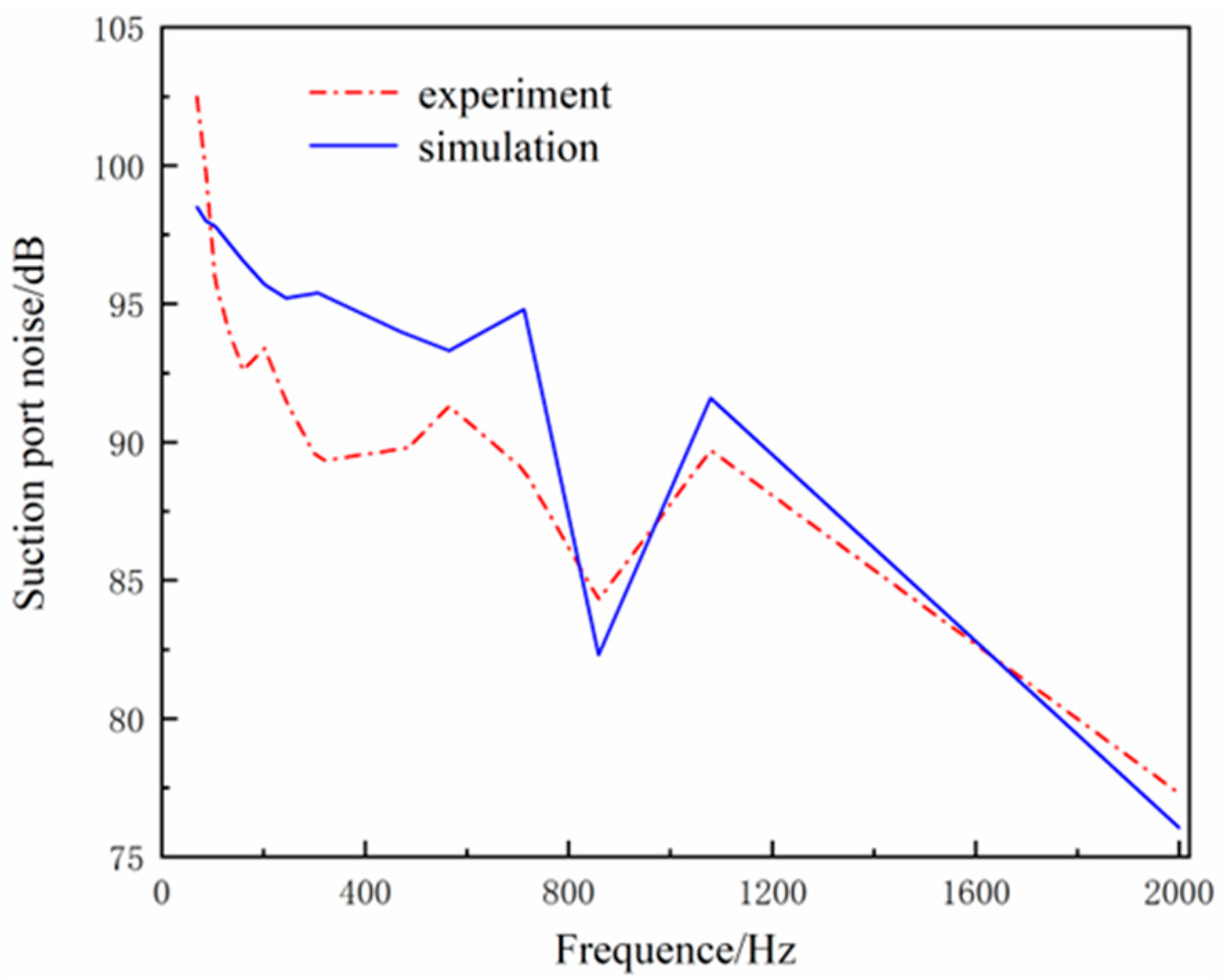



| Frequence/Hz | Noise/dB | Frequence/Hz | Noise/dB |
|---|---|---|---|
| 69 | 102.5 | 307 | 89.3 |
| 87 | 99.7 | 468 | 89.8 |
| 105 | 95.8 | 565 | 91.3 |
| 132 | 94.0 | 712 | 89.0 |
| 160 | 92.6 | 859 | 84.3 |
| 202 | 93.4 | 1079 | 89.7 |
| 244 | 91.5 | 89.7 | 77.3 |
| Variable | Lower Limit of Variable/mm | Upper Limit of Variable/mm | Initial Value/mm | Optimization Parameter Value/mm |
|---|---|---|---|---|
| the muffler suction insertion pipe length | 0 | 190 | 30 | 21.2 |
| the first cavity exhaust pipe length | 0 | 190 | 17.5 | 13.3 |
| the second cavity suction pipe length | 0 | 190 | 17.5 | 23.6 |
| the second cavity exhaust pipe length | 0 | 190 | 17.5 | 19.8 |
| the third cavity suction pipe length | 0 | 190 | 17.5 | 16.7 |
| the muffler exhaust insertion pipe length | 0 | 190 | 30 | 27.9 |
| the muffler first cavity length | 0 | 190 | 63.3 | 50.8 |
| the muffler second cavity length | 5 | 195 | 63.3 | 68.9 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, Y.; He, X.; Chen, L.; Wang, J.; Zhao, Y.; Ren, Z. Flow Field Noise Analysis and Noise Reduction Research of Twin-Screw Air Compressor Based on Multi-Field Coupling Technology. Machines 2024, 12, 577. https://doi.org/10.3390/machines12080577
He Y, He X, Chen L, Wang J, Zhao Y, Ren Z. Flow Field Noise Analysis and Noise Reduction Research of Twin-Screw Air Compressor Based on Multi-Field Coupling Technology. Machines. 2024; 12(8):577. https://doi.org/10.3390/machines12080577
Chicago/Turabian StyleHe, Yayin, Xuyang He, Lijun Chen, Junli Wang, Yongqiang Zhao, and Zhigui Ren. 2024. "Flow Field Noise Analysis and Noise Reduction Research of Twin-Screw Air Compressor Based on Multi-Field Coupling Technology" Machines 12, no. 8: 577. https://doi.org/10.3390/machines12080577
APA StyleHe, Y., He, X., Chen, L., Wang, J., Zhao, Y., & Ren, Z. (2024). Flow Field Noise Analysis and Noise Reduction Research of Twin-Screw Air Compressor Based on Multi-Field Coupling Technology. Machines, 12(8), 577. https://doi.org/10.3390/machines12080577





