Analysis of the Influence of Nozzle Structure of Dry Powder Fire Extinguishing System on Supersonic Jet Characteristics
Abstract
1. Introduction
2. Theory and Methods
2.1. Gas-Solid Two-Way Coupling Theory
2.1.1. Gas Phase Control Equations
2.1.2. Particle Phase Control Equations
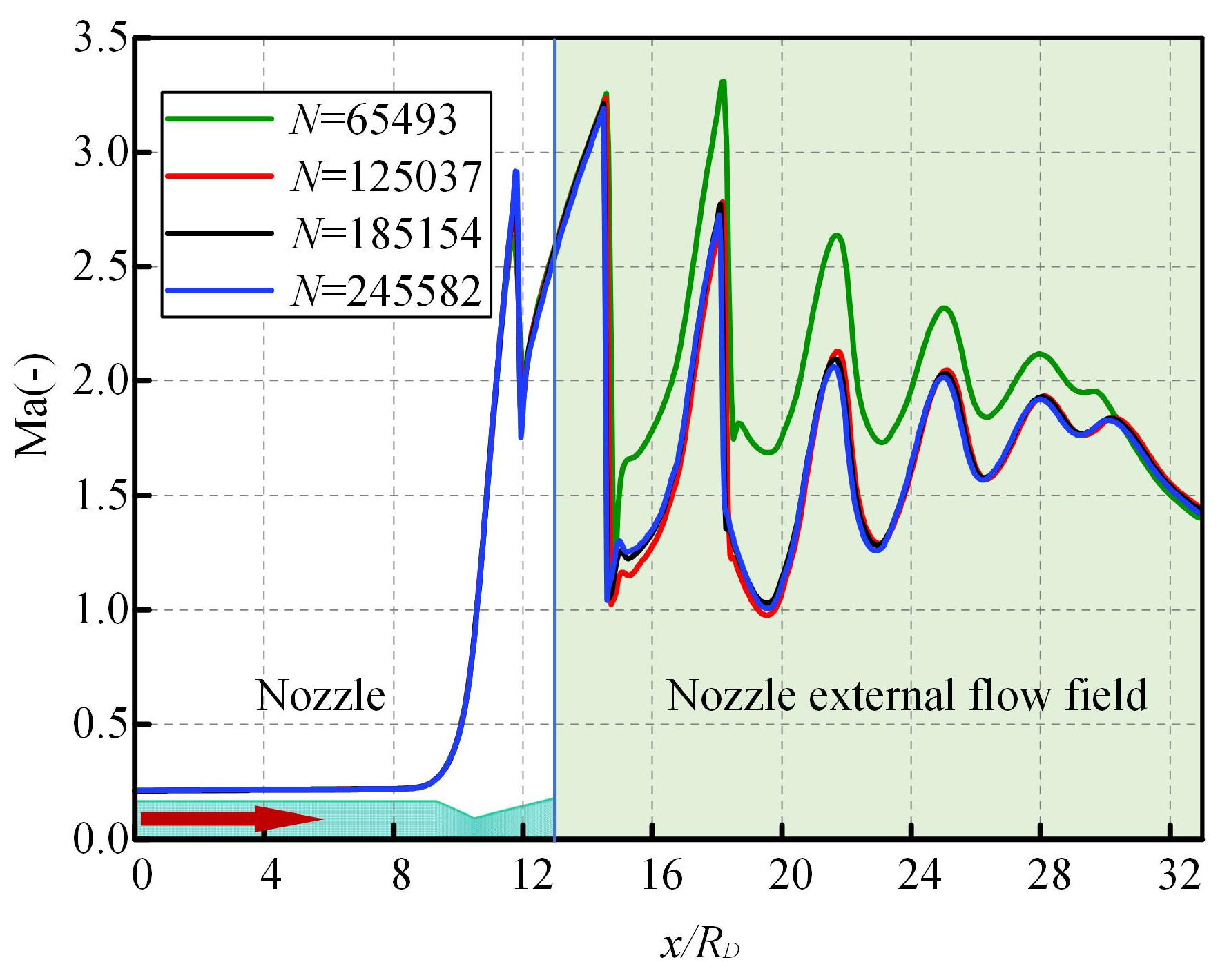
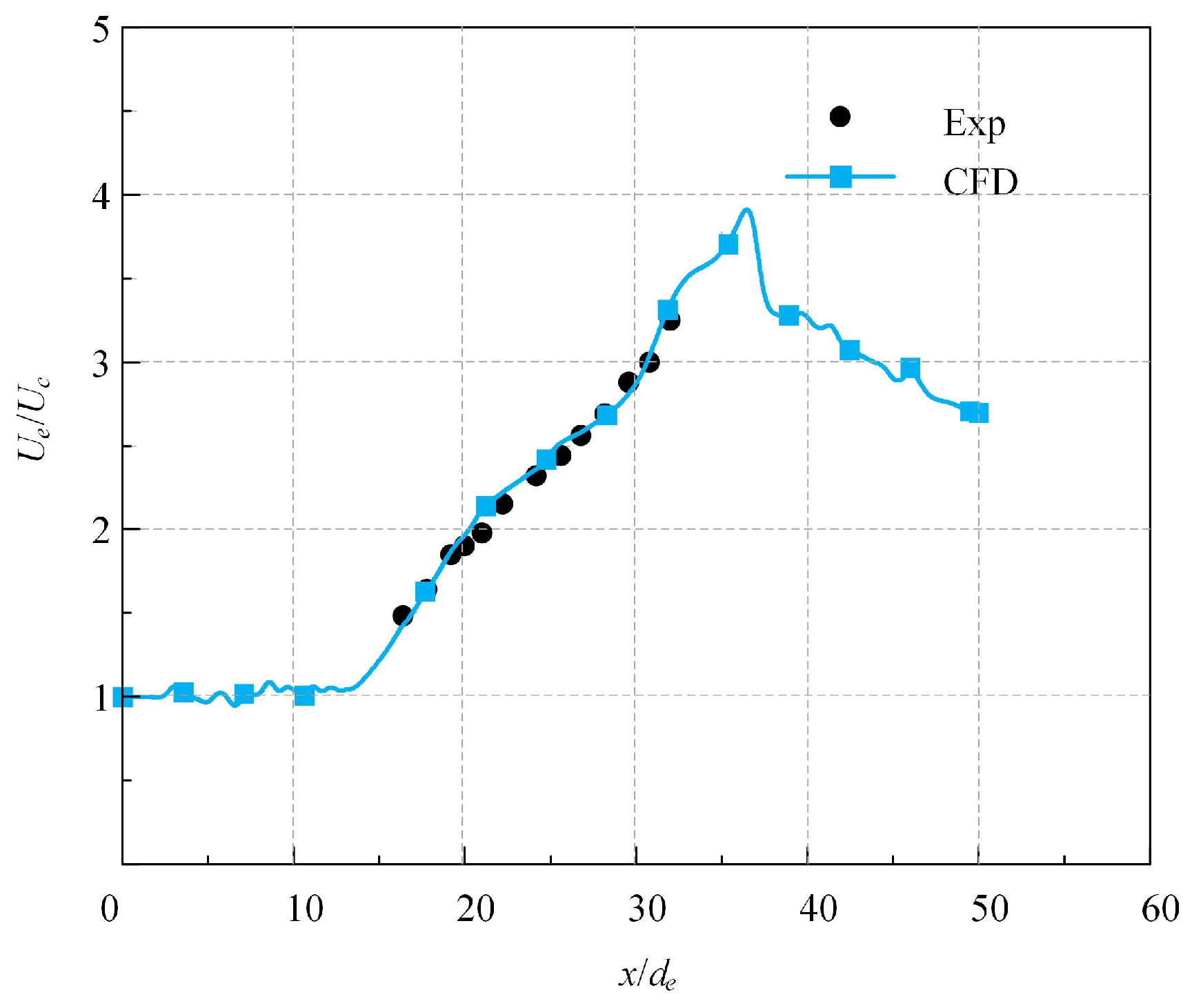
2.2. Numerical Simulation Boundary Conditions
2.3. Experimental System for Ultrafine Dry Powder Jetting and Nozzle Structure Design
3. Results and Discussion
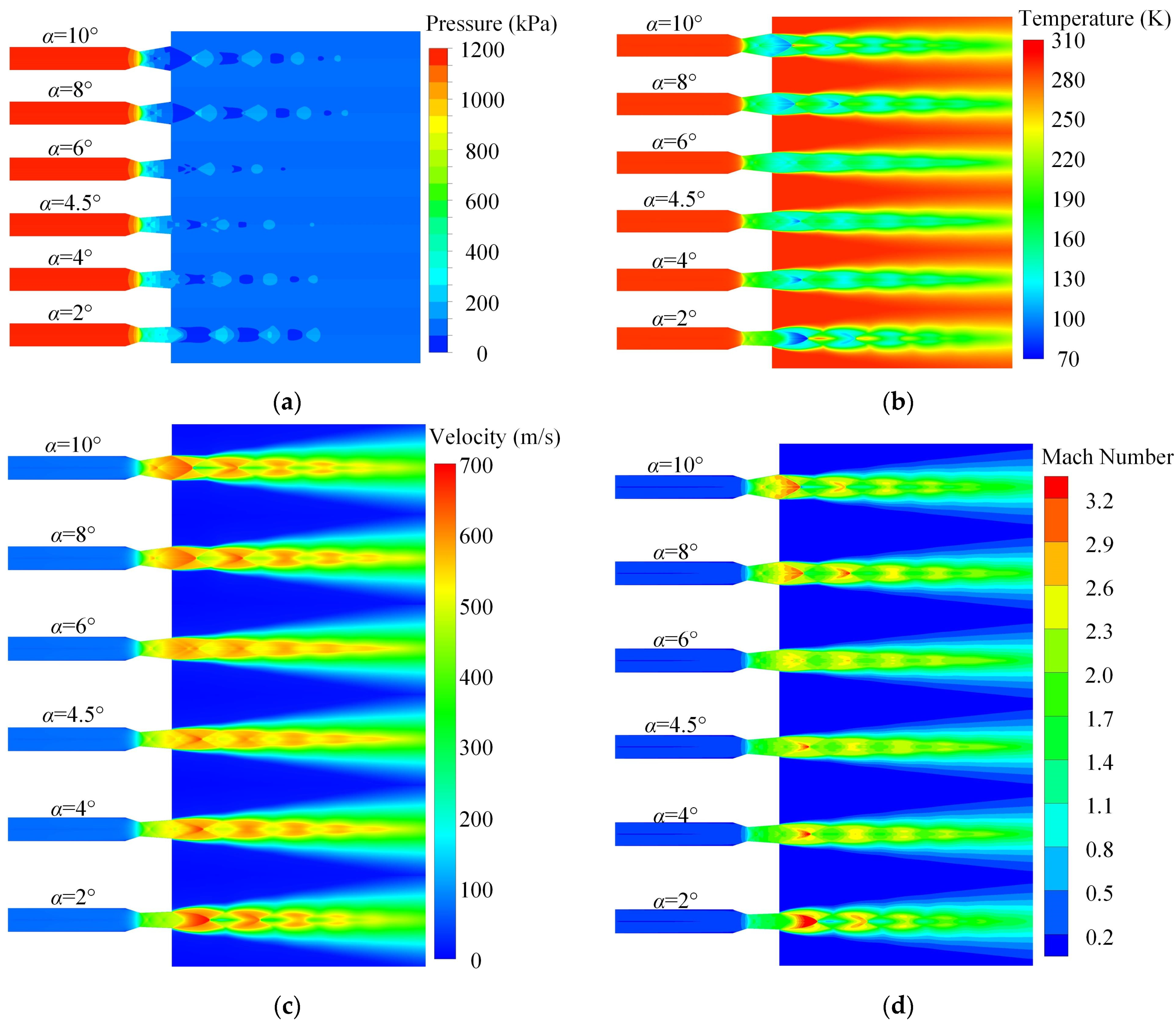
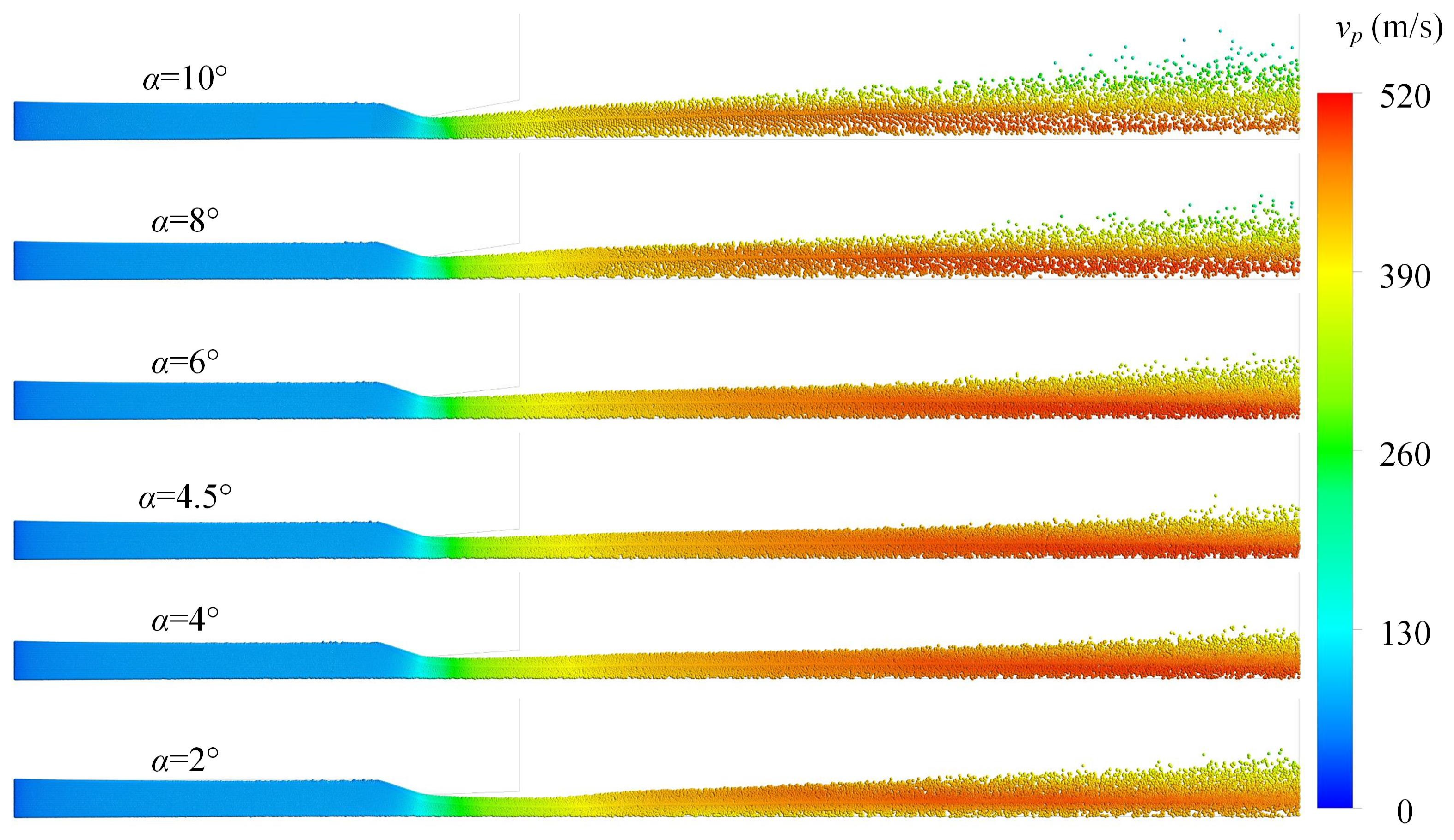
3.1. Analysis of the Influence of Semi-Expansion Angle on Dry Powder Nozzle Jet Characteristics
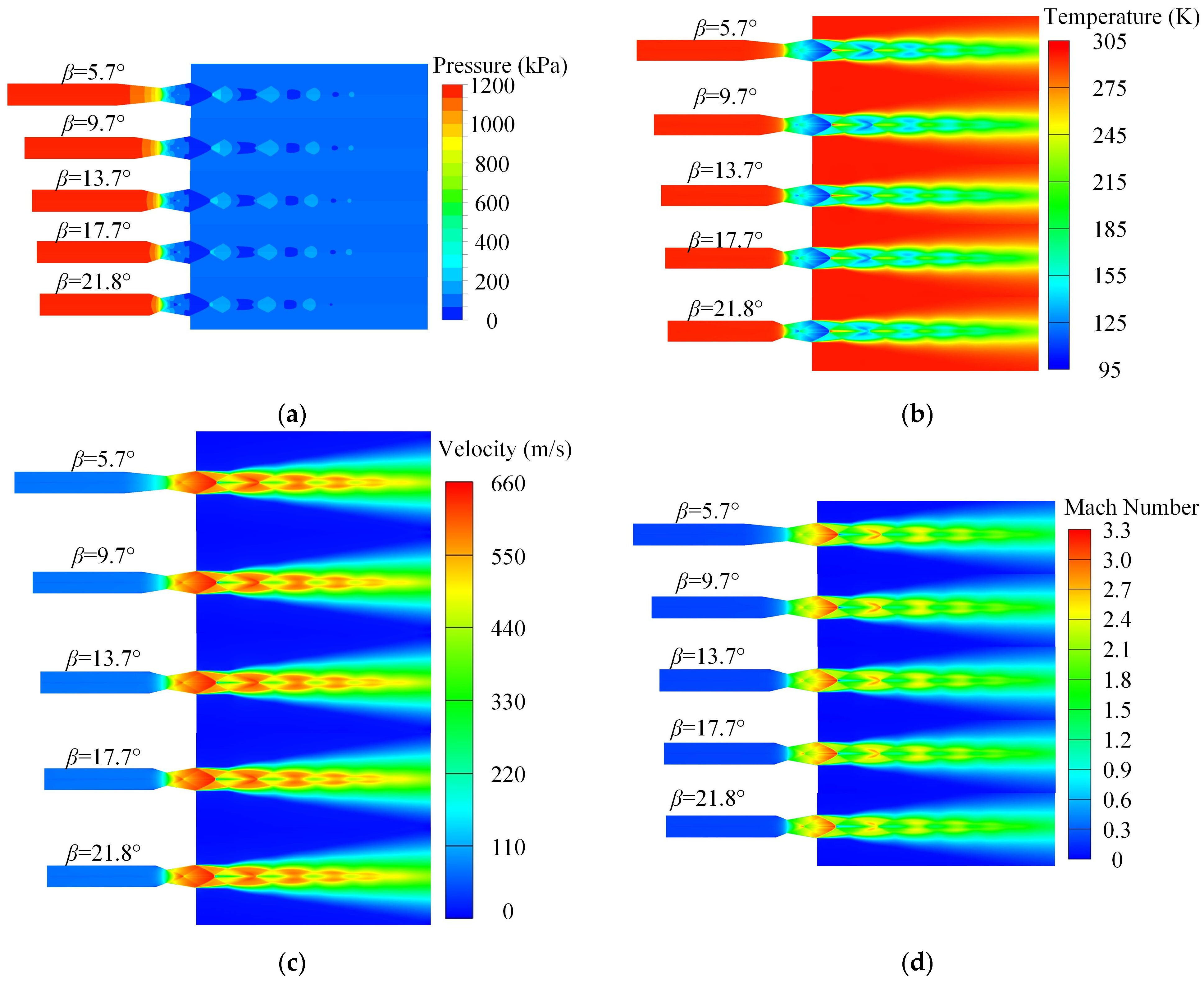
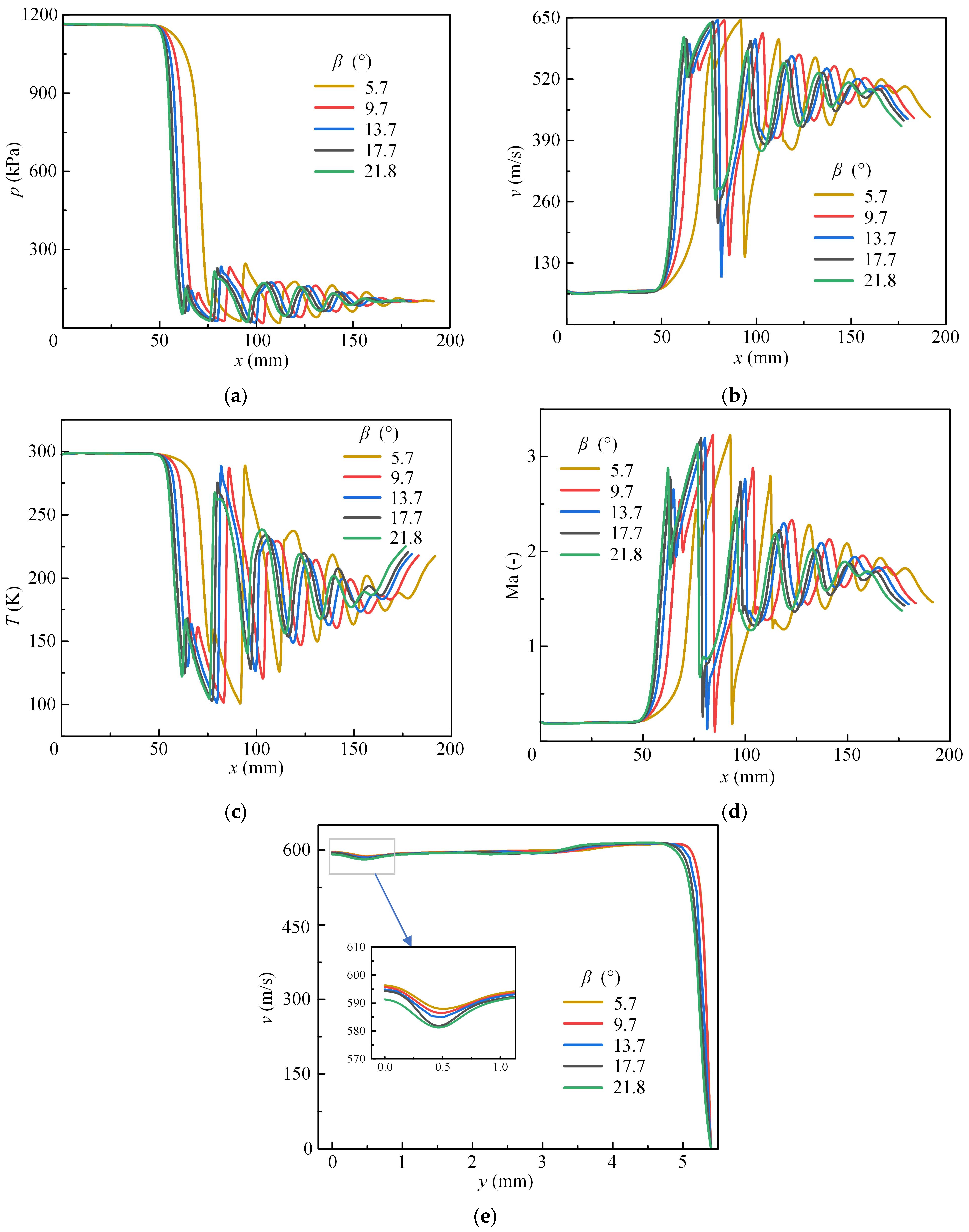
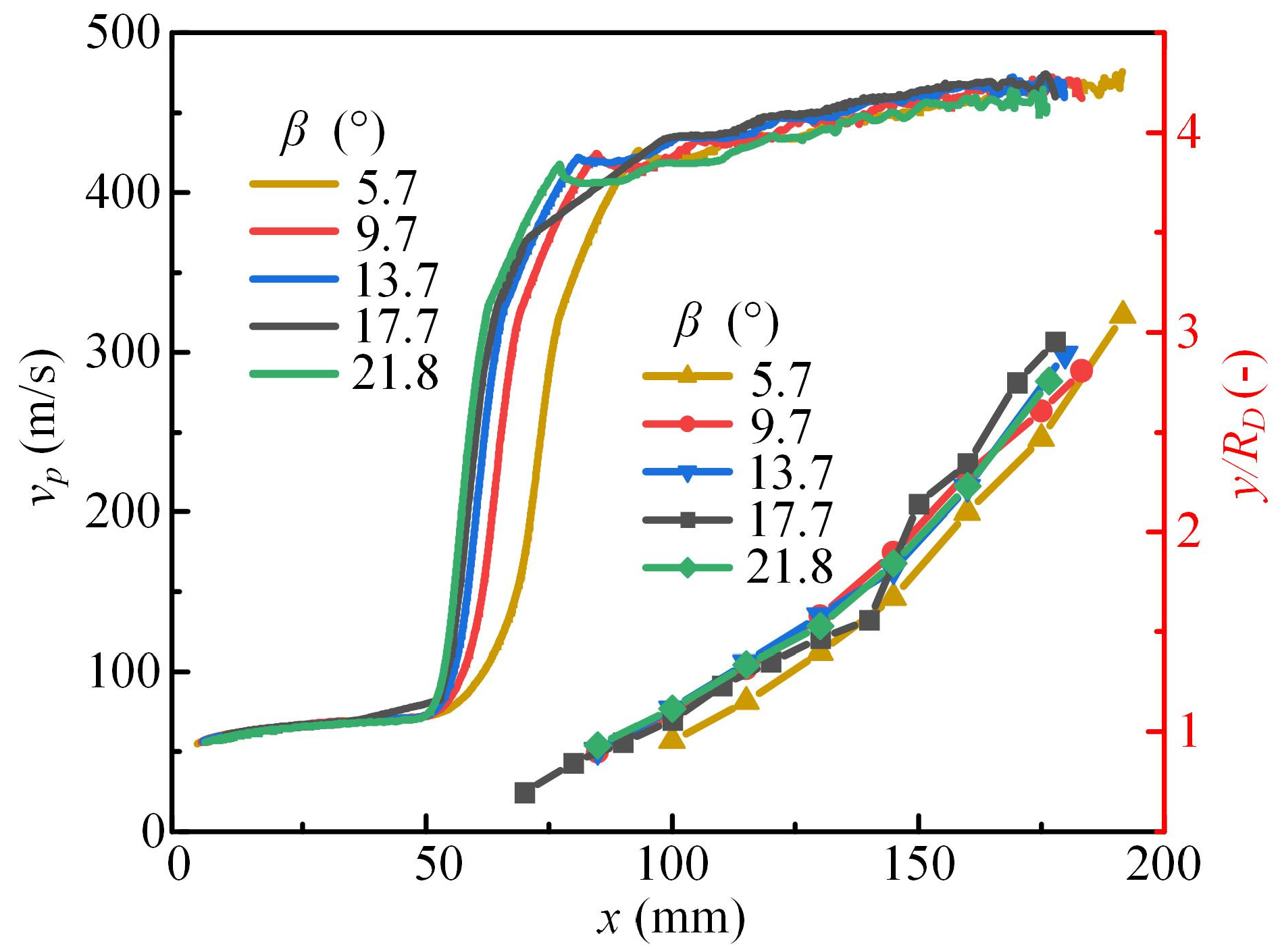
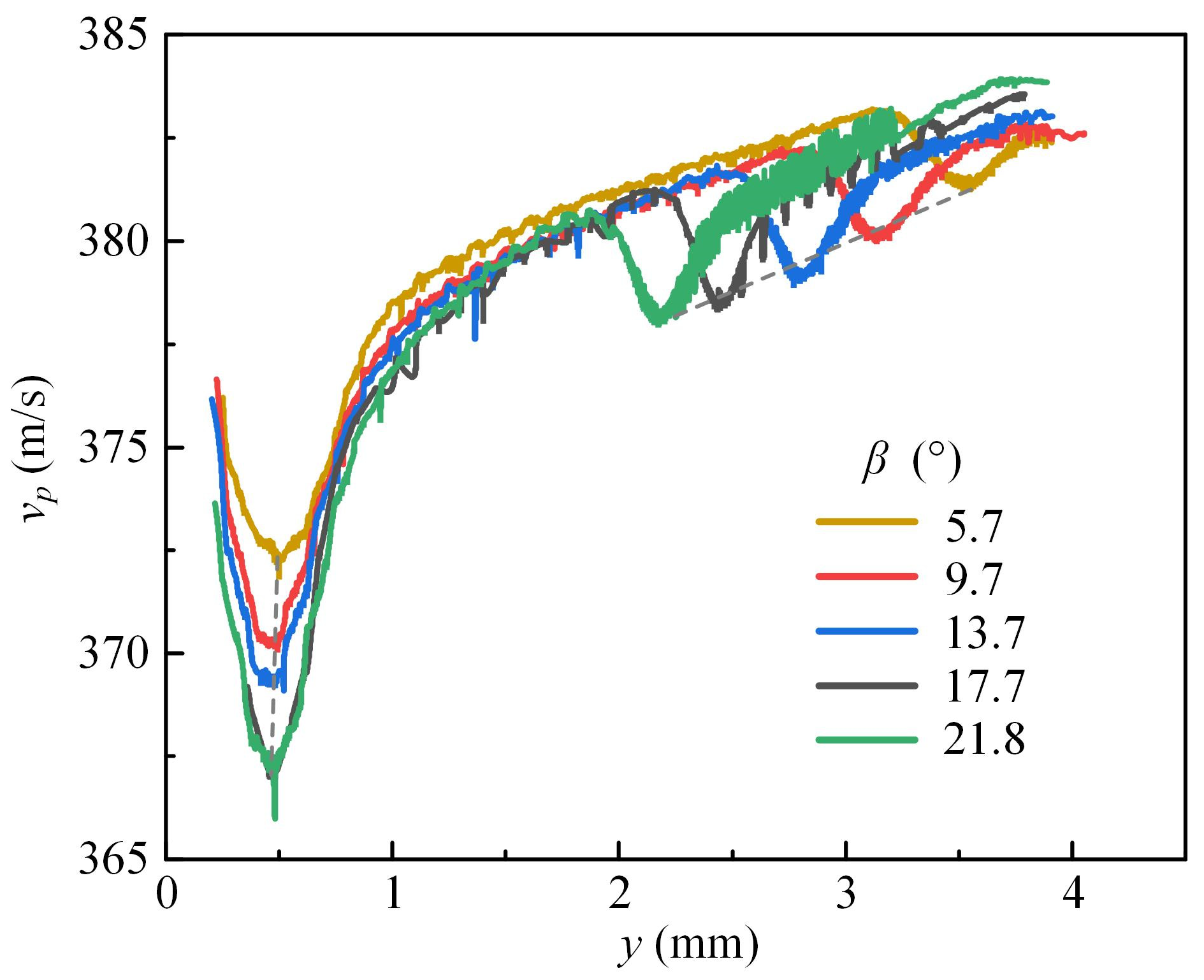
3.2. Analysis of the Influence of Semi-Contraction Angle on Dry Powder Nozzle Jet Characteristics
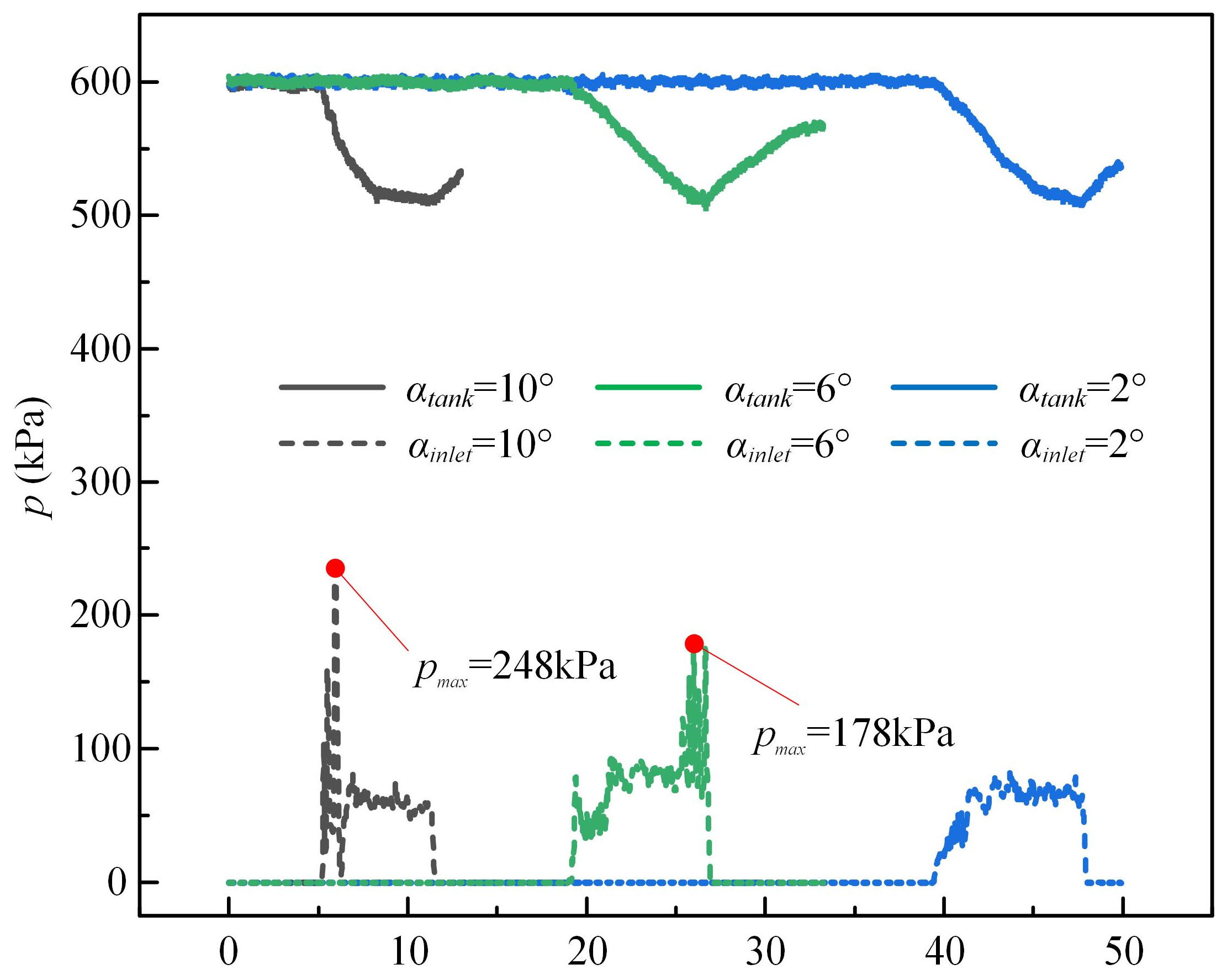
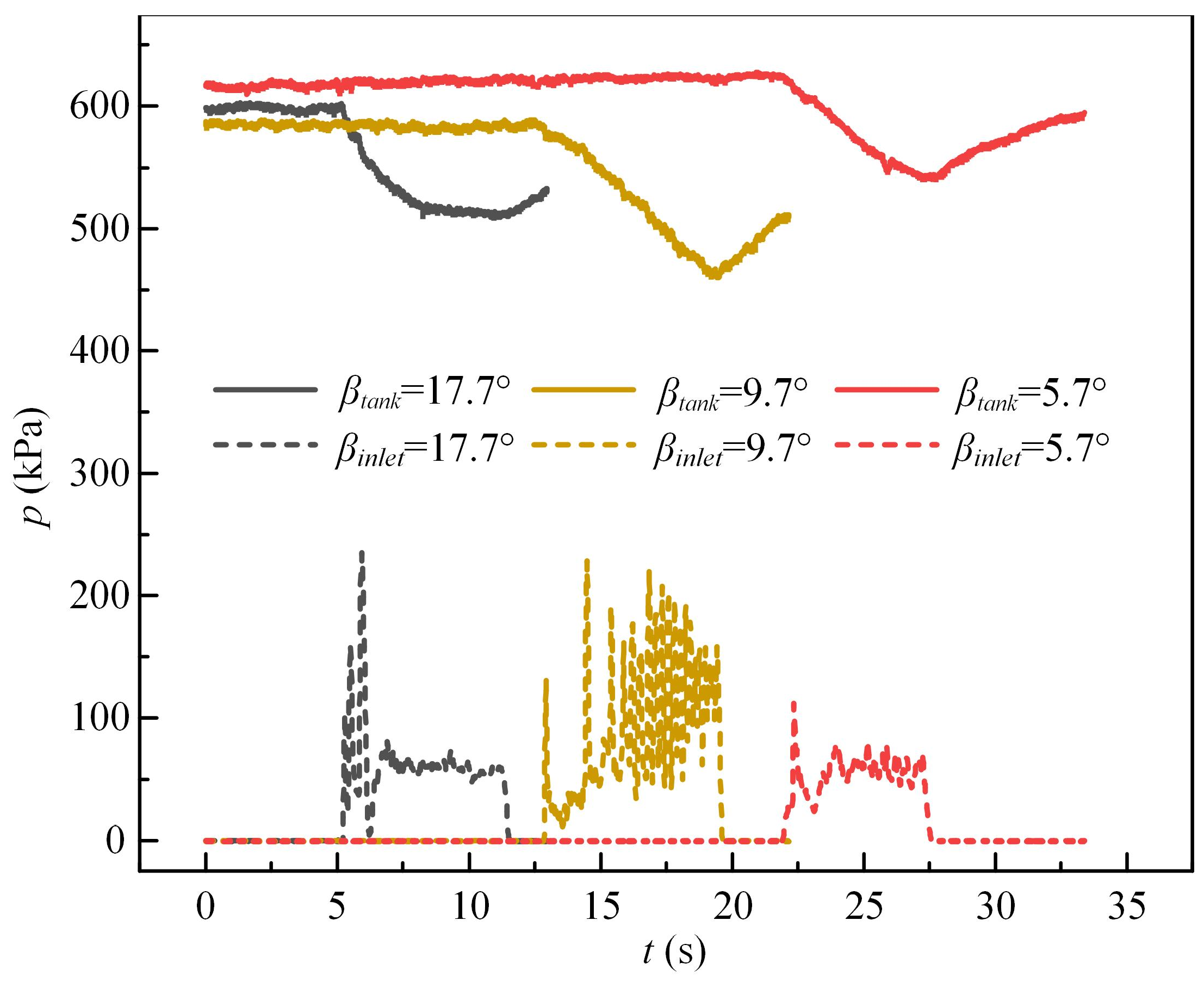
3.3. Experimental Study of Supersonic Jets with Different Nozzle Structures
4. Conclusions
- (1)
- For supersonic nozzles with gas-solid two-phase jets, altering the semi-contraction angle has minimal impact on the gas-phase flow field. The peak and valley values of gas-phase state parameters remain approximately the same, and the increase in particle jet velocity is minor. The effect of changing the expansion angle on jet characteristics is significantly greater. Under constant inlet pressure, a decrease in the expansion angle enhances particle collimation. Specifically, when the semi-expansion angle α = 2°, the gas jet is in an under-expanded state, making particles more prone to dispersion due to the stripping effect of the surrounding high-speed airflow. At α = 4.5°, the gas jet core region is the longest, providing the optimal particle acceleration effect.
- (2)
- Reducing the expansion angle alters the gas jet state. When α = 2° (under-expanded state), the dry powder exhibits a continuous diffusion trend within the x = 0 to 180 mm range, contrasting with the compression-expansion trend observed in over-expanded states. Globally, the diffusion of dry powder is more effective at α = 2° compared to α = 6°.
- (3)
- The experimental findings are largely consistent with the numerical simulation patterns. An excessively small expansion angle α is detrimental to increasing the range of the dry powder jet, and changes in the semi-contraction angle β have a relatively minor impact on the characteristics of the supersonic jet. When the structural parameters are the same, the diffusion and range of dry powder are identical for different semi-contraction angles β.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hassan, S.; Björn, K. Pneumatic Conveying of Wood Powder by Using a Steam-Jet Ejector. Biomass Bioenergy 2000, 19, 103–117. [Google Scholar] [CrossRef]
- Miyata, M.; Tamura, T.; Higuchi, Y. Development of Hot Metal Dephosphorization with Lime Powder Top Blowing: Part 1. Low Blowing Rate. ISIJ Int. 2017, 57, 1756–1761. [Google Scholar] [CrossRef]
- Varadaraajan, V.; Mohanty, P. Design and Optimization of Rectangular Cold Spray Nozzle: Radial Injection Angle, Expansion Ratio and Traverse Speed. Surf. Coat. Technol. 2017, 316, 246–254. [Google Scholar] [CrossRef]
- Cao, C.; Li, W.; Zhang, Z.; Yang, X.; Xu, Y. Cold Spray Additive Manufacturing of Ti6Al4V: Special Nozzle Design Using Numerical Simulation and Experimental Validation. Coatings 2022, 12, 210. [Google Scholar] [CrossRef]
- Gabor, T.; Akin, S.; Jun, M.B.-G. Numerical Studies on Cold Spray Gas Dynamics and Powder Flow in Circular and Rectangular Nozzles. J. Manuf. Process. 2024, 114, 232–246. [Google Scholar] [CrossRef]
- Mat, M.N.H.; Asmuin, N.Z.; Basir, M.F.M.; Goodarzi, M.; Rahman, M.F.A.; Khairulfuaad, R.; Jabbar, B.A.; Kasihmuddin, M.S.M. Influence of Divergent Length on the Gas-Particle Flow in Dual Hose Dry Ice Blasting Nozzle Geometry. Powder Technol. 2020, 364, 152–158. [Google Scholar] [CrossRef]
- Okuda, S.; Choi, W.S. Gas-Particle Mixture Flow in Various Types of Convergent-Divergent Nozzle. J. Chem. Eng. Jpn. 1978, 11, 432–438. [Google Scholar] [CrossRef]
- Zhong, L.; Lei, J.; Zuo, Z.; Tu, J.; Deng, J.; Lei, Z.; Zhao, M.; Hua, Y. Simulation Analysis of the Decontamination Effect of Different Nozzles Abrasive Jet Based on CFD-DEM. Part. Sci. Technol. 2023, 41, 864–875. [Google Scholar] [CrossRef]
- Hong, C.; Yang, R.; Huang, Z.; Liu, W.; Chen, J.; Cong, R. Experimental Investigation on Coal-Breakage Performances by Abrasive Nitrogen-Gas Jet with a Conical Nozzle. Int. J. Rock Mech. Min. Sci. 2021, 142, 104781. [Google Scholar] [CrossRef]
- Zhang, L.; Feng, Y.; Wu, S.; Jia, H. Numerical Study of the Effect of Primary Nozzle Geometry on Supersonic Gas-Solid Jet of Bypass Injected Dry Powder Fire Extinguishing Device. Fire 2024, 7, 45. [Google Scholar] [CrossRef]
- Wu, X.; Zhu, R.; Wei, G.; Dong, K. Influence of the Carrier Gas Species on CaO-Gas Mixed Injection in the EAF Steelmaking Process. Met. Mater Trans B 2019, 50, 2389–2402. [Google Scholar] [CrossRef]
- Wang, Q.; Pang, Z.; Tian, C.; Chen, J. New Design Method of a Supersonic Steam Injection Nozzle and Its Numerical Simulation Verification. ACS Omega 2023, 8, 44485–44496. [Google Scholar] [CrossRef] [PubMed]
- Lupoi, R.; Meyer, M.; Wits, W.W.; Yin, S. The Role of Particles Flow Characteristics in the Performance of Cold Spray Nozzles. CIRP Ann. 2020, 69, 189–192. [Google Scholar] [CrossRef]
- Kudryavtsev, A.; Shershnev, A.; Rybdylova, O. Numerical Simulation of Aerodynamic Focusing of Particles in Supersonic Micronozzles. Int. J. Multiph. Flow 2019, 114, 207–218. [Google Scholar] [CrossRef]
- Miao, B.; Chen, F. Optimization Simulation of Ultrafine Dry Powder Blow-Assisted Pipe Based on CFD. Math. Probl. Eng. 2022, 2022, 8304007. [Google Scholar] [CrossRef]
- Ding, H.; Zhuo, C.; Deng, H.; Hu, W.; Chen, X. Numerical Study on Coupled Flow Characteristics of a Gas-Solid Two-Phase Jet in a Supersonic Crossflow. Int. J. Multiph. Flow 2023, 168, 104583. [Google Scholar] [CrossRef]
- Yu, H.; Yang, S.; Hu, J.; Wang, H. CFD Study of Gas-Powder Injection Characteristics in a Novel Lance with Supersonic Shrouding Jet. Chem. Eng. J. 2024, 481, 148470. [Google Scholar] [CrossRef]
- Yu, H.; Yang, S.; Hu, J.; Wang, H. Jet Penetration and Particle Dispersion Behaviors of Supersonic Gas–Solid Oxygen Jet under High Ambient Temperature. Appl. Therm. Eng. 2024, 242, 122502. [Google Scholar] [CrossRef]
- Cruz, N.; Briens, C.; Berruti, F. Supersonic Attrition Nozzles in Gas–Solid Fluidized Beds. Chem. Eng. Process. Process Intensif. 2010, 49, 225–234. [Google Scholar] [CrossRef]
- Cruz, N.; Briens, C.; Berruti, F. Effect of Thrust on Supersonic Gas Jet Penetration in Gas–Solid Fluidized Beds. Powder Technol. 2011, 214, 38–46. [Google Scholar] [CrossRef]
- Liu, F.; Sun, D.; Zhu, R.; Li, Y. Characteristics of Flow Field for Supersonic Oxygen Multijets with Various Laval Nozzle Structures. Metall. Mater. Trans. B 2019, 50, 2362–2376. [Google Scholar] [CrossRef]
- Li, M.; Li, L.; Zhang, B.; Li, Q.; Wu, W.; Zou, Z. Numerical Analysis of the Particle-Induced Effect on Gas Flow in a Supersonic Powder-Laden Oxygen Jet. Metall. Mater. Trans. B 2020, 51, 1718–1730. [Google Scholar] [CrossRef]
- Sun, H.; Yu, H.; Yang, S.; Hu, J.; Wang, H. Four-Way Coupled Eulerian-Lagrangian Study of Phase Interaction Mechanism in the Supersonic Gas-Solid Two-Phase Flow. Chem. Eng. J. 2023, 473, 145265. [Google Scholar] [CrossRef]
- Yang, Q.; Yang, S.; Yu, H.; Wang, H. Impact of Laval Nozzle Structure on the Flow Characteristics of Supersonic Gas-Solid Two-Phase Flow. Powder Technol. 2024, 439, 119657. [Google Scholar] [CrossRef]
- Shi, H.; Wang, X.; Xiang, Q.; Zhang, G.; Xue, L. Experimental and Numerical Study of the Discharge Performance of Particle-Laden Turbulent Flow. J. Mar. Sci. Eng. 2022, 10, 85. [Google Scholar] [CrossRef]
- Zhang, L.; Yu, Q.; Liu, T.; Feng, Z.; Sun, M.; Jin, H. Coupled Modeling and Numerical Simulation of Gas Flows Laden with Solid Particles in de Laval Nozzles. Shock Waves 2022, 32, 213–230. [Google Scholar] [CrossRef]
- Zaman, K.B.M.Q. Asymptotic Spreading Rate of Initially Compressible Jets—Experiment and Analysis. Phys. Fluids 1998, 10, 2652–2660. [Google Scholar] [CrossRef]








| Structure | Straight | Convergent | Expansion | Inlet | Throat | Outlet | Jet | Jet |
|---|---|---|---|---|---|---|---|---|
| Symbol | LAB | LBC | LCD | RA | RC | RD | LEF | LFG |
| Size | 50 | 6.25 | 13.6 | 5 | 3 | 5.4 | 108 | 81 |
| Symbol | Simulation Conditions | Parameter Setting | Unit |
|---|---|---|---|
| p0 | Nozzle inlet pressure | 1.2 | MPa |
| p | Nozzle outlet pressure | 101,325 | Pa |
| T | Environment temperature | 300 | K |
| Gas property | N2 | perfect gas | |
| μg | Gas viscosity | Sutherland | kg/m·s |
| cpg | Specific heat coefficient of gas | 1040.67 | J·kg−1·K−1 |
| λ | Thermal conductivity of gas | 0.0242 | W/m·K |
| dp | Particle diameter | 10 | μm |
| Qp | Particle mass flow rate | 0.001 | kg/s |
| ρp | Particle density | 1800 | kg·m−3 |
| cp | Specific heat coefficient of particle | 2159 | J·kg−1·K−1 |
| Nozzle Number | Semi-Expansion Angle α (°) | Semi-Contraction Angle β (°) | Filling Ratio | Injection Pressure P |
|---|---|---|---|---|
| Nozzle 1 | 10 | 17.7 | 0.35 | 0.6 MPa |
| Nozzle 2 | 6 | 17.7 | ||
| Nozzle 3 | 2 | 17.7 | ||
| Nozzle 4 | 10 | 9.7 | ||
| Nozzle 5 | 10 | 5.7 |
| Nozzle | Number of Experiments | RD1 (mm) | S (m) | MRD (mm) | MS (m) |
|---|---|---|---|---|---|
| Nozzle1 | 1 | 52.6 | 5.01 | 54.1 | 4.84 |
| 2 | 54.5 | 4.89 | |||
| 3 | 55.3 | 4.63 | |||
| Nozzle2 | 1 | 48.9 | 4.51 | 50.1 | 4.43 |
| 2 | 50.1 | 4.46 | |||
| 3 | 51.3 | 4.32 | |||
| Nozzle3 | 1 | 49.6 | 3.34 | 50.6 | 3.48 |
| 2 | 50.3 | 3.48 | |||
| 3 | 51.8 | 3.62 | |||
| Nozzle4 | 1 | 52.8 | 5.02 | 54.3 | 4.91 |
| 2 | 54.9 | 4.91 | |||
| 3 | 55.3 | 4.82 | |||
| Nozzle5 | 1 | 53.8 | 5.32 | 54.7 | 4.99 |
| 2 | 54.1 | 4.94 | |||
| 3 | 56.1 | 4.72 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ge, H.; Zhao, P.; Zhu, C.; Zhang, X.; Liu, Y. Analysis of the Influence of Nozzle Structure of Dry Powder Fire Extinguishing System on Supersonic Jet Characteristics. Machines 2024, 12, 553. https://doi.org/10.3390/machines12080553
Ge H, Zhao P, Zhu C, Zhang X, Liu Y. Analysis of the Influence of Nozzle Structure of Dry Powder Fire Extinguishing System on Supersonic Jet Characteristics. Machines. 2024; 12(8):553. https://doi.org/10.3390/machines12080553
Chicago/Turabian StyleGe, Hongen, Peng Zhao, Cong Zhu, Xin Zhang, and Yuqi Liu. 2024. "Analysis of the Influence of Nozzle Structure of Dry Powder Fire Extinguishing System on Supersonic Jet Characteristics" Machines 12, no. 8: 553. https://doi.org/10.3390/machines12080553
APA StyleGe, H., Zhao, P., Zhu, C., Zhang, X., & Liu, Y. (2024). Analysis of the Influence of Nozzle Structure of Dry Powder Fire Extinguishing System on Supersonic Jet Characteristics. Machines, 12(8), 553. https://doi.org/10.3390/machines12080553





