Human Reliability Assessment of Space Teleoperation Based on ISM-BN
Abstract
1. Introduction
2. Materials and Methods
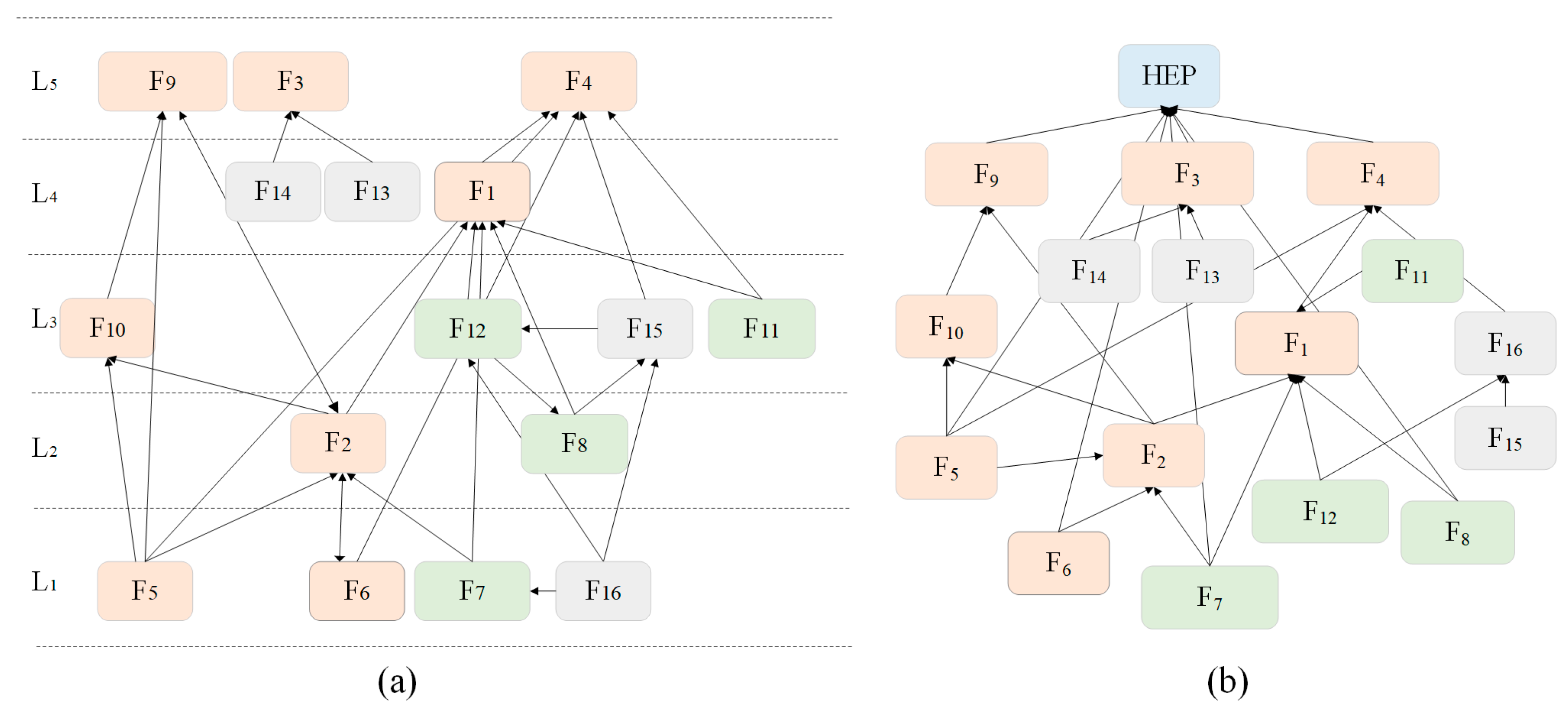
2.1. Interpretive Structural Modeling
2.2. Probabilistic Interpretation of HRA
2.3. First-Phase Update Based on Expert Judgement Data
2.4. Second-Phase Update Based on Experimental Data
3. Results
4. Discussion
4.1. Case Study
4.2. Sensitivity Analysis
4.3. Validation
5. Conclusions
- (1)
- The constructed model integrates data from expert judgment with experimental data, offering the potential for continuous model updates as more empirical data become available in the future.
- (2)
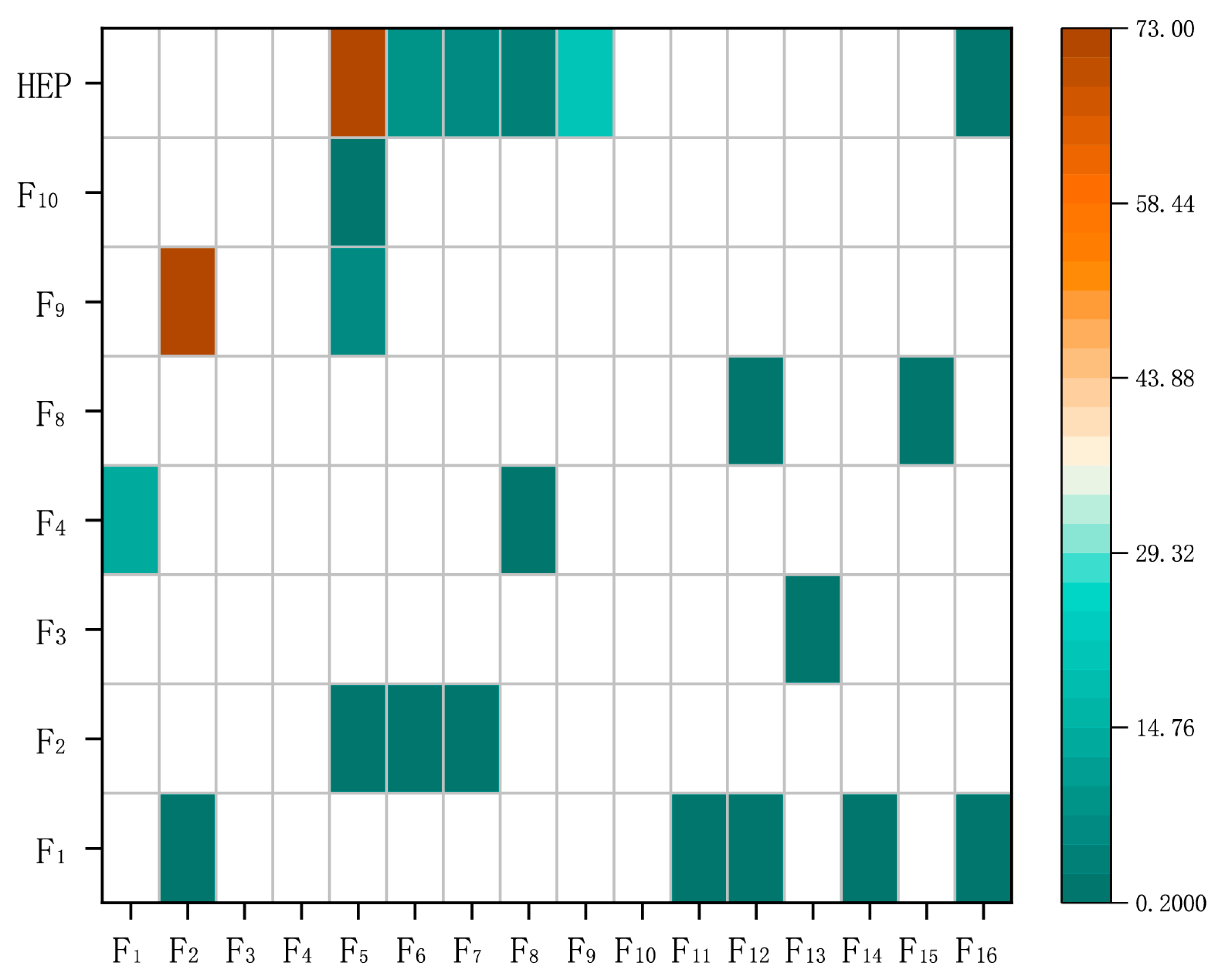
- Sensitivity analysis conducted using the HRA model shows that spatial cognitive ability (), team communication (), task complexity (), team cooperative (), and control mode () are HEP-sensitive nodes. Minor improvements in the involved factors can substantially reduce overall system risk.
- (3)
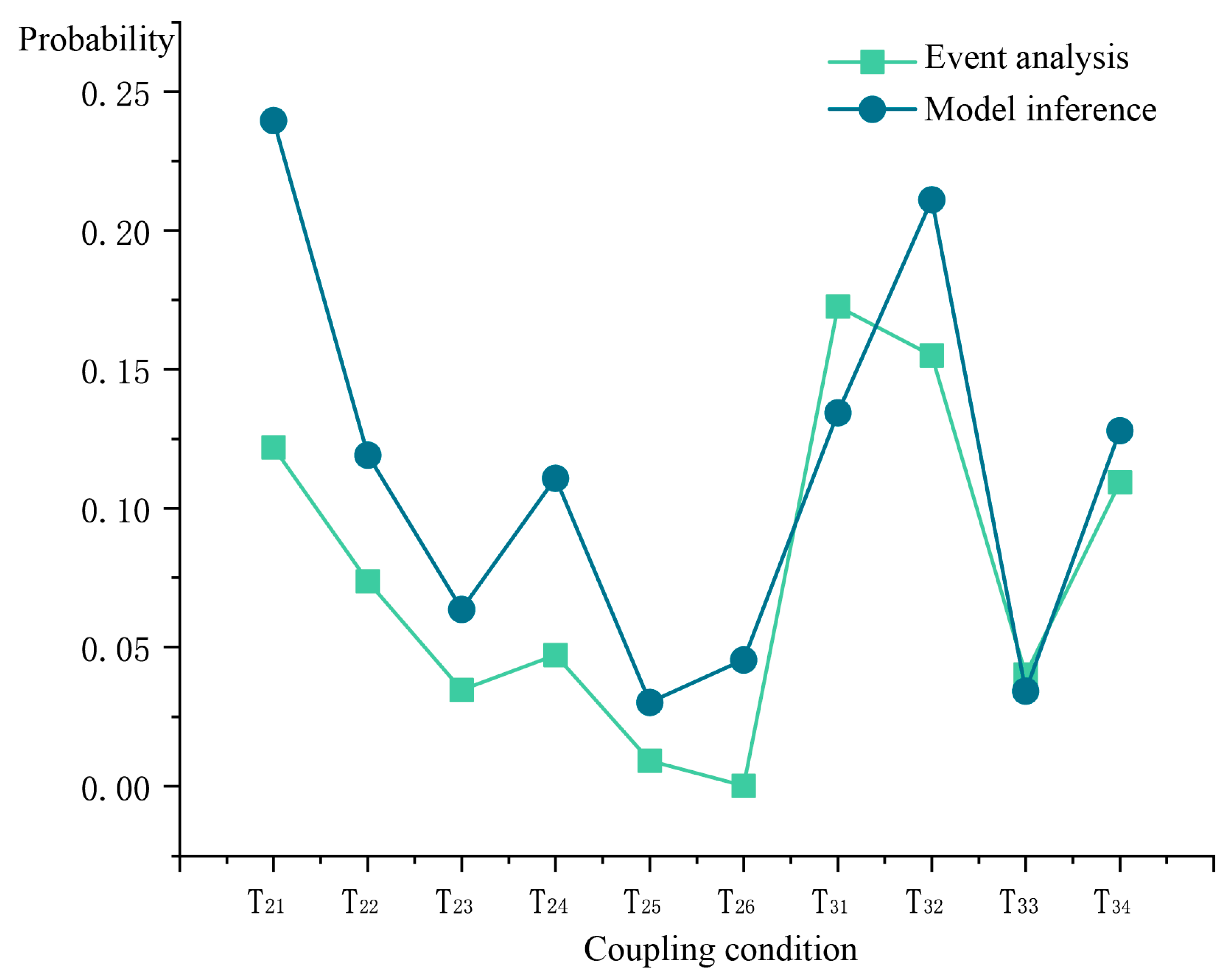
- Model validation shows that the occurrence of multi-factor coupling will be key for risk prevention. Moreover, human factors (individual and team factors) will be central to safety management.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Qi, W.; Wang, N.; Su, H.; Aliverti, A. DCNN based human activity recognition framework with depth vision guiding. Neurocomputing 2022, 486, 261–271. [Google Scholar] [CrossRef]
- Ovur, S.E.; Zhou, X.; Qi, W.; Zhang, L.; Hu, Y.; Su, H.; Ferrigno, G.; De Momi, E. A novel autonomous learning framework to enhance sEMG-based hand gesture recognition using depth information. Biomed. Signal Process. Control 2021, 66, 102444. [Google Scholar] [CrossRef]
- Zhao, J.; Lv, Y.; Zeng, Q.; Wan, L. Online policy learning-based output-feedback optimal control of continuous-time systems. IEEE Trans. Circuits Syst. II Express Briefs 2022, 71, 652–656. [Google Scholar] [CrossRef]
- Tong, M.; Chen, S.; Niu, Y.; Wu, J.; Tian, J.; Xue, C. Visual search during dynamic displays: Effects of velocity and motion direction. J. Soc. Inf. Disp. 2022, 30, 635–647. [Google Scholar] [CrossRef]
- Paglioni, V.P.; Groth, K.M. Dependency definitions for quantitative human reliability analysis. Reliab. Eng. Syst. Saf. 2022, 220, 108274. [Google Scholar] [CrossRef]
- Liu, P.; Li, Z. Human error data collection and comparison with predictions by SPAR-H. Risk Anal. 2014, 34, 1706–1719. [Google Scholar] [CrossRef] [PubMed]
- Hollnagel, E. Cognitive Reliability and Error Analysis Method (CREAM); Elsevier: Amsterdam, The Netherlands, 1998. [Google Scholar]
- Gertman, D.; Blackman, H.; Marble, J.; Byers, J.; Smith, C. The SPAR-H human reliability analysis method. US Nucl. Regul. Comm. 2005, 230, 35. [Google Scholar]
- Chang, Y.; Mosleh, A. Cognitive modeling and dynamic probabilistic simulation of operating crew response to complex system accidents. Part 2: IDAC performance influencing factors model. Reliab. Eng. Syst. Saf. 2007, 92, 1014–1040. [Google Scholar] [CrossRef]
- Wang, L.; Wang, Y.; Chen, Y.; Pan, X.; Zhang, W.; Zhu, Y. Methodology for assessing dependencies between factors influencing airline pilot performance reliability: A case of taxiing tasks. J. Air Transp. Manag. 2020, 89, 101877. [Google Scholar] [CrossRef]
- De Ambroggi, M.; Trucco, P. Modelling and assessment of dependent performance shaping factors through Analytic Network Process. Reliab. Eng. Syst. Saf. 2011, 96, 849–860. [Google Scholar] [CrossRef]
- Adedigba, S.A.; Khan, F.; Yang, M. Process accident model considering dependency among contributory factors. Process Saf. Environ. Prot. 2016, 102, 633–647. [Google Scholar] [CrossRef]
- Kim, Y.; Park, J.; Jung, W.; Jang, I.; Seong, P.H. A statistical approach to estimating effects of performance shaping factors on human error probabilities of soft controls. Reliab. Eng. Syst. Saf. 2015, 142, 378–387. [Google Scholar] [CrossRef]
- Kabir, S.; Papadopoulos, Y. Applications of Bayesian networks and Petri nets in safety, reliability, and risk assessments: A review. Saf. Sci. 2019, 115, 154–175. [Google Scholar] [CrossRef]
- Giudici, P. Bayesian data mining, with application to benchmarking and credit scoring. Appl. Stoch. Models Bus. Ind. 2001, 17, 69–81. [Google Scholar] [CrossRef]
- Martins, M.R.; Maturana, M.C. Application of Bayesian Belief networks to the human reliability analysis of an oil tanker operation focusing on collision accidents. Reliab. Eng. Syst. Saf. 2013, 110, 89–109. [Google Scholar] [CrossRef]
- Musharraf, M.; Hassan, J.; Khan, F.; Veitch, B.; MacKinnon, S.; Imtiaz, S. Human reliability assessment during offshore emergency conditions. Saf. Sci. 2013, 59, 19–27. [Google Scholar] [CrossRef]
- Johnson, K.; Morais, C.; Patelli, E.; Walls, L. A data driven approach to elicit causal links between performance shaping factors and human failure events. In Proceedings of the European Conference on Safety and Reliability 2022, Dublin, Ireland, 28 August–1 September 2022; pp. 520–527. [Google Scholar]
- Guan, L.; Abbasi, A.; Ryan, M.J. Analyzing green building project risk interdependencies using Interpretive Structural Modeling. J. Clean. Prod. 2020, 256, 120372. [Google Scholar] [CrossRef]
- Xu, X.; Zou, P.X. Analysis of factors and their hierarchical relationships influencing building energy performance using interpretive structural modelling (ISM) approach. J. Clean. Prod. 2020, 272, 122650. [Google Scholar] [CrossRef]
- Wu, W.-S.; Yang, C.-F.; Chang, J.-C.; Château, P.-A.; Chang, Y.-C. Risk assessment by integrating interpretive structural modeling and Bayesian network, case of offshore pipeline project. Reliab. Eng. Syst. Saf. 2015, 142, 515–524. [Google Scholar] [CrossRef]
- Hou, L.-X.; Liu, R.; Liu, H.-C.; Jiang, S. Two decades on human reliability analysis: A bibliometric analysis and literature review. Ann. Nucl. Energy 2021, 151, 107969. [Google Scholar] [CrossRef]
- Mkrtchyan, L.; Podofillini, L.; Dang, V.N. Methods for building conditional probability tables of bayesian belief networks from limited judgment: An evaluation for human reliability application. Reliab. Eng. Syst. Saf. 2016, 151, 93–112. [Google Scholar] [CrossRef]
- Prvakova, S.; Dang, V. A Review of the Current Status of HRA Data; Paul Scherrer Institute: Villigen, Switzerland, 2014; pp. 595–603. [Google Scholar]
- Podofillini, L.; Mkrtchyan, L.; Dang, V. Aggregating expert-elicited error probabilities to build HRA models. In Safety and Reliability: Methodology and Applications; CRC Press: Boca Raton, FL, USA, 2014; pp. 1119–1128. [Google Scholar]
- Mosleh, A.; Bier, V.M.; Apostolakis, G. A critique of current practice for the use of expert opinions in probabilistic risk assessment. Reliab. Eng. Syst. Saf. 1988, 20, 63–85. [Google Scholar] [CrossRef]
- Zhang, H.; Shanguang, C.; Wang, C.; Deng, Y.; Xiao, Y.; Zhang, Y.; Dai, R. Analysis of factors affecting teleoperation performance based on a hybrid Fuzzy DEMATEL method. Space Sci. Technol. 2024. [Google Scholar] [CrossRef]
- Podofillini, L.; Dang, V.N. A Bayesian approach to treat expert-elicited probabilities in human reliability analysis model construction. Reliab. Eng. Syst. Saf. 2013, 117, 52–64. [Google Scholar] [CrossRef]
- Atwood, C.L. Constrained noninformative priors in risk assessment. Reliab. Eng. Syst. Saf. 1996, 53, 37–46. [Google Scholar] [CrossRef]
- Greco, S.F.; Podofillini, L.; Dang, V.N. A Bayesian model to treat within-category and crew-to-crew variability in simulator data for Human Reliability Analysis. Reliab. Eng. Syst. Saf. 2021, 206, 107309. [Google Scholar] [CrossRef]
- Zhang, Z.-X.; Wang, L.; Wang, Y.-M.; Martínez, L. A novel alpha-level sets based fuzzy DEMATEL method considering experts’ hesitant information. Expert Syst. Appl. 2023, 213, 118925. [Google Scholar] [CrossRef]
- Warfield, J.N. Developing interconnection matrices in structural modeling. IEEE Trans. Syst. Man Cybern. 1974, SMC-4, 81–87. [Google Scholar] [CrossRef]
- Liu, J.; Wan, L.; Wang, W.; Yang, G.; Ma, Q.; Zhou, H.; Zhao, H.; Lu, F. Integrated fuzzy DEMATEL-ISM-NK for metro operation safety risk factor analysis and multi-factor risk coupling study. Sustainability 2023, 15, 5898. [Google Scholar] [CrossRef]
- Swain, A.D.; Guttmann, H.E. Handbook of Human-Reliability Analysis with Emphasis on Nuclear Power Plant Applications. Final Report; Sandia National Lab. (SNL-NM): Albuquerque, NM, USA, 1983. [Google Scholar]
- Groth, K.M.; Smith, C.L.; Swiler, L.P. A Bayesian method for using simulator data to enhance human error probabilities assigned by existing HRA methods. Reliab. Eng. Syst. Saf. 2014, 128, 32–40. [Google Scholar] [CrossRef]
- Schneider, W.; Shiffrin, R.M. Controlled and automatic human information processing: I. Detection, search, and attention. Psychol. Rev. 1977, 84, 1. [Google Scholar] [CrossRef]
- Zhang, M.; Zhang, D.; Yao, H.; Zhang, K. A probabilistic model of human error assessment for autonomous cargo ships focusing on human–autonomy collaboration. Saf. Sci. 2020, 130, 104838. [Google Scholar] [CrossRef]
- Chen, H.; Zhao, Y.; Ma, X. Critical factors analysis of severe traffic accidents based on Bayesian network in China. J. Adv. Transp. 2020, 2020, 8878265. [Google Scholar] [CrossRef]
- Li, C.; Mahadevan, S. Sensitivity analysis of a Bayesian network. ASCE-ASME J. Risk Uncertain. Eng. Syst. Part B Mech. Eng. 2018, 4, 011003. [Google Scholar] [CrossRef]
- Lu, Y.; Wang, T.; Liu, T. Bayesian network-based risk analysis of chemical plant explosion accidents. Int. J. Environ. Res. Public Health 2020, 17, 5364. [Google Scholar] [CrossRef] [PubMed]
- Bartone, P.T.; Roland, R.; Bartone, J.; Krueger, G.; Sciaretta, A.; Johnsen, B.H. Human adaptability for deep space exploration mission: An exploratory study. J. Hum. Performanc Extrem. Environ. 2019, 15, 2327–2937. [Google Scholar]
- Manuele, F.A. Reviewing Heinrich. Prof. Saf. 2011, 56, 52–61. [Google Scholar]
- Zhang, M.; Yu, D.; Wang, T.; Xu, C. Coupling analysis of tunnel construction safety risks based on NK model and SD causality diagram. Buildings 2023, 13, 1081. [Google Scholar] [CrossRef]
- David, S. Disasters and Accidents in Manned Spaceflight; Springer Science & Business Media: Berlin, Germany, 2000. [Google Scholar]
- Wu, B.-J.; Jin, L.-H.; Zheng, X.-Z.; Chen, S. Coupling analysis of crane accident risks based on Bayesian network and the NK model. Sci. Rep. 2024, 14, 1133. [Google Scholar] [CrossRef]
- Zhang, X.; Mahadevan, S. Bayesian network modeling of accident investigation reports for aviation safety assessment. Reliab. Eng. Syst. Saf. 2021, 209, 107371. [Google Scholar] [CrossRef]


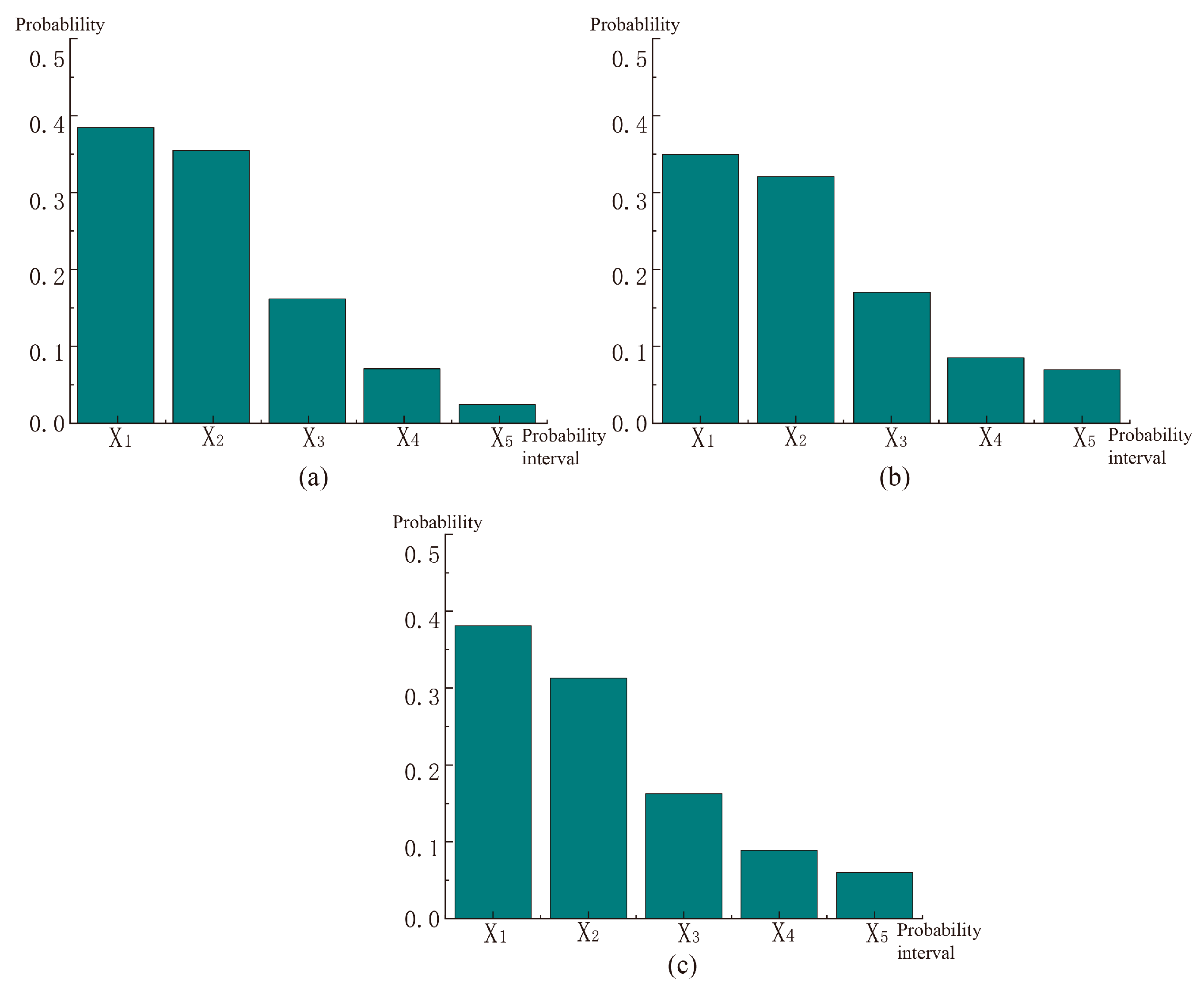


| Interval | Label | Reference Value | Probabilistic Boundary |
|---|---|---|---|
| 1 | Very low | ||
| 2 | Low | ||
| 3 | Medium | ||
| 4 | High | ||
| 5 | Very high |
| Expert | |||||
|---|---|---|---|---|---|
| h = 1 | 0.0008 | 0.0008 | 0.0008 | 0.0024 | 2 |
| h = 2 | 0.0008 | 0.004 | 0.0008 | 0.0056 | 4 |
| h = 3 | 0.0008 | 0.0008 | 0.0008 | 0.0024 | 3 |
| … | … | … | … | … | … |
| h = 35 | 0.0008 | 0.004 | 0.004 | 0.0088 | 4 |
| Combination | The Posterior Probability of HEP | ||||
|---|---|---|---|---|---|
| 5.89 × 10−1 | 4.08 × 10−1 | 1.99 × 10−3 | 2.73 × 10−4 | 2.74 × 10−4 | |
| 1.27 × 10−8 | 1.27 × 10−8 | 1.72 × 10−3 | 4.09 × 10−1 | 5.90 × 10−1 | |
| 4.86 × 10−3 | 4.86 × 10−5 | 1.76 × 10−3 | 4.08 × 10−1 | 5.88 × 10−1 | |
| 6.72 × 10−8 | 6.73 × 10−8 | 1.72 × 10−3 | 4.09 × 10−1 | 5.89 × 10−1 | |
| 2.85 × 10−1 | 2.85 × 10−2 | 3.01 × 10−2 | 3.84 × 10−1 | 5.29 × 10−1 | |
| 1.91 × 10−1 | 1.91 × 10−1 | 1.91 × 10−1 | 2.47 × 10−1 | 1.80 × 10−1 | |
| 9.99 × 10−1 | 9.37 × 10−32 | 9.42 × 10−32 | 8.96 × 10−32 | 4.23 × 10−32 | |
| 2.18 × 10−1 | 2.19 × 10−1 | 2.22 × 10−1 | 2.23 × 10−1 | 1.16 × 10−1 | |
| Condition | Frequency | Condition | Frequency | Condition | Frequency | Condition | Frequency |
|---|---|---|---|---|---|---|---|
| F0000 | 0 | F0010 | 0.0222 | F0110 | 0.0222 | F1101 | 0.0222 |
| F1000 | 0.1333 | F1100 | 0.0444 | F0101 | 0 | F1011 | 0.0444 |
| F0010 | 0.0444 | F1010 | 0.2 | F0011 | 0.1556 | F0111 | 0 |
| T21 | T22 | T23 | T24 | T25 | T26 | T31 | T32 | T33 | T34 |
| 0.0091 | 0.0736 | 0.0346 | 0.0472 | 0.1219 | 0.0002 | 0.1727 | 0.1550 | 0.0402 | 0.0993 |
| Condition | Very High | High | Medium | Low | Very Low | HEP Expectation |
|---|---|---|---|---|---|---|
| T21 | 0.5132 | 0.5255 | 0.5255 | 0.2435 | 0.0525 | 0.0301 |
| T22 | 0.9999 | 0.9999 | 0.4555 | 0.2525 | 0.1601 | 0.1192 |
| T23 | 0.9999 | 0.4816 | 0.2817 | 0.2525 | 0.0601 | 0.0636 |
| T24 | 0.0003 | 0.0723 | 0.0002 | 0.1947 | 0.2321 | 0.1408 |
| T25 | 0.0003 | 0.0721 | 0.1946 | 0.1946 | 0.2321 | 0.2397 |
| T26 | 0.0002 | 0.9999 | 0.0003 | 0.2101 | 0.0409 | 0.0455 |
| T31 | 0.2132 | 0.2255 | 0.2255 | 0.1625 | 0.2254 | 0.1345 |
| T32 | 0.3069 | 0.3254 | 0.3254 | 0.3145 | 0.3435 | 0.2112 |
| T33 | 0.5999 | 0.3817 | 0.0817 | 0.0525 | 0.0600 | 0.0342 |
| T34 | 0.0003 | 0.0072 | 0.0003 | 0.1946 | 0.2159 | 0.1080 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, H.; Chen, S.; Dai, R. Human Reliability Assessment of Space Teleoperation Based on ISM-BN. Machines 2024, 12, 524. https://doi.org/10.3390/machines12080524
Zhang H, Chen S, Dai R. Human Reliability Assessment of Space Teleoperation Based on ISM-BN. Machines. 2024; 12(8):524. https://doi.org/10.3390/machines12080524
Chicago/Turabian StyleZhang, Hongrui, Shanguang Chen, and Rongji Dai. 2024. "Human Reliability Assessment of Space Teleoperation Based on ISM-BN" Machines 12, no. 8: 524. https://doi.org/10.3390/machines12080524
APA StyleZhang, H., Chen, S., & Dai, R. (2024). Human Reliability Assessment of Space Teleoperation Based on ISM-BN. Machines, 12(8), 524. https://doi.org/10.3390/machines12080524






