The Effect of Cycloid Gear Wear on the Transmission Accuracy of the RV Reducer
Abstract
1. Introduction
2. Wear Model in Cycloid Gear
2.1. Tooth Profile of Cycloid Pinwheel Transmission
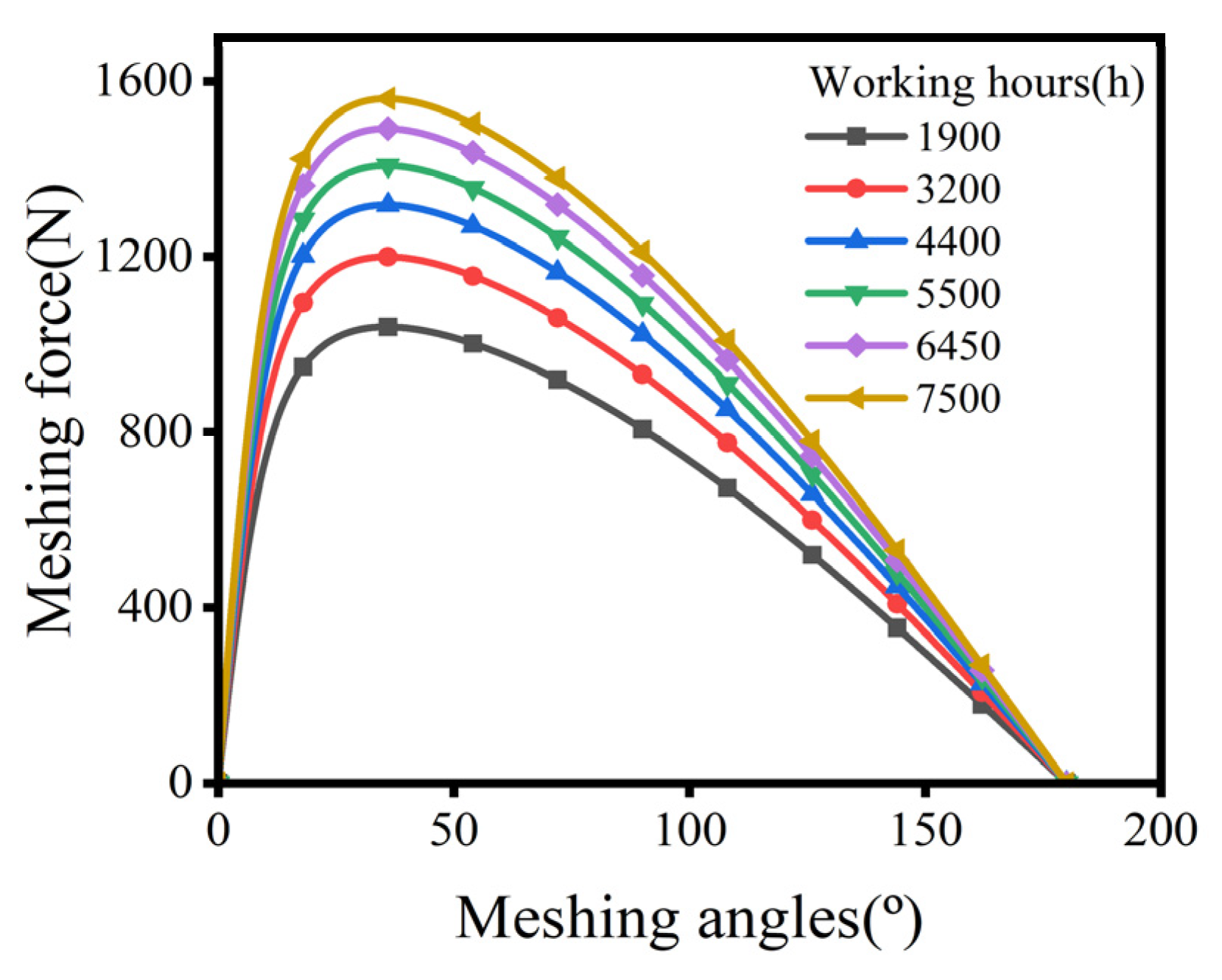
2.2. Meshing Force of the Cycloid Gear
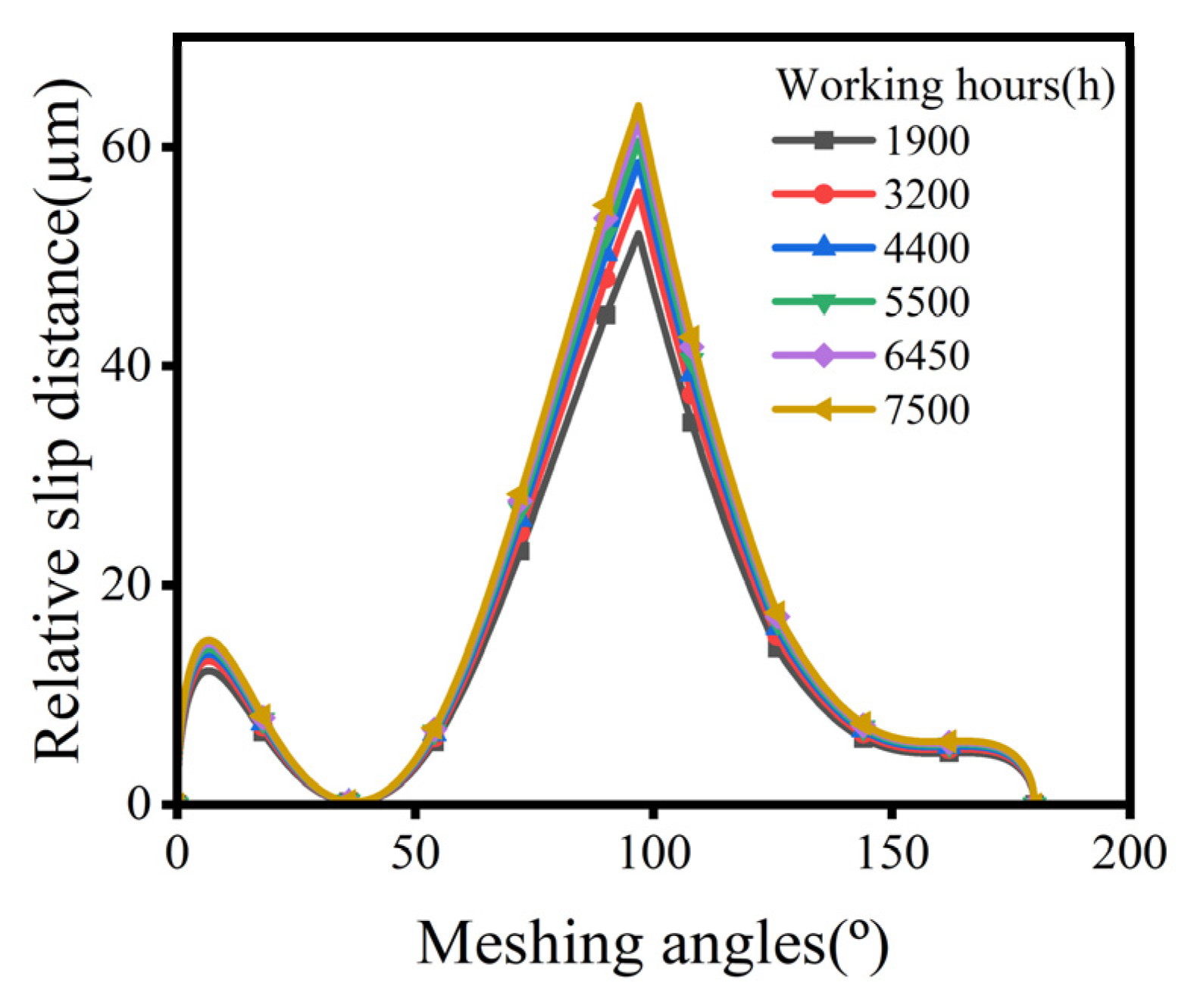
2.3. Wear Volume of the Cycloid Gear Tooth Profile
3. TE Models Considering Wear
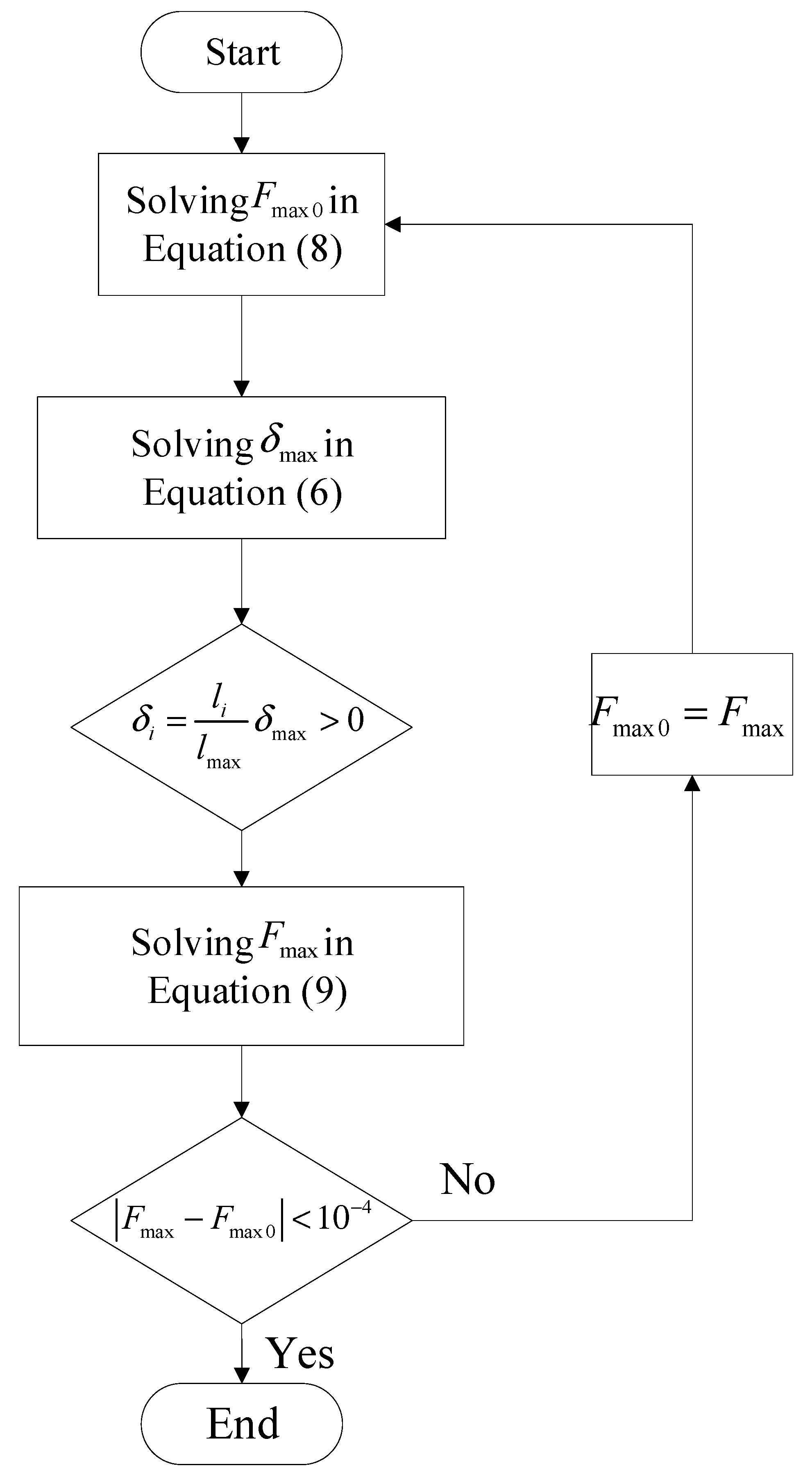
3.1. The Wear Model of Cycloid Gear
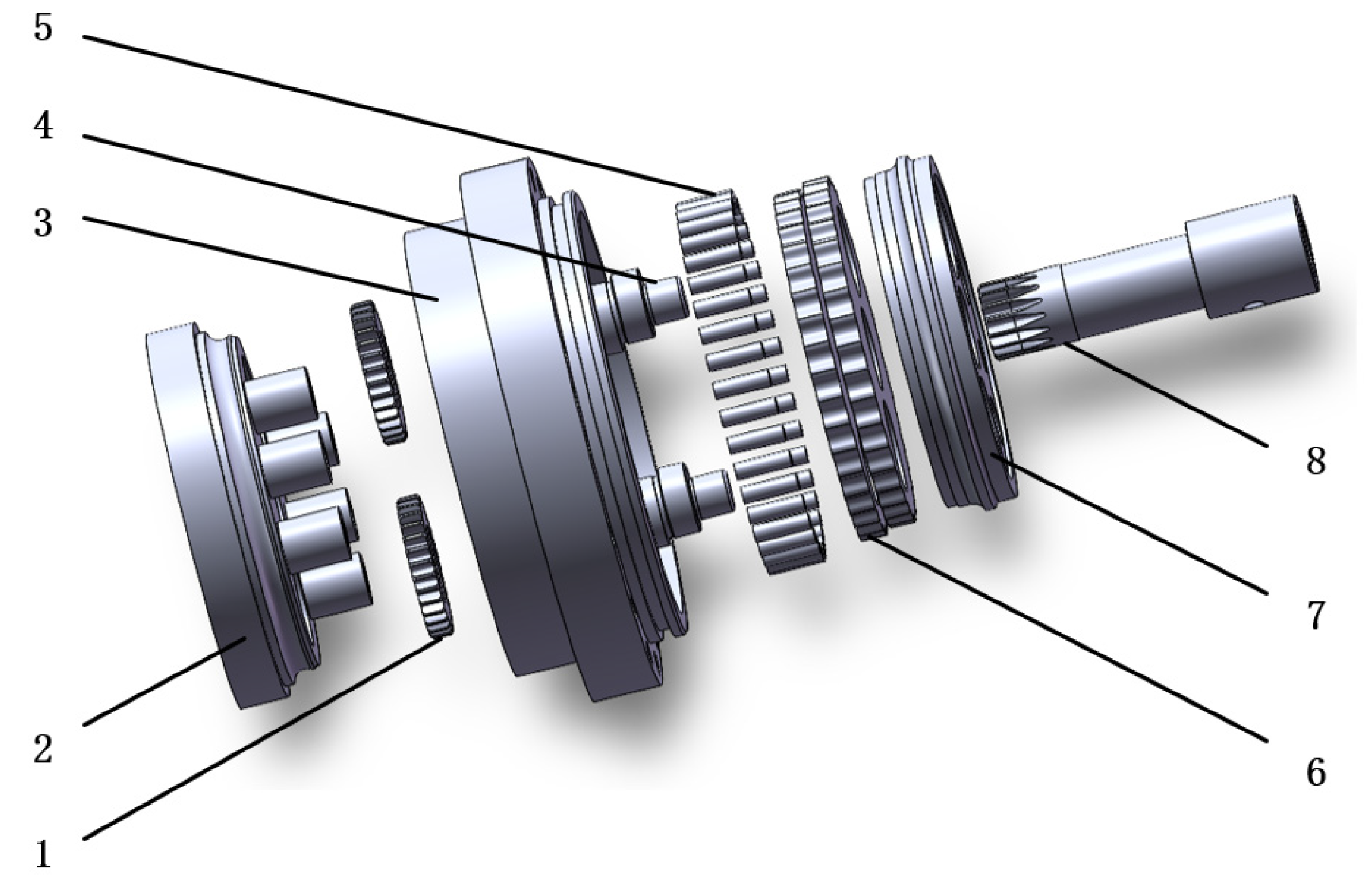
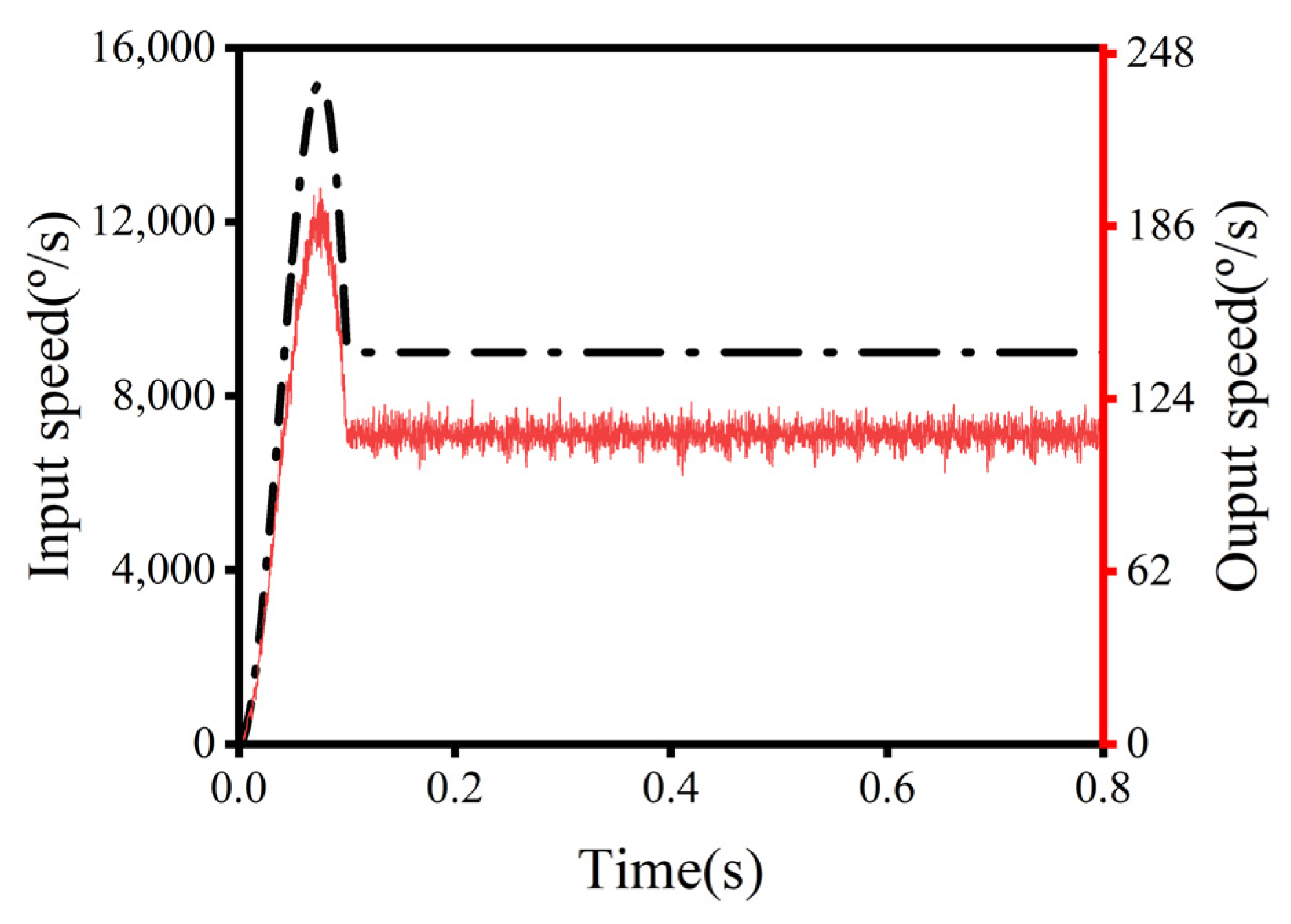
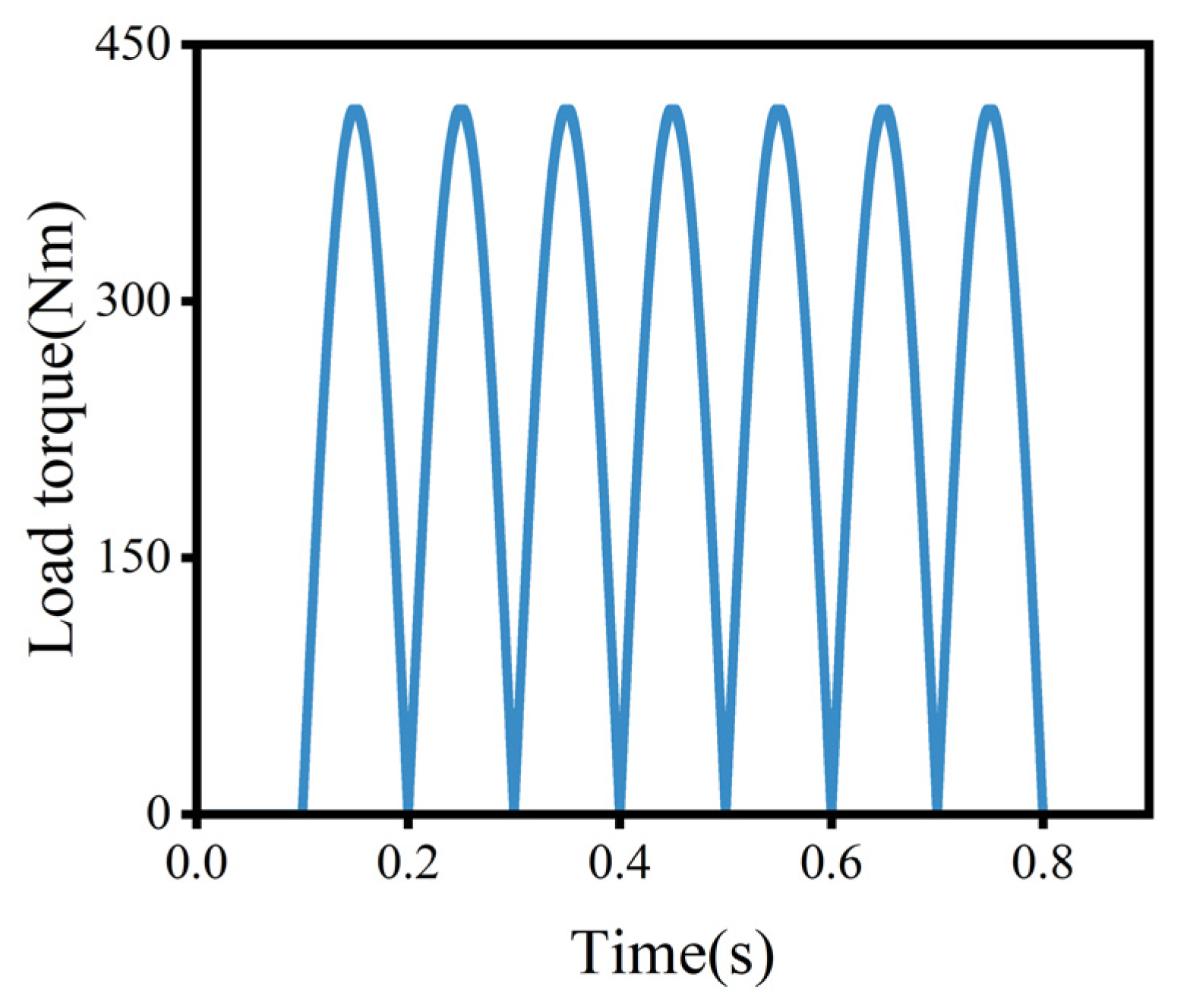
3.2. Full Rigid Body Model
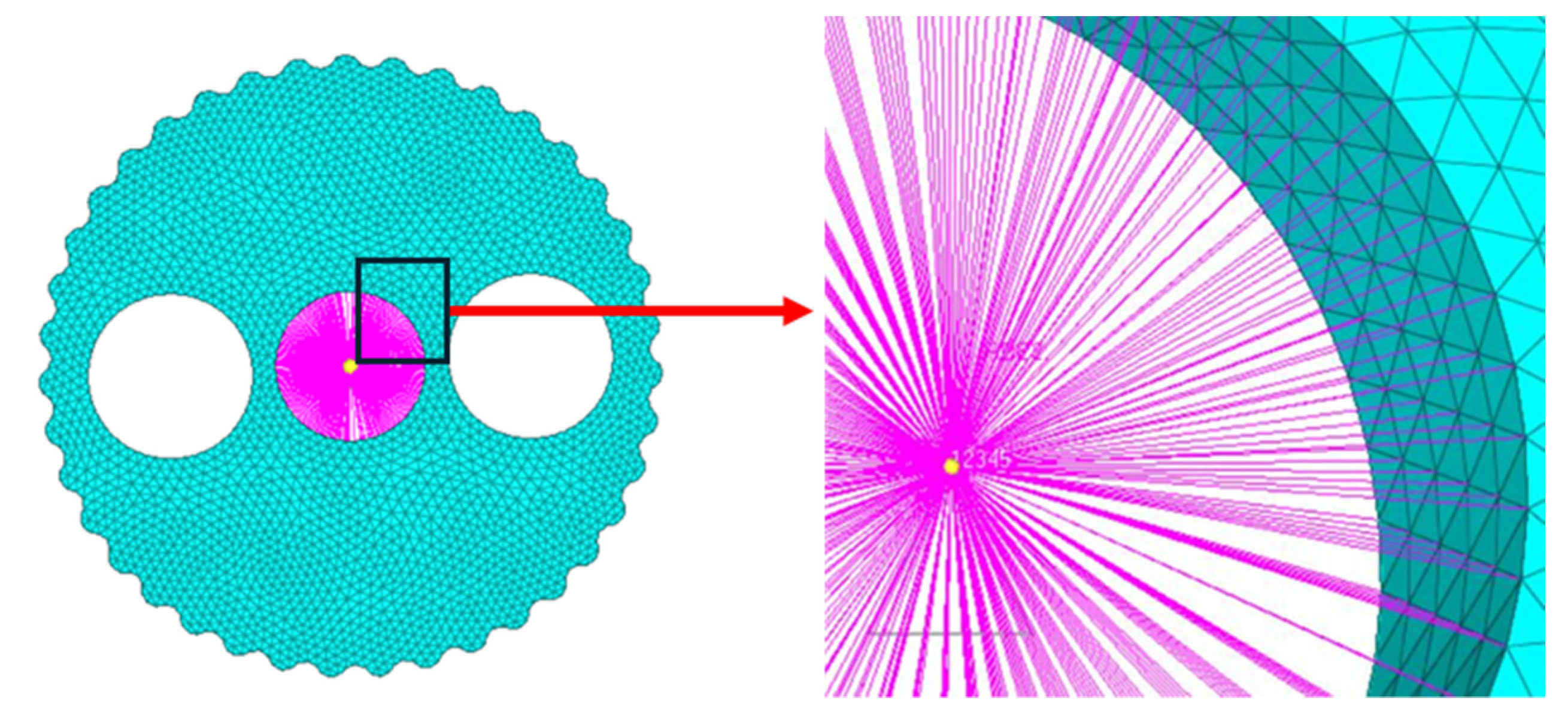
3.3. Rigid–Flexible Coupling Model
4. Results and Discussions
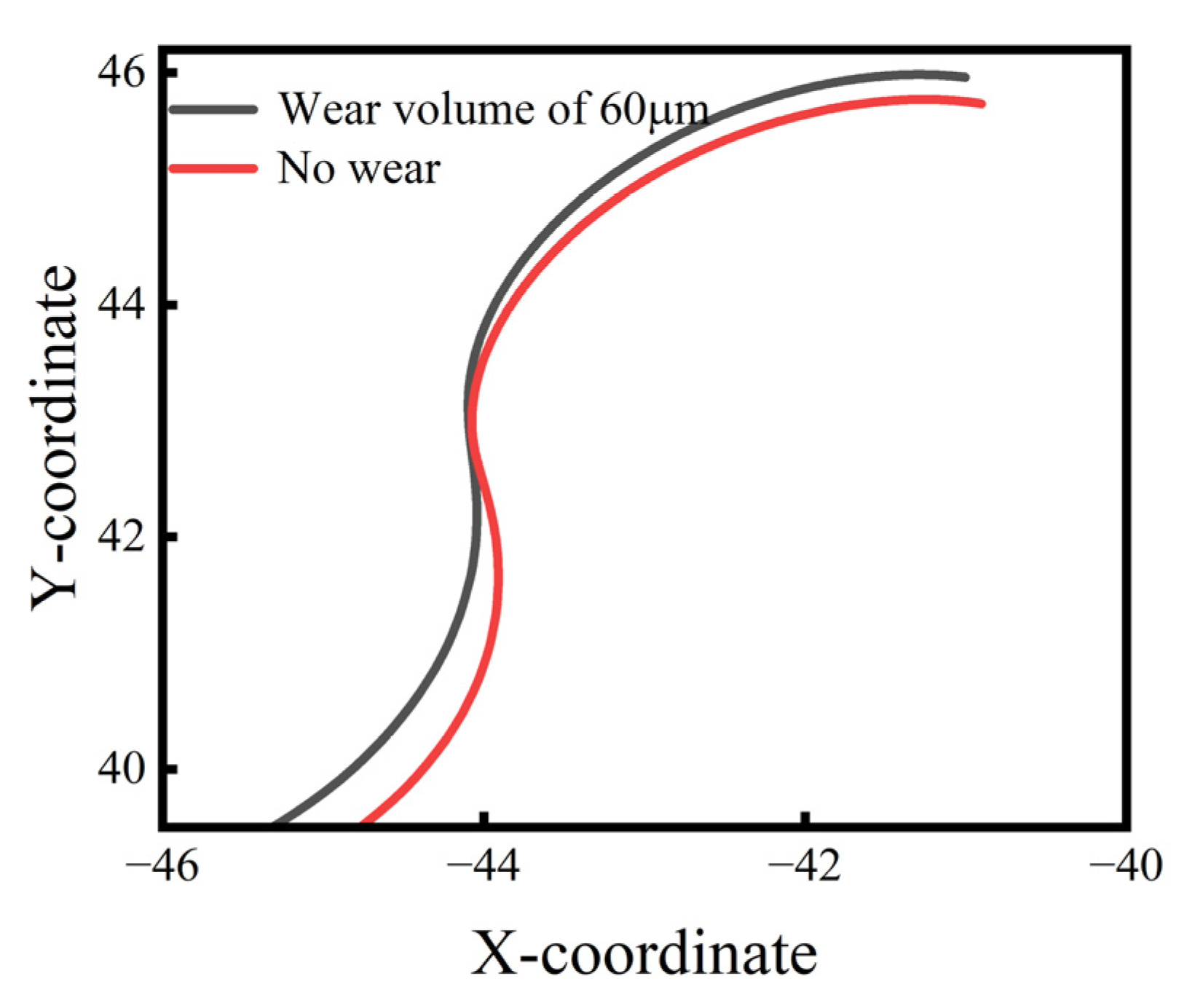
4.1. The Wear Volume on the Cycloid Gear Tooth Profile
4.2. Effects of the Cycloid Gear’s Flexibility and Output Shaft’s Load on the TE
4.3. Effects of Wear Volumes on the TE
4.3.1. The STE and DTE of the Full Rigid Model
4.3.2. The STE of the Rigid–Flexible Coupling Model
5. Conclusions
- (1)
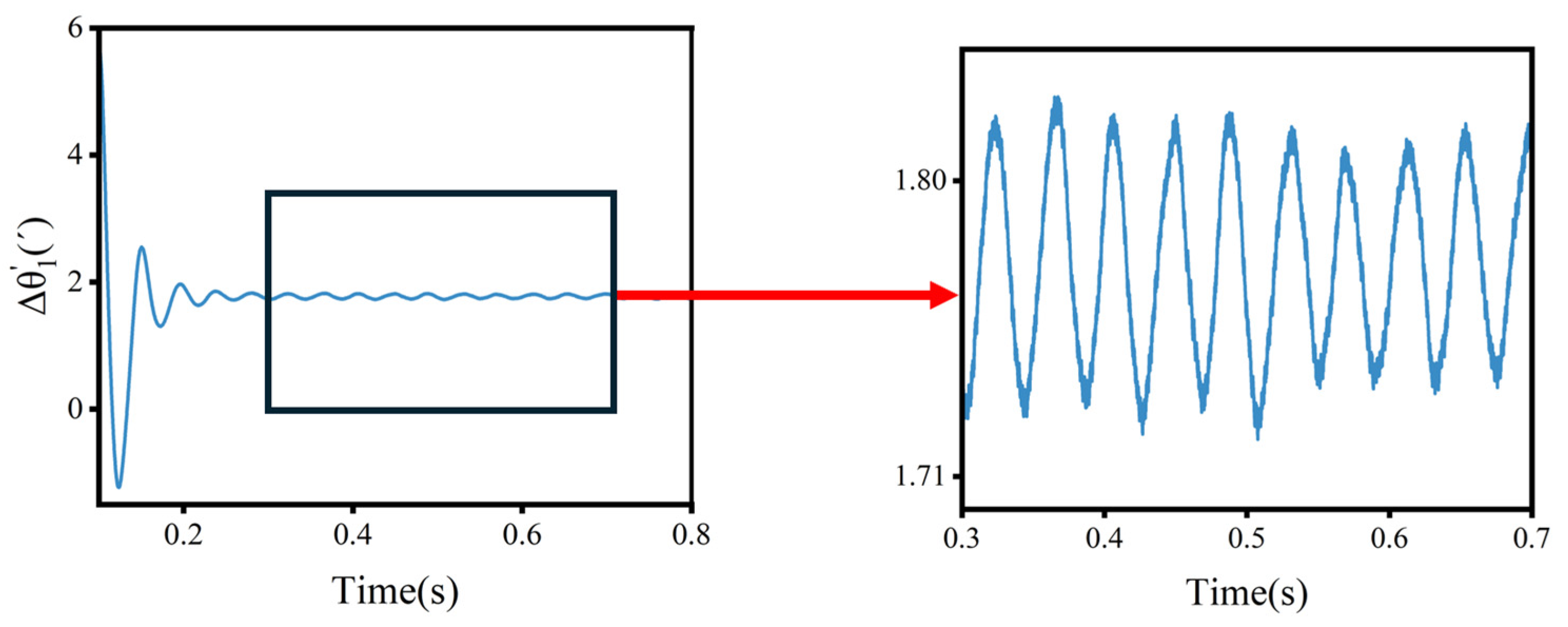
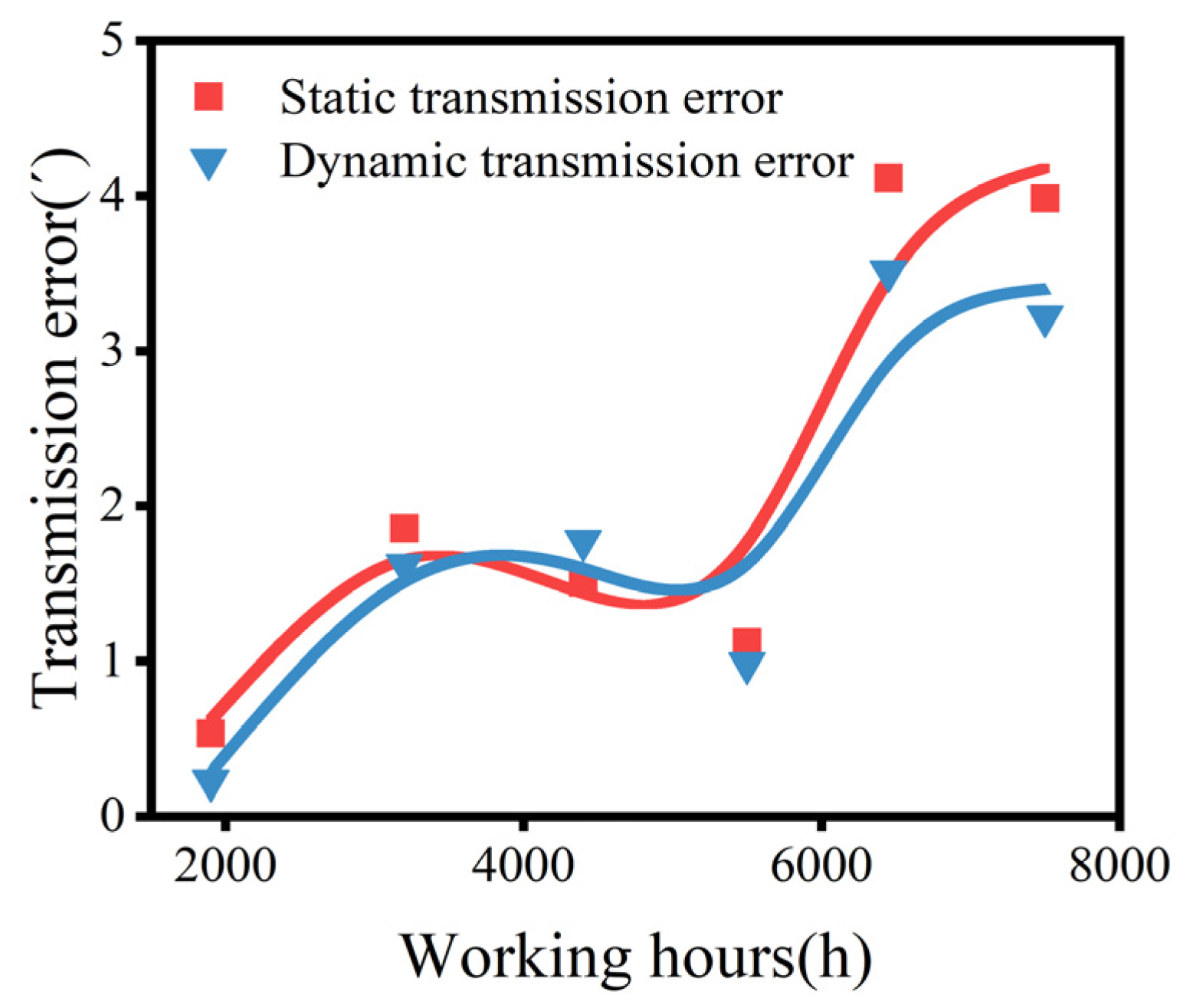
- The following fact reflects the impact of the output shaft’s load on the TE at the same volume of wear: the average value of the DTE is smaller than the STE, probably because the gap is compensated by the load. And the instability of the load leads to greater fluctuations in the DTE. The following fact also reflects the impact of the cycloid gear’s flexibility on the TE: considering the flexible deformation, both the average value and the fluctuation of the TE are larger.
- (2)
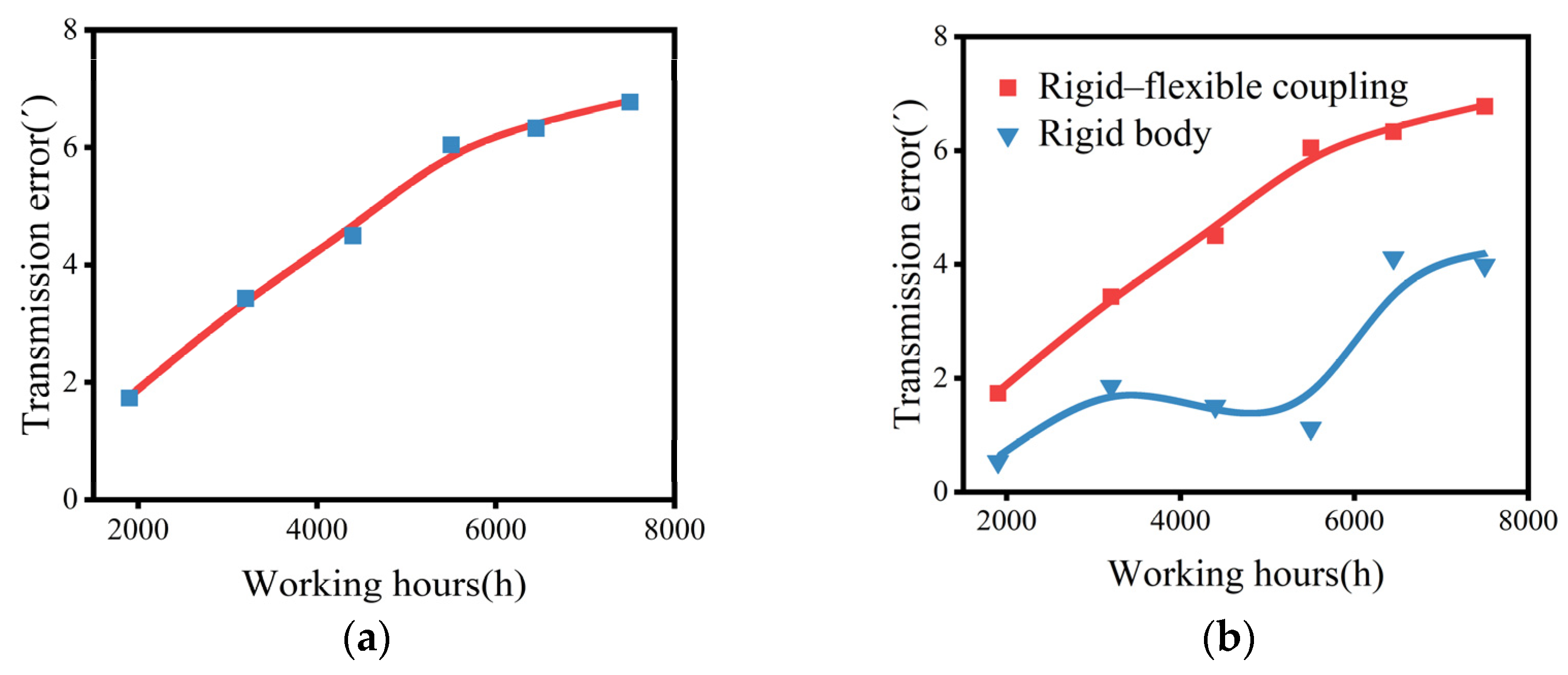
- The following fact reflects the impact of different wear volumes on the TE: for both the STE and DTE of the full rigid body model, the wear volume increases with the growth of working time. Initially, the TE increases, occasionally decreases, and eventually tends to increase. For the rigid–flexible-coupled model, the TE monotonically increases with the existing wear volumes, but the rate tends to slow down.
- (3)
- While rigid-body analysis can save computational efficiency, there are certain differences in the degradation trend and degradation quantity compared to the rigid–flexible coupling model. Considering the actual wear test trend of the RV reducer [40], it is recommended to use the rigid–flexible coupling model for analysis.
- (4)
- In actual engineering, these measures can be taken to reduce the impact of wear on transmission accuracy, such as optimizing the tooth design, regular inspection and the replenishment of lubricants, keeping clean, and so on. In the later period, it is important to monitor the transmission accuracy to ensure that the performance of the RV reducer meets the requirements for usage.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Fang, L.T. Generation and investigation of a new cycloid drive with double contact. Mech. Mach. Theory 2012, 49, 270–283. [Google Scholar]
- Jang, D.J.; Kim, Y.C.; Hong, E.P.; Kim, G.S. Geometry design and dynamic analysis of a modified cycloid reducer with epitrochoid tooth profile. Mech. Mach. Theory 2021, 164, 104399. [Google Scholar] [CrossRef]
- Li, W.; Hao, L.J. Study on the degradation law of harmonic gear drive backlash with wear and assembly errors. Eng. Fail. Anal. 2022, 140, 106614. [Google Scholar] [CrossRef]
- Lin, K.; Chan, K.; Lee, J. Kinematic error analysis and tolerance allocation of cycloidal gear reducers. Mech. Mach. Theory 2018, 124, 73–91. [Google Scholar] [CrossRef]
- Sensinger, J.W. Unified Approach to Cycloid Drive Profile, Stress, and Efficiency Optimization. J. Mech. Des. 2010, 132, 024503. [Google Scholar] [CrossRef]
- Xu, L.X.; Chen, B.K.; Li, C.Y. Dynamic modelling and contact analysis of bearing-cycloid-pinwheel transmission mechanisms used in joint rotate vector reducers. Mech. Mach. Theory 2019, 137, 432–458. [Google Scholar] [CrossRef]
- Pham, A.-D.; Ahn, H.-J. High Precision Reducers for Industrial Robots Driving 4th Industrial Revolution: State of Arts, Analysis, Design, Performance Evaluation and Perspective. Int. J. Precis. Eng. Manuf.-Green Technol. 2018, 5, 519–533. [Google Scholar] [CrossRef]
- Duan, T.; Wei, J.; Zhang, A.; Xu, Z.; Lim, T.C. Transmission error investigation of gearbox using rigid-flexible coupling dynamic model: Theoretical analysis and experiments. Mech. Mach. Theory 2021, 157, 104213. [Google Scholar] [CrossRef]
- Xu, L.X.; Zhong, J.L.; Li, Y.; Chang, L. Design and dynamic transmission error analysis of a new type of cycloidal-pin reducer with a rotatable output-pin mechanism. Mech. Mach. Theory 2023, 181, 105218. [Google Scholar] [CrossRef]
- He, W.D.; Shan, L.J. Research and Analysis on Transmission Error of RV Reducer Used in Robot. Recent Adv. Mech. Des. Robot. 2015, 33, 231–238. [Google Scholar]
- Xu, H.; Shi, Z.; Yu, B.; Wang, H. Optimal Measurement Speed and Its Determination Method in the Transmission Precision Evaluation of Precision Reducers. Appl. Sci. 2019, 9, 2146. [Google Scholar] [CrossRef]
- Li, T.; Tian, M.; Xu, H.; Deng, X.; An, X.; Su, J. Meshing contact analysis of cycloidal-pin gear in RV reducer considering the influence of manufacturing error. J. Braz. Soc. Mech. Sci. Eng. 2020, 42, 133. [Google Scholar] [CrossRef]
- Zhang, M.; Zhang, Z.; Xiong, J.; Chen, X. Accuracy Analysis of Complex Transmission System with Distributed Tooth Profile Errors. Machines 2024, 12, 459. [Google Scholar] [CrossRef]
- Han, L.; Guo, F. Global sensitivity analysis of transmission accuracy for RV-type cycloid-pin drive. J. Mech. Sci. Technol. 2016, 30, 1225–1231. [Google Scholar] [CrossRef]
- Jin, S.; Tong, X.; Wang, Y. Influencing Factors on Rotate Vector Reducer Dynamic Transmission Error. Int. J. Autom. Technol. 2019, 13, 545–556. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, Z.; He, W. Virtual prototype simulation and transmission error analysis for RV reducer. Appl. Mech. Mater. 2015, 789, 226–230. [Google Scholar] [CrossRef]
- Li, X.; Huang, J.; Ding, C.; Guo, R.; Niu, W. Dynamic modeling and analysis of an RV reducer considering tooth profile modifications and errors. Machines 2023, 11, 626. [Google Scholar] [CrossRef]
- Ren, Z.-Y.; Mao, S.-M.; Guo, W.-C.; Guo, Z. Tooth modification and dynamic performance of the cycloidal drive. Mech. Syst. Signal Process. 2017, 85, 857–866. [Google Scholar] [CrossRef]
- Jia, C.; Fang, Z.D.; Zhang, Y.Z. Topography of modified surfaces based on compensated conjugation for the minimization of transmission errors of cylindrical gears. Mech. Mach. Theory 2017, 116, 145–161. [Google Scholar] [CrossRef]
- Bruyere, J.; Velex, P.; Guilbert, B.; Houser, D. An analytical study on the combination of profile relief and lead crown minimizing transmission error in narrow-faced helical gears. Mech. Mach. Theory 2019, 136, 224–243. [Google Scholar] [CrossRef]
- Archard, J.F. Contact and Rubbing of Flat Surfaces. J. Appl. Phys. 1953, 24, 981–988. [Google Scholar] [CrossRef]
- Bajpai, P.; Kahraman, A.; Anderson, N.E. A Surface Wear Prediction Methodology for Parallel-Axis Gear Pairs. J. Tribol. 2004, 126, 597–605. [Google Scholar] [CrossRef]
- Shen, X.; Liu, Y.; Cao, L.; Chen, X. Numerical Simulation of Sliding Wear for Self-lubricating Spherical Plain Bearings. J. Mater. Res. Technol. 2012, 1, 8–12. [Google Scholar] [CrossRef][Green Version]
- Tunalioğlu, M.Ş.; Tuç, B. Theoretical and experimental investigation of wear in internal gears. Wear 2014, 309, 208–215. [Google Scholar] [CrossRef]
- Brandão, J.A.; Cerqueira, P.; Seabra, J.H.; Castro, M.J. Measurement of mean wear coefficient during gear tests under various operating conditions. Tribol. Int. 2016, 102, 61–69. [Google Scholar] [CrossRef]
- Mirparizi, M.; Fotuhi, A.R.; Shariyat, M. Nonlinear coupled thermoelastic analysis of thermal wave propagation in a functionally graded finite solid undergoing finite strain. J. Therm. Anal. Calorim. 2020, 139, 2309–2320. [Google Scholar] [CrossRef]
- Mirparizi, M.; Shariyat, M.; Fotuhi, A.R. A novel approach for generalized Green-Naghdi-type electro-magneto-thermo-hyperelasticity wave propagation and reflection investigations in near-incompressible layers under shock loads. J. Therm. Stress. 2024, 47, 743–765. [Google Scholar] [CrossRef]
- Zhang, R.H.; Zhou, J.X.; Wei, Z. Study on transmission error and torsional stiffness of RV reducer under wear. J. Mech. Sci. Technol. 2022, 36, 4067–4081. [Google Scholar] [CrossRef]
- Ishida, T.; Wang, H.; Hidaka, T.; Hashimoto, M. Rotational Transmission Error of K-H-V-Type Planetary Gears with Cycloid Gears: 2nd Report, Effects of Manufacturing and Assembly Errors on Rotational Transmission Error. Trans. Jpn. Soc. Mech. Eng. C 1994, 60, 3510–3517. [Google Scholar] [CrossRef]
- Wang, H.; Shi, Z.-Y.; Yu, B.; Xu, H. Transmission Performance Analysis of RV Reducers Influenced by Profile Modification and Load. Appl. Sci. 2019, 9, 4099. [Google Scholar] [CrossRef]
- Lu, L.S.; Zhang, F.X.; Tang, H.; Wan, Z.; Tang, Y. Equidistant & Radial-moving Modifications of Cycloidal Gear Tooth Profiles Used in RV Reducer Based on Optimized Carrying Capacity. China Mech. Eng. 2019, 30, 2022–2029. [Google Scholar]
- Su, J.X.; Li, C. Numerical Calculation and Analysis of Cycloidal Gear Wear Amount of RV Reducer. J. Mech. Transm. 2021, 45, 41–45+57. [Google Scholar]
- Zhang, J. Quasi-static-model-based wear analysis of spur gears. J. Mech. Eng. 2017, 53, 136–145. [Google Scholar] [CrossRef]
- Flodin, A.; Andersson, S. Simulation of mild wear in spur gears. Wear 1997, 207, 16–23. [Google Scholar] [CrossRef]
- Shen, Z.; Qiao, B.; Yang, L.; Luo, W.; Chen, X. Evaluating the influence of tooth surface wear on TVMS of planetary gear set. Mech. Mach. Theory 2019, 136, 206–223. [Google Scholar] [CrossRef]
- Ding, H.; Kahraman, A. Interactions between nonlinear spur gear dynamics and surface wear. J. Sound Vib. 2007, 307, 662–679. [Google Scholar] [CrossRef]
- Liang, S.F.; Deng, X.Z.; Li, T.X.; Wang, C.; Yang, J. Tooth contact analysis of cycloidal pinwheel drive in RV reducer of robot. J. Mech. Transm. 2017, 41, 17–22. [Google Scholar]
- Ambaye, G.A.; Lemu, H.G. Dynamic analysis of spur gear with backlash using ADAMS. Mater. Today Proc. 2021, 38, 2959–2967. [Google Scholar] [CrossRef]
- Cheng, M.; Qiu, C.; Li, J.F.; Zhang, J.; Zhang, W.; Feng, N.; Shi, X. Development and research of fatigue life testing device for robot reducer. J. Mech. Transm. 2019, 43, 156–160. [Google Scholar]
- Li, J.F.; Yang, Y.K.; Wang, X.F.; Yao, L.; Xiao, J. Reliability evaluation of RV reducers based on multi degenerate data. J. Mech. Transm. 2023, 47, 82–87. [Google Scholar]








| Parameters | Value |
|---|---|
| Number of cycloid gear teeth | 39 |
| Pin number | 40 |
| Eccentricity (mm) | 1.3 |
| Pin radius (mm) | 3 |
| Radius of center circle (mm) | 64 |
| Degree of overlap | 1.3 |
| Transmission ratio | 81 |
| Radius of planetary gear indexing circle (mm) | 27 |
| Pressure angle (°) | 30 |
| Cycloid gear tooth width (mm) | 8.75 |
| Rated output torque (Nm) | 412 |
| Input speed (r/min) | 1500 |
| Components | Material | Modulus of Elasticity/MPa | Poisson’s Ratio | Density/106 (kg/mm3) |
|---|---|---|---|---|
| Cycloid gear | GCr15 | 219,000 | 0.3 | 7.83 |
| Output shaft | CrMnTi20 | 212,000 | 0.289 | 7.86 |
| Crankshaft | GCr15 | 219,000 | 0.3 | 7.83 |
| Pinwheel housing | QT450 | 169,000 | 0.257 | 7.06 |
| Pinwheel | GCr15 | 219,000 | 0.3 | 7.83 |
| Number | Components | Constraints | |
|---|---|---|---|
| 1 | Pin wheel housing | Ground | Fixed |
| 2 | Rigid disk | Output shaft | Fixed |
| 3 | Planetary gear1 | Crankshaft1 | Fixed |
| 4 | Planetary gear2 | Crankshaft2 | Fixed |
| 5 | Input shaft | Ground | Revolution |
| 6 | Input shaft | Rigid disk | Revolution |
| 7 | Planetary gear1 | Rigid disk | Revolution |
| 8 | Planetary gear2 | Rigid disk | Revolution |
| 9 | Crankshaft1 | Cycloid gear1 | Revolution |
| 10 | Crankshaft1 | Cycloid gear2 | Revolution |
| 11 | Crankshaft2 | Cycloid gear1 | Revolution |
| 12 | Crankshaft2 | Cycloid gear2 | Revolution |
| 13 | Pinwheel | Pin wheel housing | Revolution |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tao, Y.; Liu, H.; Wu, M.; Zheng, N.; Pei, J. The Effect of Cycloid Gear Wear on the Transmission Accuracy of the RV Reducer. Machines 2024, 12, 511. https://doi.org/10.3390/machines12080511
Tao Y, Liu H, Wu M, Zheng N, Pei J. The Effect of Cycloid Gear Wear on the Transmission Accuracy of the RV Reducer. Machines. 2024; 12(8):511. https://doi.org/10.3390/machines12080511
Chicago/Turabian StyleTao, Yourui, Huishan Liu, Miaojie Wu, Nanxian Zheng, and Jiaxing Pei. 2024. "The Effect of Cycloid Gear Wear on the Transmission Accuracy of the RV Reducer" Machines 12, no. 8: 511. https://doi.org/10.3390/machines12080511
APA StyleTao, Y., Liu, H., Wu, M., Zheng, N., & Pei, J. (2024). The Effect of Cycloid Gear Wear on the Transmission Accuracy of the RV Reducer. Machines, 12(8), 511. https://doi.org/10.3390/machines12080511







