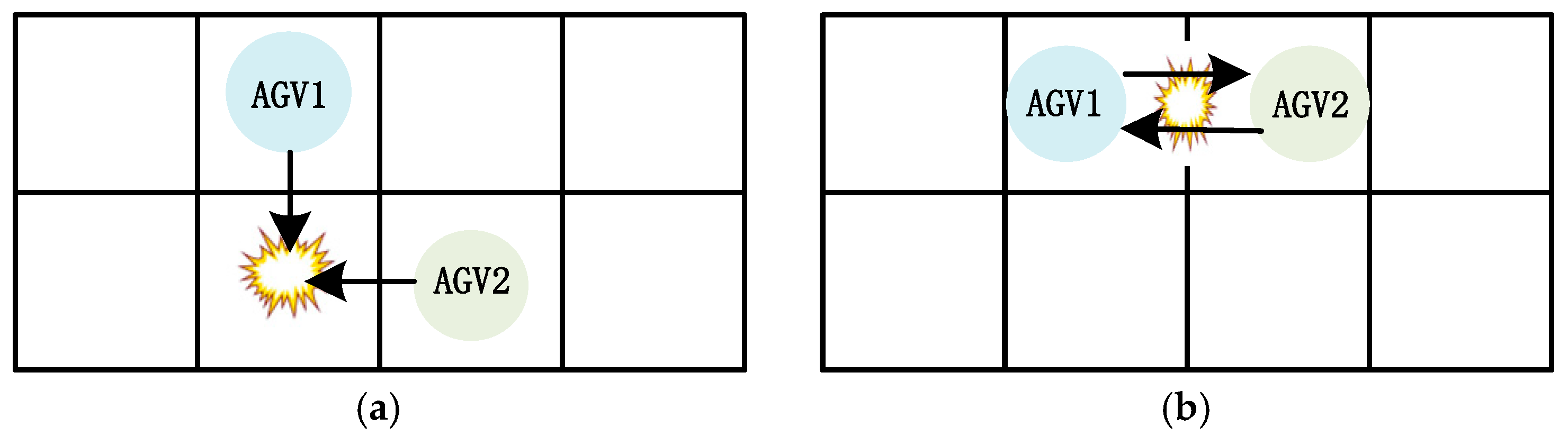
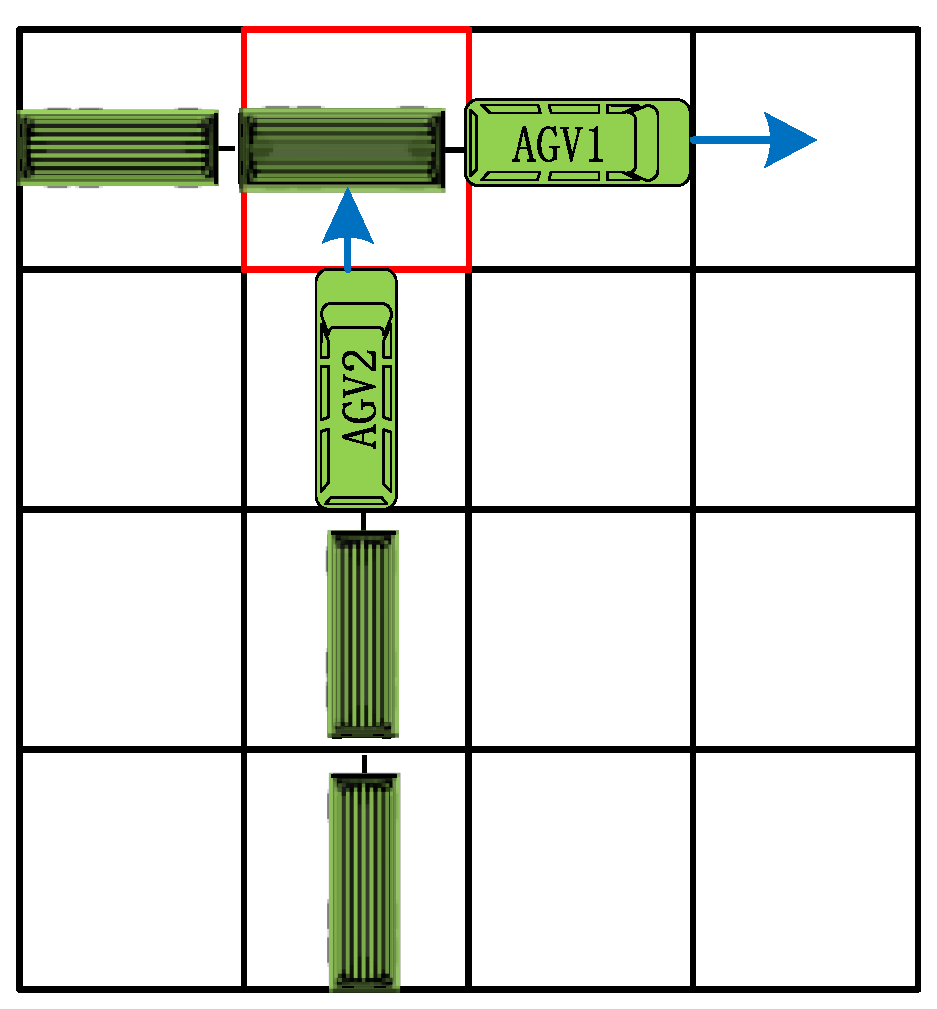
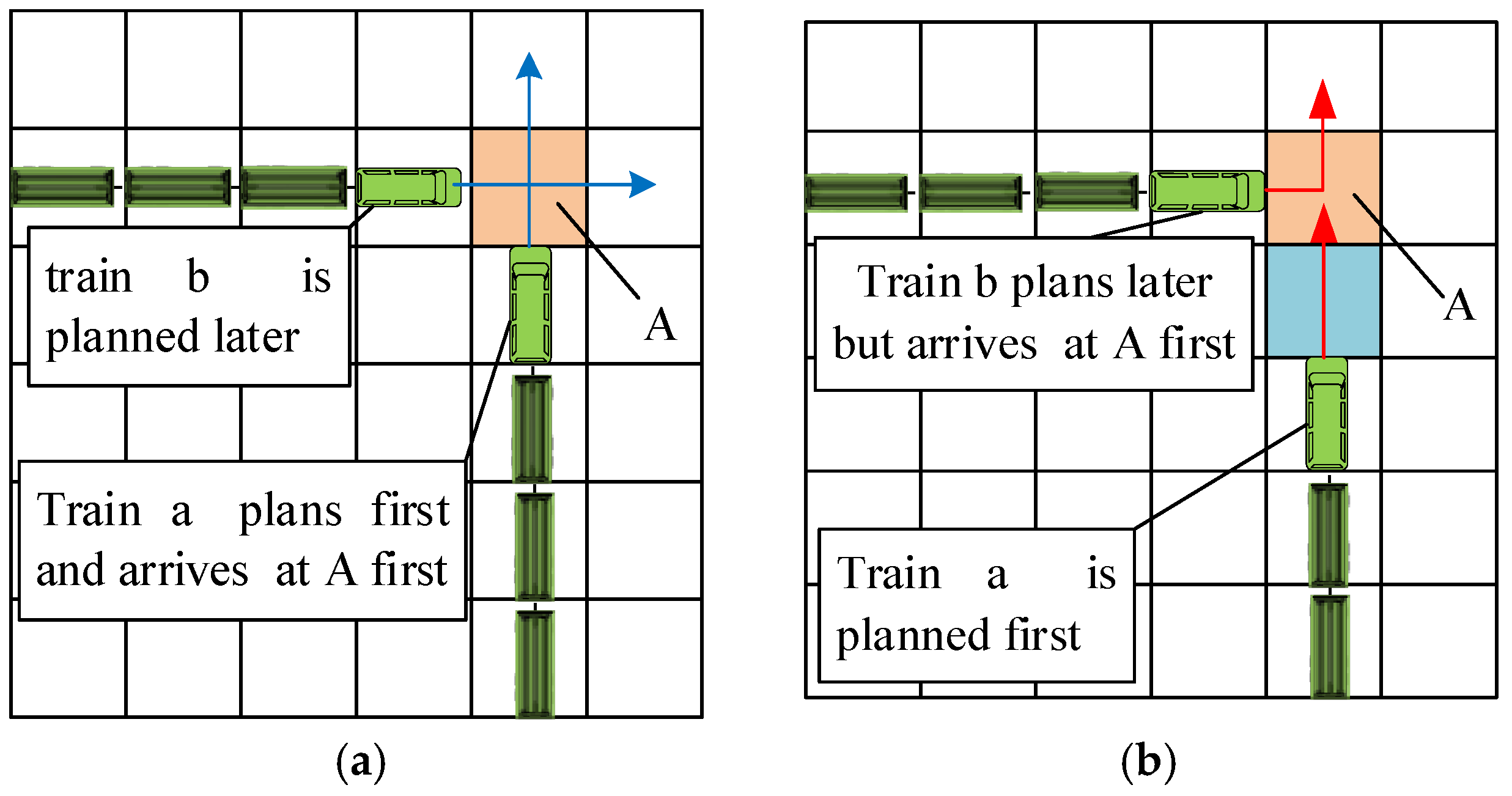
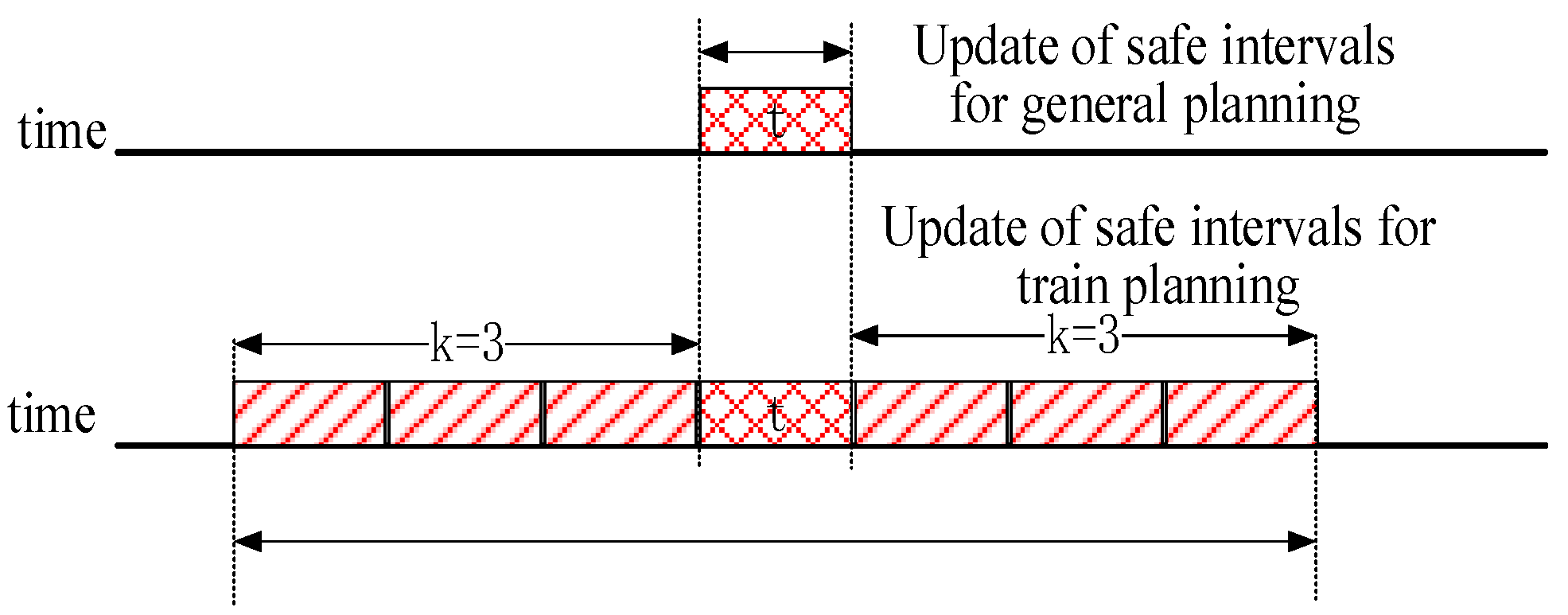
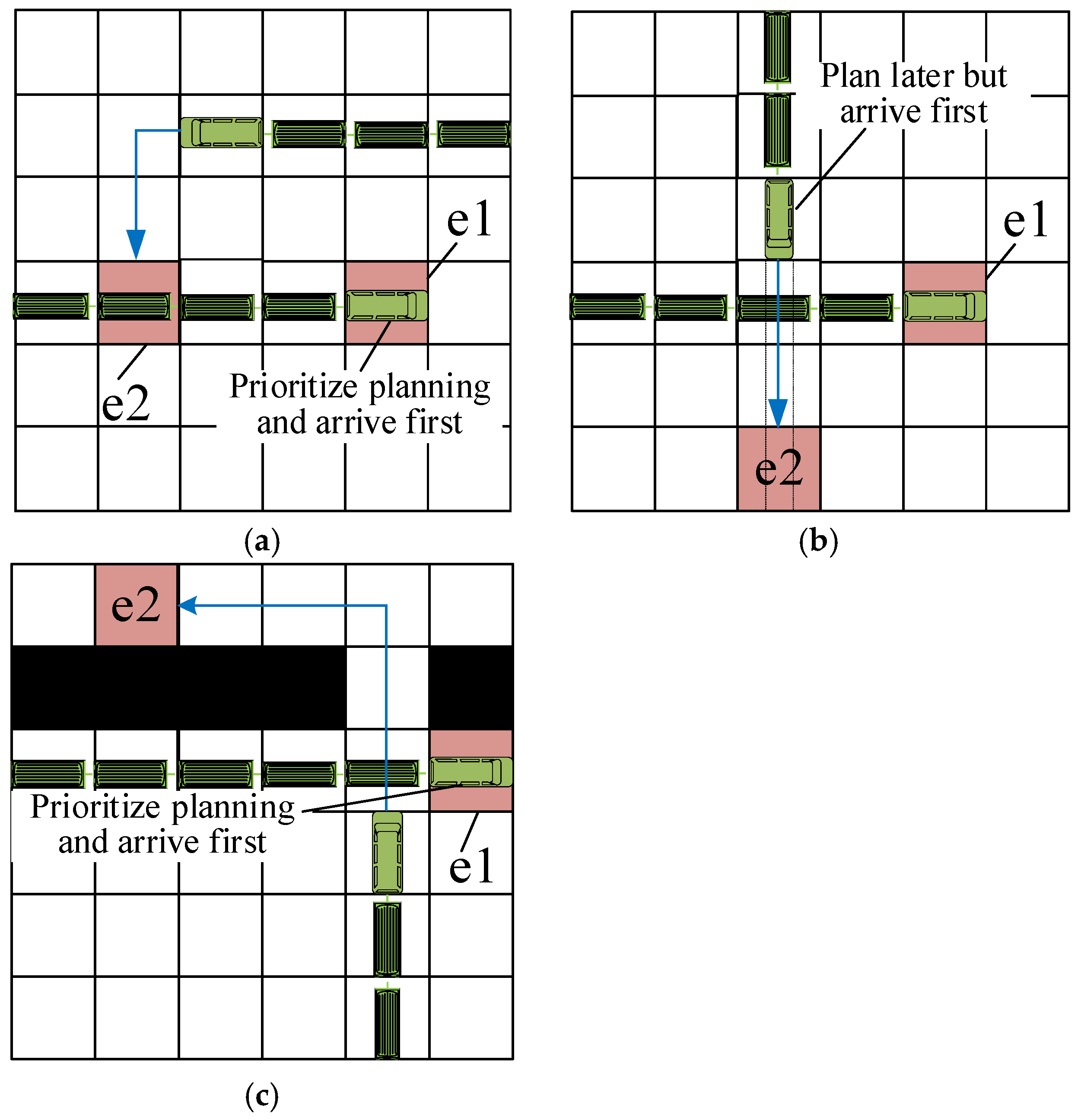
1. Introduction
Intelligent robots are increasingly being applied in smart environments and are capable of autonomously or semi-autonomously performing diverse tasks through instruction reception and execution. Particularly in scenarios necessitating that multiple robots cooperatively reach different target locations for task execution, such as in logistics [
1,
2], agriculture [
3], and factory handling [
4,
5], the technology of Multi-Agent Path Finding (MAPF) [
6] becomes pivotal. This technology aims to devise optimal and collision-free paths from starting points to target points for each robot while ensuring safety during the movement process.
In pursuit of this objective, researchers have extensively explored the field of MAPF [
7,
8,
9], introducing a variety of planning algorithms [
10,
11,
12] tailored to diverse path planning needs. Among these, Sharon et al. [
13] proposed the Conflict-Based Search (CBS) algorithm, which has made significant strides in achieving optimal and comprehensive solutions for MAPF. CBS utilizes a conflict constraint tree to expand nodes, detecting conflicts and imposing constraints based on optimal single-agent path planning. It subsequently replans conflicting robots within existing constraints until conflict-free paths are established. In order to further enhance the efficiency of the CBS algorithm, Boyarski et al. [
14] improved strategies for conflict priority and meta-agents, which effectively reduced the number of conflicting nodes. Additionally, Ariel et al. [
15] optimized the node expansion process within the CBS algorithm by introducing the Add Heuristics to Conflict-Based Search (CBSH) algorithm. By integrating heuristics as reference metrics for node selection during high-level node expansions, CBSH effectively reduces the number of expanded nodes, thereby accelerating the solving process. Building on the CBSH algorithm, Li et al. [
16] addressed the issue of long processing times for handling rectangle conflicts. By introducing different methods to infer and add rectangle conflict constraints, Li effectively reduced invalid or redundant node expansions, thereby further improving the solving efficiency of the CBSH algorithm.
Taking into account potential delays encountered by robots during actual movement, Dor et al. [
17] introduced the k-Robust Conflict-Based Search (kR-CBS) algorithm. This algorithm allocates a safety margin of time steps for each path node during planning, ensuring robots can safely execute tasks even when delays in time steps occur. This proactive approach effectively mitigates potential collision risks. To tackle the challenge of exploring large path node spaces in coupled algorithms for multi-agent planning, Phillips et al. [
18] introduced the Safe Interval Path Planning (SIPP) algorithm. This method prioritizes sequential planning of multiple robots based on their respective priorities. As robots complete their planning, they dynamically update safe intervals on the map grid, guiding subsequent robots in selecting path nodes. This decoupled and priority-driven approach ensures conflict-free paths once all robots have finalized their plans, significantly enhancing overall solving efficiency. However, Yakovlev et al. [
19] identified a limitation in the SIPP algorithm during node expansion, where each grid node permits passage for only one robot at a time, potentially resulting in scenarios where solutions are not achievable. Therefore, he introduced a Weighted Safe Interval Path Planning algorithm that maintains optimal and suboptimal nodes during path node expansion. If the optimal node path cannot be expanded further, the algorithm leverages suboptimal nodes to improve solution success rate and adaptability.
The MAPF algorithms mentioned above demonstrate adaptability for traditional robots that occupy a single grid node. However, they are not applicable to path planning problems for chain robots [
20], such as trains and serpent robots, which occupy multiple grid nodes. Chain robots, compared to traditional robot transport methods [
21,
22], offer greater flexibility by integrating multiple transport units to carry large quantities of goods. Additionally, their transport mechanism is highly efficient and energy-saving, requiring only the head unit as a power source to pull an entire train-like assembly of carriages, aligning with principles of green sustainable development. Currently, chain robots show broad application prospects across various fields, including efficient baggage handling at airports, flexible product transport in factory production lines, and convenient flower transport in greenhouse environments. For the path planning problem of chain robots, Lin et al. [
23] proposed an innovative multi-train scheduling algorithm based on simulated annealing, capable of delivering high-quality solutions within a limited timeframe. Svancara et al. [
24] introduced a novel constraint-based scheduling model for the MAPF problem, emphasizing optional activities. He et al. [
25] developed a dynamic train trajectory planning method that integrates model predictive control and multi-swarm particle swarm optimization, effectively reducing energy consumption. Zhang et al. [
26] presented a multi-objective integer nonlinear programming model aimed at minimizing passenger travel time and optimizing average train load utilization. Arsalani et al. [
27] addressed the train formation and transportation path optimization problem with a mixed-integer linear programming model, providing satisfactory solutions within a reasonable time frame. Dor et al. [
28] defined the Multi-Train Path Finding (MTPF) problem and introduced the Multi-Train Conflict-Based Search (MT-CBS) algorithm. Building on the MT-CBS algorithm, Chen et al. [
29] proposed enhanced versions including MT-ICBS, MT-CBSH, and MT-CBSH-RM, offering more comprehensive solutions for the path planning of chain robots. However, CBS-based algorithms inherently rely on node search and splitting mechanisms, which present limitations for large-scale MTPF problems. In contrast, the Safe Interval Path Planning (SIPP) algorithm utilizes safe intervals as the foundational planning element, allowing for the simultaneous detection and adjustment of multiple consecutive time steps, thereby ensuring higher search efficiency. While the MT-CBS [
28] algorithm is a recognized approach to solving MTPF problems, there is a notable gap in research on leveraging the principles of the SIPP algorithm to address these issues.
Our work aims to bridge a significant gap by substantially reducing the pathfinding complexity for chain robots, thus enhancing the success rate in solving large-scale multi-train pathfinding problems. By leveraging the principles of Safe Interval Search Algorithms, we developed a novel planning strategy called the Multi-Train Safe Interval Path Planning (MT-SIPP) algorithm, designed to efficiently address the path planning challenges that come with multiple chain robots. We introduce a new path planning framework for multi-chain robots based on the concept of safe intervals. Within this framework, conflicts are classified into train movement conflicts, waiting conflicts, and station conflicts. To resolve these conflicts, we employ robust methods for train movement conflicts, adjust the occupancy time steps for waiting conflicts, and manage station conflicts through grid checks and the addition of node constraints. To validate our approach, we conducted extensive simulations on benchmark maps of varying scales. Additionally, we visualized the planning solutions for specific instances to demonstrate the effectiveness of the proposed method.
The structure of this paper is organized as follows:
Section 2 provides an introduction to the MAPF and MTPF problems.
Section 3 elaborates on the concept of safe intervals.
Section 4 presents the k-robust planning method.
Section 5 offers a detailed description of our proposed method for resolving multi-type conflicts.
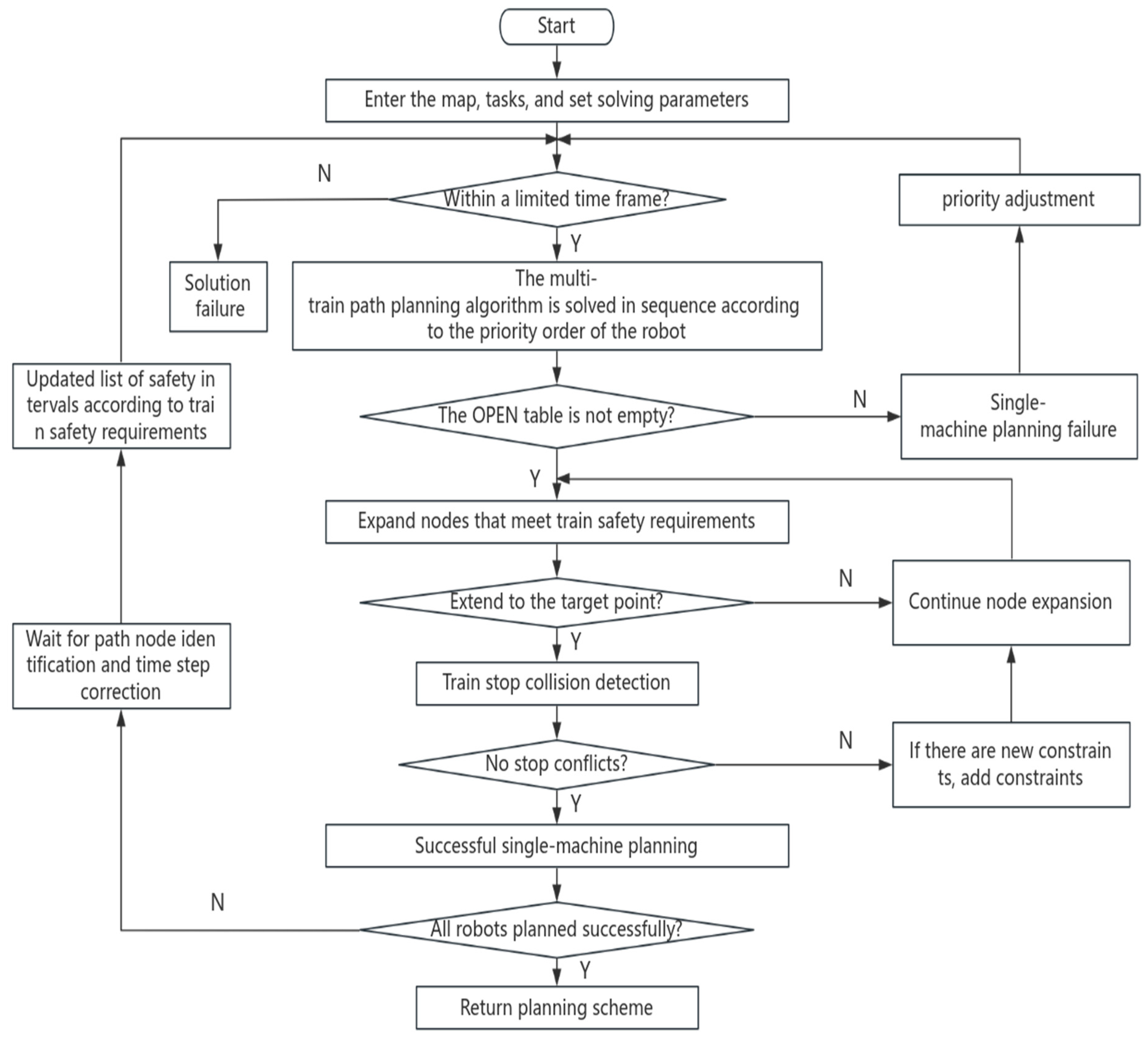
Section 6 outlines the algorithmic workflow.
Section 7 discusses the simulations conducted on three types of benchmark maps.
Section 8 concludes this study.
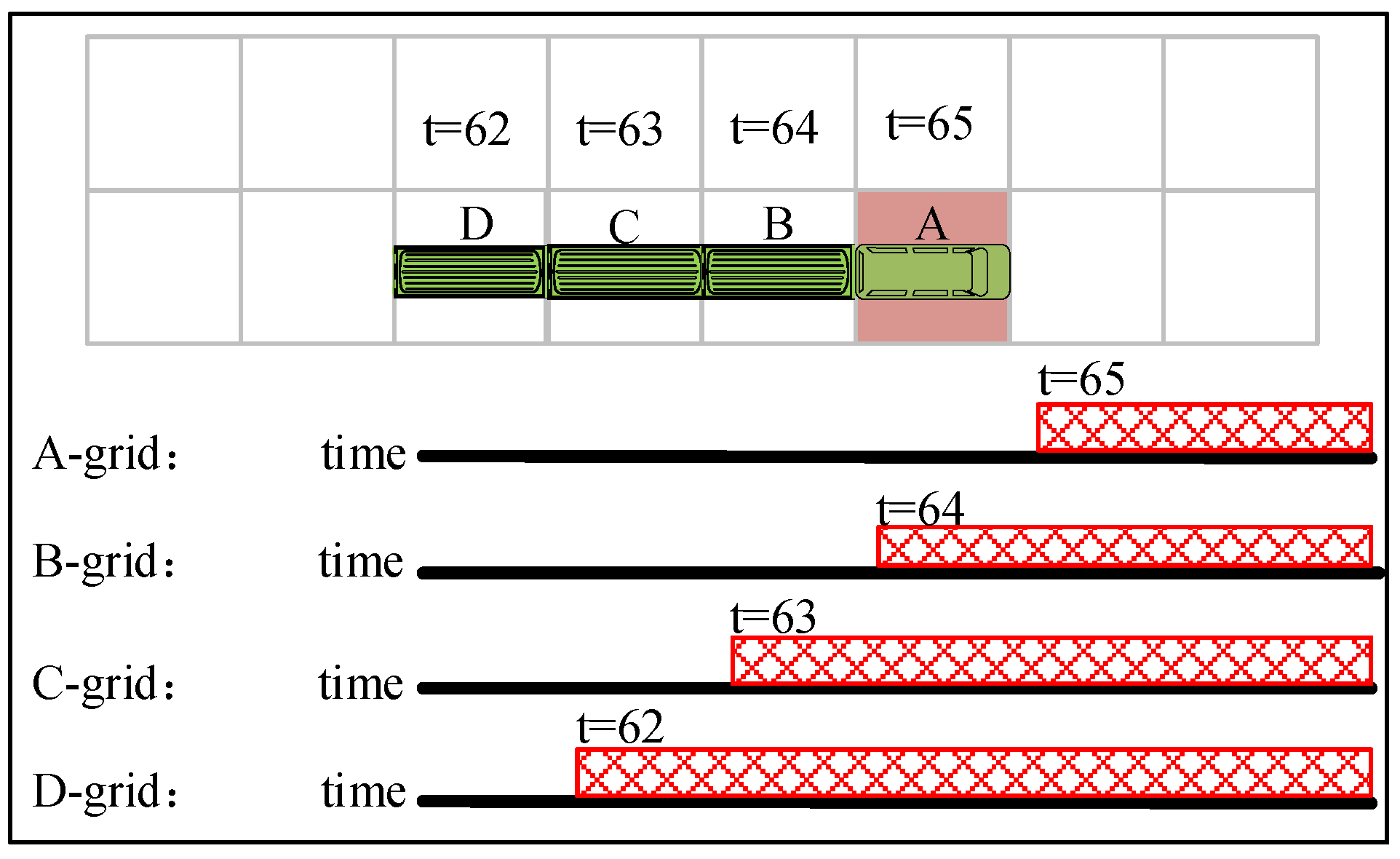
4. K-Robust Planning Methods
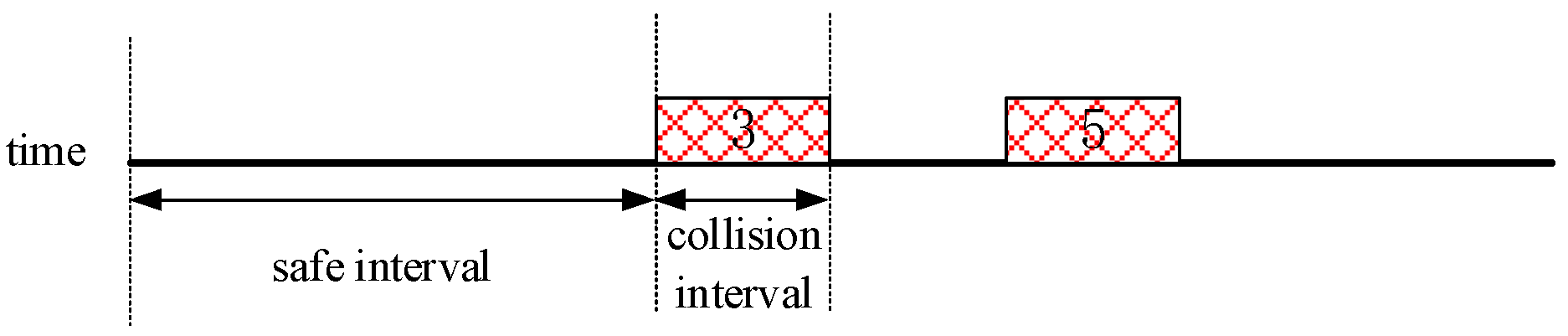
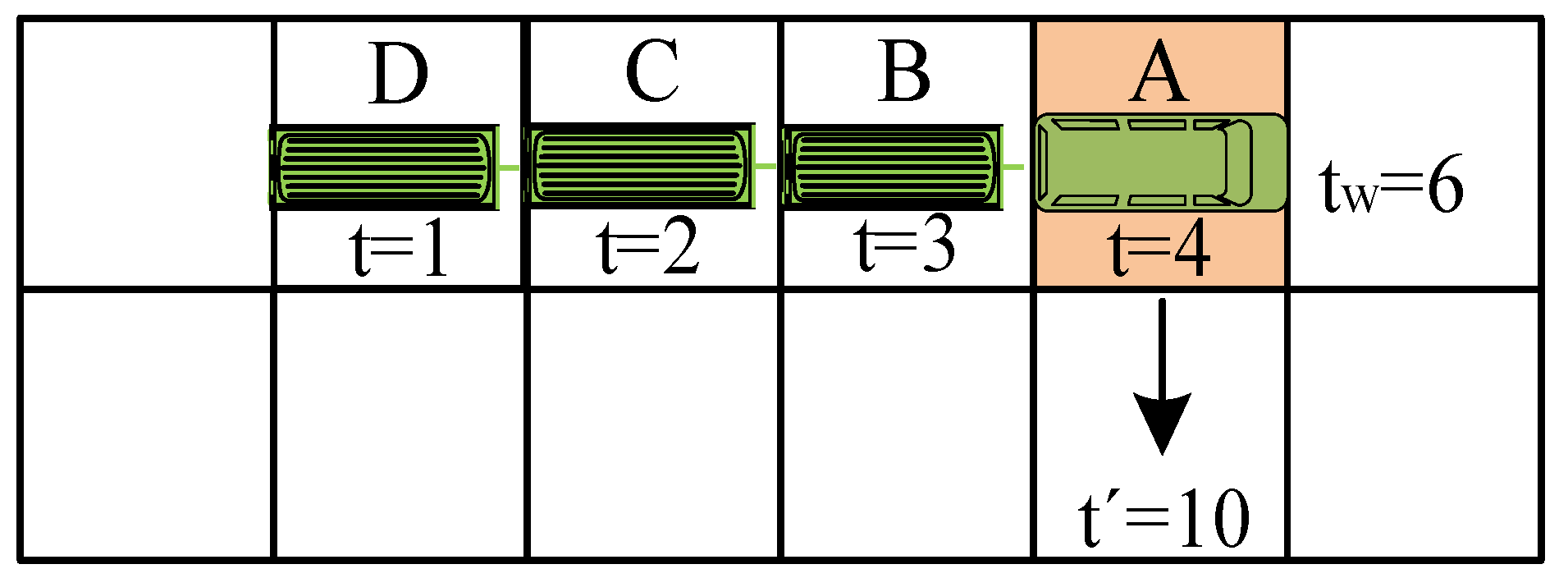
As referenced in [
17], to mitigate potential delays encountered by robots during path execution, an effective strategy involves preemptively accounting for delay factors during the planning stage and assigning suitable safety buffers for each robot. This measure significantly enhances the robustness of multi-robot path planning, enabling it to withstand delays to a certain extent. In practical implementation, since most multi-robot path planning algorithms expand nodes based on integer time steps,
K-robust planning algorithms typically simplify computations by setting
as an integer value. For instance, in
Figure 4, if Robot 1 is allocated a safety buffer of 1 time step during the planning phase (i.e.,
)), and Robot 1 passes through a grid at time step 3 while Robot 2 passes through the same grid at time step 5, the safe interval for grid A would accordingly update to
. This updating strategy ensures that robots can traverse grids safely and sequentially according to their planned paths, even in the presence of potential delays.
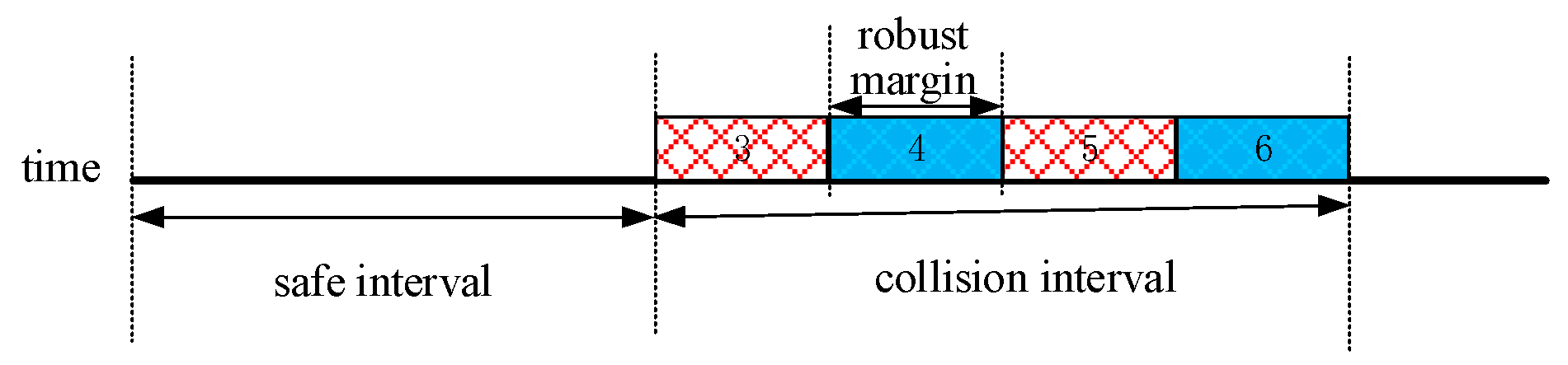
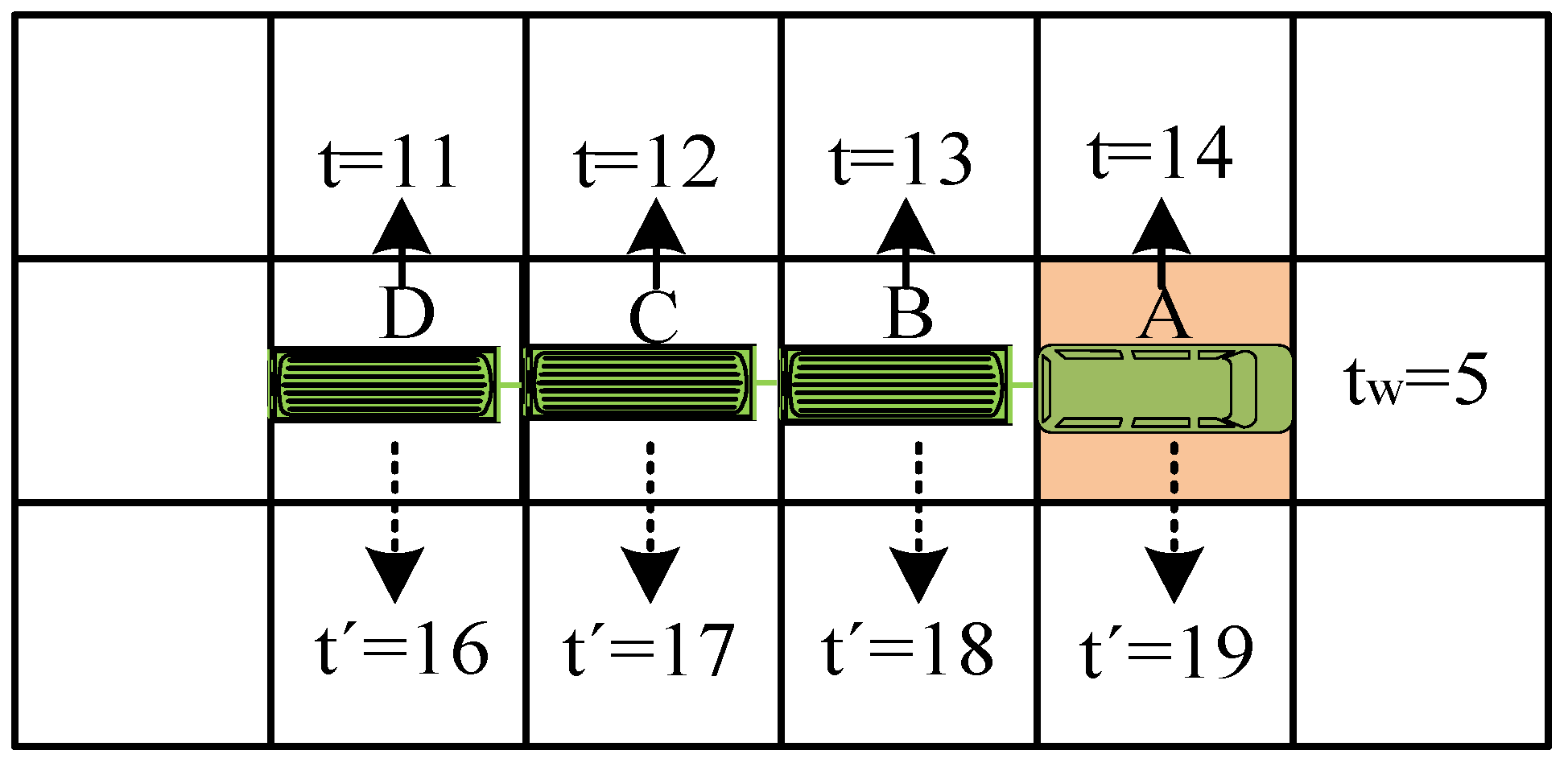
Upon comparing
Figure 3 and
Figure 4, we can clearly discern the practical application effects of the
-robust planning algorithm. This algorithm effectively extends the time duration that a robot occupies a grid from a single time step to
+ 1 time steps. Therefore, if Robot 1 or Robot 2 encounters a delay of up to
time steps upon leaving grid A, they may potentially remain on grid A during these
time steps. To mitigate this scenario, the
-robust planning algorithm assigns a safety buffer of
time steps for these robots. This approach treats the subsequent
time steps as collision intervals during planning, effectively preventing other robots from passing through grid A within
time steps. Such a strategy ensures that Robot 1 and Robot 2 can safely execute their path planning even in the presence of delays, thus minimizing potential collisions and conflicts.
7. Experimental Analysis
This paper compares five multi-train path planning algorithms, MT-CBS, MT-ICBS, MT-CBSH, MT-CBSH-RM [
29], and MT-SIPP, on three benchmark map environments [
6] (blank-empty-48-48, random-random-32-32-20, and room-room-32-32-4) for a performance evaluation. MT-CBS, MT-ICBS, MT-CBSH, and MT-CBSH-RM are based on the basic CBS (Conflict-Based Search) algorithm, the modified CBS algorithm, the CBS algorithm with heuristics, and the CBS algorithm combining the heuristics and MDD (Manhattan Distance on a Grid) for rectangular conflict reasoning is implemented in the CBS algorithm. In the experiments, the number of trains
was systematically increased, with 25 instances tested for each train count. In tables, algorithms with notably shorter average runtime under identical conditions are highlighted in bold. “-” marks denote instances where the compared algorithms failed to produce solutions under the corresponding conditions, enhancing the visual comparison of algorithm performance across different scenarios.
Our experimental setup consisted of a Windows 10 operating system, a 2.3 GHz processor, and 8 GB of memory. The algorithms MT-CBS, MT-ICBS, MT-CBSH, and MT-CBSH-RM were implemented in C++, while the MT-SIPP algorithm was implemented in Python. Each algorithm was restricted to solving individual instances within a 2 min time frame. Instances failing to provide a valid solution within this limit were categorized as unsuccessful.
7.1. Testing in a Blank Map Environment
The blank map environment is distinguished by a prominent feature: the entire map space consists of obstacle-free open areas. This environment provides optimal conditions for the unrestricted movement and efficient interaction of multiple robots. As depicted in
Figure 12, this study selected this typical blank map environment, sized 48 × 48, for evaluating algorithm performance.
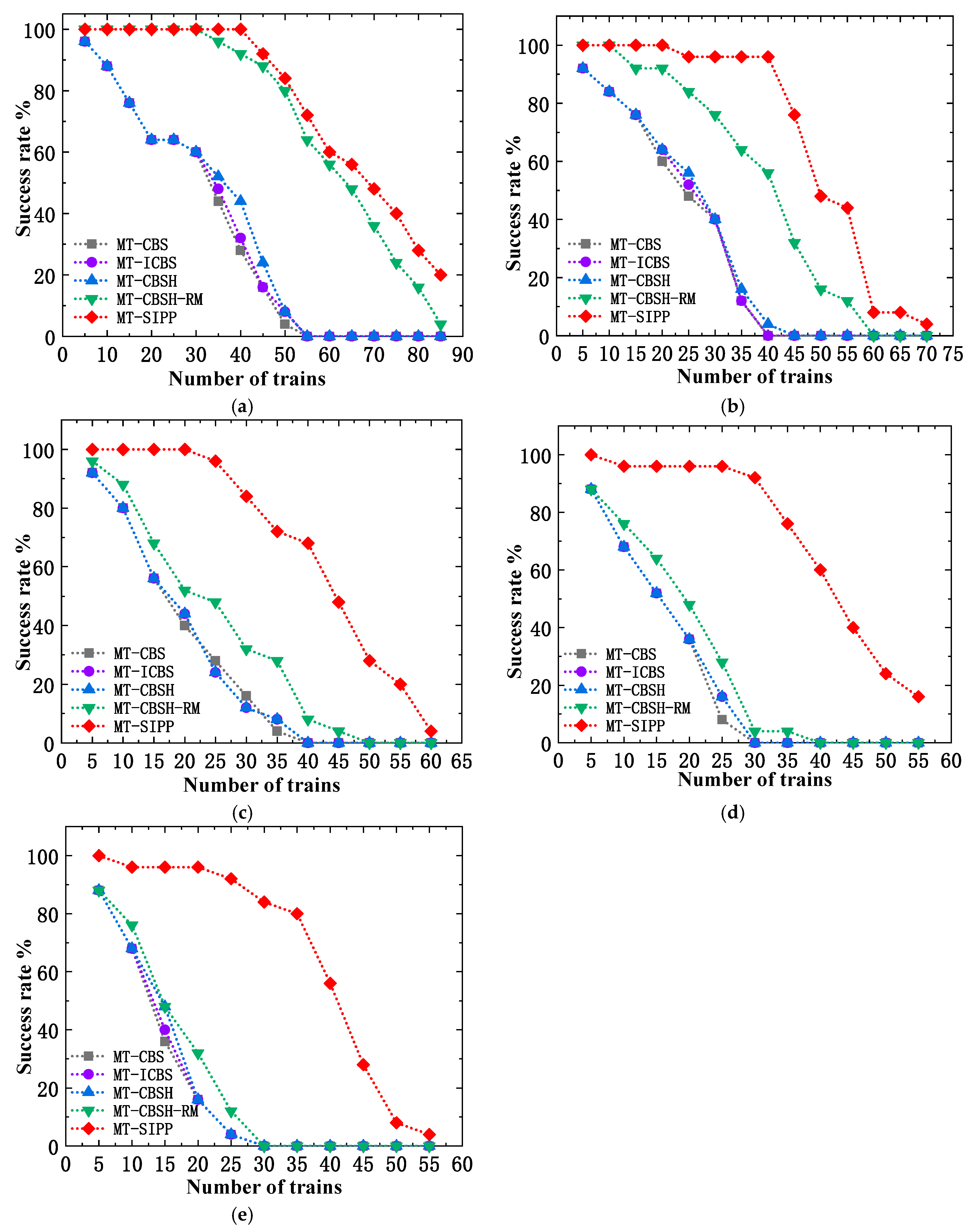
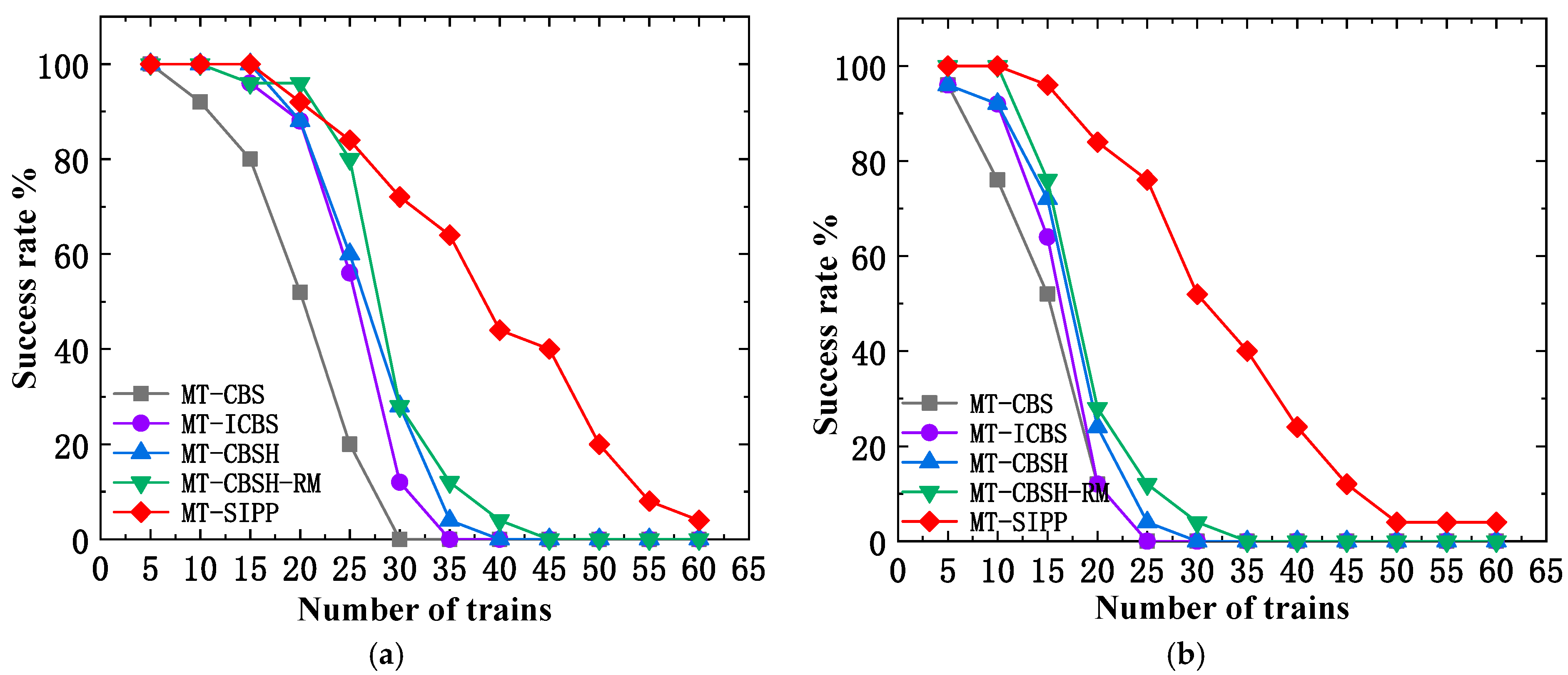
Figure 13 visually illustrates the comparative results of MT-CBS, MT-ICBS, MT-CBSH, MT-CBSH-RM, and MT-SIPP algorithms in terms of their success rates in solving problems within the blank map environment. This comparison offers a clear insight into the performance disparities among the algorithms under these specific environmental conditions.
Based on the success rate comparison depicted in
Figure 13, it is evident that among the five multi-train path planning algorithms MT-CBS, MT-ICBS, MT-CBSH, MT-CBSH-RM, and the proposed MT-SIPP algorithm consistently exhibit the highest success rates in the empty map environment. Of particular note is that although the MT-CBSH-RM algorithm, a prominent CBS-type algorithm, shows comparable success rates to the MT-SIPP algorithm when the value of
(train body length) is small, the superiority of the MT-SIPP algorithm becomes more pronounced as
increases. Detailed statistical analysis reveals that at
, the MT-SIPP algorithm exhibited average success rate improvements of 44.7%, 44%, 42.6%, and 5.6% compared to the other four algorithms. At
, these enhancements were 40%, 38%, 39%, and 17%. At
, the improvements were consistently 42%, 42%, 42%, and 33%. Notably, at
, the algorithm achieved substantial improvements of 49.1%, 48.4%, 48.4%, and 43.6%, while at
, the figures were 48%, 47.6%, 46.9%, and 44%. These findings underscore a significant performance advantage of the MT-SIPP algorithm over CBS-like multi-agent pathfinding algorithms in achieving higher success rates, with an average improvement nearing 40% in blank map environments. Furthermore, regarding the scalability in handling multiple train instances, particularly at larger
values (e.g.,
), MT-SIPP demonstrated superior capability, effectively managing nearly twice the maximum train instances compared to alternative algorithms.
In our statistical analysis of algorithm runtime (as shown in
Table 1), we compared the MT-CBSH-RM algorithm, known for its superior efficiency in CBS-like multi-train planning algorithms, with the MT-SIPP algorithm. In a blank map environment, MT-CBSH-RM demonstrates better algorithmic runtime efficiency than MT-SIPP when
(train length) is small or when solving a small number of trains. However, as the number of trains or
increases, CBS-like multi-train planning algorithms experience a rapid expansion of their solution space, resulting in a gradual decline in efficiency. This efficiency gap becomes more pronounced with increasing problem complexity.
The aforementioned results indicate that in a blank map environment, CBS-like multi-train planning algorithms, particularly the MT-CBSH-RM algorithm, excel in both success rate and runtime efficiency when values are small and the number of trains is limited. This is largely attributed to the expansive layout of the map, which allows ample maneuvering space for trains. However, as the number of trains increases or values grow larger, the available maneuvering space for trains gradually diminishes, leading to a significant decrease in the solving efficiency of CBS-like algorithms. In contrast, under these circumstances, the MT-SIPP algorithm consistently maintains higher solving efficiency, demonstrating its superior performance in handling complex multi-train pathfinding problems.
7.2. Random Map Environment Testing
In a random map environment, the distribution of obstacles is stochastic, leading to dispersed and variably-sized passable areas for trains. This variability undoubtedly presents considerable challenges for multi-train planning on such maps. As depicted in
Figure 14, this study utilized a representative random map measuring 32 × 32 for testing purposes. To thoroughly evaluate the performance of diverse algorithms in this setting, comprehensive testing was conducted, and the findings are consolidated in
Figure 15 and
Table 2.
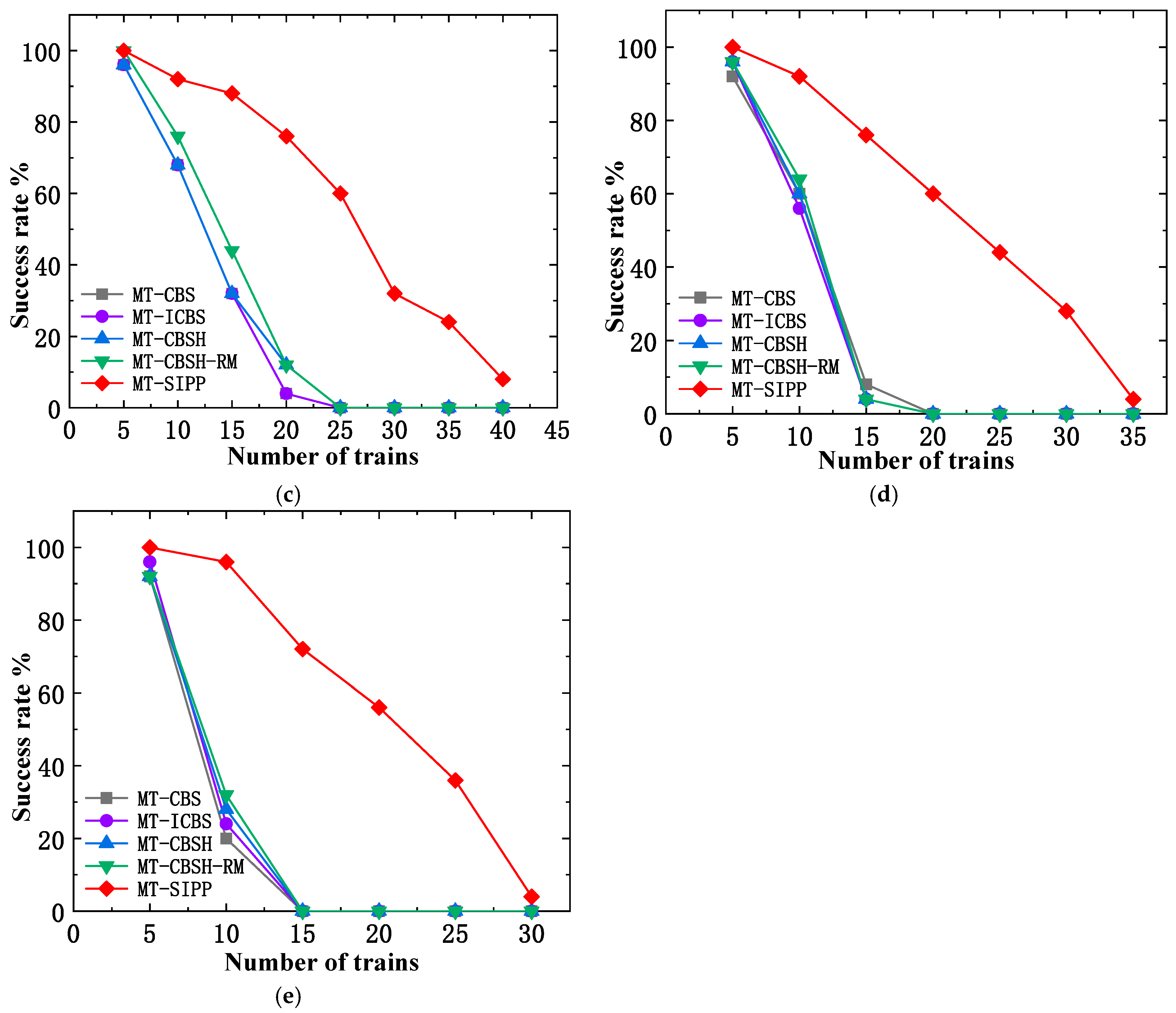
Based on the comparative results of success rates depicted in
Figure 15, it is evident that in random map environments, the high coverage of obstacles leads to an increasing number of conflicts among trains as the number of trains to be solved increases. This diminishes the available maneuvering space and gradually lowers the success rates of all algorithms. Furthermore, as the value of
(train car length) increases, the number of empty grids occupied by trains and their occupation duration also increase, thereby reducing the maximum feasible number of trains that can be effectively managed by several multi-train planning algorithms. Nevertheless, it is worth noting that across various
values, the MT-SIPP algorithm consistently achieves higher success rates than several other algorithms. This superiority is particularly evident at
. In contrast, CBS-like multi-train path planning algorithms show minimal differences in success rates, with their performance nearly converging as
increases. This trend primarily stems from the constrained passable areas in random maps. At lower
values, the enhancement strategies integrated into the MT-CBS algorithm contribute to improved success rates. However, as
increases, further reduction in passable space and rapid growth in conflict search state space diminish the effectiveness of these strategies in enhancing success rates. Overall, the MT-SIPP algorithm exhibits an average increase in success rates of approximately 30% compared to CBS-like multi-train planning algorithms. Particularly noteworthy is its ability to handle more than twice the maximum number of solvable trains compared to CBS-like algorithms when
. This robust performance underscores the superiority of MT-SIPP in addressing multi-train path planning challenges in random map environments.
According to the data analysis from
Table 2, the prevalence of numerous random obstacles in random map environments significantly complicates the task of multi-train planning. In scenarios with smaller
values and fewer trains to solve, the MT-CBSH-RM algorithm indeed exhibits shorter runtimes compared to the MT-SIPP algorithm. However, once the number of trains to be solved exceeds 10, regardless of the
value, the runtime of the MT-CBSH-RM algorithm experiences exponential growth, making it difficult to provide solutions within a reasonable time frame.
In contrast, while the MT-SIPP algorithm does experience increased runtime as the number of trains to solve increases, the magnitude of this increase is significantly smaller compared to the MT-CBSH-RM algorithm. Consequently, when solving for more than 10 trains (i.e., ), the MT-SIPP algorithm consistently demonstrates shorter runtimes than MT-CBSH-RM, sometimes averaging as little as one-tenth of the latter’s runtime. This finding strongly validates the superior performance of the MT-SIPP algorithm in addressing large-scale multi-train planning problems.
7.3. Indoor Map Environment Testing
The indoor map environment replicates the layout of partially enclosed rooms typically found in real-world scenarios, interconnected by narrow passages allowing only one train to pass at a time. In this unique map environment, characterized by spatial constraints and restricted passages, congestion between trains can readily occur, thereby greatly augmenting the complexity and challenges associated with multi-train planning. The indoor room map we tested is illustrated in
Figure 16, with comprehensive test results detailed in
Figure 17 and
Table 3.
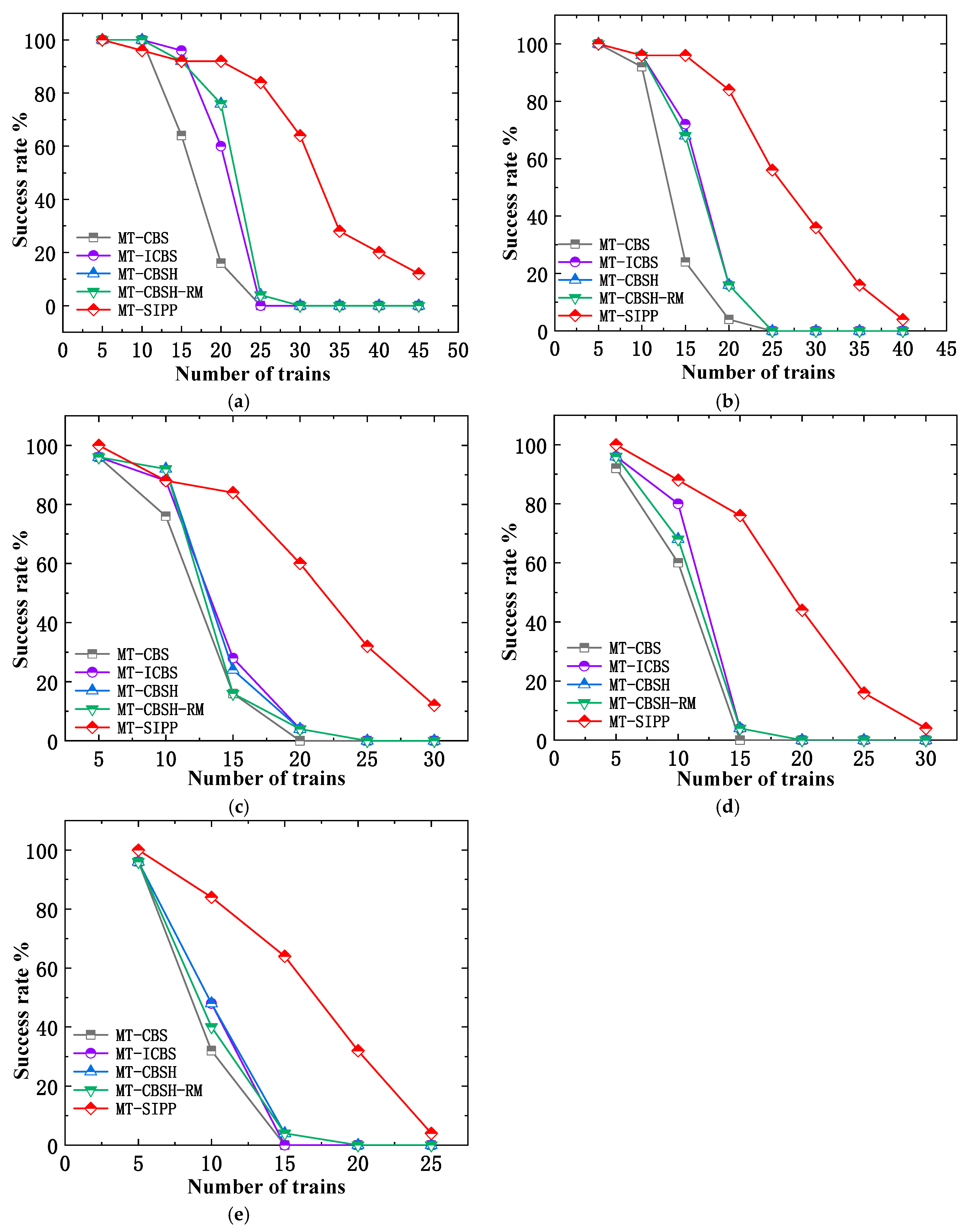
In
Figure 17, we have contrasted the success rates of several algorithms in solving room-based maps. The findings reveal that MT-CBS exhibits the lowest success rate, whereas the MT-SIPP algorithm displays the highest success rate. It is worth noting that the performance of the multi-train path planning algorithms that incorporate improvements over MT-CBS shows varying degrees of success and consistency. In specific terms, at
, both the MT-CBSH and MT-CBSH-RM algorithms achieve identical success rates, slightly edging out MT-ICBS. However, as
increases, the scenario evolves. At
and
, MT-ICBS shows slightly superior performance compared to MT-CBSH and MT-CBSH-RM. Conversely, at
, MT-CBSH-RM outperforms MT-ICBS and MT-CBSH. By
, MT-CBSH exhibits marginally better performance than MT-CBSH-RM and MT-ICBS. This inconsistency in results may be attributed to the unique characteristics of room-based maps and the high complexity inherent in multi-train path planning. In certain cases, the addition of more improvement strategies might inadvertently reduce success rates due to increased algorithmic complexity. Overall, in room-based maps, the MT-SIPP algorithm exhibits a notable average increase of approximately 27% in success rates compared to CBS-like multi-train path planning algorithms. This improvement is quite significant.
Based on the data from
Table 3, in the context of room-based map environments, it is observed that when
and the number of trains
is less than 10, the MT-CBSH-RM algorithm indeed shows shorter runtime compared to the MT-SIPP algorithm. However, across all other test conditions, the MT-SIPP algorithm consistently demonstrates shorter runtime.
It is noteworthy that many of the connecting passages between rooms in the room-based maps are single-channel, significantly restricting the throughput of trains. This structural limitation predisposes CBS-like multi-train planning algorithms to conflict generation when applied in such environments. To find conflict-free solutions, algorithms must continually search and replan numerous potential conflict nodes, which inevitably consumes substantial computational resources. Particularly in densely populated train scenarios, achieving a conflict-free solution becomes increasingly challenging. Therefore, the MT-SIPP algorithm demonstrates superior efficiency and adaptability in tackling these intricate indoor multi-train planning problems.
7.4. Analysis and Discussion of Experimental Results
The experimental results across various map environments indicate that while strategies such as integrating heuristic function -value guidance in search and employing MDD for rectangle conflict resolution can enhance the solving capabilities of the MT-CBS algorithm to some extent, its effectiveness is hindered by the CBS algorithm’s reliance on unit discretization nodes for path expansion and conflict detection mechanisms. This limitation results in an exponential increase in solution space as the number of trains and train lengths grow. Despite the incorporation of additional improvement strategies, the overall enhancement in algorithmic efficiency remains rather limited. In contrast, the MT-SIPP algorithm proposed in this study primarily expands path nodes and avoids conflicts based on global safe intervals, demonstrating a linear relationship between search space and both and . Consequently, as and increase beyond certain thresholds, the superior efficiency of the MT-SIPP algorithm in solution space becomes increasingly apparent.
All test results unequivocally demonstrate that our algorithm surpasses existing multi-train path planning algorithms (MT-CBS, MT-ICBS, MT-CBSH, MT-CBSH-RM) in several key metrics: success rate, maximum number of solvable trains, and algorithm runtime. Particularly notable is the MT-SIPP algorithm’s ability to achieve shorter runtimes and higher solving efficiency when confronted with larger numbers of trains and longer train lengths . Furthermore, our algorithm guarantees that the total cost of generated path solutions deviates from the optimal path’s total cost by no more than 10%. In scenarios involving blank maps or random and room-based maps with fewer trains, this deviation is further minimized to within 5%. This thoroughly validates the feasibility and efficacy of our algorithm. Despite making compromises in total path cost, its significant advancements in success rate, maximum solvable capacity, and solving efficiency underscore its broad applicability in the realm of multi-train path planning.
7.5. Visualization of Path Solutions
Figure 18 visually demonstrates the path planning solutions generated by the MT-SIPP algorithm across diverse map environments. The figure highlights that in open, obstacle-free blank maps, despite the absence of direct obstacles, the paths of a significantly increased number of robots become intricately intertwined, leading to higher path overlaps and potential conflicts. This underscores the necessity for multi-chain robot planning algorithms to exhibit strong conflict coordination capabilities. Conversely, in maps with random layouts or distinct room partitions, robot paths concentrate heavily on narrow passages that must be traversed. These areas serve as conflict hotspots, thereby imposing higher demands on the algorithm’s conflict management strategies.
8. Conclusions
To achieve cost savings and improve transport efficiency, snake-like robots, akin to train-like transport vehicles, are widely employed across multiple scenarios for cargo handling operations. However, in CBS-like multi-train path planning algorithms, the detection and resolution of conflicts for each segment of a snake-like robot occupying grid nodes often entail intricate processes of conflict node splitting and path searching. This significantly increases the algorithm’s runtime. At times, such complexity may prevent the algorithm from delivering feasible solutions within the allocated time, thereby failing to meet the efficient path planning requirements of multi-robot systems.
In addressing this challenge, we propose the Multi-Train Safety Interval Path Planning (MT-SIPP) algorithm in this study. This algorithm harnesses the benefits of safety intervals in solving path planning issues for snake-like robots. By directly adjusting safety intervals and incorporating additional node constraints, it efficiently mitigates conflicts among snake-like robots, thereby markedly improving path planning efficiency. The simulation test results convincingly validate the superiority of the MT-SIPP algorithm. Compared to MT-CBS, MT-ICBS, MT-CBSH, and MT-CBSH-RM algorithms, MT-SIPP demonstrates significant advancements in both solving capability and efficiency. Specifically, our algorithm shows an average 28% increase in success rate and can handle up to twice the maximum number of trains solvable by other algorithms. Particularly in scenarios with a large number of trains and longer train lengths, MT-SIPP consistently provides solutions rapidly and efficiently, thereby demonstrating its exceptional performance in the field of multi-train path planning.
In the future, we aim to significantly enhance the performance of our MT-SIPP algorithm by optimizing conflict resolution strategies for greater efficiency and robustness. Moreover, we will address more complex aspects of chain robots, such as kinematic constraints (such as precise steering times and acceleration/deceleration durations), larger scales, and extended vehicle lengths, thereby advancing solutions for industrial automation and intelligent logistics.