Abstract
The rapid development of wearable technologies is increasing research interest in on-body robotics, where relocatable robots can serve as haptic interfaces, support healthcare measurements, or assist with daily activities. However, on-body mobile robotics poses challenges in aspects such as stable locomotion and control. This article proposes a novel small robot design for moving on human limbs that consists of an open grasping mechanism with a spring linkage, where one side holds a pivoting differential drive base (PDDB) with two spherical rollers, and the other side holds an actuated roller for grasping and stabilization. The spherical rollers maintain contact at three points on the limb, optimizing stability with a minimal number of rollers and integrating DC motors within. The PDDB wheels (spherical rollers) enable directional changes on limb surfaces. The combination of the open mechanism, the PDDB, and the spherical rollers allows adaptability to diameter variations along the limb. Furthermore, the mechanism can be easily put on or removed at any point along the limb, eliminating the need to slip the robot over the hand or foot. The kinematic model for the proposed mechanism has been developed. A cascade control strategy is proposed with an outer loop for stable grasping and an inner loop for trajectory adjustments using PDDB roller velocities. An on-limb robot prototype has been built to test its applicability to human arms. Simulation and experimental results validate the design.
1. Introduction
The rapid advancement of new technologies has sparked the development and significant commercial impact of wearable smart devices that can be attached to the body to improve quality of life through safety, assistance, and entertainment [1,2,3]. The concept of wearable robotics as person-oriented systems was coined over a decade ago to primarily refer to exoskeletons, orthotic robots, and prosthetic robots [4,5]. However, the growing interest in lightweight and compact devices has broadened the notion of robot wearability to include miniature robots that can either be affixed to the body [6,7,8,9] or move along its surface. In this sense, dynamic wearable technology [10], where small robots can move on or around the human body, can extend the capabilities of wearable smart devices in applications such as healthcare measurements [11,12], haptic interfaces [13,14], fashion expression [15], and support and assistance with activities of daily living (ADL) [16,17].
Nevertheless, on-body mobile robotics is a challenging topic that requires specific research in key technological aspects such as adhesion, locomotion design, and control.
Generally, climbing robots for industrial and maintenance applications have adopted various adhesion mechanisms such as vacuum suction cups, grippers, magnetic systems, or bioinspired methods mimicking geckos or insects [18,19,20]. Even if the requirements for wearable robots differ significantly from industrial solutions [21], some studies have proposed locomotion designs that adapt some of these mechanisms to on-body robots. For instance, SkinBot [11,21] has an inch-worm locomotion system that employs two legs with suction cups to navigate on human skin and collect biosignals, yet vacuum pumps pose a challenge for achieving untethered devices. Furthermore, some works have investigated cloth climbing mechanisms that could be used for on-body robots. Thus, gripper-based locomotion can be employed to grasp fabric, taking advantage of the soft and deformable characteristics of loose clothing. Clothbot [12] employs a gripper consisting of a passive spring and two tangential differential drive wheels, allowing it to roll along the fold within the gripper. Given that movement direction is restricted by the fold, an articulated tail can use gravity to assist steering [22]. In Rubbot [23], a passive folder frame holds two grippers for differential motion. Moreover, Rovables [24] are differential drive miniature robots that use magnetic attraction between wheels and a rod that moves on the fabric’s inner side. Additionally, gecko-inspired adhesion was used for the feet of the CLASH lightweight micro-hexapod to climb on loose clothing [25]. In general, cloth-climbing robots allow for navigation on any part of the body where clothing is smooth. However, they are not suitable for applications requiring direct contact with the body, such as healthcare measurements. Moreover, their design primarily focuses on managing folds and other interactions with flexible fabric, which limits maneuverability. Alternative locomotion designs have avoided adhesion issues by employing smooth rails or tracks affixed to the clothing worn by the user [26]. The rail locomotion design of the Calico robot [14] relies on wheels, a rail attachment system, and a track-switching mechanism for bifurcations.
In contrast, on-limb mobile robots designed to move along the wearer’s arm [13,16,17,27] are based on locomotion systems that make direct contact with the limb, either on bare skin or through tight clothing. These on-limb mobile robot designs prioritize a snug fit by exerting gentle pressure against the limb, relying less on adhesion, and using surface materials and textures that favor both grip and comfort. Additionally, on-limb robots require adaptability to the varying diameters of the limb (e.g., from the wrist to the upper arm). On-limb mobile robots are related to out-of-pipe climbing robots in industrial applications [28,29]. Some pipe climbing robots [30,31] have addressed diameter variation with adaptable clamping mechanisms that can be mechanically adjusted to different pipe sizes before use, but are not designed for pipes with diameter variations along their length. In general, the designs and construction of industrial solutions are mostly unsuitable for human limbs due to their heavy and complex structures [31,32], even if current research in soft robots [33,34] aims at lighter and compliant pipe crawling mechanisms that could be suitable for human–robot interaction [35]. In this sense, Knitskin [27] is a textile sleeve-like robot designed for moving along the user’s forearm that needs a compressor for pressurizing pneumatic actuators. Nevertheless, most methods for on-limb motion rely on rigid locomotion with self-actuated electric servo-motors. Thus, the Movelet robot for positional haptic feedback [13] consists of a closed bracelet with four evenly distributed wheels connected by pairs of spring suspensions, allowing for small diameter adjustments along the forearm. The wearable bracelet robot proposed by Kimura et al. [16] is based on rolling spherical capsules with internal motors, linked by alternating rigid links and a flexible rubber band with an actuated reel for diameter adaptation. Alternatively, the bathing assistance robot proposed by Liu et al. [17] is a four-wheel mechanism designed for single-track locomotion along the user’s arm, pulling a cleaning fabric sleeve that also serves to hold the robot in place. All of these mechanisms depend on closed bracelets or sleeves that must be slid over the wearer’s hand, which limits applicability in situations where active user involvement or human assistance is challenging or unexpected, such as remote health monitoring for patients or victims.
In this work, we propose an open mechanism for on-limb locomotion that can be put on or removed at any point of the limb without slipping the robot over the hand or foot. This novel locomotion design has a minimum number of wheels: two actuated spherical rollers for differential drive and another actuated spherical roller for grasping and stabilization. A triangular configuration provides stability (i.e., three points of contact provide a stable support base for an object) and can accommodate uneven surfaces. Some studies [36,37] have demonstrated that using three fingers on robotic grippers improves the capability to grasp more complex irregular objects. In particular, spherical rollers [38] have been employed as fingertips for in-hand manipulation [36], facilitating the manipulation and reorientation of objects with different shapes and enabling continuous rotation and adaptability to changes in the contact state.
In particular, the major contributions of this article are as follows:
- A new robot designed to move on human limbs featuring an open grasping mechanism with a spring linkage. One side has a pivoting differential drive base (PDDB) with two actuated spherical rollers, and the other side has an actuated roller for grasping and stabilization.
- The kinematic analysis of the proposed robot configuration estimates the circumcenter coordinate, the current limb radius, and the actual roller contact points from the joint angle measurements. These values are necessary for estimating the actual differential drive wheel distance for motion control.
- A cascade control system, combined with the passive spring linkage, allows for adaptation to varying limb diameters. The outer loop ensures stable grasping, while the inner loop adjusts the trajectory using PDDB roller velocities. A Lyapunov stability analysis is also provided.
Additionally, the article presents experimental results from both simulations and a real on-arm prototype. To our knowledge, this is the first analysis of a locomotion system based on spherical rollers with proprioceptive estimation of limb diameter changes.
The rest of this paper is organized as follows. Section 2 presents the proposed design. Section 3 offers a kinematic analysis locomotion system. The cascade control system is described in Section 4. Section 5 discusses the experimental results. Finally, Section 6 summarizes the key findings and offers conclusions.
2. On-Limb Mobile Robot Design
This section offers an overview of the proposed design and describes the grasping model, highlighting the concept of central alignment for ensuring stability while moving on the limb.
2.1. Design Overview
The concept and main elements of the proposed robot design are illustrated in Figure 1. The system consists of an open symmetrical two-link mechanism with a passive spring joint, where the first link holds a differential drive base with a passive pivot joint. The pivoting differential drive base (PDDB) has two active spherical rollers that move along the limb. The spring joint presses the PDDB over the limb, ensuring the rollers are always in contact with it. The centerline of the PDDB is connected to Link 1 using a free pivot joint aligned with the motion axis corresponding to the measured articulation variable . Moreover, Link 1 and Link 2 are connected by a passive spring joint (measured articulation variable ) to facilitate grasping and adaptation to changes in limb diameter. The synergy between the pivot and spring joints enables stable and adaptable locomotion along the limb. The second link has a fixed (i.e., non-articulated) platform holding a 1 DoF spherical roller that provides the grasping point. Furthermore, this wheel is active to maintain an aligned robot pose relative to the limb.
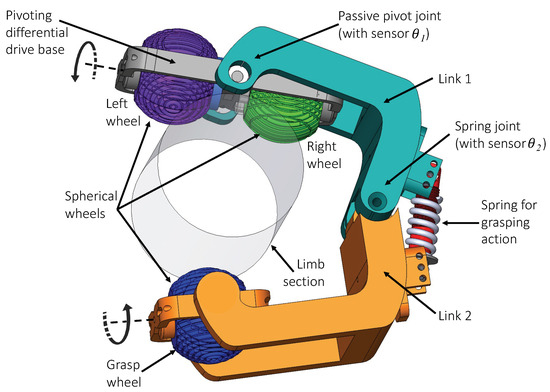
Figure 1.
Illustration of the concept and main elements of the on-limb mobile robot. Colors indicate the different parts of the locomotion system: two links with a spring joint, the pivoting differential drive base, and three actuated 1 DOF spherical rollers.
The rotation axes of the three rollers (i.e., two spherical wheels in a differential drive configuration plus an opposing grasping wheel) are in the same plane. Spherical rollers allow for stable grasps independent of its orientation [36] and limb radii. Also, the spherical design of the rollers allows them to have individual DC motors inside, with encoders for velocity control, reducing hardware size and utilizing internal volume [36]. The PDDB rollers are used to change the heading. At the same time, the actuator of the third one provides a grasping effect, holding the device on the limb with a velocity equivalent to the PDDB’s linear velocity. These rollers are suitable for curved surfaces, providing a single contact point regardless of surface curvature. Moreover, the combination of the spring joint, the free-pivoting mechanism, and the spherical rollers allows continuous 3-wheel contact with the limb surface. PDDB wheels can be used to correct the orientation of the trajectory, preventing the deterioration of the stable grasp during locomotion.
All in all, the proposed design enables adaptability to variations in the limb section: the passive spring provides continuous adaptation to size changes, the PDDB ensures contact and allows for differential drive heading corrections against shape variations, and the continuous curvature of spherical rollers provides smooth motion independent of the actual contact points. Additionally, the mechanism can be easily attached or removed at any point on the limb without requiring the robot to be slipped over the hand or foot.
2.2. Grasp Model
Figure 2 shows a cross-sectional diagram of the proposed robot configuration on a cylindrical limb. The robot can be considered planar, with all roller axles in the same plane, and the axles of the spring and pivot joints are perpendicular to this plane. In this work, point coordinates in the local robot frame are denoted by subindexes x, y, and z (e.g., ). In particular, is placed at the center of the PDDB, where the Z-axis coincides with the pivot axis, and the X-axis coincides with the rotation axle of the differential drive wheels. Hence, the pivot joint point is . For the kinematic chain, we have followed a Denavit–Hartenberg convention. The origin of the frame for Link 1, which holds the PDDB, coincides with that of the robot’s frame, with the -axis aligned with Z. Link 1 has a length and rotates around the Z-axis with a pivot joint angle measured relative to the X-axis.
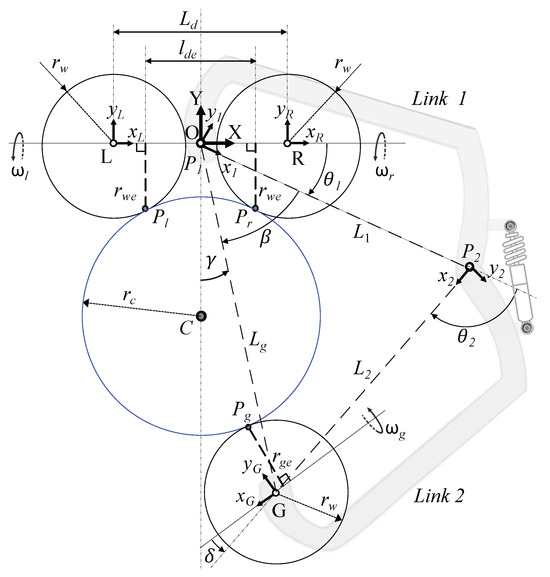
Figure 2.
Cross-sectional schematic diagram of the on-limb mobile robot mechanism. The cylindrical limb is depicted in blue.
The local frame for Link 2, which has a length , originates at the spring joint point and rotates around the -axis, with the -axis aligned with the link segment . The spring joint angle is defined between and . The joint vector is defined as .
The frames for the left, right, and grasping spherical rollers (i.e., , , and ) are placed at the respective centers L, R, and G, with rotation around the corresponding x-axis. The Cartesian coordinates for the grasp roller center G are computed from and the spring-joint angle . The contact points relevant for grasp stability and motion control are denoted as , , and for the left, right, and grasp rollers, respectively.
The locomotion of the PDDB along the limb’s longitudinal axis is illustrated in Figure 3, which shows a top view of the robot. This locomotion is characterized by independently controlled wheels (left and right) working in tandem to maintain a straight-line trajectory. The vehicle heading is parallel to the longitudinal limb axis in the centered orientation, meaning the pivot point is in the center. An off-centered state occurs when the robot deviates from the longitudinal axis. Moreover, orientation error affects the cylindrical section shape, which becomes elliptical. The PDDB’s linear velocity is denoted as V, while the right and left wheels’ linear velocities are and , respectively.
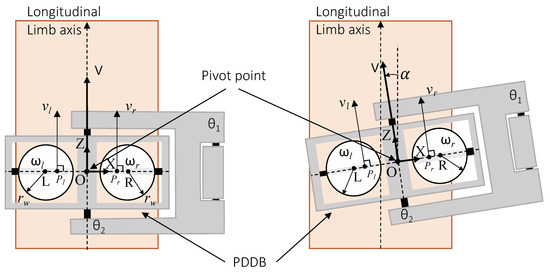
Figure 3.
Top view of the on-limb mobile robot with respect to the limb’s longitudinal axis: centered (left) and uncentered (right).
2.3. Stability of Grasp and Alignment Error
When considering grasp with d fingers under a planar friction-less grasp, a stable equilibrium grasp is achieved when the total wrench due to the finger forces is zero. In the case of the proposed circular geometry, with no frictions, the forces are pure normal forces with respect to the center of the grasped body (i.e., ). The condition for the equilibrium grasp [39] for a three finger (i.e., ) friction-less grasping is that with and (i.e., positive coefficients can be found).
In this case, the planar grasping configurations that make possible a null wrench are illustrated in Figure 4. In Figure 4a, a null wrench is possible with non-negative . Figure 4b shows the limit case, where a positive value of makes a positive Wrench under the friction-less assumption. Finally, Figure 4c shows an unstable grasping configuration. Cases (b) and (c) occur also, respectively, for negative values of . Additionally, when considering surface frictions, the Coulomb friction replaces the normal forces with a friction cone [40], making the grasping area wider and providing a bigger, more practical, and stable grasp.
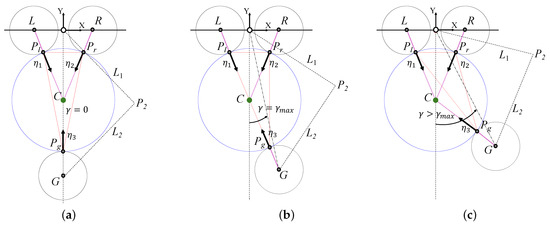
Figure 4.
Illustration of grasp stability: (a) ideal central alignment (), (b) maximum alignment error () for friction-less stable grasp, and (c) unstable grasp.
Graphically, in the desired robot grasping configuration (see Figure 4a), point G lies on the Y axis (i.e., ) so the contact points , , and form an isosceles triangle whose circumcenter coincides with C. Additionally, the angle of with respect to the Y axis is null, indicating that the contact point triangle is centrally aligned with the limb section. Static grasping stability is maintained as long as C remains within the contact point triangle. However, as the absolute value of increases, the degree of central alignment decreases, potentially causing the robot to detach from the limb when . Specifically, is reached when C lies on the segment .
Therefore, the central alignment of the contact triangle and the limb section corresponds to maximum grasping stability, and can be considered as the alignment error for controlling grasping stability. Alignment error can be computed from the joint variable measurements and , as well as the and lengths. First, the angle of with respect to is obtained using the law of sines:
Then, is given by:
3. Kinematics
This section describes the mathematical models of the robot kinematics. Figure 2 shows the schematic model, the coordinate systems, the joint variables, and the mechanism parameters. Table 1 and Table 2 define the symbols of the major parameters and relevant variables used in the formulation, respectively. The simplifying assumptions for the kinematics analysis include considering the limb as a circular cylinder with a varying radius. The desired robot’s locomotion is parallel to the cylinder’s longitudinal axis. For this reason, the plane defined by the robot contact points is considered perpendicular to the longitudinal cylinder axis, resulting in a circular section. The analysis assumes pure rolling of rigid bodies without sliding and considers steering corrections sufficiently small to neglect the ellipsoidal components of the cylinder section.

Table 1.
Design parameters.

Table 2.
Relevant variables.
3.1. Limb Radii and Differential Wheel Distance Estimation
We use the information from the joint angle measurements and the dimensions of the links to obtain the circumcenter coordinate . To solve for , we determine the equations for the bisectors of the triangle formed by the and segments, then we derive the midpoints of the segment, and finally we find the slope of its perpendicular line. Hence, is given by:
Moreover, as the PDDB is symmetrical with respect to Y, then .
Then, the limb (i.e., cylinder) radius can be obtained by applying the Pythagorean theorem from a distance between L, O, and C less the wheel radius :
As for the computation of contact points, the angle between and X is given by , where is the slope of . Then, the coordinates of the left roller contact points are:
and is symmetrical with respect to Z:
Similarly, the coordinates of contact point are:
where is the angle between and X.
A spherical roller ensures a contact point when the robot moves on a non-planar surface. However, actual contact points do not lie on the corresponding rollers’ -axis (see Figure 2), so the constant distance between the PDDB wheels centers is not suitable for differential drive computations. Moreover, the contact points of spherical wheels change along the path due to variations in the cylinder’s radius. Therefore, the distance between and is the effective differential drive wheel distance , which can be obtained from Equation (5) as:
Similarly, the effective wheel radius is defined as the perpendicular distance from the wheel rotation axis to the limb at the contact point, which is for the PDDB rollers and for the grasp roller (see Figure 2). To determine , we use the relationship defined by the right triangle formed by L, the roller radius , and the difference of the roller distance . Applying the Pythagorean theorem to this triangle we obtain as follows:
We consider the angle between and the axis , given by the mechanical design for the effective radius calculation:
3.2. Longitudinal Model
We derive the kinematic model of the PDDB to find position variation given in the following matrix:
where and are the derivatives of the robot’s position and the orientation; represents the linear velocity; and is the angular velocity.
The robot inverse Jacobian matrix describes the PDDB rollers’ surface velocities that can be established as:
where and represent the right and left rolling velocities. The linear velocity of the PDDB center is used. The grasp rolling velocity is determined as:
3.3. Heading Error
The robot’s orientation influences the grasping during locomotion. The optimal heading is considered when the PDDB centerline is aligned with the longitudinal limb axis, so the orientation angle is null, as shown in Figure 3. Adjusting the PDDB rollers’ velocities allows it to reach a centered orientation while the decentered orientation increases , causing the pivot point to move away from the centerline. Therefore, can be considered as a heading error for controlling orientation.
The estimation of the heading with respect to the limb longitudinal axis (Heading Estimation block in Figure 5) can be obtained from external sensors (e.g., sets of short-distance laser range-sensors) or by numerically integrating the Cartesian angular velocity () of the robot considering a known initial state:
This approach is affected by the deviation caused by cumulative inaccuracies in odometer measurements. However, as will be described in Section 4, additional performance information of the system () can be used to compensate for the estimation drift.
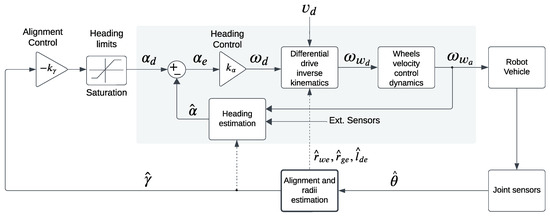
Figure 5.
The control system block diagram shows the cascade control strategy. Alignment control (outer loop) uses proportional action for grasping stability, and heading control (inner loop) adjusts the trajectory by proportional control of PDDB rollers’ velocities.
4. Control Strategy
In this section, the control strategy is formulated based on several assumptions. The pivot mechanism is assumed to be rigid and symmetric with respect to the longitudinal axis of the limb. Furthermore, the model considers a perpendicular contact point of the roller with the skin, so traction and adherence are guaranteed. Additionally, the analysis presupposes the absence of slippage. Moreover, we assume the robot’s path is continuous and does not constitute a control objective. Also, the forward velocity is constant. Dynamics analysis and the influence of gravity are excluded.
The proposed cascade control scheme is shown in Figure 5, with the alignment control represented externally and the heading control internally (within the shaded box). The variables to control are and . The aim of the control system is to minimize the error estimation and to ensure that the robot motion remains parallel to the limb (i.e., is null).
The subindexes a, d, and e (e.g., ) are used to represent their respective relationships with the actual a, the desired d, and the error e value.
4.1. Central Alignment Control
The external control follows a proportional control law , outputting a desired heading that is limited to maintain the grasp stability. The controller input is derived from the central alignment and radius error estimation block, which receives information from the joint sensors and .
Additionally, note that the alignment and radius error estimation block computes the effective differential wheel distance , radii , and based on Equations (8), (9), and (10), respectively. These data are important for calculating inverse kinematics, which determines , , and as shown in Equations (12) and (13). The heading limits saturate the central alignment control to ensure the robot stays centered within .
4.2. Heading Control
The second loop controls the heading error with a proportional control law with gain . The estimated orientation error is computed from roller odometry. The robot follows the trajectory varying the velocity of the PDDB’s rollers; these are deduced by the differential drive inverse kinematics with and as input references. The output is the desired velocity of each roller, given as =. As mentioned in Section 3.3, the drift in the odometric estimation of the heading has an effect on the overall control system. As the external control loop has a proportional control, the system error would grow proportional to the drift. To avoid this, an additional term can be added to the heading estimation (15) that compensates for the estimation error based on the integral of the error with a gain :
4.3. Velocity Control
This is an additional velocity control that provides independent control of each roller of the PDDB. A PID is implemented to control the velocity of the wheels. The feedback for this control is obtained from the encoders. A first-order system has been implemented to create a model that simulates a simplified representation of the real system. The first-order transfer function simulates the loop response of the control system, with a time constant of ms. Also, the actual velocities can be obtained as . The robot vehicle block determines the global position of the robot, integrating roller velocities from Equation (11).
4.4. Stability Analysis
This study aims to ensure the robot is stable while moving along a straight path along the cylinder’s longitudinal axis. We propose the control’s input for the grasp stability analysis. The time derivative of and are established at Equations (16) and (17):
involving the temporal variation of and , where is the angle between and and is derived in Equation (1). Distributing the term, we obtain . Solving in terms of and , the expression is:
To guarantee the convergence and stability, a Lyapunov function candidate V is chosen as , which is continuous, and positive definite . Computing the time derivative we have:
If we substitute from model Equation (18), then:
This shows that the term is semidefinite negative. This guarantees the stable behavior in the system. Additionally, achieving global asymptotic stabilization of , indicating that the system converges to a stable equilibrium point.
5. Experiments and Results
This section presents the simulation of the kinematic system outlined in Section 3 and assesses the control system for alignment and heading described in Section 4, including the definition of a boundary proximity condition. Also, experimental results of locomotion are included. The results highlight the robot’s capabilities to control the direction of the PDDB and maintain stable limb grasp alignment.
5.1. Simulation Parameters
The simulation experiments were developed using MATLAB by Mathworks (Natick, MA, USA) running on a 2.3 GHz 8-Core (Core i9) by Intel Corp. (Santa Clara, CA, USA) with 16 GB 2667 MHz DDR4 memory. For the simulations, we used parameters considered relevant for an on-arm robot: mm, mm, and rad, with radii ranging from 28 mm to 50 mm. When simulating the joint sensors and , we started from the position and determined by applying the concept of the distance between O and G. Next, we derived according to the law of cosines. In case and are equal, the equation can be simplified as: Subsequently, is found using the sum of the interior angles of the isosceles triangle , given by based on Equation (2) of and with information, we determine , that can be estimated as: .
5.2. Boundary Proximity Condition
A cylinder with varying radii represents the outer surface of the limb. A boundary proximity condition has been implemented to ensure that the simulated robot does not pass through the cylinder. The condition detects when the limb contacts the spring joint, requiring a distance between the limb border and point on the spring joint to maintain this restriction:
where , and defines a relationship between , , and . For the sake of simplicity, Equation (21) assumes .
5.3. Simulation Results
Simulated experiments have been performed to evaluate the performance of the cascade control, the effect of different limb sizes, and the compensation of drift in heading estimation.
5.3.1. Cascade Control Performance
Figure 6 presents simulation results in robot coordinates. The initial conditions of the experiment are =10 mm/s, , mm, and = = mm, where an initial alignment error of the grasp wheel is corrected while the robot follows a trajectory parallel to the longitudinal cylinder axis. The cascaded alignment and heading controls guarantee stability and locomotion on a varying radius limb. Figure 6a–c illustrate the robot’s front view, plane, at three representative moments of the simulation. Evolution of the grasping alignment error , the trajectory results of the joint angle sensors are shown in Figure 6d. The findings indicate a shift in the wheels’ position, resulting in a stable grasp on the limb and continuous grasping during locomotion.
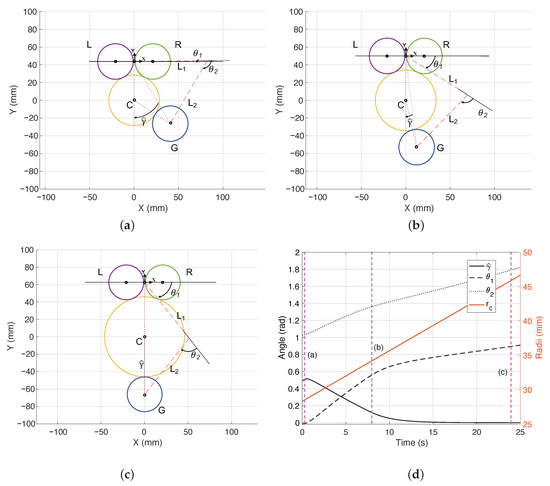
Figure 6.
Path of the grasp roller in a variable diameter limb from the front view: (a) position at s, (b) advancement of the grasp roller at s, (c) at s, and (d) evolution of , , , and variation, where instants corresponding to (a–c) are highlighted by fuchsia dashed lines.
Furthermore, we have evaluated the effect of different heading limit values in the cascaded control system, as shown in Figure 7. In particular, heading limits have been set for rad, rad, and rad. In the first case, the control system shows a slow response after reaching , resulting in an extended period before overcoming the condition. Conversely, the last test indicates the robot approaches too quickly, causing it to move faster than required. This could be problematic, as the vehicle must control the wheel speeds differently to change direction. In all simulations, the radius was considered to vary along the trajectory.
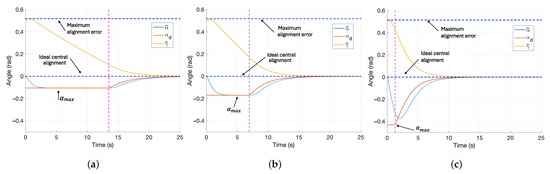
Figure 7.
Effect of in the temporal response from (with an initial value of ), , and , in a variable diameter limb. (a) = : begins to overcome the heading condition at s; (b) = : overcomes the heading condition at s; and (c) = : approaches the heading condition at s.
5.3.2. Effect of Different Limb Sizes
Table 3 presents results for different limb sizes according to minimum () and maximum () limb radii: small (S), medium (M), and large (L), which correspond to human arm radius variations between 22 and 42 mm, 24 and 44 mm, and 28 and 50 mm, respectively, [41]. Moreover, different values for the parameter (40 mm, 44 mm, and 48 mm) are considered. In these experiments, the robot starts from the wrist (). The table presents the resulting maximum alignment error , the settling time , measured as the time required for to fall within rad, and the corresponding traveled distance in that time . Increasing provokes a slight reduction in but has a negligible effect on settling time and distance. The major observed performance differences depend on limb size, with longer settling times for the L-sized arm.

Table 3.
Parameters , , and for different component sizes and configurations with = 10 mm/s, and = 0.17 rad, starting from .
5.3.3. Drift Compensation in Heading Estimation
As mentioned in Section 4.2, the deviation caused by cumulative inaccuracies in odometer measurements can be avoided either by using external sensors or by using the integral of the alignment error (15). In this work, no external sensors have been used, and the drift of odometric estimation is compensated by the alignment error, which in turn makes use of the proprioceptive sensors located in joints and . To show the compensation capability of the heading estimation block (15), a simulation experiment has been performed by adding a ramp ( deg/s), to the signal and an integral constant . Additionally, an rad and a linear velocity mm/s are used.
As shown in Figure 8, in steady state, the uncompensated heading , unlike the compensated heading , follows the simulated drift. The steady value of the is null, so the alignment error can also be null. We also believe that this approach may also compensate for the effects of non-straight limbs.
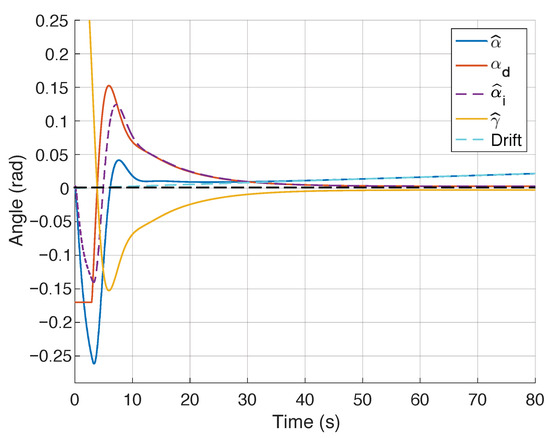
Figure 8.
Compensation of the odometric heading estimation error using the alignment error signal with a simulated drift.
5.4. 3D Visualization of Robot Locomotion
Robot locomotion visualization is shown in Figure 9, which illustrates the pivoting movement of the PDDB and the control system involved in heading adjusting. Furthermore, it shows the grasp movement along the upper arm. The simulation illustrates three positions: initial, progress, and final. Moreover, the dimensions of the limb were based on the anthropometric measurements. We establish for the wrist radius the range from 22 mm to 32 mm; for the mid-limb, between 32 mm to 44 mm; and the limb, between 42 mm to 54 mm [42]. In addition, longitudinal distances were established from the wrist to the mid-limb, with a range of 120 mm to 180 mm, and from the mid-limb to the shoulder, with a range of 165 mm to 225 mm [41]. Once the limb radius ranges were defined, we interpolated the data and conducted a fitting process, all as part of the limb modeling.
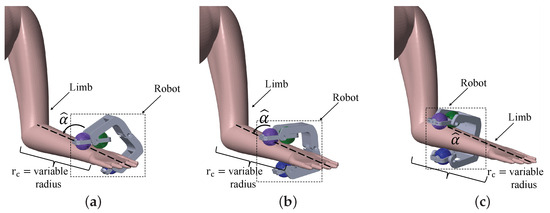
Figure 9.
Locomotion of the virtual model along the upper limb: (a) initial position at s, (b) advancement of the grasp wheel at s, and (c) final position at s.
5.5. Link Length Design
The structure design can influence the stability of the on-limb mobile robot. Therefore, we analyze the parameters of the differential wheel distance , roller radius , and the limb radius, , represented as a cylinder. We consider a range of 40 mm to 48 mm for , and for , the range is between 16 mm and 24 mm. With this data, we computed the maximum . The results are presented in Table 4, in which we compare how changes in and affect the maximum limb radius . As rises, decreases. Increasing could improve stability but also would affect the robot’s change direction as well as the navigation on the upper limb and adaptation to changes in limb dimensions. Furthermore, we establish a design criterion, , indicating that the differential wheel distance should be less than twice the wheel radius. This prevents oversizing issues that may lead to undesirable wheel contact.

Table 4.
Maximum limb radius for and design parameters.
5.6. Developed Prototype
We constructed a prototype to verify the kinematic model’s design and simulation results. The PDDB has dimensions of mm and mm, as shown in Figure 10. Link length parameters are mm, roller radii are mm, mm, and rad. The robot includes three small in-wheel DC motors, each with encoders by Pololu Robotics and Electronics (Las Vegas, NV, USA). These motors are velocity-controlled independently, and the motor shaft connects to the center of each wheel. Also, two rotary potentiometers with good performance in robotic grippers [43], muRata A01346 by Murata Manufacturing Co., Ltd. (Nagaokakyo-shi, Japan), are affixed to Link 1 to measure the pivoting and spring joint angles (i.e., and ). The wheels feature a surface pattern that hlserves to verify visually advance and the PDDB directional changes. The PDDB, links, the spherical wheels, and the spring joint brackets were 3D printed in polylactide (PLA) material. All in all, the robot weighs 250 g, including the three wheel-motor sets (26 g each). Table 5 shows the weight of each component of the robot. A Mega2560 microcontroller by Arduino (Chiasso, Switzerland) processes the angle sensor data and controls the three in-wheel motors for velocity. In the experimental prototype, this microcontroller has not been integrated on-board.

Figure 10.
Prototype of the on-limb mobile robot: (a) general view; (b) detail of the spring joint with rotatory sensor.

Table 5.
Parts and their weights.
For the passive joint mechanism, we used an aluminum alloy shock absorber designed for radio-controlled cars with an elastic constant of 60 N/m [44]. The rest, pre-load, and maximum lengths of the spring are 16 mm, mm, and 60 mm, respectively. We empirically found that this spring offered a good balance between grasping force and comfort. Moreover, both links have three spring anchor points allowing the tension to be adjusted for different users (see Figure 10).
The experimental simulation results depict and values across velocities ranging from to , utilizing the mechanical parameters: mm, mm, mm, and rad. These results are illustrated in Figure 11.
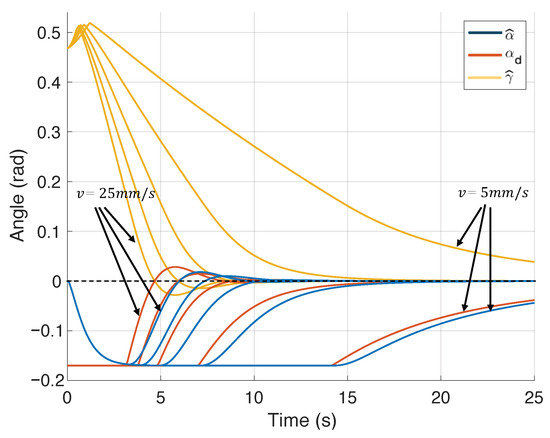
Figure 11.
Temporal evolution of and for velocities from mm/s to mm/s.
The on-limb mobile robot locomotion tests (see Figure 12) were teleoperated. We used virtual sensors based on the upper limb dimensions, thus allowing the robot to track the movements. The robot considers variations in limb sizes and dimensions. The spring joint has three positions that increase the opening range and reduce friction force. Results show that the robot moves over the limb. Also, spherical rollers offer advantages such as a circular contact area, which eliminates pressure points and thus reduces user discomfort.
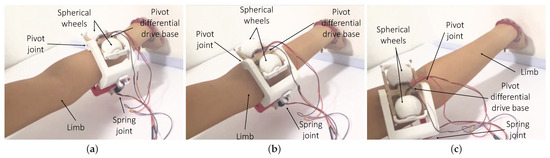
Figure 12.
Temporal progression of locomotion on a human upper limb: (a) initial position, (b) intermediate position, and (c) final position.
Even if no clinical experiments have been performed, voluntary users in preliminary lab tests described their sensations as comfortable and natural, noting the device’s smooth adaptation to the limb’s anatomical shape, the absence of annoying noises, and the perception of fluid, non-intrusive movements.
6. Conclusions
We have presented a novel on-limb mobile robot mechanism adaptable to human limb sizes. Concerning the mechanical design, the combination of the spring joint, the free pivoting mechanism, and the spherical wheels provides a solution that guarantees continuous three-wheel contact with the limb. Also, the open mechanism allows for the robot to be easily put on or removed at any point on the limb without slipping the robot over the hand or foot. While alternative solutions, such as a closed mechanisms or bracelet, offer intrinsic grasping stability, achieving mechanical stability poses a challenge in open mechanisms. Implementing a double cascade control system enables the robot to achieve grasping stability while enhancing maneuverability through differential drive steering. Moreover, the controller includes drift compensation in odometric heading estimation.
The simulations have demonstrated the effectiveness of the controller to maintain heading and central alignment. Furthermore, an on-limb robot prototype has been built to test its applicability to human arms.
Nevertheless, further work is required for practical application, including clinical experiments to evaluate user experience and comfort during extended use. Additionally, there is potential to optimize materials and robot design to reduce weight and facilitate the integration of electronics for untethered operation. Moreover, the estimation of heading error has been performed using odometry. A more accurate estimation of this value is related to the complex problem of on-body robot localization, which requires additional proprioceptive and/or exteroceptive sensors. Moreover, analyzing gravity and wheel–skin tissue interactions with terramechanics principles, involving wheel surface materials and human tissue modeling, is an open research area for on-limb robots.
Author Contributions
Conceptualization, L.M.T.-S.-C. and J.M.G.-d.-G.; methodology, L.M.T.-S.-C., J.M.G.-d.-G. and A.M.; software, L.M.T.-S.-C. and J.M.G.-d.-G.; validation, L.M.T.-S.-C. and J.M.G.-d.-G.; formal analysis, L.M.T.-S.-C., A.M. and J.M.G.-d.-G.; investigation, L.M.T.-S.-C. and J.M.G.-d.-G.; writing—original draft, L.M.T.-S.-C., A.M. and J.M.G.-d.-G.; writing—review and editing, L.M.T.-S.-C., A.M. and J.M.G.-d.-G.; visualization, L.M.T.-S.-C.; supervision, A.M. and J.M.G.-d.-G.; project administration, J.M.G.-d.-G.; funding acquisition, J.M.G.-d.-G. All authors have read and agreed to the published version of the manuscript.
Funding
This work has been funded by the “Plan Nacional de Investigacion de España” under a project with code PID2021-127221OB-I00. This publication has also been partially funded by the Universidad de Málaga.
Institutional Review Board Statement
The study was conducted in accordance with the Declaration of Helsinki, and the protocol was approved by the Ethics Committee of the University of Málaga (CEUMA) with reference 7-2023-H, 13 June 2023.
Informed Consent Statement
Not applicable.
Data Availability Statement
All data included in this study are available upon request by contact with the corresponding author.
Acknowledgments
The first author has received a research stay grant by AUIP—Programa Iberoamericano de Formación Doctoral en el área de las Ingenierías y las Ciencias Técnicas.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| DOF | Degrees of freedom |
| PDDB | Pivoting differential drive base |
References
- Park, S.; Jayaraman, S. Wearables: Fundamentals, advancements, and a roadmap for the future. In Wearable Sensors, 2nd ed.; Academic Press: Oxford, UK, 2021; Chapter 1; pp. 3–27. [Google Scholar] [CrossRef]
- Shtarbanov, A.; Zhu, M.; Colonnese, N.; Hajiagha Memar, A. SleeveIO: Modular and Reconfigurable Platform for Multimodal Wearable Haptic Feedback Interactions. In Proceedings of the Annual ACM Symposium on User Interface Software and Technology, San Francisco, CA, USA, 29 October–1 November 2023. [Google Scholar] [CrossRef]
- Minaoglou, P.; Efkolidis, N.; Manavis, A.; Kyratsis, P. A Review on Wearable Product Design and Applications. Machines 2024, 12, 62. [Google Scholar] [CrossRef]
- Pons, J. Wearable Robots: Biomechatronic Exoskeletons; John Wiley and Sons: Hoboken, NJ, USA, 2008. [Google Scholar] [CrossRef]
- Pitzalis, R.F.; Park, D.; Caldwell, D.G.; Berselli, G.; Ortiz, J. State of the Art in Wearable Wrist Exoskeletons Part II: A Review of Commercial and Research Devices. Machines 2024, 12, 21. [Google Scholar] [CrossRef]
- Chinello, F.; Malvezzi, M.; Pacchierotti, C.; Prattichizzo, D. Design and development of a 3RRS wearable fingertip cutaneous device. In Proceedings of the IEEE International Conference on Advanced Intelligent Mechatronics, Busan, Republic of Korea, 7–11 July 2015; pp. 293–298. [Google Scholar] [CrossRef]
- Mete, M.; Paik, J. Closed-Loop Position Control of a Self-Sensing 3-DoF Origami Module With Pneumatic Actuators. IEEE Robot. Autom. Lett. 2021, 6, 8213–8220. [Google Scholar] [CrossRef]
- Tong, Y.; Liu, J. Review of Research and Development of Supernumerary Robotic Limbs. IEEE CAA J. Autom. Sin. 2021, 8, 929–952. [Google Scholar] [CrossRef]
- Rahman, A.; Azim, M.A.R.; Heo, S. Take My Hand: Automated Hand-Based Spatial Guidance for the Visually Impaired. In Proceedings of the Conference on Human Factors in Computing Systems, Hamburg, Germany, 23–28 April 2023. [Google Scholar] [CrossRef]
- Dementyev, A. Dynamic Wearable Technology: Designing and Deploying Small Climbing Robots for Sensing and Actuation on the Human Body. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2019. [Google Scholar]
- Dementyev, A.; Jitosho, R.; Paradiso, J.A. Mechanical imaging of soft tissues with miniature climbing robots. IEEE Trans. Biomed. Eng. 2021, 68, 3142–3150. [Google Scholar] [CrossRef] [PubMed]
- Wu, X.; Liu, J.; Zhou, Y.; Lv, Q.; Hu, C. Movement Control and Attitude Adjustment of Climbing Robot on Flexible Surfaces. IEEE Trans. Ind. Electron. 2018, 65, 2618–2628. [Google Scholar] [CrossRef]
- Dobbelstein, D.; Stemasov, E.; Besserer, D.; Stenske, I.; Rukzio, E. Movelet: A self-actuated movable bracelet for positional haptic feedback on the user’s forearm. In Proceedings of the ACM International Symposium on Wearable Computers, Singapore, 8–12 October 2018. [Google Scholar] [CrossRef]
- Sathya, A.; Li, J.; Rahman, T.; Gao, G.; Peng, H. Calico: Relocatable On-cloth Wearables with Fast, Reliable, and Precise Locomotion. Proc. ACM Interact. Mob. Wearable Ubiquitous Technol. 2022, 6, 1–32. [Google Scholar] [CrossRef]
- Kao, H.L.; Ajilo, D.; Anilionyte, O.; Dementyev, A.; Choi, I.; Follmer, S.; Schmandt, C. Exploring interactions and perceptions of kinetic wearables. In Proceedings of the Conference on Designing Interactive Systems, Edinburgh, UK, 10–14 June 2017; pp. 391–396. [Google Scholar] [CrossRef]
- Kimura, K.; Tanaka, F. Development of a Wearable Robot that Moves on the User’s Arm to Provide Calming Interactions. In Proceedings of the ACM/IEEE International Conference on Human-Robot Interaction, Stockholm, Sweden, 13–16 March 2023; pp. 311–313. [Google Scholar] [CrossRef]
- Liu, F.; Patil, V.; Erickson, Z.; Temel, Z. Characterization of a Meso-Scale Wearable Robot for Bathing Assistance. In Proceedings of the IEEE International Conference on Robotics and Biomimetics (ROBIO), Jinghong, China, 5–9 December 2022; pp. 2146–2152. [Google Scholar] [CrossRef]
- Sikdar, S.; Rahman, M.H.; Siddaiah, A.; Menezes, P.L. Gecko-Inspired Adhesive Mechanisms and Adhesives for Robots—A Review. Robotics 2022, 11, 143. [Google Scholar] [CrossRef]
- Fang, G.; Cheng, J. Advances in Climbing Robots for Vertical Structures in the Past Decade: A Review. Biomimetics 2023, 8, 47. [Google Scholar] [CrossRef]
- Jamšek, M.; Sajko, G.; Krpan, J.; Babič, J. Design and Control of a Climbing Robot for Autonomous Vertical Gardening. Machines 2024, 12, 141. [Google Scholar] [CrossRef]
- Dementyev, A.; Hernandez, J.; Choi, I.; Follmer, S.; Paradiso, J. Epidermal Robots: Wearable Sensors that Climb on the Skin. Proc. Acm Interact. Mob. Wearable Ubiquitous Technol. 2018, 2, 1–22. [Google Scholar] [CrossRef]
- Liu, Y.; Wu, X.; Qian, H.; Zheng, D.; Sun, J.; Xu, Y. System and design of clothbot: A robot for flexible clothes climbing. In Proceedings of the IEEE International Conference on Robotics and Automation, St. Paul, MN, USA, 14–18 May 2012; pp. 1200–1205. [Google Scholar] [CrossRef]
- Chen, G.; Liu, Y.; Fu, R.; Sun, J.; Wu, X.; Xu, Y. Rubbot: Rubbing on flexible loose surfaces. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Tokyo, Japan, 3–7 November 2013; pp. 2303–2308. [Google Scholar] [CrossRef]
- Dementyev, A.; Kao, C.H.L.; Choi, I.; Ajilo, D.; Xu, M.; Paradiso, J.; Schmandt, C.; Follmer, S. Rovables: Miniature On-Body Robots as Mobile Wearables. In Proceedings of the 29th Annual Symposium on User Interface Software and Technology, Tokyo, Japan, 16–19 October 2016; pp. 111–120. [Google Scholar] [CrossRef]
- Birkmeyer, P.; Gillies, A.G.; Fearing, R.S. CLASH: Climbing vertical loose cloth. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, San Francisco, CA, USA, 25–30 September 2011; pp. 5087–5093. [Google Scholar] [CrossRef]
- Saga, T.; Munekata, N.; Ono, T. Daily support robots that move on me. In Proceedings of the SIGGRAPH Asia 2014 Emerging Technologies, Singapore, 28 November–1 December 2014; pp. 1–3. [Google Scholar] [CrossRef]
- Kim, J.H.H.; Patil, S.D.; Matson, S.; Conroy, M.; Kao, C.H.L. KnitSkin: Machine-Knitted Scaled Skin for Locomotion. In Proceedings of the Conference on Human Factors in Computing Systems, Orleans, LA, USA, 29 April–5 May 2022. [Google Scholar] [CrossRef]
- Liu, J.H.; Padrigalan, K.E. The kinematic analysis of a wind turbine climbing robot mechanism. Appl. Sci. 2022, 12, 1210. [Google Scholar] [CrossRef]
- Shah, D.; Dave, J.; Majithiya, A.; Patel, Y. Conceptual design and analysis of pipe climbing robot. J. Phys. Conf. Ser. 2021, 2115, 012004. [Google Scholar] [CrossRef]
- Li, J.; Huang, F.; Tu, C.; Tian, M.; Wang, X. Elastic Obstacle-Surmounting Pipeline-Climbing Robot with Composite Wheels. Machines 2022, 10, 874. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, Y.; Zhang, B. Development and Experiment of Clamp Type Submarine Cable Inspection Robot. Machines 2023, 11, 627. [Google Scholar] [CrossRef]
- Zheng, Z.; Zhang, W.; Fu, X.; Hazken, S.; Hu, X.; Chen, H.; Luo, J.; Ding, N. CCRobot-IV: An obstacle-free split-type quad-ducted propeller-driven bridge stay cable-climbing robot. IEEE Robot. Autom. Lett. 2021, 7, 11751–11758. [Google Scholar] [CrossRef]
- Wan, J.; Sun, L.; Du, T. Design and applications of soft actuators based on Digital Light Processing (DLP) 3D printing. IEEE Access 2023, 11, 86227–86242. [Google Scholar] [CrossRef]
- Mendoza, N.; Haghshenas-Jaryani, M. Combined Soft Grasping and Crawling Locomotor Robot for Exterior Navigation of Tubular Structures. Machines 2024, 12, 157. [Google Scholar] [CrossRef]
- Xie, D.; Liu, J.; Kang, R.; Zuo, S. Fully 3D-printed modular pipe-climbing robot. IEEE Robot. Autom. Lett. 2020, 6, 462–469. [Google Scholar] [CrossRef]
- Yuan, S.; Shao, L.; Yako, C.L.; Gruebele, A.; Salisbury, J.K. Design and control of roller grasper V2 for in-hand manipulation. In Proceedings of the 2020 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Las Vegas, NV, USA, 25–29 October 2020; pp. 9151–9158. [Google Scholar] [CrossRef]
- Backus, S.B.; Dollar, A.M. An Adaptive Three-Fingered Prismatic Gripper with Passive Rotational Joints. IEEE Robot. Autom. Lett. 2016, 1, 668–675. [Google Scholar] [CrossRef]
- Tafrishi, S.A.; Svinin, M.; Yamamoto, M.; Hirata, Y. A geometric motion planning for a spin-rolling sphere on a plane. Appl. Math. Model. 2023, 121, 542–561. [Google Scholar] [CrossRef]
- Rimon, E.; Burdick, J. Towards planning with force constraints: On the mobility of bodies in contact. In Proceedings of the 1993 Proceedings IEEE International Conference on Robotics and Automation, Atlanta, GA, USA, 2–6 May 1993; Volume 1, pp. 994–1000. [Google Scholar] [CrossRef][Green Version]
- Poonwattanachai, K.; Niparnan, N.; Sudsang, A. Computation of Three-Finger Grasping Plane. In Proceedings of the 2018 22nd International Computer Science and Engineering Conference (ICSEC), Chiang Mai, Thailand, 21–24 November 2018; pp. 1–5. [Google Scholar] [CrossRef]
- Schünke, M.; Schulte, E.; Schumacher, U.; Voll, M.; Wesker, K. LernAtlas der Anatomie; 2022. Available online: http://www.ciando.com/img/books/extract/3132420840_lp.pdf (accessed on 1 July 2024).
- Preedy, V.R. Handbook of Anthropometry: Physical Measures of Human Form in Health and Disease; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Pastor, F.; Lin-Yang, D.H.; Gómez-de Gabriel, J.M.; García-Cerezo, A.J. Dataset with Tactile and Kinesthetic Information from a Human Forearm and Its Application to Deep Learning. Sensors 2022, 22, 8752. [Google Scholar] [CrossRef] [PubMed]
- Ruiz-Ruiz, F.J.; Urdiales, C.; Gómez-de Gabriel, J.M. Estimation of the Interaction Forces in a Compliant pHRI Gripper. Machines 2022, 10, 1128. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).