Asymmetrical Four-Phase 8/6 Switched Reluctance Motor for a Wide Constant Power Region

Abstract

In this paper, the methodology for designing an asymmetrical four-phase 8/6 switched reluctance motor (SRM) that achieves approximately constant output power over a wide speed range is described. In an asymmetrical 8/6 SRM, orthogonal phase pairs are different in terms of the pole width and number of turns. The main comparison criterion between the asymmetrical and symmetrical 8/6 SRM is the power-speed characteristic, obtained for a given rated RMS phase current of the symmetrical drive. The obtained results demonstrate that the asymmetrical 8/6 SRM allows the shape of the power-speed characteristic to be modified, thereby extending the constant power region well beyond that of the symmetrical configuration with the same rated power level. To make a fair comparison between the asymmetrical and symmetrical 8/6 SRM drives, the converter volt-ampere rating, machine volume, slot fill factor, and ohmic losses per phase are kept constant in all analyzed cases. For determination of the optimal control parameters and maximal drive performance for both designs, the appropriate SRM mathematical model and differential evolution algorithm are used. The applied model includes all substantial non-linearities and mutual coupling between phases. The simulation results are verified using a Finite Element Method (FEM)-based model in the Ansys Electronics 2020 R2 software package.

1. Introduction

With qualities such as simple and cost-effective construction, good performance over a wide speed range, high reliability, and robustness, the switched reluctance motor (SRM) is a remarkable candidate for electric vehicles (EVs) and hybrid electric vehicles (HEVs), as well as home appliances [1,2,3,4]. In particular, there are a wide range of applications in which low-power SRMs can be implemented, such as electric bikes and scooters, power tools, etc. [5,6]. For the above applications, it is particularly important that the speed range in the constant power area is extended to reduce the requirement of motor rated power. The width of the constant power region depends on the SRM geometry, the power converter capability, and the employed control algorithm [1,2,7,8]. The research described in [1,2] gives the relationship between motor geometry and its constant power region width. As shown in [2], reducing the number of phases and the widths of stator and rotor poles extends the constant power region. The “pole changing” method, which ensures higher torque values at elevated speeds, is described in [9]. An improvement of the exploitation characteristic for SRMs used in home appliances is achieved in [10,11,12]. The constant power region can be extended by using improved power converter topologies and control algorithms that increase the efficiency of electromechanical energy conversion [13,14,15,16,17]. The results presented in [18,19] show that increasing the constant power range as well as the motor power can be achieved if the SRM operates in continuous conduction mode at high speeds. The asymmetrical three-phase 6/4 SRM drive with an unequal number of turns per motor phase can also provide the constant power range extension, which is experimentally verified in [20].

In this paper, an original design and control methodology of an asymmetrical four-phase 8/6 SRM that provides approximately constant output power over a wide speed range is proposed. Orthogonal phase pairs of the asymmetrical 8/6 SRM are different in terms of the pole width and number of turns compared to the symmetrical design. The main comparison criterion between the asymmetrical and symmetrical 8/6 SRM drive is the power-speed characteristic, obtained for a given rated RMS phase current of the symmetrical drive. The obtained results demonstrate that the asymmetrical 8/6 SRM allows the shape of the power-speed characteristic to be modified, thereby extending the constant power region well beyond that of the symmetrical configuration with the same rated power level. To make a fair comparison between the asymmetrical and symmetrical designs, the converter volt-ampere rating, machine volume, slot fill factor, and ohmic losses per phase are kept constant in all analyzed cases. To determine the optimal design and control parameters, a two-step optimization procedure is developed. A detailed transient asymmetrical 8/6 SRM model including mutual phase coupling effects and saturation is developed specifically for use within the optimization algorithm. The applied model is comparable to a corresponding FEM model in terms of accuracy while significantly reducing execution time. A family of optimal solutions is obtained for each set of input design parameters, thereby allowing the user to select the best design for the specific application.

This study is organized as follows: Section 2 shows basic considerations related to the proposed asymmetrical 8/6 SRM. The asymmetrical 8/6 SRM design methodology is presented in Section 3. Section 4 presents and analyzes power-speed characteristics of the asymmetrical 8/6 SRM for the optimal design and control parameters. Asymmetrical 8/6 SRM examples with approximately constant power-speed characteristics are presented in Section 5. The obtained results are verified in Section 6 by using a FEM-based model. The cost analysis of the proposed solution is carried out in Section 7. Finally, conclusions are given in Section 8.

2. Basic Considerations Related to the Proposed Asymmetrical 8/6 SRM Drive

The base speed (Ω₀) of the SRM is defined as the speed at which the induced electromotive force (EMF) becomes equal to the DC-link voltage, while the output power and phase currents of the motor are at their rated values. Below the base speed, due to the low EMF value, torque control is performed by controlling the phase currents using hysteresis current control or PWM voltage control combined with the appropriate control algorithm [1]. The control parameters in this speed range are the reference current I_ref and the turn-on and turn-off angles (θ_ON and θ_OFF, respectively). Above the base speed, in the constant power region, the high EMF value forces the SRM to operate in the single-pulse voltage control mode, with θ_ON and θ_OFF as the only influential control parameters. Namely, as the speed increases, constant power operation is achieved by reducing angles θ_ON and θ_OFF and increasing their difference θ_DWELL = θ_OFF − θ_ON. By doing so, the power is maintained at the rated value over a wide speed range. However, after reaching a certain critical speed value Ω_C, the angle θ_ON cannot be reduced any further, as this would lead to phase magnetization in the negative torque area. Consequentially, for operating speeds above Ω_C, the torque and power begin to decrease proportionally as 1/Ω² and 1/Ω, respectively.

To further extend the constant power region, i.e., to increase the critical speed Ω_C, the reduction in θ_ON with respect to the speed increase should follow a slower trend. This can be achieved either by increasing the supply voltage or by designing a machine with a reduced number of turns per phase. The supply voltage, i.e., the DC link voltage, is predefined and limited in practical applications; therefore, its increase is not an option. On the other hand, a reduced number of turns would require a converter with a higher volt-ampere (VA) rating [19].

Another option for increasing the constant power range of the symmetrical SRM is to expand the feasible range of the turn-on angle θ_ON by reducing the stator pole width. However, this would decrease the available torque of the SRM. As shown in [1], increasing the stator and rotor pole width increases the torque, but at the cost of reducing the constant speed range. Optimization of the control parameters for a given rated current with torque as the objective function is performed in [2]. It is shown that the output power significantly varies inside the theoretically constant power range, and that its value is greater compared to the one at base speed.

If an 8/6 SRM is designed in an asymmetrical manner, with one pair of orthogonal phases having a lower number of turns compared to the symmetrical design and the other pair having a higher number of turns, then the contribution of orthogonal phase pairs to the power-speed characteristic and VA requirements will be different. The reduced number of turns improves the power-speed characteristic but increases the VA requirements imposed on the converter. On the other hand, the increased number of turns decreases the constant power region width but also reduces the VA requirements. Additionally, there is a possibility that the corresponding orthogonal phase pairs of such an asymmetrical 8/6 SRM have different stator pole widths, which also has a direct influence on the power-speed characteristic and converter VA requirements.

The proposed asymmetrical 8/6 SRM needs to fulfill the following conditions with respect to the corresponding symmetrical design:

(i)

The VA demands remain unchanged.

(ii)

The magnetic circuit remains unchanged, except potentially the width of stator poles. If the stator pole widths are varied, their total volume must remain unchanged.

(iii)

The slot fill factor remains unchanged.

(iv)

The ohmic losses per phase remain unchanged.

Designing an asymmetrical 8/6 SRM drive under the given conditions allows the power-speed characteristic to be modified and achieves a uniform power distribution over a wide speed range. Though the maximal power attainable using the asymmetrical design is lower compared to the symmetrical design, the maximal power of the symmetrical 8/6 SRM often exceeds the required power significantly. Therefore, the symmetrical 8/6 SRM has unexploited power capability at low speeds, while being unable to deliver the required power at higher speeds.

On the other hand, the asymmetrical design reduces the available power in the low-speed region, while increasing the available power in the high-speed region. By properly selecting the number of turns, stator pole widths, and control parameters, the power-speed characteristic of the asymmetrical 8/6 SRM can be modified to obtain a much wider constant power range compared to the symmetrical design. The asymmetrical 8/6 SRM can essentially be viewed as a combination of two symmetrical SRMs with different pole widths and different numbers of turns per phase. Increasing the number of turns and/or the pole width results in high torque in the low-speed region, whereas reducing the number of turns and/or pole width extends the constant-power region, but at the cost of torque reduction in the low-speed region. The asymmetrical 8/6 SRM takes advantage of both benefits, thereby achieving a wider constant power region with uniform power distribution, while maintaining a satisfactory torque output at lower speeds. The methodology for optimal asymmetrical 8/6 SRM drive design is presented in the following section.

3. Asymmetrical 8/6 SRM Drive Methodology

3.1. Asymmetrical 8/6 SRM Drive Design Principles

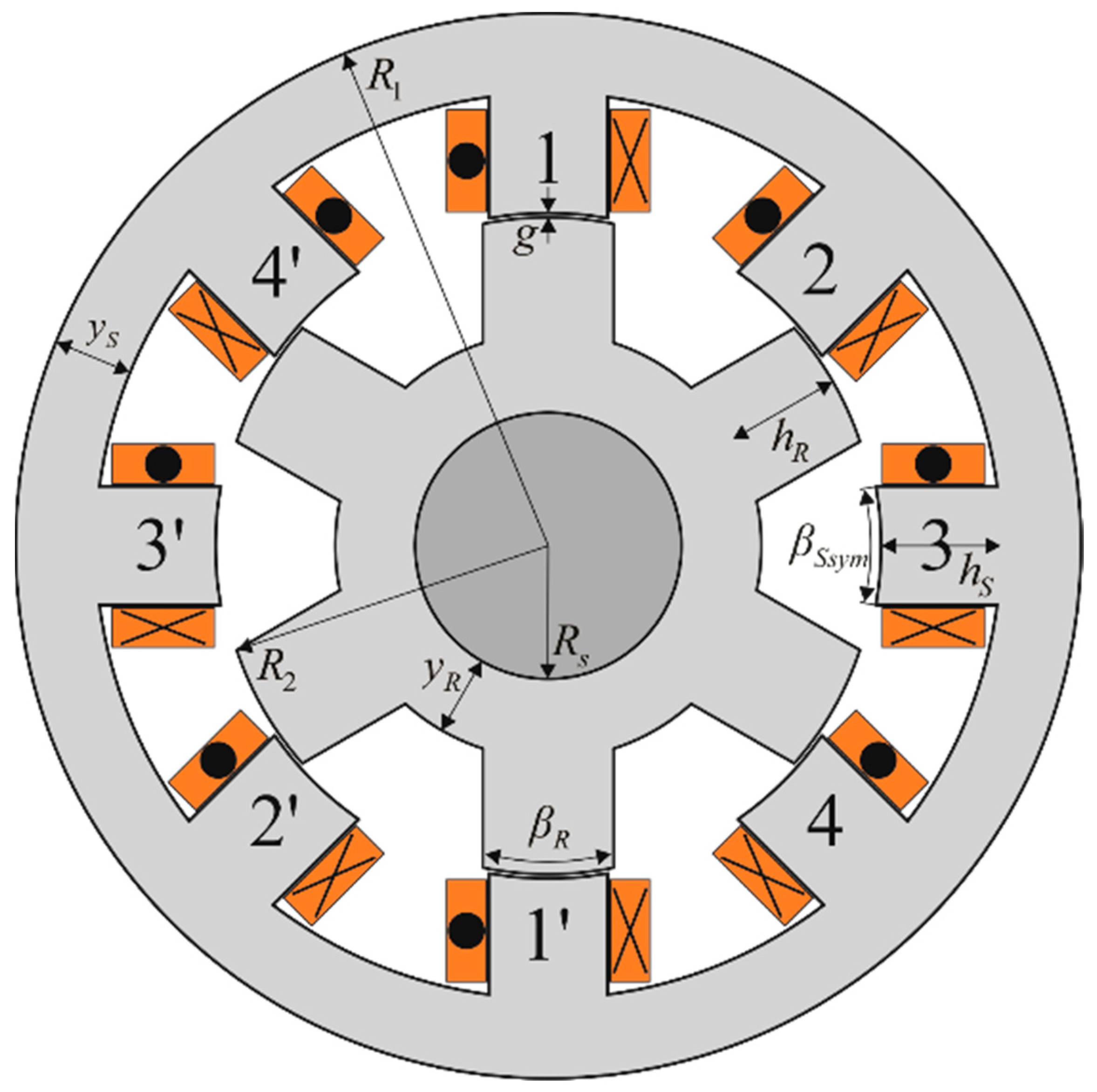
To introduce the asymmetrical 8/6 SRM, we start from the symmetrical 8/6 SRM displayed in Figure 1 with the parameters given in Appendix A. According to Figure 1, the slot cross-section area is defined as

$$A_{slot}^{sym}=\frac{1}{N_S}\left[\frac{\pi }{4}[{(2(R_2+g)+2h_S)}^2-{(2(R_2+g))}^2]-N_S{t}_{Ssym}{h}_S\right]$$

(1)

where t_Ssym = 2(R₂ + g)∙sin(β_Ssym·π/360) is the stator pole width expressed in millimeters. The symmetrical 8/6 SRM holds N_sym/2 coil sides of one phase in each slot, with N_sym being the total number of coils per phase. The total slot area occupied by conductors is

$$A_{wCu}^{sym}=N_{sym}{A}_{wCu}$$

(2)

where A_wCu is the total conductor cross-section area (including insulation).

The slot fill factor can be expressed according to (1) and (2) as

$$k_{fill}^{sym}=\frac{A_{wCu}^{sym}}{A_{slot}^{sym}}$$

(3)

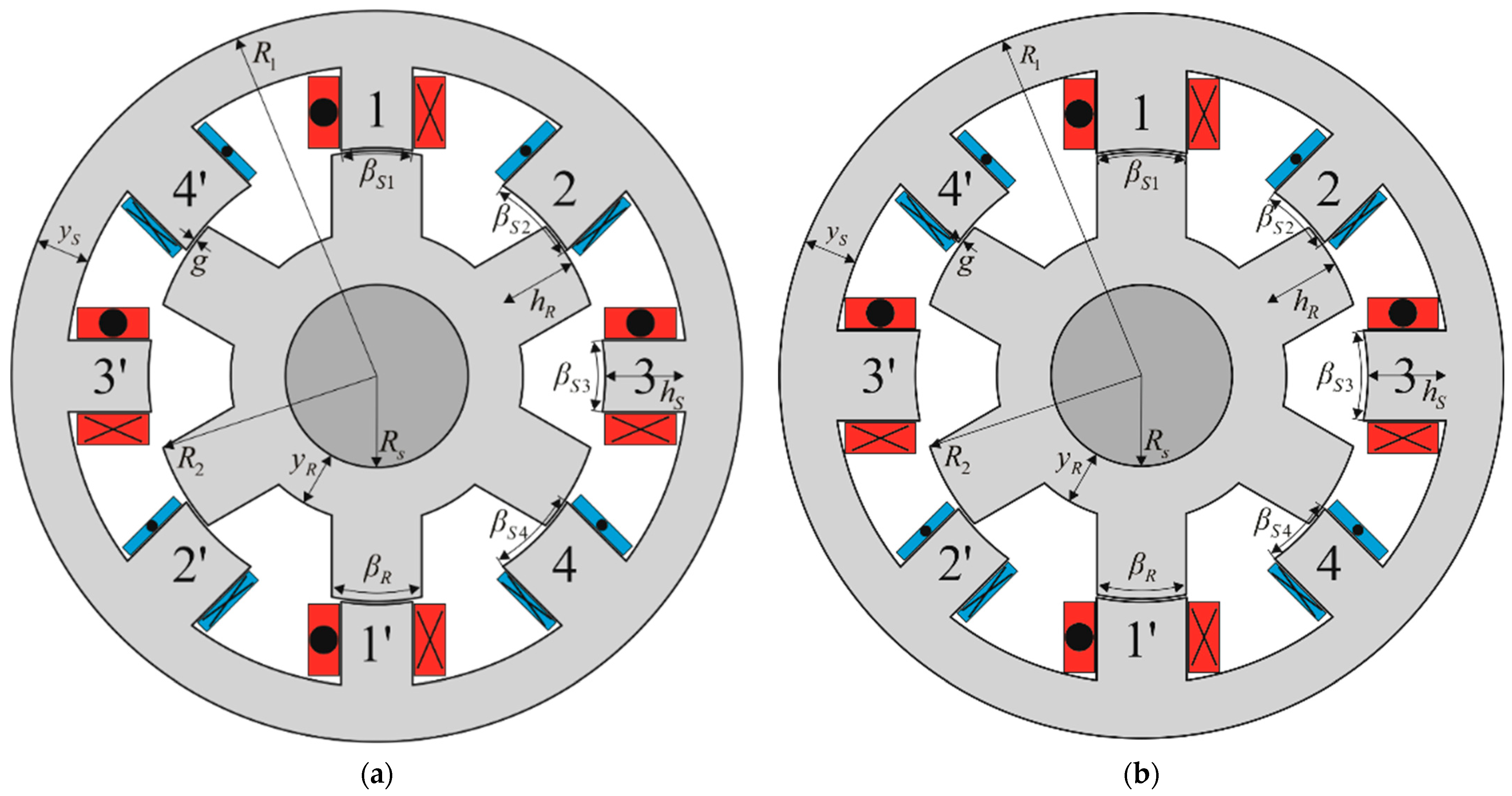
The asymmetrical 8/6 SRM concept is displayed in Figure 2. The orthogonal phases 1 and 3 have the same number of turns N₁ = N₃ = N₁₃ and stator pole span β_S1 = β_S3 = β_S13. The same holds for the other orthogonal phase pair (phases 2 and 4), namely, N₂ = N₄ = N₂₄ and stator pole span β_S2 = β_S4 = β_S24.

Two variants of the asymmetrical 8/6 SRM are analyzed and compared. In the first variant (variant 1), as shown in Figure 2a, orthogonal phases 1 and 3 have a higher number of turns compared to the symmetrical design (N₁₃ > N_sym), whereas the orthogonal phases 2 and 4 have a lower number of turns (N₂₄ < N_sym). The stator poles of phases 1 and 3 span the same or a smaller angle compared to the symmetrical design (β_S13 ≤ β_Ssym), whereas the opposite holds for phases 2 and 4 (β_S24 ≥ β_Ssym). The second variant (variant 2) differs from the first in terms of stator pole widths. In variant 2, the stator poles of phases 1 and 3 span a larger angle than the poles of the symmetrical configuration (β_S13 ≥ β_Ssym), whereas the poles of phases 2 and 4 span a smaller angle (β_S24 ≤ β_Ssym). The other parts of the magnetic circuit in both variants are unchanged compared to the symmetrical configuration, according to condition (ii).

According to Figure 2 and the machine cross-section, in an asymmetrical 8/6 SRM with N_S = 8 stator poles, N_S/2 poles have a width of t_S13 = 2(R₂ + g)·sin(β_S13·π/360), whereas the widths of the remaining N_S/2 poles equal t_S24 = 2(R₂ + g)·sin(β_S24·π/360). It should be noted that condition (ii) must be satisfied, which translates to

$${\beta }_{S13}+{\beta }_{S24}=2{\beta }_{Ssym}.$$

(4)

All slots of the asymmetrical 8/6 SRM have the same cross-section area given by

$$A_{slot}^{asym}=\frac{1}{N_S}\left[\frac{\pi }{4}[{(2(R_2+g)+2h_S)}^2-{(2(R_2+g))}^2]-\frac{N_S}{2}(t_{S13}+t_{S24})h_S\right],$$

(5)

whereas the coil-filled area of the slot equals

$$A_{wCu}^{asym}=\frac{1}{2}(N_{13}+N_{24})A_{wCu}.$$

(6)

The fill factor of the asymmetrical 8/6 SRM is determined as

$$k_{fill}^{asym}=\frac{A_{wCu}^{asym}}{A_{slot}^{asym}}.$$

(7)

If a constant K is defined as

$$K={\left(2(R_2+g)+2h_S\right)}^2-{\left(2(R_2+g)\right)}^2,$$

(8)

to simplify given relationships, and considering that the fill factors of the symmetrical and asymmetrical 8/6 SRM are mutually equal, Equations (3) and (7) can be combined to obtain the following relationship:

$$\frac{N_{13}+N_{24}}{N_{sym}}=2\frac{K-\frac{N_S}{2}(t_{S13}+t_{S24})h_S}{K-N_S{t}_{Ssym}{h}_S}.$$

(9)

After introducing coefficients, for the sake of easier manipulations,

$$k_{13}=\frac{N_{13}}{N_{sym}}$$

(10)

and

$$k_{24}=\frac{N_{24}}{N_{sym}},$$

(11)

the previous expression can be formulated as

$$k_{13}+k_{24}=2\frac{K-\frac{N_S}{2}(t_{S13}+t_{S24})h_S}{K-N_S{t}_{Ssym}{h}_S}.$$

(12)

Equation (12) defines the relationship between the number of turns and stator pole width of the symmetrical and asymmetrical 8/6 SRMs. When β_S13 = β_S24 = β_Ssym, (12) reduces to k₁₃ + k₂₄ = 2, which verifies derived relationships.

Condition (iv) defined in Section 2 states that the ohmic per-phase losses of the asymmetrical 8/6 SRM may not be greater than the corresponding losses of the symmetrical 8/6 SRM, which is expressed as

$$R_{13}{I}_{13}^2=R_{24}{I}_{24}^2=R_{Ssym}{I}_{sym}^2,$$

(13)

where R₁₃ = R₁ = R₃, R₂₄ = R₂ = R₄, and R_Ssym are the phase winding resistances, and I₁₃ = I₁ = I₃, I₂₄ = I₂ = I₄, and I_sym are the corresponding RMS phase currents of the asymmetrical and symmetrical 8/6 SRM, respectively.

Using a software package [21], it was determined that the phase winding resistances can be approximately calculated as

$$R_i=\frac{N_i}{{\sigma }_{Cu}}\frac{2.84L+1.57t_{Si}}{A_{Cu}},$$

(14)

where i should be replaced by 13, 24, or sym, depending on the observed winding and configuration, σ_Cu is copper conductivity, A_Cu is the conductor cross-section area (insulation excluded), and L is the lamination stack length. Coefficients 2.84 and 1.57 in (14) are obtained by interpolation of the huge number of resistance values for different stator pole widths and number of turns.

By combining (13) and (14), coefficients k₁₃ and k₂₄ can be formulated as

$$k_{13}=\frac{2.84L+1.57t_{Ssym}}{2.84L+1.57t_{S13}}\cdot {\left(\frac{I_{sym}}{I_{13}}\right)}^2$$

(15)

and

$$k_{24}=\frac{2.84L+1.57t_{Ssym}}{2.84L+1.57t_{S24}}\cdot {\left(\frac{I_{sym}}{I_{24}}\right)}^2$$

(16)

We further introduce

$$x_{13}=\frac{I_{sym}}{I_{13}},$$

(17)

$$x_{24}=\frac{I_{sym}}{I_{24}},$$

(18)

and

$$f(t_{S13},t_{S24},t_{Ssym})=\frac{K-\frac{N_S}{2}(t_{S13}+t_{S24})h_S}{K-N_S{t}_{Ssym}{h}_S}.$$

(19)

By substituting (15)–(19) into (12), we obtain

$$z_{13}+z_{24}=1,$$

(20)

where

$$z_{13}=\frac{2.84L+1.57t_{Ssym}}{2f(t_{S13},t_{S24},t_{Ssym})(2.84L+1.57t_{S13})}{(x_{13})}^2,$$

(21)

and

$$z_{24}=\frac{2.84L+1.57t_{Ssym}}{2f(t_{S13},t_{S24},t_{Ssym})(2.84L+1.57t_{S24})}{(x_{24})}^2.$$

(22)

According to condition (i), to obtain comparable power (torque)-speed characteristics, the asymmetrical 8/6 SRM must have the same VA demands as its symmetrical counterpart. The asymmetrical half-bridge converter (AHBC) is considered a benchmark topology for SRM supply [1]. However, supplying an 8/6 SRM from an AHBC involves three “Short Flux Path Excitation” (SFPE) modes and one “Long Flux Path Excitation” (LFPE) mode within each electrical cycle [22]. Mutual coupling between the phases causes differences in the phase current waveforms of the 8/6 SRM, and consequentially, their RMS values differ [22,23,24,25].

To fulfill condition (13), RMS current values of orthogonal phases must be equal, i.e., I₁ = I₃ and I₂ = I₄, which is possible if magnetic symmetry between phases exists. Magnetic symmetry can be achieved using industrial dual-pack modules (H-bridges) with the control algorithm [22], which ensures four SFPEs over each electrical cycle. This type of supply results in bipolar phase currents. 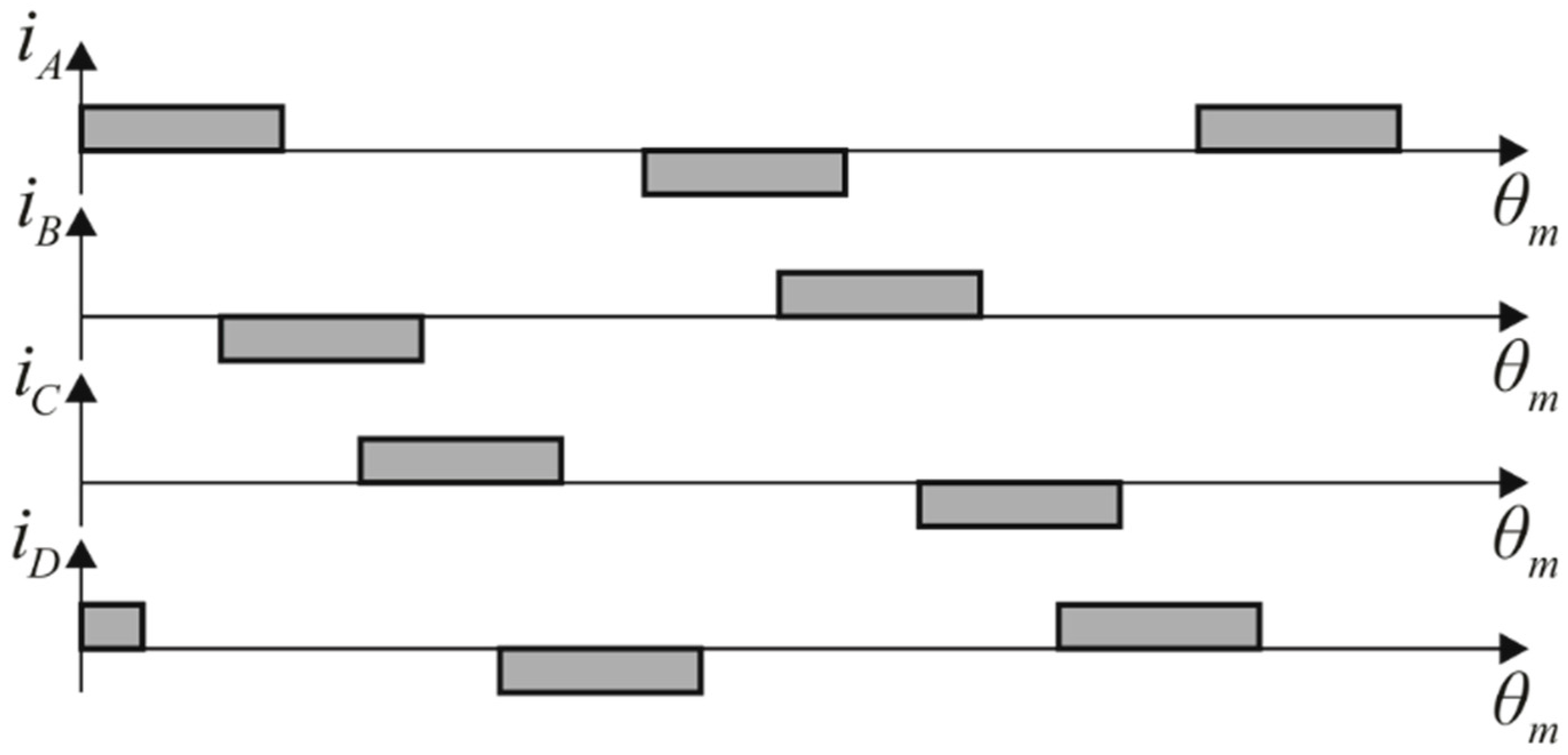A converter topology that ensures magnetic symmetry in both the symmetrical and asymmetrical 8/6 SRM consists of four separate full-bridge (H-bridge) converters, one supplying each phase [22]. The bipolar phase excitation [22] corresponding to the coil directions shown in Figure 1 and Figure 2 for maintaining a SFPE within each electrical cycle of an 8/6 SRM is illustrated in Figure 3.

When magnetic symmetry is ensured, the magnitudes of orthogonal phase currents are mutually equal. The condition (i) related to the equality of total converter VA demands of the asymmetrical and symmetrical designs can be formulated as

$$8V_{13}{I}_{13\max \_P}+8V_{24}{I}_{24\max \_P}=16V{I}_{sym\max \_P},$$

(23)

where I_{13max_P}, I_{24max_P}, and I_{symmax_P} are the maximal phase current peaks of the asymmetrical and symmetrical 8/6 SRM, respectively, whereas V₁₃, V₂₄, and V are the corresponding DC-link voltages. As all H-bridges are connected to the same DC-link, the DC-link voltages are mutually equal (V₁₃ = V₂₄ = V), and (23) is reduced to

$$I_{13\max \_P}+I_{24\max \_P}=2I_{sym\max \_P}.$$

(24)

By introducing coefficients c₁₃ = I_{13max_P}/I_{symmax_P,} and c₂₄ = I_{24max_P}/I_{symmax_P}, the previous relationship can be reformulated as

$$c_{13}+c_{24}=2.$$

(25)

3.2. Asymmetrical 8/6 SRM Drive Design and Control Optimization

The optimal 8/6 SRM design and control parameters need to be determined. To do so, the following steps are followed:

(a)

Feasible combinations of stator pole widths (β_S13, β_S24) and numbers of turns (N₁₃, N₂₄) are defined according to conditions (4) and (20);

(b)

Optimization is first performed for each of the selected β_S13/β_S24 combinations. The optimization variables are the numbers of turns N₁₃ and N₂₄ and the control parameters (reference phase currents and turn-on and turn-off angles). The optimization objective is to obtain the maximal torque while satisfying constraints (i)–(iv) defined in Section 2. Optimization is performed over a wide speed range of 400–13,200 rpm;

(c)

Optimization of control parameters is performed for selected β_S13/β_S24 and N₁₃/N₂₄ combinations from the previous step. Unlike the previous step, a fixed number of turns is now used over the entire speed range in each optimization run;

(d)

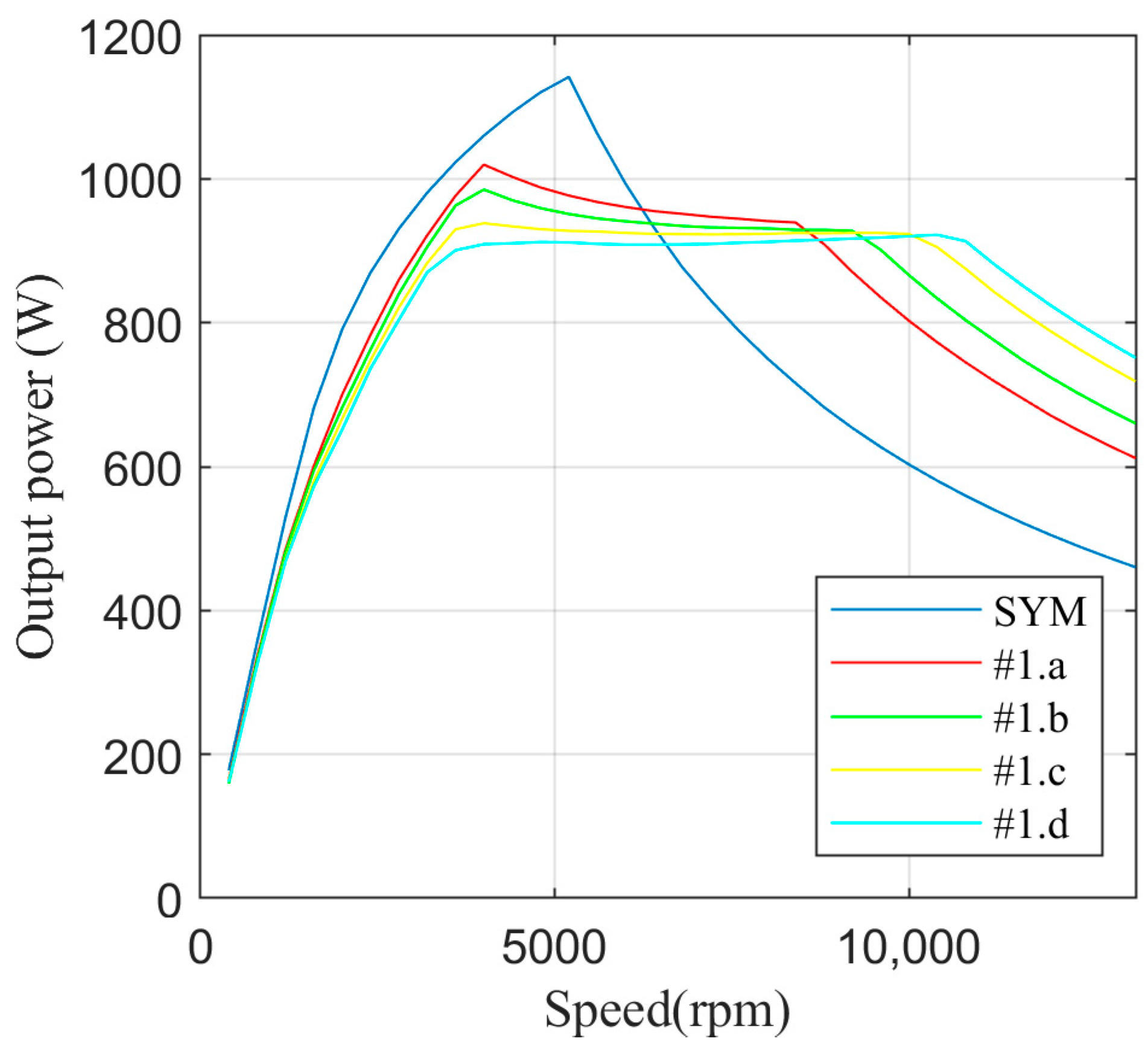
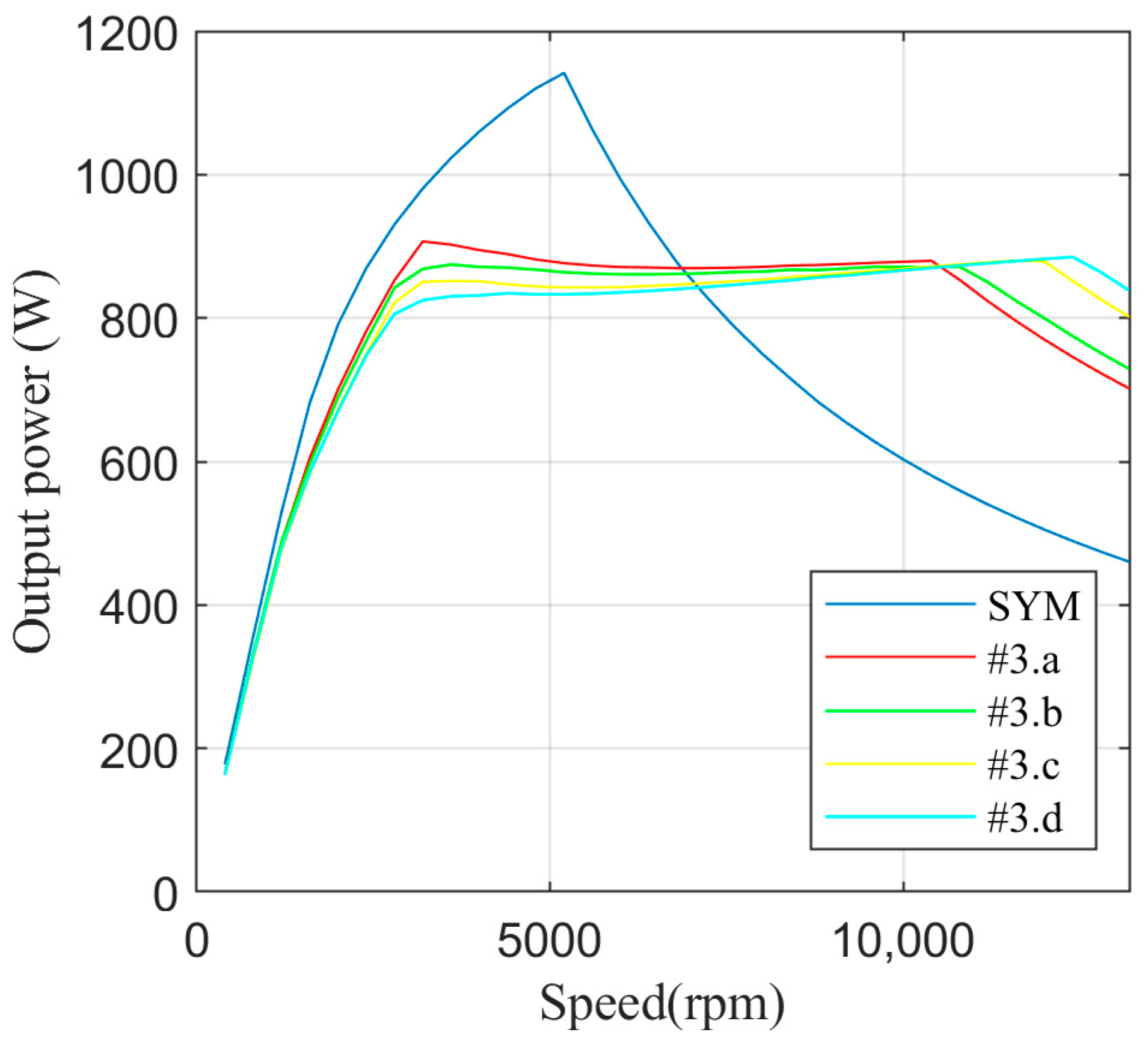
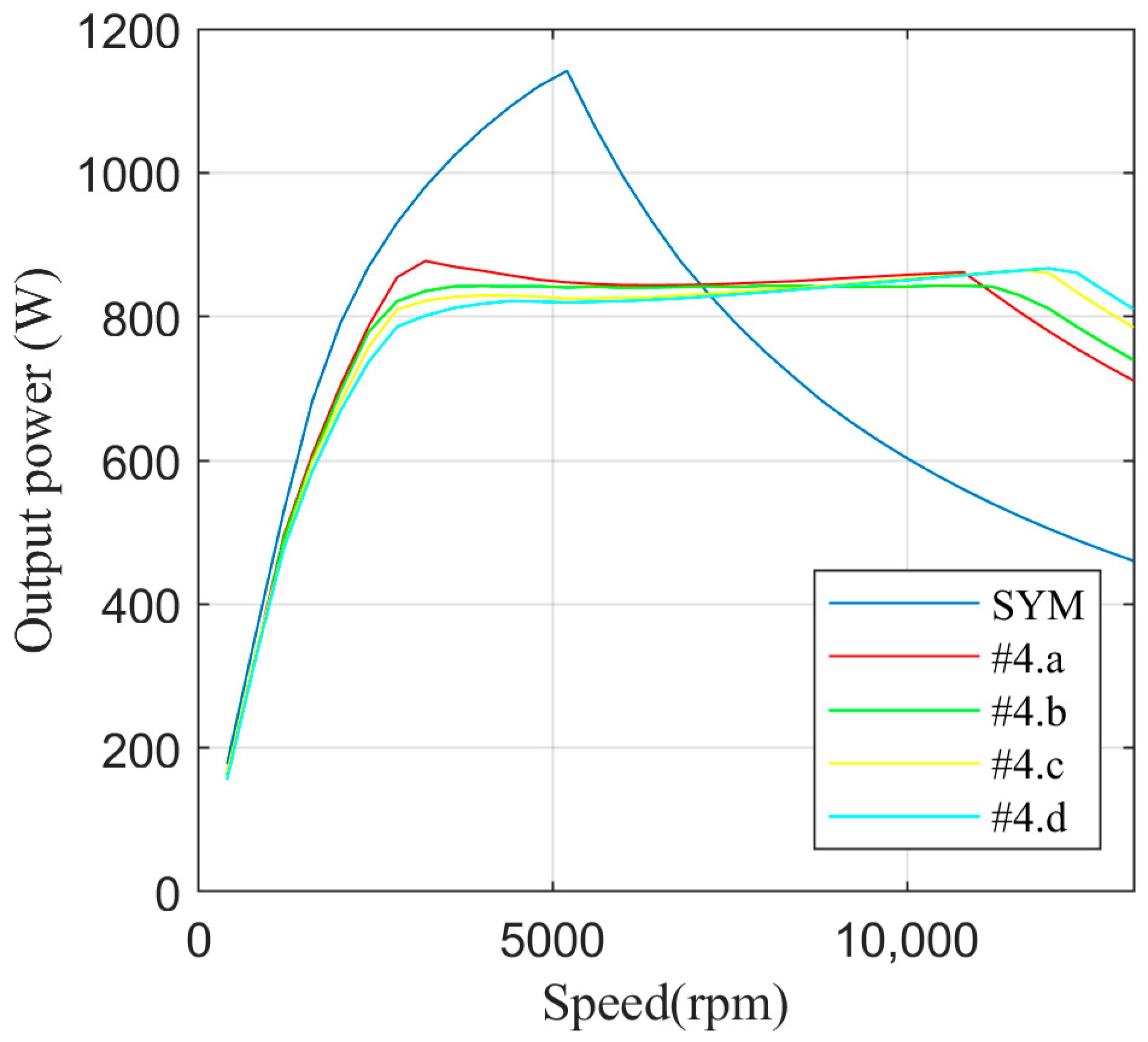
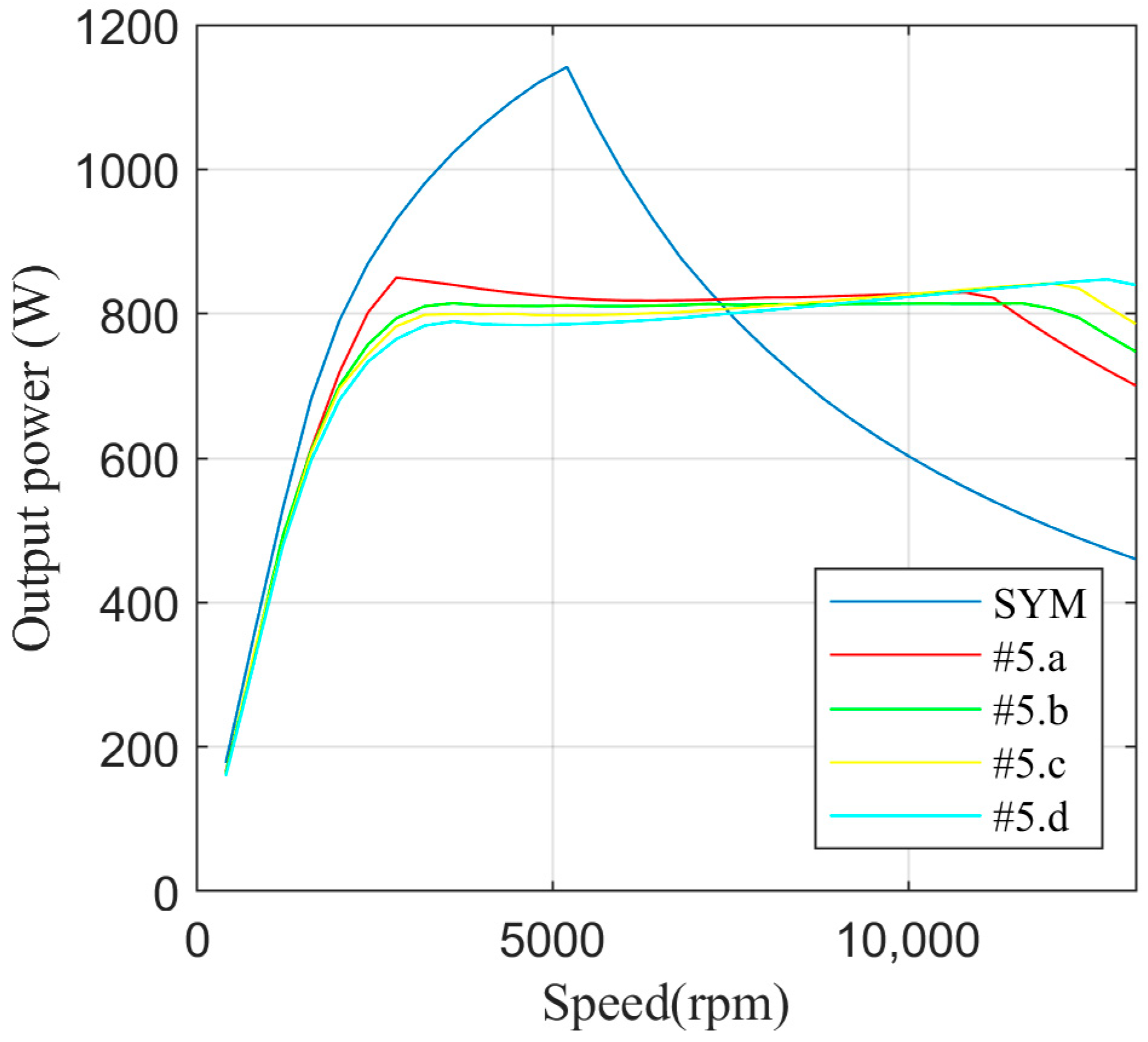
A single combination of pole widths (β_S13, β_S24) and numbers of turns (N₁₃, N₂₄) is selected and declared optimal based on the shapes of the respective power-speed characteristics obtained in the previous step.

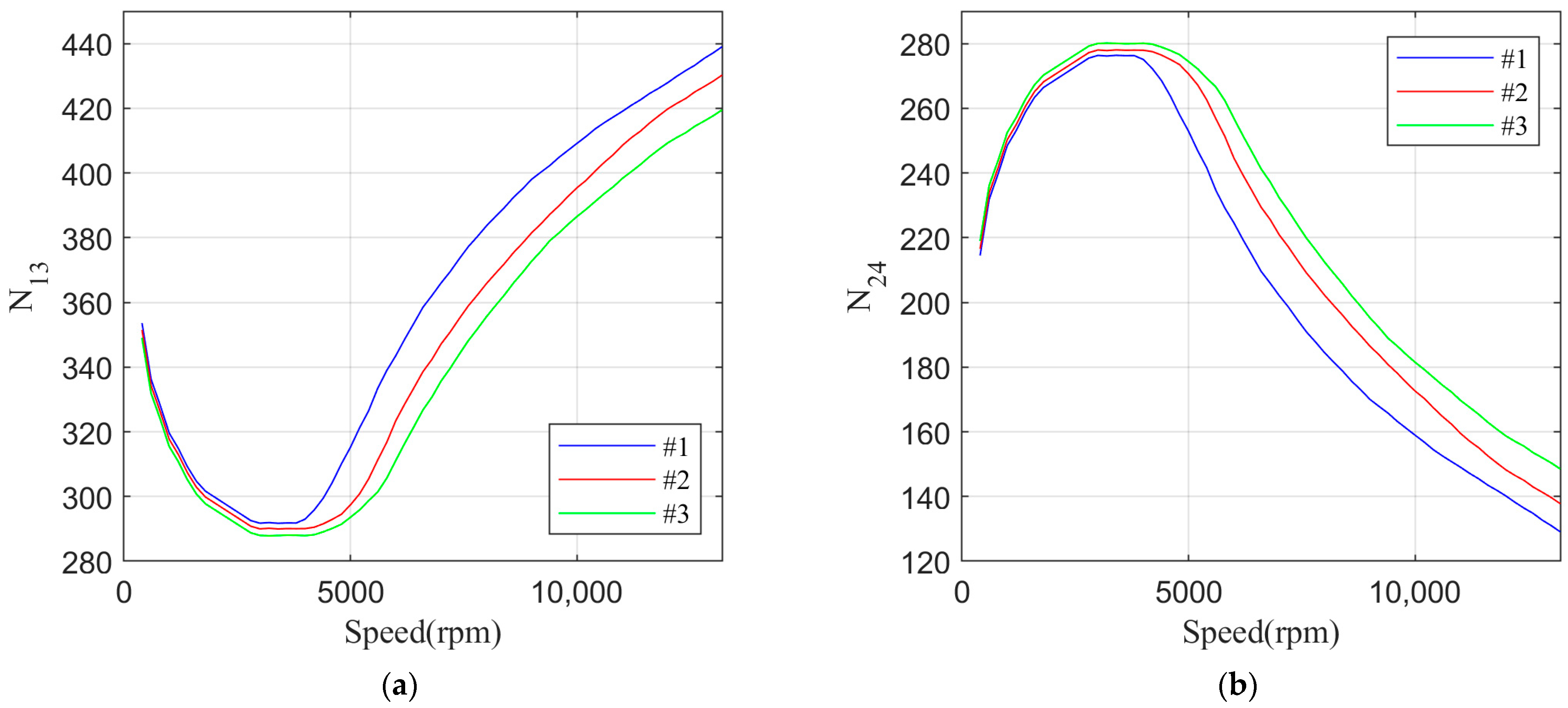
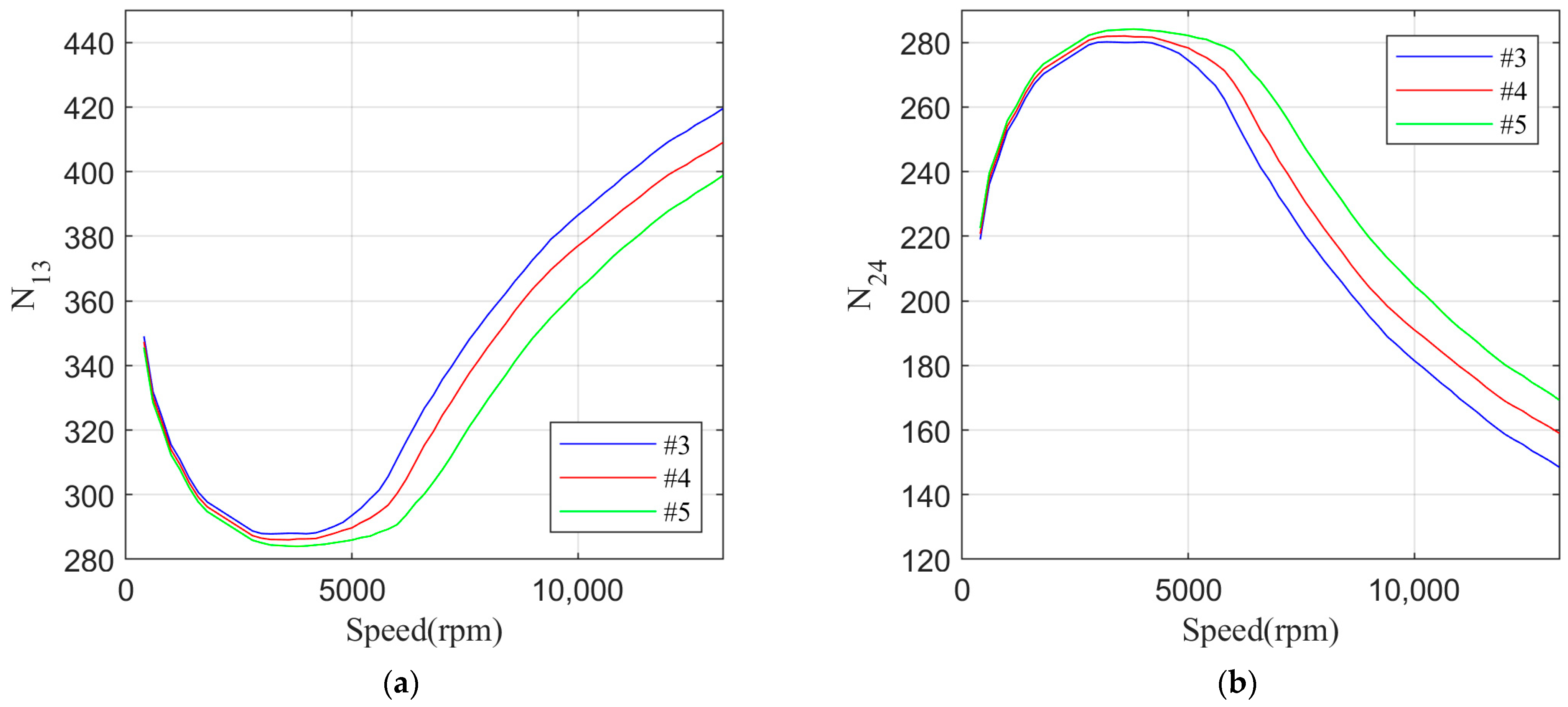
The optimization procedure requires that the ranges of optimization variables and all constraints are defined. The optimization variables are as follows:

• Coefficients z₁₃ and z₂₄;
• Coefficients c₁₃ and c₂₄;
• Turn-on angles for each set of orthogonal phases (θ_ON13, θ_ON24);
• Dwell angles for each set of orthogonal phases (θ_DWELL13, θ_DWELL24).

It should be noted that all of the listed variables are optimized only in the first stage (step (b)), when design and control optimization are conducted simultaneously. In the second stage (step (c)), only the control parameters (θ_ON13, θ_ON24, θ_DWELL13, θ_DWELL24) are optimized for a selected design obtained in step (b). Such an approach is required, as design parameters obviously cannot be modified during operation. On the other hand, the optimal set of control parameters for the selected design is determined only for a single operating point in step (b); therefore, control parameter optimization must be conducted for all other operating points. In this way, optimization in step (c) results in optimal driver performance using a specific 8/6 SRM design obtained in step (b). It should be noted that simultaneous optimization of design and control parameters in step (b) is necessary to determine optimal design parameters. A JADE (Joint Optimization Differential Evolution) algorithm [26] is used for optimization of the design and control parameters. The algorithm implements a “current-to-p-best” mutation strategy with self-adaptive values of mutation and crossover rates to ensure fast and reliable convergence. The optimization algorithm is based on randomly selecting values of optimization variables within defined ranges, each combination constituting one viable candidate solution. In each step of the optimization, the algorithm attempts to improve the candidate solutions by preserving, replacing, or modifying previous solutions based on their measure of quality.

The outline of the JADE algorithm is illustrated by the flowchart in Figure 4. Some of the specifics regarding algorithm implementation in this paper should be emphasized:

• The limit values of optimization variables are determined empirically to include all feasible design and control variants.
• The population size N_P is set to 40 in step (b) and to 24 in step (c).
• The optimization is completed if the number of iterations is higher than 100 and the standard deviation of average torque (T_avg) is lower than 0.5 Nm. If this condition is never met, the optimization procedure is ended after 400 generations.
• Individuals are ranked according to the obtained average torque T_avg. The optimization constraint is that RMS currents may not exceed predefined permissible values.

To avoid overburdening the text, only the application-specific aspects of the JADE algorithm have been addressed. For more details, particularly regarding the self-adaptation of algorithm control parameters, one should refer to [26].

Coefficients z₁₃ and z₂₄ are corelated by (20), and c₁₃ and c₂₄ are corelated by (25). Therefore, there are a total of six independent optimization variables. Note that z₁₃ and z₂₄ are complex functions of the machine dimensions, number of turns, and RMS current, whereas c₁₃ and c₂₄ are proportional to maximal phase current peaks. The stator pole width combination is not an optimization variable, as it is selected prior to each optimization run. The minimal stator pole width is limited to 360°/N_S/q = 15° due to starting requirements [1], whereas the rotor pole width β_R needs to be greater or equal to the width of the stator poles. The stator pole spans must therefore be kept within ranges β_S13 = (15°, β_Ssym) and β_S24 = (β_Ssym, β_R) in the case of variant 1, and vice versa in the case of variant 2. The selected values of pole widths must also satisfy condition (4). On the other hand, considering relationship (20), the theoretical range for coefficient z₁ would be (0, 1). However, seeing as N₁₃ > N_sym, and due to practical limitations, the actual range of z₁ is reduced to (0.5, 0.8). The range of z₂₄ is then automatically determined, as z₂₄ = 1 − z₁₃. For given (selected) values of β_S13, β_S24 and z₁₃, z₂₄, values of x₁₃ and x₂₄ are determined from (21) and (22), after which maximal RMS currents of orthogonal phase sets I₁₃ and I₂₄ are calculated from (17) and (18), respectively. Based on the RMS current values, coefficients k₁₃ and k₂₄ are obtained. The numbers of turns N₁₃ and N₂₄ are determined based on the known values of k₁₃ and k₂₄. Finally, the phase winding resistances R₁₃ and R₂₄ are calculated according to (14). Having determined all the aforementioned parameters, a feasible asymmetrical 8/6 SRM drive that satisfies constraints (ii)–(iv) is defined, i.e., a design with the same fill factor and ohmic losses as the original symmetrical 8/6 SRM. In each iteration, N_P asymmetrical designs are defined in the described way, constituting a population.

Once the asymmetrical 8/6 SRM design parameters are defined, the control parameters need to be assigned to each asymmetrical design within the population. The control parameters should ensure maximal available torque without RMS phase currents exceeding maximal permissible values I₁₃ and I₂₄. The control parameters include reference current and turn-on and turn-off angles for each set of orthogonal phase pairs. Control parameters for phases 1 and 3 are the reference current I_ref13, turn-on angle θ_ON13, and turn-off angle θ_OFF13. The given angles refer specifically to phase 1 and should be shifted by 30° for phase 3. Similarly, the reference current and turn-on and turn-off angles of phases 2 and 4 are I_ref24, θ_ON24, and θ_OFF24, respectively. The given angles refer to phase 2 and should be shifted by 30° for phase 4. If the reference angle is set so that the unaligned position of phase 1 equals 30°, the turn-on angle values are selected from ranges that depend on the stator and rotor pole widths as follows [27]:

$${\theta }_{ON13}\in \left(\frac{{\beta }_{S13}+{\beta }_R}{2},60°-\frac{{\beta }_{S13}+{\beta }_R}{2}\right),$$

(26)

$${\theta }_{ON24}\in \left(15°+\frac{{\beta }_{S24}+{\beta }_R}{2},75°-\frac{{\beta }_{S24}+{\beta }_R}{2}\right).$$

(27)

Note that the turn-off angles are defined as θ_OFF13 = θ_ON13 + θ_DWELL13 and θ_OFF24 = θ_ON24 + θ_DWELL24. The dwell angles for all phases are selected from the range (13°, 30°).

When setting the values of reference currents, the constant VA demand formulated by (25) must be fulfilled. The theoretical range of c₁₃ is (0, 2), but it is narrowed down to (0.2, 1.8) due to practical considerations. By selecting the value of c₁₃, we automatically obtain c₂₄ = 2 − c₁₃.

In order to carry out steps (b), (c), and (d), as well as the comparison of asymmetrical and symmetrical drive, it is necessary to determine the optimal control parameters of the symmetrical drive, turn-on angle (θ_ON), turn-off angle (θ_OFF), and reference current (I_ref) for which the maximum output torque is achieved, and the RMS value of the phase current does not exceed the rated value I_sym = I_nom = 3.2 A, which is given in Appendix A. 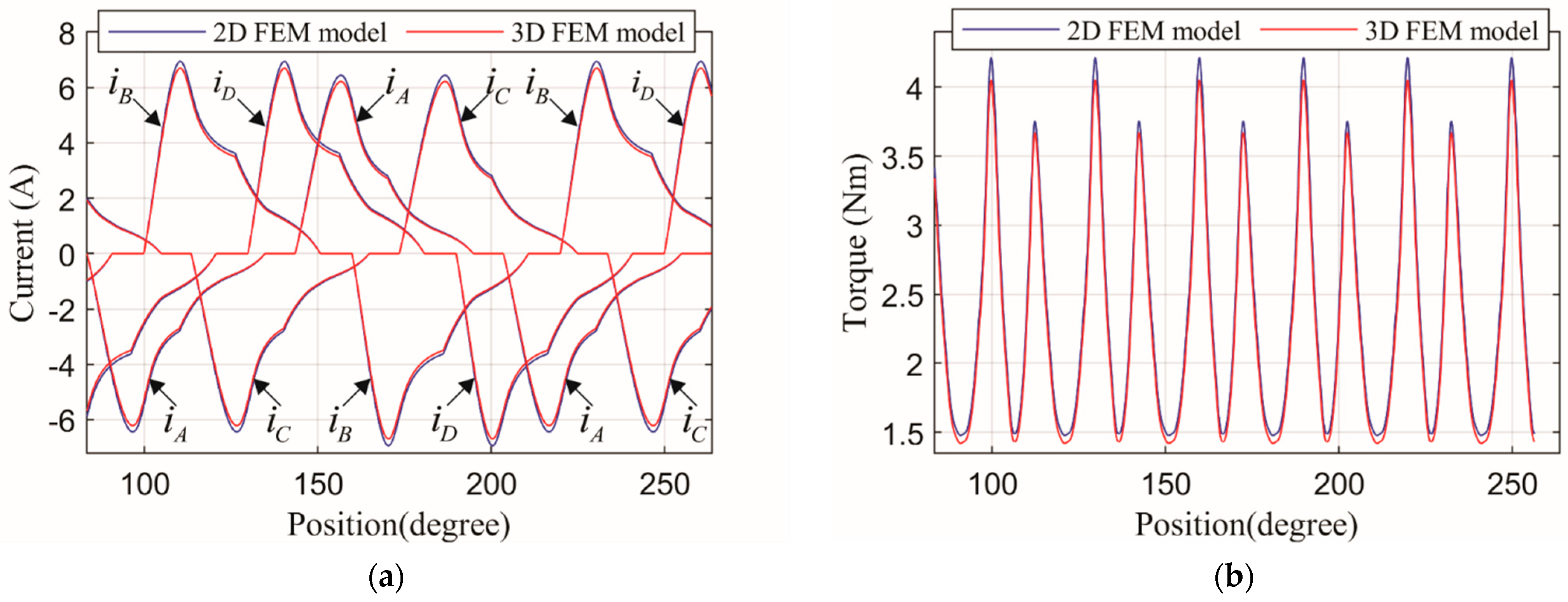To determine optimal control parameters of the symmetrical drive, model [25] is used, which includes all substantial non-linearities and mutual coupling between phases. This model is also used for the design of the asymmetrical 8/6 SRM drive, i.e., the realization of steps (b) and (c). Though using a FEM model in the optimization process would yield slightly more accurate results, such an approach would be much more time-consuming compared to using model [25]. On the other hand, it was previously shown that the results of model [25] are in very good agreement with the results of the corresponding FEM model. Further validation of the applied model is provided in Section 6. The optimization of the control parameters of the symmetrical drive was performed for a speed range between 400 and 13,200 rpm with a step of 400 rpm.

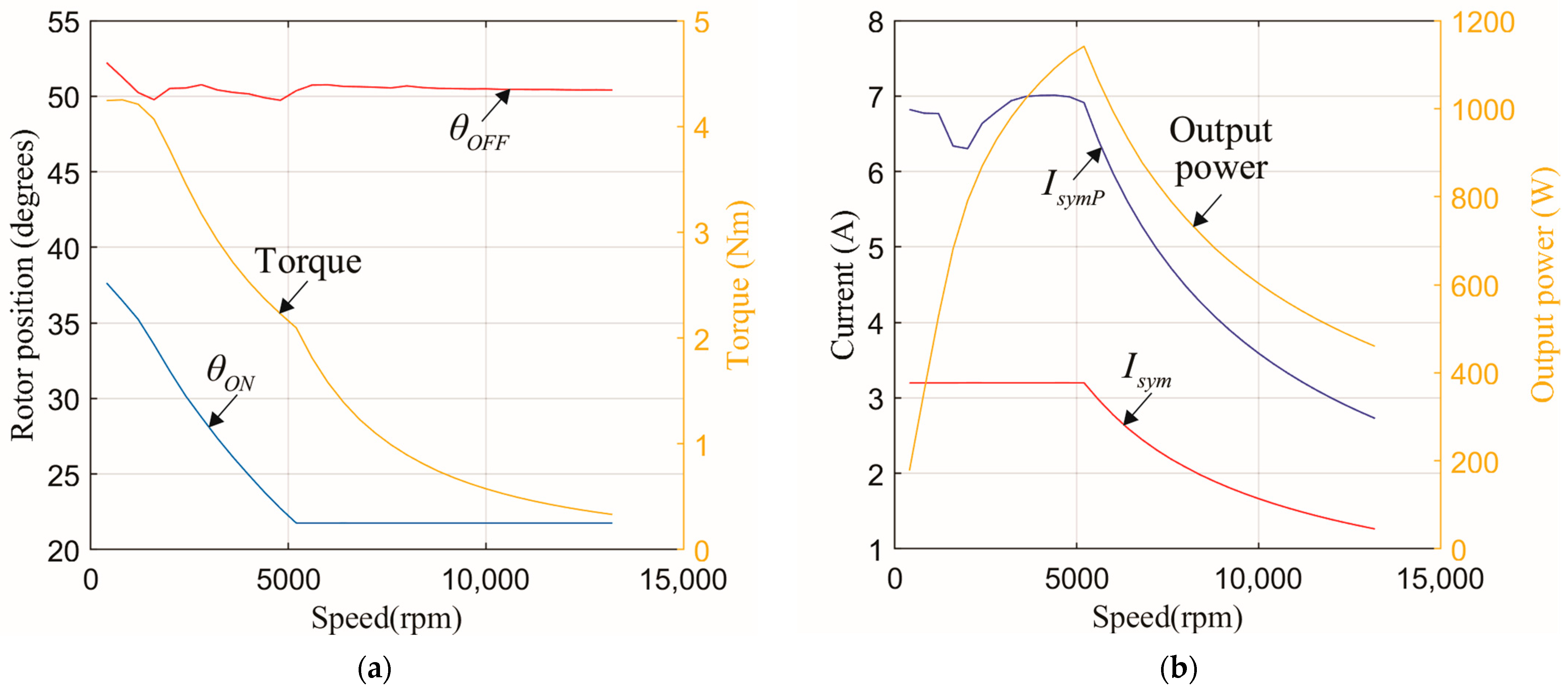
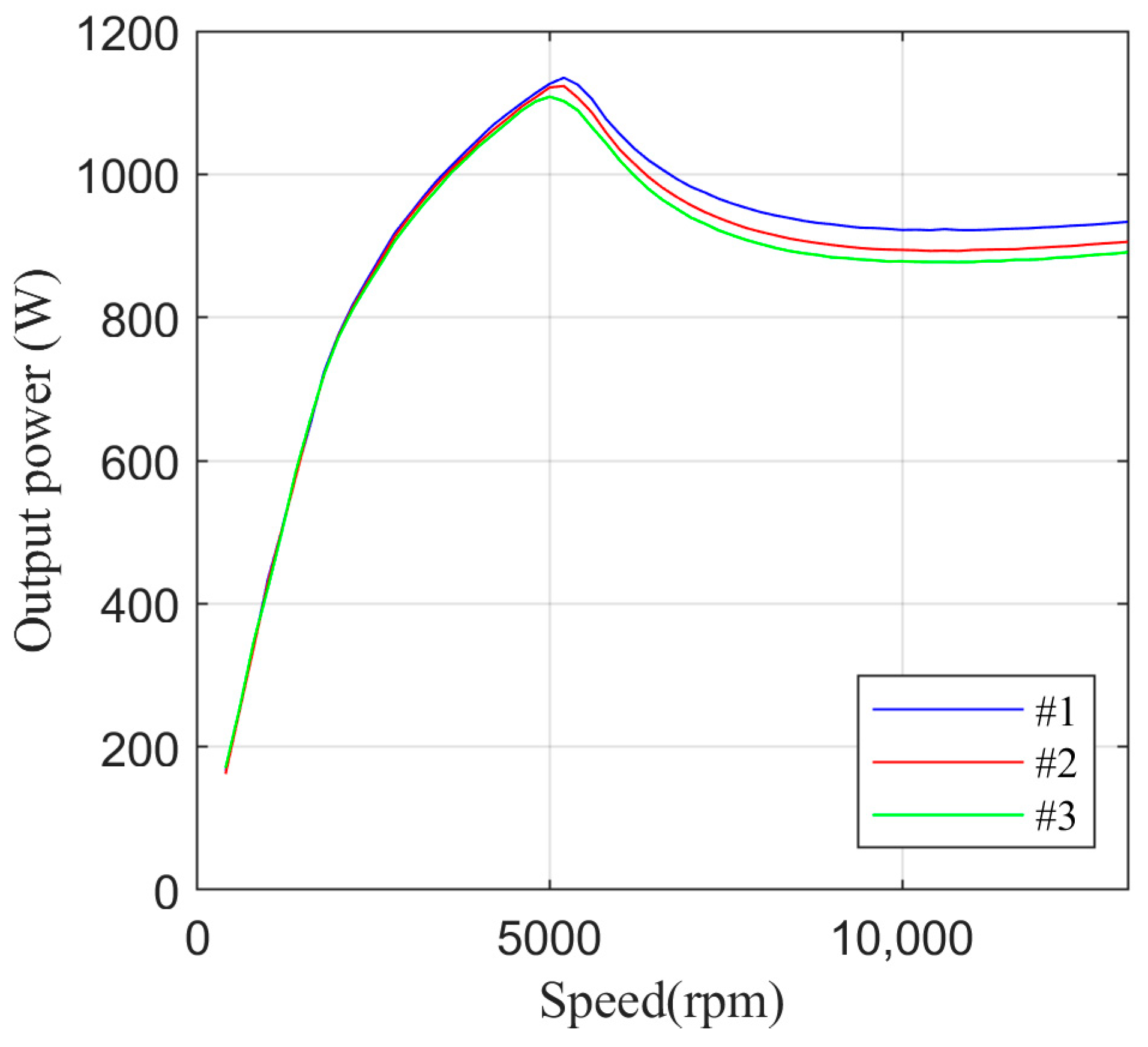
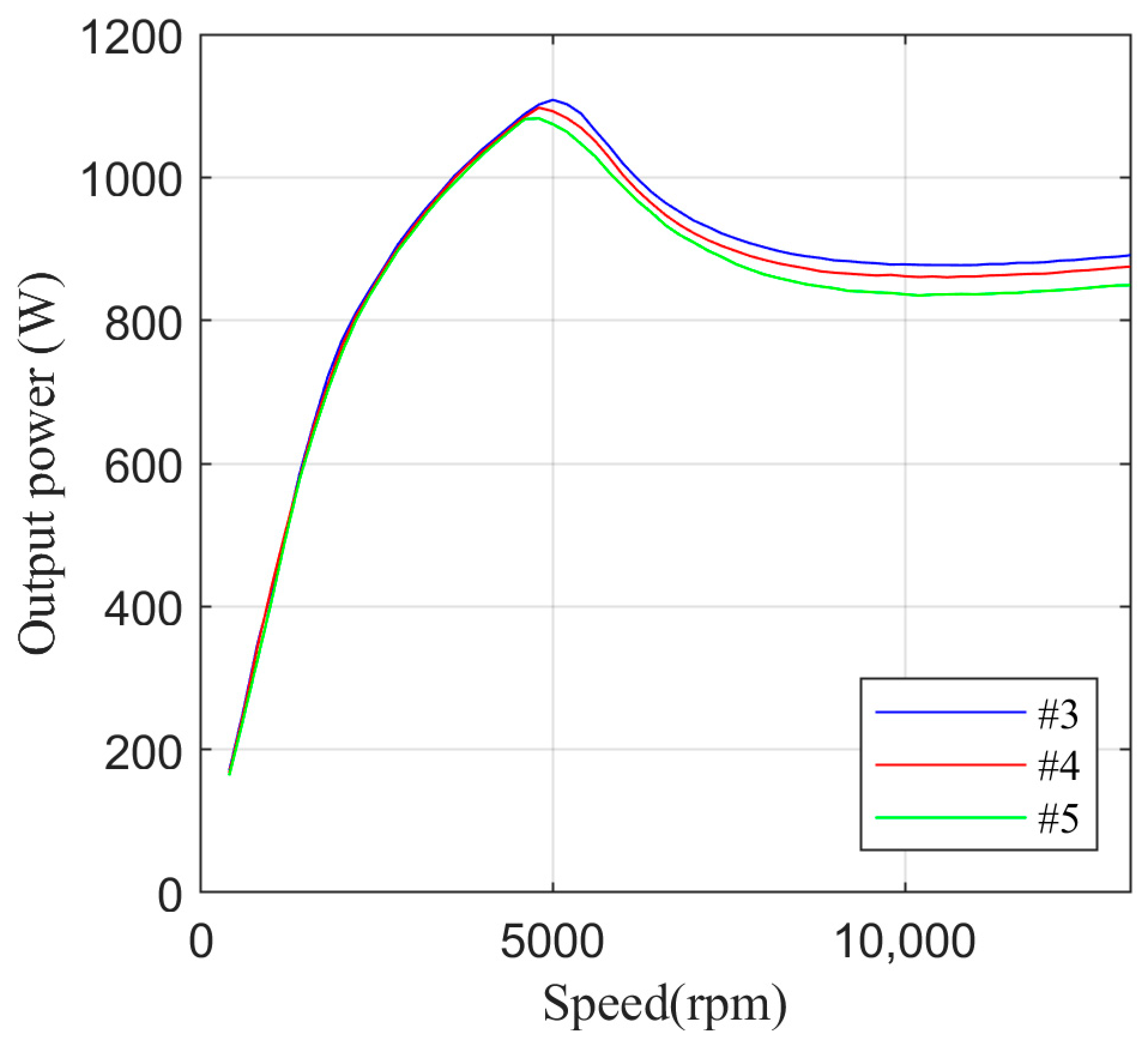
The calculation results are shown in Figure 5. The optimal control turn-on and turn-off angles together with developed torque are given in Figure 5a, and the output power, RMS phase current (I_sym), and phase current peak value (I_symP) are shown in Figure 5b. From Figure 5b, it can be seen that the maximum of I_symP is I_{symmax_P} = 7.01 A. Based on this value, the total VA requirements of the symmetrical drive are determined according to relationship (23) as 16VI_symmax__P = 16 × 220 × 7.01 = 24.675 KVA.

4. Power-Speed Characteristics of Asymmetrical 8/6 SRM for the Optimal Design and Control Parameters

The optimization procedure in step (b) defined in the previous section is conducted for numerous combinations of β_S13, β_S24 that satisfy condition (4). The optimal values of N₁₃, N₂₄, θ_ON13, θ_ON24, θ_OFF13, θ_OFF24, I_ref13, I_ref24 are obtained for each stator pole width combination and for each speed from the range 400–13,200 rpm. The purpose of this optimization stage is to obtain an optimal design for each speed, i.e., to study the influence of β_S13, β_S24, N₁₃, N₂₄ on the power-speed characteristic. Results obtained for five pole width combinations listed in

Table 1. Analyzed pole width combination.

	βS13	βS24
#1	18°	23°
#2	19.5°	21.5°
#3	20.5°	20.5°
#4	21.5°	19.5°
#5	23°	18°

are displayed in this paper. These pole width combinations cover both variants of the asymmetrical 8/6 SRM. Combinations #1 and #2 represent variant 1, combinations #4 and #5 represent variant 2, and combination #3 has the same pole widths as the symmetrical configuration. The selected pole width combinations are uniformly distributed over a wide range to provide comprehensive insight into the influence of asymmetrical pole design on 8/6 SRM performance, while maintaining the complexity of the modeling and optimization procedure at a reasonable level.

Power-speed characteristics corresponding to pole width combinations #1, #2, and #3 are compared in Figure 6. Optimal numbers of turns corresponding to each combination are shown in Figure 7. From Figure 6 and Figure 7, it is notable that maximal power at different speeds is obtained for different combinations of N₁₃ and N₂₄. As the number of turns obviously cannot be varied during SRM operation, the given characteristics are hypothetical. Namely, each operating point of each characteristic represents an optimal solution for that specific speed; therefore, a different design corresponds to every speed. It can be noted that the qualitative change in the displayed characteristics is very similar. As β_S13 increases and β₂₄ decreases, the power values over the entire speed range decrease, i.e., P(#1) > P(#2) > P(#3). These values are nearly equal until the corresponding minimum values of the turn-on angles are reached. After these limits are reached, which occurs at higher speeds, differences between the considered characteristics become more pronounced. Namely, seeing as N₁₃ > N₂₄, this limit is first reached in orthogonal phase pair 1 and 3, as already stated in Section 2.

Furthermore, seeing as β_S13(#3) > β_S13(#2) > β_S13(#1), relationship (26) implies that the turn-on angle limit is first reached for combination #3, followed by combination #2, and finally for combination #1. Therefore, the maximal output power values corresponding to the three combinations are related as P(#1) > P(#2) > P(#3). The variations in the number of turns are also much more pronounced at higher speeds, as is the difference between N₁₃ and N₂₄. Once again, it must be emphasized that a different design corresponds to each operating point, and that the displayed numbers of turns represent optimal values for the given operating speed.

The comparisons of power-speed characteristics for stator pole width combinations #3, #4, and #5 are shown in Figure 8. As β_S13(#5) > β_S13(#4) > β_S13(#3), the maximal powers are related as P(#3) > P(#4) > P(#5). This is expected, as the turn-on angle limit in variant 2 first occurs in combination #5, followed by combination #4, and finally combination #3. The optimal numbers of turns of orthogonal phase pairs corresponding to combinations #3, #4, and #5 are shown in Figure 9.

As stated previously, the number of turns of an actual asymmetrical 8/6 SRM cannot be varied during machine operation; hence, a fixed combination of N₁₃, N₂₄ needs to be selected for each pole width combination among those shown in Figure 7 and Figure 9. When a combination is selected, optimization of the control parameters is conducted for the selected combination of pole widths and numbers of turns according to step (c), which is defined in the previous section. Naturally, the 8/6 SRM performance, i.e., the power-speed characteristic, will be inferior to that obtained when using optimal numbers of turns for each speed. The goal is to select the (N₁₃, N₂₄) combination among the optimal solutions obtained in step (b), which results in the desired shape of the power-speed characteristic. By optimizing the control parameters for a given pole width/number of turns combination, the shape of the power-speed characteristic can be modified to obtain approximately constant power over a wide speed range.

Figure 6 and Figure 8 indicate that the stator pole widths also influence the power-speed characteristic. This is due to the fact that the stator pole widths directly affect the machine saliency, saturation, peak, and average torque value as well as the interval of turn-on angle variations [5]. Considering this, the goal is to select one or more combinations of β_S13, β_S24, N₁₃, N₂₄ from Figure 6, Figure 7, Figure 8 and Figure 9 that result in the required shape of the power-speed characteristic, i.e., that provide approximately constant power over a wide speed range.

5. Asymmetrical 8/6 SRM Design Examples with Approximately Constant Power-Speed Characteristics

In this section, optimization of the control parameters is performed for selected combinations of β_S13, β_S24, N₁₃, N₂₄ that satisfy conditions (4) and (20). The goal is to identify the asymmetrical 8/6 SRM design with an approximately constant power-speed characteristic over a wide speed range. The selected β_S13, β_S24 combinations are listed in Table 1. Considering the results obtained in the previous section, coefficients k₁₃ and k₂₄ are varied for each β_S13, β_S24 combination to properly perceive their influence on the power-speed characteristic. The optimization procedure is virtually unchanged compared to the previous section, except that the coefficients z₁₃, z₂₄, c₁₃, and c₂₄ are no longer optimization variables, but are included as constant inputs in each optimization run.

The parameters of asymmetrical 8/6 SRM topologies with pole widths of β_S13 = 18° and β_S24 = 23° (combination #1 of Table 1) are given in

Table 2. Design parameters of the asymmetrical 8/6 SRM drive with pole width combination #1 (β_S13 = 18° and β_S24 = 23°).

	k13	k24	R13 (Ω)	R24 (Ω)	I13 (A)	I24 (A)
a	1.3742	0.6261	3.1931	1.4912	2.7468	4.0195
b	1.4102	0.5901	3.2768	1.4054	2.7115	4.1403
c	1.4442	0.5561	3.3558	1.3244	2.6794	4.2650
d	1.4622	0.5381	3.3976	1.2815	2.6629	4.3358

. These parameters include the number of turns of each orthogonal phase pair (expressed by coefficients k₁₃ and k₂₄) and the winding resistances and maximal RMS currents of orthogonal phase pairs. In the following discussion, the notation #N.y will be used to refer to particular design combinations, where N ∈ {1, 2, 3, 4, 5} denotes the observed pole width combination, and y ∈ {a, b, c, d, e} denotes the k₁₃, k₂₄ combination. Combination #1 will be used to illustrate the main principles and benefits of the asymmetrical 8/6 SRM, whereas the main results will be displayed for other combinations as well. The values of coefficients k₁₃ and k₂₄ are proportional to the optimal numbers of turns for speeds in the vicinity of 10,000 rpm. By selecting these values, the constant-power range is extended to the corresponding speed values, as will be shown below.

The power-speed characteristics obtained for optimal control parameters corresponding to combinations defined in Table 2 are displayed in Figure 10. For the sake of comparison, the power-speed characteristic corresponding to the symmetrical drive (SYM) with optimized control parameters is shown in the same diagram. As evident from Figure 10, the proposed asymmetrical 8/6 SRM design methodology allows the shape of the power-speed characteristic to be modified. Compared to the symmetrical 8/6 SRM, the maximal power of the asymmetrical configurations is lower. However, by reducing the maximal attainable power, the asymmetrical 8/6 SRM attains a more uniform power distribution over a wide speed range. By increasing the coefficient k₁₃, i.e., the number of turns N₁₃, the maximal power decreases, and the speed range with an approximately uniform power distribution is wider compared to the symmetrical 8/6 SRM. This is in accordance with the diagrams of Figure 6, where higher optimal values of N₁₃ and lower values of N₂₄ correspond to higher speeds.

According to the results of Figure 10, among the combinations given in Table 2, combination #1.c with optimal control parameters at each speed results in a power-speed characteristic with the widest constant power zone. In other words, the widest range of the constant power region is obtained when k₁₃ = 1.4442 and k₂₄ = 0.5561 (i.e., N₁₃ = 410 and N₂₄ = 158). Namely, maximal power within the 923–938 W range is obtained between n_min = 3530 rpm and n_max = 10,040 rpm (n_max/n_min = 2.8442). On the other hand, the symmetrical drive provides output power above 923 W in the range between n_min = 2740 rpm and n_max = 6460 rpm (n_max/n_min = 2.3577). Combination #1.d results in a higher maximal speed, but at the cost of reduced power at speeds below 5000 rpm, which makes it inferior to #1.c.

Therefore, applying the asymmetrical configuration extends the constant power region by 20.6% compared to the symmetrical configuration. The power provided by the asymmetrical 8/6 SRM in the high-speed region (above 6460 rpm) is significantly higher compared to that of the symmetrical drive. On the other hand, the symmetrical configuration does provide higher power in the low-speed region. Though this may be advantageous in some specific cases, most applications would benefit much more from the extended constant power region, whereas the enhanced power capability in the low-speed region would mostly remain unexploited.

The values of turn-on and turn-off angles that ensure the widest constant power zone of the #1.c topology are displayed in Figure 11a. By observing Figure 10 and Figure 11a, it can be concluded that the constant power region begins at the speed of 3600 rpm, above which the turn-on angle θ_ON13 cannot be further reduced. Due to this limitation, for operating speeds that exceed 3600 rpm, the flux linkages and RMS currents of orthogonal phase pair 1 and 3 begin to decrease, leading to reduced torque contribution by these phases. On the other hand, Figure 11a shows that the turn-on angle θ_ON24 decreases at a slower rate as the speed increases. Consequentially, the orthogonal phase pair 2 and 4 generates maximal torque over a very wide speed range. The combined contribution of all four phases to the generated torque results in approximately constant power over a very wide speed range, with a significantly higher maximal power compared to the symmetrical drive for speeds above 6460 rpm.

According to Figure 11b, the maximum peak current values of orthogonal phase pairs (1, 3) and (2, 4) corresponding to configuration #1.c equal I_{13max_P} = 5.701 A and I_{24max_P} = 8.315 A, respectively. The total VA demands of this configuration are 24.668 kVA. This is nearly equal to the VA demands of the symmetrical configuration (24.675 kVA), which is in accordance with condition (i) defined in Section 2.

The asymmetrical 8/6 SRM configurations corresponding to stator pole width combinations #2, #3, #4, and #5 (see Table 1) are listed in

Table 3. Design parameters of the asymmetrical 8/6 SRM drive with pole width combination #2 (β_S13 = 19.5° and β_S24 = 21.5°).

	k13	k24	R13 (Ω)	R24 (Ω)	I13 (A)	I24 (A)
a	1.37403	0.62601	3.2167	1.4801	2.7367	4.0345
b	1.41003	0.59001	3.3010	1.3950	2.7015	4.1558
c	1.43003	0.57001	3.3478	1.3477	2.6826	4.2280
d	1.44403	0.55601	3.3806	1.3146	2.6695	4.2809

,

Table 4. Design parameters of the asymmetrical 8/6 SRM drive with pole width combination #3 (β_S13 = 20.5° and β_S24 = 20.5°).

	k13	k24	R13 (Ω)	R24 (Ω)	I13 (A)	I24 (A)
a	1.37400	0.62600	3.2326	1.4728	2.73	4.0445
b	1.39800	0.60200	3.2891	1.4163	2.7064	4.1243
c	1.42800	0.57200	3.3597	1.3458	2.6778	4.2311
d	1.44400	0.55600	3.3973	1.3081	2.6630	4.2915

,

Table 5. Design parameters of the asymmetrical 8/6 SRM drive with pole width combination #4 (β_S13 = 21.5° and β_S24 = 19.5°).

	k13	k24	R13 (Ω)	R24 (Ω)	I13 (A)	I24 (A)
a	1.35803	0.64201	3.2108	1.5030	2.7392	4.0036
b	1.36603	0.63402	3.2297	1.4843	2.7312	4.0288
c	1.37403	0.62601	3.2487	1.4656	2.7232	4.0545
d	1.41003	0.59001	3.3338	1.3813	2.6882	4.1763

and

Table 6. Design parameters of the asymmetrical 8/6 SRM drive with pole width combination #5 (β_S13 = 23° and β_S24 = 18°).

	k13	k24	R13 (Ω)	R24 (Ω)	I13 (A)	I24 (A)
a	1.29819	0.70211	3.0919	1.6314	2.7914	3.8428
b	1.31819	0.682102	3.1395	1.5849	2.7701	3.8988
c	1.34819	0.65209	3.2110	1.5152	2.7391	3.9875
d	1.374203	0.62609	3.2729	1.4548	2.7131	4.0694

, respectively. Optimization of the control parameters for all asymmetrical 8/6 SRM designs defined by Table 3, Table 4, Table 5 and Table 6 is performed, and the corresponding power-speed characteristics are displayed in Figure 12, Figure 13, Figure 14 and Figure 15. The power-speed characteristic of the symmetrical 8/6 SRM is added to each graph for the sake of comparison.

The displayed results demonstrate that each of the analyzed asymmetrical topologies results in a more uniform power distribution over a wider speed range compared to the symmetrical design. The influence of the number of turns, i.e., the coefficients k₁₃ and k₂₄, is qualitatively the same as with the previously analyzed designs based on stator pole width combination #1.

According to Figure 12, Figure 13, Figure 14 and Figure 15 and Table 3, Table 4, Table 5 and Table 6, combinations #2.b, #3.b, #4.b, and #5.b, respectively, are with the widest constant power zone. Compared to the symmetrical configuration, for the approximately same power level, the above-mentioned asymmetrical configurations extend the constant power region by 25.7%, 30.2%, 34.3%, and 38.1%, respectively.

To make a comprehensive comparison, Figure 16 displays the power-speed characteristics of asymmetrical topologies that ensure the largest constant power zone width for each pole width combination. The power-speed characteristic of the symmetrical configuration is again included for comparison purposes. As seen in the graphs, increasing β_S13 while decreasing β_S24 reduces the power level in the constant power region but extends the width of this region. Specifically, increasing β_S13 causes the lower speed limit of the constant power region to decrease and the upper speed limit to increase. The pole width should be selected depending on the specific application, so that the constant power region is as wide as possible while achieving the required rated power. As the required maximal power and constant power region width depend on the intended application, no general optimal solution can be derived from this analysis. The results of Figure 16 indicate that a trade-off exists between the maximal power and the constant power region width. Therefore, the design selection process is application-specific, i.e., there is no universally optimal design.

6. FEM Verification of the Proposed Methodology for Designing Asymmetrical 8/6 SRM Drive

In this section, verification of the proposed methodology for designing asymmetrical 8/6 SRM drive is performed by using an appropriate transient FEM model built in Ansys Electronics simulation software [25,28,29,30]. Various designs and operating modes will be verified using a reference 2D FEM model. Additional verification will be provided for a selected design in a single operating point. This will be conducted using a detailed 3D FEM model. As stated in Section 3, the complete optimization procedure is performed by using the transient model [25], which includes all significant nonlinear and phase coupling effects but is much less complex and slightly less accurate than the FEM model. The use of model [25] significantly reduces the computation time, and it is hypothesized in Section 3 that the loss of accuracy is negligible, based on previous findings. This assumption is verified in this section by comparing the results obtained using model [25] with the results obtained using the corresponding FEM model. Namely, FEM is the most commonly employed numerical technique for modeling electric machines due to its high accuracy. The transient FEM model, including the 8/6 SRM geometry, materials, a winding and magnetic circuit, boundary conditions, a mesh, an external supply circuit in the form of 4 H-bridges, and control is defined according to [25,29,30]. From this point on, model [25] will be referred to as the model M1.

6.1. Two-Dimensional FEM Verification

Two-dimensional FEM models of the symmetrical design and optimal asymmetrical designs obtained from the optimization procedure are developed, along with the appropriate external supply.

As an example, Figure 17 shows flux density distribution in the asymmetrical 8/6 SRM (pole width combinations #5 from Table 1) for two different rotor positions. As can be observed, the flux density distribution in the 8/6 SRM for the observed rotor positions corresponds to the SFPE, which is in accordance with the discussion in Section 3. Thanks to the defined power supply method, SFPE is achieved in the 8/6 SRM for any rotor position.

Firstly, a comparison of the phase current and electromagnetic torque waveforms obtained by the analytical and 2D FEM model is performed. Two operating regimes are chosen, one for each variant of the asymmetrical 8/6 SRM drive. The considered asymmetrical topologies and operating conditions defined by the operating speed and control parameters are given in

Table 7. Definition of considered asymmetrical topologies and corresponding operating regimes.

	#1	#4
k13	1.1190	1.4
k24	0.8818	0.6
n (rpm)	4400	8400
θON13 (°)	23.49	22.18
θON24 (°)	39.87	41.22
θOFF13 (°)	50.14	50.52
θOFF24 (°)	66.19	64.95

. A comparison of the corresponding waveforms is shown in Figure 18 and Figure 19.

Very good agreement of the results obtained from the analytical model and 2D FEM confirm the justification of using the model M1 for the determination of the optimal control parameters and maximal drive performances. This is a very significant conclusion, as the execution speed of model M1 is much higher compared to the 2D FEM model. This makes model M1 a preferred choice for the optimization algorithm, which requires a great number of simulations.

According to

Table 8. Comparison of simulation results obtained from 2D FEM and M1 models for asymmetrical topology #1 and operating conditions given in Table 7.

	IA (A)	IB (A)	IC (A)	ID (A)	Tem (Nm)
Model M1	2.9945	3.3668	2.9945	3.3668	2.3483
2D FEM model	3.0228	3.3560	3.0288	3.3560	2.3929

and

Table 9. Comparison of simulation results obtained from 2D FEM and M1 models for asymmetrical topology #4 and operating conditions given in Table 7.

	IA (A)	IB (A)	IC (A)	ID (A)	Tem (Nm)
Model M1	0.9274	3.8750	0.9274	3.8750	0.8966
2D FEM model	0.9341	3.9512	0.9341	3.9512	0.9139

, the error in the prediction of RMS values of phase currents and the mean torque values obtained using model M1 and the 2D FEM model does not exceed 2%, which justifies the use of model M1 for optimization purposes.

The power-speed characteristics of asymmetrical topologies that ensure the largest constant power zone width for each pole width combination from Table 1 are obtained using the 2D FEM model. The optimal control parameters determined based on model M1 in the previous section are used in the 2D FEM simulations. The power-speed characteristics obtained using 2D FEM are shown in Figure 20a. As can be observed, power speed characteristics are in very good agreement with the corresponding characteristics in Figure 16.

The good agreement between the results of model M1 and 2D FEM is demonstrated in Figure 20b, where overlapped power-speed characteristics obtained using the two models for the case of asymmetrical configuration #1 are displayed. This once again confirms the justification of using model M1 for the design of the asymmetrical 8/6 SRM drive. In this way, the proposed methodology to design an asymmetrical four-phase 8/6 switched reluctance motor that achieves approximately constant output power over a wide speed range is verified.

6.2. 3D FEM Verification

The 3D FEM model of the asymmetrical 8/6 SRM topology #1 from Table 7 analyzed in the previous subsection is shown in Figure 21. The symmetry of the problem allows for one quarter of the machine to be modeled. Considering the extensive amount of time required for conducting a transient 3D FEM simulation, only one design is analyzed in a single operating point. However, a potential good match between the results of the 3D and 2D FEM models would further justify the results of the optimization procedure.

The selected operating point corresponds to the operating speed of 4400 rpm. The turn-on and turn-off angles are set to values given in Table 7 for configuration #1. The current and torque waveforms obtained using the 3D and 2D FEM models are displayed in Figure 22. Slight differences between the results of the 3D and 2D models are due mostly to the end-winding leakage inductance and axial fringing field effects, which are explicitly included in the 3D model.

To provide a more comprehensive comparison, RMS current values and average torque values obtained using the 2D and 3D FEM models are given in

Table 10. Comparison of simulation results obtained from 2D and 3D FEM models for asymmetrical topology #1 and operating conditions given in Table 7.

	IA (A)	IB (A)	IC (A)	ID (A)	Tem (Nm)
2D FEM model	3.0228	3.3560	3.0288	3.3560	2.3929
3D FEM model	2.9231	3.2385	2.9231	3.2385	2.3167

. The RMS current values obtained using the 2D model differ by no more than 3.7% from those obtained using the 3D model. An average torque deviation of 3.5% is obtained.

The conducted analysis indicates that the accuracy of the 2D FEM model is quite satisfactory when compared to the reference 3D model. By the transitive property, the previously conducted verification of model M1 through comparison to the 2D FEM model is further validated.

7. Cost-Effectiveness of the Proposed Design

According to the design constraints defined in Section 2 and Section 3, the total masses of the magnetic material (steel sheets) and the windings (copper) are equal to those of the reference symmetrical design. Though the constraint considering the amount of magnetic material is expected to be fully satisfied during the manufacturing process, the total copper mass can vary significantly depending on the winding technique. As the coils of the asymmetrical design have a different number of turns, certain variations in the total conductor length and volume of such coils can be expected, as compared to the design values. Furthermore, the manufacturing expenses may be slightly higher compared to the symmetrical design due to two different coil groups, which may prolong the manufacturing process and increase the cost. However, there is no way to verify these assumptions prior to actual manufacturing of the motor. Even then, it would be difficult to estimate the cost of potential mass production, which is of particular interest for low-power drives such as the one analyzed in this paper. Therefore, only a comparison of raw material masses between the reference symmetrical design and the proposed asymmetrical design can be made unambiguously. The total masses of copper and iron are virtually identical for the symmetrical and any of the obtained asymmetrical designs. This is shown in

Table 11. Masses of magnetic circuit and windings in the asymmetrical and symmetrical design.

	Symmetrical Design	Asymmetrical Design
Stator magnetic circuit	2.325 kg	2.325 kg
Rotor magnetic circuit	1.149 kg	1.149 kg
Winding	0.912 kg	0.911 kg
Total	4.385 kg	4.386 kg

, by comparing the masses of the symmetrical design and the asymmetrical design #1 of Table 7. The masses given in Table 11 are obtained from the 3D FEM models of the machines. There is virtually no difference in the raw material mass between the symmetrical and asymmetrical models. The exact cost cannot be easily determined, as the material costs vary significantly and depend on numerous factors, such as availability, market conditions, and total amount purchased.

Considering the power converter, there may be a more pronounced cost difference between the symmetrical and asymmetrical drives. Namely, the symmetrical drive requires four identical full-bridge converters, whereas the asymmetrical drive employs two pairs of full-bridge converters of the same voltage but different current ratings. Though the total VA requirements remain unchanged, the total cost of the converter may be higher in the asymmetrical case, as the component cost is generally not directly proportional to its current rating. The maximal converter currents of selected optimal designs obtained for different pole width combinations are given in

Table 12. Maximal power converter current values corresponding to optimal asymmetrical designs.

	#1.c	#2.b	#3.b	#4.b	#5.b
I13max_P	5.701	6.067	5.958	5.753	5.622
I24max_P	8.315	7.949	8.058	8.263	8.394

. The DC link voltage equals 220 V in all cases. The maximal converter current of the symmetrical design equals 7.01 A, as stated in Section 3.2.

The switching devices can now be selected according to the maximal current values and the DC link voltage. By investigating commercially available switching devices, it was determined that virtually no half-bridge or full-bridge modules appropriate for the given voltage and current rating are available. Therefore, only discrete switching devices were considered. Given the relatively low DC link voltage and low current rating, along with the requirement for high switching frequency, power MOSFETs with antiparallel diodes are the most adequate choice. A broad palette of suitable devices is provided by Infineon Technologies [31]. To simplify the selection, only devices with the same package type (TO-220) and a rated voltage of 500 V were considered. The device’s maximal current at the junction temperature of 100 °C is selected to accommodate a current 20% higher than the projected value. The list of required components is given in

Table 13. Switching components and driver circuits required for the asymmetrical 8/6 SRM drive.

Device	Code	Quantity	Unit Price (USD)
500 V CoolMOSTM CE Power Transistor	IPA50R380CEXKSA2	8	1.19
500 V CoolMOSTM CE Power Transistor	IPA50R280CE XKSA2	8	1.51
Gate Driver IC (Half-bridge)	2ED2184S06FXUMA1	8	1.88
		TOTAL: 36.64 USD

. The maximal converter currents of the optimal topologies given in Table 12 vary only slightly; therefore, the same components are suitable for all cases. The converter for the symmetrical drive can be composed using sixteen IPA50R380CEXKSA2 power switches at the unit cost of USD 1.19, whereas the driver circuits would remain the same. Therefore, the total cost of converter components for the reference symmetrical 8/6 SRM would be USD 34.08. It should be noted that this price includes only the power switches and the driver circuits. The costs of design, assembly, DC-link, logic, protection, measurement circuits, and other components would be the same in both the symmetrical and asymmetrical drive. Therefore, the total converter cost would be approximately the same in both cases. Additionally, in the case of mass production, the unit price of individual components would certainly be lower, thereby further decreasing the price difference.

8. Conclusions

This paper describes the methodology for obtaining optimal design and control of an asymmetrical four-phase 8/6 SRM that achieves approximately constant output power over a wide speed range. In an asymmetrical 8/6 SRM, orthogonal phase pairs are different in terms of the pole width and number of turns compared to the corresponding symmetrical motor. The converter volt-ampere rating, machine volume, slot fill factor, and ohmic losses per phase of the asymmetrical and reference symmetrical drive are kept constant. Determination of the optimal design and control parameters was performed using an appropriate 8/6 SRM mathematical model and a differential evolution algorithm. The applied model includes all substantial non-linearities and mutual coupling between phases. The simulation results are verified using a Finite Element Method (FEM)-based model in the Ansys Electronics software package. A very close match between the simulation and FEM results is observed, which justifies the conducted optimization procedure. The cost comparison between the symmetrical and asymmetrical drives shows only a slight increase in the converter cost when the asymmetrical design is employed, and the copper and iron volume and mass remain virtually unchanged.

The main comparison criterion between the asymmetrical and symmetrical 8/6 SRM drive is the power-speed characteristic, obtained for a given rated RMS phase current of the symmetrical drive. The obtained results demonstrate that the asymmetrical 8/6 SRM allows the shape of the power-speed characteristic to be modified, thereby extending the constant power region well beyond that of the symmetrical configuration with the same rated power level and attaining a more uniform power distribution over a wide speed range. In the considered asymmetrical drives, the speed range in which the drive develops the given power is extended by 20–38% compared to the range of the reference symmetrical drive. The symmetrical 8/6 SRM exhibits higher maximal power in the lower speed region, which may be beneficial in some cases where high acceleration rates at low speeds are required. However, in most applications, a wide constant power region is imperative, whereas additional power capability in the low-speed region is seldom required. For low-power drives, such as the one analyzed in this paper, the most notable examples include urban transport applications such as e-bikes and electric scooters, home appliances, power tools, fan and pump motors, etc. Therefore, the asymmetrical 8/6 SRM would be a preferred choice in such cases.