Bearing Health State Detection Based on Informer and CNN + Swin Transformer
Abstract
1. Introduction
2. Test Setup and Data Acquisition
3. Models
3.1. Bearing Health Condition Diagnosis Method Combining Temperature Rise Prediction and Image Classification
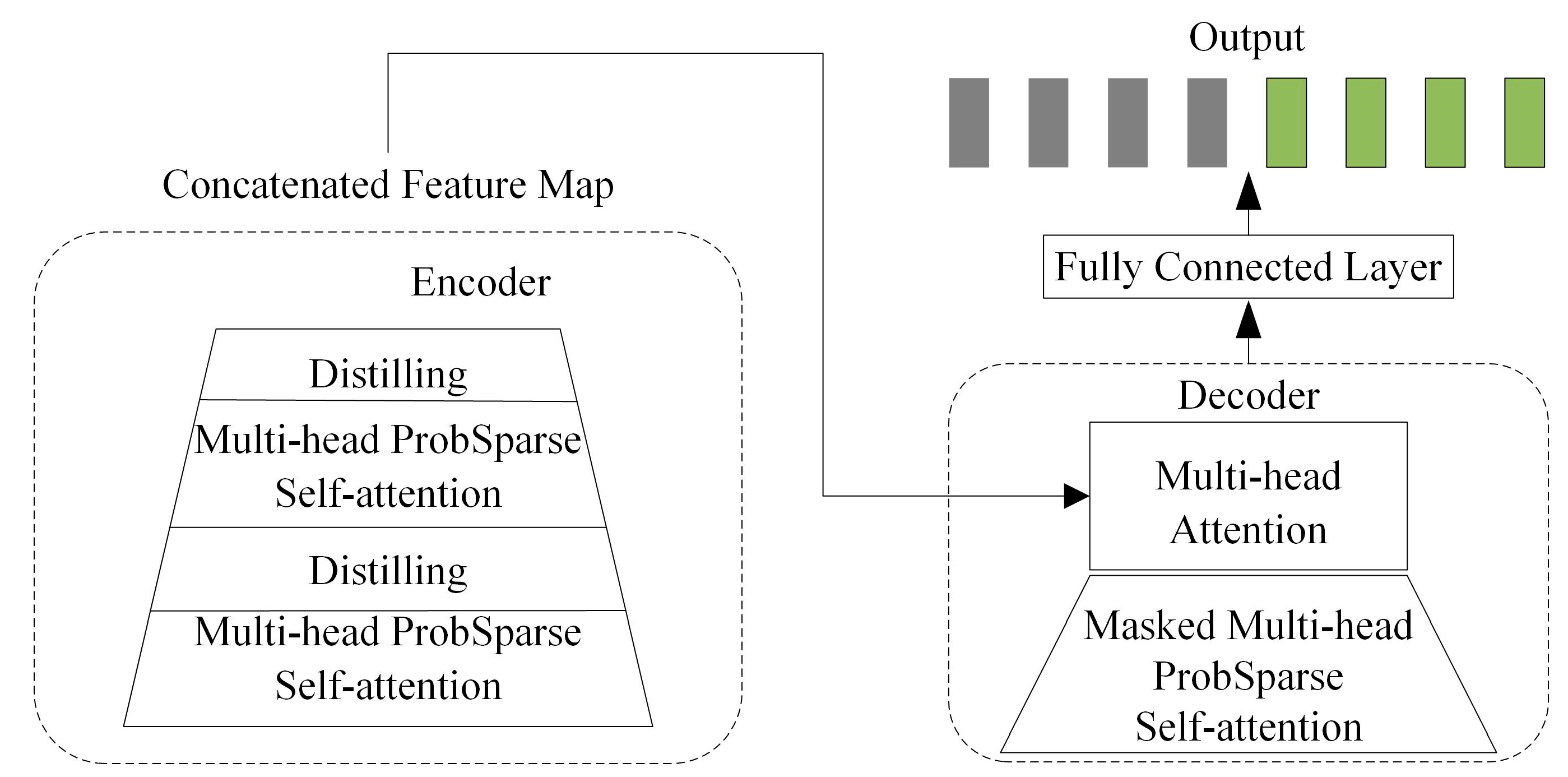
3.2. Informer
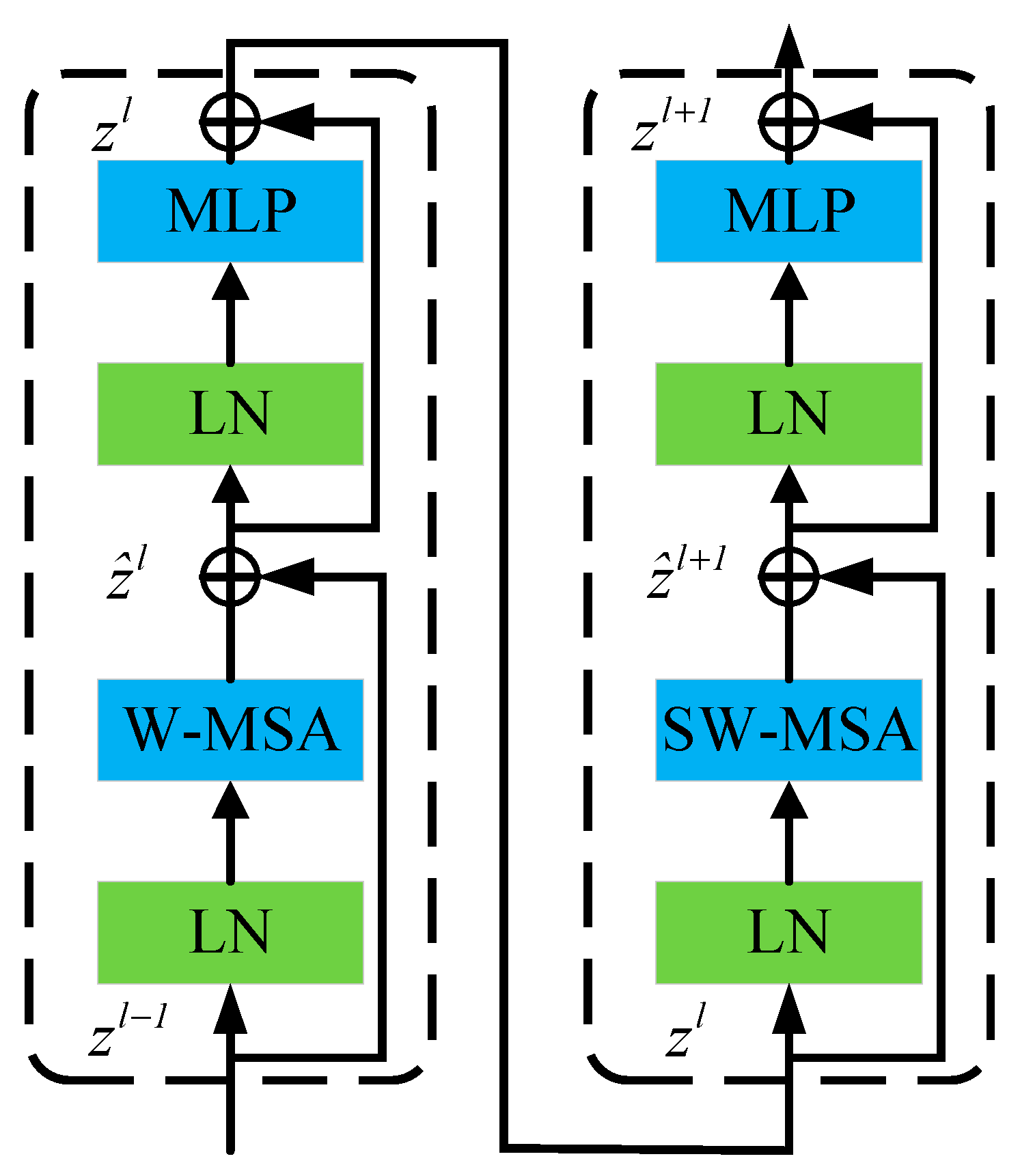
3.3. Diagnostic Modeling with a CNN + Swin Transformer
4. Testing and Analysis
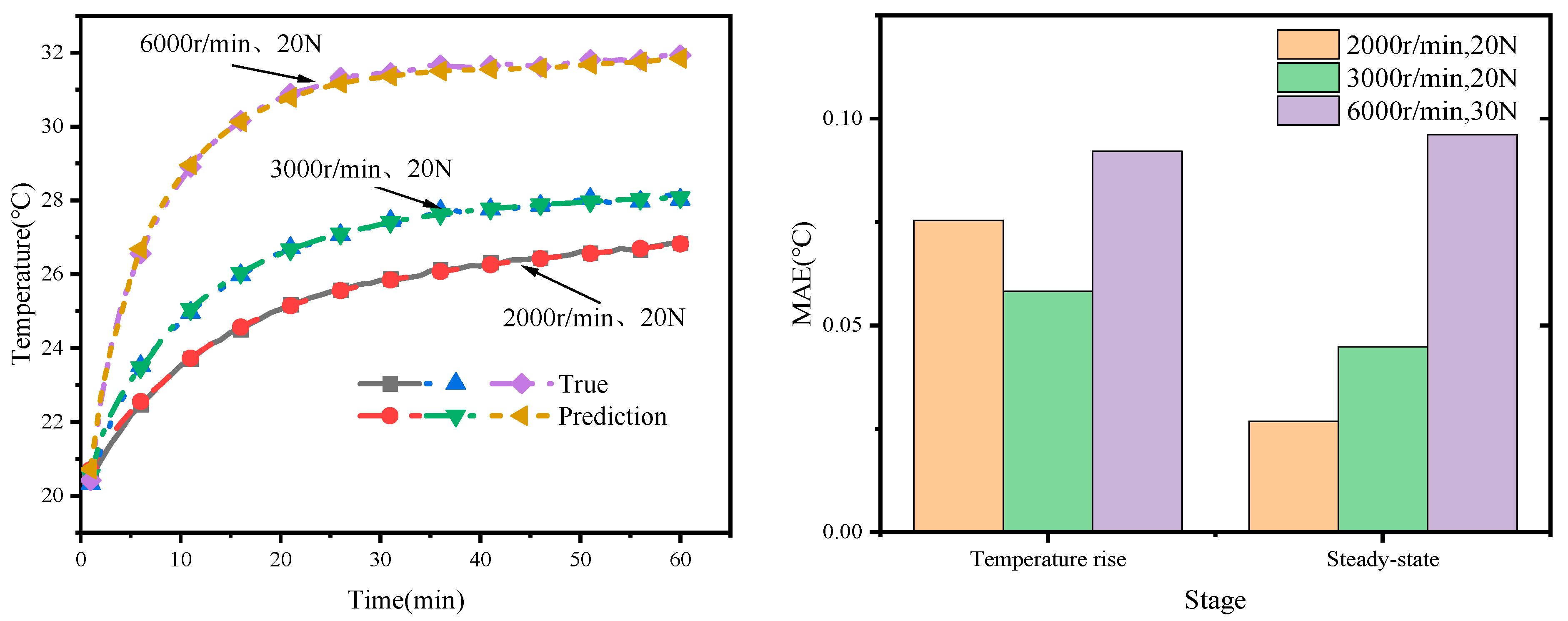
4.1. Informer Model Prediction Results
4.2. CNN + Swin Transformer Model Fault Recognition Experiments
4.3. Temperature Rise Prediction Combined with Image Recognition for Health Diagnosis
5. Conclusions
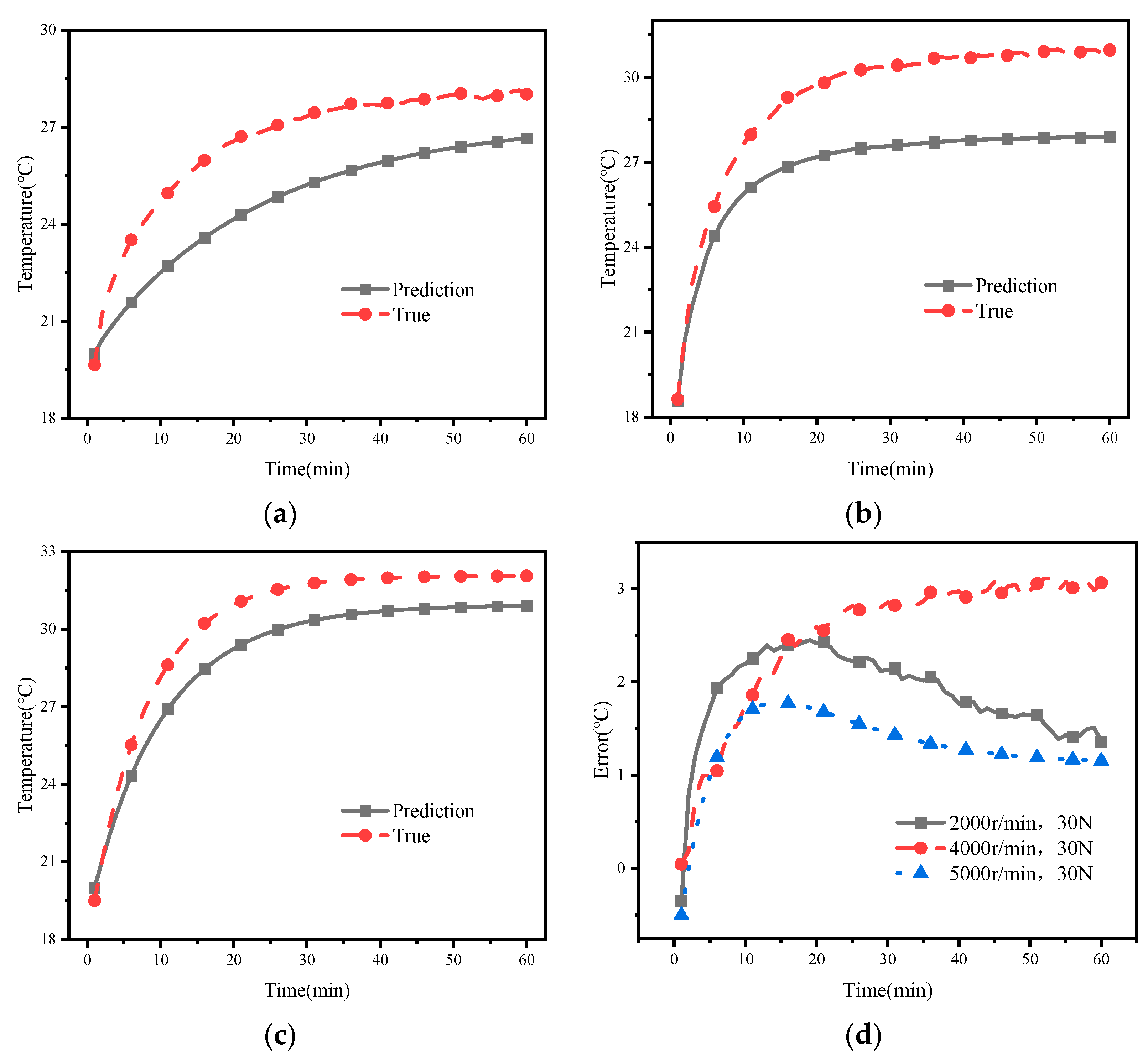
- After training the Informer model, it successfully predicts temperature variations in spindle bearings under different operating conditions. The model achieves lower prediction errors during the stable state of healthy bearings compared to the temperature rise phase. When a bearing fault occurs, there is a noticeable difference between the predicted and measured temperatures, especially during the stable operating state. This accurately reflects changes in the health status of bearings.
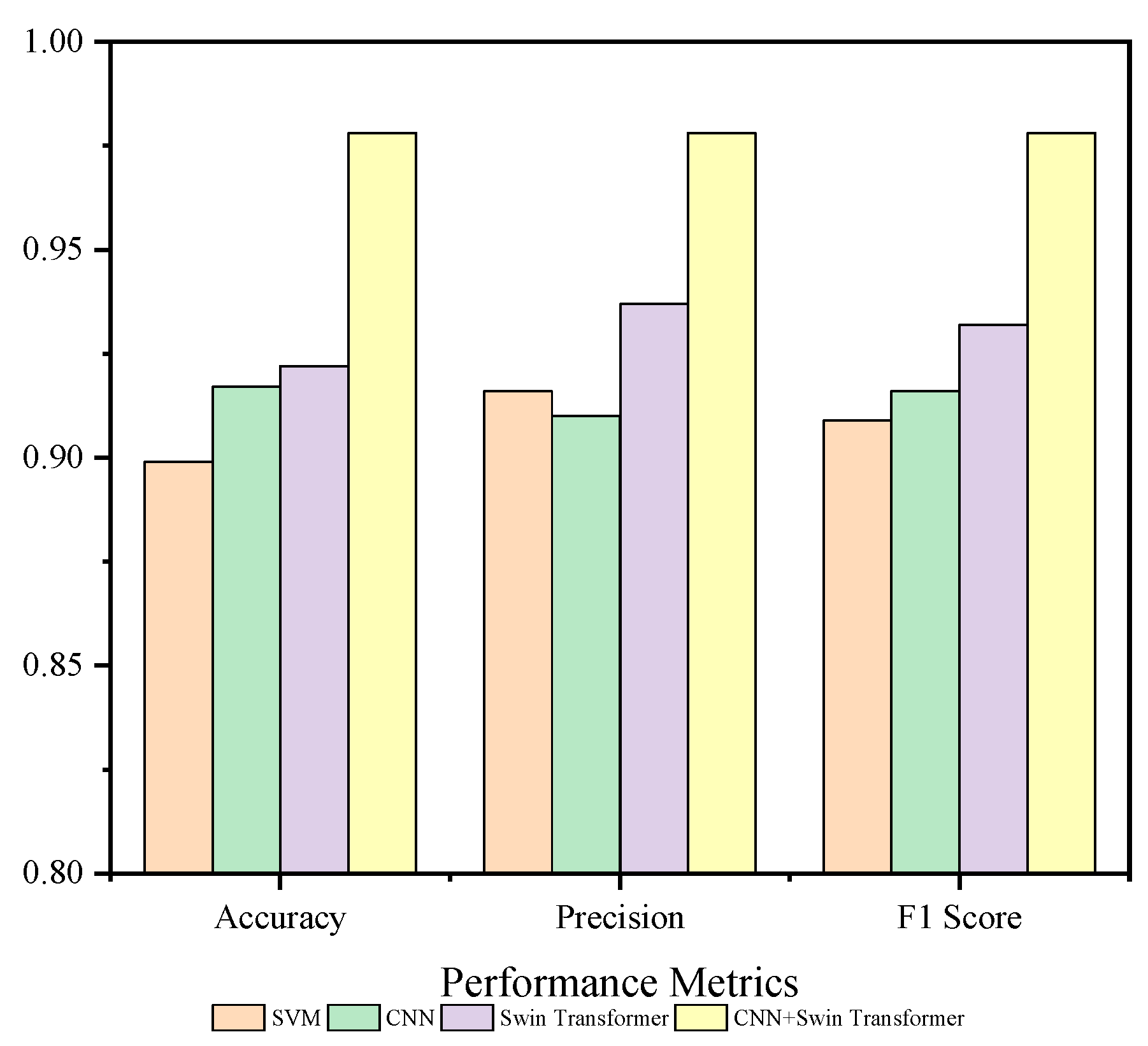
- The fault recognition model based on a CNN + Swin Transformer utilizes extracted feature maps and attention mechanisms for training and testing on the dataset. It achieves a recognition accuracy of 98.9% for identifying bearing fault states. Compared to individual models such as CNN, SVM, and Swin Transformer, the proposed method demonstrates superior recognition performance.
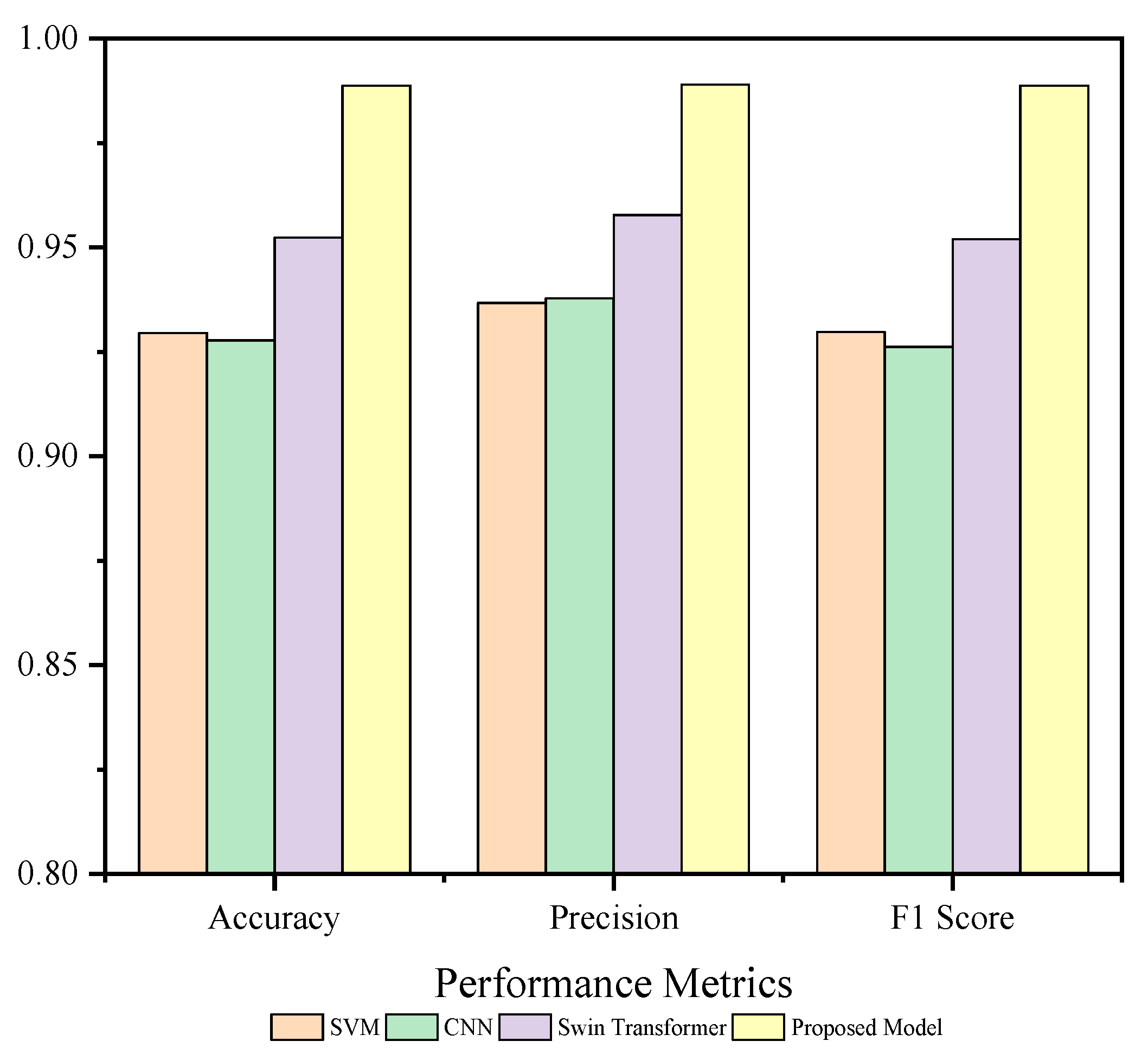
- By combining Informer temperature rise prediction with CNN + Swin Transformer fault diagnosis and recognition, a dual diagnostic approach utilizing temperature differences and image feature differences is achieved. The recognition accuracy for bearing fault states reaches 98.9%. Compared to CNN, SVM, Swin Transformer, and other models, this combined approach accurately reflects the health status of bearings. It provides a solution for assessing the health status of spindle bearings in complex operating environments.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Peng, B.; Bi, Y.; Xue, B.; Zhang, M.; Wan, S. A survey on fault diagnosis of rolling bearings. Algorithms 2022, 15, 347. [Google Scholar] [CrossRef]
- Nikula, R.P.; Karioja, K.; Pylvänäinen, M.; Leiviskä, K. Automation of low-speed bearing fault diagnosis based on autocorrelation of time domain features. Mech. Syst. Signal Process. 2020, 138, 106572. [Google Scholar] [CrossRef]
- Aasi, A.; Tabatabaei, R.; Aasi, E.; Jafari, S.M. Experimental investigation on time-domain features in the diagnosis of rolling element bearings by acoustic emission. J. Vib. Control 2022, 28, 2585–2595. [Google Scholar] [CrossRef]
- Fu, S.; Liu, K.; Xu, Y.; Liu, Y. Rolling bearing diagnosing method based on time domain analysis and adaptive fuzzy-means clustering. Shock. Vib. 2016, 2016, 9412787. [Google Scholar]
- Zhao, D.; Cui, L.; Liu, D. Bearing weak fault feature extraction under time-varying speed conditions based on frequency matching demodulation transform. IEEE/ASME Trans. Mechatron. 2022, 28, 1627–1637. [Google Scholar] [CrossRef]
- Gougam, F.; Rahmoune, C.; Benazzouz, D.; Afia, A.; Zair, M. Bearing faults classification under various operation modes using time domain features singular value decomposition fuzzy logic system. Adv. Mech. Eng. 2020, 12, 1687814020967874. [Google Scholar]
- Zhao, D.; Wang, H.; Cui, L. Frequency-chirprate synchrosqueezing-based scaling chirplet transform for wind turbine nonstationary fault feature time–frequency representation. Mech. Syst. Signal Process. 2024, 209, 111112. [Google Scholar] [CrossRef]
- Lu, Y.; Wang, Z.; Zhu, D.; Gao, Q.; Sun, D. Bearing fault diagnosis based on clustering and sparse representation in frequency domain. IEEE Trans. Instrum. Meas. 2021, 70, 1–14. [Google Scholar] [CrossRef]
- Jawad, S.M.; Jaber, A.A. Bearings health monitoring based on frequency-domain vibration signals analysis. Eng. Technol. J. 2022, 41, 86–95. [Google Scholar] [CrossRef]
- Liang, M.; Zhou, K. A hierarchical deep learning framework for combined rolling bearing fault localization and identification with data fusion. J. Vib. Control 2023, 29, 3165–3174. [Google Scholar] [CrossRef]
- Sun, Y.; Li, S. Bearing fault diagnosis based on optimal convolution neural network. Measurement 2022, 190, 110702. [Google Scholar] [CrossRef]
- Chaleshtori, A.E.; Aghaie, A. A novel bearing fault diagnosis approach using the Gaussian mixture model and the weighted principal component analysis. Reliab. Eng. Syst. Saf. 2024, 242, 109720. [Google Scholar] [CrossRef]
- Unal, M.; Onat, M.; Demetgul, M.; Kucuk, H. Fault diagnosis of rolling bearings using a genetic algorithm optimized neural network. Measurement 2014, 58, 187–196. [Google Scholar] [CrossRef]
- Tang, H.; Tang, Y.; Su, Y.; Feng, W.; Wang, B.; Chen, P.; Zuo, D. Feature extraction of multi-sensors for early bearing fault diagnosis using deep learning based on minimum unscented kalman filter. Eng. Appl. Artif. Intell. 2024, 127, 107138. [Google Scholar] [CrossRef]
- Zhang, J.; Sun, Y.; Guo, L.; Gao, H.; Hong, X.; Song, H. A new bearing fault diagnosis method based on modified convolutional neural networks. Chin. J. Aeronaut. 2020, 33, 439–447. [Google Scholar] [CrossRef]
- Su, Y.; Shi, L.; Zhou, K.; Bai, G.; Wang, Z. Knowledge-informed deep networks for robust fault diagnosis of rolling bearings. Reliab. Eng. Syst. Saf. 2024, 244, 109863. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhou, T.; Huang, X.; Cao, L.; Zhou, Q. Fault diagnosis of rotating machinery based on recurrent neural networks. Measurement 2021, 171, 108774. [Google Scholar] [CrossRef]
- An, Z.; Li, S.; Wang, J.; Jiang, X. A novel bearing intelligent fault diagnosis framework under time-varying working conditions using recurrent neural network. ISA Trans. 2020, 100, 155–170. [Google Scholar] [CrossRef]
- Yu, Y.; Si, X.; Hu, C.; Zhang, J. A review of recurrent neural networks: LSTM cells and network architectures. Neural Comput. 2019, 31, 1235–1270. [Google Scholar] [CrossRef]
- Yang, Z.; Cen, J.; Liu, X.; Xiong, J.; Chen, H. Research on bearing fault diagnosis method based on transformer neural network. Meas. Sci. Technol. 2022, 33, 085111. [Google Scholar] [CrossRef]
- Alexakos, C.T.; Karnavas, Y.L.; Drakaki, M.; Tziafettas, I.A. A combined short time fourier transform and image classification transformer model for rolling element bearings fault diagnosis in electric motors. Mach. Learn. Knowl. Extr. 2021, 3, 228–242. [Google Scholar] [CrossRef]
- Tang, X.; Xu, Z.; Wang, Z. A novel fault diagnosis method of rolling bearing based on integrated vision transformer model. Sensors 2022, 22, 3878. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.; Lin, Y.; Cao, Y.; Hu, H.; Wei, Y.; Zhang, Z.; Lin, S.; Guo, B. Swin Transformer: Hierarchical Vision Transformer Using Shifted Windows. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Virtual, 11–17 October 2021; pp. 10012–10022. [Google Scholar]
- Zhou, H.; Zhang, S.; Peng, J.; Zhang, S.; Li, J.; Xiong, H.; Zhang, W. Informer: Beyond Efficient Transformer for Long Sequence Time-Series Forecasting. In Proceedings of the AAAI Conference on Artificial Intelligence, Virtual, 2–9 February 2021; Volume 35, pp. 11106–11115. [Google Scholar]



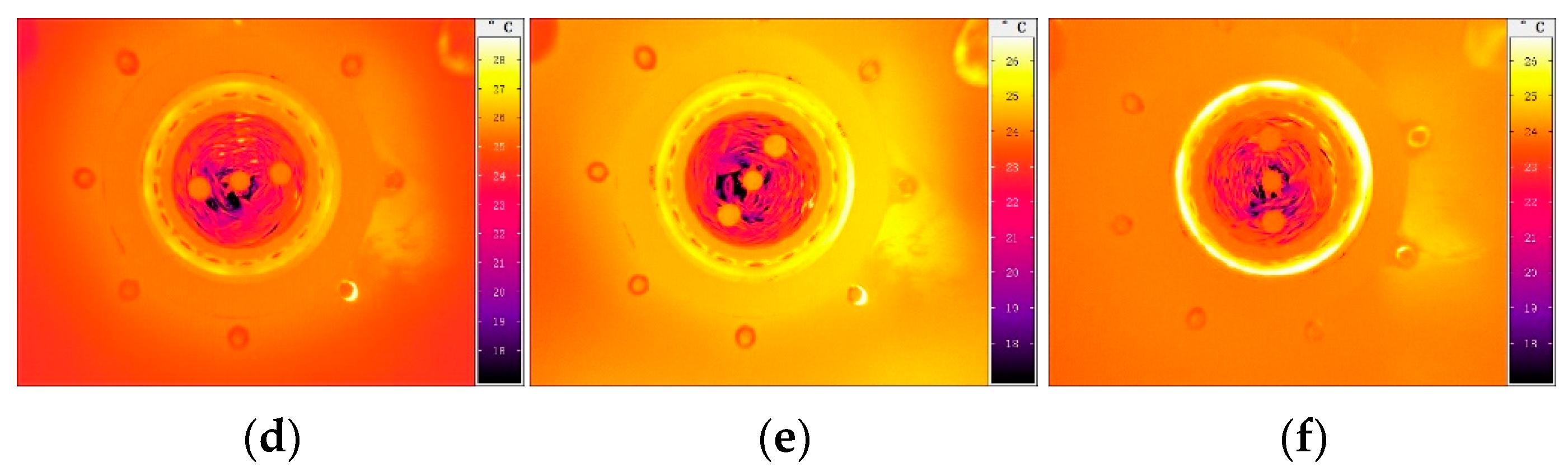


| Temperature Rise | Steady-State | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| HB | SIRF | MIRF | LIRF | SORF | MORF | LORF | HB | SIRF | MIRF | LIRF | SORF | MORF | LORF | |
| HB | 52 | 3 | 1 | 0 | 2 | 2 | 0 | 57 | 1 | 1 | 0 | 1 | 0 | 0 |
| SIRF | 3 | 53 | 2 | 2 | 0 | 2 | 1 | 1 | 59 | 0 | 0 | 0 | 0 | 0 |
| MIRF | 2 | 0 | 56 | 0 | 1 | 1 | 0 | 0 | 0 | 60 | 0 | 0 | 0 | 0 |
| LIRF | 0 | 4 | 0 | 54 | 2 | 0 | 6 | 0 | 1 | 0 | 59 | 0 | 0 | 0 |
| SORF | 2 | 0 | 0 | 1 | 55 | 2 | 0 | 1 | 0 | 0 | 0 | 58 | 0 | 1 |
| MORF | 0 | 0 | 3 | 0 | 0 | 57 | 0 | 0 | 0 | 1 | 0 | 0 | 59 | 0 |
| LORF | 0 | 0 | 0 | 0 | 1 | 0 | 59 | 0 | 0 | 0 | 0 | 0 | 1 | 59 |
| Temperature Rise | Steady-State | |||||||
|---|---|---|---|---|---|---|---|---|
| Accuracy | Precision | Recall | F1 Score | Accuracy | Precision | Recall | F1 Score | |
| HB | 0.9650 | 0.8814 | 0.8667 | 0.8740 | 0.9881 | 0.9661 | 0.95 | 0.9580 |
| SIRF | 0.9604 | 0.8833 | 0.8413 | 0.8618 | 0.9929 | 0.9672 | 0.9833 | 0.9752 |
| MIRF | 0.9767 | 0.9032 | 0.9333 | 0.9180 | 0.9952 | 0.9677 | 1 | 0.9836 |
| LIRF | 0.9650 | 0.9474 | 0.8182 | 0.8781 | 0.9976 | 0.9833 | 0.9833 | 0.9916 |
| SORF | 0.9744 | 0.9016 | 0.9167 | 0.9091 | 0.9929 | 0.9831 | 0.9667 | 0.9748 |
| MORF | 0.9767 | 0.8906 | 0.95 | 0.9193 | 0.9952 | 0.9833 | 0.9833 | 0.9833 |
| LORF | 0.9814 | 0.8939 | 0.9833 | 0.9365 | 0.9952 | 0.9833 | 0.9833 | 0.9833 |
| Bearing Condition | ||||||
|---|---|---|---|---|---|---|
| SIRF | MIRF | LIRF | SORF | MORF | LORF | |
| SIRF | 59 | 0 | 1 | 0 | 0 | 0 |
| MIRF | 1 | 59 | 0 | 0 | 0 | 0 |
| LIRF | 0 | 0 | 60 | 0 | 0 | 0 |
| SORF | 0 | 0 | 0 | 60 | 0 | 0 |
| MORF | 0 | 1 | 1 | 0 | 58 | 0 |
| LORF | 0 | 0 | 0 | 0 | 0 | 60 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, C.; Zou, W.; Hu, Z.; Li, H.; Sui, X.; Ma, X.; Yang, F.; Guo, N. Bearing Health State Detection Based on Informer and CNN + Swin Transformer. Machines 2024, 12, 456. https://doi.org/10.3390/machines12070456
Liu C, Zou W, Hu Z, Li H, Sui X, Ma X, Yang F, Guo N. Bearing Health State Detection Based on Informer and CNN + Swin Transformer. Machines. 2024; 12(7):456. https://doi.org/10.3390/machines12070456
Chicago/Turabian StyleLiu, Chunyang, Weiwei Zou, Zhilei Hu, Hongyu Li, Xin Sui, Xiqiang Ma, Fang Yang, and Nan Guo. 2024. "Bearing Health State Detection Based on Informer and CNN + Swin Transformer" Machines 12, no. 7: 456. https://doi.org/10.3390/machines12070456
APA StyleLiu, C., Zou, W., Hu, Z., Li, H., Sui, X., Ma, X., Yang, F., & Guo, N. (2024). Bearing Health State Detection Based on Informer and CNN + Swin Transformer. Machines, 12(7), 456. https://doi.org/10.3390/machines12070456






