Design and Experimental Study of Negative Pressure Spiral Separation and Reduction Device for Drilling Holes

Abstract

Currently, screw conveyors and negative pressure vacuum screens with negative pressure vibration units are used for handling drilling cuttings both domestically and internationally. However, there is currently no effective solution to address the high liquid content of drilling cuttings during their conveyance by screw conveyors. In this paper, a novel design scheme for a negative pressure spiral separation and reduction device is proposed based on an extensive literature survey. This device aims to effectively reduce the liquid content of drilling cuttings during their conveyance by screw conveyors, thereby minimizing the overall liquid content throughout the drilling process. The structural design of the negative pressure spiral separation and reduction device is conducted using theoretical analysis and 3D solid modeling methods, while strength analysis of the negative pressure suction unit is performed using a finite element method. Additionally, theoretical research on relevant process parameters is carried out, and an online real-time testing system for experiments is designed. An analysis of experimental results demonstrates that within 151 s, the liquid suction rate of the device can reach 51%, with an average flow speed of approximately 0.008 m/s, thus achieving the desired target for drilling cutting separation and reduction. By designing this new negative pressure spiral separation and reduction device, its feasibility has been verified through acceptable engineering results obtained from experimentation; furthermore, it aims to achieve an optimal liquid suction effect for drilling cuttings in order to enhance solid–liquid separation efficiency, as well as to improve drilling fluid recovery efficiency by conserving mud materials and reducing overall drilling costs.

1. Introduction

With the rapid development of the oil industry, more waste drilling fluids are being generated at drilling sites, and these waste drilling fluids will undoubtedly have a huge impact on the marine and terrestrial environments [1,2,3]. During the drilling of oil and gas wells, there are two main types of wastes produced: one is drill cuttings and the other is drilling fluid. Therefore, the recycling of drill cutting mud containing waste drilling flu-ids generated during the drilling process can greatly reduce the impact of environmental pollution caused by drilling, save mud materials, and reduce drilling costs [4]. Drill cut-tings and mud are important waste products in drilling operations [5,6]. Up to now, the most widely used drilling mud treatment method is the reinjection method, but for some inland seas, such as China’s Bohai Sea, the discharge in these seas will be subject to strict requirements, only the use of the waste liquid recycling method of drilling mud within the liquid phase of the treatment, also known as the reduction of drilling cuttings containing liquid. International researchers have carried out much research on both improving the capacity of solid control equipment and equipping reduction and treatment devices to solve the challenges of drilling waste disposal. In recent years, with the continuous improvements in drilling fluid systems, the capability of rock cutting solid control equipment and the development of treatment devices to reduce the fluid content of drill cuttings have also been significantly improved. Next, the current status of research on screw conveyor and negative pressure suction technology will be presented separately.

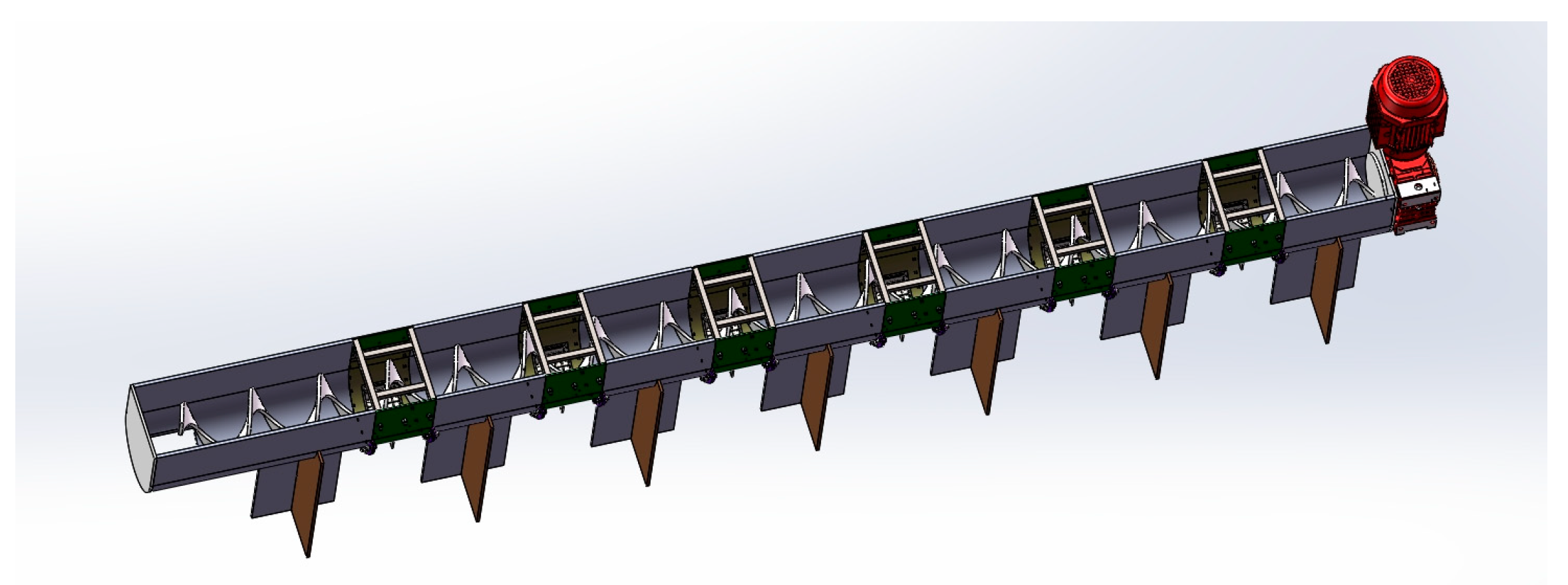
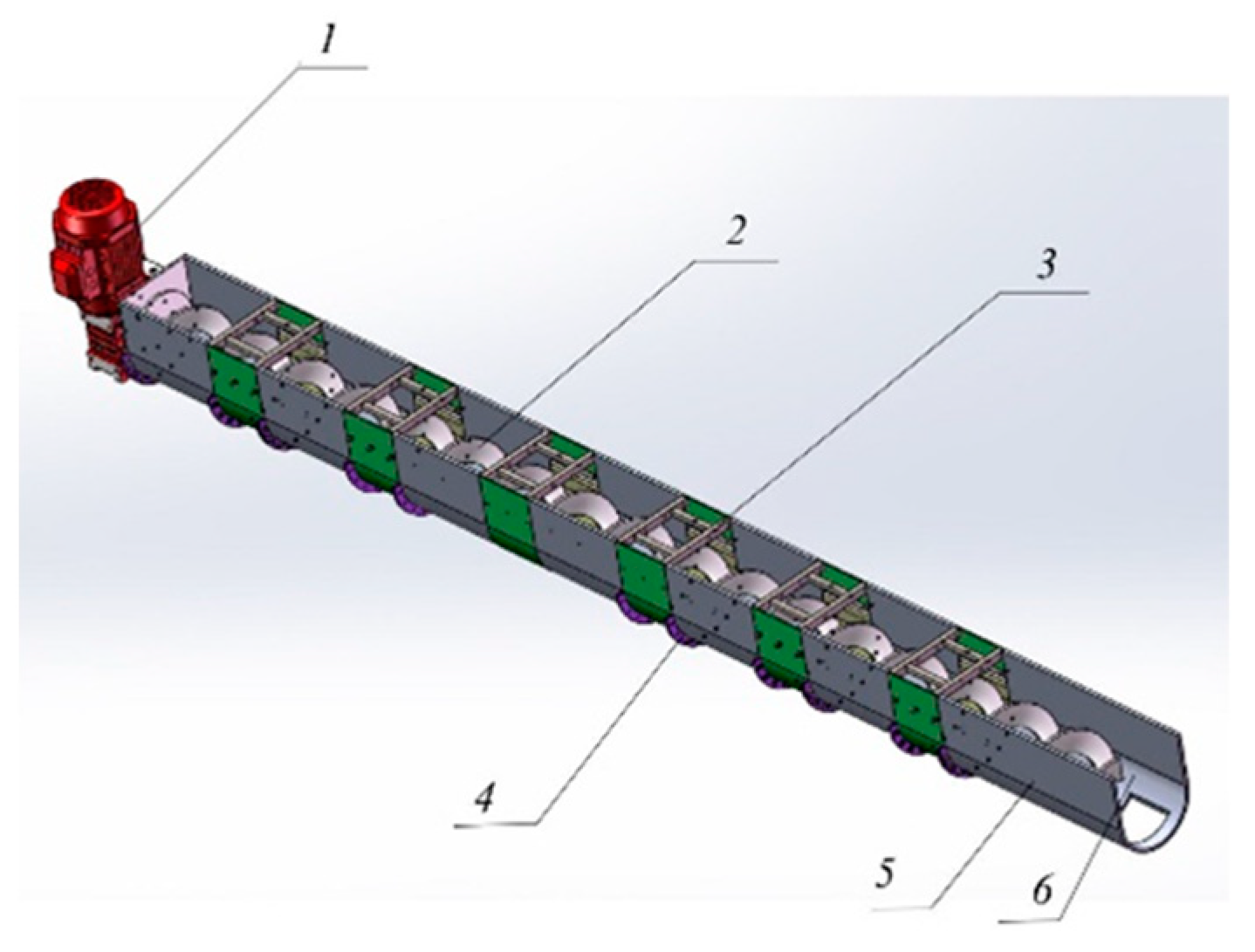
Screw conveyors are one of the best conveying systems for specific applications [7], such as in the chemical, building materials, and grain industries. Screw conveyors can be used to transport and mix more than one type of material during material transfer [8,9,10], and the 3D model is shown in Figure 1.

The rotary motion of the shaftless auger facilitates the conveying and simultaneous mixing of granular material through the discharge area [11,12]. The Shaftless Screw Conveyor has a strong anti-tangling property, which can reduce the interference of easily tangled materials and then convey materials easily and quickly, which cannot be done by a Shafted Screw Conveyor. In 2008, Merritt et al. [13] proposed a novel theoretical model to describe the total pressure gradient and torque of tunnel excavator spiral conveyors. The theory introduced new equations that establish connections between the pressure gradient and torque with the geometric characteristics, shear stress, and material flow within the spiral conveyor. In 2021, Narayani et al. [14] developed an innovative oil sludge excavation system based on spiral conveyors and devised a mathematical model to facilitate the design of a spiral conveyor capable of excavating maximum sludge per rotation. Computational fluid dynamics were employed for numerical simulations to visualize material flow in various system designs. In 2010, Zhongjun Yin et al. [15] investigated the conveying principle of open-helix conveyors from a kinematic perspective by focusing on individual particles within such conveyors. They analyzed the granular material conveying speed during the transportation process along with its influencing factors, thereby deriving design criteria for key parameters of open-helix conveyors. In 2014, Qingchun Sun [16] conducted relevant research on optimizing stiffness in two components—the spiral axis and blade—of horizontal spiral conveyors using multi-degree-of-freedom system vibration theory while also enhancing existing structural models. In 2015, Chaobin Jia [17] on the structure of the screw conveyor and its working principle, analyzed the basis of the design of the conveyor, to establish the mathematical model of its parameter design, to determine the optimization of the main variables (parameters), constraints, and objective function to establish the optimization of the mathematical model and the optimization of the main parameters and to find the optimal combination of parameters.

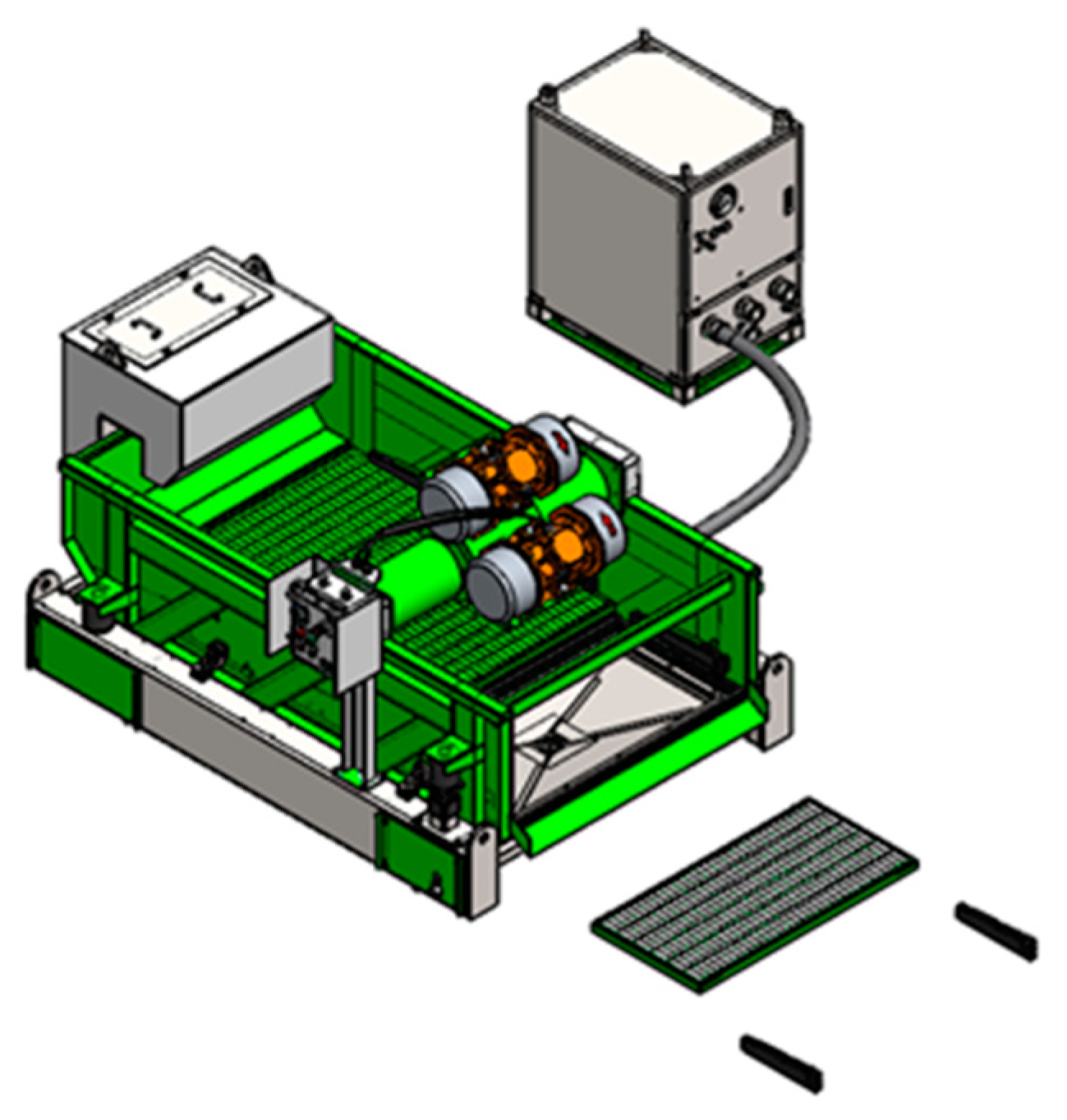
Mud solid phase control equipment is used to control the solid phase particles in the drill cutting mud [18,19,20]. Through a large amount of literature research, it was found that up to now, offshore oilfield drill cutting liquid phase reduction equipment applied to the negative pressure pumping technology is only a vibrating screen. A drilling shaker is the first stage of solid phase control equipment for recovering drilling fluids [21,22,23]. In order to improve screening efficiency, researchers have proposed the concept of “negative pressure suction”. The 3D model of a negative pressure vibrating screen is shown in Figure 2. In the 1980s, Remteck, an American company, ref. [24] pioneered the development of the MAX system. This groundbreaking innovation introduced the vacuum filtration principle commonly employed in mining to revolutionize the solid–liquid separation process of drilling fluid. By effectively extracting drilling mud through a filter belt, this technology marked a significant advancement in the field. In 2015, US-based SWACO [25] introduced a pulsed vacuum negative pressure vibrating screen that incorporates a vacuum negative pressure device at the end of the traditional vibrating screen and utilizes pulsed airflow to create a suction effect, thereby enhancing the drilling-fluid-recovery rate and reducing solid–liquid separation difficulties in mixed liquids. This technology can effectively reduce liquid content in solid-phase material from drilled rock cuttings by 20–30% after treatment, improve liquid reuse efficiency, and significantly lower drilling costs. In 2018, Sizhu Zhou et al. [26] designed an innovative type of drilling vibrating screen that leverages pressure differences to enhance the working performance and increase drilling fluid treatment capacity. They analyzed different-sized rock debris’ throwing motion under negative pressure conditions and optimized the corresponding parameters. In 2020, Wenliang Li [27] developed a sludge vacuum suction device that employs large screw air compressors to generate high-pressure airflow, which is then converted into negative pressure for generating suction force capable of drawing in drilling mud; high-pressure airflow is subsequently used for the direct discharge of mud to central treatment points.

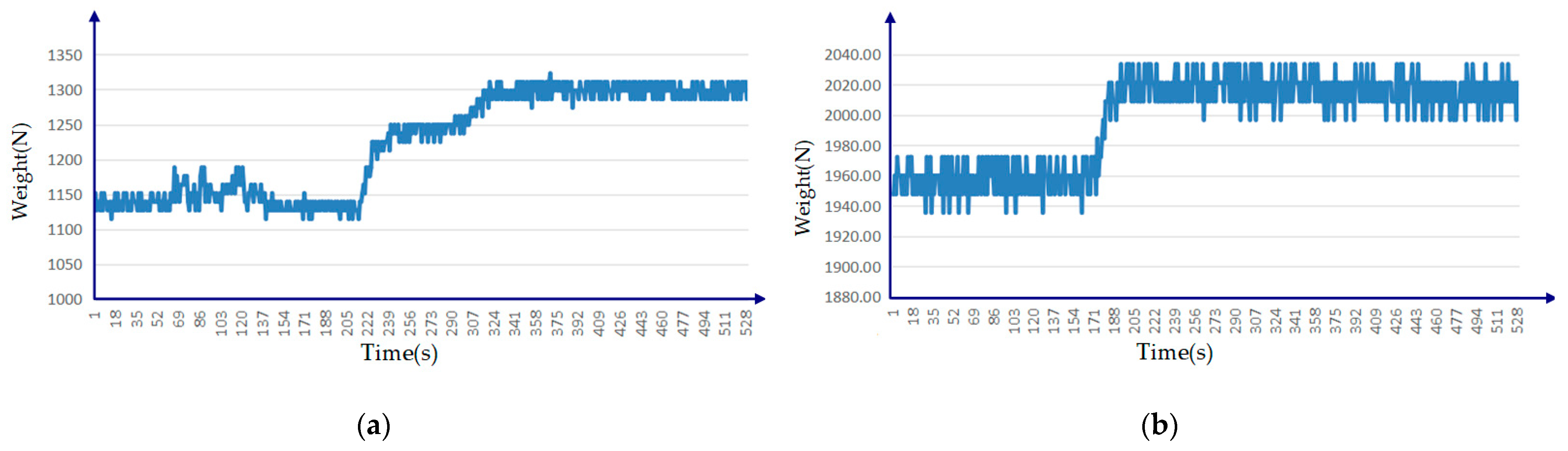
The present study aims to comprehensively investigate the feasibility of the proposed scheme through a theoretical analysis, kinematic analysis, structural design and strength analysis, fluid dynamic simulation analysis of the vacuum screen, and experimental trials on a prototype to validate the theoretical findings by assessing actual suction effects.

After conducting a comprehensive review of the relevant literature on the treatment of drilling cuttings in offshore oilfields both domestically and internationally, this paper presents a concise summary of related technologies and subsequently proposes an innovative design scheme for negative pressure spiral separation and reduction. Notably, this scheme represents the pioneering application of negative pressure suction technology to a screw conveyor. Firstly, the device’s detailed structure is meticulously designed, followed by the establishment of a 3D model and subsequent finite element strength analysis. Then the theoretical analysis of relevant process parameters was carried out, and the vacuum screening process was simulated using the coupled EDEM-Fluent method. Finally, an online real-time testing system is devised to evaluate the solid–liquid separation effect. The experimental results conclusively demonstrate that this proposed scheme enables the more efficient solid–liquid separation of drilling cuttings, enhances the drilling fluid recovery efficiency, reduces mud material consumption, and lowers drilling costs significantly while effectively conserving energy.

2. Design of a Negative Pressure Spiral Separator for Reducing Liquid Phase Content

This chapter presents the comprehensive design of the negative pressure spiral separation and reduction device, which combines the axis-less screw conveyor with the vacuum adsorption device used in the negative pressure vibrating screen from a macro perspective. After formulating the overall scheme, an analysis is conducted on the screw conveyor, encompassing its selection, structure, and kinematics during drill cuttings, conveying process to establish a relationship between the motor speed and forward speed of drill cuttings. Subsequently, a crucial component called the negative pressure suction short node is designed by integrating both the axis-less screw conveyor and vacuum adsorption device employed in the negative pressure vibrating screen. The quality of this component directly influences that of the entire device. Finally, a strength analysis is performed on the negative pressure suction short node to ensure compliance with engineering requirements.

2.1. New Design Solution and Innovation of Negative Pressure Spiral Separator for Reducing Liquid-Phase Content

Through a comprehensive domestic and international literature search and analysis, a new design of the negative pressure spiral separation device for reducing the liquid phase is proposed, as shown in Figure 3, for the reduction of the liquid phase of the negative pressure spiral separation device arrangement schematic diagram. In the existing drill cutting treatment process, the wet drill cuttings are initially screened by a vibrating screen and then directly poured into a screw conveyor, which then transports the drill cuttings to a designated location; the length of the screw conveyor is controlled by increasing or decreasing the number of short sections of the conveyor, which in turn controls the conveying distance of the conveyor. In the existing arrangement, the screw conveyor only has the function of conveying drill cuttings. In this paper, a new type of program is researched, as shown in Figure 1; the negative pressure suction short section is designed at the connection of the conveyor short section, and the conveyor is connected with the screw conveyor. The screw conveyor operates normally, and when the drill cuttings pass through the negative pressure suction short section under the impetus of the blades of the screw conveyor, the liquid phase of the drill cuttings will be sucked away by the action of the suction force and then be discharged to the liquid phase of the drill cutting collection area, and at the same time, the solid phase of the drill cuttings continues to be discharged to the solid phase collection area of the drill cuttings through the screw conveyor. This solution allows the drill cuttings to be de-liquidized again at the screw conveyor, which can better reduce the liquid content in the drill cuttings.

Arranged by the negative pressure spiral separation device used to reduce the liquid phase, the overall structure of the design equipment is shown in Figure 4. Three negative pressure suction short sections and one vacuum adsorption device are used as one set of equipment in this design, and the amount of equipment can be increased later according to the actual distance and the liquid content of the drill cuttings at the time of use. Figure 4 shows the three-dimensional model of the two sets of equipment in use. In Figure 4 of 4, for the vacuum adsorption device, this vacuum adsorption device needs an external air source, and the use of the venturi principle will come from the air source of high-pressure air jets converted to negative pressure, so as to produce a certain degree of suction; at the same time, the vacuum adsorption device can also be realized in the high-pressure discharge and will be inhaled to the liquid phase of the drill cuttings for a long-distance discharge. The vacuum adsorption device mainly consists of venturi, suction and discharge conversion valves, discharge valves, suction valves, sludge storage tanks, and control systems. In addition, this vacuum adsorption device has a mature product and can be directly purchased and used.

The technical parameters for the design of the device are as follows:

Parameters of shaftless screw conveyor:

• Motor power: 5.5 KW;
• Angular velocity: 40 rpm;
• Spiral blade diameter: $\varphi 260 \mathrm{mm}$
• Pitch of spiral: 250 mm.

Negative pressure suction short section parameters:

• Short section specifications (L × W × H): 306 × 230 × 405 mm;
• Weights: 22.56 kg;
• Specification of short section suction hole (L × W): 187 × 120 mm;
• Outside pipe coupling fitting specifications: G2.

The working process is as follows: in Figure 4, the drill cuttings are poured into the screw conveyor 2 via the top of different short sections of the screw conveyor, and the motor rotates with the blades, which in turn moves with the drill cuttings, and the vacuum adsorption device 4 negatively pumps the liquid phase portion of the material whenever it passes through the negative pressure pumping short Section 1 and discharges it into the drill cutting liquid-phase collection area 5. The six negative pressure suction short sections of the whole device can treat the liquid phase in a graded manner, and each negative pressure suction short section is connected to the vacuum adsorption device through the pipeline 3, and a valve is provided in the pipeline 3, which can control the opening and closing of a certain negative pressure suction short section through the valve. Eventually, the reduced drill cuttings will be discharged to the drill cutting solid-phase collection area 6 through the end of the screw conveyor 2.

The innovations of the design scheme of this negative pressure spiral separation and reduction device can be summarized as the following three points:

• Drawing on the pulsed negative pressure vibrating screen suction technology and structure;
• Innovative combination of negative pressure suction technology and screw conveyor, and can be embedded in the screw conveyor multi-segment node-type negative pressure suction device, efficiently realizing the solid–liquid separation of drill cuttings;
• It can realize the best match between the movement of drill cuttings and the flow rate of the suction liquid, improve the solid–liquid separation efficiency of drill cuttings, save mud materials, reduce drilling costs, and save energy effectively.

2.2. Screw Conveyor Analysis

2.2.1. Screw Conveyor Selection and Structure

Currently offshore drilling platforms mainly use screw conveyors to transfer drilling waste chips. A horizontal shaftless screw conveyor is selected according to the nature of waste chips. The waste chips have a complex composition, including water, oil, clay, and rock chips, etc., with various forms and a certain viscosity. To ensure continuous conveying and prevent leakage, the horizontal shaftless screw conveyor was selected. This conveyor is characterized by a high conveying capacity, anti-tangling, and anti-clogging, which ensures the smooth conveying of materials, and even if jamming occurs, the screw body can be released by itself, effectively avoiding clogging. In addition, since oil drilling is a continuous process, the waste chips generated need to be continuously transported to the treatment system while ensuring that they do not leak out. The advantages of choosing a horizontal shaftless screw conveyor are its large conveying capacity, resistance to entanglement, and anti-clogging characteristics, which ensure the smooth transportation of the waste chips. Even in the event of clogging, the screw body can be released elastically, which greatly improves the chances of clogging.

As shown in Figure 5, it is the SolidWorks model of the horizontal shaftless screw conveyor. The working principle is as follows: the shaftless blade 2 rotates under the drive of the motor 1, which drives the drill chips to rotate and move linearly, and they will finally be discharged from the end outlet; 3 is a square steel pipe, which plays the role of supporting the shell, so that both sides of the shell to maintain a certain degree of parallelism; 4 is the connecting ribs, so that each section of the spiral conveyor is connected by bolts. Inside the conveyor, there is a stainless steel lining plate 6 with it, which plays a protective role and can avoid the damage caused by the friction between the blades and the cylinder wall 5 of the conveyor.

2.2.2. Drill Chip Kinematic Analysis

To analyze a unit of drill cuttings in the screw conveyor, the distance of the drill cuttings from the “axis” is $d$, and the screw angle of rise is $\alpha$. With the rotation of the screw blade, the linear velocity $v_q$ is the traction speed of the unit of drill cuttings and the direction is the tangent direction of the screw. This is due to the friction between the blade and the material, the absolute speed of the unit chip material $v_a$ direction, and the normal direction to produce an angle. The motion decomposition diagram is shown in Figure 6.

As can be seen from Figure 6, the absolute velocity of the unit drill chip material can be decomposed into two directional component velocities, the axial component velocity $v_x$ and the circumferential component velocity $v_c$, for which the values can be solved using vector triangles:

$$v_x=v_a\cos (\alpha +\beta )$$

(1)

$$v_c=v_a\sin (\alpha +\beta )$$

(2)

$$v_a=\frac{v_q}{\cos \beta }=\frac{v_0\sin \alpha }{\cos \beta }$$

(3)

$$v_0=\frac{2\pi n}{60}\frac{P}{2\pi \tan \alpha }=\frac{nP}{60\tan \alpha }$$

(4)

$$v_a=\frac{nP}{60\tan \alpha }\frac{\sin \alpha }{\cos \beta }=\frac{nP\cos \alpha }{60\cos \beta }$$

(5)

$$v_x=\frac{Pn}{60}\times \frac{1-\mu \frac{P}{2\pi d}}{1+{\left(\frac{P}{2\pi d}\right)}^2}$$

(6)

$$v_c=\frac{Pn}{60}\times \frac{\mu +\frac{P}{2\pi d}}{1+{\left(\frac{P}{2\pi d}\right)}^2}$$

(7)

where $P$ is the pitch of the spiral blade (mm), take 250 mm; $v_x$ is the axial speed of the material (mm/s); $v_c$ is the circumferential velocity of the material (mm/s); $\mu$ is the coefficient of friction between the material and the spiral surface, take 0.5; $n$ is the rotational speed of the spiral shaft (rpm), take 40 rpm; $d$ is the distance between the location of the material particles to the “axis” of the spiral (mm).

In summary, substituting the data, the axial velocity of the material is found to be 0.115 m/s based on Equation (6).

2.3. Negative Pressure Suction Short Section Design and Analysis

2.3.1. Negative Pressure Suction Short Section Structure Design

The negative pressure short section is connected to the vacuum adsorption device through the pipeline, forming negative pressure inside of it to recover the liquid phase in the drill cuttings. This device can realize the optimal match between the movement of the drill cutting material and the flow rate of the suction liquid, so that it can effectively reduce the liquid content of the conveyed drill cuttings and play the role of negative pressure suction reduction.

As shown in Figure 7, for the design of the negative pressure suction short section of the structural diagram, the working principle is as follows: square steel tube 1 plays a supporting role, can maintain the parallelism of the two sides of the outer cylinder wall 5. Structure 2 for the stainless steel liner plays a protective role and can avoid friction between the blade and the negative pressure suction short section of the outer cylinder wall 5 and cause damage. Structure 7 is a support rib plate, which supports the whole negative pressure suction section. The negative pressure suction section is bolted to the screw conveyor through the connecting ribs 3. Structure 4 is a filter module; the liquid phase will enter the negative pressure bin 6 through the filter, the right side of the negative pressure bin 6 is connected to the vacuum adsorption device through the pipeline, and the liquid phase will be recovered.

The entire filter module can be divided into three parts: the upper cover plate, the intermediate support, the lower support plate, and the steel wire filter mesh, as illustrated in Figure 8. The upper cover plate and intermediate support are welded together to form a single component. The lower support plate is connected to the upper cover plate using four bolts. The space between the upper cover plate and lower support plate is utilized for placing the steel wire filter mesh. Once the filter mesh is positioned, the tightening of bolts with a screwdriver allows for lifting of the upper cover plate akin to a screw and nut structure, ensuring tight compression of the steel wire filter mesh within the frame of the filter module. Layered installation of steel wire filter mesh can be performed based on specific requirements, with the maximum thickness reaching 11 mm. Constructed entirely from 1.5 mm stainless steel plates, drilling bolt holes in the upper cover plate or threading on lower support plates is not feasible; hence, protrusions need to be welded onto these plates before drilling operations commence for hole-creation purposes. Furthermore, in order to ensure a precise welding alignment between intermediate supports and upper cover plates, positioning grooves measuring 0.5 mm thick are incorporated at both ends where contact occurs between these components; additionally, positioning protrusions measuring 0.5 mm thick are added at both ends of intermediate supports to align with corresponding positioning grooves on upper cover plates during the welding processes, as depicted in Figure 9.

2.3.2. Strength Analysis of Negative Pressure Suction Short Sections

Stress analysis of the entire negative pressure short section is carried out using simulation tools in the following steps:

• Stress analysis of the entire negative pressure short section is carried out using simulation tools in the following steps;
• Adding the load, one pressure estimate of 1000 N was applied by the drill cuttings and screw conveyor blades to the negative pressure short section in the same direction as gravity; (the pressure estimate value consists of two parts: the weight of the negative pressure suction short connector itself is 22.56 kg, and the weight of the drilling cuttings being conveyed during the working process is estimated by the formula $m=\rho v$ to be 60 kg. Then, an additional margin is set with an installed load of 1000 N);
• The delineation grid cell size is 2 mm, and the delineation is shown in Figure 10;
• Running this calculation example, the stresses are shown in Figure 11.

Through the simulation analysis of the negative pressure, the short section can be seen, and the maximum stress appears in Figure 11 of 1, with a value of $1.537\times {10}^7\mathrm{N}/{\mathrm{m}}^2$. Here, for the negative pressure warehouse support rib plate material used for Q235, the yield strength is $23.5\times {10}^7\mathrm{N}/{\mathrm{m}}^2$, so we can obtain the strength of this design to meet the requirements.

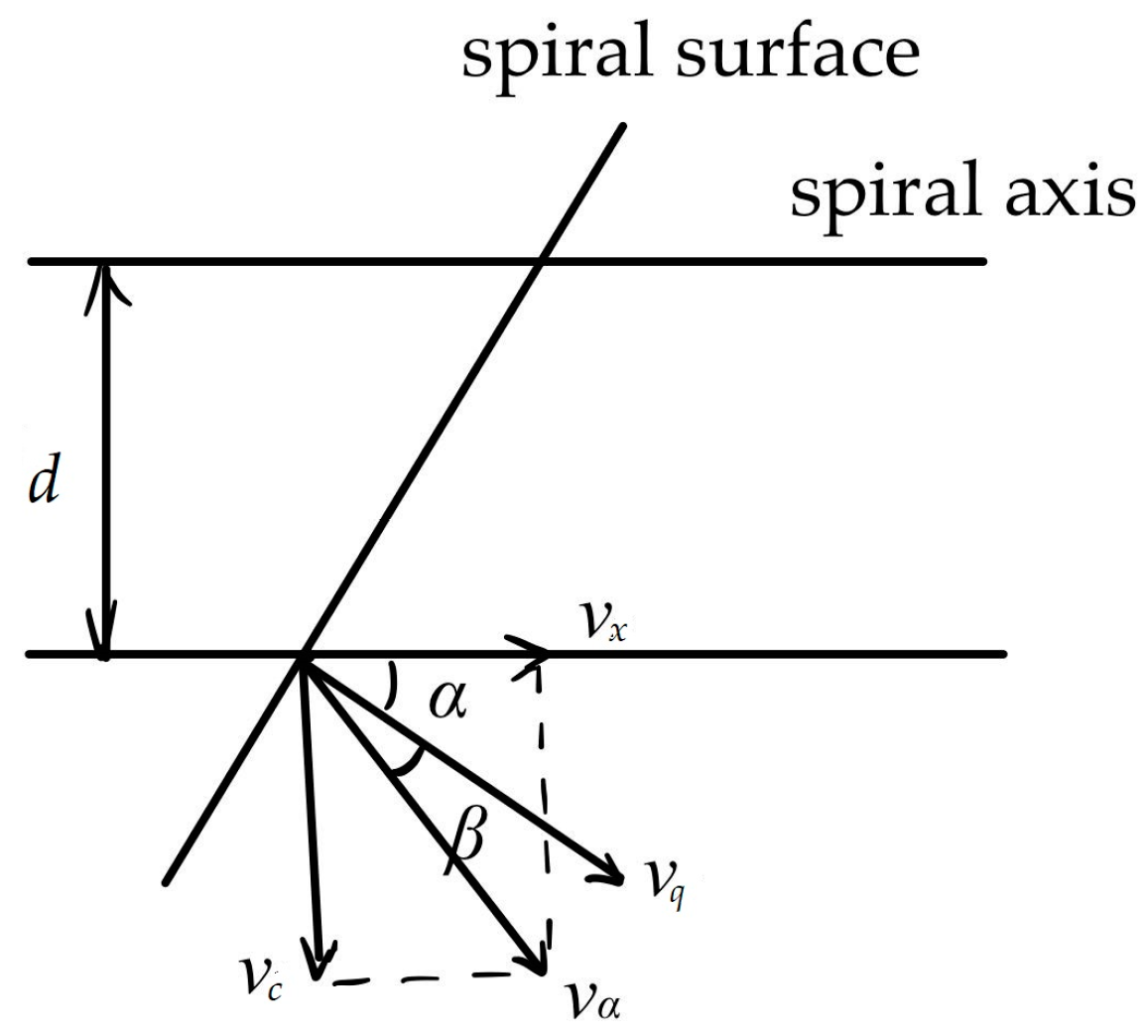
3. Theoretical Analysis of Process Parameters of Negative Pressure Spiral Separation and Reduction Device

The vacuum screening principle investigated in this study is as follows: particles enter the screening area through the material inlet located at the top of the material screening cylinder, while the bottom of the cylinder is connected to a vacuum chamber. The high-speed gas flow carries the material into the screening cylinder. Initially, during the vacuum screening process, gas and particles smaller than the mesh size pass through, whereas particles with a diameter close to or larger than that of the mesh are intercepted by it. Over time, these retained particles accumulate and form a bed, potentially leading to partial blockage of some sections of the mesh. The vacuum chamber maintains a pressure differential between the upper and lower surfaces of the mesh and facilitates gas flow, thereby enhancing the solid–liquid separation efficiency through the combined effects of the carrying capacity and pressure differential induced by the gas flow. In this chapter, we will employ an EDEM-Fluent coupled computational method to investigate screen mesh blocking patterns occurring during vacuum screening.

3.1. Numerical Simulation of Vacuum Sieving

3.1.1. Numerical Simulation Study of Gas-Solid Two-Phase

The vacuum screening process involves the calculation of the multiphase flow, which is a complex coupled process that is challenging to describe using single simulation software. In this study, we employ the EDEM-Fluent coupled method to simulate the blocking process in vacuum screening. The EDEM-Fluent computational model consists of two main models: the Eulerian–Lagrange method and the Eulerian–Eulerian method. When simulating without considering the solid-phase volume fraction, only momentum exchange between gas and solid phases needs to be considered, making the Eulerian–Lagrange coupled method suitable for calculations. This model offers a faster computation speed but is limited to working conditions where the local solid-phase volume fraction remains below 10%. On the other hand, the Eulerian–Eulerian method (also known as double Eulerian) considers interactions between solid and fluid phases, including the mass, momentum, and energy exchange [28]. As our simulation involves particle blocking and accumulation leading to local solid-phase volume fractions exceeding 10%, we choose the double Eulerian coupled model for discrete phase treatment.

3.1.2. EDEM Computational Model

The discretization of the model is based on the following assumptions [29]:

• The total deformation of the granular system is considered to be equivalent to the overall displacement of all particles within it;
• Particle–particle contact occurs through point contacts, which are localized in very small areas;
• Partial overlap may occur when particles come into contact, but the magnitude of this overlap is significantly smaller compared to the size of individual particles;
• In each computational step, no particle can instantaneously transmit external excitation to its adjacent particles. Consequently, the resultant force acting on any particle at any given time can be uniquely determined by interactions with its neighboring particles that are in contact.

The particle-motion-simulation process in EDEM 2022 software entails the movement of particles within a particle group. During the simulation, contact and collision between particles are essential, resulting in forces when particles come into contact. The discrete element method’s fundamental model is based on mutual contact, where the torque-based contact model directly determines the forces acting on the particles during analysis. In the discrete element analysis, the contact model for dispersed particles is categorized as either dry or wet based on analysis conditions. For dry particle materials without adhesion at remaining contact points, the Hertz–Mindlin basic contact model can be selected in EDEM software as it serves as both the default and suitable choice for calculating inter-particle forces [30].

$$\overrightarrow{F_{\nu }}=\frac{4}{3}{{\rm E}}_{eq}\sqrt{R_{eq}}{\alpha }^{\frac{3}{2}}$$

(8)

The format is as follows: $E_{eq}$ is the equivalent Young’s modulus, $\mathrm{GPa}$; $\alpha$ is the normal overlap, $\mathrm{mm}$; $R_{eq}$ is the equivalent contact radius.

The inter-particle normal damping force, as well as the tangential damping force, is calculated as follows [31]:

$$\begin{array}{l}{\overrightarrow{F_n}}^d=-2\sqrt{\frac{5}{6}}\beta \sqrt{S_n{m}_{eq}}{v_n}^{rel}\\ {\overrightarrow{F_t}}^d=-2\sqrt{\frac{5}{6}}\beta \sqrt{S_t{m}_{eq}}{v_t}^{rel}\end{array}$$

(9)

The format is as follows: $S_t$ is the tangential stiffness; $S_n$ is the normal stiffness; ${v_t}^{rel}$ is the tangential true velocity; ${v_n}^{rel}$ is the normalized true speed; $e$ is the coefficient of restitution; $m_{eq}$ is the equivalent mass.

3.1.3. Gas–Solid Coupling Control Equation

Laminar flow and turbulent flow are two flow states of airflow; the control equations of the two flows are the same, but the difference is that the variables have different expressions, and the turbulent transport equation needs to be attached when calculating turbulent flow. The following is the gas–solid coupling equation for laminar flow, and its N-S equation and continuity equation are as follows:

$$\left\{\begin{array}{l}\frac{\partial ({\epsilon }_g{\rho }_g)}{{\partial }_t}+\nabla \cdot ({\epsilon }_g{\rho }_g{u}_g)=0\\ \frac{\partial ({\epsilon }_g{\rho }_g{u}_g)}{{\partial }_t}+\nabla \cdot ({\epsilon }_g{\rho }_g{u}_g{\mu }_g)=-\nabla p+\nabla ({\mu }_g{\epsilon }_g\nabla u_g)-{\epsilon }_g{\rho }_{g}g-S\end{array}\right.$$

(10)

The format is as follows: ${\rho }_g$ is the density of the gas; $t$ for time; $u_g$ is the gas velocity; ${\epsilon }_g$ is the gas porosity; $p$ is the gas pressure; ${\mu }_g$ is the gas dynamic viscosity; $g$ is the acceleration due to gravity; $S$ is the phase of the momentum exchange source.

3.2. EDEM-Fluent Coupled Computational Model and Related Parameter Settings

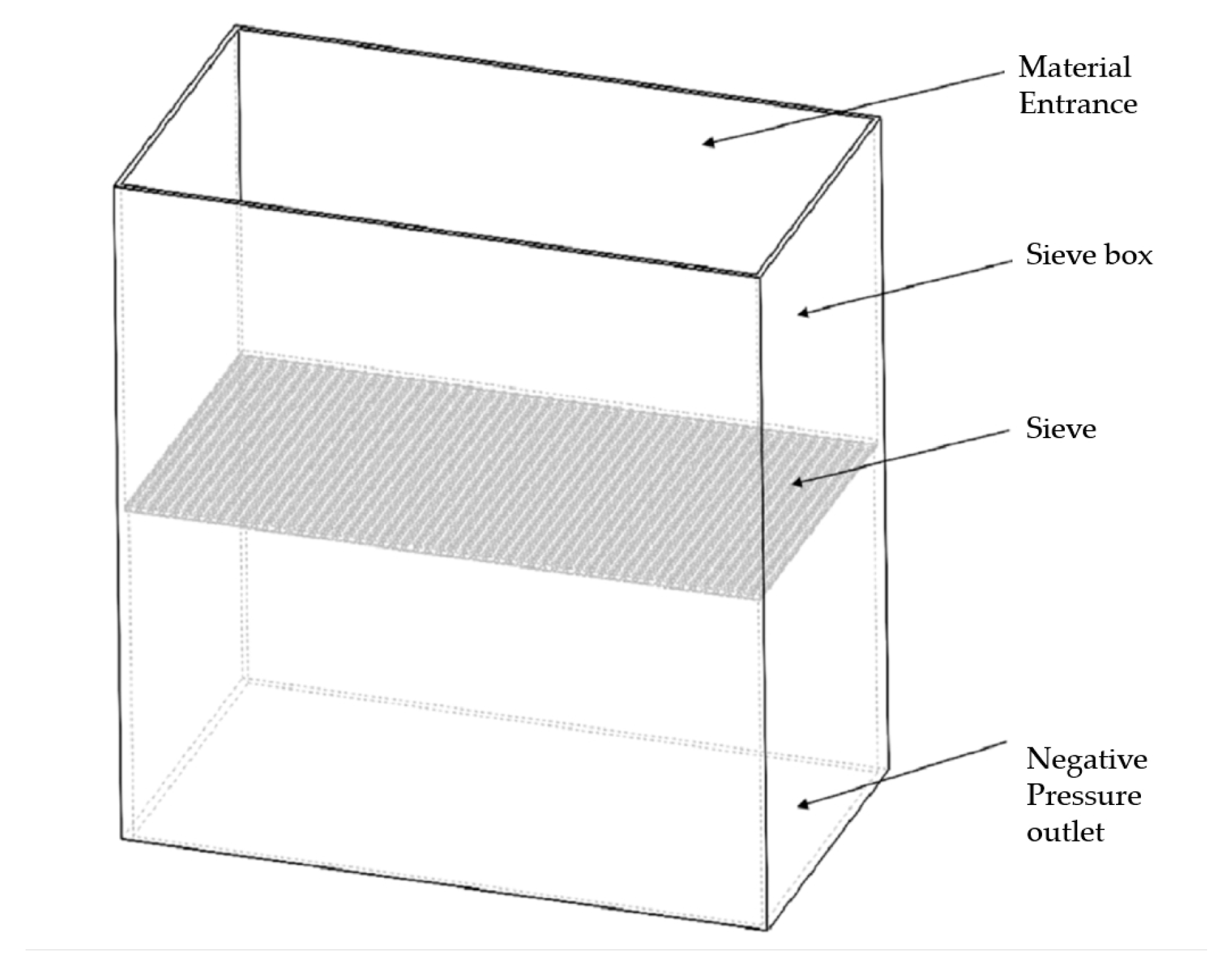
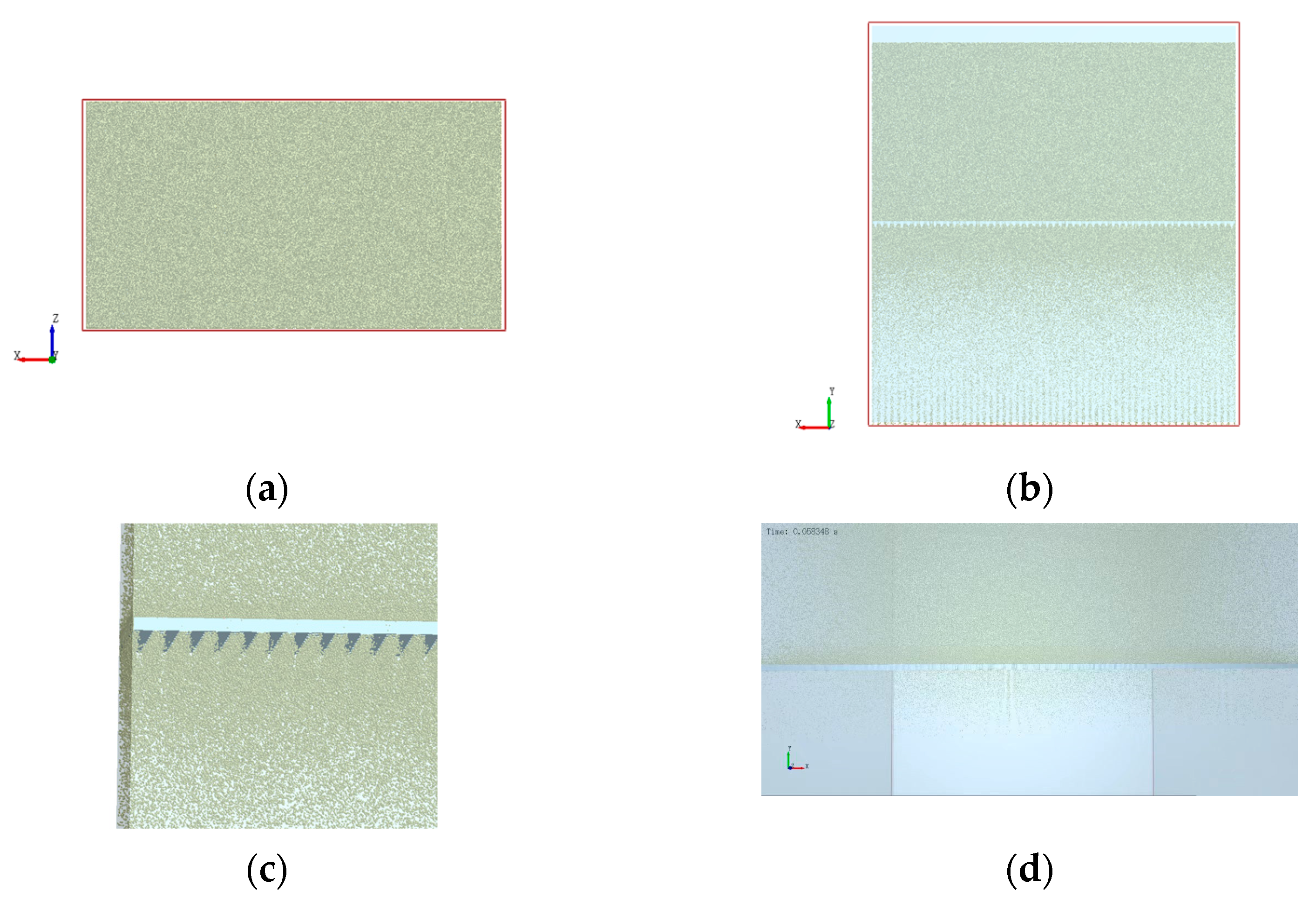
Based on the principle of vacuum screening and the reasonable simplification of the structure of the vacuum screening and filtration experimental device, the application of Solidworks2020 three-dimensional modeling software to establish a simplified three-dimensional model of the sieve bin, as shown in Figure 12, the sieve bin structure includes the material inlet, the material sieve cylinder, the sieve mesh, and the vacuum outlet.

Vacuum sieving and filtration experiments choose the effective processing area of the screen for $6739 {\mathrm{mm}}^2$, but simulation calculations need to take into account the computer computing power and calculation cycle, so the effective filtration area of the calculation model is reduced to the effective filtration area of the experimental 1/200, the screen calculation model is simplified to a porous structure but the mesh number of the screen remains unchanged, i.e., the effective area of the calculations for the 33,695 mm², the mesh size $a=0.14 \mathrm{mm}$, and the structure is square. The EDEM computational model is shown in Figure 13a, and the mesh division of the computational fluid domain in Fluent is shown in Figure 13b.

3.2.1. Solid-Phase Particle Modeling

Due to the heterogeneous particle size distribution and irregular shape and number of particles in drilling fluid, it is imperative to simplify the calculation model and reduce the simulation time. Consequently, this simulation analysis focuses on simulating particles prone to blockage, employing spherical particles as solid-phase calculation entities in the EDEM software. Several particle size distribution methods are available in EDEM for selection based on specific conditions, including a uniform particle size, average particle size distribution, normal distribution, random distribution, and user-defined particle size range. Given the irregularity of both the particle size distribution and number of solid-phase particles within a certain range only, we set the particle ratio according to

Table 1. Particle size ratio setting.

Particle Size Distribution Range	Particle Size Distribution Ratio
75–120 μm	10%
120–150 μm	40%
150–180 μm	50%

in EDEM software while opting for random distribution as the chosen method to establish our particle model.

3.2.2. Main Simulation Parameter Setup

Using the EDEM-Fluent coupled calculation method, the laws of screen mesh blockage during vacuum screening are studied. The calculation uses the EDEM 2022 version to simulate the particle phase and Fluent 2022 to simulate the gas phase. In the EDEM software, the parameters of the particles are set, and the contact model is selected as the Hertz–Mindlin frictionless contact model [32]. The gravity acceleration direction is set along the negative Y axis, with a magnitude of 9.81 m/s². After the parameters in the EDEM software are set, the coupling interface is opened, and then, the coupling file is loaded in Fluent. The two softwares are coupled together, and the solver in Fluent is selected as the pressure algorithm coupled solver, and the k-epsion model is selected. The working environment is set to atmospheric pressure. After the grid is divided for the fluid domain, the material handling cylinder outlet is set as the velocity outlet, the inlet is set as free flow into the atmospheric environment, and the outlet is set as the constant flow rate flow. The flow rate in the outlet can be controlled by changing the airflow speed, thereby achieving the goal of controlling the airflow during vacuum screening; because two softwares need to exchange data for the coupled calculation, the calculation time steps of the two softwares need to be matched. Since the calculation time step in EDEM is much smaller than that in Fluent 2022 software, it cannot be set at a ratio of 1:1, and the time step length in Fluent must be an integer multiple of the time step length in EDEM. In EDEM, the time step is set to 1 × 10⁻⁶ s, and the save time is set to 0.01 s. In Fluent, the time step is set to 0.01 s, and the iteration calculation is performed for 5000 steps, with a total calculation time of 1 s. The particle parameters can be set in EDEM software, and the physical parameters of each item are shown in

Table 2. Physical properties of materials.

	Poisson’s Ratio	Density/(kg/m3)	$\mathbf{Modulus} \mathbf{of} \mathbf{Elasticity}/\mathit{P}\mathit{a}$
Pellets	0.2	2600	5 × 107
Sieve box	0.3	7680	7 × 1010

and

Table 3. Material-to-material contact properties.

	Elastic Recovery Coefficient	Coefficient Of Static Friction	Coefficient of Kinetic Friction
Pellets-Pellets	0.03	0.3	0.01
Pellets-screen surface	0.4	0.5	0.02

.

3.3. Simulation Results of Vacuum Screening Using EDEM-Fluent

This chapter employs the EDEM-Fluent coupled computational method to investigate screen clogging patterns that arise during vacuum screening. The study primarily encompasses the analysis of screen clogging patterns, gas flow characteristics, and screen clogging severity under various operational conditions, including different particle concentrations and particle size ratios. The simulation parameters encompass simulations conducted under varying particle concentration and particle size ratio conditions.

Due to the combined action of the airflow, granule bed, and screen, there is a relatively obvious pressure difference between the upper and lower parts of the filter bed formed by the granule accumulation layer and the screen. Because the thickness of the granule layer accumulation increases and the inter-granule pores are gradually squeezed by the airflow and mutual pressure between the granules, the granule layer accumulation becomes more compact, the interception of airflow is enhanced, and the pressure drop across the screen increases as the airflow passes through the granule bed, as shown in Figure 14.

In Fluent, the pressure distribution cloud map of the fluid domain at different computational conditions when the pressure tends to stabilize under static conditions is shown in Figure 15. The post-processing analysis of the computational results in Fluent software was conducted, and the pressure distribution of the entire screening chamber was exported. The simulation results are the final simulation results. Due to the gradual compression of the interparticle pores and the increasing tightness of the particle layer, the interception of the airflow is enhanced, so a relatively obvious pressure gradient is formed in the screening chamber.

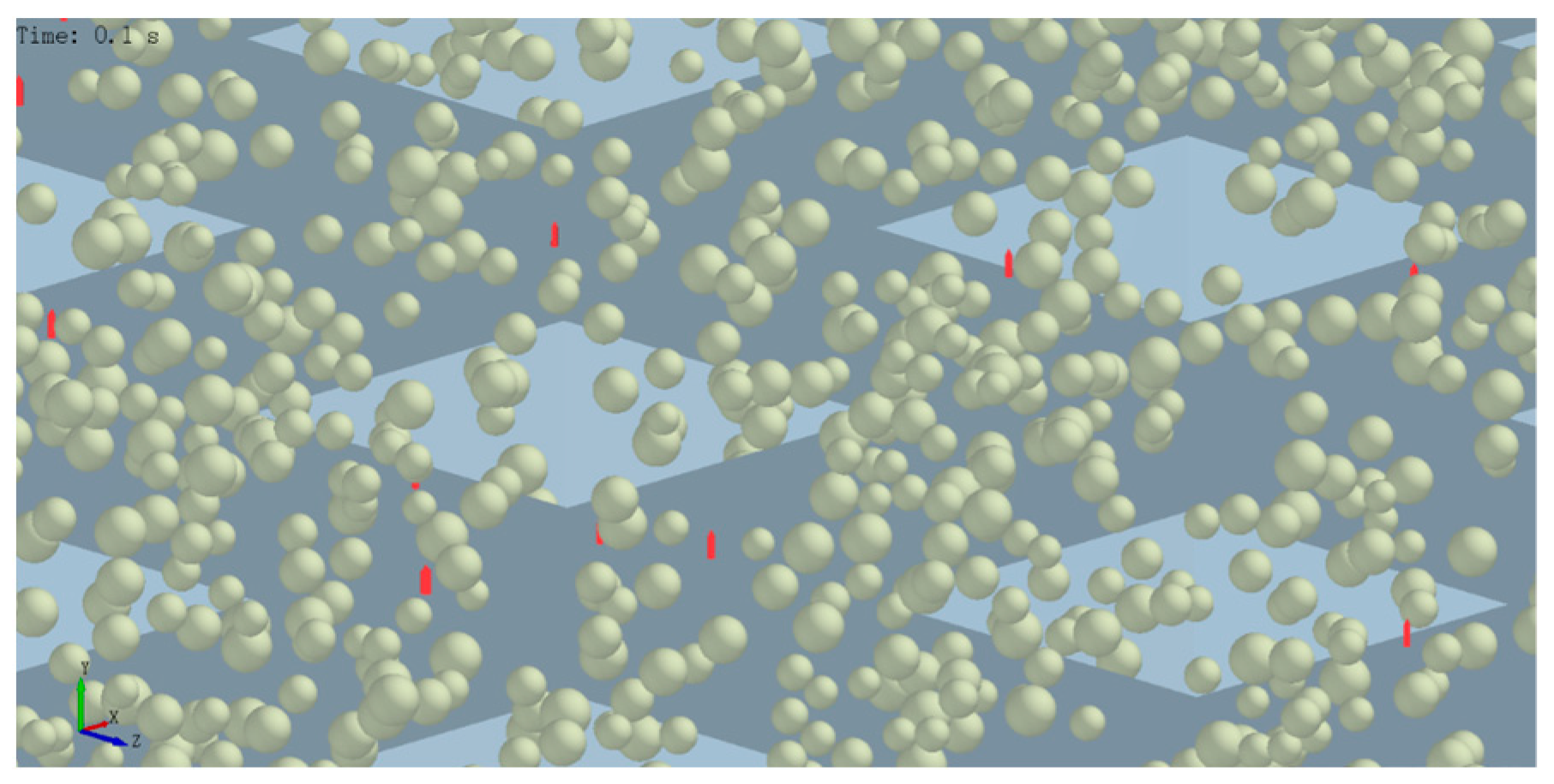
In order to elucidate the phenomenon of screen mesh blockage caused by particulate matter, partial images depicting the obstructed areas with embedded particles were extracted, as illustrated in Figure 16. The figure reveals a substantial number of particles deeply lodged within the apertures of the screen mesh, resulting in embedded blockages. Generally, there are two main causes for this type of obstruction: firstly, when the particle size closely approaches or slightly exceeds that of the mesh openings; secondly, when numerous particles agglomerate and form larger entities that become trapped within the mesh apertures. As calculations progress deeper into subsequent levels, these larger-volume particles increasingly contribute to more severe blockages. Furthermore, variations in particle size lead to differences in how deeply they embed themselves within the screen mesh holes; some particles become so deeply embedded that their removal becomes challenging.

The study used the EDEM-Fluent coupling to simulate the vacuum screening and filtration process and calculated the filtration efficiency, blockage, and pressure in the screening chamber of the vacuum screen. Due to the limited computational time of the simulation model, there are still some shortcomings in the study, and some issues have not been studied yet and need further research and discussion.

4. Design and Test of Test System for Negative Pressure Spiral Separation and Reduction Device

4.1. Test System Design

This negative pressure spiral separation and reduction device test system is mainly composed of the load cell, pressure transmitter, Delta PLC module, and computer host computer, as shown in Figure 17, wherein the Delta PLC module consists of the Delta PLC mainframe (DVP-12SA2), Delta PLC analog input module (DVP-04AD), 24 V switching power supply (a device that converts alternating current to direct current, with an output voltage of 24 V); the computer host computer applies the Delta Industrial Configuration Monitoring System (Delta Industrial Automation View) (DIAView for short) to control the whole test process. The upper computer is composed of Delta Industrial Automation View (DIAView for short) to control the whole testing process. During the actual test, two load cells are placed at the lower part of the drill cutting liquid-phase collection area and the drill cutting solid-phase collection area, respectively, and when the test starts, the weights and changes of the liquid and solid phases of the drill cuttings discharged during the working process can be measured in real time.

4.2. Negative Pressure Spiral Separation and Reduction Device Test

4.2.1. Introduction to the Test

This experiment involved injecting a solid–liquid mixture with a liquid-to-solid ratio of 1:4 into a spiral conveyor, with the mixture’s parameters shown in

Table 4. Parameters of the solid–liquid mixture used in the experiment.

Test Items		Test Results	Testing Methods
Solid content		78.5%	Oven
Water		21.6%	Karl Fischer
Particle size	Dv10	1.739 μm	Laser Particle Size Analyzer
	Dv50	14.224 μm
	Dv90	129.988 μm
Solid-phase mineral composition		Quartz (SiO2), Calcite (CaCO3), Barite (BaSO4), kaolinite (SiO2·Al2O3), sodalite (Na2O·Al2O3·6SiO2), sodium chloride (NaCl)

. During the operation of the spiral conveyor, the mass of the solid and liquid extracted under negative pressure was measured, and the data were analyzed and tabulated to calculate the suction flow rate and evaluate the solid–liquid separation suction effect. The objective was as follows:

• Testing the sealing of three negative pressure suction node connections after the injection of solid–liquid mixtures;
• By means of the calculated liquid suction flow rate, it is possible to analyze the resistance of the filter module in relation to the mesh size of the filter;
• Through the experimental extraction using a negative pressure solid conveyor (the technical parameters of which are shown in

  Table 5. Technical parameters of negative pressure solid conveying equipment.

  Model	BZVP-20
  Vacuum degree (Kpa)	85
  Processing capacity (m3/h)	≤1–20
  Air pressure requirement (Kpa)	550–690
  Inlet maximum distance (m)	≤30
  Discharge maximum distance (m)	≤300
  Air supply requirement (m3/min)	4.2~8
  Dimensions (mm)	1200 × 820 × 1470

  ), the performance of the ideal state of the negative pressure solid conveyor extraction can be obtained, thus enabling the calculation of the extraction effect for the material with a liquid-to-solid ratio of 1:4.

The principle of the whole test process is as follows: after injecting the solid–liquid mixture with liquid-solid ratio of 1:4 into the screw conveyor, the liquid level covering the three suction nodes is formed, and the negative pressure suction device is used to carry out the suction operation of the solid–liquid mixture. The solid–liquid mixture of the screw conveyor is outputted along its pipeline, and the solid phase is outputted to the drill cuttings solid-phase collection test box through the outlet of the screw conveyor; the liquid phase is outputted to the drill cutting liquid-phase collection test box through the negative-pressure suction device, and then, the quality data are outputted to the computer test system interface display and record by the sensor under the box.

This test is all parts in the factory processing and assembly and is completed according to a certain proportion of the liquid phase and solid phase mixed and poured into the screw conveyor for testing. In addition, this test uses a set of negative pressure devices, that is, three negative pressure suction short sections, and the test site as shown in Figure 18 and Figure 19.

4.2.2. Test Process Test Data Records and Results

• The real-time monitoring of the test process by the computerized supervisory system meets, as shown in Figure 20.
• The data processing of the mass change in the test data record is shown in Figure 21.
• The variation in the fluctuation curve of the steady-state value at the end of the experimental test data is shown in Figure 22. From Figure 22a, the average value of the solid-phase test data was 1298 N, and from Figure 22b, the average value of the liquid-phase experimental data was 1960 N.
• Analysis of test results

According to the previous test, data can be analyzed accordingly, and the data obtained from the test are shown in

Table 6. Parameters of test materials in the initial screw conveyor.

Liquid Mass/m1	Solid Mass/m2
12.19 kg	48.76 kg

and

Table 7. End-of-suction test parameters.

Liquid Weighing Tanks to Add Mass/m3	Solid Weighing Box to Add Mass/m4	Motor Runtime/t1	Negative Pressure Suction Device Working Time/t2	Output Tube Inner Diameter/d
6.22 kg	16.22 kg	141 s	151 s	80 mm

:

The following calculations can be made based on the data in Table 6 and Table 7:

$${\eta }_1=\frac{m_3}{m_1}$$

(11)

$$Q=\frac{{10}^{-3}{m}_3}{t_2}$$

(12)

$$V_1=\frac{4Q}{\pi d^2}$$

(13)

The measured value of the actual propulsion speed $V_2$ of the screw conveyor material is 8.4 m/min, i.e., 0.14 m/s.

$${\eta }_2=\frac{V_1}{V_2}$$

(14)

From the test data and calculated using Equations (11)–(14), respectively, the relevant data can be obtained as follows:

• ${\eta }_1$, Liquid suction rate: 0.51;
• $Q$, Average flow rate of negative pressure suction device: 2.5 L/min;
• $V_1$, Average flow rate of negative pressure solids conveyor: 0.008 L/min;
• ${\eta }_2$, The ratio of suction speed to material propulsion speed is 0.057.

From the negative pressure suction device, a dynamic pumping rate of 0.51 can be derived. If you double the number of suction units, theoretically all the liquid can be pumped out; the negative pressure suction device average flow rate of 2.5 L/min compared with the ideal state can be derived from the solid–liquid mixing state of the liquid and will be a significant decrease in the pumping rate of about 10 times. At the same time, the pumping speed and the material propulsion speed ratio are also significantly decreased by about 10 times. In order to be able to improve the suction volume and suction rate, the same as the length of the screw conveyor to increase the number of suction node units can be realized, this measure is the same as the ideal state.

5. Conclusions

This paper conducts a comprehensive literature search and analysis of negative pressure spiral separation and reduction processes and equipment, both domestically and internationally, in order to propose a novel design scheme for this project. The proposed scheme introduces an innovative process technology solution by embedding multiple segmental node-type negative pressure suction devices within the spiral conveyor. The device’s structure and strength were designed and verified, while a theoretical analysis of related process parameters was conducted. The vacuum sieving process was simulated using the coupled EDEM-Fluent method. Furthermore, a test system design was implemented along with experiments to dynamically extract solid–liquid mixtures using the negative pressure spiral separation and reduction process/equipment. Results indicated that at node 3, with a filter mesh number of 50 meshes and 2 layers under specific conditions, the negative pressure solid conveyor achieved a liquid extraction rate of 51% within 151 s at an average flow rate of approximately 0.008 m/s. Experimental verification confirmed the effectiveness of the proposed scheme in reducing the liquid content in conveyed drill cuttings, as well as improving the solid–liquid separation efficiency. However, further improvement is required regarding matching suction efficiency with basic efficiency; specifically, investigating variable-frequency speed control for motorized beltless screw conveyors would be beneficial for future research endeavors aiming to achieve optimal suction efficiency.