Comparative Study of Short Circuits and Demagnetization in Delta, Star, and Hybrid Winding Connections for Surface-Mounted Permanent Magnet Machines
Abstract
1. Introduction
- (1)
- The short-circuit analytical models of different winding connections are developed and the relationship of short-circuit peak currents is revealed. It is found that the largest 3PSC or 2PSC peak current happens in the star-side of a hybrid connection. In addition, the delta connection leads to a larger 2PSC peak current than the star connection. As for the 3PSC, the delta connection shows slightly higher peak current when the third harmonic is in phase with the fundamental back EMF. In contrast, the star connection shows a higher peak current. Additionally, the conditions resulting in the largest peak short-circuit current for each winding connection are also provided.
- (2)
- The demagnetization in different winding connections is compared by FE analysis. It is found that the hybrid connection can lead to the severest demagnetization due to the largest peak current, which is not suggested for safety-critical applications. The comparison between delta and star connections depends on PM temperature. When the 2PSC happens under relatively low PM temperature, the delta connection can lead to more severe demagnetization than the star connection, whereas the opposite condition can occur when PM temperature increases. Since the demagnetization level under high PM temperature is much more severe, which is not acceptable in most scenarios, and the difference between star and delta connections can be neglected, the star connection can be a better selection for safety-critical applications. For a similar reason, the comparison of demagnetization due to 3PSC depends on the phase of the third back-EMF harmonic.
- (3)
- It is also found that, compared to the 3PSC peak current, the 2PSC peak current is smaller in the star and hybrid connection. In the delta connection, the 3PSC and 2PSC peak currents are comparable. In addition, the 3PSC usually leads to more severe demagnetization than the 2PSC in different winding connections.
2. Winding Connections and Basic Performances
2.1. Prototype Machine
2.2. Back EMF
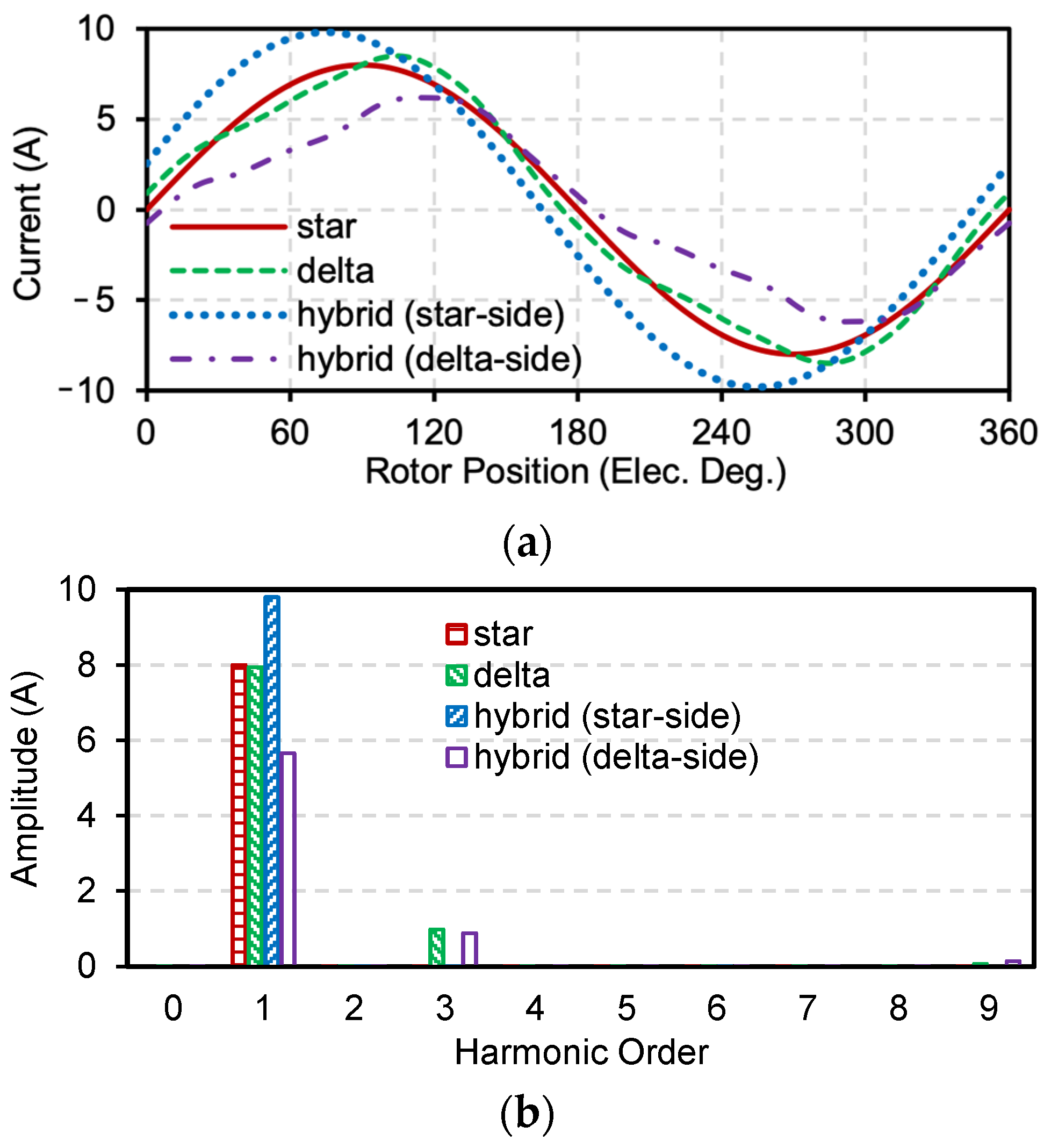
2.3. Current and Torque
3. Comparison of the 3PSC and Demagnetization
3.1. Equivalent Circuits of the 3PSC
3.2. Analytical Model of the 3PSC
3.3. FE Analysis Considering Demagnetization
3.4. Influence of PM Temperature
4. Comparison of the 2PSC and Demagnetization
4.1. Equivalent Circuits of the 2PSC
4.2. Analytical Model of the 2PSC
4.3. FE Analysis Considering Demagnetization
4.4. Influence of PM Temperature
5. Experimental Validation
5.1. Prototype Machine and Experimental Setup
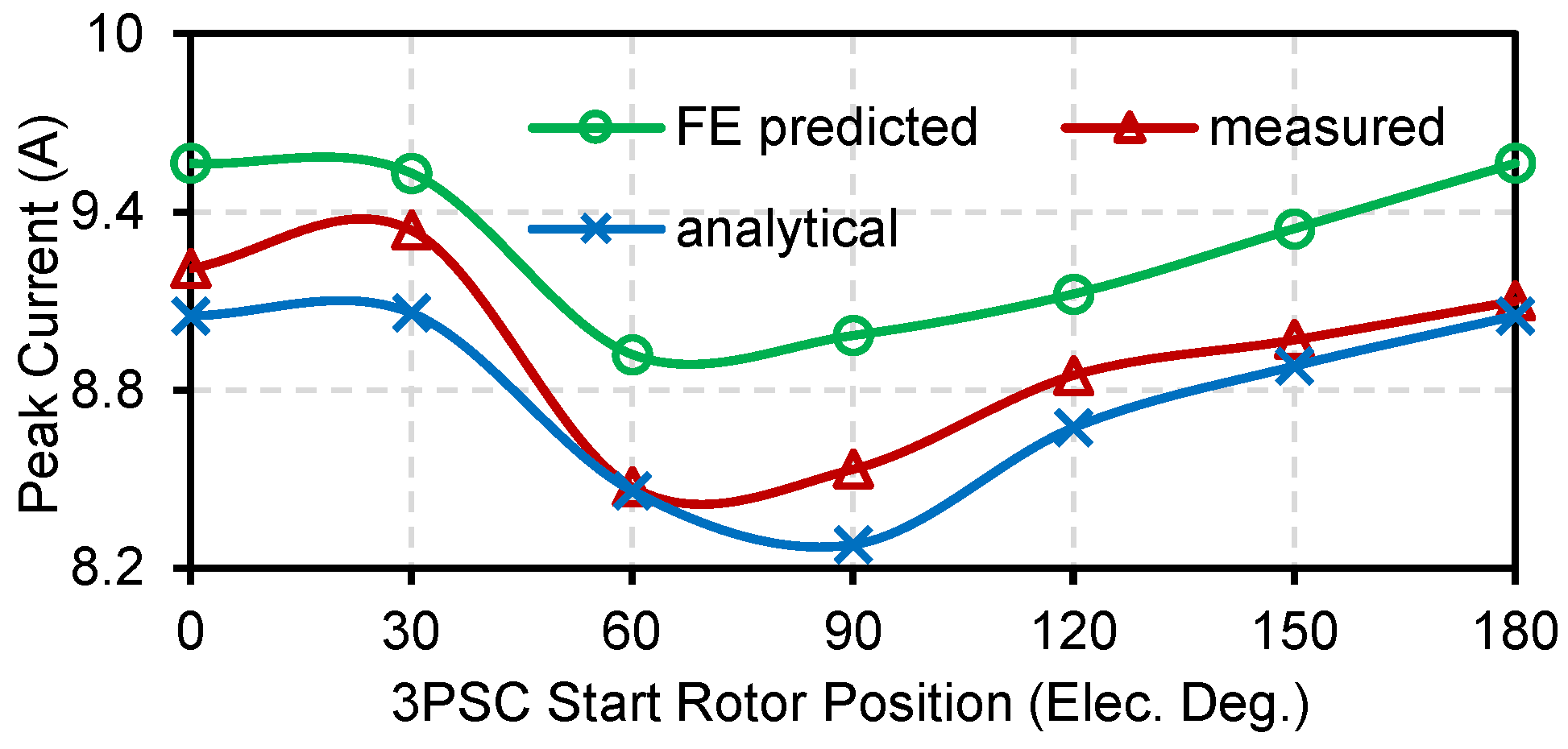
5.2. Experimental Results and Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wu, L.; Du, Y.; Chen, Z.; Guo, Y.; Wen, H.; Fang, Y. Influence of Load Characteristics on Three-Phase Short Circuit and Demagnetization of Surface-Mounted PM Synchronous Motor. IEEE Trans. Ind. Appl. 2020, 56, 2427–2440. [Google Scholar] [CrossRef]
- Darmani, M.A.; Poskovic, E.; Bramerdorfer, G.; Vaschetto, S.; Cavagnino, A.; Tenconi, A. Surface-mounted and flux-switching pm structures trade-off for automotive smart actuators. In Proceedings of the 2019 IEEE Energy Conversion Congress and Exposition (ECCE), Baltimore, MD, USA, 29 September–3 October 2019; pp. 6555–6561. [Google Scholar] [CrossRef]
- Chen, H.; El-Refaie, A.M.; Demerdash, N.A.O. Flux-Switching Permanent Magnet Machines: A Review of Opportunities and Challenges—Part I: Fundamentals and Topologies. IEEE Trans. Energy Convers. 2019, 35, 684–698. [Google Scholar] [CrossRef]
- Ibrahim, M.N.; Silwal, B.; Sergeant, P. Permanent magnet-assisted-assisted synchronous reluctance motor employing a hybrid star-delta winding for high-speed applications. In Proceedings of the 2018 XIII International Conference on Electrical Machines (ICEM), Alexandroupoli, Greece, 3–6 September 2018; pp. 379–385. [Google Scholar] [CrossRef]
- Ibrahim, M.N.; Abdel-Khalik, A.S.; Rashad, E.M.; Sergeant, P. Comparison between two combined star-delta configurations on synchronous reluctance motors performance. In Proceedings of the 2017 20th International Conference on Electrical Machines and Systems (ICEMS), Sydney, NSW, Australia, 11–14 August 2017; pp. 1–5. [Google Scholar] [CrossRef]
- Silwal, B.; Ibrahim, M.N.; Sergeant, P. Synchronous reluctance machine: Combined star-delta winding and rotor eccentricity. In Proceedings of the 2018 XIII International Conference on Electrical Machines (ICEM), Alexandroupoli, Greece, 3–6 September 2018; pp. 427–432. [Google Scholar] [CrossRef]
- Yu, J.; Yang, J.; Li, Q.; Zhao, X.; Huang, S.; Huang, S. An improved two-terminal hybrid connection method to reduce the armature winding MMF space harmonics of asymmetric six-phase machine. In Proceedings of the 2023 26th International Conference on Electrical Machines and Systems (ICEMS), Zhuhai, China, 5–8 November 2023; pp. 2594–2599. [Google Scholar] [CrossRef]
- Yang, S.; Tong, C.; Sui, Y.; Zhou, Z.; Zheng, P. Three-phase current-source inverter-based PMSM control scheme considering star and delta winding connections. In Proceedings of the 2022 25th International Conference on Electrical Machines and Systems (ICEMS), Chiang Mai, Thailand, 29 November–2 December 2022; pp. 1–5. [Google Scholar] [CrossRef]
- Decker, S.; Rollbuhler, C.; Brodatzki, M.; Rehm, F.; Liske, A.; Hiller, M. Comparison of losses in small star and delta-connected permanent magnet synchronous machines. In Proceedings of the 2021 23rd European Conference on Power Electronics and Applications (EPE’21 ECCE Europe), Ghent, Belgium, 6–10 September 2021; pp. 1–10. [Google Scholar] [CrossRef]
- Rehm, F.; Breining, P.; Decker, S.; Kolb, J.; Hiller, M. Loss comparison of small delta- and star-connected permanent magnet synchronous machines. In Proceedings of the IECON 2019—45th Annual Conference of the IEEE Industrial Electronics Society, Lisbon, Portugal, 14–17 October 2019; pp. 1171–1176. [Google Scholar] [CrossRef]
- Odawara, S.; Fujisaki, K.; Fukuhara, S. Investigation on iron loss characteristics in star-connection and delta-connection under three phase PWM inverter excitation. In Proceedings of the 2014 International Power Electronics Conference (IPEC-Hiroshima 2014 ECCE-ASIA), Hiroshima, Japan, 18–21 May 2014; pp. 289–293. [Google Scholar] [CrossRef]
- Ferreira, F.; de Almeida, A. Method for In-Field Evaluation of the Stator Winding Connection of Three-Phase Induction Motors to Maximize Efficiency and Power Factor. IEEE Trans. Energy Convers. 2006, 21, 370–379. [Google Scholar] [CrossRef]
- Ibrahim, M.N.F.; Abdel-Khalik, A.S.; Rashad, E.E.M.; Sergeant, P. An Improved Torque Density Synchronous Reluctance Machine with a Combined Star–Delta Winding Layout. IEEE Trans. Energy Convers. 2017, 33, 1015–1024. [Google Scholar] [CrossRef]
- Kasten, H.; Hofmann, W. Electrical machines with higher efficiency through combined star-delta windings. In Proceedings of the 2011 IEEE International Electric Machines & Drives Conference (IEMDC), Niagara Falls, ON, Canada, 15–18 May 2011; pp. 1374–1379. [Google Scholar] [CrossRef]
- Ibrahim, M.N.; Sergeant, P.; Rashad, E.E.M. Performance comparison of conventional synchronous reluctance machines and PM-assisted types with combined star–delta winding. Energies 2017, 10, 1500. [Google Scholar] [CrossRef]
- Ibrahim, M.N.; Sergeant, P.; Rashad, E.E.M. Combined Star-Delta Windings to Improve Synchronous Reluctance Motor Performance. IEEE Trans. Energy Convers. 2016, 31, 1479–1487. [Google Scholar] [CrossRef]
- Bianchi, N.; Cinti, L.; Contó, C.; Ortombina, L. Experimental tests of fractional-slot SPM motor with star-delta windings. In Proceedings of the 2023 IEEE Energy Conversion Congress and Exposition (ECCE), Nashville, TN, USA, 29 October–2 November 2023; pp. 4414–4420. [Google Scholar] [CrossRef]
- Wang, B.; Luo, L.; Hua, W.; Cheng, M.; Niu, S. High Performance and Strong Fault Tolerant Triple 3-phase PMA-SynRM with Star-delta Windings. IEEE Trans. Energy Convers. 2022, 37, 1977–1986. [Google Scholar] [CrossRef]
- Ferreira, F.J.T.E. On the star, delta and star-delta stator winding connections tolerance to voltage unbalance. In Proceedings of the IEEE International Electric Machines & Drives Conference (IEMDC), Coeur d’Alene, ID, USA, 10–13 May 2015; pp. 1888–1894. [Google Scholar] [CrossRef]
- Mahmouditabar, F.; Vahedi, A.; Marignetti, F. The Demagnetization Phenomenon in PM Machines: Principles, Modeling, and Design Considerations. IEEE Access 2023, 11, 47750–47773. [Google Scholar] [CrossRef]
- Choi, G.; Jahns, T.M. Post-demagnetization characteristics of permanent magnet synchronous machines. In Proceedings of the 2015 IEEE Energy Conversion Congress and Exposition, Montreal, QC, Canada, 20–24 September 2015; pp. 1781–1788. [Google Scholar] [CrossRef]
- Chen, Z.; Fan, C.; Wan, X.; Ling, Z.; Wang, F. Demagnetization fault analysis of FSCW-PMM with four-layer star-delta winding. In Proceedings of the 2023 26th International Conference on Electrical Machines and Systems (ICEMS), Zhuhai, China, 5–8 November 2023; pp. 4977–4980. [Google Scholar] [CrossRef]
- Xiao, L.; Yu, G.; Zou, J.; Xu, Y.; Zheng, B.; Liu, C. Experimental investigation of the relationship between magnetic properties of permanent magnet against temperature and pressure coupling environment. In Proceedings of the 2019 22nd International Conference on Electrical Machines and Systems (ICEMS), Harbin, China, 11–14 August 2019; pp. 1–5. [Google Scholar] [CrossRef]
- Valle, R.L.; de Almeida, P.M.; Fogli, G.A.; Ferreira, A.A.; Barbosa, P.G. Simple and Effective Digital Control of a Variable-Speed Low Inductance BLDC Motor Drive. IEEE Access 2020, 8, 13240–13250. [Google Scholar] [CrossRef]
- Du, Y.; Dong, Z.; Zhan, H.; Wu, L.; Zhou, K.; Yu, L.; Fang, Y.; Sun, L. Investigation of Post-Demagnetization Torque Ripple in Fractional-Slot Surface-Mounted PM Wind Power Generators after Short Circuit Faults. IEEE Trans. Ind. Appl. 2024, 60, 1. [Google Scholar] [CrossRef]
- Peng, W.; Kun, W.; Meng, F. Demagnetization study of permanent magnet machine under three phase short circuit. In Proceedings of the 2023 IEEE 6th International Electrical and Energy Conference (CIEEC), Hefei, China, 12–14 May 2023; pp. 2705–2710. [Google Scholar] [CrossRef]
- Welchko, B.; Jahns, T.; Soong, W.; Nagashima, J. IPM synchronous machine drive response to symmetrical and asymmetrical short circuit faults. IEEE Trans. Energy Convers. 2003, 18, 291–298. [Google Scholar] [CrossRef]
- Choi, G.; Jahns, T.M. Investigation of key factors influencing the response of permanent magnet synchronous machines to three-phase symmetrical short-circuit faults. IEEE Trans. Energy Convers. 2016, 31, 1488–1497. [Google Scholar] [CrossRef]
- Seo, M.-K.; Lee, T.-Y.; Ko, Y.-Y.; Kim, Y.-J.; Jung, S.-Y. Irreversible Demagnetization Analysis with Respect to Winding Connection and Current Ripple in Brushless DC Motor. IEEE Trans. Appl. Supercond. 2018, 28, 5203604. [Google Scholar] [CrossRef]
- Lei, Y.; Zhao, Z.; Wang, S.; Dorrell, D.G.; Xu, W. Design and Analysis of Star–Delta Hybrid Windings for High-Voltage Induction Motors. IEEE Trans. Ind. Electron. 2010, 58, 3758–3767. [Google Scholar] [CrossRef]
- Chu, W.Q.; Zhu, Z.Q. Analytical modeling and investigation of transient response of PM machines with 3-phase short-circuit fault. In Proceedings of the 2011 IEEE International Electric Machines & Drives Conference (IEMDC), Niagara Falls, ON, Canada, 15–18 May 2011; pp. 125–130. [Google Scholar] [CrossRef]























| Parameters | Value | Parameters | Value |
|---|---|---|---|
| Stator outer radius | 50 mm | Stack length | 50 mm |
| Number of turns/coil | 45 | Airgap length | 1 mm |
| Magnet thickness | 3 mm | Coil resistance | 0.19 Ω |
| Sheet material | 35WW250 | PM material | N45H |
| Volume | 9.8 × 10−5 m3 | Rated phase current (star) | 5.85 A |
| Rated speed | 500 rpm | Rated power | 265 W |
| The Largest 3PSC Peak Currents | Conditions | ||
|---|---|---|---|
| Start Rotor Position | Rotor Position after 3PSC | ||
| Star | α = kπ (k is integer) | ωt = π | |
| Delta | α = kπ | ωt = π | |
| Hybrid, star-side | α = −π/12 + kπ | ωt = π | |
| Hybrid, delta-side | α = −π/4 + kπ | ωt = π | |
| The Largest 2PSC Peak Currents | Conditions | ||
|---|---|---|---|
| Start Rotor Position | Rotor Position after 3PSC | ||
| Star | α = −π/6 + kπ (k is integer) | ωt = π | |
| Delta | α = 2π/3 + kπ | ωt = π | |
| Hybrid, star-side | α = −π/4 + kπ | ωt = π | |
| Hybrid, delta-side | α = −π/4 + kπ | ωt = π | |
| Parameters | Value | Parameters | Value |
|---|---|---|---|
| Stator outer radius | 50 mm | Rotor outer radius | 28 mm |
| Airgap length | 1 mm | Magnet thickness | 3 mm |
| Stack length | 50 mm | Pole-arc to pole-pitch ratio | 1 |
| Number of turns/coil | 70 | Coil resistance | 0.45 Ω |
| Sheet material | 35WW400 | PM material | N52 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, J.; Du, Y.; Zhan, H.; Zhou, K.; Sun, Y. Comparative Study of Short Circuits and Demagnetization in Delta, Star, and Hybrid Winding Connections for Surface-Mounted Permanent Magnet Machines. Machines 2024, 12, 401. https://doi.org/10.3390/machines12060401
Chen J, Du Y, Zhan H, Zhou K, Sun Y. Comparative Study of Short Circuits and Demagnetization in Delta, Star, and Hybrid Winding Connections for Surface-Mounted Permanent Magnet Machines. Machines. 2024; 12(6):401. https://doi.org/10.3390/machines12060401
Chicago/Turabian StyleChen, Junyi, Yidong Du, Haolan Zhan, Kai Zhou, and Yuan Sun. 2024. "Comparative Study of Short Circuits and Demagnetization in Delta, Star, and Hybrid Winding Connections for Surface-Mounted Permanent Magnet Machines" Machines 12, no. 6: 401. https://doi.org/10.3390/machines12060401
APA StyleChen, J., Du, Y., Zhan, H., Zhou, K., & Sun, Y. (2024). Comparative Study of Short Circuits and Demagnetization in Delta, Star, and Hybrid Winding Connections for Surface-Mounted Permanent Magnet Machines. Machines, 12(6), 401. https://doi.org/10.3390/machines12060401






