Analysis of Vibration Characteristics and Influencing Factors of Complex Tread Pattern Tires Based on Finite Element Method

Abstract

The vibration of the tires significantly impacts a vehicle’s ride comfort and noise level; however, the current analysis of tire vibration characteristics often involves excessive simplification in their models, leading to a reduction in model accuracy. To analyze the tire vibrational properties and the influence of its design and service conditions, a combined modeling technology was developed to construct a three-dimensional (3D) finite element model of a 205/55R16 specification radial tire with intricate tread patterns. The accuracy and reliability of the simulation model was verified through vibration modal tests. Based on the vibration mode theory, the Lanczos method provided by ABAQUS was adopted to analyze the modal characteristics of the tire under free inflation and grounded conditions, and the effects of different inflation pressures, loads, operating conditions, and belt cord angles on the tire vibration characteristics were analyzed. The results indicate that grounding constraints will suppress the low order radial modal frequency of the tire and enhance the lateral modal frequency. The higher the order of the tire vibration mode, the greater the impact of inflation pressure. As the operating conditions change, the modal frequencies of all directions have the same trend of change, and as the ground load increases, the tire is prone to misalignment at lower lateral frequencies. The radial and lateral grounding modes of the tire are slightly affected by the change of the cord angle in the belt layer, but the circumferential grounding frequency decreases as the belt layer angle increases. These research findings offer a crucial foundation for the structural design of complex tread pattern tires, and also serve as a reference for addressing vibration and comfort issues encountered in the tire matching process.

1. Introduction

As a component that directly contacts the vehicle and the road surface, tires not only support the vehicle’s load but also play a key role in buffering the vehicle against vibrations caused by uneven roads, controlling vehicle stability, generating handling force, and improving driving safety [1,2]. The vibration characteristics of tires have a significant impact on the noise, smoothness, and even safety of vehicles. Studying the vibration characteristics and influencing factors of tires is beneficial for reducing car noise and improving comfort [3]. The modal feature analysis of tires can help to better understand the vibration frequency characteristics, which plays a key role in fault diagnosis when matching tires with vehicles and avoiding resonance peaks of vehicle-related components [4,5,6].

However, when studying the mechanical characteristics of tires, it is common to reduce computational complexity by isolating and simplifying the tread to match computer performance, which can lead to a decrease in the accuracy and reliability of the results. Wu et al. [7] studied the deformation of tread rubber under different pattern shapes, loads, and speeds, and found that the set shape of tread patterns has a noticeable effect on tire deformation stiffness. Zhou et al. [8] carried out wind tunnel experiments and calculations to study the airflow patterns around heavy-duty tires with different tread patterns, revealing that complex tread patterns can greatly influence the airflow patterns surrounding tires. Pinay et al. [9] and others used acoustic foam to fill grooves, revealing that tire tread patterns and loads have an impact on groove resonance noise spectrum components. Guzzomi et al. [10] found significant torsional vibration at the tread pattern through torsional excitation experiments on tires. It can be inferred that the tread pattern has a significant impact on the performance of tires; therefore, the utilization of tires featuring intricate tread designs for investigating tire vibration characteristics would yield more precise results.

The modeling of tires with the assistance of mathematical and physical theories to investigate the vibration properties exhibited by tires requires the determination of the parameters of the structure and materials of tires [11,12]. Matsubara et al. [13] constructed a model based on a 3D ring with damping characteristics, derived steady-state response functions and frequency response functions, and discussed the feasibility of the model in verifying radial circumferential and lateral vibration of tires through experiments. Liu et al. [14] established a theoretical 3D circular tire model to describe tread vibration and steady-state response and analyzed the impact of material and structural factors on the natural frequency. Liu et al. [15] proposed a tire model with a flexible ring structure utilizing an elastic continuous base and predicted the modal of the tire under different inflation pressures. Li et al. [16] started with the grounding properties of tires, combined with experiments, and used the energy method to determine the formula for calculating the lateral stiffness of the tread unit. Based on this premise, a dynamic model was developed to analyze the impact of speed, load, and inflation pressure on tire lateral vibration in great detail.

At present, many scholars use a combination of kinematic modeling, finite element analysis, and experimental modal analysis to investigate the tire’s attributes associated with vibrations [17,18]. Combined with numerical simulation and experimental research, Guan et al. [19] found that the variation of vertical load can affect the tire vibration mode. Cheng et al. [20] studied the cross-sectional vibration properties of high aspect ratio radial load tires using experimental modal analysis and theoretical modeling methods and discovered that the tire body’s cross-sectional vibration is responsible for the observed vibration. Swami et al. [21] developed a tire model with a flexible 3D ring structure considering radial and bending modes and conducted a numerical simulation utilizing the finite element method. The findings indicated that the frequency of the tire would increase due to the increase in stiffness under static loads. Ku et al. [22] constructed a numerical model to investigate the mechanical properties of a novel flexible-spoke non-pneumatic tire under various conditions, both individually and in combination. Zhang et al. [23] analyzed the impact of usage factors on the vibration properties of the tread and sidewall from the perspective of finite element simulation and found that the vibration speed is symmetrical about the tire vertex and the vibration speed of the tread and sidewall is positively correlated with the vehicle speed and inflation pressure.

Liu et al. [24] developed a finite element model for tires and simulated the vibration characteristics of tires under different inflation pressures, rim constraints, loads, and rolling speeds. The research results showed that inflation pressure and rolling speed significantly affect tire vibration. Lv et al. [25] studied the effects of two parameters related to the structural dimensions on the stiffness and grounding properties of a self-supporting deflated tire based on finite element analysis. Liu et al. [26] developed a rigid elastic coupling model for heavy-duty radial tires using the finite difference method and investigated the parameter impacts of the transfer function inside the tread. Domestic and foreign scholars, combining finite element analysis and dynamic modeling, have demonstrated the connection between the vibration characteristics of tires and some usage factors and structural parameters. However, researchers have paid little attention to the relationship between the vibration characteristics of complex tread pattern tires and factors such as the belt layer and usage conditions. Therefore, establishing a finite element model of complex tread pattern tires and studying the correlation between the vibration properties of tires with complex tread patterns and usage conditions can offer a theoretical foundation for the design of structures.

In this paper, an experimental modal analysis and a simulated modal analysis were used to investigate the relationship between the vibration characteristics of tires with complex tread patterns and the usage conditions. Firstly, a 3D vibration modal simulation model of the tire was constructed in ABAQUS, and its feasibility was verified through hammer impact vibration modal experiments. Afterwards, simulation analysis was conducted on the radial, lateral, and circumferential vibration modes of the tires, and the effects of different application conditions on the vibration properties of complex tread pattern tires were studied, which provided a reference for solving vibration and comfort problems encountered in tire matching processes.

2. Establishment of Tire Simulation Model

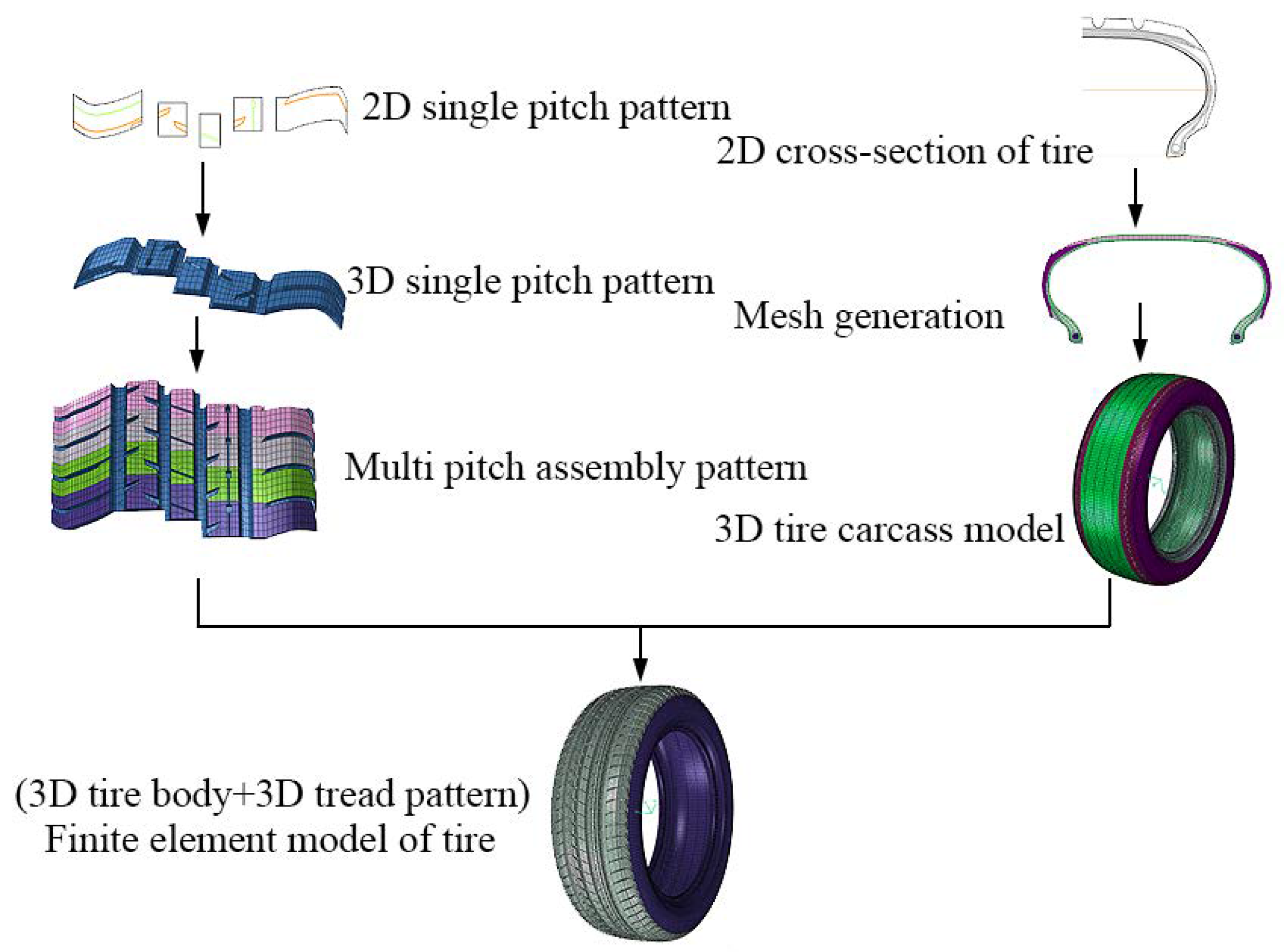
2.1. Complex Pattern Tire Model

Figure 1 displays the process of establishing a finite element simulation model of a tire considering complex patterns. A 205/55R16 specification tire was chosen as the research subject for simulation and experimental analysis. The main tire body and pattern parts of the tire were modeled separately, and then, the two were tied and constrained together using combinatorial modeling techniques to establish a simulation analysis model. Firstly, based on the conformal mapping algorithm, the top curve of the tread profile was mapped into a planar form. After obtaining the unfolded section of the tread body with a mapped pattern, we utilized its outer surface as the plane to depict the complex and tortuous pattern shape. Hypermesh was then used to partition the grid and establish a 3D pattern model. We imported the contours of the tire, including both inner and outer dimensions in a two-dimensional (2D) format, along with segmentation lines for material interlayers, into ABAQUS/CAE for model mesh division, element and node set creation, and element type specification. Finally, the axisymmetric model generation command was utilized to perform a 360° rotation of the 2D tire body model around a coordinate axis, resulting in the creation of a 3D model. Meanwhile, contour streamlines were generated to precisely define the material trajectory within the grid transmission for subsequent dynamic analysis.

The CGAX4R element, a reduced integral solid element with four nodes, was employed to simulate the tire cross-section. Additionally, the SFMGAX1 element, an axisymmetric surface element with linearly twisted double nodes, was selected to represent the tire skeleton material [27,28]. In the calculation files of the established 3D tire body model and 3D tread model, the technology of combining models was applied to establish constraints to integrate the two models and ultimately obtained a tire’s finite element model incorporating intricate tread designs. The established simulation model of the tire contains 167,960 units and a total of 222,360 nodes.

2.2. Material Settings

As a hyper elastic material, rubber has a wide variety of constitutive models, including the Mooney-Rivlin model, the Yeoh model, the Ogden model, and the G-H model [29]. The Yeoh model was chosen for simulation analysis in this paper. As a simplified polynomial model, its function for expressing the density of strain energy can be expressed as stated below:

$$W=C_{10}\left(I_C-3\right)+C_{20}{\left(I_C-3\right)}^2+C_{30}{\left(I_C-3\right)}^3,$$

(1)

where $C_{10}$, $C_{20}$, and $C_{30}$ are the parameters of the material constitutive model, and $I_C$ is the strain invariant. The Yeoh model can precisely predict the stress–strain relationship for uniaxial and planar tensile experiments and has a good ability to fit the large deformation of rubber material [30].

The distribution map of tire materials is shown in Figure 2, and the parameters used for the matrix adhesive and skeleton materials of every individual component are presented in

Table 1. Material parameters of Yeoh model for rubber materials of various tire components.

Component	C10	C20	C30
Tread	7.331 × 10−1	−2.939 × 10−2	2.840 × 10−3
Base	7.408 × 10−1	8.522 × 10−3	1.857 × 10−3
Belt	1.012 × 100	3.899 × 10−2	3.590 × 10−4
Carcass	1.142 × 100	2.660 × 10−2	8.713 × 10−4
Sidewall	5.279 × 10−1	−2.698 × 10−2	1.027 × 10−3
Triangle	2.026 × 100	−1.004 × 10−1	5.329 × 10−3
Inner liner	5.594 × 10−1	−6.73 × 10−4	1.558 × 10−3
Rim cushion	1.215 × 100	−4.336 × 10−2	3.816 × 10−3

and

Table 2. Module parameters of tire skeleton materials.

Parameter	Crown Strips	Belt	Carcass	Bead Ring
Elastic modulus (GPa)	9.14	110.98	9.36	210
Poisson’s Ratio	0.4	0.33	0.4	0.33

, correspondingly.

3. Experimental Validation

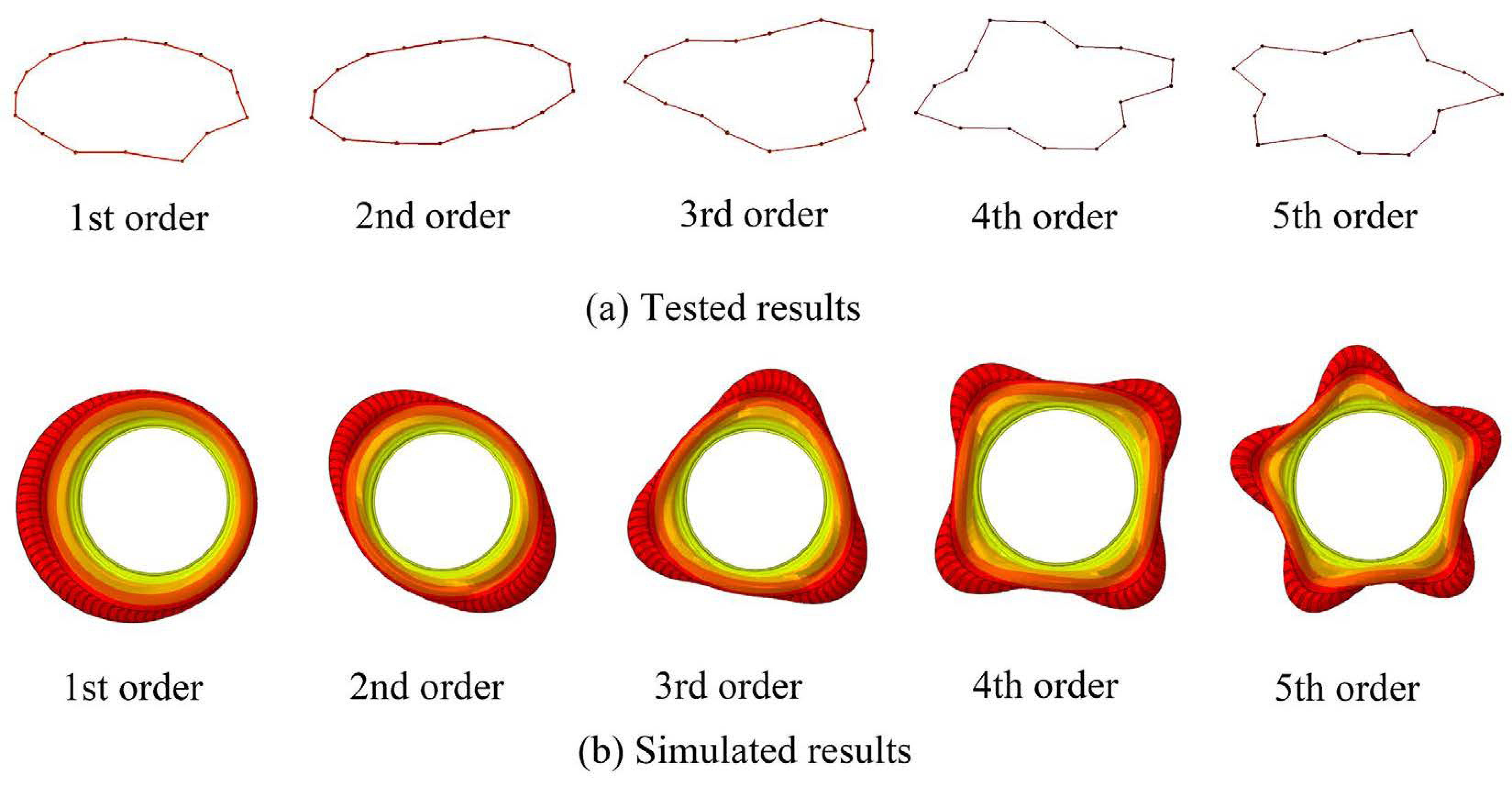
3.1. Tire Vibration Modal Testing

To authenticate the accuracy of the established tire numerical simulation model, the tire’s modal properties were experimentally verified utilizing the hammering method. As shown in Figure 3, a German Siemens LMS vibration modal testing analyzer (Siemens, Munich, Germany) and LMS Test Lab 16A analysis software were used to perform modal testing and vibration mode identification on a tire in a freely suspended state, with air pressure for inflation at 250 kPa. During the experiment, nylon material was used to lift the tire to achieve the original support effect, and the tire’s natural frequency is extremely low (below 1 Hz), significantly lower than its first-order natural frequency; therefore, the measurement effect on the tire modal parameters can be ignored.

The multi-point excitation and single-point response method was adopted. At the center line of tire tread, 16 vibration picking points uniformly distributed along the circumference were selected. The PCB three-way sensors were adhered to the tread pattern, and each pattern block was excited point by point by moving the force hammer to obtain each row element in the frequency response function matrix, where the single row element includes all modal information of the tire.

3.2. Analysis of Vibration Mode Results

Considering that the high-order frequencies of the tire have a small impact on vehicle performance, the first five natural frequencies and modes of the tire were selected for analysis. Figure 4 shows the findings of the radial mode shapes of the first 5 orders at an inflation pressure of 250 kPa obtained from the experiment and simulation. Based on the illustration, it is evident that the radial mode shape is approximately petal shaped and the number of petals increases from 1st to 5th order. In addition, comparing the simulated and experimental findings of the radial vibration mode, it can be seen that the changes in both are basically consistent.

The comparison between the 1st–5th order frequencies automatically recognized by LMS 16A testing software and the modal simulation results is shown in Figure 5. The simulation and experimental results in the figure have an error of around 3 Hz in the first two orders, and after the third order, the error is greater than 7 Hz, but the trend is consistent. In summary, the established numerical simulation model for tires with complex patterns can be used to analyze the vibration characteristics and influencing factors.

4. Results and Discussion

4.1. Finite Element Analysis of Vibration Characteristics

4.1.1. Vibration Modal Theory

The essence of vibration modal analysis is to convert the vibration differential equation system’s physical coordinates in a linear steady system to modal coordinates, decouple the equation system, and become a collection of unconnected equations described by modal coordinates and modal parameters, and then, calculate the system’s modal characteristics. The matrix for transforming coordinates is the vibration mode matrix, and each column represents each order of vibration modes. The linear combination of each order of modes can obtain the dynamic response of the structural system [31]. Based on the fundamental principles of dynamic systems, the fundamental formula for resolving the dynamic reaction is as follows:

$$M\ddot{a}(t)+C\dot{a}(t)+Ka(t)=Q(t),$$

(2)

where $\ddot{a}(t)$ represents the vector that describes the acceleration of the node, $\dot{a}(t)$ represents the velocity vectors, $a(t)$ is the displacement vector, $M$ is the mass matrix vector of the system, $C$ represents the damping matrix vector, $K$ is the stiffness matrix vector, and $Q(t)$ is the nodal load vector.

The system’s inherent frequency for a tire in the free vibration state is

$$f_0=\frac{1}{2\pi }\sqrt{\frac{K}{M}},$$

(3)

The displacement resonance frequency of the tire in its system in the state of forced vibration is as follows:

$$f=f_0\sqrt{1-\frac{1}{2Q_m^2}},$$

(4)

where $Q_m$ is the mechanical quality factor.

The speed resonance frequency of the system is

$$f=f_0,$$

(5)

The acceleration resonance frequency is

$$f=f_0\cdot Q_m\sqrt{\frac{2}{2Q_m^2-1}},$$

(6)

An automatic multi-level substructure (AMS) solver and the Lanczos method are the commonly used eigenvalue solvers provided in ABAQUS. The Lanczos method is a vector orthogonalization method that obtains a feature spectrum with fast high-frequency convergence and a large number of low-frequency convergence iterations. This method is suitable for large symmetric mass structures and has fast stiffness matrix convergence. It can handle a large number of vibration mode problems with 50,000 to 100,000 degrees of freedom and can effectively handle rigid body vibration modes [32,33]. Based on the structural characteristics of tire modeling, the Lanczos method was selected in ABAQUS 2020 software to analyze the tire’s vibration properties in free and ground modes.

4.1.2. Shape and Modal Frequency Analysis

To ensure good computational efficiency while maintaining the simulation accuracy, a rigid wheel was added to constrain the rim cushion of the tire in the process of free vibration modal analysis. In addition to the rim constraint, a rigid road surface was also added to constrain the grounding area during the ground vibration modal analysis. The interaction between the tire and the road was characterized as surface-to-surface contact. Figure 6 illustrates the radial vibration mode of the tire in a grounded state at a standard inflation pressure of 250 kPa. The first five lateral vibration modes of the tire in free and grounded states are shown in Figure 7. It can be concluded that there is a strong correlation between the radial vibration pattern and the change in modal order, with each mode having more lobes than the modal order. Meanwhile, in both free and grounded states, as the order increases, the lateral twisting of the tire increases.

Figure 8 shows the comparison of free and grounded modal frequencies under different conditions. The results indicate that, for the radial mode, the grounding constraint has a frequency suppression effect on the first-order grounding mode and the constraints added to the rim cushion and contact area can change the pattern of the grounding mode and the free vibration mode. For lateral mode vibration, grounding constraints did not suppress lateral vibration. Instead, as a result of the grounding effect, the inner air pressure increases and the tire stiffness increases, leading to a rise in the frequency of lateral modes.

4.2. The Influencing Factors of Vibration Characteristics

The vibration modal characteristics of tires mainly influence the ride comfort and tire noise of vehicles. By changing parameters such as inflation pressure, operating conditions, grounding load, and belt angle, the interrelationships between tire vibration characteristics and usage conditions and structural parameters can be revealed.

4.2.1. Inflation Pressure

The standard inflation pressure and load of the 205/55R16 tire selected in this paper are 250 kPa and 615 kg, respectively. When conducting free mode and ground mode vibration simulation analysis under different air pressures, the load was set at 80% standard load (492 kg), and the inflation pressures were selected as 70% (175 kPa), 75% (187.5 kPa), 80% (200 kPa), 85% (212.5 kPa), 90% (225 kPa), and 95% (237.5 kPa) standard inflation pressures, respectively.

Figure 9 shows the effects of different inflation pressures on the radial, lateral, and circumferential frequencies in free and grounded states. The radial vibration mode of the tire causes bending deformation of the tire in the plane, affecting the comfort and smoothness of the vehicle. The lateral vibration mode causes lateral bending deformation, which has a significant impact on the handling stability of the vehicle. For radial and lateral natural frequencies, the 1st–5th order simulation results were selected. The circumferential vibration mode reflects the torsional deformation of the tire along the circumference. As a result of the limitation of degrees of freedom, there is only one rotational degree of freedom in the circumferential direction. Therefore, this calculation only obtained the first circumferential vibration mode of the tire.

It is observable in Figure 9 that as the tire’s inflation pressure increases, the natural frequencies of each order of the tire also increase accordingly. And the higher the vibration mode order, the greater its vulnerability to the impact of inflation pressure, because inflation pressure directly affects the stiffness of the tire. Therefore, increasing tire pressure can lead to a decrease in vehicle smoothness. After the tire is grounded, ground constraints have a suppressive effect on its natural frequency, but under the same load, the trend of the impact of inflation pressure on the natural frequency is consistent. At the same time, the natural frequency change of the tire is relatively weakened between the inflation pressure of 200 kPa and 212.5 kPa: that is, the alteration in the tire’s natural frequency is relatively small near 80% of the standard inflation pressure.

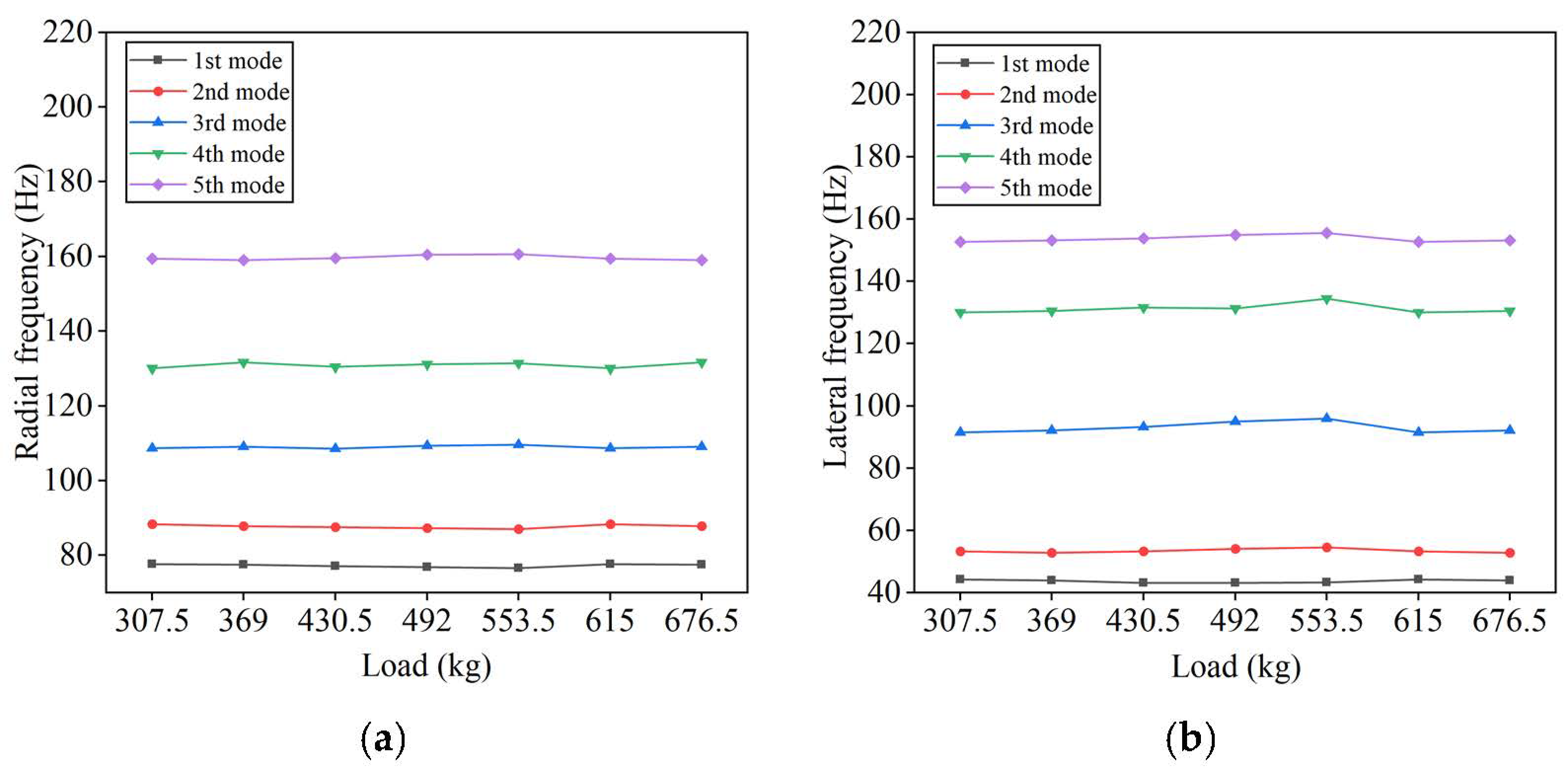
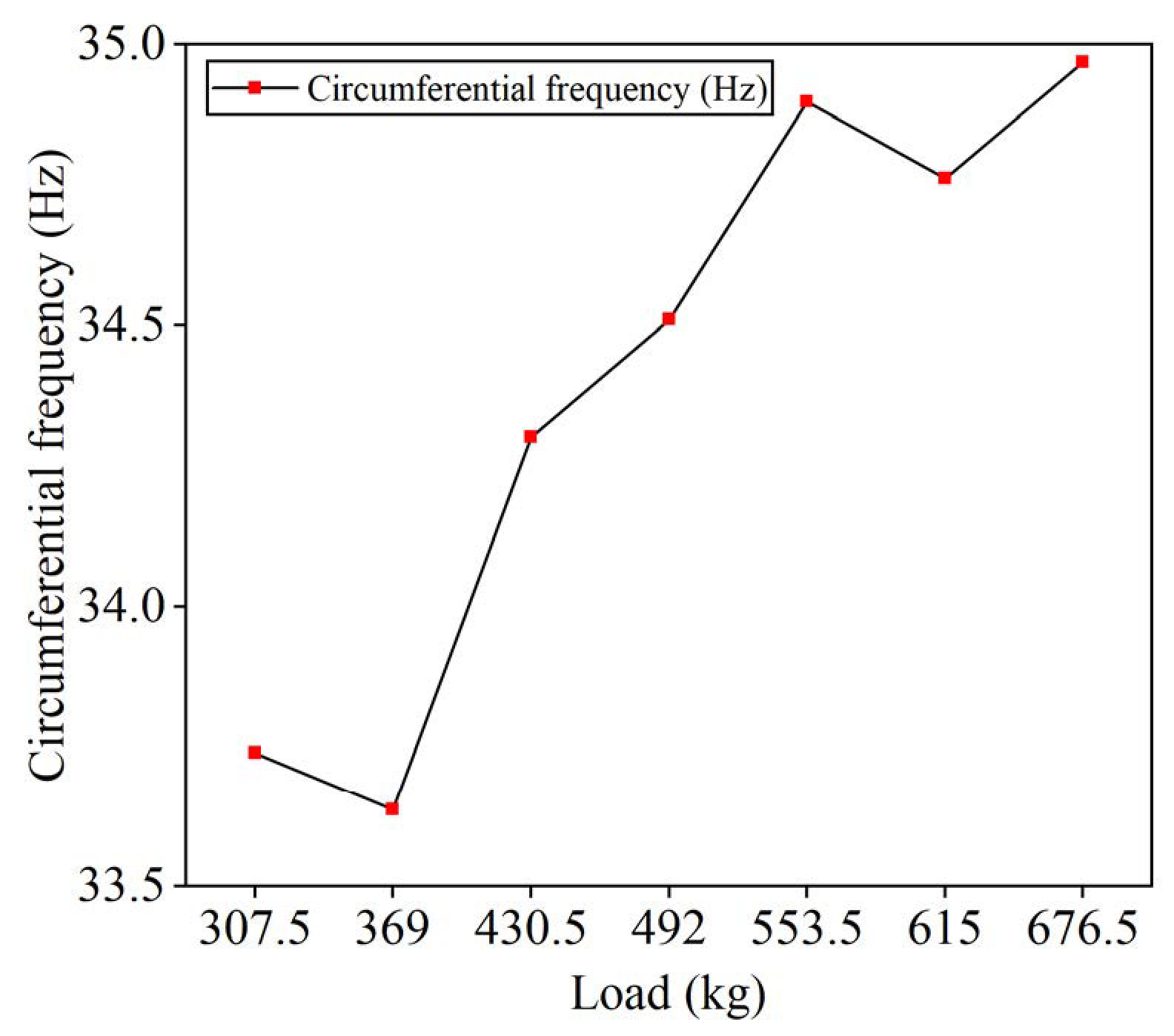
4.2.2. Tire Load

A simulation analysis of the tire’s grounded mode was conducted under the same air pressure and different loads. The air pressure was set to 210 kPa, and the load application range was 50~110% of the standard load. The influence of tire load variation on radial and lateral natural frequencies is shown in Figure 10. It is evident that the change in load does not exert a noteworthy impact on the radial grounding mode of the tire. Only the first two orders decrease as the load rises, indicating that the rise in load has a suppressive effect on frequency. After the third order, the radial frequency change is very small, within 0.4 Hz. The lateral 1st and 2nd vibration frequencies exhibit slight fluctuations with increasing load. When the order is above 3, it rises in proportion to the load’s increment and begins to reduce at 90% of the standard load (553 kg). This indicates that as the load increases, the tire is prone to misalignment and becomes unstable at lower lateral frequencies.

Figure 11 shows the relationship curve between circumferential vibration frequency and load variation. It can be seen that, at 60% standard load (369 kg), there is a turning point in the circumferential frequency change, and then, the circumferential frequency increases significantly with the increase of load. Combining the variation of lateral vibration frequency at lower loads, the deduction can be made that when the actual load borne by the tire is lower, it will make it difficult to determine the calculated frequency trend.

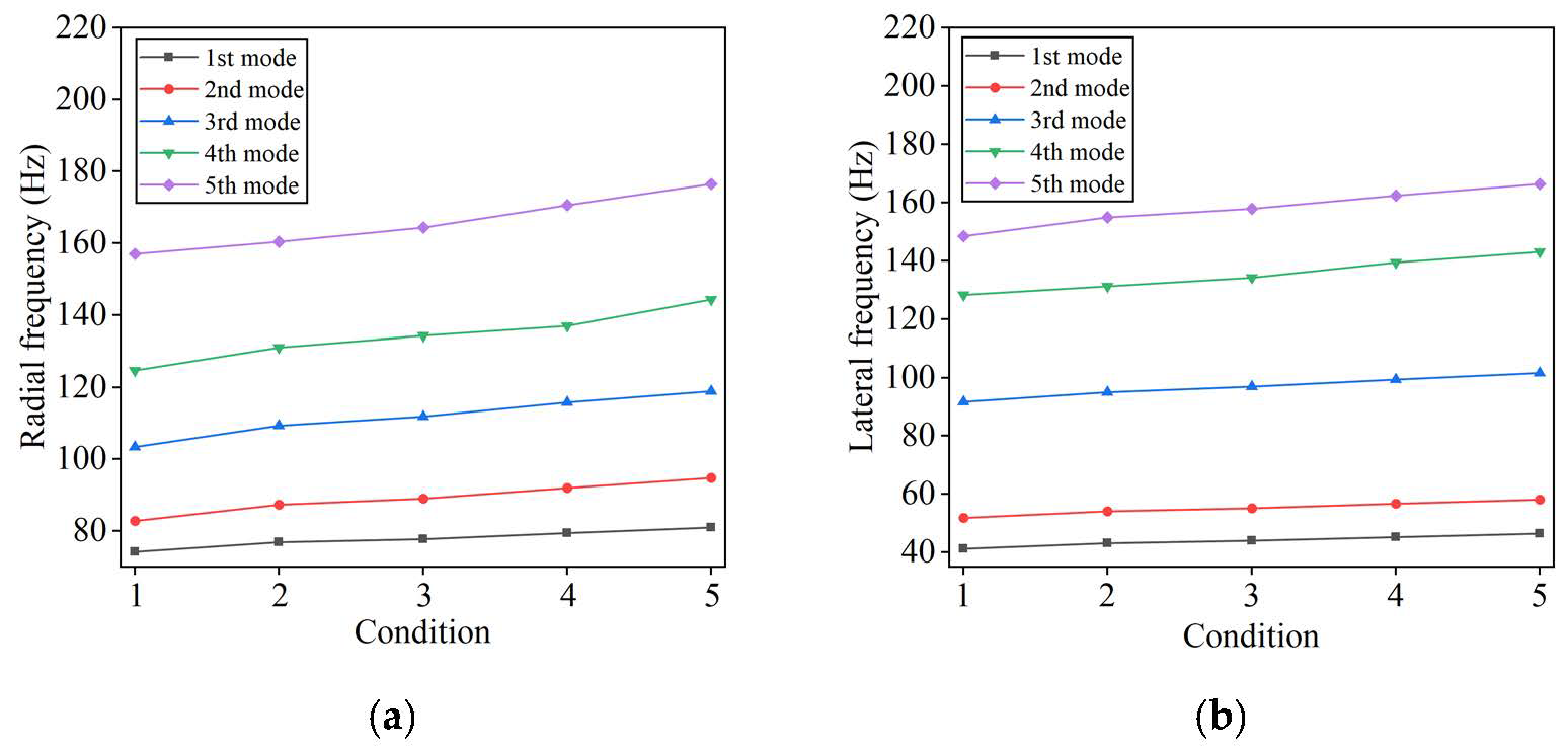
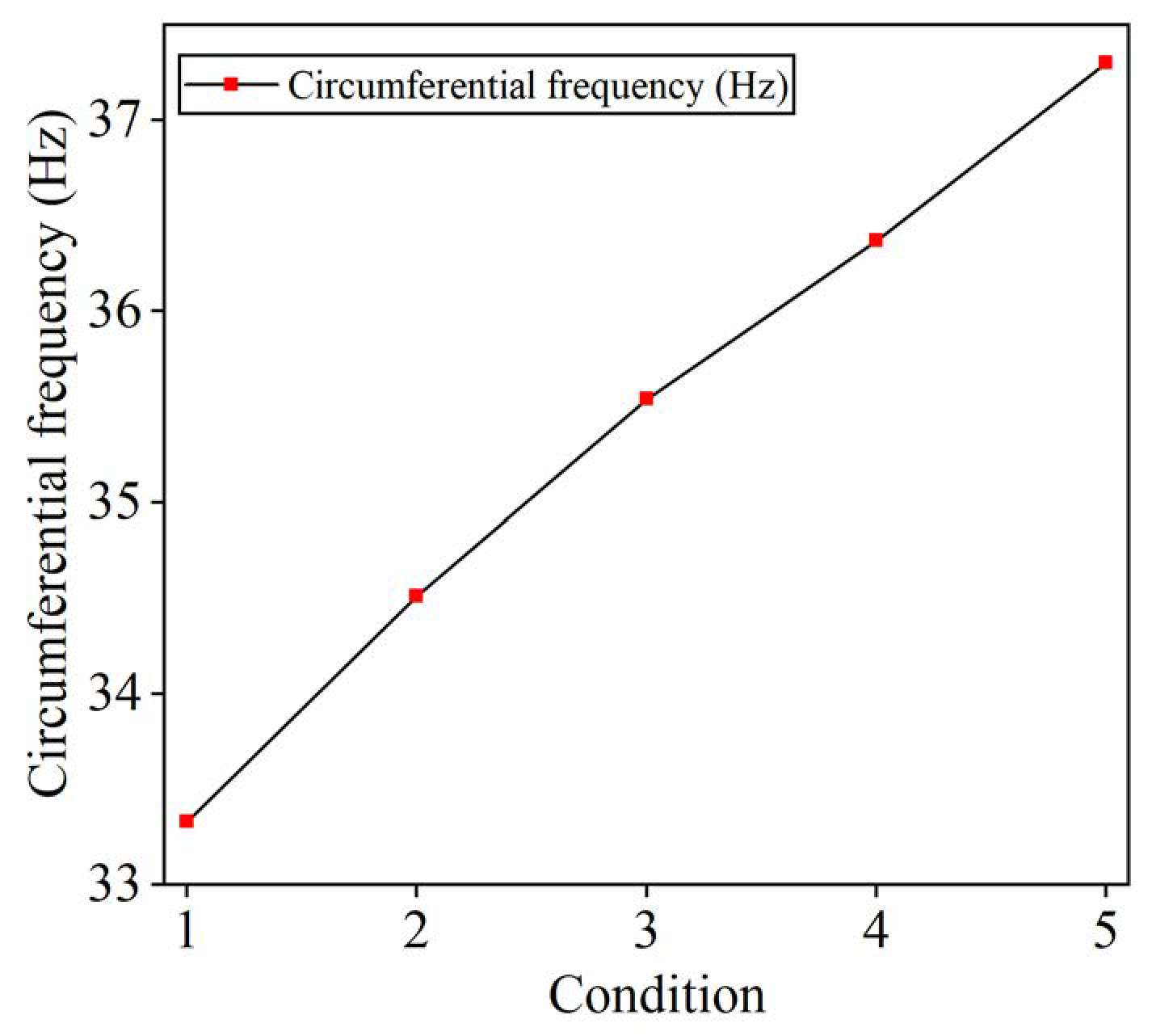
4.2.3. Operating Condition

By setting different combinations of inflation pressure and load, the vibration frequency characteristics of tires under different operating conditions can be analyzed. In this paper, five typical tire operating conditions were selected for analysis, and the operating conditions for this study are detailed in

Table 3. Utilization conditions.

Condition	1	2	3	4	5
Pressure (kPa)	175	210	225	250	275
Load (kg)	430.5	492	553.5	615	676.5

.

Figure 12 shows the frequency variation curves of the radial and lateral vibration of the tire under five selected typical operating conditions. Observing the curve changes, it can be seen that according to the order of operating conditions 1–5, the radial and lateral frequency changes have the same trend and gradually increase. The influence of operating conditions on circumferential vibration frequencies is displayed in Figure 13. From condition 1 to condition 5, the circumferential vibration frequency of the tire shows a significant increase trend. The changing trend of these curves reflects that the overall stiffness of the tire increases from condition 1 to condition 5.

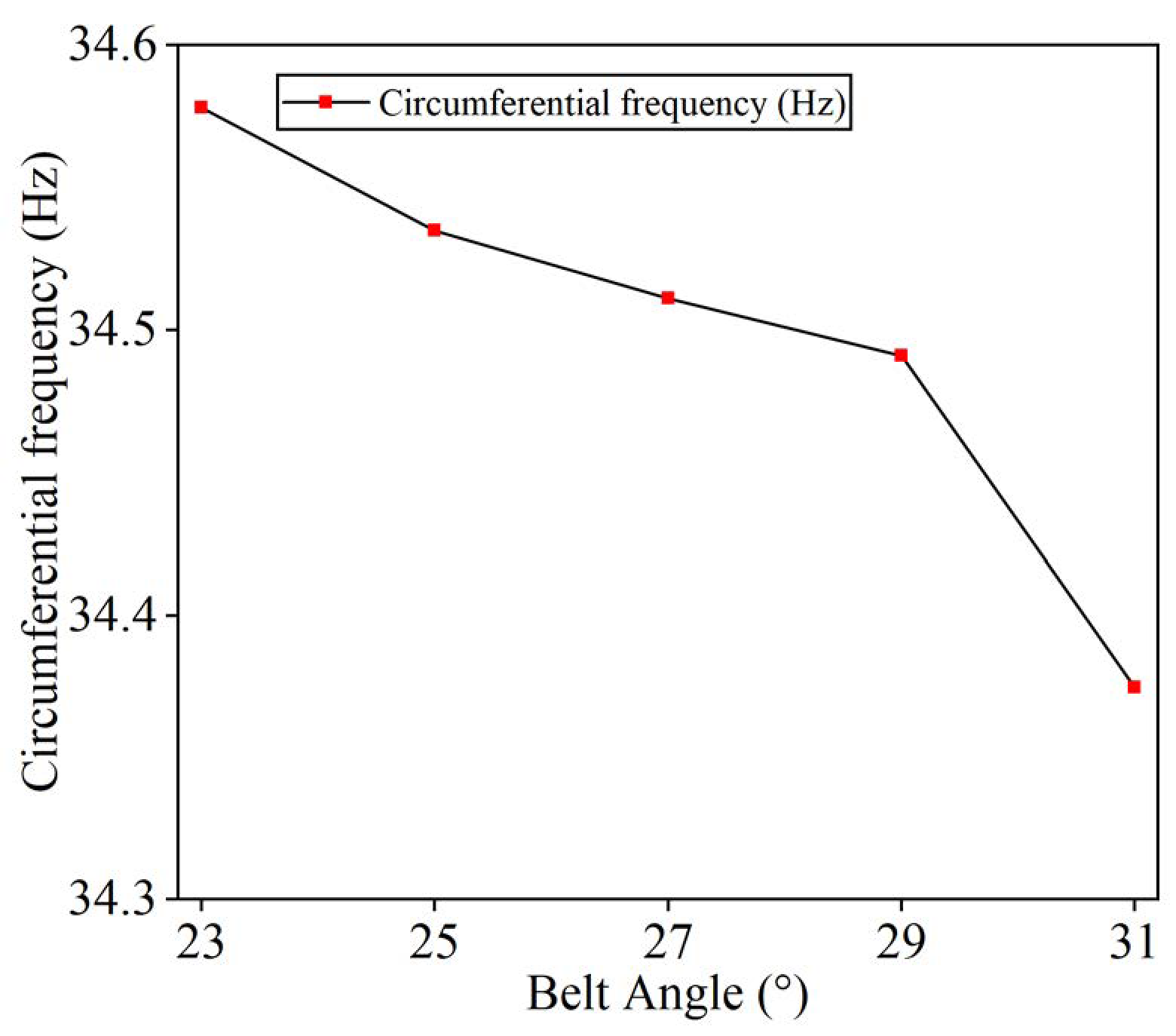
4.2.4. Belt Angle

The belt layer, located below the base of the tire surface, has the function of buffering impact and clamping the tire body. Generally, high strength and high modulus curtain wires arranged at different angles are used as reinforcement materials for the belt layer. In order to analyze the influence caused by changes in belt angle on the modal characteristics of tire vibration, the tire pressure and load were kept constant at 210 kPa and 492 kg, respectively. The belt angles were set at 23°, 25°, 27°, 29°, and 31° for simulation analysis.

The variation relationships between the radial and lateral frequencies and the belt angle extracted from the vibration mode simulation analysis are displayed in Figure 14. It is obvious that under the same air pressure and load, the angle change of the belt layer has no significant effect on the tire’s grounding mode. However, from the comparison of the radial and lateral data, it can be seen that the first order radial and lateral frequencies have a turning point when the belt angle is 29°, indicating that the stiffness of the tire changes at 29°. The radial and lateral frequencies of other orders decrease as the angle of the belt layer increases.

The relationship curve between the circumferential vibration frequency and the belt angle is illustrated in Figure 15. It is clear based on the graph that the circumferential frequency decreases with the rise in the belt angle, but the trend of change is small between 25° and 29°. This explains why the belt angle is often set within the range of 24° to 29° in the tire design and production process.

5. Conclusions

In order to analyze the vibration properties and influencing factors of tires with complex tread patterns, a 3D numerical simulation model of radial tires with complex tread patterns was constructed in this paper. From the perspectives of simulation and experiments, the feasibility of the model was verified through vibration mode experiments. Based on vibration mode theory, the relationship between the vibration characteristics of tires with complex tread patterns and four influencing factors, namely, inflation pressure, load, operating conditions, and belt angle, was analyzed. The following conclusions were drawn:

(1)

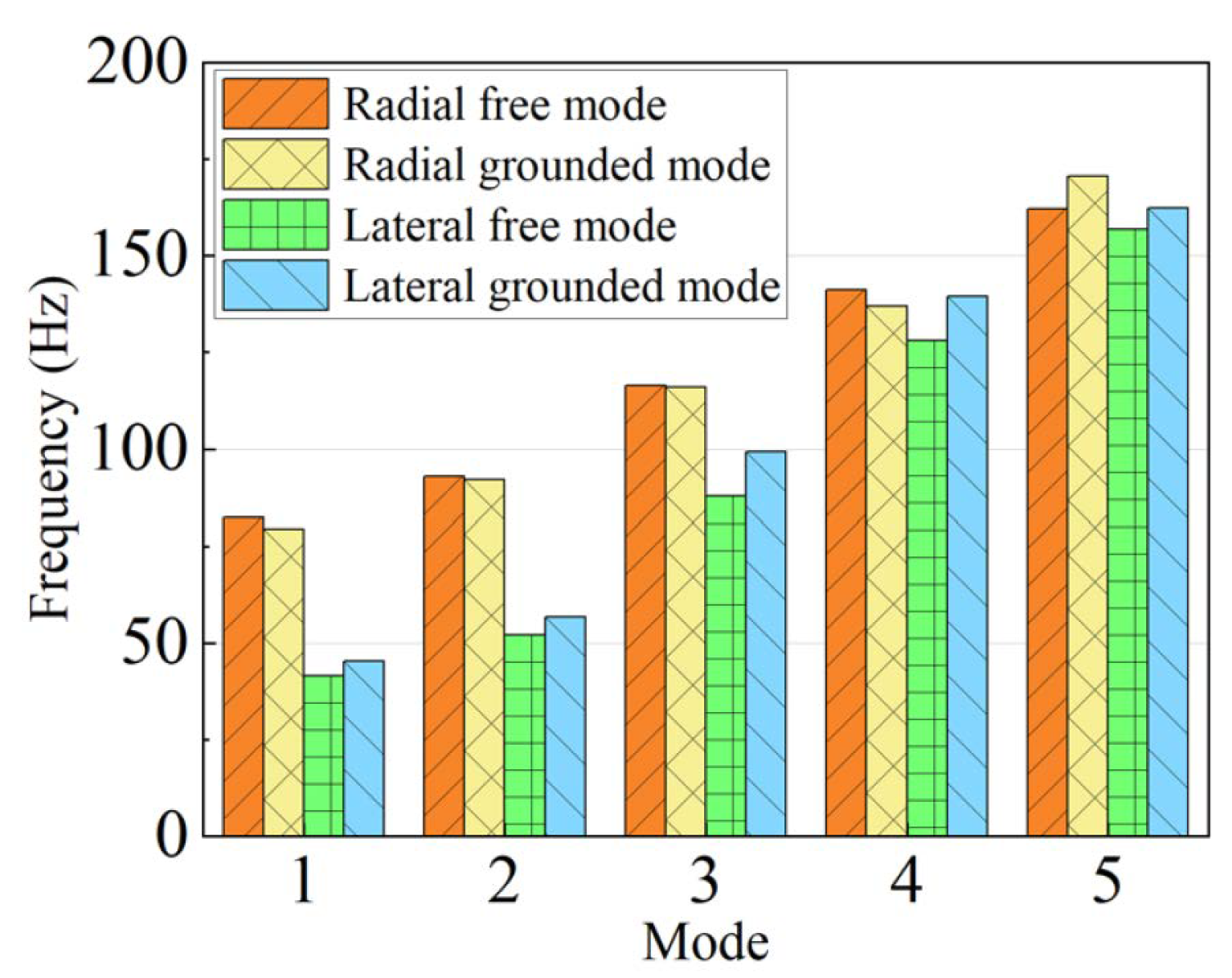
Through experimental comparisons, it was verified that the combination modeling technique used to establish the simulation model of a tire with complex tread patterns is reliable. Compared to the free vibration mode, the radial vibration of the tire with complex patterns shows a suppressed effect under the constraint state of the ground. For the lateral vibration mode, the grounding effect increases the internal air pressure and tire rigidity, which enhances the vibration frequency of the lateral mode.

(2)

In both free mode and grounded mode, the change in inflation pressure will directly affect the stiffness of the tire, thereby changing the natural frequency of the tire, and the higher the vibration mode order, the greater the impact of inflation pressure.

(3)

The overall stiffness of tires with complex patterns increases as the load and air pressure rise under different operating conditions. The change in load exerts minimal impact on the radial grounding mode of the tire, but the rise in load has a suppressive effect on the first two vibration frequencies. The lateral low order frequency of the tire is unstable, and when subjected to lower loads, the lateral 1st and 2nd order vibration frequencies fluctuate with load changes, making the tire prone to misalignment at the lateral low order frequency.

(4)

At the same pressure and load, except for the radial and lateral first-order vibration frequencies that undergo a turning point at a belt angle of 29°, all other frequencies decrease with increasing belt angle. Meanwhile, the increase in belt angle leads to a decrease in the circumferential grounding frequency, but the variation is small between 25° and 29°. Therefore, in the tire design and production process, the belt angle is often set in the range of 25° to 29°.

(5)

The analysis of tire vibration characteristics in this paper takes into account the influences of inflation pressure, load, working conditions, and belt layer angle. Further research can be conducted to explore the impacts of environmental temperature, rubber compound, and belt layer cord density and width on tire vibration characteristics.