An Improved Fault Diagnosis Method for Rolling Bearings Based on 1D_CNN Considering Noise and Working Condition Interference
Abstract
1. Introduction
- (1)
- An end-to-end fault diagnosis method for rolling bearings with strong feature extraction capability is proposed, which is especially suitable for the fault diagnosis of bearings that often work under an interference environment.
- (2)
- A network design idea is proposed, in which a multi-scale convolutional layer is placed at the first layer of a 1D convolutional fault diagnosis model, thus obtaining multi-scale initial features that contain rich information. Meanwhile, the key fault features are further enhanced adaptively by introducing a self-attention mechanism.
- (3)
- A composite loss function containing cross-entropy loss and mutual information loss is constructed. By maximizing the mutual information between the final convolutional feature vector and the original input, as well as the mutual information between the final convolutional feature vector and the intermediate convolutional feature map, redundant environmental information in the feature is eliminated, resulting in a more powerful fault feature extraction capability.
2. Theoretical Background
2.1. One-Dimensional Convolutional Neural Network
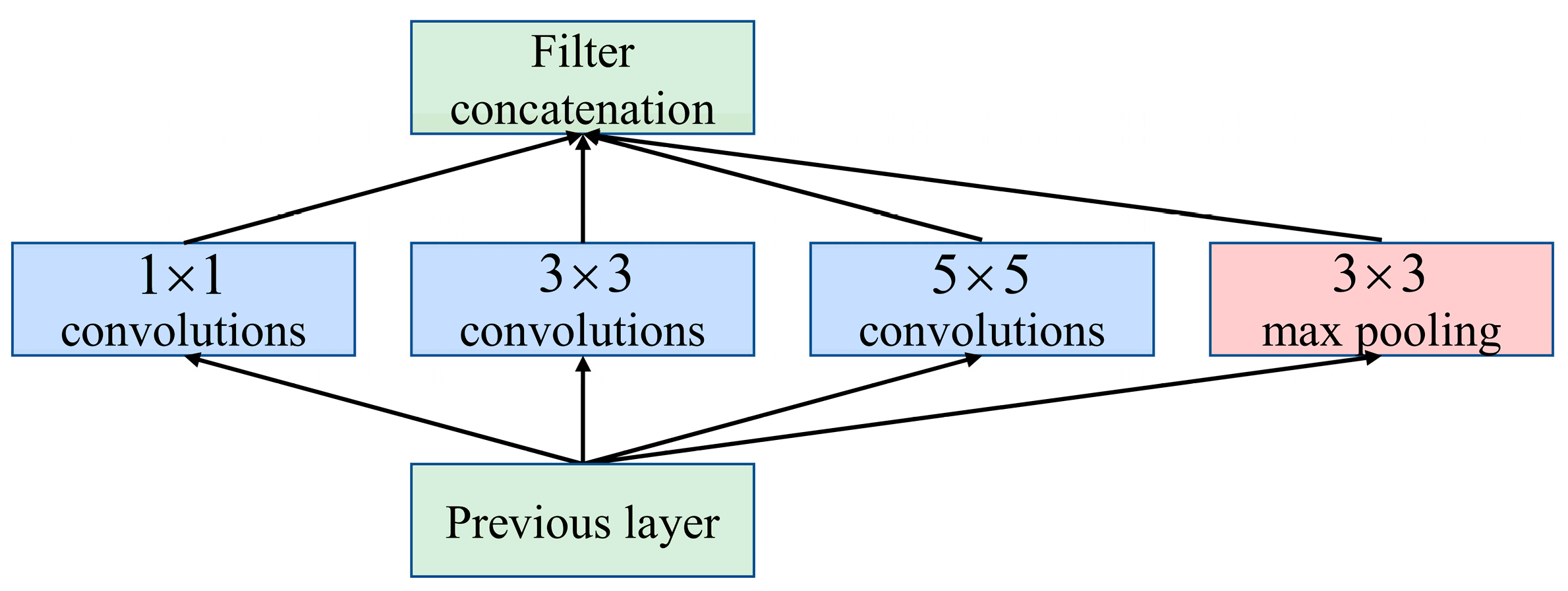
2.2. Inception Module
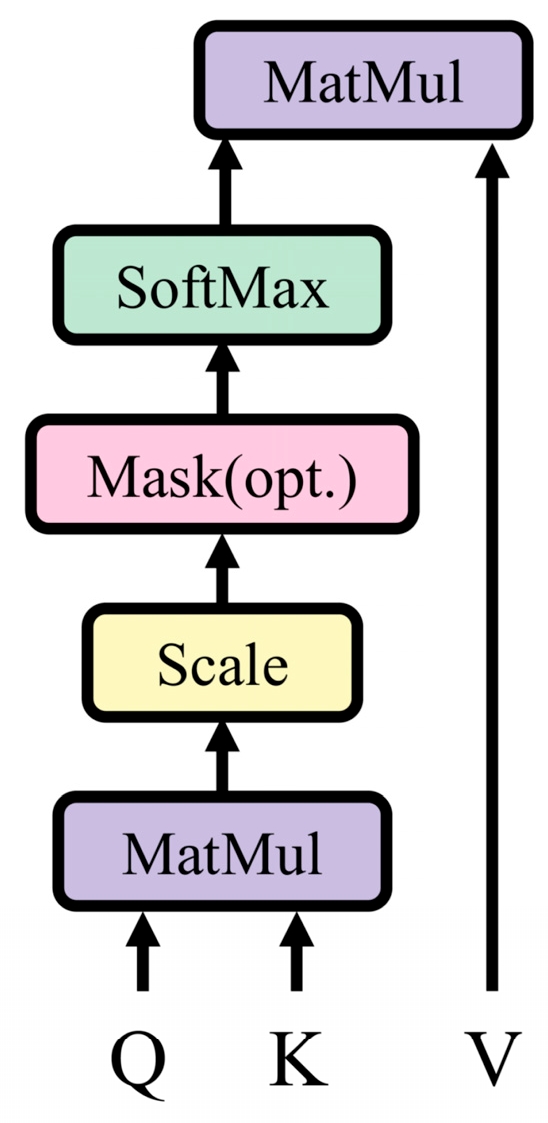
2.3. Scaled Dot-Product Attention
2.4. Mutual Information
3. Proposed Method
3.1. Multi-Scale Feature Extraction Network
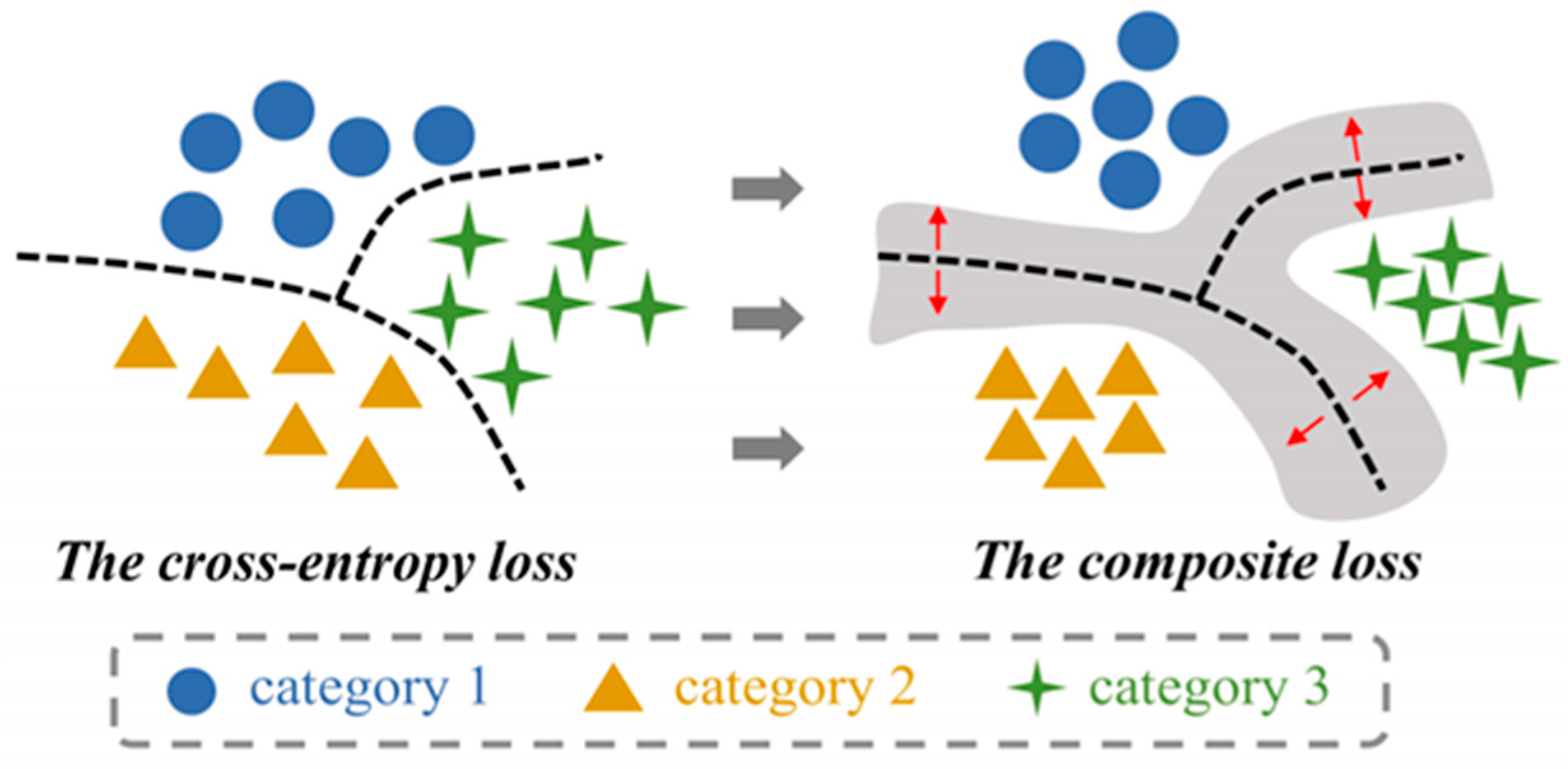
3.2. Composite Loss Function Construction
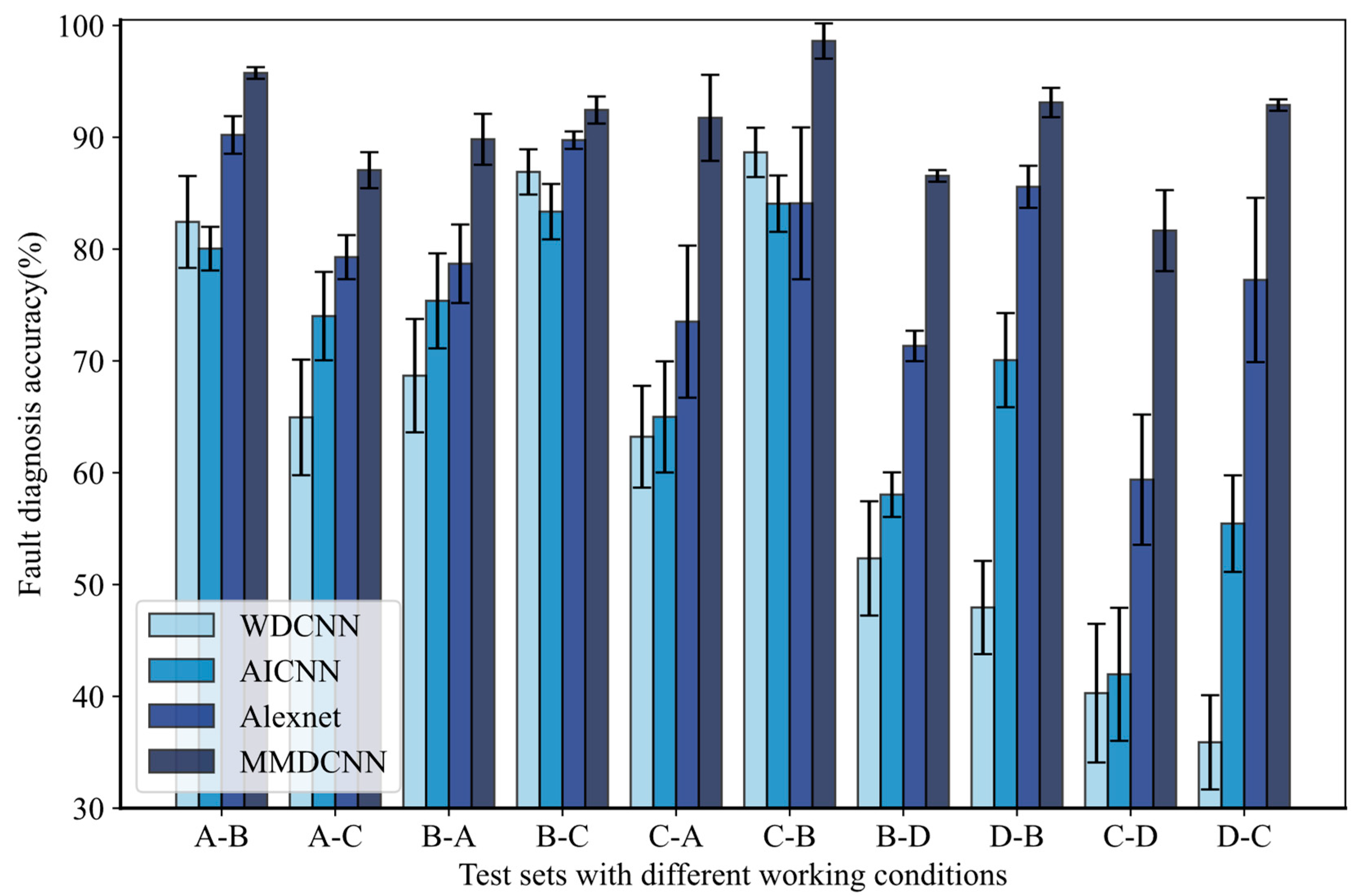
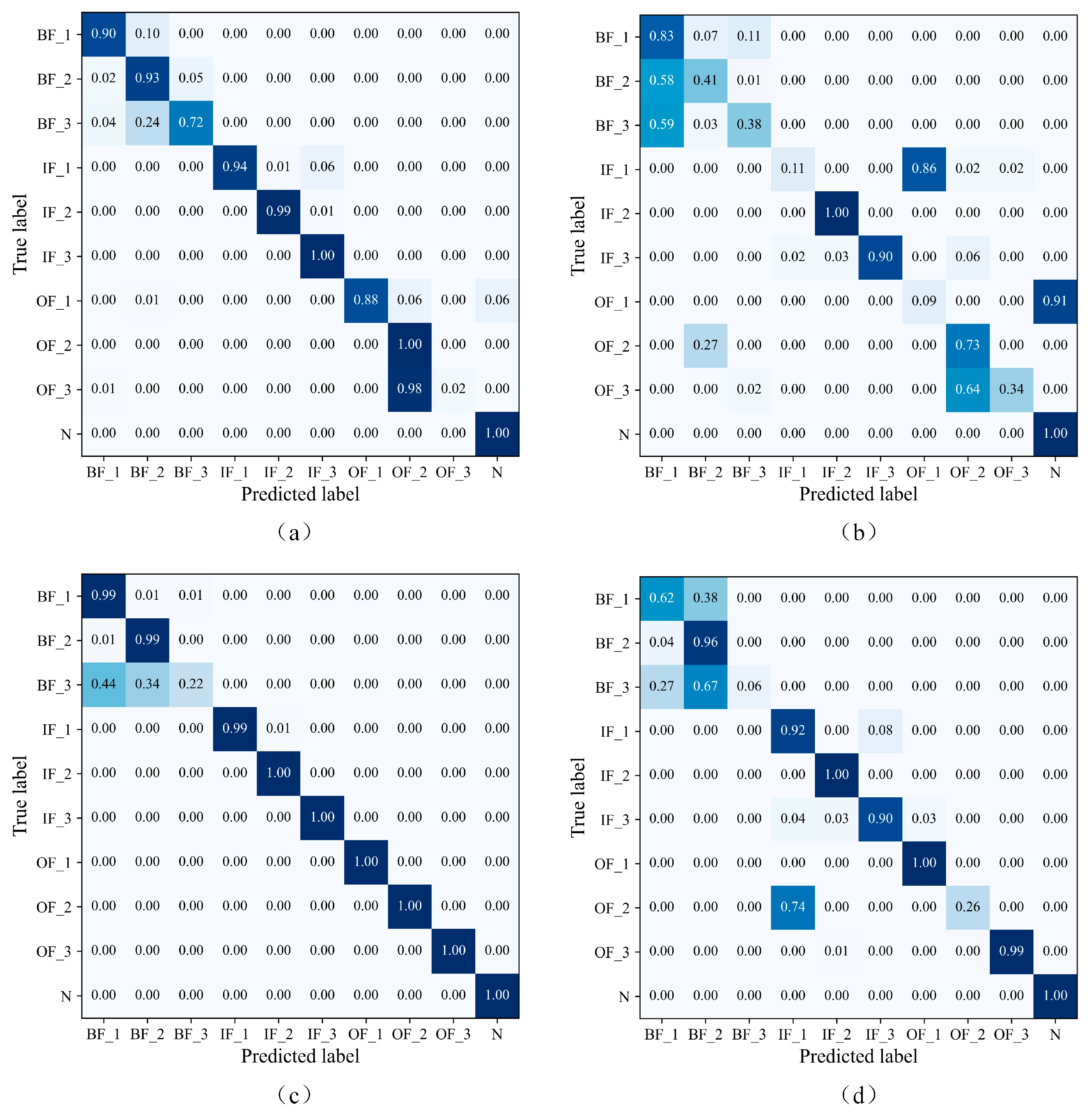
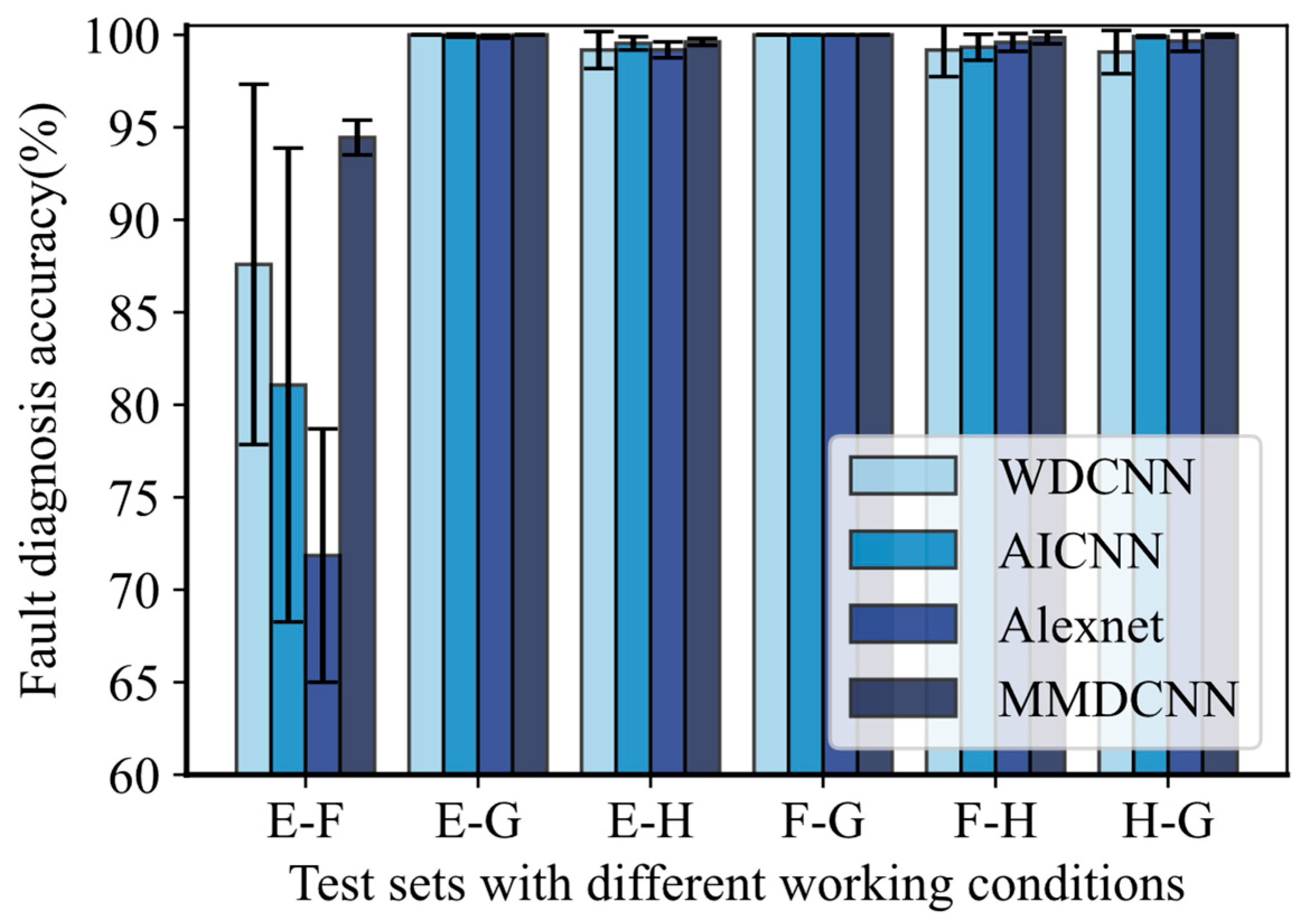
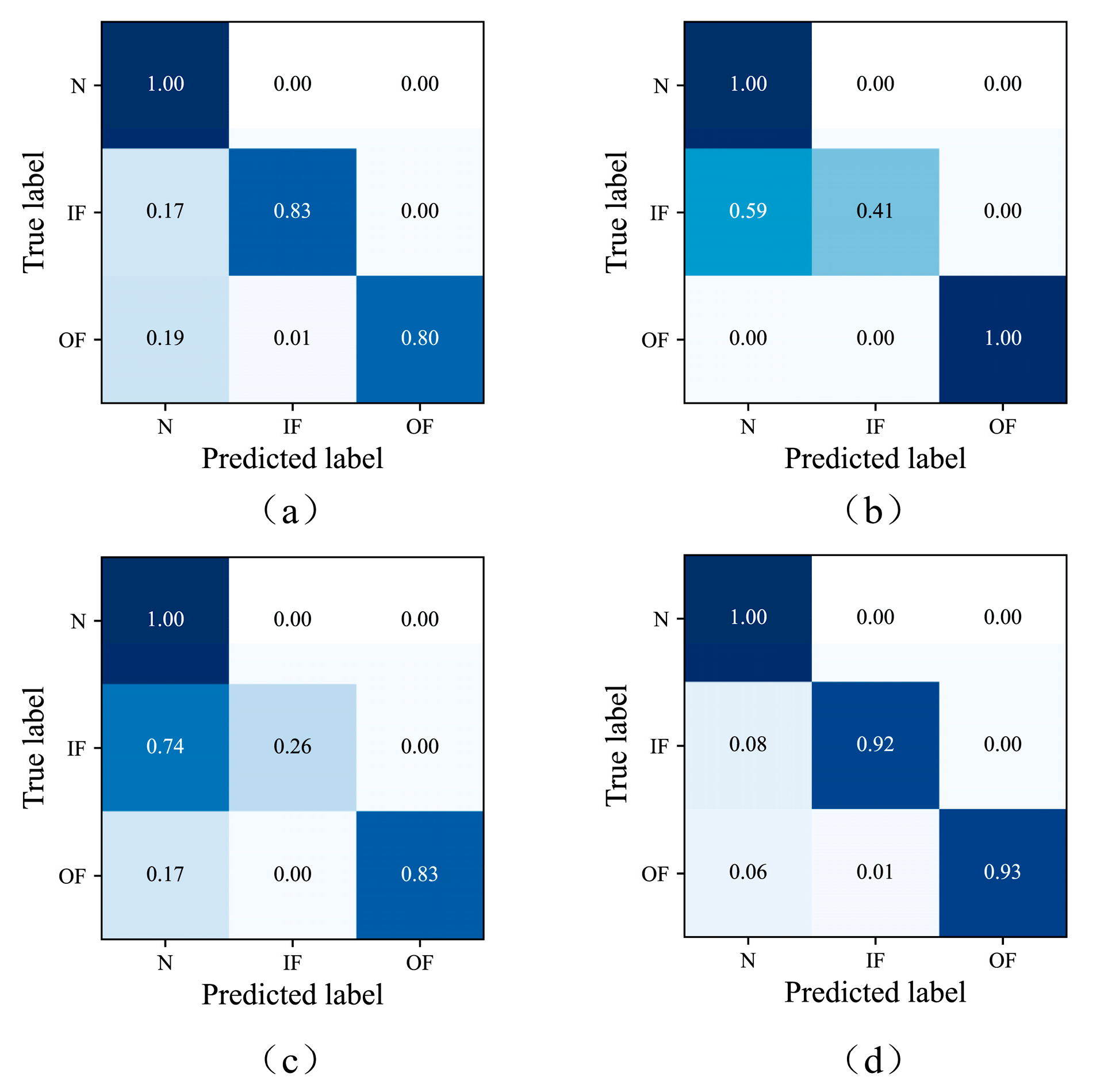
4. Experimental Validation and Analysis
4.1. Case 1: Experiments on Spindle Bearing Simulation Fault Dataset
4.2. Case 2: Experiments on the Paderborn University (PU) Dataset
4.3. Ablation Experiments
4.4. Computational Cost Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. The Ablation Study on Dataset D under Varying Noise
| Methods | Accuracy (%) | |
|---|---|---|
| SNR = 0 dB | ||
| SNR = −2 dB | SNR = 2 dB | |
| MMDCNN without multi-scale convolution part | 82.61 ± 0.62 | 87.33 ± 0.44 |
| MMDCNN without mutual information part | 83.33 ± 0.83 | 87.66 ± 0.62 |
| MMDCNN without all contributive parts | 80.88 ± 1.00 | 85.99 ± 0.95 |
| MMDCNN | 84.07 ± 0.13 | 88.70 ± 0.58 |
Appendix B. The Comparison Experiment on Dataset E under Varying Noise
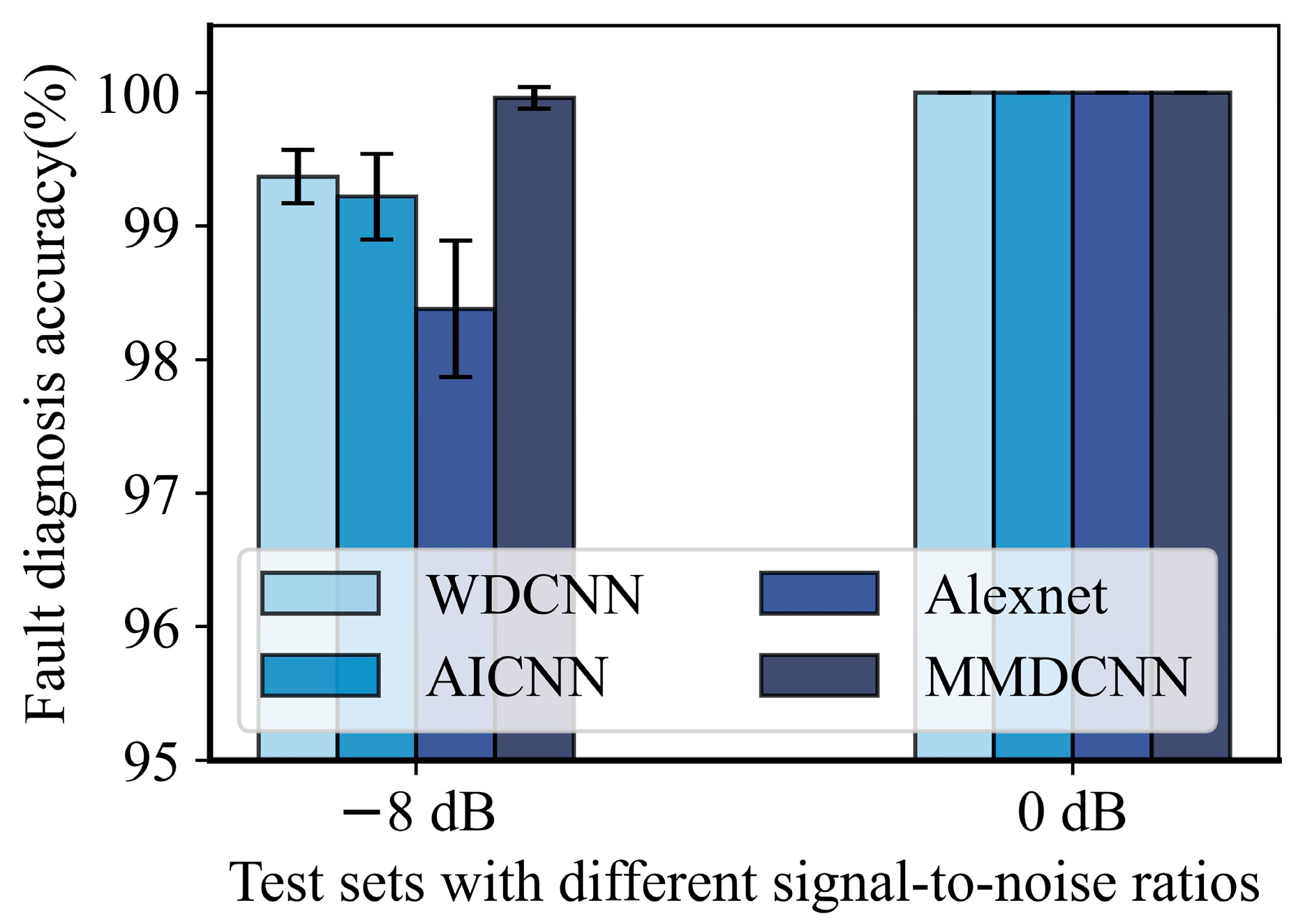
References
- Wang, H.; Xu, J.; Yan, R.; Gao, R.X. A New Intelligent Bearing Fault Diagnosis Method Using SDP Representation and SE-CNN. IEEE Trans. Instrum. Meas. 2020, 69, 52377–52389. [Google Scholar] [CrossRef]
- Gao, D.; Huang, K.; Zhu, Y.; Zhu, L.; Yan, K.; Ren, Z.; Soares, C.G. Semi-supervised small sample fault diagnosis under a wide range of speed variation conditions based on uncertainty analysis. Reliab. Eng. Syst. Saf. 2024, 242, 109746. [Google Scholar] [CrossRef]
- Wang, X.; Shen, C.; Xia, M.; Wang, D.; Zhu, J.; Zhu, Z. Multi-scale deep intra-class transfer learning for bearing fault diagnosis. Reliab. Eng. Syst. Saf. 2020, 202, 107050. [Google Scholar] [CrossRef]
- Gao, H.; Liang, L.; Chen, X.; Xu, G. Feature extraction and recognition for rolling element bearing fault utilizing short-time Fourier transform and non-negative matrix factorization. Chin. J. Mech. Eng. 2015, 28, 96–105. [Google Scholar] [CrossRef]
- Dybała, J.; Zimroz, R. Rolling bearing diagnosing method based on empirical mode decomposition of machine vibration signal. Appl. Acoust. 2014, 77, 195–203. [Google Scholar] [CrossRef]
- Wang, D.; Kwok-Leung, T.; Yong, Q. Optimization of segmentation fragments in empirical wavelet transform and its applications to extracting industrial bearing fault features. Measurement 2019, 133, 328–340. [Google Scholar] [CrossRef]
- Yu, J. Local and nonlocal preserving projection for bearing defect classification and performance assessment. IEEE Trans. Ind. Electron. 2011, 59, 2363–2376. [Google Scholar] [CrossRef]
- Soualhi, A.; Kamal, M.; Noureddine, Z. Bearing health monitoring based on Hilbert–Huang transform, support vector machine, and regression. IEEE Trans. Instrum. Meas. 2014, 64, 52–62. [Google Scholar] [CrossRef]
- Yu, W.; Zhao, C. Robust monitoring and fault isolation of nonlinear industrial processes using denoising autoencoder and elastic net. IEEE Trans. Control Syst. Technol. 2019, 28, 1083–1091. [Google Scholar] [CrossRef]
- Yu, W.; Zhao, C.; Huang, B. MoniNet with concurrent analytics of temporal and spatial information for fault detection in industrial processes. IEEE Trans. Cybern. 2021, 52, 8340–8351. [Google Scholar] [CrossRef]
- LeCun, Y.; Boser, B.; Denker, J.S.; Henderson, D.; Howard, R.E.; Hubbard, W.; Jackel, L.D. Backpropagation applied to handwritten zip code recognition. Neural Comput. 1989, 1, 541–551. [Google Scholar] [CrossRef]
- Long, Y.; Zhou, W.; Luo, Y. A fault diagnosis method based on one-dimensional data enhancement and convolutional neural network. Measurement 2021, 180, 109532. [Google Scholar] [CrossRef]
- Wen, L.; Li, X.; Gao, L.; Zhang, Y. A new convolutional neural network-based data-driven fault diagnosis method. IEEE Trans. Ind. Electron. 2017, 65, 5990–5998. [Google Scholar] [CrossRef]
- Chen, H.; Hu, N.; Cheng, Z.; Zhang, L.; Zhang, Y. A deep convolutional neural network based fusion method of two-direction vibration signal data for health state identification of planetary gearboxes. Measurement 2019, 146, 268–278. [Google Scholar] [CrossRef]
- He, Z.; Shao, H.; Zhong, X.; Zhao, X. Ensemble transfer CNNs driven by multi-channel signals for fault diagnosis of rotating machinery cross working conditions. Knowl.-Based Syst. 2020, 207, 106396. [Google Scholar] [CrossRef]
- Yu, W.; Zhao, C. Broad convolutional neural network based industrial process fault diagnosis with incremental learning capability. IEEE Trans. Ind. Electron. 2019, 67, 5081–5091. [Google Scholar] [CrossRef]
- Huo, C.; Jiang, Q.; Shen, Y.; Zhu, Q.; Zhang, Q. Enhanced transfer learning method for rolling bearing fault diagnosis based on linear superposition network. Eng. Appl. Artif. Intell. 2023, 121, 105970. [Google Scholar] [CrossRef]
- Tang, G.; Yi, C.; Liu, L.; Xu, D.; Zhou, Q.; Hu, Y.; Zhou, P.; Lin, J. A parallel ensemble optimization and transfer learning based intelligent fault diagnosis framework for bearings. Eng. Appl. Artif. Intell. 2024, 127, 107407. [Google Scholar] [CrossRef]
- Ganin, Y.; Ustinova, E.; Ajakan, H.; Germain, P.; Larochelle, H.; Laviolette, F.; March, M.; Lempitsky, V. Domain-Adversarial Training of Neural Networks. In Domain Adaptation in Computer Vision Applications; Advances in Computer Vision and Pattern Recognition; Csurka, G., Ed.; Springer International Publishing: Cham, Switzerland, 2017; pp. 189–209. [Google Scholar] [CrossRef]
- Wang, Y.-Q.; Zhao, Y.-P. A novel inter-domain attention-based adversarial network for aero-engine partial unsupervised cross-domain fault diagnosis. Eng. Appl. Artif. Intell. 2023, 123, 106486. [Google Scholar] [CrossRef]
- Ren, H.; Wang, J.; Zhu, Z.; Shi, J.; Huang, W. Domain fuzzy generalization networks for semi-supervised intelligent fault diagnosis under unseen working conditions. Mech. Syst. Signal Process. 2023, 200, 110579. [Google Scholar] [CrossRef]
- Chen, L.; Li, Q.; Shen, C.; Zhu, J.; Wang, D.; Xia, M. Adversarial Domain-Invariant Generalization: A Generic Domain-Regressive Framework for Bearing Fault Diagnosis Under Unseen Conditions. IEEE Trans. Ind. Inform. 2022, 18, 31790–31800. [Google Scholar] [CrossRef]
- Zhao, C.; Shen, W. Mutual-assistance semisupervised domain generalization network for intelligent fault diagnosis under unseen working conditions. Mech. Syst. Signal Process. 2023, 189, 110074. [Google Scholar] [CrossRef]
- Zhu, H.; Ning, Q.; Lei, Y.J.; Chen, B.C.; Yan, H. Rolling bearing fault classification based on attention mechanism-Inception-CNN model. J. Vib. Shock 2020, 39, 84–93. [Google Scholar]
- Zhang, K.; Wang, J.; Shi, H.; Zhang, X.; Tang, Y. A fault diagnosis method based on improved convolutional neural network for bearings under variable working conditions. Measurement 2021, 182, 109749. [Google Scholar] [CrossRef]
- Li, S.; An, Z.; Lu, J. A novel data-driven fault feature separation method and its application on intelligent fault diagnosis under variable working conditions. IEEE Access 2020, 8, 113702–113712. [Google Scholar] [CrossRef]
- Szegedy, C.; Liu, W.; Jia, Y.; Sermanet, P.; Reed, S.; Anguelov, D.; Erhan, D.; Vanhoucke, V.; Rabinovich, A. Going deeper with convolutions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. In Proceedings of the Annual Conference on Neural Information Processing Systems 2017, Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Hjelm, R.D.; Fedorov, A.; Lavoie-Marchildon, S.; Grewal, K.; Bachman, P.; Trischler, A.; Bengio, Y. Learning deep representations by mutual information estimation and maximization. arXiv 2018, arXiv:1808.06670. [Google Scholar]
- Kingma, D.P.; Welling, M. Auto-encoding variational bayes. arXiv 2013, arXiv:1312.6114. [Google Scholar]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. Adv. Neural Inf. Process. Syst. 2012, 25, 1097–1105. [Google Scholar] [CrossRef]
- Zhang, W.; Peng, G.; Li, C.; Chen, Y.; Zhang, Z. A new deep learning model for fault diagnosis with good anti-noise and domain adaptation ability on raw vibration signals. Sensors 2017, 17, 425. [Google Scholar] [CrossRef]
- Lessmeier, C.; Kimotho, J.K.; Zimmer, D.; Sextro, W. Kat-Datacenter, Chair of Design and Drive Technology. Paderborn University. Available online: https://mb.uni-paderborn.de/kat/forschung/kat-datacenter/bearing-datacenter (accessed on 27 May 2024).






| Type | Layer | Kernel Size/Stride/Depth | Input Size | Output Size |
|---|---|---|---|---|
| Multi-scale feature convolutional module | Inception | N | (N/2, 48) | |
| Self-attention mechanism | (N/2, 48) | (N/2, 48) | ||
| Conv Module1 | Convolution | 3/1/64 (Zero padding) | (N/2, 48) | (N/4, 64) |
| BN | / | |||
| Max Pooling | 2/2/64 | |||
| Conv Module2 | Convolution | 3/1/64 (Zero padding) | (N/4, 64) | (N/8, 64) |
| BN | / | |||
| Max Pooling | 2/2/64 | |||
| Conv Module3 | Convolution | 3/1/64 (Zero padding) | (N/8, 64) | (N/16, 64) |
| BN | / | |||
| Max Pooling | 2/2/64 | |||
| Conv Module4 | Convolution | 3/1/64 | (N/16, 64) | ((N/16 − 2)/2, 64) |
| BN | / | |||
| Max Pooling | 2/2/64 | |||
| Self-attention mechanism | ((N/16 − 2)/2, 64) | ((N/16 − 2)/2, 64) | ||
| Fully connected layer | Fc layer | / | ((N/16 − 2)/2) × 64 | 100 |
| Output layer | Fc layer | / | 100 | y |
| FC_VAE_1 | Fc layer | / | 64 | 64 |
| FC_VAE_2 | Fc layer | / | 64 | 64 |
| LI_FC_1 | Fc layer | / | (N/8) × 2 × 64 | 64 |
| LI_FC_2 | Fc layer | / | 64 | 64 |
| LI_FC_3 | Fc layer | / | 64 | 64 |
| LI_FC_4 | Fc layer | / | 64 | 1 |
| GI_FC_1 | Fc layer | / | 2 × 64 | 64 |
| GI_FC_2 | Fc layer | / | 64 | 64 |
| GI_FC_3 | Fc layer | / | 64 | 64 |
| GI_FC_4 | Fc layer | / | 64 | 1 |
| Dataset | A | B | C | D |
|---|---|---|---|---|
| Speed (rpm) | 2100 | 2100 | 2100 | 1500 |
| Axil load (kN) | 1 | 2 | 3 | 2 |
| Methods | Accuracy (%) |
|---|---|
| MMDCNN without multi-scale convolution part | 81.41 ± 2.17 |
| MMDCNN without mutual information part | 89.06 ± 3.18 |
| MMDCNN without all contributive part | 77.24 ± 7.35 |
| MMDCNN | 92.88 ± 0.51 |
| Method | Training Time/Testing Time (s) | |
|---|---|---|
| Spindle Bearing Simulation Fault Dataset | PU Dataset | |
| WDCNN | 0.15/0.0001 | 0.15/0.0001 |
| AICNN | 0.23/0.0001 | 0.23/0.0001 |
| Alexnet | 0.32/0.0001 | 0.31/0.0001 |
| MMDCNN | 2.46/0.0001 | 2.32/0.0001 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, K.; Zhu, L.; Ren, Z.; Lin, T.; Zeng, L.; Wan, J.; Zhu, Y. An Improved Fault Diagnosis Method for Rolling Bearings Based on 1D_CNN Considering Noise and Working Condition Interference. Machines 2024, 12, 383. https://doi.org/10.3390/machines12060383
Huang K, Zhu L, Ren Z, Lin T, Zeng L, Wan J, Zhu Y. An Improved Fault Diagnosis Method for Rolling Bearings Based on 1D_CNN Considering Noise and Working Condition Interference. Machines. 2024; 12(6):383. https://doi.org/10.3390/machines12060383
Chicago/Turabian StyleHuang, Kai, Linbo Zhu, Zhijun Ren, Tantao Lin, Li Zeng, Jin Wan, and Yongsheng Zhu. 2024. "An Improved Fault Diagnosis Method for Rolling Bearings Based on 1D_CNN Considering Noise and Working Condition Interference" Machines 12, no. 6: 383. https://doi.org/10.3390/machines12060383
APA StyleHuang, K., Zhu, L., Ren, Z., Lin, T., Zeng, L., Wan, J., & Zhu, Y. (2024). An Improved Fault Diagnosis Method for Rolling Bearings Based on 1D_CNN Considering Noise and Working Condition Interference. Machines, 12(6), 383. https://doi.org/10.3390/machines12060383






