Establishment and Analysis of Load Spectrum for Bogie Frame of High-Speed Train at 400 km/h Speed Level
Abstract
1. Introduction
2. Materials and Methods
2.1. Bogie Frame Load Series
2.2. Load Identification Method
2.3. Static Calibration Test
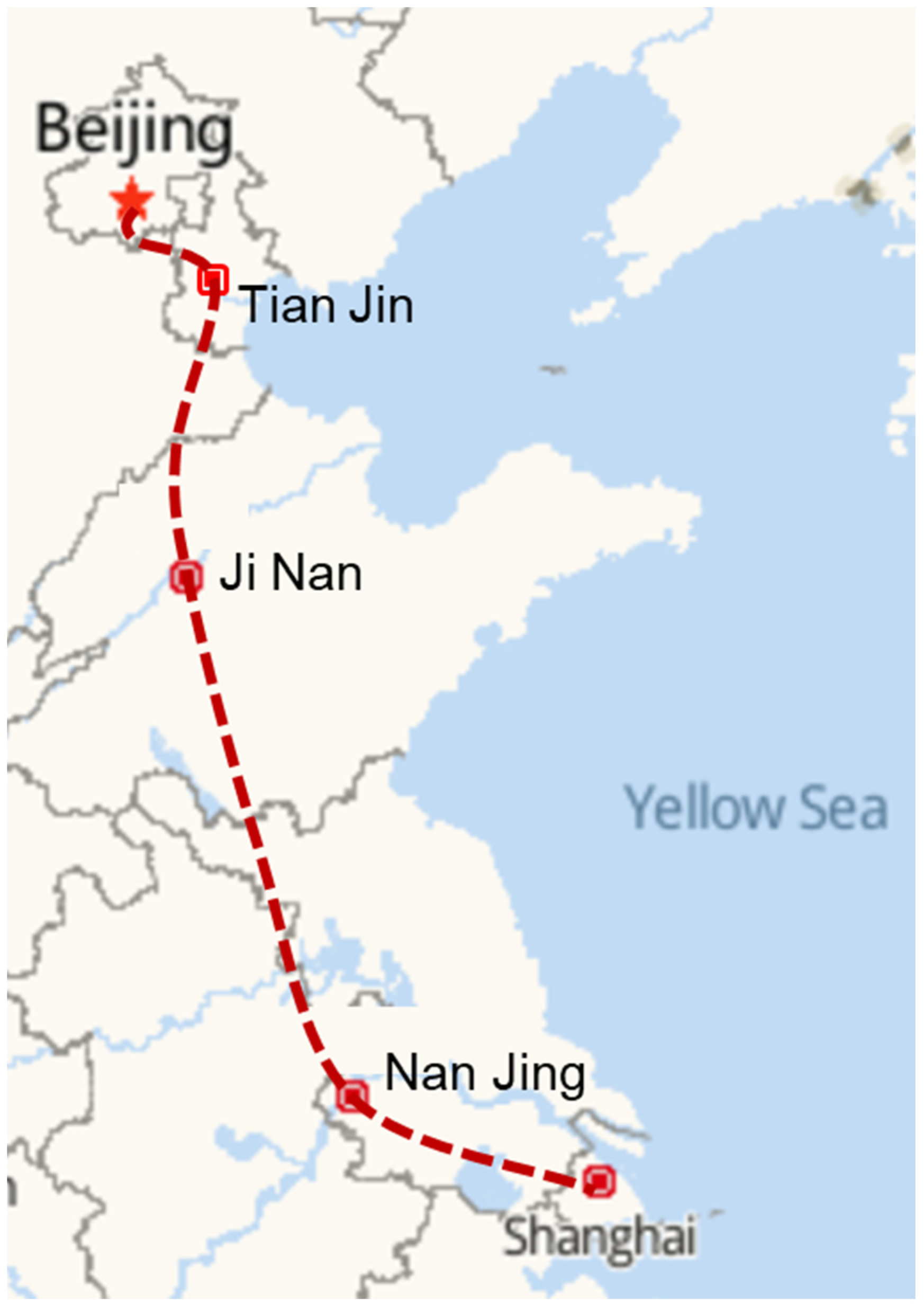
2.4. Track Test
3. Load Characteristics and Load Spectrum
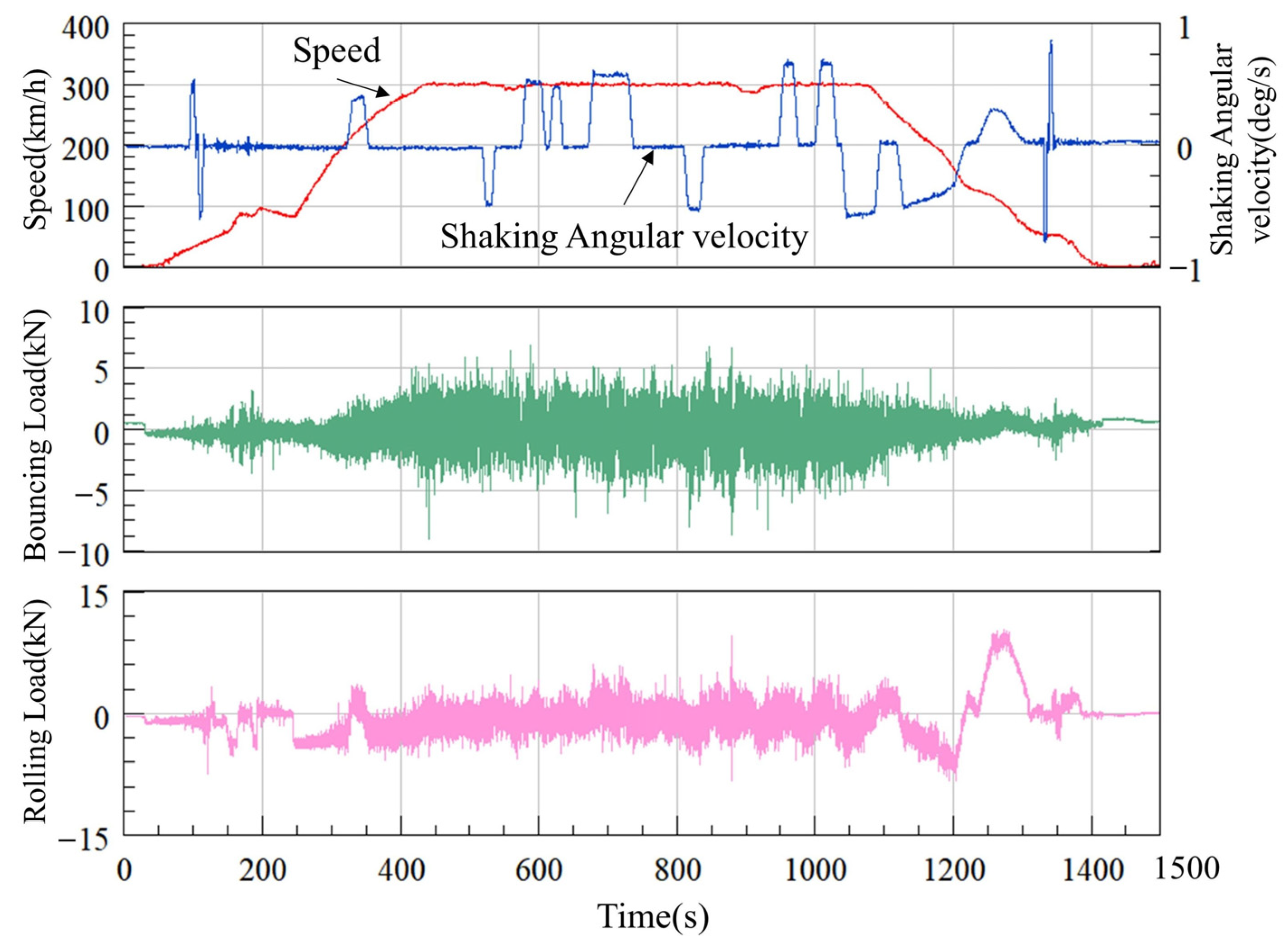
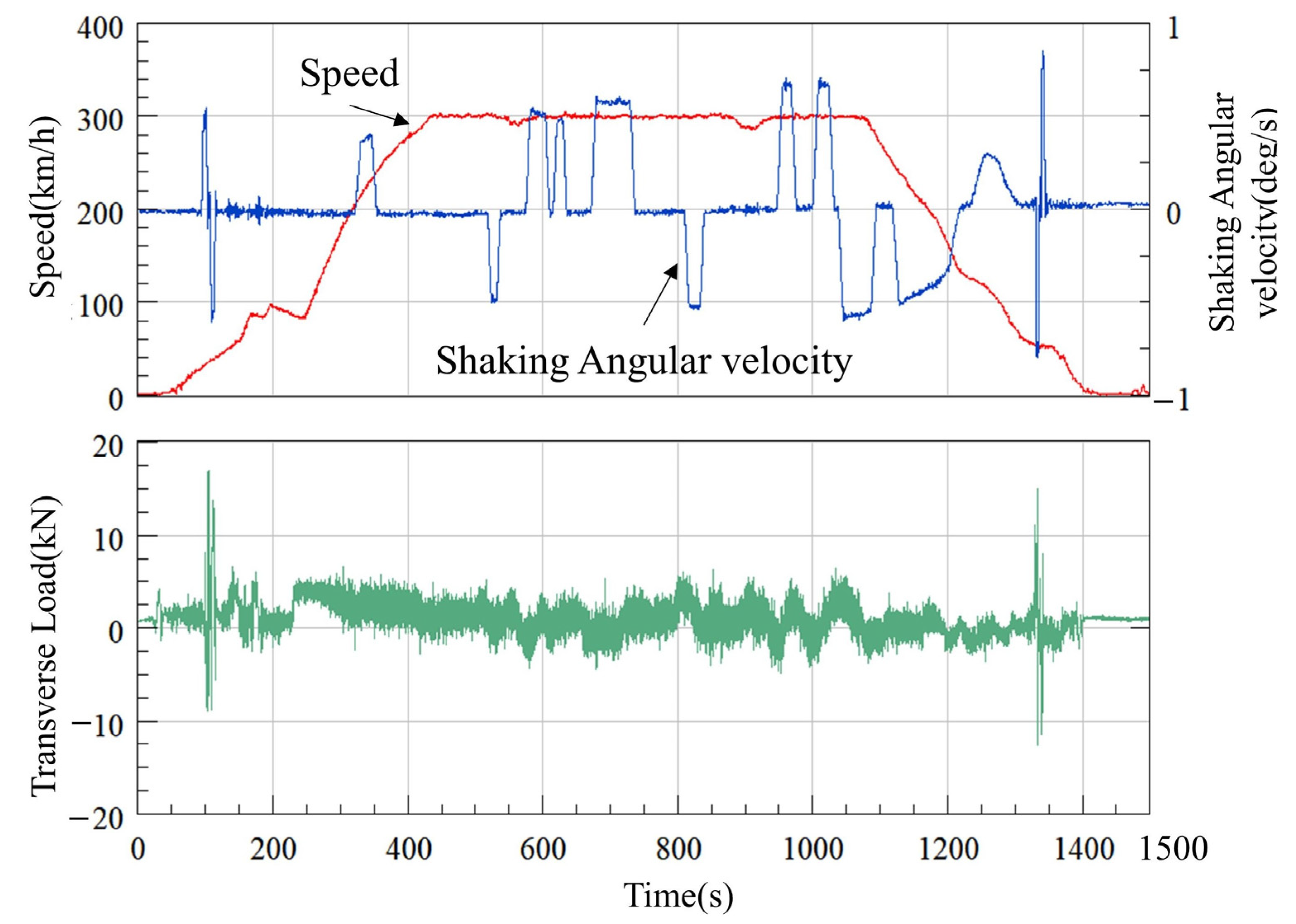
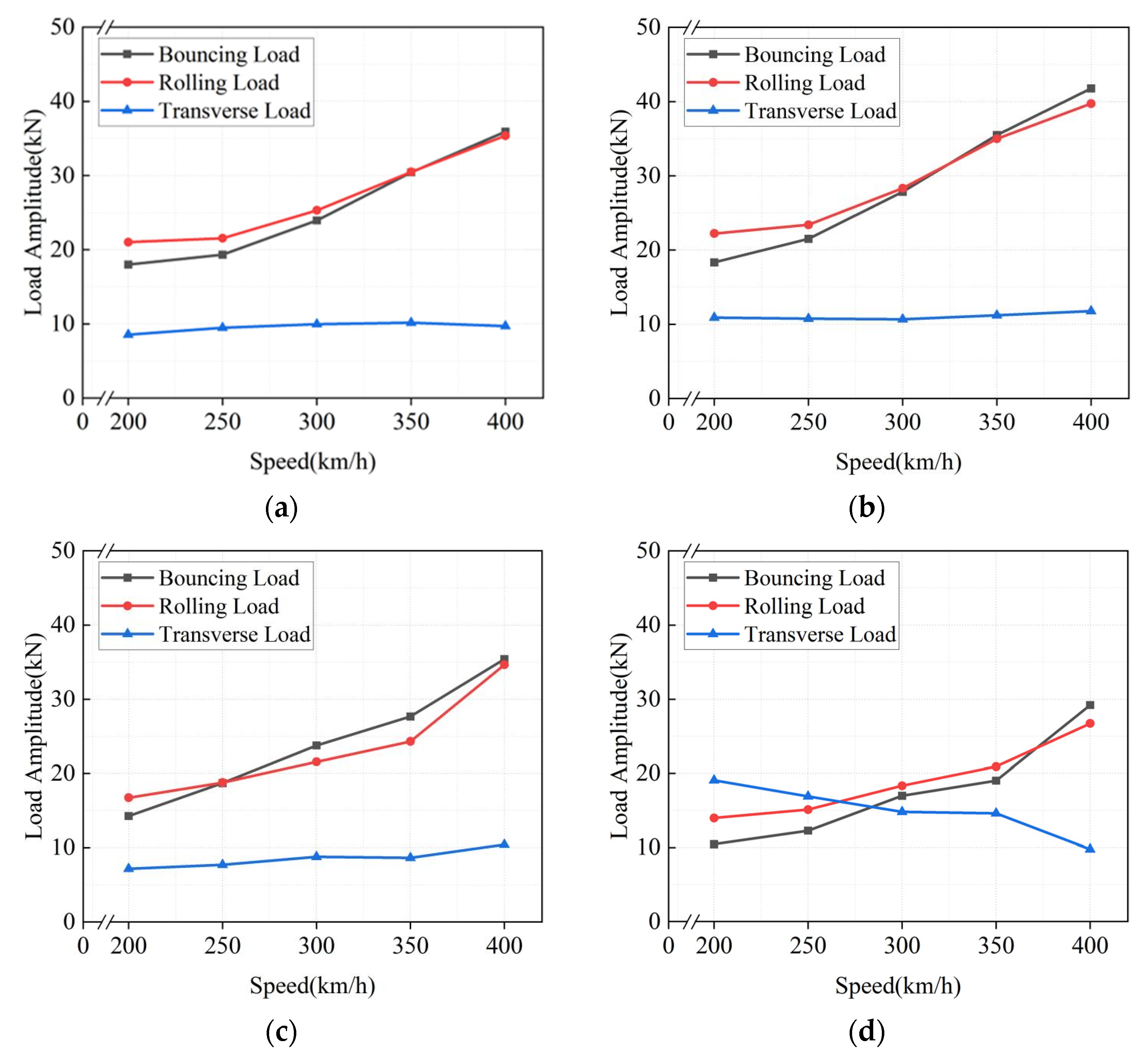
3.1. Time-Domain Characteristics of Typical Loads
3.1.1. Vertical Load
3.1.2. Transverse Load
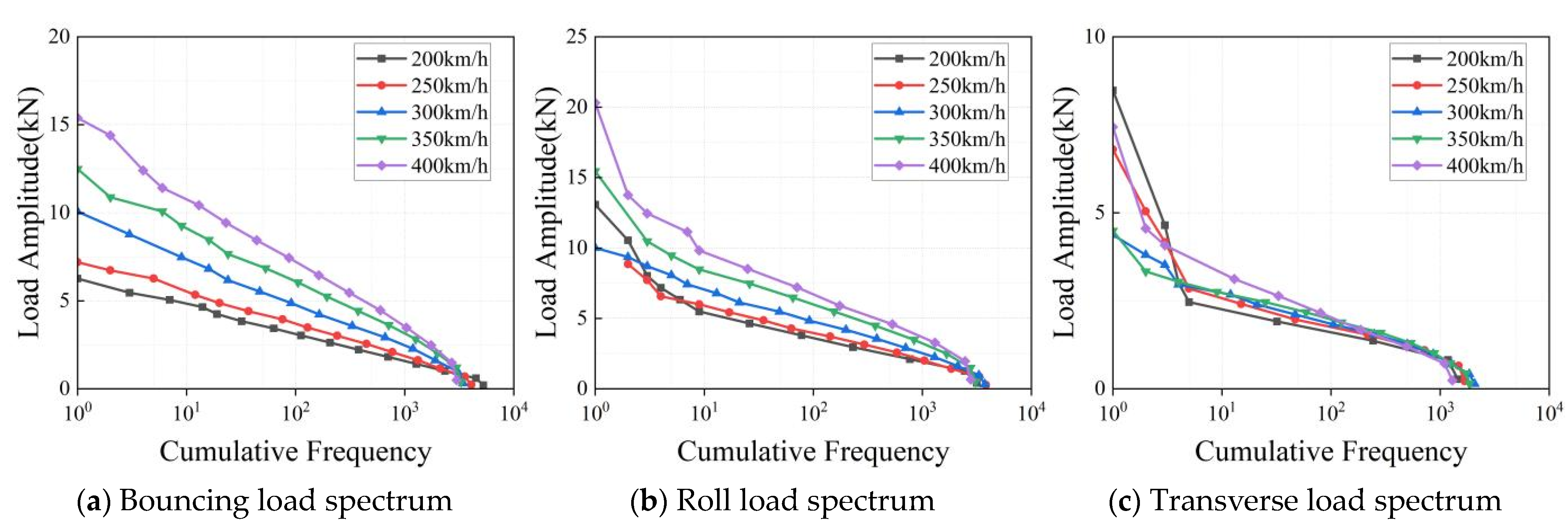
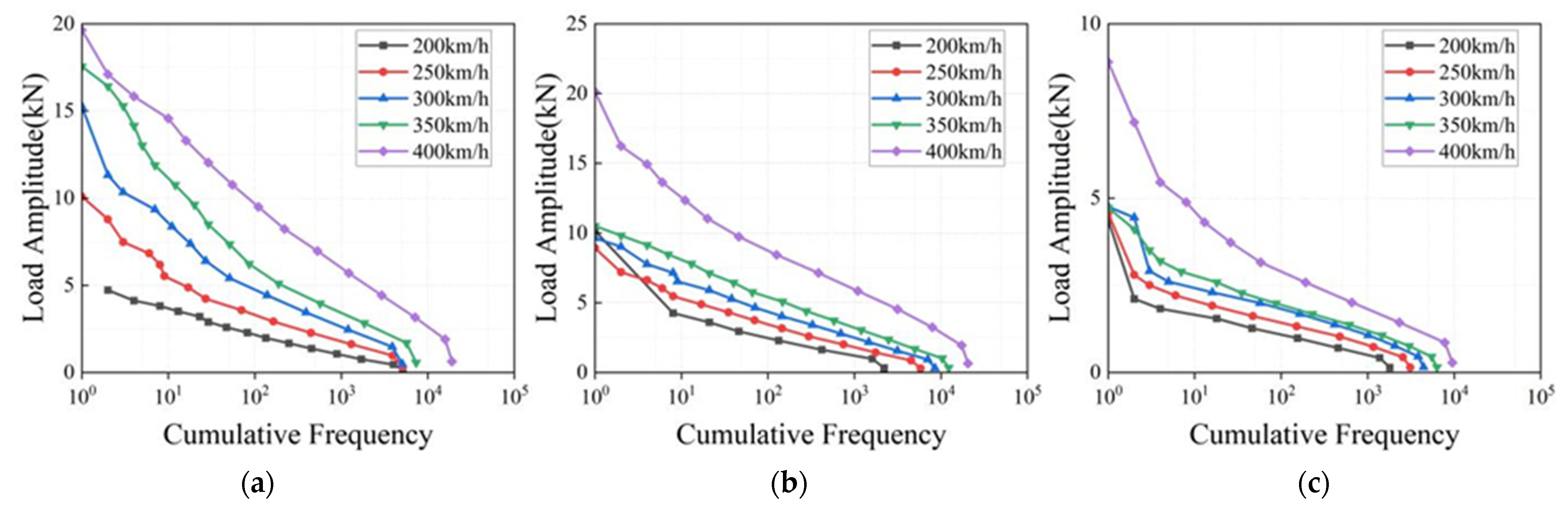
3.2. Load Spectrum Compilation
3.3. Equivalent Load Amplitude
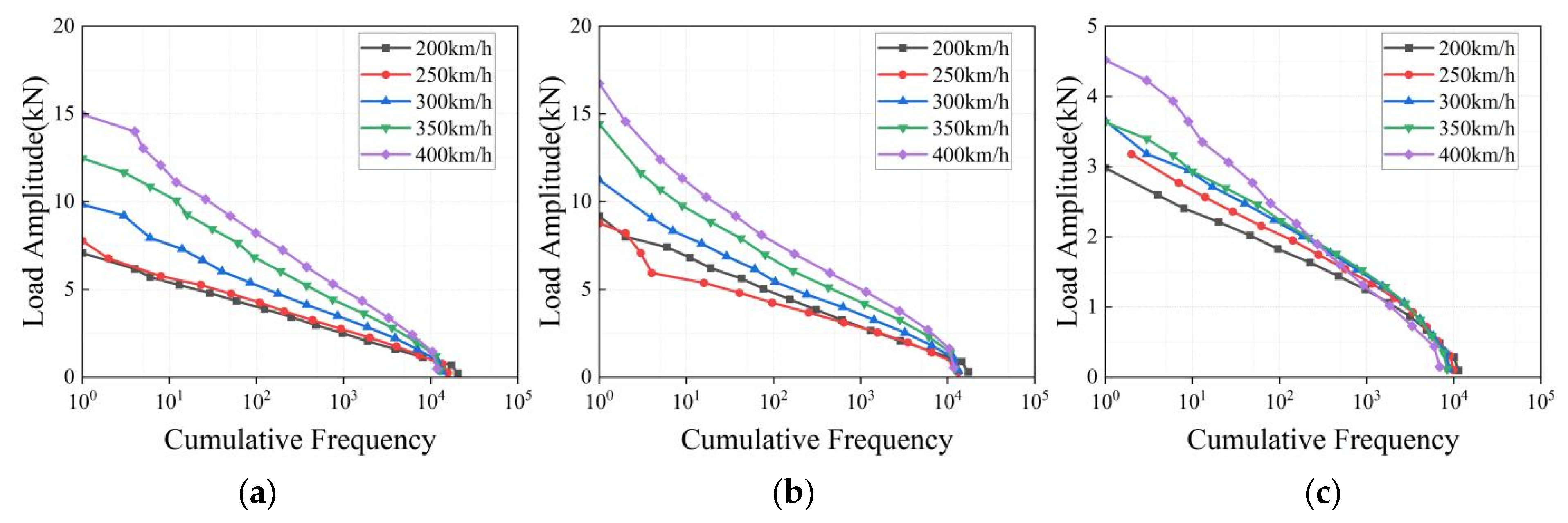
4. Construction of Load Spectrum for Higher Speed Class
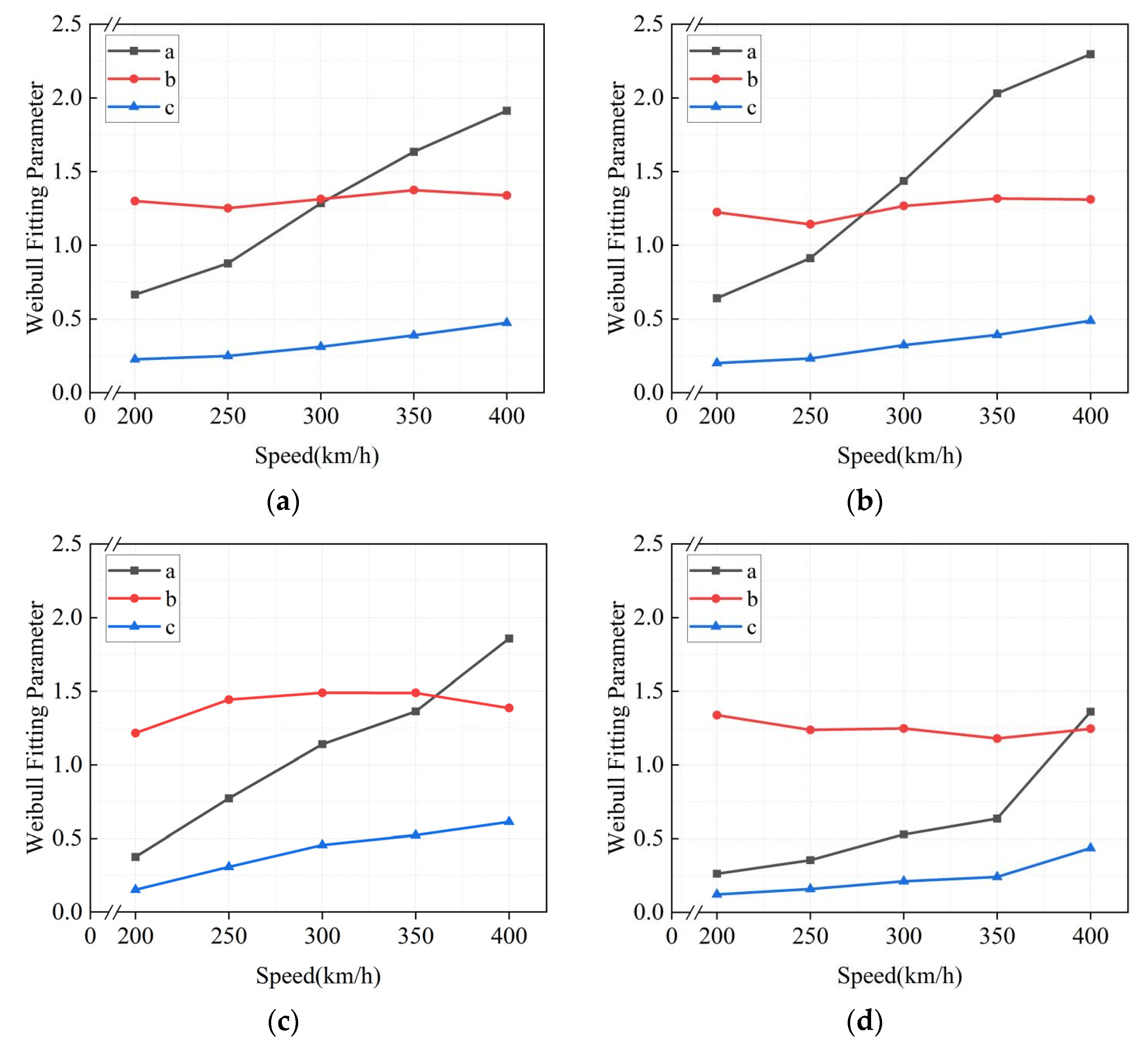
4.1. Load Spectrum Shape Fitting
4.2. Maximum Load Amplitude and Cumulative Frequency
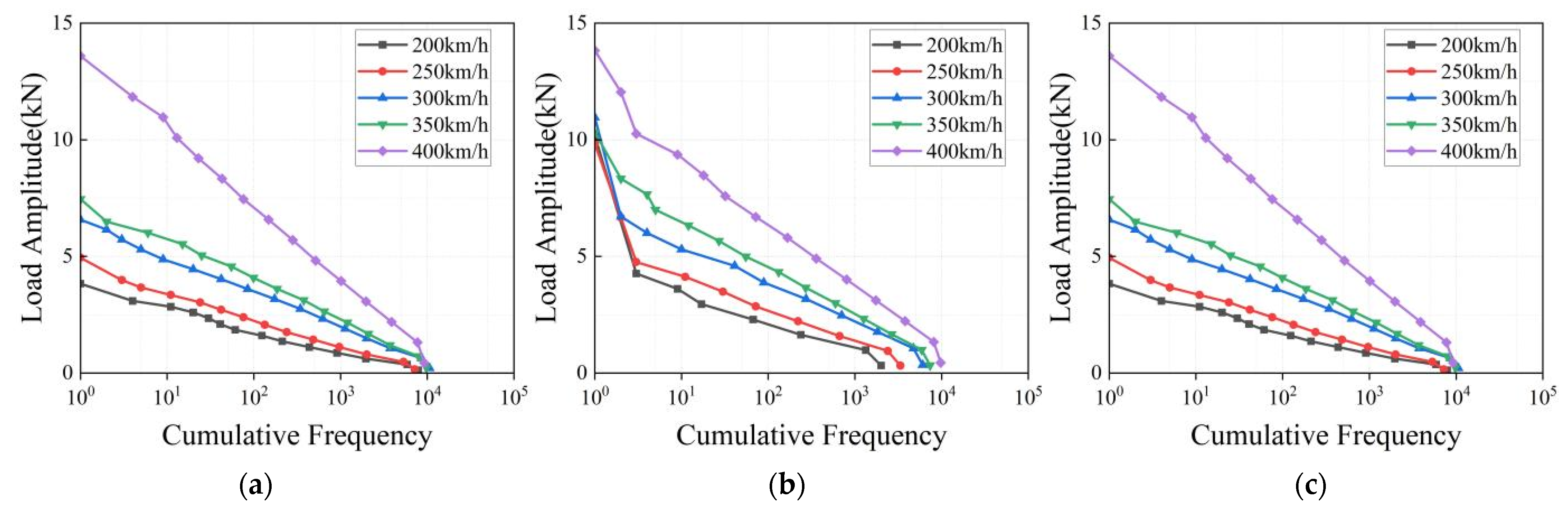
4.3. Construction of Load Spectrum for 450 km/h Speed Class
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- EN 13749:2011(E); Railway Applications—Wheelsets and Bogies—Method of Specifying the Structural Requirements of Bogie Frames. European Committee for Standardization: Brussels, Belgium, 2011; pp. 19–50.
- UIC 615-4; Tractive Units Bogies and Running Gear Bogie Frame Structure Strength Tests. International Union of Railways: Paris, France, 2003; pp. 2–12.
- JIS E 4207:2004(E); Truck Frames for Railway Rolling Stock-General Rules for Design. Japanese Standards Association: Tokyo, Japan, 2004; pp. 4–5.
- Ren, Z.; Cao, J.; Li, Y.; Wang, B.; Wei, X. The Load Character of The Bogie frame of High-Speed Emus. Eng. Mech. 2021, 38, 242–256. [Google Scholar]
- Yang, G.; Li, G.; Zhou, J.; Feng, Y. Study on Traction Rod Load Characteristics of High-Speed Train. J. Mech. Eng. 2020, 56, 200–206. [Google Scholar]
- Xing, B.; Zhang, J.; Xu, Y. Simulation and Optimization Design of CRH380A EMU Bogie Frame. IOP Conf. Ser. Mater. Sci. Eng. 2020, 790, 012117. [Google Scholar] [CrossRef]
- Ji, C.; Sun, S.; Yang, G.; Meng, Q. Study on Torsional Load Characteristics of High-speed Train Bogie Frame. J. Mech. Eng. 2021, 57, 147–157. [Google Scholar]
- Tao, G.; Wang, W.; Feng, Y.; Li, G. Research on Bench Test Method for Bogie Frame Based on Measured Line Load. J. Mech. Eng. 2023, 59, 213–221. [Google Scholar]
- Zhu, N.; Sun, S.; Li, Q.; Zou, H. Theoretical Research and Experimental Validation of Elastic Dynamic Load Spectra on Bogie Frame of High-speed Train. Chin. J. Mech. Eng. 2016, 29, 498–506. [Google Scholar] [CrossRef]
- Kassner, M. Fatigue strength analysis of a welded railway vehicle structure by different methods. Int. J. Fatigue 2012, 34, 103–111. [Google Scholar] [CrossRef]
- Wang, B.J.; Li, Q.; Ren, Z.S.; Sun, S.G. Improving the fatigue reliability of metro vehicle bogie frame based on load spectrum. Int. J. Fatigue 2020, 132, 105389. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, G.; Wang, J.; Jiang, H.; Zhang, R. Compilation method of power train load spectrum of engineering vehicle. Trans. Chin. Soc. Agric. Eng. 2011, 27, 179–183. [Google Scholar]
- Ji, C.; Sun, S.; Li, Q.; Ren, Z.; Yang, G. Realistic fatigue damage assessment of a high-speed train bogie frame by damage consistency load spectra based on measured field load. Measurement 2020, 166, 108164. [Google Scholar] [CrossRef]
- Wang, T.; Sun, W.; Wang, Q.; Zhang, Z.; He, Y.; Zhou, J. Generation of vibration load spectrum for fatigue analysis of equipment mounted on bogie frame of railway vehicle based on fatigue damage spectrum. Proc. Inst. Mech. Eng. Part F-J. Rail Rapid Transit 2023, 237, 1082–1093. [Google Scholar] [CrossRef]
- Xiu, R.; Spiryagin, M.; Wu, Q.; Yang, S.; Liu, Y. Fatigue life prediction for locomotive bogie frames using virtual prototype technique. Proc. Inst. Mech. Eng. Part F-J. Rail Rapid Transit 2021, 235, 1122–1131. [Google Scholar] [CrossRef]
- Ma, S.; Sun, S.; Wang, B.; Wang, N. Estimating load spectra probability distributions of train bogie frames by the diffusion-based kernel density method. Int. J. Fatigue 2020, 132, 105352. [Google Scholar] [CrossRef]
- Chen, D.; Xiao, Q.; Mou, M.; Sun, S.; Li, Q. Study on establishment of standardized load spectrum on bogie frames of high-speed trains. Acta Mech. Sin. 2019, 35, 812–827. [Google Scholar] [CrossRef]
- Xiu, R.; Spiryagin, M.; Wu, Q.; Yang, S.; Liu, Y. Fatigue life assessment methods for railway vehicle bogie frames. Eng. Fail. Anal. 2020, 116, 104725. [Google Scholar] [CrossRef]
- Li, F.; Wu, P.; Zeng, J.; Wang, J. Study on the Differences between the Three Common Fatigue Strength Analysis Methods for Bogie Frame. J. Mech. Eng. 2014, 50, 170–176. [Google Scholar] [CrossRef]
- Wang, B.J.; Xie, S.Q.; Li, Q.; Ren, Z.S. Fatigue damage prediction of metro bogie frame based on measured loads. Int. J. Fatigue 2022, 154, 106532. [Google Scholar] [CrossRef]
- Wang, B.; Sun, S.; Wang, X.; Zhang, L.; Dong, L.; Jiang, C. Research on Characteristics of Operation Loads and Fatigue Damage of Metro Train Bogie Frame. J. China Railw. Soc. 2019, 41, 53–60. [Google Scholar]
- Zhang, Z. Study on Load Spectrum of 400 km/h EMU Bogie Frame. Master’s Thesis, Beijing Jiaotong University, Beijing, China, 2018. [Google Scholar]
- Ji, C.; Sun, S.; Li, Q.; Wang, W.; Ren, Z.; Yang, G. A novel method for the general application of measured load spectra to different high-speed train bogie frames based on virtual track irregularity. Measurement 2022, 198, 111369. [Google Scholar] [CrossRef]
- Wen, Z.Z. Fatigue Load Spectra Study of c70 Type Railway Freight Car. Master’s Thesis, Southwest Jiaotong University, Chengdu, China, 2011. [Google Scholar]
- Yuan, Z.; Chen, X.J.; Ma, L.J.; Li, Q.; Sun, S.; Wei, Y. A segmented load spectrum model for high-speed trains and its inflection stress as an indicator for line quality. Int. J. Fatigue 2021, 148, 106221. [Google Scholar] [CrossRef]
- Wang, B.; Sun, S.; Li, Q.; Tang, Q. Research on the Improvement of Speed Increase Passenger Car Bogie Frame Reliability Based on Load Spectrum. J. China Railw. Soc. 2019, 41, 23–30. [Google Scholar] [CrossRef]
- Rennert, R. Measured load spectra of rail vehicle car-bodies and their application as design loads. Int. J. Fatigue 2021, 144, 106030. [Google Scholar] [CrossRef]
- Cousineau, D. Fitting the Three-Parameter Weibull Distribution: Review and Evaluation of Existing and New Methods. IEEE Trans. Dielectr. Electr. Insul. 2009, 16, 281–288. [Google Scholar] [CrossRef]
- Mei, G.; Luo, Q.; Qiao, W.; Huang, Z.; Lu, J.; Wang, J. Study of load spectrum compilation method for the pantograph upper frame based on multi-body dynamics. Eng. Fail. Anal. 2022, 135, 106099. [Google Scholar] [CrossRef]
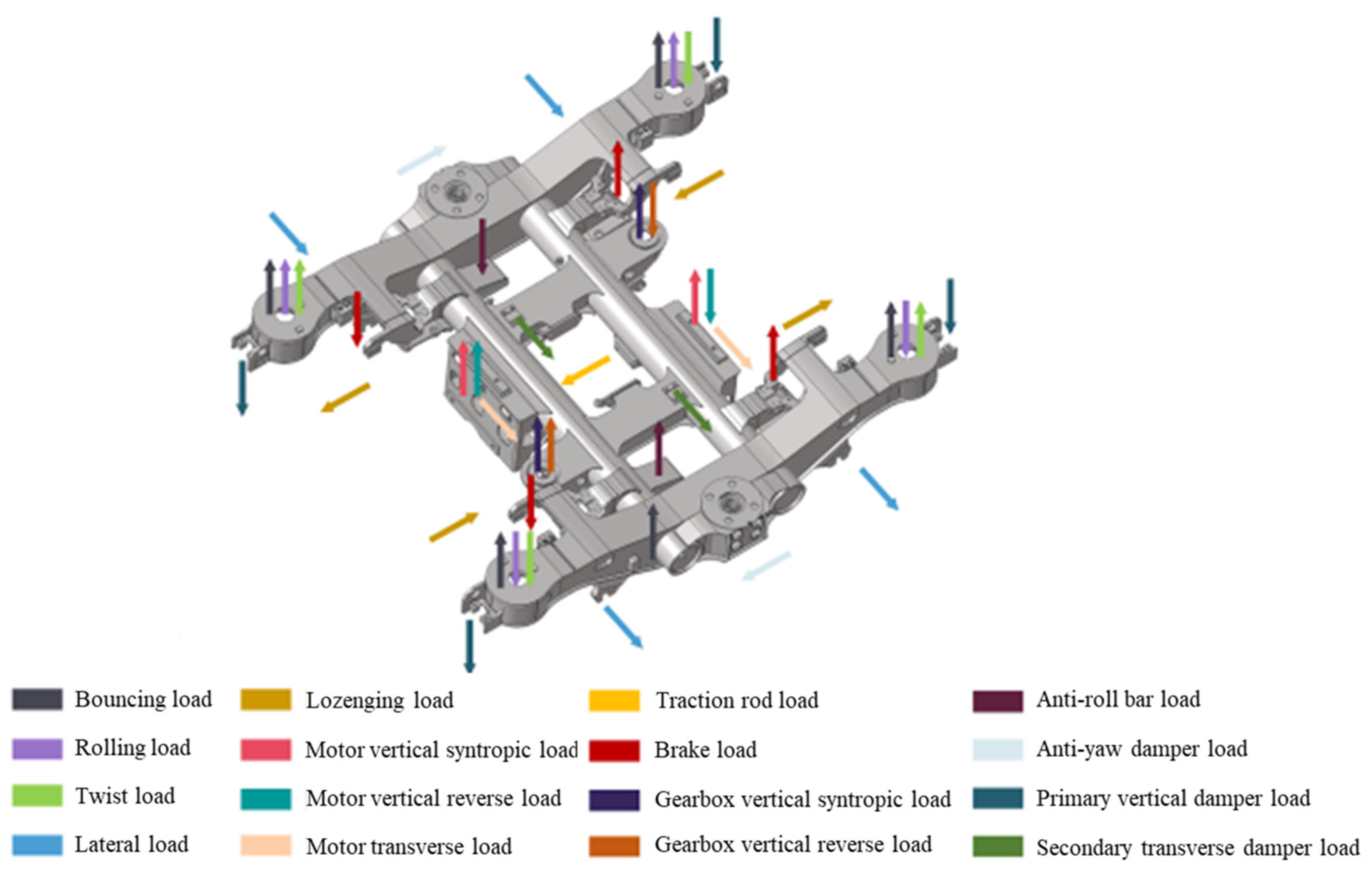
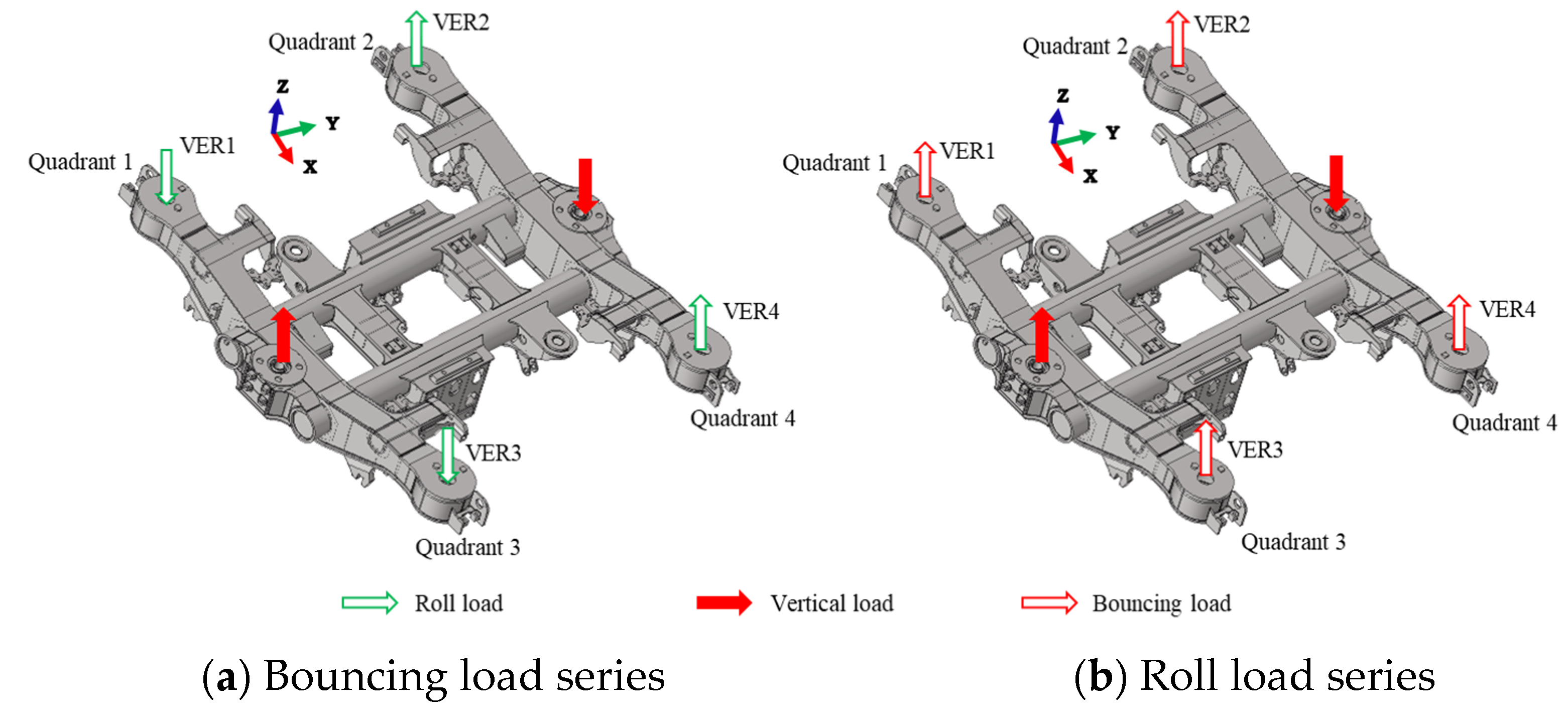
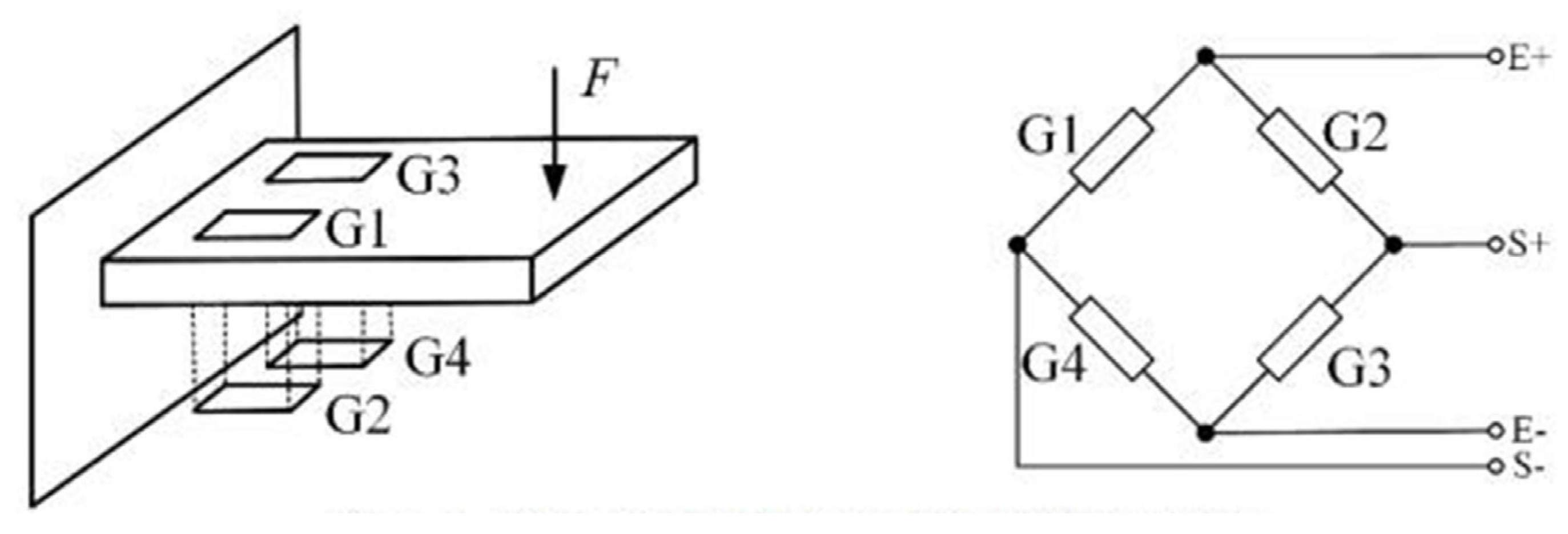

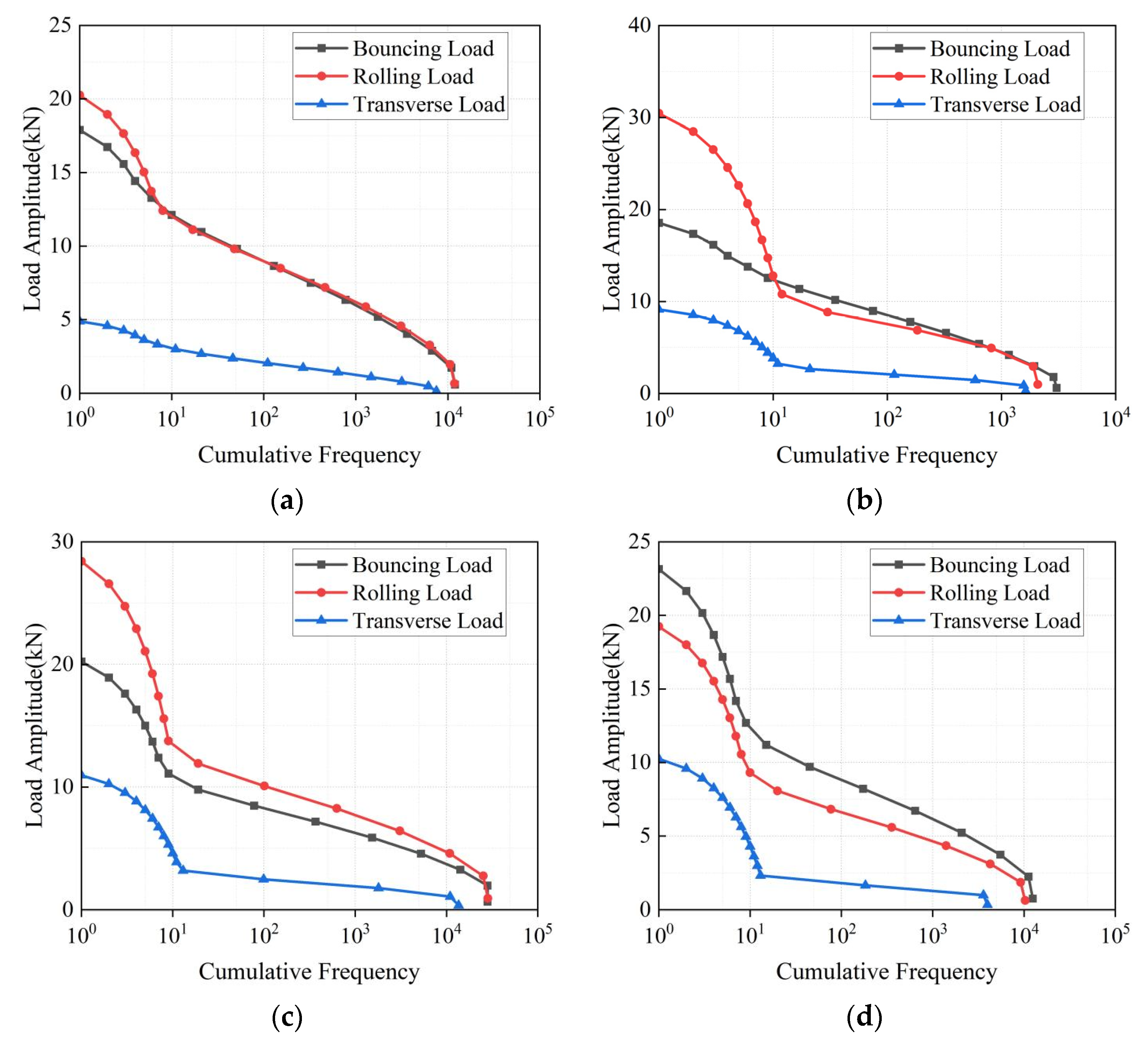
| Operation Condition | Load Name | Bouncing Load | Rolling Load | Transverse Load | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Fitting Parameters | a | b | c | a | b | c | a | b | c | |
| Constant speed operation on straight line | G | 4.62 × 10−6 | 5.81 × 10−7 | 2.94 × 10−6 | 1.03 × 10−5 | −2.17 × 10−6 | 1.44 × 10−6 | −1.60 × 10−5 | −1.60 × 10−5 | 5.58 × 10−7 |
| E | 4.48 × 10−3 | 9.08 × 10−5 | −5.24 × 10−4 | 1.24 × 10−3 | 2.30 × 10−3 | 3.33 × 10−4 | 9.81 × 10−3 | 9.81 × 10−3 | −1.15 × 10−4 | |
| F | −4.58 × 10−1 | 1.22 | 2.07 × 10−1 | 1.12 × 10−1 | 9.27 × 10−1 | 1.43 × 10−1 | −7.86 × 10−1 | −7.86 × 10−1 | 9.61 × 10−2 | |
| Constant speed operation on curved line | G | 3.08 × 10−6 | 3.09 × 10−7 | 2.26 × 10−6 | 2.26 × 10−6 | 1.87 × 10−5 | 1.28 × 10−5 | 3.84 × 10−6 | 4.23 × 10−5 | 7.20 × 10−6 |
| E | 7.77 × 10−3 | 7.92 × 10−4 | 9.65 × 10−5 | 9.65 × 10−5 | −1.02 × 10−2 | −6.67 × 10−3 | −1.96 × 10−3 | −2.90 × 10−2 | −4.04 × 10−3 | |
| F | −1.10 | 9.87 × 10−1 | 8.41 × 10−2 | 8.41 × 10−2 | 2.74 | 1.18 | 9.62 × 10−1 | 6.29 | 6.93 × 10−1 | |
| Acceleration operation | G | 7.50 × 10−6 | 1.93 × 10−6 | −5.44 × 10−6 | 5.96 × 10−5 | 2.07 × 10−5 | 1.75 × 10−5 | 4.41 × 10−7 | 1.99 × 10−5 | 5.55 × 10−6 |
| E | 2.45 × 10−3 | −2.98 × 10−5 | 5.52 × 10−3 | −3.05 × 10−2 | −1.32 × 10−2 | −9.28 × 10−3 | 1.39 × 10−3 | −1.16 × 10−2 | −2.98 × 10−3 | |
| F | −3.63 × 10−1 | 1.17 | −7.32 × 10−1 | 4.50 | 3.34 | 1.48 | 5.41 × 10−2 | 3.00 | 5.21 × 10−1 | |
| Deceleration operation | G | 4.15 × 10−5 | 5.60 × 10−6 | 9.99 × 10−6 | 2.43 × 10−5 | 1.77 × 10−5 | 5.59 × 10−6 | −2.00 × 10−5 | −2.02 × 10−5 | 2.54 × 10−4 |
| E | −1.80 × 10−2 | −2.45 × 10−3 | −4.11 × 10−3 | −1.03 × 10−2 | −1.17 × 10−2 | −2.46 × 10−3 | 1.27 × 10−2 | 1.66 × 10−2 | −1.93 × 10−1 | |
| F | 2.22 | 1.45 | 5.48 × 10−1 | 1.72 | 3.24 | 5.57 × 10−1 | −1.18 | −1.44 | 3.68 × 10+1 | |
| Load Name | Fitting Parameters | Operation Conditions | |||
|---|---|---|---|---|---|
| Constant Speed Operation on Straight Line | Constant Speed Operation on Curved Line | Acceleration Operation | Deceleration Operation | ||
| Bouncing load | a | 2.493 | 3.017 | 2.258 | 2.509 |
| b | 1.380 | 1.406 | 1.552 | 1.478 | |
| c | 0.566 | 0.586 | 0.652 | 0.722 | |
| Roll load | a | 2.758 | 3.241 | 2.851 | 2.023 |
| b | 1.522 | 1.927 | 1.614 | 1.566 | |
| c | 0.585 | 0.783 | 0.847 | 0.582 | |
| Transverse load | a | 0.583 | 0.860 | 0.770 | 0.559 |
| b | 1.215 | 1.820 | 1.805 | 1.850 | |
| c | 0.157 | 0.284 | 0.305 | 0.320 | |
| Load name | Fitting Parameters | Operation Conditions | |||
|---|---|---|---|---|---|
| Constant Speed Operation on Straight Line | Constant Speed Operation on Curved Line | Acceleration Operation | Deceleration Operation | ||
| Bouncing load | G | 8.62 × 10−5 | 6.46 × 10−5 | −2.55 × 10−4 | 3.75 × 10−4 |
| E | −1.18 × 10−2 | 8.31 × 10−3 | 2.26 × 10−1 | −1.68 × 10−1 | |
| F | 5.75 | 1.72 | −3.03 × 10+1 | 2.28 × 10+1 | |
| Rolling load | G | 8.29 × 10−5 | 5.77 × 10−4 | 6.54 × 10−4 | 2.45 × 10−4 |
| E | −6.75 × 10−3 | −3.02 × 10−1 | −3.55 × 10−1 | −1.24 × 10−1 | |
| F | 6.50 | 4.96 × 10+1 | 5.59 × 10+1 | 2.53 × 10+1 | |
| Transverse load | G | 9.95 × 10−6 | −2.92 × 10−4 | 2.28 × 10−4 | −4.35 × 10−4 |
| E | 1.04 × 10−3 | 2.75 × 10−1 | −1.24 × 10−1 | 2.28 × 10−1 | |
| F | 2.34 | −5.55 × 10+1 | 2.07 × 10+1 | −1.28 × 10+1 | |
| Load Name | Operation Conditions | |||
|---|---|---|---|---|
| Constant Speed Operation on Straight Line | Constant Speed Operation on Curved Line | Acceleration Operation | Deceleration Operation | |
| Bouncing load | 17.9 | 18.6 | 19.9 | 23.1 |
| Roll load | 20.3 | 30.4 | 28.4 | 19.2 |
| Transverse load | 4.8 | 9.1 | 11.0 | 10.3 |
| Load Name | Fitting Parameters | Operation Conditions | |||
|---|---|---|---|---|---|
| Constant Speed Operation on Straight Line | Constant Speed Operation on Curved Line | Acceleration Operation | Deceleration Operation | ||
| Bouncing load | G | 2.08 × 10−1 | 5.62 × 10−2 | 9.47 × 10−1 | 1.41 × 10−1 |
| E | −1.65 × 10+2 | −4.46 × 10+1 | −5.15 × 10+2 | −6.67 × 10+1 | |
| F | 4.48 × 10+4 | 1.18 × 10+4 | 7.22 × 10+4 | 1.47 × 10+4 | |
| Rolling load | G | 1.42 × 10−1 | −7.93 × 10−2 | 4.82 × 10−1 | 5.52 × 10−3 |
| E | −1.15 × 10+2 | 5.41 × 10+1 | −2.08 × 10+2 | 3.18 × 10+1 | |
| F | 3.49 × 10+4 | −6.16 × 10+3 | 2.60 × 10+4 | −4.63 × 10+3 | |
| Transverse load | G | 8.44 × 10−2 | 1.55 × 10−3 | 2.19 × 10−1 | 1.38 × 10−1 |
| E | −6.92 × 10+1 | −1.67 | −9.22 × 10+1 | −6.58 × 10+1 | |
| F | 2.19 × 10+4 | 5.90 × 10+2 | 1.19 × 10+4 | 7.94 × 10+3 | |
| Load Name | Operation Conditions | |||
|---|---|---|---|---|
| Constant Speed Operation on Straight Line | Constant Speed Operation on Curved Line | Acceleration Operation | Deceleration Operation | |
| Bouncing load | 12,476 | 3145 | 32,172 | 13,243 |
| Roll load | 11,963 | 2130 | 29,911 | 10,794 |
| Transverse load | 7792 | 1771 | 14,770 | 5423 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tao, G.; Liu, Z.; Ji, C.; Yang, G. Establishment and Analysis of Load Spectrum for Bogie Frame of High-Speed Train at 400 km/h Speed Level. Machines 2024, 12, 382. https://doi.org/10.3390/machines12060382
Tao G, Liu Z, Ji C, Yang G. Establishment and Analysis of Load Spectrum for Bogie Frame of High-Speed Train at 400 km/h Speed Level. Machines. 2024; 12(6):382. https://doi.org/10.3390/machines12060382
Chicago/Turabian StyleTao, Guidong, Zhiming Liu, Chengxiang Ji, and Guangxue Yang. 2024. "Establishment and Analysis of Load Spectrum for Bogie Frame of High-Speed Train at 400 km/h Speed Level" Machines 12, no. 6: 382. https://doi.org/10.3390/machines12060382
APA StyleTao, G., Liu, Z., Ji, C., & Yang, G. (2024). Establishment and Analysis of Load Spectrum for Bogie Frame of High-Speed Train at 400 km/h Speed Level. Machines, 12(6), 382. https://doi.org/10.3390/machines12060382




