A Thorough Procedure to Design Surface-Mounted Permanent Magnet Synchronous Generators

Abstract

This paper sets forth a thorough procedure to design surface-mounted permanent magnet synchronous generators. Since synchronous generators generate the majority of electrical energy, their relevance in society nowadays is substantial. As a consequence, the methodology to design these electrical machines also holds great importance. However, even though a considerable amount of works addresses the matter, it is difficult to find a complete and thoroughly explained design procedure. The proposed method is based on analytical equations to fully consider PM generator fundamentals with a few simplifications, which implies in a considerable number of design equations and parameters. Differently from most papers on the design of PM synchronous generators, a significant level of detail and explanation is presented, all design choices are discussed, and the suggested ranges for the design parameters are shown. This results in a straightforward procedure that allows non-experienced designers to easily replicate the results and effectively enhance the comprehension of permanent magnet synchronous machines, and provides a guideline for researchers from other fields who may need to understand and perform a synchronous generator design. To show the effectiveness of the proposed design procedure, a PM generator is designed, and the results are compared with a finite element simulation, showing good accuracy.

1. Introduction

After the second industrial revolution, electricity became a big necessity for basically all industry sectors and, gradually, for all of society. Thus, energy generation also became a fundamental matter for countries all over the world due to the fact that energy consumption increases every year. Except for solar energy, all other significant primary energy sources, such as hydraulic, coal, nuclear, natural gas, wind, biomass, etc., need electric generators to convert the mechanical energy provided by the primary mover into electricity [1].

Synchronous generators are the most used electrical machines in electric energy production, regardless of the primary sources mentioned above [1,2,3,4,5,6]. There are two types of synchronous generators regarding field production: those with a wound rotor and those with permanent magnets. Wound-rotor synchronous generators (WRSGs) have field windings on the rotor, supplied with DC power by an excitation system, to create the main magnetic field. On the other hand, permanent magnet synchronous generators have permanent magnets (PMs) attached to the rotor surface or buried in the rotor, creating the rotor magnetic field [2].

Given their substantial importance in society nowadays, the design of synchronous generators has also gained considerable attention. Extensive knowledge of electrical machine design can be found with ease in several bibliography materials [2,3,4,5,6]. Furthermore, an expressive number of papers also address synchronous machine design [1,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24]. Even though most of these works are about permanent magnet synchronous generators, only a few have a detailed design methodology and present all the design equations and parameters. Essential details of the design are not discussed. The focus is on specific parts of the design [7,8,9,10,11,12], determining the machine’s outer dimensions [13,14], presenting the highlights of the designed machine and its results [15,16,17,18], or exploring a new machine topology [19,20,21,22]. There are also those focused on synchronous machine design optimization [25,26,27,28,29,30], where the focus is mainly on finding a machine with improved performance, efficiency, or cost. Thus, the design equations are not presented, and the design procedure is only mentioned as one of the optimization models, with very little information about it.

In [1], a step-by-step design procedure for synchronous generators is developed, but it focuses on salient-pole WRSGs. The authors of [23] present a detailed design procedure and design equations for permanent magnet synchronous generators with surface PMs for direct-driven wind turbines. This type of generator has a non-salient pole construction that allows the armature reaction components to be calculated analytically, and thus, the machine terminal voltage can be found more effortlessly. However, the authors do not show how to perform adjustments during the design process to meet the calculated terminal voltage to the specified value with the designed generator. Furthermore, the design procedure starts with stator sizing rather than the rotor, in which the stator slots are dimensioned to fit a calculated conductor surface. This can lead to long and thin stator teeth, causing saturation problems and leading to excessive losses and vibration, especially with inexperienced designers.

The authors of [24] present the design of a synchronous generator with a PM buried within the rotor, which is a salient-pole geometry that is more complex to model and design than surface PM machines. However, the authors do not show design procedure specifics concerning the PM and the design choices, which makes it challenging for others to replicate. Moreover, being a salient-pole machine, the method to obtain the direct and quadrature axis reactances used to calculate the generator’s terminal voltage is not addressed.

Thus, this paper intends to reduce the literature gap regarding PM synchronous generator design, presenting a thorough design procedure. Throughout this manuscript, all the design stages, along with their equations and parameters, are explained. Even though the procedure is composed of a considerable number of equations, it is not an overly complex method, and it fully considers PM generator fundamentals, with a few simplifications. Differently from [23], the proposed design method sizes the armature conductors based on the slot dimensions, which are imposed by the designer. This allows for a feasible generator since a reasonable range of each imposed parameter is provided. Furthermore, a significant amount of information concerning imposed values and procedure specifics is presented, as well as how necessary adjustments in output power, terminal voltage, etc., can be made in the proposed design method.

The proposed method is not intended to reach a competitive design or to be optimized in terms of efficiency, power density, or cost but rather to present a framework for others to incorporate into their research or build upon for further development. Being a simplified procedure that accounts for the permanent magnet generator’s main fundamentals, it is easy to replicated and, thus, it can be used in a variety of applications:

• Beginners in designing PM synchronous generators can use it to replicate the results and gain experience;
• Experienced designers can easily improve it by eliminating the simplifications, incorporating complexity and new physics, and finding an optimal design according to their objectives;
• Fellow researchers from other fields, such as power electronics, control, or optimization, can use it to quickly find the parameters of the generator for their studies.

This paper has been structured in sections; Section 1 is the introduction and literature review. Section 2 presents the proposed design method, including a description of the PM generator geometry, the design procedure, and the analytical design equations. The imposed design parameters and their suggested ranges are also included in this section. The designed PM generator results and the finite element simulations of this generator under no-load and full-load conditions are presented in Section 3. Finally, the conclusions are drawn in Section 4.

2. Materials and Methods

This section concentrates the information about the proposed design methodology. Firstly, Section 2.1 describes the surface-mounted permanent magnet generator geometry in detail, presenting all of its dimensions. Secondly, Section 2.2 explains the stages of the design method and how this iterative process works. Then, in Section 2.3, every step of the design is described, i.e., all the design equations are presented and explained. Lastly, Section 2.4 explains the imposed parameters used during the design process and their suggested ranges so readers can easily replicate or adapt the presented method.

2.1. Permanent Magnet Generator Geometry

The proposed procedure was developed for surface-mounted permanent magnet generators, which can be seen in Figure 1. Even though the methodology was developed for this very conventional rotor topology in the literature [4,5,6], it can also be adapted to other PM machines. For example, Equation (6) and the rest of the rotor sizing would be slightly different for a straight PM rotor. Changes in the rotor geometry may require a new phasor diagram for the generator, similar to the one for WRSGs from [1].

The main geometric parameters of the surface-mounted PM generator depicted in Figure 1 are organized as follows: Figure 1a shows the diameters and air gap length; Figure 1b shows the full and effective pole pitches, the slot pitch, the slot angle at the top, and the stator yoke height; the rotor dimensions are shown in Figure 1c; and the stator topology is shown in Figure 1d.

This type of construction, with surface-mounted magnets, has less mechanical robustness since, with the magnets attached to the rotor surface, they are exposed to centrifugal forces, which worsen at high speeds [31,32]. To address this issue, a non-magnetic sleeve to retain the PMs on the rotor surface can be used. The sizing of the sleeve is not included in the presented procedure, but criteria for its use and sizing can be found in [33,34,35,36,37].

2.2. Design Procedure

Before initiating the design, a few basic characteristics must be defined, such as the machine type (asynchronous, synchronous, etc.) and type of construction (external rotor, internal rotor, axial flux, radial flux). Thereafter, the first step of the design consists of defining the specifications of the generator, such as the apparent power, desired power factor, rated angular speed, rated frequency, rated terminal voltage, and number of phases [3]. Using this information, it is possible to obtain the physical dimensions of the electrical machine, define the material properties winding characteristics, and draw up manufacturing instructions.

Even though the specifications can be the same for different types of machines, a single design procedure does not apply to all types of machines. Therefore, adaptations to well-established methodologies to better adapt to the particular needs of the designer become relevant [4]. Thus, the proposed design methodology for surface-mounted permanent magnet synchronous generators (PMSGs) is based on the design procedure developed in [1] for salient pole wound-rotor synchronous generators. The rotor sizing part of the design was entirely developed in this paper, whereas the stator sizing is very similar to the mentioned reference.

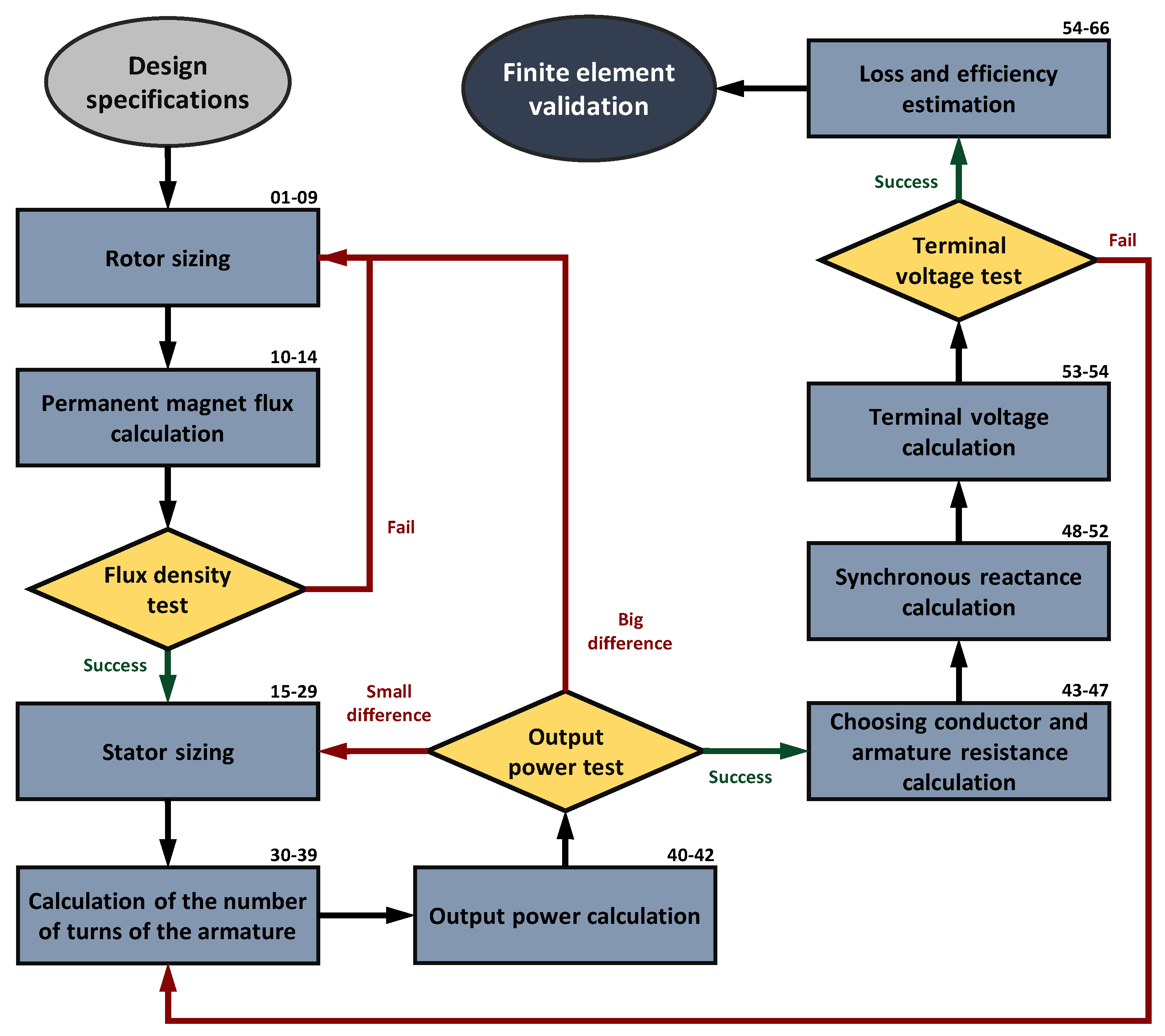
The proposed design methodology is composed of 66 analytical equations, and the general flowchart is shown in Figure 2. From the specifications, the majority of the generator dimensions, presented in Section 2.1, are calculated with analytical equations, and the remaining dimensions are found using parameters imposed by the designer. The proposed method is an iterative design procedure that allows for adjustments of dimensions and parameters so that the calculated values match the design specifications in a very straightforward manner. The iterations within the procedure happen with the flux density, output power, and terminal voltage tests. Furthermore, the rectangular blocks in the flowchart of Figure 2 represent the design stages of the procedure, and each one has a subsection dedicated to explaining its steps. Every stage is composed of a set of equations (steps), and the numbers can be seen in the right corner of the corresponding stage in Figure 2.

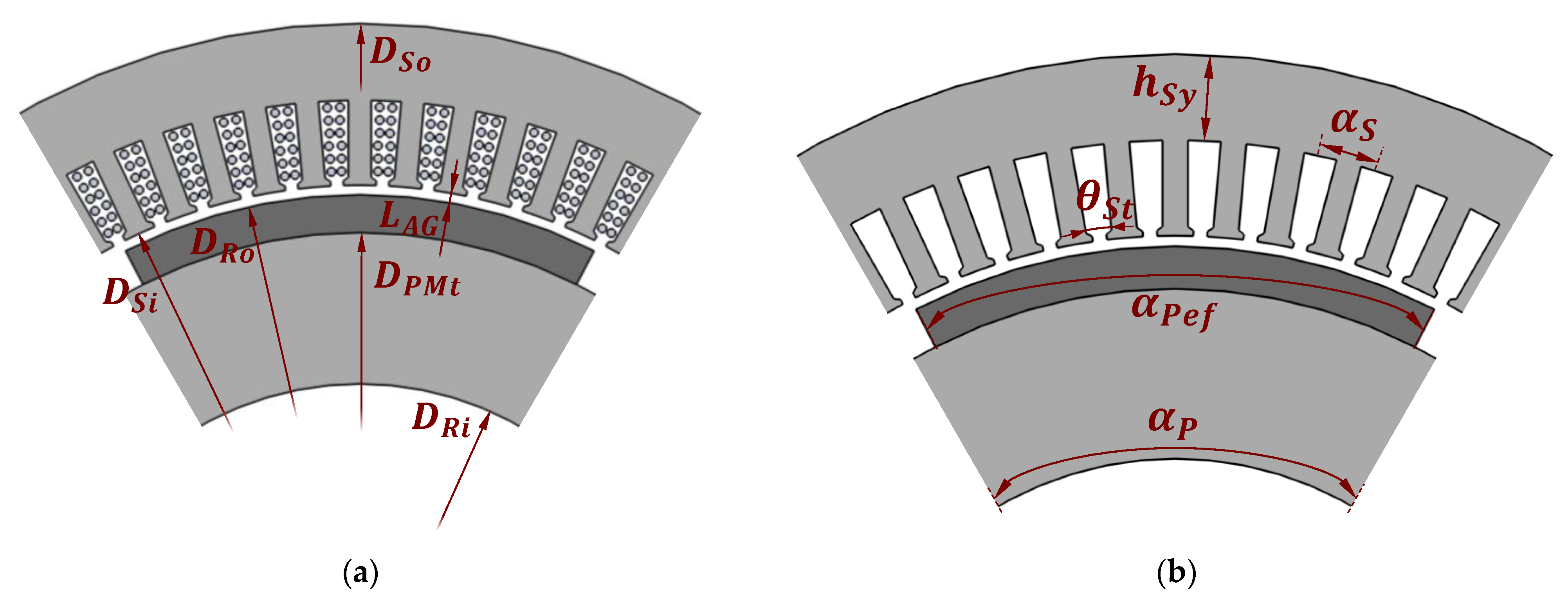
As shown in Figure 2, the proposed design procedure begins with the specifications, followed by sizing the rotor and stator to find all their dimensions. In the rotor sizing (Section 2.3.1), the first steps depend on defining the rotor external diameter. This design methodology considers it an input parameter known by the designer, either from a previous calculation (which can be found in [3,4,11,19]) or by experience. The remaining rotor dimensions, such as the PM dimensions and the rotor internal diameter, are found using a few imposed parameters and with the desired magnetic flux density in the rotor core, respectively.

Knowing all PM dimensions, and after defining the PM type, operative temperature, and permeance coefficient, the design proceeds to PM flux calculation (Section 2.3.2), as Figure 2 shows. Thus, with the air gap length and the generator axial length, the flux in the air gap is calculated and used to find the air gap flux density. If this flux density is not within the desired range, the PM permeance coefficient can be increased or decreased to have more or less magnetic flux density in the air gap, respectively. Another solution would be changing the PM grade, which is a specification that indicates its energy. However, higher grades also mean higher PM costs [5].

According to Figure 2, with an acceptable air gap flux density, the design proceeds to stator sizing (Section 2.3.3), where a few imposed parameters are used once more and the stator teeth and slot dimensions are found. Then, the armature windings are defined (Section 2.3.4), with the armature conductor surface being the final obtained parameter. Based on the previously calculated flux of the air gap, the number of turns per coil of the armature winding is found using an imposed no-load voltage value. With the slot surface and the number of turns, the armature conductor surface can be found. Considering the previously set maximum conductor current density, the conductor surface is then used to obtain the armature current.

As shown in Figure 2, the next step is the output power calculation. By using the desired terminal voltage value and the armature current from the previous step, the admissible output power can be calculated (Section 2.3.5). Even though the specified terminal voltage value is used, this is not an inconsistency of the proposed design methodology since the procedure is only completed after matching the calculated terminal voltage value with the specifications (explained further in this subsection). Calculating the admissible output power at this early stage of the procedure allows the designer to assess whether the machine’s latest size and dimensions correspond to a solution not too far from the desired output power.

If this value does not correspond to the apparent power from the specifications, a few parameters can be adjusted, either from the rotor or from the stator design, as depicted in Figure 2. Since the terminal voltage is a design specification (meaning its value is fixed), output power adjustments must be made that target the armature current by changing the conductor cross-section, either by changing the slot dimensions or by reducing the number of turns of the windings. Since in this design methodology the stator sizing defines an armature conductor that can be fitted in the slots, for minor differences, this can be done by adjusting the machine’s stack length or the slot geometry.

For example, increasing the generator length would result in more flux linked by the armature coils; thus, fewer turns are required to match the terminal voltage, and consequently, a bigger conductor cross-section may be used. Ultimately, this results in a bigger value of admissible current while maintaining both the same slot area and the specified current density. On the other hand, increasing the slot area directly allows for a bigger conductor surface when maintaining the number of turns in the armature coils. Thus, more armature current is admissible while keeping the same current density. Evidently, this logic can be applied when adjustments must be made to decrease the admissible output power of the generator.

If the admissible power is too far from the specified value, more significant changes are necessary. In this case, parameters in the rotor sizing should be adjusted since the current PM volume does not produce the flux that, when linked by the armature coils, corresponds to the desired output power. Either the PM flux is less than what is needed and more turns are required, which reduces the conductor surface, or too much flux is produced and fewer turns are needed to match the imposed voltage value, which allows for a bigger conductor. In this case, the rotor outer diameter or the effective pole pitch can be adjusted. The latter must be more carefully altered since it greatly impacts flux leakage. It is not recommended to alter the armature current density since this value is usually chosen to guarantee operation under maximum temperature or is determined by a thermal model.

The proposed method has a noteworthy difference from other design methodologies concerning the output power calculation and the iterative process discussed previously. As seen in Figure 2 and explained earlier in this subsection, the proposed design comes from rotor sizing to stator sizing, where the slot area is defined; then, with the number of turns of the armature coils, the conductor cross-section that can be fitted within the slots is calculated, the armature current is found and, consequently, the admissible output power is found. In other design methodologies ([9,23,24], for example), this part is inverted, where, with the specified output power and terminal voltage, the armature current is calculated, which is then used to find the conductor cross-section after defining the armature current density. Thus, the slot dimensions are found so that the slot area can accommodate the previously found conductor. With this approach, the design is susceptible to resulting in a too-large stator compared to the rotor and would only be noticed by the designer when the generator is drawn. On the other hand, with the proposed approach, the designer deals directly with the dimensions and quickly assesses their relation to the output power. Furthermore, performing the iterative process of the output power test, the relation between the generator rotor and stator dimensions becomes clearer and clearer.

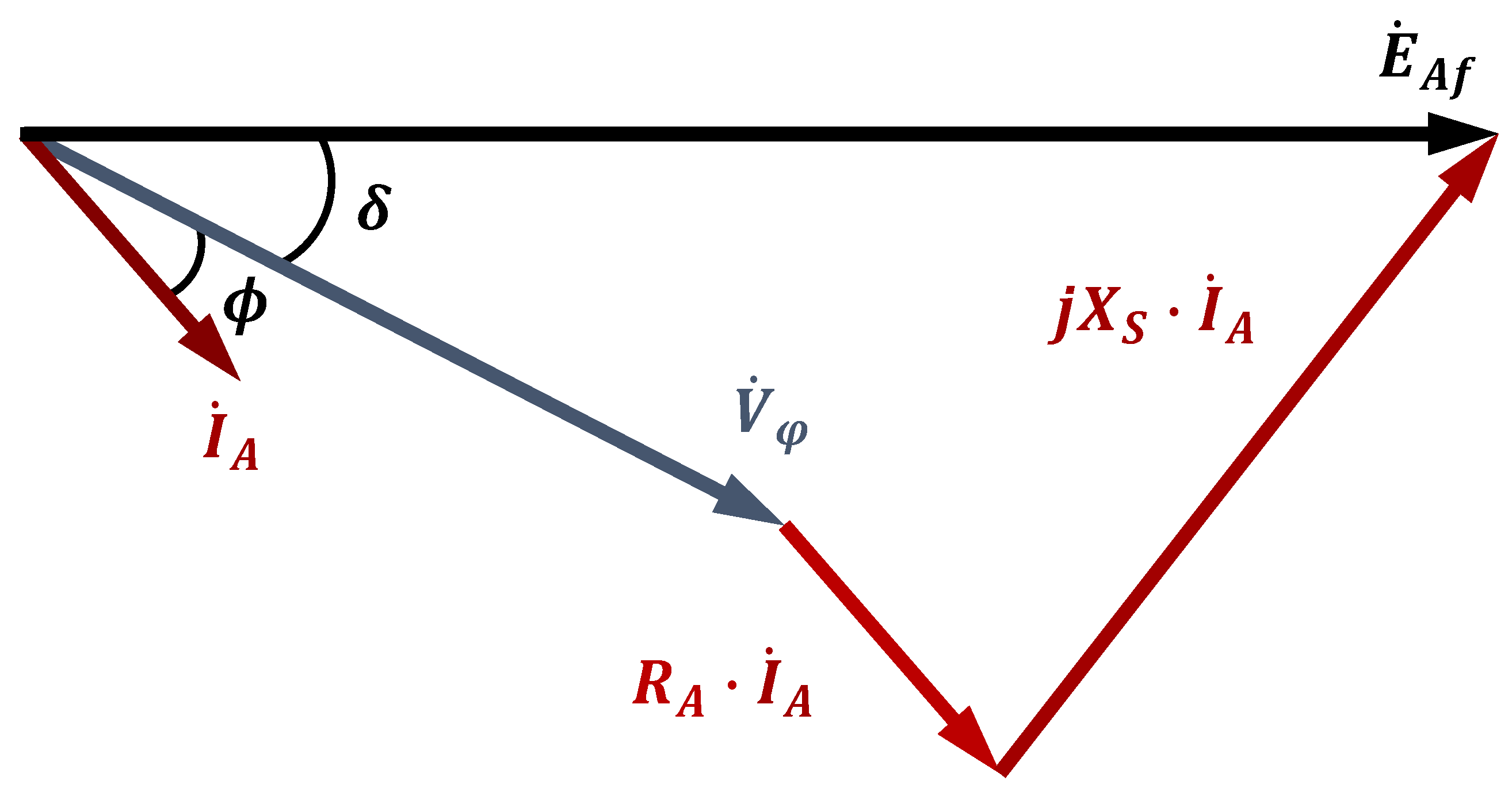
At the end of the output power design stage, all generator dimensions are known, and then the loading effects have to be considered before proceeding with the design method, as Figure 2 shows. Firstly, a combination of copper conductors (or a single one) is chosen to match the calculated armature conductor surface. From its specifications, the armature resistance is found (Section 2.3.6). During load operation, the armature current creates a magnetic field that interacts with the rotor magnetic field, resulting in distorted net flux density with a decreased or an increased value, depending on the load. This corresponds to a smaller or bigger terminal voltage (with inductive and capacitive loads, respectively). This armature reaction field can be electrically represented by a reactance, so obtaining this value is an essential design step. For non-salient pole PM machines, the reluctance of the air gap is constant, regardless of the position of the rotor, as the magnetic permeability of the magnets is very close to that of air. Thus, the armature reaction reactance does not assume different values depending on the rotor position and can be analytically calculated since the rotor geometry is less complex than in other types of PM machines.

In addition to the armature reaction reactance, the armature coils also have a leakage inductance, which becomes leakage reactance when multiplied by the synchronous speed of the machine. Adding these two reactance values results in the synchronous reactance of the generator (Section 2.3.7). After calculating the voltage drops in the armature resistance and the synchronous reactance, the terminal voltage is estimated (Section 2.3.8) and should be compared with the desired voltage value from the specifications. As shown in Figure 2, in the case of a difference, the designer should adjust the imposed voltage used in the design step that calculates the number of turns of the armature coils per phase. A new value would result in more or fewer turns for the same rotor dimensions and air gap flux. Since the design is taken back to the armature definitions, the output power assumes a new value in the next stage, and naturally, adjustments should be performed. How to perform these adjustments was discussed earlier, where minor differences require less effort from the designer, and a big difference may take a few more iterations and eventually take the design back to stator or rotor sizing.

When the terminal voltage matches its desired value, the next stage consists of a loss estimation (Section 2.3.9) to further compute the generator efficiency, as Figure 2 shows. The proposed design procedure considers copper losses in armature windings, iron losses in the stator core, and permanent magnet losses. Finally, after calculating the efficiency, the surface-mounted permanent magnet generator design is completed. If the designer is satisfied with the designed generator, then a finite element simulation should be carried out. This way, a thorough analysis can be realized, and the designed machine can be eventually verified.

2.3. Design Stages and Equations

This section describes in detail all the steps of the design procedure, where each subsection corresponds to a design stage depicted in Figure 2, resulting in a total of 66 steps.

2.3.1. Rotor Sizing

From the specified operative electrical frequency $f$ (Hz) and rotational speed $\omega$ (rad/s), the first step of the rotor sizing can be executed, which is the calculation of the number of poles of the machine $P$:

$$P=\frac{120·f}{\omega }.$$

(1)

The number of poles determines the pole pitch ${\alpha }_P$ ($°$), which is the angle available for each pole:

$${\alpha }_P=\frac{2·\pi }{P}.$$

(2)

The pole pitch factor ($k_{\alpha P}$) is used to define the angle occupied by the permanent magnet, called the effective pole pitch ${\alpha }_{Pef}$ ($°$):

$${\alpha }_{Pef}={\alpha }_P·k_{\alpha P}.$$

(3)

The generator air gap length $L_{AG}$ (mm) is an extremely important parameter, usually imposed by the designer. In the proposed procedure, it is determined using the rotor outer diameter $D_{Ro}$ (mm) and the air gap factor ($k_{AG}$):

$$L_{AG}=D_{Ro}·k_{AG}.$$

(4)

By imposing a permeance coefficient ($PC$) value, the permanent magnet height $h_{PM}$ (mm) can be found with:

$$h_{PM}=PC·L_{AG}.$$

(5)

In the arc-shaped PM rotor in Figure 1, the outer surface is wider than the inner surface attached to the rotor yoke. Thus, to calculate the permanent magnet’s width, the arc length at its center is used:

$$W_{PM}=\left(\frac{D_{Ro}}{2}-\frac{h_{PM}}{2}\right)·{\alpha }_{Pef}.$$

(6)

The rotor yoke height $H_{Ry}$ (mm) is found using the PM operative flux density $B_{PM}$ (T) and after setting the desired magnetic flux density in the rotor yoke $B_{Ry}$ (T) at no load:

$$h_{Ry}=\frac{B_{PM}}{B_{Ry}}·\frac{W_{PM}}{2}.$$

(7)

As one of the last dimensions in rotor sizing, the diameter at the permanent magnet top $D_{PMt}$ (mm) is calculated:

$$D_{PMt}=D_{Ro}-2·h_{PM}.$$

(8)

With the last dimension, the rotor inner diameter $D_{Ri}$ (mm) is found:

$$D_{Ri}=D_{PMt}-2·h_{Ry}.$$

(9)

2.3.2. Permanent Magnet Flux Calculation

Once the permanent magnet type (component material and its temperature ratings), its grade, and the desired permeance coefficient have been chosen, the operative permanent magnet flux density $B_{PM}$ (T) can be determined. Thus, the permanent magnet flux ${\phi }_{PM}$ (Wb) is calculated with:

$${\phi }_{PM}=B_{PM}·W_{PM}·L_G,$$

(10)

where $L_G$ (mm) is the generator stack length, which is an imposed parameter by the designer. In this design methodology, it is found by determining the machine shape factor $k_{MS}$:

$$L_G=D_{Ro}·k_{MS}.$$

(11)

The air gap flux ${\phi }_{AG}$ (Wb) can then be calculated with:

$${\phi }_{AG}={\phi }_{PM}·{∆\phi }_{PMAG},$$

(12)

where ${∆\phi }_{PMAG}$ is the permanent magnet to air gap leakage flux factor. To assess whether the designed PM corresponds to the desired air gap magnetic flux density, the length of the arc at the middle of the air gap $L_{AGa}$ (mm) must be found:

$$L_{AGa}=\left(\frac{{D_{Ro}+L}_{AG}}{2}\right)·{\alpha }_P·k_{\alpha P}.$$

(13)

Finally, the air gap magnetic flux density $B_{AG}$ (T) is calculated with:

$$B_{AG}=\frac{W_{PM}}{L_{AGa}}·B_{PM}·{∆\phi }_{PMAG}.$$

(14)

This last equation is part of the flux density test in Figure 2, detailed in Section 2.2.

2.3.3. Stator Sizing

With the rotor sizing completed and the air gap flux determined, the stator sizing begins with the stator inner diameter $D_{Si}$ (mm):

$$D_{Si}=D_{Ro}+2·L_{AG}.$$

(15)

Then, the slot opening and tooth tips must be defined. Firstly, using the slot opening factor $k_{Sow}$ and the number of slots of the stator $N_S$, the slot opening width $W_{So}$ (mm) is found:

$$W_{So}=\frac{D_{Ro}}{N_S}·k_{Sow}.$$

(16)

Then, the heights of the slot opening $h_{So}$ (mm) and wedge $h_{Sw}$ are related to $W_{So}$, with the slot opening height factor $k_{Soh}$ and the wedge height factor $k_{Sw}$:

$$h_{So}=W_{So}·k_{Soh},$$

(17)

$$h_{Sw}=W_{So}·k_{Sw}.$$

(18)

With these two height values, the diameter at the top of the slot can be calculated:

$$D_{St}=D_{Si}+2·\left(h_{So}+h_{Sw}\right).$$

(19)

To continue the stator sizing, the slot pitch ${\alpha }_S$ ($°$) must be determined:

$${\alpha }_S=\frac{2·\pi }{N_S}.$$

(20)

Since the slot pitch corresponds to one slot and one stator tooth, the proportion between them can be determined with the tooth-to-slot-width factor $k_{TS}$:

$${\theta }_{St}=\frac{{\alpha }_S}{1+k_{TS}}.$$

(21)

With the angle of the slot on the top ${\theta }_{St}$ ($°$), the widths of the slot on the top $W_{St}$ (mm) and of the tooth $W_t$ (mm) are calculated:

$$W_{St}=D_{St}·\tan {\displaystyle \frac{{\theta }_{St}}{2}}$$

(22)

$$W_t=D_{St}·\mathit{tan}{\displaystyle \frac{{\alpha }_S-{\theta }_{St}}{2}}$$

(23)

With slot width at the top, the slot wedge width $W_{Sw}$ (mm) can be found:

$$W_{Sw}=\frac{W_{St}-W_{So}}{2}.$$

(24)

The next stator dimension to be determined is the height of the stator yoke $h_{Sy}$ (mm), found after choosing a value for the permanent-magnet-width-to-stator-yoke factor $k_{PMSy}$:

$$h_{Sy}=W_{PM}·k_{PMSy}.$$

(25)

Another factor is used to ensure a proper proportionality between the stator yoke height and the slot height, called the stator-yoke-to-slot-height factor $k_{SyS}$:

$$h_S=h_{Sy}·k_{SyS}.$$

(26)

In low-voltage machines, the stator teeth usually have the same width at the top and bottom. This means that a constant flux density is maintained throughout their length (neglecting flux leakage crossing the slots), and the slots increase in width along their height. Thus, to keep the teeth parallel, the inclination angle of the slot edge ${\theta }_{Sei}$ ($°$) must be:

$${\theta }_{Sei}=\frac{{\alpha }_S}{2}.$$

(27)

The last slot dimension to be found is the bottom width $W_{Sb}$ (mm):

$$W_{Sb}=W_{St}+2·h_S·\tan {\theta }_{Sei}.$$

(28)

To complete the stator sizing, the stator outer diameter $D_{So}$ (mm) is calculated with:

$$D_{So}=D_{St}+2·\left(h_S+h_{Sy}\right).$$

(29)

2.3.4. Armature Winding Definitions

In this design stage, all the characteristics of the armature windings are defined and calculated. The armature windings are coils with a certain number of turns inserted in the stator slots. With the slot pitch and pole pitch, it is possible to determine how many slots correspond to one pole pitch and which slot a phase coil enters or exits. This distance is the armature coil pitch ${\alpha }_{Ac}$ ($rad$), found after defining a value for the armature coil-shortening factor $k_{Ac}$:

$${\alpha }_{Ac}={\alpha }_P·k_{Ac}·\frac{P}{2}.$$

(30)

By multiplying it by the number of pole pairs, this angle goes from mechanical to electrical radians.

As the coil is shortened, the flux linked by the armature coil is decreased [3]. The reduction factor due to coil shortening ${∆\phi }_{Cs}$ is:

$${∆\phi }_{Cs}=\sin \frac{{\alpha }_{Ac}}{2}.$$

(31)

After defining the number of slots $N_S$ and the number of phases of the generator $N_{ph}$, the number of slots per pole per phase $q$ is found:

$$q=\frac{N_S}{N_{ph}·P}.$$

(32)

The fact that the armature coils are spatially distributed within the stator slots means that the sum of the voltages generated in each coil is not the same as if there were only one coil (concentrated winding) since the voltage of each coil has a lag in relation to the others. Therefore, a reduction factor due to winding distribution ${∆\phi }_{Wd}$ must be considered in this step of the design:

$${∆\phi }_{Wd}=\frac{\sin \left(q·\frac{{\alpha }_{Ac}}{2}·\frac{P}{2}\right)}{q·\sin \left(\frac{{\alpha }_{Ac}}{2}·\frac{P}{2}\right)}.$$

(33)

With these coil factors, the next step would be to calculate the number of turns in the armature winding per phase $T_A$. In the proposed design methodology, to find this winding parameter, the designer must impose a voltage value $E_{Af}$ (V):

$$T_A=\frac{E_{Af}}{\sqrt{2}·\pi ·f·{∆\phi }_{Cs}·{∆\phi }_{Wd}·{\phi }_{AG}·{∆\phi }_{AGA}}.$$

(34)

A thorough discussion on how this voltage value should be determined can be seen in Section 2.4.4. The air-gap-to-armature factor ${∆\phi }_{AGA}$ is a flux-leakage factor used to adjust the number of turns. By choosing a number of parallel paths of armature windings $N_{Cp}$ and the consequent pole factor $K_{Cop}$, the number of coils in series per phase $N_{Cs}$ is found:

$$N_{Cs}=\frac{P}{N_{Cp}·k_{Cop}}.$$

(35)

Then, by defining the number of slot layers $N_{Sl}$, the number of coils per pole per phase $N_{Cpp}$ is found:

$$N_{Cpp}=q·\frac{k_{Cop}·N_{Sl}}{2}.$$

(36)

Finally, the number of turns of the armature winding per coil $T_{Ac}$ can be calculated with:

$$T_{Ac}=\frac{T_A}{N_{Cpp}·N_{Cs}}.$$

(37)

To complete the armature definition, the conductor surface $S_{Ac}$ (mm²) should be found. Firstly, since the stator slot is trapezoidal, its surface $S_S$ (mm²) is:

$$S_S=\frac{\left(W_{Sb}+W_{St}\right)}{2}·h_S.$$

(38)

The conductor surface is calculated after considering the slot fill factor $k_{Sf}$:

$$S_{Ac}=\frac{S_S·k_{Sf}}{T_{Ac}·N_{Sl}}.$$

(39)

2.3.5. Output Power Calculation

By defining the armature current density $J_A$ (A/mm²) and with the area of the armature conductor, the allowable armature current $I_A$ (A) can be found:

$$I_A=S_{Ac}·J_A.$$

(40)

With the desired terminal voltage value $V_{Td}$ (V) from the specifications, the apparent output power of the generator $S_E$ (VA) is:

$$S_E=\sqrt{3}·V_{Td}·I_A.$$

(41)

With this equation, the output power test of the procedure depicted in Figure 2 is performed. The iterative process involving this test is detailed in Section 2.2. Lastly, with the specified power factor $PF$, the output active power $P_E$ (W) is found with:

$$P_E=S_E·PF.$$

(42)

2.3.6. Armature Resistance Calculation

To find the armature winding resistance, it is necessary to know the total length first. The distance between the entering slot and the exiting slot of a turn of the coil is an arc, so the arc length between two slots $L_C$ (mm) of the same coil is:

$$L_C=\left(D_{St}+h_S\right)·\frac{{\alpha }_{Ac}}{P}.$$

(43)

Similarly to in Equation (30), the number of poles is used to convert the armature coil pitch back to mechanical radians.

Assuming that the coil end has the shape of a half-circle, $L_C$ is its diameter and, thus, the coil length end $L_{Ce}$ (mm) is:

$$L_{Ce}=\pi ·\frac{L_C}{2}.$$

(44)

Naturally, the total length of the armature coils $L_{At}$ (mm) is:

$$L_{At}=2·L_{Ce}+2·L_G.$$

(45)

The total length of the armature coils is necessary because copper conductors’ resistance depends on their length. Thus, the armature resistance $R_{Aref}$ (Ω) at the reference temperature can be obtained with:

$$R_{Aref}=R_{km}·L_{At}·T_A,$$

(46)

after defining the resistance per kilometer of the selected conductor $R_{km}$ (Ω/km), specified by its manufacturer. Considering that, due to Joule effect, the conductor’s temperature will be increased, the resistance value should be corrected [4]:

$$R_A=R_{Aref}·\frac{243.5 °\mathrm{C}+T_{op}}{243.5 °\mathrm{C}+T_{ref}},$$

(47)

where $T_{op}$ (°C) is the operating temperature and $T_{ref}$ (°C) is the reference temperature from the manufacturer. The value of $243.5 °\mathrm{C}$ is the ratio of the copper resistance at 20 °C, which is usually the reference temperature at which the manufacturer measured the wire resistance.

2.3.7. Synchronous Reactance Calculation

Non-salient pole PM generators have a much simpler rotor geometry; thus, the armature reaction can be easily calculated with analytical equations. The synchronous inductance $L_S$ (H) of surface PM generators is composed by the air gap inductance $L_{ag}$ (H), the air gap mutual inductance $M_{ag}$ (H), and the slot-leakage inductance $L_{sl}$ (H) [4]. The armature winding coil end inductance is not considered in the proposed method since the verification finite element simulations are in 2D. Thus, it does not account for this end inductance, and providing the calculated value to the simulation model would not alter the results.

The air gap inductance ($L_{ag}$) can be obtained with:

$$L_{ag}=\frac{{\mu }_0·\pi ·{T_A}^2·L_G·D_{Si}}{4·{\left(\frac{P}{2}\right)}^2·\left(L_{AG}+h_{PM}\right)},$$

(48)

in which ${\mu }_0$ is the vacuum magnetic permeability. From [4], the air gap mutual inductance ($M_{ag}$) can be calculated with:

$$M_{ag}=-\frac{L_{ag}}{3} .$$

(49)

Lastly, according to [3], the slot-leakage inductance ($L_{sl}$) can be found with:

$$L_{Sl}=4·\frac{N_{ph}}{N_S}·{\mu }_0·L_G·{T_A}^2·\left(\frac{h_S}{3·W_{St}}+\frac{h_{So}}{W_{So}}+\frac{h_{Sw}}{W_{St}-W_{So}}·\ln \left(\frac{W_{St}}{W_{So}}\right)\right).$$

(50)

With all its components, the generator’s synchronous inductance can be found:

$$L_S=L_{ag}+L_{Sl}-M_{ag}.$$

(51)

Finally, the synchronous reactance for the non-salient pole PM generator $X_S$ (Ω) is calculated with:

$$X_S=2·\pi ·f·L_S.$$

(52)

2.3.8. Terminal Voltage Calculation

The generator phasor diagram is presented in Figure 3. The analysis developed with this diagram that results in the following equations does not consider either the harmonic content or transients, only the fundamental component at steady state.

In the phasor diagram of Figure 3, $\varphi$ ($°$) is the displacement angle between the terminal voltage and the armature current, and δ ($°$) is the load angle. To find the phase value of the terminal voltage $V_{\phi }$ (V), the phasor diagram clarifies that the voltage drops in the armature resistance and the synchronous reactances must be known. To that end, both the amplitude value of the armature and its phase must be known. The first is found with Equation (40), and the latter is the sum of $\varphi$ and δ. The displacement angle between the terminal voltage and the armature current is essentially a design specification, equal to the arc cosine of the machine power factor ($PF$). Thus, the last parameter needed is the load angle value:

$$\delta ={\sin }^{-1}\frac{I_A·X_S·\cos \varphi -I_A·R_A·\sin \varphi }{E_{Af}}.$$

(53)

Then, knowing all the presented parameter values, the phase value of the terminal voltage is:

$${\dot{V}}_{\phi }={\dot{E}}_{Af}-{\dot{I}}_A·\left(R_A+j{X}_S\right).$$

(54)

This last equation is used to perform the terminal voltage test shown in Figure 2, and the related iterative process is explained in Section 2.2.

2.3.9. Losses and Efficiency Estimation

A simplified loss estimation is determined by calculating the losses on the armature windings, on the stator core, and in the permanent magnets. The copper loss $P_{Ac}$ (W), due to the Joule effect in the armature windings, is the simplest to find:

$$P_{Ac}=3·R_A·{I_A}^2.$$

(55)

In the proposed methodology, the iron loss estimation is derived from [38]. As a first step, the volumes of the stator yoke $V_{Sy}$ (mm³) and the stator teeth $V_{St}$ (mm³) are found:

$$V_{Sy}=\frac{\pi }{4}·L_G·\left[{D_{So}}^2-{\left(D_{So}-2·h_{Sy}\right)}^2\right],$$

(56)

$$V_{St}=N_S·L_G·\left[W_t·h_S+\left(W_t+W_{Sw}\right)·h_{Sw}+\left(W_t+W_{Sw}\right)·h_{So}\right].$$

(57)

Next, the stator yoke and the teeth magnetic flux densities have to be known:

$$B_{Sy}=B_{PM}·{\displaystyle \frac{\raisebox{1ex}{$W_{PM}$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}{h_{Sy}}}·{∆\phi }_{AGA}·{∆\phi }_{PMAG}$$

(58)

$$B_{St}=B_{PM}·{\displaystyle \frac{W_{PM}}{\raisebox{1ex}{$N_S$}\!\left/ \!\raisebox{-1ex}{$P$}\right.·W_t}}$$

(59)

Using the losses per kilogram due to Foucault $P_F$ (W/kg), hysteresis $P_h$ (W/kg), and the mass density ${\rho }_{ee}$ (g/cm³), the iron losses on the stator yoke can be calculated. The hysteresis $P_{Syh}$ (W) and Foucault $P_{SyF}$ (W) losses on the stator yoke are:

$$P_{Syh}=k_{Syh}·V_{Sy}·{\rho }_{ee}·P_h·\frac{f}{50 \mathrm{H}\mathrm{z}}·{\left(\frac{B_{Sy}}{1.5T}\right)}^2,$$

(60)

$$P_{SyF}=k_{SyF}·V_{Sy}·{\rho }_{ee}·P_F·{\left(\frac{f}{50 \mathrm{H}\mathrm{z}}\right)}^2·{\left(\frac{B_{Sy}}{1.5T}\right)}^2.$$

(61)

Similarly, the stator teeth hysteresis $P_{Sth}$ (W) and Foucault losses $P_{StF}$ (W) can be calculated with:

$$P_{Sth}=k_{Sth}·V_{St}·{\rho }_{ee}·P_h·\frac{f}{50 \mathrm{H}\mathrm{z}}·{\left(\frac{B_{St}}{1.5T}\right)}^2,$$

(62)

$$P_{StF}=k_{StF}·V_{St}·{\rho }_{ee}·P_F·{\left(\frac{f}{50 \mathrm{H}\mathrm{z}}\right)}^2·{\left(\frac{B_{St}}{1.5T}\right)}^2.$$

(63)

Last, the permanent magnet losses $P_{PMs}$ (W) of the generator can be calculated:

$$P_{PM}=P·k_{PM}·W_{PM}·L_G,$$

(64)

where $k_{PM}$ (W/m²) is the PM specific loss. Ultimately, the total loss $P_T$ (W) should still consider stray losses; thus, the stray loss factor $k_{Sl}$ is used [3]:

$$P_T=\left(1+k_{Sl}\right)·\left(P_{Ac}+P_{Syh}+P_{SyF}+P_{Sth}+P_{StF}+P_{PM}\right).$$

(65)

Finally, the efficiency $\eta$ is calculated:

$$\eta =\frac{P_E}{P_E+P_T},$$

(66)

and all design steps are completed.

2.4. Imposed Parameters and Their Suggested Ranges

In the proposed design procedure, the designer has to determine a considerable number of imposed parameters. Thus, this section addresses these parameters seen throughout Section 2.3 since they significantly impact the generator’s results. To explain in the most straightforward manner possible, this section follows the same order as the previous section, going from rotor sizing all the way to losses and efficiency estimation. The suggested ranges are mostly based on the literature and papers that address the matter; they may be seen in summary in

Table 1. Imposed parameters.

Symbol	Unit	Description	Suggested Range	Value
$D_{Ro}$	mm	Rotor outer diameter	1	410
$k_{\alpha P}$	-	Pole pitch factor	1/2–4/5	4/5
$k_{AG}$	-	Air gap factor	0.01–0.015	0.01
$PC$	-	Permeance coefficient	3–8	5
$B_{PM}$	T	Operative permanent magnet flux density	2	0.98
$B_{Ry}$	T	Magnetic flux density in the rotor yoke	1.0–1.5 T	1.3
$k_{MS}$	-	Machine shape factor	1	0.212
${∆\phi }_{PMAG}$	-	PM-to-air-gap-leakage factor	3	0.973
$N_S$	slots	Number of slots	4	36
$k_{Sow}$	-	Slot-opening factor	0.25–1	0.702
$k_{Soh}$	-	Slot-opening height factor	0.25–1	0.313
$k_{Sw}$	-	Wedge height factor	0.25–1	0.250
$k_{TS}$	-	Tooth-to-slot-width factor	0.8–3	2.08
$k_{PMSy}$	-	PM-width-to-stator-yoke factor	0.25–1	0.374
$k_{SyS}$	-	Stator-yoke-to-slot-height factor	0.25–1	0.752
$k_{Ac}$	-	Coil-shortening factor	2/3 or 5/6 5	5/6
$k_{Cop}$	-	Consequent pole factor	1 or 2	1
$N_{Sl}$	layers	Number of slot layers	1 or 2	2
${∆\phi }_{AGA}$	-	Air-gap-to-armature-leakage factor	3	1.00
$E_{Af}$	V	Induced voltage value	6	292
$N_{Cp}$	paths	Number of parallel paths in the armature windings	1 or 2 7	1
$k_{Sf}$	-	Slot fill factor	0.3–0.6	0.5
$J_A$	A/mm2	Armature current density	4–6.5	5.75
$R_{km}$	Ω/km	Conductor resistance per kilometer	8	0.643
$T_{ref}$	°C	Reference temperature	9	20
$T_{op}$	°C	Operating temperature	100–140	120
${\rho }_{ee}$	g/cm3	Electrical steel mass density	9	7.75
$P_F$	W/kg	Foucault loss per kilogram	9	3.68
$P_h$	W/kg	Hysteresis loss per kilogram	9	3.68
$k_{Syh}$	-	Hysteresis loss factor (yoke)	2	2
$k_{SyF}$	-	Foucault loss factor (yoke)	1.8	1.8
$k_{Sth}$	-	Hysteresis loss factor (teeth)	1.2	1.2
$k_{StF}$	-	Foucault loss factor (teeth)	2.5	2.5
$k_{PM}$	W/m2	PM-specific loss factor	100–300	200
$k_{Sl}$	-	Stray loss factor	0.01–0.02	0.02

¹ A straightforward range of values cannot be suggested since it will depend on the intended generator output power. ² Found with the PM demagnetization curve after choosing its grade and temperature, and the permeance coefficient. ³ Obtained through magnetostatic FES. ⁴ Recommended to lead to an integer $N_{Cpp}$. ⁵ These are conventional suggestions, but other values can be chosen. ⁶ Determined to match the calculated terminal voltage with the specifications. ⁷ Or multiples of the number of poles. ⁸ Equivalent resistance of 7 wires of AWG 14 in parallel with 9 wires of AWG 16 at 20 °C. ⁹ Mass density and losses per kilogram of the electrical steel M400-50A E170.

.

As explained in Section 2.2, after defining the design specifications, the rotor outer diameter ($D_{Ro}$) should be chosen. To simplify the design procedure, the equations that guide the external rotor diameter calculation were not included since they can be found in several works in the literature ([3,4,11,19]). Thus, the proposed method treats it as an imposed parameter, allowing the designer to find it with one of the methods in the mentioned literature or to freely choose it based on their experience. Alternatively, it is possible to follow the “ABC” procedure presented by [4], where the torque per unit of rotor volume (and consequently the rotor external diameter) is obtained from the electric and magnetic loadings, assuring proper temperature rise. This procedure can be carried out by adopting the range values suggested by [3]. The imposed $D_{Ro}$, presented in Table 1, implies on the values of electric loading (A/m) and flux densities (T) according to reference values from [3].

After analyzing the electrical machine design equations, it becomes clear that the machine’s electrical power is proportional to its volume (considering the same rotational speed). This means that it is not possible to suggest a range for the rotor outer diameter since it heavily depends on the desired output power of the generator. Even though stator dimensions also affect the outer diameter of the machine (and consequently its volume), most of the stator dimensions are attached to the PM dimensions, which in turn are proportional to the rotor outer diameter (which can be seen in Section 2.3.1).

2.4.1. Rotor Parameters

Regarding rotor sizing, four parameters need to be imposed by the designer: the pole pitch factor ($k_{\alpha P}$), air gap factors ($k_{AG}$), the permeance coefficient ($PC$), and the desired magnetic flux density in the rotor yoke ($B_{Ry}$). Firstly, the pole pitch factor determines the angle occupied by the PM, defining how much of the entire pole pitch (${\alpha }_P$) can be effectively used to produce flux (${\alpha }_{Pef}$). Permanent magnet machines, in general, should not utilize the entire pole pitch. Utilizing the entire pole pitch in surface-mounted machines would mean that the permanent magnets of adjacent poles would be in contact with each other, resulting in significant leakage flux since the flux lines will feel a path of lesser reluctance compared to the one crossing the air gap. It is also not advised for the PM to occupy less than half of the pole, resulting in low rotor volume utilization.

The generator air gap length ($L_{AG}$) is an extremely important parameter, and it is recommended to keep it as small as possible to maximize the PM flux. However, in addition to torque ripple under load operation, other vibration sources can cause contact between the rotor and stator; thus, a safety margin should be considered. To ensure a reasonable proportion between the air gap length and rotor size, the value of the air gap factor ($k_{AG}$) should be determined considering manufacturing and mechanical aspects. A good reference would be to keep the value between 0.01 and 0.015 (meaning an air gap length of 1% to 1.5% of the rotor’s outer diameter) [1].

Since the permeance coefficient ($PC$) is better explained in the next section, the last imposed parameter of the rotor sizing is the magnetic flux density in the rotor yoke ($B_{Ry}$). At no-load operation, the flux density in the rotor yoke tends to be proportional to the PM width since the PM flux divides itself in the yoke on both sides. Thus, by dividing the PM operative flux density by the desired flux density in the yoke (at no load) and multiplying by the PM width, the yoke height ($h_{Ry}$) is found. According to [3], the flux density in the rotor yoke should be between 1.0 and 1.5 T during full-load operation. Therefore, since the $B_{Ry}$ value is imposed in a no-load part of the design, the designer should consider a safety margin to ensure that this range is still respected during full load.

2.4.2. Permanent Magnet Flux Parameters

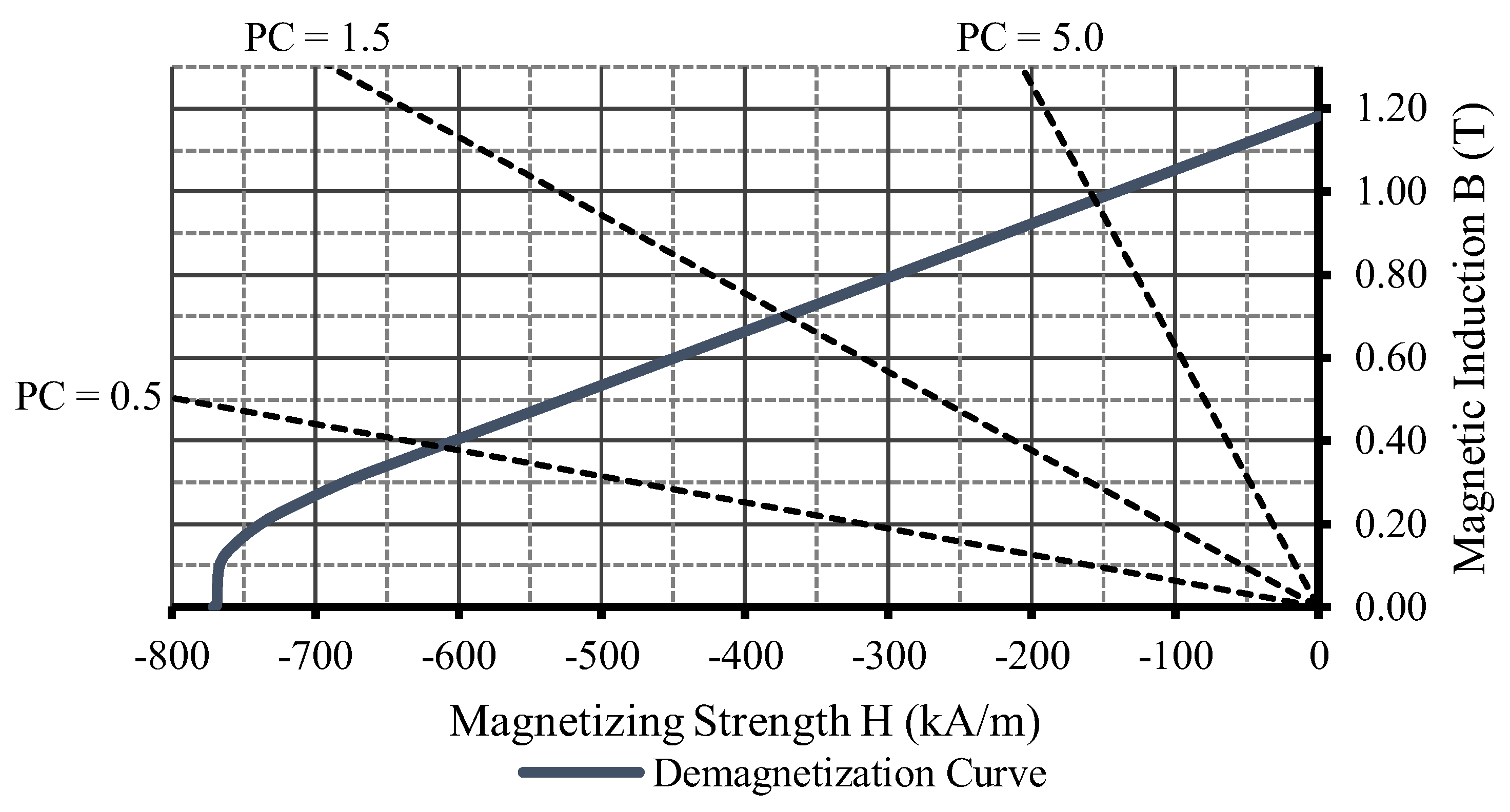
In the permanent magnet flux calculation, one of the most important values is the operative permanent magnet flux density ($B_{PM})$, which is obtained from the PM demagnetization curve. Even though it was first used in a previous section, the permeance coefficient ($PC$) is a paramount parameter for the PM flux calculation. To better explain how this operative flux density is extracted and the PC influences this process, the demagnetization curve of the neodymium–iron–boron PM N42SH from [39] is depicted in Figure 4.

The $PC$ is the inclination of the load lines (dotted) that intersect the permanent magnet demagnetization curve (blue continuous line) in Figure 4. Each intersection corresponds to a PM operating magnetic flux density ($B_{PM}$) at no load. Assuming that the cross-sectional areas of the permanent magnet and the air gap are very close values, that the air gap flux leakage is low, and that the permeability of the electrical steel used in electric machines is thousands of times greater than that of air, with both Ampère’s and Gauss’s laws the PC can be described as $PC=h_{PM}/L_{AG}$ [5]. Therefore, with the air gap length, choosing the permeance coefficient defines the PM height ($h_{PM})$ and its operative magnetic flux density at no load.

As shown with the different $PC$ values in Figure 4, increasing it moves the no-load operating flux density towards the PM remanent flux density, which is the maximum that the PM can generate (while maintaining the same temperature). On the other hand, smaller values correspond to a smaller operating flux density, bringing the PM operating point closer to the knee of the demagnetization curve, which could cause permanent demagnetization [4]. There is no consensus concerning a correct range for the $PC$ value. The authors of [6] suggest a $PC$ of between 5 and 15, whereas the authors of [4] suggest a smaller range of 5 to 10, and the authors of [15,23] follow the range indicated by [5], which is between 4 and 6.

In the proposed design methodology, values between 3 and 8 can be used as long as the designer is conscious that a safety margin should ensure that during load operation (and even under overload transients) the PM is not under the possibility of having permanent demagnetization. Additionally, even though the permeance coefficient may assume values more in the middle of the suggested range (or even towards the upper limit), too-small PM heights are usually more complicated to manufacture [4,5,6]. Values close to the top end of the suggested range would result in a bigger PM height (and volume) and no-load operative flux density. Normally, this would also increase the machine cost; however, shortening the machine stack length could adjust the generator price and result in the same flux linked by the coils as a smaller PC.

At the very beginning of the design procedure, a permanent magnet and its permeance coefficient are chosen. In the performed design of Section 3, the neodymium–iron–boron of grade 42 and thermal class SH was selected. Moreover, as the demagnetization curve depends on the operating temperature of the PM, a maximum temperature rise of 100 °C was considered. This results in an operative temperature ($T_{op}$) of 120 °C if the ambient temperature is considered to be around 20 °C. Therefore, the correct demagnetization curve of the N42SH from the spreadsheet of its manufacturer [39] is the one for 120 °C, as shown in Figure 4.

Another parameter necessary to calculate the PM flux is the generator stack length ($L_G$), found by imposing a value for the machine shape factor ($k_{MS})$, which usually assumes values between 0.5 and 2. For the lower half of this range, the axial length of the rotor is smaller than its diameter, resulting in more rotor inertia than upper values in the suggested range. Additionally, the efficiency of the machine tends to be lower, as there is relatively more copper in the coil ends. For values between one and two, the rotor has lower mechanical stress, but cooling the machine becomes more costly [19].

To find the flux in the air gap of the machine, the permanent magnet to air gap leakage factor (${∆\phi }_{PMAG}$) is used to consider the leakage flux that tends to return to the adjacent pole (or even the opposite side of the same PM) and does not reach the air gap. Its value can be obtained with reluctance networks or finite element simulations (FESs) of the generator under no-load operation. With this factor value, the designer can more accurately assess whether the designed PM corresponds to the desired air gap magnetic flux density, which should be between 0.85 and 1.05 T [3].

Similarly to the permanent magnet to air gap leakage factor that accounts for the leakage flux from the PM that does not reach the air gap, the air gap to armature leakage flux factor (${∆\phi }_{AGA}$) is used in the calculation of the number of turns of armature winding ($T_A$) to consider the flux that is not linked by the coils, returning to the air gap through the stator teeth. This factor may also be adjusted after performing a magnetostatic no-load finite element simulation of the machine, which does not take more than a few seconds.

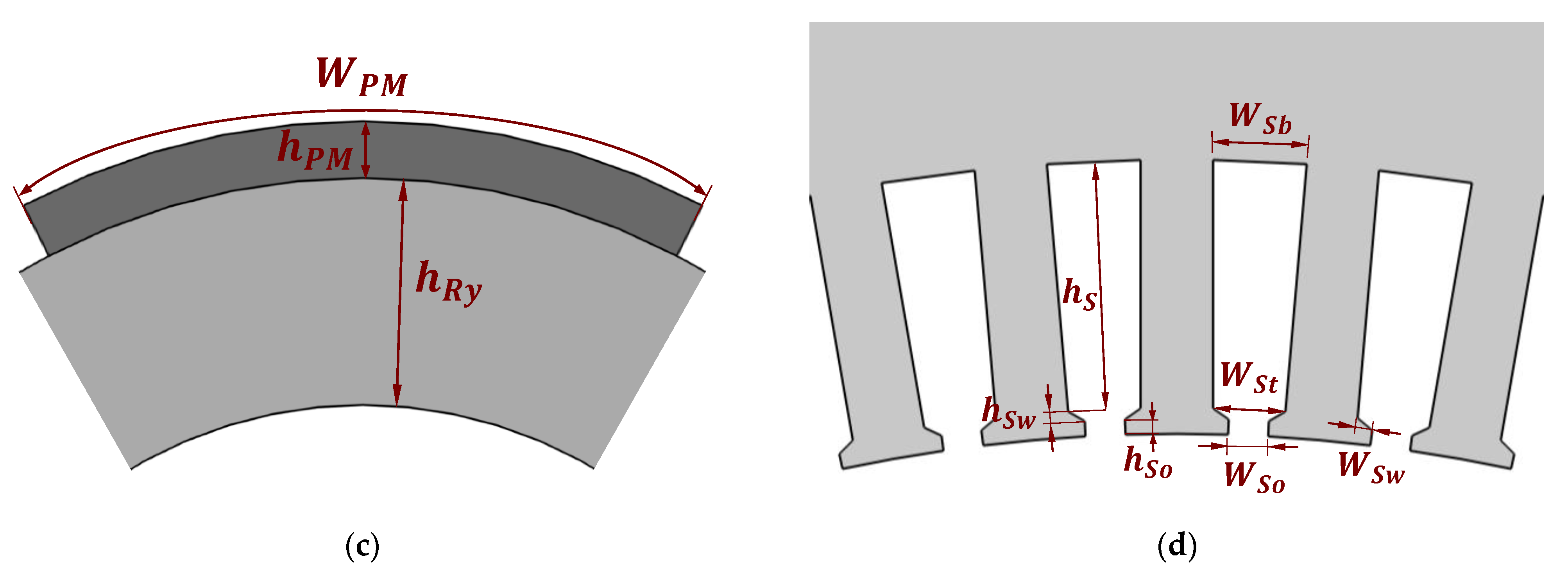
2.4.3. Stator Parameters

The stator sizing begins with choosing the number of slots ($N_S$), which is strictly linked to the number of poles since their ratio strongly affects the machine’s winding scheme and the presence of harmonics of certain orders. Additionally, the ratio between the number of poles and slots, together with the slot opening width, influences the presence of cogging torque. Furthermore, this tends to become a constrained choice since the number of slots and their layers are limited by production feasibility and winding manufacturability aspects [3]. Therefore, since synchronous machine winding is an extensive topic alone, the recommendation here is to choose the number of stator slots so that the number of coils per pole per phase is an integer, preferably between 1 and 4. As a reminder, this is a recommendation; other values (even non-integer ones) could be used as long as the designer knows the subject very well and its repercussions for the design.

Subsequently, the slot sizing requires definitions of the slot opening and the tooth dimensions. These dimensions have an impact on the cogging torque and Foucault losses, demanding special care and experience from the designer [5]. Due to their significance in the overall result, in this design procedure they are linked in an attempt to maintain reasonable proportions and allow inexperienced designers to find an appropriate PM generator geometry.

Firstly, the slot opening width ($W_{So}$) is bounded to the rotor outer diameter and the number of stator slots, ensuring that proportion with the overall size and number of slots of the machine is established. To adjust this proportion, aiming for the slot width to be feasible (in terms of manufacturability) and allowing the armature conductors to be inserted in the slots, the slot opening factor ($k_{Sow}$) is used. It is not elementary to suggest a range of values for this imposed parameter since it can vary substantially, but a range between 0.25 and 1 should cover most cases.

The remaining tooth tip dimensions being linked to the slot opening (seen in Equations (17) and (18)) would avoid excessively thin or too-long and -fragile tooth tips. Both the slot opening height factor ($k_{Soh}$) and the wedge height factor ($k_{Sw}$) could assume values between 0.25 and 1. Ultimately, the tooth tip proportions can only be verified when the stator sizing is finished and the generator cross-section is drawn. However, with the slot wedge dimensions (imposed slot wedge height and slot wedge width calculated with Equation (24)), the wedge inclination ${\theta }_{Sw}={\tan }^{-1}\left(h_{Sw}/W_{Sw}\right)$ can be found and analyzed. An imbalance between wedge height and width can be easily noticed if this value becomes smaller than 20$°$ or bigger than 40$°$.

Also during the stator sizing, a proportion of how much of the slot pitch corresponds to the slot or the stator teeth is defined by the tooth-to-slot-width factor ($k_{TS}$). As the value of this imposed parameter increases, the slot begins to occupy a smaller portion of the slot pitch, reducing the total slot area, which reduces the armature conductor surface and, therefore, the power produced in the stator volume. On the other hand, decreasing the value of this imposed parameter reduces the tooth width ($W_t$) and increases its flux density, which can lead to saturation. Therefore, this parameter could assume values within the 0.8 to 3 range. The designer can assess whether the stator teeth are close to saturation at no-load operation by calculating the teeth average magnetic flux density $B_{St}=B_{PM}·\left(W_{PM}/W_t\right)·\left(P/N_S·k_{\alpha P}\right)$. The flux density in the stator teeth should be between 1.5 and 2.0 T [3] at full-load operation; thus, similar to the imposed rotor yoke flux density, the $k_{TS}$ should also consider a margin so that the stator teeth will not saturate when the generator feeds a rated load. The magnetostatic simulation used to adjust the leakage flux factors can also be used to verify whether this range is respected and whether there is a reduced risk of saturation.

Seeking to establish a certain relationship with the flux density produced by the magnets with the maximum flux density in the stator yoke, its height ($h_{Sy}$) is chosen to be a portion of the width of the magnets—seen in Equation (25). Keeping the permanent magnet width to stator yoke factor ($k_{PMSy}$) to between 0.25 and 1 makes it possible to avoid designing an unnecessarily large stator with a low air gap flux density or an overly saturated one. The flux density in the stator yoke should be kept between 1.0 and 1.5 T [3] at full load. Thus, using $B_{Sy}=B_{PM}·\left(W_{PM}/2·h_{Sy}\right)$, the designer can assess whether a margin is reasonable and ensure that this would not exceed the flux density recommended by [3]. Lastly, for PM generators with many poles, defining the stator yoke height only by its desired flux density can lead to excessively thin yokes. In this case, a mechanical constraint can be incorporated.

Lastly, the slot height ($h_S$) is tied to the stator yoke height with the stator yoke to slot height factor ($k_{SyS}$). Even more than the width, the slot height influences the power density of the machine, as with larger slots it is possible to increase the conductor’s surface, allowing for more current. As discussed in Section 2.2, with this approach, in essence, the designer freely defines the generator output power by imposing the last two factors instead of choosing an armature conductor based on the output power and then finding the slot dimensions to fit the conductors. Additionally, a proportionality between the volume of magnets and the volume of copper in the stator is also ensured indirectly. The suggested range is also between 0.25 and 1.

2.4.4. Armature Winding Parameters

During the armature-winding definitions, a coil-shortening factor ($k_{Ac}$) is defined to calculate the armature coil pitch (${\alpha }_{Ac}$). Usually, the coil pitch is shortened so that the length of the coil end becomes shorter and the total copper mass is reduced [4]. This results in a smaller armature resistance and fewer copper losses, which increases the efficiency of the generator since it is the most significant loss in synchronous generators. Furthermore, with the correct factor value, the shortened coil can attenuate the harmonic content of the air gap flux density and result in a more sinusoidal linked flux compared to a full-pitch coil [3].

The armature coil-shortening factor is a fraction of the original pole pitch, composed of values multiple of the original pitch, resulting in an integer shortened pitch. Since many combinations between the number of poles and stator slots are possible, this fraction can be composed of a large quantity of multiples. Shortening factors of 2/3 and 5/6 are more conventional, known to reduce significantly third and ninth-order components and fifth and seventh-order components, respectively [1,3].

To find the component of the winding factor (i.e., the winding distribution factor ${∆\phi }_{Wd}$), the number of slots per pole per phase must be found, which depends on the number of phases of the generator ($N_{ph}$). This can be selected freely in principle, but since most supply networks are three-phase, most electrical machines are three-phase [3].

Further regarding the proposed design methodology, one of the most important parameters is defined: the number of armature-winding turns per phase ($T_A$), calculated with Equation (34). This equation is basically Faraday’s law, i.e., the voltage induced in a coil depends on the time variation of the linked flux and the number of turns, with the addition of flux linkage reduction factors due to coil shortening (${∆\phi }_{Cs}$), winding distribution (${∆\phi }_{Wd}$), and flux leakage (${∆\phi }_{AGA}$). Thus, in essence, the number of turns is found based on the flux produced by the PM and the imposed voltage value ($E_{Af}$).

To more effectively elucidate how this voltage value can be chosen, the WRSG design is used. In this case, the voltage value used to calculate the number of turns is the no-load voltage, given that for both no-load and full-load conditions it is possible to adjust the rotor-winding excitation and maintain the specified terminal voltage [1]. This is not the case for permanent magnet generators since the PM flux cannot be adjusted dynamically according to the generator load. Therefore, for PMSG, the voltage value used to calculate the number of turns of the armature winding must be the induced voltage estimated to be generated when feeding a load, which has to be big enough to be equal to the desired terminal voltage after the voltage drops in the armature resistance and due to the armature reaction.

This is an iterative stage of the design (depicted in Figure 2) since it is very unlikely that the first imposed voltage value will precisely correspond to the desired terminal voltage in the specifications. However, matching the calculated terminal voltage to the specified value usually takes only a few iterations. An adequate first guess could be a voltage 1.3 times bigger than the phase value of the specified terminal voltage. After calculating the terminal voltage with Equation (54), this value is adjusted, but related parameters should eventually be adjusted concurrently.

For example, increasing $E_{Af}$ would result in more turns per coil; thus, a smaller conductor cross-section can be fitted in the slots. Considering that the stator geometry (slot dimensions) and the stator current density are not altered, less armature current is admissible, corresponding to less admissible output power. To correct that, the generator stack length could be adjusted, meaning more linked flux, and the number of turns would be restored to the previous value (this is the simpler way to deal with that since the cross-section of the generator remains the same). Another way would be to adjust the slot size, allowing a bigger conductor surface that results in the original output power. However, the designer should know that this changes the value of the air-gap-to-armature-leakage factor (${∆\phi }_{AGA}$).

Instead of just imposing a generic number of turns, defining a voltage value ($E_{Af}$) is more palpable since it would be the equivalent of expecting a voltage regulation (of 30%, for example). Furthermore, if the proposed method were to be implemented in optimization software, the algorithm itself would be capable of finding the exact value of $E_{Af}$, because the terminal voltage and output power are fixed variables.

The last imposed parameters that define the armature windings are the consequent pole factor ($k_{Cop}$), the number of slot layers ($N_{Sl}$), and the number of parallel paths in the armature windings ($N_{Cp}$). Both $k_{Cop}$ and $N_{Sl}$ are either 1 or 2. For the consequent pole factor, a value of 2 would be chosen to have a consequent pole armature winding. The number of parallel paths in the armature windings is a multiple of the number of poles [1]. For example, for a six-pole generator, $N_{Cp}$ could be 1, 2, 3, or even 6. However, in this paper the suggestion is either 1 or 2. Again, this is a recommendation; other values can be used for specific cases or applications as long as the designer is aware that this will deeply impact the generator’s winding scheme. With these values, both the number of coils in series per phase ($N_{Cs}$) and the number of coils per pole per phase ($N_{Cpp}$) are found.

Lastly, before moving on to the armature current ($I_A$) calculation, the designer must impose values for the slot fill factor ($k_{Sf}$) and the admissible armature current density ($J_A$). Considering that it is not possible to fill the slot entirely with conductors due to the conductor’s insulation and manufacturability aspects, a slot fill factor is considered. The main aspects include the techniques available during manufacturing (allowing perfectly nested conductors or not), square or round conductors, and single- or double-layer [6]. Usually, slot fill factors between 40 and 45% are a bit optimistic for random-wound coils, and for higher values, rectangular wires more precisely fitted are required [4]. Thus, in this paper, a range between 30% and 60% is suggested.

Finally, the current density in the armature conductors must be carefully analyzed, considering two major aspects. The first is the operation temperature of the generator, which is intensely related to the thermal class of the conductors’ insulation. High-thermal-class insulation materials can sustain higher operation temperatures, thus allowing more current density. The last is the cooling system chosen, with a high-efficiency cooling method allowing more current density. In more complex design procedures that include a thermal model of the generator, the operating temperature of the armature winding can be an imposed parameter, so the conductor current density is a free parameter. To simplify the design procedure, the imposed current density in the armature conductors is suggested to be within 4 and 6.5 A/mm² [3].

2.4.5. Armature Resistance Parameters

To find the resistance per kilometer of the conductor ($R_{km}$), firstly, the designer should choose the number of wires that correspond to a conductor. If a single wire is used, then its surface should be very close to the armature conductor surface (calculated with Equation (39)), and the resistance per kilometer can be found on the spreadsheet of the conductor’s manufacturer. Suppose two or more wires of different sizes are chosen. In that case, a combination of these wires (each with a different size) is found to closely match the armature conductor surface ($S_{Ac}$), and the resistance per kilometer of this conductor is then the equivalent resistance considering all wires in parallel.

Finally, to find the armature-winding resistance ($R_A$), the temperature must be corrected [4]. From the spreadsheet, the reference temperature in which the manufacturer measured the resistance ($T_{ref}$) can be found. The operating temperature ($T_{op}$) would be accurately calculated with a thermal model of the machine. However, for simplification purposes, it can be estimated to be between 100 and 140 °C. These values should also be considered when choosing the PM, as they influence its grade and temperature class.

2.4.6. Loss Parameters

The proposed design methodology estimates the iron losses based on the method from [38]. This method takes into account the loss per kilogram value ($P_F$ and $P_h$) provided by the electrical steel manufacturer and is divided into hysteresis ($P_{Syh}$ and $P_{Sth}$) and eddy current losses ($P_{SyF}$ and $P_{StF}$). From this same spreadsheet, the mass density (${\rho }_{ee}$) of the selected material can also be found. Furthermore, as the stator yoke and teeth may have different magnetic flux densities, these two elements must have their losses estimated separately. Furthermore, empirical factors are used to account for Foucault and hysteresis losses ($k_{SyF}$ and $k_{StF}$, and $k_{Syh}$ and $k_{Sth}$, respectively), the values of which naturally should be based on the recommendations of [38].

Therefore, the hysteresis and Foucault empirical factors are 2 and 1.8 for the stator yoke and 1.3 and 2.5 for the stator teeth. Another empirical factor used in the loss estimation is PM specific loss factor ($k_{PM}$). This is roughly based on the current loading of the machine, being between 100 and 300 W/m², with the higher value for higher current loadings [38]. Finally, the total loss ($P_T$) still considers stray losses, which usually are between 0.1% and 0.2% of the total value [3] (which means a stray loss factor ($k_{Sl}$) of between 0.1 and 0.2).

3. Results and Discussion

This section presents the results of a generator designed with the proposed procedure, described throughout Section 2, to show its effectiveness. As seen in Figure 2, the PMSG design starts with the generator specifications shown in

Table 2. PMSG design specifications.

Symbol	Unit	Description	Value
$S_{Ed}$	VA	Desired output power	100,000
$V_{Td}$	V	Desired terminal voltage	380
$PF$	-	Power factor	0.9
$f$	Hz	Electrical frequency	60
$n$	rpm	Rotation	1200

. To complete the design of the generator and find its complete geometry, a handful of parameters must be imposed. All the values of these design choices are shown in Table 1, as well as the suggested ranges discussed in Section 2.4.

With the values from Table 1 and Table 2, it is possible to employ the design procedure detailed in Section 2 and obtain all the dimensions and parameters of the PM generator. The main generator results are shown in

Table 3. Main generator results.

Symbol	Unit	Description	Value
$P$	poles	Number of poles	6
$L_{AG}$	mm	Air gap length	4.1
$h_{PM}$	mm	PM height	20.5
$W_{PM}$	mm	PM width	163.2
$L_G$	mm	Generator stack length	87
${\phi }_{PM}$	mWb	PM flux	13.9
${\phi }_{AG}$	mWb	Air gap flux	13.5
$B_{AG}$	T	Air gap flux density	0.897
$W_{So}$	mm	Slot-opening width	8.0
$h_{So}$	mm	Slot-opening height	2.5
$h_{Sw}$	mm	Slot wedge height	2.0
$W_t$	mm	Teeth width	25.2
$B_{St}$	T	Stator teeth flux density	1.32
$W_{St}$	mm	Width at the top of the slot	12.1
$W_{Sb}$	mm	Width at the slot bottom	20.2
$h_{Sy}$	mm	Stator yoke height	61.0
$B_{Sy}$	T	Stator yoke flux density	1.28
$h_S$	mm	Slot height	45.9
$D_{So}$	mm	Stator outer diameter	641
$N_{Cpp}$	coils	Number of coils per pole per phase	2
$T_{Ac}$	turns	Number of turns per coil	7.0
$S_{Ac}$	mm2	Armature conductor surface	26.5
$R_A$	Ω	Armature resistance 1	0.05
$X_S$	Ω	Synchronous inductance	0.748
$\delta$	°	Load angle	19.8

.

It is worth mentioning that this is a generic generator designed purely for methodology explanation rather than to match or present advantages when compared with commercial machines. To provide a graphical representation of the generator dimensions presented in Table 3, Figure 5 shows the generator cross-section when constructed in Ansys Maxwell software (2023 R2 version).

This is the cross-section of the generator designed as an example. The losses and the efficiency of the designed PMSG are presented in

Table 4. Losses and efficiency.

Symbol	Unit	Description	Value
$P_{Ac}$	kW	Armature copper losses	3.47
$P_{Syh}$	kW	Stator yoke hysteresis losses	0.478
$P_{SyF}$	kW	Stator yoke Foucault losses	0.517
$P_{Sth}$	kW	Stator teeth hysteresis losses	0.128
$P_{StF}$	kW	Stator teeth Foucault losses	0.320
$P_{PMs}$	kW	Permanent magnet losses	0.02
$P_T$	kW	Total losses	4.93
$\eta$	%	Estimated efficiency	94.8

.

The validation of the designed PM synchronous generator was carried out with finite element simulations, which were all carried out with Ansys Maxwell in 2D. These time-stepping simulations take into account the ferromagnetic saturation, naturally. The no-load and full-load flux lines and densities are presented in Figure 6 and Figure 7, respectively.

Other important results extracted from the performed FES are the phase-to-phase voltages, shown in Figure 8, and the phase armature currents, presented in Figure 9, both under full-load operation. Moreover, Ansys Maxwell also allows for a harmonic content calculation for both curves through fast Fourier transformation (FFT).

The total harmonic content (THD) of the phase-to-phase voltages in Figure 8 was 5.15%, whereby the 11th- and 13th-order components were the most significant—at 3.88% and 1.28%, respectively. The FFT of the armature currents in Figure 9 resulted in a THD of 7.67%, where the third-order component was the most significant, contributing 6.89%, followed by the ninth-order component, with 1.02%.

The main electromagnetic results are shown in

Table 5. Main electromagnetic results.

Symbol	Unit	Design	FES	Difference (%)
$B_{AG}$ 1	T	0.897	0.899	0.285
$V_T$	V	378.1	389.4	2.89
$I_A$	A	152.1	155.3	2.06
$S_E$ 2	kVA	99.6	104.7	4.89
$P_E$ 3	kW	89.6	94.7	5.35

¹ Flux density during no-load operation with the flux measured at the middle of the air gap. ² The FES result is the product of rms values of $V_T$, $I_A$, and $\sqrt{3}$. ³ FES result obtained by the mean value of the instantaneous power.

, and a percentual difference with the finite element simulation (in Maxwell 2D) is also presented. From the difference values, it is clear that the proposed design methodology presented good accuracy, with the differences between the design model and finite element simulation being around 2% for terminal voltage and armature current. The 5% difference in the output power was a consequence of the terminal voltage and armature current differences and is within an acceptable range, thus not affecting the overall merit of the method.

4. Conclusions

A comprehensive and detailed procedure to design surface-mounted permanent magnet synchronous generators has been presented. With the ever-growing indispensability of electrical energy in modern society, the significance of synchronous generators cannot be overemphasized. This paper focuses on closing a lacuna in the literature on PM synchronous generator design methodology, providing a comprehensive and thoroughly explained procedure, presenting all the design equations, and unraveling the specifics of the design and its choices.

The proposed method fully considers the fundamentals of permanent magnet generator operation, with some simplifications. Moreover, the procedure; its stages, parameters, and iterative loops; and the related designer decisions are explained and discussed with clear guidelines. This significant amount of detail allows designers (even inexperienced ones) to replicate the presented results easily and provides a robust framework for experienced ones to improve on.

To verify the accuracy of the proposed method, finite element simulations were used to compare the results, and an acceptable match between their outcomes is presented. It is pertinent to highlight that while the proposed design method includes simplifications (such as disregarding iron reluctance and saturation), finite element simulations meticulously account for core reluctance and saturation, thus reinforcing the credibility of the developed design procedure.

Overall, many researchers can benefit from this procedure to design surface-mounted PM synchronous generators. Fellow researchers from other areas, such as control, optimization, power electronics, and power systems, can easily replicate the results or quickly obtain the parameters of a new generator that suits their purposes. Furthermore, acquainted machine designers can lightly improve the proposed method by incorporating other features, such as techniques to reduce the harmonic content or reluctance networks, or even by developing it into a more elaborate method, including more physics in the model, like an equivalent thermal circuit.