Mechanical Modeling of Viscous Fluid Damper with Temperature and Pressure Coupling Effects
Abstract
1. Introduction
2. Experimental Study
3. Results and Discussion
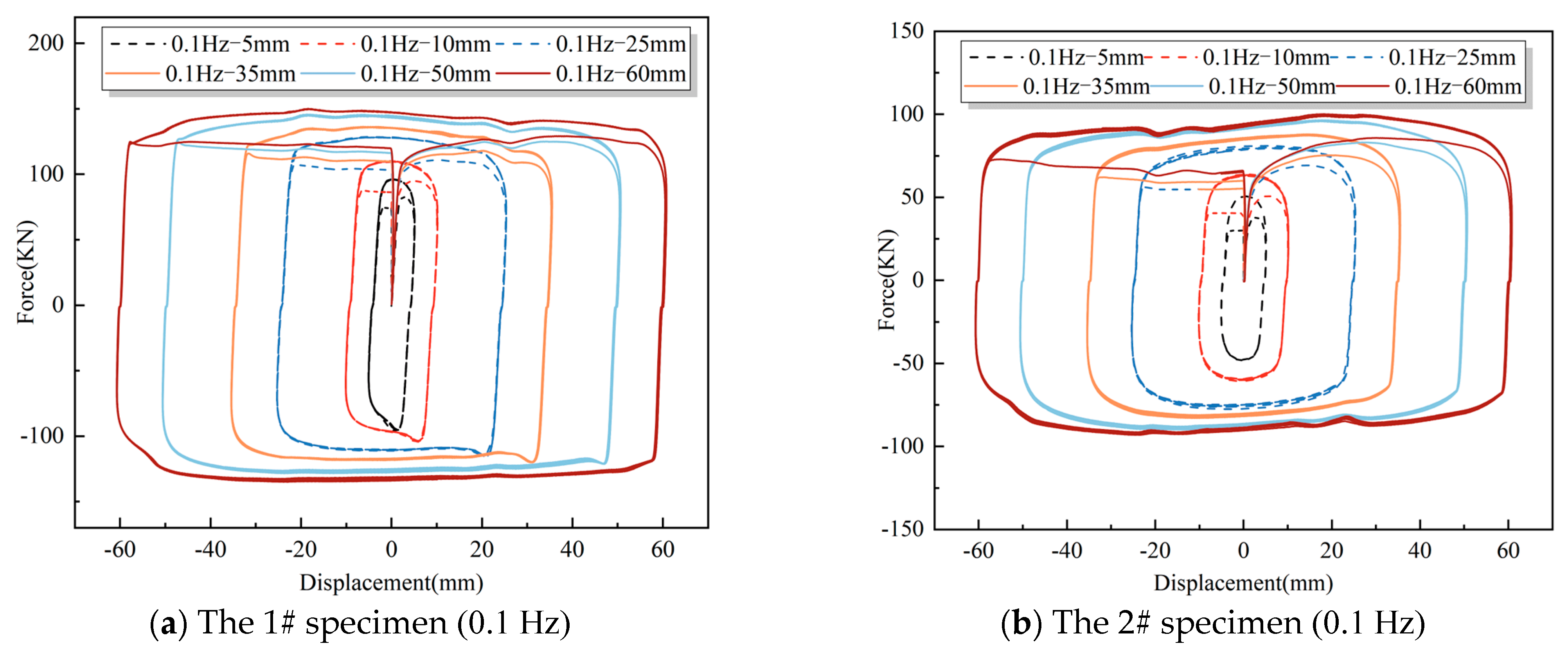
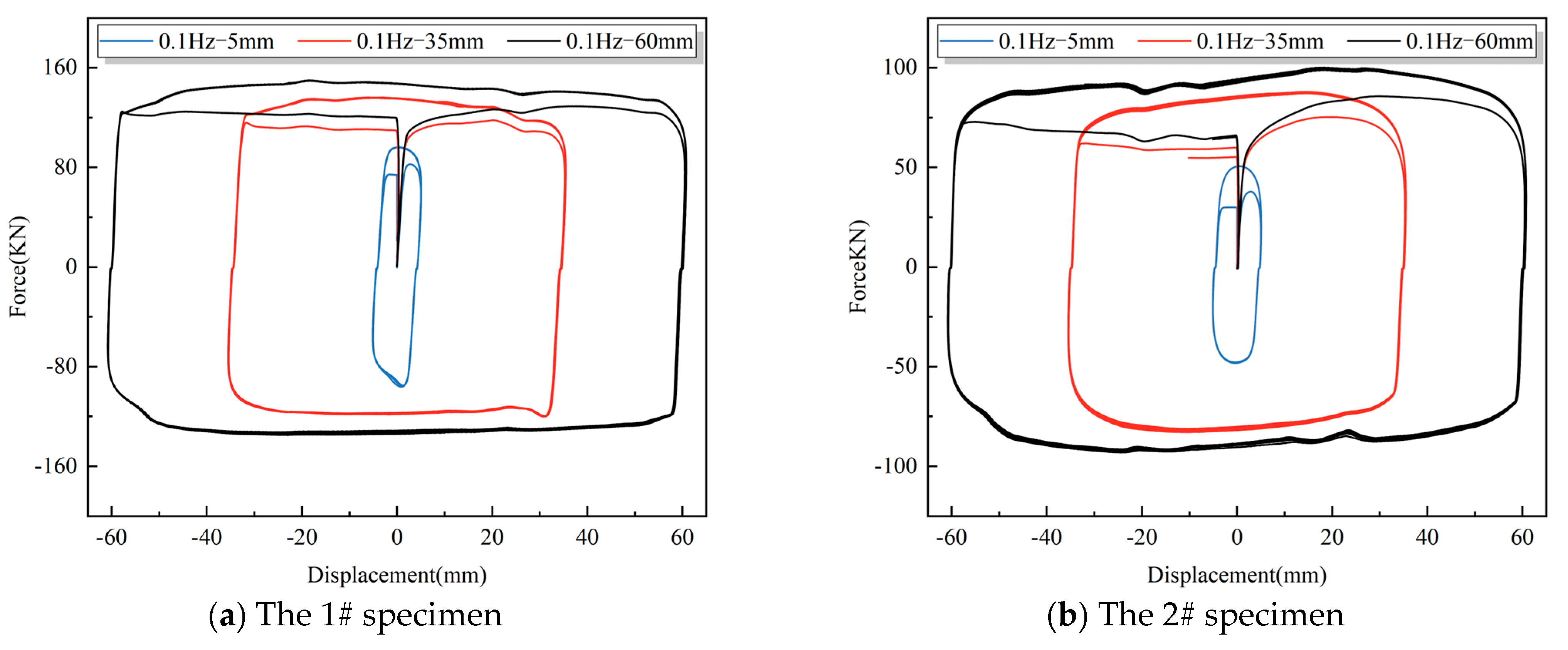
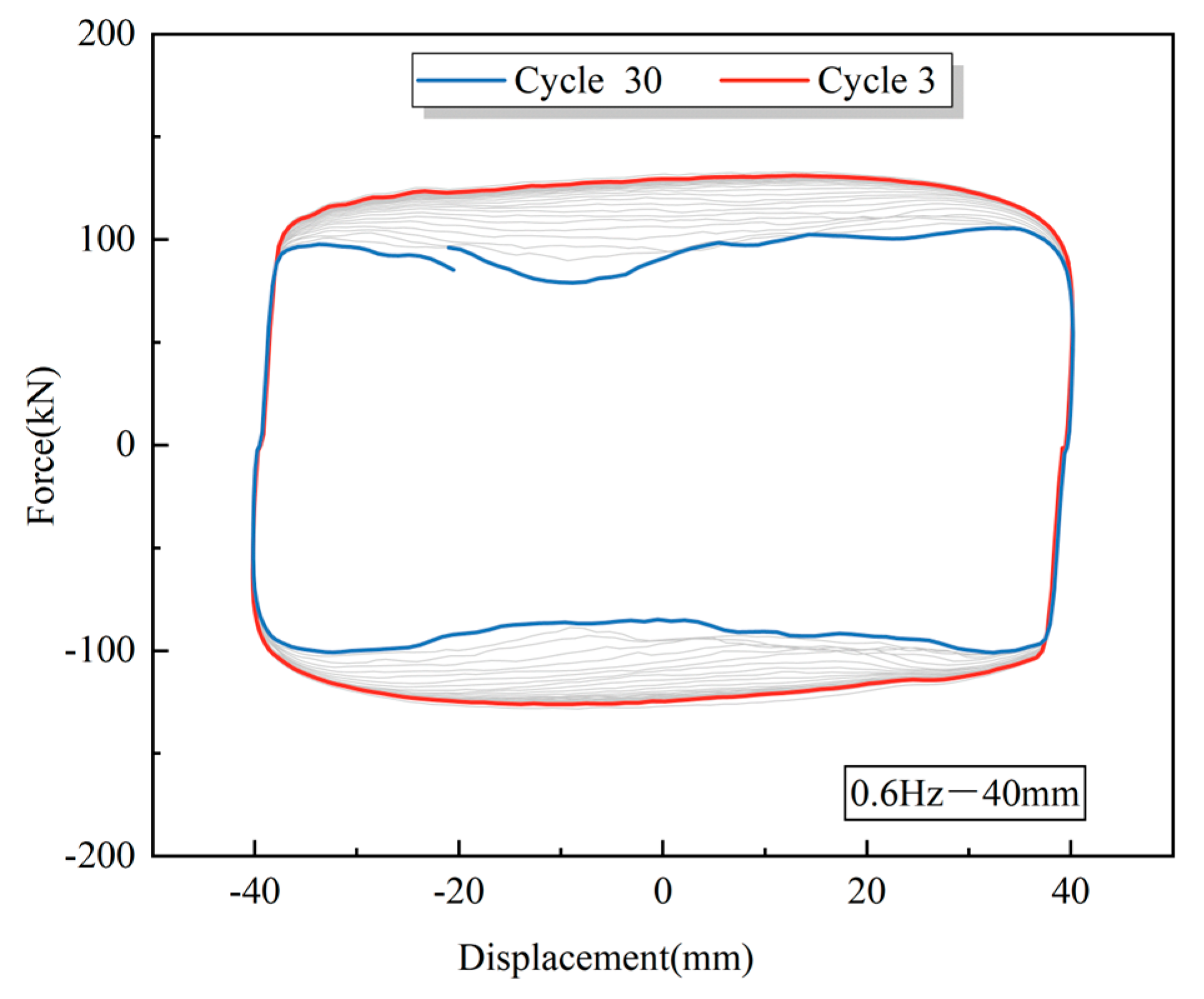
3.1. Experimental Results
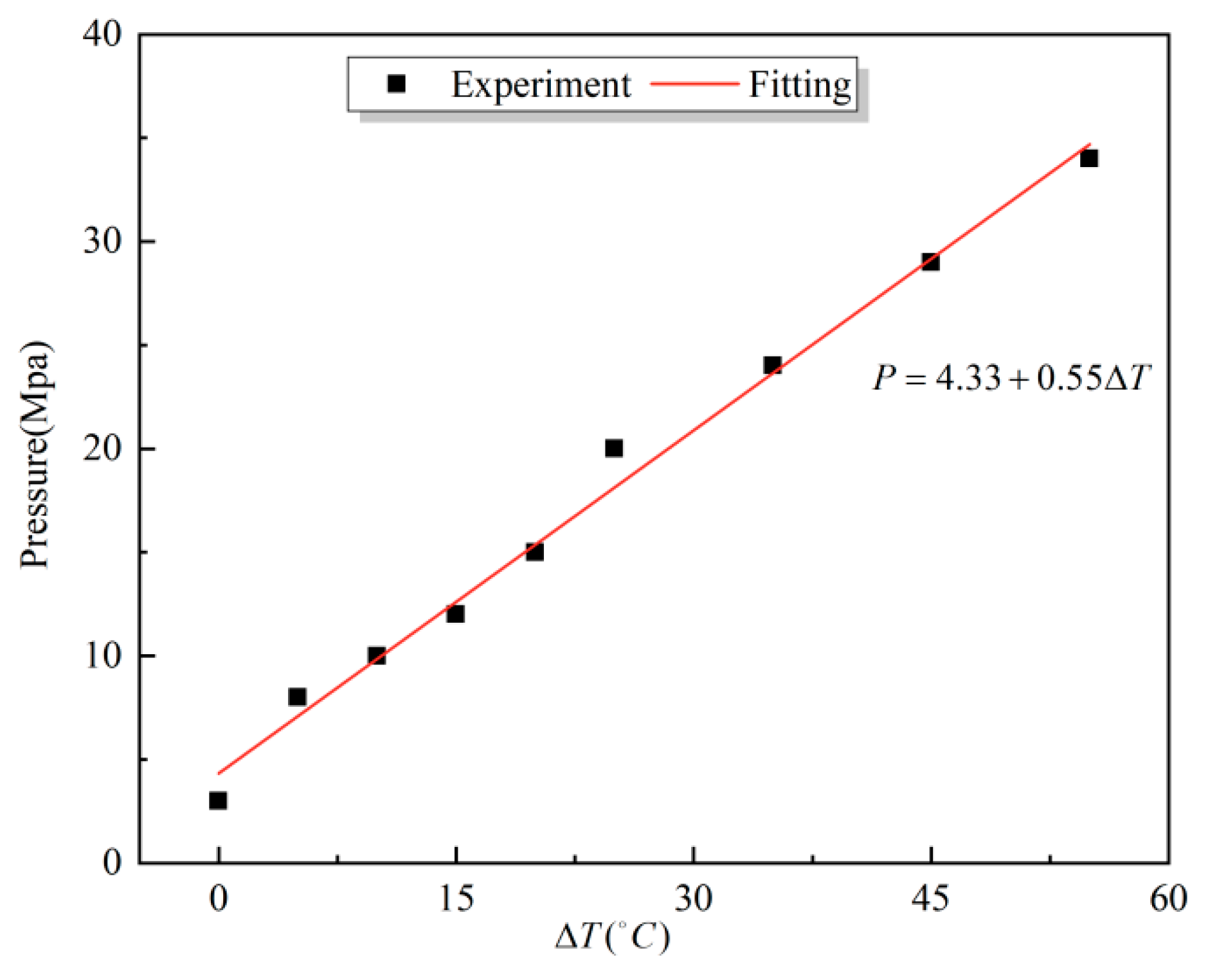
3.2. Relationship of Temperature and Pressure
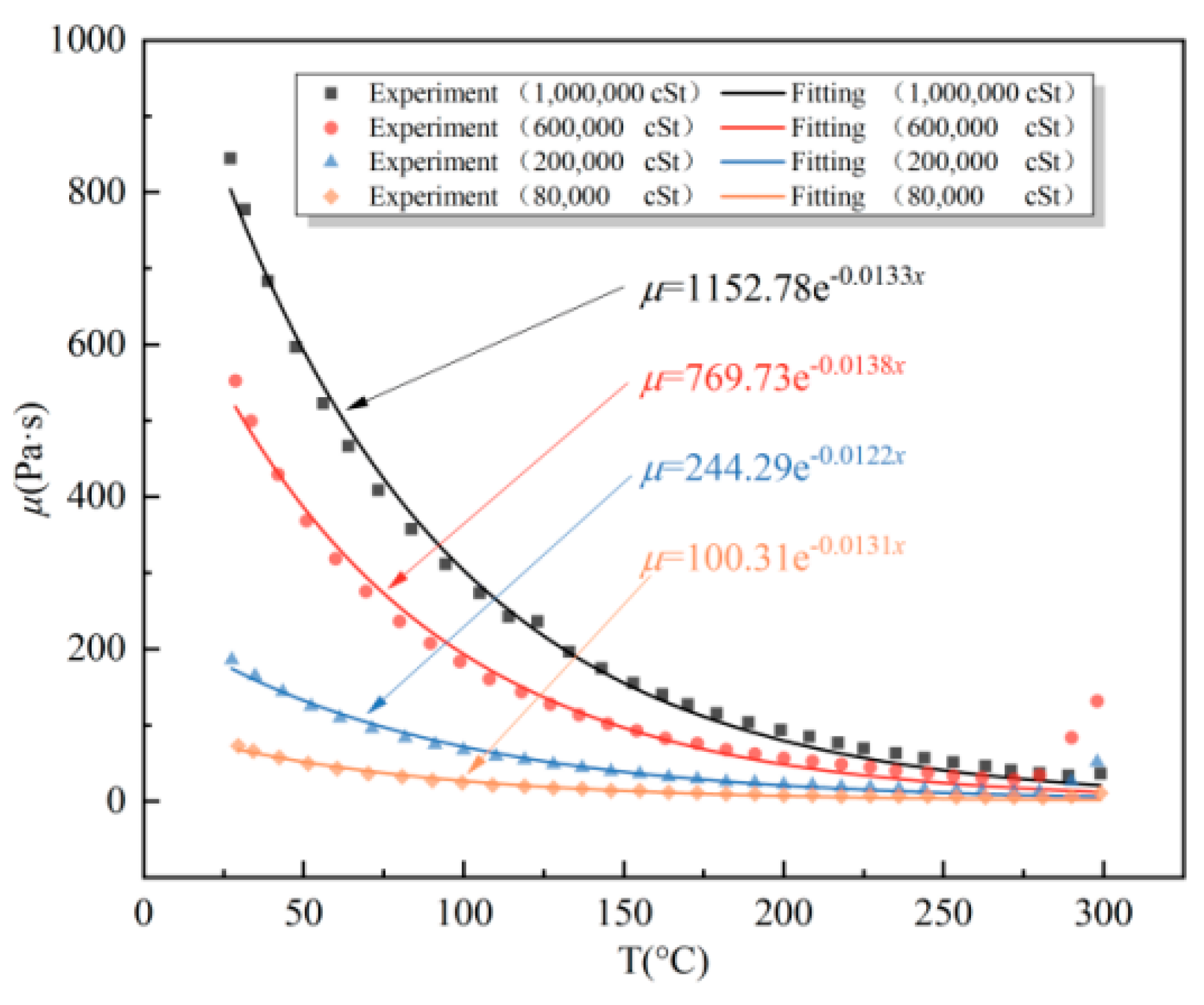
3.3. Effect of Kinematic Viscosity
4. Mathematical Model
4.1. Boundary Conditions
4.2. Theoretical Derivation
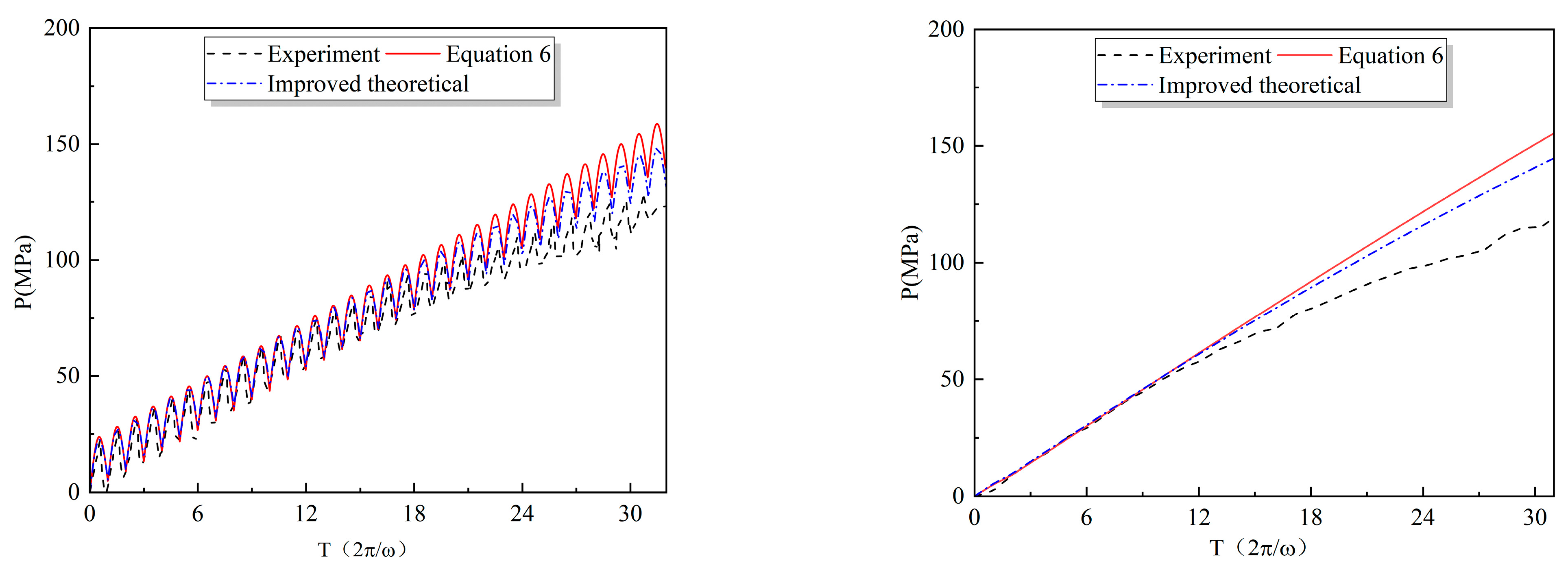
5. Comparison of Numerical and Experimental Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ngatu, G.T.; Wereley, N.M.; Kothera, C.S. Hydromechanical analysis of a fluid-elastomeric lag damper incorporating temperature effects. J. Aircraft. 2012, 49, 1212–1221. [Google Scholar] [CrossRef]
- Martínez-Rodrigo, M.D.; Filiatrault, A. A case study on the application of passive control and seismic isolation techniques to cable-stayed bridges: A comparative investigation through non-linear dynamic analyses. Eng. Struct. 2015, 99, 232–252. [Google Scholar] [CrossRef]
- Wang, J.; Zhao, S.; Wu, D.; Jing, X. The interior working mechanism and temperature characteristics of a fluid based micro-vibration isolator. J. Sound Vibr. 2016, 360, 1–16. [Google Scholar] [CrossRef]
- Buclny, D.D.; Wiggert, D.C.; Hatfield, F.J. The influence of structural damping on internal-pressure during a transient pipe-flow. J. Fluids Eng.-Trans. ASME 1991, 113, 424–429. [Google Scholar]
- He, X.; Wu, T.; Wang, Y. Modeling and characteristics of viscous damper using throttled fluid mixed with air. J. Vib. Shock 2014, 33, 95–100. [Google Scholar]
- Kitayama, S.; Constantinou, M.C. Fluidic self-centering devices as elements of seismically resistant structures description, testing, modeling, and model validation. J. Struct. Eng. 2017, 143, 04017050. [Google Scholar] [CrossRef]
- Liang, G.; Zhao, T.; Li, N.; Wei, Y.; Savaresi, S.M. Magnetorheological damper temperature characteristics and control-oriented temperature-revised model. Smart Mater. Struct. 2021, 30, 125005. [Google Scholar] [CrossRef]
- Xu, W.; Du, D.; Kasai, K.; Wang, S. Optimization layout of viscous dampers and its application in retrofitting of a high-rise steel structure. J. Build. Struc. 2022, 43, 32–44. [Google Scholar]
- Xu, W.; Wang, Y.; Guo, H.; Du, D.; Wang, S. Theoretical and experimental investigation on the seismic performance of a novel variable-damping viscous fluid damper. J. Build. Eng. 2022, 53, 104537. [Google Scholar] [CrossRef]
- Makris, N.; Constantinou, M.C. Fractional-derivative maxwell model for viscous dampers. J. Struct. Eng. 1991, 117, 2708–2724. [Google Scholar] [CrossRef]
- Makris, N.; Constantinou, M.C.; Dargush, G.F. Analytical model of viscoelastic fluid dampers. J. Struct. Eng. 1993, 119, 3310–3325. [Google Scholar] [CrossRef]
- Yu, Q.; Xu, D.; Zhu, Y.; Guan, G.; Li, Q. Damping characteristic modeling and numerical simulation analysis of the viscous damper of a clearance hydrocylinder. J. Vib. Shock 2020, 39, 161–167. [Google Scholar]
- Constantinou, M.C.; Symans, M.D. Experimental & Analytical Investigation of Seismic Response of Structures with Supplemental Fluid Viscous Dampers. 1992. Available online: https://www.buffalo.edu/mceer/catalog.host.html/content/shared/www/mceer/publications/NCEER-92-0032.detail.html (accessed on 21 May 2024).
- Ou, J.; Ding, J. Theory and performance experiment of viscous damper of clearance hydrocylinder. Earthq. Eng. Eng. Vib. 1999, 19, 82–89. [Google Scholar]
- Ding, J.; Ou, J. Theoretical study and performance experiment for cylinder-with-holes viscous damper. World Earthq. Eng. 2001, 17, 30–35. [Google Scholar]
- Black, C.J.; Makris, N. Viscous heating of fluid dampers experimental studies. In Proceedings of the SPIE’s 7th Annual International Symposium on Smart Structures and Materials, Newport Beach, CA, USA, 5–9 March 2000. [Google Scholar]
- Black, C.J.; Makris, N. Viscous heating of fluid dampers under small and large amplitude motions: Experimental studies and parametric modeling. J. Eng. Mech. 2007, 133. [Google Scholar] [CrossRef]
- Hou, C.Y. Fluid dynamics and behavior of nonlinear viscous fluid dampers. J. Struct. Eng. 2008, 134, 56–63. [Google Scholar] [CrossRef]
- Makris, N. Viscous heating of fluid dampers. I: Small-amplitude motions. J. Eng. Mech. 1998, 124, 1210–1216. [Google Scholar] [CrossRef]
- Makris, N.; Roussos, Y.; Whittaker, A.S.; Kelly, J.M. Viscous heating of fluid dampers. II: Large-amplitude motions. J. Eng. Mech. 1998, 124, 1217–1223. [Google Scholar] [CrossRef]
- He, L.; Zheng, G. Feedback effect of viscous heating and heat balance of fluid damper. Chin. J. Appl. Mech. 2006, 505–510+691. [Google Scholar]
- He, L.; Yang, Q.; Zheng, G. Effect of viscous heating of the fluid damper on the whole-spacecraft vibration isolation. Chin. J. Mech. Eng. 2007, 43, 31–64. [Google Scholar] [CrossRef]
- He, L.; Yang, Q.; Zheng, G. Effect of temperature of fluid isolator on whole-spacecraft vibration isolation. Aerosp. Shanghai 2008, 44–47+57. [Google Scholar] [CrossRef]
- Amangeldi, M.; Wang, Y.; Perveen, A.; Zhang, D.; Wei, D. An iterative approach for the parameter estimation of shear-rate and temperature-dependent rheological models for polymeric liquids. Polymers 2021, 13, 4185. [Google Scholar] [CrossRef] [PubMed]
- Chmielowiec, A.; Wo’s, W.; Gumieniak, J. Viscosity approximation of PDMS using Weibull function. Materials 2021, 14, 6060. [Google Scholar] [CrossRef] [PubMed]
- Venczel, M.; Bognár, G.; Veress, Á. Temperature-dependent viscosity model for silicone oil and its application in viscous dampers. Processes 2021, 9, 331. [Google Scholar] [CrossRef]
- Lak, H.; Zahrai, S.M. Self-heating of viscous dampers under short- & long-duration loads: Experimental observations and numerical simulations. Structures 2023, 48, 275–287. [Google Scholar]
- Du, D.; Song, B.; Xu, W. Seismic retrofit of a high-rise steel structure considering long-period and long-duration ground motions. J. Eng. Mech. 2020, 37, 189–200. [Google Scholar]
- Deng, J.; Fang, Y.; Qin, H.; Xu, F. The filling material viscidity characteristic of helicopter fluidlastic damper. Helicopter Tech. 2007, 2, 7–11. [Google Scholar]
- Makris, N.; Dargush, G.F.; Constantinou, M.C. Dynamic Analysis of Generalized Viscoelastic Fluids. J. Eng. Mach. 1993, 119, 1663–1679. [Google Scholar] [CrossRef]




| Specimen | L/mm | D/mm | d/mm | Gap /mm | D0/mm | Silicone Fluid |
|---|---|---|---|---|---|---|
| 1# | 50 | 80 | 30 | 0.30 | 79.40 | 600,000 cSt |
| 2# | 50 | 80 | 30 | 0.30 | 79.40 | 80,000 cSt |
| Test Case | Case | Frequency (Hz) | Displacement (mm) | Number of Cycles | Maximum Velocity (m/s) |
|---|---|---|---|---|---|
| Ultimate displacement | 1 | 0.01 | 75 | 2 | 0.00 |
| Low frequency | 2 | 0.1 | 5 | 5 | 0.00 |
| 3 | 10 | 0.01 | |||
| 4 | 25 | 0.02 | |||
| 5 | 35 | 0.02 | |||
| 6 | 50 | 0.03 | |||
| 7 | 60 | 0.04 | |||
| Medium frequency | 8 | 0.6 | 5 | 5 | 0.02 |
| 9 | 10 | 0.04 | |||
| 10 | 25 | 0.09 | |||
| 11 | 35 | 0.13 | |||
| 12 | 45 | 0.17 | |||
| Durability performance | 13 | 0.6 | 40 | 30 | 0.15 |
| T1 (°C) | 25 | 30 | 35 | 40 | 45 | 50 | 60 | 70 | 80 |
| Pressure (MPa) | 3 | 8 | 10 | 12 | 15 | 20 | 24 | 29 | 34 |
| ΔT | 0 | 5 | 10 | 15 | 20 | 25 | 35 | 45 | 55 |
| Parameter | Viscosity | |||
|---|---|---|---|---|
| 1,000,000 cSt | 600,000 cSt | 200,000 cSt | 80,000 cSt | |
| a | 1152.78 | 769.73 | 244.29 | 100.31 |
| b | −0.0133 | −0.0138 | −0.0122 | −0.0131 |
| Temperature | Viscosity (Rate of Change) | |||
|---|---|---|---|---|
| 1,000,000 cSt | 600,000 cSt | 200,000 cSt | 80,000 cSt | |
| 25 °C | 850 | 565 | 200 | 80 |
| 50 °C | 560 (34.12%) | 369 (34.69%) | 130 (35.00%) | 50 (37.50%) |
| 75 °C | 390 (54.12%) | 256 (54.69%) | 90 (55.00%) | 34.6 (56.75%) |
| 100 °C | 293 (65.53%) | 182 (67.79%) | 67.5 (66.25%) | 25 (68.75%) |
| 150 °C | 160 (81.18%) | 97 (82.83%) | 38 (81.00%) | 14.3 (82.13%) |
| 200 °C | 94 (88.94%) | 57 (89.91%) | 22.4 (88.80%) | 8 (90.00%) |
| Viscosity | 1,000,000 cSt | 600,000 cSt | 200,000 cSt | 80,000 cSt |
| Viscosity–temperature coefficient | 0.572 | 0.575 | 0.578 | 0.596 |
| Cycle | Temperature Ratio | ΔT | ΔP | Cycle | Temperature Ratio | ΔT | ΔP |
|---|---|---|---|---|---|---|---|
| 1 | 0.990 | 8.510 | 4.698 | 16 | 0.991 | 7.387 | 4.079 |
| 2 | 0.990 | 8.425 | 4.651 | 17 | 0.991 | 7.323 | 4.043 |
| 3 | 0.990 | 8.341 | 4.605 | 18 | 0.991 | 7.260 | 4.008 |
| 4 | 0.990 | 8.259 | 4.560 | 19 | 0.992 | 7.198 | 3.974 |
| 5 | 0.990 | 8.179 | 4.515 | 20 | 0.992 | 7.136 | 3.940 |
| 6 | 0.990 | 8.100 | 4.472 | 21 | 0.992 | 7.076 | 3.907 |
| 7 | 0.991 | 8.022 | 4.429 | 22 | 0.992 | 7.017 | 3.874 |
| 8 | 0.991 | 7.946 | 4.387 | 23 | 0.992 | 6.959 | 3.842 |
| 9 | 0.991 | 7.872 | 4.346 | 24 | 0.992 | 6.902 | 3.811 |
| 10 | 0.991 | 7.799 | 4.306 | 25 | 0.992 | 6.846 | 3.780 |
| 11 | 0.991 | 7.727 | 4.266 | 26 | 0.992 | 6.790 | 3.749 |
| 12 | 0.991 | 7.657 | 4.227 | 27 | 0.992 | 6.736 | 3.719 |
| 13 | 0.991 | 7.588 | 4.189 | 28 | 0.992 | 6.683 | 3.689 |
| 14 | 0.991 | 7.520 | 4.152 | 29 | 0.992 | 6.630 | 3.660 |
| 15 | 0.991 | 7.453 | 4.115 | 30 | 0.992 | 6.578 | 3.632 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Xu, W.; Wang, S.; Du, D.; Geng, Y. Mechanical Modeling of Viscous Fluid Damper with Temperature and Pressure Coupling Effects. Machines 2024, 12, 366. https://doi.org/10.3390/machines12060366
Zhang Y, Xu W, Wang S, Du D, Geng Y. Mechanical Modeling of Viscous Fluid Damper with Temperature and Pressure Coupling Effects. Machines. 2024; 12(6):366. https://doi.org/10.3390/machines12060366
Chicago/Turabian StyleZhang, Yunlong, Weizhi Xu, Shuguang Wang, Dongsheng Du, and Yan Geng. 2024. "Mechanical Modeling of Viscous Fluid Damper with Temperature and Pressure Coupling Effects" Machines 12, no. 6: 366. https://doi.org/10.3390/machines12060366
APA StyleZhang, Y., Xu, W., Wang, S., Du, D., & Geng, Y. (2024). Mechanical Modeling of Viscous Fluid Damper with Temperature and Pressure Coupling Effects. Machines, 12(6), 366. https://doi.org/10.3390/machines12060366






