Application of a Multi-Criterion Decision-Making Method for Solving the Multi-Objective Optimization of a Two-Stage Helical Gearbox

Abstract

This paper provides a novel application of a multi-criterion decision-making (MCDM) method to the multi-objective optimization problem of designing a two-stage helical gearbox. This study’s goal is to identify the ideal primary design elements that increase gearbox efficiency while reducing the gearbox cross-section area. In this work, three primary design parameters were selected for investigation: the gear ratio of the first stage and the coefficients of wheel face width (CWFW) of the first and second stages. The multi-objective optimization problem was further split into two phases: phase 1 solved the single-objective optimization problem of minimizing the gap between the variable levels, and phase 2 solved the multi-objective optimization issue of identifying the ideal key design factors. Moreover, the multi-objective optimization problem was handled by the SAW method as an MCDM approach, and the weight criteria were computed using the entropy approach. This study’s significant characteristics are as follows: First, a multi-objective optimization problem was successfully solved using the MCDM approach (SAW technique) for the first time. Second, the power losses in idle motion were investigated in this work in order to determine the efficiency of a two-stage helical gearbox. From this study’s findings, the ideal values for three major design parameters can be determined for the design of a two-stage helical gearbox.

1. Introduction

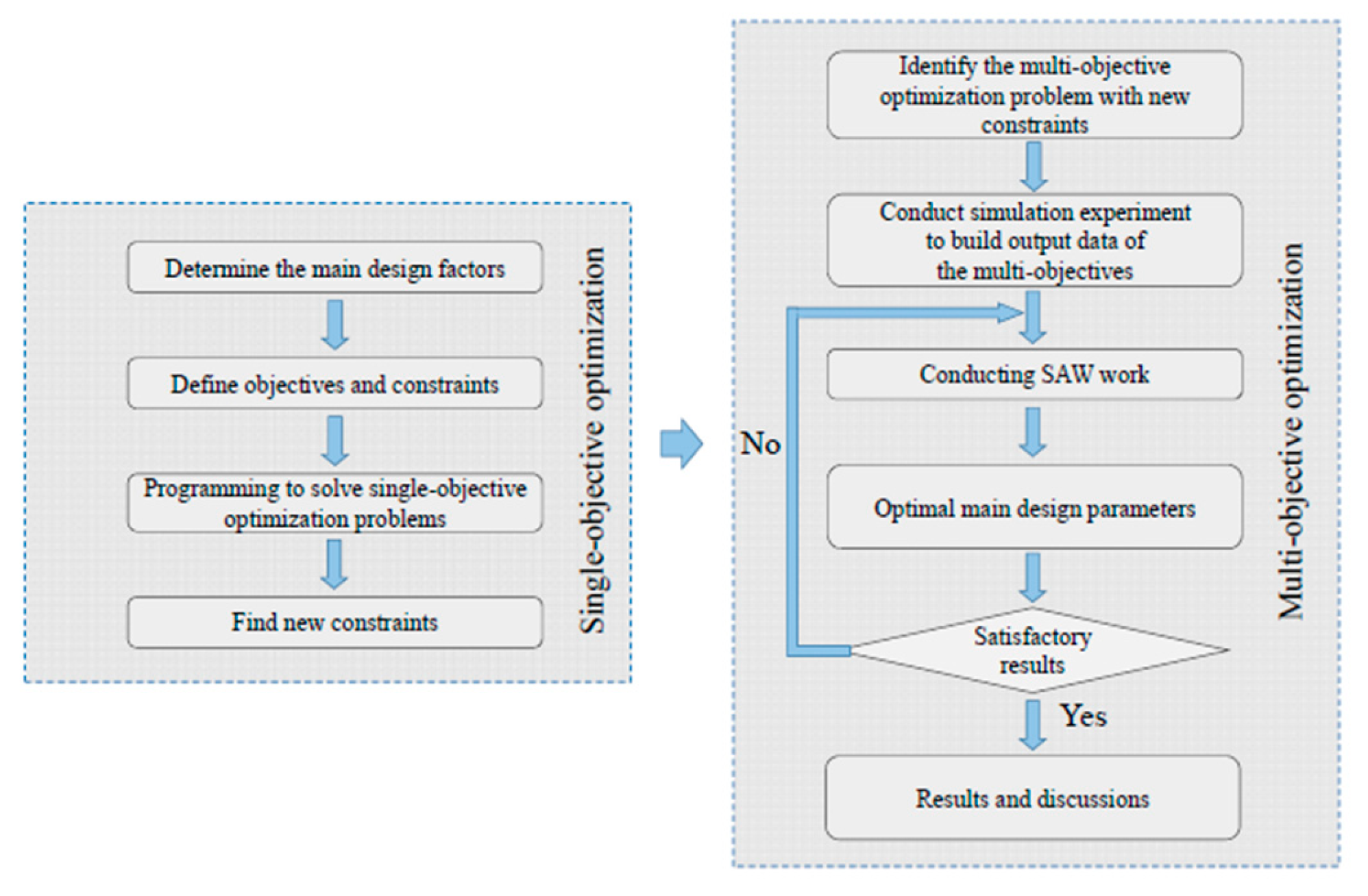
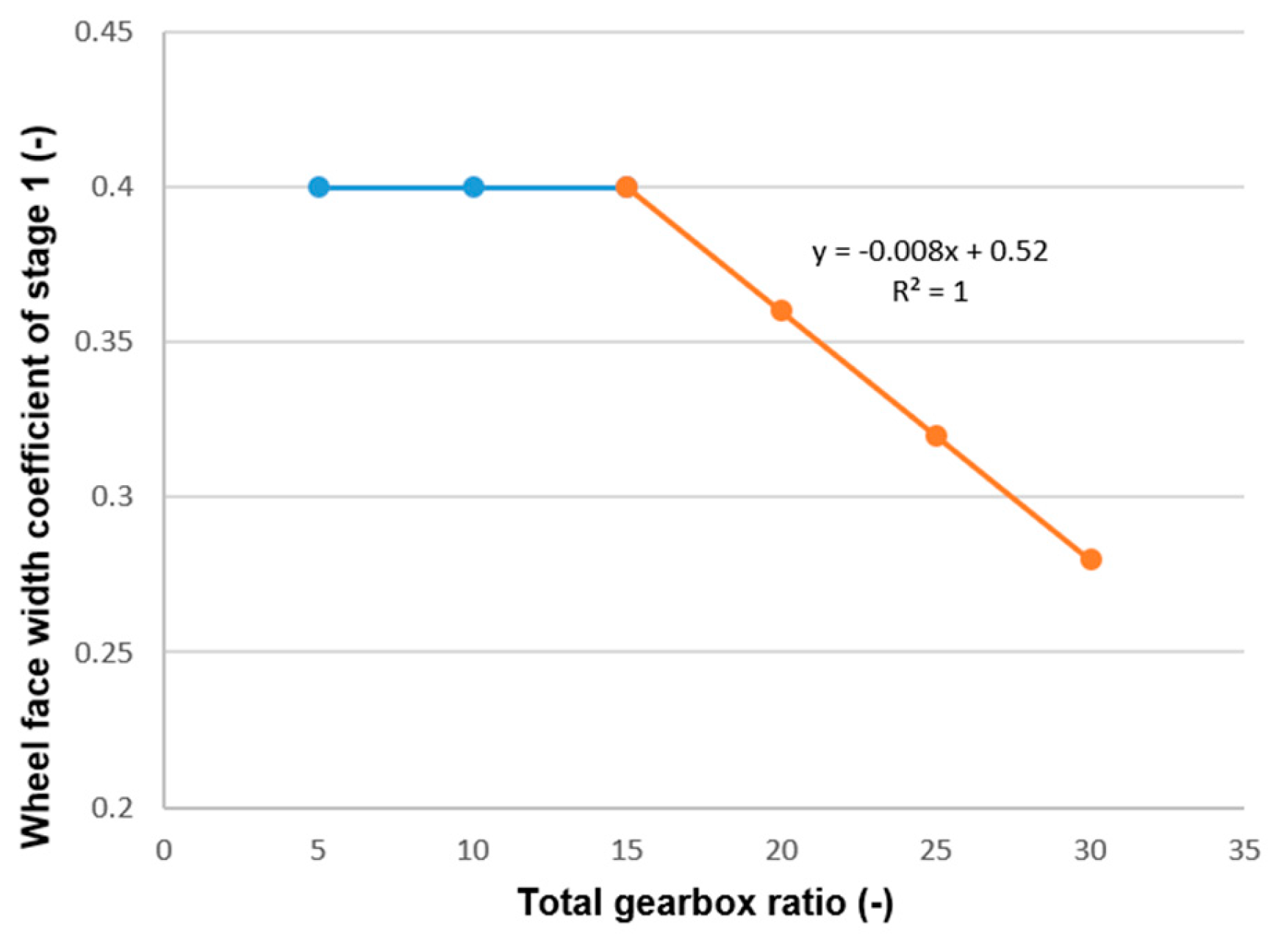
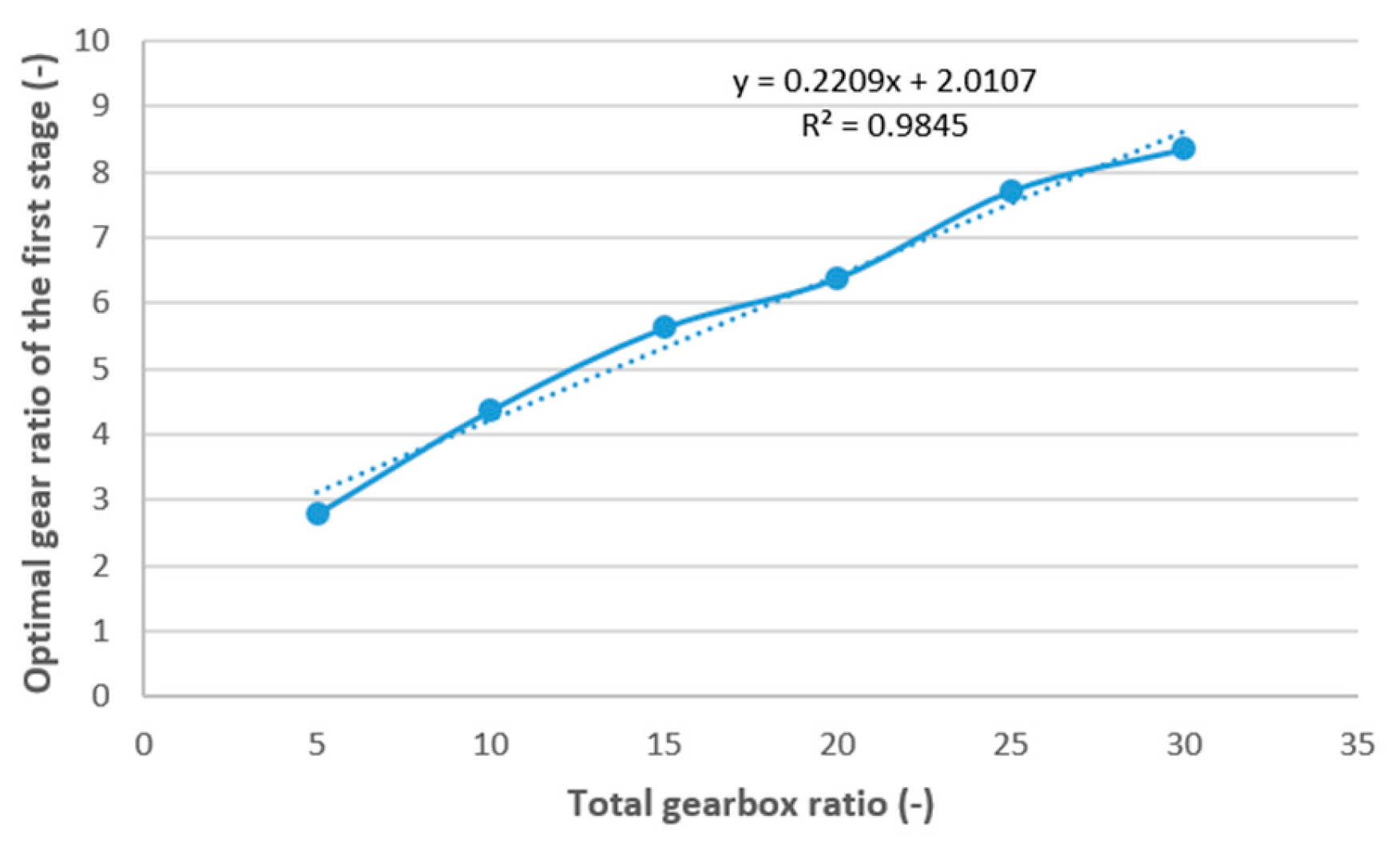
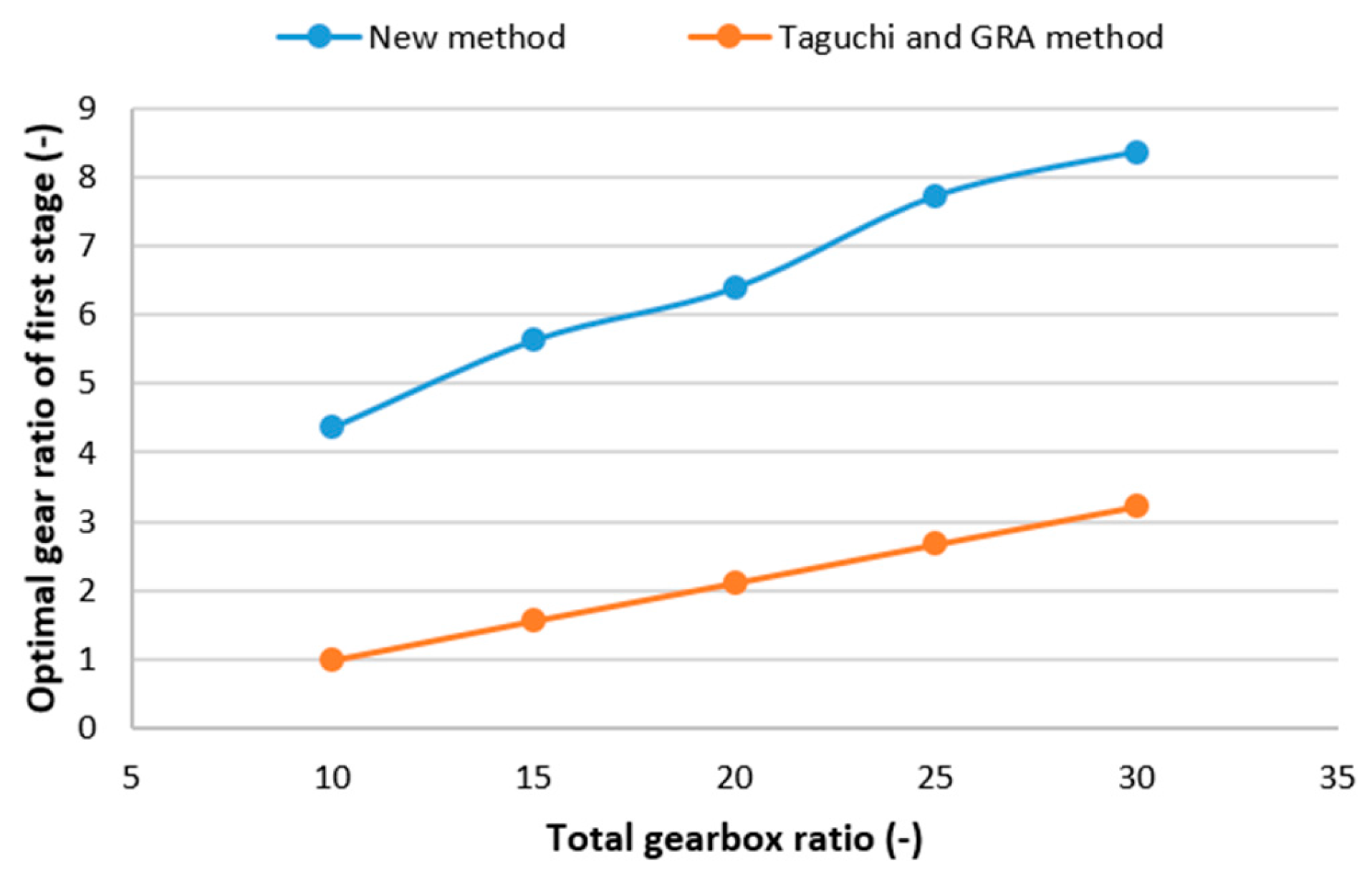
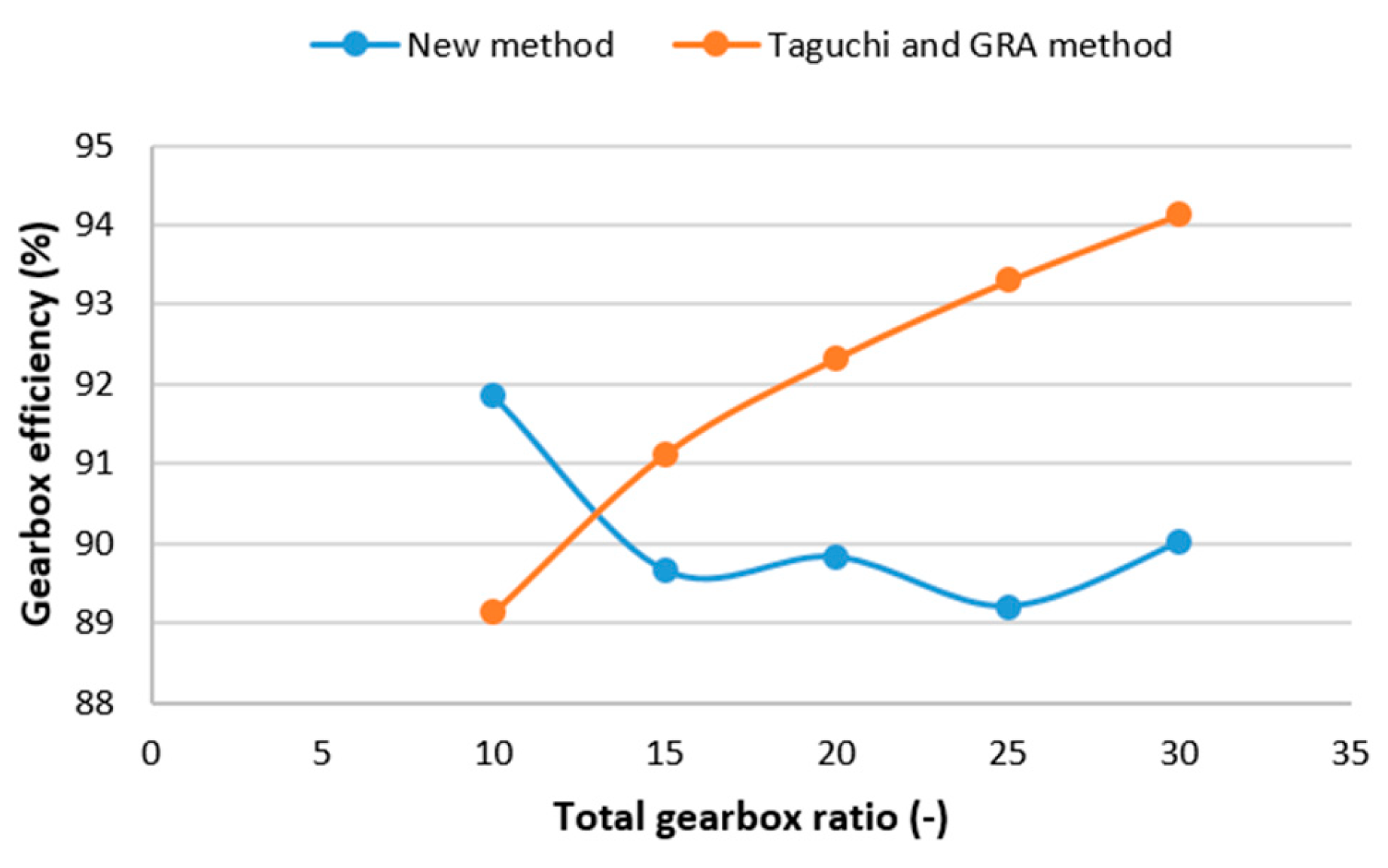
The most crucial component of a mechanical drive system is the gearbox. It facilitates the lowering of the torque and speed transfer from the motor shaft to the working shaft. Because of this, numerous experts are working on optimization of the gearbox. In practice, multi-objective optimization refers to optimization issues in practice that involve the simultaneous optimization of two or more objective functions. Maximizing multiple performance parameters at once, including efficiency, size, mass, and load-carrying capability, can be difficult and complex when building a gearbox utilizing multi-objective optimization. In order to solve these issues, numerous optimization approaches have been created.

Using the response surface method, H. Wang et al. conducted a multi-objective optimization research for the helical gear in a centrifugal compressor [1]. Two specific goals were chosen for this project: the minimal gear mass and the highest gear stress. According to reports, the helical gear’s maximum stress is within permissible bounds and its mass has decreased by 27.4%. The Non-Dominated Sorting Genetic Algorithm II methodology (NSGA-II) was employed by D. Miller et al. [2] in a multi-objective spur gear pair optimization investigation. Enhancement of gear efficiency and decrease in gear volume were this study’s goals. It was observed that a trade-off between efficiency and volume was necessary and that a lower gear module, a lower face width, greater profile shift coefficients, and a higher pinion tooth count all worked well together to achieve these goals. A mono-objective self-adaptive algorithm approach was used in [3] to solve the optimization of tooth changes for spur and helical gears. The PSO (particle swarm optimization) method was the foundation of this strategy. Multi-objective optimization enhanced the transmission error signal’s maximal contact pressures and root mean square values. Edmund S. Maputi and Rajesh Arora [4] used the NSGA-II and the TOPSIS (Technique for Order of Preference by Similarity to Ideal Solution) approach to solve multi-objective optimization by concurrently taking three objectives into consideration: volume, power output, and center distance. Their study’s findings can provide insight into the design of small gearboxes. In [5], a planetary gearbox was optimized using the NSGA-II method while taking into account crucial tribological and regular mechanical restrictions. Comparing the results of single-objective optimization with and without tribological restrictions, the multi-objective optimization result demonstrated a considerable reduction in weight and power loss. In order to minimize gear weight, contact stress throughout the contact path, and optimal film thickness at the contact point, Jawaz Alam and Sumanta Panda [6] established a strategy for spur gear set design optimization. In order to guarantee a notable decrease in weight and contact stress of a profile-modified spur gear set with sufficient film thickness at the site of contact, this work used particle swarm optimization, particle swarm optimization-based teaching–learning optimization, and Jaya algorithms. The gear design was considerably better with optimum addendum coefficient values within the design space than with conventional designs, according to the study’s findings. A unique multi-objective optimization of a two-stage spur gearbox utilizing the NSGA-II method was introduced by M. Patil et al. [7]. Two goal functions—minimal gearbox volume and minimum gearbox power losses—were involved in this effort. Their study’s findings suggest that solutions derived from single-objective minimization had a significant likelihood of wear failure. Additionally, when utilizing multi-goal optimization as opposed to single-objective optimization, the overall power loss was cut in half. Chrystopher V.T. et al. [8] used the MCDM method to find the ideal gear material for a gearbox in order to enhance surface fatigue and boost its wear resistance. Their study aimed to enhance surface fatigue resistance and maximize its efficiency when applied to a gearbox. In [9], the multi-objective design of helical gear pair transmission was taken into consideration. The objective functions included gear volumes and opposing number of overlap ratio. In this study, the Parameter-Adaptive Harmony Search Algorithm (PAHS) was used to address the optimization problem. Recently, X.H. Le and N.P. Vu [10] explored the multi-objective optimization problem of designing a two-stage helical gearbox using the Taguchi technique and grey relation analysis (GRA). Finding the optimal primary design parameters that maximize gearbox efficiency while minimizing gearbox mass was the goal of their study. This method was also used in [11] to identify the best major design parameters for a two-stage bevel helical gearbox with the goal of maximizing gearbox efficiency and reducing gearbox volume. A multi-target optimization research for the two-stage gearbox of xEV-axle drives was carried out by M. Hofstetter et al. [12]. Three specific goals were chosen for this work’s investigation: gearbox efficiency, packaging metric, and total expenses. Additionally, a closed loop of choosing the gearbox design parameters and then performing a gearbox analysis was included in the optimization process. The above study’s findings suggested that the benchmark solution could still be improved, particularly in light of the cost and packaging trade-off. In order to build a drive system for electric vehicles, Istenes G. and J. Polák [13] carried out research to jointly optimize an electric motor and a gearbox. The goal of their effort was to minimize both the driving system’s weight and the overall energy waste. To highlight the additional potential of cooperative optimization, the optimization results were contrasted with earlier findings. If a drive system is optimized overall, it has been stated that increasing the gear ratio increases the system’s overall efficiency. The most effective power flow solutions for a power system, taking into account the electric market and renewable energy, more particularly, nodal prices and wind turbine placement, were presented in [14]. The placement of wind turbines was optimized in this study to increase transmission power systems’ profits. Nevertheless, the study did not take into account the possibility of reducing power loss in the wind turbine system by improving the gearbox’s efficiency. To enhance the hypoid gears’ operational features, a multi-objective optimization technique was developed [15]. The maximum tooth contact pressure, the minimum transmission error, the minimum gear mesh temperature, and the maximum gear pair efficiency were the four goals to be studied. The model was also solved using the NSGA-II approach. In [16], a study on the mechanical efficiency forecasting model and energy loss for aero-engine bevel gear power transmission was presented. Based on the research findings, a novel model for predicting energy loss and mechanical efficiency was put forth, utilizing enhanced thermal elastohydrodynamic lubrication analysis and taking into account the non-Newtonian fluid effect and entrainment angle. Higher and higher degrees of aero-engine bevel gear production efficiency and design sustainability were made possible by this approach. It can offer essential access to geometric and physical evaluations that can enhance the aero-engine power transmission system’s overall energy generation, conversion, transfer, and usage.

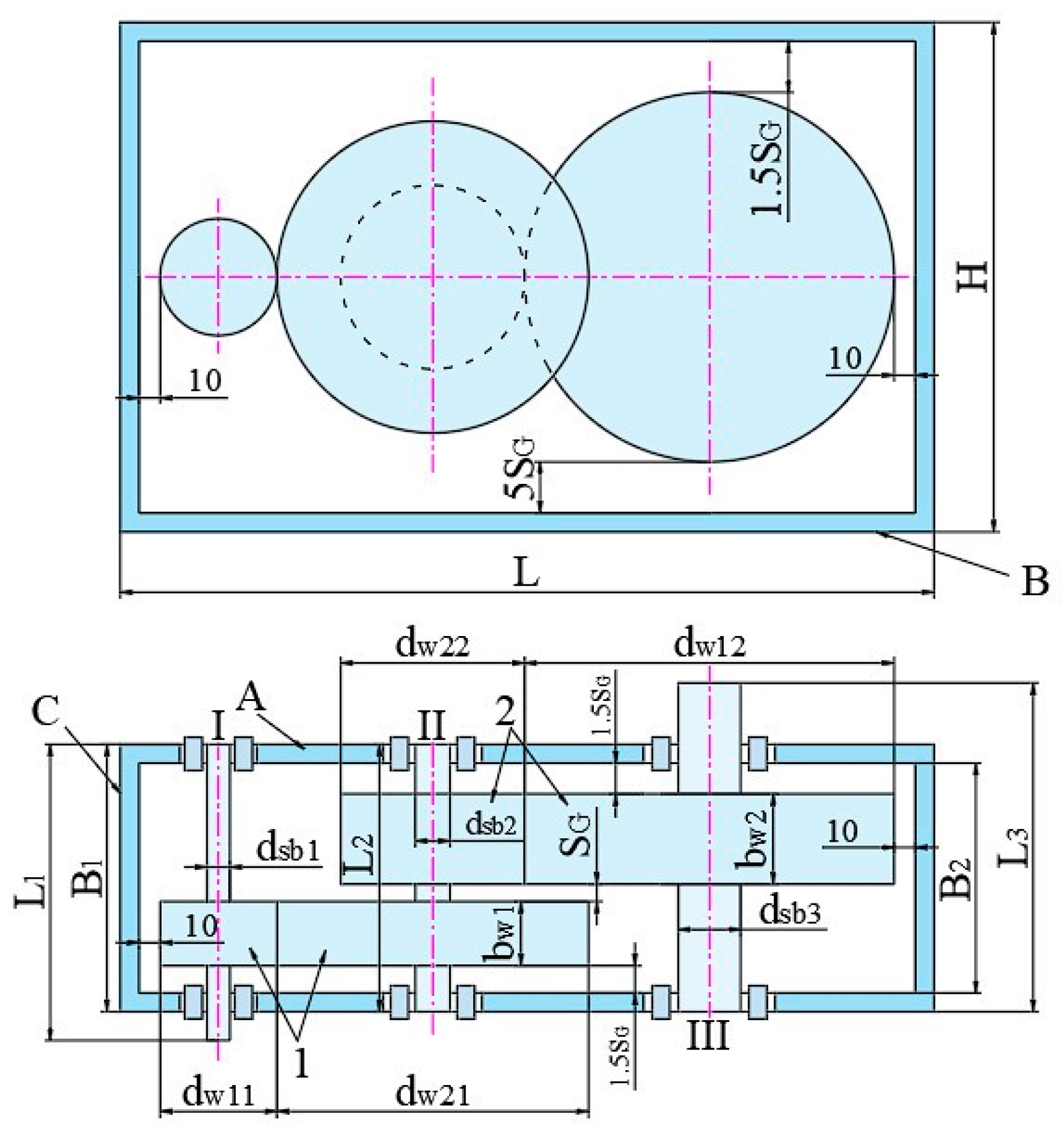
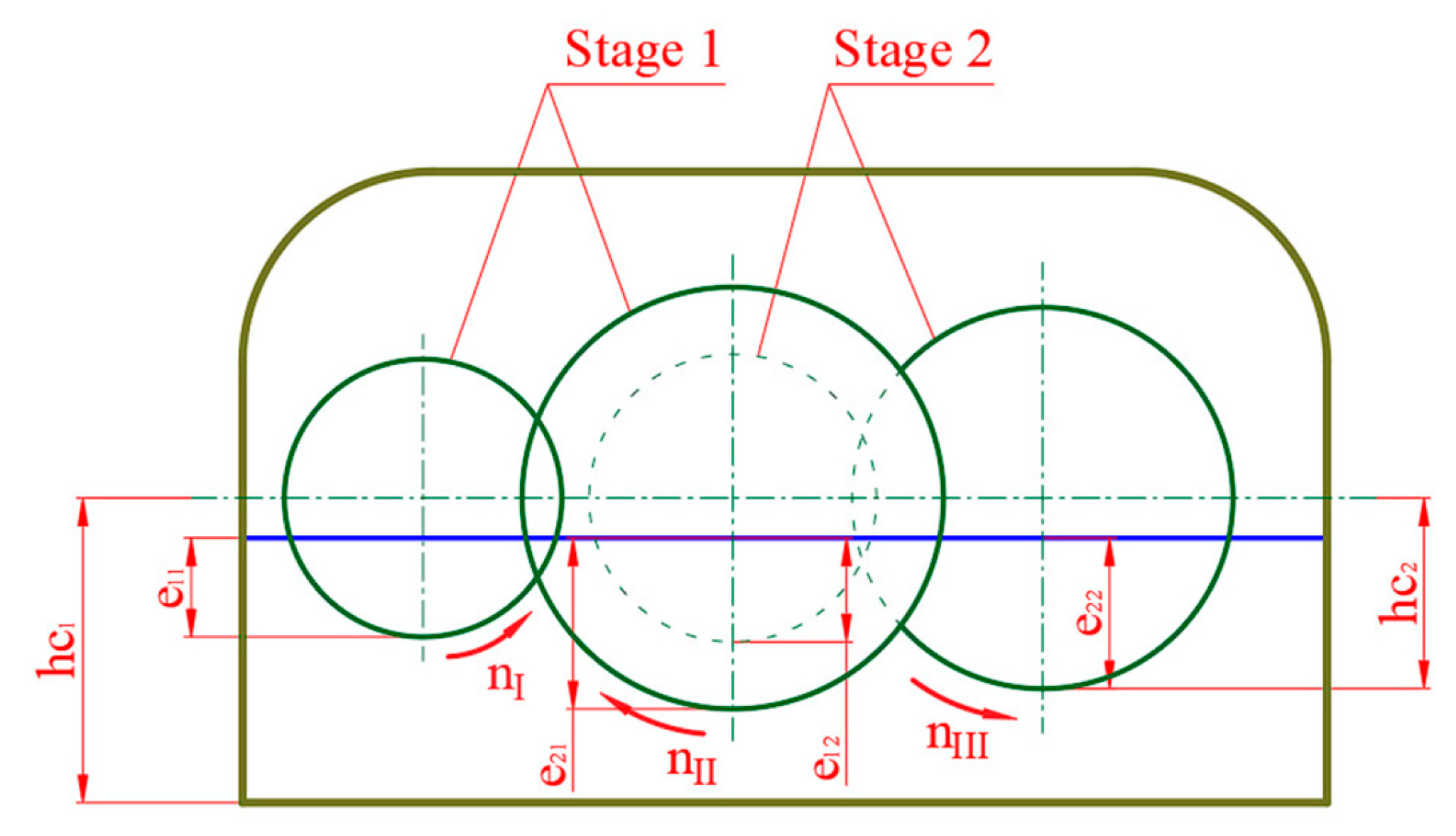
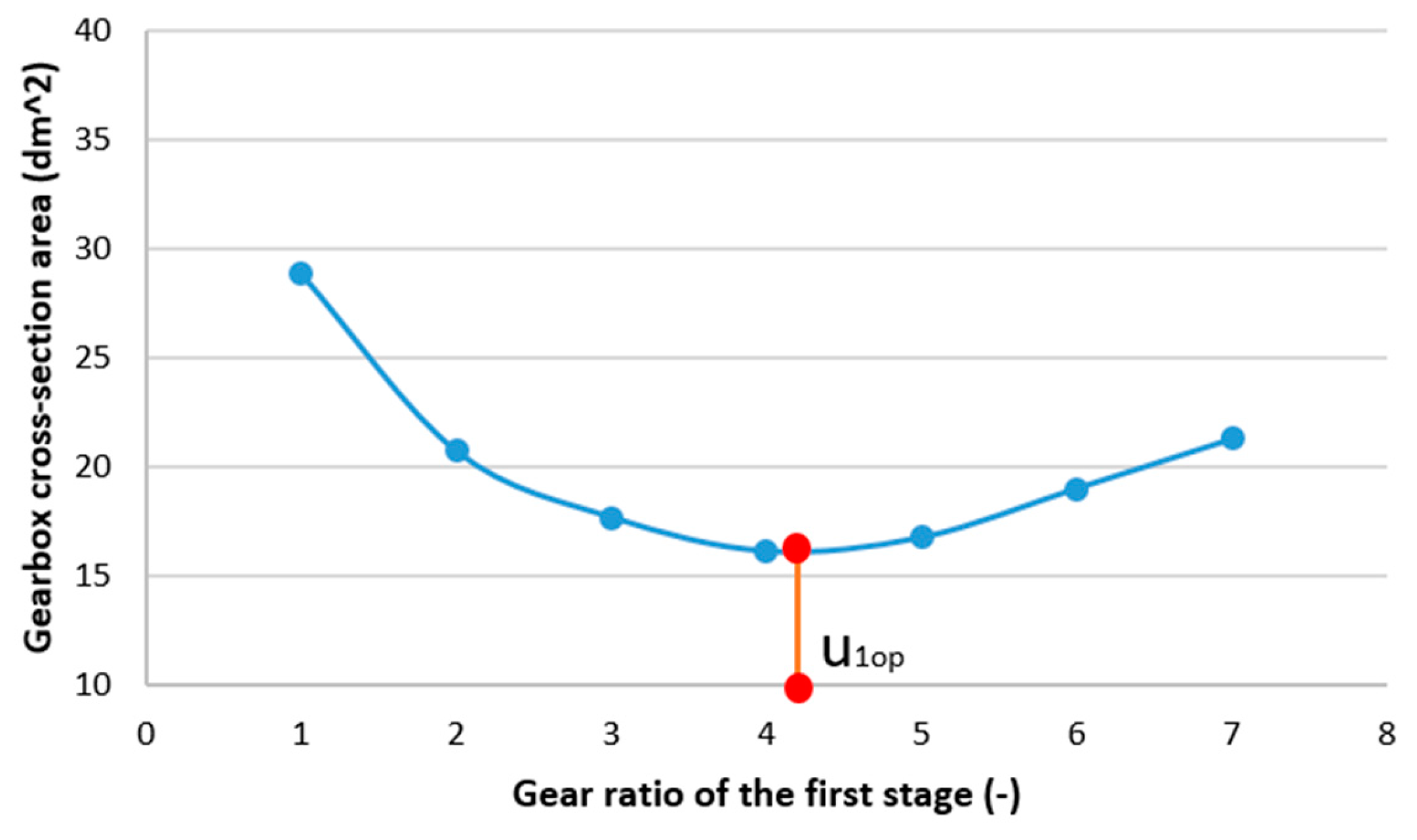
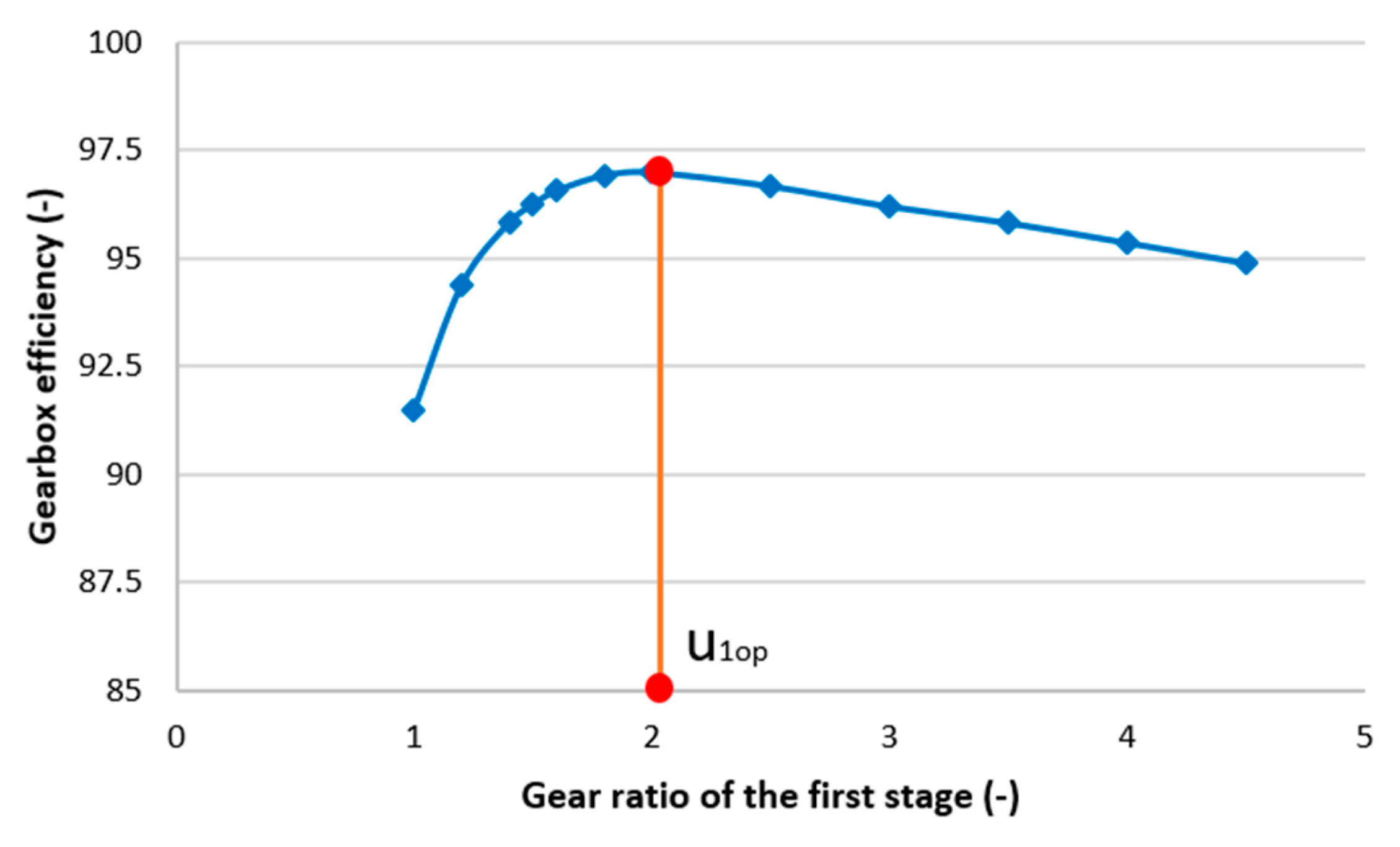
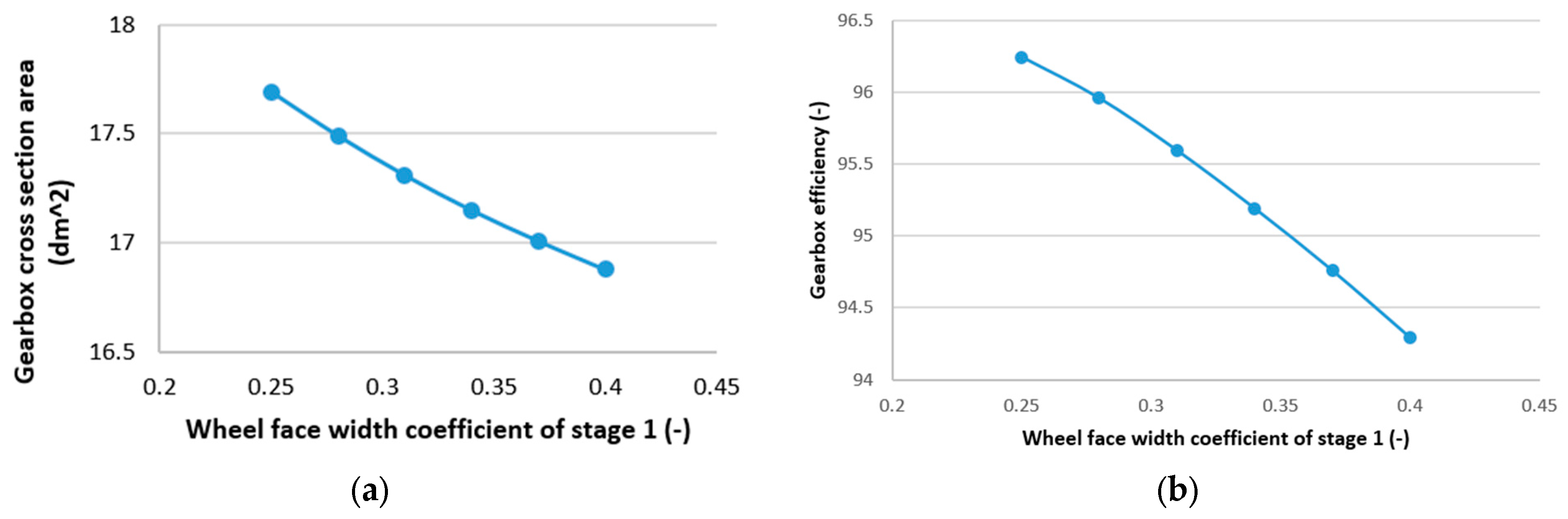
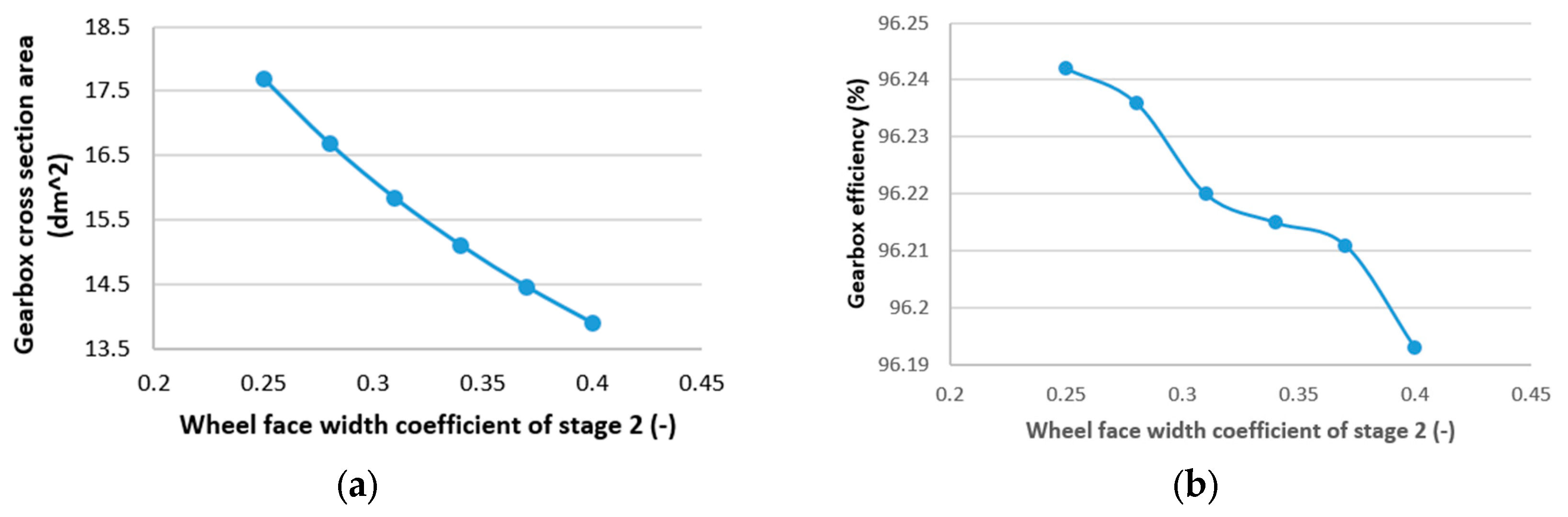
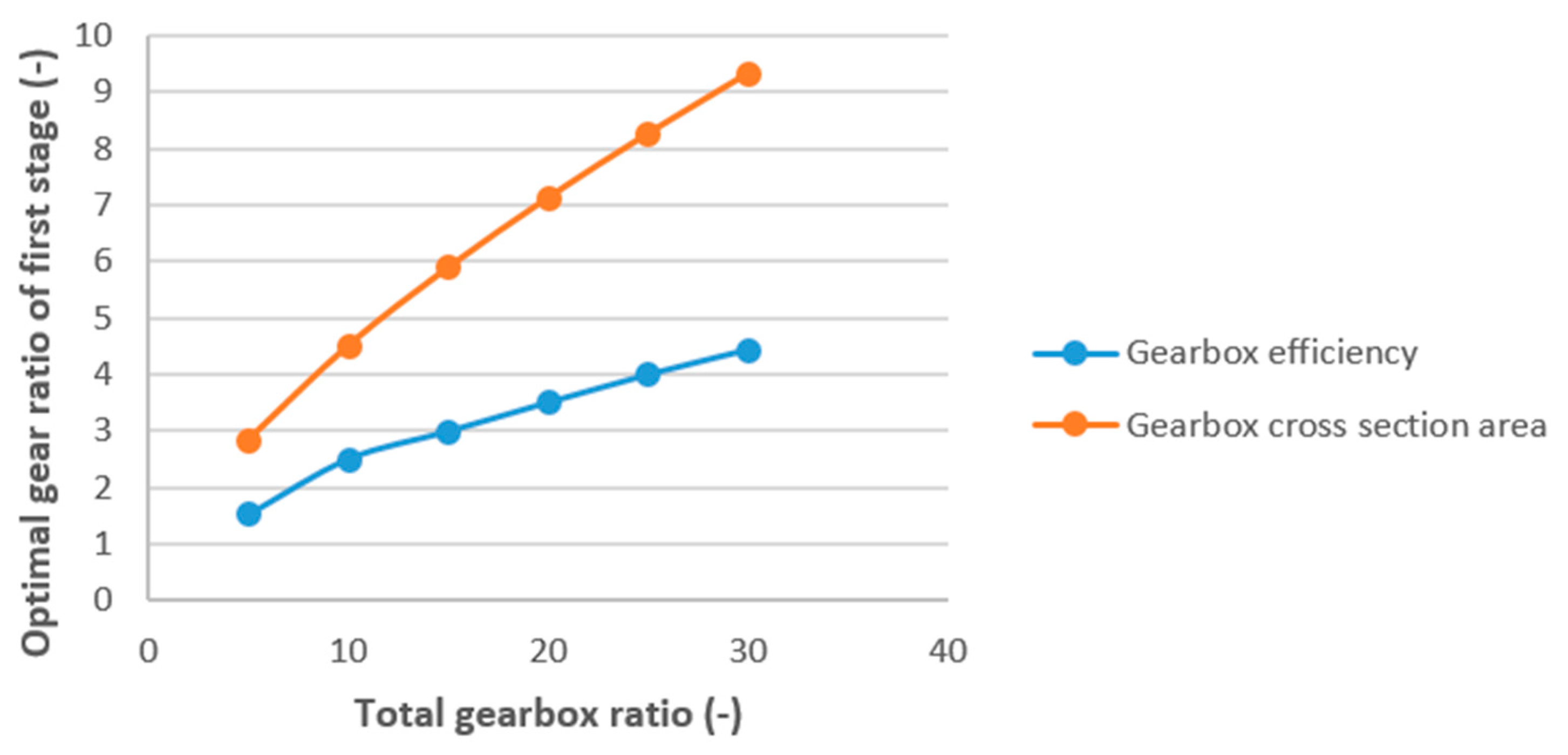
It can be found from previous studies that the best primary design parameters for helical gearboxes have not been found using the MCDM technique, despite a great deal of research on multi-objective optimization for helical gearboxes. The present study reports on a multi-objective optimization study carried out for a two-stage helical gearbox, with two particular goals in mind: increasing gearbox efficiency and minimizing the gearbox cross-section area. The three optimum main design features for the two-stage helical gearbox were examined in this study: the gear ratio of the first stage and the CWFW of both stages. Additionally, the SAW method was selected to solve the multi-objective optimization issue, and the entropy methodology was used to establish the weights of the criteria. One of the primary research conclusions recommends using an MCDM technique in conjunction with two-step problem solving to address multi-objective optimization problems as well as single- and multi-objective problems. Furthermore, the solutions to the challenge out-perform those from previous research.

2. Optimization Problem

In order to construct the optimization problem, the gearbox cross-section areas and gearbox efficiency are first calculated in this section. The stated objective functions and limitations are then provided.

Table 1. The nomenclatures used in the optimization work.

Parameters	Nomenclature	Units
Allowable contact stress of stage 1	AS1	MPa
Allowable contact stress of stage 2	AS2	MPa
Allowable shear stress of shaft material	[τ]	MPa
Arc of approach on i stage	${\beta }_{\mathrm{a}\mathrm{i}}$
Arc of recess on i stage	${\beta }_{\mathrm{r}\mathrm{i}}$
Base-circle radius of the pinion	$R_{01i}$	mm
Base-circle radius of the gear	$R_{02i}$	mm
Contacting load ratio for pitting resistance	kHβ	-
Center distance of stage 1	aw1	mm
Center distance of stage 2	aw2	mm
Diameter of shaft i	dsi	mm
Efficiency of a helical gearbox	ηhb	-
Efficiency of the i stage of the gearbox	ηgi	-
Efficiency of a helical gear unit	ηhg	-
Efficiency of a rolling bearing pair	ηb	-
Friction coefficient	f	-
Friction coefficient of bearing	fb	-
Gearbox cross-section area	Agb	dm2
Gearbox length	L	dm
Gearbox height	H	dm
Gear ratio of stage 1	u1	-
Gear ratio of stage 2	u2	-
Gearbox ratio	ugb	-
Gear width of stage 1	bw1	mm
Gear width of stage 2	bw2	mm
Hydraulic moment of power losses	TH	Nm
ISO viscosity grade number	VG40
Length of shaft i	lsi	mm
Load of bearing i	Fi	N
Material coefficient	ka	MPa1/3
Output torque	Tout	Nmm
Outside radius of the pinion	$R_{e1i}$	mm
Outside radius of the gear	$R_{e2i}$	mm
Outside diameter of the gear of stage i	da2i	mm
Peripheral speed of bearing	vb	m/s
Pitch diameter of the pinion of stage 1	dw11	mm
Pitch diameter of the gear of stage 2	dw21	mm
Pitch diameter of the pinion of stage 2	dw12	mm
Pitch diameter of the gear of stage 2	dw22	mm
Power loss in the gears	Plg	kW
Power loss in the bearings	Plb	kW
Power loss in the seals	Pls	kW
Power loss in the idle motion	Pzo	kW
Pressure angle	α	rad.
Sliding velocity of gear	v	m/s
Total power loss in the gearbox	Pl
Torque on the pinion of stage i	T1i	Nmm
Wheel face width coefficient of stage 1	Xba1	-
Wheel face width coefficient of stage 2	Xba2	-

lists the nomenclatures used in the optimization problem to make calculations easier.

2.1. Determination of Gearbox Cross-Section Area

The gearbox cross-section area, $A_{gb},$ is determined by

$$A_{gb}=L·H$$

(1)

where L and H (Figure 1) are calculated by the following [17]:

$$L={(d}_{w11}+d_{w21}/2+d_{w12}/2+d_{w22}/2+22.5)/0.975$$

(2)

$$H=max\left(d_{w21};d_{w22}\right)+8.5·S_G$$

(3)

$$S_G=0.005·L+4.5$$

(4)

In the above equations,

$$d_{w1i}=2·a_{wi}/(u_i+1)$$

(5)

$$d_{w2i}=2·a_{wi}·u_i·/(u_i+1)$$

(6)

$$b_{w1}=X_{ba1}{·a}_{w1}$$

(7)

$$b_{w2}=X_{ba2}{·a}_{w2}$$

(8)

In them, a_wi is calculated by the following equation based on contact strength condition (for the involute gear profile with a pressure angle of 20 degrees) [18]:

$$a_{wi}=k_a·(u_i+1)·\sqrt[3]{T_{1i}·k_{H\beta }/({\left[{AS}_i\right]}^2·u_i·X_{bai})}$$

(9)

with

$$T_{1i}=\frac{T_r}{\prod _{j=i}^3{(u}_i·{\eta }_{hg}^{3-i}·{\eta }_{be}^{4-i})}$$

(10)

2.2. Determination of Gearbox Efficiency

The efficiency of a two-stage helical gearbox (%) can be found by

$${\eta }_{gb}=100-\frac{100·P_l}{P_{in}}$$

(11)

wherein P_l is calculated by [19]

$$P_l=P_{lg}+P_{lb}+P_{ls}+P_{Z0}$$

(12)

where P_lg, P_lb, P_ls, and P_zo are determined by the following:

+) Calculation of power loss in the gears, P_lg:

$$P_{lg}=\sum _{i=1}^2{P}_{lgi}$$

(13)

where

$$P_{lgi}=P_{gi}·\left(1-{\eta }_{gi}\right)$$

(14)

In this, ${\eta }_{gi}$ is determined by [20]

$${\mathsf{\eta }}_{\mathrm{g}\mathrm{i}}=1-\left(\frac{1+1/{\mathrm{u}}_{\mathrm{i}}}{{\mathsf{\beta }}_{\mathrm{a}\mathrm{i}}+{\mathsf{\beta }}_{\mathrm{r}\mathrm{i}}}\right)·\frac{{\mathrm{f}}_{\mathrm{i}}}{2}·\left({\mathsf{\beta }}_{\mathrm{a}\mathrm{i}}^2+{\mathsf{\beta }}_{\mathrm{r}\mathrm{i}}^2\right)$$

(15)

with ${\beta }_{\mathrm{a}\mathrm{i}}$ and ${\beta }_{\mathrm{r}\mathrm{i}}$ calculated by [20]

$${\mathsf{\beta }}_{\mathrm{a}\mathrm{i}}=\frac{{\left({\mathrm{R}}_{\mathrm{e}2\mathrm{i}}^2-{\mathrm{R}}_{02\mathrm{i}}^2\right)}^{1/2}-{\mathrm{R}}_{2\mathrm{i}}·\mathrm{s}\mathrm{i}\mathrm{n}\mathsf{\alpha }}{{\mathrm{R}}_{01\mathrm{i}}}$$

(16)

$${\mathsf{\beta }}_{\mathrm{r}\mathrm{i}}=\frac{{\left({\mathrm{R}}_{\mathrm{e}1\mathrm{i}}^2-{\mathrm{R}}_{01\mathrm{i}}^2\right)}^{1/2}-{\mathrm{R}}_{1\mathrm{i}}·\mathrm{s}\mathrm{i}\mathrm{n}\mathsf{\alpha }}{{\mathrm{R}}_{01\mathrm{i}}}$$

(17)

From the data in [20], f in (15) can be determined by the following regression equations [10]:

-

If v ≤ 0.424 (m/s):

$$\mathrm{f}=-0.0877·\mathrm{v}+0.0525$$

(18)

-

If v > 0.424 (m/s):

$$\mathrm{f}=0.0028·\mathrm{v}+0.0104$$

(19)

+) Calculation of power loss in bearings P_lb [19]:

$$P_{lb}=\sum _{i=1}^6{f}_b·F_i·v_i$$

(20)

where i = 1 ÷ 6 and $f_b=0.0011$ because the radical ball bearings with angular contact were used [19].

+) Calculation of power loss in seals, Ps [19]:

$$P_s=\sum _{i=1}^2{P}_{si}$$

(21)

where i is the ordinal number of seal (i = 1÷2), and $P_{si}$ can be determined by

$$P_{si}=\left[145-1.6·t_{oil}+350·\mathit{log}\mathit{log}\left({VG}_{40}+0.8\right)\right]·d_s^2·n·{10}^{-7}$$

(22)

+) Calculation of power loss in idle-motion Pzo [19]:

$$P_{Zo}=\sum _{i=1}^k{T}_{Hi}·\frac{\pi ·n_i}{30}$$

(23)

where k is the total number of gear pairs (k = 2), n is the number of revolution of driven gear, and T_Hi is calculated by [19]

$$T_{Hi}=C_{Sp}·C_1·e^{\frac{C_2·v}{v_{t0}}}$$

(24)

where $C_{Spi}=1$ for stage 1 when the involved oil mast to pass till the mesh, and, for stage, 2 $C_{Spi}$ can be found by (Figure 2)

$$C_{Spi}={\left(\frac{4·e_{max}}{3·h_{Ci}}\right)}^{1.5}·\frac{2·h_{Ci}}{l_{hi}}$$

(25)

In the above, l_hi can be found by the following [19]:

$${\mathrm{l}}_{\mathrm{h}\mathrm{i}}=\left(1.2÷2.0\right)·{\mathrm{d}}_{\mathrm{a}2\mathrm{i}}$$

(26)

In (24), C_1i and C_2i (i = 1 ÷ 2) are determined by the following [19]:

$${\mathrm{C}}_{1\mathrm{i}}=0.063·\left(\frac{{\mathrm{e}}_{1\mathrm{i}}+{\mathrm{e}}_{2\mathrm{i}}}{{\mathrm{e}}_0}\right)+0.0128·\left(\frac{{\mathrm{b}}_{\mathrm{w}\mathrm{i}}}{{\mathrm{b}}_0}\right)$$

(27)

$${\mathrm{C}}_{2\mathrm{i}}=\frac{{\mathrm{e}}_{1\mathrm{i}}+{\mathrm{e}}_{2\mathrm{i}}}{80·{\mathrm{e}}_0}+0.2$$

(28)

2.3. Objective Functions and Constrains

2.3.1. Objective Functions

In this work, the multi-objective optimization problem consists of two single objectives:

-

Minimizing the gearbox cross-section area:

$$\mathrm{m}\mathrm{i}\mathrm{n} f_1\left(X\right)=V_{gb}$$

(29)

-

Maximizing the gearbox efficiency:

$$\mathrm{m}\mathrm{i}\mathrm{n} f_2\left(X\right)={\mathsf{\eta }}_{\mathrm{g}\mathrm{b}}$$

(30)

where X is the vector that represents the design variables. A two-stage helical gearbox has five main design parameters: u₁, X_ba1, X_ba2, AS₁, and AS₂ [10]. Moreover, it has been demonstrated that the maximum values of AS₁ and AS₂ match their ideal values [10]. Consequently, u₁, X_ba1, and X_ba2—the three main design factors—have been selected as variables for the optimization issue in this work. Consequently, we have the following:

$$X=\left\{u_1,{Xba}_1,{Xba}_2\right\}$$

(31)

2.3.2. Constrains

The multi-objective function needs to be subject to the following constraints:

$$1\le u_1\le 9 \mathrm{and} 1\le u_2\le 9$$

(32)

$$0.25\le {Xba}_1\le 0.4 \mathrm{and} 0.25\le {Xba}_2\le 0.4$$

(33)

3. Methodology

3.1. Method to Solve Multi-Objective Optimization

In this work, the two objectives of the multi-objective optimization problem are the lowest gearbox cross-section area and the best gearbox efficiency. Furthermore, the optimization problem selects three main design factors to be variables, as noted in Section 2. These variables are listed in

Table 2. Input parameters.

Parameters	Symbol	Lower Bound	Upper Bound
Gearbox ratio of the first stage	u1	1	9
CWFW of stage 1	Xba1	0.25	0.4
CWFW of stage 2	Xba2	0.25	0.4

along with the lowest and maximum values. In practice, an MCDM method is difficult to use to solve the MOO (multi-objective optimization) problem. The reason is that, for solving an MOO problem, the number of possible solutions or possibilities is very large. In this work, with three parameters and their limits as shown in Table 2, and the step between variables being 0.02 (to ensure the accuracy of the parameters and not miss the solution of the optimization problem), the number of options (or number of experimental runs) that need to be determined and compared is $(9-1)/0.02·(0.4-0.25)/0.02·(0.4-0.25)/0.02=22.500$ (runs). With such a large number of options, it is impossible to directly use the MCDM method to solve the OMO problem. This paper uses the SAW method to solve the MCDM problem and the entropy methodology to establish the criterion weights. To supply the input data for the multi-objective optimization problem for a two-stage helical gearbox in the MCDM problem, a simulation experiment is built. The number of experiments that can be conducted by applying the full-factorial design is unlimited because this is a simulation experiment. The total number of experiments is 5³ = 125 because there are three experimental variables (as previously mentioned) and five levels for each variable. A method for resolving multi-objective problems is presented in order to lessen this discrepancy, save time, and enhance the correctness of the results (Figure 2). This process is divided into two stages: phase 1 factors solve the single-objective optimization problem to narrow the gap between levels, and phase 2 factors solve the multi-objective optimization problem to identify the best primary design. Furthermore, if the levels of the variables are not sufficiently close to one another or if the best answer is not appropriate for the requirement, the SAW issue is rerun using the smaller distance between two levels of the u₁ in order to address the multi-objective problem (see Figure 3).

3.2. Method to Solve the MCDM Problem

The SAW approach was first suggested in 2006 [21]. The stages of implementing this method are as follows.

-

Creating initial decision-making matrix:

$$\mathrm{X}=\begin{array}{c}\\ {\mathrm{A}}_1\\ {\mathrm{A}}_2\\ \cdots \\ {\mathrm{A}}_{\mathrm{m}}\end{array}\begin{array}{c}\begin{array}{cccc}{\mathrm{C}}_1& {\mathrm{C}}_2& \cdots & {\mathrm{C}}_{\mathrm{n}}\end{array}\\ \left[\begin{array}{cccc}{\mathrm{y}}_{11}& {\mathrm{y}}_{12}& \cdots & {\mathrm{y}}_{1\mathrm{n}}\\ {\mathrm{y}}_{21}& {\mathrm{x}\mathrm{y}}_{22}& \cdots & {\mathrm{y}}_{2\mathrm{n}}\\ \cdots & \cdots & \cdots & \cdots \\ {\mathrm{y}}_{\mathrm{m}1}& {\mathrm{y}}_{\mathrm{m}2}& \cdots & {\mathrm{y}}_{\mathrm{m}\mathrm{n}}\end{array}\right]\end{array}$$

(34)

In which, m and n are alternative and criterion numbers.

-

Finding the normalized matrix by

$$n_{\mathrm{ij}}=\frac{r_{ij}}{max{r}_{ij}}$$

(35)

$$n_{\mathrm{ij}}=\frac{min{r}_{ij}}{r_{ij}}$$

(36)

Equation (35) is used for the criterion as gearbox efficiency, while (36) is used for the criterion as the gearbox cross-section area.

-

Determine the preference value for each option:

$$V_{\mathrm{i}}=\sum _{j=1}^n{w}_j·n_{ij}$$

(37)

-

Rank the options according to the principle that the option with the highest V_i is the best one.

3.3. Method to Find the Weight of Criteria

The weights of the criteria in this research were determined using the entropy technique. This technique can be implemented following the steps outlined below [22].

-

Determining indicator-normalized values:

$$p_{\mathrm{ij}}=\frac{x_{\mathrm{ij}}}{m+{\sum }_{i=1}^m{x}_{\mathrm{ij}}^2}$$

(38)

-

Finding the entropy for each indicator:

$$m{e}_j=-{\sum }_{i=1}^m\left[p_{ij}\times ln\left(p_{ij}\right)\right]-\left(1-{\sum }_{i=1}^m{p}_{ij}\right)\times ln\left(1-{\sum }_{i=1}^m{p}_{ij}\right)$$

(39)

-

Calculating the weight of each indicator:

$${\mathrm{w}}_{\mathrm{j}}=\frac{1-{\mathrm{m}\mathrm{e}}_{\mathrm{j}}}{{\sum }_{\mathrm{j}=1}^{\mathrm{m}}\left(1-{\mathrm{m}\mathrm{e}}_{\mathrm{j}}\right)}$$

(40)

4. Single-Objective Optimization

In this work, the single-objective optimization problem is solved using the direct-search approach. Furthermore, two single-objective problems—maximizing gearbox efficiency and minimizing gearbox cross-section area—have been investigated using a Excel computer program (Device ID: D4FEAEE3-C716-5EEE-850A-8F37FAFD3C23). Several figures and observations from the program’s findings are listed below: The relationship between u₁ and A_gb is depicted in Figure 4. A_gb reaches its lowest value when u₁ is at its ideal value (Figure 4). The relation between η_gb and u₁ is described in Figure 5. From the figure, it is clear that there is an ideal value of u₁ at which η_gb reaches its maximum. The relationships between X_ba1 and X_ba2 and A_gb and η_gb, respectively, are depicted in Figure 6 and Figure 7. These findings (Figure 6 and Figure 7) show that a rise in X_ba1 and X_ba2 will cause A_gb and η_gb to fall.

The values of the optimal major design factors of two single-objective functions, A_gb and η_gb, are shown in

Table 3. Optimum main design factors of two single objectives.

Objective	Factor	ut
		5	10	15	20	25	30
	u1	2.82	4.49	5.88	7.12	8.26	9.33
Agb	Xba1	0.4	0.4	0.4	0.4	0.4	0.4
	Xba2	0.4	0.4	0.4	0.4	0.4	0.4
	u1	1.51	2.49	2.98	3.49	3.98	4.42
ηgb	Xba1	0.25	0.25	0.25	0.25	0.25	0.25
	Xba2	0.25	0.25	0.25	0.25	0.25	0.25

. This table makes it clear that the A_gb function takes the maxi-mum values of X_ba1 and X_ba2 (X_ba1 = 0.4 and X_ba2 = 0.4) as the ideal values for X_ba1 and X_ba2. This is because, in order for A_gb to be the smallest, d_w21 and d_w22—which are determined using Equation (6)—must also be the smallest. In order to decrease a_w1 and a_w2, X_ba1 and X_ba2 must now be at their highest values (Equation (9)). As opposed to the A_gb function, the η_gb function has the biggest (ideal) value when X_ba1 and X_ba2 (X_ba1 = 0.25 and X_ba2 = 0.25) have the smallest values. This is because the smallest values of P_lg, P_lb, P_ls, and P_zo correspond to the maximum value of the η_gb function. X_ba1 and X_ba2 have a significant impact on power loss in the idle-motion P_zo among these performance factors. In order for P_zo to be small, C_1i must also be small (Equation (27)). In this case, in order for b_w1 and b_w2 to be tiny, X_ba1 and X_ba2 must have small values (Equations (7) and (8)).

From Table 3, the relationship between the total gearbox ratio (u_t) and the ideal gear ratio for the first stage u₁ for both single objectives (A_gb and η_gb) is depicted in Figure 8. Furthermore, freshly computed constraints for the variable u₁ are shown in

Table 4. New constraints of u₁.

ut	u1
	Lower Limit	Upper Limit
5	1.41	2.92
10	2.39	4.59
15	2.88	5.98
20	3.39	7.22
25	3.88	8.36
30	4.32	9.43

.

5. Multi-Objective Optimization

In this study, for solving the OMO problem, a simulation experiment was designed and conducted. In this experiment, different variations of the main design factors of a two-stage helical gearbox were established, and the gearbox cross-section area and efficiency (or the output factors) were calculated for use as the input data for the MCDM problem. To conduct simulation experiments, a computer program was developed. For the analysis, the gearbox ratios 5, 10, 15, 20, 25, and 30 were all taken into account. The solutions to this u_t = 20 problem are shown below. For the first 125 testing cycles, this gearbox ratio was utilized overall (as indicated in Section 3). To solve the multi-objective optimization issue, SAW received the gearbox cross-section area and the efficiency, which were the experiment’s output values. Until there was less than 0.02 between two levels of u₁, this process was repeated.

Table 5. Main design parameters and output results for u_t = 20 in the fourth run of SAW.

Trial	u1	Xba1	Xba2	Agb (dm2)	ηgb (%)
1	6.36	0.25	0.25	17.44	93.41
2	6.36	0.25	0.29	16.23	93.39
3	6.36	0.25	0.33	15.25	93.38
4	6.36	0.25	0.36	14.57	93.36
5	6.36	0.25	0.40	14.28	93.39
6	6.36	0.29	0.25	17.18	92.36
…
23	6.36	0.40	0.33	14.49	88.33
24	6.36	0.40	0.36	13.69	88.31
25	6.36	0.40	0.40	13.02	88.35
…
50	6.37	0.40	0.40	13.02	88.33
51	6.38	0.25	0.25	17.42	93.39
52	6.38	0.25	0.29	16.21	93.37
…
71	6.38	0.40	0.25	16.6	88.32
72	6.38	0.40	0.29	15.43	88.3
73	6.38	0.40	0.33	14.47	88.29
…
94	6.39	0.36	0.36	13.82	89.7
95	6.39	0.36	0.40	13.14	89.74
96	6.39	0.40	0.25	16.59	88.3
…
123	6.4	0.40	0.33	14.46	88.24
124	6.4	0.40	0.36	13.67	88.22
125	6.4	0.40	0.40	13	88.26

displays the main design parameters and output responses for u_t = 20 in the SAW experiment’s fourth and final run. The entropy technique (see Section 3.3) was used to determine the weights of the criterion in the following manner: First, we obtained the normalized values of p_ij utilizing Equation (38). The entropy value of each indicator m_ej was found using Equation (39). Lastly, we determined the weight of the condition w_j using Equation (40). For the latest SAW work run, the weights of A_gb and η_gb were found to be 0.5676 and 0.4324, respectively. How to use the SAW technique for the MCDM process is explained in Section 3.2. First, we computed the decision-making matrices using Equation (31). The first matrix was then normalized using Equations (35) and (36). After that, V_i was computed using Equation (37). In the end, we sorted the options so that the optimal option had the highest V_i. The options’ ranking and number of computed results for u_t = 20 (the most recent SAW work run) are shown in

Table 6. Several calculated results and ranking of alternatives by SAW for u_t = 20.

Trial	nịj		Vi	Rank
	Agb	ηgb
1	0.7454	1.0000	0.8555	120
2	0.8010	0.9998	0.8870	99
3	0.8525	0.9997	0.9161	75
4	0.8922	0.9995	0.9386	46
5	0.9104	0.9998	0.9490	24
6	0.7567	0.9888	0.8570	109
…
23	0.8972	0.9456	0.9181	70
24	0.9496	0.9454	0.9478	37
25	0.9985	0.9458	0.9757	14
…
50	0.9985	0.9456	0.9756	15
51	0.7463	0.9998	0.8559	115
52	0.8020	0.9996	0.8874	92
…
71	0.7831	0.9455	0.8533	124
72	0.8425	0.9453	0.8870	98
73	0.8984	0.9452	0.9186	67
…
94	0.9407	0.9603	0.9491	23
95	0.9893	0.9607	0.9770	1
96	0.7836	0.9453	0.8535	122
…
123	0.8990	0.9447	0.9188	66
124	0.9510	0.9444	0.9482	33
125	1.0000	0.9449	0.9762	9

. The table shows that option 95 is the best option out of all the options provided. As a result, Table 5 reveals the ideal values for the three main design features: u₁ = 6.39, X_ba1 = 0.36, and X_ba2 = 0.4.

Building on the preceding discussion,

Table 7. Optimum main design parameters.

No.	ut
	5	10	15	20	25	30
u1	2.79	4.37	5.63	6.39	7.72	8.36
Xba1	0.4	0.4	0.4	0.36	0.32	0.28
Xba2	0.4	0.4	0.4	0.4	0.4	0.4

presents the ideal values for the primary design parameters that correspond to the remaining u_t values of 5, 10, 20, 25, and 30. The data shown in this table allow for the following deductions to be made:

+) X_ba2 selects the highest value (X_ba2 = 0.4) while X_ba1 selects the highest value (X_ba1 = 0.4) if u_t ≤ 15, and it decreases gradually when 15 ≤ u_t ≤ 30 (Figure 9). These values are relatively close to the A_gb function’s ideal values for X_ba1 and X_ba2. This is because it has been discovered that the average weights of A_gb and η_gb are, respectively, 0.57 and 0.43. Briefly, the A_gb function will typically be served by the ideal values of X_ba1 and X_ba2. When 15 ≤ u_t ≤ 30, X_ba2 can be calculated using the following equation (with R² = 1):

$${Xba}_2=-0.008·u_t+0.52$$

(41)

+) An obvious first-order relationship exists between the ideal values of u₁ and u_t (Figure 10). Additionally, it has been discovered that the ideal values of u₁ may be calculated using the regression equation that follows (with R² = 0.9845):

$$u_1=0.2209·u_t+2.0107$$

(42)

The following equation can be used to find the ideal value of u₂ once u₁ has been established:

$$u_2=u_t/u_1$$

(43)

To assess the model’s results for identifying the ideal values when derived using the SAW technique (new method), the findings of this study are compared with those acquired using the Taguchi and grey relational analysis method (old method) in [23]. The ideal values of u₁ corresponding to different u_t determined by the two approaches are shown in Figure 11. Figure 12 and Figure 13, respectively, show the gearbox cross-section area and the efficiency numbers as derived by the old and new methodologies. These statistics demonstrate that the new method generates a substantially smaller gearbox cross-section area (from 28.9 to 45.03%) compared to the calculations obtained using the previous method. However, when u_t > 13, the maximum efficiency values determined by the new method are marginally less (less than 4.5%) than those determined by the previous method. For example, when u_t = 10, the gearbox cross-section area decreases $\left(21.43-11.78\right)·100/21.43=45.03$ (%), and the gearbox efficiency increases $\left(91.85-89.14\right)·100/91.85=2.95$ (%). When u_t=30, the gearbox cross-section area decreases to $\left(20.24-14.39\right)·100/20.24=28.90$ (%) using new method, but the new method’s gearbox efficiency $\left(94.13-90.02\right)·100/94.13=4.57$ (%) is lower than the old method’s.

6. Conclusions

The SAW technique was utilized in this study to solve the multi-objective optimization problem related to the design of a two-stage helical gearbox. This study’s goal was to determine the most critical design parameters that maximized gearbox efficiency while reducing the gearbox cross-section area. To achieve this, three crucial design components were chosen: the CWFW for the first and second stages and the first-stage gear ratio. In addition, there were two phases in the multi-objective optimization problem solution process. Phase 1 was centered on solving the single-objective optimization problem of reducing the difference between variable values, whereas phase 2 was concerned with determining the optimal primary design factors. The following findings were drawn from this work:

-

The single-objective optimization problem speeded up and simplified the resolution of the multi-objective optimization problem by bridging the gap between variable levels.

-

Two single goals—the maximum gearbox efficiency and the minimum gearbox cross-section area—were assessed in connection with the important design elements.

-

By using the SAW technique repeatedly until the required results were reached, the multi-objective optimization problem could be solved more precisely (u₁ had an accuracy of less than 0.02).

-

The three main design parameters for a two-stage helical gearbox—Equations (41) and (42) and Table 7—were recommended to have optimal values based on this study’s findings.

-

Regression Equation (42), with R² = 0.9845, proved that the experimental data’s extraordinary degree of concordance with the proposed model of u₁ verified their reliability.

-

The results showed that the novel approach to the multi-objective optimization issue produced better findings when compared with the prior methods (the Taguchi and GRA approaches).