Simplified Strategy for Trajectory Tracking Application of a Passive Suspension Rover-Type Mobile Robot
Abstract
1. Introduction
- (i)
- A simplified kinematic model for a rover-type mobile robot, which allows a robot with complex suspension systems to be controlled using an easy control law.
- (ii)
- A control strategy that can be used as the basis for trajectory tracking or autonomous navigation in a rover-type mobile robot with only one position and orientation sensor.
- (iii)
- The verification of the control algorithm for trajectory tracking, which is implemented in the embedded system at a low cost.
2. Description of the Rover Prototype
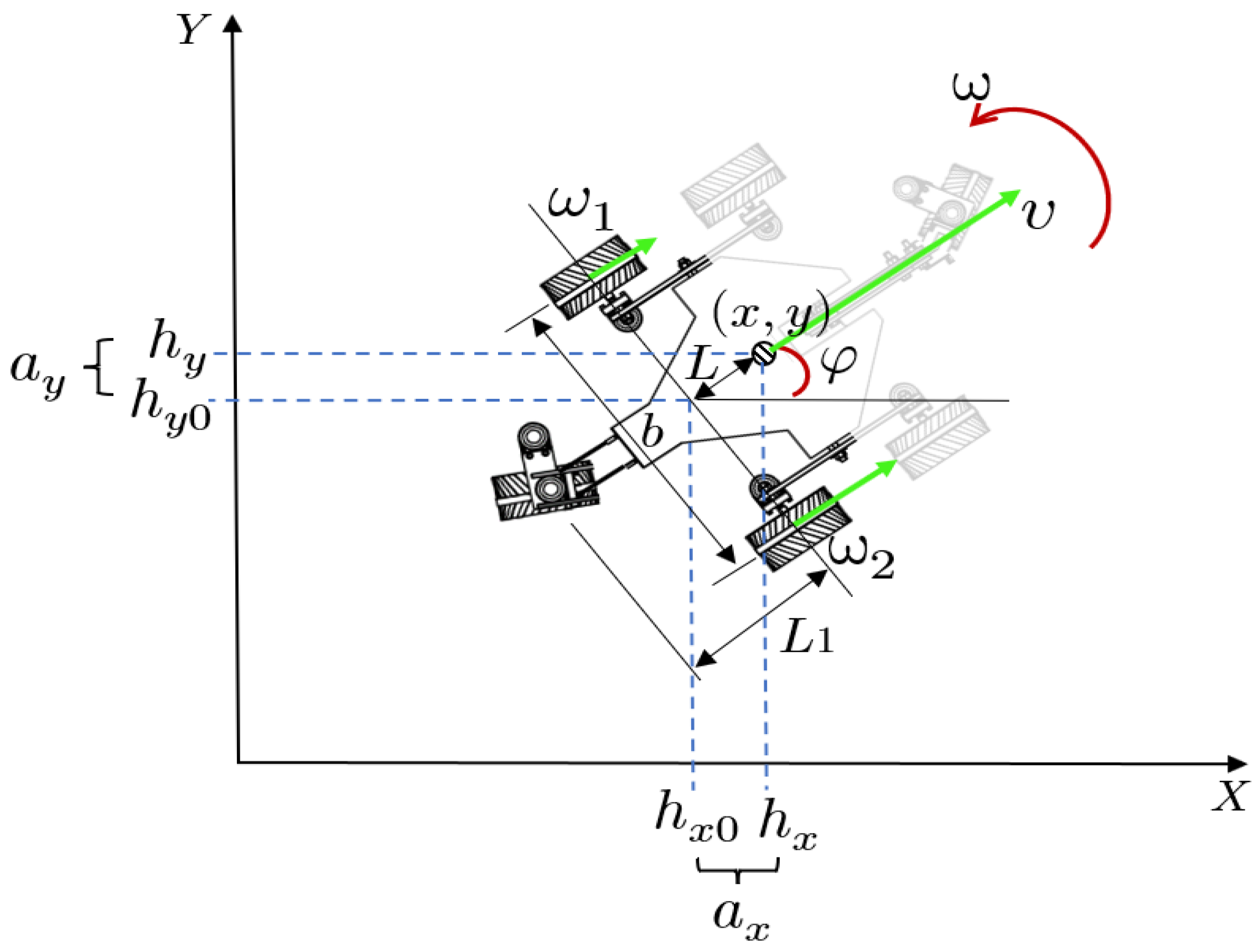
3. Kinematic Model
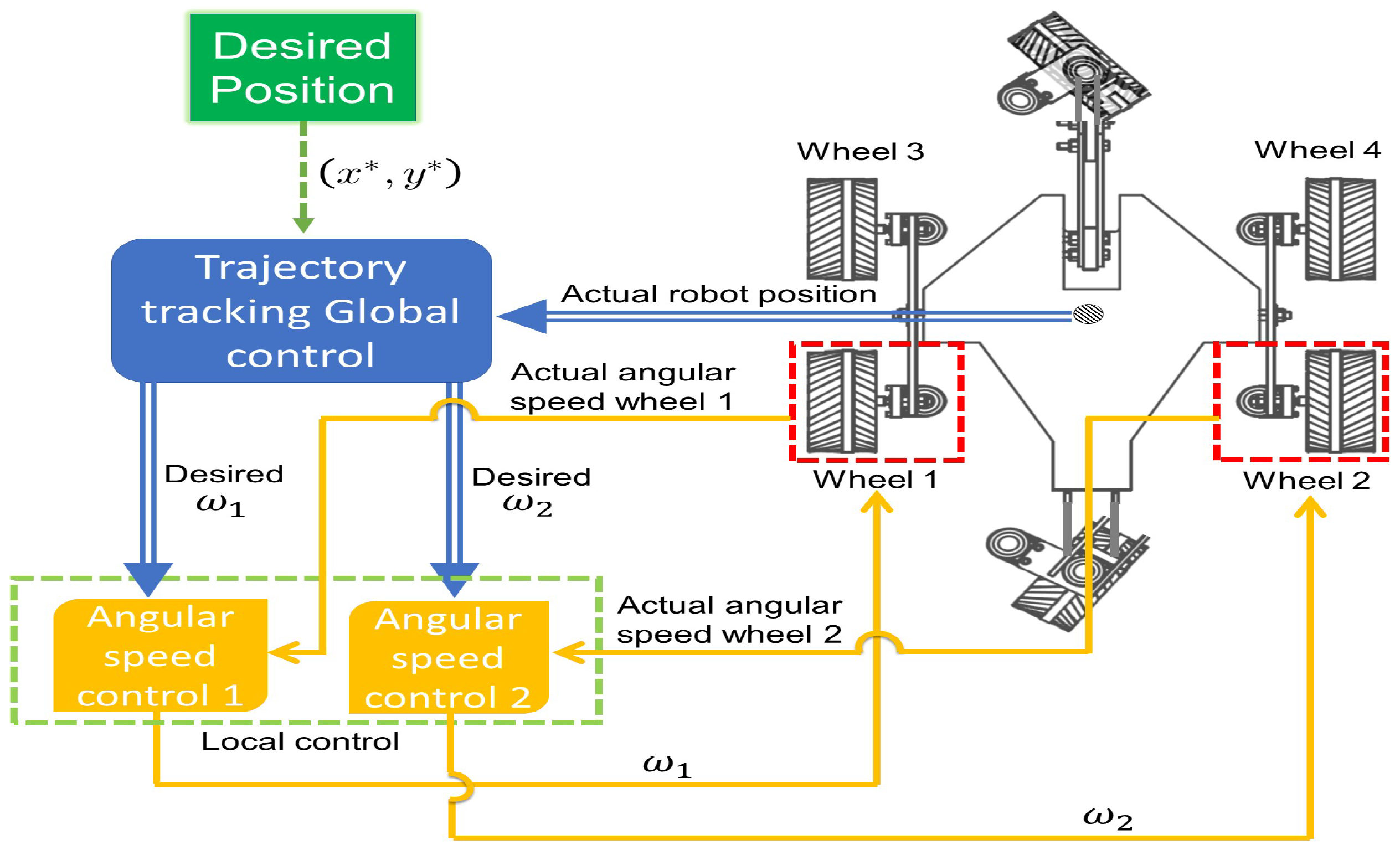
4. Control Strategy
4.1. Trajectory Tracking Control—Global Control
4.2. Locomotion Subsystem Control—Local Control
4.3. Reference Signals for Motion Subsystem Controls
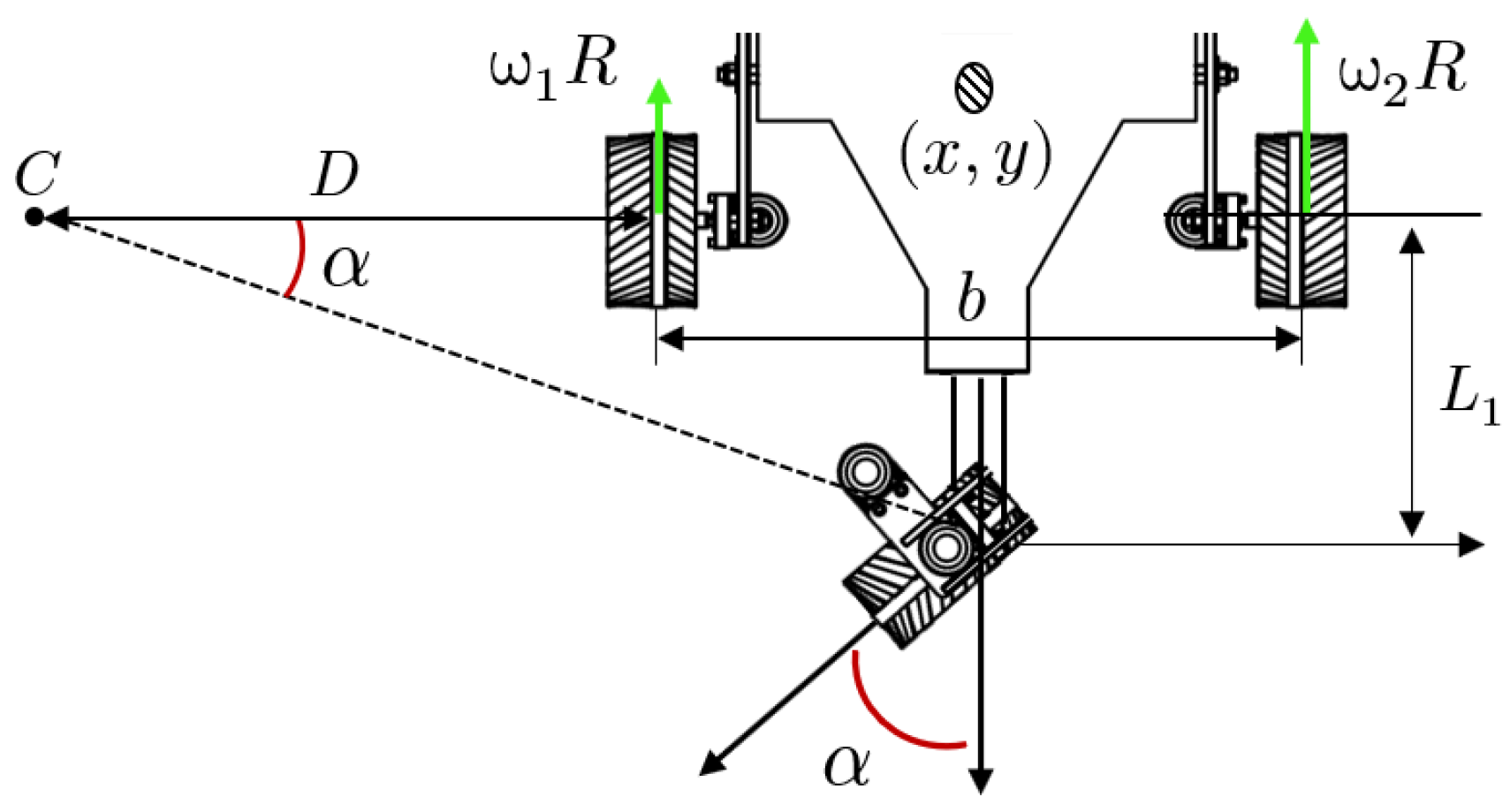
4.3.1. Angle for Steering Mechanism
4.3.2. Front and Rear Wheel Angular Velocity
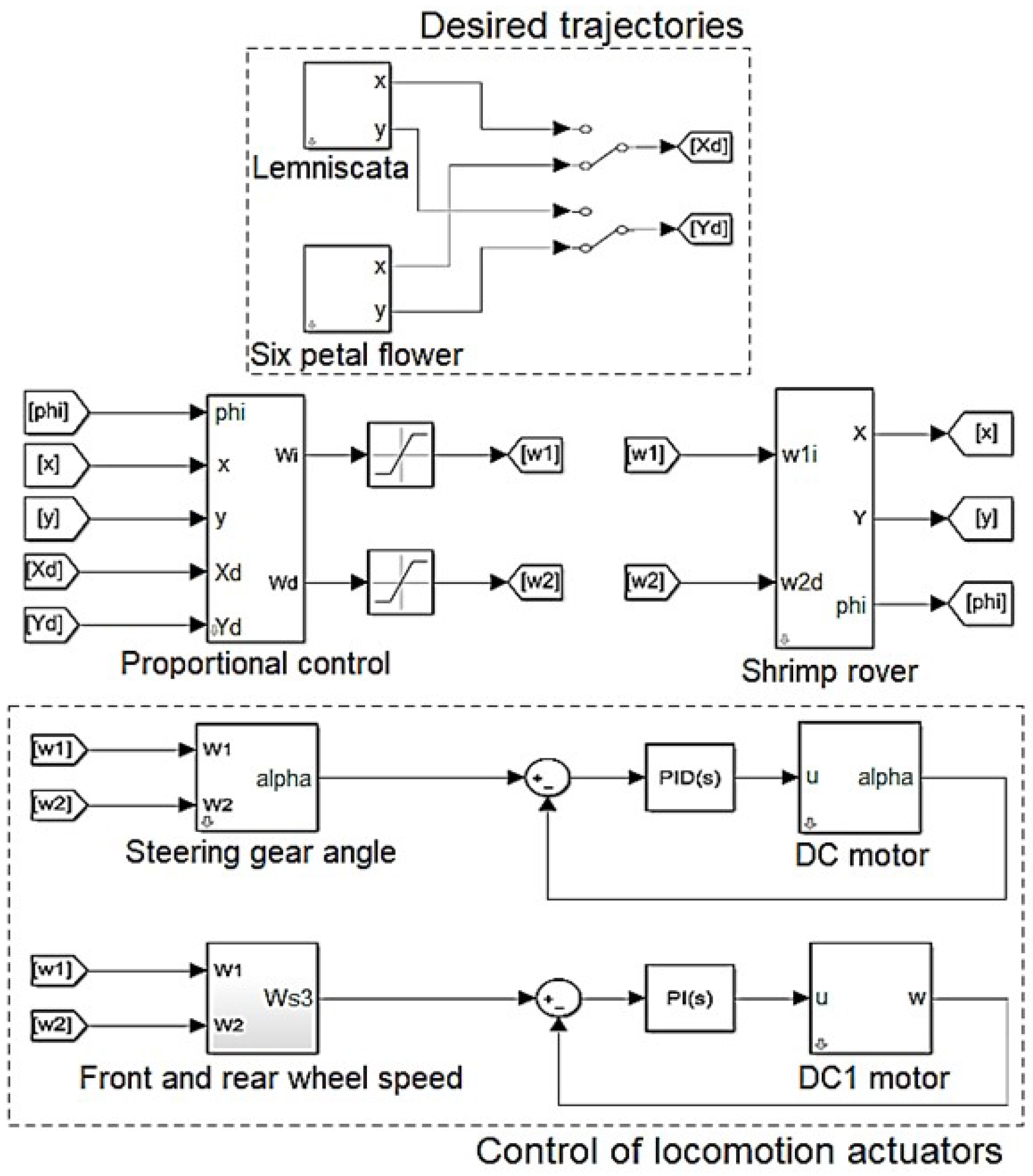
5. Numerical Simulation
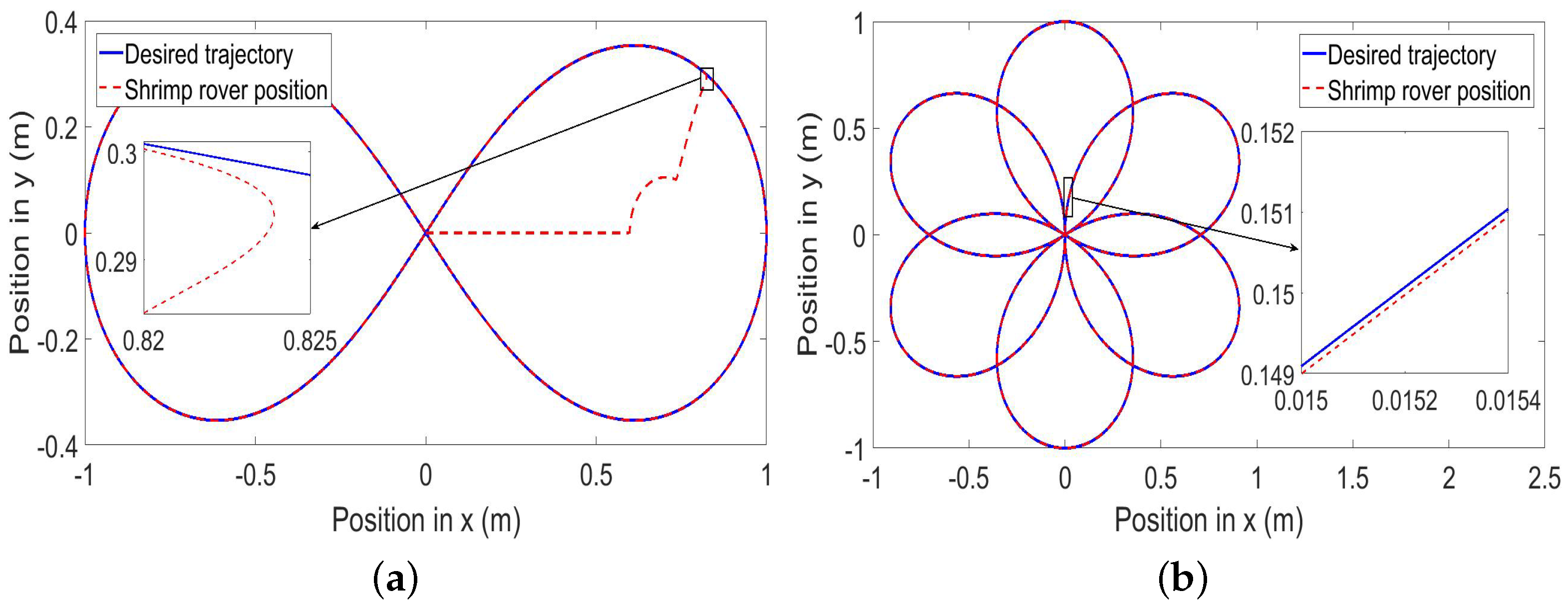
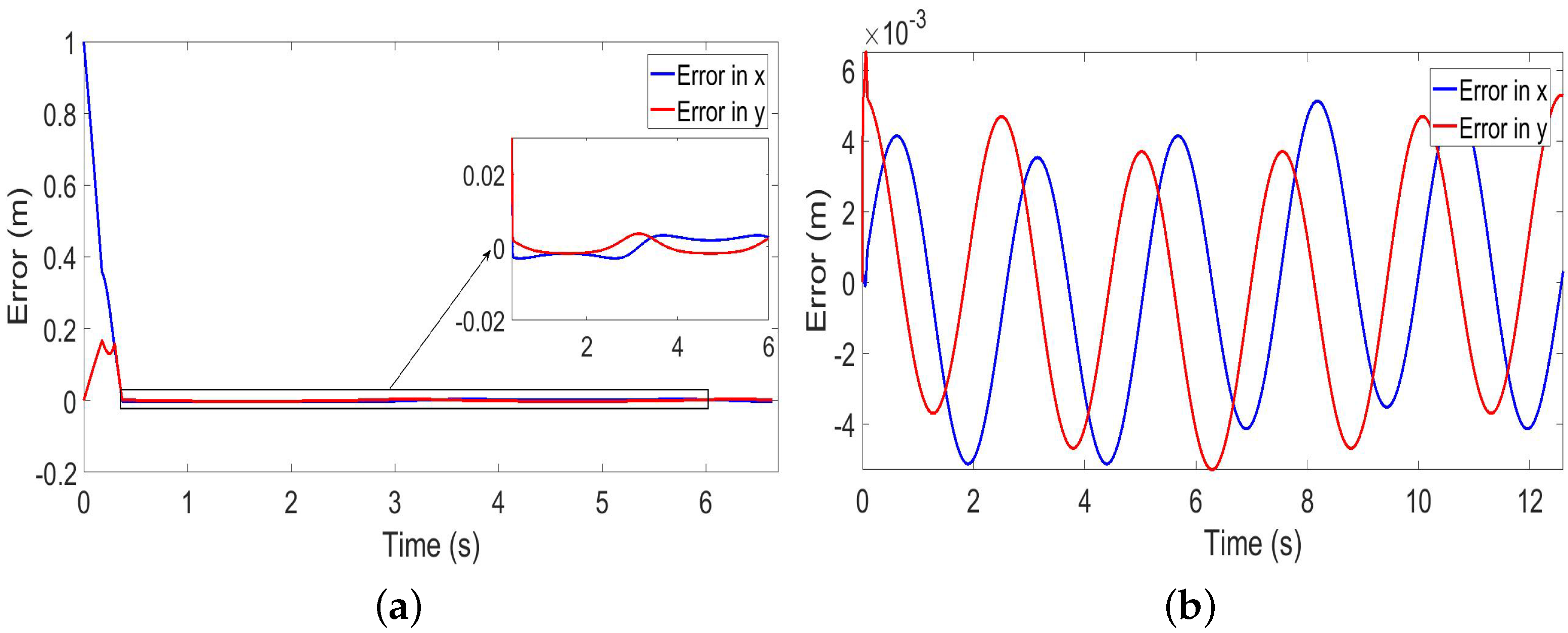
5.1. Simulation Results of Trajectory Tracking
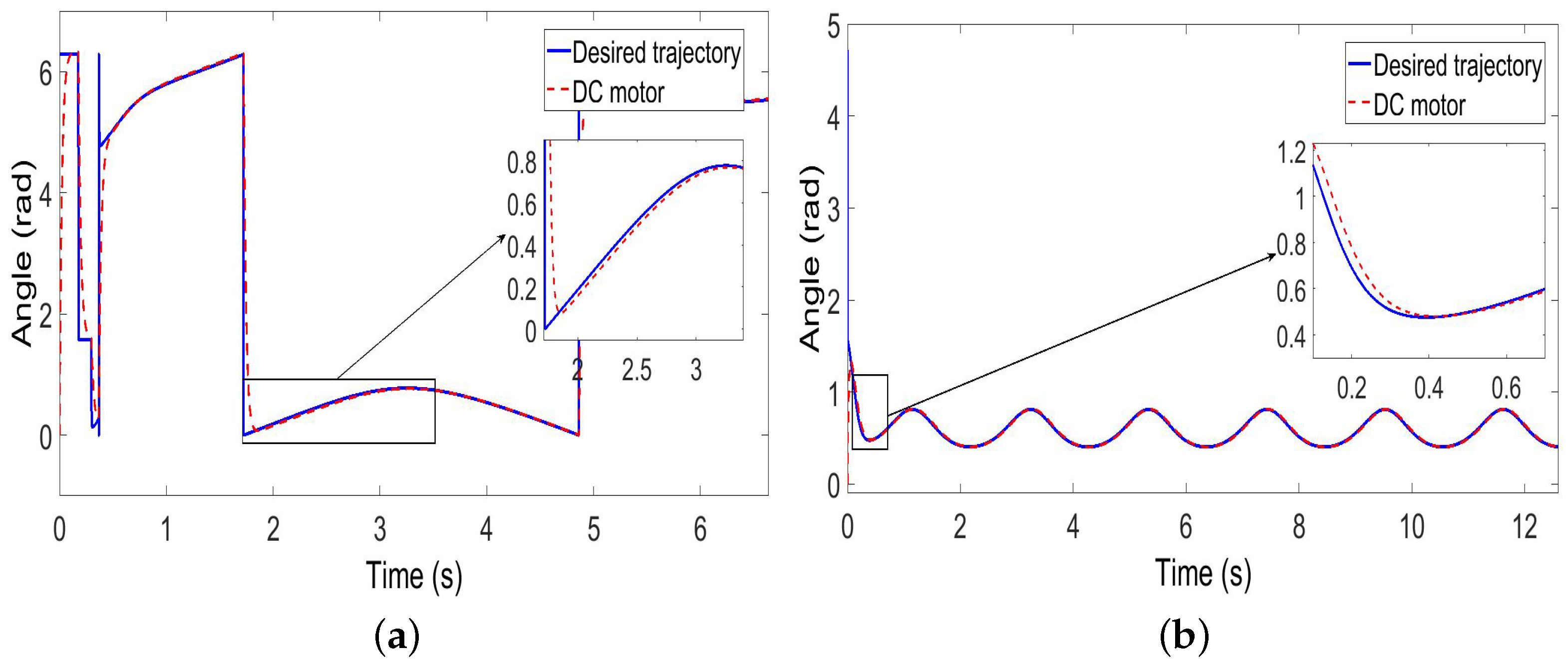
5.2. Control Results of Steering Mechanisms
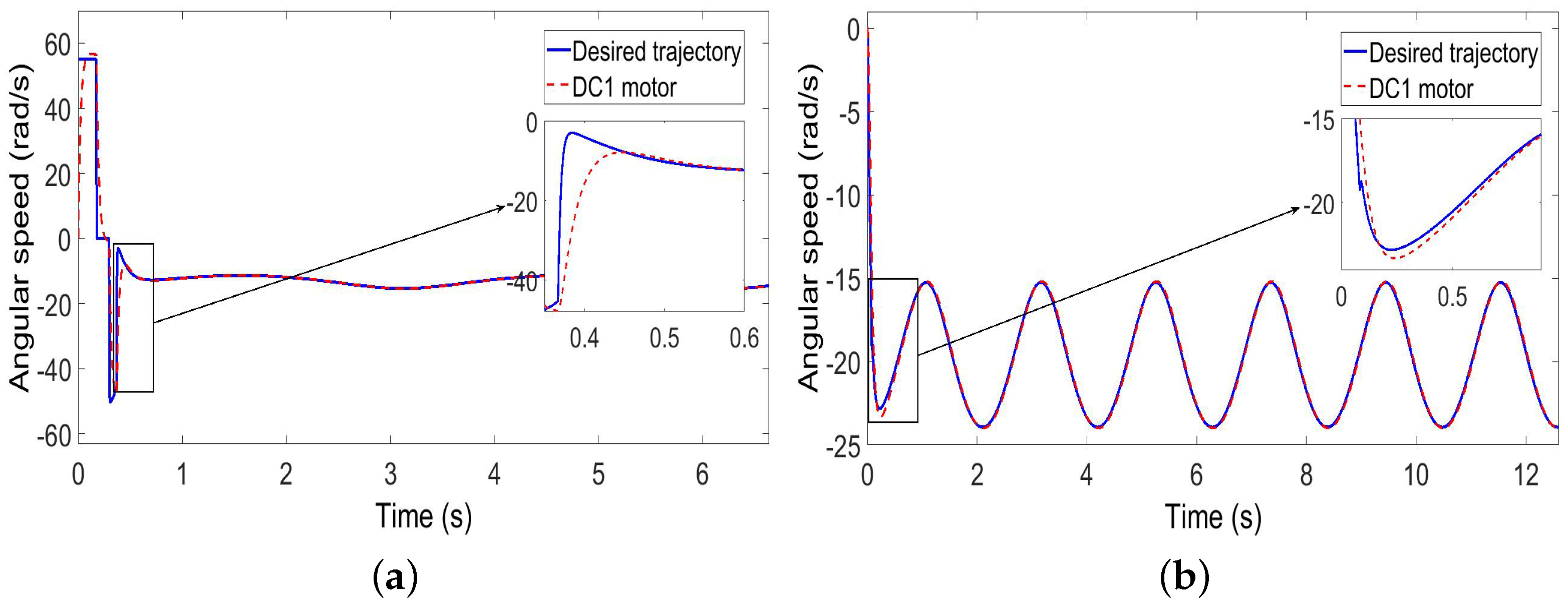
5.3. Wheel Speed Control Results
6. General Implementation and Experimental Testing
Experimental Results
7. Conclusions
- The kinematic model allows us to treat the mobile system with a simplified approach that resembles a differential robot with a geometric centre at an eccentric point with respect to the axis centre. This configuration is very important to ensure holonomic restrictions in the system, reducing the control synthesis to a set of classic controls with a simple inverse gain compensation. Most approaches tend to use differential robot-based kinematic models with non-holonomic restrictions that are not addressed.
- Even when the mechanical design and control ensure robustness against disturbances and certain slopes, actual applications demand a higher scale in both the size of the vehicle and the wheel radius to improve the capacity in rougher terrains.
- The presented design obtains its position measurements using a GPS, and even when the system has an RGB-D camera, it is only used for obstacle detection, which may not be robust in practical tasks. In this sense, an area of opportunity consists of the inclusion of more sensors as well as the active use of an RGB-D camera to improve the robustness and accuracy of the position sensing by means of alternative approaches such as sensor fusion.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sutoh, M. Traveling performance analysis of planetary rovers using a repeatable test system in vacuum. J. Terramech. 2021, 95, 15–24. [Google Scholar] [CrossRef]
- Lopez-Arreguin, A.J.R.; Montenegro, S. Machine learning in planetary rovers: A survey of learning versus classical estimation methods in terramechanics for in situ exploration. J. Terramech. 2021, 97, 1–17. [Google Scholar] [CrossRef]
- Bajracharya, M.; Maimone, M.W.; Helmick, D. Autonomy for Mars Rovers: Past, Present, and Future. Computer 2008, 41, 44–50. [Google Scholar] [CrossRef]
- Chen, C.; Shu, M.; Wang, Y.; Ding, L.; Gao, H.; Liu, H.; Zhou, S. Simultaneous control of trajectory tracking and coordinated allocation of rocker-bogie planetary rovers. Mech. Syst. Signal Process. 2021, 151, 107312. [Google Scholar] [CrossRef]
- Parsons IV, J.R.; Mazzoleni, A.P. Modeling and experimental investigation of the dynamics of a spherical Transforming Roving Rolling Explorer (TRREx) prototype. Acta Astronaut. 2021, 181, 92–111. [Google Scholar] [CrossRef]
- Sasiadek, J.; Green, D. Guidance and Control of Autonomous Planetary Rover. IFAC Proc. Vol. 1997, 30, 241–246. [Google Scholar] [CrossRef]
- Caracciolo, L.; De Luca, A.; Iannitti, S. Trajectory tracking control of a four-wheel differentially driven mobile robot. In Proceedings of the 1999 IEEE International Conference on Robotics and Automation (Cat. No. 99CH36288C), Detroit, MI, USA, 10–15 May 1999; Volume 4, pp. 2632–2638. [Google Scholar]
- Yang, J.M.; Kim, J.H. Sliding mode control for trajectory tracking of nonholonomic wheeled mobile robots. IEEE Trans. Robot. Autom. 1999, 15, 578–587. [Google Scholar] [CrossRef]
- Sasiadek, J.; Lu, Y. Path tracking of an autonomous LHD articulated vehicle. IFAC Proc. Vol. 2005, 38, 55–60. [Google Scholar] [CrossRef]
- Grand, C.; Benamar, F.; Plumet, F. Motion kinematics analysis of wheeled–legged rover over 3D surface with posture adaptation. Mech. Mach. Theory 2010, 45, 477–495. [Google Scholar] [CrossRef]
- Arabi, A.A.; Sakib, H.U.; Sarkar, P.; Proma, T.P.; Anowar, J.; Amin, M.A. Autonomous Rover Navigation Using GPS Based Path Planning. In Proceedings of the 2017 Asia Modelling Symposium (AMS), Kota Kinabalu, Malaysia, 4–6 December 2017; pp. 89–94. [Google Scholar] [CrossRef]
- Polash, M.M.H.; Tumpa, S.N.; Saumik, S.S.; Samia, M.B.R.; Rafid, M.F.; Elahi, S.S.B.; Moumi, P.K.; Dipta, S.R.; Inan, T.T.; Oishwee, S.J.; et al. Explorer-0100: An autonomous next generation Mars rover. In Proceedings of the 2017 20th International Conference of Computer and Information Technology (ICCIT), Dhaka, Bangladesh, 22–24 December 2017; pp. 1–7. [Google Scholar] [CrossRef]
- Zhang, W.; Gai, J.; Zhang, Z.; Tang, L.; Liao, Q.; Ding, Y. Double-DQN based path smoothing and tracking control method for robotic vehicle navigation. Comput. Electron. Agric. 2019, 166, 104985. [Google Scholar] [CrossRef]
- Qi, L.; Zhang, T.; Xu, K.; Pan, H.; Zhang, Z.; Yuan, Y. A novel terrain adaptive omni-directional unmanned ground vehicle for underground space emergency: Design, modeling and tests. Sustain. Cities Soc. 2021, 65, 102621. [Google Scholar] [CrossRef]
- Khan, R.; Malik, F.M.; Raza, A.; Mazhar, N. Comprehensive study of skid-steer wheeled mobile robots: Development and challenges. Ind. Robot. Int. J. Robot. Res. Appl. 2020, 48, 142–156. [Google Scholar] [CrossRef]
- Meghdari, A.; Mahboobi, S.; Gaskarimahalle, A.L. Dynamics modeling of “cedra” rescue robot on uneven terrains. In Proceedings of the ASME International Mechanical Engineering Congress and Exposition, Anaheim, CA, USA, 13–19 November 2004; Volume 47063, pp. 991–1001. [Google Scholar]
- Li, S.; Liu, J.; Sun, M.; Wen, W.; Bi, S. Optimal design for a self-adaptive mobile robot based on virtual center of motion. In Proceedings of the 2009 IEEE International Conference on Robotics and Biomimetics (ROBIO), Guilin, China, 19–23 December 2009; pp. 414–419. [Google Scholar]
- Xu, M.; Yang, R.; Cheng, Y.; Xu, H. Kinematics modeling and step climbing study of an all-terrain wheeled mobile robot on uneven terrains. In Proceedings of the 2011 International Conference on Electronic & Mechanical Engineering and Information Technology, Harbin, China, 12–14 August 2011; Volume 5, pp. 2725–2728. [Google Scholar]
- Aguirre-Anaya, J.A. Diseño y Construcción de un Móvil Tipo Rover de Arquitectura Abierta. Master’s Thesis, Instituto Politecnico Nacional—Unidad Profesional Interdisciplinaria en Ingeniería y Tecnologías Avanzadas, Ciudad de México, Mexico, 2016. Available online: https://cloud.upiita.ipn.mx/s/bRRCGpjFXawpzrN (accessed on 13 March 2024).
- Baturone, A.O. Robótica: Manipuladores y Robots Móviles; Marcombo, 2005. [Google Scholar]
- Sugisaka, M.; Hazry, D. Development of a proportional control method for a mobile robot. Appl. Math. Comput. 2007, 186, 74–82. [Google Scholar] [CrossRef]
- Haytham, A.; Elhalwagy, Y.; Wassal, A.; Darwish, N. Modeling and simulation of four-wheel steering unmanned ground vehicles using a PID controller. In Proceedings of the 2014 International Conference on Engineering and Technology (ICET), Cairo, Egypt, 19–20 April 2014; pp. 1–8. [Google Scholar]
- Kanojiya, R.G.; Meshram, P. Optimal tuning of PI controller for speed control of DC motor drive using particle swarm optimization. In Proceedings of the 2012 International Conference on Advances in Power Conversion and Energy Technologies (APCET), Mylavaram, India, 2–4 August 2012; pp. 1–6. [Google Scholar]
- Sira-Ramirez, H.; Agrawal, S.K. Differentially Flat Systems, 1st ed.; CRC Press: Boca Raton, FL, USA, 2004. [Google Scholar]
- Luviano-Juárez, A.; Cortés-Romero, J.; Sira-Ramírez, H. Trajectory tracking control of a mobile robot through a flatness-based exact feedforward linearization scheme. J. Dyn. Syst. Meas. Control. 2015, 137, 051001. [Google Scholar] [CrossRef]
- Hanson, B.A.; Seeger, C.J. Apps for Collecting GPS Tacks: MyTracks-The GPS-Logger. 2015. Available online: https://store.extension.iastate.edu/product/Apps-for-Collecting-GPS-Tracks-myTracks-The-GPS-Logger (accessed on 14 November 2023).
- Mars Society. University Rover Challenge. 2006. Available online: https://urc.marssociety.org/home/requirements-guidelines (accessed on 14 November 2023).


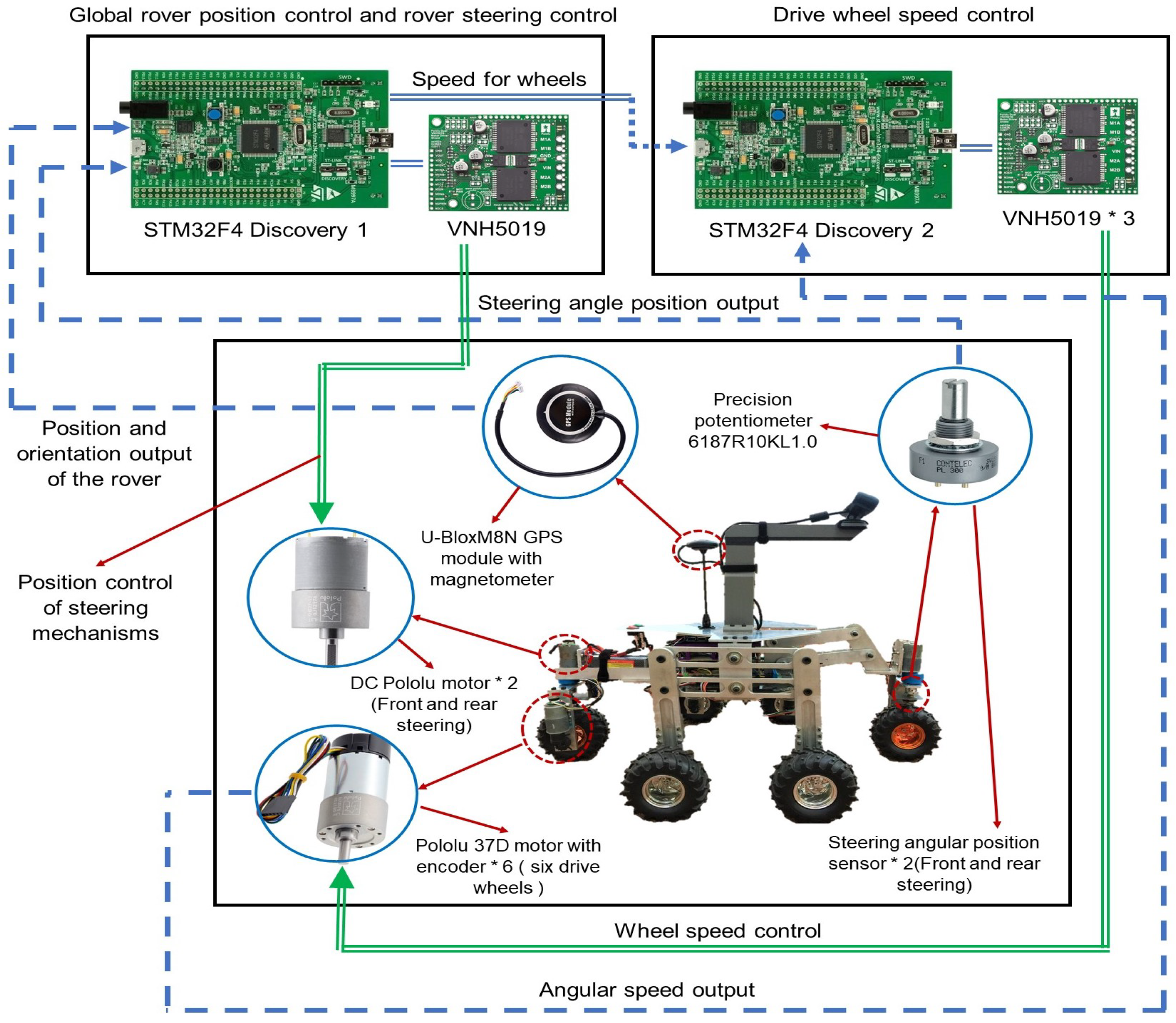


| Features | Description |
|---|---|
| Prototype dimensions | 50.5 cm × 75 cm × 60 cm |
| Model dimensions | L = 0.105 m, = 0.315 m, R = 0.062 m, b = 0.445 m |
| Weight | 9.5 kg |
| Number of wheels | 6 |
| Suspension system | Parallelogram |
| Traction system | Each wheel is actuated |
| Steering system | Works independently on front and rear wheels |
| Obstacles to overcome | Obstacles with a height of twice its wheel diameter |
| Processing cards | 2 STM32F4 Discovery microcontrollers |
| Localisation module | GPS U-BloxM8N |
| Actuators | Geared motors with encoder pololu 37D-131.25:1 |
| Motor controllers | 4 drivers pololu VNH5019 Dual |
| Trajectory | Variable | Quantity |
|---|---|---|
| Lemniscate | Maximum position error in x | 0.0032 mm |
| Maximum position error in y | 0.0036 mm | |
| Initial conditions | (0, 0) m | |
| Wheels’ maximum angular velocity | 55 rad/s | |
| Time to reach the desired trajectory | <1 s | |
| Controller’s gains | 277, 277 | |
| Six-petal flower | Maximum position error in x | 0.0051 mm |
| Maximum position error in y | 0.0053 mm | |
| Initial conditions | (0, 0) m | |
| Wheels’ maximum angular velocity | 55 rad/s | |
| Time to reach the desired trajectory | <1 s | |
| Controller’s gains | 283, 283 |
| Parameter | Units | Value |
|---|---|---|
| Initial position | ∘ | Lat = 19.512416, Long = −99.127674 |
| Initial orientation | rad | 5.7596 |
| Desired coordinate | ∘ | lat = 19.513616, long = −99.128438 |
| Max. wheel speed | r/min | 40 |
| Controller constants | 278; 278 | |
| Travel time | min | 11.267 |
| Distance covered | m | 174 |
| Mean travel speed | m/s | 0.2574 |
| Final position | ∘ | Lat = 19.513605, Long = −99.128425 |
| Positioning error | m | 1.9 |
| L | m | 0.105 |
| m | 0.315 | |
| R | m | 0.062 |
| b | m | 0.445 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Diaz-Ortega, J.D.; Gutiérrez-Frías, O.; Aguirre-Anaya, J.A.; Luviano-Juárez, A. Simplified Strategy for Trajectory Tracking Application of a Passive Suspension Rover-Type Mobile Robot. Machines 2024, 12, 322. https://doi.org/10.3390/machines12050322
Diaz-Ortega JD, Gutiérrez-Frías O, Aguirre-Anaya JA, Luviano-Juárez A. Simplified Strategy for Trajectory Tracking Application of a Passive Suspension Rover-Type Mobile Robot. Machines. 2024; 12(5):322. https://doi.org/10.3390/machines12050322
Chicago/Turabian StyleDiaz-Ortega, Jheison Duvier, Octavio Gutiérrez-Frías, José Alejandro Aguirre-Anaya, and Alberto Luviano-Juárez. 2024. "Simplified Strategy for Trajectory Tracking Application of a Passive Suspension Rover-Type Mobile Robot" Machines 12, no. 5: 322. https://doi.org/10.3390/machines12050322
APA StyleDiaz-Ortega, J. D., Gutiérrez-Frías, O., Aguirre-Anaya, J. A., & Luviano-Juárez, A. (2024). Simplified Strategy for Trajectory Tracking Application of a Passive Suspension Rover-Type Mobile Robot. Machines, 12(5), 322. https://doi.org/10.3390/machines12050322






