Study on Performance Improvement through Reducing Axial Force of Ferrite Double-Layer Spoke-Type Permanent Magnet Synchronous Motor with Core Skew †
Abstract
1. Introduction
1.1. Summary
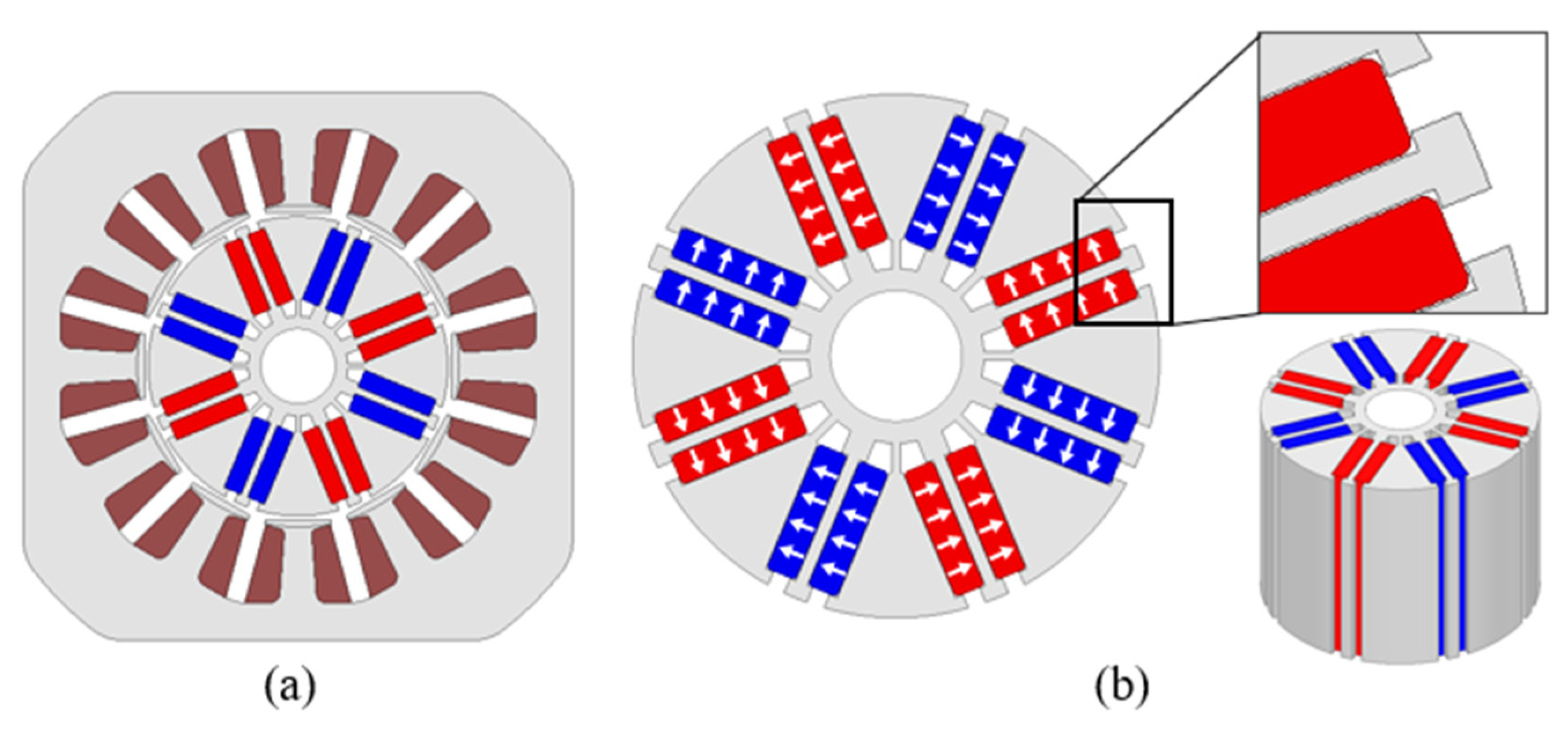
1.2. Conventional Model Specifications
2. Equation and Analysis of Axial Force
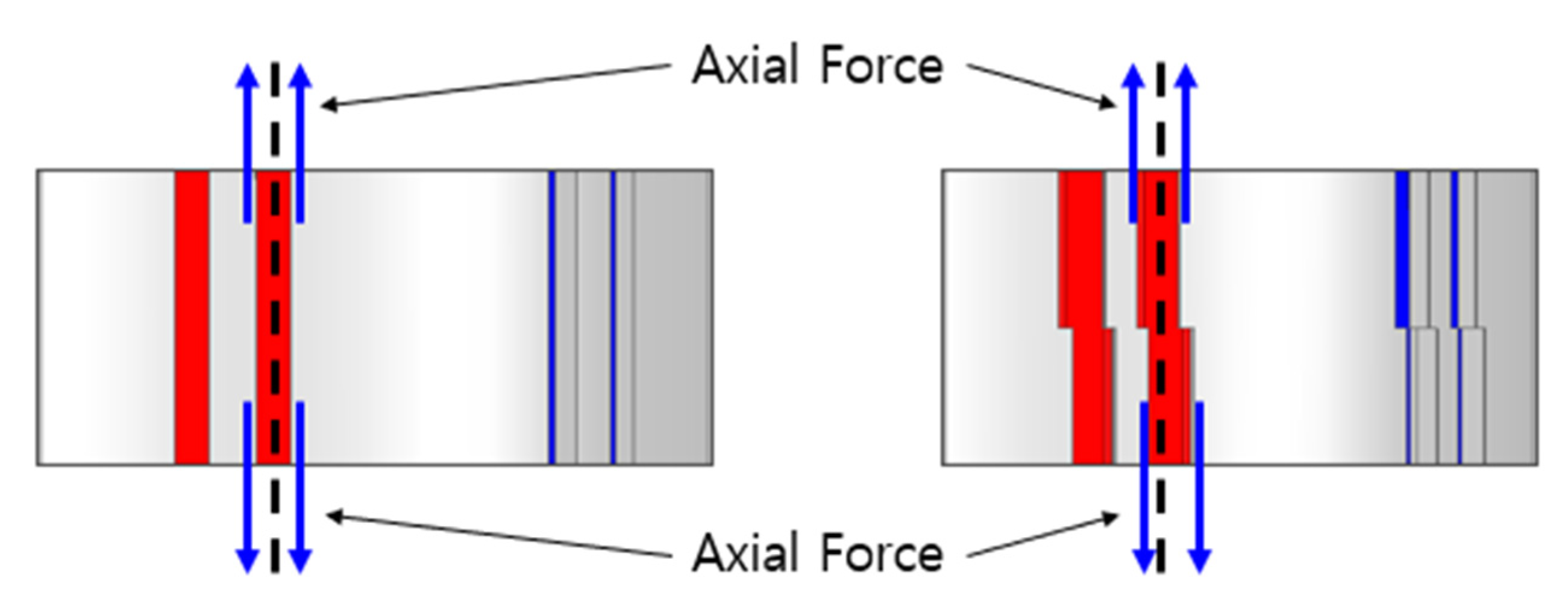
2.1. Equation for Axial Force
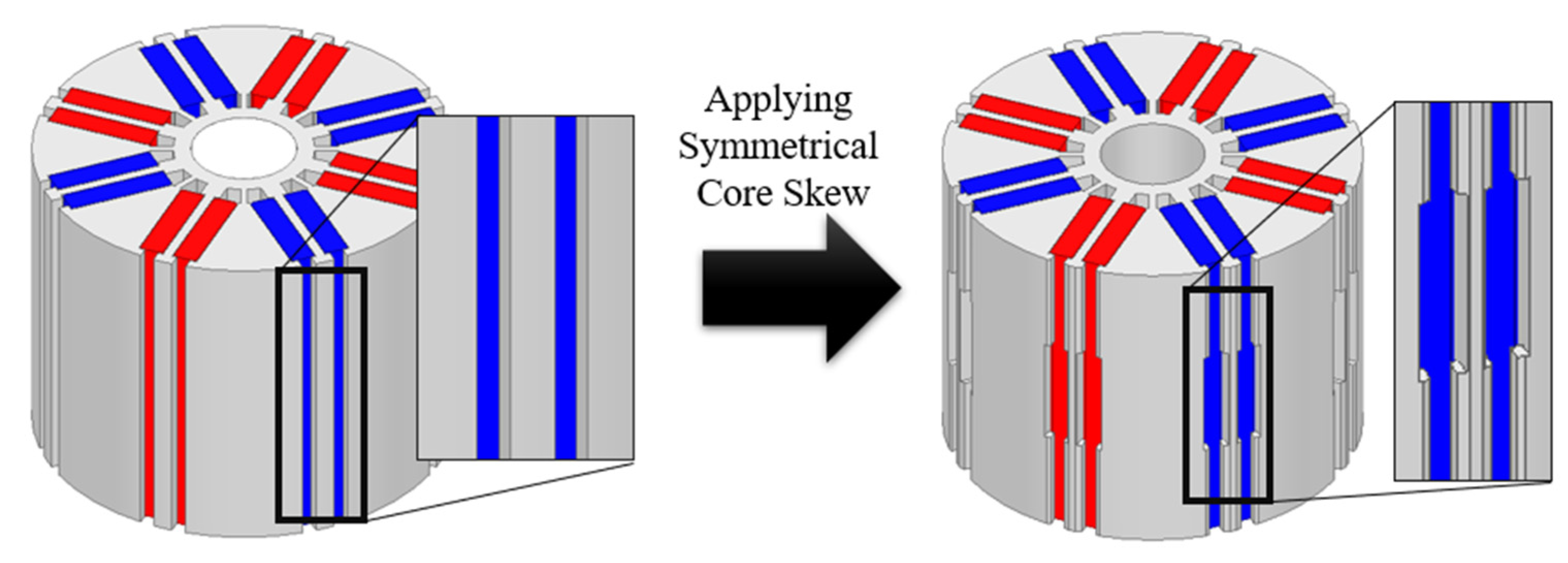
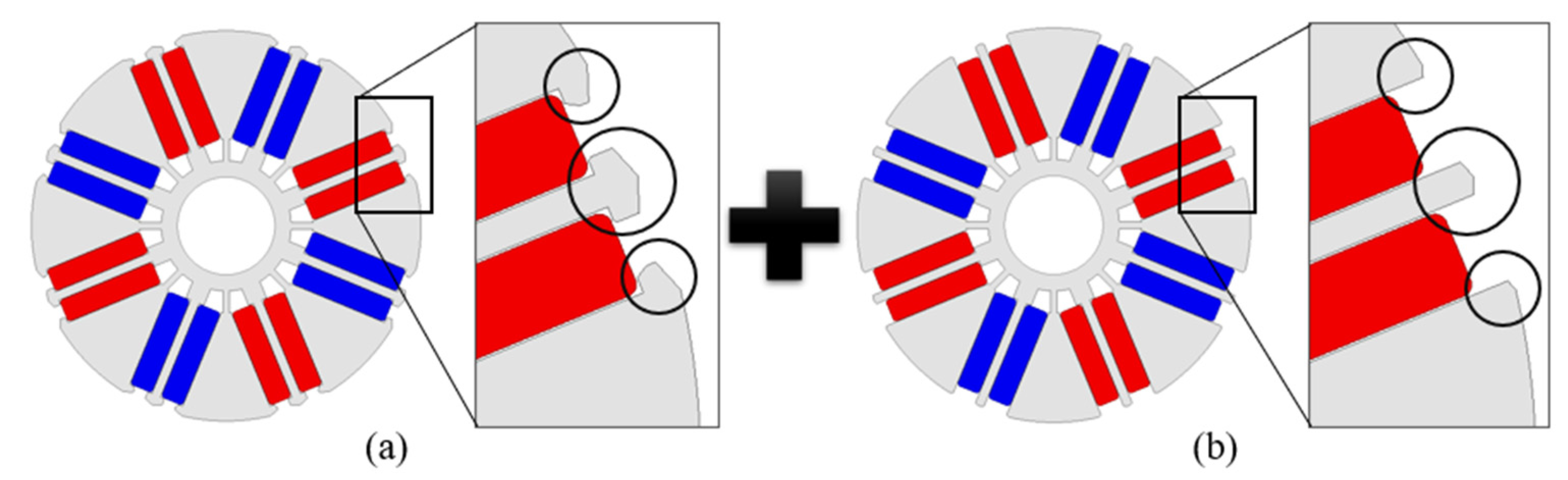
2.2. Analysis of the Cause of Core Skew
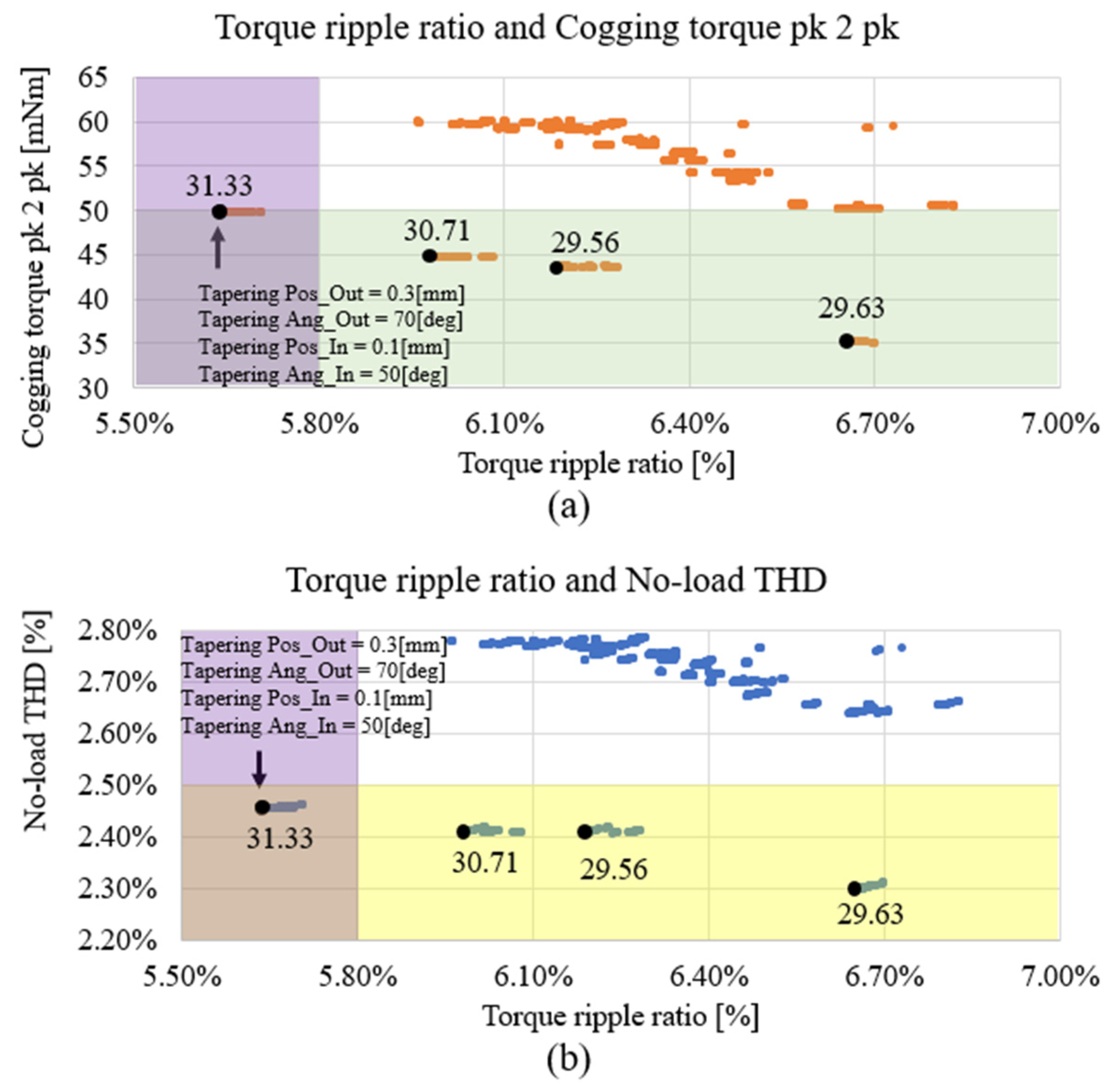
3. Geometric Variables and Their Effects on 2D FEA
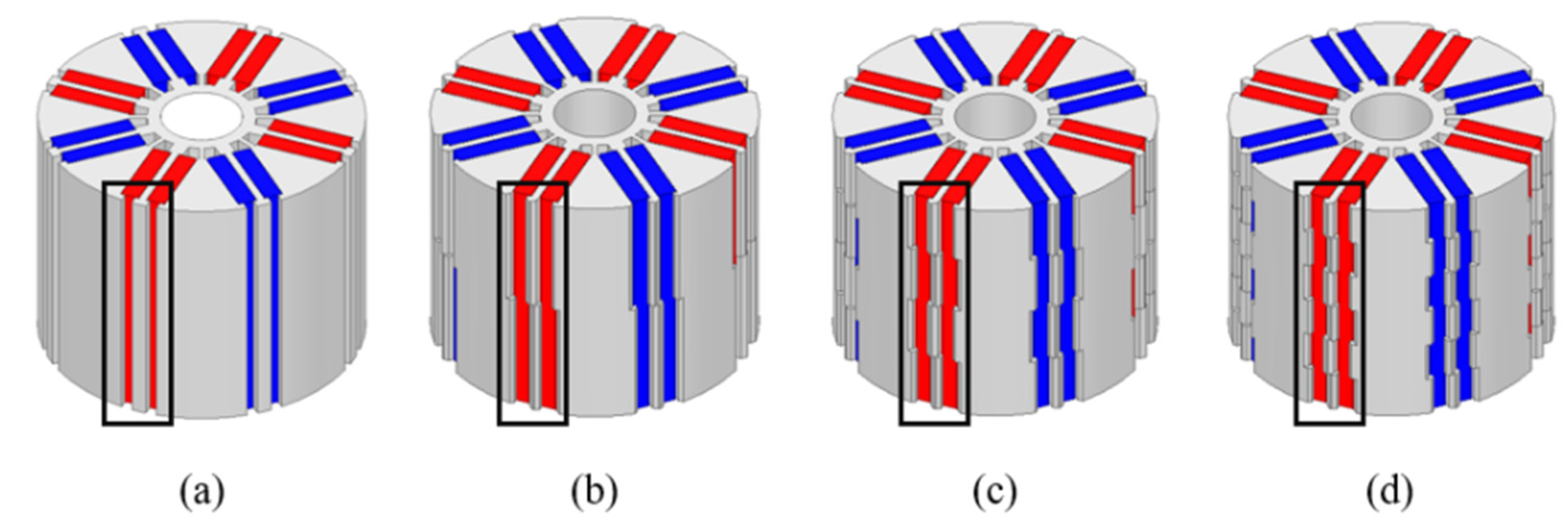
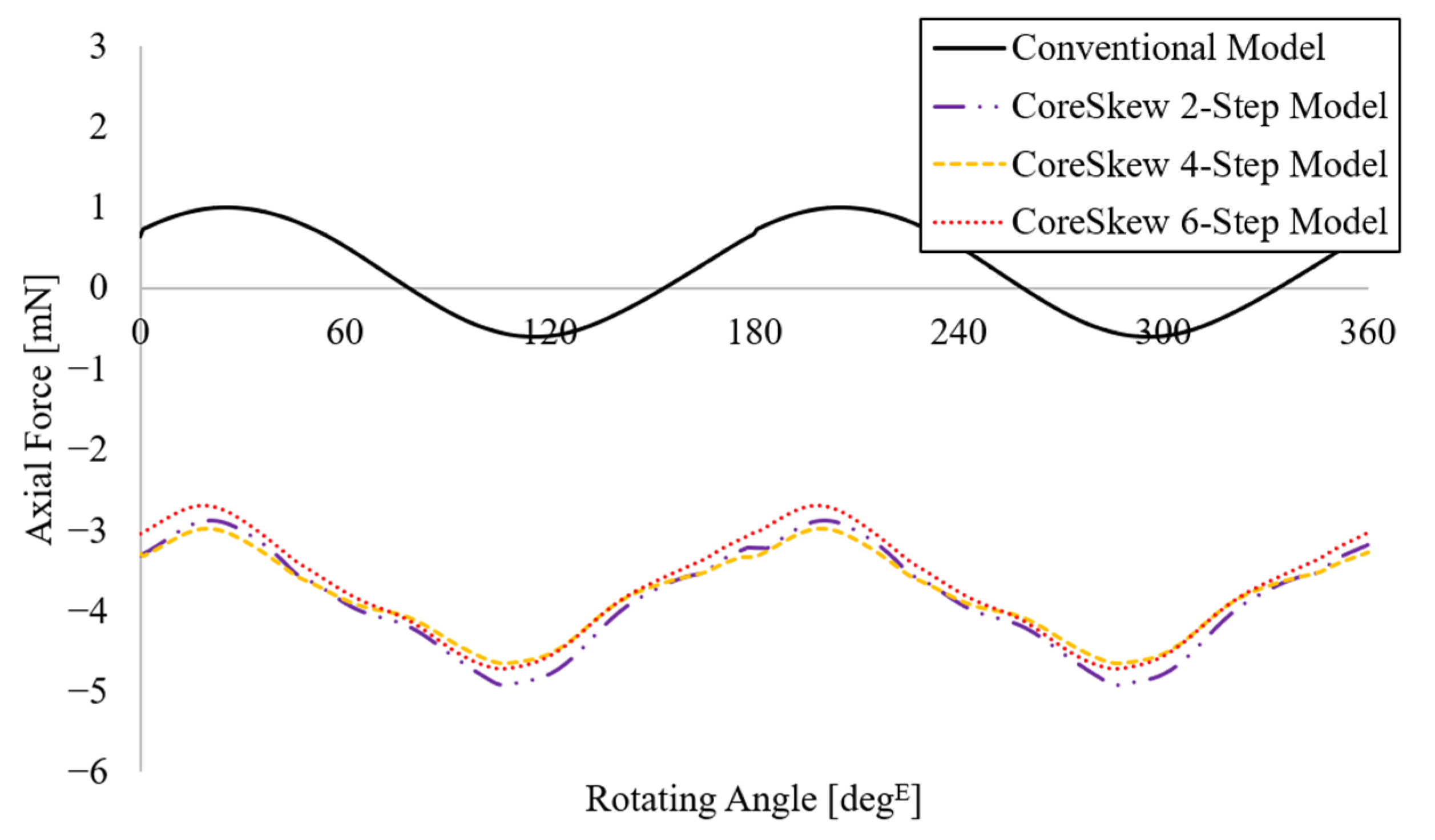
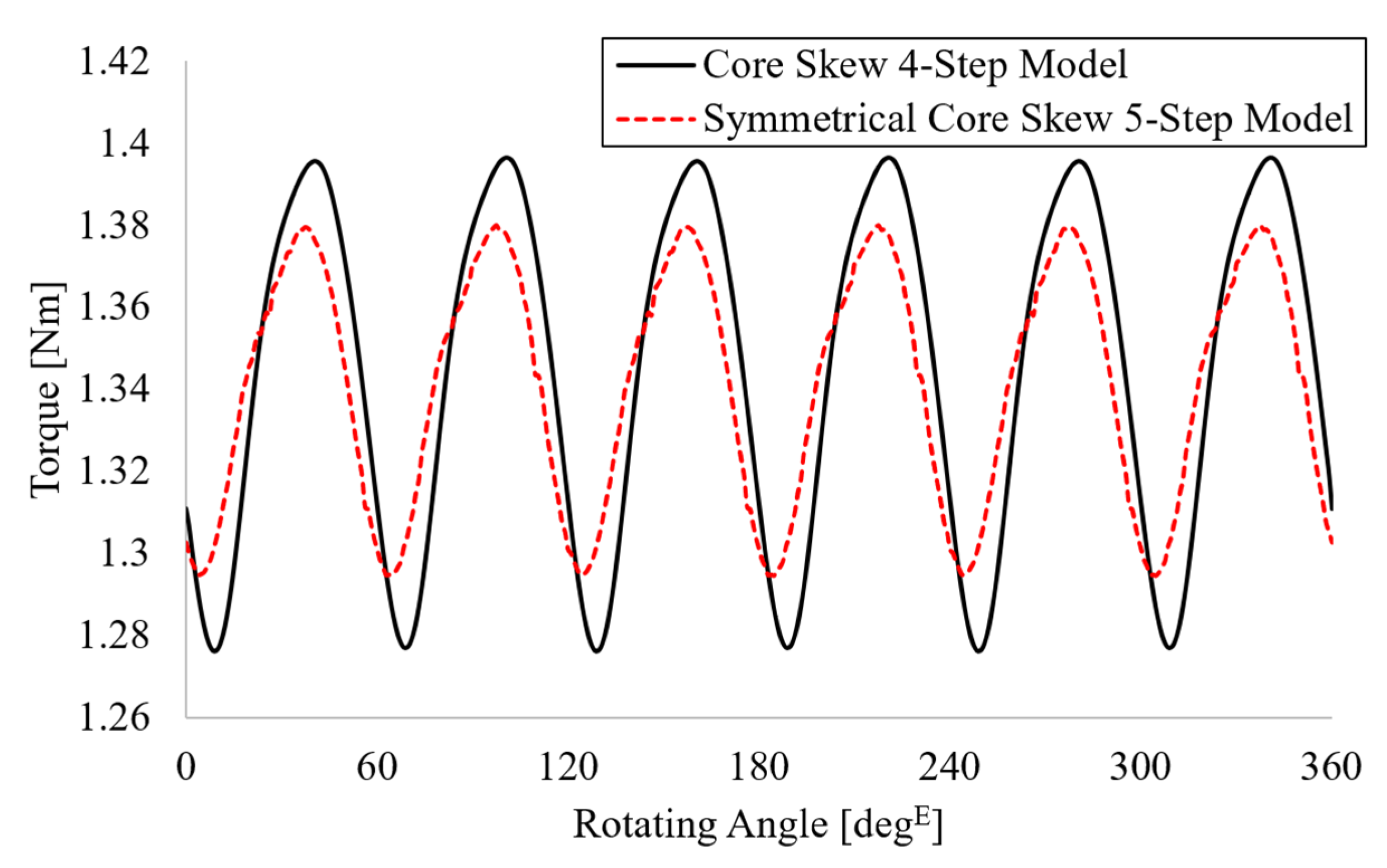
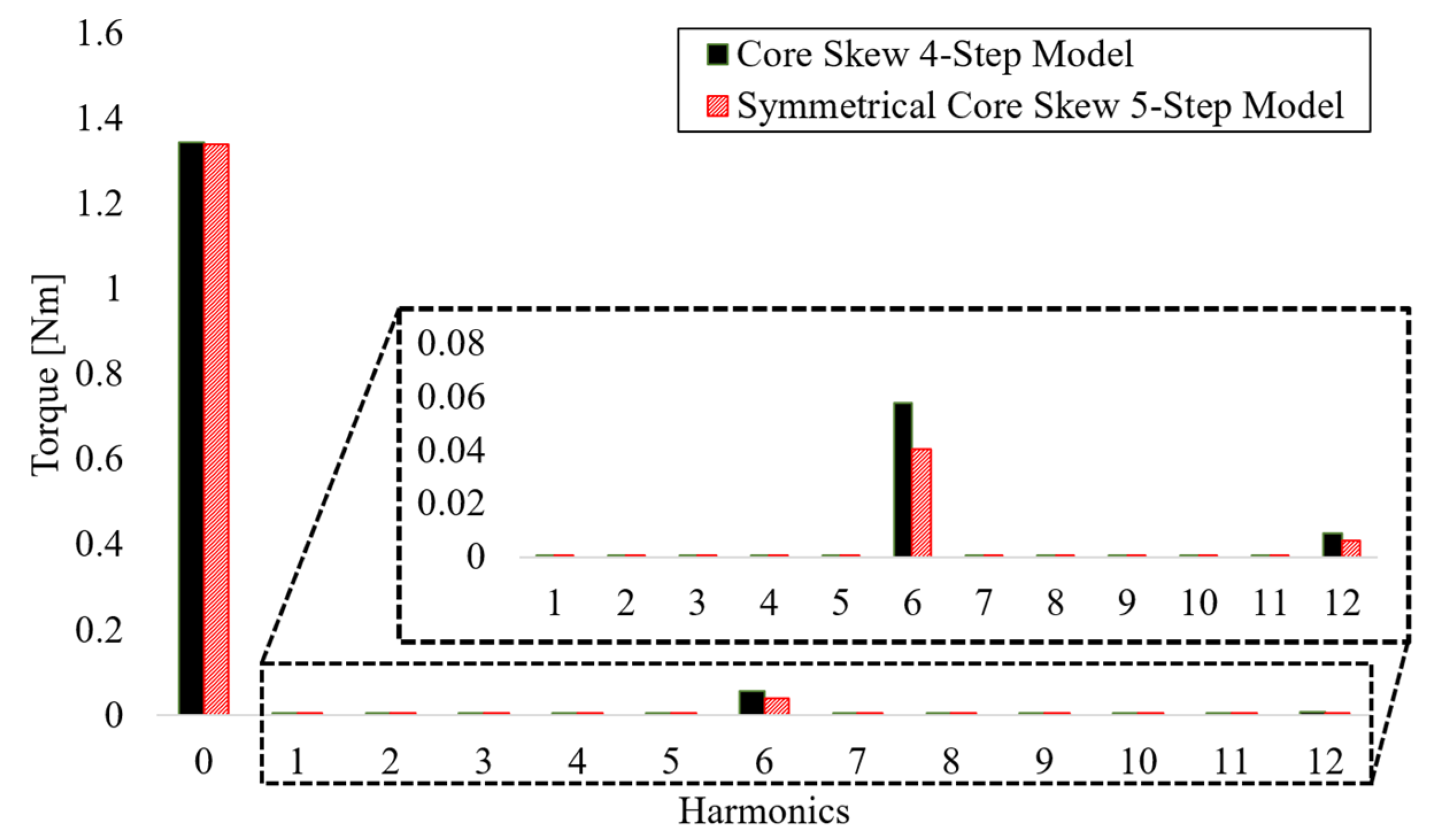
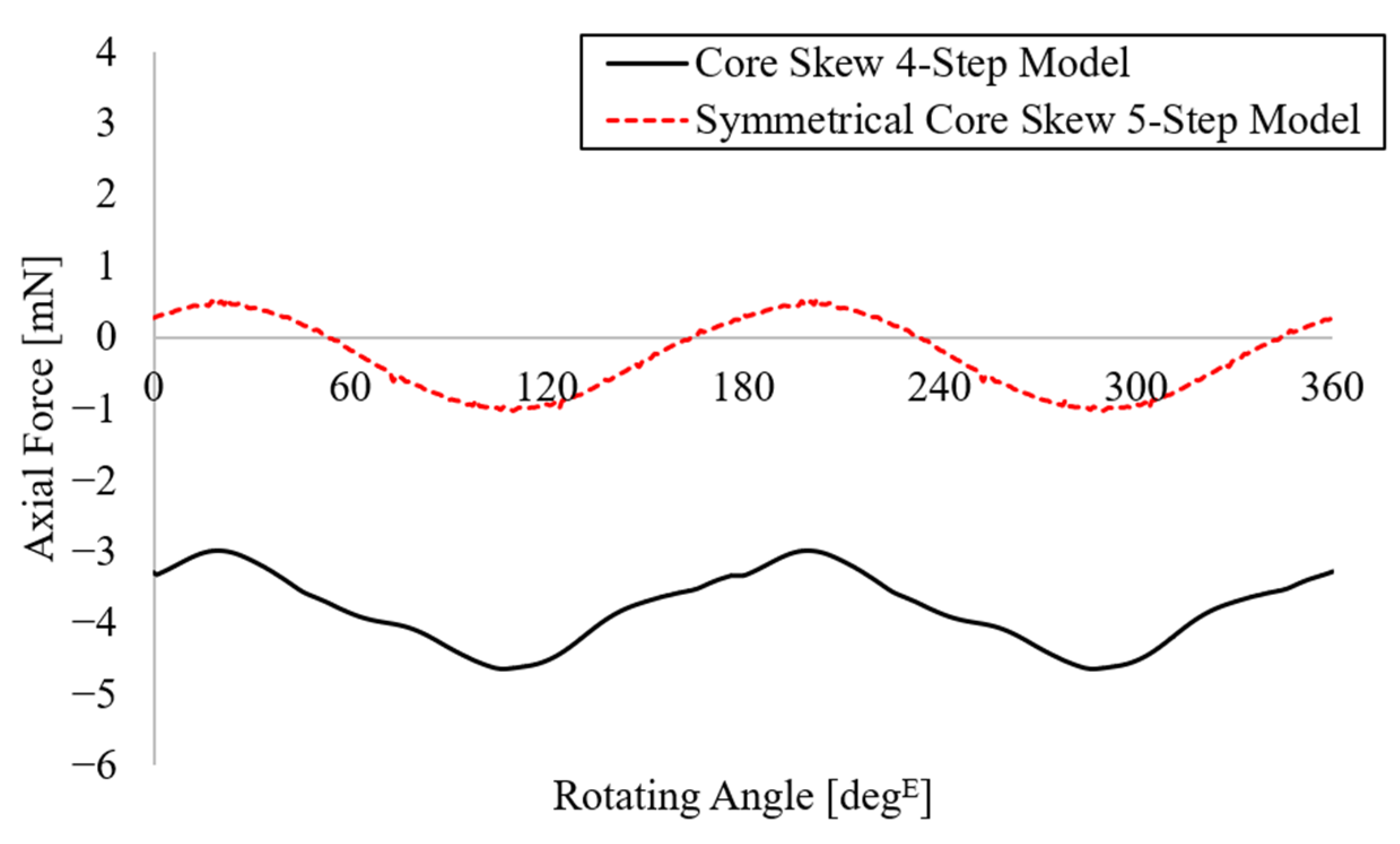
4. Three-Dimensional FEA Based on Several Modeling Steps
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Dorrell, D.G.; Hsieh, M.-F.; Knight, A.M. Alternative rotor designs for high performance brushless permanent magnet machines for hybrid electric vehicles. IEEE Trans. Magn. 2012, 48, 835–838. [Google Scholar] [CrossRef]
- Rahman, M.M.; Kim, K.-T.; Hur, J. Design and optimization of neodymium-free SPOKE-type motor with segmented wing-shaped PM. IEEE Trans. Magn. 2014, 50, 7021404. [Google Scholar] [CrossRef]
- Kim, S.I.; Park, S.; Park, T.; Cho, J.; Kim, W.; Lim, S. Investigation and experimental verification of a novel spoke-type ferrite-magnet motor for electric-vehicle traction drive applications. IEEE Trans. Ind. Electron. 2014, 61, 5763–5770. [Google Scholar]
- Kim, K.-C. A novel method for minimization of cogging torque and torque ripple for interior permanent magnet synchronous motor. IEEE Trans. Magn. 2014, 50, 7019604. [Google Scholar] [CrossRef]
- Bianchini, C.; Immovilli, F.; Lorenzani, E.; Bellini, A.; Davoli, M. Review of design solutions for internal permanent-magnet machines cogging torque reduction. IEEE Trans. Magn. 2012, 48, 2685–2693. [Google Scholar] [CrossRef]
- Zhu, Z.Q.; Liu, Y.; Howe, D. Minimizing the influence of cogging torque on vibration of PM brushless machines by direct torque control. IEEE Trans. Magn. 2006, 42, 3512–3514. [Google Scholar] [CrossRef]
- Zhu, Z.Q.; Howe, D. Influence of design parameters on cogging torque in permanent magnet machines. IEEE Trans. Energy Convers. 2000, 15, 407–412. [Google Scholar] [CrossRef]
- Zhu, L.; Jiang, S.Z.; Zhu, Z.Q.; Chan, C.C. Analytical methods for minimizing cogging torque in permanent-magnet machines. IEEE Trans. Magn. 2009, 45, 2023–2031. [Google Scholar] [CrossRef]
- Nam, D.-W.; Lee, K.-B.; Kim, W.-H. A study on core skew considering manufacturability of double-layer spoke-type PMSM. Energies 2021, 14, 610. [Google Scholar] [CrossRef]
- Yao, B.; Tian, Z.; Zhan, X.; Li, C.; Yu, H. Study on Rotor-Bearing System Vibration of Downhole Turbine Generator under Drill-String Excitation. Energies 2024, 17, 1176. [Google Scholar] [CrossRef]
- Meessen, K.J.; Paulides, J.J.H.; Lomonova, E.A. Force calculations in 3-D cylindrical structures using fourier analysis and the maxwell stress tensor. IEEE Trans. Magn. 2013, 49, 536–545. [Google Scholar] [CrossRef]
- Park, G.-J.; Kim, Y.-J.; Jung, S.-Y. Design of IPMSM applying v-shape skew considering axial force distribution and performance characteristics according to the rotating direction. IEEE Trans. Appl. Supercond. 2016, 26, 7021404. [Google Scholar] [CrossRef]
- Yang, I.-J.; Lee, S.-H.; Jang, I.-S. A process to reduce the electromagnetic vibration by reducing the spatial harmonics of air gap magnetic flux density. IEEE Trans. Magn. 2021, 57, 8103006. [Google Scholar] [CrossRef]





| Parameter | Value | Unit |
|---|---|---|
| Stator Outer Diameter | 134 | mm |
| Rotor Outer Diameter | 60 | mm |
| Air Gap | 0.75 | mm |
| Stack Length | 46 | mm |
| Parameter | Conventional Model | Core Skew 2-Step Model | Core Skew 4-Step Model | Core Skew 6-Step Model | Unit |
|---|---|---|---|---|---|
| torque ripple | 4.29 | 9.04 | 8.94 | 8.81 | % |
| axial force | 0.2 | −3.86 | −3.81 | −3.72 | mN |
| Parameter | Range | Step | Unit |
|---|---|---|---|
| PO | 0.1~0.7 | 0.1 | mm |
| AO | 10~70 | 10 | deg |
| PI | 0.1~0.3 | 0.1 | mm |
| AI | 10~60 | 10 | deg |
| Parameter | X(c) (Conventional Model) | Y(t) (Analysis Model) | Significance Factor | Weight Score |
|---|---|---|---|---|
| torque ripple ratio | XT(c) | YT(t) | ST |
(XT(c) − YT(t))/ XT(c) × ST |
| cogging torque pk 2 pk | XC(c) | YC(t) | SC |
(XC(c) − YC(t))/ XC(c) × SC |
| no-load THD | XH(c) | YH(t) | SH |
(XH(c) − YH(t))/ XH(c) × SH |
| Parameter | Conventional Model | Core Skew Model | Symmetrical Core Skew Model | Unit |
|---|---|---|---|---|
| torque | 1.35 | 1.37 | 1.37 | Nm |
| torque ripple | 7.68 | 8.92 | 5.78 | % |
| Parameter | Symmetrical Core Skew 3-Step Model | Symmetrical Core Skew 5-Step Model | Symmetrical Core Skew 7-Step Model | Unit |
|---|---|---|---|---|
| torque | 1.34 | 1.34 | 1.34 | Nm |
| torque ripple ratio | 6.49 | 6.37 | 6.41 | % |
| axial force | −0.48 | −0.23 | −0.49 | mN |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nam, D.-W.; Lee, K.; Song, S.-W.; Kim, W.-H.; Lee, J.-J. Study on Performance Improvement through Reducing Axial Force of Ferrite Double-Layer Spoke-Type Permanent Magnet Synchronous Motor with Core Skew. Machines 2024, 12, 280. https://doi.org/10.3390/machines12040280
Nam D-W, Lee K, Song S-W, Kim W-H, Lee J-J. Study on Performance Improvement through Reducing Axial Force of Ferrite Double-Layer Spoke-Type Permanent Magnet Synchronous Motor with Core Skew. Machines. 2024; 12(4):280. https://doi.org/10.3390/machines12040280
Chicago/Turabian StyleNam, Dong-Woo, Kangbeen Lee, Si-Woo Song, Won-Ho Kim, and Jae-Jun Lee. 2024. "Study on Performance Improvement through Reducing Axial Force of Ferrite Double-Layer Spoke-Type Permanent Magnet Synchronous Motor with Core Skew" Machines 12, no. 4: 280. https://doi.org/10.3390/machines12040280
APA StyleNam, D.-W., Lee, K., Song, S.-W., Kim, W.-H., & Lee, J.-J. (2024). Study on Performance Improvement through Reducing Axial Force of Ferrite Double-Layer Spoke-Type Permanent Magnet Synchronous Motor with Core Skew. Machines, 12(4), 280. https://doi.org/10.3390/machines12040280








