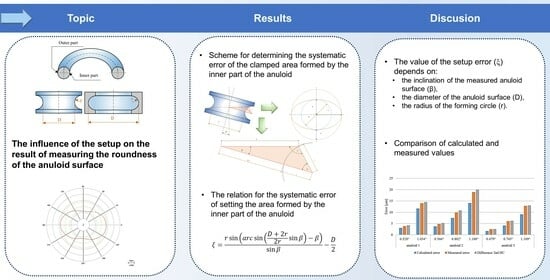
The Influence of the Setup on the Result of Measuring the Roundness of an Anuloid Surface
Abstract
1. Introduction
2. Materials and Methods
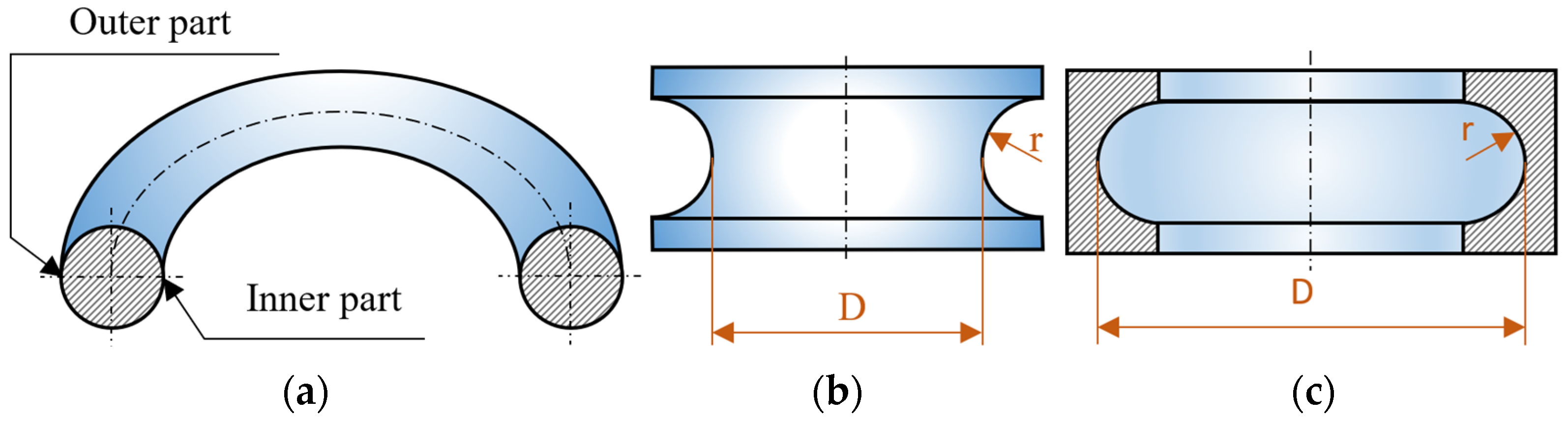
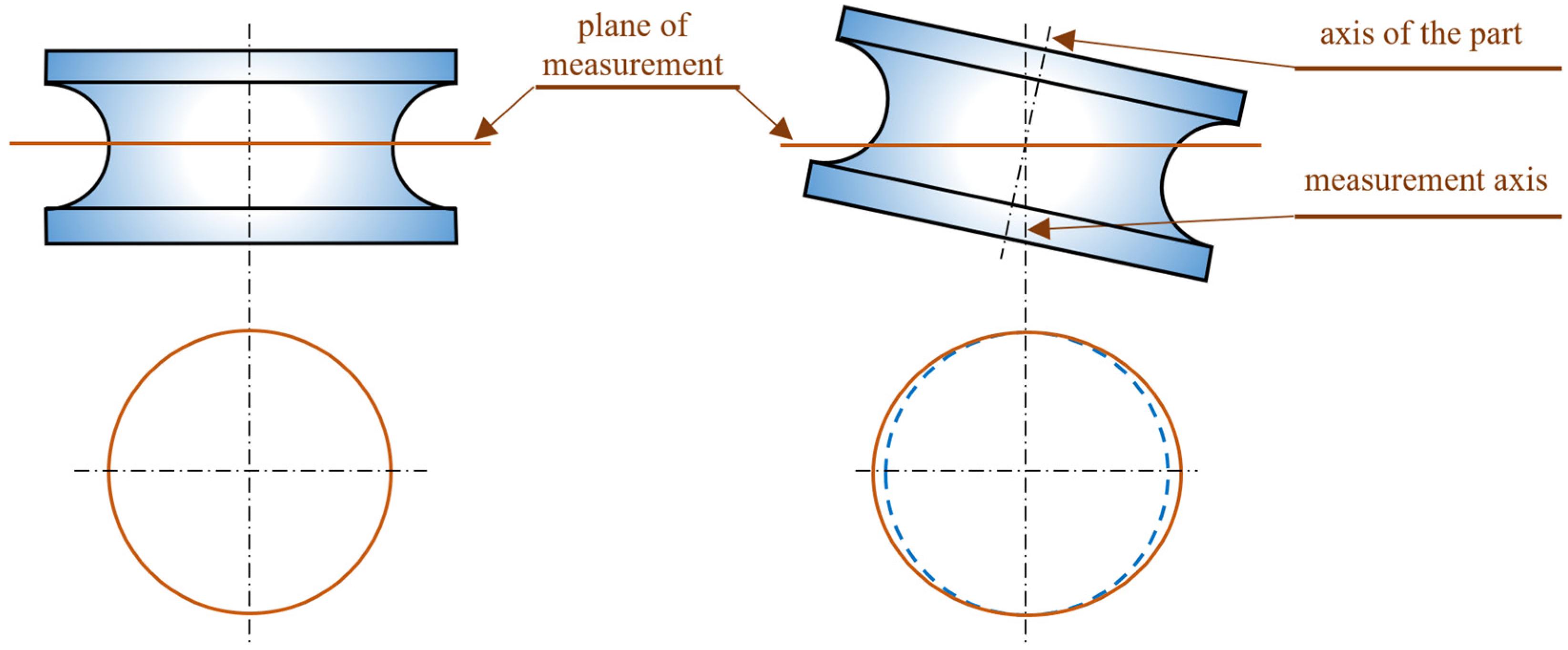
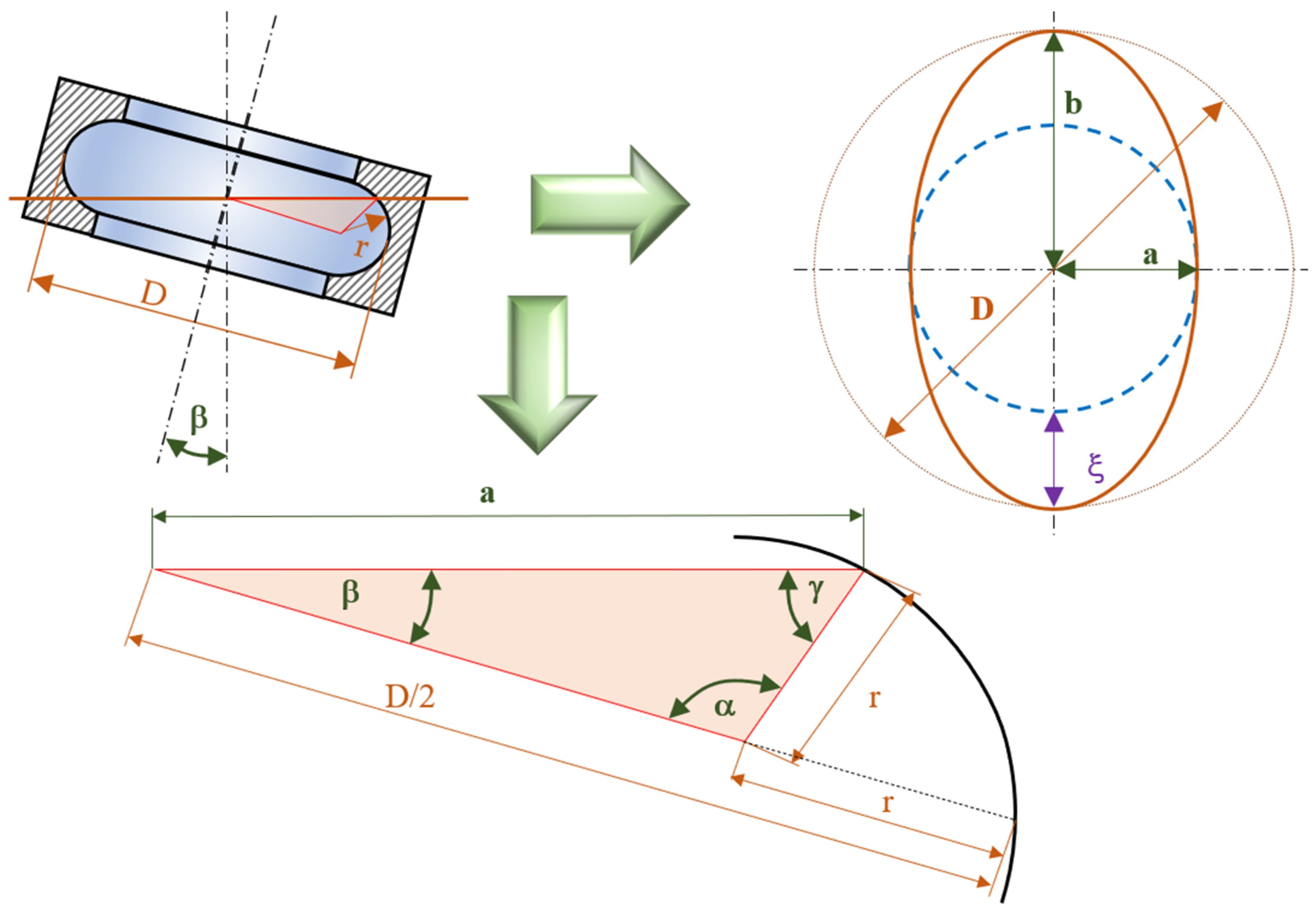
Defining the Problem
3. Results
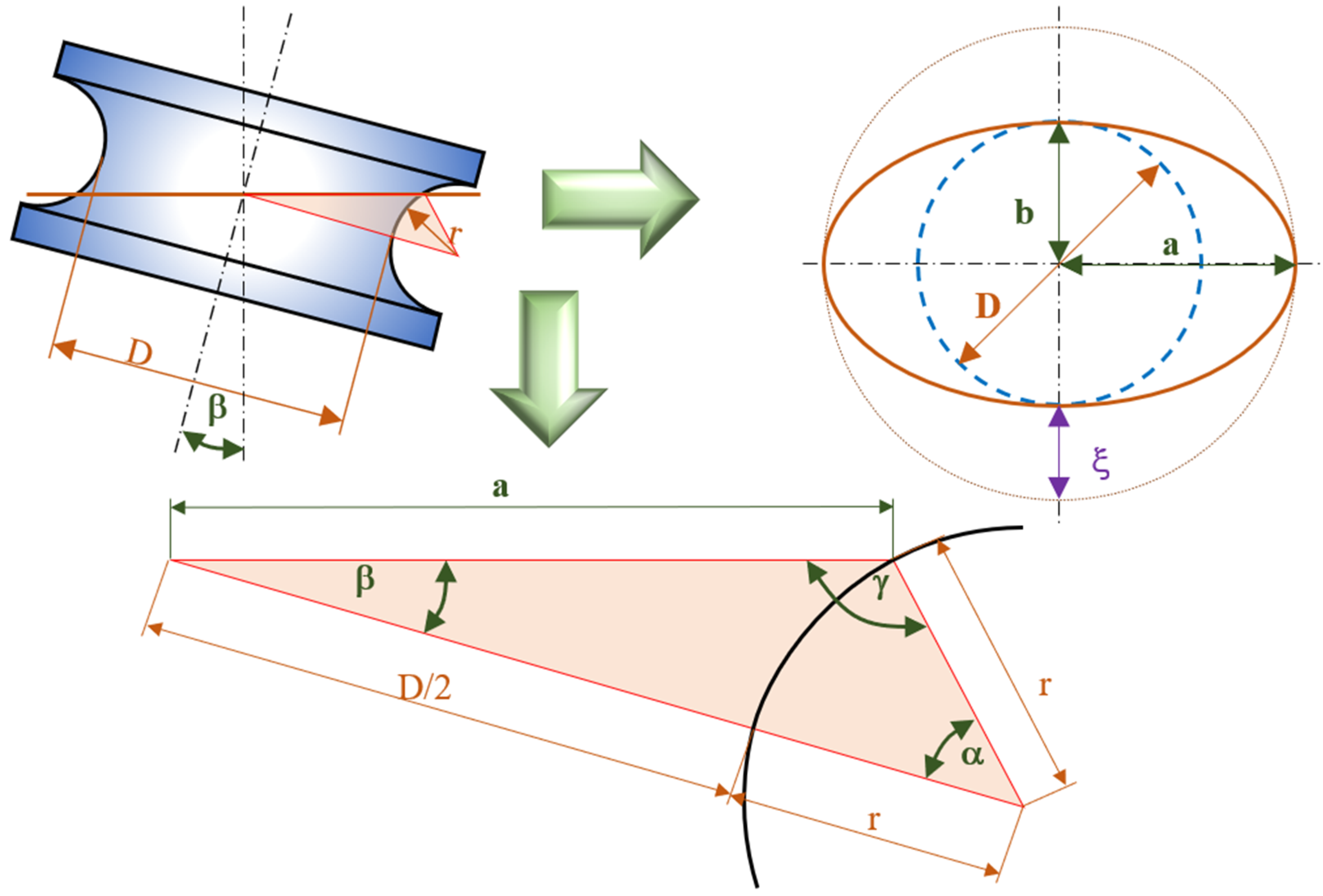
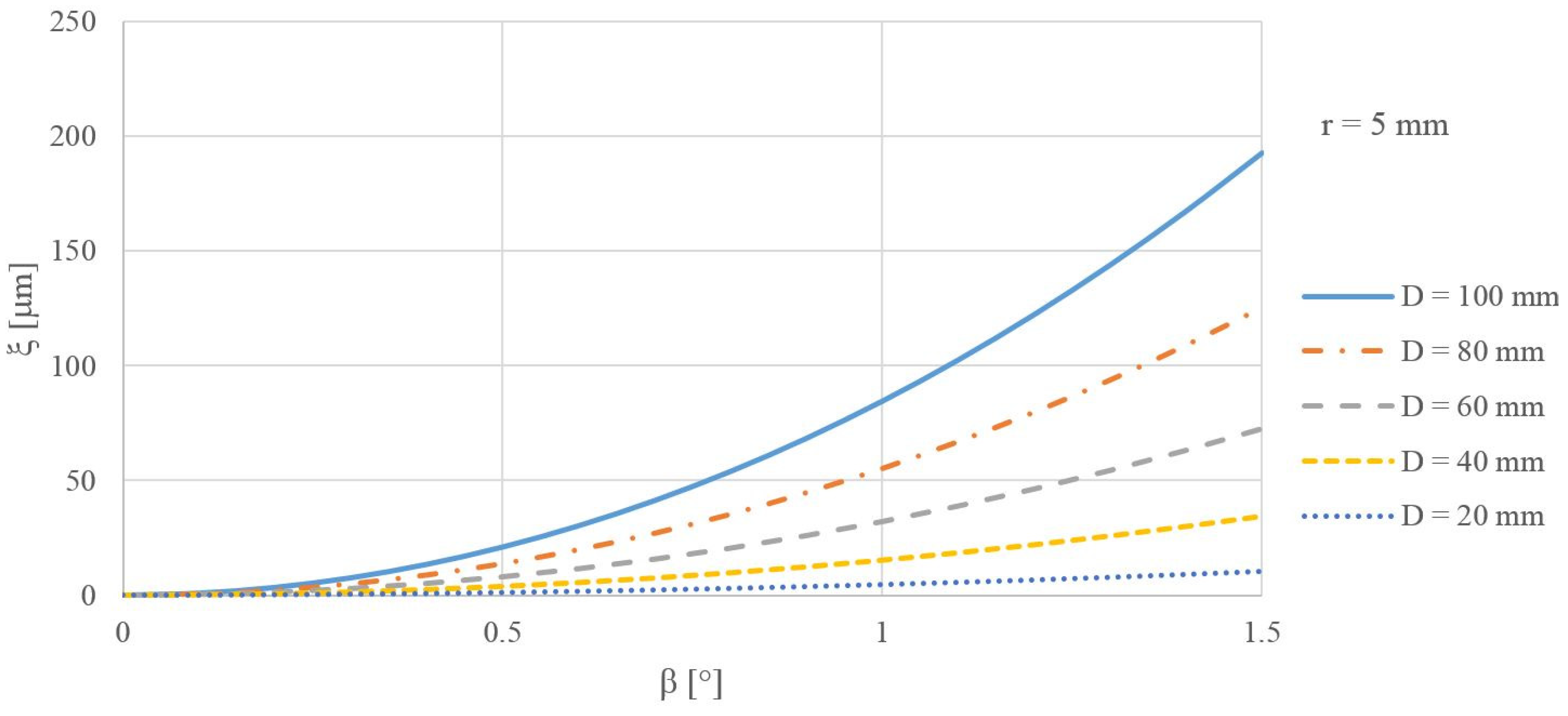
3.1. Calculation of the Systematic Error of the Clamped Area Formed by the Inner Part of the Anuloid
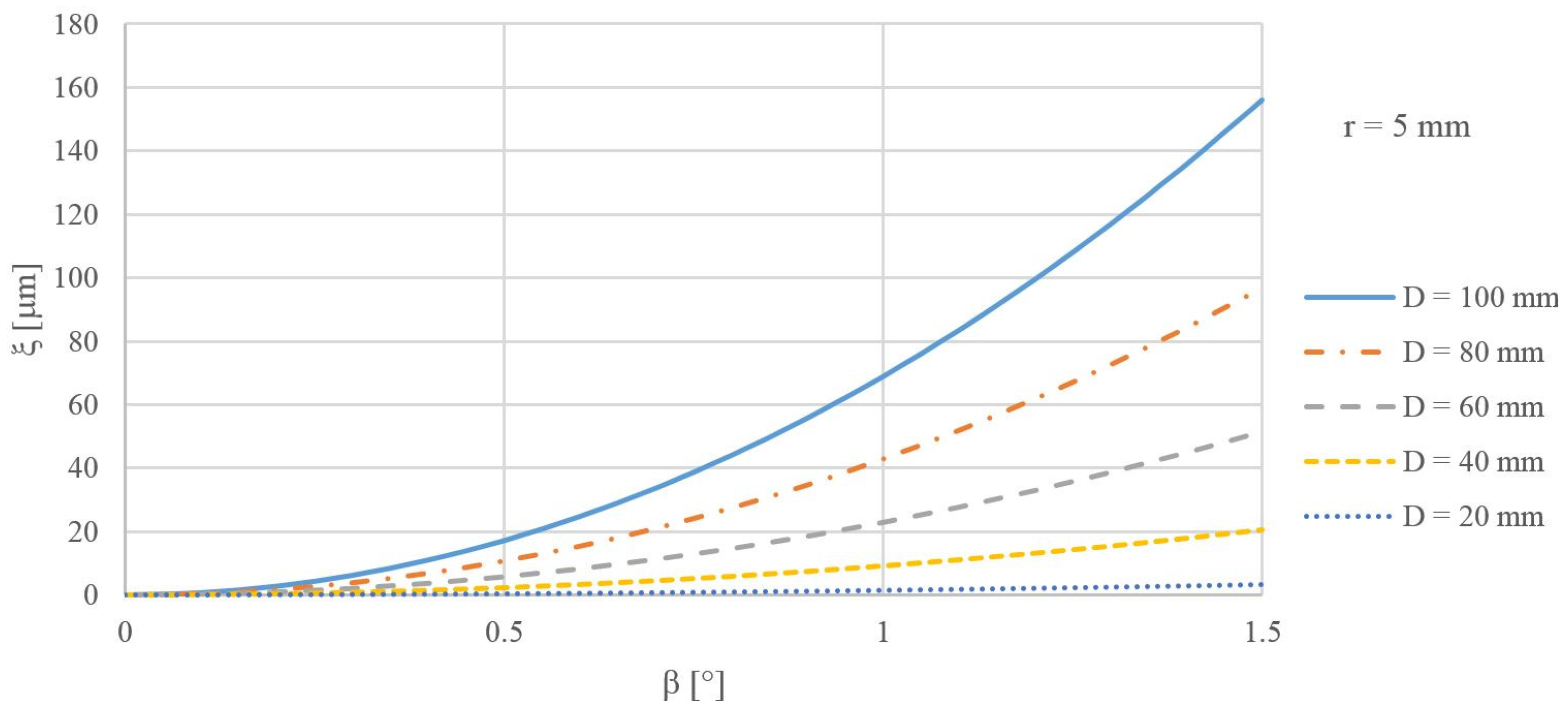
3.2. Calculation of the Systematic Error of the Clamped Area Formed by the Outer Part of the Anuloid
4. Discussion
Comparison of Calculated and Measured Values
- Rotation precision: (0.02 + 6 H/10,000) µm (H is the height from the table top to the measuring point in mm).
- Number of measured points for the roundness measurement: 3600.
- Method of roundness evaluation: MZC (the minimum zone circle).
- The filter used to evaluate the roundness was a Gauss low 150 UPR (undulations per revolution).
- Measurement speed (rotation): 4.0 min−1.
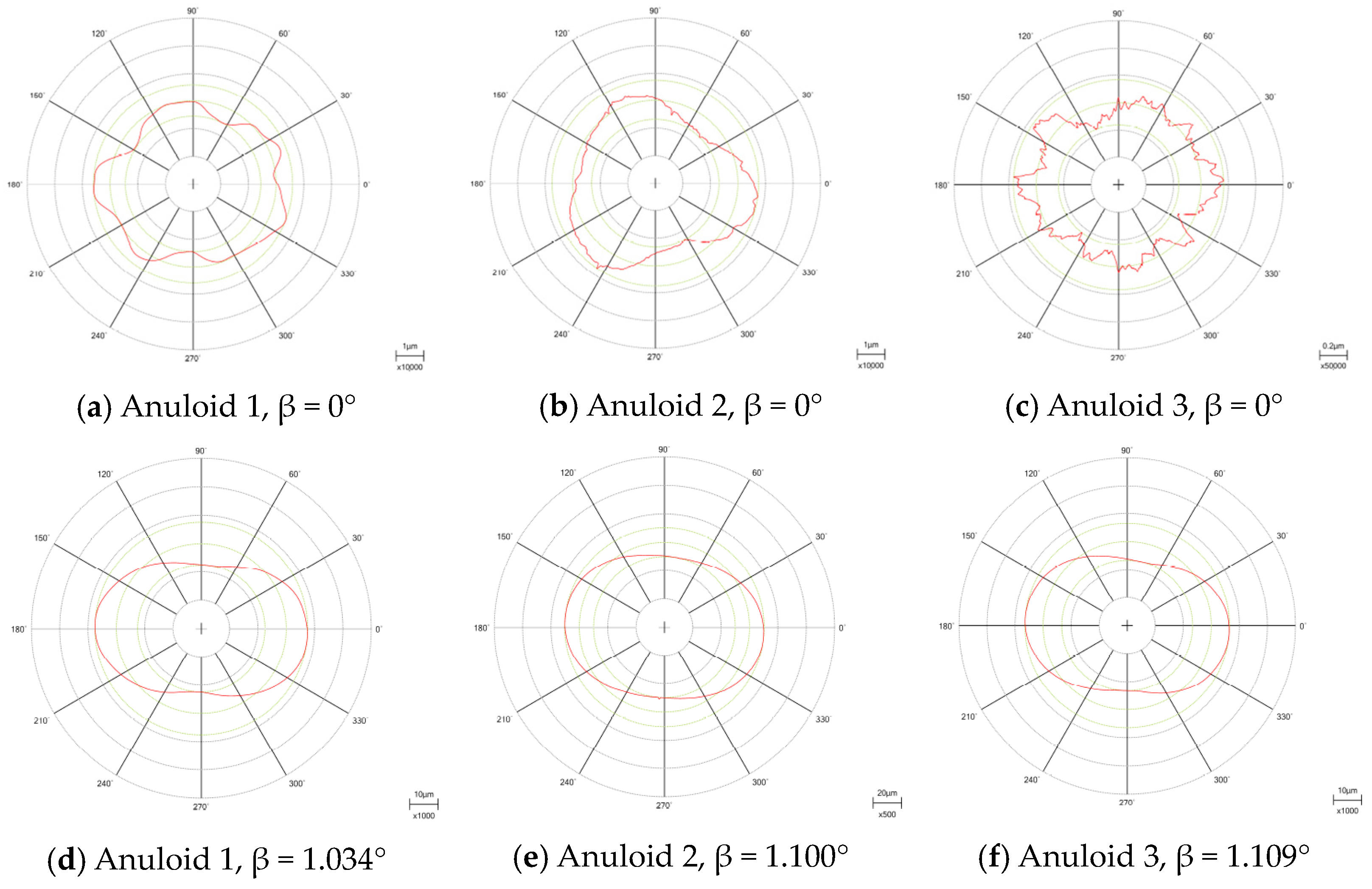
- Anuloid 1: surface diameter D = 29.3 mm and radius of the forming circle r = 3.5 mm; the measured profiles are presented in Figure 10a,d.
- Anuloid 2: surface diameter D = 26.5 mm and radius of the forming circle r = 5 mm; the measured profiles are presented in Figure 10b,e.
- Anuloid 3: surface diameter D = 42.5 mm and radius of the forming circle r = 9 mm; the measured profiles are presented in Figure 10c,f.
5. Conclusions
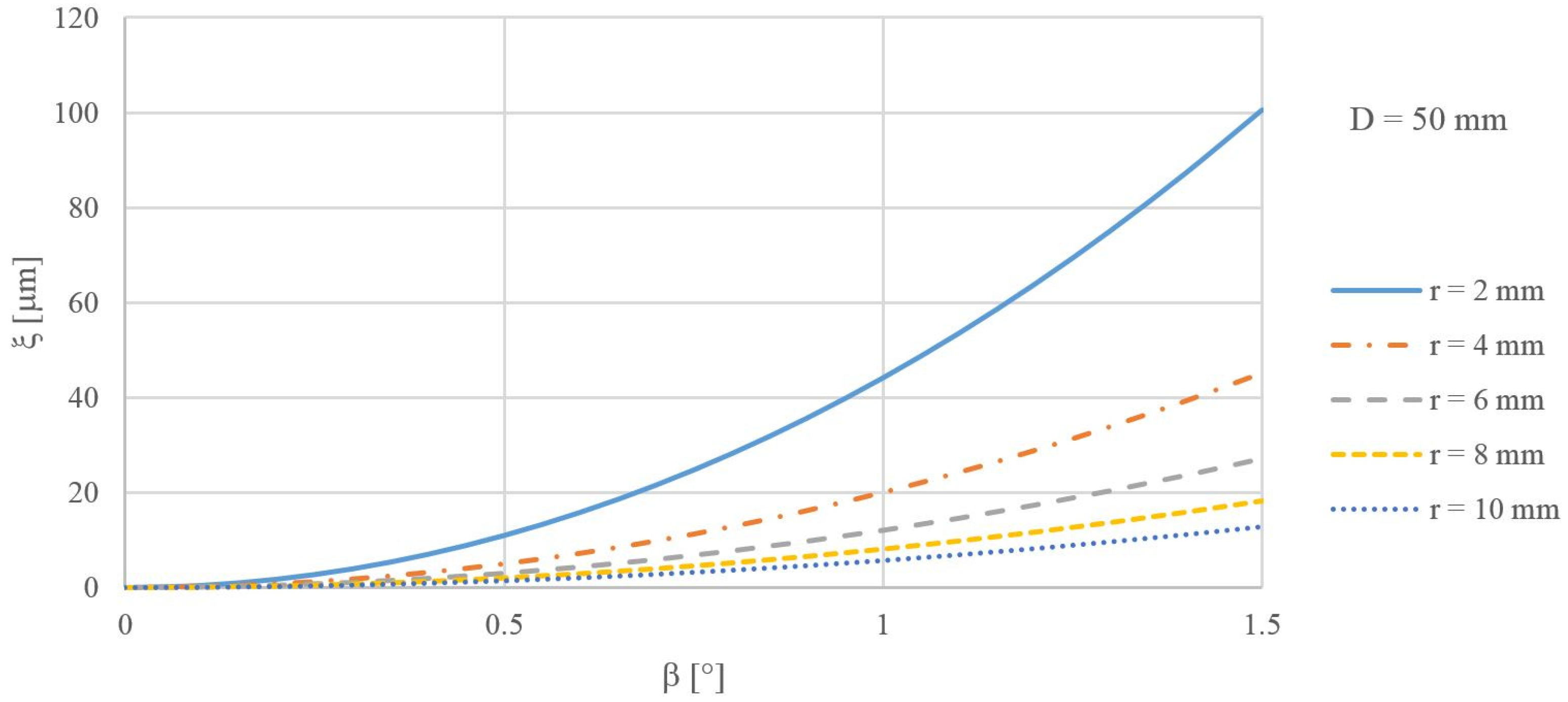
- The value of the setup error (ξ) depended on:
- ○
- the inclination of the measured anuloid surface (β);
- ○
- the diameter of the anuloid surface (D);
- ○
- the radius of the forming circle (r).
- As the angle of inclination of the measured surface (β) increased, the calculated error also increased.
- As the diameter of the measured area (D) increased, the calculated error also increased.
- As the radius of the forming circle (r) increased, the calculated error decreased.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Askary, F.; Sullivan, N. Importance of measurement accuracy in statistical process control. In Proceedings of the Metrology, Inspection, and Process Control for Microlithography XIV, Santa Clara, CA, USA, 27 February–3 March 2000; Volume 3998. [Google Scholar] [CrossRef]
- Whitehouse, D.J. Surface metrology. Meas. Sci. Technol. 1997, 8, 955–972. [Google Scholar] [CrossRef]
- Muralikrishnan, B.; Raja, J. Computational Surface and Roundness Metrology; Springer: London, UK, 2009; ISBN-13:9781848002968. [Google Scholar]
- Sun, C.; Wang, L.; Tan, J.; Zhao, B.; Zhou, T.; Kuang, Y. A high-accuracy roundness measurement for cylindrical components by a morphological filter considering eccentricity, probe offset, tip head radius and tilt error. Meas. Sci. Technol. 2016, 27, 085008. [Google Scholar] [CrossRef]
- Nozdrzykowski, K.; Janecki, D. Comparative studies of reference measurements of cylindrical surface roundness profiles of large machine components. Metrol. Meas. Syst. 2014, 21, 67–76. [Google Scholar] [CrossRef]
- Kupriyanov, O. The influence of measurement error on the risks of the consumer and the manufacturer when completing connections. Ukr. J. Mech. Eng. Mater. Sci. 2020, 6, 22–29. [Google Scholar] [CrossRef]
- Aston, R.; Davis, J.; Stout, K. A probing question: A customer’s investigation into the directional variability of a coordinate measuring machine touch trigger probe. Int. J. Mach. Tools Manuf. 1997, 10, 1375–1382. [Google Scholar] [CrossRef]
- Desa, D.O.J. Instrumentation Fundamentals for Process Control; CRC Press: Boca Raton, FL, USA, 2001; p. 566. ISBN 9781560329015. [Google Scholar]
- Ostrowska, K.; Gaska, A.; Sladek, J. Determining the uncertainty of measurement with the use of a Virtual Coordinate Measuring Arm. Int. J. Adv. Manuf. Technol. 2014, 71, 529–537. [Google Scholar] [CrossRef]
- Blanco, D.; Valino, G.; Fernandez, P.; Rico, C.; Mateos, S. Influence of part material and sensor adjustment on the quality of digitised point-clouds using conoscopic holography. Precis. Eng. 2015, 42, 42–52. [Google Scholar] [CrossRef]
- Prabhu, B.S. An experimental investigation on the misalignment effects in journal bearings. Tribol. Trans. 1997, 40, 235–242. [Google Scholar] [CrossRef]
- Bouyer, J.; Fillon, M. An experimental analysis of misalignment effects on hydrodynamic plain journal bearing performances. In: Journal of Tribology. Am. Soc. Mech. Eng. 2002, 127, 313–319. [Google Scholar] [CrossRef]
- Howard, S.A. Misalignment in gas foil journal bearings: An experimental study. In: Journal of Engineering for Gas Turbines and Power. Am. Soc. Mech. Eng. 2009, 1, 741–749. [Google Scholar] [CrossRef]
- Shi, J.; Cao, H.; Chen, X. Effect of angular misalignment on the dynamic characteristics of externally pressurized air journal bearing. J. Eng. Tribol. Proc. Inst. Mech. Eng. 2019, 234, 205–228. [Google Scholar] [CrossRef]
- Ma, J.; Fu, C.; Zhang, H.; Chu, F.; Shi, Z.; Gu, F.; Ball, A.D. Modelling non-Gaussian surfaces and misalignment for condition monitoring of journal bearings. Measurement 2021, 174, 108983. [Google Scholar] [CrossRef]
- Oktaviana, L.; Tong, V.-C.; Hong, S.-W. Skidding analysis of angular contact ball bearing subjected to radial load and angular misalignment. J. Mech. Sci. Technol. 2019, 33, 837–845. [Google Scholar] [CrossRef]
- Yang, Z.; Zhang, Y.; Zhang, K.; LI, S. Wear analysis of angular contact ball bearing in multiple-bearing spindle system subjected to uncertain initial angular misalignment. In: Journal of Tribology. Am. Soc. Mech. Eng. 2021, 143, 091703. [Google Scholar] [CrossRef]
- Ye, Z.; Wang, L.; Gu, L.; Zhang, C. Effects of tilted misalignment on loading characteristics of cylindrical roller bearings. Mech. Mach. Theory 2013, 69, 153–167. [Google Scholar] [CrossRef]
- Tong, V.-C.; Hong, S.-W. The effect of angular misalignment on the running torques of tapered roller bearings. Tribol. Int. 2016, 95, 76–85. [Google Scholar] [CrossRef]
- Zhao, Z.; Wang, X.; Hou, Y. Measurement of the roller tilt angle in a double-row tapered roller bearing with strain gauges. Measurement 2024, 226, 114106. [Google Scholar] [CrossRef]
- Šimunović, V.; Baršić, G. Evaluating the spindle error of the roundness measurement device. Meas. Sens. 2024, 32, 101038. [Google Scholar] [CrossRef]
- Li, Q.; Shimizu, Y.; Wang, X.; Li, X.; Gao, W. High-accuracy roundness measurement of small cylindrical workpieces by a high-frequency filtering method. Precis. Eng. 2024, 85, 241–246. [Google Scholar] [CrossRef]
- Tiainen, T.; Viitala, R. Effect of positional errors on the accuracy of multi-probe roundness measurement methods. Mech. Syst. Signal Process. 2020, 144, 106883. [Google Scholar] [CrossRef]
- Görög, A.; Görögová, I. Application of Fourier series for evaluation of roundness profiles in metrology. Adv. Sci. Technol. Res. J. 2019, 13, 30–38. [Google Scholar] [CrossRef]
- Görög, A. Influence of the Setting on the Result of Measuring the Roundness of the Cylindrical and Conical Surface. Manuf. Technol. 2022, 22, 408–413. [Google Scholar] [CrossRef]


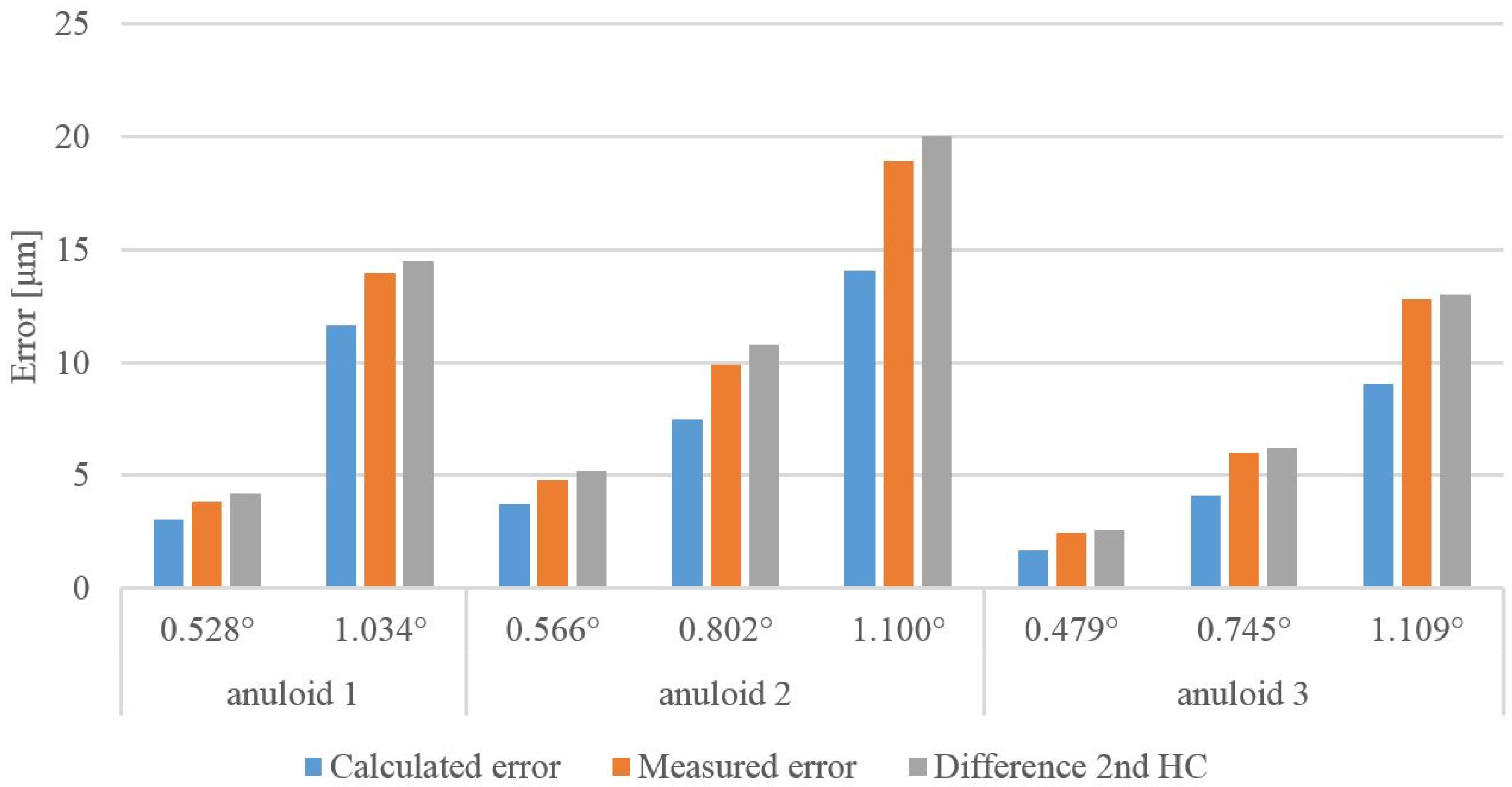
| Surface | Tilt β (°) | Roundness (μm) | 2nd HC (μm) | Calculated Error (μm) | Measured Error (μm) | Differ. 2nd HC (μm) |
|---|---|---|---|---|---|---|
| Anuloid 1 | 0 | 1.396 | 0.278 | - | - | - |
| Anuloid 1 | 0.528 | 5.207 | 2.368 | 3.034 | 3.811 | 4.180 |
| Anuloid 1 | 1.034 | 15.357 | 7.510 | 11.644 | 13.961 | 14.464 |
| Anuloid 2 | 0 | 1.437 | 0.193 | - | - | - |
| Anuloid 2 | 0.566 | 6.243 | 2.781 | 3.710 | 4.806 | 5.176 |
| Anuloid 2 | 0.802 | 11.336 | 5.580 | 7.454 | 9.899 | 10.774 |
| Anuloid 2 | 1.100 | 20.366 | 10.215 | 14.042 | 18.929 | 20.044 |
| Anuloid 3 | 0 | 0.328 | 0.056 | - | - | - |
| Anuloid 3 | 0.479 | 2.777 | 1.333 | 1.691 | 2.449 | 2.554 |
| Anuloid 3 | 0.745 | 6.305 | 3.153 | 4.091 | 5.977 | 6.194 |
| Anuloid 3 | 1.109 | 13.139 | 6.549 | 9.073 | 12.811 | 12.986 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Görög, A.; Kuruc, M. The Influence of the Setup on the Result of Measuring the Roundness of an Anuloid Surface. Machines 2024, 12, 258. https://doi.org/10.3390/machines12040258
Görög A, Kuruc M. The Influence of the Setup on the Result of Measuring the Roundness of an Anuloid Surface. Machines. 2024; 12(4):258. https://doi.org/10.3390/machines12040258
Chicago/Turabian StyleGörög, Augustín, and Marcel Kuruc. 2024. "The Influence of the Setup on the Result of Measuring the Roundness of an Anuloid Surface" Machines 12, no. 4: 258. https://doi.org/10.3390/machines12040258
APA StyleGörög, A., & Kuruc, M. (2024). The Influence of the Setup on the Result of Measuring the Roundness of an Anuloid Surface. Machines, 12(4), 258. https://doi.org/10.3390/machines12040258