Abstract
The measurement of the ground forces on a real structure or mechanism in operation can be time-consuming and expensive, particularly when production cannot be halted to install sensors. In cases in which disassembling the parts of the system to accommodate sensor installation is neither feasible nor desirable, observing the structure or mechanism in operation and quickly deducing its force trends would facilitate monitoring activities in industrial processes. This opportunity is gradually becoming a reality thanks to the coupling of artificial intelligence (AI) with design techniques such as the finite element and multi-body methods. Properly trained inferential models could make it possible to study the dynamic behavior of real systems and mechanisms in operation simply by observing them in real time through a camera, and they could become valuable tools for investigation during the operation of machinery and devices without the use of additional sensors, which are difficult to use and install. In this paper, the idea presented is developed and applied to a simple mechanism for which the reaction forces during operating conditions are to be determined. This paper explores the implementation of an innovative vision-based virtual sensor that, through data-driven training, is able to emulate traditional sensing solutions for the estimation of reaction forces. The virtual sensor and relative inferential model is validated in a scenario as close to the real world as possible, taking into account interfering inputs that add to the measurement uncertainty, as in a real-world measurement scenario. The results indicate that the proposed model has great robustness and accuracy, as evidenced by the low RMSE values in predicting the reaction forces. This demonstrates the model’s effectiveness in reproducing real-world scenarios, highlighting its potential in the real-time estimation of ground reaction forces in industrial settings. The success of this vision-based virtual sensor model opens new avenues for more robust, accurate, and cost-effective solutions for force estimation, addressing the challenges of uncertainty and the limitations of physical sensor deployment.
1. Introduction
In recent years, the Internet of Things (IoT) has paved the way for new methods of obtaining and processing large amounts of data, playing a crucial role in a variety of applications, such as mobility, industrial automation, and smart manufacturing. The necessity for a large number of sensors to monitor crucial production variables in order to ensure consistent product quality and optimize energy consumption [1] has caused the emergence of virtual sensors, software-based models that emulate the functioning of physical sensors. The main advantage of virtual sensors is related to their cost-effectiveness, gaining an advantage especially in those cases where the installation and maintenance of physical sensors is difficult and expensive [2,3]. The flexibility of virtual sensors, which are easily adaptable to different process conditions and environments, makes them easy to integrate into industrial settings with different aims, ranging from predictive maintenance [4] to process optimization [5]. Generally, soft sensors are divided into two categories: those based on mathematical models and those based on data-driven methods. The foundational concept of virtual sensors originates from the utilization of mathematical models to estimate critical quantities, without direct measurement. Hu et al. extrapolated the force exerted at the catheter tip within the human body with a mathematical model, exploiting a sensor positioned on the exterior of the catheter tube [6]. In recent years, with the advent of new technologies that provide enhanced data storage capabilities, data-driven methods have gained significant attention thanks to the development of new machine learning algorithms [7,8]. This innovative data-driven approach offers a new, effective means of obtaining accurate readings along the entire processing chain, without installing expensive hardware, providing an effective tool for the online estimation of quantities that are important but difficult to measure with traditional sensors. A clear example of a data-driven virtual sensor is presented by Sabanovic et al. in their work, where different architectures of artificial neural networks are exploited to estimate vertical acceleration in vehicle suspension [9]. Leveraging technological advancements in computational power and increasingly efficient algorithms, recent developments have paved the way for the use of vision-based virtual sensors (i.e., based on image analysis). Indeed, the use of cameras, even across various spectral ranges, allows for real-time information gathering in a non-invasive manner, enabling installation and data acquisition even on pre-existing structures that were not designed for the use of physical sensors. Moreover, the extreme versatility of these systems allows for their use remotely or in dangerous or hard-to-reach situations (i.e., through the use of robots or unmanned aerial vehicles (UAVs) [10]). Byun et al. introduce a methodology for the use of image-based virtual vibration measurement sensors to monitor vibration in structures, offering an alternative to traditional accelerometers [11]. Wang et al. introduce a model-based approach for the design of virtual binocular vision systems using a single camera and mirrors to improve the 3D haptic perception in robotics [12]. Ögren et al. develop vision-based virtual sensors with the aim of estimating the equivalence ratio and concentration of major species in biomass gasification reactors, using image processing techniques and regression models on real-time light reaction zone image data, demonstrating the applicability and effectiveness of vision-based monitoring for process control in a complex industrial setting [13]. Alarcon et al. discuss the integration of Industry 4.0 technologies into fermentation processes by implementing complex culture conditions that traditional technologies cannot achieve. In this context, computer vision techniques are exploited to develop a virtual sensor to detect the end of the growth phase and a supervisory system to monitor and control the process remotely [14]. There are many cases found in the literature related to the use of virtual sensors to measure forces. Physics-informed neural networks (PINNs) are used to estimate equivalent forces and calculate full-field structural responses, demonstrating high accuracy under various loading conditions and offering a promising tool for structural health monitoring [15]. Marban et al. introduce a model based on a recurrent and convolutional neural network for the sensor-less force measurement of the interaction forces in a robotic surgical application. Using video sequences and surgical instrument data, the model estimates the forces applied during surgical tasks, improving the haptic feedback in minimally invasive robot-assisted surgery [16]. Ko et al. developed a vision-based system to estimate the interaction forces between the robot grip and objects by combining RGB-D images, robot positions, and motor currents. By incorporating proprioceptive feedback with visual data, the proposed model achieves high accuracy in force estimation [17]. In the context of smart manufacturing, Chen et al. develop a real-time milling force monitoring system, using sensory data to accurately estimate the forces involved in the process, thus enabling real-time adjustment to optimize the cutting operation [18]. Bakhshandeh et al. propose a digital-twin-assisted system for machining process monitoring and control. Virtual models, integrated with real-time sensor data, are used to measure the cutting forces, enabling adaptive control, anomaly detection, and precision applications without physical sensors [19].
1.1. Novel Work and Motivation
In this research, we intend to demonstrate that properly trained inferential models have the potential to revolutionize the study of the dynamic behavior of real systems and mechanisms. By exploiting virtual sensing techniques, we intend to observe these systems in operation in real time through a camera, eliminating the need for additional, often bulky and difficult-to-install sensors. Our goal is to validate this approach using a simple mechanism as a test case, illustrating how these models can become valuable tools in studying the operation of machinery and devices with ease, efficiency, and robustness. This study is intended to explore the feasibility and effectiveness of inferential models in capturing and analyzing the complex dynamics of mechanical systems, paving the way for their widespread application in industry. Even in the case in which accurate multi-body models or digital twins of the mechanism are available, delivering real-time input to these models can be challenging. Simulating the actual scenario for a multi-body model requires knowledge of the actual motion of law and demands significant computational effort, especially in the case of very complex models. The measurement of the motion law is easy in the case of synchronous motors since their speed is correlated to the frequency of the AC power supply and the number of poles of the motor itself. However, in an industrial context, asynchronous motors are frequently used, and the measurement of their speed is not straightforward. External sensors such as encoders become necessary, demanding both excessive time and high costs for their installation. Our research investigates the implementation of an innovative vision-based virtual sensor that, through data-driven training, is able to emulate traditional sensing solutions for the estimation of reaction forces. The implemented virtual sensor and related multi-layer perceptron (MLP) architecture are trained and tested using a simple mechanism, exploiting a multi-body model. The first model is trained with the ideal inputs and outputs, while the second is instead trained on a dataset that takes into account the uncertainty in the measurement of the input quantities (i.e., closely replicating a real-world scenario). The developed models are tested with new and unobserved trajectories to further assess their effectiveness and robustness.
The motivation behind our study lies in the challenge of studying the dynamics of operational machines that lack installed sensors. In many cases, halting production for the installation of sensors is impractical and time-consuming, despite the potential benefits in terms of analysis, control, and overall system reliability. The interest in exploring non-invasive alternatives, to obtain accurate estimations of machine behavior without disrupting ongoing operations, drove us to implement a specific virtual sensor for the estimation of ground reaction forces in industrial machines.
The concept revolves around exploiting verified multi-body models of machines to train AI-based virtual sensors. These sensors can then be employed to gather real-time information by processing data from cameras, eliminating the need for physical force sensors. Our aim is to develop a robust method that enables the generation of virtual sensors capable of providing valuable insights into the dynamics of existing operational machines. Our approach is well suited for the real-time estimation of forces and other relevant values and it accounts for the variability introduced by various factors, such as the camera positioning, significantly enhancing the reliability and robustness of the sensor. In summary, our study paves the way for the establishment of a robust framework for the creation of virtual sensors that can monitor and gauge the condition of moving machines solely by visually observing them.
1.2. Contribution
The contribution of our work to the existing body of knowledge lies in the development and application of a vision-based virtual sensor, in the context of industrial processes and mechanical systems. The main key points of our study are the following.
- This paper introduces a non-invasive virtual sensor as an alternative to traditional sensing systems, using cameras and leveraging data-driven inferential models to measure the forces involved in a mechanism.
- The exploitation of the proposed vision-based virtual sensor is an efficient solution in reducing the need for external sensors like force transducers or encoders, whose installation is often time-consuming and expensive.
- The virtual sensor has been developed also considering datasets with uncertainties, thus assessing the robustness of the overall measurement system to real-world disturbances.
- This study demonstrates the adaptability of the proposed solution in capturing and analyzing the dynamics of mechanical systems for real-time solutions.
1.3. Organization of the Paper
The article is structured as follows. Section 2 details the design of the multi-body model, the camera model used to simulate frame acquisition, the methodology used for data collection, and the implementation of an AI-based virtual sensor to estimate ground reaction forces. The results of the training of two different models are presented in Section 3. The models thus trained are finally compared with the results that would have been obtained through the use of the multi-body model.
2. Materials and Methods
To first assess the feasibility of the method, the implementation of a vision-based virtual sensor to estimate the reaction forces in industrial mechanisms is applied to a simple but fundamental mechanical system, the four-bar linkage mechanism, with a verified multi-body model (Figure 1). This system is chosen for its basic but significant role in the study of mechanical systems, providing a clear framework to test our hypotheses. The approach focuses on the development of an AI-based virtual sensor designed to estimate the reaction forces (constraint reactions) within the mechanism based solely on visual observation. This method is similar to extracting hypothetical data from a camera monitoring the moving mechanism, mimicking real-world scenarios where direct force measurement is not feasible. The main objective is to demonstrate the practicality of using AI-based algorithms to extract reaction forces in real time. The implemented AI-based virtual sensor is responsible for estimating the ground reaction forces of the mechanism. It processes the mechanism position data, which serve as the input, enabling real-time analysis and estimation. This approach is critical in replicating and predicting the forces in operational industrial environments, showing the potential of virtual sensors in optimizing the performance, monitoring the operation, and ensuring the safety of mechanical systems in a real industrial scenario. In this section, we will describe the multi-body model of the mechanism used to build our training dataset; then, the model of the camera used in the software to replicate the monitoring of the mechanism is presented. This camera model will be replicated with an analytical model that will be used to generate different datasets taking into account various sources of uncertainty, which will be described in the section related to data collection. Finally, the design of the AI-based virtual sensor and its architecture will be presented in the last subsection.
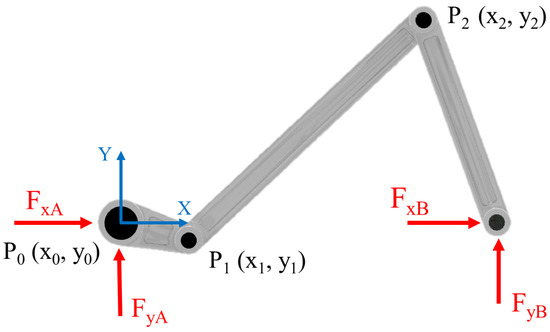
Figure 1.
CAD model of the four-bar linkage mechanism. Ground reaction forces , , , are represented in red. The crank center of rotation is identified by point , where a fixed reference frame represented in blue is indicated to evaluate the position of the joints identified by points and .
2.1. Multi-Body Model
The 3D model of the mechanism, designed in Autodesk Inventor 2024, uploaded on the multi-body software RecurDyn 24, is shown in Figure 1. In the multi-body software, the definition of joints has to be meticulously performed, by taking into account the degrees of freedom (DoF) of each body in the space and avoiding the redundancy of the constraints. The objective is to achieve a mechanism with a single DoF, specifically the rotation of the crank. The two grounded joints are defined as “revolute” joints, restricting all translations and rotations of the links, except for the rotation within the plane of the image. The joint between the crank and the connecting rod is defined as the “universal” joint, permitting two rotations, one of which is in the plane of the image. To prevent redundancy in the constraints, the joint between the connecting rod and the rocker is defined as a “spherical” joint, constraining only the three relative translations. The resulting system has one degree of freedom (DoF), corresponding to the rotation of the crank. As shown in Figure 1, the point corresponding to the crank center of rotation is labeled as , the point identifies the joint between the crank and the connecting rod, while point is used to describe the position of the joint between the connecting rod and the rocker.
2.2. Camera Model
Autodesk Inventor 2023 has been utilized to simulate a real-life sensor and to create dynamic videos of the mechanism for further analysis through computer vision. To incorporate a camera within the Inventor Studio environment, it is necessary to specify both the target point position and the spatial coordinates of the camera. The orientation of the camera aligns with the line connecting it to the target point, allowing us to configure the camera precisely. We constrain the target position to the same plane where the mechanism exists, limiting the range of its coordinates to two, while the camera’s three spatial coordinates and roll angle remain adjustable. The type of camera employed in the software is an orthographic projection rather than a perspective camera, with the horizontal angular field of view (AFOV) and resolution as customizable parameters. In the specific case, an AFOV of 28° is fixed and the resolution of the captured image is set equal to 2240 × 1200, as shown in Figure 2. Once the intrinsic parameters of the camera have been chosen, the adjustable parameters related to its position and orientation have to be set. In Table 1, the definitions of these parameters and their values used to identify the standard configuration of the sensor are reported.
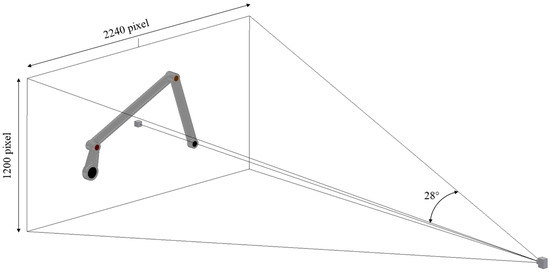
Figure 2.
Four-bar linkage mechanism in Inventor Studio and definition of camera.

Table 1.
Parameters of standard configuration of camera in Inventor Studio.
To bypass the need for Inventor Studio and the extensive rendering time required for each video, an analytical model of the camera has been developed. This model is an effective tool, accepting as input the values of the adjustable parameters outlined in Table 1 and the spatial position of a point. It outputs the corresponding location of this point, in pixels, within the frame captured by the camera. In Figure 3, an example of the application of this model is represented: a point p (green) in space is defined by its coordinates with the respect to the world frame (), while the positions of the camera and the target are defined, respectively, by the coordinates () and (). The orientation of the camera is defined by the line connecting the camera and the target, and the image plane is orthogonal to this line and centered in the target. The point p is orthogonally projected on the image plane, resulting in the point P (red). Finally, its coordinates and (expressed in mm) with respect to the image reference frame () are computed.
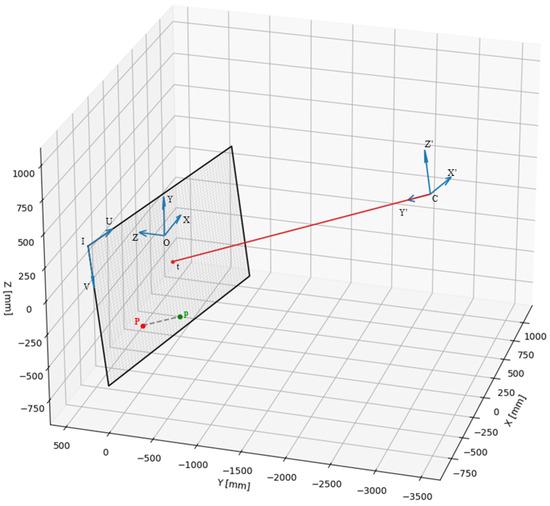
Figure 3.
Example of application of analytical model of camera. The world reference frame () centered at O, the position of the camera C and its frame (), and the position of the target t are presented. The point p defined in the world reference frame is projected onto the plane image and defined in the image reference frame () in pixels.
The model has been tested and validated under standard camera conditions, with its results benchmarked against those obtained from the Autodesk Inventor camera. In anticipation of exploring the impact of uncertainties on the AI-based virtual sensor, the analytical model has been adapted to accept deviations in the camera’s customizable parameters from their standard settings, as well as the coordinates of any point in space. This enhanced model facilitates the generation of varied datasets to account for uncertainties related to the camera’s position, thus significantly reducing the time required to produce highly consistent datasets. Our research focuses on replicating the camera model used by Autodesk Inventor, given its focus on a simulated model. However, it is crucial to acknowledge that, within real-world applications, a variety of camera models could be implemented, each offering different perspectives and characteristics.
2.3. Data Collection
Data to train the model are sourced from simulations conducted on the multi-body model within the RecurDyn environment, which facilitates the simulation of the mechanical system’s dynamics. Following the workflow shown in Figure 4, a known motion is imposed on the mechanism, and it is observed by the camera sensor modeled in Section 2.2.
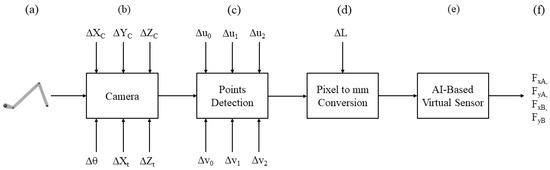
Figure 4.
Workflow of the reaction force estimation procedure: the four-bar linkage mechanism (a) motion is captured by a sensor camera (b); images are processed by a computer vision algorithm (c), and position of significant points are computed in mm (d); positions data are fed to the AI-based virtual sensor (e) that estimates ground reaction forces of the mechanism (f).
Thus, mechanism (a) is observed from camera sensor (b), the position of which is defined by . From the captured frame, points , and , expressed in pixels, are identified by computer vision algorithms (c), based on HSV color segmentation. The image is then calibrated based on known dimensions (i.e., crank length L) and such points’ positions are converted from pixels to millimeters and referenced to the reference system centered at (d), as shown in Figure 1. The positions of the points and expressed in millimeters are then fed to the model (e) such that the constraining reactions , , , (f) are predicted. The use of vision-based measurement systems introduces sources of uncertainty that could alter the input data given to the model: the positioning of the camera might be different with respect to the standard configuration; therefore, the uncertainty related to the sensor position is defined as the deviation from the reference position (). The detection of the three points’ coordinates, performed by the computer vision algorithm, is characterized by some noise related to the position of the pixel in the frame, corresponding to the detected point. Moreover, in this case, the uncertainty is defined as the deviation from the real position of the three centroids (). Finally, the conversion from pixels to mm, implemented in the algorithm, is influenced by the measurement of the crank length, which may suffer from some error (). Therefore, to generate datasets that take into account the presence of these sources of uncertainty, the analytical model of the camera can be used to generate data related to a large variety of camera configurations. The output of the analytical model, which represent the positions of , , and , can be further rearranged, adding artificial noise (in pixels) on the six coordinates, for each frame, simulating the computer vision algorithm. Finally, the conversion from pixels to mm can be carried out by taking into account the error in the length measurement.
2.4. AI-Based Virtual Sensor for Ground Reaction Force Estimation
A multi-layer perceptron (MLP) regression model is built in order to estimate the ground reaction forces using the linkage joints’ position coordinates, extrapolated from the camera data. The use of MLP networks can be remarkably effective, despite their simplicity, even when compared to more complex deep neural network (DNN) models, such as convolutional neural networks (CNNs) [20]. The advantage of the MLP lies in its utilization of lightweight and fast models, typically around the order of 0.1 Mb, offering a stark contrast to the often much heavier advanced DNN models. This efficiency makes MLP an appealing choice in various scenarios where a balance between performance and resource utilization is crucial. The purpose of the model is to predict, at each instant , the reaction forces exchanged on the ground by the articulated quadrilateral (Figure 4a). Since the time history of the input influences the value of the output, the model receives as input a vector of shape (20, 1), consisting of the 2D coordinates of the two points and of the mechanism from instant to , measured as explained in Section 2.3. As output, it returns a vector of shape (4, 1), consisting of the two components of the ground reaction forces (Figure 5).
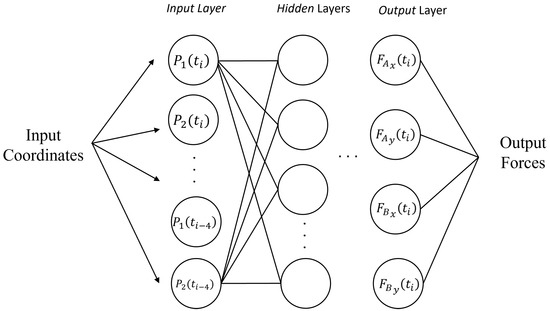
Figure 5.
The proposed MLP architecture takes as input two points and of the mechanism from instant to , and it returns as output (i.e., predicts) the two components of the ground reaction forces and .
The input and output data are normalized to enhance the convergence and the stability of the neural network during the training. Each column of both the input and the output datasets is independently normalized, by scaling the values within each column to the range . The normalization formula is given by
where X is the original value, is the minimum value in the column, and is the maximum value in the column. A Bayesian optimization technique for hyperparameter tuning, as detailed in [21], is utilized to determine the optimal numbers of layers, neurons per layer, and model hyperparameters that minimize the loss function. This technique of hyperparameter optimization is widely tested in various fields and is proven to be superior to other techniques, such as grid search and random search [22,23]. This technique performs training many times with different sets of numbers of layers, neurons, and hyperparameters. The method initially tests the function n times by assigning random values to its variables in order to diversify the exploration space. Then, based on the values obtained in the previous step, the actual optimization begins. At each step, the algorithm evaluates the past model information to select new optimal parameter values that increase the performance of the new model according to the described method [24,25]. The initial phase involves defining the function that requires optimization. Considering the problem at hand, the target function represents the training procedure of the neural network, accepting multiple parameters for input and yielding the mean absolute error (MAE) as its result. The optimizer’s exact goal is to reduce this coefficient value to its minimum. The MAE, chosen as the loss function, is expressed in Equation (3), where n is the number of observations, is the ground truth input, and is the predicted value. The function to be optimized is defined in Equation (2), where x and y are the input and ground truth batches of the network in the training process, respectively.
After selecting the function for optimization, it is essential to identify the specific input parameters that need refinement and establish their limits, given that the approach is one of bounded optimization. The parameters and their ranges, selected based on prior knowledge and preliminary experimental data, are listed in Table 2, with the following.

Table 2.
Hyperparameters involved in the Bayesian optimization technique and their corresponding bounds.
- Batch size : specifies the number of training samples processed in one iteration.
- Learning rate : determines the rate at which the model weights are updated during training.
- Optimizer o: updates the model based on the loss function. Options include SGD, Adam, RMSprop, Adadelta, and Adagrad [26].
- Number of layers : specifies the total number of layers in the network.
- Number of neurons per layer : specifies the number of neurons in each layer.
The number of training epochs is set at 1000, with an early stopping level of 50 for the validation loss [27]. Each iteration is cross-validated by the K-fold method with three folds; the result of each iteration is expressed as the average MAE of the three iterations minus the standard deviation [28].
3. Results
With the work presented, we have shown that properly trained inferential models can be used to effectively study the dynamic behavior of real systems and mechanisms in operation simply by observing them in real time through a camera. This approach has been validated by applying it to a simple mechanism, demonstrating its potential as a valuable tool for investigation during the operation of machinery and devices, without the need for additional sensors, which are often difficult to use and install. Our results confirm that such models are not only feasible but also effective in capturing and analyzing complex dynamic interactions in mechanical systems. The methodologies described in the previous section are used to train a model for the prediction of the reaction forces in a simple mechanism (Section 3.1). Two separate models are trained. The first one, labeled as Model 1, is trained by using the dataset coming from the multi-body simulation, which does not take into account the presence of uncertainties. A second dataset, which takes into account all sources of uncertainty described in Section 2.3, is generated by using the camera model described in Section 2.2, and it is used to train the second model, labeled as Model 2. Both models are subsequently tested on motion laws not previously encountered, to assess their capability in predicting the forces in every scenario (Section 3.2). Finally, a comparison between a virtual sensor based on the multi-body model and the one based on the inferential model is performed with an emphasis on their ability to respond to different interfering inputs (i.e., noise) (Section 3.3).
3.1. Model Training
Following the methodology described in Section 2.3, a known motion law is imposed on the mechanism in order to use the collected data as a training dataset for the virtual sensor model. As shown in Figure 6, the motion law comprises a combination of several sinusoidal functions with different amplitudes and frequencies, with the objective of introducing a degree of randomness in the dynamics of the mechanism.
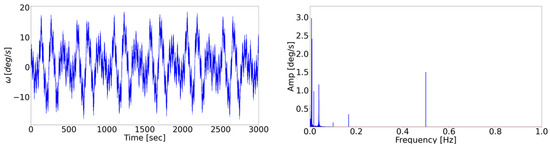
Figure 6.
From left to right: crank rotational speed motion law imposed on the mechanism to build the training dataset and its FFT transform.
The camera sensor records the scene for 3000 s at 60 frames per second (fps) for a total of 180,000 samples. For each sample, the reaction forces are known. Following the procedure described in Section 2.3, the positions of points and are calculated for each frame. Two training datasets are created with the collected data.
- Dataset 1:
- −
- Uses ideal data from the simulation. This dataset is designed to represent the best-case scenario without any external interference or noise, serving as a benchmark for optimal model performance.
- Dataset 2:
- −
- Accounts for possible interfering inputs (e.g., noise) within the measurement chain, simulating a real use case. The incorporation of such disturbances aims to mimic the challenges encountered in real case scenarios.
The use of vision-based measurement systems introduces sources of uncertainty that could alter the input data given to the model. These sources of uncertainty are considered during dataset generation to enhance the inferential model’s robustness. As reported in Figure 4, thirteen sources of uncertainty are identified, relating to the six DoFs of the camera positioning (), six uncertainties associated with the coordinates identifying the three points plotted by the computer vision algorithm (), and the extent of the crank length (L) used for the pixel-to-millimeter conversion of these coordinates. To introduce the effects of these uncertainties into the dataset generation process, a Gaussian normal distribution is imposed for each of the thirteen sources of uncertainty, specifying the mean and standard deviation of the error introduced, around a standard case. Table 3 shows the value distribution for each of the thirteen sources of uncertainty. Only the input dataset has been manipulated, while the output remains unchanged.

Table 3.
The table shows the limits within which the various sources of uncertainty are made to vary uniformly for the generation of Dataset 2.
Following the data pre-processing steps explained in Section 2.3, the final dataset consists of an input file containing 179,996 entries (the overall dataset consists of 180,000 time instants, but the first batch consists of five consecutive acquisitions; from this, it follows that the first useful batch starts at the fifth acquisition). The corresponding output file consists of the same number of entries, containing the values of the four reaction forces. Dataset 1 and Dataset 2 are used to train two models (i.e., Model 1 and Model 2) following the hyperparameter training and optimization procedure explained in Section 2.4 with (i.e., the number of optimization iterations). At the end of the optimization process, Model 1 and Model 2 reach an MAE of 0.004 and 0.005, respectively, with the hyperparameters shown in Table 4.

Table 4.
Selected hyperparameters for cost function minimization (i.e., MAE) for Model 1 and Model 2 training.
3.2. Model Testing
The testing procedure has been carried out by subjecting Model 1 and Model 2 to an input dataset, firstly generated by simulating a 15 s scenario in RecurDyn, keeping the same number of steps per second (i.e., 60 fps), and then altered taking into account the uncertainties described in Section 2.3. This dataset is henceforth referred to as Dataset 3. As shown in Figure 7, the motion law used for the simulation on Dataset 3 differs significantly from the one used during the testing procedure, comprising step functions available in the multi-body software. The introduction of a new motion law aims to ensure that Model 1 and Model 2 are indeed able to generalize to a new scenario without overfitting on the training dataset.
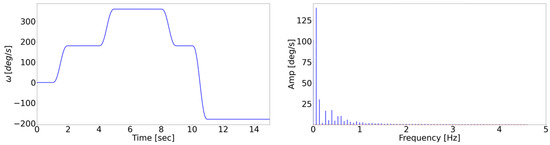
Figure 7.
From left to right: the crank rotational speed motion law imposed on the mechanism to build the testing dataset and its FFT transform.
The uncertainties discussed in Section 2.3 are taken into account in Dataset 3 in order to introduce a realistic level of noise in the acquired data, by sampling from their respective Gaussian distributions. Table 5 shows the sampled values for each source of uncertainty used in the testing procedure. The corresponding reaction forces predicted by Model 1 and Model 2 have been compared with the solution coming from the multi-body simulation (Reference—Figure 8 and Figure 9): the root mean squared error (RMSE) is computed for each reaction force, providing a quantitative measure to assess the quality of the models under the testing conditions (i.e., Dataset 3). Complete results are reported in Table 6.

Table 5.
Sampled uncertainty values for the generation of the dataset used for the comparison.
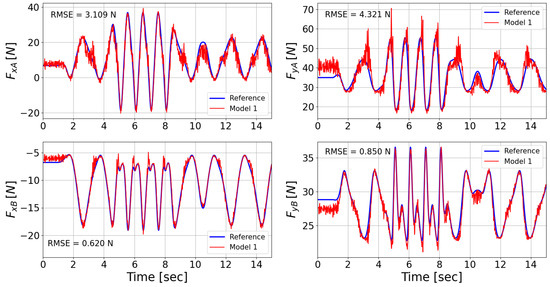
Figure 8.
Prediction of the four reaction forces performed by the model trained with the unmodified dataset, with respective RMSEs.
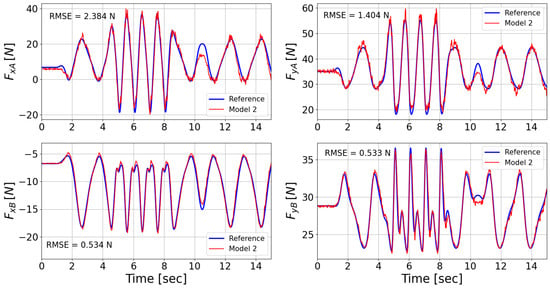
Figure 9.
Prediction of the four reaction forces performed by the model trained with the modified dataset, with respective RMSEs.

Table 6.
Comparison of the quality of the estimation of the two models on each of the four reaction forces.
The obtained results highlight the effectiveness of the second model in mitigating the noise introduced by the different sources of uncertainty. The higher performance of the second model is reflected in the lower RMSE obtained for each of the four reaction force estimations. Figure 8 and Figure 9 show the differences between the two models in predicting all four reaction forces exchanged between the mechanism and the ground. While both Model 1 and Model 2 show their ability to predict the behavior of the reaction forces, the second model offers higher precision.
3.3. Multi-Body vs. Inferential Model
The direct use of the multi-body model as a virtual sensor, instead of the implemented AI-based sensor, is possible but challenging, since it would required the imposition of the motion law as input. In the case of synchronous motors, the speed of the actuated joint is directly determined by the frequency of the AC power supply, the number of poles in the motor, and the transmission ratio. On the other hand, in asynchronous motors, which are widely applied in industrial settings, the speed is not directly determined, and external measures such as encoders or tachometers are often required. To avoid the use of external physical sensors, which have large time and cost requirements for installation and maintenance, the already proposed vision-based system can be used, tracking the crank joints’ positions over time to compute the angular values. However, the already presented sources of uncertainty may introduce noise in the evaluation of the motion law, especially in the speed and acceleration computations, derived numerically from the angular positions. This noise is reflected in the output of the multi-body model. A comparison between the virtual sensor based on the multi-body model and the AI-based one has been carried out to assess their robustness. The evaluation has been carried out by using the same dataset used for the previous evaluations, with the same sampled sources of uncertainty reported in Table 5. The multi-body virtual sensor requires a filter to be implemented in order to smooth the behavior of the numerical derivatives of the angular position, while the AI-based sensor receives only the data relative to the positions of the two joints. A real-time low-pass filter has been implemented to filter the numerical derivatives of the motion law. The filtered motion laws have been applied to the multi-body model, and the resulting outputs are presented in Figure 10, where a comparison between the latter model and Model 2, in terms of the R2 score, is reported.
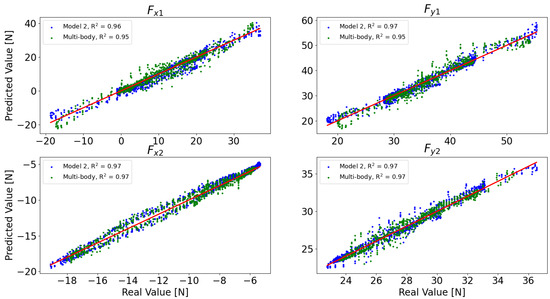
Figure 10.
Comparison of the results obtained by Model 2 and the multi-body model receiving motion law data from the computer vision algorithm, with real-time filtering.
The presented result indicates good agreement between the prediction of the reaction forces performed by the AI-based virtual sensor and the one performed by the multi-body model. Both methods show high reliability in the estimation, reflected in the high values of the R2 score. The high reliability of the obtained result, together with the low computational effort required, makes the implemented AI-based virtual sensor a powerful solution for this type of application.
4. Conclusions
In this research, we implemented and studied the feasibility of an innovative virtual sensor with the aim of studying the dynamics of operating machines without integrated sensors. This can be of vital importance in all cases where stopping production to install sensors would be impractical and time-consuming, despite the potential benefits in terms of analysis, control, and overall system reliability. As a test case, the study focused on a four-bar linkage mechanism, developing an AI-based virtual sensor for ground reaction force estimation based on visual observation. Two multi-layer perceptron regression models were trained using data from a multi-body simulation. The second model took into account the measurement uncertainties of the input quantities (i.e., the measurement uncertainties of the vision-based system).
The research showcased the effectiveness of the AI-based virtual sensor in estimating the ground reaction forces, even in the presence of significant uncertainties introduced by the vision-based system (i.e., camera position, computer vision algorithm, and crank length measurements). Furthermore, the study compared the AI-based virtual sensor with a multi-body based virtual sensor, both exploiting the vision-based system output as the input. The results indicated the ability of the AI-based proposed approach to filter out uncertainties and provide real-time estimation with low computational effort.
In conclusion, the developed virtual sensor presents a promising solution for the estimation of the reaction forces in the proposed mechanism, offering a non-invasive and cost-effective solution. Further developments would require the experimental validation of the proposed methodology on a real mechanism exploiting real camera sensors.
Author Contributions
Conceptualization, H.G. and N.G.; methodology, N.G.; software, D.F. and N.G.; validation, M.C. and N.G.; formal analysis, H.G. and N.G.; investigation, N.G.; data curation, D.F.; writing—original draft preparation, D.F. and N.G.; writing—review and editing, N.G. and M.C.; supervision, H.G.; project administration, H.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data are not publicly available.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Souza, F.A.; Araújo, R.; Mendes, J. Review of soft sensor methods for regression applications. Chemom. Intell. Lab. Syst. 2016, 152, 69–79. [Google Scholar] [CrossRef]
- Calvanese, L.; Carnevale, M.; Facchinetti, A. Fiber optic system to extend the measuring frequency range of pantograph contact force. In Proceedings of the 2022 Joint Rail Conference, JRC 2022, Virtual, 20–21 April 2022. [Google Scholar] [CrossRef]
- Carnevale, M.; Collina, A.; Palmiotto, M. Condition monitoring of railway overhead lines: Correlation between geometrical parameters and performance parameters. In Proceedings of the 1st World Congress on Condition Monitoring 2017, WCCM 2017, London, UK, 13–16 June 2017. [Google Scholar]
- Peinado-Asensi, I.; Montés, N.; García, E. Virtual Sensor of Gravity Centres for Real-Time Condition Monitoring of an Industrial Stamping Press in the Automotive Industry. Sensors 2023, 23, 6569. [Google Scholar] [CrossRef] [PubMed]
- Tang, Z.; Zhang, Z. The multi-objective optimization of combustion system operations based on deep data-driven models. Energy 2019, 182, 37–47. [Google Scholar] [CrossRef]
- Hu, X.; Cao, L.; Luo, Y.; Chen, A.; Zhang, E.; Zhang, W.J. A Novel Methodology for Comprehensive Modeling of the Kinetic Behavior of Steerable Catheters. IEEE/ASME Trans. Mechatron. 2019, 24, 1785–1797. [Google Scholar] [CrossRef]
- Etxegarai, M.; Camps, M.; Echeverria, L.; Ribalta, M.; Bonada, F.; Domingo, X. Virtual Sensors for Smart Data Generation and Processing in AI-Driven Industrial Applications. In Industry 4.0—Perspectives and Applications; IntechOpen: London, UK, 2022. [Google Scholar]
- Sun, Q.; Ge, Z. A Survey on Deep Learning for Data-Driven Soft Sensors. IEEE Trans. Ind. Inform. 2021, 17, 5853–5866. [Google Scholar] [CrossRef]
- Sabanovic, E.; Kojis, P.; Ivanov, V.; Dhaens, M.; Skrickij, V. Development and Evaluation of Artificial Neural Networks for Real-World Data-Driven Virtual Sensors in Vehicle Suspension. IEEE Access 2024, 12, 13183–13195. [Google Scholar] [CrossRef]
- Giulietti, N.; Allevi, G.; Castellini, P.; Garinei, A.; Martarelli, M. Rivers’ Water Level Assessment Using UAV Photogrammetry and RANSAC Method and the Analysis of Sensitivity to Uncertainty Sources. Sensors 2022, 22, 5319. [Google Scholar] [CrossRef] [PubMed]
- Byun, E.; Lee, J. Vision-based virtual vibration sensor using error calibration convolutional neural network with signal augmentation. Mech. Syst. Signal Process. 2023, 200, 110607. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, L.; Li, T.; Jiang, Y. A Model-based Analysis-Design Approach for Virtual Binocular Vision System with Application to Vision-based Tactile Sensors. IEEE Trans. Instrum. Meas. 2023, 72, 5010916. [Google Scholar] [CrossRef]
- Ögren, Y.; Tóth, P.; Garami, A.; Sepman, A.; Wiinikka, H. Development of a vision-based soft sensor for estimating equivalence ratio and major species concentration in entrained flow biomass gasification reactors. Appl. Energy 2018, 226, 450–460. [Google Scholar] [CrossRef]
- Alarcon, C.; Shene, C. Fermentation 4.0, a case study on computer vision, soft sensor, connectivity, and control applied to the fermentation of a thraustochytrid. Comput. Ind. 2021, 128, 103431. [Google Scholar] [CrossRef]
- Li, Y.; Ni, P.; Sun, L.; Xia, Y. Finite element model-informed deep learning for equivalent force estimation and full-field response calculation. Mech. Syst. Signal Process. 2024, 206, 110892. [Google Scholar] [CrossRef]
- Marban, A.; Srinivasan, V.; Samek, W.; Fernández, J.; Casals, A. A recurrent convolutional neural network approach for sensorless force estimation in robotic surgery. Biomed. Signal Process. Control 2019, 50, 134–150. [Google Scholar] [CrossRef]
- Ko, D.K.; Lee, K.W.; Lee, D.H.; Lim, S.C. Vision-based interaction force estimation for robot grip motion without tactile/force sensor. Expert Syst. Appl. 2023, 211, 118441. [Google Scholar] [CrossRef]
- Chen, K.; Zhao, W.; Zhang, X. Real-time milling force monitoring based on a parallel deep learning model with dual-channel vibration fusion. Int. J. Adv. Manuf. Technol. 2023, 126, 2545–2565. [Google Scholar] [CrossRef]
- Bakhshandeh, P.; Mohammadi, Y.; Altintas, Y.; Bleicher, F. Digital twin assisted intelligent machining process monitoring and control. CIRP J. Manuf. Sci. Technol. 2024, 49, 180–190. [Google Scholar] [CrossRef]
- Ksiazek, K.; Romaszewski, M.; Głomb, P.; Grabowski, B.; Cholewa, M. Blood Stain Classification with Hyperspectral Imaging and Deep Neural Networks. Sensors 2020, 20, 6666. [Google Scholar] [CrossRef]
- Giulietti, N.; Caputo, A.; Chiariotti, P.; Castellini, P. SwimmerNET: Underwater 2D Swimmer Pose Estimation Exploiting Fully Convolutional Neural Networks. Sensors 2023, 23, 2364. [Google Scholar] [CrossRef]
- Giulietti, N.; Discepolo, S.; Castellini, P.; Martarelli, M. Neural Network based Hyperspectral imaging for substrate independent bloodstain age estimation. Forensic Sci. Int. 2023, 39, 111742. [Google Scholar] [CrossRef]
- Giulietti, N.; Discepolo, S.; Castellini, P.; Martarelli, M. Correction of Substrate Spectral Distortion in Hyper-Spectral Imaging by Neural Network for Blood Stain Characterization. Sensors 2022, 22, 7311. [Google Scholar] [CrossRef]
- Nogueira, F. Bayesian Optimization: Open Source Constrained Global Optimization Tool for Python. 2014. Available online: https://github.com/fmfn/BayesianOptimization (accessed on 11 April 2024).
- Agrawal, T. Bayesian Optimization. In Hyperparameter Optimization in Machine Learning; Apress: Berkeley, CA, USA, 2020; pp. 81–108. [Google Scholar] [CrossRef]
- Abdulkadirov, R.; Lyakhov, P.; Nagornov, N. Survey of Optimization Algorithms in Modern Neural Networks. Mathematics 2023, 11, 2466. [Google Scholar] [CrossRef]
- Bai, Y.; Yang, E.; Han, B.; Yang, Y.; Li, J.; Mao, Y.; Niu, G.; Liu, T. Understanding and improving early stopping for learning with noisy labels. Adv. Neural Inf. Process. Syst. 2021, 34, 24392–24403. [Google Scholar]
- Raschka, S. Model evaluation, model selection, and algorithm selection in machine learning. arXiv 2018, arXiv:1811.12808. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).