Abstract
This article describes a proposed procedure for multiparametric optimization of the quality of machined surfaces, including mathematical models that can predict the high quality of a precisely machined surface and, at the same time, the high productivity of the process in WEDM of tool steels. The experimental research was carried out using the full DoE factorial design method, which has four technological parameters. The measured output qualitative parameter Surface Roughness (SR) and the output quantitative parameter Material Removal Rate (MRR) were evaluated using the Grey Relational Analysis (GRA) and Analysis of Variance (ANOVA) methods. Multiple Regression Models (MRM) were developed to represent the multiple responses of the investigated tool steels using a regression tool set. The results of the multiparametric optimization revealed a correlation between the input variable parameters of the electrical discharge process, while the favorable results of the observed output-dependent parameters SR and MRR were coupled to the parameters of low peak current I, low value of pulse on-time duration ton, low voltage of discharge U, and high value of pulse off-time duration toff. Based on the multiparametric optimization, key results were obtained that demonstrated the mutual dependence of the observed output process parameters. An optimum SR value of 1.50 μm was obtained with L8-level settings for the input variable parameters I, ton, U, and toff (2 A, 32 μs, 90 V, and 20 μs, respectively) and an MRR value of 12.50 mm3·min−1 was achieved.
1. Introduction
The need to increase the quality of machined surfaces is real issue in almost all production technologies. Wire Electrical Discharge Machining (WEDM) technology is no exception. The problem, however, is that increasing the quality of the machined area, especially in precision WEDM, is associated with deterioration in productivity and overall process efficiency. In order for this technology to become generally competitive, it must reflect the high demands of the current state of science and technology, which is oriented toward achieving high-quality machined surfaces and, at the same time, high productivity of machining processes [1,2,3]. Multiparametric optimization appears to be a suitable solution to this problem. As part of multiparametric optimization, it is necessary to pay particular attention to qualitative indicators of the machined surface that have a significant impact on the overall quality of the finished product while significantly affecting the overall productivity of the electrical discharge process [4,5,6]. The execution of multiparametric optimization of the quality of a machined surface is based on the search for a suitable combination of settings for the main technological parameters. Technological parameters include peak current I, voltage of discharge U, pulse on-time duration ton, and pulse off-time duration toff. Process parameters represent the mechanical and physical properties of the machined material, the properties of the wire electrode, the tension of the wire electrode, the diameter of the wire, the properties of the dielectric liquid, and other factors of the machining process that significantly affect the quality of the machined surface and the productivity of the electroerosion process. A suitable combination of the settings of the main technological and process parameters of the electroerosion process is sought with regard to finding the optimal values of the output indicators MRR and SR [7,8,9,10].
On the basis of an analysis of the current state of the given issue, it can be concluded that several relevant experimental studies have been carried out to date, the aim of which was to contribute to the improvement of the quality of machined surfaces after EDM with a wire electrode in terms of dimensional and geometric accuracy and precise surface quality in terms of roughness parameters from the point of view of low thermal impact on surface and subsurface layers [11,12,13]. These experiments were performed from different points of view. Several experimental investigations were carried out, the aim of which was to contribute to the reduction of wear of the wire tool electrode (TWR) while increasing the MRR and the overall productivity of the electrical discharge process. Most of these experimental studies included new approaches to solving shortcomings in the process of EDM with a wire electrode, including identification of the morphology of the machined surface, modeling, optimization, and direct application of the results obtained from experimental research to applications in science and technology in the field of EDM of selected types of materials [14]. However, very few researchers have devoted themselves to the mutual optimization of the abovementioned output qualitative and quantitative parameters of the electrical discharge process. In their work, Kumar et al. [15] claim that a good surface finish and a high material removal rate cannot be achieved at the same time. This is a long-standing problem that scientists from different countries are constantly trying to resolve. Most of them consider a rough cut followed by several finishing (offset) cuts to be the most likely cause. Singh et al. [16] tried to solve this problem through the design of an empirical cutting speed model with subsequent optimization of the electrical discharge process. They included factors such as pulse on-time duration (ton), peak current (I), and voltage of discharge (U) in the process and predicted the ideal cutting speed setting using a mathematical model based on RSM. However, during the research, they came to the conclusion that if the voltage of discharge is too low, the removed material and the tool wire may not be properly cleaned by the dielectric fluid, which leads to an excessive electric arc and the destruction of the wire electrode, thereby reducing the productivity of the electrical discharge process. Vikasa et al. [17], in turn, demonstrated the influence of various input factors during EDM with a wire electrode on the resulting qualitative indicator of the machined surface of the EN41 material. They found out that the SR parameter is rather significantly affected by the peak current I. They considered the influence of other parameters to be negligible. At the same time, they considered the given process to be stochastic, which requires sufficient mathematical representation and optimization. Sharma et al. [18], used the Taguchi L9 and ANOVA methods to solve the given problem, through which they analyzed the response of the MRR in relation to the peak current I and the machining time of the tool steel D2. In an experimental study, they found that the pulse off-time duration toff was the most influential and significant parameter for all responses, followed by the pulse on-time duration ton, while the effects of peak current and wire electrode tension were negligible. Using response modeling (RSM), genetic algorithms (GAs), and ANOVA, they optimized the parameters of the electrical discharge process in the machining of high-strength low-alloy steel (HSLA) using a brass wire electrode. At the same time, using the Taguchi L9 method, analysis of variance (ANOVA), and the signal-to-noise ratio (S/N), they determined the optimal parameters of the electrical discharge process when machining AISI 1045 alloy. To solve the given problem, the authors recommended the use of experiment-based multiparametric optimization, which includes multiple responses and variable parameters. Their study was further developed by Huang et al. [19], who confirmed through Grey Relational Analysis (GRA) and the S/N ratio that ton has a major effect on both MRR and SR. In a recent experimental study using similar methods, Kumar et al. [20] reduced the number of input parameters used in the electrical discharge process to four. They found that the optimal setting of the input parameters of the electrical discharge process had the greatest impact on increasing the MRR when machining D2 steel. Further progress in maximizing the productivity of the electrical discharge process was made by Zhu et al. [21], who changed the properties of the dielectric liquid to which they added TiC-based powder. This allowed them to significantly increase the productivity of the electrical discharge process. However, it caused the worsening of the total machined surface quality with regard to the roughness parameters. Many others have tried to observe the effects of different input factors and their levels on the output quality and performance parameters of the electroerosion process. However, such research often focused only on certain types of materials in the context of machining performance parameters with subsequent modeling of the material properties of the workpiece and the tool electrode. Therefore, a different approach to resolving the low productivity of the electroerosion process by optimization was attempted by Pradhan et al. [22]. As part of their research, they applied the approach to the response of selected input factors to the quality of the machined surface. They identified the parameters that are crucial in maximizing the productivity of the electroerosion process. Using ANOVA and the S/N ratio, they obtained the significant process parameters and the optimal combination of the selected process parameters. They found that the performance of the electrical discharge process is mainly influenced by the peak current I. At the same time, they developed mathematical models to determine the relationship between various important process parameters and performance criteria in the EDM process depending on the selected input technological and process parameters using the ANOVA method. Equivalent experimental research in this area was carried out by Somashekhar et al. [23], who devoted themselves to the optimization of the input parameters of the electrical discharge process using the artificial neural network (ANN) method. To predict a better MRR, they developed a neural network model using MATLAB programming and its subsequent simulation. They then used genetic algorithms (GAs) to determine the optimal process parameters for the desired output value of the machining characteristics [24,25,26,27,28,29]. They demonstrated that the proposed neural network model enhanced with optimized machining parameters is effective in estimating the MRR. The extensive experimental research carried out, as described in the works of several authors [30,31,32,33,34], demonstrates that there is a wide range of input parameters for the electrical discharge process, which significantly affect the output qualitative parameters of machined surfaces in addition to the quantitative performance parameters of the process. Therefore, researchers [35,36,37,38,39,40,41,42], who solved the problem of multi-objective optimization of various Non-Traditional Machining processes (NTM) using an a priori approach, provided a different perspective on the issue. In the a priori approach, the multi-objective optimization problem is transformed into a single-objective optimization problem by assigning an appropriate priority weight to each objective. This eventually leads to a unique optimal solution. However, the solution obtained via this optimization technique largely depends on the weights assigned to the different objective functions [43,44,45,46]. Therefore, the a posteriori approach is preferable, which is suitable for solving multifactor optimization problems in NTM processes, where extreme variability of input parameters leads to significant changes in the order of their importance [47,48].
For today’s modern industry, the influence of machining factors on overall performance is important, especially in terms of achieving a higher MRR, good dimensional accuracy, and excellent SR [49,50,51,52]. At the same time, the problems of low productivity in precision WEDM continue to persist. For this reason, multiparametric optimization with multiple responses in the machining of tool steels appears to be a highly topical issue. Therefore, the aim of the performed experimental research was to achieve a significant step in the optimization of the quality of machined surfaces while maintaining high productivity of the electrical discharge process. The research also contributed to the database of existing knowledge through clear formulation of individual laws in connection with the events that take place during the electrical discharge process with respect to the MRR and SR. Accordingly, an experimental study was carried out to investigate the influence of the input parameters of the process on the selected output qualitative parameters of the machined surface of tool steels and the output quantitative parameters of the electrical discharge process. On the basis of the experimental results, multiparametric optimization of the selected qualitative indicator of the machined surface was performed to maximize the productivity of the electrical discharge process. Through the performed prediction of specific settings of the main input factors, the productivity of the electrical discharge process was maximized with regard to the optimal qualitative level of the machined surface. Thus, the main contribution of the experimental research was obtaining Multiple Regression Models (MRM) to predict the setting of selected input technological parameters with regard to maximizing the productivity of the electrical discharge process while achieving a high-quality machined surface.
2. Materials and Methods
2.1. Material and Technological Equipment Used in the Performed Experimental Research
During the experimental research, three tool steels were used to make the samples: a low-alloy tool steel with the designation EN X37CrMoV5-1 (W.-Nr. 1.2343); a medium-alloy tool steel with the designation EN 35CrMo8 (W.-Nr. 1.2311); and a high-alloy tool steel with the designation EN X210Cr12 (W.-Nr. 1.2080). EN X37CrMoV5-1 is a chromium–molybdenum–silicon–vanadium tool steel, which is suitable for hardening in oil and air, with very good hardenability, high heat strength, and tempering resistance. It has good toughness and plastic properties at normal and elevated temperatures, with resistance to cracking. It is suitable for heat treatment to a strength of Rm ≥ 1800 N·mm−2. It is well machinable and hot-formable. It is used for the production of die-casting molds for aluminum, zinc, and magnesium alloys and their fixed and movable parts, hot forming tools (die and die liners), and water-cooled tools such as dies, mandrels, jaws, punches, shears etc. EN 35CrMo8 is a chromium–molybdenum tool steel characterized by very good hardenability and good heat strength. It is suitable for nitriding, cementing, and hardening, with a strength of Rm ≥ 2000 N·mm−2. It has good machinability in an annealed state; therefore, it is used for parts of molds and tools for hot forming and for thermally stressed tools. It is also suitable for large injection molds for plastic materials and die-casting molds. EN X210Cr12 is a chrome ledeburite tool steel with a content of alloying elements of 1.80–2.05% C and 11.0–12.5% Cr and is characterized by high resistance to wear by abrasion, while it can withstand dimensional changes even in elevated temperatures. It is suitable for hardening in oil and air to a strength of Rm ≥ 2300 N·mm−2. It has good cutting properties, very high compressive strength, and very low toughness. These properties make it optimal for the production of highly stressed and complex-shaped cold shearing tools. It is also suitable for simple and symmetrical tools for pressing and tools for hot rolling. It is also used for the production of small molds with a long service life for forming plastic and powder materials, glass, porcelain, ceramic materials, etc. The basic mechanical and physical properties of tool steels EN X37CrMoV5-1, EN 35CrMo8, and EN X210Cr12, including their chemical compositions, are shown in Table 1 and Table 2.

Table 1.
Chemical composition of tool steels EN X37CrMoV5-1, EN 35CrMo8, and EN X210Cr12.

Table 2.
Mechanical and physical properties of tool steels EN X37CrMoV5-1, EN 35CrMo8 and EN X210Cr12.
All these tool steels are difficult to machine using classic technologies. However, progressive WEDM technology is suitable for their machining. The experimental samples were prepared on an AgieCharmilles CUT E 350 (GF Machining Solutions—Headquarters, Biel, Switzerland) electrical discharge machine (Figure 1). The basic technical parameters of the AgieCharmilles CUT E 350 wire electrical discharge equipment are listed in Table 3.

Figure 1.
AgieCharmilles CUT E 350 wire electrical discharge equipment.

Table 3.
Basic parameters of the AgieCharmilles CUT E 350.
The AgieCharmilles CUT E 350 wire electrical discharge equipment is a modern, compact, and autonomous electroerosion device by the Swiss manufacturer GF, which is used for cutting metallic electrically conductive materials using a wire tool electrode. This electroerosion device has a number of unique systems and functions, such as the ergonomic AC CUT HMI interface with 19” touch screen, a wire preparation system using the Thermocut module, automatic wire threading, the possibility of bevel cutting, and many others.
Electrical discharge machining (EDM) of the experimental samples was performed in the presence of a liquid dielectric based on demineralized water with an electrical conductivity of less than 10 μS·cm−1. A wire electrode ∅ 0.25 mm marked AC Brass LP 1000 was used as a tool. The electrode is a multi-purpose brass electrode that is designed for a wide range of operations performed on modern electrical discharge devices. It is especially suitable for precise machining, taking into account the economic efficiency of the electrical discharge process, so it is categorized as a universal wire electrode. The stability of the performance of the electrical discharge process is ensured by the material composition of the wire electrode in the ratio of Cu 63%/Zn 37%. The process of experimental sample production from the tool steels is shown in Figure 2.

Figure 2.
The process of production of experimental samples from the tool steels.
As already mentioned in the introduction, the quality of the machined surface and the performance of the electrical discharge process in WEDM of tool steels are largely dependent on the combination of settings of the main input technological parameters. At the same time, based on the performed analysis, it can be assumed that the peak current I (A), the pulse on-time duration ton (μs), the pulse off-time duration toff (μs), and the discharge voltage U (V) have a significant influence on the assessed output parameters SR and MRR of the electrical discharge process.
Table 4 shows the Low Value (LV) and High Value (HV) of settings of the input independent Main Technological Parameters (MTPs) for WEDM of tool steels EN X37CrMoV5-1, (W.-Nr. 1.2343), EN 35CrMo8 (W.-Nr. 1.2311), and EN X210Cr12 (W.-Nr. 1.2080) using a ∅ 0.25 mm AC Brass wire electrode LP 1000.

Table 4.
The LV and HV settings of MTPs for WEDM of tool steels using a brass wire electrode.
The above ranges of LV and HV settings of the input-independent MTPs were chosen to ensure the stability of the electroerosion process during WEDM of tool steels. In doing so, the LV setting of the input-independent process parameters I and ton allowed the lowest value of the output-dependent quality indicator of the machined surface SR to be obtained. In contrast, the HV settings of the input-independent parameters I and ton made it possible to achieve the highest value of the output-dependent performance parameter MRR during the electroerosion process. The stability of the electrical discharge process was maintained using a combination of the input-independent parameters toff and U.
2.2. Analysis of Aspects of Multiparametric Optimization of the Output Parameters MRR and SR of the Electrical Discharge Process
Properly performed multiparametric optimization of the output parameters SR and MRR of the electrical discharge process is subject to several considerations. The key step in achieving a relevant multiparametric optimization of the output qualitative parameter SR of the machined surface and the output quantitative performance parameter MRR of the electrical discharge process is the careful design of Multiple Regression Models (MRMs). Therefore, deterministic methods were applied in the design, which, unlike classic optimization methods, are not subject to such strict mathematical logic [53,54]. However, classical methods based on gradient are not always suitable for modeling because it is sometimes difficult to obtain relevant gradient data, thereby making it impossible to obtain objective functions [55,56,57]. Stochastic and metaheuristic approaches, relative to classical approaches, provide an advantage in that no additional data are required for their introduction [58,59,60,61]. In addition, these approaches introduce a random step size within the calculation-based numerical iteration. This means that, in many cases, algorithms in this category do not require any initial guess values owing to random initialization [62,63]. Nevertheless, multi-parametric optimization must be preceded by preparation of the experiment plan DoE, including the analysis of the influence of selected input factors on the quality of the machined surface and the performance of the electroerosion process in the machining of high-speed steels [64]. In doing so, evaluating the effect of each input technology parameter of the electrical discharge process on the multiple responses using ANOVA is useful to find the percentage contribution and to identify the effects. At the same time, it is possible to exclude factors from the MRR without any adverse effect on the output monitored indicators SR and MRR. The performed analysis allowed separation of the total response variability (the sum of the squared deviations around the grand mean) into the contributions of each parameter and the error. The p-value (probability of significance) is generally calculated based on the F-value or Fisher’s F-ratio to obtain information about the significance of the selected response. A p-value was used to determine the significance, with a p-value ˂ 0.05 representing significant input factors that affect the response variable. Conversely, a value of p ˃ 0.05 represented input factors that do not affect the response variable and, therefore, could be removed from the MRR without any adverse impact. To evaluate the Mean Square (MS), degrees of freedom (DF) and determination of the availability of independent information are needed to evaluate the Sum of Squares (SS). In ANOVA analysis, Mean Square Deviation (MSD) and F-values are calculated as MS = SS/DF and F = MS for Source Parameter/MS for error.
However, as mentioned above, the productivity MRR of the electroerosion process, and also the final quality of the machined surface SR, are determined by a mutual combination of the input MTP settings. Thus, in the process of multiparametric optimization of machined surface quality and the maximization of productivity during WEDM of tool steels by mathematical modeling, it is inevitable to approach these two output indicators of the electroerosion process in a complex way. The traditional Taguchi method can optimize only one objective, and it cannot resolve multiple parameters at the same time. This means that the SR and MRR parameters can only be optimized separately by this method, while the optimal setting of one response parameter does not ensure that the other parameters are also optimal within the same limit. Therefore, it is better to apply a method that provides the optimal settings of the input parameters while optimizing all objectives. For this reason, the Grey Relational Analysis (GRA) method was applied, which enables analysis of the correlation between several response parameters in the process of multiparametric optimization [65,66]. This method also includes the normalization of the response parameters and calculation of the Grey Relation Coefficient (GRC). The overall relational degree is then determined by averaging the GRC relational coefficient for each selected response, which can be used to evaluate the performance of the electrical discharge process with multiple responses. Subsequently, the optimal parametric combination represents the transformation of the multi-response problem to a single-response optimization situation, resulting in the highest degree Grey Relation. The optimal parametric combination is then the one that achieves the highest Grey Relation class.
When generating the relation for the SR parameter, the minimization of the given output qualitative parameter can be considered as a corresponding criterion in the optimization process in accordance with the relation
When generating the relation for the MRR, it is true that the maximization of the given output performance parameter in accordance with the relation is considered as the corresponding criterion in the optimization process:
where is the sequence after data preprocessing, is the original sequence, is the largest value of , and is the smallest value of .
If a certain target value (TV) is to be achieved, then the original sequence must be normalized in the form
Alternatively, the natural order can be normalized by deriving the original sequence from the first value of the sequence according to the following relation:
where xi(k) is the value after Grey Relation generation (data processing), and yi(k) is the original sequence.
Here, yi(k) (k = 1, 2, 3, …, m) is an ideal sequence of answers. In addition, the GRC needs to be determined in order to establish a relationship for the actual and ideal normalized experimental results by preprocessing the data in the form
where is the Grey Relation Coefficient, = 1.0, = 0.0, and , whereas denotes sequences of deviations of the reference sequence , and ξ is the distinguishing coefficient between 0 and 1.
The mean of the GRC is then defined using the GRC parameter γ according to the following relation:
where = 1, 2, 3, … 16 (L16), is the Grey Relation Coefficient of the k-th response in the i-th experiment, and n is the number of process responses.
The optimal levels of the input MTPs of the electrical discharge process are then defined by the level with the highest Grey Relational Grade (GRG) value. Subsequently, the optimal levels of the input MTPs of the electrical discharge process are determined using the highest GRG, which indicates a better quality of the machined surface in terms of the output parameter SR and the highest value of the MRR productivity parameter in WEDM of tool steels.
3. Results and Discussion
3.1. Design of Experimental Plan Using the DoE Method
The design of the experimental plan was based on the DoE method. In this method, a 4-factor analysis was applied at two levels of MTP-dependent input settings. In doing so, the peak current I, the pulse on-time duration ton, the pulse off-time duration toff, and the discharge voltage U were considered, resulting in 16 experimental samples for each tool steel. This amounted to a total of 48 experimental samples. Figure 3 shows the experimental samples made from the EN X37CrMoV5-1, EN 35CrMo8, and EN X210Cr12 tool steels using WEDM technology. The individual surfaces with dimensions of 30 mm × 15 mm were made at the L1 level of the MTP setup.

Figure 3.
Experimental samples of tool steels EN X37CrMoV5-1, EN 35CrMo8, and EN X210Cr12 made using WEDM technology at the L1 level of the MTP settings.
The setting of the input-independent MTPs was carried out at two levels, Low Value (LV) and High Value (HV), in the specified order of parameters I, ton, toff a, and U (LV- 2 A, 8 μs, 1 μs, and 70 V; HV- 19 A, 32 μs, 20 μs, and 90 V) from Table 4. The experimental results for the quality of the machined surface SR and the performance of the electrical discharge process given by the MRR parameter during WEDM of tool steels No. 1 (EN X37CrMoV5-1), No. 2 (EN 35CrMo8), and No. 3 (EN X210Cr12) with a wire electrode are shown in Table 5.

Table 5.
Experimental results for SR and MRR according to 4-factor 2-level DoE.
Based on the results of the experimental measurements listed in Table 5, it can be concluded that a lowest value of SR = 0.18 μm was recorded for tool steel No. 3 (EN X210Cr12) with the input-independent MTPs of the electrical discharge process being set to level L3 (I = 2 A, ton = 8 μs, toff = 20 μs, and U = 70 V). The highest value of SR = 3.98 μm was recorded for tool steel No. 1 (EN X37CrMoV5-1), with the input-independent MTPs of the electrical discharge process set to level L14 (I = 19 A, ton = 32 μs, toff = 1 μs, and U = 90 V). The highest value of MRR = 26.87 mm3·min−1 was recorded for tool steel No. 1, with the input-independent MTPs set to level L14. The lowest value of MRR = 3.21 mm3·min−1 was recorded for tool steel No. 3, with the input-independent MTPs set to level L3. Based on the results of the experimental measurements, it can be concluded that the required values of the output parameters (minimum value of Ra and maximum MRR) of the electroerosion process are inconsistent with each other. At the same time, it can be observed that at identical settings of the input-independent MTPs, the lowest values of both output-dependent parameters were recorded for tool steel No. 3. However, the highest values were recorded for tool steel No. 1. This implies that the properties of the machined material contribute to the deviation of the resulting output parameters of the electroerosion process, even when the input-independent MTPs are the same. This deviation during WEDM of tool steels No.1, No.2, and No.3 ranged from 0.02 to 0.07 μm for the output quality parameter SR of the machined surface and from 0.02 to 0.07 mm3·min−1 for the output performance parameter MRR of the electroerosion process. For the following analysis and multiparametric optimization, the mean value of the output-dependent parameters SR and MRR were taken into account. Based on the recorded data, DoE factor analysis was subsequently performed to determine the main influence of the selected process input-independent parameter MTPs on the machined surface quality parameter SR (Figure 4) and the performance parameter MRR of the electroerosion process (Figure 5) during WEDM machining of tool steels.
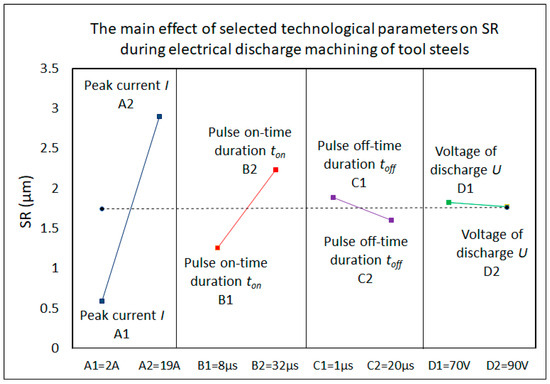
Figure 4.
Graph of the main effects of input MTPs on the quality of the machined surface SR when machining tool steels using WEDM.
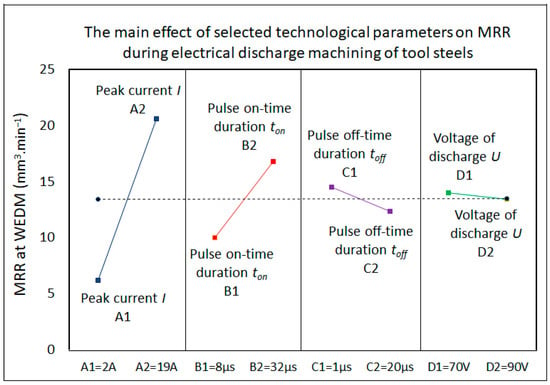
Figure 5.
Graph of the main effects of selected MPTs on the performance of the electrical discharge process MRR when machining tool steels using WEDM.
From the analysis results of the main effects of the chosen input factors on the quality of the SR of the machined surface (Figure 4) and the performance of the electrical discharge process MRR (Figure 5) during WEDM of tool steels, it is apparent that the peak current I has the greatest influence on both monitored output parameters. The voltage of discharge U and the pulse off-time duration toff have the least influence on both considered output process parameters.
3.2. Analysis of the Output Parameters SR and MRR during Electroerosion of Tool Steels Using the GRA Method
In multi-parametric optimization of the output qualitative parameter SR and the quantitative performance parameter MRR of the electroerosion process, it is desirable for the SR parameter to reach lower values (SB) and the MRR parameter to reach higher values (HB). In Table 6, the average values of the output qualitative parameter SR of the machined surface and the quantitative performance parameter MRR are shown for the EDM of tool steels with a wire electrode.

Table 6.
Calculated average values of the output parameters SR and MRR during WEDM of tool steels.
From Table 6, it can be observed that the lowest average value (SB) of the output quality parameter SR = 0.20 μm for WEDM of tool steels was recorded when the input-independent MTPs of the electrical discharge process were set at the L3 level. The highest average value (HB) of the output quantitative performance parameter MRR = 26.81 mm3·min−1 was recorded when the input-independent MTPs were set at the L14 level. Table 7 shows the GRC and GRG of the output observed parameters SR and MRR during WEDM of tool steels, which were obtained during analysis using the GRA method.

Table 7.
Results of the analysis (GRC and GRG parameters) of output process parameters SR and MRR during WEDM of tool steels using the GRA method.
It is true that the higher the considered GRG value, the stronger the relational degree between the ideal sequence and the given sequence . Therefore, the ideal sequence is the best response to the process in the experimental setup. It follows that the highest GRG corresponds to the combination of process input parameters that are closest to their optimal setting. In our case, this corresponds to the combination of the input MTPs of the electrical discharge process, which was applied in experiments L3 and L14. At the same time, the combination of the settings of the input-independent MTPs during WEDM of tool steels with the primary emphasis on minimizing the parameter SR corresponded to the setting at the L3 level, and with the primary emphasis on maximizing the parameter MRR, the setting of the input parameters corresponded to the L14 level. In order, the next suitable levels with optimal MTP settings were L13, L4, and L1. Table 8 shows the main effects on the mean value of GRG for the output quality parameter SR of the machined surface and the output performance parameter MRR during WEDM of tool steels.

Table 8.
Main effects on mean GRG.
The optimal parametric combination of the input-independent MTPs of the electrical discharge process was selected based on the highest mean values of GRG from Table 8. A higher GRG value indicates a stronger correlation with the reference sequence and better performance, that is, higher mean GRG values indicate minimum SR values and maximum MRR values. The GRG weight for SR is 0.50895, and the GRG weight for MRR is 0.49105, which indicates the higher importance of the output quality parameter of the machined surface during WEDM of tool steels with a wire electrode. The optimal setting for input technological parameters of multiple responses of SR during WEDM of tool steels is I1-ton1-toff2-U1, which corresponds to a combination of parameter settings of I = 1 A, ton = 8 μs, toff = 20 μs, and U = 70 V. The differences in the max and min values of the mean GRG for SR ranked in sequential order from highest to lowest (0.42203, 0.17028, 0.05011, and 0.01069) correspond to the order of the main input technological parameters of the electrical discharge process I, ton, toff, and U. A higher value represents a higher weight of the parameter. From this, it is evident that I has the greatest influence on the multiple responses during WEDM of tool steels. Figure 6 shows plots of the main effects of GRG on SR during WEDM of tool steels.

Figure 6.
Plots of the main effects of GRG on SR.
The optimal setting of input-independent MTPs of multiple responses for MRR during WEDM of tool steels is I2-ton2-toff1-U2, which is a combination of input parameter settings of I = 19 A, ton = 32 μs, toff = 1 μs, and U = 90 V. The differences in the max and min values of the mean GRG for the MRR sorted in sequential order from highest to lowest (0.34291, 0.21145, 0.07372, and 0.00206) correspond to the order of the input MTPs of the electrical discharge process I, ton, toff, and U. Figure 7 shows plots of the main effects of GRG on the MRR during WEDM of tool steels.
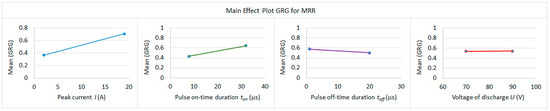
Figure 7.
Plots of the main effect of GRG on MRR.
A lower value of the difference between the max and min of the GRG indicator represents a lower weight of the input MTP. From this, it is evident that U has the least influence on the multiple responses during WEDM of tool steels.
3.3. Analysis of the Recorded Values of the Input and Output Parameters of the Electroerosion Process Using the ANOVA Method with Regard to GRG
After determining the optimal combination of input-independent MTP settings during WEDM of tool steels, the next step was to investigate their influence on the quality of the machined surface SR and the performance of the electrical discharge process MRR using the Analysis of Variance (ANOVA) method. The objective was to assess the effect of significant input technological parameters affecting the multiple responses at the 95% confidence level, thereby providing important information about the experimental data.
The results of the analysis of the input MTPs during WEDM of tool steels using the ANOVA method with respect to GRG are shown in Table 9.

Table 9.
The results of data evaluation using the ANOVA method with regard to GRG.
The ANOVA table shows that the significant parameters of the electrical discharge process affecting multiple responses are I, ton, and toff, as their p-values are less than 0.05.
After determining the significance of the influence of individual input parameters of the electrical discharge process on the output indicators SR and MRR during WEDM of tool steels, the next step was to improve the GRG indicator by performing a confirmatory experiment. The predicted value of the GRG indicator for the optimal level can be obtained by applying the formula
where γm is the overall average GRG, is the average GRG at the optimal level of each parameter, and O is the number of significant process parameters. The results of the performed validation test of the obtained empirical and experimental values of the improvement of the GRG indicator are presented in Table 10.

Table 10.
Results of the verification test of the obtained empirical and experimental values of SR and MRR.
By performing a verification test of the obtained empirical and experimental values of SR and MRR during WEDM of tool steels with respect to GRG, improvements in both responses of the output-dependent parameters was found, with improvements of 2.8% for the SR parameter and 1.6% for the MRR parameter. The improvement of the GRG indicator for SR was identified at the level of 0.03514 for the predicted input parameters of the electrical discharge process and 0.06622 for the experimental ones. The improvement of the GRG indicator for the MRR was at the level of 0.08058 for the predicted input parameters of the electrical discharge process and 0.11142 for the experimental ones.
3.4. Proposal of MRM for the Prediction of SR and MRR Output Parameters during WEDM of Tool Steels
For the purposes of multiparametric optimization of the output dependent qualitative indicator SR of the machined surface and the quantitative performance indicator MRR of the electrical discharge process in the machining of tool steels using a wire electrode, Multiple Regression Models (MRMs) were compiled at the 95% confidence level. Peak current I, pulse on-time duration ton, and pulse off-time duration toff were considered as MRM input parameters for prediction of the SR and MRR parameters. The input parameter voltage of discharge U was not taken into account during the design of MRM because, based on the performed analysis (Table 9), it appears to be insignificant. The validity of the proposed MRM was evaluated using the values of determination coefficients (R2). The higher the value of the determination coefficient R2 approaching the value of 1, the greater the validity of the compiled MRM. The following MRM Equation (8) was compiled based on experimental results with regard to the minimization of the SR parameter.
The accuracy of the determined MRM is indicated by the determination coefficient R2, which for the output quality parameter SR takes a value of 0.9972. This represents a deviation of experimentally measured values from empirically determined values at the level of 0.28%.
Figure 8 shows the prediction and optimization report for Multiple Regression of the output quality parameter SR during WEDM of tool steels.
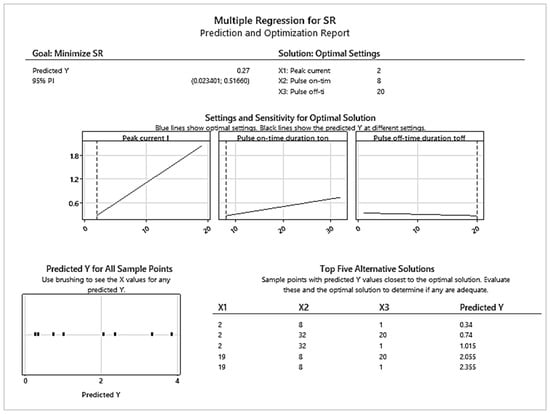
Figure 8.
Report of Multiple Regression for the output quality parameter SR during WEDM of tool steels.
Based on the results of Multiple Regression for SR presented in Figure 8, it is possible to observe the prediction of the influence of the individual input factors I, ton, and toff on the output qualitative parameter SR of the machined surface during WEDM of tool steels with regard to its minimization. At the same time, the predicted combination of five settings of the given input factors with regard to the minimization of the achieved parameter SR in the range of 0.34 to 2.355 μm is presented.
The following MRM Equation (9) was compiled based on the experimental results with regard to the maximization of the MRR parameter:
The value of the determination coefficient R2 for the determined MRM of the output performance parameter MRR takes a value of 0.9987, which represents a deviation of experimentally measured values from empirically determined values at the level of 0.13%.
Figure 9 shows the prediction and optimization report for Multiple Regression of the output quantitative performance parameter MRR during WEDM of tool steels.
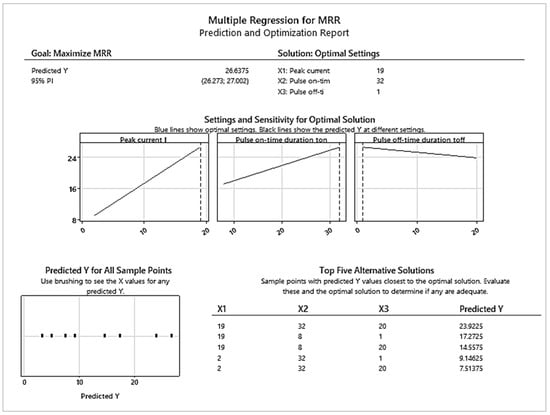
Figure 9.
Report of Multiple Regression for the output quantitative performance parameter MRR during WEDM of tool steels.
The results of Multiple Regression for MRR presented in the report in Figure 9 predict the influence of the individual input factors I, ton, and toff on the output quantitative performance parameter of the electrical discharge process in the machining of tool steels with regard to its maximization. At the same time, the predicted combination of five settings of the mentioned input factors is given with regard to the maximization of the achieved MRR parameter in the range of 23.9225 to 7.51375 mm3·min−1.
Based on the Multiple Regression reports obtained for the prediction and optimization of the output dependent quality parameter SR of the machined surface and the performance parameter MRR during WEDM of tool steels, several facts can be observed. First, it can be observed that with decreasing values of the parameters I and ton and an increasing value of the toff parameter during WEDM of tool steels, there is a significant increase in the output quality parameter SR, which with the combination of I = 2 A, ton = 23 μs, and toff = 20 μs, yields value of 0.74 μm. However, with the given combination of input-independent MTPs, the MRR productivity value of the electrical discharge process is at a low level of 7.51375 mm3·min−1. Conversely, with increasing values of the I and ton parameters and a decreasing value of the toff parameter during WEDM of tool steels, there is a significant increase in the output quantitative parameter MRR, which with the combination of I = 19 A, ton = 8 μs and toff = 1 μs, yields a value of 17.2725 mm3·min−1. With the given combination of input MTPs, the value of the output qualitative parameter of the machined surface is SR = 2.355 μm.
3.5. Optimization of the Quality Parameter SR of the Machined Surface with Regard to the Maximization of MRR Productivity during WEDM of Tool Steels
On the basis of the obtained data, a mutual optimization of the output qualitative indicator of the machined surface SR was subsequently carried out with regard to the maximization of the productivity of the electrical discharge process MRR during WEDM of tool steels. Figure 10 shows the graphic optimization of the output parameter SR with regard to the maximization of the MRR parameter, performed on the basis of their predicted values, which were obtained through the MRM defined by Formulas (8) and (9).
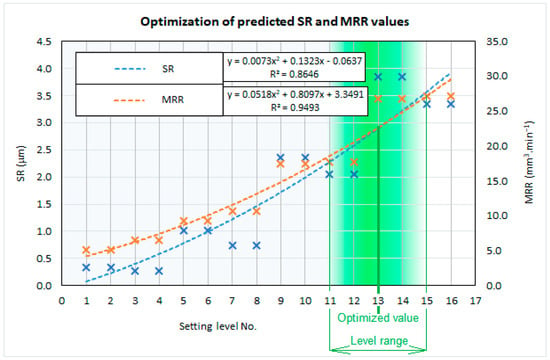
Figure 10.
Optimization of the qualitative parameter SR of the machined surface with regard to the maximization of the quantitative performance parameter MRR during WEDM of tool steels based on the values predicted through MRM.
From the graphical dependencies shown in Figure 10, it can be observed that with the increasing value of the output quantitative parameter of the electrical discharge process MRR during WEDM of tool steels, the predicted value of the output qualitative parameter of the machined surface SR also increases. When setting the input technological parameters at the L1 level, the predicted value of SR = 0.05 μm and the MRR = 5.05 mm3·min−1. When the input technological parameters are set at the L16 level, the predicted value of SR = 3.75 μm and the MRR = 29.5 mm3·min−1. Based on the performed optimization, during WEDM of tool steels, the most suitable combination of input technological parameter settings appears to be at the L13 level, with a combination of I = 19 A, ton = 32 μs, and toff = 1 μs. At this setting level, the predicted value of SR = 2.75 μm and the value of MRR = 22.50 mm3·min−1. A suitable optimization extent is in the range of settings at levels L11 to L15. The predicted value of SR for the given settings ranges from 2.25 to 3.50 μm, and the MRR ranges from 18.0 to 27.50 mm3·min−1.
Subsequently, on the basis of the experimentally obtained values, a graphical optimization of the output parameter SR was performed without emphasizing the maximization of the MRR parameter, as shown in Figure 11.
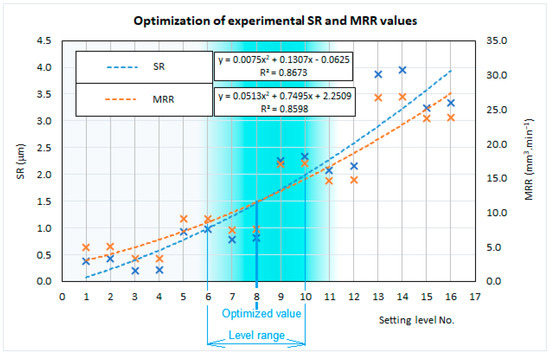
Figure 11.
Optimization of the qualitative parameter SR of the machined surface without emphasis on the maximization of the quantitative performance parameter MRR during WEDM of tool steels, performed on the basis of experimentally obtained values.
Based on the performed graphical optimization of the real values of the quality parameter SR of the machined surface without emphasis on the maximization of the quantitative performance parameter MRR during WEDM of tool steels shown in Figure 11, the same trend as in the predicted values can be observed. This means that with the increasing value of the output quantitative parameter of the electrical discharge process MRR during WEDM of tool steels, the real value of the output qualitative parameter SR of the machined area also increases. When setting the input MTP at the L1 level, the real value of SR = 0.18 μm and the MRR = 4.95 mm3·min−1. When setting the input MTPs at the L16 level, the real value of SR = 3.95 μm and the MRR = 26.75 mm3·min−1. Based on the performed graphical optimization, the most suitable combination of input MTP settings appears to be at the L8 level during WEDM of tool steels, which comprises a combination of I = 2 A, ton = 32 μs, and toff = 20 μs. At this setting level, the real value of SR = 1.50 μm and the MRR = 12.50 mm3·min−1. A suitable optimization extent is in the range of settings at levels L6 to L10. The real SR value for the given range of settings occurs from 0.98 to 2.33 μm, and the MRR occurs from 9.14 to 17.19 mm3·min−1.
4. Conclusions
The goal of the experimental research was the prediction and multiparametric optimization of the output-dependent parameters SR and MRR during WEDM of tool steels with a brass wire electrode of 0.25 mm diameter. Prediction and multiparametric optimization of the SR and MRR parameters was performed in relation to MTP settings. From the perspective of MTPs, four input variables (I, ton, toff, and U) were assessed, of which discharge current I was identified as the most influential parameter during WEDM with respect to SR and MRR, followed by ton and toff. On the basis of the Mean GRG values, a suitable combination (I1-ton1-toff2-U1) of settings for the input MTPs of multiple responses for SR during WEDM of tool steels was identified (I = 1 A, ton = 8 μs, toff = 20 μs, and U = 70 V). It was found that the output-dependent responses SR and MRR had a non-linear nature during WEDM of tool steels and are suitable for modeling using regression models. Despite the fact that the WEDM process has a phase dependence on the MTPs, the developed MRMs generated for the selected output response variables represent experimental results with small negligible errors that support the optimization of the models. For the MRR parameter, the deviation of values is 0.13%, and for SR, the deviation of values is 0.28%, which confirms their excellent predictability. The findings were analyzed using GRA to determine maximum MRR and minimum SR. A higher value of the weighted Mean GRG = 0.50895 for SR compared with the weighted GRG = 0.49105 for MRR indicates higher importance of the output qualitative parameter of the machined surface during WEDM of tool steels. By performing a verification test to improve the GRG indicator at settings of I1-ton1-toff2-U1 and I2-ton2-toff1-U2 of the input (predicted/experimental) technological parameters during WEDM of tool steels with respect to their initial setting at levels of I1-ton1-toff1-U1 and I2-ton2-toff2-U2, an improvement of the GRG indicator for SR was found at 0.03514/0.06622, and an improvement of the GRG indicator for the MRR was found at the level of 0.08058/0.11142. The deviations between the confirmation experiment and the values obtained by graphic optimization are 2.8% for SR and 1.6% for the MRR. Within the experimental research, it was found that the results of the performed multiparametric optimization with respect to the optimal value of the output-dependent parameter SR reflect the combination of the predicted settings of the input-independent MTPs during WEDM of tool steels at the L13 level. The optimal value of 2.75 μm identified for the SR parameter reflects the maximization of the output power parameter MRR. The optimum value of the qualitative parameter SR of the machined area without emphasizing the maximization of the quantitative performance parameter MRR during WEDM of tool steels determined using experimentally obtained values was 1.50 μm at the L8 level of the MTP settings. Within the framework of the experimental research, a wider spectrum of tool steels covering low-, medium-, and high-alloy steels was applied. Therefore, the experimental results obtained by multi-parametric optimization can be applied to the entire class of alloy tool steels.
Author Contributions
Conceptualization, Ľ.S.; methodology, I.Č.; validation, Ľ.S.; formal analysis, I.Č.; investigation, Ľ.S.; data curation, Ľ.S.; writing—original draft preparation, Ľ.S.; visualization, I.Č.; project administration, Ľ.S.; funding acquisition, Ľ.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Scientific Grant Agency of the Ministry of Education, Science, Research, and Sport of the Slovak Republic, grant number VEGA 1/0371/23.
Data Availability Statement
Data is contained within the article.
Acknowledgments
The authors would like to thank the grant agency for supporting research work via the project VEGA 1/0371/23.
Conflicts of Interest
The authors declare no conflicts of interest.
Nomenclature
| ANOVA | Analysis of Variance |
| ANN | Artificial Neural Network |
| DoE | Design of Experiments |
| GA | Genetic Algorithm |
| GRA | Grey Relational Analysis |
| GRC | Grey Relation Coefficient |
| GRG | Grey Relational Grade |
| HB | Higher is Better |
| HV | High Value |
| LV | Lower Value |
| MRM | Multiple Regression Models |
| MRR | Material Removal Rate |
| MS | Mean Square |
| MSD | Mean Square Deviation |
| NTM | Non-Traditional Machining |
| SB | Smaller is Better |
| SR | Surface Roughness |
| TV | Target Value |
| TWR | Tool Wear Rate |
| WEDM | Wire Electrical Discharge Machining |
| I | Peak Current (A) |
| ton | Pulse On-time Duration (µs) |
| toff | Pulse Off-time Duration (µs) |
| U | Voltage of Discharge (V) |
| R2 | Determination Coefficient |
| Sequence After Data Preprocessing, | |
| Original Sequence | |
| Largest Value of | |
| Simply the Smallest Value of |
References
- Aggarwal, V.; Khangura, S.S.; Garg, R.K. Parametric modeling and optimization for wire electrical discharge machining of Inconel 718 using response surface methodology. Int. J. Adv. Manuf. Technol. 2015, 79, 31–47. [Google Scholar] [CrossRef]
- Dzionk, S.; Siemiatkowski, M.S. Studying the effect of working conditions on WEDM machining performance of super alloy Inconel 617. Machines 2020, 8, 54. [Google Scholar] [CrossRef]
- Dodun, O.; Slătineanu, L.; Nagîț, G.; Hrițuc, A.; Mihalache, A.M.; Beșliu-Băncescu, I. WEDM-generated slot width variation modelling. Micromachines 2022, 13, 1231. [Google Scholar] [CrossRef]
- Nowicki, R.; Świercz, R.; Oniszczuk-Świercz, D.; Rozenek, M. Experimental investigation of technological indicators and surface roughness of hastelloy C-22 after electrical discharge machining using POCO graphite electrodes. Materials 2022, 15, 5631. [Google Scholar] [CrossRef]
- Mičietová, A.; Neslušan, M.; Čilliková, M. Influence of surface geometry and structure after non-conventional methods of parting on the following milling operations. Manuf. Technol. 2013, 13, 199–204. [Google Scholar] [CrossRef]
- Fassi, I.; Modica, F. Editorial for the special issue on micro-electro discharge machining: Principles, Recent advancements and applications, volume II. Micromachines 2023, 14, 29. [Google Scholar] [CrossRef]
- Gorgani, H.H.; Jahazi, A.; Pak, A.J.; Shabani, S. A hybrid algorithm for adjusting the input parameters of the wirecut EDM machine in order to obtain maximum customer satisfaction. SN Appl. Sci. 2023, 5, 37. [Google Scholar] [CrossRef]
- Grigoriev, S.N.; Kozochkin, M.P.; Gurin, V.D.; Malakhinsky, A.P.; Porvatov, A.N.; Melnik, Y.A. Display of WEDM quality indicators of heat-resistant alloy processing in acoustic emission parameters. Sensors 2023, 23, 8288. [Google Scholar] [CrossRef]
- Wang, J.; Sanchez, J.A.; Izquierdo, B.; Ayesta, I. Experimental and numerical study of crater volume in wire electrical discharge machining. Materials 2020, 13, 577. [Google Scholar] [CrossRef]
- Evin, E.; Tomáš, M.; Kmec, J. Optimization of electro-discharge texturing parameters for steel sheets’ finishing rollers. Materials 2020, 13, 1223. [Google Scholar] [CrossRef]
- Kiyak, M. Investigation of effects of cutting parameters on surface quality and hardness in the wire-EDM process. Int. J. Adv. Manuf. Technol. 2021, 119, 647–655. [Google Scholar] [CrossRef]
- Mouralova, K.; Zahradnicek, R.; Houska, P. Evaluation of surface quality of X210Cr12 steel for forming tools machined by WEDM. MM Sci. J. 2016, 5, 1366–1369. [Google Scholar] [CrossRef]
- Kosaraju, S.; Bobba, B.P.; Salkuti, S.R. Optimization and microstructural studies on the machining of Inconel 600 in WEDM using untreated and cryogenically treated zinc electrodes. Materials 2023, 16, 3181. [Google Scholar] [CrossRef]
- Straka, L.; Dittrich, G. Influence of tool steel properties on surface quality after electrical discharge machining by wire electrode. Int. J. Adv. Manuf. Technol. 2020, 106, 1617–1632. [Google Scholar] [CrossRef]
- Kumar, M.; Singh, H. Multi response optimization in wire electrical discharge machining of Inconel X-750 using Taguchi’s technique and grey relational analysis. Cogent Eng. 2016, 3, 1266123. [Google Scholar] [CrossRef]
- Singh, B.; Misra, J.P. Empirical Modelling of Wear Ratio during WEDM of Nimonic 263. Mater. Today Proc. 2018, 5, 23612–23618. [Google Scholar] [CrossRef]
- Vikasa, A.K.R.; Kumarb, K. Effect and optimization of various machine process parameters on the MRR, over-cut and surface roughness in EDM for an EN41 material using grey-taguchi approach. Int. J. Appl. Eng. Res. 2014, 9, 8963–8966. [Google Scholar]
- Sharma, S.; Vates, U.K.; Bansal, A. Parametric optimization in wire EDM of D2 tool steel using Taguchi method. Mater. Today Proc. 2021, 45, 757–763. [Google Scholar] [CrossRef]
- Huang, J.T.; Liao, Y.S. Optimization of machining parameters of Wire-EDM based on Grey relational and statistical analyses. Int. J. Prod. Res. 2003, 41, 1707–1720. [Google Scholar] [CrossRef]
- Kumar, A.; Jagota, V.; Shawl, R.Q.; Sharma, V.; Sargam, K.; Shabaz, M.; Tanveer Khan, M.; Rabani, B.; Gandhi, S. Wire EDM process parameter optimization for D2 steel. Mater. Today Proc. 2021, 37, 2478–2482. [Google Scholar] [CrossRef]
- Zhu, S.; Chen, W.; Zhan, X.; Ding, L.; Zhou, J. Parameter optimisation of laser cladding repair for an Invar alloy mould. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2019, 233, 1859–1871. [Google Scholar] [CrossRef]
- Pradhan, B.B.; Masanta, M.; Sarkar, B.R.; Bhattacharyya, B. Investigation of electro-discharge micro-machining of titanium super alloy. Int. J. Adv. Manuf. Technol. 2009, 41, 1094–1106. [Google Scholar] [CrossRef]
- Somashekhar, K.P.; Ramachandran, N.; Mathew, J. Optimization of material removal rate in micro-EDM using artificial neural network and genetic algorithms. Mater. Manuf. Process. 2010, 25, 467–475. [Google Scholar] [CrossRef]
- Meena, V.K.; Azad, M.S. Grey relational analysis of micro-EDM machining of Ti-6Al-4V alloy. Mater. Manuf. Process. 2012, 27, 973–977. [Google Scholar] [CrossRef]
- Kopytowski, A.; Świercz, R.; Oniszczuk-Świercz, D.; Zawora, J.; Kuczak, J.; Żrodowski, Ł. Effects of a New Type of Grinding Wheel with Multi-Granular Abrasive Grains on Surface Topography Properties after Grinding of Inconel 625. Materials 2023, 16, 716. [Google Scholar] [CrossRef]
- Mouralova, K.; Bednar, J.; Benes, L.; Prokes, T.; Zahradnicek, R.; Fries, J. Mathematical models for machining optimization of Ampcoloy 35 with different thicknesses using WEDM to improve the surface properties of mold parts. Materials 2023, 16, 100. [Google Scholar] [CrossRef]
- Ming, W.; Guo, X.; Zhang, G.; Hu, S.; Liu, Z.; Xie, Z.; Zhang, S.; Duan, L. Optimization of process parameters and performance for machining Inconel 718 in renewable dielectrics. Alex. Eng. J. 2023, 79, 164–179. [Google Scholar] [CrossRef]
- Pi, V.N.; Tam, D.T.; Cuong, N.M.; Tran, T.H. Multi-objective optimization of PMEDM process parameters for processing cylindrical shaped parts using taguchi method and grey relational analysis. Int. J. Mech. Prod. Eng. Res. Dev. 2020, 10, 669–678. [Google Scholar]
- Zhu, Z.; Guo, D.; Xu, J.; Lin, J.; Lei, J.; Xu, B.; Wu, X.; Wang, X. Processing Characteristics of Micro Electrical Discharge Machining for Surface Modification of TiNi Shape Memory Alloys Using a TiC Powder Dielectric. Micromachines 2020, 11, 1018. [Google Scholar] [CrossRef]
- Meshram, D.B.; Puri, Y.M. Optimized curved electrical discharge machining-based curvature channel. J. Braz. Soc. Mech. Sci. 2020, 42, 82. [Google Scholar] [CrossRef]
- Rafaqat, M.; Mufti, N.A.; Ahmed, N.; Rehman, A.U.; AlFaify, A.Y.; Farooq, M.U.; Saleh, M. Hole-making in D2-Grade steel tool by electric-discharge machining through non-conventional electrodes. Processes 2022, 10, 1553. [Google Scholar] [CrossRef]
- Selvarajan, L.; Venkataramanan, K. Si3N4–TiN conductive ceramic composites: Topography on EDMed surfaces and precise drilled holes. Mater. Sci. Technol. 2023, 39, 2006–2017. [Google Scholar] [CrossRef]
- Panda, A.; Anisimov, V.M.; Anisimov, V.V.; Diadiura, K.O.; Pandova, I.V.E.T.A. Increasing of wear resistance of linear block-polyurethanes by thermal processing methods. MM Sci. J. 2021, 10, 731–4735. [Google Scholar] [CrossRef]
- Seshaiah, S.; Sampathkumar, D.; Mariappan, M.; Mohankumar, A.; Balachandran, G.; Kaliyamoorthy, M.; Rajendran, B.; Gopal, R. Advanced Materials for Promoting. Sustainability 2022, 2022, 6022550. [Google Scholar]
- Jagadish; Ray, A. Multi-objective optimization of green EDM: An integrated theory. J. Inst. Eng. Ser. C 2015, 96, 41–47. [Google Scholar] [CrossRef]
- Padhi, P.C.; Mahapatra, S.S.; Yadav, S.N.; Tripathy, D.K. Multi-objective optimization of wire electrical discharge machining (WEDM) process parameters using weighted sum genetic algorithm approach. J. Adv. Manuf. Syst. 2016, 15, 85–100. [Google Scholar] [CrossRef]
- Abhishek, T.; Mandal, A.; Kumar, K. Multi-objective optimization of electro-chemical machining by non-dominated sorting genetic algorithm. Mater. Today Proc. 2015, 2, 2569–2575. [Google Scholar]
- Kalita, K.; Chakraborty, S.; Ghadai, R.K.; Chakraborty, S. Parametric optimization of non-traditional machining processes using multi-criteria decision making techniques: Literature review and future directions. Multiscale Multidiscip. Model. Exp. Des. 2023, 6, 1–40. [Google Scholar] [CrossRef]
- Shankar, C.; Chatterjee, P.; Protim, D.P. A DoE–TOPSIS method-based meta-model for parametric optimization of non-traditional machining processes. J. Model. Manag. 2019, 14, 430–455. [Google Scholar]
- Ganesh, N.; Ghadai, R.K.; Bhoi, A.K.; Kalita, K.; Gao, X.Z. An intelligent predictive model-based multi-response optimization of EDM process. Comput. Model. Eng. Sci. 2020, 124, 459–476. [Google Scholar] [CrossRef]
- Chakraborty, S. Multi-objective optimization of EDM process on AISI P-20 Tool steel using multi-criteria decision-making technique. In Machine Learning Applications in Non-Conventional Machining Processes; IGI Global: Hershey, PA, USA, 2021; pp. 33–44. [Google Scholar]
- Ram Prasad, A.V.S.; Ramji, K.; Kolli, M.; Krishna, G.V. Multi-response optimization of machining process parameters for wire electrical discharge machining of lead-induced Ti-6Al-4V alloy using AHP–TOPSIS method. J. Adv. Manuf. Sys. 2019, 18, 213–236. [Google Scholar] [CrossRef]
- Mouralova, K.; Benes, L.; Zahradnicek, R.; Bednar, J.; Zadera, A.; Fries, J.; Kana, V. WEDM Used for machining high entropy alloys. Materials 2020, 13, 4823. [Google Scholar] [CrossRef]
- Singh, D.P.; Mishra, S. Effect of different reinforcements in wire electric discharge machining of various geometrical profiles in metal matrix composites. Int. J. Interact. Des. Manuf. 2023, 18, 351–373. [Google Scholar] [CrossRef]
- Straka, L.; Pitel, J.; Corny, I. Influence of the main technological parameters and material properties of the workpiece on the geometrical accuracy of the machined surface at WEDM. Int. J. Adv. Manuf. Technol. 2021, 115, 3065–3087. [Google Scholar] [CrossRef]
- Singh, V.; Sharma, A.K.; Goyal, A.; Saxena, K.K.; Negi, P.; Rao, P.C.S. Electric discharge machining performance measures and optimisation: A review. Adv. Mater. Process. Technol. 2023, 1–14. [Google Scholar] [CrossRef]
- Świercz, R.; Oniszczuk-Świercz, D.; Zawora, J.; Marczak, M. Investigation of the Influence of Process Parameters on Shape Deviation after Wire Electrical Discharge Machining. Arch. Metall. Mater. 2019, 64, 1457–1462. [Google Scholar] [CrossRef]
- Takale, A.M.; Chougule, N.K.; Selmokar, P.H.; Gawari, M.G. Multi-response optimization of micro-WEDM process parameters of Ti49.4-Ni50.6 shape memory alloy for orthopedic implant application. Adv. Mater. Res. 2018, 1150, 1–21. [Google Scholar] [CrossRef]
- Sahu, N.K.; Singh, M.K.; Sahu, A.K.; Sahu, A.K. Multi Parametric Investigation for Improvement in Machining Characteristics on Aluminium Boron Carbide Composite in WEDM. In Springer Proceedings in Materials; Springer: Singapore, 2023; Volume 26, pp. 81–93. [Google Scholar]
- Choudhary, P.; Desale, Y.B.; Ranjan, G.; Naik, B.K.; Singh, V.K. Parametric optimization of wire EDM process for single crystal pure tungsten using Taguchi-Grey relational analysis. Sādhanā 2023, 48, 152. [Google Scholar] [CrossRef]
- Wang, S.M.; Wu, J.X.; Gunawan, H.; Tu, R.Q. Optimization of Machining Parameters for Corner Accuracy Improvement for WEDM Processing. Appl. Sci. 2022, 12, 10324. [Google Scholar] [CrossRef]
- Yu, T.; Zhao, J. Quantifying the mechanisms of keyhole pore evolutions and the role of metal-vapor condensation in laser powder bed fusion. Addit. Manuf. 2023, 72, 103642. [Google Scholar] [CrossRef]
- Rimár, M.; Abraham, M.; Fedák, M.; Kulikov, A.; Oravec, P.; Váhovský, J. Methods of increasing the efficiency of cogeneration based energy equipment. MM Sci. J. 2019, 6, 2935–2938. [Google Scholar] [CrossRef]
- Van, D.N.; Van, B.P.; Huu, P.N. Application of Deng’s similarity-based analytic hierarchy process approach in parametric optimization of the electrical discharge machining process of SDK11 die steel. Trans. Can. Soc. Mech. Eng. 2020, 44, 294–310. [Google Scholar] [CrossRef]
- Rani, S.S.; Sundari, V.K.; Jose, P.S.H.; Sivaranjani, S.; Stalin, B.; Pritima, D. Enrichment of material subtraction rate on Eglin steel using electrical discharge machining process through modification of electrical circuits. Mater. Today 2020, 33, 4428–4430. [Google Scholar] [CrossRef]
- Świercz, R.; Oniszczuk-Świercz, D. Experimental Investigation of Surface Layer Properties of High Thermal Conductivity Tool Steel after Electrical Discharge Machining. Metals 2017, 7, 550. [Google Scholar] [CrossRef]
- Oniszczuk-Świercz, D.; Świercz, R.; Michna, Š. Evaluation of prediction models of the microwire EDM process of Inconel 718 using ANN and RSM methods. Materials 2022, 15, 8317. [Google Scholar] [CrossRef]
- Mouralova, K.; Benes, L.; Prokes, T.; Zahradnicek, R.; Fries, J.; Plichta, T. Analysis of the machinability of different types of sintered carbides with WEDM in both water and oil baths. Int. J. Adv. Manuf. Technol. 2023, 125, 2705–2715. [Google Scholar] [CrossRef]
- Židek, K.; Piteľ, J.; Adámek, M.; Lazorík, P.; Hošovský, A. Digital Twin of Experimental Smart Manufacturing Assembly System for Industry 4.0 Concept. Sustainability 2020, 12, 3658. [Google Scholar] [CrossRef]
- Hašová, S.; Straka, Ľ. Design and verification of software for simulation of selected quality indicators of machined surface after WEDM. Acad. J. Manuf. Eng. 2016, 14, 13–20. [Google Scholar]
- Straka, Ľ.; Čorný, I.; Piteľ, J.; Hašová, S. Statistical Approach to Optimize the Process Parameters of HAZ of Tool Steel EN X32CrMoV12-28 after Die-Sinking EDM with SF-Cu Electrode. Metals 2017, 7, 35. [Google Scholar] [CrossRef]
- Vagaská, A.; Gombár, M.; Straka, Ľ. Selected mathematical optimization methods for solving problems of engineering practice. Energies 2022, 15, 2205. [Google Scholar]
- Rouniyar, A.K.; Shandilya, P. Fabrication and experimental investigation of magnetic field assisted powder mixed electrical discharge machining on machining of aluminum 6061 alloy. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2019, 233, 2283–2291. [Google Scholar] [CrossRef]
- Wang, G.; Han, F.A. Comparative study on the surface integrity of single-step and multi-step sequential machining in electric discharge machining. Int. J. Adv. Manuf. Technol. 2021, 114, 1803–1817. [Google Scholar] [CrossRef]
- Oniszczuk-Swiercz, D.; Swiercz, R.; Chmielewski, T.; Salacinski, T. Experimental investigation of influence WEDM parameters on surface roughness and flatness deviation. Metal 2020, 29, 611–617. [Google Scholar]
- Grigoriev, S.N.; Pivkin, P.M.; Kozochkin, M.P.; Volosova, M.A.; Okunkova, A.A.; Porvatov, A.N.; Zelensky, A.A.; Nadykto, A.B. Physicomechanical nature of acoustic emission preceding wire breakage during wire electrical discharge machining (WEDM) of advanced cutting tool materials. Metals 2021, 11, 1865. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).