Milling Tool Wear Monitoring via the Multichannel Cutting Force Coefficients
Abstract
1. Introduction
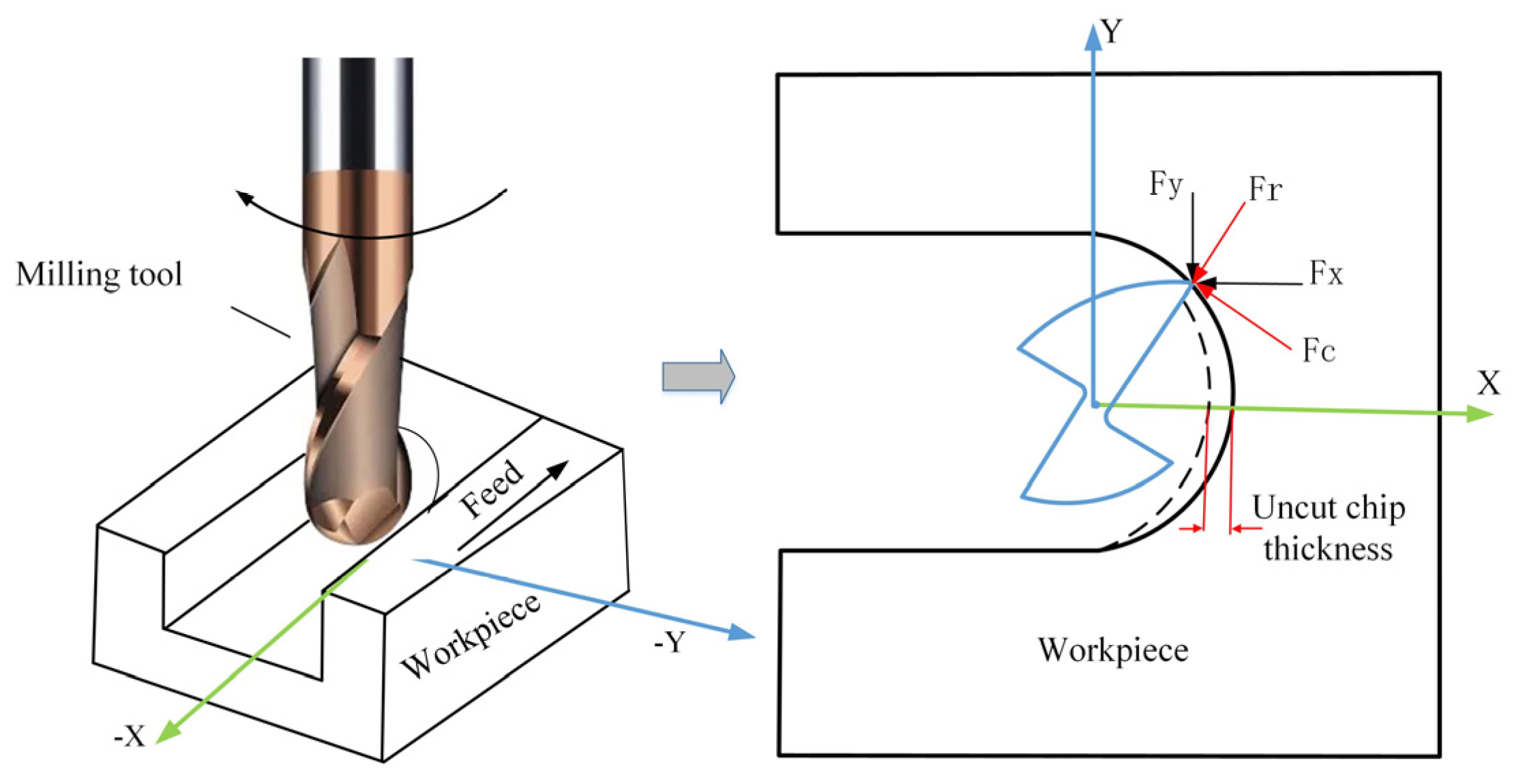
2. Cutting Force Model and Cutting Force Coefficient Extraction
2.1. Mechanistic Cutting Force Model for the Milling Process
2.2. Identification of the Multichannel Cutting Force Coefficients
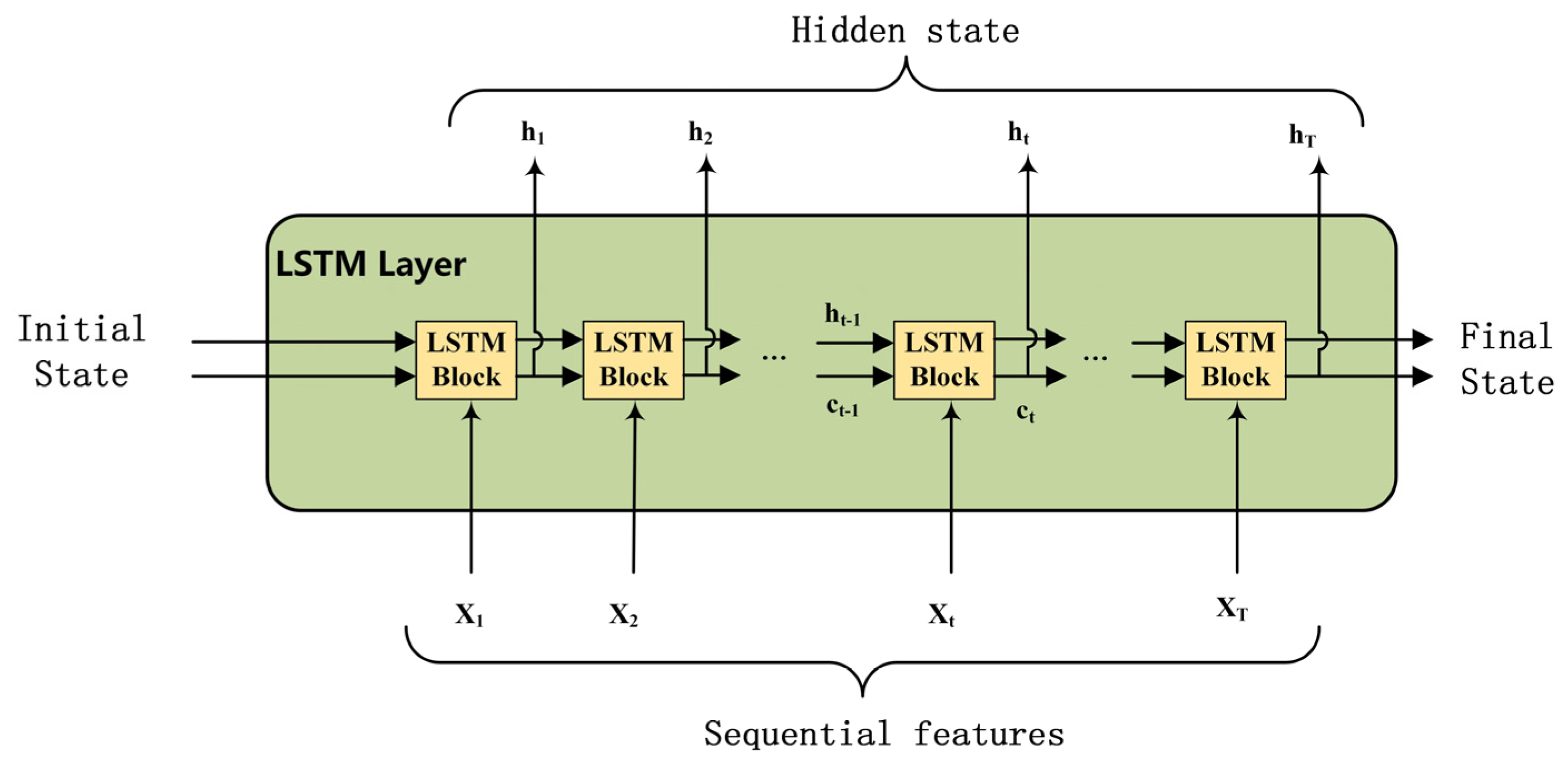
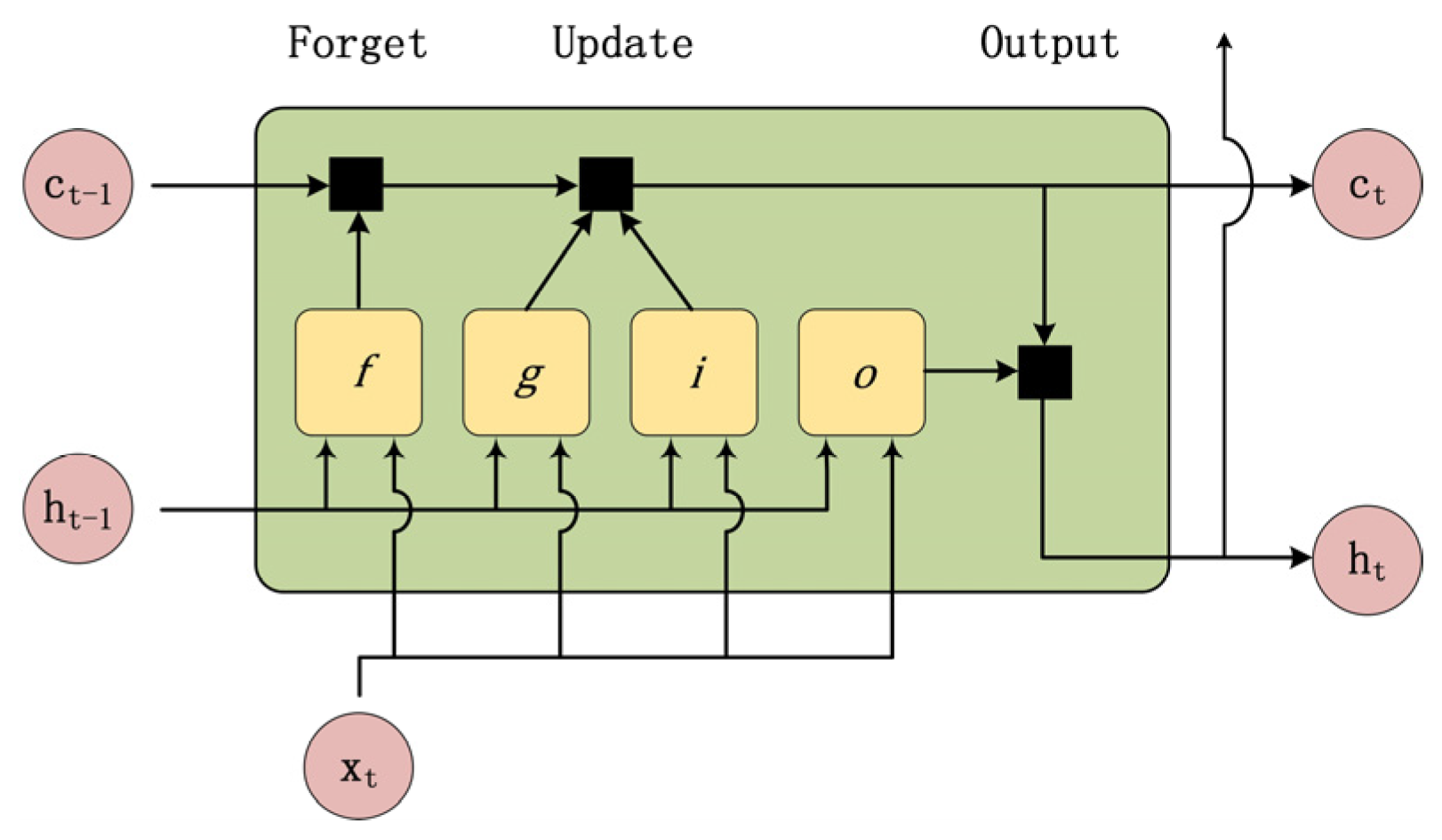
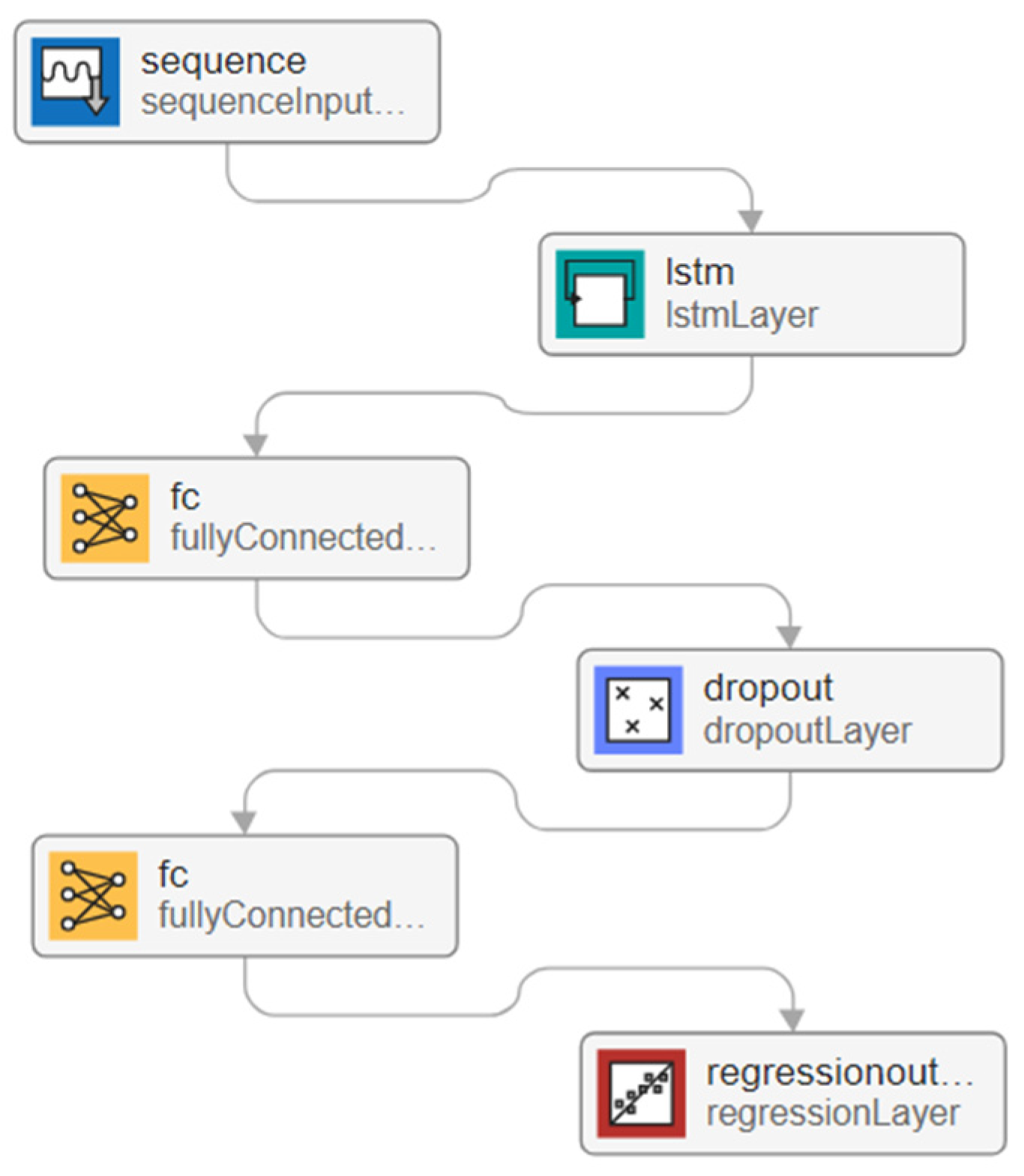
3. Tool Wear Monitoring with LSTM and the Multichannel Cutting Force Coefficients
4. Experimental Validations and Analysis
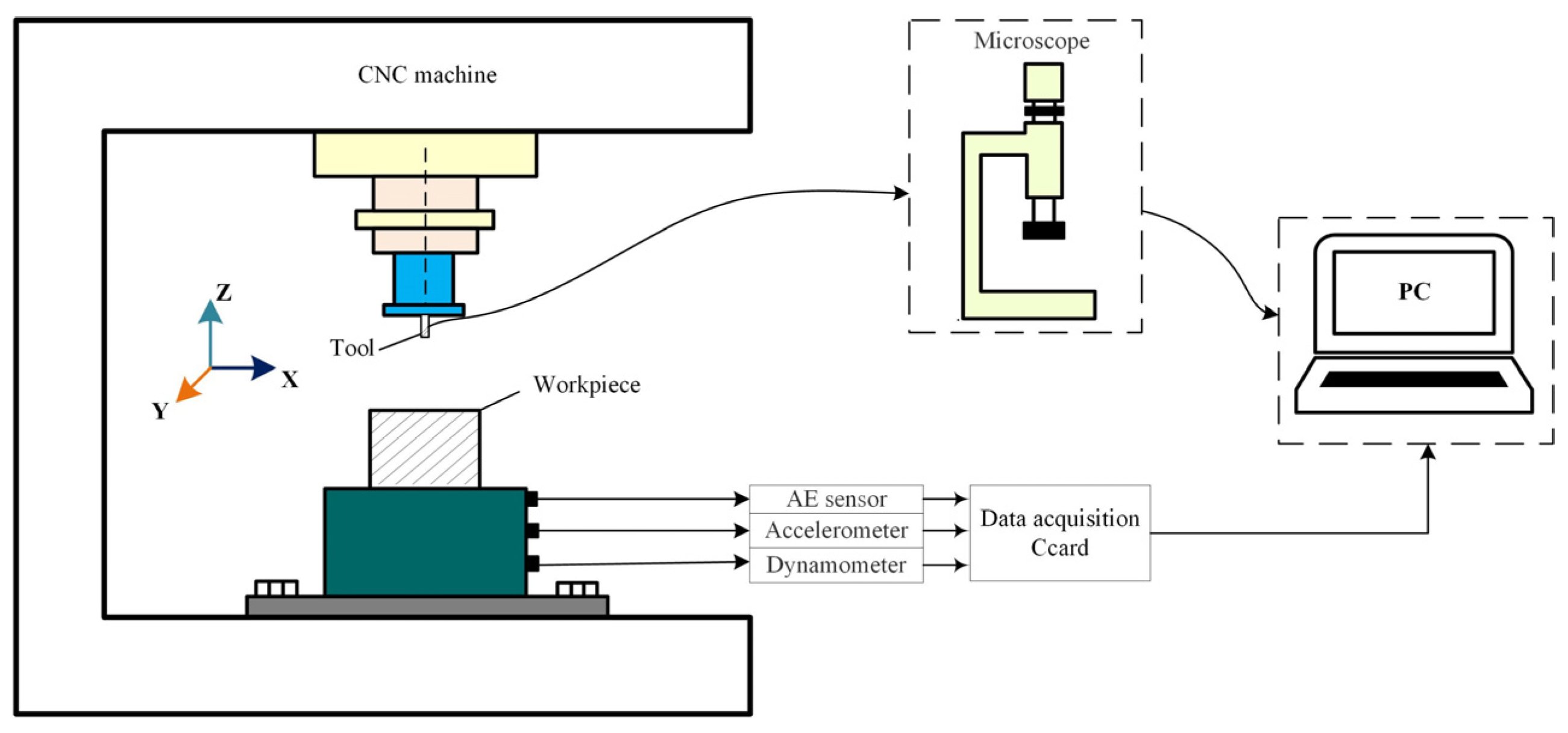
4.1. Experimental Setup
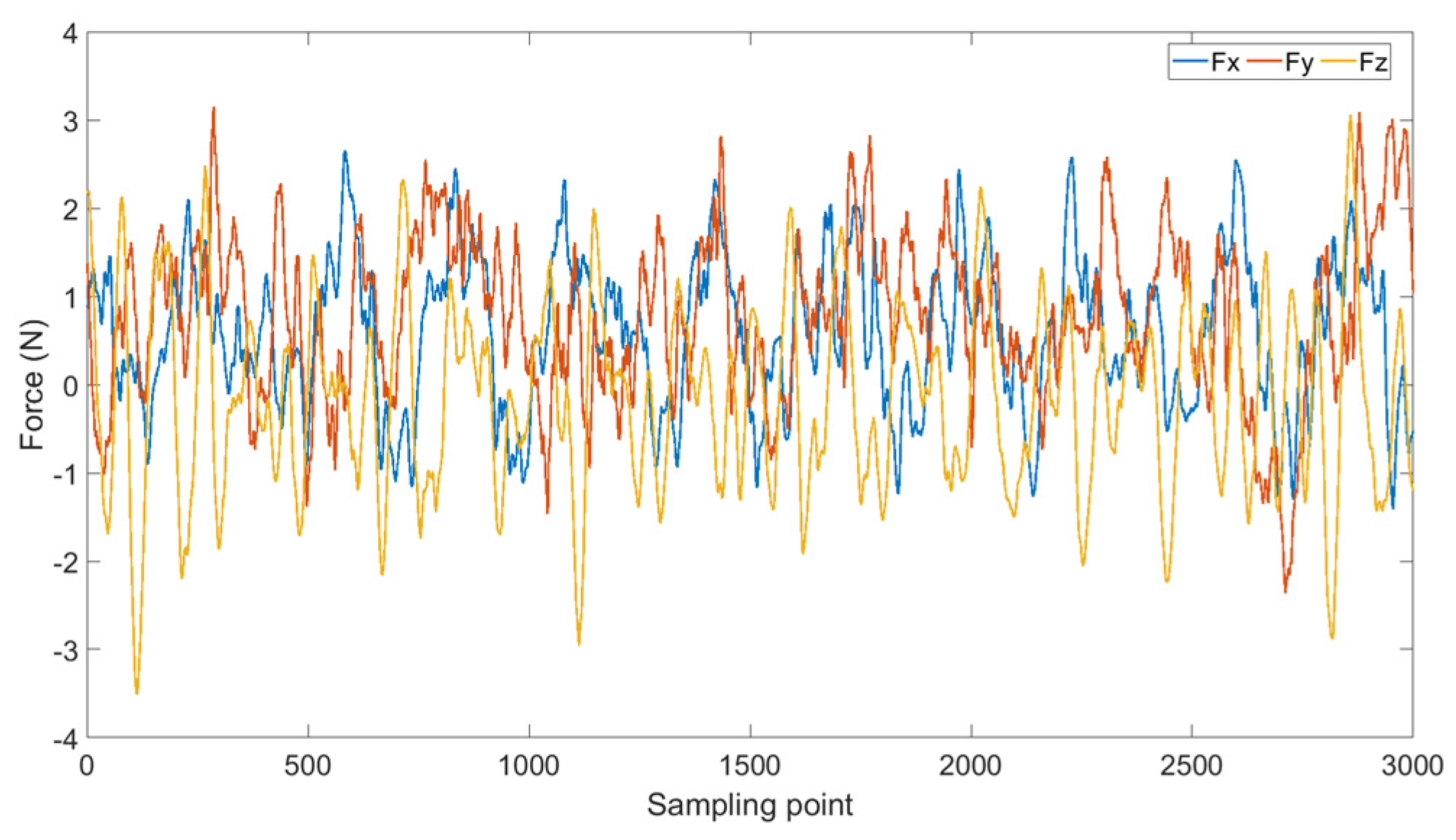
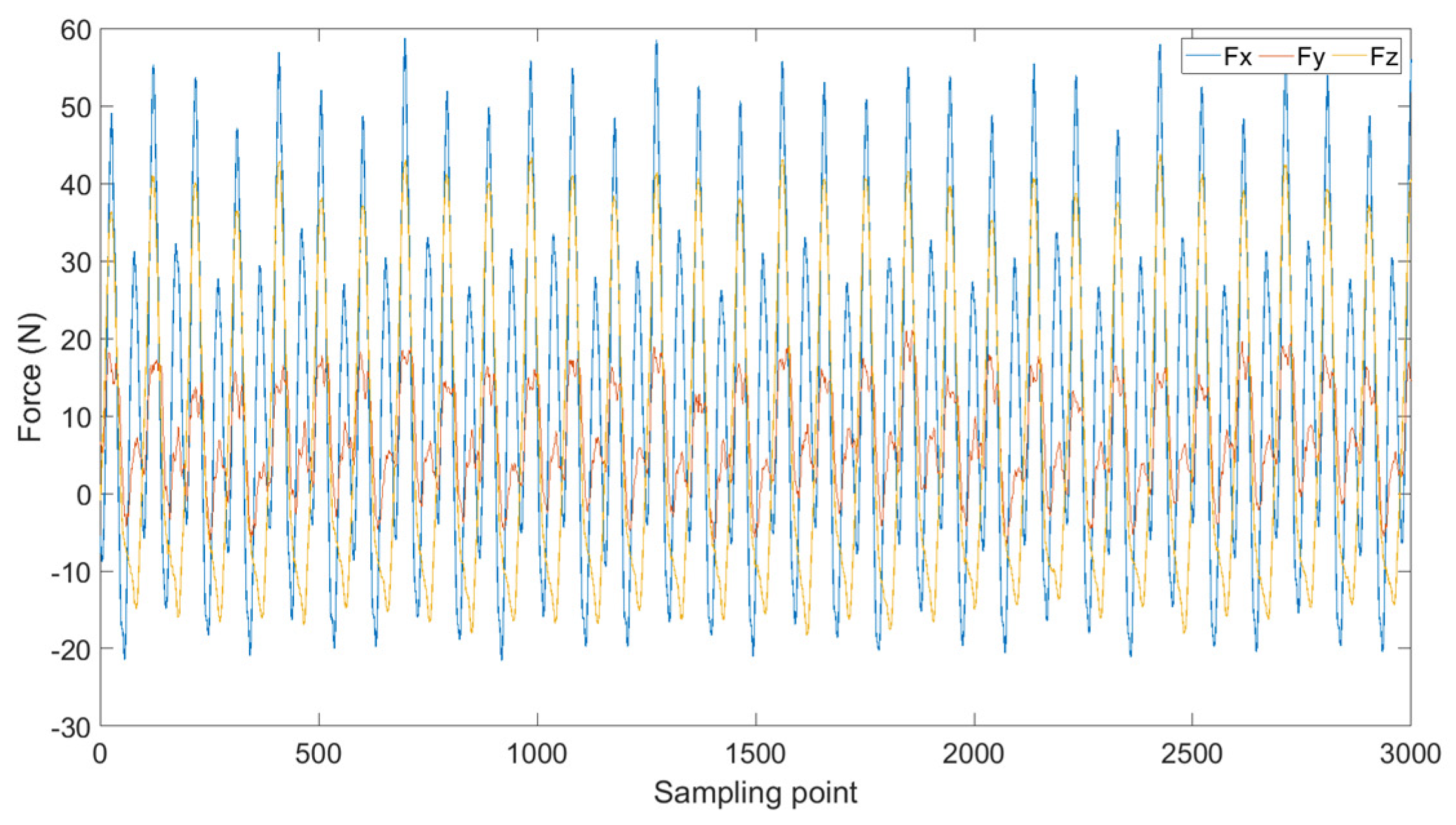
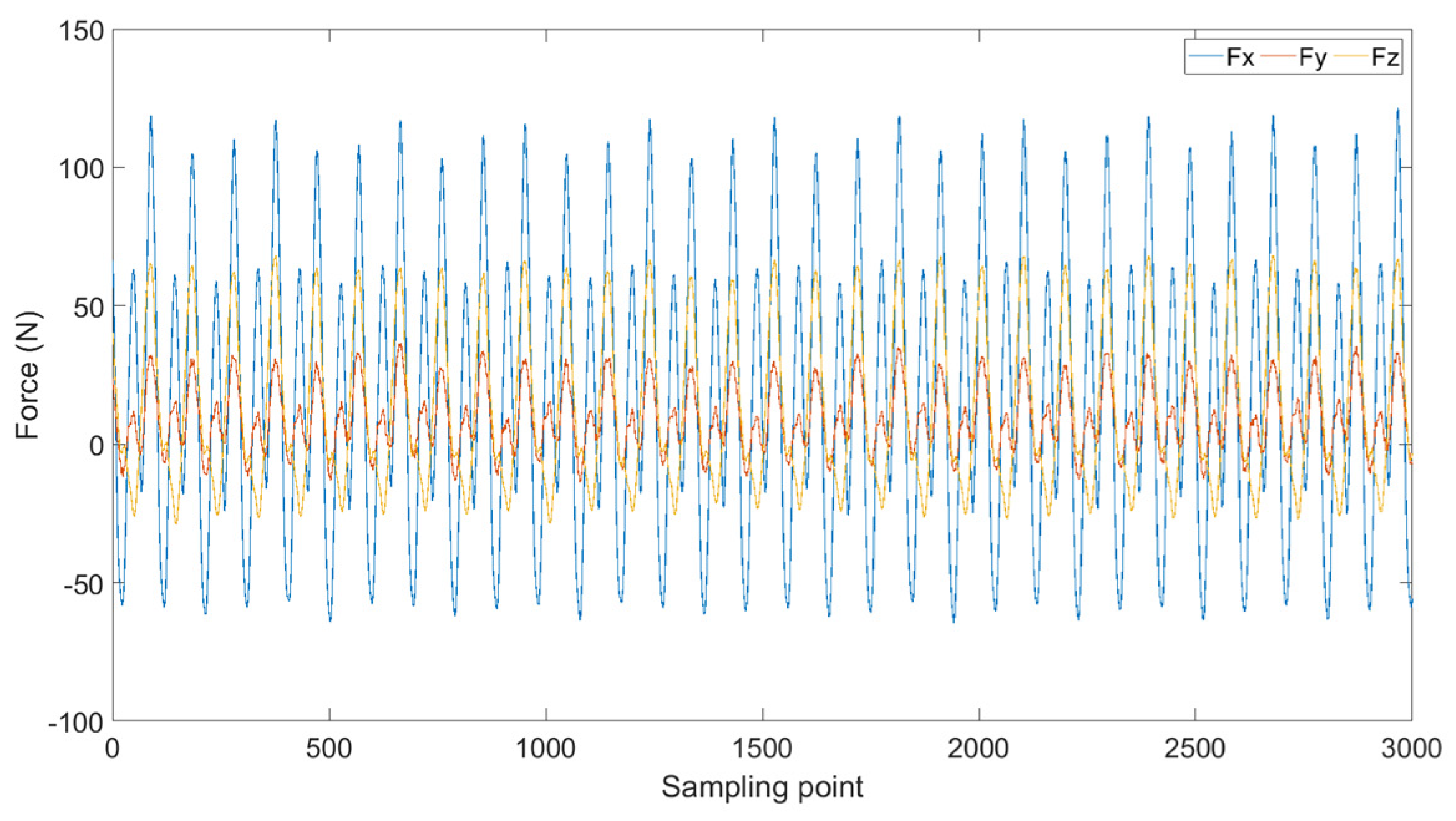
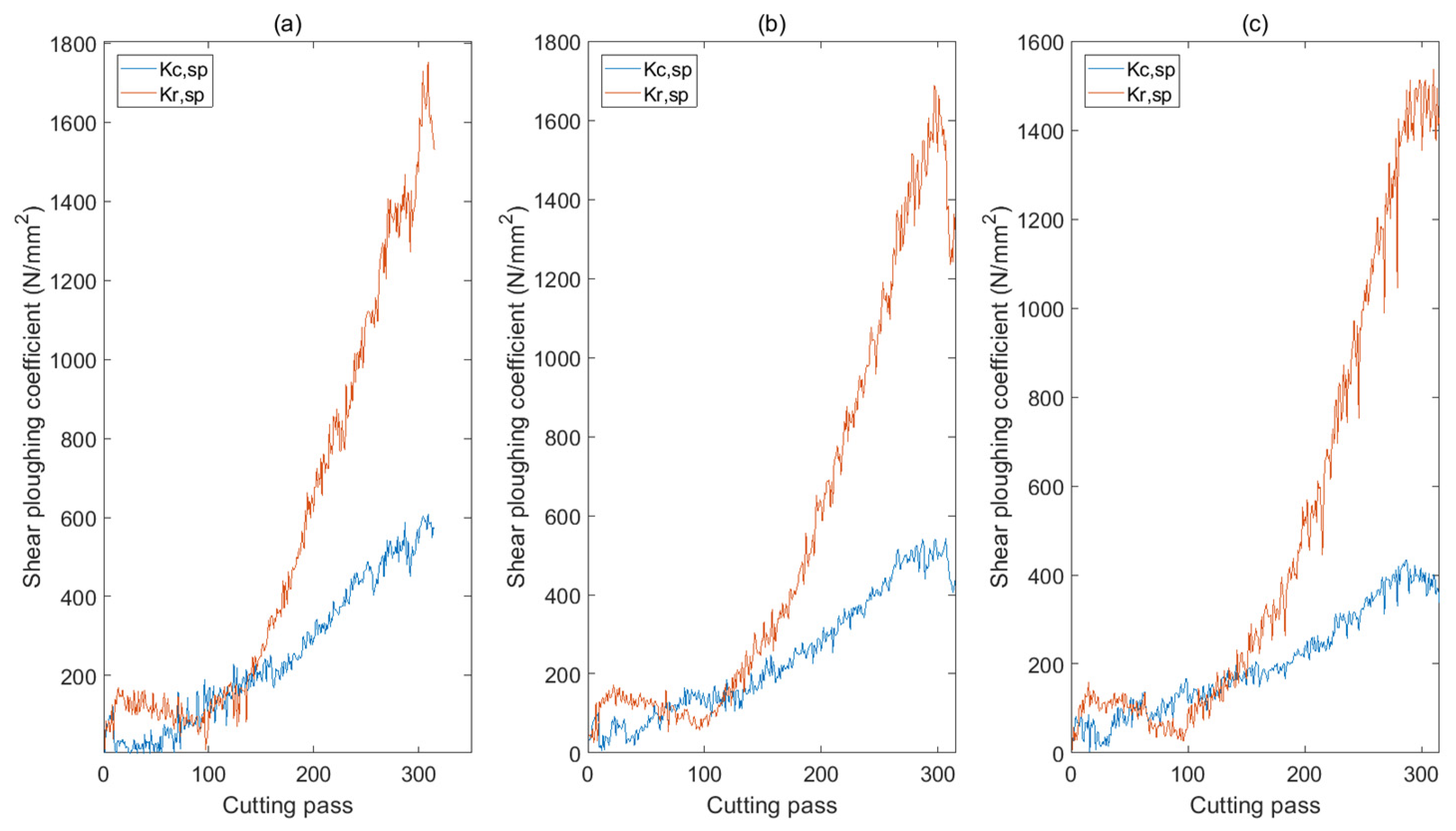
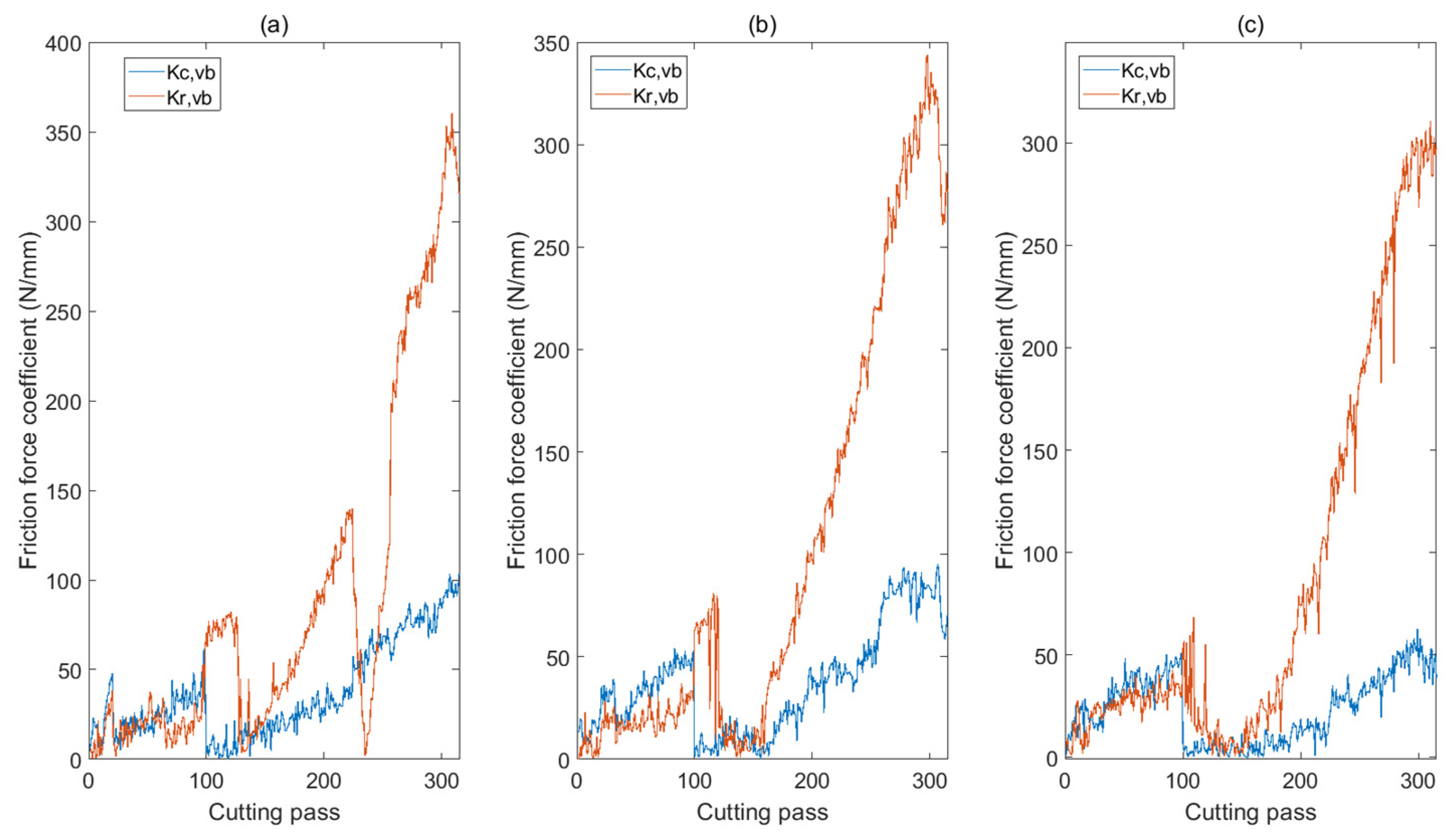
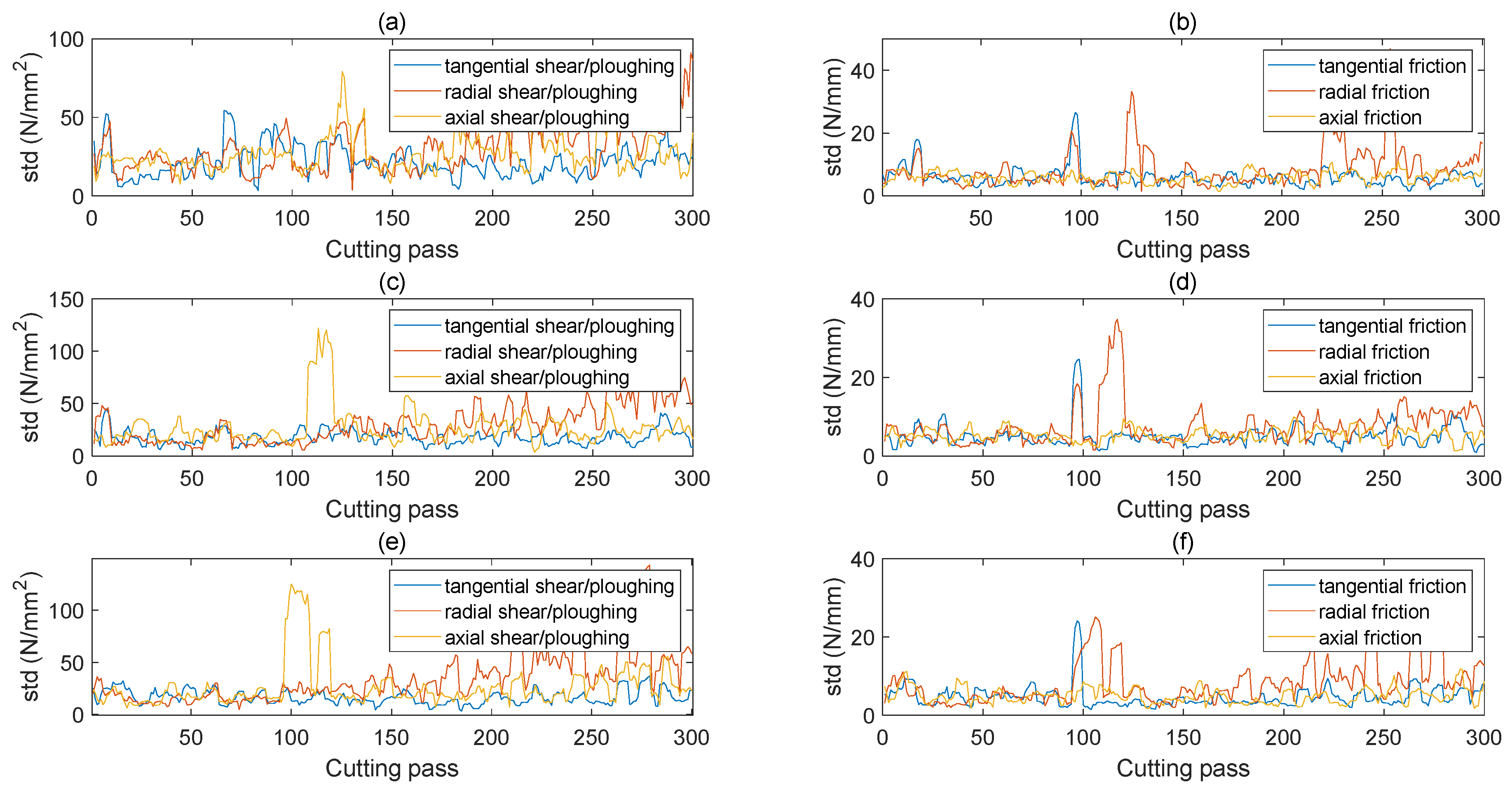
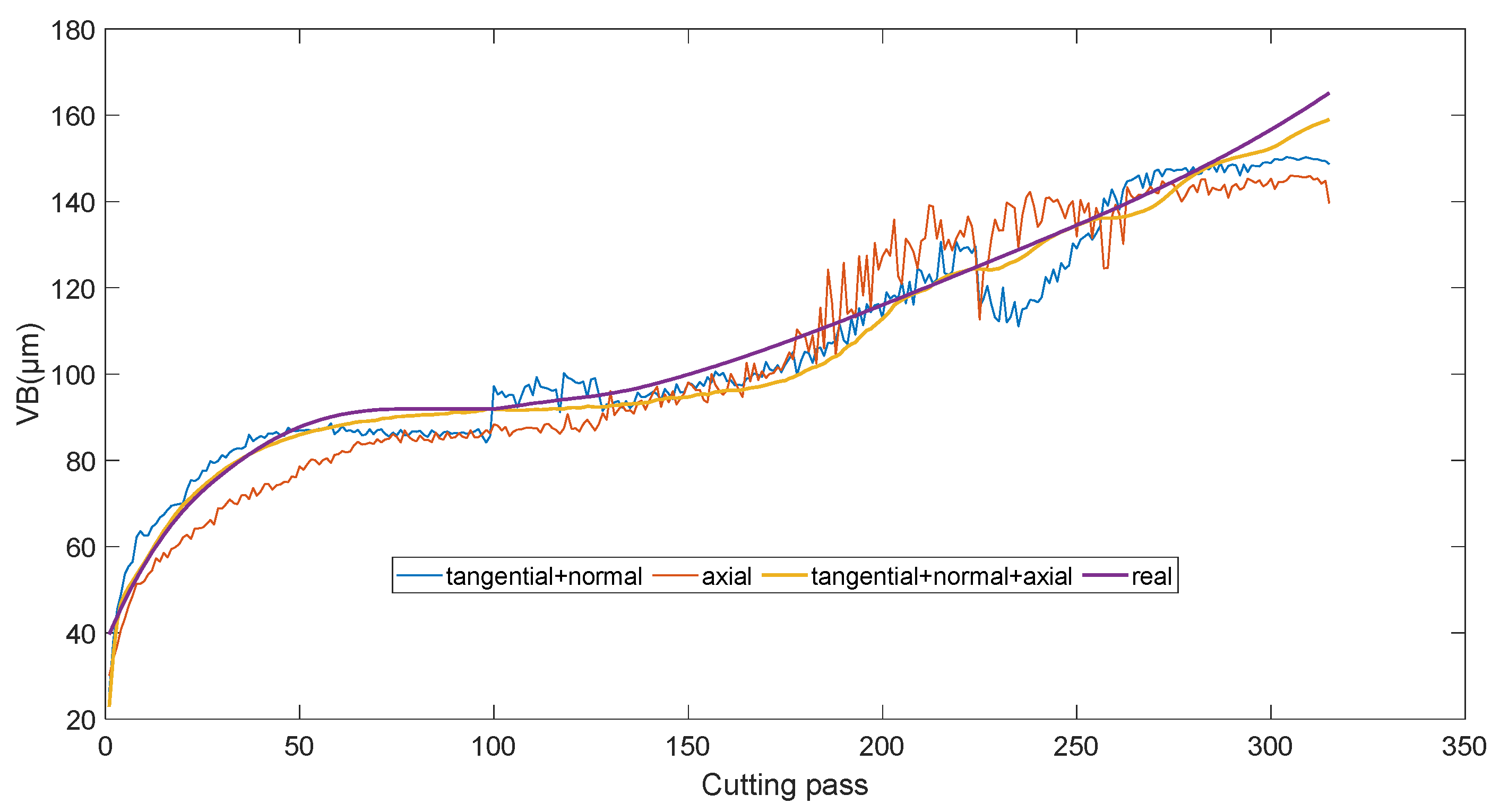
4.2. Tool Wear Feature Extraction and Analysis
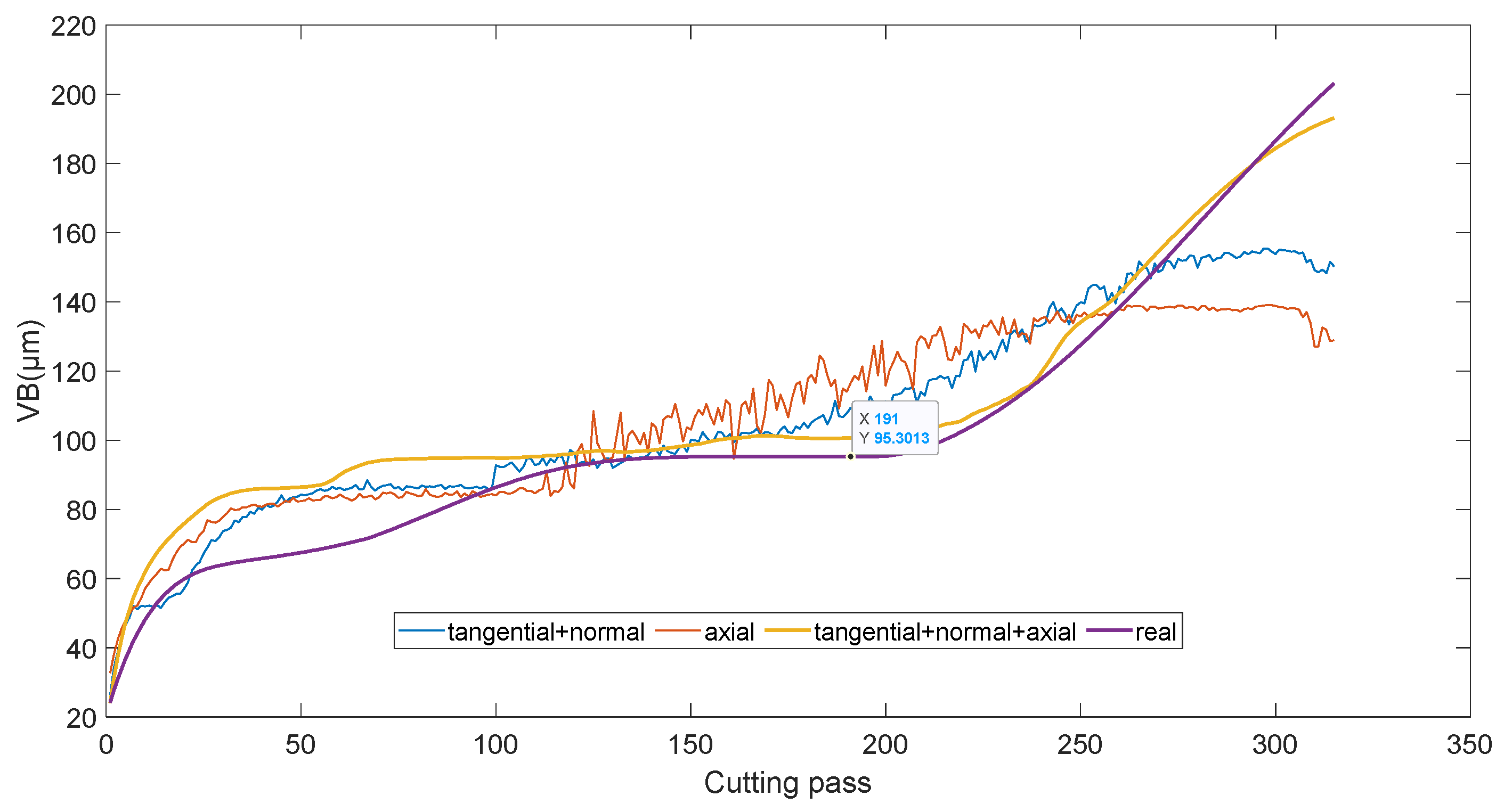
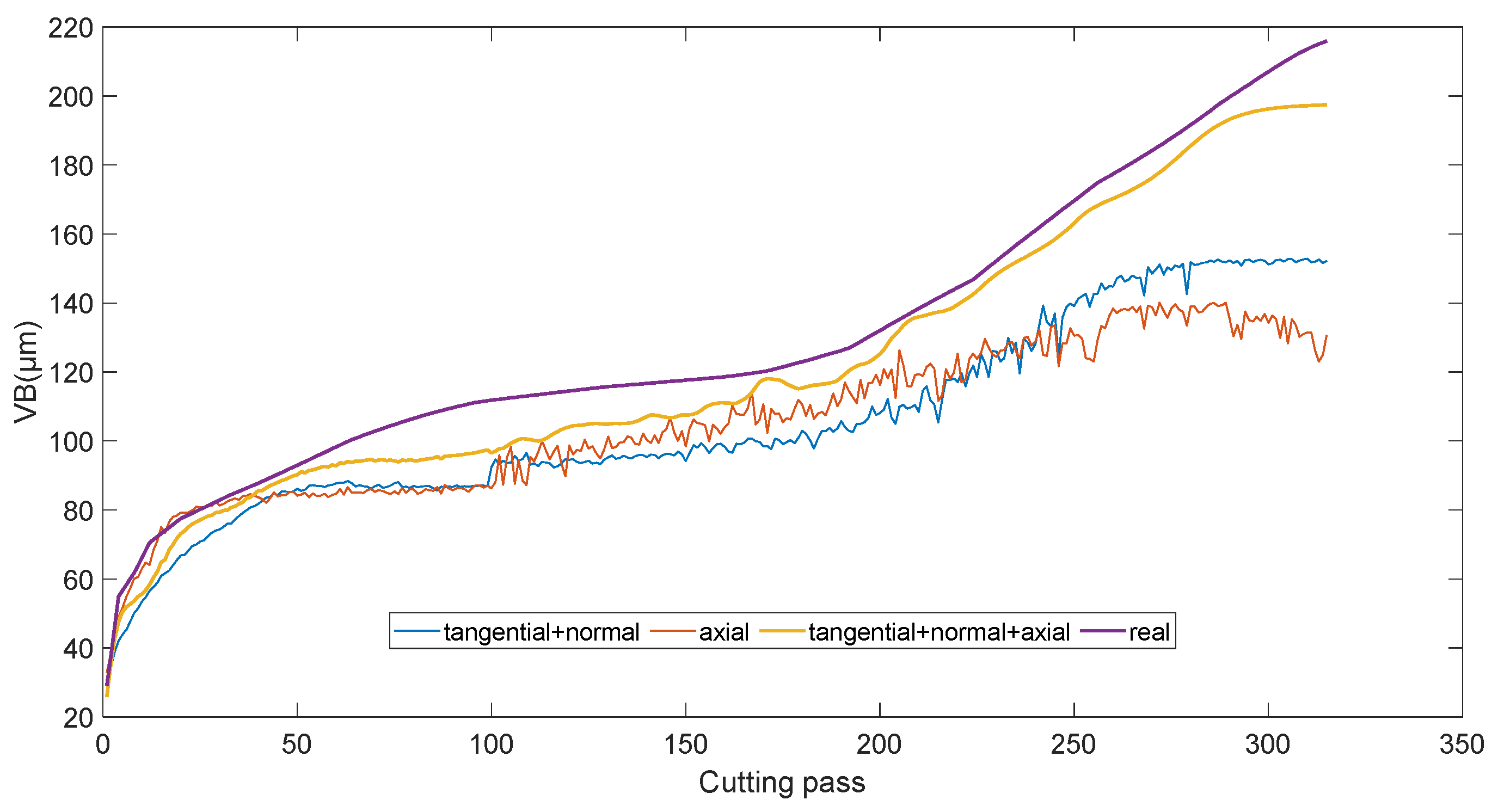
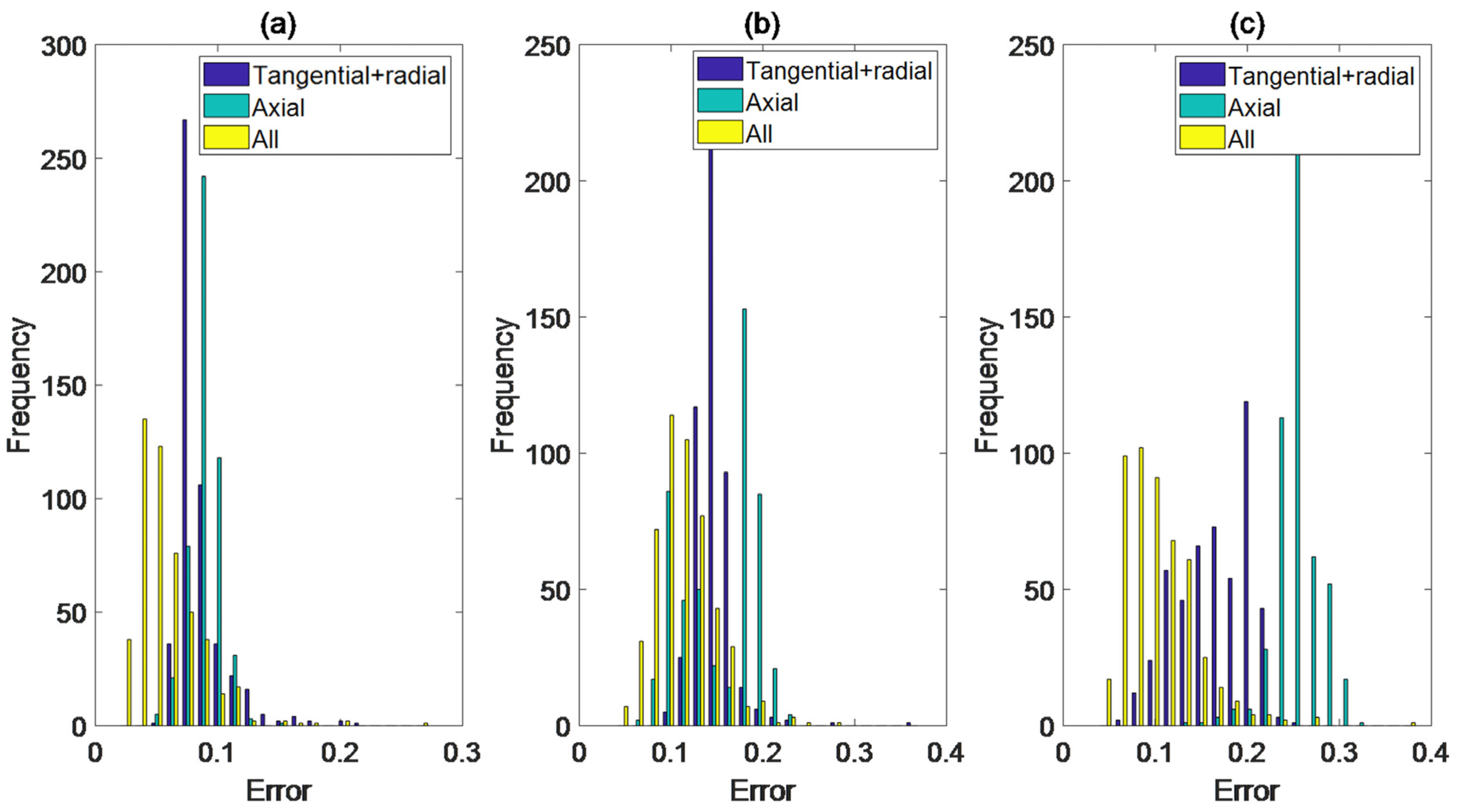
4.3. Tool Wear Monitoring Results and Analysis
5. Conclusions
- (1)
- The tangential, radial, and axial cutting force coefficients were sensitive to the tool wear condition.
- (2)
- With the fusion of the multichannel cutting force coefficients, the monitoring accuracy improved by 2.74–6.35%.
- (3)
- The shear/ploughing coefficient was bigger than the friction force coefficient and was more sensitive to the tool wear condition in milling Inconel 718.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Xie, Y.; Lian, K.; Liu, Q.; Zhang, C.; Liu, H. Digital twin for cutting tool: Modeling, application and service strategy. J. Manuf. Syst. 2021, 58, 305–312. [Google Scholar] [CrossRef]
- Peng, Y.; Song, Q.; Wang, R.; Yang, X.; Liu, Z.; Liu, Z. A tool wear condition monitoring method for non-specific sensing signals. Int. J. Mech. Sci. 2024, 263, 108769. [Google Scholar] [CrossRef]
- Liu, C.; Zhu, H.; Tang, D.; Nie, Q.; Zhou, T.; Wang, L.; Song, Y. Probing an intelligent predictive maintenance approach with deep learning and augmented reality for machine tools in IoT-enabled manufacturing, Robot. Comput. Integr. Manuf. 2022, 77, 102357. [Google Scholar] [CrossRef]
- Zhu, L.; Liu, C. Recent progress of chatter prediction, detection and suppression in milling, Mech. Syst. Sig. Process. 2020, 143, 106840. [Google Scholar] [CrossRef]
- Zhu, K.; Mei, T.; Ye, D. Online condition monitoring in micromilling: A force waveform shape analysis approach. IEEE Trans. Ind. Informat. 2015, 62, 3806–3813. [Google Scholar] [CrossRef]
- Asadzadeh, M.Z.; Eib¨ock, A.; G¨anser, H.-P.; Klünsner, T.; Mücke, M.; Hanna, L.; Teppernegg, T.; Treichler, M.; Peissl, P.; Czettl, C. Tool damage state condition monitoring in milling processes based on the mechanistic model goodness-of-fit metrics. J. Manuf. Process. 2022, 80, 612–623. [Google Scholar] [CrossRef]
- Hsieh, W.H.; Lu, M.C.; Chiou, S.J. Application of backpropagation neural network for spindle vibration-based tool wear monitoring in micro-milling. Int. J. Adv. Manuf. Technol. 2012, 61, 53–61. [Google Scholar] [CrossRef]
- Liu, B.; Liu, C.; Zhou, Y.; Wang, D.; Dun, Y. An unsupervised chatter detection method based on AE and merging GMM and K-means. Mech. Syst. Sig. Process. 2023, 186, 109861. [Google Scholar] [CrossRef]
- Díaz-Saldaña, G.; Osornio-Ríos, R.A.; Zamudio-Ramírez, I.; Cruz-Albarrán, I.A.; Trejo-Hernández, M.; Antonino-Daviu, J.A. Methodology for Tool Wear Detection in CNC Machines Based on Fusion Flux Current of Motor and Image Workpieces. Machines 2023, 11, 480. [Google Scholar] [CrossRef]
- Zhang, X.; Gao, Y.; Guo, Z.; Zhang, W.; Yin, J.; Zhao, W. Physical model-based tool wear and breakage monitoring in milling process. Mech. Syst. Sig. Process. 2023, 184, 109641. [Google Scholar] [CrossRef]
- Bernini, L.; Albertelli, P.; Monno, M. Mill condition monitoring based on instantaneous identification of specific force coefficients under variable cutting conditions. Mech. Syst. Sig. Process. 2023, 185, 109820. [Google Scholar] [CrossRef]
- Sousa, V.F.C.; Silva, F.J.G.; Fecheira, J.S.; Lopes, H.M.; Martinho, R.P.; Casais, R.B.; Ferreira, L.P. Cutting forces assessment in CNC machining processes: A critical review. Sensors 2020, 20, 4536. [Google Scholar] [CrossRef] [PubMed]
- Altintas, Y. Manufacturing Automation: Metal Cutting Mechanics, Machine Tool Variations, and CNC Design, 2nd ed.; Cambridge University Press: New York, NY, USA, 2012. [Google Scholar]
- Lu, X.; Wang, F.; Jia, Z.; Si, L.; Zhang, C.; Liang, S.Y. A modified analytical cutting force prediction model under the tool flank wear effect in micro-milling nickel-based superalloy. Int. J. Adv. Manuf. Technol. 2017, 91, 3709–3716. [Google Scholar] [CrossRef]
- Zhou, L.; Deng, B.; Peng, F.; Yang, M.; Yan, R. Semi-analytic modelling of cutting forces in micro ball-end milling of NAK80 steel with wear-varying cutting edge and associated nonlinear process characteristics. Int. J. Mech. Sci. 2020, 169, 105343. [Google Scholar] [CrossRef]
- Nouri, M.; Fussell, B.K.; Ziniti, B.L.; Linder, E. Real-time tool wear monitoring in milling using a cutting condition independent method. Int. J. Mach. Tools. Manuf. 2015, 89, 1–13. [Google Scholar] [CrossRef]
- Hou, Y.; Zhang, D.; Wu, B.; Luo, M. Milling force modeling of worn tool and tool flank wear recognition in end milling. IEEE/ASME Trans. Mechatron. 2014, 20, 1024–1035. [Google Scholar] [CrossRef]
- Pan, T.; Zhang, J.; Zhang, X.; Zhao, W.; Zhang, H.; Lu, B. Milling force coefficients-based tool wear monitoring for variable parameter milling. Int. J. Adv. Manuf. Technol. 2022, 120, 4565–4580. [Google Scholar] [CrossRef]
- Liu, T.; Zhu, K.; Wang, G. Micro-milling tool wear monitoring under variable cutting parameters and runout using fast cutting force coefficient identification method. Int. J. Adv. Manuf. Technol. 2020, 111, 3175–3188. [Google Scholar] [CrossRef]
- Jing, X.; Lv, R.; Chen, Y.; Tian, Y.; Li, H. Modelling and experimental analysis of the effects of run out, minimum chip thickness and elastic recovery on the cutting force in micro-end-milling. Int. J. Mech. Sci. 2020, 176, 105540. [Google Scholar] [CrossRef]
- Li, K.; Zhu, K.; Mei, T. A generic instantaneous undeformed chip thickness model for the cutting force modeling in micromilling. Int. J. Mach. Tool. Manu. 2016, 105, 23–31. [Google Scholar] [CrossRef]
- Yu, Y.; Si, X.; Hu, C.; Zhang, J. A review of recurrent neural networks: LSTM cells and network architectures. Neural Comput. 2019, 31, 1235–1270. [Google Scholar] [CrossRef]
- Beale, M.H.; Hagan, M.T.; Demuth, H.B. Deep Learning Toolbox; User’s Guide; The MathWorks, Inc.: Natick, MA, USA, 2018; Available online: https://research.iaun.ac.ir/pd/mahdavinasab/pdfs/UploadFile_4309.pdf (accessed on 1 May 2023).
- Li, X.; Lim, B.S.; Zhou, J.H.; Huang, S.; Phua, S.J.; Shaw, K.C.; Er, M.J. Fuzzy neural network modelling for tool wear estimation in dry milling operation. In Proceedings of the Annual Conference of the PHM Society, San Diego, CA, USA, 27 September–1 October 2009; Volume 1. [Google Scholar]
- Sagheer, A.; Hamdoun, H.; Youness, H. Deep LSTM-Based Transfer Learning Approach for Coherent Forecasts in Hierarchical Time Series. Sensors 2021, 21, 4379. [Google Scholar] [CrossRef] [PubMed]

| Shear/Ploughing | Friction in Flank Region | |
|---|---|---|
| Tangential | Kc,sp (N/mm2) | Kc,vb (N/mm) |
| Radial | Kr,sp (N/mm2) | Kr,vb (N/mm) |
| Axial | Ka,sp (N/mm2) | Ka,vb (N/mm) |
| CNC Machine | Röders Tech RFM760 (Soltau, Germany) |
|---|---|
| Tool type | Ball nose milling cutter |
| Number of flutes | 3 |
| Workpiece material | Stainless steel (HRC52) |
| Spindle speed | 10,400 rpm |
| Feed rate | 1555 mm/min |
| Radial cutting depth | 0.125 mm |
| Axial cutting depth | 0.2 mm |
| Number of cuts per experiment | 315 |
| Number | Training Data | Testing Data |
|---|---|---|
| 1 | C4 and C6 | C1 |
| 2 | C1 and C6 | C4 |
| 3 | C1 and C4 | C6 |
| Number | Tangential + Radial | Axial | Tangential + Radial + Axial |
|---|---|---|---|
| 1 | 8.53% | 8.98% | 5.79% |
| 2 | 14.70% | 15.38% | 11.33% |
| 3 | 16.58% | 25.39% | 10.23% |
| Number | MLP | Single-Layer LSTM | Stacked LSTM |
|---|---|---|---|
| 1 | 10.37% | 9.24% | 5.79% |
| 2 | 16.73% | 14.95% | 11.33% |
| 3 | 16.58% | 18.17% | 10.23% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xing, Q.; Zhang, X.; Wang, S.; Yu, X.; Liu, Q.; Liu, T. Milling Tool Wear Monitoring via the Multichannel Cutting Force Coefficients. Machines 2024, 12, 249. https://doi.org/10.3390/machines12040249
Xing Q, Zhang X, Wang S, Yu X, Liu Q, Liu T. Milling Tool Wear Monitoring via the Multichannel Cutting Force Coefficients. Machines. 2024; 12(4):249. https://doi.org/10.3390/machines12040249
Chicago/Turabian StyleXing, Qingqing, Xiaoping Zhang, Shuang Wang, Xichen Yu, Qingsheng Liu, and Tongshun Liu. 2024. "Milling Tool Wear Monitoring via the Multichannel Cutting Force Coefficients" Machines 12, no. 4: 249. https://doi.org/10.3390/machines12040249
APA StyleXing, Q., Zhang, X., Wang, S., Yu, X., Liu, Q., & Liu, T. (2024). Milling Tool Wear Monitoring via the Multichannel Cutting Force Coefficients. Machines, 12(4), 249. https://doi.org/10.3390/machines12040249






