Effect of Floating Support Parameters on the Load-Sharing Performance of EDPGS Based on Mathematical Statistical Methods
Abstract
1. Introduction
2. The Physical Model of the EDPGS
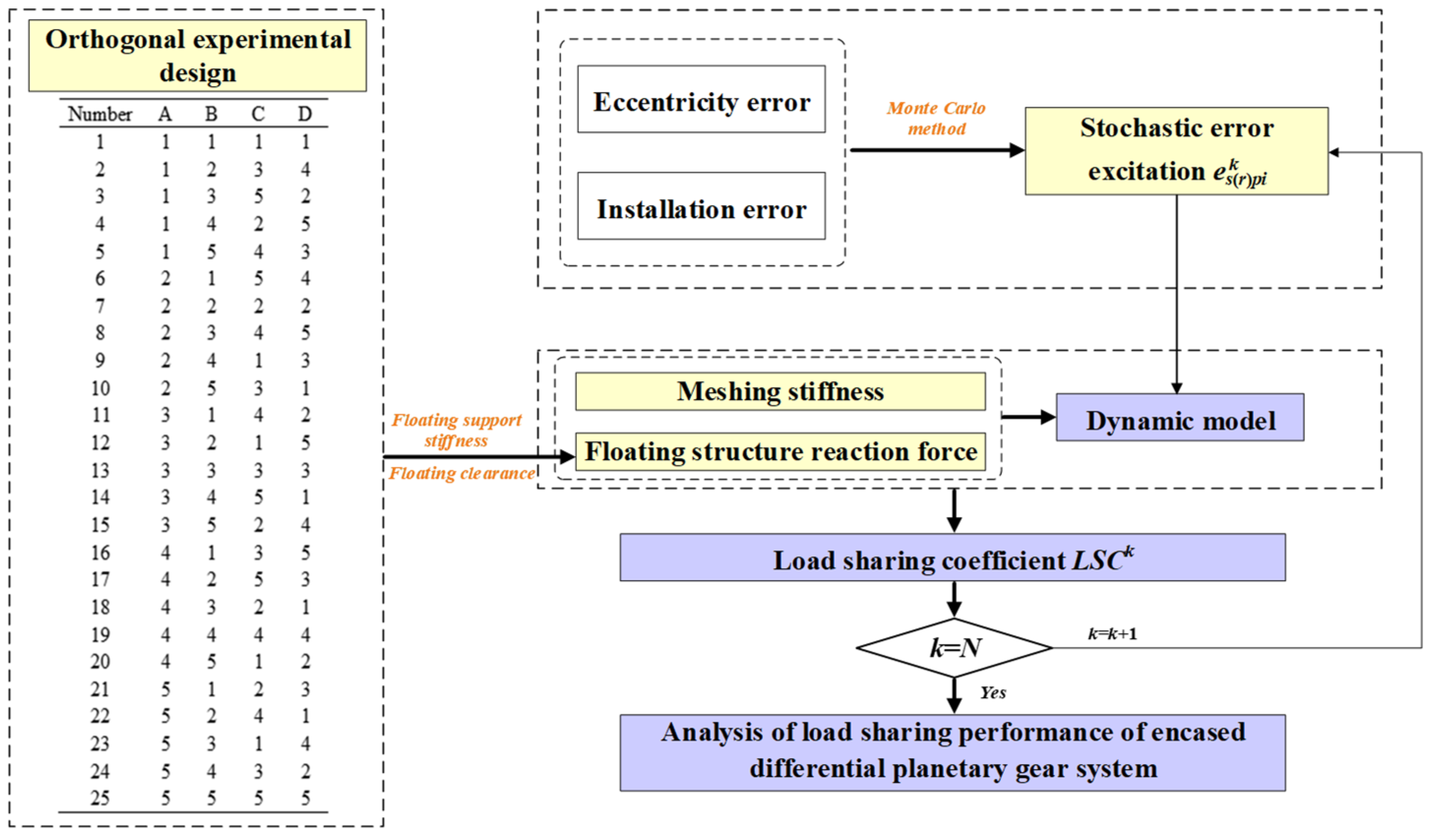
3. Dynamic Model of the EDPGS Based on the Monte Carlo Method
3.1. Time-Varying Meshing Stiffness
3.2. Stochastic Equivalent Meshing Error Based on the Monte Carlo Method
- (1)
- The influence of the eccentricity error and installation error is mainly considered, and the error schematic diagram of the sun gear and planetary gear is shown in Figure 2.
- (2)
- The Monte Carlo method is used to simulate random eccentricity error and installation error. Assuming that the error machining accuracy in this paper is grade 5, the range of the tolerance band is considered to be between grade 4 and grade 6.
3.3. Dynamic Modeling of Support Reaction Forces in Floating Structures
3.4. Overall System Dynamic Model
(i = 1, 2, …, M, j = 1, 2, …, N)
3.5. Calculation Model of Load-Sharing Coefficient
4. The Analysis of the Load-Sharing Characteristics of the EDPGS
4.1. Dynamic Parameter of the Encased Differential Planetary System
4.2. Orthogonal Experimental Design Based on Floating Support Stiffness and Clearance
- (1)
- Determine the experimental factors and levels.
- (2)
- Build the experimental matrix X, ensuring that each level of each experimental factor appears exactly once and that every pair of columns in the experimental matrix is orthogonal. The building method can refer to a Latin hypercube, orthogonal fractional array, etc.
- (3)
- Conduct experiments according to the design in the experimental matrix and record the resulting data.
4.3. Analysis Process of EDPGS Based on Mathematical Statistical Methods
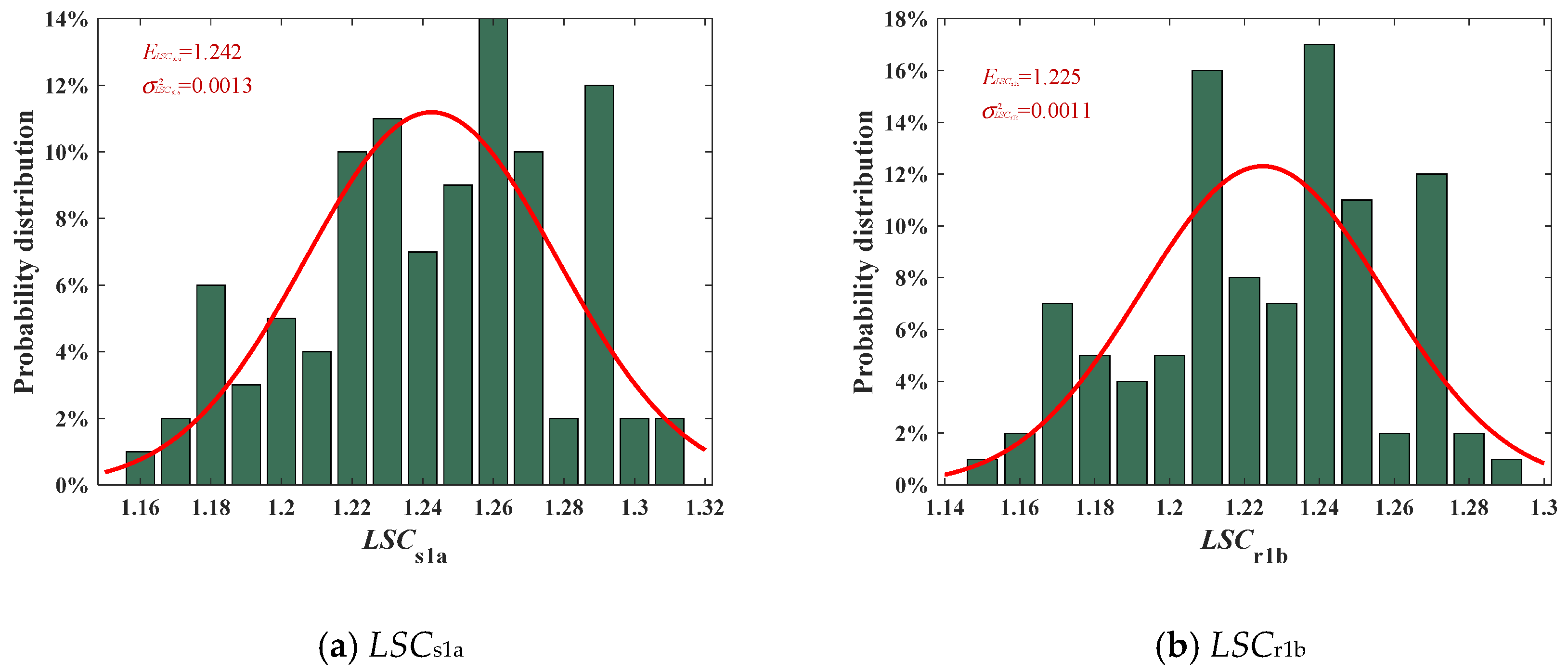
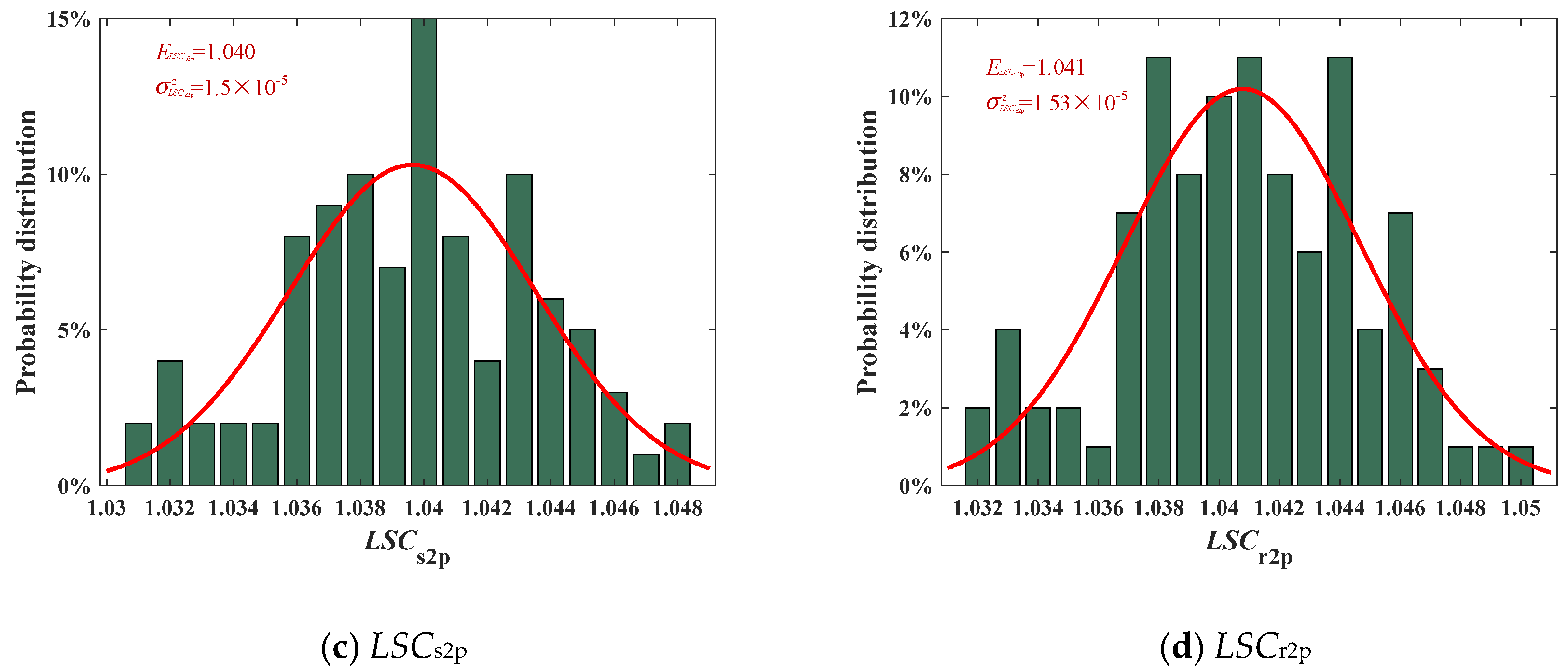
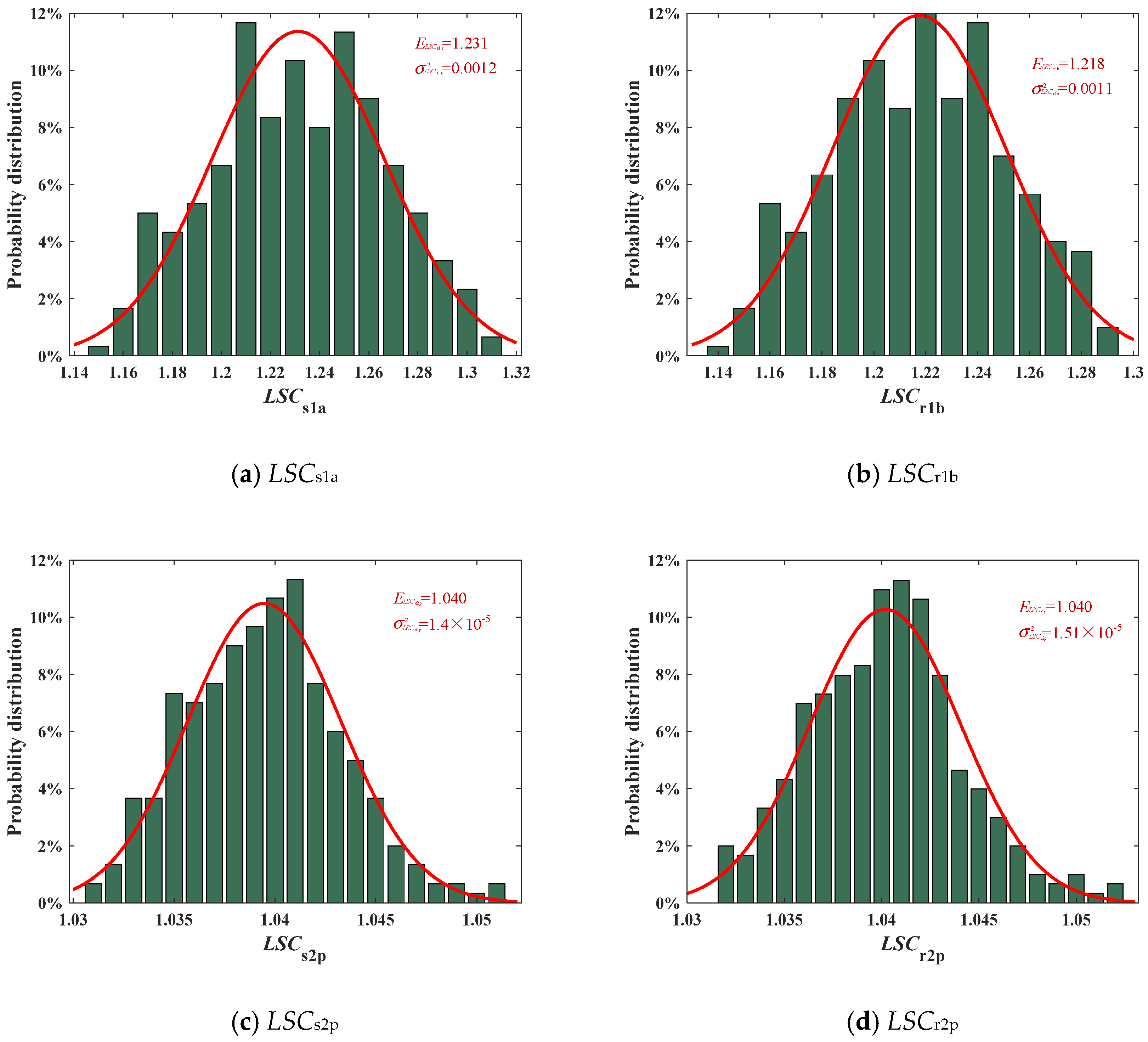
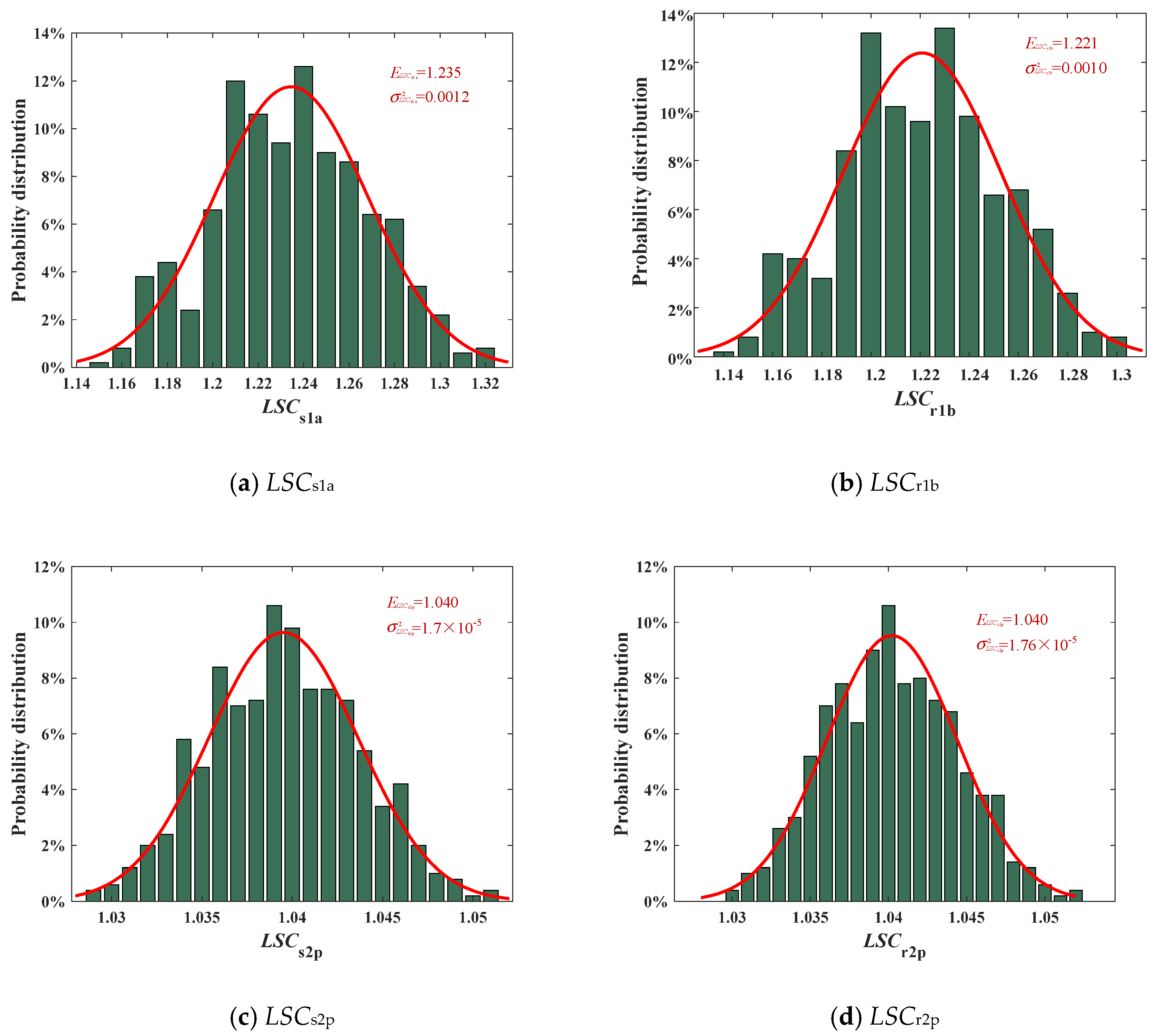
4.4. Analysis of Load-Sharing Performance of EDPGS Based on the Monte Carlo Method
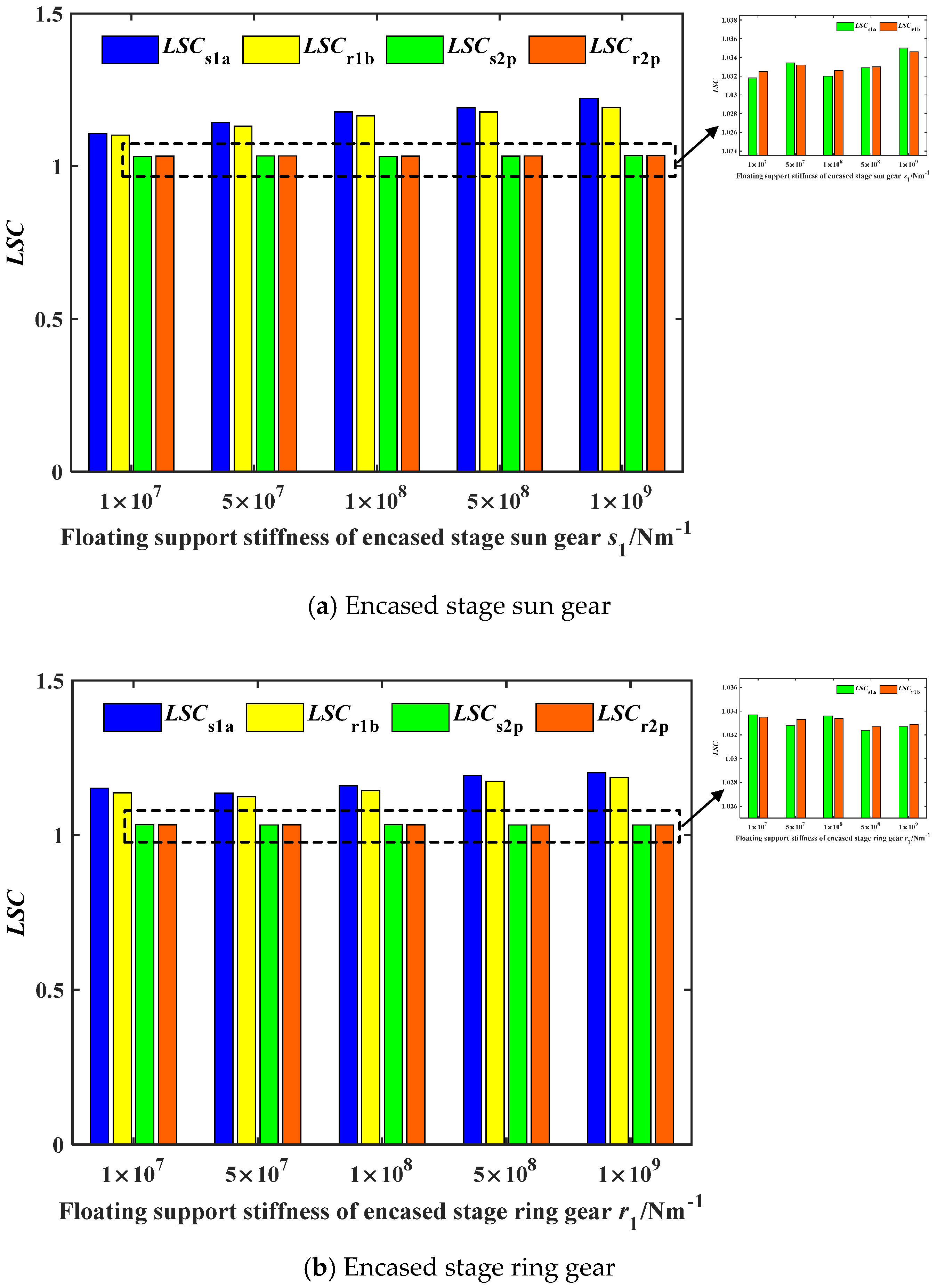
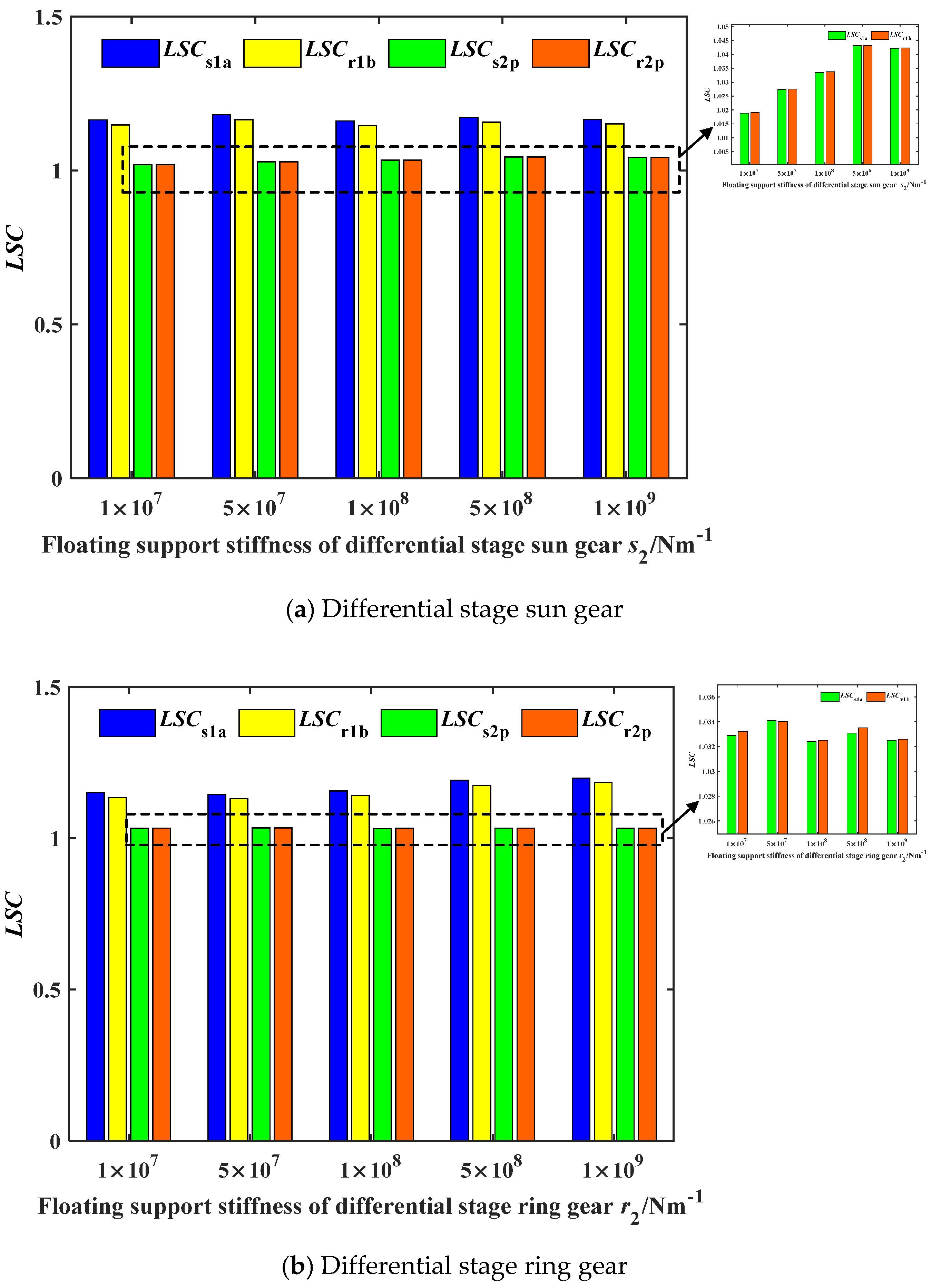
4.5. The Effect of Floating Support Stiffness on the Load-Sharing Performance of EDPGS
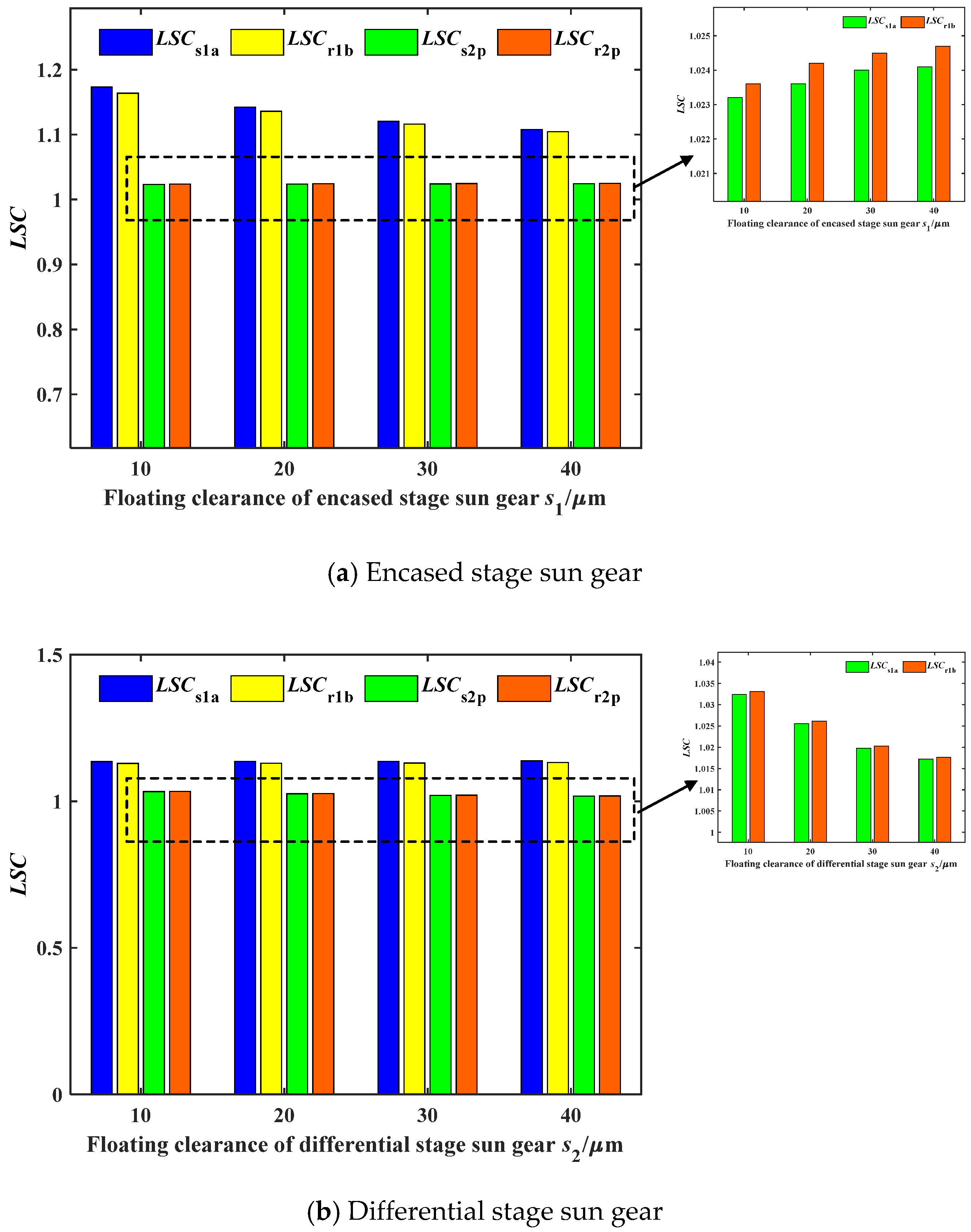
4.6. The Effect of Floating Clearance of the Sun Gear on the Load-Sharing Performance of the EDPGS
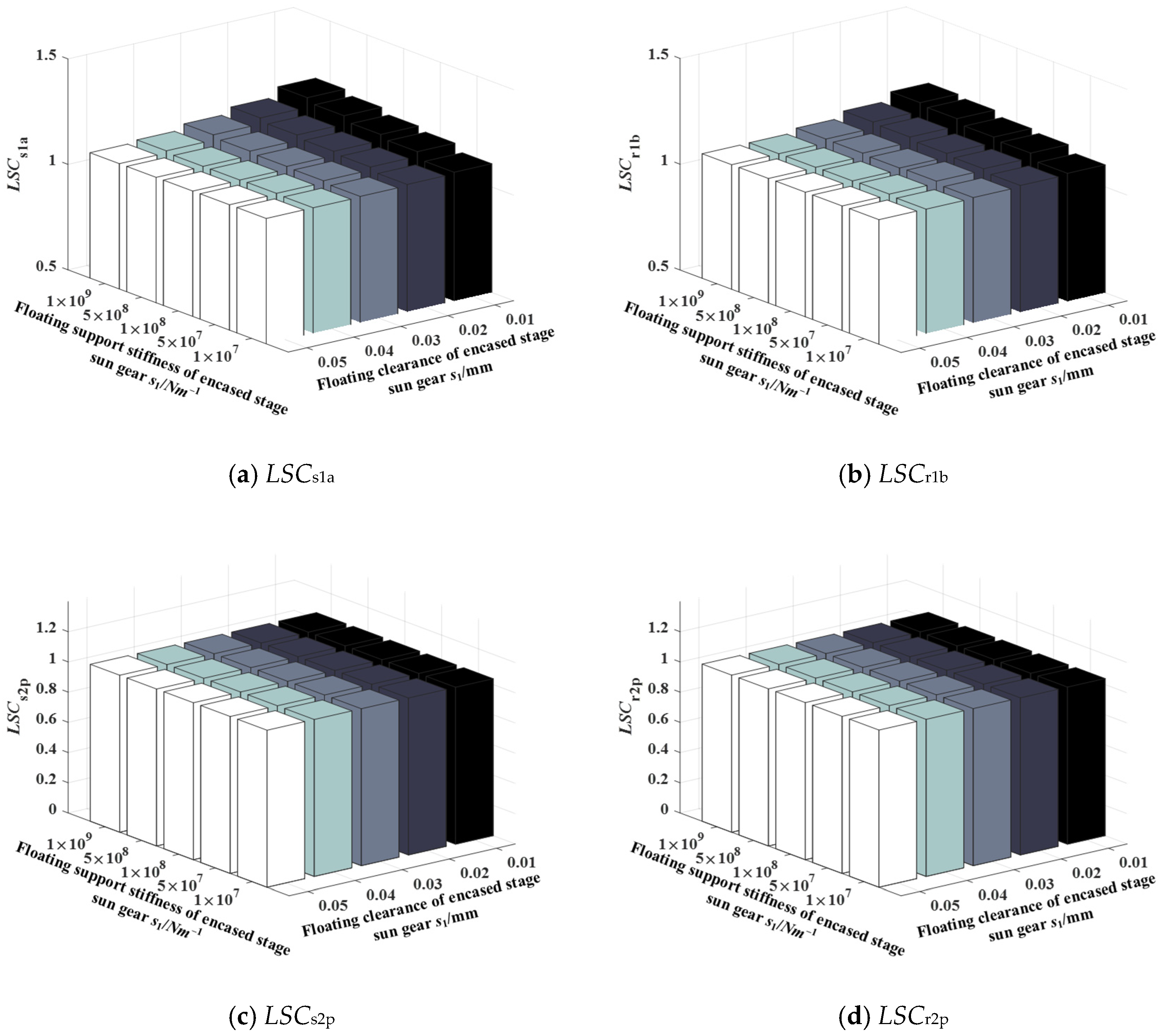
4.7. The Coupling Effect of Floating Sun Gear Parameter on the Load-Sharing Performance of the EDPGS
5. Conclusions
- (a)
- The probability distribution, expectation, and variance under the sample number with 100, 300, and 500 were compared. When the sample number N = 100, the probability distribution significantly deviated from the fitted Gaussian distribution, and the fitting degree improved at N = 300 and 500. However, the expectation and variance were less affected by the sample number.
- (b)
- The load-sharing coefficient of the encased stage system increases with the increase in the floating support stiffness, and the load-sharing coefficient of the differential stage system increases with the increase in the floating support stiffness of s2.
- (c)
- The load-sharing coefficient of the encased stage system decreased with the increase in the floating clearance of s1. In contrast, the load-sharing coefficient of the differential stage system increased with the increase in the floating clearance of s1 and decreased with the increase in the floating clearance of s2.
- (d)
- The impact of floating support stiffness on load-sharing performance was more pronounced when the floating clearance of s1 was smaller, leading to an increase in the load-sharing coefficient as the floating support stiffness increased. Conversely, a higher floating support stiffness of s1 amplified the influence of floating clearance on load-sharing performance, causing the load-sharing coefficient to decrease with the increase in the floating clearance.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Number | ks1 (N/m) | ks2 (N/m) | kr1 (N/m) | kr2 (N/m) | LSCs1a | LSCr1b | LSCs2p | LSCr2p |
|---|---|---|---|---|---|---|---|---|
| 1 | 1 × 107 | 1 × 107 | 1 × 107 | 1 × 107 | 1.0669 | 1.0590 | 1.0186 | 1.0192 |
| 2 | 1 × 107 | 5 × 107 | 1 × 108 | 5 × 108 | 1.1146 | 1.1085 | 1.0271 | 1.0276 |
| 3 | 1 × 107 | 1 × 108 | 1 × 109 | 5 × 107 | 1.1163 | 1.1152 | 1.0319 | 1.0328 |
| 4 | 1 × 107 | 5 × 108 | 5 × 107 | 1 × 109 | 1.1183 | 1.1154 | 1.0412 | 1.0420 |
| 5 | 1 × 107 | 1 × 109 | 5 × 108 | 1 × 108 | 1.1149 | 1.1099 | 1.0402 | 1.0409 |
| 6 | 5 × 107 | 1 × 107 | 1 × 109 | 5 × 108 | 1.1812 | 1.1638 | 1.0205 | 1.0204 |
| 7 | 5 × 107 | 5 × 107 | 5 × 107 | 5 × 107 | 1.1104 | 1.1000 | 1.0277 | 1.0281 |
| 8 | 5 × 107 | 1 × 108 | 5 × 108 | 1 × 109 | 1.1782 | 1.1632 | 1.0336 | 1.0335 |
| 9 | 5 × 107 | 5 × 108 | 1 × 107 | 1 × 108 | 1.1240 | 1.1131 | 1.0436 | 1.0425 |
| 10 | 5 × 107 | 1 × 109 | 1 × 108 | 1 × 107 | 1.1249 | 1.1128 | 1.0414 | 1.0413 |
| 11 | 1 × 108 | 1 × 107 | 5 × 108 | 5 × 107 | 1.1794 | 1.1665 | 1.0179 | 1.0182 |
| 12 | 1 × 108 | 5 × 107 | 1 × 107 | 1 × 109 | 1.1877 | 1.1769 | 1.0266 | 1.0269 |
| 13 | 1 × 108 | 1 × 108 | 1 × 108 | 1 × 108 | 1.1451 | 1.1315 | 1.0327 | 1.0333 |
| 14 | 1 × 108 | 5 × 108 | 1 × 109 | 1 × 107 | 1.1968 | 1.1828 | 1.0413 | 1.0422 |
| 15 | 1 × 108 | 1 × 109 | 5 × 107 | 5 × 108 | 1.1779 | 1.1658 | 1.0417 | 1.0423 |
| 16 | 5 × 108 | 1 × 107 | 1 × 108 | 1 × 109 | 1.2332 | 1.2174 | 1.0180 | 1.0178 |
| 17 | 5 × 108 | 5 × 107 | 1 × 109 | 1 × 108 | 1.2379 | 1.2211 | 1.0265 | 1.0263 |
| 18 | 5 × 108 | 1 × 108 | 5 × 107 | 1 × 107 | 1.1152 | 1.1054 | 1.0341 | 1.0345 |
| 19 | 5 × 108 | 5 × 108 | 5 × 108 | 5 × 108 | 1.2377 | 1.2192 | 1.0413 | 1.0422 |
| 20 | 5 × 108 | 1 × 109 | 1 × 107 | 5 × 107 | 1.1350 | 1.1218 | 1.0446 | 1.0441 |
| 21 | 1 × 109 | 1 × 107 | 5 × 107 | 1 × 108 | 1.1572 | 1.1317 | 1.0191 | 1.0197 |
| 22 | 1 × 109 | 5 × 107 | 5 × 108 | 1 × 107 | 1.2534 | 1.2142 | 1.0289 | 1.0287 |
| 23 | 1 × 109 | 1 × 108 | 1 × 107 | 5 × 108 | 1.2465 | 1.2116 | 1.0351 | 1.0348 |
| 24 | 1 × 109 | 5 × 108 | 1 × 108 | 5 × 107 | 1.1808 | 1.1521 | 1.0486 | 1.0470 |
| 25 | 1 × 109 | 1 × 109 | 1 × 109 | 1 × 109 | 1.2743 | 1.2462 | 1.0431 | 1.0429 |
| ks1 (N/m) | ks2 (N/m) | kr1 (N/m) | kr2 (N/m) | |
|---|---|---|---|---|
| k1 (LSCs1a) | 1.1062 | 1.1636 | 1.1520 | 1.1514 |
| k2 (LSCs1a) | 1.1437 | 1.1808 | 1.1358 | 1.1444 |
| k3 (LSCs1a) | 1.1774 | 1.1603 | 1.1597 | 1.1558 |
| k4 (LSCs1a) | 1.1918 | 1.1715 | 1.1927 | 1.1916 |
| k5 (LSCs1a) | 1.2224 | 1.1654 | 1.2013 | 1.1983 |
| R (LSCs1a) | 0.1162 | 0.0205 | 0.0655 | 0.0539 |
| k1 (LSCr1b) | 1.1016 | 1.1477 | 1.1365 | 1.1348 |
| k2 (LSCr1b) | 1.1306 | 1.1641 | 1.1237 | 1.1311 |
| k3 (LSCr1b) | 1.1647 | 1.1454 | 1.1445 | 1.1415 |
| k4 (LSCr1b) | 1.1770 | 1.1565 | 1.1746 | 1.1738 |
| k5 (LSCr1b) | 1.1912 | 1.1513 | 1.1858 | 1.1838 |
| R (LSCr1b) | 0.0896 | 0.0059 | 0.0621 | 0.0527 |
| k1 (LSCs2p) | 1.0318 | 1.0188 | 1.0337 | 1.0329 |
| k2 (LSCs2p) | 1.0334 | 1.0274 | 1.0328 | 1.0341 |
| k3 (LSCs2p) | 1.0320 | 1.0335 | 1.0336 | 1.0324 |
| k4 (LSCs2p) | 1.0329 | 1.0432 | 1.0324 | 1.0331 |
| k5 (LSCs2p) | 1.0350 | 1.0422 | 1.0327 | 1.0325 |
| R (LSCs2p) | 0.0032 | 0.0244 | 0.0013 | 0.0017 |
| k1 (LSCr2p) | 1.0325 | 1.0191 | 1.0335 | 1.0332 |
| k2 (LSCr2p) | 1.0332 | 1.0275 | 1.0333 | 1.0340 |
| k3 (LSCr2p) | 1.0326 | 1.0338 | 1.0334 | 1.0325 |
| k4 (LSCr2p) | 1.0330 | 1.0432 | 1.0327 | 1.0335 |
| k5 (LSCr2p) | 1.0346 | 1.0423 | 1.0329 | 1.0326 |
| R (LSCr2p) | 0.0021 | 0.0241 | 0.0008 | 0.0015 |
| Number | Rs1 (μm) | Rs2 (μm) | LSCs1a | LSCr1b | LSCs2p | LSCr2p |
|---|---|---|---|---|---|---|
| 1 | 10 | 10 | 1.1747 | 1.1660 | 1.0325 | 1.0330 |
| 2 | 10 | 20 | 1.1714 | 1.1627 | 1.0254 | 1.0260 |
| 3 | 10 | 30 | 1.1710 | 1.1615 | 1.0192 | 1.0196 |
| 4 | 10 | 40 | 1.1747 | 1.1639 | 1.0156 | 1.0159 |
| 5 | 20 | 10 | 1.1420 | 1.1350 | 1.0323 | 1.0330 |
| 6 | 20 | 20 | 1.1417 | 1.1355 | 1.0254 | 1.0260 |
| 7 | 20 | 30 | 1.1414 | 1.1352 | 1.0196 | 1.0200 |
| 8 | 20 | 40 | 1.1438 | 1.1376 | 1.0172 | 1.0176 |
| 9 | 30 | 10 | 1.1186 | 1.1135 | 1.0323 | 1.0331 |
| 10 | 30 | 20 | 1.1205 | 1.1157 | 1.0255 | 1.0260 |
| 11 | 30 | 30 | 1.1199 | 1.1162 | 1.0201 | 1.0205 |
| 12 | 30 | 40 | 1.1213 | 1.1182 | 1.0179 | 1.0184 |
| 13 | 40 | 10 | 1.1044 | 1.0989 | 1.0324 | 1.0331 |
| 14 | 40 | 20 | 1.1080 | 1.1043 | 1.0256 | 1.0262 |
| 15 | 40 | 30 | 1.1084 | 1.1057 | 1.0204 | 1.0209 |
| 16 | 40 | 40 | 1.1097 | 1.1080 | 1.0181 | 1.0186 |
| Rs1 (μm) | Rs2 (μm) | |
|---|---|---|
| k1 (LSCs1a) | 1.1730 | 1.1349 |
| k2 (LSCs1a) | 1.1422 | 1.1354 |
| k3 (LSCs1a) | 1.1201 | 1.1352 |
| k4 (LSCs1a) | 1.1076 | 1.1374 |
| R (LSCs1a) | 0.0654 | 0.0025 |
| k1 (LSCr1b) | 1.1635 | 1.1284 |
| k2 (LSCr1b) | 1.1358 | 1.1296 |
| k3 (LSCr1b) | 1.1159 | 1.1297 |
| k4 (LSCr1b) | 1.1042 | 1.1319 |
| R (LSCr1b) | 0.0593 | 0.0035 |
| k1 (LSCs2p) | 1.0232 | 1.0324 |
| k2 (LSCs2p) | 1.0236 | 1.0255 |
| k3 (LSCs2p) | 1.0240 | 1.0198 |
| k4 (LSCs2p) | 1.0241 | 1.0172 |
| R (LSCs2p) | 0.0009 | 0.0152 |
| k1 (LSCr2p) | 1.0236 | 1.0331 |
| k2 (LSCr2p) | 1.0242 | 1.0261 |
| k3 (LSCr2p) | 1.0245 | 1.0203 |
| k4 (LSCr2p) | 1.0247 | 1.0176 |
| R (LSCr2p) | 0.0011 | 0.0155 |
References
- Wang, C. The effect of planetary gear/star gear on the transmission efficiency of closed differential double helical gear train. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2020, 234, 4215–4223. [Google Scholar] [CrossRef]
- Kuznetsova, N.A.; Tetyushev, A.A.; Shandybina, I.M. Dynamic Model of Differential Closed Planetary Gearing and the Spectrum of its Eigenfrequencies. Chem. Pet. Eng. 2018, 54, 488–492. [Google Scholar] [CrossRef]
- Zhu, Z.; Zhu, R.; Bao, H.; Jin, G. Analysis of dynamic floating displacement of center gear for encased differential planetary train. J. Cent. South Univ. 2012, 43, 497–504. [Google Scholar]
- Zhu, Z.; Zhu, R. Meshing stiffness variation instabilities in encased differential planetary gear train. J. Mech. Eng. 2016, 52, 25–33. [Google Scholar] [CrossRef]
- Zhu, Z.; Cheng, L.; Xu, R.; Zhu, R. Impacts of Backlash on Nonlinear Dynamic Characteristic of Encased Differential Planetary Gear Train. Shock Vib. 2019, 2019, 9347925. [Google Scholar] [CrossRef]
- Zhang, D.; Zhu, R.; Li, M.; Tan, W.; Li, P. Meshing Stiffness Parametric Vibration of Coaxial Contrarotating Encased Differential Gear Train. Math. Probl. Eng. 2021, 2021, 8950945. [Google Scholar] [CrossRef]
- Zhang, D.; Zhu, R.; Fu, B.; Tan, W. Mesh Phase Analysis of Encased Differential Gear Train for Coaxial Twin-Rotor Helicopter. Math. Probl. Eng. 2019, 2019, 8421201. [Google Scholar] [CrossRef]
- Zhang, D.; Zhu, R.; Fu, B.; Tan, W. Modal Properties of Contra-rotating Encased Differential Gear Train Used in Coaxial Helicopter. J. Vib. Eng. Technol. 2020, 8, 799–814. [Google Scholar] [CrossRef]
- Yang, J.; Yue, Y.; Zhu, R.; Chen, W.; Li, M. Dynamic Characteristics of Encased Differential Gear Train with Journal Bearing. Math. Probl. Eng. 2020, 2020, 2436191. [Google Scholar] [CrossRef]
- Yang, J.; Lin, T.; Jiang, L.; Xiang, Y.; Wei, J. Load sharing performance analysis of planetary gear system considering the coupling effects of gear pair and journal bearing. J. Vib. Control 2023, 10775463231177775. [Google Scholar] [CrossRef]
- Ryali, L.; Talbot, D. A dynamic gear load distribution model for epicyclic gear sets with a structurally compliant planet carrier. Mech. Mach. Theory 2023, 181, 105225. [Google Scholar] [CrossRef]
- Che, X.; Zhu, R. Dynamic behavior analysis of planetary gear transmission system with bolt constraint of the flexible ring gear. Meccanica 2023, 58, 1173–1204. [Google Scholar] [CrossRef]
- Zhang, C.; Wei, J.; Niu, R.; Hou, S.; Zhang, S. Similarity and experimental prediction on load sharing performance of planetary gear transmission system. Mech. Mach. Theory 2023, 180, 105163. [Google Scholar] [CrossRef]
- Yoo, H.-G.; Chung, W.-J.; Kim, B.-S.; Park, Y.-J.; Kim, S.-C.; Lee, G.-H. Application of flexible pin for planetary gear set of wind turbine gearbox. Sci. Rep. 2022, 12, 1713. [Google Scholar] [CrossRef] [PubMed]
- Xu, Z.; Yu, W.; Shao, Y.; Yang, X.; Nie, C.; Peng, D. Dynamic modeling of the planetary gear set considering the effects of positioning errors on the mesh position and the corner contact. Nonlinear Dyn. 2022, 109, 1551–1569. [Google Scholar] [CrossRef]
- Zhang, H.; Shang, H.; Yang, C. Influence of floating support on the dynamic characteristics of compound planetary gear set. J. Vibroengineering 2022, 24, 272–289. [Google Scholar] [CrossRef]
- Fang, Y.; Zuo, M.J.; Li, Y. Investigation of Gear Dynamic Characteristics under Stochastic External Excitations. In Proceedings of the 2019 International Conference on Advances in Materials, Mechanical and Manufacturing (AMMM 2019), Beijing, China, 22–24 March 2019; IOP Publishing: Bristol, UK, 2019; Volume 576. [Google Scholar] [CrossRef]
- Diez-Ibarbia, A.; Sanchez-Espiga, J.; Fernandez-Del-Rincon, A.; Calvo-Irisarri, J.; Iglesias, M.; Viadero, F. Probabilistic analysis of the mesh load factor in wind-turbine planetary transmissions: Tooth thickness errors. Mech. Mach. Theory 2023, 185, 105341. [Google Scholar] [CrossRef]
- Jun, Z.; Wei-Min, T.; Qin, C.; Tao, C. Reliability sensitivity analysis of tooth modification on dynamic transmission error of helical planetary gears. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2020, 234, 3903–3918. [Google Scholar] [CrossRef]
- Hajnayeb, A.; Sun, Q. Study of gear pair vibration caused by random manufacturing errors. Arch. Appl. Mech. 2022, 92, 1451–1463. [Google Scholar] [CrossRef]
- Jin, G.H.; Xu, X.T.; Zhu, R.P. Analysis of load sharing mechanism and parameter matching of gear split torque drive system. J. Aerosp. Power 2020, 35, 71–80. [Google Scholar]
- Hu, C.; Geng, G.; Spanos, P.D. Stochastic dynamic load-sharing analysis of the closed differential planetary transmission gear system by the Monte Carlo method. Mech. Mach. Theory 2021, 165, 104420. [Google Scholar] [CrossRef]
- ISO 6336-1; Calculation of Load Capacity of Spur and Helical Gears Part 1: Basie Principles, Introduction and General Influence Factors. ISO: Geneva, Switzerland, 2006.
- Shuai, M.; Ting, Z.; Guo-Guang, J.; Xiao-lin, C.; Han-Jun, G. Analytical investigation on load sharing characteristics of herringbone planetary gear train with flexible support and floating sun gear. Mech. Mach. Theory 2020, 144, 103670. [Google Scholar] [CrossRef]
- Wu, H. Research on the Dynamic Characteristics of Rolling Element Bearings and the Dynamic Model of Bearing Rotor System. Ph.D. Dissertation, East China University of Science and Technology, Shanghai, China, 2011. (In Chinese). [Google Scholar]
- Dong, H.; Zhang, H.Q.; Zhao, X.L.; Duan, L.L. Study on dynamic load-sharing characteristics of face gear dual-power split transmission system with backlash, support and spline clearance. Mech. Sci. 2021, 12, 573–587. [Google Scholar] [CrossRef]
- Zhanfei, S.; Jianxing, Z.; Xiangfeng, Z.; Hong, J.; Yuan, S.; Xu, G. Study on dynamic characteristics of wind turbine planetary gear transmission system considering tooth shape error. Acta Energiae Solaris Sin. 2017, 43, 315. [Google Scholar]
- Li, S.; Wu, S.; Wang, X. Analysis of the Dynamic Load Sharing Characteristic of Two-stage Planetary Transmission. J. Mech. Transm. 2016, 40, 11–16. [Google Scholar]
- Li, X. Nonlinear Dynamic Modeling and Comprehensive Performance Optimization Design for NW Wind Turbine Gearbox. Ph.D. Dissertation, Dalian University of Technology, Dalian, China, 2018. (In Chinese). [Google Scholar]
- Guan, P.; DeSmidt, H.A. Passive suppression of planetary gear transmission vibration via discrete boundary struts. In Proceedings of the AHS 72nd Annual Forum, West Palm Beach, FL, USA, 17–19 May 2016. [Google Scholar]
- Wang, C.L.; Wei, J.; Wu, Z.H.; Lu, L.; Gao, H. Load sharing performance of herringbone planetary gear system with flexible pin. Int. J. Precis. Eng. Manuf. 2019, 20, 2155–2169. [Google Scholar] [CrossRef]
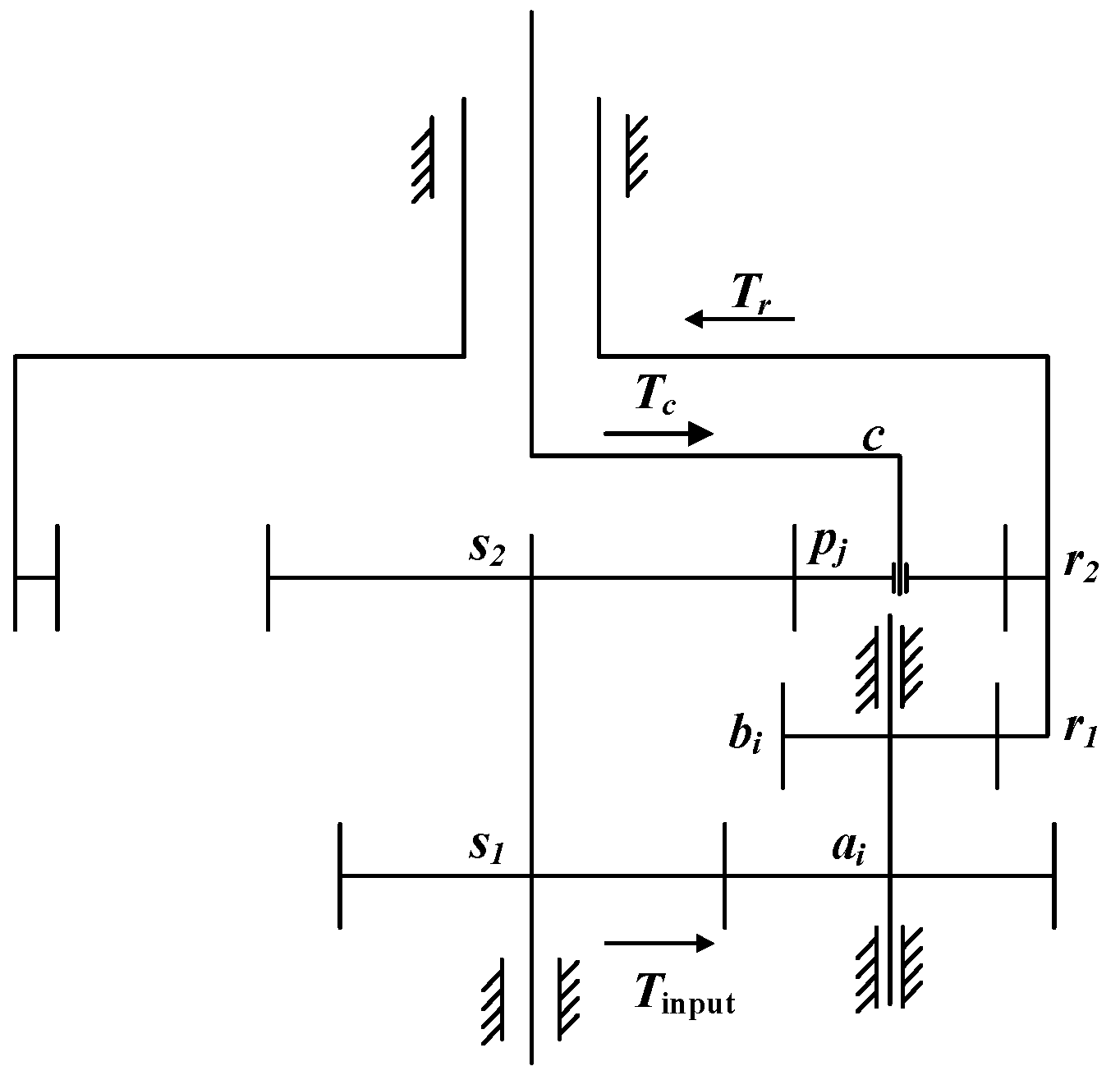
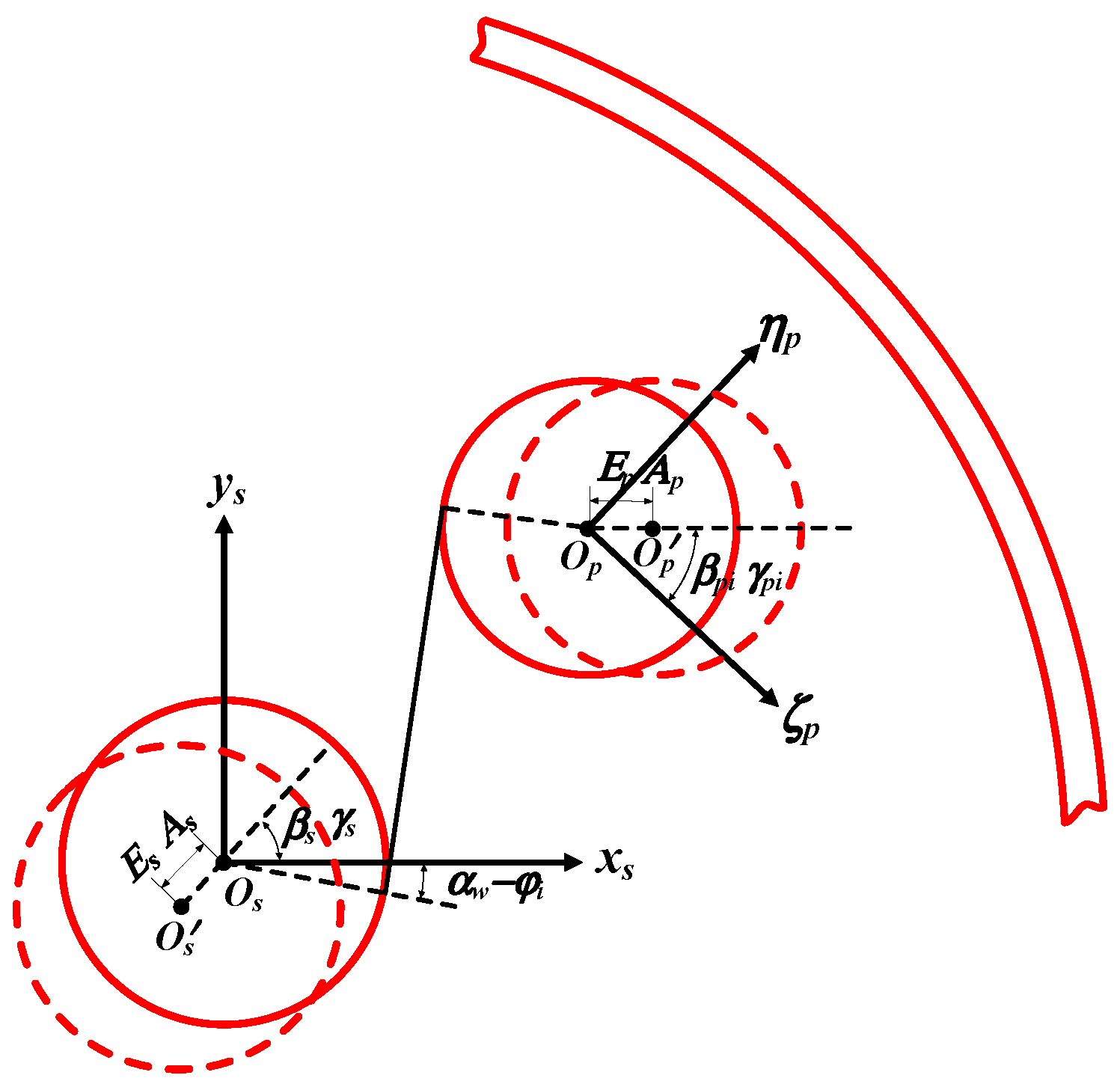
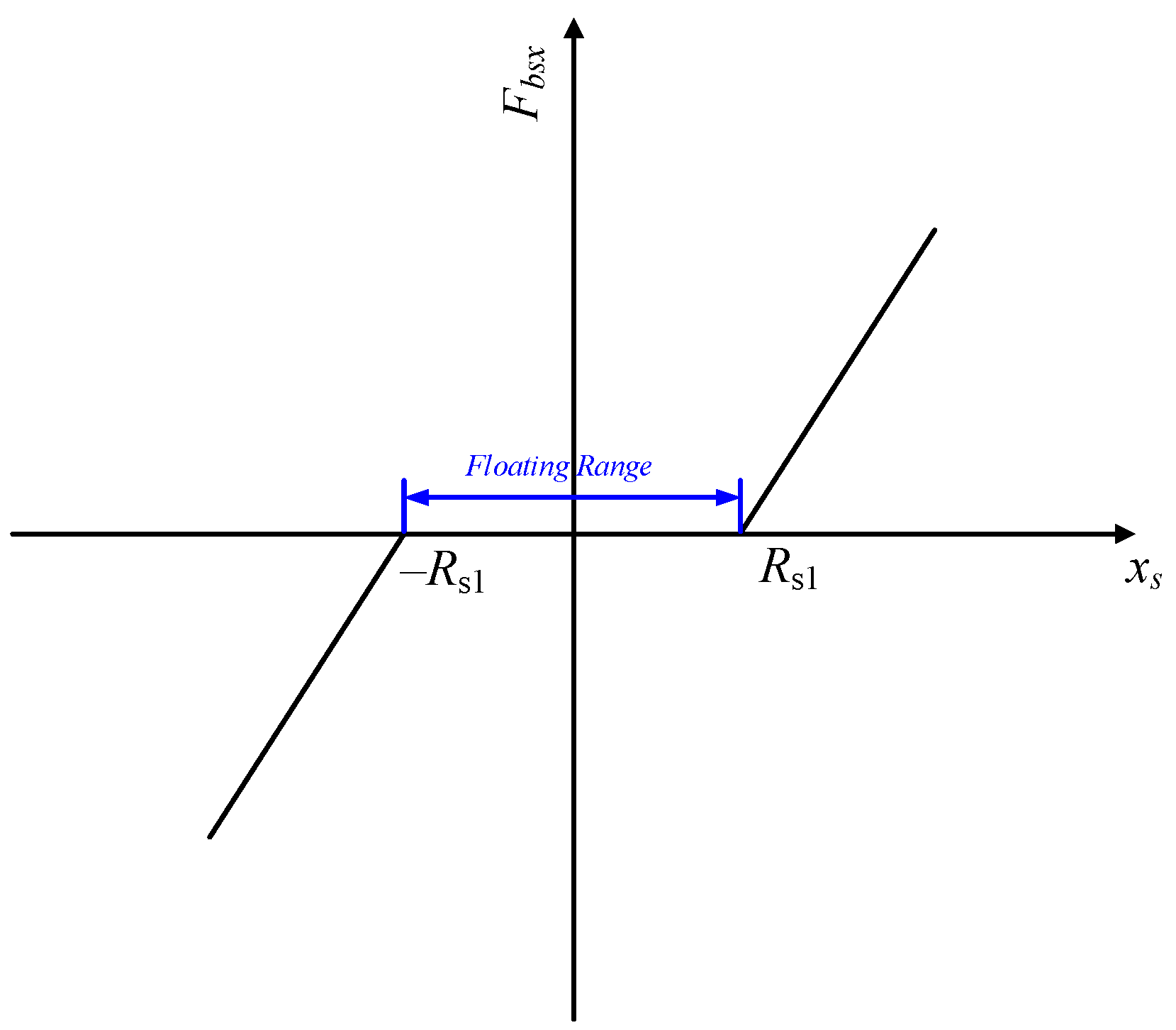
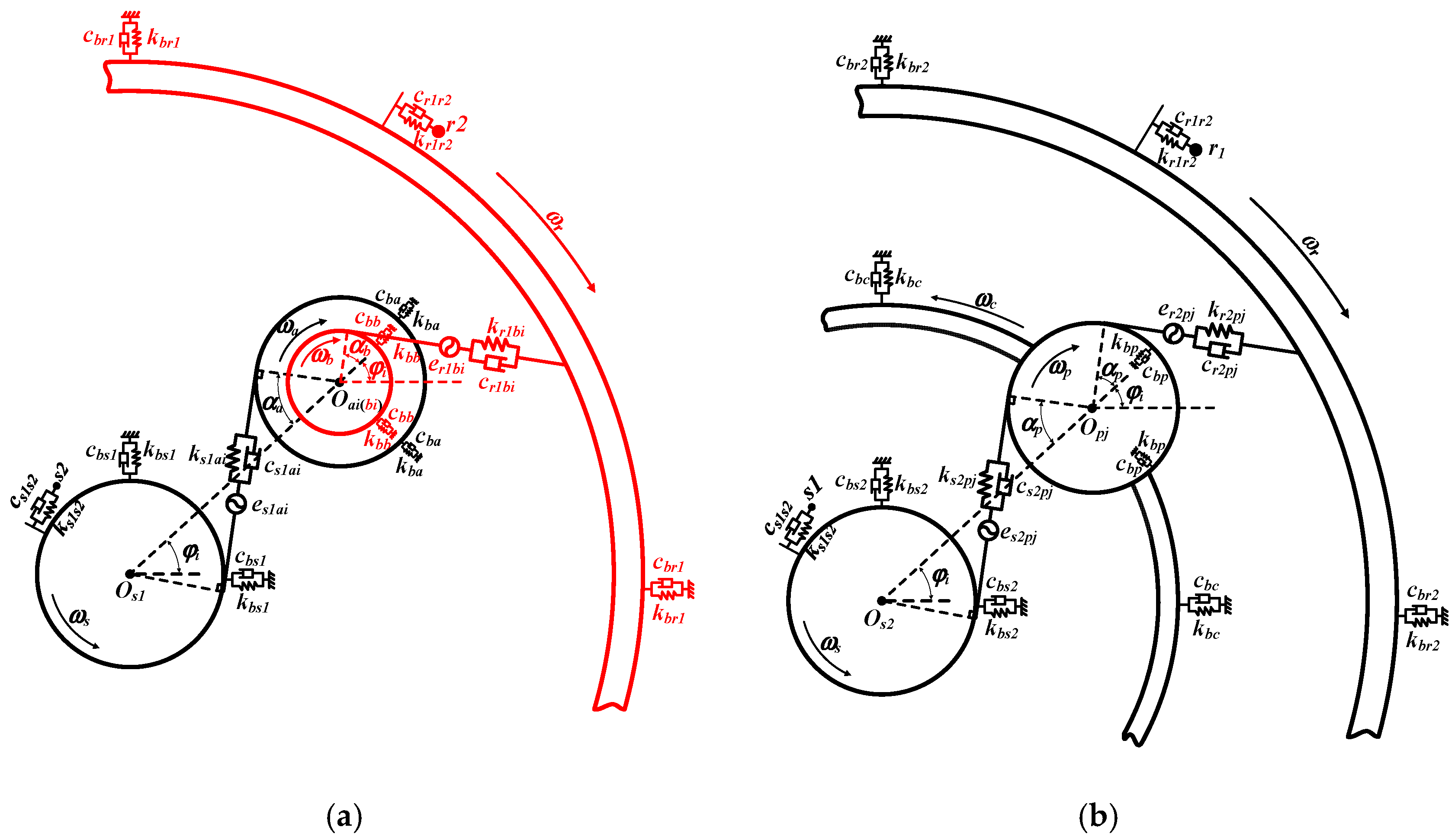


| Component | Tooth Number | Module/mm | Pressure Angle/° | Modification Coefficient |
|---|---|---|---|---|
| s1 | 57 | 2.75 | 20 | 0.4618 |
| a | 54 | 2.75 | 20 | 0.45 |
| b | 18 | 3.5 | 20 | 0.5038 |
| r1 | 107 | 3.5 | 20 | 0.2935 |
| s2 | 38 | 4 | 20 | 0 |
| p | 25 | 4 | 20 | 0 |
| r2 | 88 | 4 | 20 | 0 |
| Dynamic Parameter | Value |
|---|---|
| Support stiffness (N/m) | ks = 3.5 × 108, ka = 2.6 × 108, kb = 3.5 × 108, kp = 5.2 × 108, kr = 6.2 × 108 |
| Torsional stiffness (Nm/rad) | kts12 = 2.4 × 106, ktab = 8.5 × 105, ktr12 = 5.7 × 108 |
| Radial coupling stiffness (N/m) | krs12 = 2.1 × 108, krab = 1.8 × 109, krr12 = 6.2 × 1010 |
| Grade 4 | Grade 6 | |||
|---|---|---|---|---|
| E/mm | A/mm | E/mm | A/mm | |
| Sun gear | 8 | 8 | 16 | 19 |
| Star gear/planetary gear | 8 | 8 | 16 | 19 |
| Inner ring gear | 10 | 8 | 21 | 19 |
| Number | A | B | C | D |
|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 1 |
| 2 | 1 | 2 | 3 | 4 |
| 3 | 1 | 3 | 5 | 2 |
| 4 | 1 | 4 | 2 | 5 |
| 5 | 1 | 5 | 4 | 3 |
| 6 | 2 | 1 | 5 | 4 |
| 7 | 2 | 2 | 2 | 2 |
| 8 | 2 | 3 | 4 | 5 |
| 9 | 2 | 4 | 1 | 3 |
| 10 | 2 | 5 | 3 | 1 |
| 11 | 3 | 1 | 4 | 2 |
| 12 | 3 | 2 | 1 | 5 |
| 13 | 3 | 3 | 3 | 3 |
| 14 | 3 | 4 | 5 | 1 |
| 15 | 3 | 5 | 2 | 4 |
| 16 | 4 | 1 | 3 | 5 |
| 17 | 4 | 2 | 5 | 3 |
| 18 | 4 | 3 | 2 | 1 |
| 19 | 4 | 4 | 4 | 4 |
| 20 | 4 | 5 | 1 | 2 |
| 21 | 5 | 1 | 2 | 3 |
| 22 | 5 | 2 | 4 | 1 |
| 23 | 5 | 3 | 1 | 4 |
| 24 | 5 | 4 | 3 | 2 |
| 25 | 5 | 5 | 5 | 5 |
| Number | A | B |
|---|---|---|
| 1 | 1 | 1 |
| 2 | 1 | 2 |
| 3 | 1 | 3 |
| 4 | 1 | 4 |
| 5 | 2 | 1 |
| 6 | 2 | 2 |
| 7 | 2 | 3 |
| 8 | 2 | 4 |
| 9 | 3 | 1 |
| 10 | 3 | 2 |
| 11 | 3 | 3 |
| 12 | 3 | 4 |
| 13 | 4 | 1 |
| 14 | 4 | 2 |
| 15 | 4 | 3 |
| 16 | 4 | 4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Che, X.; Zhu, R. Effect of Floating Support Parameters on the Load-Sharing Performance of EDPGS Based on Mathematical Statistical Methods. Machines 2024, 12, 247. https://doi.org/10.3390/machines12040247
Che X, Zhu R. Effect of Floating Support Parameters on the Load-Sharing Performance of EDPGS Based on Mathematical Statistical Methods. Machines. 2024; 12(4):247. https://doi.org/10.3390/machines12040247
Chicago/Turabian StyleChe, Xiaoyu, and Rupeng Zhu. 2024. "Effect of Floating Support Parameters on the Load-Sharing Performance of EDPGS Based on Mathematical Statistical Methods" Machines 12, no. 4: 247. https://doi.org/10.3390/machines12040247
APA StyleChe, X., & Zhu, R. (2024). Effect of Floating Support Parameters on the Load-Sharing Performance of EDPGS Based on Mathematical Statistical Methods. Machines, 12(4), 247. https://doi.org/10.3390/machines12040247






