Underwater Low-Frequency Acoustic Wave Detection Based on a High-Q CaF₂ Resonator

Abstract

Whispering gallery mode (WGM) resonators with an ultra-high quality (Q) factor provide a new idea for high-precision underwater acoustic sensing. However, acoustic energy loss due to watertight encapsulation has become an urgent problem for its underwater application. In order to solve this problem, this paper proposes a hollowed-out array structure. The finite element simulation shows that the acoustic wave transmission loss is improved by 30 dB compared with that of the flat plate encapsulation structure. Using a calcium fluoride (CaF₂) resonator with a Q factor of 1.2 × 10⁸ as an acoustic sensitive unit, the amplitude and frequency of the loaded acoustic wave are retrieved by means of the dispersion coupling response mechanism. The resonator’s underwater experimental test range is 100 Hz–1 kHz, its acoustic sensing sensitivity level reaches −176.3 dB re 1 V/µPa @ 300 Hz, and its minimum detectable pressure can be up to 0.87 mPa/Hz^1/2, which corresponds to a noise-equivalent pressure (NEP) of up to 58 dB re 1 µPa/Hz^1/2.

1. Introduction

Hydrophones play an important role in seabed exploration [1], underwater ranging [2], underwater localization and rescue [3], and environmental monitoring [4]. Compared with traditional micro-electro-mechanical system (MEMS) hydrophones, optical hydrophones have a higher underwater acoustic sensitivity and are less susceptible to electromagnetic interference [5]. Cavity optomechanical systems have received increasing attention among various optical acoustic sensors due to their high sensitivity, wide bandwidth, low power consumption, and chip-level integration. In cavity optomechanical systems, the strain induced by the acoustic wave, and hence the refractive index change or shape deformation, is converted into a change in the intensity of the detectable light or the spectral properties of the device [6]. Therefore, cavity optomechanical systems are ideal sensing platforms for realizing acoustic wave conversion and hold significant promise for acoustic sensing applications [7,8].

Low-frequency acoustic signals with low transmission loss in water can be transmitted over long distances and are important signals for marine applications, such as environmental awareness, target monitoring, resource exploration, and information collection [9]. Whispering gallery mode (WGM) resonators are characterized by their small size [10] and high-quality (Q) factor [11], which can effectively capture underwater acoustic waves as the sensitive element of the cavity optomechanical system and can also make the whole underwater sensing structure more compact. The WGM resonator binds the photons inside the cavity, causing them to continuously circulate inside the cavity and thus accumulate energy [12]. Its inherent high Q factor makes the photons circulate inside the cavity for a longer period, thus enhancing the light–matter interaction [13,14,15]. In recent years, WGM resonators have been rapidly developed in the field of acoustic sensing, and a variety of acoustic sensors with excellent performance have emerged.

In 2019, Hao Chen et al. fabricated a ring-structured underwater acoustic resonator with a Q value of up to 10⁴ using a tapered optical fiber with a size of about 200 μm. They performed underwater high-frequency acoustic measurements using a simple spectral side-filtering technique, and the test results showed that the resonator could operate over a range of 3–6 MHz [16]. In 2020, Ke Huang et al. proposed a microdisk resonator for underwater acoustic signal detection and processing, extending the application of cavity optomechanical systems for underwater acoustic wave detection [17]. In 2023, Jialve Sun et al. performed ultrasonic sensing using an optical WGM polymer microcavity coupled to a microprobe formed by a u-type microfiber with a Q factor of up to 10⁶ and achieved a noise equivalent pressure (NEP) of 1.07 mPa/Hz^1/2; the broadband response was 150 MHz with a large detection angle of 180° [18]. The emergence of these sensors has extended the range of acoustic sensing applications of WGM optical resonant cavities. However, most of the microresonator-based acoustic sensors use a microring or microdisk, in which case the complex production process and the requirement for nanoimprinting systems increase the cost of device fabrication [15], and most of the signal bands investigated by these microresonators focus on high-frequency signals. There is still little research on the use of cavity optomechanical systems to detect underwater low-frequency acoustic signals.

This paper reports on an underwater low-frequency acoustic sensor based on a calcium fluoride (CaF₂) optical resonator. The sensor consists of a WGM CaF₂ optical resonator coupled with a tapered optical fiber and uses a novel hollowed-out array package structure, which increases the acoustic transmittance by 30 dB compared to flat-panel packages. The sensor operates on the principle that acoustic pressure is applied to the CaF₂ resonator, which deforms and changes its refractive index and radius to affect the resonance wavelength. When the resonator is deformed by pressure, the change in the resonance wavelength changes the strength of the transmitted field through the resonator. Thus, the acoustic signal can be demodulated by detecting the intensity of the reflected light. We performed finite element simulations and experimental verification of the sensor performance. The test results show that the acoustic pressure sensitivity of the sensor is up to 0.92 mV/Pa, with a sensitivity level of −176.3 dB re 1 V/μPa at 300 Hz, and the minimum detectable pressure (MDP) is 0.87 mPa/Hz^1/2, which corresponds to an NEP of up to 58 dB re 1 µPa/Hz^1/2.

2. Theoretical Analysis and Discussion

The CaF₂ resonator consists of a CaF₂ cavity and a tapered optical fiber. In the CaF₂ resonator, the tapered optical fiber acts as a straight waveguide to couple light into the CaF₂ cavity and circulate it along the equatorial wall of the CaF₂ cavity, allowing the photons to move in the optical path for a longer time. The resonant wavelength of the CaF₂ resonator can be deduced from the standing wave condition of the WGM mode:

$$\mathrm{m}\lambda =2\pi nR$$

(1)

where n and R are the effective refractive index and radius of the CaF₂ resonator, respectively, and m is the order of the resonant mode. Changes in both R and n of the CaF₂ resonator cause a resonance wavelength (λ) shift [19], which can be expressed by Equation (2):

$$\frac{∆\lambda }{\lambda }=\frac{∆\mathrm{n}}{n}+\frac{∆R}{R}$$

(2)

In an acoustic sensing system with a CaF₂ resonator as the sensitive unit, the external acoustic pressure induces mechanical deformation of the resonator, with a consequent change in the radius and effective refractive index of the resonator [20], leading to resonance shifts. In this case, the change in refractive index is the change in the relative refractive index caused by the elastic–optical effect. The sensitivity of an underwater acoustic sensor based on the WGM can be expressed as [21]:

$$S=\frac{dT}{dP}=\frac{dT}{d\lambda }\frac{d\lambda }{dP}$$

(3)

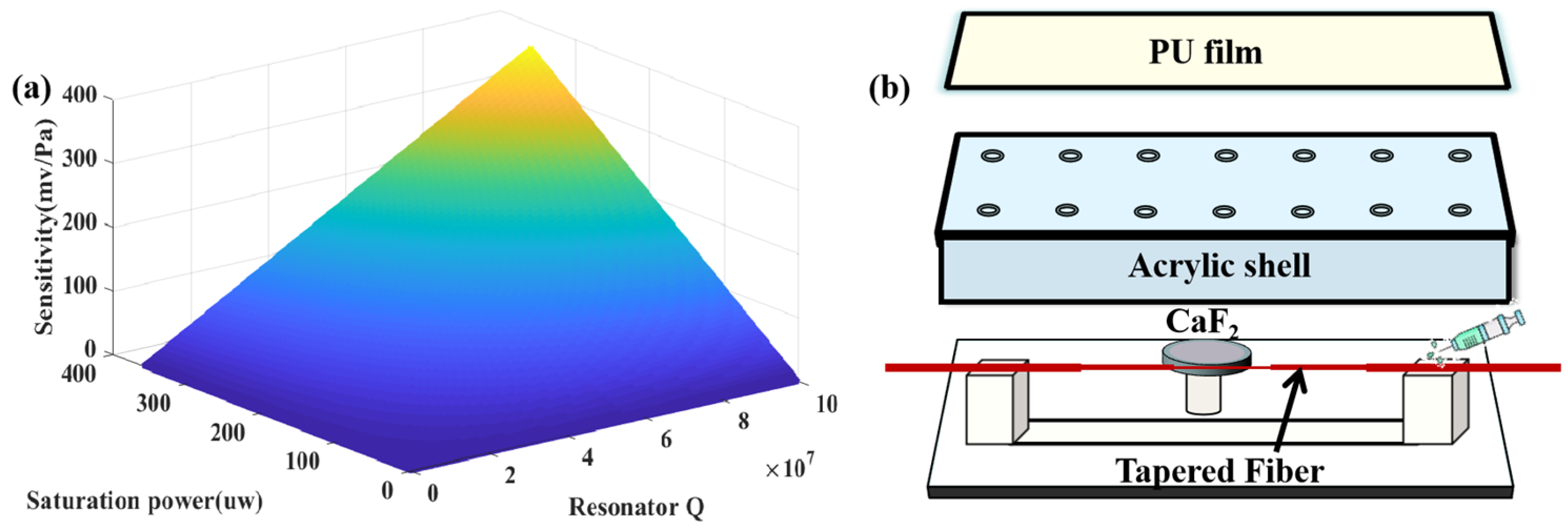
Here, T is the transmission spectrum of the resonator, and P is the underwater acoustic pressure. dT/dλ denotes the slope of the transmission spectrum, which is proportional to the Q-factor of the resonator, indicating that the higher the Q-factor, the higher the S. dλ/dP is the resonance wavelength shift caused by the change in the R and n of the resonator in response to the acoustic pressure. Figure 1a shows the cloud plot of the acoustic sensor sensitivity distribution when the nonresonant laser output is 0–360 μW and the calcium fluoride resonator Q has 0–1 × 10⁸ magnitude.

The tapered optical fiber itself is fragile and highly susceptible to interference from the aqueous environment that leads to changes in the coupling state of the resonator, so a coupling encapsulation of the resonator system is required. There are two common resonator encapsulation methods [22]: the full package fixation method and the point package fixation method. The full package fixation method utilizes UV glue with a low refractive index to wrap the resonator coupling system, which can effectively isolate the influence of the external environment on the coupling state. However, the UV glue may reduce the Q factor of the resonator during the injection and curing process, and the expansion of the UV glue itself will also change the original coupling state. Using the point encapsulation fixation method [23], only the contact area between the tapered fiber and the resonator needs to be fixed, but its stability is far less than that of full encapsulation fixation.

Compared with the above encapsulation methods, we used a new encapsulation method, and the encapsulation schematic is shown in Figure 1b. The tapered optical fiber was straightened and attached to the processed fiber holder, the resonant cavity was coupled with the tapered optical fiber by adjusting the three-dimensional precision displacement stage, and the coupling system was fixed by using UV glue. The whole resonator system was isolated from the outside world by using an acrylic encapsulation shell. The acoustic permeability of the encapsulation shell is extremely important for the CaF₂ resonator acoustic sensing system [24]. Since the acoustic impedance of the acrylic shell does not match the acoustic impedance of water, the acoustic transmissive cap of the hydrophone is usually made of acoustically transmissive polyurethane material. Therefore, we punched holes in the upper surface of the customized acrylic shell and added a layer of acoustically transmissive waterproof polyurethane film on the upper surface of the punched holes. This film prevents water from destroying the coupling state of the resonator and also reduces the blocking of underwater sound by the encapsulated shell.

We used Comsol finite element software to analyze the sound transmission effects of acrylic encapsulation shells and acrylic encapsulation shells with perforations on the upper surface plus thermoplastic urethane (TPU) film. Sound transmission effects can be compared by using the sound transmission loss (STL). The STL is the logarithmic ratio of the total incident power in the sound field (P_in) to the total transmitted power in the sound field (P_tr) of the structure, expressed as [25]:

$$STL=10{\log }_{10}\frac{P_{in}}{P_{tr}}$$

(4)

Therefore, the lower the acoustic transmission loss, the better the sound transmission of the structure. Referring to Figure 1 to establish the simulation model, the sound source field, as an ideal diffusion field, is placed directly above the encapsulation shell, and the sound wave passes through the encapsulation shell and is then transmitted to the ideal anechoic field by the air layer to avoid the error caused by sound-wave reflections. The acrylic encapsulation shell used in the simulation is 2 mm thick, 25.4 mm wide, and 76.2 mm long, and for the perforated encapsulation scheme, the array of holes is 3 × 12, and the radius of each hole, which runs completely through the entire acrylic shell, is set to 1 mm. The thickness of the polyurethane film on the upper surface of the acrylic shell is 0.1 mm, and the sound intensity and the STL of the two structures are simulated by applying an acoustic pressure of 1 Pa using the acoustic–solid coupling module in the frequency domain of the finite element software [25,26,27].

From the simulation results obtained in Figure 2a, the sound intensity of the perforated structure is three orders of magnitude higher than that of the unpunched structure. After fitting the simulated data, it can be seen from Figure 2a that the sound loss of the single acrylic shell is significantly higher than that of the shell coated with 30 dB perforated polyurethane film. This indicates that the scheme of the acrylic shell perforated with an acoustically transmissive film applied to it transmits the sound better.

To investigate the effect of acoustic signals of different frequencies on disk deformation, we simulated in detail a CaF₂ resonator with a perforated encapsulation structure. The resonator was tightly coupled to the support post, the tapered optical fiber, and the encapsulated shell. The CaF₂ resonator system was wrapped by an air layer, and the whole was encapsulated by the proposed arrayed acrylic shell encapsulation structure. The model was placed in the water, and the system was studied using the frequency domain acoustic–solid coupling module. Through the pressure acoustics module, a fixed-position acoustic source was generated 40 mm directly above the encapsulation shell, and an acoustic pressure of 1 Pa was applied to the top of the encapsulation shell in the form of a plane wave. At the same time, the solid mechanics module imposed a fixed constraint on the bottom of the encapsulated shell. Given that the entire resonator was located in the air domain, a minimum grid size of one-sixth of the air sound velocity divided by the maximum frequency of the simulation was used for rational meshing. This simulation model helps us gain a deeper understanding of the effect of acoustic signal frequency on the deformation of the CaF₂ resonator system.

The deformation curves of CaF₂ resonators with different radii at 1 Pa sound pressure are simulated and analyzed in Figure 2b. It can be seen that the larger the radius of the CaF₂ resonator, the larger the deformation of the signal subjected to sound pressure. This means that the subsequent optimization of the sensitivity can be carried out by changing the size and dimensions of the CaF₂ resonator. The parameters used in the simulation are shown in the following

Table 1. Parameters used in the simulation.

Property	Value
Poisson Ratio of CaF2	0.26
Young’s Modulus of CaF2	75.8 [GPa]
Poisson Ratio of TPU	0.42
Young’s Modulus of TPU	62.5 [MPa]
Poisson Ratio of acrylic	0.35
Young’s Modulus of acrylic	3.5 [GPa]

.

3. Result

Experimental Validation

The CaF₂ resonator with a radius of 5 mm and a thickness of 0.5 mm was prepared by single-point diamond cutting and mechanical polishing, as shown in the inset of Figure 3a. We encapsulated the CaF₂ resonator according to the package scheme shown in Figure 1. Tested by the linewidth method, the device exhibited a high Q-factor (1.2 × 10⁸) and remained highly stable under normal atmospheric conditions. Figure 3a shows the scanning transmission spectrum of the packaged CaF₂ resonator. Figure 3b shows the packaged CaF₂ resonator.

The experimental setup for underwater testing is shown in Figure 4. A narrow linewidth (<200 kHz) tunable laser (Toptica laser) with a wavelength of 1550 nm is used to emit the detection light, and an isolator is added between the laser and the subsequent optical path to prevent the laser from entering the laser in the reverse direction. The optical signal from the laser is attenuated and passes through the polarization controller into the CaF₂ resonator fiber optic coupling system. The optical signal from the resonator system is divided into two photodetectors to convert the optical signal into an electrical signal, one of which will be connected back to the laser through Pound–Drever–Hall (PDH) frequency-locked technology to regulate the laser frequency to the resonance frequency of the WGM in real time. The other is connected to a frequency spectrometer and an oscilloscope for real-time observation of the underwater test signals of the CaF₂ resonator system. A function generator is utilized to perform laser frequency sweeps to help find the high-Q spectral lines in the resonant cavity. The sound source used for the underwater test is placed at the bottom of a cylindrical tank, and the source signal is given by a signal generator through a power amplifier. The hydrophone to be tested is placed at the same height underwater as the standard hydrophone, and the frequency of the signal generator is adjusted so that the source emits a standard sinusoidal acoustic signal at different frequencies. At the same time, the voltage signal of the standard hydrophone is connected to an oscilloscope and a spectrometer to observe the changes due to the acoustic signal, and the signals in the frequency and time domains of the hydrophone to be tested and the standard hydrophone at 100 Hz–1 kHz are recorded.

4. Experimental Results and Discussion

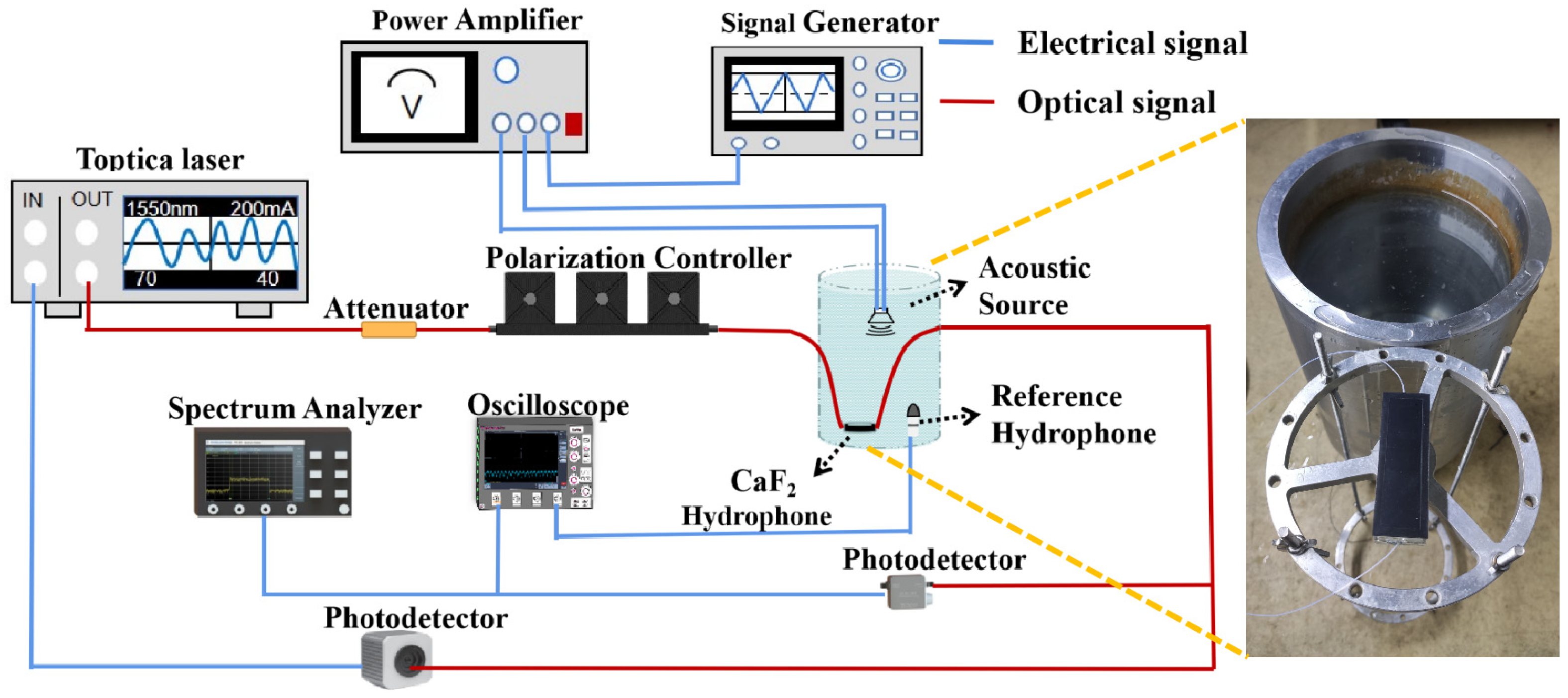
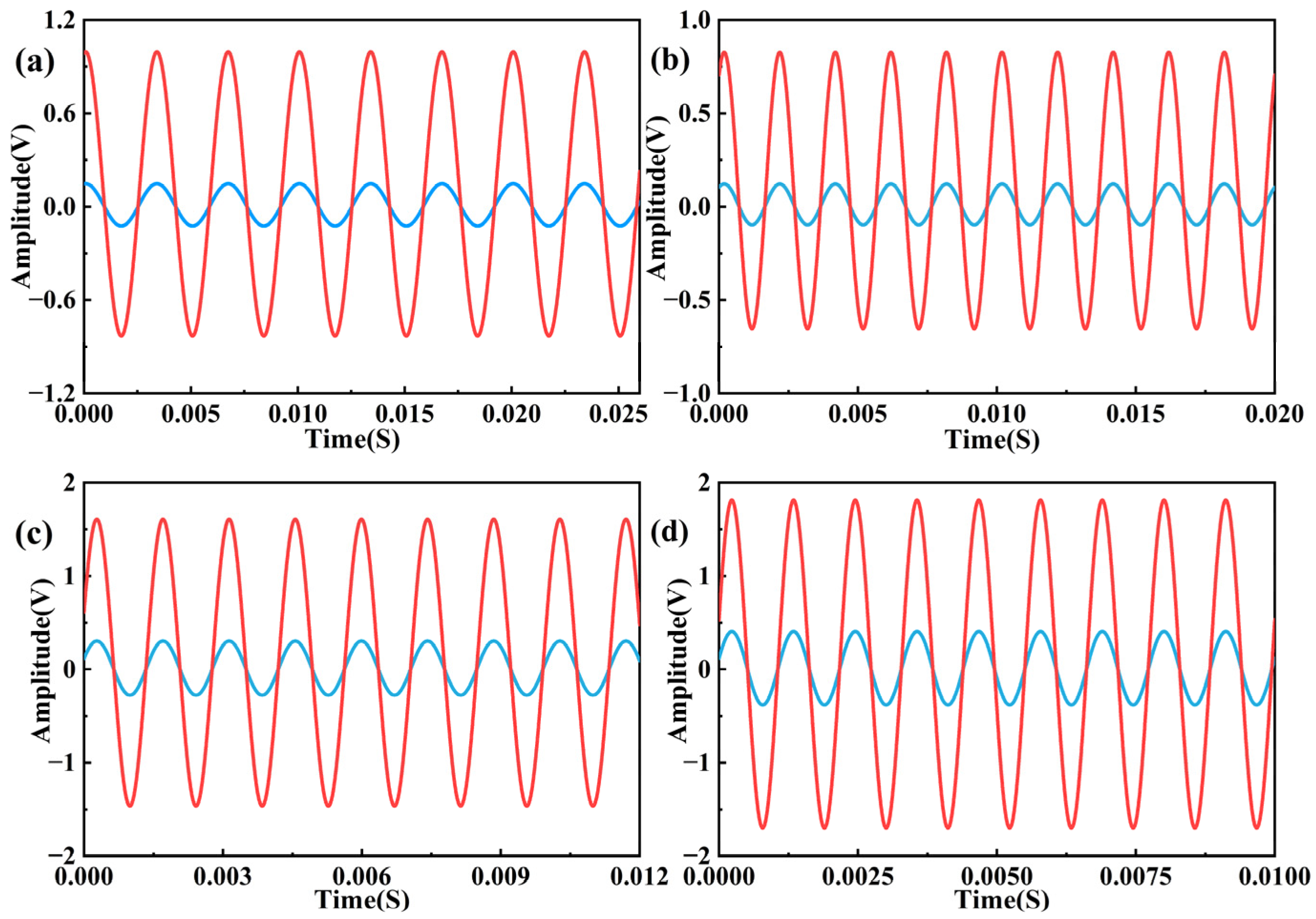
Experiments are conducted using standard sinusoidal sound pressure signals at different frequencies to test the temporal response of CaF₂ resonator hydrophones. At each single test frequency, the amplitude of the sinusoidal sound pressure signal output from a standard sound source is adjusted to an appropriate value and kept constant. The experimental results show that the CaF₂ resonator hydrophone is effective over the entire frequency range tested, with the time response results at several representative frequencies of the CaF₂ resonator hydrophone shown in Figure 5. 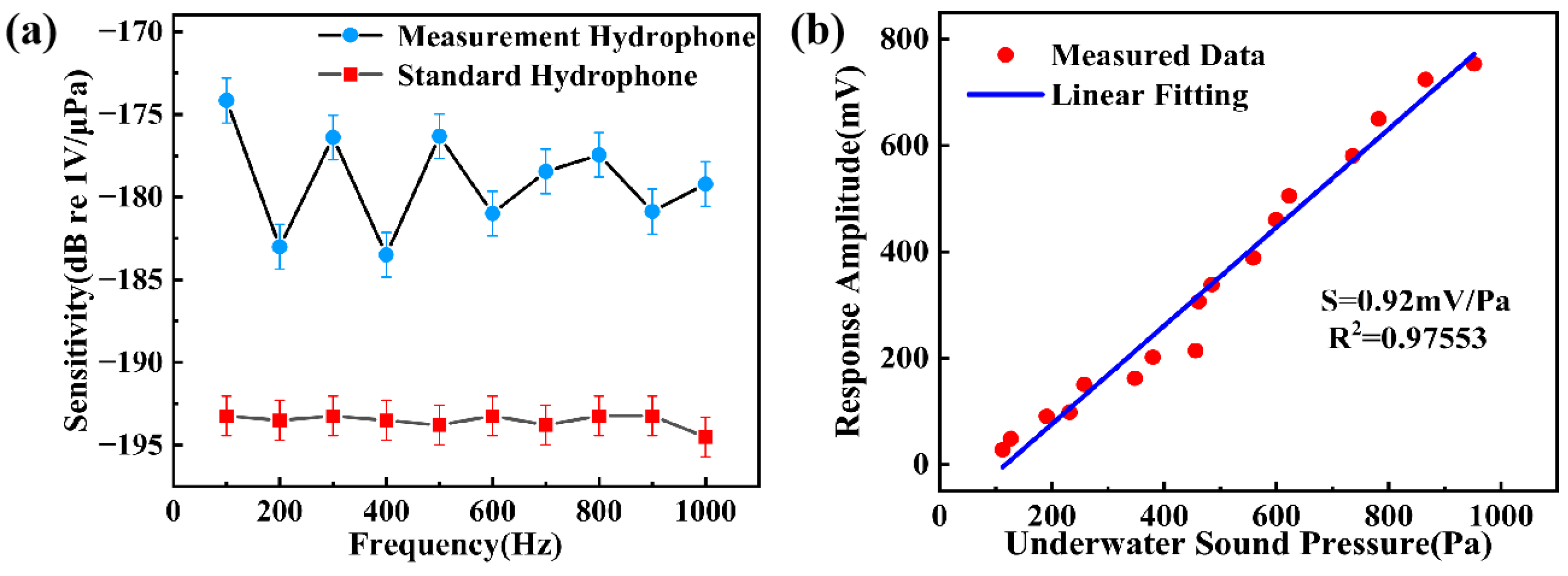The differences in signal amplitudes at the four frequency points in Figure 5 are due to the different amplitudes of the sound pressure signals used for the tests at each frequency point. The standard hydrophone used in the experiment is the RHS-30 manufactured by Hangzhou Maihuang Technology Limited (Hangzhou, China), which is a broadband standard piezoelectric ceramic hydrophone.

The sensitivity level of the standard hydrophone used in the experiments is −193 dB re 1 V/μPa, and the sensitivity level of the hydrophone to be tested is calculated as follows: S = 20 log₁₀(U₁/U₂) − 193 dB, where U₁ and U₂ are the output voltages of the hydrophone to be tested and the standard hydrophone, respectively, when the same sound pressure signal is applied. After testing, the proposed resonator hydrophone had a test sensitivity level of −174 dB–−183 dB re 1 V/μPa, as shown in Figure 6a. The results show that the sensitivity level of the resonator hydrophone is −176.4 dB @ 300 Hz, which is 16.6 dB higher than that of the standard hydrophone. The acoustic pressure of the hydrophone to be tested underwater can be obtained by dividing the RMS value of the voltage of the standard hydrophone at the same moment by the voltage sensitivity of the standard hydrophone and the gain multiplier of the standard hydrophone. We used a standard hydrophone with a voltage sensitivity of 0.22 mV/Pa and a gain multiplier of 10. By fitting the data obtained from the tests, we obtained a sensitivity of 0.92 mV/Pa for the resonator-type hydrophone, as shown in Figure 6b.

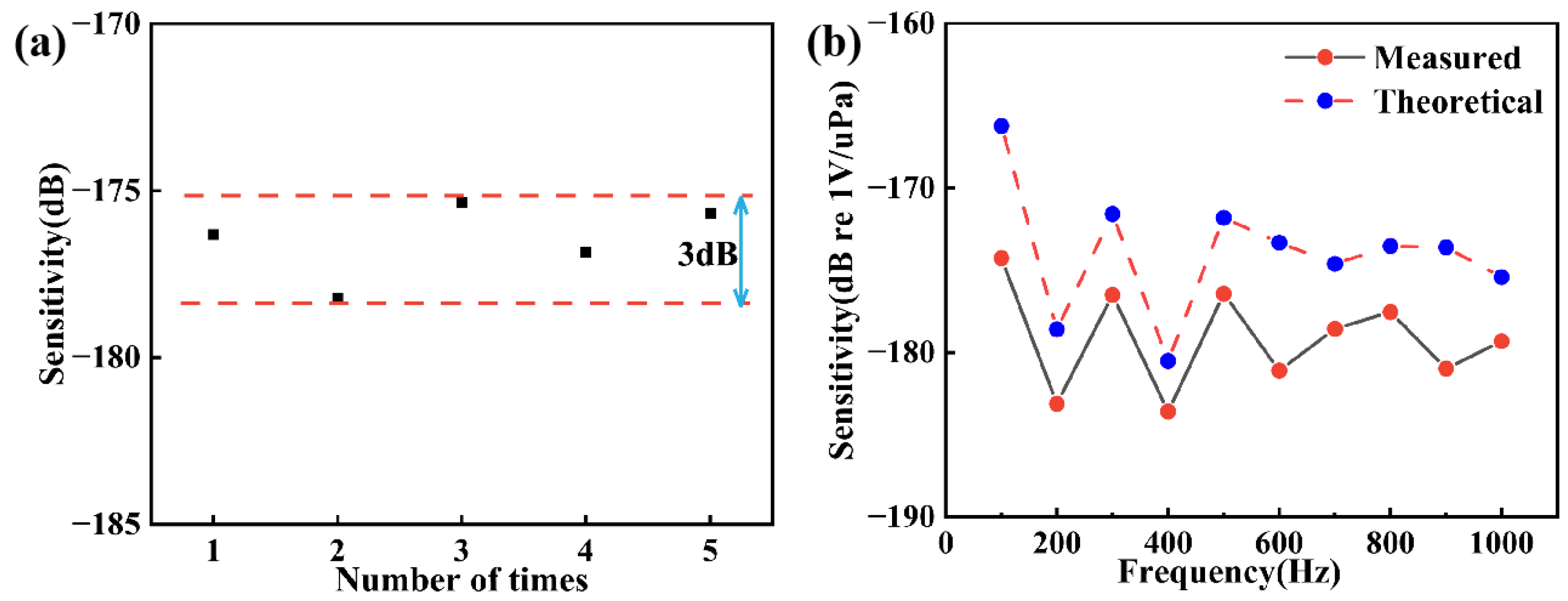
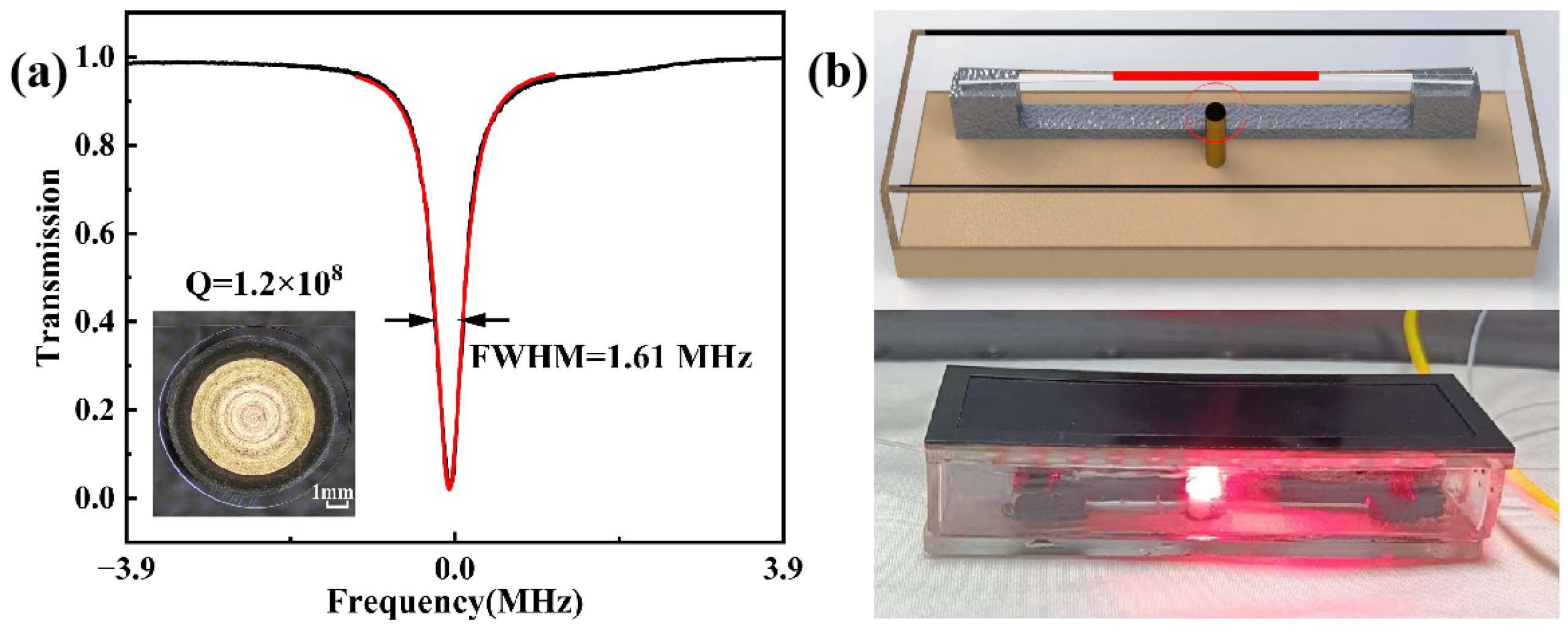
To verify the stability of the sensor, we repeated the experiments on the hydroacoustic sensor at different times, and the fluctuation of the sensitivity level during the experiments may have been caused by the fluctuation of the experimental ambient noise and the instability of the frequency locking system. As shown in Figure 7a, the experimental sensitivity level at 300 Hz fluctuates within a range of 3 dB, and the theoretical acoustic sensing sensitivity at a Q-value of 1.2 × 10⁸ is calculated based on Equation (3) and the shape variables obtained from the simulation with a resonator radius of 5 mm. As shown in Figure 7b, the experimental results are in good agreement with the theoretical values. There is still a gap between the theoretical sensitivity and the experimental data. We believe that there are two main reasons for this phenomenon. The first is that the material of the CaF₂ has a high Young’s modulus, which leads to insensitivity to acoustic signals of a certain frequency, resulting in a gap between the experimental results and the theory. The second reason is the response speed of the lock-in amplifier module and the proportional–integral module, which is also one of the factors affecting the sensitivity of the sensor.

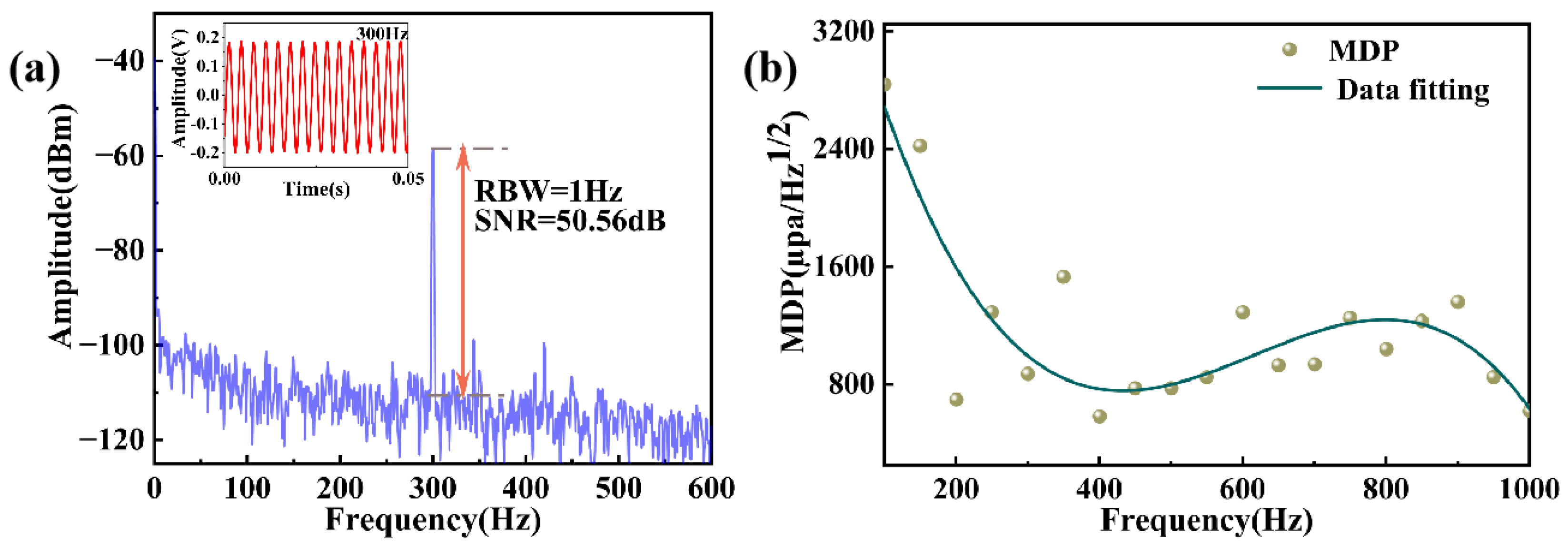
The signal-to-noise ratio (SNR) of the hydrophone is defined as the amplitude of the received signal at the resonant frequency of the hydrophone when an excitation signal is input into the sensor divided by the amplitude when there is no excitation voltage. As the excitation voltage to the sensor increases, the transmitted signal increases, and the signal-to-noise ratio increases. Figure 8a demonstrates the SNR of the hydrophone to be tested at 300 Hz for an acoustic pressure of 500 Pa with a value of 50.56 dB. For all acoustic frequencies tested, the SNR of the CaF₂ resonator hydrophone exceeded 18 dB. These results strongly suggest that the proposed hydrophone device is capable of effectively detecting low-frequency acoustic signals. The noise equivalent pressure (NEP) spectral level of the hydrophone reflects the minimum measurable sound pressure level of the hydrophone, which is the ability of the system to recognize the MDP and is also the lower limit of the dynamic range in the dynamic range test. We measured the phase noise of the entire system when no excitation signal was applied and derived the MDP at 300 Hz to be 0.87 mPa/Hz^1/2 by dividing the system phase noise by the sound pressure sensitivity over the entire measured frequency band [28], which corresponds to an NEP of 58 dB for a sound pressure of 1 µPa/Hz^1/2 in the reference water. This indicates that the fabricated CaF₂ resonator has a very low NEP. Figure 8b shows the MDP versus the frequency for the CaF₂ resonator hydrophone.

5. Conclusions

In this article, we fabricated and tested a hydroacoustic sensor based on a WGM CaF₂ optical crystal resonator in a hollowed array package structure. The characteristics of the hydroacoustic sensor fabricated using this structure were analyzed using finite element software. The simulation results show that a package structure with hollowed-out holes at the top of the housing can effectively reduce acoustic wave loss. The sensor has a sensitivity level of −176.4 dB re 1 V/µPa at 1550 nm wavelength at 300 Hz, and an MDP of 0.87 mPa/Hz^1/2 is obtained at 300 Hz, which corresponds to an NEP of up to 58 dB re 1 µPa/Hz^1/2. The response of the whole system matches well with the trend of the theoretical simulation results and verifies that the acoustic field changes with the regularity of the acoustic field change. In addition, the sensitivity of this hydroacoustic sensor can be further improved by optimizing the Q-factor and size parameters of the resonator.