Various Feature-Based Series Direct Current Arc Fault Detection Methods Using Intelligence Learning Models and Diverse Domain Exclusion Techniques
Abstract
1. Introduction
2. Hardware Specifications and Data Processing
2.1. Hardware Specifications
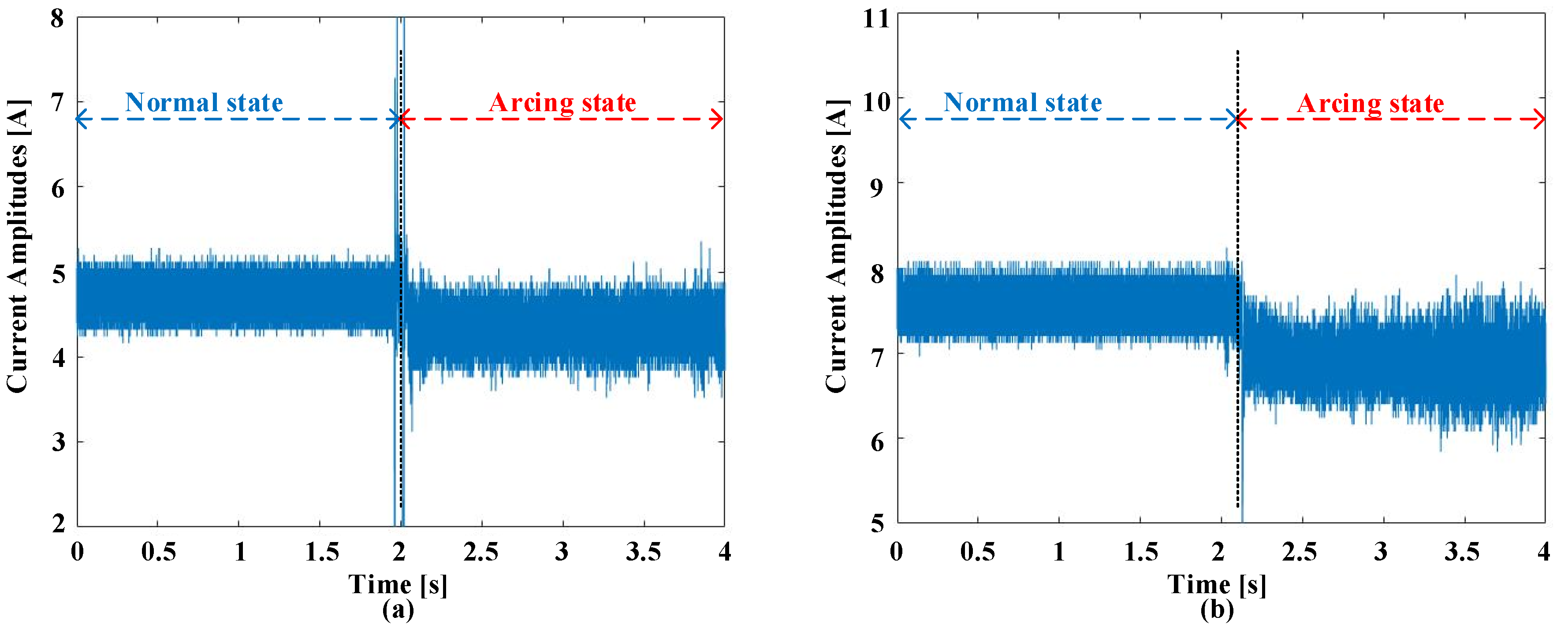
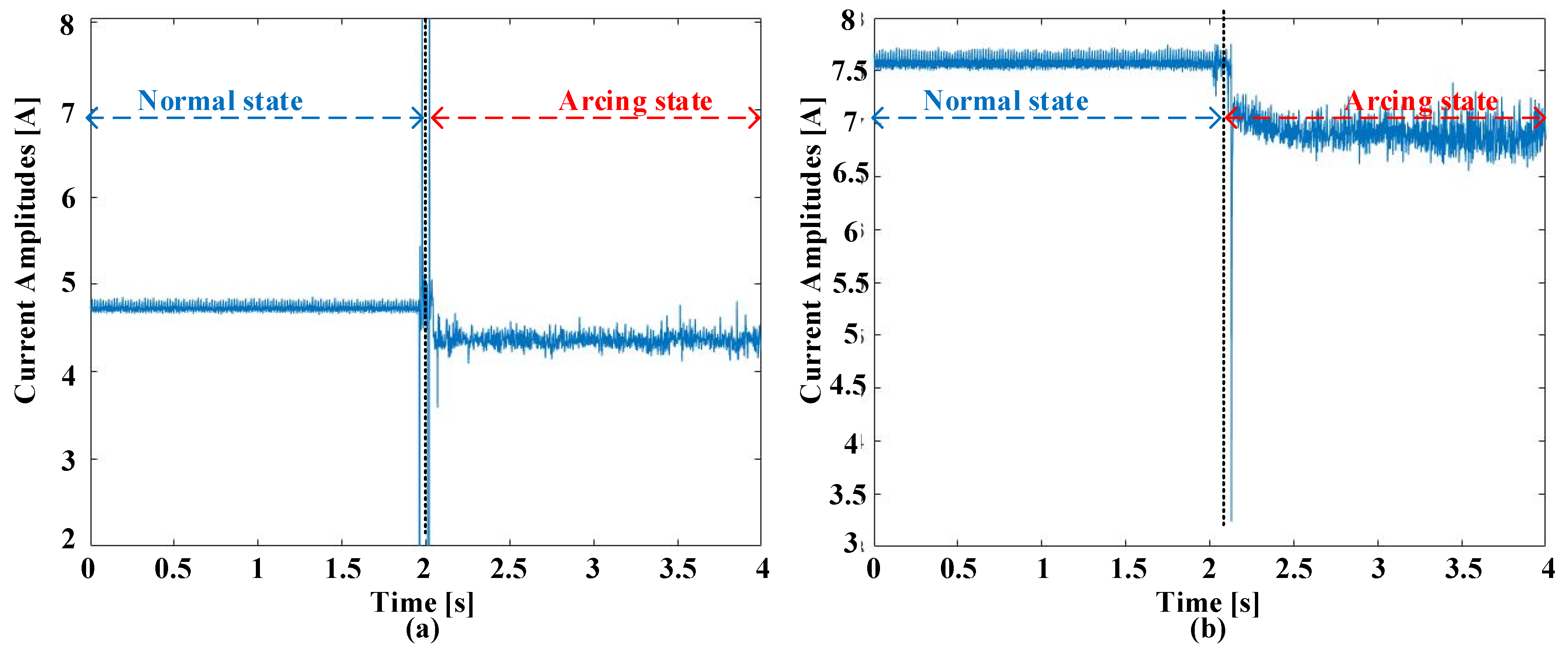
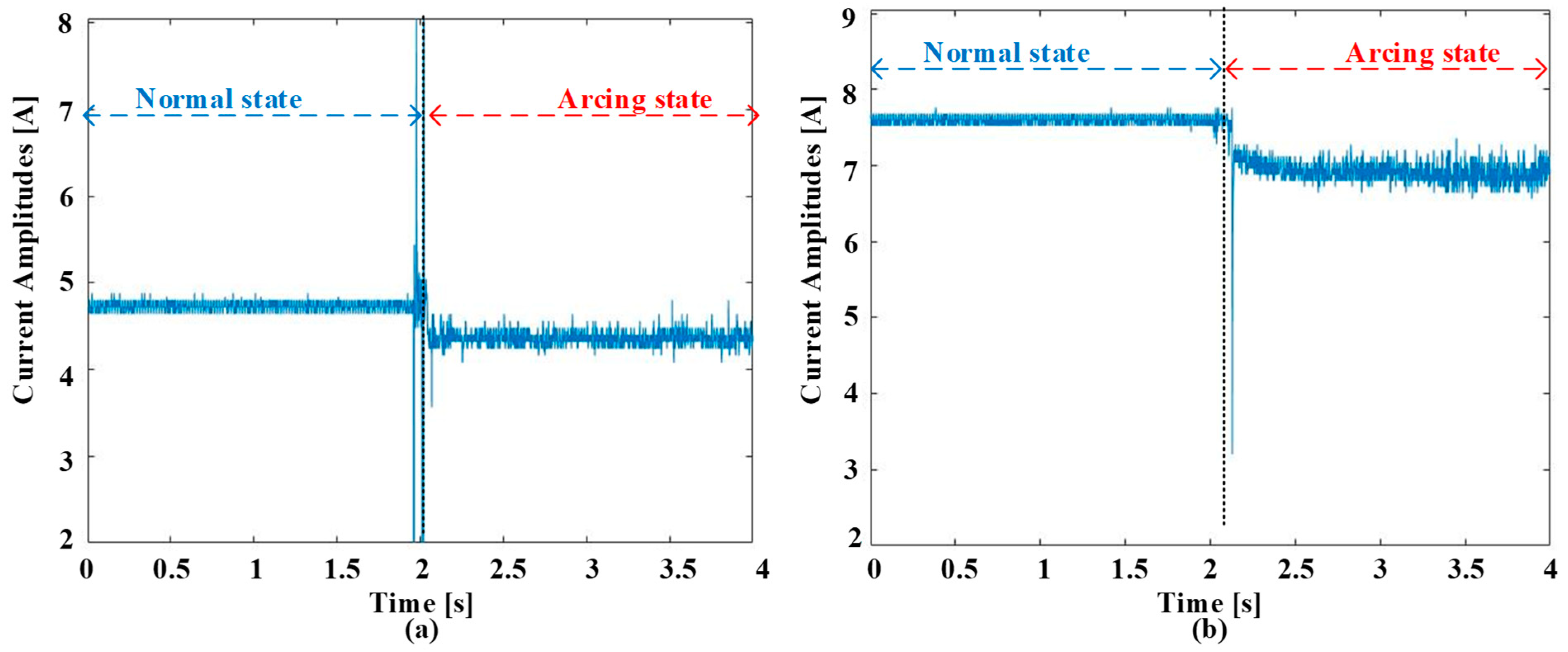
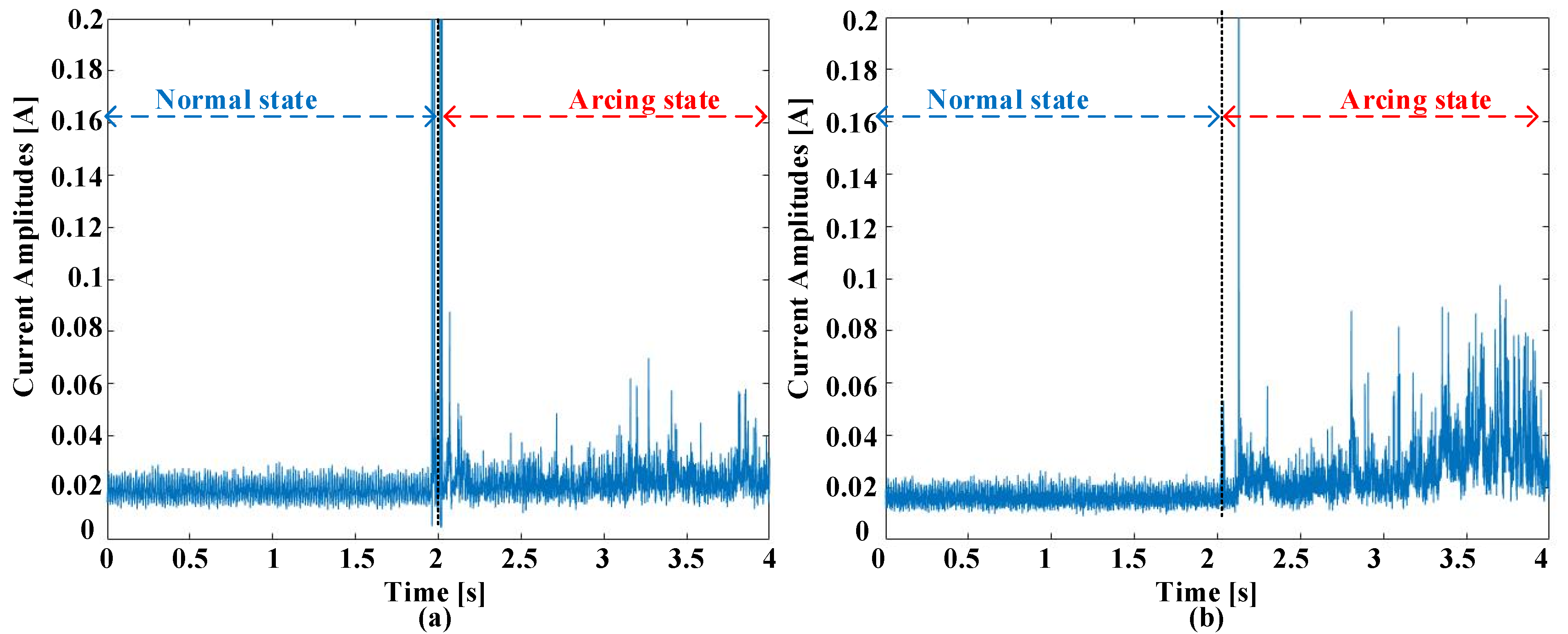
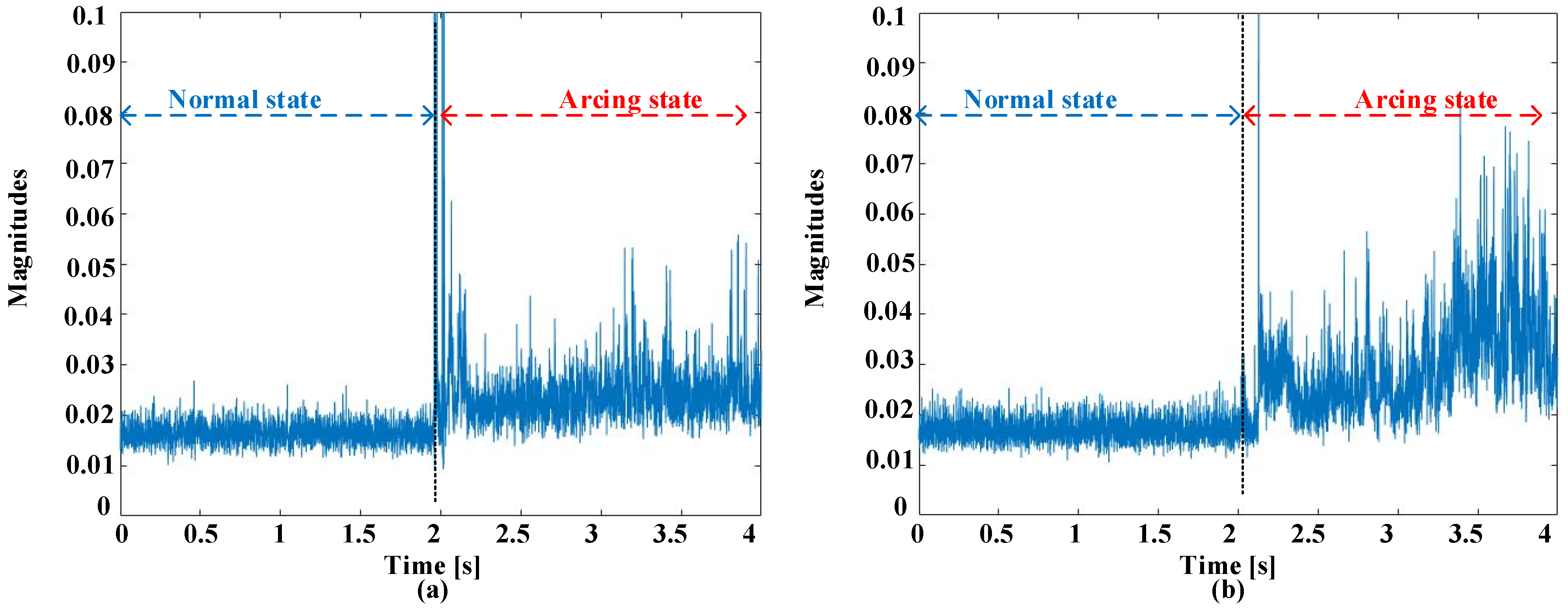
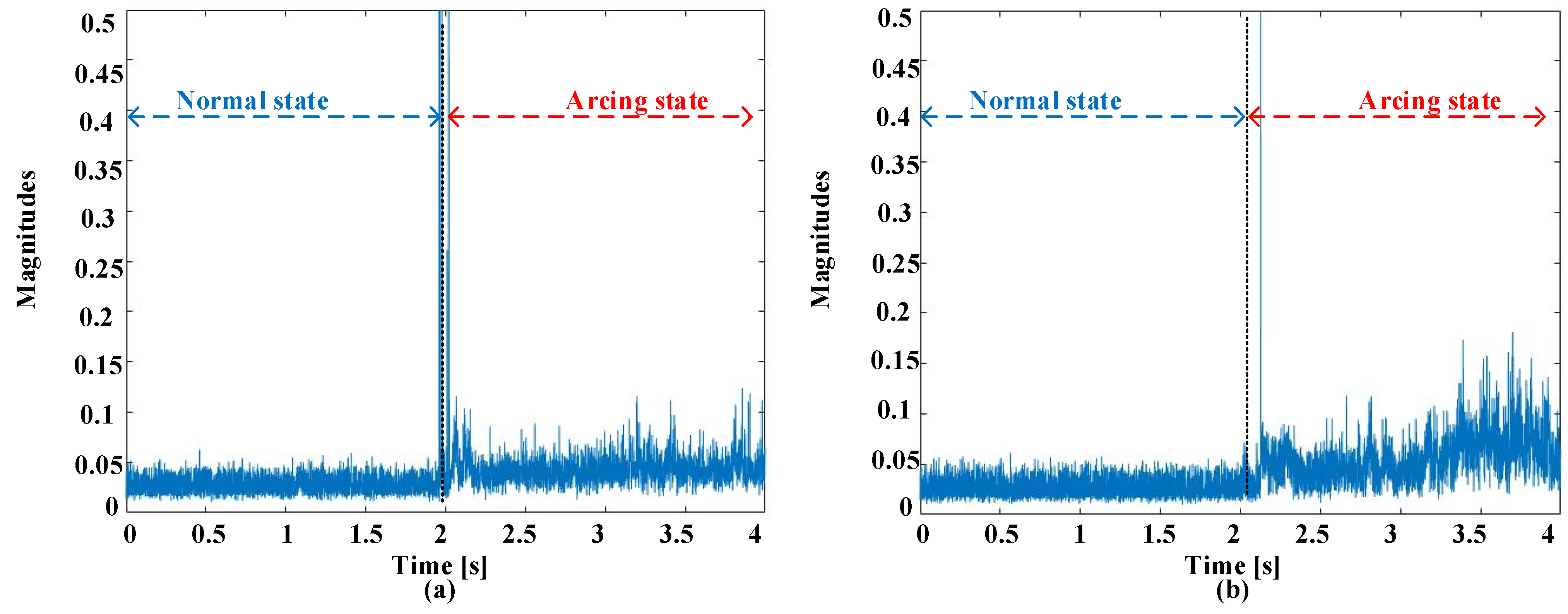
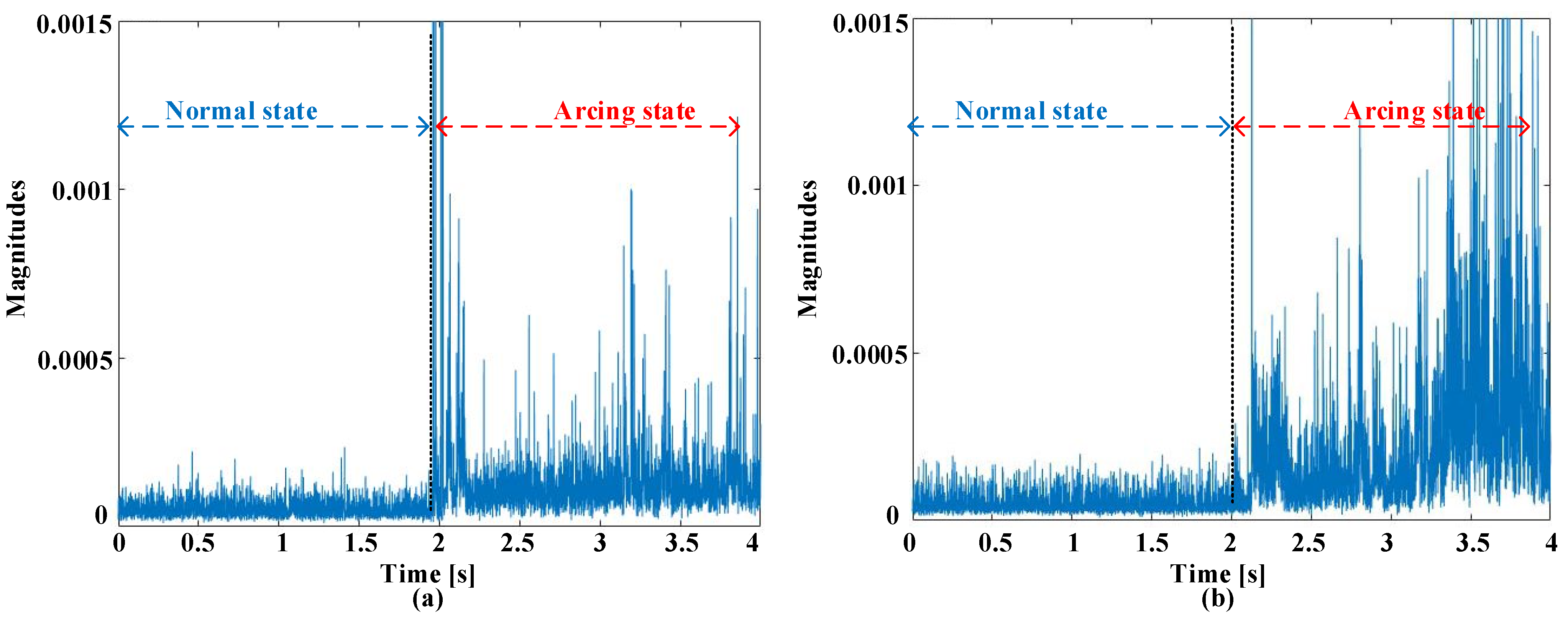
2.2. Failure Event Descriptions
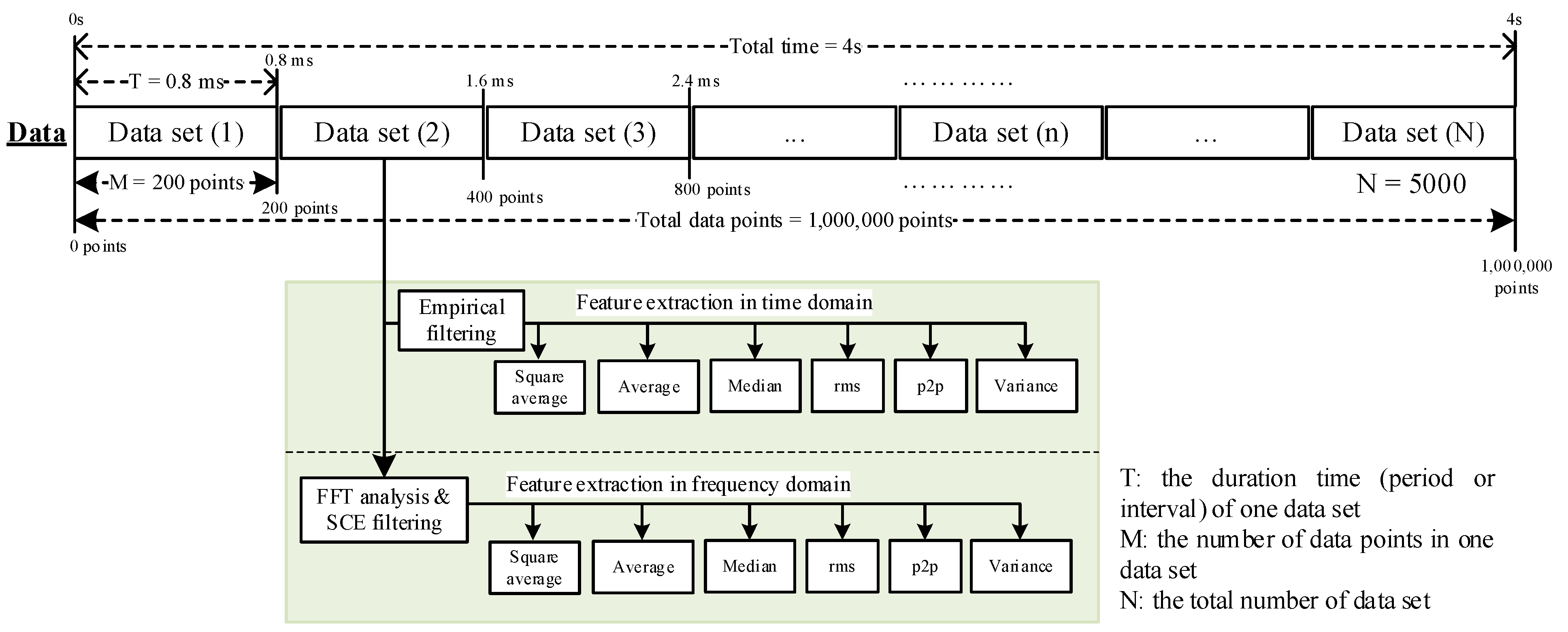
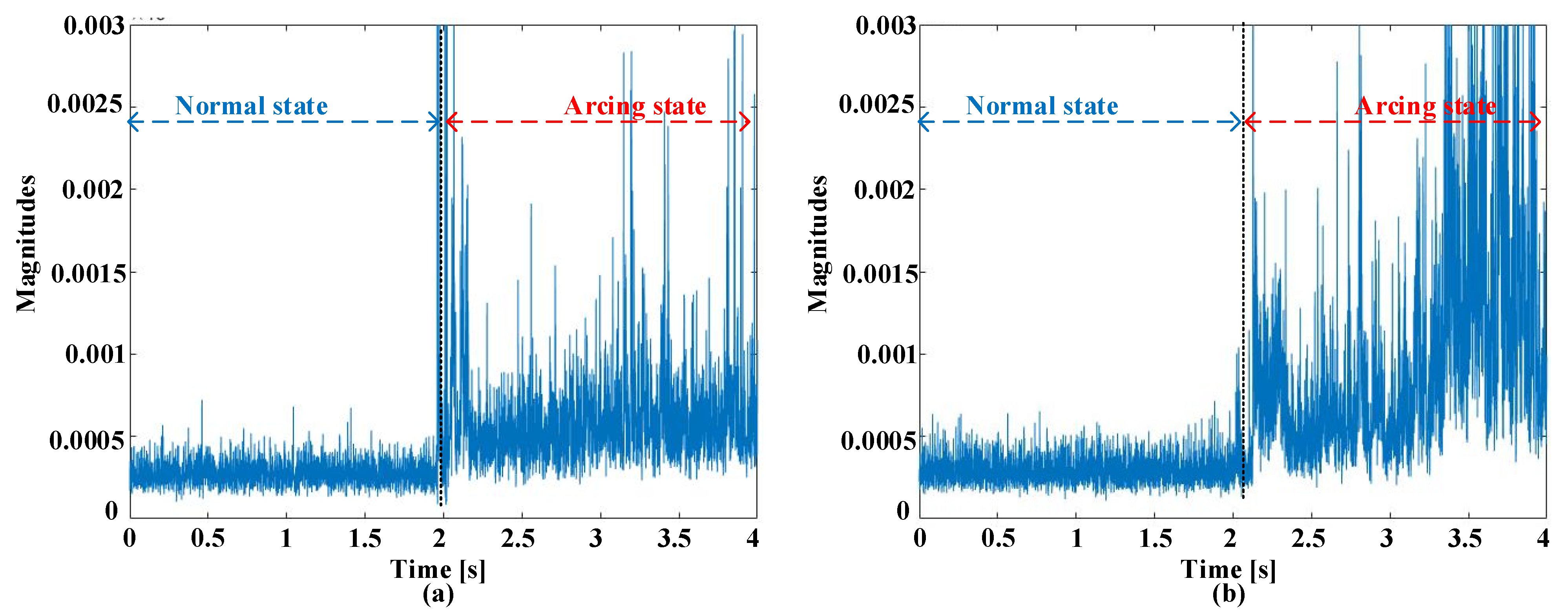
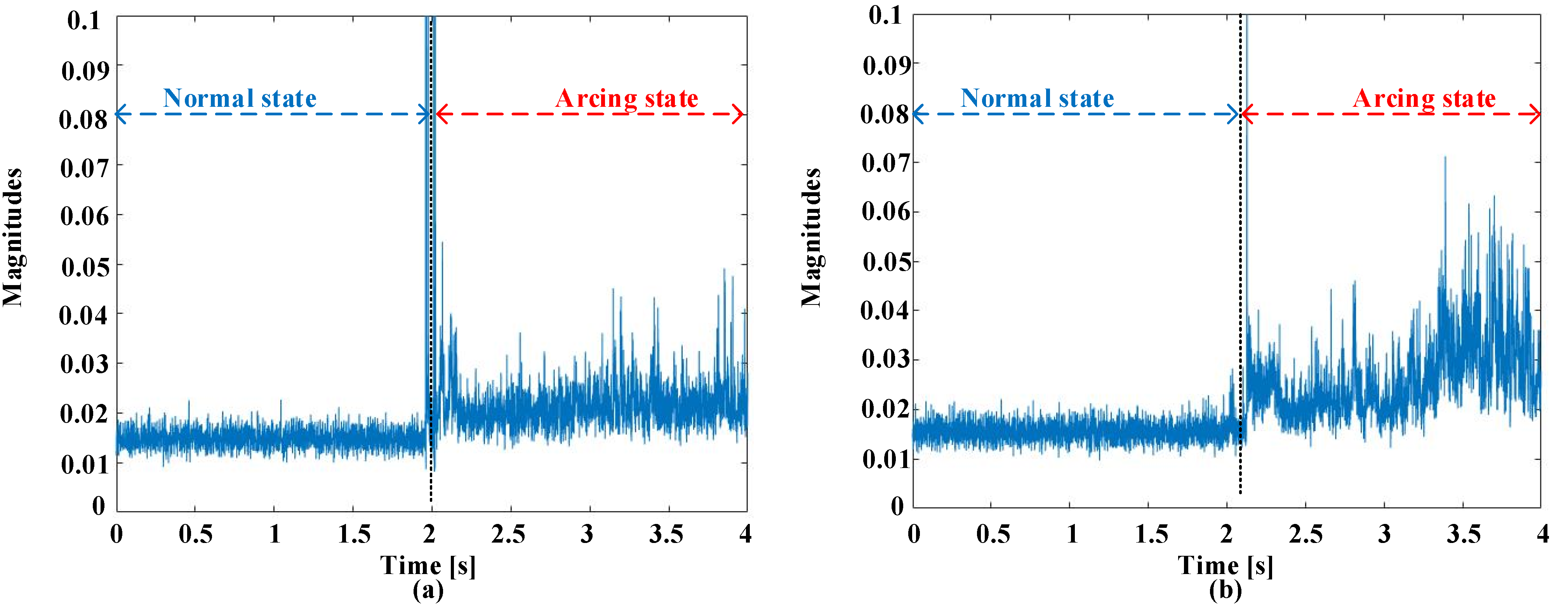
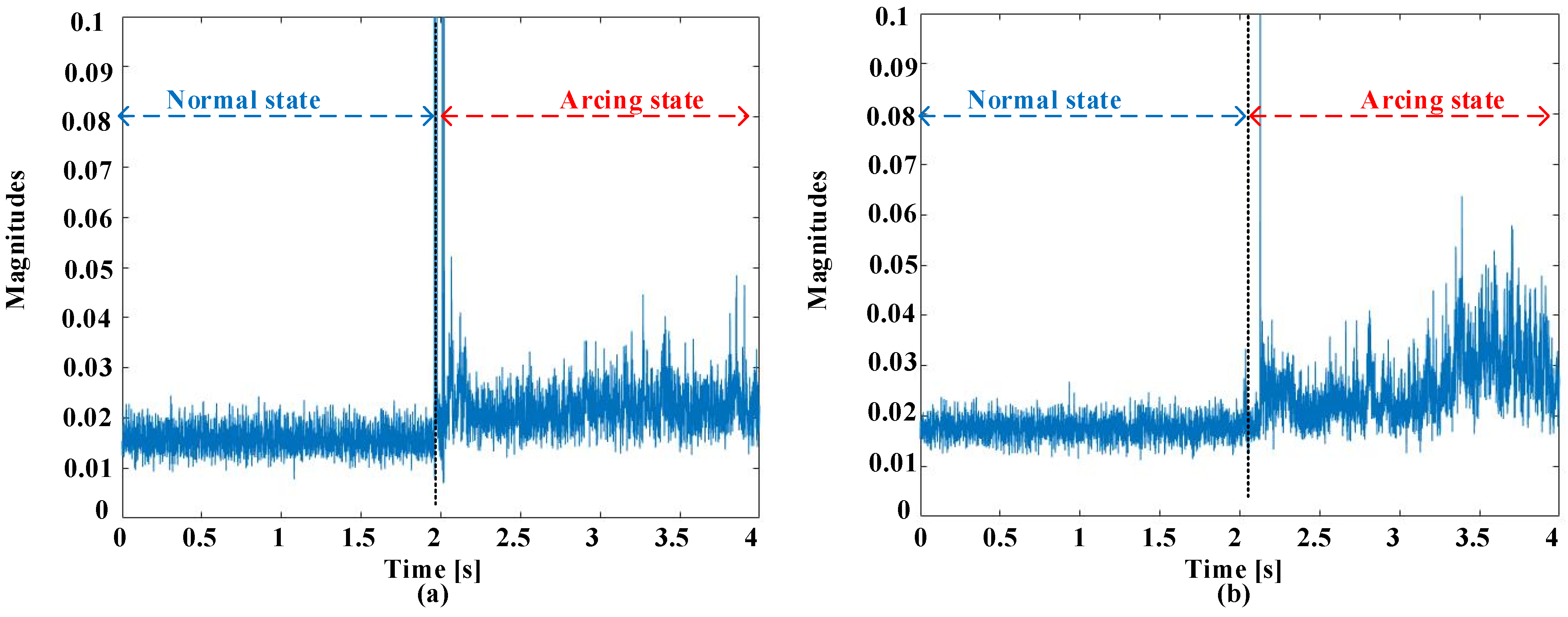
2.3. Screening Procedures in Time and Frequency Domains
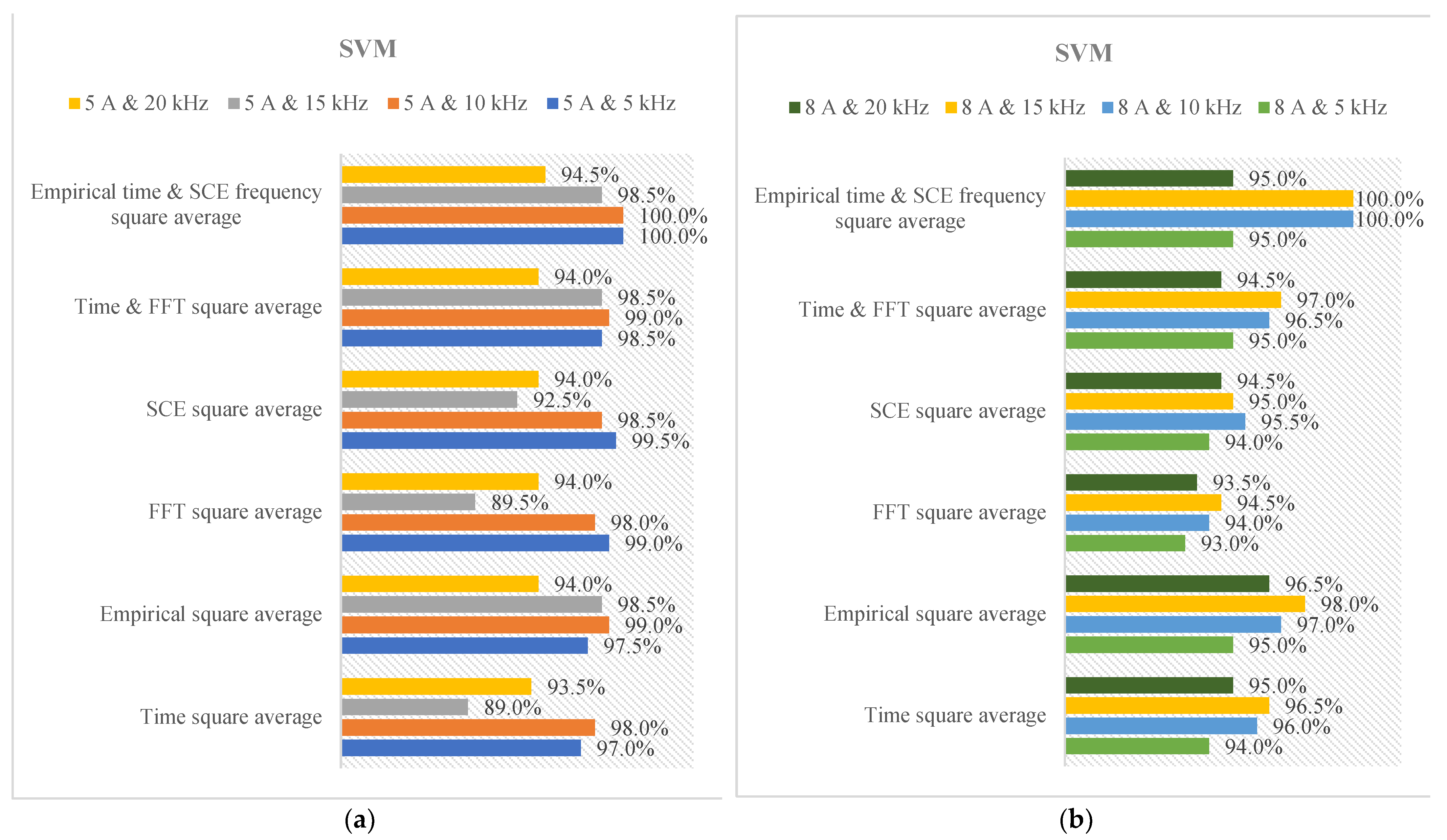
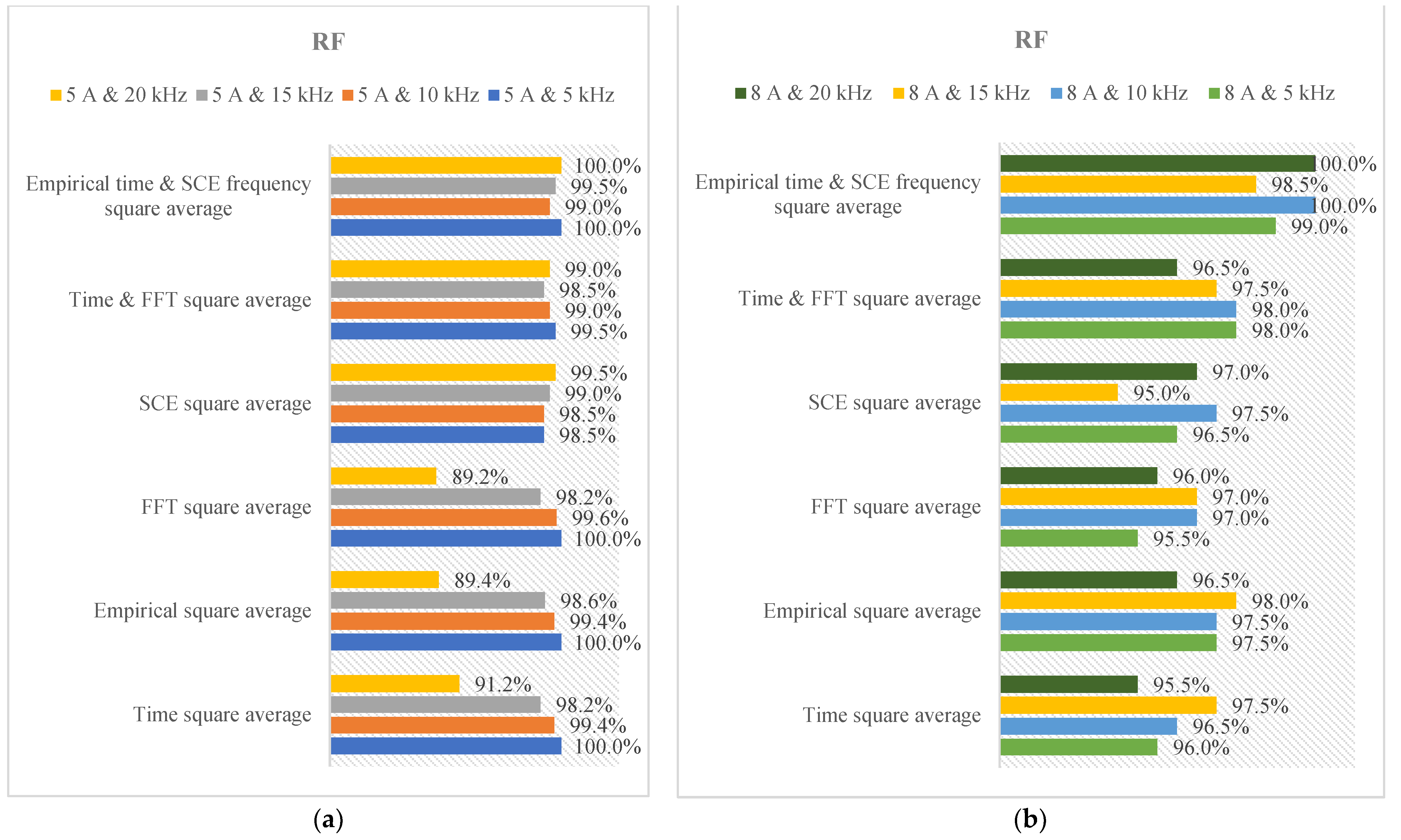
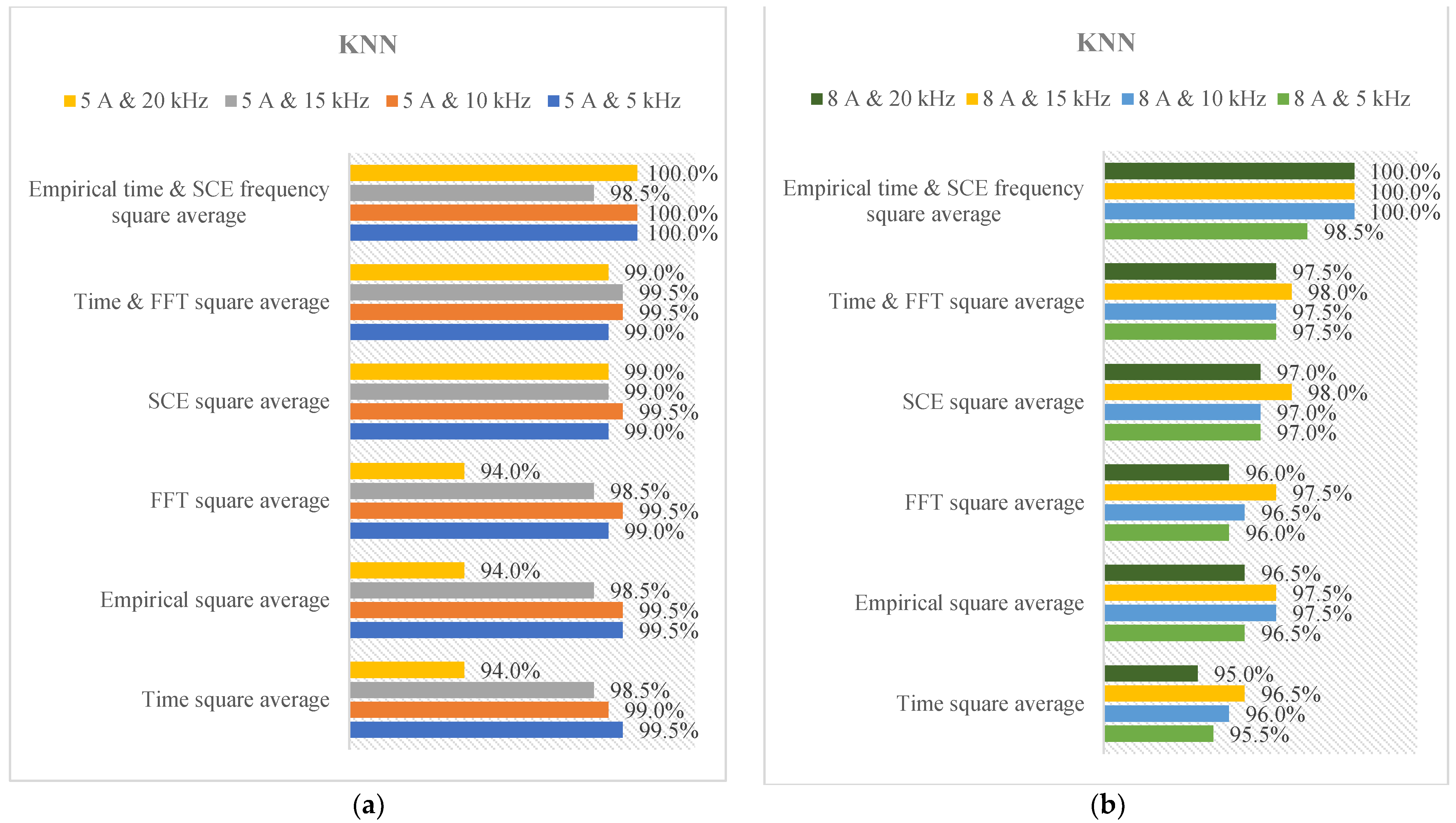
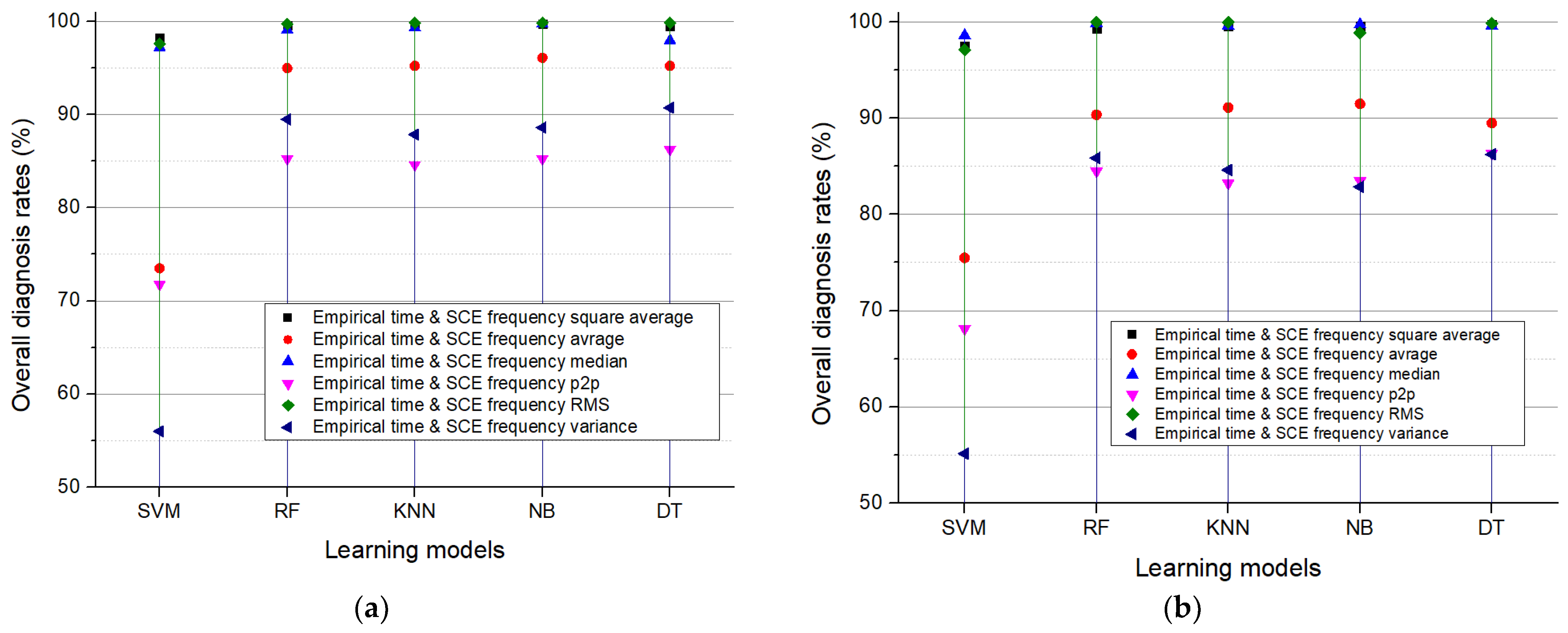
3. Diagnosis of DC Arc Failure Using Various Indexes with Intelligence Learning Models
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lee, S.; Kim, H. A study on low-voltage DC circuit breakers. In Proceedings of the 2013 IEEE International Symposium on Industrial Electronics, Taipei, Taiwan, 28–31 May 2013; pp. 1–6. [Google Scholar]
- Gammon, T.; Lee, W.J.; Zhang, Z.; Johnson, B.C. A review of commonly used DC arc models. IEEE Trans. Ind. Appl. 2015, 51, 1398–1407. [Google Scholar] [CrossRef]
- Klement, K. DC arc flash studies for solar photovoltaic systems: Challenges and recommendations. IEEE Trans. Ind. Appl. 2015, 51, 4239–4244. [Google Scholar] [CrossRef]
- Zhao, S.; Wang, Y.; Niu, F.; Zhu, C.; Xu, Y.; Li, K. A Series DC Arc Fault Detection Method Based on Steady Pattern of High-Frequency Electromagnetic Radiation. IEEE Trans. Plasma Sci. 2019, 47, 4370–4377. [Google Scholar] [CrossRef]
- Park, S.Y.; Choi, H.S. Operation characteristics of DC circuit breaker using arc induction technique according to the magnetism of the superconducting magnet. J. Electr. Eng. Technol. 2024, 19, 845–850. [Google Scholar] [CrossRef]
- Georgijevic, N.L.; Jankovic, M.V.; Srdic, S.; Radakovic, Z. The detection of series arc fault in photovoltaic systems based on the arc current entropy. IEEE Trans. Power Electron. 2016, 31, 5917–5930. [Google Scholar] [CrossRef]
- Chae, S.; Park, J.; Oh, S. Series DC arc fault detection algorithm for DC microgrids using relative magnitude comparison. IEEE J. Emerg. Sel. Top. Power Electron. 2016, 4, 1270–1278. [Google Scholar] [CrossRef]
- Ahn, J.-B.; Jo, H.-B.; Ryoo, H.-J. Real-Time DC Series Arc Fault Detection Based on Noise Pattern Analysis in Photovoltaic System. IEEE Trans. Ind. Electron. 2023, 70, 10680–10689. [Google Scholar] [CrossRef]
- Khamkar, A.; Patil, D.D. Arc fault and flash signal analysis of DC distribution system sing artificial intelligence. In Proceedings of the 2020 International Conference on Renewable Energy Integration into Smart Grids: A Multidisciplinary Approach to Technology Modelling and Simulation (ICREISG), Bhubaneswar, India, 14–15 February 2020; pp. 10–15. [Google Scholar]
- Dang, H.-L.; Kwak, S.; Choi, S. Different Domains Based Machine and Deep Learning Diagnosis for DC Series Arc Failure. IEEE Access 2021, 9, 166249–166261. [Google Scholar] [CrossRef]
- Ni, Y.; Zhang, X.; Chen, Q.; Huang, Y.; Wang, Q. Performance comparison of surface-inset machines with two layer equal/unequal magnet-arc halbach magnets. J. Electr. Eng. Technol. 2024, 19, 845–850. [Google Scholar] [CrossRef]
- Xiong, Q.; Feng, X.; Gattozzi, A.L.; Liu, X.; Zheng, L.; Zhu, L.; Ji, S.; Hebner, R.E. Series Arc Fault Detection and Localization in DC Distribution System. IEEE Trans. Instrum. Meas. 2020, 69, 122–134. [Google Scholar] [CrossRef]
- Yao, X.; Wang, J.; Schweickart, D.L. Review and recent developments in DC arc fault detection. In Proceedings of the 2016 IEEE International Power Modulator and High Voltage Conference (IPMHVC), San Francisco, CA, USA, 6–9 July 2016; pp. 467–472. [Google Scholar]
- Wang, Y.; Zhang, F.; Zhang, S. A new methodology for identifying arc fault by sparse representation and neural network. IEEE Trans. Instrum. Meas. 2018, 67, 2526–2537. [Google Scholar] [CrossRef]
- Laldingliana, J.; Biswas, P.K. Artificial intelligence based fractional order PID control strategy for active magnetic bearing. J. Electr. Eng. Technol. 2022, 17, 3413–3426. [Google Scholar] [CrossRef]
- Uriarte, F.M.; Gattozzi, A.L.; Herbst, J.D.; Estes, H.B.; Hotz, T.J.; Kwasinski, A.; Hebner, R.E. A DC arc model for series faults in low voltage microgrids. IEEE Trans. Smart Grid 2012, 3, 2063–2070. [Google Scholar] [CrossRef]
- Som, S.; Samantaray, S.R. Wavelet based fast fault detection in LVDC micro-grid. In Proceedings of the 2017 7th International Conference on Power Systems (ICPS), Pune, India, 21–23 December 2017; pp. 87–92. [Google Scholar]
- Dang, H.-L.; Kwak, S.; Choi, S. DC Series Arc Fault Diagnosis Scheme Based on Hybrid Time and Frequency Features Using Artificial Learning Models. Machines 2024, 12, 102. [Google Scholar] [CrossRef]
- Gu, J.-C.; Lai, D.-S.; Wang, J.-M.; Huang, J.-J.; Yang, M.-T. Design of a DC Series Arc Fault Detector for Photovoltaic System Protection. IEEE Trans. Ind. Appl. 2019, 55, 2464–2471. [Google Scholar] [CrossRef]
- Dang, H.-L.; Kwak, S.; Choi, S. DC Series Arc Failure Diagnosis using Artificial Machine Learning with Switching Frequency Component Elimination Technique. IEEE Access 2023, 11, 119584–119595. [Google Scholar] [CrossRef]
- UL 1699B; Outline of Investigation for Photovoltaic (PV) dc Arc-Fault Circuit Protection, Issue 2. Underwriters Laboratories, Inc.: Northbrook, IL, USA, 2013.
- Boser, B.E.; Guyon, I.M.; Vapnik, V.N. A training algorithm for optimal margin classifiers. In Proceedings of the Fifth Annual Workshop on Computation Learning Theory (COLT’92), Pittsburgh, PA, USA, 27–29 July 1992; pp. 144–152. [Google Scholar]
- Dang, H.-L.; Kwak, S.; Choi, S. Empirical Filtering-Based Artificial Intelligence Learning Diagnosis of Series DC Arc Faults in Time Domains. Machines 2023, 11, 968. [Google Scholar] [CrossRef]
- Cover, T.; Hart, P. Nearest neighbor pattern classification. IEEE Trans. Inf. Theory 1967, 13, 21–27. [Google Scholar] [CrossRef]
- Breiman, L.; Friedman, J.; Olshen, R.; Stone, C. Classification and Regression Trees; ser. Statistics/Probability Series; Wadsworth and Brooks: Belmont, CA, USA, 1984. [Google Scholar]
- Dang, H.-L.; Kwak, S.; Choi, S. Identifying DC Series and Parallel Arcs Based on Deep Learning Algorithms. IEEE Access 2022, 10, 76386–76400. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Langley, P.; Iba, W.; Thompson, K. An analysis of Bayesian classifiers. In Proceedings of the 10th National Conference on Artificial Intelligence, San Jose, CA, USA, 12–16 July 1992; pp. 223–228. [Google Scholar]







| Learning Models | ||||||
|---|---|---|---|---|---|---|
| SVM | KNN | NB | DT | RF | ||
| Specifications | Regulation parameter C = 1 | Distance metric: Euclidean | Classifier type: Gaussian | Decision type: classification and regression trees (CART) | Forest type: bootstrap aggregation | |
| Kernel function: radial basis function | K neighbor: 20 | Hyperparameter optimization: Bayesian | Depth of tree: 4 | Number of DT: 500 | ||
| Degree = 3 | Algorithm type: brute force | Distribution: normal | Leaf nodes: 14 | |||
| Gamma: auto | ||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dang, H.-L.; Kwak, S.; Choi, S. Various Feature-Based Series Direct Current Arc Fault Detection Methods Using Intelligence Learning Models and Diverse Domain Exclusion Techniques. Machines 2024, 12, 235. https://doi.org/10.3390/machines12040235
Dang H-L, Kwak S, Choi S. Various Feature-Based Series Direct Current Arc Fault Detection Methods Using Intelligence Learning Models and Diverse Domain Exclusion Techniques. Machines. 2024; 12(4):235. https://doi.org/10.3390/machines12040235
Chicago/Turabian StyleDang, Hoang-Long, Sangshin Kwak, and Seungdeog Choi. 2024. "Various Feature-Based Series Direct Current Arc Fault Detection Methods Using Intelligence Learning Models and Diverse Domain Exclusion Techniques" Machines 12, no. 4: 235. https://doi.org/10.3390/machines12040235
APA StyleDang, H.-L., Kwak, S., & Choi, S. (2024). Various Feature-Based Series Direct Current Arc Fault Detection Methods Using Intelligence Learning Models and Diverse Domain Exclusion Techniques. Machines, 12(4), 235. https://doi.org/10.3390/machines12040235






