Abstract
In this paper, we introduce a novel method to formally represent elements of control engineering knowledge in a suitable data structure. To this end, we first briefly review existing representation methods (RDF, OWL, Wikidata, ORKG). Based on this, we introduce our own approach: The Python-based imperative representation of knowledge (PyIRK) and its application to formulate the Ontology of Control Systems Engineering (OCSE). One of its main features is the possibility to represent the actual content of definitions and theorems as nodes and edges of a knowledge graph, which is demonstrated by selected theorems from Lyapunov’s theory. While the approach is still experimental, the current result already allows the application of methods of automated quality assurance and a SPARQL-based semantic search mechanism. The feature set of the framework is demonstrated by various examples. The paper concludes with a discussion of the limitations and directions for further development.
1. Introduction
This paper presents and discusses an approach to facilitate the transferability of control engineering knowledge, both within the field (i.e., between different niches of control theory) as well as from the field into potential fields of application.
A major motivation is the following: over the past years, the first author received many requests regarding support in controller design from other mechanical or electrical engineers in the process of developing new or improving existing devices. The questions raised indicate that those experts in their respective application domains typically lack control-related knowledge that would be beneficial for their creative work. For instance, in one of such consultations, only after answering several questions on model predictive control was it revealed that there was a misunderstanding (due to wrong terminology) and actually model-based control (of a nonlinear system) was the topic of interest.
This anecdotal evidence can be underpinned by structural considerations: Contemporary control engineering is characterized by wide and heterogeneous spectra of methods (such as advanced linear algebra [1], differential geometry [2,3], functional analysis [4]) and domains of application (such as robotics [5], automotive systems [6], process engineering [7], chemical engineering [8]). This inherent two-dimensional interdisciplinarity makes it hard for outsiders to obtain a systematic overview. However, such an overview is necessary to identify and examine suitable solution approaches for the respective problem at hand.
Furthermore, the number of control-related publications (i.e., the amount of relevant knowledge) is rapidly growing (see, e.g., the bibliometric study [9] for the specific subfield of fractional order control and [10,11] for the general trend), which, together with the limited capacity of human brains, creates the necessity of increasing specialization (in mathematics, the problem is known as “one brain barrier”, cf. e.g., [12]). In other words, the field of control engineering is fragmenting into specialized niches, each of which naturally develops its own methods, notation and jargon. With the progression of this effect, knowledge transfer between these niches (which can be very fruitful as the transfer of the backstepping-method from ODE to PDE systems demonstrates [13]) is significantly handicapped.
To facilitate knowledge transfer, it is worthwhile to consider the representation of that knowledge. Currently, the prevalent representation is in the form of textbooks and scientific papers. In other words, knowledge is represented by an accumulation of text of natural language possibly enriched by formulas and graphics. Such documents are tailored to be consumed directly by humans, and thus, computers can only be of limited use by providing access to the very specific knowledge that is needed in a particular use case in research and development. Of course, this insight is far from new, and consequently, formal knowledge representation and semantic technologies (such as knowledge graphs and ontologies which are discussed in Section 2) have been investigated and applied for decades [14,15]. Recently, in the Strategic Research and Innovation Agenda (SRIA) of the European Commission [16], semantic technologies were identified as important to achieve interoperability between disciplines, i.e., to foster knowledge transfer [17].
These technologies have had huge impact on life sciences, see, e.g., [18], and also some influence on engineering (see [19] for a general overview and [20] for the example of the robotics field). However, they rarely have been used in control engineering. To the author’s knowledge, the frame-based approach described in [21,22] is the only serious attempt to apply semantic technologies to control-theoretic knowledge, apart from our own work [23,24,25,26,27,28].
Our initial endeavors to encode serious pieces of linear and nonlinear control theory with the established standard Web Ontology Language (OWL) and related technologies (see Section 2 and Section 3.1) revealed that they lack the expressive power to precisely formulate the actual relevant content of control theory, i.e., definitions, theorems and similar constructs.
To overcome this specific problem and in general facilitate knowledge transfer, within this paper, we make the following contributions:
- Firstly, we present the PyIRK framework [29] for imperative representation of knowledge.
- Secondly, we present the Ontology of Control Systems Engineering (OCSE, [30]) which is based on that framework, and focus on how contents from Lyapunov’s theory can be modeled.
- Thirdly, we demonstrate possible applications of that formally represented knowledge.
Besides many foundational concepts from mathematics and control engineering, the OCSE contains a relevant fraction of concepts, definitions and theorems from Lyapunov’s theory, all of which are related to stability analysis of linear and nonlinear dynamical systems. This choice was made because Lyapunov’s theory forms a good compromise: On the one hand, it is not “trivial” knowledge, like the stability analysis of linear SISO systems, which would have called into question the necessity of formal knowledge representation in general. On the other hand, it is not a specialized niche result as, for instance, controlling a vertical gradient freeze crystal growth process [13] or distributed converter circuits [31], where the unfamiliar content might distract from understanding the representation method. Furthermore, established approaches like quantifier elimination [32,33] based on Lyapunov’s theory make heavy use of formal logic and sophisticated computational methods, therefore a certain amount of receptiveness for our formal approach can be presumed.
To anticipate the conclusion, this paper does not claim to present the definitive solution on how to formally represent control engineering knowledge, nor does it claim to provide results that can already undoubtedly be called useful. To the best of the authors’ knowledge, it demonstrates a novel and “engineering-compatible” method of formal knowledge representation (PyIRK) and its application to control engineering (OCSE). While it is very far from completely covering Lyapunov’s theory—let alone the whole field of control theory in absolute terms—it is in relative terms the most complete approach that currently exists.
Critically examining our approach (and formal knowledge representation in general), the major questions are (1) whether it actually enables improvements in knowledge transfer (see above) and (2) whether so-called large language models [34] are not better suited to reach this goal. Answering these questions is beyond the scope of this paper, and is left to further research. Instead, in this contribution we demonstrate that formal knowledge representation is indeed an approach worth considering and that PyIRK can serve as a backend for a possible future assistant system (i.e., frontend) to facilitate knowledge transfer.
The rest of the paper is structured as follows: Section 2 briefly reviews existing approaches to formal knowledge representation, whereas Section 3 motivates and presents our own approach (PyIRK and OCSE) in more detail. Next, Section 4 recapitulates the relevant aspects of Lyapunov’s theory from the established literature while Section 5 demonstrates how this knowledge can be formalized by our approach, before Section 6 discusses how this formalization can provide some use. The paper closes with Section 7, which draws a conclusion and discusses possible future developments. The Appendix A contains a list of implemented concepts that are related to Lyapunov’s theory.
2. Formal Knowledge Representation
2.1. Overview
Traditionally, human knowledge is mostly represented by words (including numbers, formulas, etc.), which can be accumulated in texts and books. For some kinds of knowledge, more specialized representations evolved such as tables. They have the advantage of being easily processable (e.g., searchable), especially if they are implemented as a relational database in a computer. However, tables are very inflexible because of their fixed column structure. In contrast, texts are extremely flexible, i.e., they have a high expressive power but are much more difficult to process by computers.
Undoubtedly the field of natural language processing has made huge progress in recent years, mostly driven by so-called large language models (LLMs); see, e.g., [34] for a recent overview. However, such approaches rely on the consumption of huge amounts of texts as training data, which makes it practically impossible to ensure the factual quality of the input. Issues arise, for example, from outdated or wrong sources or simply the ambiguous character of natural language.
An alternative method of knowledge representation is knowledge graphs (KGs). A KG is a digitally represented directed graph, i.e., a collection of labeled nodes and labeled edges. Roughly speaking, the nodes are the “things” to which the knowledge refers, while the edges specify the relations between these nodes. In principle. a KG can have (almost) the flexibility and expressive power of a natural language text but also possesses the precision and suitability for automated processing like tabular knowledge.
Although LLMs currently dominate the artificial intelligence (AI)-related headlines, for the representation of complex scientific knowledge such as Lyapunov’s theory, a KG seems to be the adequate approach because of its explicit data representation. Of course, this by no means prevents LLM-based technology from being used in combination with a KG, e.g., for pre- or post-processing.
2.2. Established Knowledge Graph Concepts: Semantic Triples and Computational Ontologies
Each edge of a KG, along with its start and end node, can be considered a “semantic triple” with a subject–predicate–object structure. A significant aspect of knowledge representation involves converting complex knowledge structures into a large collection of such triples.
A closely related (and partially overlapping) concept is a (computational) ontology. The Greek-stemming word literally translates as “the study of being” and originally refers to a branch of theoretical philosophy. In the context of computer science, an ontology is a formal (i.e., machine-actionable) specification of a shared conceptualization (semantic coverage) of a knowledge domain [35]. In other words, an ontology specifies which concepts do exist in a domain and how they are related to another [18,36,37].
Different technical approaches for the machine-actionable representation of ontologies have been proposed, such as the Ressource Description Framework (RDF) for semantic triples, the Web Ontology Language (OWL, [38]) or the Knowledge Interchange Format (KIF, [39]). Therefore, OWL can be interpreted as an additional layer on top of RDF and enables knowledge representation by means of so-called Description Logics [40,41] which are so-called decidable fragments of first-order predicate logic. The added value of such an ontological formalization is that it enables automatic reasoning for a knowledge base. However, while the decidability requirement ensures favorable computational properties, it drastically restricts the expressive power of OWL, which makes it unpractical to represent complex mathematical knowledge.
As is the case with programming languages, the choice of an optimal representation method depends (a) on the task (or problem field) and (b) on individual factors such as a priori knowledge. Another analogy to programming languages can be drawn: while due to different strengths and weaknesses there is no objectively best formalism (and probably never will be), it is worthwhile to innovate on representation frameworks (i.e., the “language”) to achieve better results. In any case, the ability to retrieve the formalized knowledge through suitable queries is a key feature of a useful representation method.
2.3. APIs and SPARQL Interface
To be of use to a wide audience, knowledge graphs such as Wikidata [42] have to provide suitable access to potential users. This typically is conducted via an application programming interface (API), via a so-called SPARQL interface or both (“SPARQL” is a so-called recursive acronym which expands to “SPARQL Protocol and RDF Query Language”).
An API allows fine-grained access to specific features of the knowledge base and thus depends on the concrete backend. For example, the ORKG-API [43,44] allows the retrieval of an entire subgraph of a certain entity as a so-called bundle, whereas the Wikidata API does not offer this particular functionality.
In contrast to the backend-dependent API, SPARQL is a widespread standard to retrieve data stored in RDF format [45,46,47]. This query language is explicitly designed to make use of the triple structure, where the subject, predicate and object are typically so-called uniform resource identifiers (URIs) or literal values (such as strings or numbers). The strength of this approach is that via a boolean combination of such atomic queries, results can be retrieved which are not explicitly present in the knowledge base. For example, the simple SPARQL in Listing 1 retrieves a list of persons who have Aleksandr Lyapunov in their “academic lineage”.
| Listing 1. SPARQL Example: “academic lineage” of A. Lyapunov. |
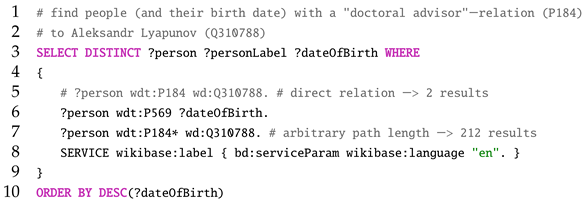 |
Remark 1.
The relation between an API and a SPARQL endpoint can be summarized as follows: while many objectives can be achieved either by using the API or the SPARQL interface, both interfaces are tailored towards different use cases and thus have different strengths and drawbacks.
3. Imperative Knowledge Representation with PyIRK and OCSE
3.1. Imperative versus Declarative Knowledge Representation
Typically, knowledge representation is declarative or passive, e.g., as XML- or RDF-files which need to be interpreted by some program to actually interact with the contained knowledge [48,49,50]. This has the advantage of clearly separating the knowledge from the algorithms to process it. However, when developing a new knowledge representation system, this separation has the disadvantage that one needs to co-develop both the processing code and the representation format. This has to be solved without a priori knowing specifically regarding what features both components might need because this would imply already having a consistent formalization of the domain knowledge available. Furthermore, it poses an additional usability hurdle that potential users or contributors have to familiarize themselves with the representation format (or some adequate interface).
Thus, after some not so successful experiments with declarative approaches, we opted for a different approach which we call imperative representation of knowledge. It basically means to express the respective knowledge as part of the source code of the knowledge processing software. This is obviously possible since hard-coded strings or variable values are a standard technique in software development. While it is usually a good idea to separate this kind of data from the actual program logic because it might be subject to change independently (e.g., error correction or translation), this separation can be achieved not only by loading declarative data files but also by suitable modularization of the programming code.
The main advantages of the imperative representation of knowledge are (a) that it allows automation of the construction of semantic triples and thus allows for a more compact formulation (in terms of the size of the source code) and (b) that it spares the user from learning an additional declarative language like, e.g., the OWL Manchester syntax (assuming that potential users are familiar with the respective programming language).
Remark 2.
Our wording “imperative representation of knowledge” should not be confused with the word group “imperative knowledge” which is in use as a synonym of “procedural knowledge” and refers to knowledge which can be demonstrated by exercise, e.g., by using a specific tool or playing an instrument which might be hard to be expressed using words. The respective counter-term is “descriptive knowledge” for which the synonym “declarative knowledge” is in use and which should also not be confused with the “declarative representation of knowledge”.
3.2. Basic Concepts of PyIRK
As the name “PyIRK” suggests, this framework for the imperative representation of knowledge is implemented in the Python programming language. That is because Python has been proven useful in many applications of science and engineering, and thus a high degree of dissemination in the target group can be assumed. Also, the dynamic features of Python (e.g., creating new functions and classes at runtime) support the compact representation of complex knowledge, like evaluated ternary operators such as Lie derivatives.
In Python, “everything” (apart from reserved words such as if or for) is an object and thus has a type. The important types (i.e., classes) for PyIRK are Entity (with subclasses Item and Relation), and Statement.
A Statement models a branch of the knowledge graph, i.e., a subject–predicate–object triple. Therefore, the predicate is always a reference to a relation, while the subject and object role can be taken by all entities.
For unambiguous identification of objects in knowledge graphs or ontologies usually one of two paradigms is used: either (a) “unique identifier and arbitrary label” (e.g., BFO_0000006 for the class with label ‘spatial region’ in the Basic Formal Ontology BFO [51]) or (b) “unique descriptive label” (e.g., TransferFunctionSystemModel in [22]). While (b) is favorable for usability, variant (a) clearly has scalability advantages for example when modeling concepts that are homonymous like “distribution” or “field” or supporting multiple languages. In PyIRK, variant (a) is chosen: Every entity has a URI, which specifies the module and the concrete object within that module via a short key I<n> (for items) or R<n> (for relations), where <n> can be replaced by any string consisting of at least one digit. Nevertheless, to achieve the favorable usability of having consistent labels present in the source code, every entity accepts a valid label as “index”, which is implemented like a dictionary lookup, i.e., using square brackets. Thus, the two lines in Listing 2 are practically equivalent PyIRK source code: in both cases, the function called is_true receives the exact same arguments and thus return the same value (True). However, the second line has the advantage that the entity references are both precise for a computer and directly understandable for a human. Technically, this behavior is achieved by overloading the _get_item_ method of the class Entity. This method checks the label (see Section 3.8) and then returns self, i.e., the object itself.
| Listing 2. Unlabled and labled identifiers in two semantically equivalent lines. |
The possibility of using such labeled identifiers enables users to directly understand and create PyIRK source code without the help of additional tools (of course, auxiliary tools, e.g., for autocompletion and visualization are very useful but they are not necessary). This property allows us to make use of established technologies and best practices for source code version control. In particular, the distributed version control system git is the de facto standard and public repository hosting services such as github, gitlab or codeberg provide useful functionality for collaborative source-code-related work such as tracking the change history, parallel branches, merge requests, and code reviews. Most importantly managing the source-code-based knowledge base in a public git repository makes it easy to create a fork of the whole project, i.e., an independent copy that can be changed and extended without the consent of the original authors. Apart from technical measures, this is also facilitated by the appropriate open-source license (GPLv3+). This “forkability” is important because it prevents the individual control of the knowledge and thus encourages people to experiment with their own fork and eventually exchange contributions.
The approach of representing knowledge as (versioned) software is also consistent with the principle of “continuous provisionality”. This means to accept that the knowledge base will never be complete and that it likely will contain bugs, as is the case with most complex software systems, but nevertheless might be useful for some task.
3.3. Modules
The knowledge represented in PyIRK is structured in modules. A PyIRK module is a Python file containing source code which, when executed, creates PyIRK entities and statements. Modules can import other modules and collections of closely related modules can be bundled to form a PyIRK package. Such a package consists of at least one module, a configuration file, some documentation and unit tests.
3.3.1. Builtin Entities
The most basic module is builtin_entities which is an integral part of the PyIRK framework. It creates abstract items like I1[“general item”], I2[“Metaclass”], I11[“general property”], I12[“mathematical object”] and fundamental relations like R1[“has label”], R2[“has description”], R3[“is subclass of”], R4[“is instance of”], R17[“is subproperty of”] etc.
Apart from the mere definition of items and relations, the module also provides auxiliary Python classes and functions such as instance_of. (Note that there is also the notion of PyIRK classes, which is a category of PyIRK items. Thus, we make the intended meaning explicit, when it is not obvious from the context.) This function creates a new item with the generic label (R1) and description (R2) and an R4[“is instance of”] statement edge to the provided class (PyIRK item). For example, this allows to create matrix instance; see Listing 3.
| Listing 3. Demonstration of PyIRK instantiation. |
Note that I9904[“matrix”] is not defined in builtin_entities but in math1 which is part of the OCSE package (see Section 3.3.2).
3.3.2. Ontology of Control Systems Engineering (OCSE)
Obviously, control theory is not the only field of science for which formal knowledge representation might be worthwhile. It is, therefore, sensible to separate between the PyIRK framework and the actual domain-specific content. From the perspective of ontology engineering, builtin_entities is an upper-level ontology [52], whereas the Ontology of Control Systems Engineering (OCSE) represents a domain ontology.
From a pragmatic perspective, the OCSE is just a PyIRK package containing three different modules:
- agents1 which contains humans, institutions and source documents, which might be referenced by the other modules. It also contains corresponding relations such as R3474[“has ORCID”] and R8439[“is described by source”] and auxiliary functions like create_person.
- math1 which contains mathematical concepts and relations such as I9904[“matrix”], I6709[“Lipschitz continuity”], R4963[“is neighborhood of”]. It also contains auxiliary Python classes like IntegerRangeElement and functions like symbolic_expression_to_graph_expression.
- control_theory1 which contains concepts and relations such as I7208[“BIBO stability”], I1347[“Lie derivative of scalar field”], R5031[“has trajectory”], I1664[“limit cycle”]. This module is also the place where the Lyapunov-related knowledge is implemented, mostly in form of instances of the builtin items I14[“mathematical proposition”] and I20[“mathematical definition”]; see Section 5.
The first use case for the OCSE was to serve as controlled vocabulary for tagging models of dynamical systems in the context of the model catalog which is part of the “Automatic Control Knowledge Repository” [23,25,28].
3.4. Qualifiers
As explained in Section 3.2, basic statements in PyIRK are modeled as triples of the form (subject, predicate, object). For example, using the respective entities from the OCSE module math1, the PyIRK snippet to express that A. Lyapunov worked at the National University of Kharkiv is shown in Listing 4. Note that, in contrast to natural languages for a semantic triple, the predicate does typically not carry any temporal information.
| Listing 4. Single statement without qualifiers. |
Expressing more complex knowledge artifacts by just using triples is not trivial. Wikidata popularized an approach called qualifiers. Thereby, for every statement (i.e., triple), which should be further described an additional “statement item” is introduced by using the original predicate URI but in a special name space. This statement item can then serve as subject for those further statements. For details see [53]. PyIRK follows a similar approach where Statement instances (Python objects) are used to serve as nodes in the knowledge graph. Together with some auxiliary functions like start_time and end_time, it is possible to make the statement from Listing 4 more precise; see Listing 5.
| Listing 5. Single statement with two qualifiers. |
 |
Therefore, the objects start_time(“1885”) and end_time(“1902”)are placeholders which are interpreted by PyIRK such that the appropriate builtin relations R48[“has start time”] and R48[“has end time”] are used together with the provided literal arguments once the primary statement object has been created.
3.5. Operators and Representation of Formulas
Representation of mathematical knowledge requires modeling of the application of operators. In PyIRK this is achieved by making those items which have a R4[“is instance of”] relation to I4895[“mathematical operator”] callable. This allows expressions like I5177[“matmul”](A, B), which create new items. In this example snippet, a new I9904[“matrix”] instance is created, because I5177[“matmul”] defines this via R11[“has range of result”]. This instance is then related to the operator item via R35[“is applied mapping of”] and to the arguments via R36[“has argument tuple”] and thus carries all necessary information. Note that operators can have an arbitrary (but fixed) number of arguments.
While this mechanism allows the representation of arbitrary mathematical expressions as part of the knowledge graph, it is inconvenient for humans to read and write a formula like with an expression like in Listing 6.
| Listing 6. Formula representation with direct operator calls. |
The flexibility of Python-based imperative knowledge representation allows us to solve this problem by facilitating the computer algebra package SymPy [54]. In particular, the module math1.py defines the functions items_to_symbols and symbolic_expression_to_ graph_expression (short: se_to_ge) to convert between SymPy and PyIRK objects in both directions; see Listing 7. While this requires a prior definition of the symbols (line 1), the actual representation of the formula is much easier to understand (line 2).
| Listing 7. Formula representation via SymPy. |
Remark 3.
It is worth mentioning that SymPy also supports parsing 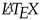 strings. This offers the possibility to denote formulas in a more widely used syntax if desired.
strings. This offers the possibility to denote formulas in a more widely used syntax if desired.
3.6. Scopes
Many knowledge artifacts (such as theorems or definitions) consist of multiple simpler statements which are in a specific semantic relation to each other. Consider the following version of the well known Pythagorean theorem:
Theorem 1.
Let be the sides of a triangle, ordered from shortest to longest, and the respective lengths. If the angle between a and b is a right angle, then the equation holds.
Such a theorem consists of several “semantic parts”, which in the context of PyIRK are called scopes. In particular, we have the three following scopes:
- 1.
- setting: “Let be the sides of a triangle, ordered from shortest to longest, and (la, lb, lc) the respective lengths”.
- 2.
- premise: “If the angle between a and b is a right angle”.
- 3.
- assertion: “then the equation holds”.
The concepts “premise” and “assertion” are usually used to refer to parts of theorems and similar artifacts and can be considered self-explanatory. The “setting” scope is used to refer to those auxiliary statements which “set the stage” to properly formulate the premise and the assertion (e.g., by introducing and specifying the relevant objects). In the literature (formulated in natural language), much of this information is usually provided by the text preceding the actual theorem or by introductory phrases like “Let …”.
To represent the actual content of a theorem in PyIRK, this theorem has first to be created as an item. In Listing 8, we continue the example of the simplified Pythagorean theorem for demonstration purposes.
| Listing 8. Creation of the theorem item as implication instance. |
 |
Now, we can create three scope items as instances of I16[“scope”], associate them to the theorem item by means of R21[“is scope of”] and specify them with R64[“has scope type”] as setting, premise, and assertion. These scope items can then be “attached” via a R20[“has defining scope”] qualifier to a statement, to express that this statement is not a “top level statement” but instead a part of a theorem structure. For example, a statement which has an R20 qualifier edge to a premise scope is considered to express a condition. In principle, all these item and qualifier creations could be expressed directly but to provide a more convenient way PyIRK makes use of Python’s context managers—indented code blocks introduced by a with statement. Listing 9 shows this technique being applied to the Pythagorean theorem. The whole process of representing a theorem in PyIRK, i.e., the content of Listings 8 and 9, is summarized by the flow chart in Figure 1.
Figure 1.
Flow chart for the PyIRK representation of a theorem as given in Listing 8 and 9.
| Listing 9. Specification of the content of the Pythagorean theorem. |
 |
3.7. Rule-Based Reasoning
One major advantage of description-logic-based ontologies (represented in OWL) is the availability of so-called reasoners or inference engines. These are pieces of software that are able to infer logical consequences from a set of “facts”, i.e., asserted statements [55]. In addition to OWL, the Semantic Web Rule Language (SWRL) is supported by some reasoners. However, even the expressiveness of both approaches combined is not sufficient for a meaningful representation of mathematical knowledge. For example, while such reasoners can easily infer new statements (edges in the knowledge graph) involving already known entities (nodes in the knowledge graph, “individuals” in OWL-terminology), it is impossible to infer the existence of new entities. A different reasoning approach which overcomes this limitation is known as “existential rules” see, e.g., [56,57].
Being an experimental knowledge representation framework, PyIRK has the flexibility to use its own rule-based inference engine (the alternative would have been to implement an interface to an existing inference engine, which possibly would compromise flexibility and expressive power). It follows the principle that the rules themselves should be part of the overall knowledge graph (instances of I41[“semantic rule”]). The content of each rule can be expressed (analogously to a mathematical theorem) by means of “setting”, “premise” and “assertion”; see Figure 1. Therefore, the first two scopes define to which entities (nodes) the rule matches, whereas the third scope defines the consequences of such a match, i.e., the creation of new statements or items. Listing 10 shows a simple example that expresses the transitivity of being a subproperty: if is a subproperty of and is a subproperty of , then should also be a subproperty of .
| Listing 10. Definition of a Semantic Rule. |
 |
In order to apply such a rule, PyIRK uses the VF2 algorithm [58] implemented in the package NetworkX [59] to find so-called subgraph monomorphisms. These are subsets of nodes and edges of the overall knowledge graph which match the structure defined by the scopes “setting” and “premise”. For all such subgraph monomorphisms, the relations of the scope “assertion” are created (with the respective bindings). For example, without applying any rule, the property I9642[“local exponential stability”] is only a subproperty (R17) of I4900[“local asymptotic stability”]. However, after applying rule I4731 from Listing 10, this property is also a subproperty of I2931[“local Lyapunov stability”] and Item I5082[“local attractiveness”]. As a consequence, it is possible to find systems that have a locally exponentially stable equilibrium point via a SPARQL search even when searching for the more general property local Lyapunov stability. For a control theory expert, this might seem trivial, but for users who are not familiar with the subtle relations between different stability concepts, this is a significant facilitation.
To implement existential rules, i.e., rules that have new nodes as consequence, PyIRK offers the mechanism of so-called “consequent functions” which are attached to an item in assertion scope. They can contain arbitrary code and thus can be used to create new items or relations. A similar mechanism, called “condition function” (attached to an item in premise scope), can be used to improve or simplify the subgraph matching for finding all relevant subgraphs for a given rule.
Remark 4.
In the current development state of PyIRK, it is not yet possible to convert the information contained in condition and consequent functions into semantic triples when exporting the graph to RDF format. However, implementation is planned as one of the next development steps.
The main applications of semantic rules in PyIRK are (a) to derive “new” knowledge and (b) to implement measures of quality assurance (see Section 3.8). While it would be possible to implement these types of algorithms directly in the source code of the framework, one must recognize that such algorithms are also relevant knowledge and thus should be a regular part of the overall knowledge graph.
To demonstrate the capabilities (and remaining limitations) of the rule engine, a formalized version of “Einsteins zebra riddle”—a famous and comparatively hard logical puzzle attributed to Albert Einstein [60]—is included as part of the PyIRK test suite; see [29] (unfortunately, the relevant code is too long to be included here). A logic puzzle was chosen to explain how “new” knowledge is meant: creating new relations between entities that follow logically from given ones. In other words, the knowledge has already been there, but only in implicit form, and thus hard to access, for example, for use in query-answering.
3.8. Quality Assurance via Type and Consistency Checking
From our own experience in research and teaching, it is obvious that intellectual activity is, in principle, error-prone: texts and formulas contain typos, calculations contain errors, and software contains bugs. Mechanisms like careful double-checking and peer review can reduce this effect, but formal knowledge representation additionally allows for automatic checks (similar to unit tests in software engineering). In particular, PyIRK offers several automated checks:
Firstly, almost every labeled identifier (cf. Listing 2) in an expression like I38[“positive integer”] is checked for consistency against the actual label (R1) of the referenced entity. In this example snippet, this is not the case, as the correct label for item I38 would be “non-negative integer”. In other words, this mechanism prevents mistakenly using the wrong items in the modeling process. It is worth mentioning that this mechanism is compatible with the multilinguality of PyIRK. For example, the expression I39[“positive Ganzzahl”@de] is valid. One exception to this label validation mechanism are the “magic” item I000 and the “magic” relation R000, because they can be used with an arbitrary label. Their purpose is to allow (temporary) reference to entities which are not yet existing.
Secondly, due to the inheritance (via R3[“is subclass of”]) and instantiation (via R4[“is instance of”]), it is possible to check the types of relations or operator items (see Section 3.5) which are applied to other items.
Finally, semantic rules (see Section 3.7) can be used for more specialized consistency checking, e.g., ensuring that only matrices are multiplied according to their column and row numbers.
3.9. Modeling Strategy and Implementation State
A major challenge in knowledge representation is to define the limits of the domain of discourse or, in other words, to answer the question “Where to begin and where to end?”. This becomes increasingly difficult if the principal ambition of the framework is, like in the case of PyIRK, the capability to consistently represent all relevant scientific knowledge traditionally contained in books or articles.
PyIRK approaches this challenge in a pragmatic way: items can be introduced as instances of I50[“stub”] which indicates that this item is not yet completely modeled and serves as placeholder. This is inspired by Wikipedia’s practice of stub articles, see https://en.wikipedia.org/wiki/Wikipedia:Stub (accessed on 30 December 2023). Nevertheless, such stub items can be used in semantic triples with other items and thereby already model valuable knowledge. If deemed necessary, the stub items can be modeled more precisely at a later time point, e.g., by introducing other stub items and thereby pushing the limits “outwards”, away from the more relevant items.
For instance, the example in Listing 9 refers to I2917[“planar triangle”]. In a first step, this could be introduced as a stub item. Later, this could be made more precise by introducing a new stub item “planar polygon” and making I2917 a subclass of it. Finally, one might decide to introduce an elaborated taxonomy of geometric objects and integrate triangles and polygons into it. The major advantage of the stub approach is that non-trivial taxonomic modeling effort can be deferred when the current focus is on some concrete problem like representing the lengths of the sides of a triangle.
Having properly set taxonomic relations via R4[“is instance of”] and R3[“is subclass of”] often is not enough to formally explain what a concept really means. PyIRK handles this challenge by instances of I20[“mathematical definition”], which, like propositions or rules, can have setting, premise and assertion scopes. For example, I5325[“Hurwitz polynomial”] is first introduced as an instance of item I4239[“abstract monovariate polynomial”] and then made more precise via I5325[“Hurwitz polynomial”].set_relation(p.R37[“has definition”], I4455[“definition of Hurwitz polynomial”]), where I4455 specifies (via the three scopes) that, if the set of roots of that polynomial is a subset of the open left half-plane of , then it is a Hurwitz polynomial.
Obviously, this approach is tedious, especially in the beginning. However, once a “critical mass” of items and relations is accumulated, it becomes easier as fewer new entities have to be introduced to express the actual intention, e.g., a new theorem.
At the time of writing, the OCSE (version 0.3) and the underlying framework PyIRK (version 0.12) are still under heavy development. When all three OCSE modules are loaded, the knowledge graph contains ≈850 items, of which ≈450 are automatically created, e.g., scope items, applied operators, etc. Between nodes, there exist ≈7600 edges (statements), each of which is specified by one of ≈140 relations. Additionally, there are ≈600 qualifier statements.
Ironically, despite the resulting data structure being called knowledge graph, a meaningful depiction of the whole data is surprisingly difficult, as Figure 2 demonstrates. A more useful visualization can be achieved when considering only a sub-graph, as, e.g., in Figure 3.

Figure 2.
Visualization of the whole knowledge graph. While it is impossible to extract meaningful details from this picture, it illustrates the high degree of interconnection. Edges of type R3["is subclass of”] are blue, R4["is instance of”] are orange and all other edges types are black.
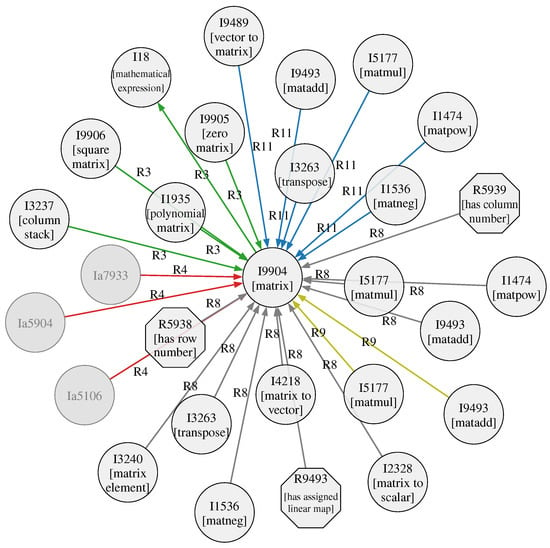
Figure 3.
Visualization of a sub-graph with I9904["matrix”] as the center and only direct neighbors. For the sake of displayability, only some of the automatically created instance items (key starting with Ia...) are displayed. The arrow colors correspond to the respective relations.
In its current development state, however, a PyIRK knowledge graph can be exported to the RDF standard without the qualifier statements. This is not a limitation in principle but is simply not yet implemented.
The RDF export is the basis for the SPARQL interface, which can be used to perform a semantic search; see Section 6.3. As for other knowledge management systems, the full functionality of the framework is only available via the API, i.e., using the Python library; see also Remark 1.
4. Lyapunov Theory
The study of nonlinear dynamical systems revolves around a number of nonlinear analysis tools. Usually, the stability of a feedback system is of particular interest. One widely used concept for the analysis of nonlinear systems is Lyapunov’s stability theory. This section presents the basic concepts of Lyapunov’s theory, starting with time-invariant systems.
The following definitions and theorems are based on the extensive descriptions in [61] (Section 4.1), [62] (Section 3.4.2) and [63] (Chapters 1–3).
4.1. Stability of Equilibrium Points
Consider the nonlinear time-invariant dynamical system
where the map f: is a local Lipschitz map and maps from to . Assume is an equilibrium point of system (1), meaning that it satisfies f (. Without loss of generality, we can assume that the equilibrium point is the origin .
Definition 1.
The equilibrium point of (1) is called stable (in the sense of Lyapunov), if for any there exists a , such that .
Definition 2.
The equilibrium point of (1) is called asymptotically stable, if it is stable and there exists a , such that .
In order to assess whether an equilibrium point has any of these properties, a criterion is needed. As an inspiration, we consider a pendulum near its lower equilibrium point. The energy of the system is lowest in its (lower) equilibrium point and increases in an environment around the equilibrium. Thus, if the energy of the system always decreases along its trajectory, it will eventually reach the equilibrium point.
The same argument holds for other physical systems. One can examine the energy of such systems along their trajectory to evaluate the stability of the equilibrium. Lyapunov showed that this concept can be generalized to specific scalar functions that allow the determination of stability of an equilibrium point, even if energy might not be a meaningful concept for the given system.
We denote with the Lie derivative of the scalar field h:D → ℝ along the vector field f of (1).
Theorem 2.
Let x* = 0 be an equilibrium of (1) and D ⊂ ℝn be an open environment of 0. If there exists a scalar function V:D → ℝ, then
- V is positive definite on D.
- = LfV is negative semi-definite on D.
- x* = 0 is called locally stable (LS). If is an even negative definite, x* is locally asymptotically stable (LAS).
Remark 5.
Technically speaking, the previous theorem consists of two separate theorems. Since most of the setting are the same, one usually formulates the statement like in Theorem 2. We will recall this fact later in Section 5.
If such a function V exists, it is called Lyapunov function. Additionally, it is called weak/non-strict, if is negative semi-definite and strong/strict, if is negative definite.
In order to generalize the concept of local asymptotic stability to the global case, one has to make sure that the definiteness conditions of V hold not just in a neighborhood of the origin, but in the entire state space. Additionally, the Lyapunov function V needs to be radially unbounded.
Definition 3.
Let be an equilibrium of (1). If there exists a scalar function , then
- V is (globally) positive definite.
- is (globally) negative definite.
- (V is radially unbounded).
- x* = 0 is called globally asymptotically stable (GAS).
4.2. Construction of Lyapunov Functions
In general, the previous theorems are only sufficient but not necessary, leading to the problem of finding a suitable Lyapunov function for a given system. While there is no general approach to finding a Lyapunov function, there is, however, a number of publications regarding Lyapunov functions for specific systems or under certain conditions.
In the case of the linear system,
a candidate for a Lyapunov function is given by the quadratic form
with the positive definite Matrix P. When evaluating the time derivative of along the system’s trajectory, one obtains
with the symmetric matrix Q. Here,
is called the Lyapunov Equation.
To show that V is indeed a Lyapunov function, we have to prove that the matrix Q is positive definite (see Theorem 2). To satisfy both conditions, one usually starts by choosing a positive definite matrix Q and solves the Lyapunov Equation (5) for the matrix P. If P is also positive definite, is indeed a Lyapunov function.
Theorem 3.
Remark 6.
To make the universal quantifier in the previous statement more explicit, one might reformulate the theorem in short notation
In the case of nonlinear systems, several approaches to construct a Lyapunov function have been discussed (see [64] for an overview). Most of these methods make assumptions about the system, limiting the applicability of the presented method to a certain class of system.
For demonstration purposes w.r.t. knowledge transfer, our contribution aims at helping to find the suitable method for a given system. To this end, the requirements and assumptions of different approaches are of particular interest to the knowledge representation. Subsequently, we recall two methods of constructing Lyapunov functions with different conditions.
4.2.1. Recursive Algorithm of Vannelli and Vidyasagar (Theorem 4 in [65])
This algorithm is applicable to time-invariant systems of dimension two or greater, which can be written as
with homogeneous functions of degree i and under the assumption, the linearized system
is asymptotically stable. Starting with solving the Lyapunov Equation for the linearized system (which has a solution, since the linearized system is stable), a recursive system of equations is defined. Solving these equations leads to a Lyapunov function. For details, see [65] (Theorem 4).
4.2.2. Algorithm by Goubault et al. [66]
This algorithm can be used to examine time-invariant polynomial systems of the form
with an equilibrium in the origin. Now with the use of so-called Darboux polynomials, one can search for so-called differential variants of the system via so-called Sum-Of-Squares programming. If a solution exists, the differential variant can be used to calculate a Lyapunov function. What this means exactly is beyond the scope of this paper. It is only important that some conditions on the applicability of the algorithm are imposed, which can be represented in our KG.
In the following section, the implementation of some selected theorems in PyIRK will be discussed.
5. Lyapunov-Theory-Related Knowledge Representation
As mentioned before (see Section 3.9), a challenge in knowledge representation is where to begin. Therefore, for now, we focused only on implementing the necessary mathematical basics that are needed to formulate important theorems in the context of Lyapunov’s theory. That means that different concepts are implemented in different levels of detail, meaning there will be items with rigorous (mathematical) definitions, items with meaningful (semantic) descriptions and relations and stub items (see Section 3.9). As it becomes necessary, new items or information about an item may be added on demand.
Consider Theorem 2. The theorem itself is represented by an item defined in the OCSE module control_theory1; see Listing 11.
| Listing 11. Theorem item for Lyapunov stability. |
 |
This item by itself only has a label (R1), a short description (R2) and the type I15[“implication proposition”] (assigned via R4). At this point, the item has no relation to any of the concepts in Theorem 2, such as stability. To formally define the content of the theorem and build the corresponding relations in the knowledge graph, we can use the structure of scopes (introduced in Section 3.6) to formulate setting, premise and assertion. To do so, we require the existence of various (mathematical) concepts, such as system, equilibrium point, scalar function, positive definiteness and Lie-derivative, to name a few. Some of these concepts need to be specified even more, e.g., the system (meaning system of ordinary differential equations) has to have an associated vector field to calculate the Lie-derivative and the concept of positive definiteness needs its own definition. Assuming all of the above-mentioned items are defined, Theorem 2 can be implemented as shown in Listing 12.
Listing 12 mainly consists of three scopes—setting, premise and assertion. In the first scope, the setting, variables are defined that are needed in premise and assertion. Naturally, we start by defining the system of equations (lines 3–5). Since Theorem 2 refers to the autonomous time-invariant system (1), the statement is restricted to systems with these properties by lines 6–7 (even though a similar statement can be made for systems without these properties). The corresponding state space D of the system is defined in line 9 and is immediately put into relation with its system via line 10. To specify the dimension of the state space, some positive integer n (line 13), is put into relation with the state space (line 14). Next, the origin of the state space (lines 15–16) is defined. As mentioned before, the system is described by its drift vector field f, which is defined in lines 18–19. To prepare the discussion of properties of the scalar field V and its derivative in the premise, V and its Lie derivative are formally defined in lines 21–22. Note that I1347["Lie derivative of scalar field"] is an item of type operator that takes the two arguments V, f and returns an evaluated mapping (see Section 3.5) of type ma.I9923[“scalar field”] (not visible here). This first part of the code corresponds with the first two lines of Theorem 2. Now, all required tools are available, to formulate the implication. The premise is rather short. Two conditions need to be fulfilled for the assertion to be true: V(x) ≻ 0 (lines 25–26) and
(x) ⪯ 0 (lines 27–28). These definiteness conditions need only hold in the neighborhood of the origin, which we describe by adding a qualifier to the statement, which restricts the statement to the condition of the qualifier. In the assertion, we create a new relation between the origin of the system and the item for local Lyapunov stability (line 31). The last line 33 is not necessarily part of the theorem and takes the place of a terminological remark, stating that the function V is called a weak Lyapunov function.
| Listing 12. Theorem for local Lyapunov stability of state space systems. |
 |
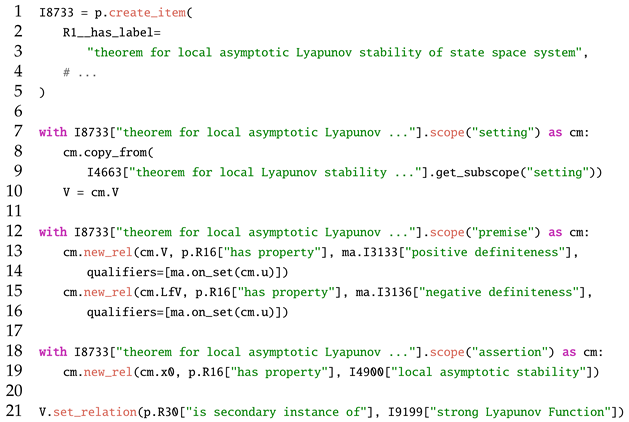
When adapting this definition for asymptotic stability, we can reuse the setting of Listing 12 via cm.copy_from; see Listing 13.
Listing 13 copies the setting of the previous theorem. With the slight change of using item ma.I3137[“negative definiteness”] instead of ma.I3136[“negative semidefiniteness”] in line 15, one can formulate the statement for local asymptotic stability.
In a similar fashion, statements regarding the construction of the Lyapunov function can be stated. For instance, Listing 14 is a PyIRK representation of Theorem 3.
Note that this is an equivalence proposition (I17) rather than an implication proposition (I15), meaning that the statement is also true, if premise and assertion are switched. For the sake of brevity, the creation of some items and relations is omitted here. Note further that lines 9–12 feature three type-conversion operators to ensure type safety during the statement of matrix equations. Lastly, lines 14–16 use the “universally quantified” expression to create the matrix Q, since the premise has to hold for all positive definite matrices Q.
| Listing 13. Theorem for local asymptotic Lyapunov stability of state space systems. |
 |
| Listing 14. Setting of Theorem 3. |
 |
In the premise in Listing 15, a statement about the existence of a specific matrix P is made.
Note the existential quantifier in line 3. Afterwards, additional conditions are imposed on the matrix P. Therefore, the SymPy-based formula representation is used; see Section 3.5.
In the assertion (Listing 16), we assign the property of global asymptotic stability to the origin and define the Lyapunov function V in relation to the matrix P.
Other approaches to finding a suitable Lyapunov function for a given system are implemented in a similar fashion. In particular, it is made clear what the requirements of an approach are and to what kind of system it is applicable to. Steps towards an application of this knowledge are proposed in Section 6.3.
| Listing 15. Premise of Theorem 3. |
 |
| Listing 16. Assertion of Theorem 3. |
 |
In addition to the aforementioned theorems, many items and relations were implemented in the context of Lyapunov’s theory (see Appendix A). Overall, in its current development state the OCSE is comprised of ≈800 items (As mentioned in Section 3.9 there are 848 total items, including 55 builtin items.).
6. Discussion: Benefits, Applications, Limitations and Reproducibility
With PyIRK and the OCSE, knowledge is formally represented in a way understandable for humans and machines alike. As announced in Section 1 the aim of the current contribution is not to provide a doubtlessly useful product, but instead to present a possible backend for such a knowledge-based application. Nevertheless, the current development state enables some advantages of formal knowledge representation.
6.1. Hierarchies and Dependencies
By explicitly stating the relationships between items and having to explicitly decide the type of every used item or variable in a theorem, the underlying knowledge graph consists of densely connected nodes. This enables the user to infer information about a node (an item) by examining its relations. With the R4[“is instance of”] or R3[“is subclass of”] relations, a hierarchical structure is imposed on an item. For example, I5677[“global asymptotic stability”] is an instance of I5236[“general trajectory property”], which in turn is an instance of the metaclass I54[“mathematical property”]. This categorizes the item in a broad way. Additional relations, such as R17[“is subproperty of”], relate the item to other items in the graph. In this case, I5677[“global asymptotic stability”] is a subproperty of I8744[“global Lyapunov stability”], I8059[“global attractiveness”] and I4900[“local asymptotic stability”]. These relations are transitive, implying that, if the property GAS applies, the property LAS applies as well. Or, in other words, if the trajectory is not LAS, it cannot be GAS (see also Section 3.7).
In the context of learning and teaching, the graph of relations between different pieces of information might be helpful to understand which concepts depend on each other, meaning, e.g., what kind of mathematical concepts, such as positive definiteness, are necessary to understand about Lyapunov functions. The careful reader might have noticed that in the previous code snippets, two different items with the label “positive definiteness” were used (I3133[“positive definiteness”] and I3648[“positive definiteness (matrix)”]). This is because the concept of a positive definite scalar function differs from the concept of a positive definite matrix, although the two are related.
6.2. Quality Assurance
Even though written publications are usually proof-read multiple times, random mistakes and typos, especially in formulas, might still occur. Such errors might include confounding the vector field and scalar field in a Lie derivative, forgetting a transposition sign on a vector or messing up an index notation. With the information in the OCSE being machine-readable, we can automate the process of finding such errors. This can be conducted by formulating dedicated rules (instances of I47[“constraint rule”]), which are part of the knowledge graph itself; see Section 3.7. Currently, three means of quality assurance are applied, as summarized by Figure 4.
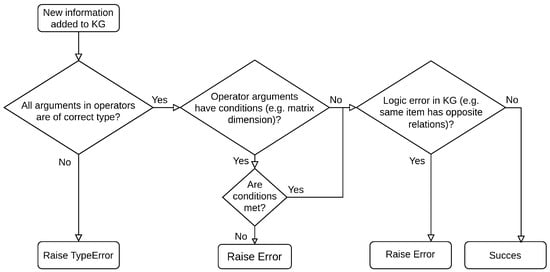
Figure 4.
Process of quality assurance when adding data to the KG.
First, mathematical operators such as multiplication and addition, but also Lie derivative and scalar field only accept arguments of specific types. For example, the I1347[“Lie derivative of scalar field”] takes two arguments, one of type vector field and one of type scalar field. An erroneous implementation of Lhf, meaning the Lie derivative of a vector field along a scalar field, would result in a raised WrongArgType-error.
The second powerful means for quality control is to make sure, that, e.g., the matrix multiplication operator only accepts matrices of adequate size. Keep in mind that PyIRK does not evaluate any numerical multiplication, but it only stores the operation and its arguments. The quality assurance is thus again carried out by the suitable rules (see Section 3.7) and can be implemented for all kinds of operators.
A third tool for quality control is the detection of problematic statements, i.e., incompatible statements or logic errors. An example would be that the same equilibrium point cannot be locally stable and unstable at the same time. Consider the exemplary statement in Listing 17.
| Listing 17. Contradicting statements. |
 |
This would result in an error, since strict Lyapunov instability and local Lyapunov stability have opposite relations, meaning they cannot be true at the same time. Due to the transitivity of property relations, the same error would occur if line 8 was exchanged for line 9.
6.3. Semantic Searchability
With the help of the SPARQL interface (see Section 2.3), we can query the KG for specific information. One might be interested in finding a Lyapunov function for a given system. This can be facilitated by defining the system and its important properties as part of the KG and then running a SPARQL query to search for theorems that apply to this concrete system. For instance, the system in question could be time-invariant and its differential equations could be polynomial. One would define this system as shown in Listing 18.
| Listing 18. Definition of test system. |
 |
Remark 7.
When speaking about dynamical systems, one usually attributes certain properties to them. To avoid ambiguity, the OCSE distinguishes between properties of the system, such as time-variance, properties of the mathematical representation of the system, such as linearity and properties of a trajectory of the system, such as local stability.
With the item testsys in the KG, one can use the following SPARQL query (Listing 19) to search for all theorems applicable to this system.
| Listing 19. SPARQL query for applicable theorems. |
 |
Note that ?th matches all items in the KG with the two specified conditions: (a) They have to be related to mathematical proposition (I14) via an arbitrary combination of R4 and R3, which includes, e.g., implication theorems and equivalence propositions. (b) They have to apply to the system of interest. Consequently, the result of the query, shown in Listing 20 consists of the two algorithms that are applicable to time-invariant polynomial systems.
| Listing 20. Result of the SPARQL query. |
Analogously, all three algorithms of Section 4.2 would be returned if the test system was a linear time-invariant system.
The logic behind the relation R80[“applies to”] examines all theorems and makes sure that conditions expressed in their setting scopes match with the conditions of all the systems in the KG. Each match between the theorem and system is connected with the R80 relation.
Although this is a rather rudimentary example, the SPARQL interface can prove a powerful tool, especially if compared to ordinary text-based search. This becomes even more obvious in the next example, as shown in Listing 21.
| Listing 21. SPARQL query for affine systems with a stable and an unstable equilibrium. |
 |
This query returns systems in the system model catalog [28] that have (at least) two different equilibrium points—one stable and one unstable. Additionally, only control affine models with at least four state components are selected. In this case, the model catalog includes six matching results:
- Model of triple pendulum;
- Model of furuta pendulum;
- Model of cartpole system;
- Model of acrobot;
- Model of inertia wheel pendulum;
- Model of pendubot.
Remark 8
(Intermediate Summary). To summarize Section 6.1, Section 6.2 and Section 6.3, the formal representation of control engineering knowledge in the OCSE along with the feature set of PyIRK allows to access this knowledge in new ways. We stress that our goal is not to develop new methods, but rather to facilitate the knowledge transfer within the field of control engineering and towards application domains and enable the user to find the right method or theorem for the respective problem.
6.4. Limitations
While, until now, we have mainly discussed the advantages of our approach, we also want to address the weaknesses—some of which might be solved in the future.
Two related issues are performance and scalability. With the current size of the KG, the OCSE’s unit tests (which include the means of quality assurance described above) run for 8 s (on an Intel Core i7-1360P processor in a 2023 consumer notebook), and the PyIRK tests take about 30 s. While an explicit performance analysis has not yet been carried out, it was observed during development that these times increase with the size of the knowledge graph, mainly caused by the rule-based reasoning tasks. This lets us estimate that scalability issues might arise for KG sizes > nodes. This number is significantly lower than the currently ≈108 nodes of Wikidata [67]. Nevertheless, we are confident that PyIRK KGs can be large enough to be useful in scientific niches such as control theory while still being sufficiently performant. It should also be noted that possible future performance issues are irrelevant for use cases that only aim at knowledge retrieval (rather than reasoning and consistency checking) because the SPARQL interface operates on the RDF export of the KG.
We want to point out that the current focus of PyIRK and OCSE development is to demonstrate the usefulness of formal knowledge representation. Given limited development resources, progress towards this goal is made by accepting compromises with reference to performance and scalability. The most obvious example of this strategy is the fundamental choice to drop OWL and its favorable description-logic-based computability properties, and instead, to choose a (comparatively slow) Turing-complete programming language for knowledge representation to achieve more expressive power.
Another issue is usability. To facilitate knowledge transfer, engineers should be able to use PyIRK within a few minutes. A crucial point for using the framework is to have convenient access to all the keys such as I9820[“equilibrium point”] or R16[“has property”]. Again, Wikidata gives a good orientation that this challenge can be tackled by a combination of good documentation, a decent collection of examples and a user interface (UI) with automatic syntax completion based on fuzzy search. A similar approach is used for PyIRK: the documentation available at https://pyirk-core.readthedocs.io (accessed on 30 December 2023) covers the most important concepts, the unit tests contain several examples and there exist two approaches for key auto-completion-based on search results over the labels and descriptions of entities (see https://github.com/ackrep-org/pyirk-django/ (accessed on 30 December 2023) and https://github.com/ackrep-org/irk-fzf/ (accessed on 30 December 2023)). However, all three usability components have to be improved significantly. Therefore, the biggest challenge is the creation of a suitable UI—both for entering new knowledge and retrieving (and presenting) existing knowledge.
Finally, the fact that the OCSE in its current version only covers a very limited amount of control engineering knowledge is obviously a limitation. A reasonable direction for extension would be to incorporate concepts and statements for the stability analysis of time discrete systems or distributed parameter systems. However, the main, yet unsolved, issue in this regard is (apart from the technical scalability issues discussed above) how to incentivize and organize the contribution process such that it becomes self-sustained.
6.5. Reproducibility
The major motivation for PyIRK and the OCSE is to facilitate knowledge transfer. Since in our approach the knowledge is represented as source code, it is a crucial requirement that this code is executable and produces the correct results on any system it runs on, especially the local systems of possible users. This might sound trivial, but experience from decades of computation-based research shows that it is not [25,68]. To ensure this, we publish our source code along with the respective suite of over 100 unit tests. Furthermore, we facilitate a continuous integration service to ensure that the tests not only pass on our local development systems but also in an explicitly defined containerized test environment.
7. Conclusions and Outlook
In this contribution, we present a novel imperative approach for the formal representation of control engineering knowledge with a focus on concepts and theorems from Lyapunov’s theory. We demonstrate that it is possible to model this kind of complex information in a way that enables subsequent applications such as automated quality assurance and enhanced search. Therefore, the basic approach is to exploit the expressive power of a full-featured programming language as opposed to the various OWL profiles, which are optimized for reasoning computability and performance at the cost of expressiveness. This facilitates techniques like scopes, applied operators, or convenient formulas. Nevertheless, the resulting knowledge graph can be exported to RDF and thus is compatible with the most widespread standard of the semantic web.
The benefits and applications shown (see Section 6) mainly serve as proof of concept. The long-term goal is to develop assistance software, which, e.g., helps to find a suitable Lyapunov function for a given dynamical system or to solve other control problems. Such assistant software might improve the accessibility of the large corpus of control theory and thus facilitate the knowledge transfer between various niches of control engineering, as well as into (new) potential application domains.
In any case, the availability of an open and multilingual domain-specific knowledge repository can be seen as a value by itself, as it helps to communicate progress (and formulate questions) precisely and with little effort (just by issuing a merge-request). The git-based infrastructure greatly supports this usage as it makes it easy to have different (experimental) versions of the knowledge base available (in git branches) and also allows precisely tracking every change to the knowledge with reference to the author, commit time and commit message.
While this paper shows that formal representation of non-trivial control-engineering content is possible, many questions remain open for future research and development, for example:
- How can contributions to the OCSE (new entities and statements, but also manual quality assurance) be incentivized?
- How exactly can the KG be processed to provide useful information and thus facilitate the desired knowledge transfer?
- How can the computational performance be improved to maintain current loading and reasoning times (some seconds) also when the number of nodes and relations increases by an order of magnitude?
- Is there a relevant educational effect of formalizing knowledge or peer-reviewing formalized knowledge? (This question is based on the observation that the formalization process requires a deep understanding of the respective propositions and the related concepts.)
- Assuming that there will be a relevant number of external contributions, how should the plurality of possible perspectives (different concepts, methods, notations, theories) on scientific questions be dealt with?
However, based on the direct feedback we obtained over the last two years, the biggest open question is how our KG-based approach (i.e., “symbolic AI”) compares to and can be combined with learning-based approaches (“numeric AI”) such as LLMs. In recent years, LLM-based systems (such as ChatGPT) have impressively demonstrated both their capabilities as well as their shortcomings. Our expectation is that the availability of a precise knowledge base such as a KG can be used to overcome the problem of neural network hallucination, or at least to detect it.
Another possible combination is to use an LLM to extract distinct kinds of knowledge directly from selected source files (such as papers) and convert it to PyIRK source code. This could drastically reduce the manual effort necessary for formalizing knowledge. Consequently, this could make it realistic to formalize a significant part of the control engineering knowledge.
Answering the question of whether the symbolic-based (KG) or the numeric-based (LLM) approach is better for knowledge representation will probably be very sensitive with reference to the concrete task and the definition of “better”. In any case, a major advantage of the symbolic approach will always be the explainability, i.e., the direct and transparent link between the result and the source data (the knowledge graph).
Author Contributions
Conceptualization, C.K. and J.F.; methodology, C.K. and J.F.; software, C.K. and J.F.; validation, C.K., J.F. and S.E.; writing—original draft preparation, C.K. and J.F.; writing—review and editing, C.K., J.F. and S.E.; visualization, C.K. and S.E.; All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
All data relevant for this paper is available in public repositories: See [29] for the PyIRK source code and [30] for the OCSE knowledge base (also represented as source code).
Acknowledgments
The authors thank the anonymous reviewers for their valuable remarks, questions and suggestions. Furthermore, we cordially thank Romy Müller for providing lots of very helpful comments based on the preprint (v1) and Kilian Göller for his useful remarks during the preparation phase.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A. List of Items and Relations in the Context of Lyapunov Theory
The following list of items, which relate to Lyapunov’s theory, is implemented in the OCSE.

Table A1.
List of implemented items relating to Lyapunov’s theory.
Table A1.
List of implemented items relating to Lyapunov’s theory.
| I1347 | Lie derivative of scalar field |
| I6229 | Definition of Lie derivative of scalar field |
| I3133* | Positive definiteness |
| I3134* | Definition of positive definiteness |
| I3135* | Positive semidefiniteness |
| I3136* | Negative definiteness |
| I8492* | Definition of negative definiteness |
| I3137* | Negative semidefiniteness |
| I3648* | Positive definiteness (matrix) |
| I6117* | Definition of positive definiteness (matrix) |
| I5753* | Radially unboundedness |
| I5082 | Local attractiveness |
| I8059 | Global attractiveness |
| I2931 | Local Lyapunov stability |
| I8744 | Global Lyapunov stability |
| I4900 | Local asymptotic stability |
| I5677 | Global asymptotic stability |
| I9642 | Local exponential stability |
| I5100 | Global exponential stability |
| I8303 | Strict Lyapunov instability |
| I2933 | Lyapunov Function |
| I9208 | Weak Lyapunov Function |
| I9199 | Strong Lyapunov Function |
| I5483 | Control Lyapunov Function |
| I3369 | Sontags formula |
| I4663 | Theorem for local Lyapunov stability of state space system |
| I8733 | Theorem for local asymptotic Lyapunov stability of state space system |
| I2983 | Theorem for global asymptotic Lyapunov stability of state space system |
| I3503 | Input-to-state stability |
| I6994 | Chetaev instability theorem |
| I3303 | Attractor |
| I5106 | Repulsor |
| I9875 | Region of attraction |
| I9903 | LaSalle’s invariance principle |
| I6338 | Lyapunov Equation |
| I3712 | Theorem on Lyapunov Equation and Stability |
| I4432 | Vannelli recursive algorithm to find Lyapunov function |
| I8142 | Theorem by Vannelli for Lyapunov functions for homogeneous systems |
| I4274 | Theorem by Goubault for Lyapunov functions for polynomial systems |
| I7006 | Goubault algorithm to find Lyapunov function |
| I2613 | Theorem for Lyapunov functions for linear systems |
Note that items with an asterisk live in the math module. Note further that positive definiteness appears twice since there are two different properties with this label (relating to positive definite scalar function and positive definite matrix). The detail of the information implemented differs for each item. Some items have rigorous definitions, most items are sorted into the existing hierarchy, meaning they have a parent class and some relations to other meaningful items, and some small amount of items are implemented as stub items, with little more information than their label.
References
- Faulwasser, T.; Flaßkamp, K.; Ober-Blöbaum, S.; Worthmann, K. Towards Velocity Turnpikes in Optimal Control of Mechanical Systems. In Proceedings of the 11th IFAC Symposium on Nonlinear Control Systems NOLCOS, Vienna, Austria, 4–6 September 2019; pp. 490–495. [Google Scholar]
- Franke, M.; Zaiczek, T.; Röbenack, K. Simulation of Nonholonomic Mechanical Systems Using Algorithmic Differentiation. In Proceedings of the 7th Vienna International Conference on Mathematical Modelling (MATHMOD), Vienna, Austria, 14–17 February 2012. [Google Scholar]
- Schöberl, M. Contributions to the Analysis of Structural Properties of Dynamical Systems in Control and Systems Theory: A Geometric Approach; Shaker: Aachen, Germany, 2014. [Google Scholar]
- Irscheid, A.; Deutscher, J.; Gehring, N.; Rudolph, J. Output Regulation for General Heterodirectional Linear Hyperbolic PDEs Coupled with Nonlinear ODEs. Automatica 2023, 148, 110748. [Google Scholar] [CrossRef]
- de Wit, C.C.; Siciliano, B.; Bastin, G. Theory of Robot Control; Springer Science & Business Media: London, UK, 2012. [Google Scholar]
- Isermann, R. Automotive Control: Modeling and Control of Vehicles; Springer: Berlin/Heidelberg, Germany, 2022. [Google Scholar]
- Urbas, L.; Krause, A.; Ziegler, J. Process Control Systems Engineering; Oldenbourg: Munich, Germany, 2012. [Google Scholar]
- Rudolph, J.; Winkler, J.; Woittennek, F. Flatness Based Control of Distributed Parameter Systems: Examples and Computer Exercises from Various Technological Domains; Shaker: Aachen, Germany, 2003. [Google Scholar]
- Shah, P.; Sekhar, R.; Sharma, D.; Penubadi, H.R. Fractional Order Control: A Bibliometric Analysis (2000–2022). Results Control Optim. 2024, 14, 100366. [Google Scholar] [CrossRef]
- Bornmann, L.; Mutz, R. Growth Rates of Modern Science: A Bibliometric Analysis Based on the Number of Publications and Cited References. J. Assoc. Inf. Sci. Technol. 2015, 66, 2215–2222. [Google Scholar] [CrossRef]
- National Science Board. Publications Output: U.S. Trends and International Comparisons. 2019. Available online: https://ncses.nsf.gov/pubs/nsb20206/ (accessed on 11 February 2024).
- Kohlhase, M. Mathematical Knowledge Management: Transcending the One-Brain-Barrier with Theory Graphs. Eur. Math. Soc. (EMS) Newsl. 2014, 92, 22–27. [Google Scholar]
- Ecklebe, S.; Gehring, N. Backstepping-Based Tracking Control of the Vertical Gradient Freeze Crystal Growth Process. In Proceedings of the 22nd IFAC World Congress, Yokohama, Japan, 9–14 July 2023; pp. 8171–8176. [Google Scholar]
- Berners-Lee, T.; Hendler, J.; Lassila, O. The Semantic Web. Sci. Am. 2001, 284, 34–43. [Google Scholar] [CrossRef]
- Patel, A.; Jain, S. Present and Future of Semantic Web Technologies: A Tesearch Statement. Int. J. Comput. Appl. 2021, 43, 413–422. [Google Scholar] [CrossRef]
- Directorate-General for Research and Innovation (European Commission); EOSC Executive Board. Strategic Research and Innovation Agenda (SRIA) of the European Open Science Cloud (EOSC); Publications Office of the European Union: Luxembourg, 2022. [Google Scholar]
- Rossenova, L.; Schubotz, M.; Shigapov, R. The Case for a Common, Reusable Knowledge Graph Infrastructure for NFDI. In Proceedings of the Conference on Research Data Infrastructure, Karlsruhe, Germany, 12–14 September 2023; Volume 1. [Google Scholar]
- Dessimoz, C.; Škunca, N. (Eds.) The Gene Ontology Handbook; Springer: New York, NY, USA, 2017. [Google Scholar]
- Darlington, M.; Culley, S. Investigating Ontology Development for Engineering Design Support. Adv. Eng. Inform. 2008, 22, 112–134. [Google Scholar] [CrossRef]
- Haidegger, T. Taxonomy and Standards in Robotics. In Encyclopedia of Robotics; Ang, M.H., Khatib, O., Siciliano, B., Eds.; Springer Nature: Berlin, Germany, 2021. [Google Scholar]
- Benavides, C.; Garcia, I.; Alaiz, H.; Alfonso, J.; Redondo, C.; Alonso, A. Ontologies as Knowledge Representation Structures for CACSD Software. In Proceedings of the 2008 IEEE International Conference on Computer-Aided Control Systems, San Antonio, TX, USA, 3–5 September 2008; pp. 1277–1282. [Google Scholar]
- Benavides, C.; García, I.; Alaiz, H.; Quesada, L. An Ontology-Based Approach to Knowledge Representation for Computer-Aided Control System Design. Data Knowl. Eng. 2018, 118, 107–125. [Google Scholar] [CrossRef]
- Knoll, C.; Heedt, R. “Automatic Control Knowledge Repository”—A Computational Approach for Simpler and More Robust Reproducibility of Results in Control Theory. In Proceedings of the 24th International Conference on System Theory, Control and Computing (ICSTCC), Sinaia, Romania, 8–10 October 2020; pp. 130–136. [Google Scholar]
- Knoll, C. Examining the ORKG towards Representation of Control Theoretic Knowledge–Preliminary Experiences and Conclusions. In Proceedings of the Web Conference (Companion Proceedings), Lyon France, 25–29 April 2022; pp. 810–817. [Google Scholar]
- Knoll, C.; Heedt, R. Tool-based Support for the FAIR Principles for Control Theoretic Results: The “Automatic Control Knowledge Repository”. Syst. Theory Control Comput. J. 2021, 1, 56–67. [Google Scholar] [CrossRef]
- Heedt, R.; Knoll, C.; Röbenack, K. Formal Semantic Representation of Methods in Automatic Control. In Proceedings of the VDI Mechatroniktagung, Darmstadt, Germany, 24–25 March 2021. (In Germany). [Google Scholar]
- Fiedler, J.; Gerwien, M.; Knoll, C. A Hybrid Tactical Decision-Making Approach in Automated Driving Combining Knowledge-Based Systems and Reinforcement Learning. In Proceedings of the IEEE 25th International Conference on Intelligent Transportation Systems (ITSC), Macau, China, 8–12 October 2022; pp. 3478–3483. [Google Scholar]
- Fiedler, J.; Knoll, C. Catalog of Dynamical System Models with Semantic Metadata. PAMM 2023, 23, e202300049. [Google Scholar] [CrossRef]
- Knoll, C.; Fiedler, J. Python-based Imperative Knowledge Representation (PyIRK)—-Source Repository on GitHub. 2023. Available online: https://github.com/ackrep-org/pyirk-core (accessed on 30 December 2023).
- Knoll, C.; Fiedler, J. Ontology of Control Systems Engineering (OCSE)—Source Repository on GitHub. 2023. Available online: https://github.com/ackrep-org/ocse (accessed on 30 December 2023).
- Röbenack, K.; Palis, S. Set-Point Control of a Spatially Distributed Buck Converter. Algorithms 2023, 16, 55. [Google Scholar] [CrossRef]
- Röbenack, K.; Voßwinkel, R.; Richter, H. Calculating Positive Invariant Sets: A Quantifier Elimination Approach. J. Comput. Nonlinear Dyn. 2019, 14, 074502. [Google Scholar] [CrossRef]
- Gerbet, D.; Röbenack, K. Application of LaSalle’s Invariance Principle on Polynomial Differential Equations Using Quantifier Elimination. IEEE Trans. Autom. Control 2022, 67, 3590–3597. [Google Scholar] [CrossRef]
- Naveed, H.; Khan, A.U.; Qiu, S.; Saqib, M.; Anwar, S.; Usman, M.; Akhtar, N.; Barnes, N.; Mian, A. A Comprehensive Overview of Large Language Models. arXiv 2023, arXiv:2307.06435. [Google Scholar]
- Guarino, N.; Oberle, D.; Staab, S. What is an Ontology? In Handbook on Ontologies; Springer: Berlin/Heidelberg, Germany, 2009; pp. 1–17. [Google Scholar]
- Bergman, M.K. Knowledge Representation Practionary; Springer: Berlin/Heidelberg, Germany, 2018. [Google Scholar]
- Keet, M. An Introduction to Ontology Engineering, v1.5; College Publications: Cape Town, South Africa, 2020. [Google Scholar]
- Allemang, D.; Hendler, J.; Gandon, F. Semantic Web for the Working Ontologist: Effective Modeling for Linked Data, RDFS, and OWL, 3rd ed.; Morgan & Claypool: Kentfield, CA, USA, 2020; Volume 33. [Google Scholar]
- Pease, A.; Niles, I. IEEE Standard Upper Ontology: A Progress Report. Knowl. Eng. Rev. 2002, 17, 65–70. [Google Scholar] [CrossRef]
- Baader, F.; Calvanese, D.; McGuinness, D.; Patel-Schneider, P.; Nardi, D.; Patel-Schneider, P.F. The Description Logic Handbook: Theory, Implementation and Applications; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Krötzsch, M.; Marx, M.; Ozaki, A.; Thost, V. Attributed Description Logics: Ontologies for Knowledge Graphs. In Proceedings of the International Semantic Web Conference, Vienna, Austria, 21–25 October 2017; Springer: Berlin/Heidelberg, Germany, 2017; pp. 418–435. [Google Scholar]
- Vrandečić, D.; Krötzsch, M. Wikidata: A Free Collaborative Knowledgebase. Commun. ACM 2014, 57, 78–85. [Google Scholar] [CrossRef]
- Jaradeh, M.Y.; Oelen, A.; Farfar, K.E.; Prinz, M.; D’Souza, J.; Kismihók, G.; Stocker, M.; Auer, S. Open Research Knowledge Graph: Next Generation Infrastructure for Semantic Scholarly Knowledge. In Proceedings of the 10th International Conference on Knowledge Capture, Marina Del Rey, CA, USA, 19–21 November 2019; pp. 243–246. [Google Scholar]
- Auer, S.; Stocker, M.; Vogt, L.; Fraumann, G.; Garatzogianni, A. ORKG: Facilitating the Transfer of Research Results with the Open Research Knowledge Graph. Res. Ideas Outcomes 2021, 7, e68513. [Google Scholar] [CrossRef]
- Pérez, J.; Arenas, M.; Gutierrez, C. Semantics and Complexity of SPARQL. In Proceedings of the International Semantic Web Conference, Athens, GA, USA, 5–9 November 2006; Springer: Berlin/Heidelberg, Germany, 2006; pp. 30–43. [Google Scholar]
- World Wide Web Consortium and Others. SPARQL 1.1 Overview. 2013. Available online: https://www.w3.org/TR/sparql11-overview (accessed on 11 February 2024).
- Ali, W.; Saleem, M.; Yao, B.; Hogan, A.; Ngomo, A.C.N. A Survey of RDF Stores & SPARQL Engines for Querying Knowledge Graphs. VLDB J. 2022, 31, 1–26. [Google Scholar]
- Grimm, S.; Hitzler, P.; Abecker, A. Logic, Ontologies and Semantic Web Languages. In Semantic Web Services: Concepts, Technologies, and Applications; Springer: London, UK, 2007. [Google Scholar]
- Xue, Y.; Ghenniwa, H.H.; Shen, W. Frame-Based Ontological View for Semantic Integration. J. Netw. Comput. Appl. 2012, 35, 121–131. [Google Scholar] [CrossRef]
- Baader, F.; Horrocks, I.; Lutz, C.; Sattler, U. Introduction to Description Logic; Cambridge University Press: Cambridge, UK, 2017. [Google Scholar]
- Arp, R.; Smith, B.; Spear, A.D. Building Ontologies with Basic Formal Ontology; MIT Press: Cambridge, MA, USA, 2015. [Google Scholar]
- Munn, K.; Smith, B. (Eds.) Applied Ontology—An Introduction; De Gruyter: Berlin, Germany, 2008. [Google Scholar]
- Wikibooks Contributors. SPARQL/WIKIDATA Qualifiers, References and Ranks—Wikibooks, The Free Textbook Project, 2021. Available online: https://en.wikibooks.org/w/index.php?title=SPARQL/WIKIDATA_Qualifiers,_References_and_Ranks&oldid=3967507 (accessed on 14 December 2023).
- Meurer, A.; Smith, C.P.; Paprocki, M.; Čertík, O.; Kirpichev, S.B.; Rocklin, M.; Kumar, A.; Ivanov, S.; Moore, J.K.; Singh, S.; et al. SymPy: Symbolic Computing in Python. PeerJ Comput. Sci. 2017, 3, e103. [Google Scholar] [CrossRef]
- Lamy, J.B. Owlready: Ontology-Oriented Programming in Python with Automatic Classification and High Level Constructs for Biomedical Ontologies. Artif. Intell. Med. 2017, 80, 11–28. [Google Scholar] [CrossRef] [PubMed]
- Carral, D.; Dragoste, I.; González, L.; Jacobs, C.; Krötzsch, M.; Urbani, J. Vlog: A Rule Engine for Knowledge Graphs. In Proceedings of the 18th International Semantic Web Conference, Part II, Auckland, New Zealand, 26–30 October 2019; Springer: Berlin/Heidelberg, Germany, 2019; pp. 19–35. [Google Scholar]
- Ivliev, A.; Ellmauthaler, S.; Gerlach, L.; Marx, M.; Meißner, M.; Meusel, S.; Krötzsch, M. Nemo: First Glimpse of a New Rule Engine. In Proceedings of the 39th International Conference on Logic Programming (ICLP 2023), London, UK, 9–15 July 2023; Pontelli, E., Costantini, S., Dodaro, C., Gaggl, S., Calegari, R., Garcez, A.D., Fabiano, F., Mileo, A., Russo, A., Toni, F., Eds.; Volume 385, pp. 333–335. [Google Scholar]
- Cordella, L.P.; Foggia, P.; Sansone, C.; Vento, M. A (Sub) Graph Isomorphism Algorithm for Matching Large Graphs. IEEE Trans. Pattern Anal. Mach. Intell. 2004, 26, 1367–1372. [Google Scholar] [CrossRef] [PubMed]
- Hagberg, A.; Schult, D.; Swart, P. Exploring Network Structure, Dynamics, and Function using NetworkX. In Proceedings of the 7th Python in Science Conference (SciPy2008), Pasadena, CA, USA, 19–24 August 2008; pp. 11–15. [Google Scholar]
- Wikipedia Contributors. Zebra Puzzle—Wikipedia, The Free Encyclopedia. 2023. Available online: https://en.wikipedia.org/w/index.php?title=Zebra_Puzzle&oldid=1183109914 (accessed on 27 December 2023).
- Khalil, H. Nonlinear Control; Pearson: London, UK, 2014. [Google Scholar]
- Slotine, J.J.E.; Li, W. Applied Nonlinear Control; Prentice Hall: Englewood Cliffs, NJ, USA, 1991; Volume 199. [Google Scholar]
- Adamy, J. Nonlinear Systems and Controls; Springer: Berlin/Heidelberg, Germany, 2022. [Google Scholar]
- Giesl, P.; Hafstein, S. Review on Computational Methods for Lyapunov Functions. Discret. Contin. Dyn. Syst.-B 2015, 20, 2291–2331. [Google Scholar]
- Vannelli, A.; Vidyasagar, M. Maximal Lyapunov Functions and Domains of Attraction for Autonomous Nonlinear Systems. Automatica 1985, 21, 69–80. [Google Scholar] [CrossRef]
- Goubault, E.; Jourdan, J.H.; Putot, S.; Sankaranarayanan, S. Finding Non-Polynomial Positive Invariants and Lyapunov Functions for Polynomial Systems Through Darboux Polynomials. In Proceedings of the 2014 American Control Conference, Portland, OR, USA, 4–6 June 2014; pp. 3571–3578. [Google Scholar]
- Wikidata Contributors. Wikidata:Statistics. Available online: https://www.wikidata.org/w/index.php?title=Wikidata:Statistics&oldid=1876166148 (accessed on 11 February 2024).
- Merali, Z. Computational science: …Error. Nature 2010, 467, 775–777. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).