Abstract
High-precision tracking of an electro-hydraulic servo material testing machine’s force control system was achieved using a proposed integral sliding mode control method based on feedback linearization to improve the machine’s force control performance and anti-interference ability. First, the electro-hydraulic servo system’s nonlinear mathematical model was established, and its input–output linearization was realized using differential geometry theory. Second, integral sliding mode control was introduced into the controller and the feedback-linearized integral sliding mode controller was designed. The controller’s stability was proven based on the Lyapunov stability principle. Finally, a simulation model of the electro-hydraulic servo material testing machine’s force control system was established using AMESim/Simulink software. The designed controller was simulated and verified, and the control effects of the system’s different amplitudes and frequency signals were analyzed. The results showed that the feedback-linearized integral sliding mode control algorithm could effectively improve the system’s force tracking accuracy and parameter adaptability, yielding better robustness and a better control effect.
1. Introduction
Fatigue is a material’s response to the cyclic stress or cyclic strain it is subjected to during use and is an accumulation of the material’s damage process [1]. Every year during production and real-world usage, every year due to fatigue caused by mechanical equipment, building, bridge, and ship failures occur due to mechanical equipment fatigue, resulting in countless losses across all aspects. With the continuous growth of China’s economy and the continuous improvement in people’s living standards, the demand for high-quality mechanical and industrial products has gradually increased; this increasing demand has produced new challenges.
A material testing machine is commonly used to test a material’s fatigue life. Testers perform fatigue tests on material samples and then analyze the material’s properties according to the test results to predict a material’s lifespan [2].
The material testing machine developed in this study uses an electro-hydraulic servo system to control loading. The high-speed, precise, and highly reliable electro-hydraulic servo system proposed by the Massachusetts Institute of Technology was quickly adopted for use in the industry and has been widely used in robot motion control [3,4,5], missile steering gear [6,7], material performance test equipment [8,9], and so on. However, the electro-hydraulic servo system has nonlinear characteristics, such as parametric uncertainties, uncertain nonlinearities, and external interference, which seriously affect its control performance. Research aimed at solving these problems has primarily been conducted by building system mathematical models [10,11,12] and a control algorithm [13]. In recent years, domestic and foreign experts have conducted a significant amount of research regarding control algorithms and proposed a variety of control methods.
Ref. [14] addressed the system instability and control accuracy reduction caused by load stiffness changes and described an adaptive control strategy based on the dominant pole reference model that effectively suppresses the load stiffness change’s influence on the electro-hydraulic servo system’s dynamic characteristics. However, this method is limited by the adaptive coefficient R; when R is too large, the system overshoots. Ref. [15] designed a feedback-linearized sliding mode controller to realize relatively high precision tracking of the electro-hydraulic servo system in view of the impact of changes in load, hydraulic oil viscosity, and system pressure on the electro-hydraulic servo system’s control accuracy. Ref. [16] designed a fuzzy PID controller with self-tuning parameters to effectively improve the electro-hydraulic servo system’s anti-interference ability to address the reduction of its control accuracy by environmental interference and cross coupling. However, fuzzy rules rely on empirical judgment and are not universal. Ref. [17] designed an adaptive robust controller to address uncertain interference in the electro-hydraulic servo system, which could effectively suppress external interference and improve the system’s tracking accuracy. Ref. [18] proposed that information fusion and the backpropagation Levenberg–Marquardt algorithm be applied to the electro-hydraulic servo system to effectively suppress the influence of position disturbance on control accuracy. The controller designs of Refs. [17,18] were complex and not conducive to practical application. Ref. [19] designed a hybrid force/bit controller to solve the electro-hydraulic servo system’s residual force problem. Designing an appropriate control rate smoothed the force/bit control switch and reduced the residual force interference. Ref. [20] proposed that the electro-hydraulic servo system can be divided into two subsystems, a linear subsystem and a nonlinear subsystem, with the nonlinear subsystem tracking the linear subsystem, thus creating a cascade sliding mode controller to effectively improve the electro-hydraulic servo system’s tracking accuracy. Ref. [21] combined the levy flight beetle antennae search algorithm with the PID controller to effectively improve the electro-hydraulic servo system’s control performance. Refs. [19,20,21] did not consider the influence of external interference on the controller when designing their controllers. Ref. [22] designed a sliding mode controller based on radial basis function (RBF) neural network compensation, which effectively improved the electro-hydraulic servo system’s robustness regarding uncertain interference and nonlinear characteristic interference. However, the compensation of this RBF control algorithm was easily affected by the external interference system, which led to a lack of robustness in the controller.
In terms of feedback linearization, Ref. [23] proposed a control strategy that combined feedback linearization theory with sliding mode variable structure theory to eliminate the sliding mode control buffeting problem, effectively improving the electro-hydraulic position servo system’s tracking quality and robustness. Ref. [24] introduced fuzzy control into feedback-linearized sliding mode control, which effectively improved the electro-hydraulic position servo system’s adaptive ability and accelerated its response velocity. The single test signal and evaluation index presented in Refs. [23,24] could not effectively show the controller’s performance. Ref. [25] proposed a control strategy combining sliding mode control based on input and output feedback linearization with a nonlinear interference observer, which effectively improved the electro-hydraulic position servo system’s tracking performance under external interference. Ref. [26] combined neural network control with feedback linearization to compensate for uncertain parameters in the control process and improved the electro-hydraulic position servo system’s control accuracy. Ref. [27] proposed a linearized nonlinear control method based on a dynamic neural network with input and output feedback and adopted a particle swarm optimization algorithm to select controller gain and deep neural network weight, effectively improving the electro-hydraulic position servo system’s robustness. The controllers designed in Refs. [25,26,27] were complicated, difficult to apply to engineering practice, and difficult to use with set parameters.
In terms of sliding mode control, Ref. [28] established the continuous control law equation based on the open-loop transfer function state–space model and then designed a continuous sliding mode controller that could effectively overcome the electro-hydraulic position servo system’s uncertainty and disturbance. However, the influence of external interference on the controller was not considered in that paper. Ref. [29] proposed using the singular disturbance theory to reduce the order of the electro-hydraulic servo system’s mathematical model; then, the mathematical model of the reduced order pump-controlled electro-hydraulic position servo system was obtained, and the extended state observer was used to observe the system interference online. This observer could also estimate the piston rod’s position and velocity signals, which were then used to design the sliding mode controller. This controller could accurately estimate interference, which greatly improved its robustness. Ref. [30] proposed a new smooth and continuous sliding mode control law for the suppression of unmatched interference in an electro-hydraulic position servo system and combined the sliding mode control law with the reverse step recurrence controller design method to design a sliding mode reverse step recurrence controller. This could effectively suppress unknown unmatched interference and output jailing in an electro-hydraulic position servo system. Ref. [31] combined a high-gain observer with sliding mode control and replaced the symbol function with the continuous change function in the sliding mode controller. This effectively improved the electro-hydraulic position servo system’s response velocity and tracking accuracy. The controller designed in Refs. [29,30,31] had good control performance, but the control design was complicated and difficult to apply in engineering. Ref. [32] combined the disturbance observer with sliding mode control, which achieved accurate position control and had good robustness; however, there is an inevitable buffeting problem due to the use of sliding mode control.
Offline iterative control is widely used in automated production [33] in industrial fields such as robot motion planning [34] and process control systems [35]. It optimizes production processes through a pre-set control strategy and automatically adjusts parameters without manual intervention to improve production efficiency and product quality. However, such control methods often rely on precise system models and presuppositions and have a limited ability to address uncertainty and nonlinear problems.
Using a feedback-linearized integral sliding mode control algorithm provides an effective solution to these challenges. The algorithm combines the advantages of feedback linearization and integral sliding mode control to achieve global stability control of nonlinear systems while providing stronger robustness to deal with system parameter uncertainty and external interference. Feedback-linearized integral sliding mode control has significant advantages over the off-line iterative control traditionally used in electro-hydraulic servo material testing machines. It can not only ensure the accuracy and repeatability of the test process but also adapt to dynamic system changes and disturbances from the external environment by adjusting the control strategy in real time to ensure higher test data reliability and equipment performance stability. The application of this control algorithm enables electro-hydraulic servo material testing machines to maintain efficient and accurate operation in the face of complex and changeable test conditions, which greatly improves material testing’s accuracy and efficiency.
To solve the problems mentioned above, a feedback-linearized integral sliding mode (FLISM) controller was designed. The controller has a simple design and requires few tuning parameters. After the electro-hydraulic servo system is linearized by feedback, the influence of nonlinear terms on the control effect can be reduced. The buffeting problem caused by sliding mode control can be effectively avoided by combining feedback linearization with sliding mode control. An integral term is introduced into sliding mode control to improve the controller’s anti-interference performance.
This paper is organized as follows: Section 2 introduces the structure of the electro-hydraulic servo material testing machine addressed in this study. Section 3 introduces the electro-hydraulic servo control structure of the electro-hydraulic servo material testing machine and deduces the system’s state equation. Section 4 presents a feedback-linearized integral sliding mode controller using feedback linearization theory and the integral sliding mode control method and describes how the system’s stability was tested using the Lyapunov function. Section 5 presents an analysis of the simulation results.
2. Structure of Electro-Hydraulic Servo Material Testing Machine
The structure of the electro-hydraulic servo material testing machine designed by the authors is shown in Figure 1: 1 is the upper beam, 2 is the lifting cylinder, 3 is the fuselage, 4 is the column, 5 is the beam lock, 6 is the main hydraulic cylinder, 7 is the accumulator, 8 is the middle beam, and 9 is the servo valve. The upper beam is tightly locked with the column through the beam lock so that it forms a hydraulic frame with load-bearing capacity [36]. The hydraulic cylinder is fixed on the middle beam, and the piston rod inside the hydraulic cylinder is connected with the lower fixture through that part. A diagram of the electro-hydraulic servo material testing machine’s hydraulic system is shown in Figure 2: 1.1~1.5 are tanks, 2.1 is the filter, 3.1 is the motor, 4.1 is hydraulic pump, 5.1 is the relief valve, 6.1 is the check valve, 7.1~7.3 are directional control valves, 8.1 is the servo valve, 9.1~9.2 are pilot-operated check valves, 10.1~10.2 are throttle valves, 11.1~11.2 are plunger cylinders, 12.1 is the piston cylinder, M is the motor, and m is the load quality simulation driven by the hydraulic cylinder.
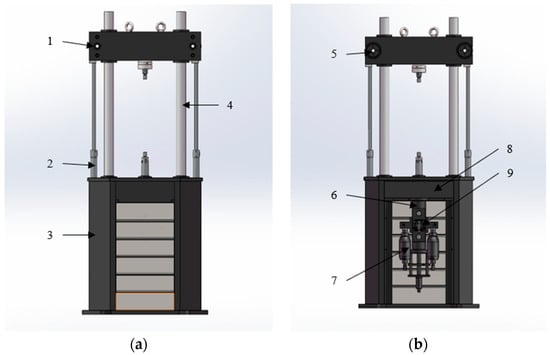
Figure 1.
Illustrations of electro-hydraulic servo material testing machine: (a) front view and (b) rear view.
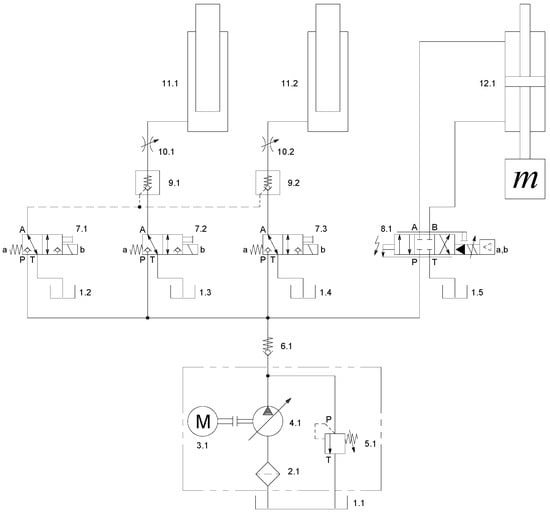
Figure 2.
Diagram of the electro-hydraulic servo material testing machine’s hydraulic system.
3. Force Servo Control System of Electro-Hydraulic Servo Material Testing Machine
3.1. Structure of Force Servo Control System of Electro-Hydraulic Servo Material Testing Machine
The electro-hydraulic servo material testing machine’s force servo control system’s structure is shown in Figure 3.
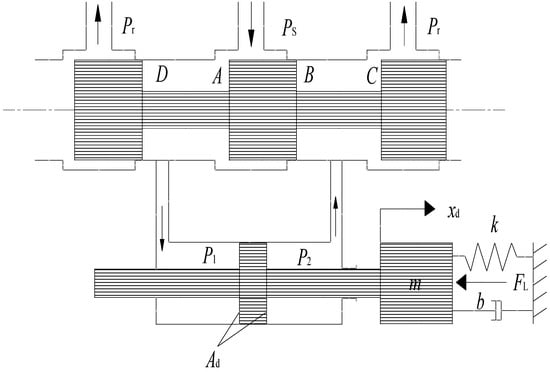
Figure 3.
Diagram of the electro-hydraulic servo material testing machine’s force servo control system’s structure. A and B are oil inlets; C and D are oil outlets.
The electro-hydraulic servo material testing machine’s force servo control system is composed of a hydraulic cylinder, electro-hydraulic servo valve, load mass, spring, and damping.
3.2. Mathematical Modeling of Electro-Hydraulic Servo Valve-Controlled Hydraulic Cylinder Force Control System
The hydraulic cylinder’s flow continuity equations are as follows:
where [] and [] are the two-chamber flow rates from the servo valve to the hydraulic cylinder; [] is the internal leakage coefficient of the hydraulic cylinder; [] is the external leakage coefficient of the hydraulic cylinder; [] is the effective bulk elastic modulus of the hydraulic oil; [] is the piston rod displacement of the hydraulic cylinder; [] is the effective area of the hydraulic cylinder; [] and [] are the two-chamber load pressures of the hydraulic cylinder; and [] and [] are the two-chamber volumes of the hydraulic cylinder.
The expressions of volumes and are as follows:
where V0 [] is the initial volume of the two-chamber of the hydraulic cylinder and L [] is the stroke of the hydraulic cylinder.
The equations for flow rate through the servo valve metering ports are as follows:
where
where [] is the flow coefficient of the servo valve; [V] is the control voltage of the servo valve; [] is the oil supply pressure; and [] is the oil return pressure.
The force balance equation of the electro-hydraulic servo system is as follows:
where m [] is the equivalent load; [] is the equivalent load damping; k [] is the equivalent load stiffness; and [] is the external load.
Piston rod displacement , piston rod velocity , pressure in the hydraulic cylinder’s left chamber, and pressure in the hydraulic cylinder’s right chamber are selected as state vectors; then, the state variables of the nonlinear mathematical model of the system are as follows:
If force is selected as the output, the system’s equation of state is expressed as follows:
where
4. Design of Feedback Linearized Integral Sliding Mode Controller
4.1. Feedback Linearization Design of Nonlinear Mathematical Model
Equation (11) is rewritten in the standard form of a nonlinear system as follows:
where
Calculating Equation (13) yields
According to the definition of relative order, the electro-hydraulic servo material testing machine’s electro-hydraulic servo system has a relative order of 1. Because the order of the system is 4, which is greater than its relative order of 1, the system has a dynamic internal subsystem. According to the input and output feedback linearization method, the transformation relationship between the new state variable and the original state variables is constructed as follows:
The new equations of state can be obtained as follows:
where is the control quantity of the new system, and the relationship between it and the control quantity of the original system is as follows:
By inverting the coordinates of control quantity of the linear system, control quantity of the original nonlinear system is obtained as follows:
4.2. Design of the Integrated Sliding Mode Controller
Sliding mode control has strong robustness to parametric uncertainties, uncertain nonlinearities, external interference, etc., but it needs to know the derivative of the system output. However, as the force derivative does not exist in practice, it cannot achieve accurate system tracking. To solve this problem, the integral term of the tracking error is added to the sliding mode surface function, and each error term in the sliding mode surface function is replaced by the system’s corresponding state variable. This paper proposes combining integrated sliding mode control with the feedback linearization model.
The tracking error of the load force driven by the hydraulic cylinder is defined as follows:
where is the hydraulic cylinder’s expected output force.
After feedback linearization, the system model that can be obtained is a first-order linear system, so the sliding mode surface can be designed as follows:
where is an optional constant.
The equivalent control is determined, and the derivation of Equation (23) can be obtained as follows:
Combined with Equation (19), it can be obtained as follows:
Let and equivalent control be obtained as follows:
To ensure the generation of sliding mode, is required, so the switching control quantity is selected as follows:
where is the switching control gain, .
Then, the output of integral sliding mode control can be expressed as follows:
Define the Lyapunov function , when , ; when , , so is positive and definite. Its derivation is obtained as follows:
It can be seen from Equation (29) that the sliding mode control system designed by meets the conditions of the Lyapunov stability theory, thus proving that the integral sliding mode control system under the new coordinates is stable.
According to Equations (21) and (28), the improved feedback-linearized integral sliding mode control law can be obtained as follows:
5. Simulation Experiment Analysis
5.1. Establishment of Simulation Model
AMESim software (https://ww2.mathworks.cn/products/connections/product_detail/simcenter-amesim.html, accessed on 19 February 2024) is powerful, used in many system modules, such as hydraulics, mechanical, control, and electrical modules, and contains many commonly used system components. Users only need to drag the required system components to the work area and connect them into a loop to complete the modeling. The Simulink toolbox, an important component of MATLAB software (https://ww2.mathworks.cn/products/matlab.html, accessed on 19 February 2024), has powerful computing functions. Users can establish a control system through the toolbox module or write a control program in the S-Function module, and then connect the module to the established control block diagram for simulation. To sum up, AMESim–Simulink co-simulation can build a nonlinear physical model of the electro-hydraulic servo system through AMESim software and avoid the system’s complicated and accurate mathematical modeling steps. In addition, a control system simulation model can be built in the Simulink toolbox to process data and images, verify simulation results, and make full use of their advantages.
A model of the electro-hydraulic servo valve-controlled hydraulic cylinder force control system was manufactured according to the schematic diagram shown in Figure 4, and the AMESim portion of the simulation was established as shown in Figure 5. The model included a power unit, a servo control unit, a load execution unit, and a trajectory-tracking control algorithm unit [37]. To test the feasibility of the proposed control strategy, MATLAB/Simulink adopted the ode45 algorithm, set the step size as , and calculated the relative error as . The model’s relevant parameters are shown in Table 1.
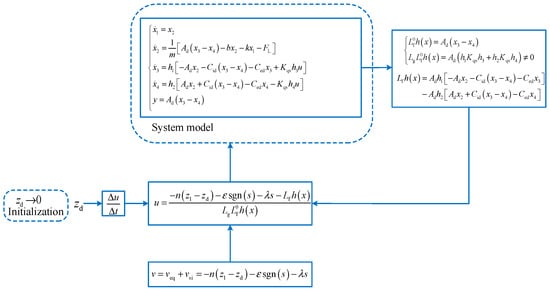
Figure 4.
Diagram of FLISM controller’s control block.
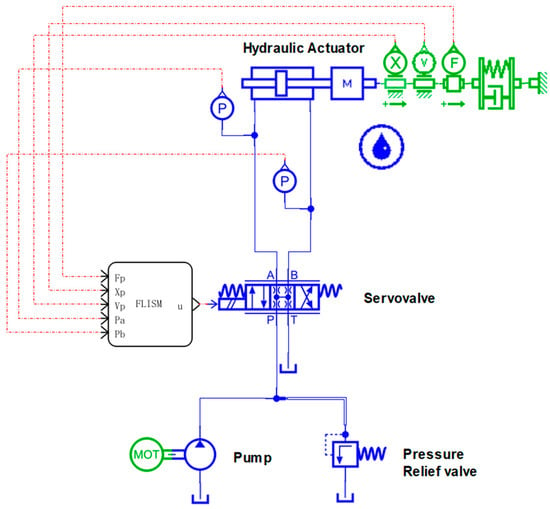
Figure 5.
AMESim simulation diagram of the electro-hydraulic servo valve-controlled hydraulic cylinder force control system.

Table 1.
Model parameters of electro-hydraulic servo system.
To verify the FLISM control’s parameter adaptability, different amplitude and frequency input signals were applied based on setting the same parameter, and the method was compared with feedback-linearized sliding mode (FLSM) control and conventional PID control. The maximum PID parameter P was adopted to minimize the system’s tracking error and ensure that sinusoidal signal tracking did not produce jitter. The sinusoidal signal scheme adopted in the simulation is shown in Table 2.

Table 2.
Different signal schemes.
5.2. Analysis of Simulation Results
During the simulation process, the FLISM controller’s parameters were as follows: was , was , and was . The parameters of the FLSM controller were as follows: was 60, was 1, and was 100. And the parameters of the PID controller were as follows: was 0.1, was 0.02, and was 10. The authors used sinusoidal signal I to conduct simulations. Figure 6 shows the tracking error curves of the FLISM, FLSM, and PID controllers for force control tracking curves.
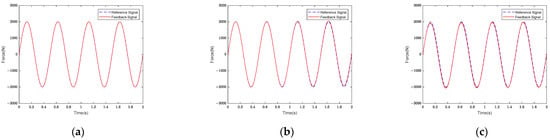
Figure 6.
Force control tracking curves of (a) FLISM controller, (b) FLSM controller, and (c) PID controller.
Figure 7 shows the FLISM, FLSM, and PID controllers’ tracking error curves.
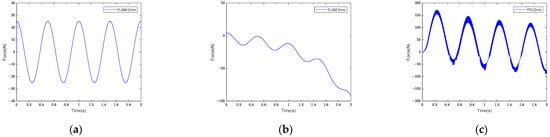
Figure 7.
Force control tracking error curves of (a) FLISM controller, (b) FLSM controller, and (c) PID controller.
As can be seen in Figure 7, the maximum tracking error of sinusoidal signal I under the PID controller was 171.70 N. Under the action of the FLSM controller, the maximum tracking error was 91.16 N, and the control error showed an increasing trend. Under the action of the FLISM controller, the maximum tracking error was 25.13 N, and the error was stable. The maximum tracking error of the FLISM controller was reduced by 72.43% compared with that of the FLSM controller and by 85.36% compared with that of the PID controller. When analyzing the three control algorithms’ control errors, the average tracking error was used to measure the control quality. The average tracking error is defined as follows:
According to the analysis of Equation (31), the FLISM controller’s average tracking error was 15.98 N, the FLSM controller’s was 30.50 N, and the PID controller’s was 47.88 N. According to the average tracking error analysis, the FLISM controller’s control effect was reduced by 47.10% compared with that of the FLSM controller and by 66.20% compared with that of the PID controller. The results showed that the FLISM controller’s control effect was better than that of the FLSM and PID controllers.
To verify the tracking effect of changing the signal frequency under the same FLISM, FLSM, and PID controller parameters, sinusoidal signal II was applied during simulations. Figure 8 shows the tracking error curves of the FLISM, FLSM, and PID controllers for force control tracking curves.
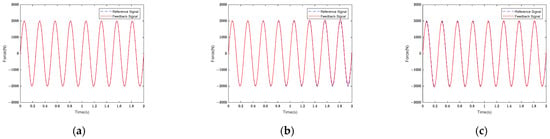
Figure 8.
Force control tracking curves of (a) FLISM controller, (b) FLSM controller, and (c) PID controller.
Figure 9 shows the FLISM, FLSM, and PID controllers’ force control tracking error curves.
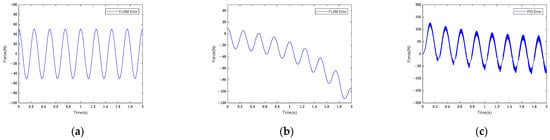
Figure 9.
Force control tracking error curves of (a) FLISM controller, (b) FLSM controller, and (c) PID controller.
As can be seen in Figure 9, the maximum tracking error of sinusoidal signal II under the PID controller was 127.00 N. The maximum tracking error was 112.90 N under the action of the FLSM controller, and the control error showed an increasing trend. The maximum tracking error was 50.25 N under the action of the FLISM controller, and the control error maintained a stable range. The FLISM controller’s maximum tracking error was reduced by 55.49% compared with that of the FLSM controller and by 60.43% compared with that of the PID controller. According to the analysis of Equation (31), the FLISM controller’s average tracking error was 31.95 N, the FLSM controller’s was 40.38 N, and the PID controller’s 44.15 N. According to the average tracking error analysis, the control effect of the FLISM controller was reduced by 20.88% compared with that of the FLSM controller and by 27.63% compared with that of the PID controller. According to the analysis results, the control effect of the FLISM controller remained better than that of the FLSM and PID controllers after changing the signal frequency.
To verify the tracking effect of changing signal amplitude under the same FLISM, FLSM, and PID controller parameters, sinusoidal signal III was applied during simulations. Figure 10 shows the tracking error curves of the FLISM, FLSM, and PID controllers for force control tracking curves.
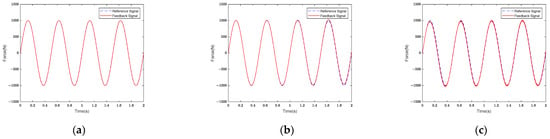
Figure 10.
Force control tracking curves of (a) FLISM controller, (b) FLSM controller, and (c) PID controller.
Figure 11 shows the FLISM, FLSM, and PID controllers’ force control tracking error curves.
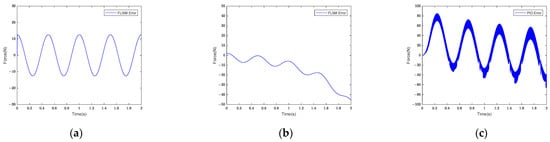
Figure 11.
Force control tracking error curves of (a) FLISM controller, (b) FLSM controller, and (c) PID controller.
As can be seen in Figure 11, the maximum tracking error of sinusoidal signal III under the action of the PID controller was 85.17 N, and it presented significant buffeting. The maximum tracking error was 45.58 N under the action of the FLSM controller, and the error showed an increasing trend. The maximum tracking error was 12.55 N under the action of the FLISM controller, and the error tended to be stable. The FLISM controller’s maximum tracking error was reduced by 85.18% compared with that of the PID controller and by 38.78% compared with that of the FLSM controller. According to the analysis of Equation (31), the FLISM controller’s average tracking error was 7.99 N, the FLSM controller’s was 15.02 N, and the PID controller’s was 26.23 N. According to the average tracking error analysis, the FLISM controller’s control effect was reduced by 46.80% compared with that of the FLSM controller and by 69.53% compared with that of the PID controller. According to the analysis results, the FLISM controller’s control effect remained better than that of the FLSM and PID controllers after the signal amplitude was changed.
A random 200 N amplitude interference signal based on sinusoidal signal I was added to verify the designed FLISM controller’s anti-interference performance. Figure 12 shows the FLISM, FLSM, and PID controllers’ force control tracking curves.
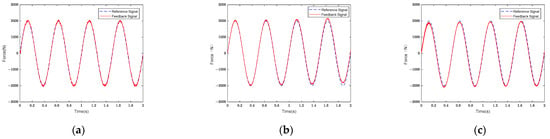
Figure 12.
Force control tracking curves of (a) FLISM controller, (b) FLSM controller, and (c) PID controller.
Figure 13 shows the FLISM, FLSM, and PID controllers’ force control tracking error curves.
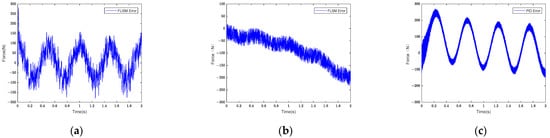
Figure 13.
Force control tracking error curves of (a) FLISM controller, (b) FLSM controller, and (c) PID controller.
According to the analysis of Equation (31), the average tracking error values of the FLISM, FLSM, and PID controllers were 61.34 N, 87.11 N, and 98.91 N, respectively, after the interference signal was applied. According to the average tracking error analysis, the FLISM controller’s control effect was reduced by 29.58% compared with that of the FLSM controller and by 38.13% compared with that of the PID controller. The results showed that the FLISM controller’s control effect remained better than that of the FLSM and PID controllers after external interference was applied.
The sine wave is the most commonly used and most easily produced waveform; it is the basis of all wave patterns. In many studies, a sinusoidal wave is chosen as the desired motion trajectory to test the effectiveness of control algorithms. However, during actual equipment operation, there are inevitable uncertainties regarding various parameters and external disturbances. To express these effects, waveform representation methods, such as step, slope, and triangle wave signals, are used. To test the FLISM controller’s adaptability to these three types of wave patterns, it was necessary to ensure that the control system’s parameters were consistent with those of the sinusoidal signal and that the system’s tracking error did not exceed the allowable limit.
Figure 14 shows the FLISM, FLSM, and PID controllers’ displacement tracking curves when the input signal was a step signal.

Figure 14.
Force control tracking curves of (a) FLISM controller, (b) FLSM controller, and (c) PID controller.
According to the analysis presented in Figure 14, under the control of the PID controller, the step signal was tracked but the tracking effect was not ideal, and the adjustment time was as high as 0.031 s. Under the control of the FLSM controller, the tracking effect significantly improved, and the adjustment time increased to 0.008 s. However, the integration term was introduced into the FLSM controller’s design. After the FLISM controller’s improvement, the tracking effect of the step signal improved again, and the adjustment time was reduced to 0.003 s. Taking the adjustment time as the evaluation index, the FLISM controller’s step signal tracking effect improved by 62.50% compared with that of the FLSM control and by 90.33% compared with that of the PID control. It was observed that after the signal type changed, the FLISM controller’s tracking effect remained better than that of the FLSM and PID controllers.
Figure 15 shows the FLISM, FLSM, and PID controllers’ displacement tracking curves when the input signal was a slope signal.
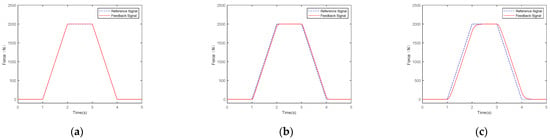
Figure 15.
Force control tracking curves of (a) FLISM controller, (b) FLSM controller, and (c) PID controller.
Figure 16 shows the FLISM, FLSM, and PID controllers’ force control tracking error curves.
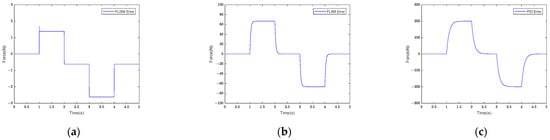
Figure 16.
Force control tracking error curves of (a) FLISM controller, (b) FLSM controller, and (c) PID controller.
As can be seen in Figure 16, the maximum tracking error of the slope signal was 199.98 N under the PID controller, 66.67 N under the FLSM controller, and 1.67 N under the FLISM controller (which was 99.16% lower than that of the PID controller and 97.45% lower than that of the FLSM controller). According to the analysis of Equation (31), the average tracking errors of the FLISM, FLSM, and PID controllers were 1.05 N, 26.66 N, and 79.98 N, respectively, under the slope displacement trajectory. As can be seen from the tracking errors presented in Figure 16, when the input signal was a slope signal, the tracking error under the action of the FLISM controller was smaller than it was under the action of the FLSM and PID controllers.
Figure 17 shows the FLISM, FLSM, and PID controllers’ displacement tracking curves when the input signal was a triangle wave signal.
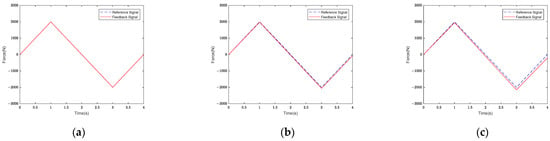
Figure 17.
Force control tracking curves of (a) FLISM controller, (b) FLSM controller, and (c) PID controller.
Figure 18 shows the FLISM, FLSM, and PID controllers’ force control tracking error curves.
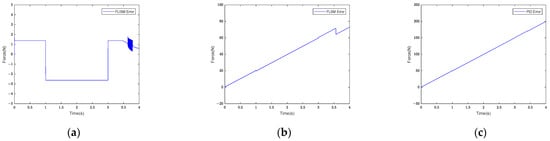
Figure 18.
Force control tracking error curves of (a) FLISM controller, (b) FLSM controller, and (c) PID controller.
As can be seen in Figure 18, the triangular wave signal achieved a good and stable tracking effect under the action of the FLISM controller, while the control errors of the FLSM and PID controllers increased over time. According to the analysis of Equation (31), the FLISM controller’s average tracking error was 1.94 N, the FLSM controller’s was 39.22 N, and the PID controller’s was 99.97 N. Taking the average tracking error as the evaluation index, the FLISM controller’s tracking effect improved by 95.05% compared with that of the FLSM controller and by 98.06% compared with that of the PID controller. According to the analysis results, the FLISM controller’s tracking effect remained better than that of the FLSM and PID controllers when the input signal was a triangular wave signal.
6. Conclusions
Focusing on the difficult problem of force control in electro-hydraulic servo material testing machines, a nonlinear state equation was established by taking piston rod displacement, piston rod velocity, and hydraulic cylinder two-chamber pressure as state variables. In a previous study, the authors used a feedback linearization method to linearize the equation of the state of nonlinear systems and, combined with sliding mode control, designed an FLSM controller that could effectively suppress the disturbance of nonlinear terms. However, some problems remained, such as parameters that were not self-adaptive and had weak anti-interference ability. To solve these problems, we introduced an integral term into sliding mode control, combined with feedback linearization, which effectively improved the adaptability of parameters and anti-interference performance and yielded a better control effect.
The results are as follows:
- (1)
- The simulation results show that the proposed FLISM controller reduced the force average tracking error compared with that of the FLSM and PID controllers. The FLISM controller was not affected by input signal changes and the control effect was worse, and after introducing a random interference signal, the FLISM control maintained good control performance. Compared with the FLSM and PID controllers, the system’s tracking effect was significantly improved.
- (2)
- Through the feedback linearization design, the FLISM controller could suppress the influence of nonlinear factors on the electro-hydraulic servo system’s force tracking accuracy and improve the system’s control accuracy and anti-interference performance.
- (3)
- Applying the FLISM controller in the electro-hydraulic servo material testing machine’s force control system could effectively improve the testing machine’s force output control precision, and it significantly helped improve the material’s test accuracy.
Author Contributions
Conceptualization, J.L.; methodology, C.S.; writing—original draft, C.S. and J.L.; writing—review and editing, Y.T. and Z.D. All authors have read and agreed to the published version of this manuscript.
Funding
This work was supported by the Major Science and Technology Special Project of the Yunnan Science and Technology Department (No. 202202AC080008).
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no potential conflicts of interest.
References
- Ma, M.Y. Design and Implementation of Measurement and Control System for Material Low Cycle Fatigue Testing Machine. Master’s Thesis, Henan University of Science and Technology, Luoyang, China, 2020. [Google Scholar]
- Wang, H. Research on Adaptive Sliding Mode Control of Electro-Hydraulic Servo Fatigue Testing Machine Based on RBFNN. Master’s Thesis, Northeastern University, Shenyang, China, 2020. [Google Scholar]
- Zhao, J.; Yang, T.; Ma, Z.; Yang, C.; Wang, Z.; Wang, C. Energy consumption minimizing for electro-hydraulic servo driving planar parallel mechanism by optimizing the structure based on genetic algorithm. IEEE Access 2019, 7, 47090–47101. [Google Scholar] [CrossRef]
- Shao, J.; Bian, Y.; Yang, M.; Liu, G. High precision adaptive fuzzy control method for hydraulic robot joint. In Proceedings of the 13th International Conference on Mechanical and Intelligent Manufacturing Technologies, Cape Town, South Africa, 26–28 May 2023. [Google Scholar]
- Guo, K.; Li, M.; Shi, W.; Pan, Y. Adaptive tracking control of hydraulic systems with improved parameter convergence. IEEE Trans. Ind. Electron. 2021, 69, 7140–7150. [Google Scholar] [CrossRef]
- Gu, F.; Yue, R.; Ma, Q.; Wang, J.; Wang, B. Frequency characteristic test of electro-hydraulic servo mechanism based on ADSTK. In Proceedings of the 29th Chinese Control and Decision Conference, Yichang, China, 20–22 May 2017. [Google Scholar]
- Fu, Y.L.; Chen, H.; Liu, H.S.; Qi, X. Research on missile electro-hydraulic Steering System based on active disturbance rejection Control. Acta Astronaut. Sin. 2010, 31, 1051–1055. [Google Scholar]
- Liu, X.; Liu, C. Testing and manufacture to shock absorber electro-hydraulic servo-testing system. In Proceedings of the 3rd Information Technology and Mechatronics Engineering Conference, Chongqing, China, 15–17 September 2017. [Google Scholar]
- Essa, M.E.S.M.; Aboelela, M.A.; Hassan, M.M.; Abdrabbo, S.M. Hardware in the loop of position tracking control of hydraulic servo mechanism. In Proceedings of the 13th International Computer Engineering Conference, Cairo, Egypt, 27–28 December 2017. [Google Scholar]
- Li, B.; Chen, J.; Zhang, W.M.; Zhang, Z.; Chen, Y. Research Status of Modeling, Identification and Control of Electro-Hydraulic Servo System. Mach. Tool Hydraul. 2016, 44, 168–172. [Google Scholar]
- Wang, L.H.; Wu, B.; Du, R.S.; Yang, S. Nonlinear Dynamic Characteristics of Hydraulic Cylinder Motion. Chin. J. Mech. Eng. 2007, 43, 12–19. [Google Scholar] [CrossRef]
- Jiang, W.L.; Zhu, Y.; Zheng, Z. Research Status and Prospect of Dynamic Characteristics of Electro-Hydraulic Servo System. Mach. Tool Hydraul. 2014, 42, 169–173. [Google Scholar]
- Sun, C.; Yuan, R.B. Adaptive robust cross-coupling position synchronization control of a hydraulic press slider-leveling. Sci. Prog. 2021, 104, 0036850420987037. [Google Scholar] [CrossRef]
- Li, C.C.; Jin, X.H.; Wang, K.; Zhang, S. Study on Adaptive Control of Dominant Pole Model for Electro-hydraulic Systems with Variable Stiffness. Mech. Electr. Eng. 2019, 37, 764–769. [Google Scholar]
- Wei, Q.; Zhou, G.; Hu, X.Y. Research on Force Trajectory Feedback Linearized sliding mode Tracking Control of Electro-hydraulic Servo System. J. Henan Polytech. Univ. (Nat. Sci. Ed.) 2023, 42, 108–113. [Google Scholar]
- Zhou, T.; Cheng, H. Design of Self-Tuning Fuzzy PID Controller for Electro-Hydraulic Servo System. Mach. Tool Hydraul. 2020, 48, 135–139+145. [Google Scholar]
- Li, B.; Rui, G.C.; Fang, L.; Sa, Y.; Tang, Y.; Shen, G. Research on Adaptive Disturbance Rejection Control of Electro-Hydraulic Servo System. Chin. Hydraul. Pneum. 2019, 12, 57–62. [Google Scholar]
- Jiang, S.X. Research on Control Strategy of Electro-Hydraulic Servo System Based on Data Fusion and Neural Network. Master’s Thesis, Beijing Jiaotong University, Beijing, China, 2022. [Google Scholar]
- Sidhom, L.; Chuhu, I.; Smaoui, M. Automation of a Hybrid Control for Electrohydraulic Servo-Actuators with Residual Dynamics. Appl. Sci. 2022, 12, 2856. [Google Scholar] [CrossRef]
- Xiao, L.; Flu, B.B.; Yu, B.; Ye, Z. Cascaded sliding mode force control for a single-rod electrohydraulic actuator. Neurocomputing 2015, 156, 117–120. [Google Scholar] [CrossRef]
- Fan, Y.Q.; Shao, J.P.; Sun, G.T.; Shao, X. Improved beetle antennae search algorithm-based Lévy flight for tuning of PID controller in force control system. Math. Probl. Eng. 2020, 2020, 1–22. [Google Scholar] [CrossRef]
- Lu, X.L.; Du, F.P.; Jia, Q.; Ren, B.; Wang, X. Sliding mode force control of an electrohydraulic servo system with RBF neural network compensation. Mechanics 2019, 25, 32–37. [Google Scholar] [CrossRef]
- Min, L.; Zhang, H.X.; Zhao, Q.H.; Fang, L.; Du, S. Research on Feedback Linearized sliding Mode Control of Electro-hydraulic Position Servo System. J. Qingdao Univ. (Eng. Technol. Ed.) 2021, 36, 9–14. [Google Scholar]
- Zhang, Z.; Li, H.J.; Qu, X.Y.; Zhang, Z. Robust Feedback Linearization Control of Electro-Hydraulic Position Servo System. Mach. Tool Hydraul. 2016, 44, 148–152. [Google Scholar]
- Wang, X.G.; Rui, G.C.; Ding, X.Y.; Shen, G. Feedback Linearized Sliding Mode Control of Electro-Hydraulic Servo System Based on Interference Observer. Chin. Hydraul. Pneum. 2018, 06, 8–13. [Google Scholar]
- Li, Y.M.; Guo, L. Feedback Linearized Asymmetric Systems based on Neural Networks. Appl. Comput. Syst. 2012, 21, 166–169+221. [Google Scholar]
- Pedro, J.O.; Dangor, M.; Dahunsi, O.A.; Ali, M.M. Intelligent feedback linearization control of nonlinear electrohydraulic suspension systems using particle swarm optimization. Appl. Soft Comput. 2014, 24, 50–62. [Google Scholar] [CrossRef]
- Dai, M.C.; Xu, T.Y.; Zhang, J.J.; Lan, Y. Trajectory Tracking Control of Electro-hydraulic Servo System Based on Continuous Sliding Mode Control. Mach. Tool Hydraul. 2021, 49, 54–58. [Google Scholar]
- Guo, X.P.; Wang, C.W.; Liu, H.; Zhang, Z.; Ji, X.; Zhao, B. Sliding mode control of pump-controlled electro-hydraulic Servo System based on Extended state observer. J. Beijing Univ. Aeronaut. Astronsutics 2020, 46, 1159–1168. [Google Scholar]
- Ji, X.H.; Wang, C.W.; Chen, S.; Zhang, Z.Y. Sliding Mode Reverse Step Control Method for Valve-controlled Electro-hydraulic Position Servo System. J. Cent. South Univ. (Nat. Sci. Ed.) 2020, 51, 1518–1525. [Google Scholar]
- Xu, G.; Lu, N.; Lv, G. High-gain observer-based sliding mode force control for the single-rod electrohydraulic servo actuator. IEEE Access 2019, 7, 161849–161857. [Google Scholar] [CrossRef]
- Han, G.Y.; Shi, G.L.; Guo, Q.Y. Sliding Mode Position Control of Electro-hydraulic Proportional System Based on Disturbance Observer. Modul. Mach. Tool Autom. Process. Technol. 2019, 01, 97–100. [Google Scholar]
- De Cuyper, J.; Verhaegen, M.; Swevers, J. Off-line feed-forward and H∞ feedback control on a vibration rig. Control. Eng. Pract. 2003, 11, 129–140. [Google Scholar] [CrossRef]
- Xia, J.; Li, Y.; Huang, D.; Yang, J.; Xing, X.; Ma, L. Spatial Iterative Learning Control with Human Guidance and Visual Detection for Path Learning and Tracking. IEEE Trans. Autom. Sci. Eng. 2022, 20, 1772–1784. [Google Scholar] [CrossRef]
- Li, X.; Wang, L.; Xia, X.; Liu, Y.; Zhang, B. Iterative learning-based negative effect compensation control of disturbance to improve the disturbance isolation of system. Sensors 2022, 22, 3464. [Google Scholar] [CrossRef]
- Wan, J.S. Structure Design and Optimization of Four-Column Hydraulic Brick Machine. Master’s Thesis, North China University of Water Resources and Electric Power, Zhengzhou, China, 2021. [Google Scholar]
- Sun, C.G. Research on Electro-Hydraulic Control System of Plastic Molding Hydraulic Press with Slider Guide. Ph.D. Thesis, Zhejiang University, Hangzhou, China, 2018. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).