Design and Testing of a New Type of Planetary Traction Drive Bearing-Type Reducer
Abstract
1. Introduction
2. Theoretical Analysis of Bearing-type Reducer
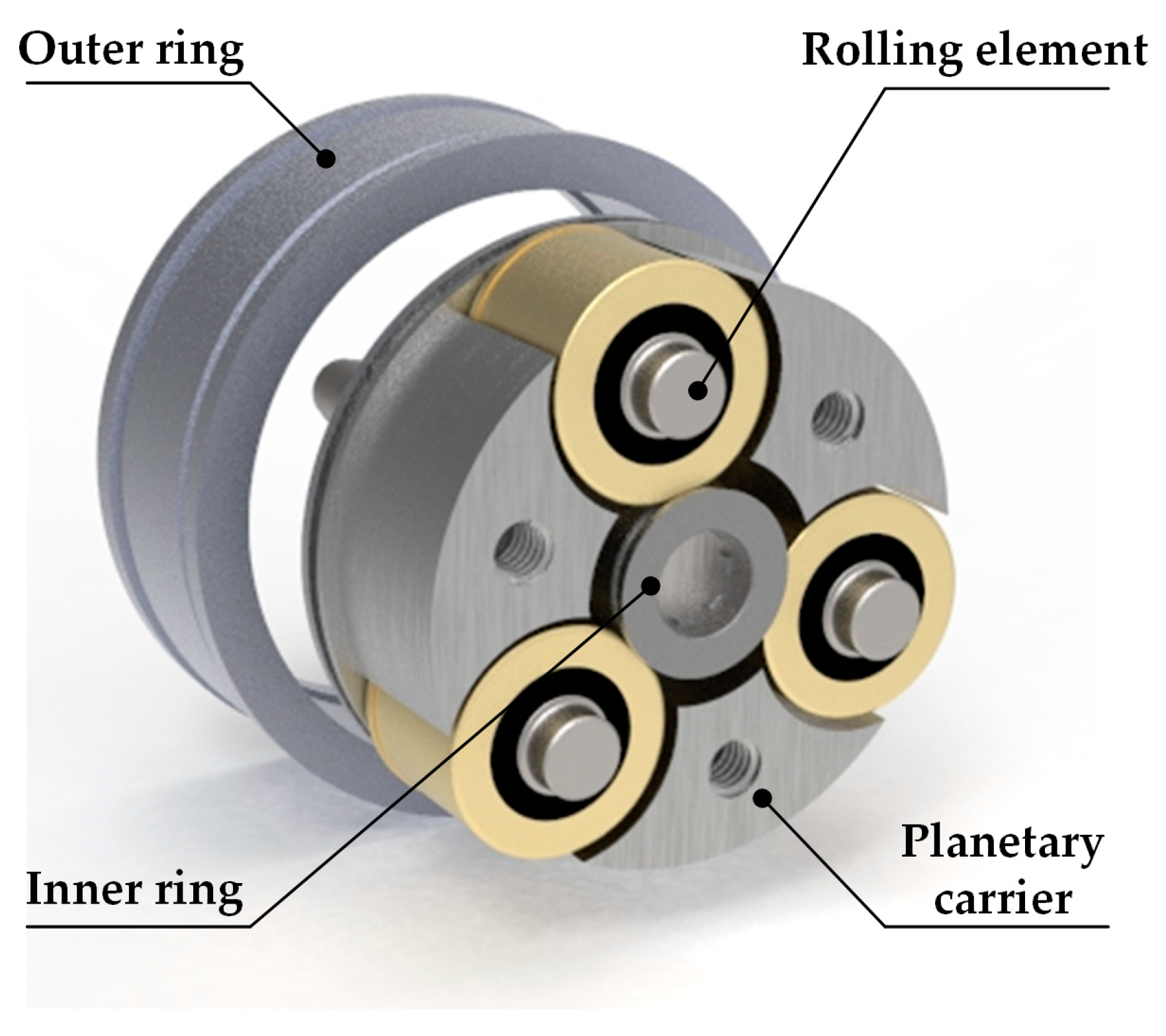
2.1. Structure of the Bearing-type Reducer
2.2. Mechanism of Traction Oil Film Formation
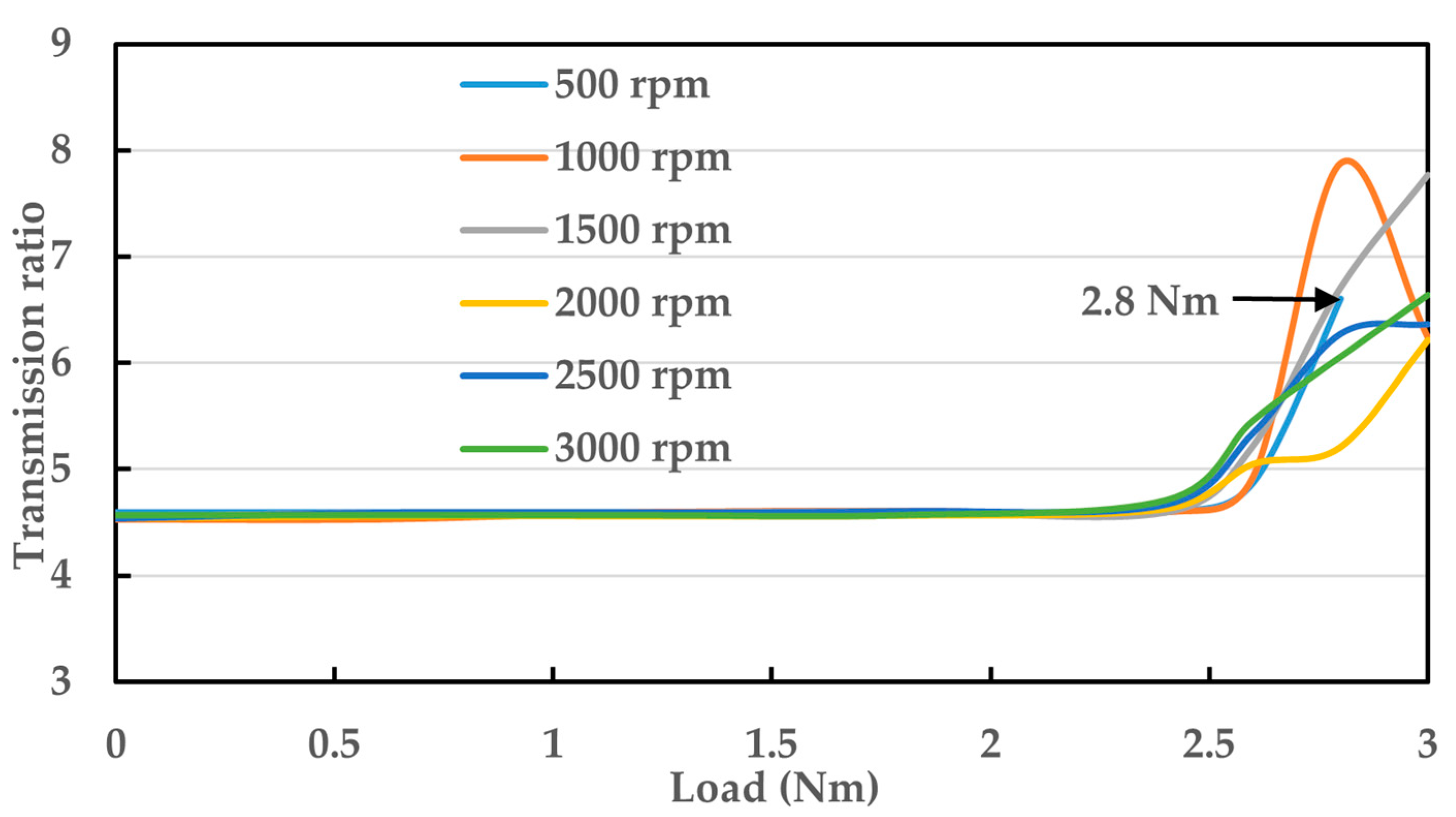
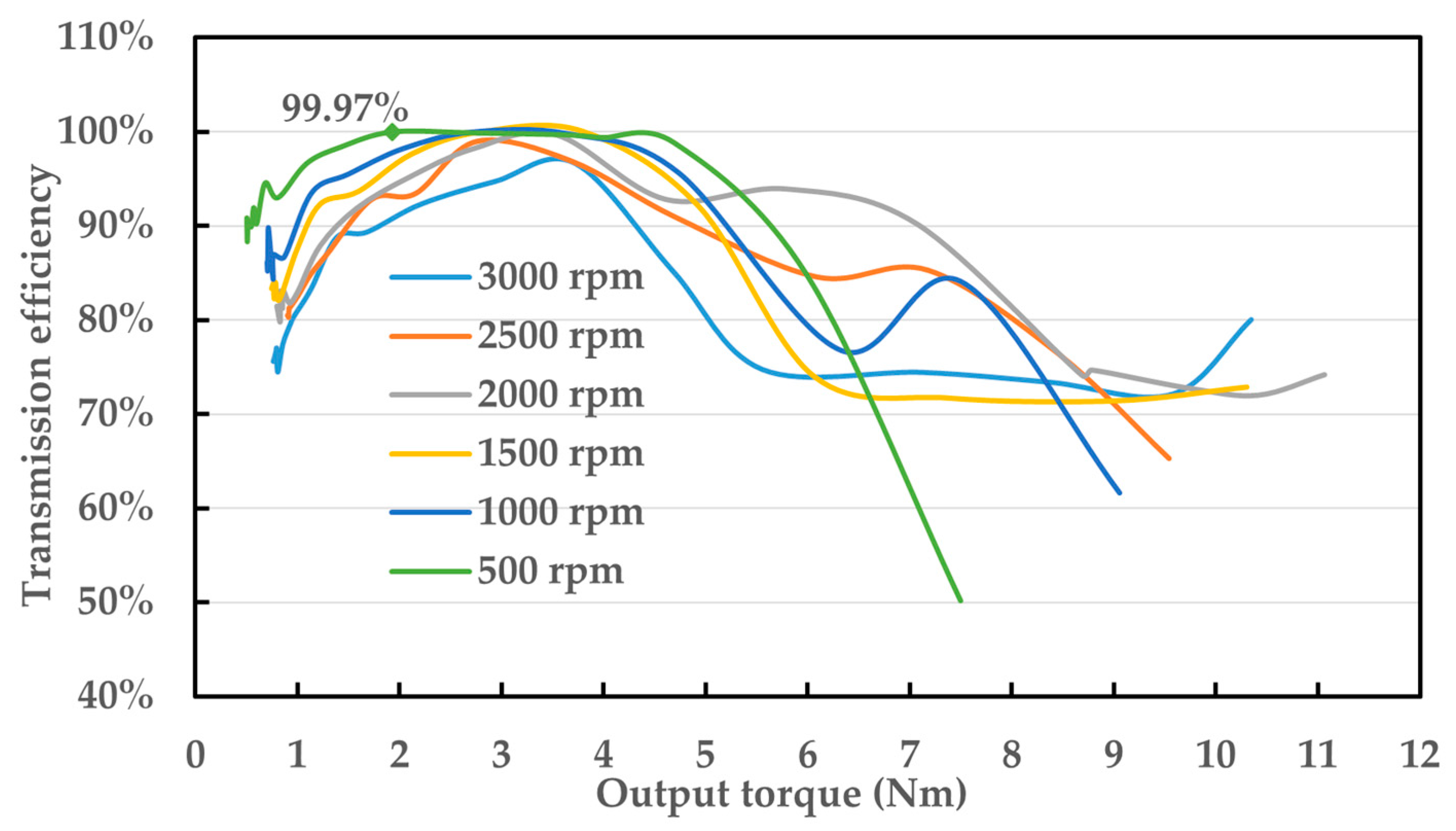
2.3. Transmission Ratio and Transmission Efficiency Analysis
3. Development and Design of Bearing-type Reducer
3.1. Overall Structure of Bearing-type Reducer
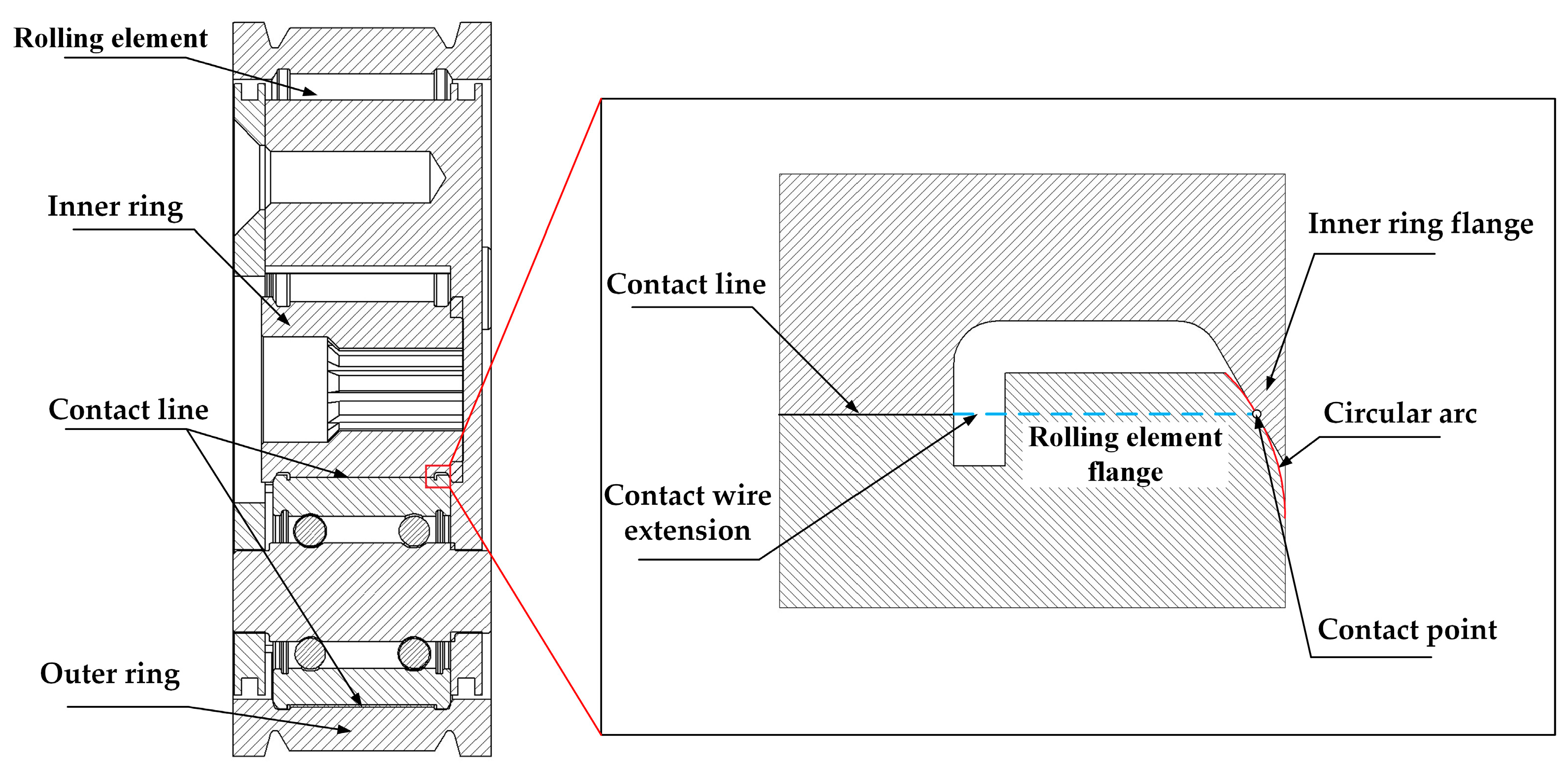
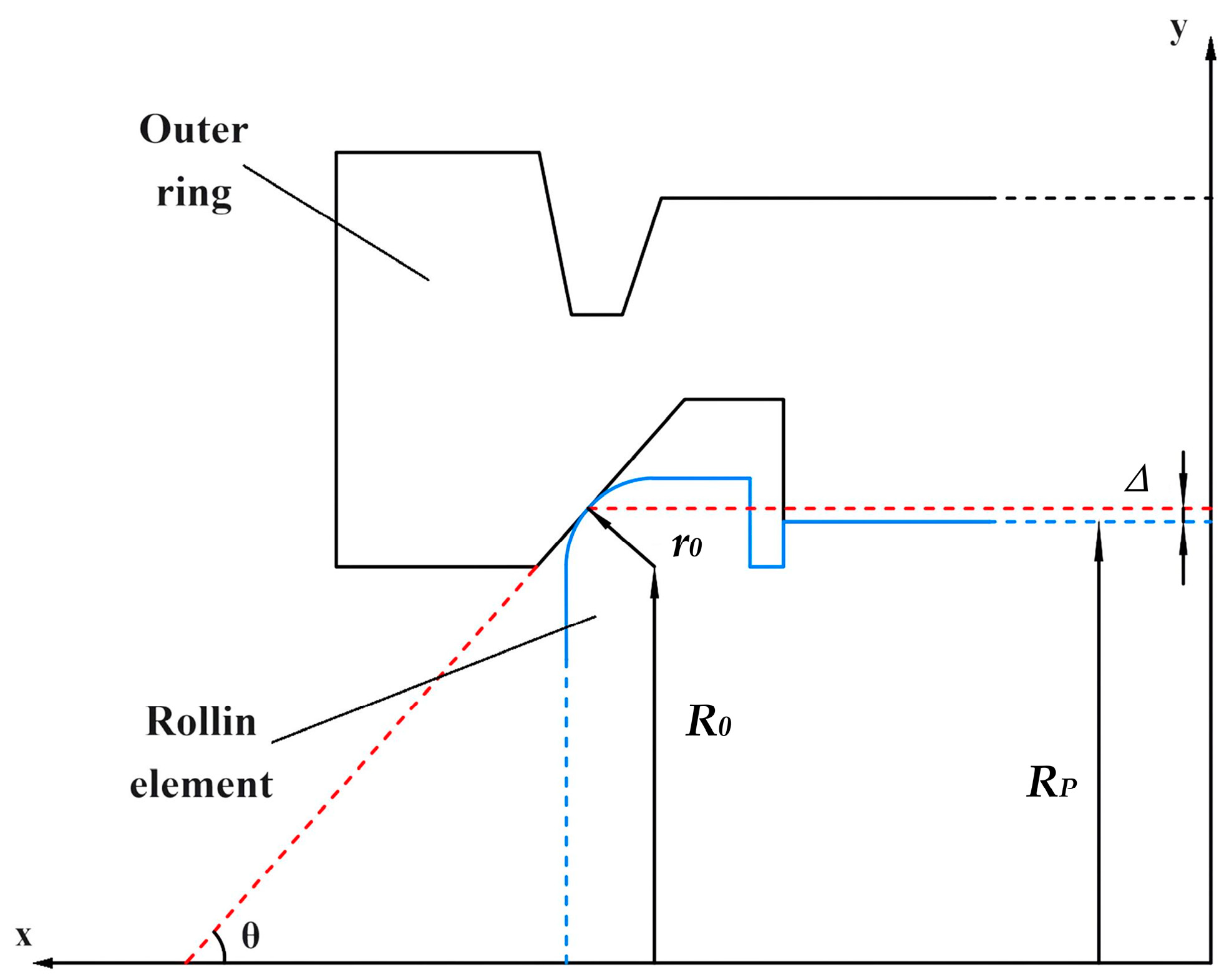
3.2. Geometric Design and Analysis at the Flange
3.3. Bearing-type Reducer Design Program
3.3.1. Basic Dimensions’ Design
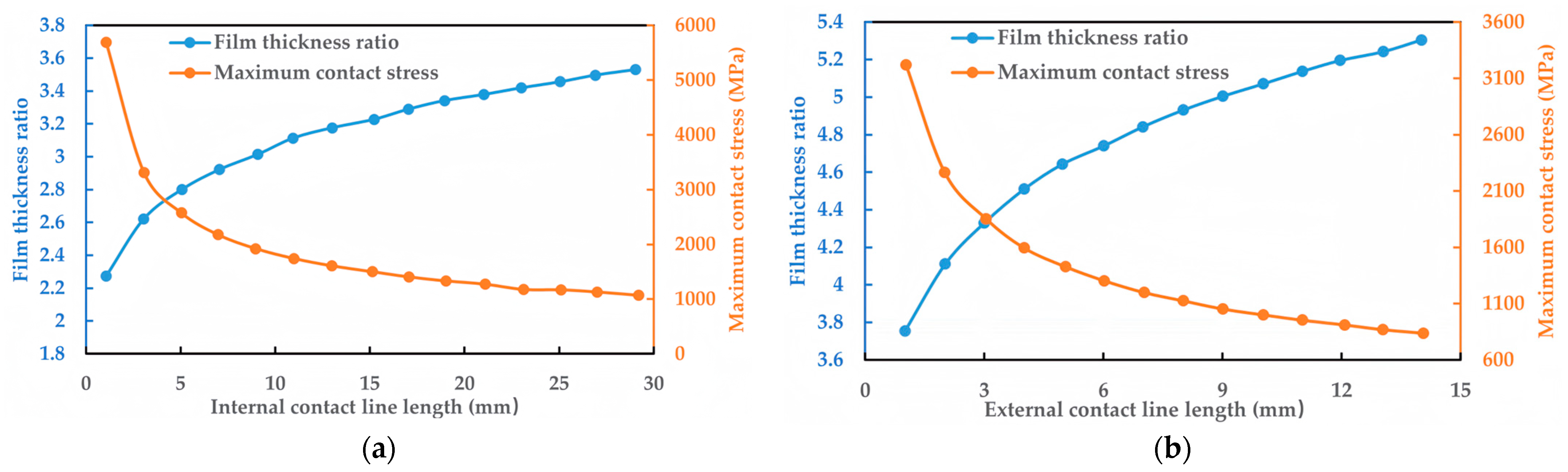
3.3.2. Design of Contact Line Length
3.3.3. Minimum Positive Pressure Design
3.3.4. Interference Design
4. Dynamic Analysis of Bearing-type Speed Reducer
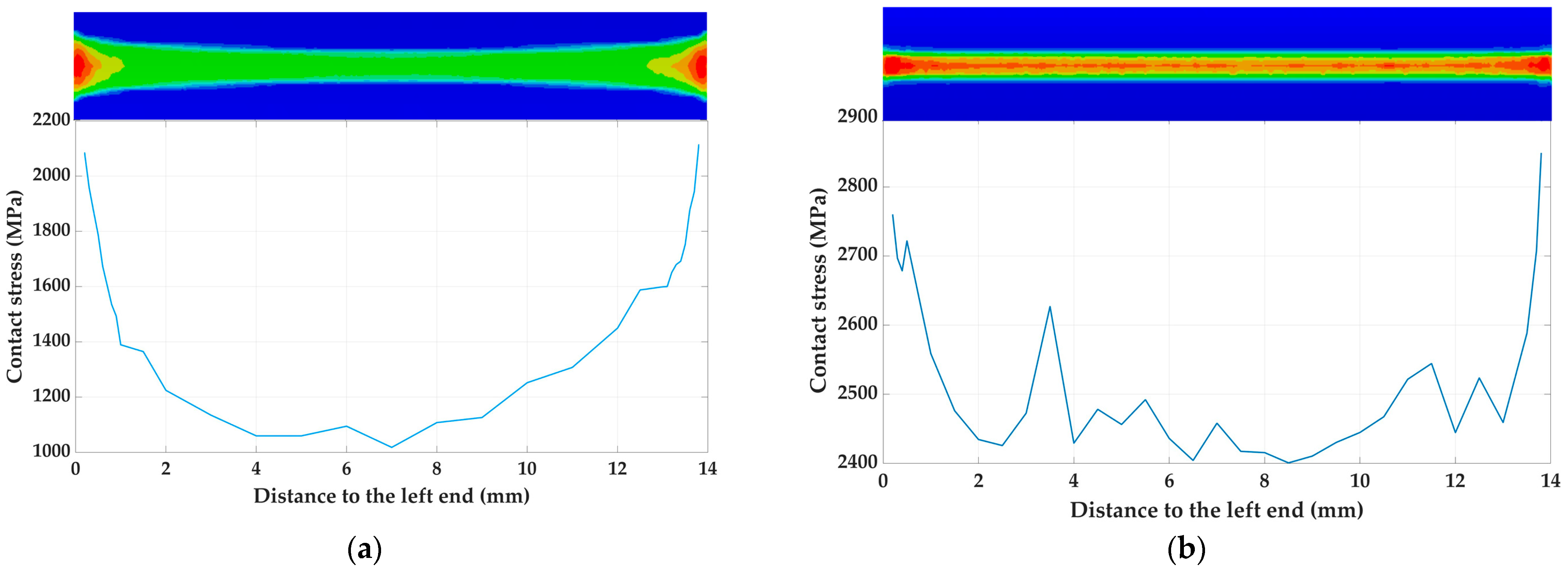
4.1. Analysis of Contact Stress at the Contact Line of the Bearing-type Reducer
4.2. Bearing-type Reducer Contour Line Modification
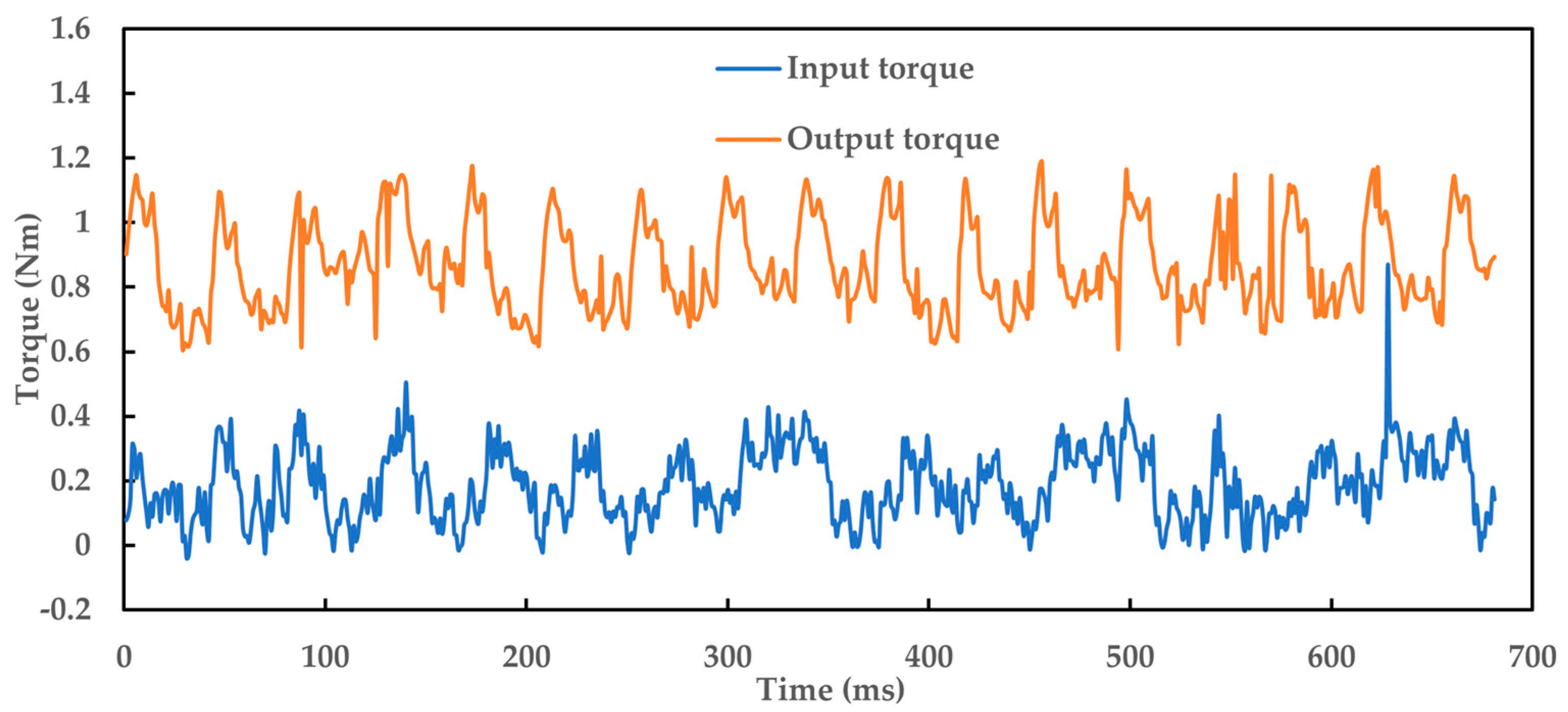
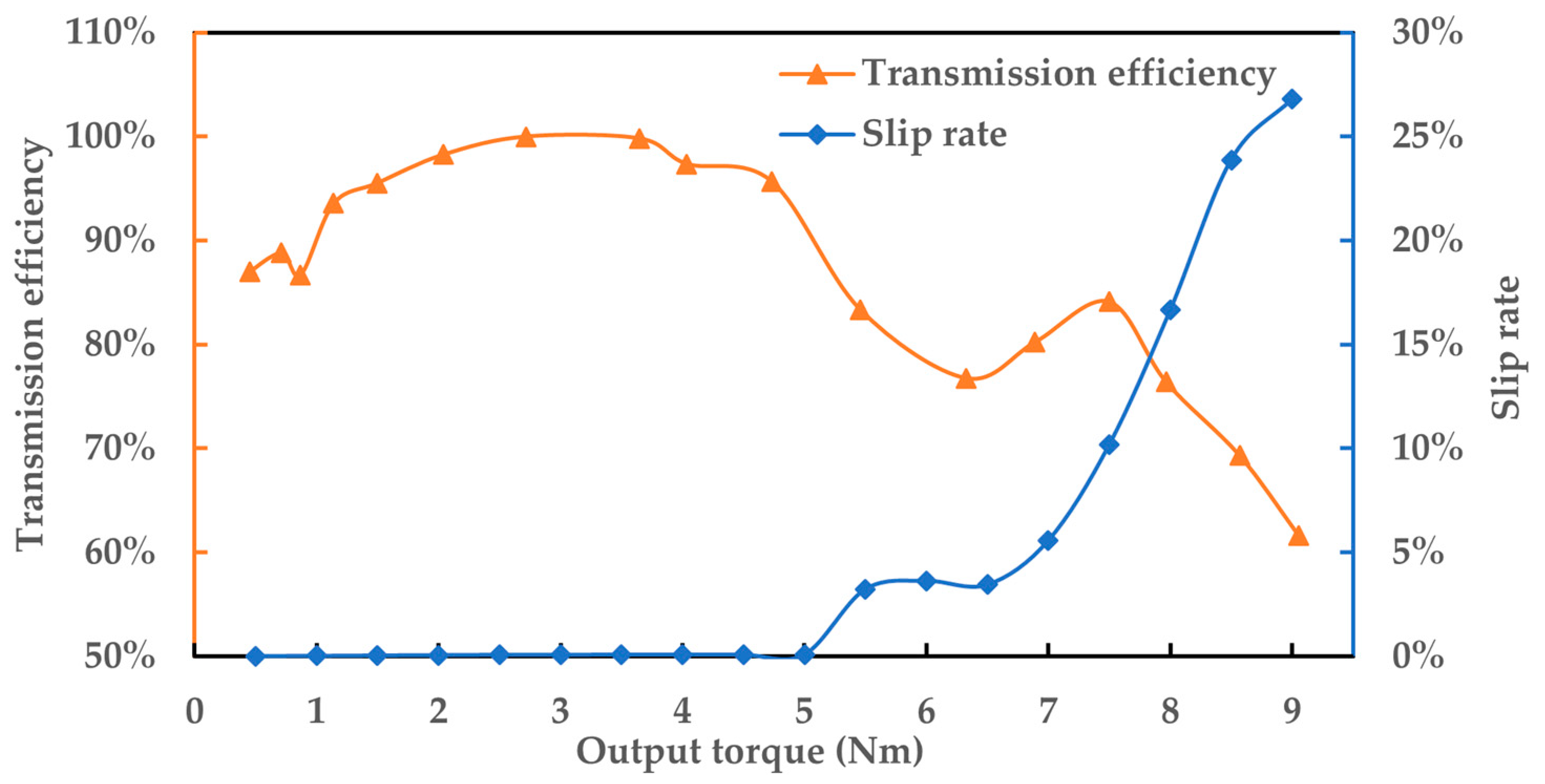
5. Application Examples and Experimental Testing
6. Conclusions
- Based on the target speed, torque, and transmission ratio, the compression force and interference of the bearing-type reducer were designed. By choosing an appropriate oil film thickness formula and incorporating contact stress, the contact line length was designed, subsequently determining the basic dimensions of the bearing-type reducer.
- A strategic design enables the planetary wheel, the outer ring, and the contact line of the sun wheel, as well as the axial and radial contact of the flange, to align on a traction line, and the structure allows the bearing-type reducer to achieve bi-directional bearing (in both axial and radial directions). Additionally, it automatically adjusts to prevent planetary wheel eccentricity during work. The implementation of centering, to prevent planetary wheel eccentricity caused by collision or other factors, simplifies the structure while enhancing the traction transmission capacity.
- Drawing on the shaping method used for bearing rollers, the contour line of the outer ring of the bearing-type reducer was refined. A method of using a full circular arc profile to shape the outer ring was determined to be suitable. When the outer ring’s convexity was set to 10 μm with a 1 mm chamfer, the stress difference between the middle and ends of the outer ring contact line reduced from the original 900 MPa to 400 MPa. This resulted in a more uniform stress distribution and a less notable edge effect.
- By designing a bearing-type reducer test rig and performing experiments on transmission efficiency and transmission ratio, their variation patterns for the bearing-type reducer with changes in the load and speed were acquired. It was verified to be highly efficient in transmission, with a peak efficiency of 99.97%. Moreover, no wear or significant heat loss was observed during the experiments.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Xie, X. Design and Analysis of Hub Motor Traction Reducer for Electric Scooter. Master’s Thesis, Chongqing University, Chongqing, China, 2012. [Google Scholar]
- Sun, X.; Han, L.; Wang, J. Tooth modification and loaded tooth contact analysis of China Bearing Reducer. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2019, 233, 6240–6261. [Google Scholar] [CrossRef]
- Stanojević, M.; Tomović, R.; Ivanović, L.; Stojanović, B. Critical Analysis of Design of Ravigneaux Planetary Gear Trains. J. Eng. Appl. Sci. 2022, 7, 32–44. [Google Scholar] [CrossRef]
- Hu, Y.; Talbot, D.; Kahraman, A. A Load Distribution Model for Planetary Gear Sets. ASME J. Mech. Des. 2018, 140, 053302. [Google Scholar] [CrossRef]
- Luo, Q. Study on Transmission Characteristics of Self-Adaptive Loading Ball Type Traction Reducer. Master’s Thesis, Chongqing University, Chongqing, China, 2022. [Google Scholar]
- Loewenthal, S.H.; Anderson, N.E.; Rohn, D.A. Evaluation of a High-Performance Fixed-Ratio Traction Drive. J. Mech. Des. 1981, 103, 410–417. [Google Scholar] [CrossRef]
- Cretu, O.S.; Glovnea, R.P. Traction Drive With Reduced Spin Losses. J. Tribol.-Trans. ASME 2003, 125, 507–512. [Google Scholar] [CrossRef]
- Flugrad, D.R.; Qamhiyah, A.Z. A Self-Actuating Traction-Drive Speed Reducer. J. Mech. Des. 2005, 127, 631–636. [Google Scholar] [CrossRef]
- Georgiev, N.; Burdick, J. Design and Analysis of the Bearingless Planetary Reducer. In Proceedings of the IEEE/RJS International Conference on Intelligent Robots and Systems, Vancouver, BC, Canada, 24–28 September 2017; pp. 1987–1994. [Google Scholar]
- Chen, D.S.; Pan, R. A Review of Traction Drive Research. J. Mech. Drives 2009, 33, 108–110. [Google Scholar]
- Katayama, E.; Ueda, K.; Takebayashi, H.; Rokkaku, K. Traction Drive Spindle Device. U.S. Patent 4,960,405, 2 October 1990. [Google Scholar]
- Qian, L.X.; Lu, J.Y.; Wang, X.X. Research on High-Speed Planetary Traction Speed-Increasing Mechanism. J. Mech. Transm. 1997, 1, 21. [Google Scholar]
- Qian, L.X. Research on Several Issues in the Development of Ultra-High-Speed Rotor Test Bed. Ph.D. Thesis, Zhejiang University, Zhejiang, China, 1998. [Google Scholar]
- Chen, C.Y. Design Analysis and Experimental Research of Planetary Traction Reducer for Hub Motors. Master’s Thesis, Chongqing University, Chongqing, China, 2016. [Google Scholar]
- Hewko, L.O. Roller Traction Drive Unit for Extremely Quiet Power Transmission. J. Hydronaut. 2013, 2, 160–167. [Google Scholar] [CrossRef]
- Ai, X.L.; Rybkoski, T.J. Traction Drive Transmission. U.S. Patent 6,095,940, 29 August 2000. [Google Scholar]
- Yan, D.Y.; Guo, J.J.; Zhang, X.H. A New Type of Symmetrically Loaded Planetary Traction Drive Reducer. J. Beijing Univ. Aeronaut. Astronaut. 1999, 25, 229–231. [Google Scholar]
- Pan, N.F.; Chen, D.S. Research on Self-Adaptive Loading Mechanism of Planetary Roller Friction Transmission. J. Mech. Des. 2013, 30, 102–108. [Google Scholar]
- Ai, X.L. Development of Zero-Spin Planetary Traction Drive Transmission: Part 1—Design and Principle of Performance Calculation. J. Tribol. 2002, 124, 386–391. [Google Scholar] [CrossRef]
- Ai, X.L. Development of Zero-Spin Planetary Traction Drive Transmission: Part 2—Performance Testing and Evaluating. J. Tribol. 2002, 124, 392–397. [Google Scholar] [CrossRef]
- Ai, X.L.; Wilmer, M.; Lawrentz, D. Development of Friction Drive Transmission. J. Tribol. 2005, 127, 857–864. [Google Scholar] [CrossRef]
- Shen, C.J.; Yuan, S.H.; Wei, C. Sliding Characteristics of Hydraulic Compression Traction Drive Device. J. South China Univ. Technol. 2012, 40, 82–86. [Google Scholar]
- Shen, C.J. Research on Traction Drive Characteristics of Double Cone Traction Drive Device. Ph.D. Thesis, Beijing Institute of Technology, Beijing, China, 2015. [Google Scholar]
- Yuan, S.H.; Yin, Z.X.; Wu, W.; Shi, B.S. Research on Cone-Ring Type Traction Drive Device Self-Help Speed Change Mechanism. J. Beijing Inst. Technol. 2015, 35, 461–466. [Google Scholar]
- Wang, W.; Durack, J.M.; Durack, M.J.; Zhang, J.; Zhao, P. Automotive Traction Drive Speed Reducer Efficiency Testing. J. Autom. Innov. 2021, 4, 81–92. [Google Scholar] [CrossRef]
- Shu, H.Y.; Yao, Z.J. Sliding Characteristics Analysis of Automotive Electric Wheel Traction Drive Reducer. J. Mech. Trans. 2018, 42, 30–35. [Google Scholar]
- Yao, Z.J. Design Analysis and Experimental Research of Planetary Traction Reducer Bearing for Automotive Electric Wheel. Master’s Thesis, Chongqing University, Chongqing, China, 2018. [Google Scholar]
- Zhou, Y.P.; Yuan, J.Q. Research and Practice of Traction Drive Design Method. J. Mod. Mech. 1999, 3, 52–53. [Google Scholar]
- Ouyang, H.B.; Wen, B. Lubrication Status Map of Planetary Rolling Mechanism. J. Lubr. Seal. 1991, 6, 35–37. [Google Scholar]
- Zhang, P.S.; Zhu, B.K.; Liu, S.C.; Qi, L.L. Study on the Measurement of Elastic Flow Film Thickness by Capacitance Method. Lubr. Seals. 1982, 2, 18–24. [Google Scholar]
- Dowson, D.; Higginson, G.R. Elasto-Hydrodynamic Lubrication; Pergamon Press: Oxford, UK, 1977. [Google Scholar]
- Department of Mechanical Principles and Mechanical Parts, Northwestern Polytechnical University. Mechanical Principles, 7th ed.; Higher Education Press: Beijing, China, 2006. [Google Scholar]
- Wu, W.; Yuan, S.H.; Guo, K.; Zhou, Z.H. Investigation of a Self-Actuating Traction Drive Device. In Proceedings of the 2009 International Conference on Mechatronics and Automation, Changchun, China, 9–12 August 2009; pp. 4133–4138. [Google Scholar]
- Huang, Z.D. Mechanical Design; Beijing Institute of Technology Press: Beijing, China, 1992; pp. 73–74. [Google Scholar]
- Ding, C.A.; Zhang, L.; Zhou, F.Z.; Zhu, J.; Zhao, S.K. Analytical Algorithm of Elastic Contact Deformation for Line Contact. Tribol. J. 2001, 2, 135–138. [Google Scholar]
- Zhang, L.; Yi, X.; Yu, J.; Li, J. Finite Element Analysis on Convexity for Tapered Roller with Arc-Line Modification Profile. Adv. Mater. Res. 2012, 591–593, 569–572. [Google Scholar] [CrossRef]
- Wang, X.; Qi, Q.S. Treatment of Stress Singularity Problems in Finite Element Analysis. J. Mech. Eng. Autom. 2014, 3, 61–63. [Google Scholar]
- Strozzi, A.; Baldini, A.; Giacopini, M. Normalization of the Stress Concentrations at the Rounded Edges of a Shaft-Hub Interference Fit. J. Strain Anal. Eng. Des. 2011, 46, 478–491. [Google Scholar] [CrossRef]
- Zhang, W.; Deng, S.; Chen, G. Study on the Impact of Roller Convexity Excursion of High-Speed Cylindrical Roller Bearing on Roller’s Dynamic Characteristics. J. Mech. Mach. Theory. 2016, 103, 21–39. [Google Scholar] [CrossRef]
- Jiang, Y.H.; Ding, S.Z.; Zhang, J.; Li, X.B.; Liu, J. Research on Optimal Design of Whole Bolt Roller Needle Bearing Roller Generatrix. Mach. J. Tool Hydraul. 2022, 50, 45–49. [Google Scholar]










| Parameters | Value |
|---|---|
| Maximum axial size/mm | 100 |
| Maximum radial dimension/mm | 75 |
| Target ratio | 20 |
| Motor torque/Nm | 2.29 |
| Motor power/kW | 1.2 |
| Motor speed/(r/min) | 5000 |
| Parameters | Value |
|---|---|
| Small inner ring outer diameter/mm | 11.5 |
| Large inner ring outer diameter/mm | 17 |
| Small inner ring axial length/mm | 19.5 |
| Large inner ring axial length/mm | 19.5 |
| Small rolling element axial length/mm | 17.2 |
| Large rolling element axial length/mm | 17.2 |
| Small outer ring axial length/mm | 27 |
| Large outer ring axial length/mm | 25 |
| Small reduction transmission ratio | 5.28 |
| Large reduction transmission ratio | 4.57 |
| Combined ratio | 26.6 |
| Parameters | Value/mm |
|---|---|
| Small inner ring outer diameter | 11.56 |
| Large inner ring outer diameter | 17.08 |
| Small rolling element outer diameter | 19 |
| Large rolling element outer diameter | 22 |
| Small inner diameter of the outer ring | 49.5 |
| Large outer diameter of the outer ring | 61 |
| Small outer ring thickness | 4.5 |
| Large outer ring thickness | 4.5 |
| Small outer diameter | 59.5 |
| Large outer diameter | 71 |
| Length of the contact line | 14 |
| Component | Material | Density (kg/m2) | Young’s Modulus (MPa) | Poisson’s Ratio |
|---|---|---|---|---|
| Inner ring | GCr15 | 7900 | 207,000 | 0.3 |
| Rolling element | GCr15 | 7900 | 207,000 | 0.3 |
| Outer ring | GCr15 | 7900 | 207,000 | 0.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shu, H.; Yu, Y.; Shu, R.; Wang, W.; Pan, C. Design and Testing of a New Type of Planetary Traction Drive Bearing-Type Reducer. Machines 2024, 12, 107. https://doi.org/10.3390/machines12020107
Shu H, Yu Y, Shu R, Wang W, Pan C. Design and Testing of a New Type of Planetary Traction Drive Bearing-Type Reducer. Machines. 2024; 12(2):107. https://doi.org/10.3390/machines12020107
Chicago/Turabian StyleShu, Hongyu, Yijie Yu, Ran Shu, Wenjie Wang, and Changjiang Pan. 2024. "Design and Testing of a New Type of Planetary Traction Drive Bearing-Type Reducer" Machines 12, no. 2: 107. https://doi.org/10.3390/machines12020107
APA StyleShu, H., Yu, Y., Shu, R., Wang, W., & Pan, C. (2024). Design and Testing of a New Type of Planetary Traction Drive Bearing-Type Reducer. Machines, 12(2), 107. https://doi.org/10.3390/machines12020107






