Abstract
This paper offers a comprehensive examination of the development and implementation of advanced safety protocols in the Patient Positioning System (PPS) for radiosurgery. In an era where precision and safety are increasingly crucial in medical procedures, particularly radiosurgery, the implementation of sophisticated safety measures in PPS is vital. This research delves into the detailed design of the system, emphasizing the sensor and controller mechanisms employed. A significant focus is placed on comparing single-loop and dual-loop control systems, assessing their impact on the precision, accuracy, and repeatability of the PPS. The study showcases how dual-loop control demonstrates superior performance in these areas, leading to enhanced patient safety and treatment outcomes. Additionally, the paper discusses the integration of these safety protocols within the system’s architecture, underscoring the practical implications of these advanced measures in augmenting patient safety and treatment effectiveness.
1. Introduction
Radiosurgery is known for its high accuracy and minimally invasive approach, but achieving this requires precise patient positioning. Our team has developed a new Patient Positioning System (PPS) prototype, designed to enhance the performance of radiosurgical procedures. A standout feature of our prototype is its exceptional precision, capable of positioning patients with an accuracy of 0.1 mm, which is vital for effective treatment.
The effectiveness of radiosurgery is closely linked to the ability of the PPS to accurately position patients. Our prototype represents a significant advancement in this area. It is not just about placing the patient correctly; it is about doing so with unparalleled precision [1].
Our study involved a thorough review of existing research on PPS. We found that advanced control systems play a crucial role in these systems. For instance, a study by Johnson and Patel (2022) highlights that a PPS with dual control loops is more accurate and dependable than those with a single loop [2]. This finding is critical for ensuring patient safety and precise treatment. Another research piece by Nguyen and Garcia (2021) underscores the importance of robust safety features in PPS, which help reduce risks and improve patient outcomes [3]. In addition to ongoing research, the market has seen recent contributions from major companies such as Siemens and Samsung, who are in competition to deliver superior products. While Samsung’s patient table design is integral to their radiotherapy treatment system, it does not facilitate movement during treatment. Siemens, conversely, emphasizes the load capacity of their solutions [4,5]. However, the two most competitive systems currently are the 6-DoF Robotic Couch System by gKteso GmbH, which boasts an absolute accuracy of 0.5 mm, and the Hexapods 6-Axis Patient Positioning Couches for Radiotherapy by PI (Physik Instrumente), known for their precision albeit with a limited travel range [6,7]. Our prototype surpasses these offerings by providing not just absolute accuracy up to 0.1mm but also a wider travel range, positioning it as a unique and advanced solution in the field of PPS [8].
This paper extends these findings by exploring the development and application of advanced safety protocols in our PPS prototype for radiosurgery. We offer a detailed comparison between single-loop and dual-loop control systems, shedding light on how these sophisticated features can improve patient safety and the effectiveness of treatment. The inclusion of these safety protocols in our PPS design reflects the ongoing advancements in technology and the increasing focus on precision and safety in medical procedures [9]. This paper is divided into several key sections to provide a thorough understanding of the topic:
- Patient Positioning System Characteristics: Here, we explore the detailed design elements of PPS, focusing on sensor and controller mechanisms, and how they contribute to the system’s overall functionality and safety [10].
- Comparison of Control Systems: This critical section compares single-loop and dual-loop control systems, presenting data and research findings that highlight the superiority of dual-loop systems in terms of precision and reliability.
- Safety Protocols and System Integration: This part discusses the advanced safety protocols integrated into the PPS, emphasizing their importance in enhancing patient safety and treatment outcomes [11].
- Results: This section shows the testing outcomes, with clear evidence of how well the dual-loop system improves accuracy and quick response to errors.
- Discussion and Future Directions: The section summarizes the findings of the paper and discusses potential areas for future research and development in the field of PPS and radiosurgery.
- Conclusion: The final section summarizes the findings of the paper and discusses potential areas for future research and development in the field of PPS and radiosurgery.
2. Patient Positioning System Characteristics
As a 6-degree-of-freedom (DOF) robotic patient bed, it has been ingeniously engineered to position patients accurately and precisely. It does so by aligning the clinical targets with the Mechanical Isocenter (MIC), ensuring an accurate delivery of the prescribed radiation. The PPS operates as a comprehensive unit, comprised of three key elements: a Linear Rail System, a Linkage System, and a Tabletop, see Figure 1.
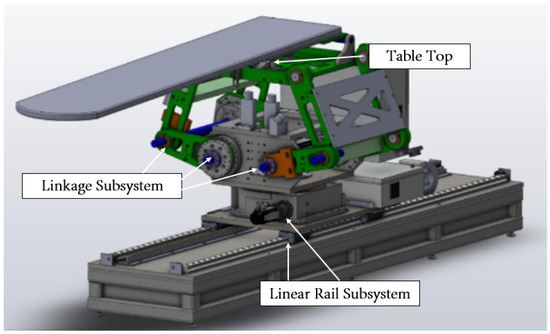
Figure 1.
Patient Positioning Table (PPT) Subsystems.
2.1. Design Overview
This subsection gives a quick look at the key parts and choices that form our system.
2.1.1. The Linear Rail System
The Linear Rail System forms the foundation of the PPS, tasked with controlling movement across two axes. It maneuvers the main plate in relation to the bottom base plate along a rail system and employs a rotary table to effectuate the rotation of the Linkage System relative to the main plate. This linear motion capability offers the flexibility to move the patient in and out of the operating area conveniently as shown in Figure 2.
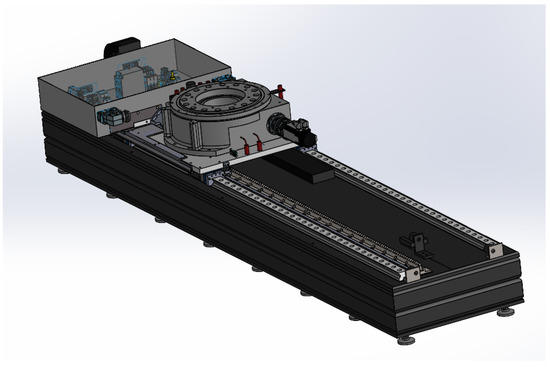
Figure 2.
Linear Rail System.
2.1.2. The Linkage System
The centerpiece of the PPS includes four linkage arms, three active and one passive. This system is anchored to a stationary weldment directly linked to the rotary table. Precision-driven shafts connect the two primary arms, while another driven shaft connects the remaining pair. Each pair of adjacent arms is interconnected by independent shafts. The active arms, driven by three motors, facilitate motion in a 2D plane and offer a sizable envelope size. The servo-driven gearbox propels the movements of three out of four linkage arms as shown in Figure 3. Notably, the Linkage System can be adjusted to varying heights for accommodating elderly or disabled patients and can be raised to the necessary height for treatment. To ensure precision for minute motor movements, such as correcting tumor misalignment during patient positioning, the motors are redundantly encoded [10].
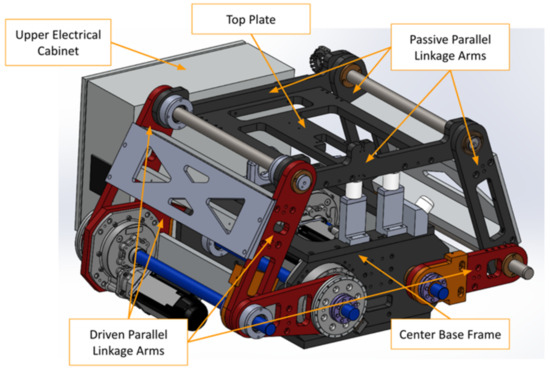
Figure 3.
Linkage Major Components.
2.1.3. Tabletop
Completes the system with its capacity to create pitching movements as shown in Figure 4. This functionality is achieved through a helical cam following system, driven by a servo motor Figure 5.
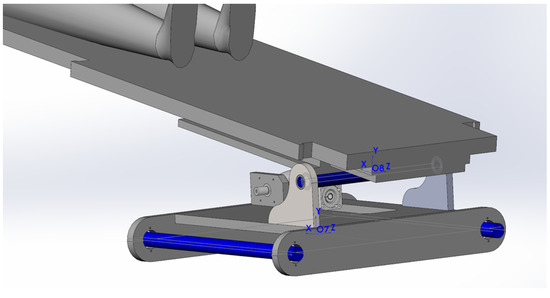
Figure 4.
Table Top Pitching Axis.
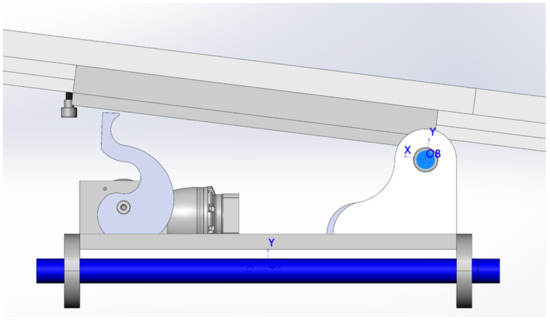
Figure 5.
Side view of Pitching Helical Cam.
The Helical Cam’s shape is designed such that the radius—as measured from the axis of rotation to the outer surface—and the angle of rotation have a linear relationship.
The PPS, through its distinctive components and operational capabilities, manifests an intricate control system for the patient’s position and orientation, fulfilling the exacting demands of radiosurgery treatment. It represents a tangible and pivotal achievement in realizing our goal of developing an effective motion control system for PPS. The 6-DOF in the 3D space of the PPS, represented by positional and orientation data [pitch (), yaw (), and roll ()], makes this system a comprehensive solution for precise patient positioning in the field of radiosurgery.
2.2. Patient Positioning System Coordinate System
The origin of the coordinate system coincides with the Mechanical Isocenter (MIC), which is a virtual point in space that lies on the z-axis. A description of each axis of the coordinate system is shown in the Table 1.

Table 1.
PPS Dimensions and Mass.
Figure 6 showcases the subsystems of the PPS, along with the associated coordinate frame.
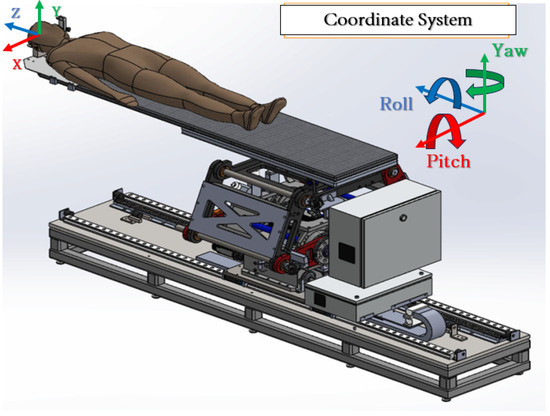
Figure 6.
Patient Positioning Coordinate System.
Note: In our frame visualizations, the axes are color-coded for clarity:
- X-axis is represented by the Red color (R).
- Y-axis is represented by the Green color (G).
- Z-axis is represented by the Blue color (B).
The PPS dimensions and mass are summarized in Table 1.
2.3. Design Components
Our device is engineered with a suite of sophisticated components, each meticulously selected for its role in ensuring optimal performance. At the core of the system lies a high-performance controller, responsible for managing the intricate motions and operations of the device. The drives, exemplified by the advanced Kollmorgen series, provide the necessary power and precision for the motion control, essential for the system’s functionality. These components are interconnected through a robust and efficient network, ensuring seamless communication and coordination. This integration of state-of-the-art components forms the backbone of our system, enabling it to meet the stringent demands of precision and reliability required in its application [12]. Figure 7 shows the axes numbering and the network connection of the PPS Subsystem Motion Controller and Drives.
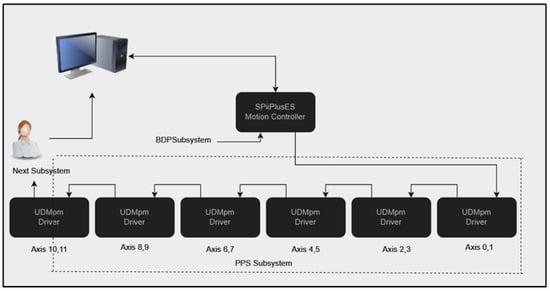
Figure 7.
PPS Subsystem Motion Controller, Drives.
2.3.1. Drives
The Universal Dual and Single Axis Motion Platform Module (UDMPM) is a sophisticated EtherCAT drive, designed to offer versatile control in both dual and single-axis applications. This drive stands out due to its compatibility with a broad range of power inputs, functioning efficiently with a single-phase supply ranging from 85 to 265 Vac or a DC supply from 120 to 375 Vdc. Such a wide power input range ensures adaptability across various operational environments. Figure 8 shows the UDMPM ACS Drive.

Figure 8.
UDMPM ACS Drive.
Furthermore, the UDMPM is engineered to cater to diverse operational demands, offering a spectrum of continuous and peak current options. These include 2.5 A/5 A, 5 A/10 A, and 7.5 A/15 A, thereby accommodating a wide range of power requirements and enhancing its suitability for different radiosurgery applications. This versatility in power handling is crucial for precision and safety in patient positioning systems, ensuring stable and controlled motion, which is essential in delicate radiosurgical procedures.
The integration of EtherCAT technology underscores the UDMPM’s capability for rapid, real-time communication, a critical factor in synchronizing complex motion sequences in radiosurgery. This allows for seamless integration with other system components, ensuring a cohesive and responsive patient positioning system.
2.3.2. Controller
The controller at the heart of our system is powered by a robust MPU, featuring the Intel® AtomTM N2600 processor with a clock speed of 1.6 GHz (Figure 9). This high-performance unit is specifically chosen for its enhanced processing capabilities, essential for managing the complex demands of radiosurgical applications [13].

Figure 9.
Motion Controller.
Key Features of the SPiiPlusEC Controller:
- High Processing Capacity: Capable of managing up to 16 axes simultaneously at a high update rate of 5 kHz. This power is crucial for executing intricate motion sequences in real time, a fundamental requirement in precision-driven radiosurgery.
- Dual EtherCAT Ports: The inclusion of two EtherCAT ports provides a robust mechanism for network failure detection and swift recovery, vital in maintaining continuous operation and ensuring patient safety [14].
- Gigabit Ethernet Connectivity: Includes an Ethernet host communication port capable of supporting speeds up to 1GbE, ensuring rapid data transfer and efficient communication.
- Multiple Communication Options: Equipped with two RS232 serial communication ports, offering versatile connectivity and facilitating easy integration with various peripherals.
- Mounting Flexibility: Offers both panel and Din-rail mounting options, allowing for customization based on specific operational requirements.
- LED Indicators: The inclusion of LED indicators provides immediate visual feedback regarding the system’s operational status, aiding in monitoring and maintenance.
2.3.3. Kollmorgen Servo Motors
In our system, a range of Kollmorgen servo motors are employed (Figure 10), each chosen for their specific strengths in precision and control. These motors are integral for various functions, from linear motion to complex linkage control. Below, we present a detailed breakdown of each motor’s role and specifications Table 2, [15].

Figure 10.
Kollmorgen Servo Motors.

Table 2.
Specifications of Kollmorgen Servo Motors.
2.3.4. Secondary Encoder
Incorporating the Renishaw 26-bit BiSS-C encoders, specifically the RESA30USA200B and RA26BAA200B50F models, into our system plays a pivotal role in enhancing precision in all axes. These encoders are selected for their exceptional resolution and accuracy, critical for the high-precision requirements of our application, Renishaw readhead shown in Figure 11. The BiSS-C (Bidirectional Serial Synchronous Communication) interface of these encoders ensures high-speed and real-time feedback, which is essential for maintaining the integrity and accuracy of the system’s motion control. The 26-bit resolution of these encoders allows for extremely detailed and accurate positional feedback. Additionally, the configuration of the read head and ring in these models facilitates precise tracking of the rotational positions, thereby ensuring meticulous control over motion in all axes. The integration of these high-end encoders underscores our commitment to achieving unparalleled accuracy and reliability in our system’s performance [16].

Figure 11.
Renishaw Readhead.
3. Comparison of Control Systems
The control architecture is a pivotal element of the Patient Positioning System (PPS), integral to its precision, safety, and efficacy. It employs advanced control strategies to accurately manage the system’s 6-DOF (Degrees of Freedom) robotic movements. This section delves into the control architecture, highlighting its core principles and operational mechanisms. Our focus is on two types of control loops: Single-loop and Dual-loop. Single-loop control offers straightforward feedback mechanisms, while Dual-loop control introduces an additional control layer, enhancing system robustness and accuracy [17].
3.1. Single Loop Control
Our device features a single-loop control system, streamlined for efficiency and reliability. At its core, a primary encoder within the brushless Kollmorgen servo motor monitors the device’s output. This encoder continuously compares the actual performance to a pre-set goal. Should any deviation occur between the encoder’s readings and this target, the system automatically adjusts the motor’s output to realign with the intended performance [18].
3.1.1. Cascaded Control Loops
Cascaded control loops are commonly used in advanced control systems. These loops are arranged hierarchically and consist of the following:
- Current Loop: This is the innermost control loop and is responsible for regulating the current in the system.
- Velocity Loop: This loop controls the speed of the system and receives its command from the outer position loop.
- Position Loop: This is the outermost loop and generates a command that is fed into the velocity loop.
The hierarchical arrangement works as follows:
- The Position Loop generates a command for the Velocity Loop.
- The Velocity Loop, in turn, generates a command for the Current Loop.
The block diagram in Figure 12 illustrates the cascading relationship between these loops.
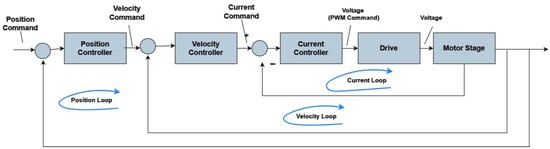
Figure 12.
Block diagram illustrating cascaded control loops.
3.1.2. Cascaded Control Loops Transfer Functions
Each closed loop in a cascaded control system functions as a low-pass filter within the overarching control architecture. A higher bandwidth of an inner loop typically enhances the stability of the subsequent outer loop.
The current control loop forms the foundational layer of our control system, ensuring the precision regulation of the motor’s current and, consequently, its torque output. The current controller is typically configured as a Proportional-Integral (PI) controller. The corresponding control strategy is depicted in Figure 13.
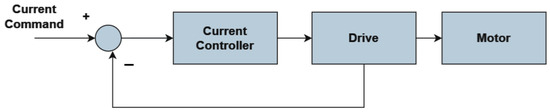
Figure 13.
Current Loop Command.
The transfer function for the PI current controller is given by:
where and denote the proportional and integral gains, respectively. The drive and motor dynamics are collectively modeled as a first-order linear system:
where is the motor gain, and is the motor time constant. The overall closed-loop transfer function, describing the system’s response to the current command input, is thus formulated as:
Following the current control loop, the velocity control loop regulates the motor’s speed to match the desired velocity command. Figure 14 illustrates the schematic of the velocity control loop.
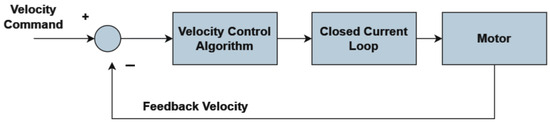
Figure 14.
Velocity Command.
The velocity control algorithm, often a Proportional-Integral (PI) controller, computes the necessary current command to achieve the target velocity based on the feedback velocity. The transfer function for the velocity controller is typically expressed as:
where is the proportional gain and is the integral gain for the velocity control.
The closed-loop transfer function, taking into account the dynamics of the current loop defined in Equation (3), can be represented as:
This equation describes the response of the velocity control loop to velocity command inputs, accounting for the motor’s current response as an integral part of the control system.
The outermost layer of control is the position loop, which ensures that the motor’s output shaft reaches and maintains the desired position. The position control loop and its elements are depicted in Figure 15.
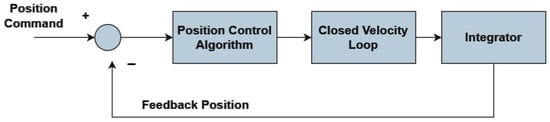
Figure 15.
Position Command.
The position control algorithm typically employs a Proportional-Integral (PI) approach to generate the required velocity command based on the position error, which is the difference between the position command and the feedback position. The transfer function for the position controller is given by:
where and are the proportional and integral gains, respectively.
An integrator is used to accumulate the velocity command over time, contributing to the position change. The closed-loop transfer function, incorporating the velocity loop from Equation (5), can be modeled as:
Equation (7) captures the dynamics of the position control loop, detailing how the system achieves precise positioning through the integration of velocity commands over time.
3.2. Dual-Loop Control
Dual Loop control is often employed to mitigate issues arising from mechanical slack between the motor and the load. Unlike Single Loop control, which can experience diminished dynamic performance due to such slack and backlash, Dual Loop control remains largely unaffected and maintains performance [19].
Dual Loop Basics
In Dual Loop control, users have the flexibility to assign feedback either from multiple channels or from an analog input directly to the axis. However, there is a condition that both the axis and the channels should be connected to the same Servo Processor. Dual Loop control relies on at least two distinct sources of feedback:
- Load position feedback: Serves as the input for the Position Loop.
- Motor position feedback: Acts as the input for the Velocity Loop, as well as for the motor’s commutation.
In our PPS, we employ dual-loop control for several reasons: to overcome backlash, achieve enhanced accuracy, and implement safety procedures. The following Figure 16 A block diagram illustrating the different components involved in a Dual Loop control system is provided for better understanding.
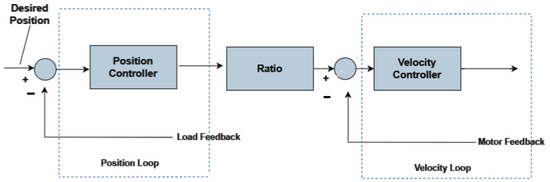
Figure 16.
Controller in Dual Loop Block Diagram.
4. Safety Protocols and System Integration
Accuracy in radiation delivery is paramount, as deviations can compromise patient health and treatment outcomes. The management of involuntary patient movements, such as breathing, presents another layer of complexity, necessitating real-time motion tracking. Furthermore, stringent equipment maintenance and calibration protocols are critical to circumvent dosimetric errors. The multidisciplinary nature of radiosurgery amplifies the need for flawless communication and synchronized efforts to preempt safety oversights.
4.1. Implementation and Safety in Patient Positioning System
The implementation of our PPS is underscored by an unwavering commitment to safety. This is realized through an ecosystem of emergency stops, fault detection capabilities, limit sensors and rigorous daily initialization procedures that together form a bulwark against potential risks [20].
4.2. Fault Classification
Faults within the PPS can be broadly classified into two categories Figure 17:
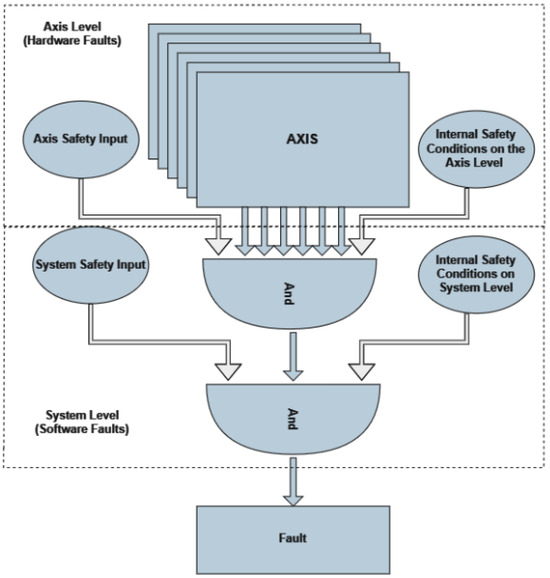
Figure 17.
ACS Fault Handling.
- Axis Faults: Pertaining to motor motion. These faults primarily arise from issues related to the mechanical components responsible for movement.
- System Faults: Directly associated with the controller program. These faults can originate from software glitches, erroneous commands, or disruptions in the control processes.
4.3. PPS Internal Safety Conditions
In the Patient Positioning System (PPS), the “internal safety condition” refers to the system’s built-in checks and measures that monitor operational states. If any irregularities or deviations are detected, the PPS automatically takes preventive actions to ensure safe operation, such as halting movements or triggering alerts as shown in Figure 18. This ensures the machinery operates without causing unexpected hazards or errors.
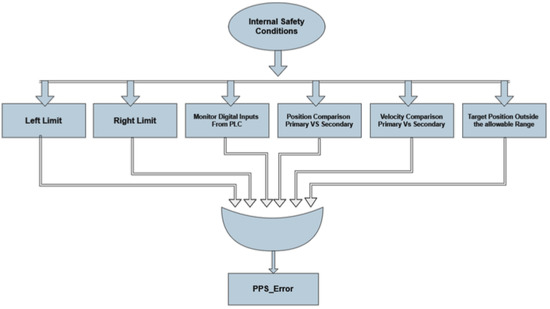
Figure 18.
Internal safety Conditions Diagram.
We have detailed this intricate process through various safety conditions and have visually represented their workings in a flowchart, as discussed below:
- Primary/Secondary Encoder Slipping Check: Both the primary and secondary encoders undergo rigorous checks for position and velocity slipping (Figure 19). Any discrepancies observed between expected and actual readings flag an immediate safety alert [21].
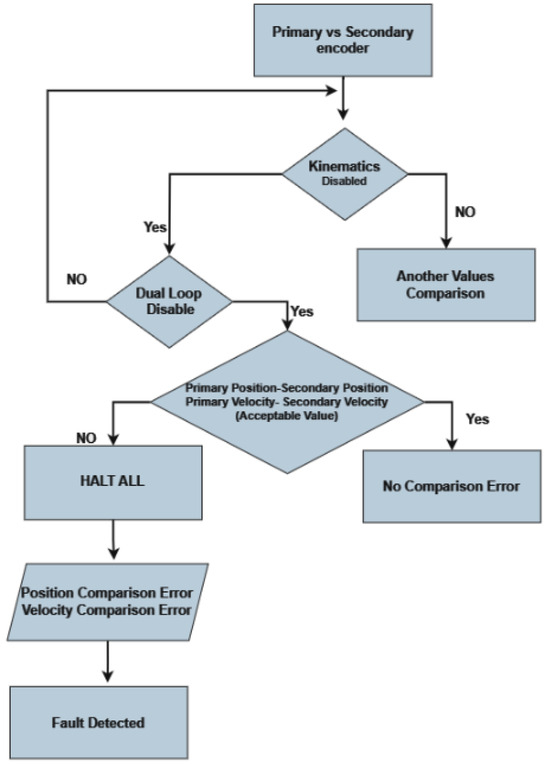 Figure 19. Slipping check Flowchart.
Figure 19. Slipping check Flowchart. - Target Position Monitoring: It is vital that the machine’s target position stays within an allowable range. For a sequential understanding of how this monitoring occurs, please consult the flowchart in Figure 20.
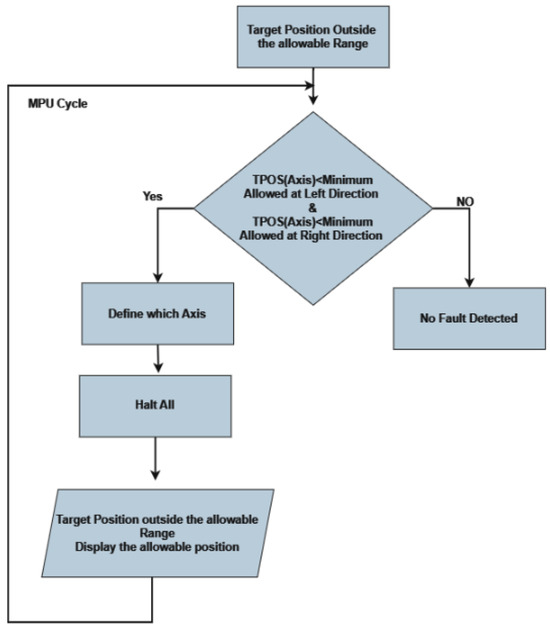 Figure 20. Target Position check Flowchart.
Figure 20. Target Position check Flowchart. - Digital Inputs from PLC Monitoring: Digital inputs from the PLC (Programmable Logic Controller) are continuously monitored. The flowchart in Figure 21 further elucidates this monitoring process [22].
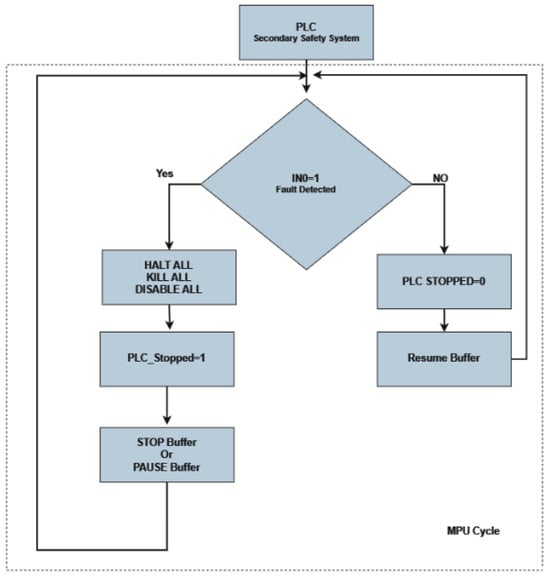 Figure 21. Monitoring Input from PLC.
Figure 21. Monitoring Input from PLC. - Left/Right Limit Check: This safety feature ensures that the machine operates within the defined left and right boundaries (Figure 22).
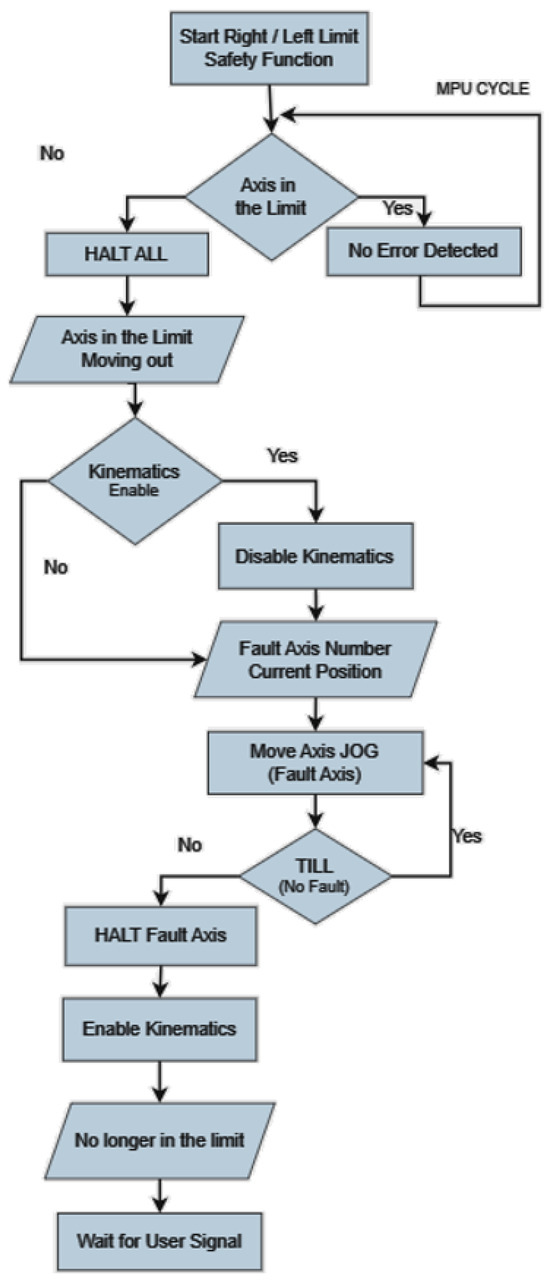 Figure 22. Left/Right Limit checking flowchart.
Figure 22. Left/Right Limit checking flowchart.
The importance of safety and fault handling in the Patient Positioning System (PPS) for radiotherapy cannot be overstated. The incorporation of emergency stops, continuous monitoring for fault detection, and limit sensors ensures the system can promptly respond to any anomalies, thereby safeguarding patient and operator well-being [23].
5. Results
5.1. Analysis of DualLoop vs. SingleLoop Systems
This analysis aims to evaluate and compare the performance of two systems: DualLoop and SingleLoop, in terms of their precision in achieving target positions. The data consist of target coordinates and the corresponding errors from both systems in achieving those targets.
5.2. Measurement Methodology
The precision of our Patient Positioning System (PPS) was assessed using a triangulation-based approach with three Optitrack cameras. These high-accuracy cameras tracked a marker placed on the target point of our PPS, which we define as the home position at coordinates = (0, 1036, 0). This position was meticulously calibrated to serve as the reference for all subsequent measurements.
5.2.1. Data Collection Protocol
The assessment was conducted by examining each axis independently to isolate the positional accuracy achievable by the control system. The procedure involved:
- Fixing the Y and Z-axes and moving along the X-axis from its minimum to maximum limit. This movement was repeated three times to ensure the consistency and repeatability of the results.
- Conducting similar movements along the Y-axis, with the X and Z-axes held stationary.
- Finally, repeating the procedure along the Z-axis while keeping the X and Y-axes fixed.
This process was performed separately for both the single loop and dual loop control systems. Each traversal from minimum to maximum represented a full sweep along that axis.
5.2.2. Error Calculation
The position error for each axis was computed by comparing the recorded positions from the Optitrack system against the PPS’s known target positions. The error was defined as the difference between the measured position and the home position for the X, Y, and Z coordinates, respectively. The data set comprised the accumulated positional readings from each sweep across the axes.
The statistical measures of mean, standard deviation, minimum, and maximum error values were calculated for each axis, providing a comprehensive error profile for the control systems. These values are presented in Table 3, enabling a direct comparison of the single and dual loop control systems’ positional accuracy.

Table 3.
Error Analysis for Single and Dual Loop Control Systems.
The error analysis, as quantified in millimeters, is instrumental in evaluating the precision of the control loops within the PPS. By detailing the measurement protocol and subsequent data analysis, we ensure that the reported errors reflect the true positional accuracy of our system under test conditions that closely mimic its intended operational environment.
5.3. Visualization Analysis
Given the multi-faceted nature of our observations, we have employed a suite of visualization tools to articulate our findings. This subsection delves into the comparative analysis of error performance between Single Loop Control and Dual Loop Control systems.
The trajectory designed for the system’s evaluation consisted of a series of coordinated movements across all axes, thereby simulating the intricate maneuvers required in radiosurgery. This trajectory was not confined to linear translations but encompassed a sequence of motions that tested the control systems’ precision in three-dimensional space. As such, the trajectory included a combination of linear, sinusoidal, and static segments, representing various operational demands.
The visualization depicted in Figure 23 provides an insightful representation of the error evolution for the X, Y, and Z-axes, showcasing the comparative performance of the two control systems. In this analysis, the ‘nominal’ positions were determined through a predetermined trajectory within the design’s permissible workspace, extensively vetted during the calibration phase. The ‘real’ positions were captured using a high-precision Optitrack system with markers located on the target point of the PPS, which was set at (0, 1036, 0 mm) in the calibrated home position.
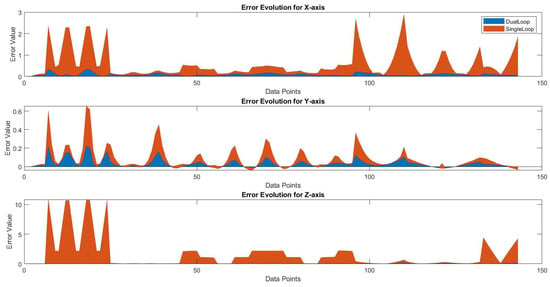
Figure 23.
Error evolution for X, Y, and Z axes (mm).
For clarity, the errors demonstrated in the figure are presented in millimeters (mm), offering a quantifiable perspective on the precision achievable by the Single Loop versus the Dual Loop Control systems. The data points represent a series of positions recorded during the system’s motion, with the error being the deviation from the expected trajectory. The marked reduction in error magnitude with the Dual Loop Control system underscores its enhanced accuracy and reliability for critical applications such as patient positioning in radiosurgery.
5.4. Internal Safety Conditions Test
5.4.1. Encoder Slipping
Figure 24 illustrates the encoder readings over time, described as follows: Figure 24 described as follows:
- The blue line represents the encoder readings across various time points.
- At time point 4 (marked by the red dashed line), a significant spike in the readings indicates the slipping event.
- Following this event, the encoder readings drop to zero, as shown by the portion of the graph following time point 4. This drop to zero, highlighted by the green dashed line, represents the system’s ’kill motion’ response, effectively stopping all motion for safety.
- These time points are measured instances that correspond to the data collection frequency, such as every second or millisecond, as defined by the system’s monitoring capabilities.
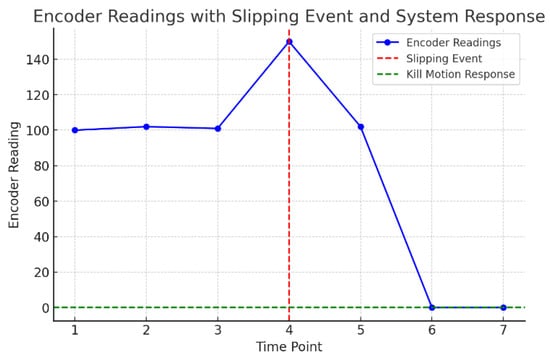
Figure 24.
Primary Vs Secondary Encoder.
5.4.2. Left and Right Limits Test
Figure 25 presents two separate line graphs, each representing a scenario for the Left Limit Check and Right Limit Check of your system on the Z axis:
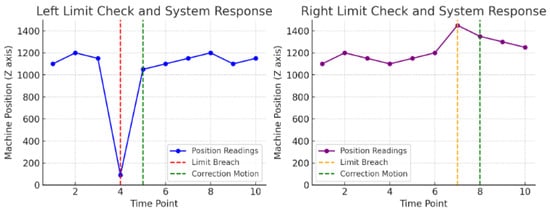
Figure 25.
Left/Right Limits.
Left Limit Check
- Normal Operation: The blue line shows normal operation within the allowable range.
- Limit Breach: At time point 4 (red dashed line), the machine position drops below the minimum allowable limit (100), indicating a breach of the left limit.
- Correction Motion: Immediately after the breach, at time point 5 (green dashed line), the system responds by applying a corrective motion, bringing the machine position back into the allowable range.
Right Limit Check
- Normal Operation: The purple line indicates normal operation within the allowable range.
- Limit Breach: At time point 7 (orange dashed line), the machine position exceeds the maximum allowable limit (1400), signaling a breach of the right limit.
- Correction Motion: Following this breach, at time point 8 (green dashed line), the system executes a corrective motion in the opposite direction, ensuring the machine returns to within the safe operating range.
These time points are measured instances that correspond to the data collection frequency, such as every second or millisecond, as defined by the system’s monitoring capabilities.
5.4.3. Digital Safety Signal from PLC
Figure 26 visually represents a scenario where the reception of a signal from the Programmable Logic Controller (PLC) leads to the immediate cessation of machine motion.
- The blue line shows the machine’s motion over time, initially moving continuously.
- At time point 11, marked by the red dot, the system receives a critical signal from the PLC.
- Following the reception of this signal, the machine’s motion stops abruptly, as indicated by the blue line remaining constant after time point 11.
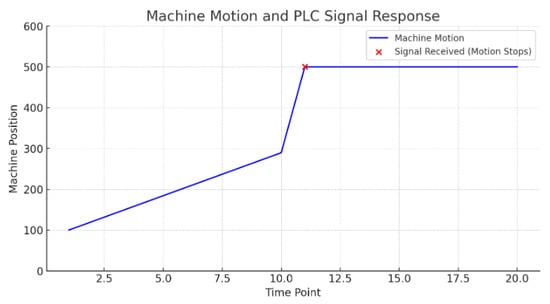
Figure 26.
Error Signal from PLC.
6. Discussion
This study’s exploration into the intricate safety protocols within the Patient Positioning System (PPS) for radiosurgery highlights the paramount importance of precision and reliability in medical procedures. The findings clearly demonstrate the efficacy of dual-loop control systems over single-loop systems, particularly in terms of precision, accuracy, and repeatability. These attributes are critical in radiosurgery, where even minimal deviations can have significant consequences.
The visual analyses presented, such as the line graphs depicting the encoder readings and machine motion in response to safety triggers, reinforce the robustness of the safety mechanisms. The immediate cessation of motion upon detecting the encoder slipping or breaching pre-set limits underscores the system’s responsiveness. This rapid response capability is vital in preventing potential errors that could compromise patient safety.
The comparison between single-loop and dual-loop systems provides valuable insights. While single-loop systems are simpler and may suffice in less critical applications, our study illustrates that for applications demanding high precision and reliability, dual-loop systems are clearly superior. The additional feedback loop in a dual-loop system offers a significant increase in accuracy, a critical factor in ensuring the safety and effectiveness of radiosurgery treatments.
Practical Implications and Future Directions
The integration of these advanced safety protocols into the PPS’s architecture is not just a theoretical enhancement but a practical necessity. The real-world implications of these improvements are profound, as they directly contribute to heightened patient safety and better treatment outcomes. The enhanced safety measures provide a buffer against unforeseen operational anomalies, ensuring the system remains within safe operational parameters at all times.
Looking forward, the continual refinement of these safety protocols, along with the incorporation of emerging technologies like AI and machine learning, could offer even greater precision and reliability. Future research could focus on integrating predictive analytics into the PPS, allowing for proactive adjustments before potential safety issues arise.
7. Conclusions
In conclusion, this study affirms the critical role of advanced safety protocols in the PPS for radiosurgery. The implementation of these protocols, particularly the adoption of dual-loop control systems, marks a significant advancement in ensuring patient safety and treatment efficacy. This research contributes to the ongoing evolution of radiosurgery, pushing the boundaries of what is possible in precision medical treatment.
8. Patents
The Patient Positioning System (PPS) is presently undergoing the patenting process, holding the application number PCT/US2019/048205.
Author Contributions
Conceptualization, L.F., A.S., J.H., E.T. and J.S.; methodology, L.F., A.S., J.H., E.T., J.S. and L.M. software, A.S., J.H., L.F., T.K. and M.K.; validation, A.S., D.T., P.P., J.S. and L.M.; formal analysis, A.S.; investigation, A.S., J.S., J.H. and L.M.; resources, E.T., L.F., J.H., A.S., J.S. and L.M.; data curation, A.S., T.K., M.K. and L.M.; writing—original draft preparation, A.S.; writing—review and editing, A.S. and G.H.; visualization, A.S. and L.F.; supervision, G.H., E.T., D.M. and X.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This project was funded by the National Research Development and Innovation, Fund of the Ministry of Innovation and Technology.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Acknowledgments
Gratitude is extended to the contributors from Spinotron Kft, Hungary, and the Medical Beams Laboratory, USA. Their indispensable assistance was instrumental in the system’s prototyping and examination phases conducted in Hungary.
Conflicts of Interest
Laszlo Fadgyas, Donald Medlin, and Xiaoran Zheng are employed by Medical Beam Laboratories. Jad Saud is employed by Spinotron Kft. Jason Henderson is employed by Quiverent LLC. Tibor Koroknai, Máté Koroknai, David Takacs, and Peter Panko are employed by Medikai Innováció Kft. There are no other conflicts of interest, and the companies had no role in this study. The authors declare no further conflicts of interest.
References
- Sadashiva, N.; Tripathi, M. Safety checklist for gamma knife radiosurgery. Asian J. Neurosurg. 2019, 14, 1308–1311. [Google Scholar] [CrossRef] [PubMed]
- Johnson, K.L.; Patel, S.R. Enhancing Precision in Radiosurgery: A Comparative Analysis of Single-Loop and Dual-Loop Control Systems in Patient Positioning. J. Med. Robot. Autom. 2022, 28, 455–467. [Google Scholar]
- Nguyen, H.T.; Garcia, M. Integrating Advanced Safety Protocols in Radiosurgical Patient Positioning Systems: Impacts on Clinical Outcomes. Int. J. Radiosurgery Patient Saf. 2021, 19, 122–134. [Google Scholar]
- Siemens. SOMATOM go. Platform—CT Scanners for Radiation Therapy Planning. Available online: https://www.siemens-healthineers.com/en-us/radiotherapy/ct-for-rt/somatomgoup (accessed on 18 January 2024).
- Samsung Hospital. Introduction to Radiotherapy Process. Available online: https://www.samsunghospital.com/ (accessed on 18 January 2024).
- gKteso GmbH. 6 DoF Couch for Medical Physicists. Available online: https://www.radiotherapy-patient-system.com/medical-physicists/6-dof-couch/ (accessed on 18 January 2024).
- PI (Physik Instrumente). Hexapods Enable Precise 6-Axis Patient Positioning Couches for Radiotherapy. Available online: https://www.pi-usa.us/en/tech-blog/hexapods-enable-precise-6-axis-patient-positioning-couches-for-radiotherapy (accessed on 18 January 2024).
- Saadah, A.; Medlin, D.; Saud, J.; Zheng, X.R.; Husi, G. A State-of-the-Art Design: Applying Forward Kinematics to Improve Patient Positioning in Radiosurgery. In Proceedings of the 2023 International Conference on Microelectronics (ICM), Abu Dhabi, United Arab Emirates, 17–20 December 2023; pp. 86–90. [Google Scholar]
- Das, I.J.; Dawes, S.L.; Dominello, M.M.; Kavanagh, B.; Miyamoto, C.T.; Pawlicki, T.; Santanam, L.; Vinogradskiy, Y.; Yeung, A.R. Quality and safety considerations in stereotactic radiosurgery and stereotactic body radiation therapy: An ASTRO safety white paper update. Pract. Radiat. Oncol. 2022, 12, e253–e268. [Google Scholar] [CrossRef] [PubMed]
- Saadah, A.; Medlin, D.; Saud, J.; Zheng, X.R.; Géza, H. Kinematics Study for Linkage System (Parallel Robotics System): Linkage system of patient positioning system PPS to accurately position a human body for radiosurgery treatment. In Proceedings of the 2023 Advances in Science and Engineering Technology International Conferences (ASET), Dubai, United Arab Emirates, 20–23 February 2023; pp. 1–6. [Google Scholar]
- Kim, K.H.; Lee, H.; Sohn, M.J.; Mun, C.W. In-house developed surface-guided repositioning and monitoring system to complement in-room patient positioning system for spine radiosurgery. Prog. Med. Phys. 2021, 32, 40–49. [Google Scholar] [CrossRef]
- Gerlach, S.; Schlaefer, A. Robotic systems in radiotherapy and radiosurgery. Curr. Robot. Rep. 2022, 3, 9–19. [Google Scholar] [CrossRef]
- Palmer, J.D.; Sebastian, N.T.; Chu, J.; DiCostanzo, D.; Bell, E.H.; Grecula, J.; Arnett, A.; Blakaj, D.M.; McGregor, J.; Elder, J.B.; et al. Single-isocenter multitarget stereotactic radiosurgery is safe and effective in the treatment of multiple brain metastases. Adv. Radiat. Oncol. 2020, 5, 70–76. [Google Scholar] [CrossRef] [PubMed]
- Al-Hallaq, H.; Batista, V.; Kügele, M.; Ford, E.; Viscariello, N.; Meyer, J. The role of surface-guided radiation therapy for improving patient safety. Radiother. Oncol. 2021, 163, 229–236. [Google Scholar] [CrossRef] [PubMed]
- Shi, J.; Gu, H.; Shi, C. Research and Realization of Servo Control System Based on Medical Centrifuge. J. Phys. Conf. Ser. 2022, 2383, 012153. [Google Scholar] [CrossRef]
- Iafolla, L.; Filipozzi, M.; Freund, S.; Zam, A.; Rauter, G.; Cattin, P.C. Proof of concept of a novel absolute rotary encoder. Sens. Actuators Phys. 2020, 312, 112100. [Google Scholar] [CrossRef]
- Sabarianand, D.V.; Karthikeyan, P.; Muthuramalingam, T. A review on control strategies for compensation of hysteresis and creep on piezoelectric actuators based micro systems. Mech. Syst. Signal Process. 2020, 140, 106634. [Google Scholar] [CrossRef]
- Gambhire, S.J.; Kishore, D.R.; Londhe, P.S.; Pawar, S.N. Review of sliding mode based control techniques for control system applications. Int. J. Dyn. Control. 2021, 9, 363–378. [Google Scholar] [CrossRef]
- Yang, L.; Zhang, L. Motion control in magnetic microrobotics: From individual and multiple robots to swarms. Annu. Rev. Control Robot. Auton. Syst. 2021, 4, 509–534. [Google Scholar] [CrossRef]
- Azarkaman, A.; Deilamani, P.R.; Ghorbani, N. Medical Devices Engineering Textbook 1; Nobel TM: Tehran, Iran, 2022. [Google Scholar]
- Wang, K.; Johnson, C.W.; Bennett, K.C.; Johnson, P.A. Predicting fault slip via transfer learning. Nat. Commun. 2021, 12, 7319. [Google Scholar] [CrossRef] [PubMed]
- Stoicuta, O.; Riurean, S.; Burian, S.; Leba, M.; Ionica, A. Application of optical communication for an enhanced health and safety system in underground mine. Sensors 2023, 23, 692. [Google Scholar] [CrossRef] [PubMed]
- Pal, A.; Restrepo, V.; Goswami, D.; Martinez, R.V. Exploiting mechanical instabilities in soft robotics: Control, sensing, and actuation. Adv. Mater. 2021, 33, 2006939. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).