Abstract
This paper presents the structure and model of a hybrid modular structure of a robotic system for lower limb rehabilitation. It is made of two modules identical in structure, including an active 3-PRRR manipulator for moving the patient’s foot and a passive orthosis based on the RRR mechanism for supporting the lower limb. A mathematical model has been developed to describe the positions for the links of the active and passive mechanisms of two modules, as a function of the angles in the joints of the passive orthosis, considering constraints for attaching the active manipulators to the moving platform and their configurations. A method has been formulated for a parametric synthesis of the hybrid robotic system proposed with modular structure, taking into account the generated levels of parametric constraints depending on the ergonomic and manufacturability features. The proposed design is based on a criterion in the form of a convolution, including two components, one of which is based on minimizing unattainable points of the trajectory, considering the characteristics of anthropometric data, and the other is based on the compactness of the design. The results of the mathematical modeling are discussed as well as the analysis results towards a prototype validation.
1. Introduction
One of the most pressing and complex problems of medicine and neurology is the rehabilitation of patients. The number of people who need rehabilitation is growing every day. According to investigations [1,2], 419,000 people diagnosed with stroke were registered in the Russian Federation in 2014. According to the Ministry of Health of the Russian Federation, in 2017, 427,963 people were registered for whom acute cerebrovascular disorders were first detected. Patients who have experienced acute attacks of this disease type either cannot move without help or are completely deprived of the opportunity to move independently. Currently, over one million stroke survivors live in Russia. A third of this number are people of working age. At the same time, only every fourth of working people return to work after a stroke [2]. Violations of the limbs must undergo a rehabilitation process in order to restore the normal functioning of the limbs. Lower limb rehabilitation or treatment has been a hot topic in recent years, since robotized systems promised effective results and led to significant improvements in the recovery of patients using robotic physiotherapy, as pointed out in [3].
It Is widely recognized that a person’s locomotion depends both on basic patterns generated at the level of the spine and on the prognosis and reflex-dependent precise control of these patterns at different levels [4,5,6]. These physiological movements recorded in healthy people are applied as exercises in patients with disorders of the lower limbs. These data sequences for the joints of the lower limbs are called gait data (walking pattern) [5]. In addition to gait data, the lower limbs perform movements such as hip flexion and extension, knee flexion and extension, ankle flexion, and back flexion. Gait training restores synchronization of muscle action in lower limbs and is processed separately to strengthen each motor joint, to then strengthen each joint of the leg.
Currently, there are many devices available for lower limb rehabilitation. The Gait Trainer [7] is a wheeled device that helps a person who cannot walk independently. The BIT LExoChair [8] mobility-assisted wheelchair has a modular design for user’s locomotion mobility with the aim of assisting autonomy, exercising, and rehabilitation. The design is based on a traditional wheelchair design that uses a force sensor for controlled operation with different equipment as a function of the environment and aim of usage. The rehabilitation system WalkTrainer [9] has a mobile frame design, which includes a system for unloading weight. Thus, it is possible to regulate the dynamic load on the patient’s lower limbs. There are also rehabilitation devices that are based on treadmills. It is worth noting the Lokomat rehabilitation system [10] and the CDLR cable robot for lower limb rehabilitation [11]. The functionality of those devices does not allow for the rehabilitation of the lower limbs of patients in the early stages of rehabilitation; therefore, these devices are not suitable for patients who are only able to be in a sitting and lying position, impaired with lower limbs.
Among rehabilitation systems, which are available in the early stages of rehabilitation, one can point out the LokoHelp movement therapy station [12], which is an electromechanical gait trainer with a weight-unloading system. However, this system is not applicable to patients who cannot be suspended. A gait rehabilitation device based on a 3DOF parallel arm [13] generates the required gait pattern by moving the patient’s foot while the body weight is supported by a seat belt system. The KARR rehabilitation system [14] allows the rehabilitation of patients in a sitting position. Also worth noting is the Lambda robot rehabilitation system [15], which can be applied to the rehabilitation of bedridden patients by mobilizing the ankle joint. An upright table with an integrated orthopedic device and synchronized functional electrical stimulation, Erigo Pro [16], allows for intensive cyclic movement therapy in the form of passive dynamic movements of the lower limbs of recumbent patients. However, the above-mentioned devices for physiotherapeutic movements provide flexion–/extension in the knee joint, while a movement such as adduction–abduction in the hip joint is impossible, with a significant drawback. The CUBE cable rehabilitation device [17] allows for the rehabilitation of both the upper and lower limbs. However, with this design, active robot-assisted therapy for flexion/extension in the ankle joint is rather difficult.
In general, in rehabilitation procedures, the treatment of patients with disabilities of impaired motor functions of the lower limbs occurs in a critical sitting or lying position. These conditions are because patients at this stage cannot control the movement of their limbs. In this regard, the treatment of patients using only the BWS (body weight support) system is difficult, since this requires a certain level of physical fitness. CPM (continuous passive motion) is one of the conventional therapies at the initial stage of treatment when patients have weak or even uncontrolled limbs.
Analysis of the literature sources has revealed that most rehabilitation systems have an active orthosis within their mechanical design. This orthosis has a simple structure, but its dynamic characteristics are low due to the presence of drives in the orthosis system. Other types of rehabilitation systems have linear drives and high dynamic performance. However, these types of rehabilitation systems have a limited workspace with limited movement of linear drives, or do not include supporting frames or orthopedic systems. Many manipulators are based on CPM and are intended for continuous or repeated treatments. In addition, these manipulators cannot provide the required quality when performing continuous passive movements due to their complex design, high dynamic loads, and bulkiness.
In order to overcome the above limitations, in this work, the popular Cartesian parallel manipulator, Tripteron [18,19], is taken as a basis for a novel solution. It consists of three legs, each having a prismatic–revolute–revolute–revolute joint arrangement with an active prismatic joint and each leg being mounted on the base platform [18]. The major difficulty in off-planar movement is the movement of the actuator assembly, as they are mounted in single plane. Thus, the proposed system combines a parallel manipulator based on Tripteron, with a serial passive orthosis which can give four degrees of freedom to the lower limb. The dynamics of the separate right and left modules of the system were considered in [20,21]. The Euler–Lagrangian approach is used to formulate the dynamics of the manipulator for a simulated performance analysis. The papers [20,21] also present an augmented proportional-derivative (PD) controller for gravity compensation in motion control. This control method transforms the closed-loop dynamics of the manipulator into a decoupled behavior for a more convenient analysis of motion performance. The numerical simulations showed that the augmented PD controller enables us to obtain a reliable control strategy. In the works [22,23], a method for optimizing the geometric parameters of a robotic system based on one Tripteron module for the rehabilitation of one limb is discussed. Nevertheless, it has a number of limitations for the case of application to the proposed two-module system, which include as follows:
- The location of the drive guides of the active manipulator, because of the intersection of their axes at one point in the upper right side of a patient user;
- Not a convenient shape for the moving platform, as in the form of an equilateral triangle;
- Limited location of fastenings of mechanisms to the platform center;
- The used optimization algorithms for the generation of random parameters and search by climbing to the top;
- Consideration of intersections of only active manipulator links;
- The use of the average size of a human limb with no customizing capability.
Based on the aforementioned flaws, the main contributions of this paper can be summarized as follows:
- A novel hybrid modular structure of a robotic system for the rehabilitation of the lower limbs is designed as based on two modules identical in structure, including an active 3-PRRR manipulator for moving the patient’s foot and a passive orthosis based on the RRR mechanism for supporting the lower limbs;
- A method for parametric synthesis of a hybrid robotic system with a modular structure is formulated, taking into account the generated levels of parametric constraints depending on the ergonomics and manufacturability of the proposed design.
The paper is organized as follows: Section 2 provides motion requirements from the lower limb biomechanics. The dimensions of the lower limbs of people of different nationalities are considered and the necessary trajectory is formulated. Section 3 provides a mathematical model of the proposed robotic system. Design parameters for the robotic system are considered. Section 4 presents an optimization problem for the design of the proposed solution. Section 5 is devoted to numerical simulation. Section 6 reviews experimental studies for validation and characterization purposes.
2. Motion Requirements from Lower Limb Biomechanics
In early rehabilitation after injuries, surgical interventions on the musculoskeletal system and neurological treatments such as the so-called CPM therapy (Continuous Passive Motion) have shown high efficiency [24]. The last is a rehabilitation technique that is associated with continuous passive exercise of human joints. This technique is based on implementing long-term repetitive movements of the joints using a specialized robot simulator without the participation of the patient’s own muscle strength.
Biomechanical parameters for a motion therapy activity may include volume, direction of movement, degree of applied force, velocity, and accuracy of task reproduction. An assisting device should also be used for safe exercise with no functional overstrain, cognitive discomfort, and psycho-emotional over excitation.
In general, the main movements of the lower limb are carried out in the sagittal plane. However, the possibility of additional rotational and frontal movements due to the hip joint has a synergistic effect on the restoration of motion also in the main plane. Therefore, a statically balanced passive orthosis model, where the limb can be placed, should allow for synchronization of movements in the hip, knee, and ankle joints. In this case, the main requirement for the correct operation of an assisting device is the precise positioning of the hip joint and of the device, relative to the patient’s hip joint.
The hip joint can be modeled as a ball-shaped joint of a limited type (cup-shaped joint), and therefore allows movement, although not as extensive as in a free ball joint (for example, in the shoulder), around three main axes: frontal, sagittal and vertical. Lateral and medial rotation occurs relative to the vertical axis, extension and flexion occurs relative to the frontal axis, and abduction and adduction occurs relative to the sagittal axis, as indicated in Figure 1.
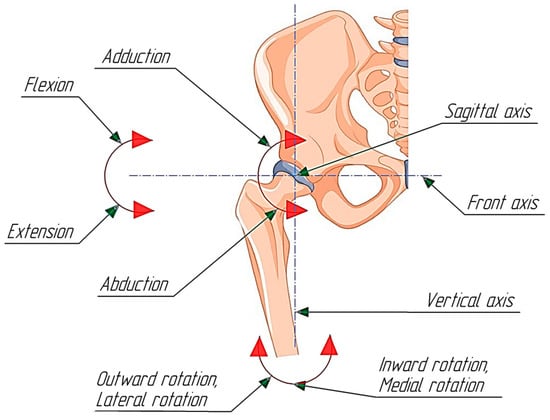
Figure 1.
Axes of rotations of the hip joint [25].
Referring to Figure 1 [25], flexion and extension of the lower limb occurs around the frontal axis. Flexion has the greatest range due to the absence of tension in the fibrous capsule of the joint, which has no attachment to the femoral neck from behind. When the knee joint is bent, it can real (118–130°), so that the lower limb, with its maximum flexion, can be pressed against the stomach. With an extended knee joint, the range of motion is less as in the round (84–90°), since it is inhibited by the tension of the muscles on the back of the thigh. Extension from the vertical position, taken as 0°, is limited by the tension of the joint ligaments and in most cases is limited to 10° (but can reach 20°).
Around the sagittal axis, the limb is abducted and adducted. The counting is carried out from the center line (0°). Abduction is possible at up to 50°, and reduction at up to 30°.
During the rehabilitation process, it is required to activated required angles in the hip, knee, and ankle joint. In particular, the angle of abduction in the hip joint is 30 degrees, as well as angles corresponding to the imitation of human gait; flexion in the hip joint is from −20 to 10 degrees, as well as flexion in the knee joint being from −60 to 0 degrees.
The trajectory of the limb movement, which will be used further during optimization, is built on the basis of repetitive movements corresponding to the human gait and abduction of the limb at the hip joint.
By imitation of gait, we mean the movement of each limb in accordance with the following law:
where is the limb index (1—left, 2—right), , are minimum and maximum angle of flexion of the hip joint, and , are the knee joint. To increase the working range of hip joint flexion training, was taken equal to . The remaining constraints on the angles in the joints were adopted in accordance with the clinical information above, that is, , .
Thus, a sequence of movements has been planned with the following steps:
- The limbs are not abducted (leg abduction angle ) while performing one cycle () of gait simulation;
- Abduction of the left leg to ;
- Performing one cycle of gait simulation;
- Simultaneous adduction of the left leg to the angle and abduction of the right leg to ;
- Performing one cycle of gait simulation;
- Abduction of the right leg .
Figure 2 shows the planned sequence of movements as a reference for joint trajectories. Figure 2a shows the sequence for flexion of the hip joint, Figure 2b shows the knee, and Figure 2c shows abduction of the hip joint.
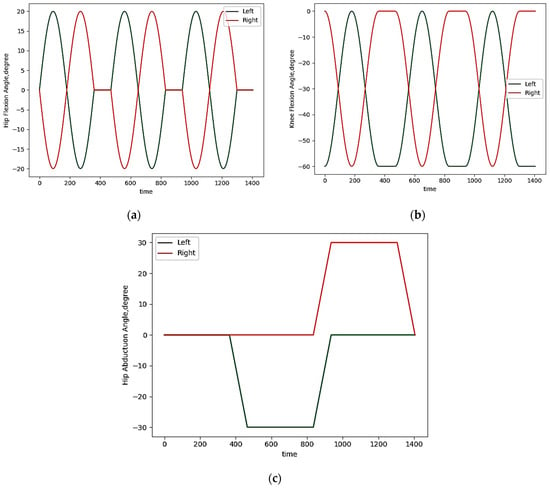
Figure 2.
The planned sequence of movements as reference joint trajectories: (a) Hip joint flexion ; (b) Knee joint flexion ; (c) Hip joint abduction .
The proposed system should provide the ability to rehabilitate patients with different anthropometric data. Table 1 presents the main anthropometric measurements of the lower limbs based on statistical data from national populations, in accordance with [26]. Each size is presented for P95 (95th percentile, that is, the maximum statistical size without taking into account the five percent of people who have unusually small limb sizes) based on individual samples for adults in different countries, taking into account gender. As a result of the analysis of the statistical data, a data set was generated as in Table 2, which is used as a reference for designing the geometric parameters of the robotic system. The set of sizes, without taking into account the orthosis, was obtained based on the choice of the maximum value of each limb size among the values in Table 1. Since the limb dimensions are used according to P95 (95th percentile, that is, the maximum statistical size without taking into account the five percent of people who have unusually small limb sizes) this will ensure the possibility of lower limb rehabilitation for more than 95 percent of people. The choice for maximum dimensions is justified by the presence, in this case, of the maximum area of movement of the human foot during the development of the trajectory, as well as the most complicated task of eliminating the collision of the links of the robotic system with the limbs.

Table 1.
Anthropometric measurements of the lower limbs, [26].

Table 2.
Set of anthropometric data for modeling, mm.
Considering the dimensions of the orthosis, which includes the frame and structural elements used to protect the limb, the dimensions have been adjusted. Based on the thickness of the human leg orthosis, equal to 15 mm, the thigh width is taken to be 30 mm larger (15 mm∙2), and the thigh circumference is 95 mm larger (15 mm = 94.25 mm). Considering the increased thickness of the calf orthosis, equal to 30 mm, taking into account the possibility of adding additional safety elements, the circumference of the calf muscle is increased by 188 mm, the length of the foot by 30 mm, and the width of the foot by 60 mm. Also, taking into account the possibility of adding safety-structural elements, the length of the lower leg has been increased by 200 mm. Taking into account the dimensions of the reference data, the trajectory of the reference movement is designed as in Figure 2, as the assumed trajectory of assisted joints by the rehabilitation system. Figure 3 shows the change in the position of the center of the ankle joint, taking into account the planned sequence of movements and the selected dimensions of the orthosis.
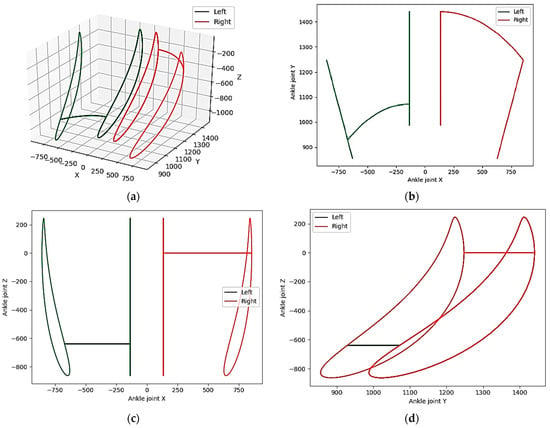
Figure 3.
Reference movement of the center of the ankle joint: (a) three-dimensional view; (b) in projection on the XY plane; (c) in projection on the XZ plane; (d) in projection on the YZ plane.
3. Mathematical Model
The proposed hybrid robotic system consists of two modules identical in structure, each of which is based on an active 3-PRRR mechanism of a parallel structure, which ensures the movement of the patient’s fixed foot, and a planar RRRR mechanism of a serial structure as a passive cut to support the lower limb, as sketched in Figure 4. The modular structure allows for a change to the parameters of the systems depending on the method of rehabilitation and, depending on the anthropometry and characteristics of the disease, the use of one and two modules simultaneously. The mutual movement of the end-effector of the two manipulators makes it possible to simulate the gait of a healthy person, while safe movement algorithms are implemented taking into account possible intersections (collisions) of the links.
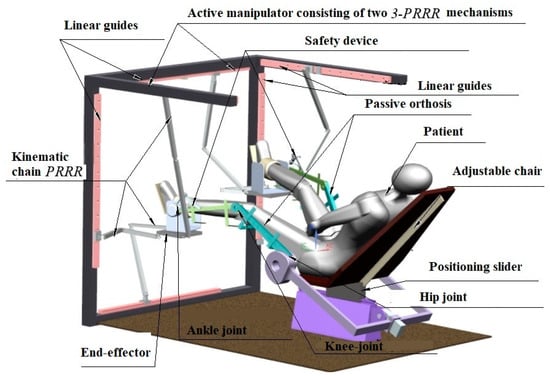
Figure 4.
A 3D model of a two-module hybrid robotic system.
The design in Figure 4 is better explained by the model in Figure 5. Figure 5a shows the kinematic design with labels for all of the joints of the active manipulators, as well as the joints and angles of the passive orthoses. In Figure 5a, where I is for the left module for the rehabilitation of the left limb, and II is for the rehabilitation of the right limb. The 3-PRRR mechanism, which provides movement of the patient’s limb through active actuators, consists of three kinematic chains, a fixed base, and a moving platform. The 3-PRRR mechanism (Tripteron) provides the necessary degrees of freedom (translational movements along three axes) and the absence of singularity, since the Jacobian matrix of the mechanism is a unit matrix. Each chain contains one drive prismatic joint (P) and three rotation joints (R). Linear actuators are connected to active linear translational pairs, which in turn are connected to guides and passive RRR chains connected to the moving platform. The configurations of kinematic chains, (hereinafter in the formulas i is the module index: 1—left module, 2—right module, j—index of kinematic chains of active manipulators), are variable, which means the possibility of bending chains in different directions is present. Each of the chains have two possible configurations that are designated as in Figure 5b. Also, the presented structure, in comparison with a single-module structure, assumes the use of the platform shape , not in the form of a regular triangle, but in the form of a right triangle with variability in the options for attaching kinematic chains to the platform (Figure 6). This assumes that the joints can be located on different sides, relative to the center of the platform (—can be located in both the negative and positive directions along the Y–axis, —along the X–axis, —along the Z–axis). The active manipulator is connected to the passive orthosis through the link GP, connecting the G joint from the ankle joint of the passive orthosis and the center P from the movable platform of the active manipulator. Each of the passive sections includes four rotational joints, two of which correspond to the hip joint ( with angles flexion/extension and abduction/adduction of the joint), one knee ( with angle flexion/extension of the joint) and one ankle ( with the angle of joint flexion/extension). The point corresponding to the toe of the human foot is designated as . The relative position of the active manipulator and the passive orthosis, as well as the relative position of the two active manipulators, are determined by the value of two constant coordinates of each of the active manipulator’s guides, relative to the base coordinate system located in the center of the patient’s pelvis. Figure 5a shows the effect of changing the coordinates of the guides on the system configuration, using the example of the second guide of the left module (), which has a lower Z coordinate value compared to the first guide () of the left leg module and the first and second guides of the right leg module ( and ).
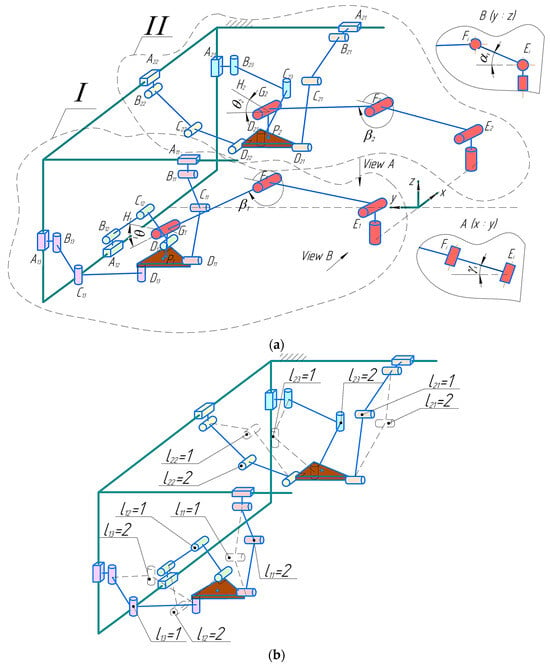
Figure 5.
Kinematic scheme of rehabilitation system: (a) the kinematic design (I is the left module for the left limb; II is the right module for the right limb), (b) an alternative design for the kinematic design.
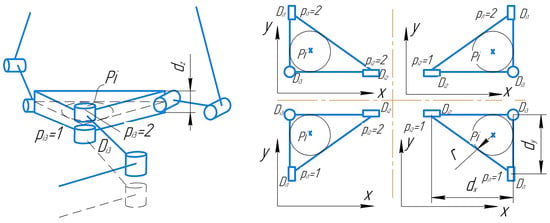
Figure 6.
Attaching kinematic chains to the platform.
To check the reachability of the robotic system position, taking into account the intersections of the links, it is necessary to determine the position of all links of the active manipulator and passive orthosis. The input data are the dimensions of the links and the angles in the patient’s joints: of the hip joint flexion, of the hip joint abduction, of the knee joint flexion, and of the ankle joint flexion. In this case referring to X, Y, Z in Figure 5, we define the coordinates of the joint centers as follows:
Taking into account the angles and , the coordinates of the joint centers are given as follows:
Let’s substitute (3) into (4) to achieve the following:
Taking into account the angle , the coordinates of the centers of the joints are given as follows:
Let’s substitute (7) into (6) to achieve the following:
Taking into account the angle , we define the coordinates of the extreme point of the link corresponding to the human foot as follows:
Let’s substitute (7), (8) into (9) to achieve the following:
We define the coordinates of the centers of the moving platforms of active manipulators as follows:
Let’s substitute (7), (8) into (12) to achieve the following::
The center of the moving platforms is understood as a point that is located along the X– and Y–axes in the center of a circle inscribed in the triangle of the platform with legs and , and along the Z–axis in the middle of the platform, having a thickness of .
To determine the coordinates of the joint centers , we will consider options for attaching the kinematic platforms (Figure 6).
Let us denote the options for fastening the joint by the variable , which can take the value 1 (in the case of fastening in a negative direction along the corresponding coordinate axis relative to a right angle) or 2 (in a positive direction). To use values 1 and 2 in joint coordinate formulas, introduce the following function, which in the case of argument 1 returns the value −1, and in the case of argument 2 returns the value 1, as follows:
Taking into account (15), we define the coordinates of the centers of the joints as the centers as follows:
where is the index of kinematic chains of active manipulators: 1—a chain with linear movement of the guide along the Y–axis; 2—along the X–axis; 3—along the Z–axis —the radius of the inscribed circle of the platform, which is determined by the following formula:
Let’s substitute (13), (14) into (16), (17) and achieve the following:
The coordinates of the joint centers in two dimensions depend on the position of the guides (coordinates that do not depend on the position of the platform) and in the third, they correspond to the coordinate of the joint center , that is as follows:
Let’s substitute (18)–(23) into (24) to achieve the following:
Let us denote the variants of configurations of kinematic chains as ; they take values 1 and 2 in accordance with Figure 5a. Considering that the center of the joint is located at the intersection of a circle with center and radius and a circle with center and radius , the coordinates can be determined as follows:
where , , , are coordinates of the joint centers D, which in accordance with (18)–(23) are defined as follows:
To ensure the operability of the robotic system and the accessibility of the positions of the working platforms of two modules in the space required for the rehabilitation process, while excluding their possible collisions during operation and mutual intersections in the presence of a large number of links of two modules, it is necessary to provide a condition that defines these criteria. To do this, using the expressions obtained for the coordinates of the connection centers (3)–(33), which can be used for the design and operation of the system, we check the orientation of the mechanisms for possible intersections of their links. For links connected by the joint, intersection checking can be performed by calculating the angle between the links and comparing it to the minimum acceptable value. For links that are not connected to each other, intersections can be checked using the geometric approach discussed in [27]. The method is based on determining the minimum distance between the segments drawn between the center of the joints of each link; it is as follows. Let us imagine the links in the form of spherocylinders (capsules). Let and be the segments connecting the centers of the joints of the links (Figure 7a).
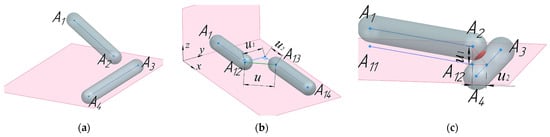
Figure 7.
Checking the links intersection: (a) model for links; (b) first case type; (c) second type case.
In this case, the condition of no intersections is written as follows:
where are the radii of the links and ,, are the distance between the nearest points of the segments along each of the axes, defined as follows:
The values of and are determined similarly. If condition (35) is not met, the following check is carried out for the absence of intersections, when the minimum distance between the segments and is greater than the sum of the radii of the links .
Let’s consider two cases of a mutual arrangement of links.
In case 1, the links are parallel. Let’s determine the minimum distance between the segments by rotating the segments relative to point so that they become perpendicular to the YOZ plane. Let’s designate points ,, after the rotation as ,,, respectively. The distance between the segments is defined as follows:
where is the distance between the segments and in the projection onto the YOZ plane, and is the distance between the nearest points of the segments along the X–axis.
Figure 7b shows an example of checking for the first case of intersection of links, when and , with . In this case there is no intersection.
In case 2, the links are not parallel. Let’s construct an auxiliary plane in which the segment will lie, with the segment parallel to this plane. In this case, the distance between the segments is determined by Formula (36), where is the distance between the segment.
and the auxiliary plane, , is the distance between the nearest points of the segments and the projection of the segment onto the auxiliary plane.
To determine , we calculate the normal vector .
Let’s determine the distance using the following:
where .
To determine , we rotate the auxiliary plane around point , which is the projection of point onto the auxiliary plane, so that the auxiliary plane becomes parallel to the YOZ plane. Let’s denote points ,, and the projection of point onto the auxiliary plane after rotation as , and , respectively. As a result, determining is reduced to the problem of calculating the distance between the nearest points of the segments and on a two-dimensional plane.
Figure 7c shows an example of checking for the second case of intersection of links, , that is, the segments do not intersect in the projection, but for , respectively, the segments intersect.
Let us write down the condition for the unattainability of the position of the moving platform, expressed by the lengths of the active manipulator links, which has the following form:
where = .
We will further use the resulting inequality to solve problems of parametric synthesis and select the optimal robotic system configurations.
4. Optimization Design Problem
The optimization problem consists in the selection of parameters to ensure the compactness of the mechanism when performing the trajectory of rehabilitation of the lower limbs. Various methods can be used for optimization including multi-objective robust design optimization method for a mechatronic system [28] and mechanical structure optimization followed by FEM analysis to verify the changes made [29]. By optimization of the task placement, a reduction in energy costs in parallel manipulators is achieved [30], and nonlinear optimization problems can be solved using the reconfiguration of a parallel manipulator [31]. The problem under consideration is non-trivial. Let us formulate the optimization problem with the following steps:
- Selection of optimization parameters, which includes both continuous and discrete.
- 1.1.
- We use the link lengths as continuous optimization parameters , , guide positions ,,,,, (Figure 5), and horizontal dimensions of the platforms.
- 1.2.
- Selection of optimization criterion. Due to the fact that as a result of optimization it is necessary to determine the geometric parameters at which the compactness of the structure is ensured, we write the criterion function in the following form:
- The optimization constraint is the reachability of all points of the trajectory described earlier in Section 2 and the absence of intersections for each of these points, that is as follows:where is the number of trajectory points in discrete form, taking into account the given accuracy , which are unattainable.
Due to the significant reduction in the range of permissible parameter values and the optimization limitation, as well as the possibility of using the limitation as part of the criterion function in the form , we will exclude the optimization limitation, but we will take it into account in the criterion function (39) as follows:
where, is a given penalty coefficient, is the Heaviside function in the following:
As an optimization algorithm, we use a parallel modification of the PSO algorithm [32], which has successfully proven itself for solving a wide range of optimization problems.
The requirements of ergonomics and manufacturability of a robotic system may impose additional constraints on the optimized parameters and thereby limit the range of feasible solutions. For a balanced selection of geometric parameters from a wide range of possible ones but taking into account the ergonomics and manufacturability of the robot design, modeling was performed for four levels of constraints as in Table 3.

Table 3.
Levels of constraints based on ergonomics and manufacturability.
5. Numerical Simulation
Let us assign the initial platform data and algorithm optimization parameters. Based on the perpendicular position of the foot relative to the shin, we take the angle at the ankle joints . The dimensions of the links of passive orthoses (Table 4) are set in accordance with the anthropometric data given in Table 2.

Table 4.
The dimensions of the passive orthosis links.
Let us take the diameters of the active manipulator links to be equal to mm. To ensure that can move under the platform without colliding with the links and the condition must be met, therefore we will take the size mm. To avoid collisions between the orthosis links and the links , we calculate the size as follows:
Optimization parameter ranges can be considered as follows:
- Continuous:
- Link sizes: , ;
- Coordinates of the guides:
- Platform sizes: , .
- Discrete:
- Options for attaching kinematic chains to moving platforms ;
- Variants of configurations of kinematic chains
The time step when checking trajectory points is , and penalty coefficient is . The PSO algorithm parameters are the number of individuals in the initial population , number of generations , number of groups , values of free parameters . To increase efficiency, each iteration of searching for optimal configurations is performed in two stages. At the first stage, the optimal solution is searched for with the original parameter ranges; at the second stage, the range of each parameter is reduced five times; and the center of the new ranges coincides with the best solution found based on the result of the first stage.
To perform optimization of the parameters, a software package has been developed, including an optimization module in the C++ programming language, using parallel computing for simultaneous calculation of the criterion function of various individuals of the PSO algorithm population. In addition, visualization modules are formulated in Python, which allow us to construct graphs of changes in the position of joint centers and to visualize the movement of the robotic system with link interference to check optimal configurations. An example of visualization using the developed software package is shown in Figure 8. In the case of intersection, the links are depicted in blue.
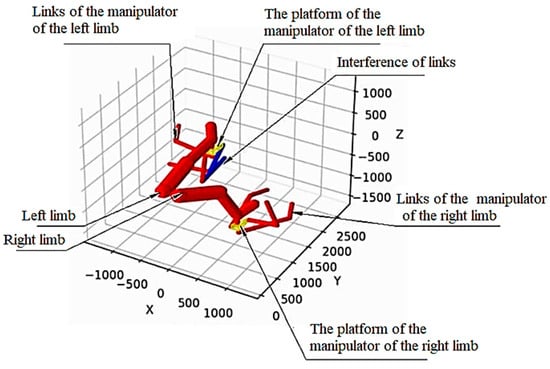
Figure 8.
Example of visualization.
Numerical simulation is performed not only to obtain structural parameters, but also to verify the correctness of the selected structure.
5.1. Constraint Level 1
Due to the non-monotonic nature of the criterion function (40) and the large dimension of the search space during the iterative search for optimal configurations, as a result of executing the algorithm, various configuration options corresponding to local extrema can be obtained. Iterative optimization was performed. Iterative computations are worked out to obtain optimal solutions using the PSO (Particle Swarm Optimization) algorithm [32]. Each iteration is performed independently of each other to obtain results at different local minima. In each iteration, an optimal set of parameters is obtained. The distribution of each of the continuous parameters is shown in the box plot (Figure 9). Local minima were obtained with a value of the criterion function within the range from 7040.7 (the minimum value) to 8700.3, whereas the arithmetic mean value of the criterion function in local minima was computed as 7686.3. The corresponding design parameter values for the minimum value of the criterion function are shown in Table 5, Table 6 and Table 7 in the first row for Level 1.
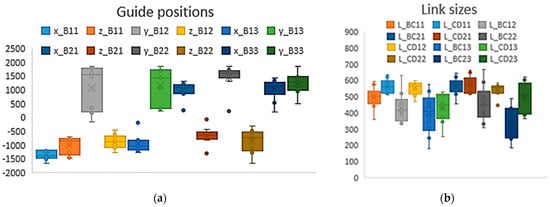
Figure 9.
Distribution of continuous parameters for constraint level 1: (a) guide positions; (b) link sizes.
Let us introduce additional constraints related to ergonomics and manufacturability of the design, corresponding to the second level.
5.2. Constraint Level 2
At the second level, a constraint has been added on the equality of the coordinates of all guides, that is, , as well as the equality of the coordinates of the guides for the left and right legs, that is, and . This makes it possible to reduce the dimension of the parameter space and provide a more ergonomic and technological design of the robotic system. Figure 10 shows a comparison example of the relative position of the drive guides for the first and second level of constraints. As can be seen from the figure, the constraint allows us to obtain more ordered robotic system configurations.
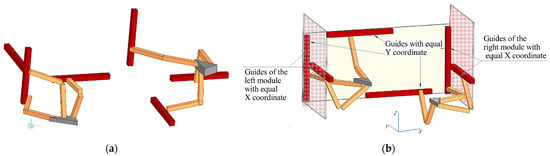
Figure 10.
An example of the relative position of guides at different levels of constraints: (a) Level 1; (b) Level 2.
Iterative optimization was performed. In each iteration, an optimal set of parameters is obtained. The distribution of each of the continuous parameters is shown in the box plot (Figure 11).
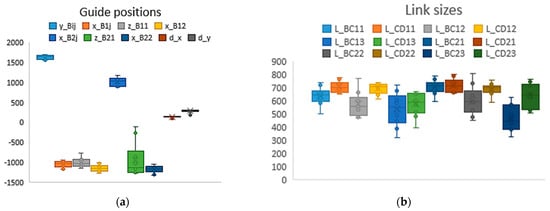
Figure 11.
Distribution of continuous parameters for constraint level 2: (a) guide positions; (b) link sizes.
Local minima were obtained with value of the criterion function within the range from 7265.1 (the minimum value) to 7898.2, whereas the arithmetic mean value of the criterion function in local minima was computed as 7552.4. The corresponding design parameters values for the minimum value of the criterion function are shown in Table 5, Table 6 and Table 7, in the second row for Level 2. The addition of the constraint affected the minimum value of the criterion function, which is 3.19% more than the value of the criterion function for level 1, which is 7040.7.
5.3. Constraint Level 3
Within the third level, in addition to the constraints of the second level, constraints have been added based on the ranges of variable coordinates of the guides, suggesting the location of the guides for each of the chains within 300 mm above or below the range of changes in the variable coordinates of the guides (Figure 12). In addition to the second level limitation, it also increases the ergonomics and manufacturability of the robotic system design.
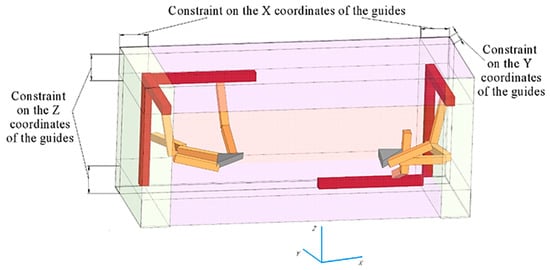
Figure 12.
Example of the relative position of guides at level 3 constraints.
This constraint can be written as follows:
where and are the limits of the range of movement of the guides, and are the range of , is the upper limit of the range of movement y_Bi1. Based on the kinematics of the robotics system, which assumes the equalities , , ,, it follows that the boundaries of the ranges of movement of the guides are determined based on the ranges of movement of the center of the platform. The graph of changes in the coordinates of the centers of the platforms during the trajectory development process is shown in Figure 13.
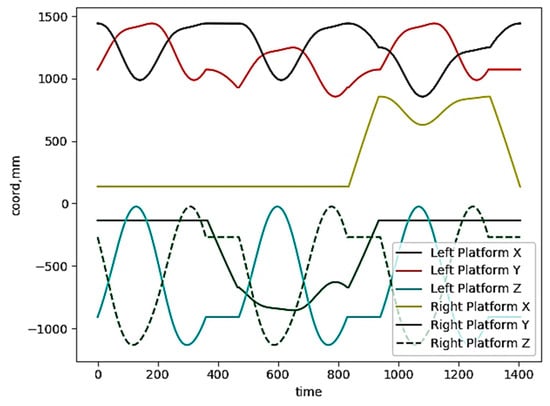
Figure 13.
Changing the coordinates of the center of the platforms during the trajectory development process.
Due to the ambiguity in determining the position of the platform, according to the equality , we accept the assumption to calculate the parametric constraints. Taking into account the range of changes in the coordinates of the center of the platforms , the ranges of optimization parameters corresponding to the coordinates of the guides for constraint level 3 have the following values:
The distribution of each of the continuous parameters is shown in the box plot (Figure 14).
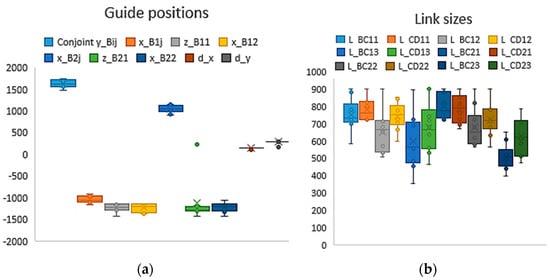
Figure 14.
Distribution of continuous parameters for constraint level 3: (a) guide positions; (b) link sizes.
Local minima were obtained with value of the criterion function within the range from 7739.7 (the minimum value) to 9320.9, whereas the arithmetic mean value of the criterion function in local minima was computed as 8332.9. The corresponding design parameter values for the minimum value of the criterion function are shown in Table 5, Table 6 and Table 7, in the third row for Level 3. The consequence of adding additional constraints of the third level is an increase in the value of the criterion function (7739.7) by 6.5%, compared to the second level. However, this made it possible to significantly improve the ergonomics and manufacturability of the design, which can be clearly assessed when comparing configurations of level 2 (Figure 10b) and level 3 (Figure 12).
5.4. Constraint Level 4
For level 4, in addition to the constraints of the 3rd level, we will add a constraint on the equality of the lengths of module links , . In this case, the number of parameters is reduced by six to twenty-seven. The distribution of each of the continuous parameters is shown in the box plot (Figure 15). Local minima were obtained with the value of the criterion function within the range from 7784.1 (the minimum value) to 8735.5, whereas the arithmetic mean value of the criterion function in local minima was computed as 8439.7. The corresponding design parameters values for the minimum value of the criterion function are shown in Table 5, Table 6 and Table 7, in the fourth row for Level 4.
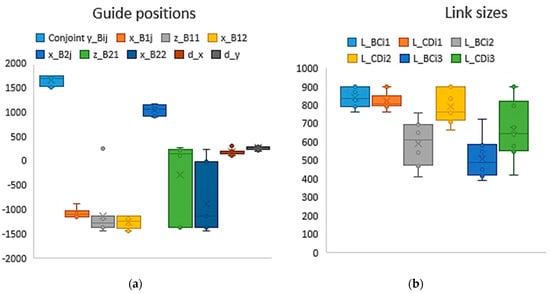
Figure 15.
Distribution of continuous parameters for constraint level 4: (a) guide positions; (b) link sizes.

Table 5.
Computed optimal configurations for constraint levels.
Table 5.
Computed optimal configurations for constraint levels.
| Level | Target Function | Platform Connection | Chain Configuration | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Left (I) Module Chains | Right (II) Module Chains | Left (I) Module Chains | Right (II) Module Chains | ||||||||||
| 1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 | ||
| 1 | 7040.7 | 1 | 2 | 2 | 1 | 2 | 2 | 2 | 2 | 1 | 1 | 2 | 1 |
| 2 | 7265.1 | 1 | 1 | 1 | 2 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 3 | 7739.7 | 2 | 2 | 2 | 2 | 1 | 2 | 1 | 1 | 1 | 1 | 1 | 1 |
| 4 | 7784.1 | 1 | 1 | 1 | 2 | 2 | 2 | 1 | 2 | 1 | 1 | 1 | 1 |

Table 6.
Computed optimal configuration for constraint levels (continued).
Table 6.
Computed optimal configuration for constraint levels (continued).
| Level | Guide Positions (mm) | Platforms | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Left (I) Module | Right (II) Module | d_x (mm) | d_y (mm) | |||||||||||
| x_B11 | z_B11 | y_B12 | z_B12 | x_B13 | y_B13 | x_B21 | z_B21 | y_B22 | z_B22 | x_B23 | y_B23 | |||
| 1 | −1028.0 | −629 | 2000 | −957 | −1114 | 1227 | 419 | −1162 | 1844 | −355 | 682 | 2000 | ||
| 2 | −1042.6 | −1031.0 | 1588.2 | −1092.6 | −1042.6 | 1588.2 | 1165.1 | −861.4 | 1588.2 | −1096.6 | 1165.1 | 1588.2 | 140.8 | 272.7 |
| 3 | −1066.5 | −1239.2 | 1567.9 | −1208.0 | −1066.5 | 1567.9 | 1043.0 | −1280.4 | 1567.9 | −1283.0 | 1043.0 | 1567.9 | 152.5 | 300.0 |
| 4 | −884.6 | 247.1 | 1677.1 | −1300.6 | −884.6 | 1677.1 | 891.6 | 148.7 | 1677.1 | −25.0 | 891.6 | 1677.1 | 148.9 | 281.7 |

Table 7.
Computed optimal configuration for constraint levels (continued).
Table 7.
Computed optimal configuration for constraint levels (continued).
| Level | Link Sizes (mm) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Left (I) Module | Right (II) Module | |||||||||||
| L_ BC11 | L_ CD11 | L_ BC12 | L_ CD12 | L_ BC13 | L_ CD13 | L_ BC21 | L_ CD21 | L_ BC22 | L_ CD22 | L_ BC23 | L_ CD23 | |
| 1 | 519.3 | 573.8 | 900.0 | 443.4 | 408.5 | 569.0 | 656.7 | 631.8 | 685.9 | 544.6 | 285.2 | 822.5 |
| 2 | 603.1 | 777.0 | 467.4 | 726.6 | 674.2 | 397.4 | 675.7 | 661.9 | 450.7 | 704.3 | 382.7 | 744.1 |
| 3 | 780.6 | 725.0 | 568.8 | 783.5 | 559.8 | 465.5 | 725.0 | 814.9 | 628.0 | 682.1 | 494.2 | 512.3 |
| 4 | 790.9 | 799.0 | 599.1 | 757.0 | 393.8 | 552.2 | 790.9 | 799.0 | 599.1 | 757.0 | 393.8 | 552.2 |
The increase in the minimum value of the criterion function for the fourth level in comparison with the third level was 0.57%. The increase in the value of the criterion function in comparison with the first level was 10.56%. Configuration 9, with the minimum value of the criterion function significantly exceeds the other nine found configurations of the fourth level and provides the opportunity to unify the links in comparison with level 3. To verify configuration 9, a visualization of the movement along the generated trajectory was visualized, successfully completed without link interference (Figure 16).
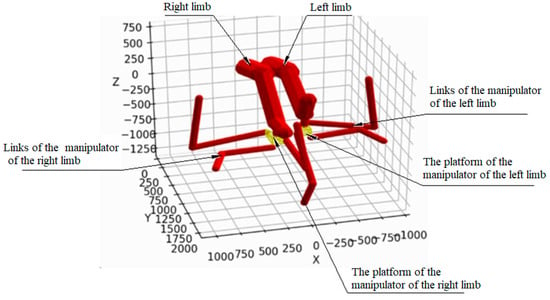
Figure 16.
Visualization of the movement of the selected optimal configuration.
Based on the insignificant difference in the criterion function, with a significant increase in manufacturability and ergonomics, we will choose the level 9 configuration as the final one for the production of the prototype.
6. Experimental Investigations
A prototype rehabilitation robot was built with the optimal design solution. The prototype was made according to drawings obtained as a result of the design algorithm implemented to NX CAD/CAE system to make the system assembly. The prototype consists of two modules (I and II Figure 5) identical in structure, which can be controlled independently of each other (Figure 17). Each module according to the proposed design, it includes 3-PRRR manipulator (with three kinematic chains according to the Figure 5) and passive orthosis ().
A controller has been selected that provides precise control of the system and maximum safety for the patient. To control the prototype, an industrial logic controller OWEN PLC 210 (LLC "Production Association OWEN", Moscow, Russia) was used. The controller uses the development environment (IDE) CODESYS V3.5. CODESYS supports IEC 61131-3 programming languages and the additional CFC language, which allows to develop a human–machine interface and configure data exchange with devices. To control the robot system, a control interface for the operator was created and visualized. Data exchange with servo motor drivers are carried out via the RS-485 interface.
When the prototype runs, calibration is performed using limit sensors, and moving the slider (Figure 5) along the guide during operation is determined from data received from an encoder mounted on the servomotor. The control system, as shown in Figure 18, provides for standard motion control of six engines, implementation of control blocking for all engines, as well as an emergency stop button. To test and verify the operating modes of the prototype, control programs have been created that implement the developed motion trajectories for conducting rehabilitation exercises.
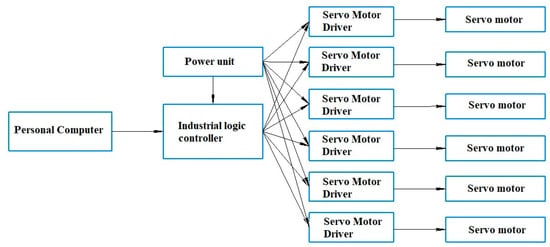
Figure 18.
Control system block diagram for the prototype in Figure 17.
To ensure the seating of patients with different anthropometric data, a chair is used that can be adjusted to three positions: tilting the back of the chair, as well as longitudinal and transverse movement of the chair in the plane of the base of the rehabilitation system. For longitudinal movement of the chair, a stepper motor with a torque of 20 kg/cm is used, and for transverse movement, a stepper motor is used, the torque of which is 34 kg/cm. To control these motors, programmable stepper motor controllers SMSD-4.2 are used. The chair is moved using ball screws along two linear guides.
To prevent injury to the patient when the limb moves into a position not intended by physiology, the orthosis is connected to the end-effector (platform with center according to the Figure 5) of the manipulator by a suspended safety device with elastic elements that provide shock absorption when a dangerous load occurs. Gas lift GL105 was used as elastic elements, providing the required forces to meet the safety requirements of rehabilitation exercises.
Experimental tests of the developed prototype were carried out, which include as follows:
- Operation of the mechanical safety device to ensure patient safety.
- Practicing the movement of limbs in the sagittal plane.
The safety device is the link between the active 3-PRRR mechanism and the passive orthosis. In the initial position, there are no external forces acting on the orthosis, all elastic elements of the safety device are in a relaxed state, their length is maximum (Figure 19).

Figure 19.
Test position of the safety device: (a) without applying load, (b) compression of the upper pair of elastic elements and movement of the orthosis when the load directed along the Y–axis is exceeded.
When the orthosis is exposed to a force exceeding the rigidity of the elastic elements, directed along the Y–axis, the upper pair of elastic elements is compressed, and the orthosis is displaced in the direction opposite to the direction of the force.
Similarly, when the orthosis is exposed to a force exceeding the rigidity of the elastic elements, directed along the X–axis, the lower pair of elastic elements is compressed, and the orthosis is displaced in the opposite direction (Figure 20).

Figure 20.
Test compression of elastic elements with simultaneous excess load along: (a) X–axis, simultaneously along the X and Y, (b) when a movement causes a simultaneous excess of load on both axes, compression of all pairs of elastic elements occurs.
Based on the results of experimental tests, it can be noted that the safety device functions correctly, operates under the required load, and allows for safety when performing rehabilitation movements of the lower limbs.
The prototype was used to test the trajectory of movement during the rehabilitation process. The acquired trajectory of movement of the end-effector point of the active manipulator is shown in Figure 21. The trajectory is obtained using Equations (7)–(14), taking into account the following dimensions of a real patient’s orthosis: mm, mm, mm. The obtained trajectory clearly shows the movement of the end-effector during the experimental investigations with suitable characteristics in reproducing a typical human trajectory.
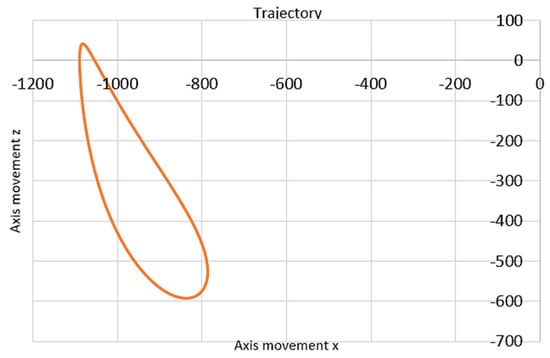
Figure 21.
Acquired trajectory of test movement of the end-effector of the active manipulator during the rehabilitation process.
A comparison was made of the simulated and experimentally obtained values of the angles in the hip and knee joints when moving along the rehabilitation trajectory. The discrepancy was measured to assess how accurately the experimental sample allows for a change in angles in the patient’s joints (Figure 22).
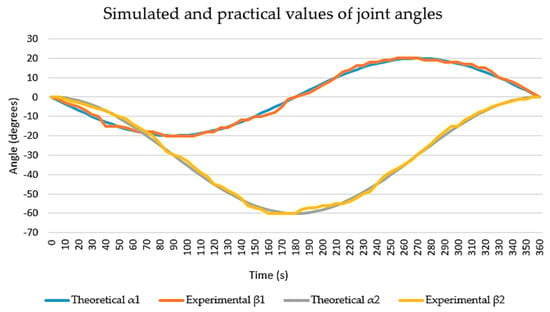
Figure 22.
Simulated and tested values of angles in joints during a rehabilitation operation.
Figure 23 graphically shows the difference between the experimental and theoretical values of the patient’s joint angles.
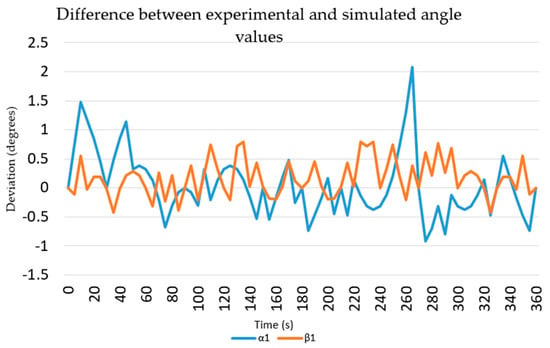
Figure 23.
Discrepancy between experimental and simulated values of angles when practicing rehabilitation movements.
The maximum discrepancy between the theoretical and experimental angle values was 2.82 deg, and the average discrepancy was 1.2 deg. This discrepancy is due to the design features of the passive orthosis, which are difficult to take into account when designing and calculating the mechanism. Experimental tests have shown that the final version of the prototype of a robotic system for the rehabilitation of the lower extremities allows you to perform the required therapeutic movements with a given accuracy, and a safety device ensures the safety of performing exercises. Discrepancies between the simulation and practical angles in the patient’s joints do not have a critical effect within the framework of therapeutic movements of rehabilitation of the lower limbs, but they can be compensated by correcting errors in the control system of the active mechanism.
7. Conclusions
Based on the results of a numerical experiment, the best configuration for design was obtained. It has been established that an increase in the level of parametric constraints reduces the design compactness in the range from 0.57 to 10.56%. But at the same time, a significant improvement in the ergonomics and manufacturability of the design is achieved. An experimental sample of a two-module hybrid robotic system was designed and manufactured, which successfully passed experimental tests. To ensure safety, the use of a suspended safety device has been proposed and experimentally confirmed to compensate for the excess load acting on the patient’s limb from the active manipulator, which allows, due to elastic elements, compensation for the movements of the active manipulator that are unacceptable by the patient’s physiology.
Author Contributions
Conceptualization, D.M. and M.C.; methodology, D.M. and V.P.; software, D.M.; validation, M.C. and V.P.; formal analysis, V.P.; investigation, D.M. and V.P.; resources, V.P.; data curation, V.P.; writing—original draft preparation, D.M. and V.P.; writing—review and editing, M.C.; visualization, D.M.; supervision, M.C.; project administration, V.P.; funding acquisition, D.M. and V.P. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the state assignment of Ministry of Science and Higher Education of the Russian Federation under Grant FZWN-2020-0017.
Data Availability Statement
Data are contained within the article.
Acknowledgments
The work realized using equipment of High Technology Center at BSTU named after V.G. Shukhov.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Samorodskaya, I.V.; Zayratyants, O.V.; Perkhov, V.I.; Andreev, E.M.; Vaisman, D.S. Trends in stroke mortality rates in Russia and the USA over a 15-year period. Arch. Pathol. 2018, 80, 30–37. [Google Scholar] [CrossRef]
- Temirova, A.R.; Syzdykov, M.B.; Kaparov, S.F.; Kairbekova, T.E.; Sarsenova, R.E.; Bekenova, L.T. Early rehabilitation of patients after acute ischemic stroke. Sci. Healthc. 2014, 2, 103–105. (In Russian) [Google Scholar]
- Vashisht, N.; Puliyel, J. Polio programme: Let us declare victory and move on. Indian J. Med. Ethics 2012, 9, 114–117. [Google Scholar] [CrossRef]
- Truelsen, T.; Bonita, R. The worldwide burden of stroke: Current status and future projections. Handb. Clin. Neurol. 2009, 92, 327–336. [Google Scholar] [CrossRef] [PubMed]
- Loeb, G.E. Neural control of locomotion. BioSciences 1989, 39, 800–804. [Google Scholar] [CrossRef]
- Stein, P.S.G.; Stuart, D.G.; Grillner, S.; Selverston, A.I. Neurons, Networks, and Motor Behavior Cambridge; MIT Press: Cambridge, MA, USA, 1999; ISBN 9780262692274. [Google Scholar]
- Hesse, S.; Uhlenbrock, D. A mechanized gait trainer for restoration of gait. J. Rehabil. Res. Dev. 2000, 37, 701–708. [Google Scholar] [PubMed]
- Huang, G.; Ceccarelli, M.; Zhang, W.; Huang, Q. Modular Design Solutions of BIT Wheelchair for Motion Assistance. In Proceedings of the IEEE International Conference on Advanced Robotics and its Social Impacts (ARSO), Beijing, China, 31 October–2 November 2019; pp. 90–96. [Google Scholar] [CrossRef]
- Bouri, M.; Stauffer, Y.; Schmitt, C.; Allemand, Y.; Gnemmi, S.; Clavel, R. The WalkTrainerTM: A Robotic System for Walking Rehabilitation. In Proceedings of the International Conference on Robotics and Biomimetics, Kunming, China, 17–20 December 2006. [Google Scholar] [CrossRef]
- Colombo, G.; Joerg, M.; Schreier, R.; Dietz, V. Treadmill training of paraplegic patients using a robotic orthosis. J. Rehabil. Res. Dev. 2000, 37, 693–700. [Google Scholar]
- Wang, Y.-L.; Wang, K.-Y.; Zhang, Z.-X.; Chen, L.-L.; Mo, Z.-J. Mechanical Characteristics Analysis of a Bionic Muscle Cable-Driven Lower Limb Rehabilitation Robot. J. Mech. Med. Biol. 2020, 20, 2040037. [Google Scholar] [CrossRef]
- Freivogel, S.; Mehrholz, J.; Husak-Sotomayor, T.; Schmalohr, D. Gait training with the newly developed ‘LokoHelp’-system is feasible for non-ambulatory patients after stroke, spinal cord and brain injury. A Feasibility Study. Brain Inj. 2008, 22, 625–632. [Google Scholar] [CrossRef] [PubMed]
- Rios, A.; Hernandez, E.; Moreno, J.A.; Keshtkar, S.; De la Garza, R. Kinematics Analysis of a New 3DOF Parallel Manipulator as Walking Rehabilitation Device. In Proceedings of the 15th International Conference on Electrical Engineering, Computing Science and Automatic Control (CCE), Mexico City, Mexico, 5–7 September 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Almaghout, K.; Tarvirdizadeh, B.; Alipour, K.; Hadi, A. Design and control of a lower limb rehabilitation robot considering undesirable torques of the patient’s limb. Proc. Inst. Mech. Eng. Part H J. Eng. Med. 2020, 234, 1457–1471. [Google Scholar] [CrossRef]
- Bouri, M.; Le Gall, B.; Clavel, R. A new concept of parallel ro-bot for rehabilitation and tness: The Lambda. In Proceedings of the 2009 IEEE International Conference on Robotics and Biomimetics (ROBIO), Guangxi, China, 19–23 December 2009; pp. 2503–2508. [Google Scholar] [CrossRef]
- Erigo Pro Homepage. Available online: https://www.hocoma.com/solutions/erigo/ (accessed on 30 December 2023).
- Cafolla, D.; Russo, M.; Carbone, G. CUBE, a cable-driven device for limb rehabilitation. J. Bionic. Eng. 2019, 16, 492–502. [Google Scholar] [CrossRef]
- Kong, X.; Gosselin, C.M. Type Synthesis of Parallel Mechanisms; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar] [CrossRef]
- Gosselin, C. Compact dynamic models for the Tripteron and Quadrupteron parallel manipulators. Proc. Inst. Mech. Eng. Part I J. Syst. Control. Eng. 2009, 223, 1–11. [Google Scholar] [CrossRef]
- Sunilkumar, P.; Mohan, S.; Mohanta, J.K.; Wenger, P.; Rybak, L. Design and motion control scheme of a new stationary trainer to perform lower limb rehabilitation therapies on hip and knee joints. Int. J. Adv. Robot. Syst. 2022, 19, 1–20. [Google Scholar] [CrossRef]
- Sunilkumar, P.; Choudhury, R.; Mohan, S.; Rybak, L. Dynamics and Motion Control of a Three Degree of Freedom 3-PRRR Parallel Manipulator. Mech. Mach. Sci. 2020, 89, 103–111. [Google Scholar] [CrossRef]
- Malyshev, D.; Mohan, S.; Rybak, L.; Rashoyan, G.; Nozdracheva, A. Determination of the Geometric Parameters of a Parallel-Serial Rehabilitation Robot Based on Clinical Data. Mech. Mach. Sci. 2021, 601, 556–566. [Google Scholar] [CrossRef]
- Malyshev, D.; Rybak, L.; Mohan, S.; Cherkasov, V.; Pisarenko, A. The Method of Optimal Geometric Parameters Synthesis of Two Mechanisms in the Rehabilitation System on Account of Relative Position. Commun. Comput. Inf. Sci. 2021, 1514, 230–245. [Google Scholar] [CrossRef]
- Lenssen, T.A.F.; van Steyn, M.J.A.; Crijns, Y.H.F.; Waltjé, E.M.H.; Roox, G.M.; Geesink, R.J.T.; van den Brandt, P.A.; De Bie, R.A. Effectiveness of prolonged use of continuous passive motion (CPM), as an adjunct to physiotherapy, after total knee arthroplasty. BMC Musculoskelet. Disord. 2008, 9, 60. [Google Scholar] [CrossRef]
- Bilich, G.L.; Nikolenko, V.N. Atlas of Human Anatomy; Phoenix: Rostov-on-Don, Russia, 2014. (In Russian) [Google Scholar]
- ISO/TR 7250-2:2010; Basic Human Body Measurements for Technological Design. Part 2: Statistical Summaries of Body Measurements from National Populations. ISO: Geneva, Switzerland, 2010.
- Behera, L.; Rybak, L.; Malyshev, D.; Gaponenko, E. Determination of Workspaces and Intersections of Robot Links in a Multi-Robotic System for Trajectory Planning. Appl. Sci. 2021, 11, 4961. [Google Scholar] [CrossRef]
- Bilel, N.; Mohamed, N.; Zouhaier, A.; Lotfi, R. Multi-objective robust design optimization of a mechatronic system with uncertain parameters, using a polynomial chaos expansion method. Proc. Inst. Mech. Eng. Part I J. Syst. Control. Eng. 2017, 231, 729–739. [Google Scholar] [CrossRef]
- Pisla, D.; Pop, N.; Gherman, B.; Ulinici, I.; Luchian, I.; Carbone, G. Efficient FEM Based Optimization of a Parallel Robotic System for Upper Limb Rehabilitation. Mech. Mach. Sci. 2021, 88, 517–532. [Google Scholar] [CrossRef]
- Scalera, L.; Boscariol, P.; Carabin, G.; Vidoni, R.; Gasparetto, A. Optimal Task Placement for Energy Minimization in a Parallel Manipulator. Mech. Mach. Sci. 2021, 88, 12–22. [Google Scholar] [CrossRef]
- Llopis-Albert, C.; Valero, F.; Mata, V.; Pulloquinga, J.L.; Zamora-Ortiz, P.; Escarabajal, R.J. Optimal Reconfiguration of a Parallel Robot for Forward Singularities Avoidance in Rehabilitation Therapies. A Comparison via Different Optimization Methods. Sustainability 2020, 12, 5803. [Google Scholar] [CrossRef]
- Malyshev, D.; Cherkasov, V.; Rybak, L.; Diveev, A. Synthesis of Trajectory Planning Algorithms Using Evolutionary Optimization Algorithms. Commun. Comput. Inf. Sci. 2023, 1739, 153–167. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).