A Multi-Objective Optimization Design Method for High-Aspect-Ratio Wing Structures Based on Mind Evolution Algorithm Backpropagation Surrogate Model
Abstract
1. Introduction
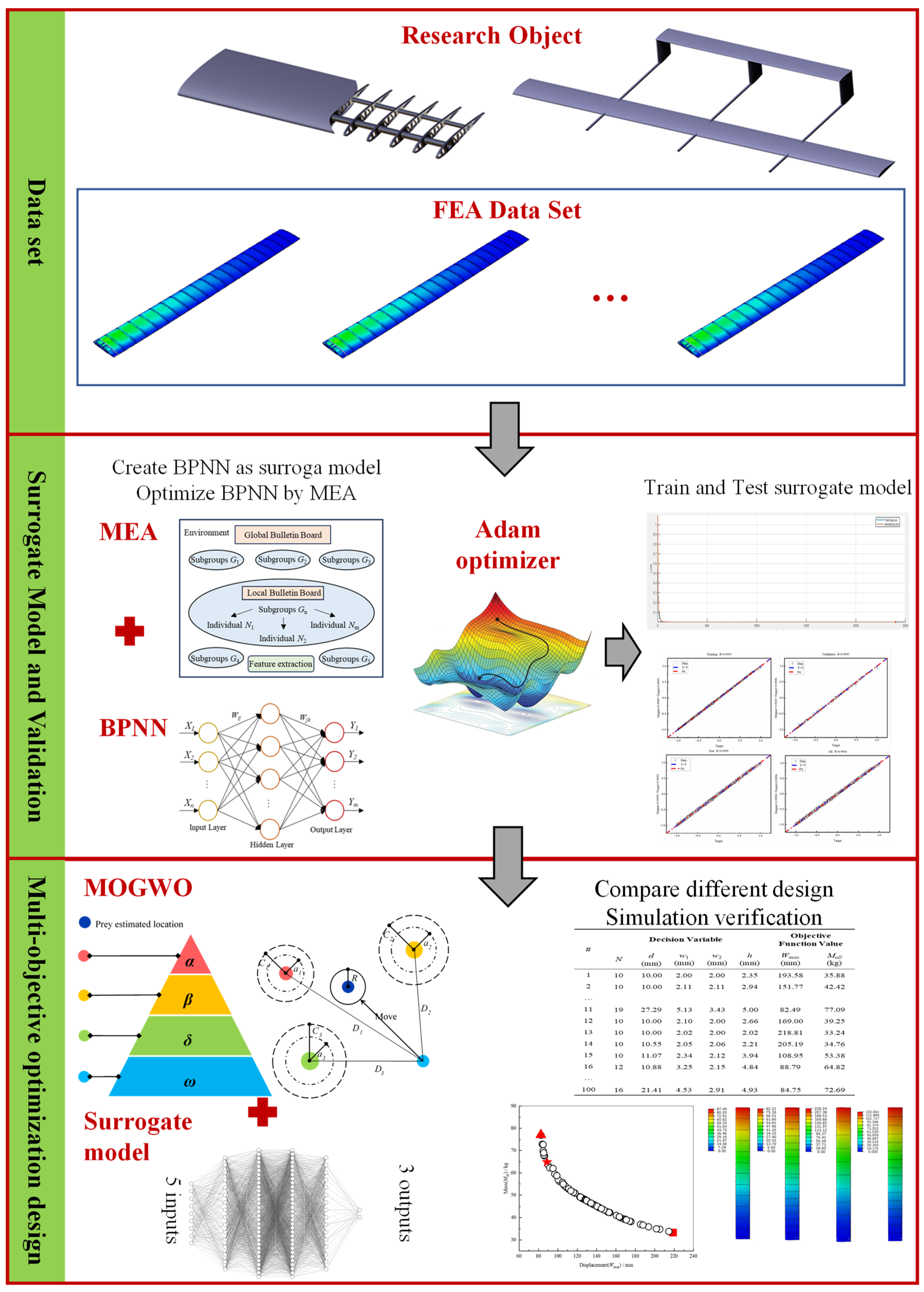
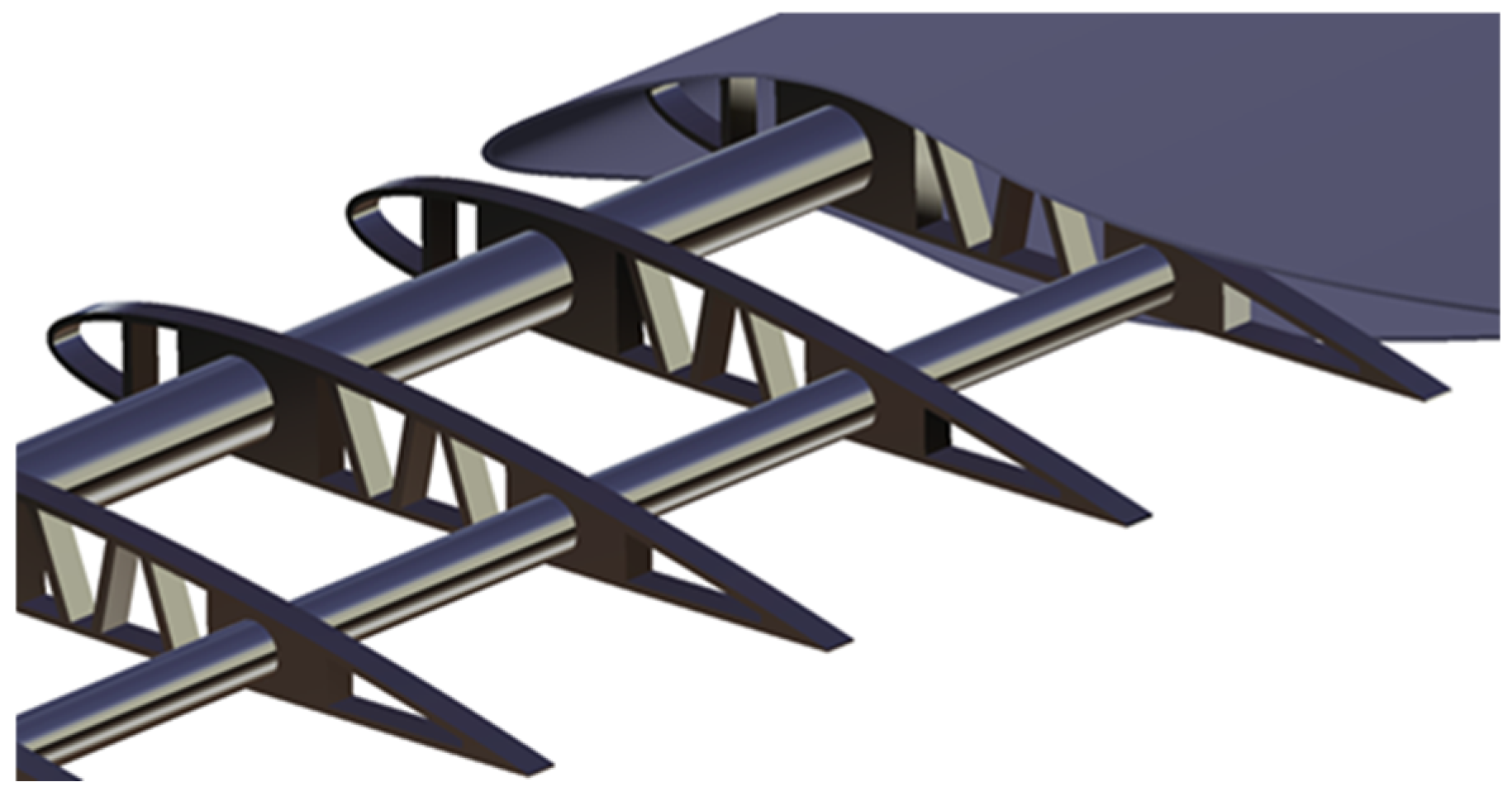
2. Research Object
3. Research Contents
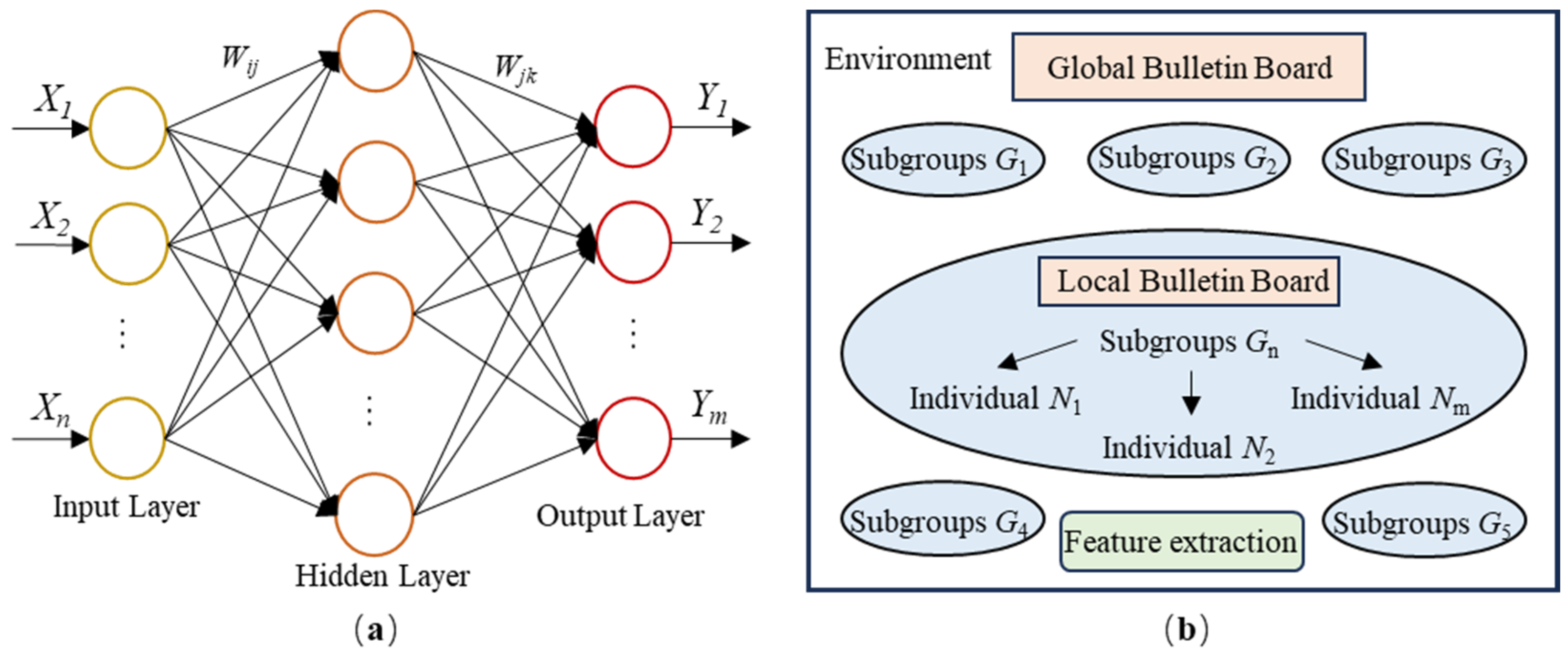
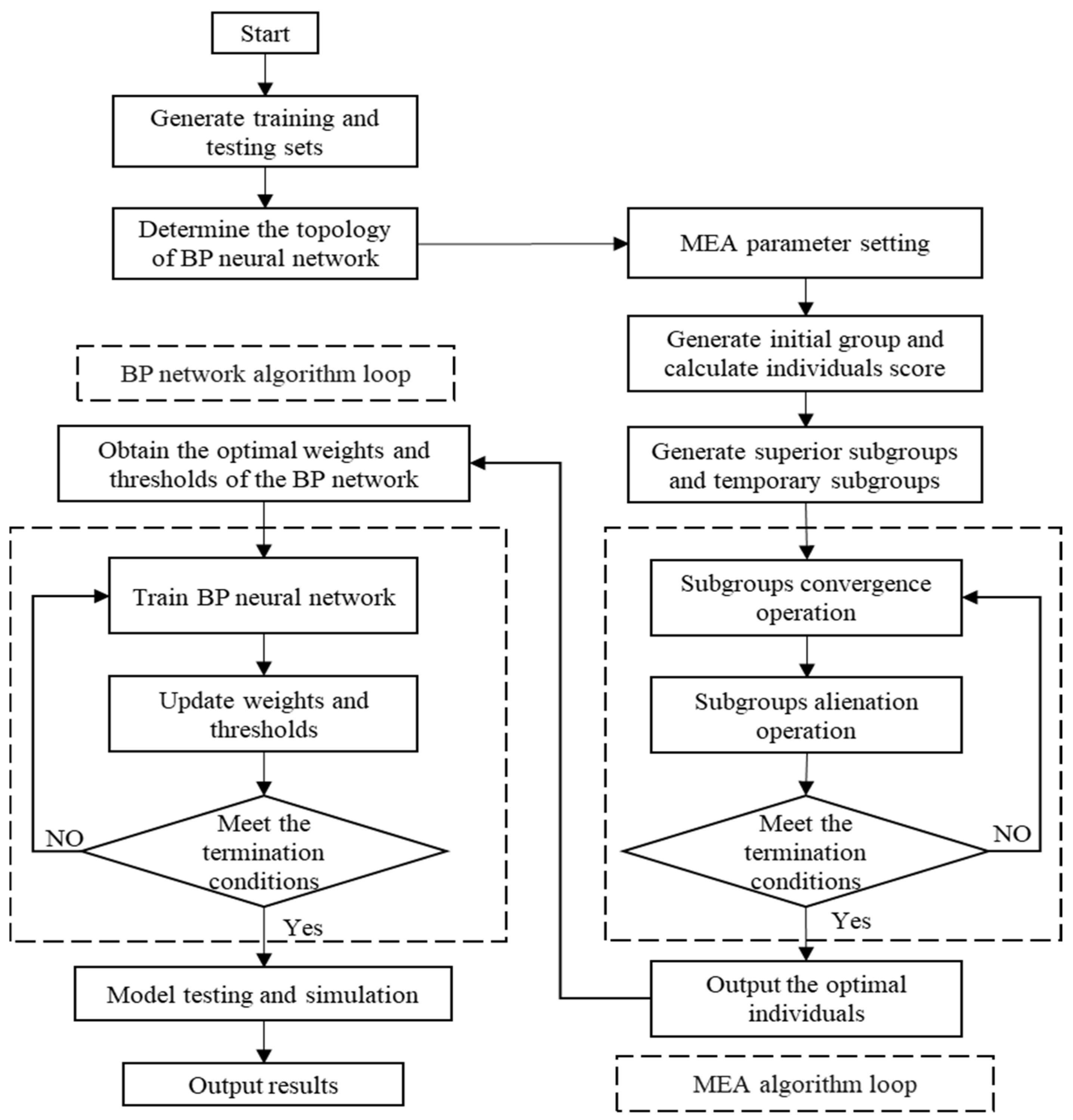
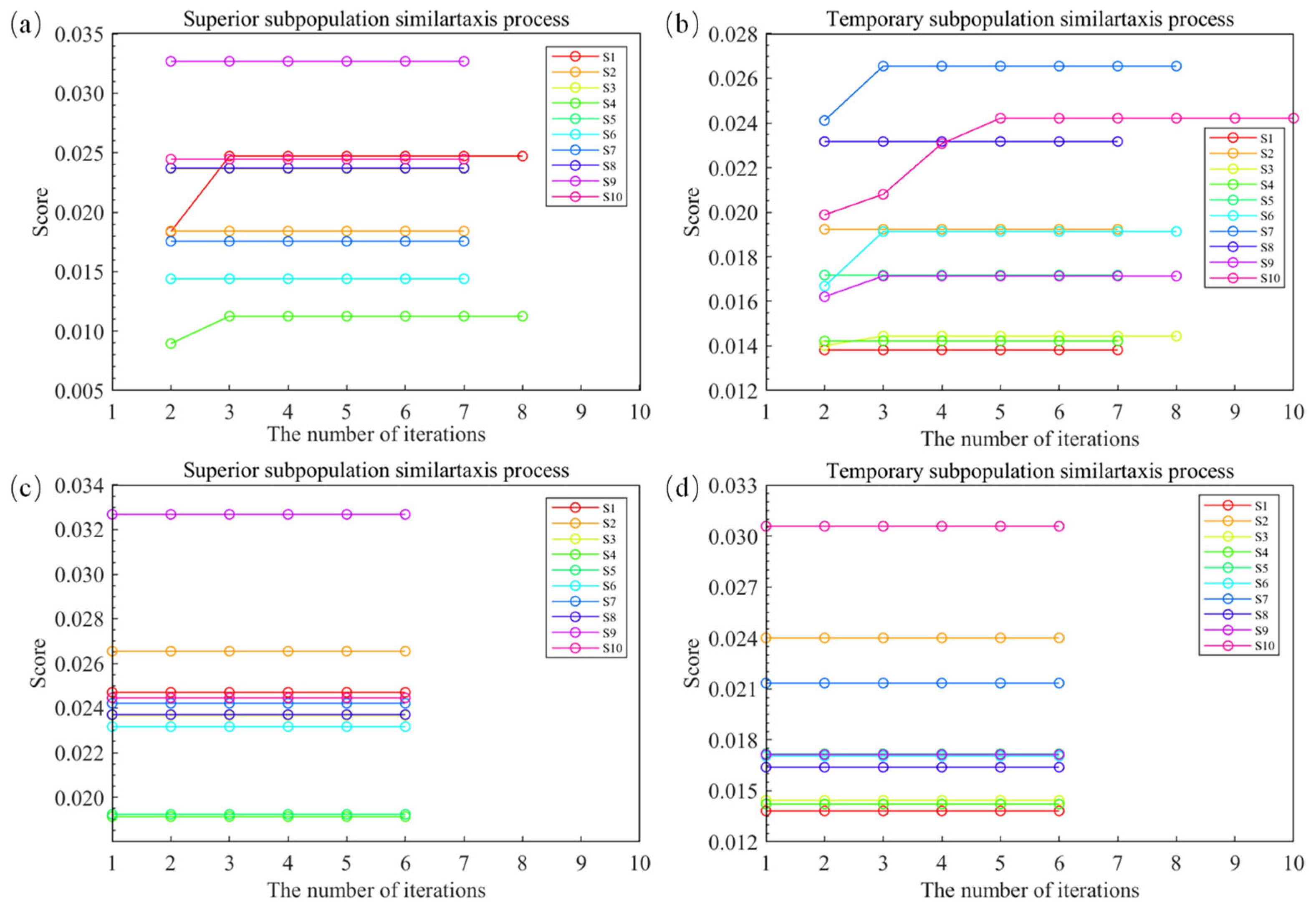
3.1. MEA-BP Surrogate Model
- Data Preprocessing and Model Construction: Generate training and testing samples for the MEA-BP model and construct the topology of the BP neural network.
- MEA Parameter Setting: Define parameters such as the number of iterations, population size, and the size of the superior and temporary subpopulations.
- Initial Population Generation and Scoring: Randomly generate the initial population and score the individuals, with the highest-scoring individuals designated as superior and temporary individuals.
- Generation of Superior and Temporary Subpopulations: Generate superior and temporary subpopulations centered around the superior and temporary individuals.
- Convergence and Divergence: Perform convergence operations within subpopulations to obtain local optimal individuals, followed by divergence operations between subpopulations to retain the high-scoring subpopulations.
- Iterative Optimization: Repeatedly perform convergence and divergence operations until the maximum number of iterations is reached or the score of the optimal individual no longer changes.
- Assign Optimal Weights and Biases: Decode the optimal individual found by MEA according to encoding rules to obtain the initial weights and biases of the BP neural network.
- Train BP Neural Network: Perform iterative training until stopping criteria are met and output the final prediction results.
3.2. MOGWO Algorithm
- Initialization: Randomly generate an initial set of solutions as the grey wolf pack and initialize parameters a, A, and C.
- Evaluation and Archiving: Calculate the fitness values of each solution based on the objective functions and use an external archive to store non-dominated solutions.
- Leader Selection: Use the roulette wheel selection strategy to select the leaders (α, β, and δ wolves) based on fitness values.
- Position Update: Update the positions of other individuals in the pack using the leaders’ positions and calculate the fitness values of the updated individuals.
- Non-dominated Sorting and Archive Update: Perform non-dominated sorting on the new population and update the archive. If the archive is full, remove the least crowded solution.
- Iteration Termination: Check if the maximum number of iterations is reached. If so, terminate the iteration.
- Result Output: Output the Pareto optimal solution set from the archive as the optimization result.
4. Simulation Experiment Content
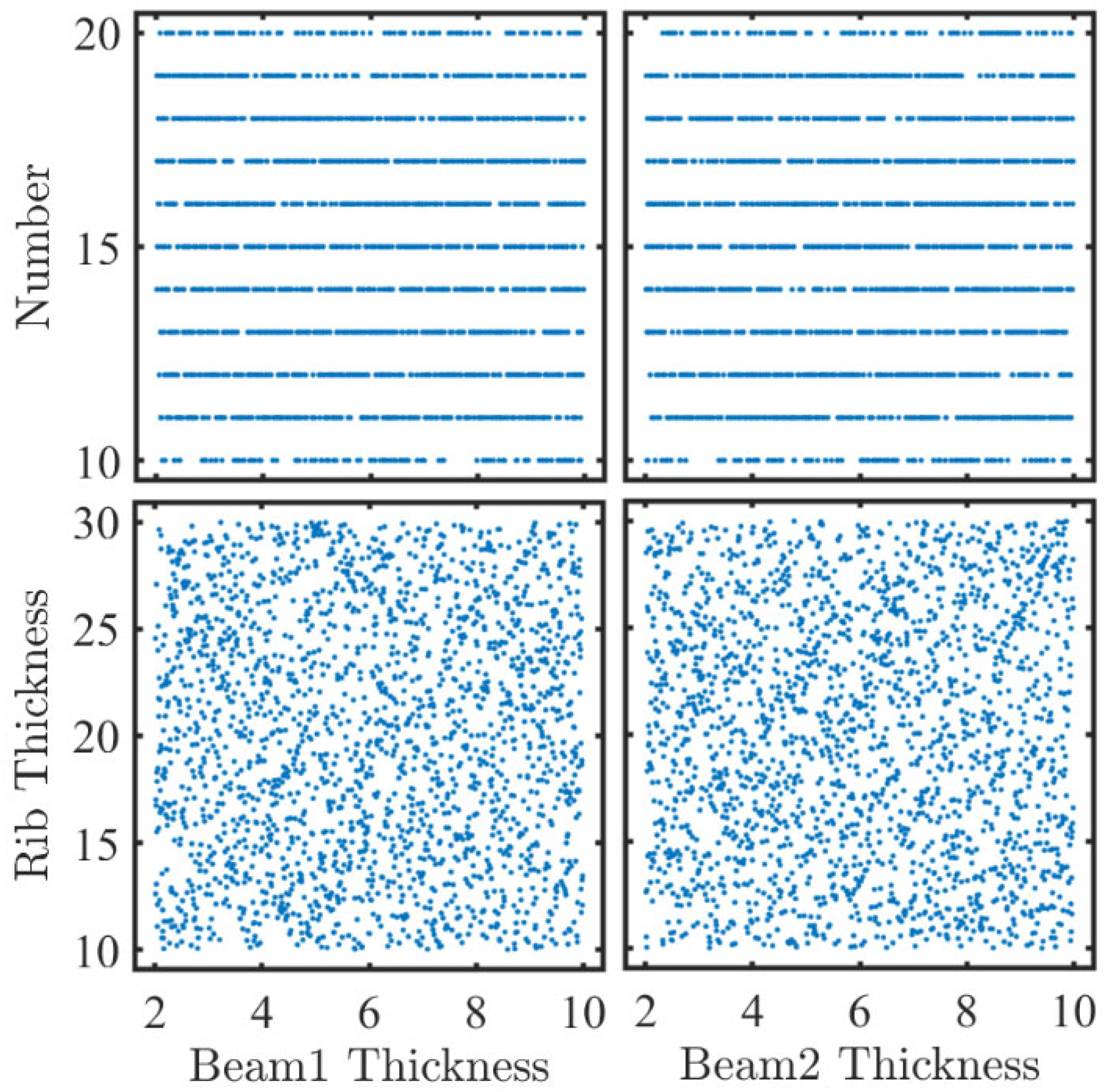
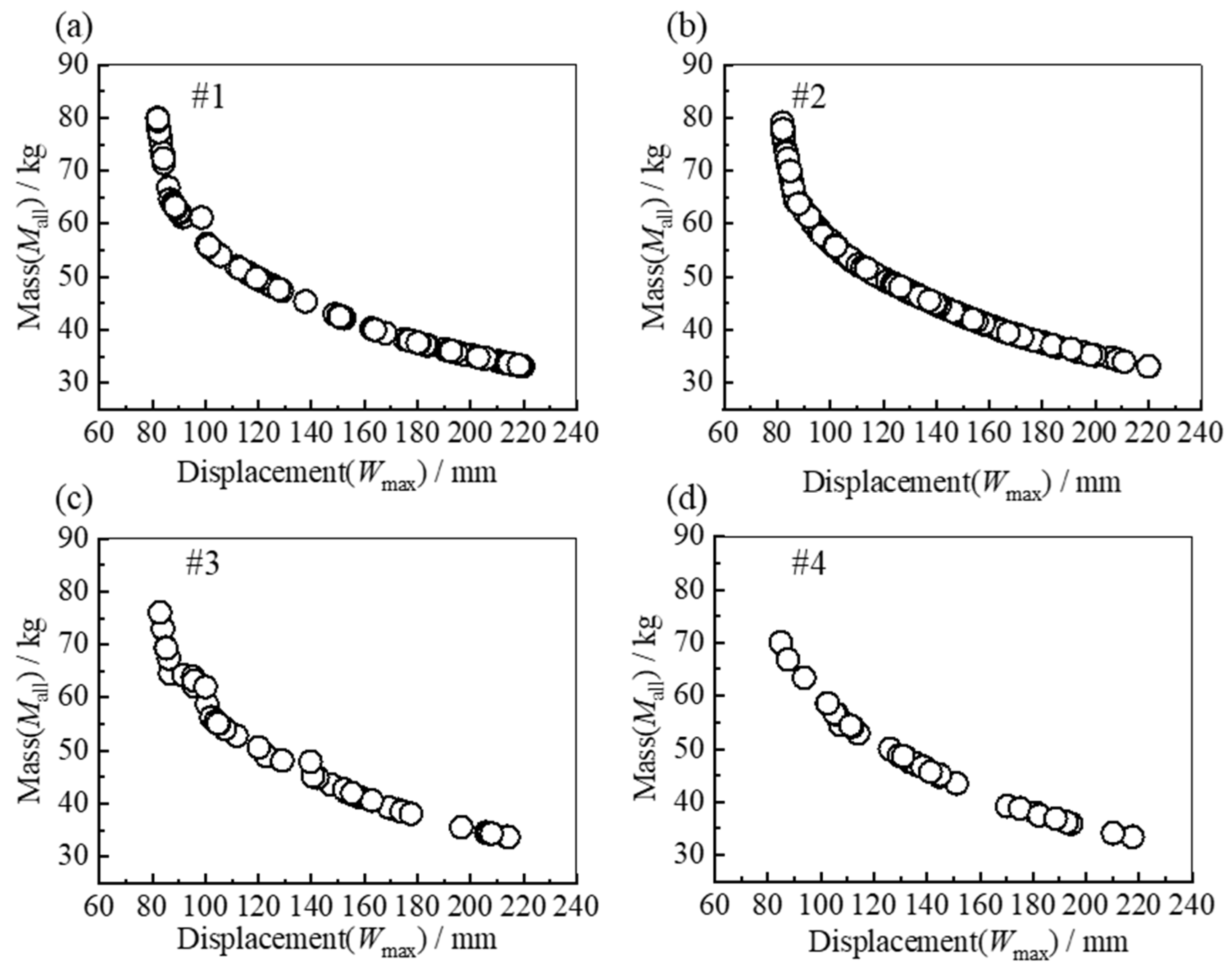
4.1. Acquisition of Training Data
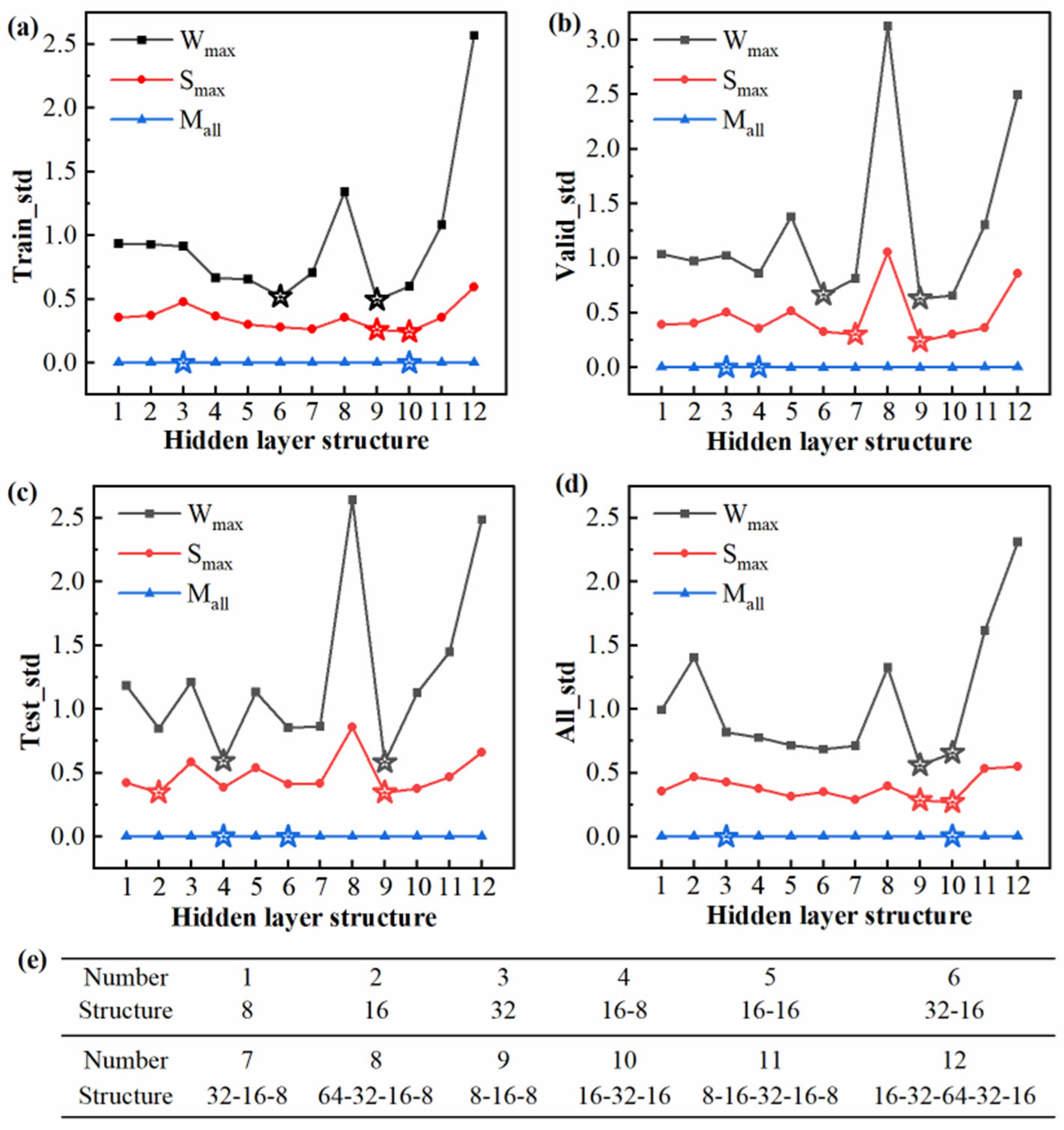
4.2. Training Method
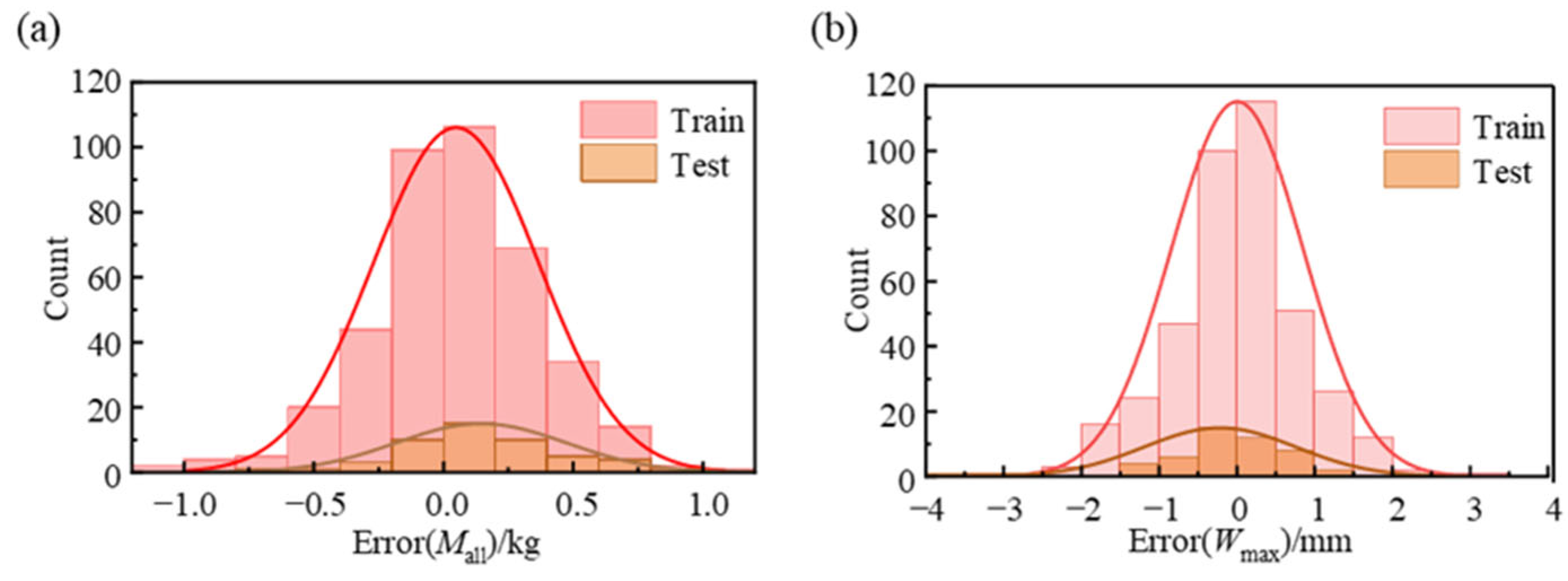
4.3. Model Performance Evaluation
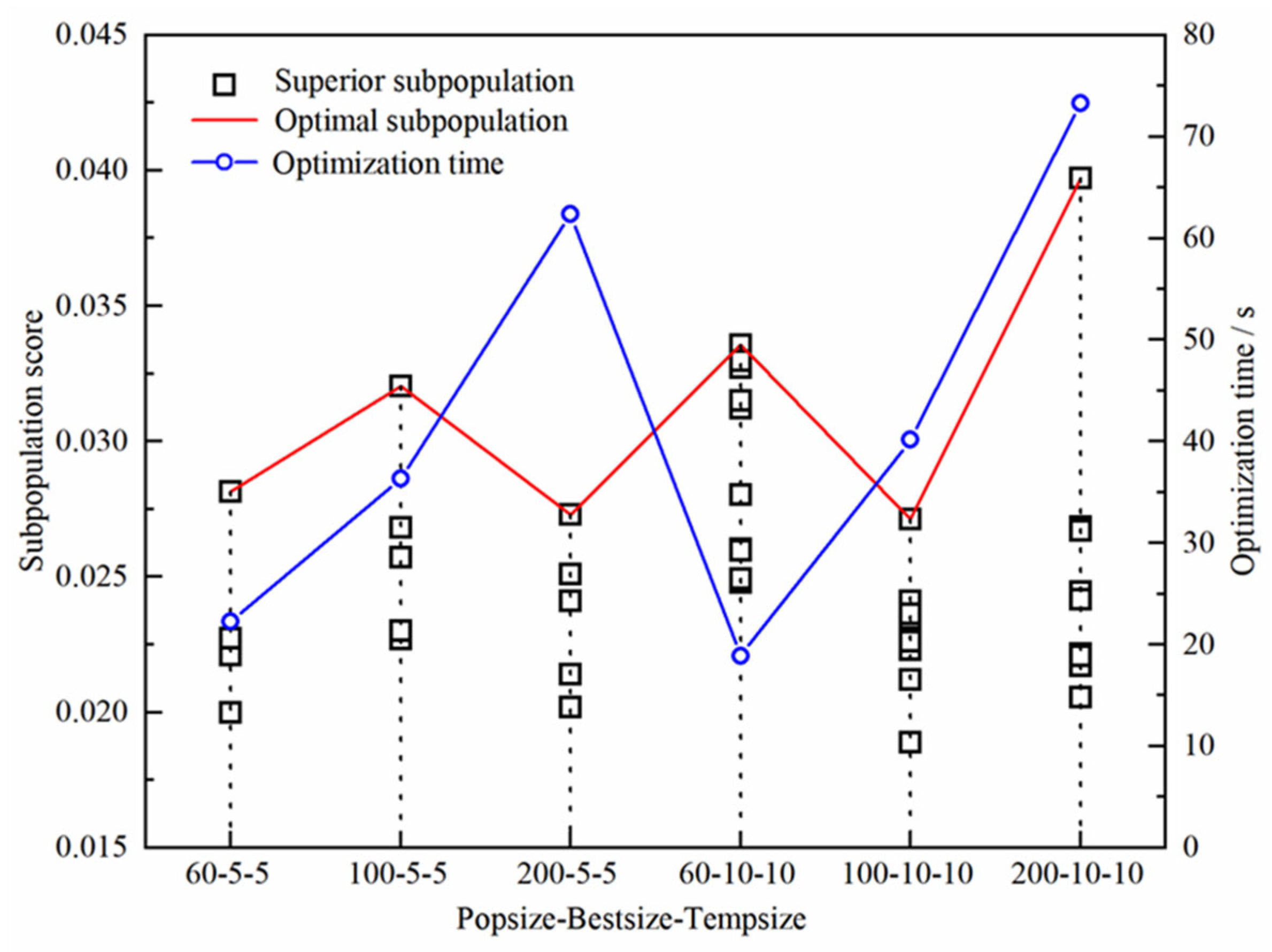
4.4. Optimization Design Method
5. Results and Discussion
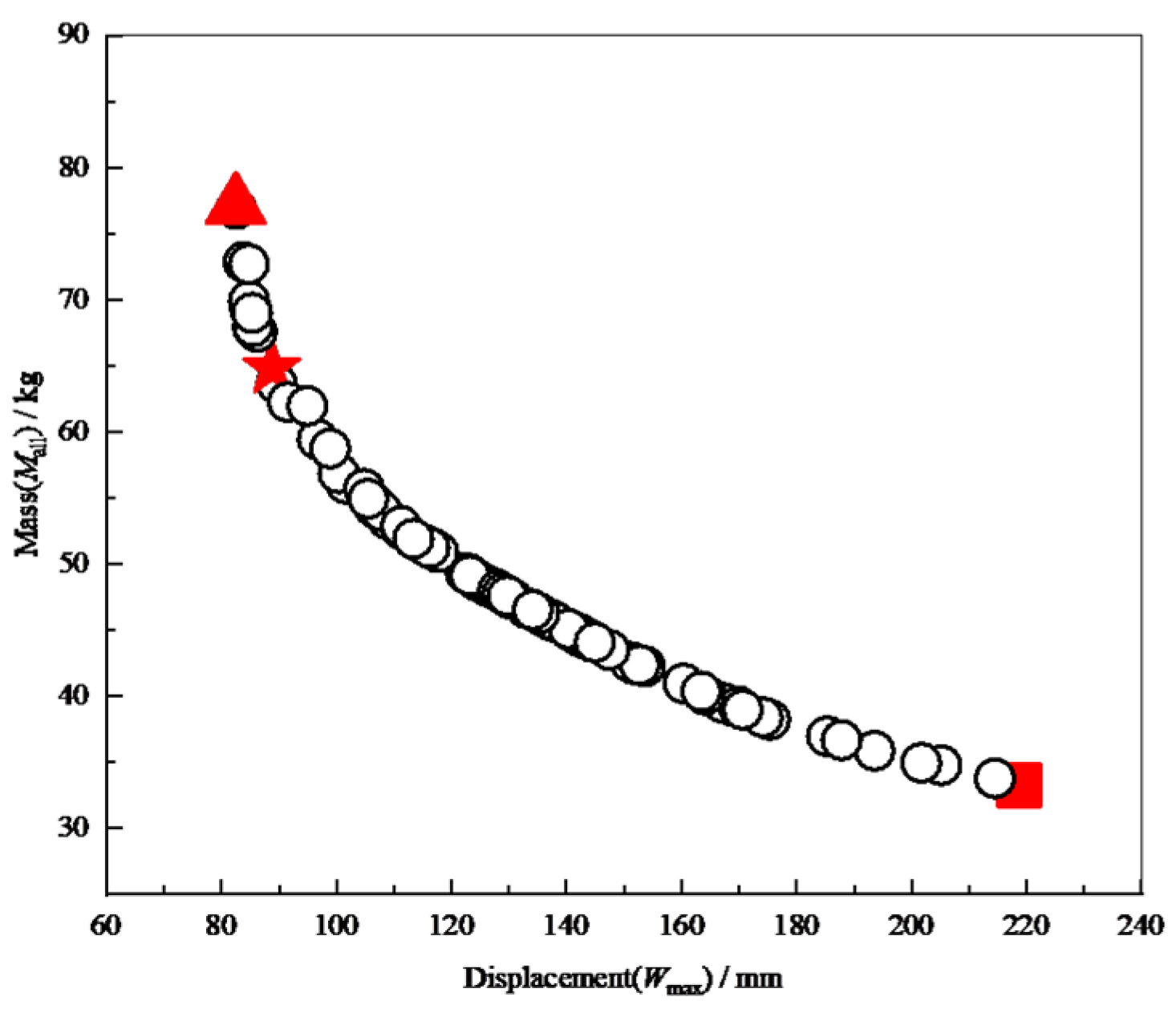
5.1. Optimization Effect Verification
5.2. Optimization Scheme Analysis
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Abro, G.E.M.; Zulkifli, S.A.B.; Masood, R.J.; Asirvadam, V.S.; Laouiti, A. Comprehensive Review of UAV Detection, Security, and Communication Advancements to Prevent Threats. Drones 2022, 6, 284. [Google Scholar] [CrossRef]
- Oh, T.H. Conceptual design of small unmanned aerial vehicle with proton exchange membrane fuel cell system for long endurance mission. Energy Convers. Manag. 2018, 176, 349–356. [Google Scholar] [CrossRef]
- Lapeña-Rey, N.; Blanco, J.A.; Ferreyra, E.; Lemus, J.L.; Pereira, S.; Serrot, E. A fuel cell powered unmanned aerial vehicle for low altitude surveillance missions. Int. J. Hydrogen Energy 2017, 42, 6926–6940. [Google Scholar] [CrossRef]
- Ma, Y.; Elham, A. Designing high aspect ratio wings: A review of concepts and approaches. Prog. Aerosp. Sci. 2024, 145, 100983. [Google Scholar] [CrossRef]
- Fu, J.; Shyy, W.; Qiu, H. Effects of aspect ratio on vortex dynamics of a rotating wing. AIAA J. 2017, 55, 4074–4082. [Google Scholar] [CrossRef]
- Zhu, L.; Li, N.; Childs, P.R.N. Light-weighting in aerospace component and system design. Propuls. Power Res. 2018, 7, 103–119. [Google Scholar] [CrossRef]
- Ren, R.; Ma, X.; Yue, H.; Yang, F.; Lu, Y. Stiffness enhancement methods for thin-walled aircraft structures: A review. Thin-Walled Struct. 2024, 201, 111995. [Google Scholar] [CrossRef]
- Wang, L.; Song, B.; Sun, Z.; Yang, X. Review on ultra-lightweight flapping-wing nano air vehicles: Artificial muscles, flight control mechanism, and biomimetic wings. Chin. J. Aeronaut. 2023, 36, 63–91. [Google Scholar] [CrossRef]
- Hammer, P.R.; Garmann, D.J.; Visbal, M.R. Effect of Aspect Ratio on Swept-Wing Dynamic Stall. AIAA J. 2023, 61, 4367–4377. [Google Scholar] [CrossRef]
- Wang, J.; Li, J.; Lei, S.; Ren, Z.; He, Y. Geometric Nonlinear Static Aeroelastic Characteristics Analysis of High-Aspect-Ratio Wing with Large Deformation. Int. J. Aeronaut. Space Sci. 2022, 23, 315–325. [Google Scholar] [CrossRef]
- Christensen, R.M. Review of the Basic Elastic Mechanical Properties and Their Realignment to Establish Ductile Versus Brittle Failure Behaviors. Appl. Mech. Rev. 2023, 75, 030801. [Google Scholar] [CrossRef]
- Meng, Y.S.; Yan, L.; Huang, W.; Zhang, T.T.; Du, Z.B. Structural design and analysis of a composite wing with high aspect ratio. J. Zhejiang Univ. A 2019, 20, 781–793. [Google Scholar] [CrossRef]
- Kilimtzidis, S.; Kostopoulos, V. Multidisciplinary structural optimization of novel high-aspect ratio composite aircraft wings. Struct. Multidiscip. Optim. 2023, 66, 150. [Google Scholar] [CrossRef]
- Guo, S.; Li, D.; Liu, Y. Multi-objective optimization of a composite wing subject to strength and aeroelastic constraints. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2012, 226, 1095–1106. [Google Scholar] [CrossRef]
- Wansasueb, K.; Pholdee, N.; Panagant, N.; Bureerat, S. Multiobjective meta-heuristic with iterative parameter distribution estimation for aeroelastic design of an aircraft wing. Eng. Comput. 2022, 38, 1–19. [Google Scholar] [CrossRef]
- Bons, N.P.; Martins, J.R.R.A. Aerostructural design exploration of a wing in transonic flow. Aerospace 2020, 7, 118. [Google Scholar] [CrossRef]
- Stamatelos, D.; Labeas, G. Towards the design of a multispar composite wing. Computation 2020, 8, 24. [Google Scholar] [CrossRef]
- Tang, Z.; Chen, Y.; Zhang, L.; Périaux, J. Solving the two objective evolutionary shape optimization of a natural laminar airfoil and shock control bump with game strategies. Arch. Comput. Methods Eng. 2019, 26, 119–141. [Google Scholar] [CrossRef]
- Sleesongsom, S.; Kumar, S.; Bureerat, S. Multi-Objective Reliability-Based Partial Topology Optimization of a Composite Aircraft Wing. Symmetry 2023, 15, 305. [Google Scholar] [CrossRef]
- Stewart, E.C.; Patil, M.J.; Canfield, R.A.; Snyder, R.D. Parametric representation and shape optimization of flaping micro air vehicle wings. Int. J. Micro Air Veh. 2012, 4, 179–202. [Google Scholar] [CrossRef]
- Wu, Q.; Wu, H.; Jiang, Z.; Tan, L.; Yang, Y.; Yan, S. Multi-objective optimization and driving mechanism design for controllable wings of underwater gliders. Ocean Eng. 2023, 286, 115534. [Google Scholar] [CrossRef]
- Nebro, A.J.; Durillo, J.J.; Garcia-Nieto, J.; Coello, C.C.; Luna, F.; Alba, E. SMPSO: A new PSO-based metaheuristic for multi-objective optimization. In Proceedings of the IEEE Symposium on Computational Intelligence in Multi-Criteria Decision-Making (MCDM), Nashville, TN, USA, 30 March–2 April 2009; pp. 66–73. [Google Scholar]
- Venter, G.; Sobieszczanski-Sobieski, J. Multidisciplinary optimization of a transport aircraft wing using particle swarm optimization. Struct. Multidiscip. Optim. 2004, 26, 121–131. [Google Scholar] [CrossRef]
- Vindigni, C.R.; Orlando, C.; Milazzo, A. Computational analysis of the active control of incompressible airfoil flutter vibration using a piezoelectric v-stack actuator. Vibration 2021, 4, 369–394. [Google Scholar] [CrossRef]
- Quintana, A.; Graves, G.; Hassanalian, M.; Abdelkefi, A. Aerodynamic analysis and structural integrity for optimal performance of sweeping and spanning morphing unmanned air vehicles. Aerosp. Sci. Technol. 2021, 110, 106458. [Google Scholar] [CrossRef]
- Zhang, Q.; Miao, W.; Liu, Q.; Xu, Z.; Li, C.; Chang, L.; Yue, M. Optimized design of wind turbine airfoil aerodynamic performance and structural strength based on surrogate model. Ocean Eng. 2023, 289, 116279. [Google Scholar] [CrossRef]
- Rajpal, D.; Mitrotta, F.M.A.; Socci, C.A.; Sodja, J.; Kassapoglou, C.; De Breuker, R. Design and testing of aeroelastically tailored composite wing under fatigue and gust loading including effect of fatigue on aeroelastic performance. Compos. Struct. 2021, 275, 114373. [Google Scholar] [CrossRef]
- Tulshibagwale, N.; Brodnik, N.; Muir, C.; Hilmas, A.; Kiser, J.D.; Smith, C.E.; Almansour, A.S.; Presby, M.J.; Daly, S. Acoustic Emission in Ceramic Matrix Composites. Appl. Mech. Rev. 2024, 76, 040801. [Google Scholar] [CrossRef]
- Su, J.; Sun, G.; Tao, J. A novel inverse design method for morphing airfoil based on deep reinforcement learning. Aerosp. Sci. Technol. 2024, 145, 108895. [Google Scholar] [CrossRef]
- Bugała, P.; Sznajder, J.; Sieradzki, A. Numerical Modelling of Static Aeroelastic Deformations of Slender Wing in Aerodynamic Design. Trans. Aerosp. Res. 2023, 2023, 52–70. [Google Scholar] [CrossRef]
- Choi, W.; Park, H. Optimized design and analysis of composite flexible wing using aero-nonlinear structure interaction. Compos. Struct. 2019, 225, 111027. [Google Scholar] [CrossRef]
- Buehler, M.J. MechGPT, a Language-Based Strategy for Mechanics and Materials Modeling That Connects Knowledge Across Scales, Disciplines, and Modalities. Appl. Mech. Rev. 2024, 76, 021001. [Google Scholar] [CrossRef]
- Shi, Q.; Wang, H.; Cheng, H.; Cheng, F.; Wang, M. An Adaptive Sequential Sampling Strategy-Based Multi-Objective Optimization of Aerodynamic Configuration for a Tandem-Wing UAV via a Surrogate Model. IEEE Access 2021, 9, 164131–164147. [Google Scholar] [CrossRef]
- Liu, F.; Han, Z.H.; Zhang, Y.; Song, K.; Song, W.P.; Gui, F.; Tang, J.B. Surrogate-based aerodynamic shape optimization of hypersonic flows considering transonic performance. Aerosp. Sci. Technol. 2019, 93, 105345. [Google Scholar] [CrossRef]
- Jin, H.; Zhang, E.; Espinosa, H.D. Recent advances and applications of machine learning in experimental solid mechanics: A review. Appl. Mech. Rev. 2023, 75, 061001. [Google Scholar] [CrossRef]
- Díaz-Manríquez, A.; Toscano, G.; Barron-Zambrano, J.H.; Tello-Leal, E. A review of surrogate assisted multiobjective evolutionary algorithms. Comput. Intell. Neurosci. 2016, 2016, 9420460. [Google Scholar] [CrossRef]
- Jin, T.; Cheng, X.; Xu, S.; Lai, Y.C.; Zhang, Y.H. Deep learning aided inverse design of the buckling-guided assembly for 3D frame structures. J. Mech. Phys. Solids 2023, 179, 105398. [Google Scholar] [CrossRef]
- Yan, Q.Y. Structural Design and Analysis of 40 kg Composite Solar Unmanned Aerial Vehicle. Master’s Thesis, Civil Aviation Flight University of China, Deyang, China, 2022. [Google Scholar] [CrossRef]
- Basheer, I.A.; Hajmeer, M. Artificial neural networks: Fundamentals, computing, design, and application. J. Microbiol. Methods 2000, 43, 3–31. [Google Scholar] [CrossRef]
- Yu, W.; Li, B.; Jia, H.; Zhang, M.; Wang, D. Application of multi-objective genetic algorithm to optimize energy efficiency and thermal comfort in building design. Energy Build. 2015, 88, 135–143. [Google Scholar] [CrossRef]
- Wang, S.; Zhang, N.; Wu, L.; Wang, Y. Wind speed forecasting based on the hybrid ensemble empirical mode decomposition and GA-BP neural network method. Renew. Energy 2016, 94, 629–636. [Google Scholar] [CrossRef]
- Wang, W.; Tang, R.; Li, C.; Liu, P.; Luo, L. A BP neural network model optimized by mind evolutionary algorithm for predicting the ocean wave heights. Ocean Eng. 2018, 162, 98–107. [Google Scholar] [CrossRef]
- Zhang, J.; Li, P.; Yin, X.; Wang, S.; Zhu, Y. Back analysis of surrounding rock parameters in Pingdingshan mine based on BP neural network integrated mind evolutionary algorithm. Mathematics 2022, 10, 1746. [Google Scholar] [CrossRef]
- Mirjalili, S.; Saremi, S.; Mirjalili, S.M.; Coelho, L.D.S. Multi-objective grey wolf optimizer: A novel algorithm for multi-criterion optimization. Expert Syst. Appl. 2016, 47, 106–119. [Google Scholar] [CrossRef]
- Heidari, A.; Imani, D.M.; Khalilzadeh, M.; Sarbazvatan, M. Green two-echelon closed and open location-routing problem: Application of NSGA-II and MOGWO metaheuristic approaches. Environ. Dev. Sustain. 2023, 25, 9163–9199. [Google Scholar] [CrossRef] [PubMed]
- Ala, A.; Goli, A.; Mirjalili, S.; Simic, V. A fuzzy multi-objective optimization model for sustainable healthcare supply chain network design. Appl. Soft Comput. 2024, 150, 111012. [Google Scholar] [CrossRef]
- Agajie, E.F.; Agajie, T.F.; Amoussou, I.; Fopah-Lele, A.; Nsanyuy, W.B.; Khan, B.; Bajaj, M.; Zaitsev, I.; Tanyi, E. Optimization of off-grid hybrid renewable energy systems for cost-effective and reliable power supply in Gaita Selassie Ethiopia. Sci. Rep. 2024, 14, 10929. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey wolf optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]

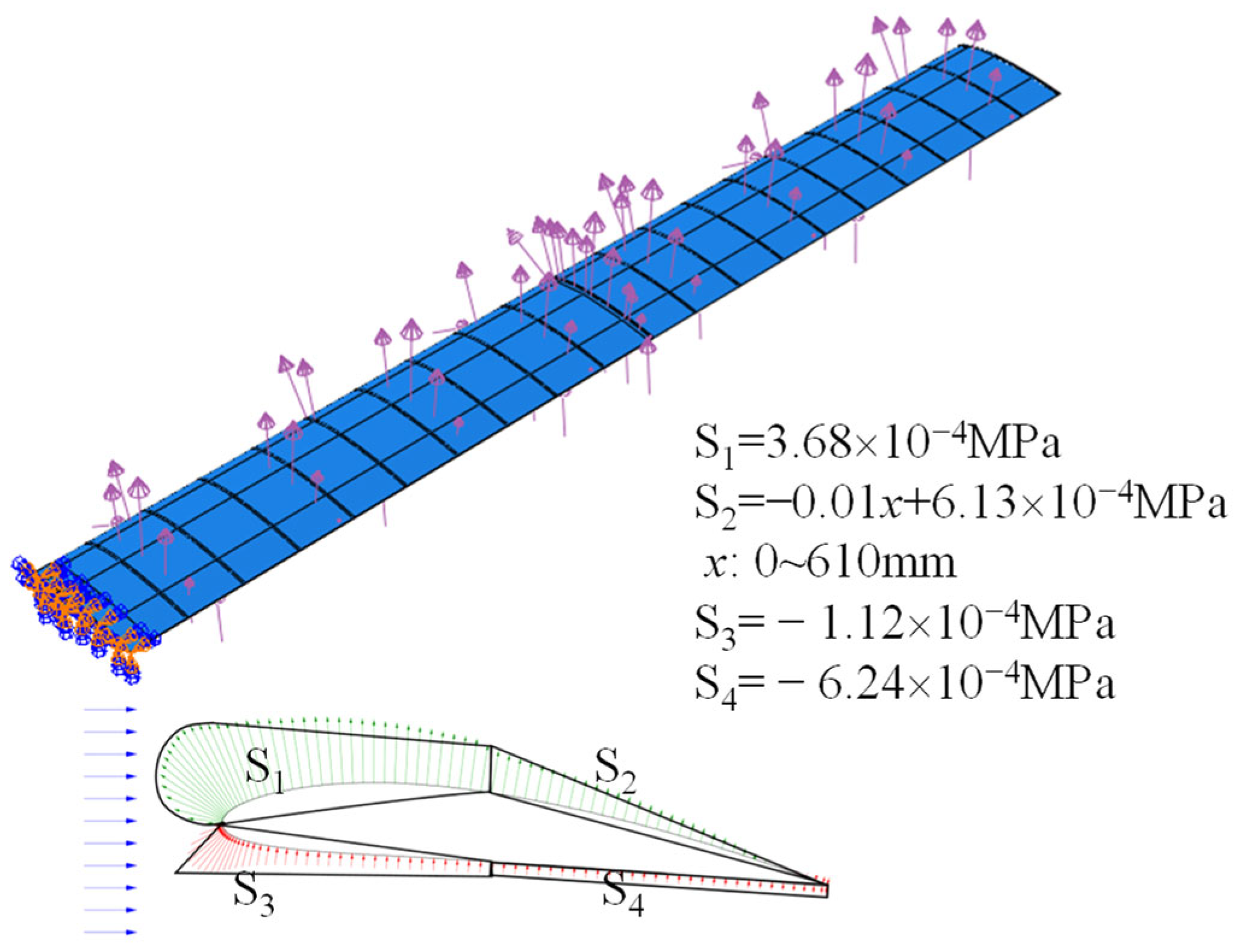



| # | T300 | SW100A-100a |
|---|---|---|
| Density (kg/m3) | 1.43 × 103 | 1.782 × 103 |
| E11/GPa | 62.4 | 38.36 |
| E22/GPa | 62.4 | 38.36 |
| E33/GPa | 8.10 | 8.10 |
| G12/GPa | 3.14 | 4.14 |
| G13/GPa | 3.14 | 4.14 |
| G23/GPa | 1.312 | 1.312 |
| μ12 | 0.33 | 0.26 |
| μ13 | 0.33 | 0.26 |
| μ23 | 0.33 | 0.26 |
| Variables | Wing Rib Number | Rib Thickness (mm) | Beam 1 Thickness (mm) | Beam 2 Thickness (mm) | Skin Thickness (mm) |
|---|---|---|---|---|---|
| Lower Limit | 10 | 10 | 2 | 2 | 2 |
| Upper Limit | 20 | 30 | 10 | 10 | 5 |
| Decision Variable | Objective Function Value | ||||||
|---|---|---|---|---|---|---|---|
| N | d (mm) | w1 (mm) | w2 (mm) | h (mm) | Wmax (mm) | Mall (mm) | |
| 1 | 10 | 10.00 | 2.00 | 2.00 | 2.35 | 193.58 | 35.88 |
| 2 | 10 | 10.00 | 2.11 | 2.11 | 2.94 | 151.77 | 42.42 |
| … | … | … | |||||
| 11 | 19 | 27.29 | 5.13 | 3.43 | 5.00 | 82.49 | 77.09 |
| 12 | 10 | 10.00 | 2.10 | 2.00 | 2.66 | 169.00 | 39.25 |
| 13 | 10 | 10.00 | 2.02 | 2.00 | 2.02 | 222.61 | 31.48 |
| 14 | 10 | 10.55 | 2.05 | 2.06 | 2.21 | 205.19 | 34.76 |
| 15 | 10 | 11.07 | 2.34 | 2.12 | 3.94 | 108.95 | 53.38 |
| 16 | 12 | 10.88 | 3.25 | 2.15 | 4.84 | 88.79 | 64.82 |
| … | … | … | |||||
| 100 | 16 | 21.41 | 4.53 | 2.91 | 4.93 | 84.75 | 72.69 |
| # | Grey Wolf Number | Maximum Iterations | Archive Size |
|---|---|---|---|
| 1 | 200 | 200 | 200 |
| 2 | 200 | 50 | 50 |
| 3 | 50 | 50 | 200 |
| 4 | 50 | 200 | 50 |
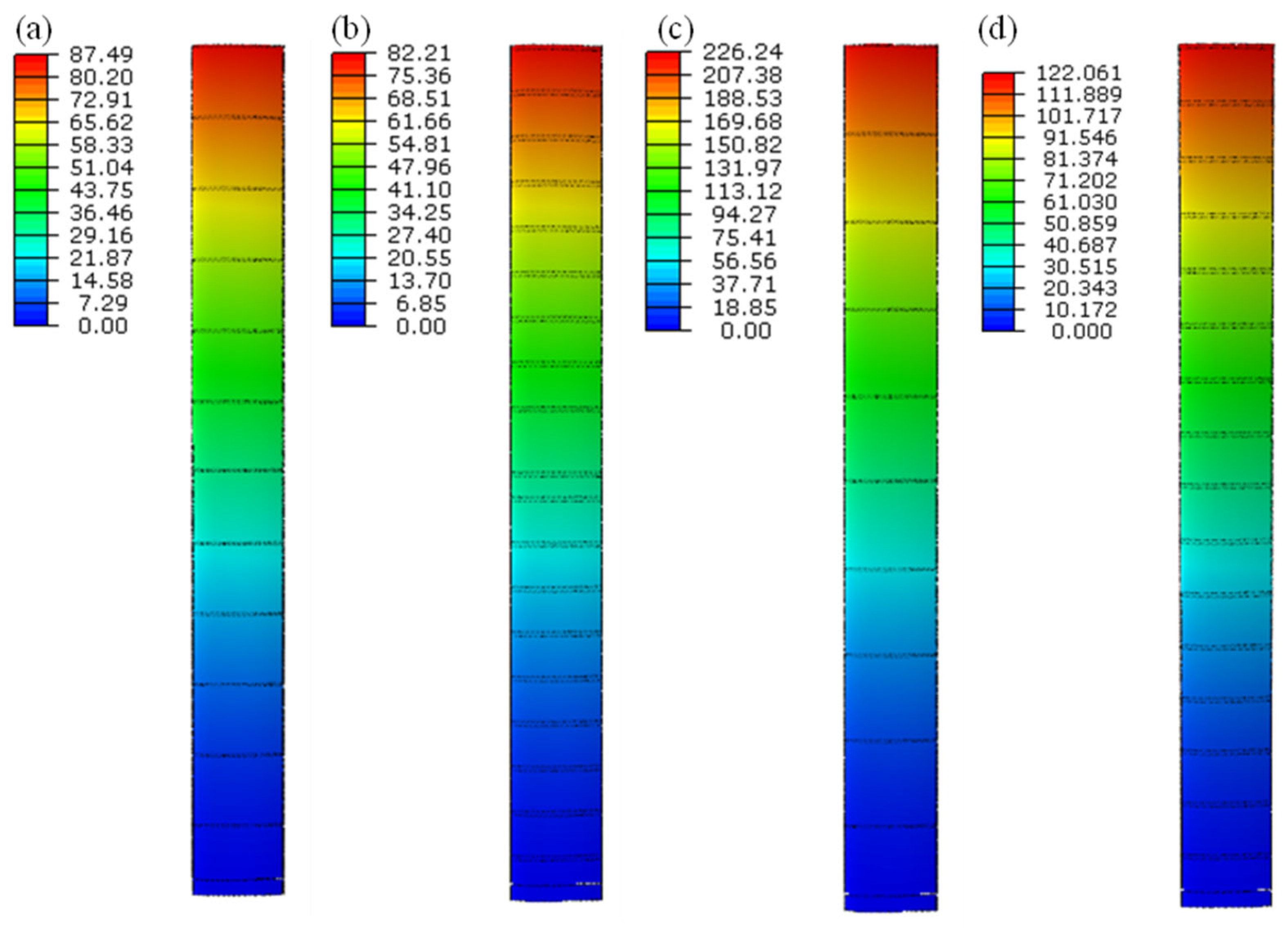
| Variables | Optimal Model | Minimal Wmax Model | Minimal Mall Model | Original Model |
|---|---|---|---|---|
| N | 12 | 19 | 10 | 16 |
| d (mm) | 10.88 | 27.29 | 10.00 | 25 |
| w1 (mm) | 3.25 | 5.13 | 2.02 | 6 |
| w2 (mm) | 2.15 | 3.43 | 2.00 | 6 |
| h (mm) | 4.84 | 5.00 | 2.02 | 3.5 |
| σmax (MPa) | 39.12 | 38.10 | 61.16 | 46.48 |
| Wmax (mm) | 87.49 | 82.21 | 226.24 | 122.06 |
| Wmax_BP (mm) | 88.79 | 82.49 | 222.61 | / |
| |Wmax − Wmax_BP| (mm) | 1.3 | 0.28 | 3.63 | / |
| Mall (kg) | 64.91 | 77.78 | 31.14 | 60.85 |
| Mall_BP (kg) | 64.82 | 77.09 | 31.28 | / |
| |Mall − Mall_BP| (kg) | 0.09 | 0.69 | 0.14 | / |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nan, J.; Zheng, J.; Jiang, B.; Li, Y.; Chen, J.; Fan, X. A Multi-Objective Optimization Design Method for High-Aspect-Ratio Wing Structures Based on Mind Evolution Algorithm Backpropagation Surrogate Model. Machines 2024, 12, 907. https://doi.org/10.3390/machines12120907
Nan J, Zheng J, Jiang B, Li Y, Chen J, Fan X. A Multi-Objective Optimization Design Method for High-Aspect-Ratio Wing Structures Based on Mind Evolution Algorithm Backpropagation Surrogate Model. Machines. 2024; 12(12):907. https://doi.org/10.3390/machines12120907
Chicago/Turabian StyleNan, Jin, Junhua Zheng, Bochuan Jiang, Yuhang Li, Jiayun Chen, and Xuanqing Fan. 2024. "A Multi-Objective Optimization Design Method for High-Aspect-Ratio Wing Structures Based on Mind Evolution Algorithm Backpropagation Surrogate Model" Machines 12, no. 12: 907. https://doi.org/10.3390/machines12120907
APA StyleNan, J., Zheng, J., Jiang, B., Li, Y., Chen, J., & Fan, X. (2024). A Multi-Objective Optimization Design Method for High-Aspect-Ratio Wing Structures Based on Mind Evolution Algorithm Backpropagation Surrogate Model. Machines, 12(12), 907. https://doi.org/10.3390/machines12120907






